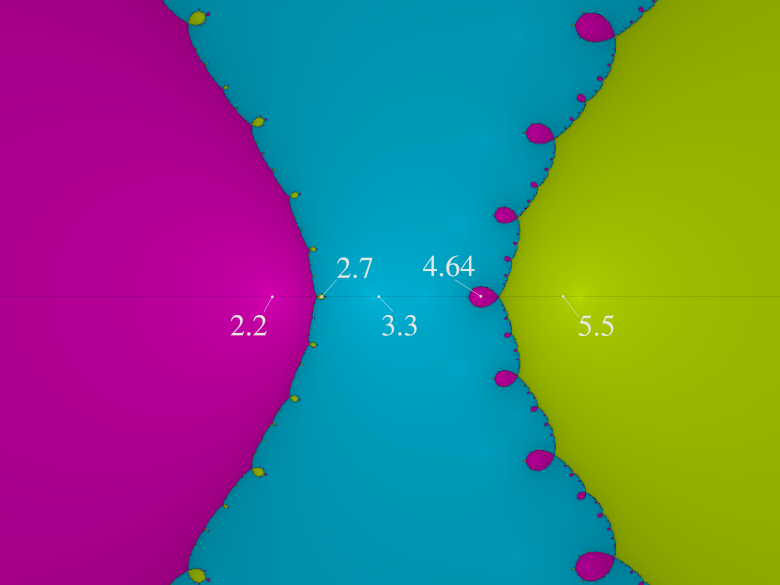Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 30 Dec 2020
Benjamin Franklin and the Exercises of Ignatius
Recently I learned of the Spiritual Exercises of St. Ignatius. Wikipedia says (or quotes, it's not clear):
Morning, afternoon, and evening will be times of the examinations. The morning is to guard against a particular sin or fault, the afternoon is a fuller examination of the same sin or defect. There will be a visual record with a tally of the frequency of sins or defects during each day. In it, the letter 'g' will indicate days, with 'G' for Sunday. Three kinds of thoughts: "my own" and two from outside, one from the "good spirit" and the other from the "bad spirit".
This reminded me very strongly of Chapter 9 of Benjamin Franklin's Autobiography, in which he presents “A Plan for Attaining Moral Perfection”:
My intention being to acquire the habitude of all these virtues, I judg'd it would be well not to distract my attention by attempting the whole at once, but to fix it on one of them at a time… Conceiving then, that, agreeably to the advice of Pythagoras in his Golden Verses, daily examination would be necessary, I contrived the following method for conducting that examination.
I made a little book, in which I allotted a page for each of the virtues. I rul'd each page with red ink, so as to have seven columns, one for each day of the week, marking each column with a letter for the day. I cross'd these columns with thirteen red lines, marking the beginning of each line with the first letter of one of the virtues, on which line, and in its proper column, I might mark, by a little black spot, every fault I found upon examination to have been committed respecting that virtue upon that day.
I determined to give a week's strict attention to each of the virtues successively. Thus, in the first week, my great guard was to avoid every the least offense against Temperance, leaving the other virtues to their ordinary chance, only marking every evening the faults of the day.
So I wondered: was Franklin influenced by the Exercises? I don't know, but it's possible. Wondering about this I consulted the Mighty Internet, and found two items in the Woodstock Letters, a 19th-century Jesuit periodical, wondering the same thing:
The following extract from Franklin’s Autobiography will prove of interest to students of the Exercises: … Did Franklin learn of our method of Particular Examen from some of the old members of the Suppressed Society?
(“Woodstock Letters” Volume XXXIV #2 (Sep 1905) p.311–313)
I can't guess at the main question, but I can correct one small detail: although this part of the Autobiography was written around 1784, the time of which Franklin was writing, when he actually made his little book, was around 1730, well before the suppression of the Society.
The following issue takes up the matter again:
Another proof that Franklin was acquainted with the Exercises is shown from a letter he wrote to Joseph Priestley from London in 1772, where he gives the method of election of the Exercises. …
(“Woodstock Letters” Volume XXXIV #3 (Dec 1905) p.459–461)
Franklin describes making a decision by listing, on a divided sheet of paper, the reasons for and against the proposed action. And then a variation I hadn't seen: balance arguments for and arguments against, and cross out equally-balanced sets of arguments. Franklin even suggests evaluations as fine as matching two arguments for with three slightly weaker arguments against and crossing out all five together.
I don't know what this resembles in the Exercises but it certainly was striking.
[Other articles in category /book] permanent link
Sat, 26 Dec 2020This tweet from Raffi Melkonian describes the appetizer plate at his house on Christmas. One item jumped out at me:
basterma (err, spicy beef prosciutto)
I wondered what that was like, and then I realized I do have some idea, because I recognized the word. Basterma is not an originally Armenian word, it's a Turkish loanword, I think canonically spelled pastırma. And from Turkish it made a long journey through Romanian and Yiddish to arrive in English as… pastrami…
For which “spicy beef prosciutto” isn't a bad description at all.
[Other articles in category /lang/etym] permanent link
Tue, 15 Dec 2020The world is so complicated! It has so many things in it that I could not even have imagined.
Yesterday I learned that since 1949 there has been a compact between New Mexico and Texas about how to divide up the water in the Pecos River, which flows from New Mexico to Texas, and then into the Rio Grande.
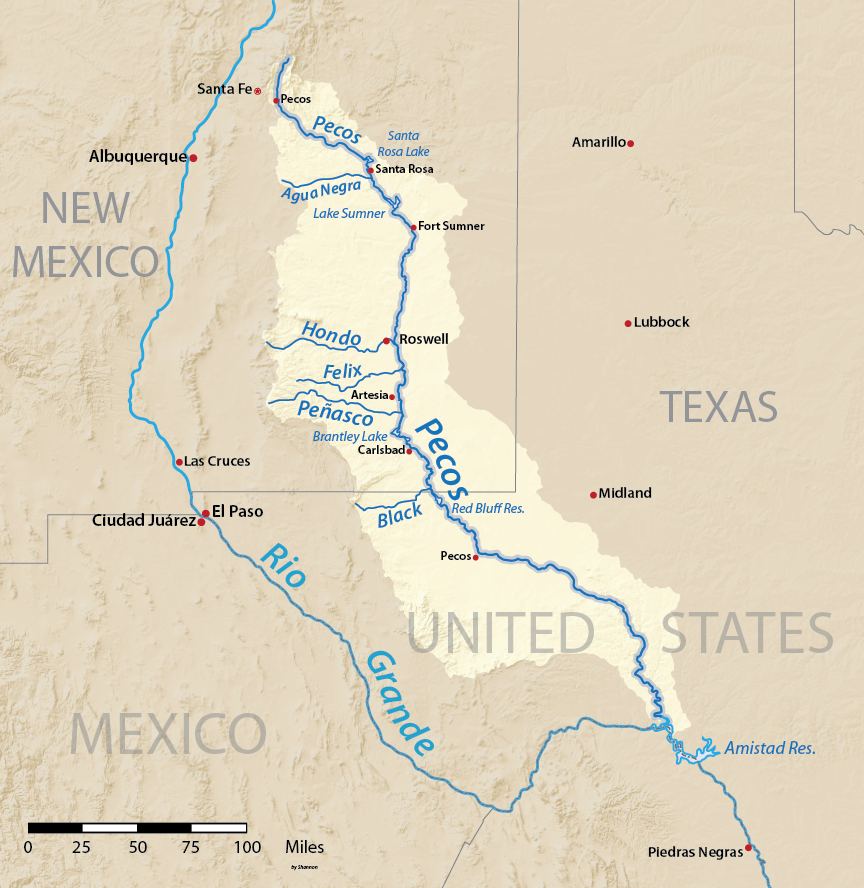
New Mexico is not allowed to use all the water before it gets to Texas. Texas is entitled to receive a certain amount.
There have been disputes about this in the past (the Supreme Court case has been active since 1974), so in 1988 the Supreme Court appointed Neil S. Grigg, a hydraulic engineer and water management expert from Colorado, to be “River Master of the Pecos River”, to mediate the disputes and account for the water. The River Master has a rulebook, which you can read online. I don't know how much Dr. Grigg is paid for this.
In 2014, Tropical Storm Odile dumped a lot of rain on the U.S. Southwest. The Pecos River was flooding, so Texas asked NM to hold onto the Texas share of the water until later. (The rulebook says they can do this.) New Mexico arranged for the water that was owed to Texas to be stored in the Brantley Reservoir.
A few months later Texas wanted their water. "OK," said New Mexico. “But while we were holding it for you in our reservoir, some of it evaporated. We will give you what is left.”
“No,” said Texas, “we are entitled to a certain amount of water from you. We want it all.”
But the rule book says that even though the water was in New Mexico's reservoir, it was Texas's water that evaporated. (Section C5, “Texas Water Stored in New Mexico Reservoirs”.)
[ Addendum 20230528: To my amazement this case has come to my attention again, because legal blogger Adam Unikowsky cited it as one of “the [ten] least significant cases of the decade”. I wrote a brief followup about why I enjoy Unikowsky's Legal Newsletter. ]
[Other articles in category /law] permanent link
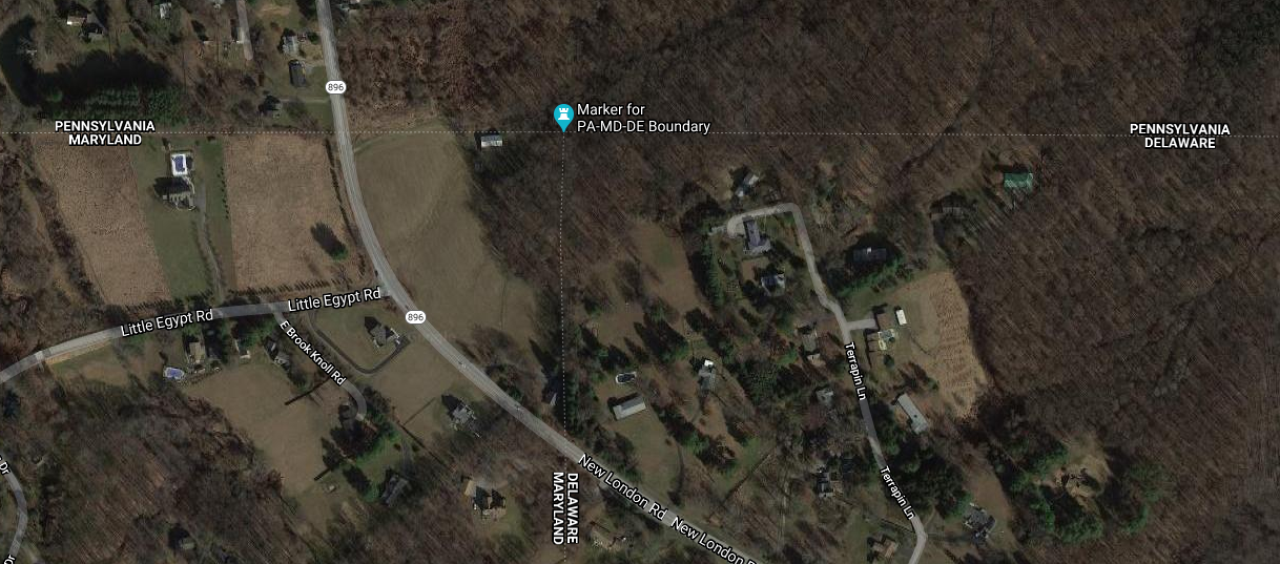
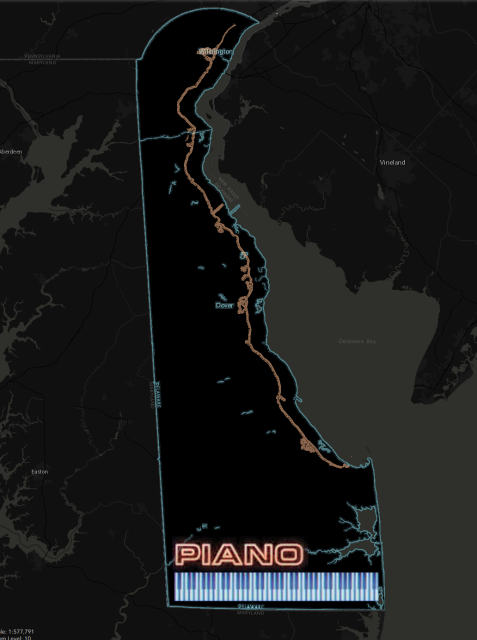
Thu, 10 Dec 2020I see that the Pennsylvania-Delaware-Maryland triple border is near White Clay Creek State Park, outside of Newark, DE. That sounds nice, so perhaps I will stop by and take a look, and see if there really is white clay in the creek.
I had some free time yesterday, so that is what I did. The creek is pretty. I did not see anything that appeared to be white clay. Of course I did not investigate extensively, or even closely, because the weather was too cold for wading. But the park was beautiful.
There is a walking trail in the park that reaches the tripoint itself. I didn't walk the whole trail. The park entrance is at the other end of the park from the tripoint. After wandering around in the park for a while, I went back to the car, drove to the Maryland end of the park, and left the car on the side of the Maryland Route 896 (or maybe Pennsylvania Route 896, it's hard to be sure). Then I cut across private property to the marker.
The marker itself looks like this:
As you see, the Pennsylvania sides of the monument are marked with ‘P’ and the Maryland side with ‘M’. The other ‘M’ is actually in Delaware. This Newark Post article explains why there is no ‘D’:
The marker lists only Maryland and Pennsylvania, not Delaware, because in 1765, Delaware was part of Pennsylvania.
This does not explain the whole thing. The point was first marked in 1765 by Mason and Dixon and at that time Delaware was indeed part of Pennsylvania. But as you see the stone marker was placed in 1849, by which time Delaware had been there for some time. Perhaps the people who installed the new marker were trying to pretend that Delaware did not exist.
[ Addendum 20201218: Daniel Wagner points out that even if the 1849 people were trying to depict things as they were in 1765, the marker is still wrong; it should have three ‘P’ and one ‘M’, not two of each. I did read that the surveyors who originally placed the 1849 marker put it in the wrong spot, and it had to be moved later, so perhaps they were just not careful people. ]
Theron Stanford notes that this point is also the northwestern corner of the Wedge. This sliver of land was east of the Maryland border, but outside the Twelve-Mile Circle and so formed an odd prodtrusion from Pennsylvania. Pennsylvania only reliquinshed claims to it in 1921 and it is now agreed to be part of Delaware. Were the Wedge still part of Pennsylvania, the tripoint would have been at its southernmost point.
Looking at the map now I see that to get to the marker, I must have driven within a hundred yards of the westmost point of the Twelve-Mile Circle itself, and there is a (somewhat more impressive) marker there. Had I realized at the time I probably would have tried to stop off.
I have some other pictures of the marker if you are not tired of this yet.
[ Addendum 20201211: Tim Heany asks “Is there no sign at the border on 896?” There probably is, and this observation is a strong argument that I parked the car in Maryland. ]
[ Addendum 20201211: Yes, ‘prodtrusion’ was a typo, but it is a gift from the Gods of Dada and should be treasured, not thrown in the trash. ]
[Other articles in category /misc] permanent link
Sat, 21 Nov 2020
Testing for divisibility by 19
[ Previously, Testing for divisibility by 7. ]
A couple of nights ago I was keeping Katara company while she revised an essay on The Scarlet Letter (ugh) and to pass the time one of the things I did was tinker with the tests for divisibility rules by 9 and 11. In the course of this I discovered the following method for divisibility by 19:
Double the last digit and add the next-to-last.
Double that and add the next digit over.
Repeat until you've added the leftmost digit.
The result will be a smaller number which is a multiple of 19 if and only if the original number was.
For example, let's consider, oh, I don't know, 2337. We calculate:
- 7·2+3 = 17
- 17·2 + 3 = 37
- 37·2 + 2 = 76
76 is a multiple of 19, so 2337 was also. But if you're not sure about 76 you can compute 2·6+7 = 19 and if you're not sure about that you need more help than I can provide.
I don't claim this is especially practical, but it is fun, not completely unworkable, and I hadn't seen anything like it before. You can save a lot of trouble by reducing the intermediate values mod 19 when needed. In the example above above, after the first step you get to 17, which you can reduce mod 19 to -2, and then the next step is -2·2+3 = -1, and the final step is -1·2+2 = 0.
Last time I wrote about this Eric Roode sent me a whole compendium of divisibility tests, including one for divisibility by 19. It's a little like mine, but in reverse: group the digits in pairs, left to right; multiply each pair by 5 and then add the next pair. Here's 2337 again:
- 23·5 + 37 = 152
- 1·5 + 52 = 57
Again you can save a lot trouble by reducing mod 19 before the multiplication. So instead of the first step being 23·5 + 37 you can reduce the 23·5 to 4·5 = 20 and then add the 37 to get 57 right away.
[ Addendum: Of course this was discovered long ago, and in fact Wikipedia mentions it. ]
[ Addendum 20201123: An earlier version of this article claimed that the double-and-add step I described preserves the mod-19 residue. It does not, of course; the doubling step doubles it. It is, however, true that it is zero afterward if and only if it was zero before. ]
[Other articles in category /math] permanent link

[Other articles in category /misc] permanent link
Mon, 02 Nov 2020
A better way to do remote presentations
A few months ago I wrote an article about a strategy I had tried when giving a talk via videochat. Typically:
The slides are presented by displaying them on the speaker's screen, and then sharing the screen image to the audience.
I thought I had done it a better way:
I published the slides on my website ahead of time, and sent the link to the attendees. They had the option to follow along on the web site, or to download a copy and follow along in their own local copy.
This, I thought, had several advantages:
Each audience person can adjust the monitor size, font size, colors to suit their own viewing preferences.
The audience can see the speaker. Instead of using my outgoing video feed to share the slides, I could share my face as I spoke.
With the slides under their control, audience members can go back to refer to earlier material, or skip ahead if they want.
When I brought this up with my co-workers, some of them had a very good objection:
I am too lazy to keep clicking through slides as the talk progresses. I just want to sit back and have it do all the work.
Fair enough! I have done this.
If you package your slides with page-turner, one instance becomes the “leader” and the rest are “followers”. Whenever the leader moves from one slide to the next, a very simple backend server is notified. The followers periodically contact the server to find out what slide they are supposed to be showing, and update themselves accordingly. The person watching the show can sit back and let it do all the work.
But! If an audience member wants to skip ahead, or go back, that works too. They can use the arrow keys on their keyboard. Their follower instance will stop synchronizing with the leader's slide. Instead, it will display a box in the corner of the page, next to the current slide's page number, that says what slide the leader is looking at. The number in this box updates dynamically, so the audience person always knows how far ahead or behind they are.

| 
|
| Synchronized | Unsynchronized |
At left, the leader is displaying slide 3, and the follower is there also. When the leader moves on to slide 4, the follower instance will switch automatically.
At right, the follower is still looking at slide 3, but is detached from the leader, who has moved on to slide 007, as you can see in the gray box.
When the audience member has finished their excursion, they can click the gray box and their own instance will immediately resynchronize with the leader and follow along until the next time they want to depart.
I used this to give a talk to the Charlotte Perl Mongers last week and it worked. Responses were generally positive even though the UI is a little bit rough-looking.
Technical details
The back end is a tiny server, written in Python 3 with Flask. The server is really tiny, only about 60 lines of code. It has only two endpoints: for getting the leader's current page, and for setting it. Setting requires a password.
@app.route('/get-page')
def get_page():
return { "page": app.server.get_pageName() }
@app.route('/set-page', methods=['POST'])
def set_page():
…
password = request.data["password"]
page = request.data["page"]
try:
app.server.update_pageName(page, password)
except WrongPassword:
return failure("Incorrect password"), status.HTTP_401_UNAUTHORIZED
return { "success": True }
The front end runs in the browser. The user downloads the front-end
script, pageturner.js, from the same place they are getting the
slides. Each slide contains, in its head element:
<LINK REL='next' HREF='slide003.html' TYPE='text/html; charset=utf-8'>
<LINK REL='previous' HREF='slide001.html' TYPE='text/html; charset=utf-8'>
<LINK REL='this' HREF='slide002.html' TYPE='text/html; charset=utf-8'>
<script language="javascript" src="pageturner.js" >
</script>
The link elements tell page-turner where to go when someone uses
the arrow keys. (This could, of course, be a simple counter, if your
slides are simply numbered, but my slide decks often have
slide002a.html and the like.) Most of page-turner's code
is in
pageturner.js,
which is a couple hundred lines of JavaScript.
On page switching, a tiny amount of information is stored in the
browser window's sessionStorage object. This is so that after the
new page is loaded, the program can remember whether it is supposed to
be synchronized.
If you want page-turner to display the leader's slide number when the
follower is desynchronized, as in the example above, you include an
element with class phantom_number. The phantom_click handler
resynchronizes the follower:
<b onclick="phantom_click()" class="phantom_number"></b>
The password for the set-page endpoint is embedded in the
pageturner.js file. Normally, this is null, which means that the
instance is a follower. If the password is null, page-turner won't
try to update set-page. If you want to be the leader, you change
"password": null,
to
"password": "swordfish",
or whatever.
Many improvements are certainly possible. It could definitely look a lot better, but I leave that to someone who has interest and aptitude in design.
I know of one serious bug: at present the server doesn't handle SSL,
so must be run at an http://… address; if the slides reside at an
https://… location, the browser will refuse to make the AJAX
requests. This shouldn't be hard to fix.
Source code download
Patches welcome.
License
The software is licensed under the Creative Commons Attribution 4.0 license (CC BY 4.0).
You are free to share (copy and redistribute the software in any medium or format) and adapt (remix, transform, and build upon the material) for any purpose, even commercially, so long as you give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
Share and enjoy.
[Other articles in category /talk] permanent link
Sun, 18 Oct 2020
Newton's Method and its instability
While messing around with Newton's method for last week's article, I built this Desmos thingy:
The red point represents the initial guess; grab it and drag it around, and watch how the later iterations change. Or, better, visit the Desmos site and play with the slider yourself.
(The curve here is !!y = (x-2.2)(x-3.3)(x-5.5)!!; it has a local maximum at around !!2.7!!, and a local minimum at around !!4.64!!.)
Watching the attractor point jump around I realized I was arriving at a much better understanding of the instability of the convergence. Clearly, if your initial guess happens to be near an extremum of !!f!!, the next guess could be arbitrarily far away, rather than a small refinement of the original guess. But even if the original guess is pretty good, the refinement might be near an extremum, and then the following guess will be somewhere random. For example, although !!f!! is quite well-behaved in the interval !![4.3, 4.35]!!, as the initial guess !!g!! increases across this interval, the refined guess !!\hat g!! decreases from !!2.74!! to !!2.52!!, and in between these there is a local maximum that kicks the ball into the weeds. The result is that at !!g=4.3!! the method converges to the largest of the three roots, and at !!g=4.35!!, it converges to the smallest.
This is where the Newton basins come from:
Here we are considering the function !!f:z\mapsto z^3 -1!! in the complex plane. Zero is at the center, and the obvious root, !!z=1!! is to its right, deep in the large red region. The other two roots are at the corresponding positions in the green and blue regions.
Starting at any red point converges to the !!z=1!! root. Usually, if you start near this root, you will converge to it, which is why all the points near it are red. But some nearish starting points are near an extremum, so that the next guess goes wild, and then the iteration ends up at the green or the blue root instead; these areas are the rows of green and blue leaves along the boundary of the large red region. And some starting points on the boundaries of those leaves kick the ball into one of the other leaves…
Here's the corresponding basin diagram for the polynomial !!y = (x-2.2)(x-3.3)(x-5.5)!! from earlier:
The real axis is the horizontal hairline along the middle of the diagram. The three large regions are the main basins of attraction to the three roots (!!x=2.2, 3.3!!, and !!5.5!!) that lie within them.
But along the boundaries of each region are smaller intrusive bubbles where the iteration converges to a surprising value. A point moving from left to right along the real axis passes through the large pink !!2.2!! region, and then through a very small yellow bubble, corresponding to the values right around the local maximum near !!x=2.7!! where the process unexpectedly converges to the !!5.5!! root. Then things settle down for a while in the blue region, converging to the !!3.3!! root as one would expect, until the value gets close to the local minimum at !!4.64!! where there is a pink bubble because the iteration converges to the !!2.2!! root instead. Then as !!x!! increases from !!4.64!! to !!5.5!!, it leaves the pink bubble and enters the main basin of attraction to !!5.5!! and stays there.
If the picture were higher resolution, you would be able to see that the pink bubbles all have tiny yellow bubbles growing out of them (one is 4.39), and the tiny yellow bubbles have even tinier pink bubbles, and so on forever.
(This was generated by the Online Fractal Generator at usefuljs.net; the labels were added later by me. The labels’ positions are only approximate.)
[ Addendum: Regarding complex points and !!f : z\mapsto z^3-1!! I said “some nearish starting points are near an extremum”. But this isn't right; !!f!! has no extrema. It has an inflection point at !!z=0!! but this doesn't explain the instability along the lines !!\theta = \frac{2k+1}{3}\pi!!. So there's something going on here with the complex derivative that I don't understand yet. ]
[Other articles in category /math] permanent link
Fixed points and attractors, part 3
Last week I wrote about a super-lightweight variation on Newton's method, in which one takes this function: $$f_n : \frac ab \mapsto \frac{a+nb}{a+b}$$
or equivalently
$$f_n : x \mapsto \frac{x+n}{x+1}$$
Iterating !!f_n!! for a suitable initial value (say, !!1!!) converges to !!\sqrt n!!:
$$ \begin{array}{rr} x & f_3(x) \\ \hline 1.0 & 2.0 \\ 2.0 & 1.667 \\ 1.667 & 1.75 \\ 1.75 & 1.727 \\ 1.727 & 1.733 \\ 1.733 & 1.732 \\ 1.732 & 1.732 \end{array} $$
Later I remembered that a few months back I wrote a couple of articles about a more general method that includes this as a special case:
The general idea was:
Suppose we were to pick a function !!f!! that had !!\sqrt 2!! as a fixed point. Then !!\sqrt 2!! might be an attractor, in which case iterating !!f!! will get us increasingly accurate approximations to !!\sqrt 2!!.
We can see that !!\sqrt n!! is a fixed point of !!f_n!!:
$$ \begin{align} f_n(\sqrt n) & = \frac{\sqrt n + n}{\sqrt n + 1} \\ & = \frac{\sqrt n(1 + \sqrt n)}{1 + \sqrt n} \\ & = \sqrt n \end{align} $$
And in fact, it is an attracting fixed point, because if !!x = \sqrt n + \epsilon!! then
$$\begin{align} f_n(\sqrt n + \epsilon) & = \frac{\sqrt n + \epsilon + n}{\sqrt n + \epsilon + 1} \\ & = \frac{(\sqrt n + \sqrt n\epsilon + n) - (\sqrt n -1)\epsilon}{\sqrt n + \epsilon + 1} \\ & = \sqrt n - \frac{(\sqrt n -1)\epsilon}{\sqrt n + \epsilon + 1} \end{align}$$
Disregarding the !!\epsilon!! in the denominator we obtain $$f_n(\sqrt n + \epsilon) \approx \sqrt n - \frac{\sqrt n - 1}{\sqrt n + 1} \epsilon $$
The error term !!-\frac{\sqrt n - 1}{\sqrt n + 1} \epsilon!! is strictly smaller than the original error !!\epsilon!!, because !!0 < \frac{x-1}{x+1} < 1!! whenever !!x>1!!. This shows that the fixed point !!\sqrt n!! is attractive.
In the previous articles I considered several different simple functions that had fixed points at !!\sqrt n!!, but I didn't think to consider this unusally simple one. I said at the time:
I had meant to write about Möbius transformations, but that will have to wait until next week, I think.
but I never did get around to the Möbius transformations, and I have long since forgotten what I planned to say. !!f_n!! is an example of a Möbius transformation, and I wonder if my idea was to systematically find all the Möbius transformations that have !!\sqrt n!! as a fixed point, and see what they look like. It is probably possible to automate the analysis of whether the fixed point is attractive, and if not to apply one of the transformations from the previous article to make it attractive.
[Other articles in category /math] permanent link
Tue, 13 Oct 2020
Newton's Method but without calculus — or multiplication
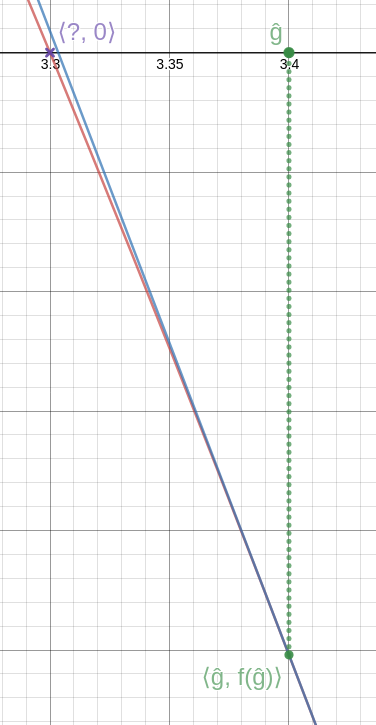
Newton's method goes like this: We have a function !!f!! and we want to solve the equation !!f(x) = 0.!! We guess an approximate solution, !!g!!, and it doesn't have to be a very good guess.
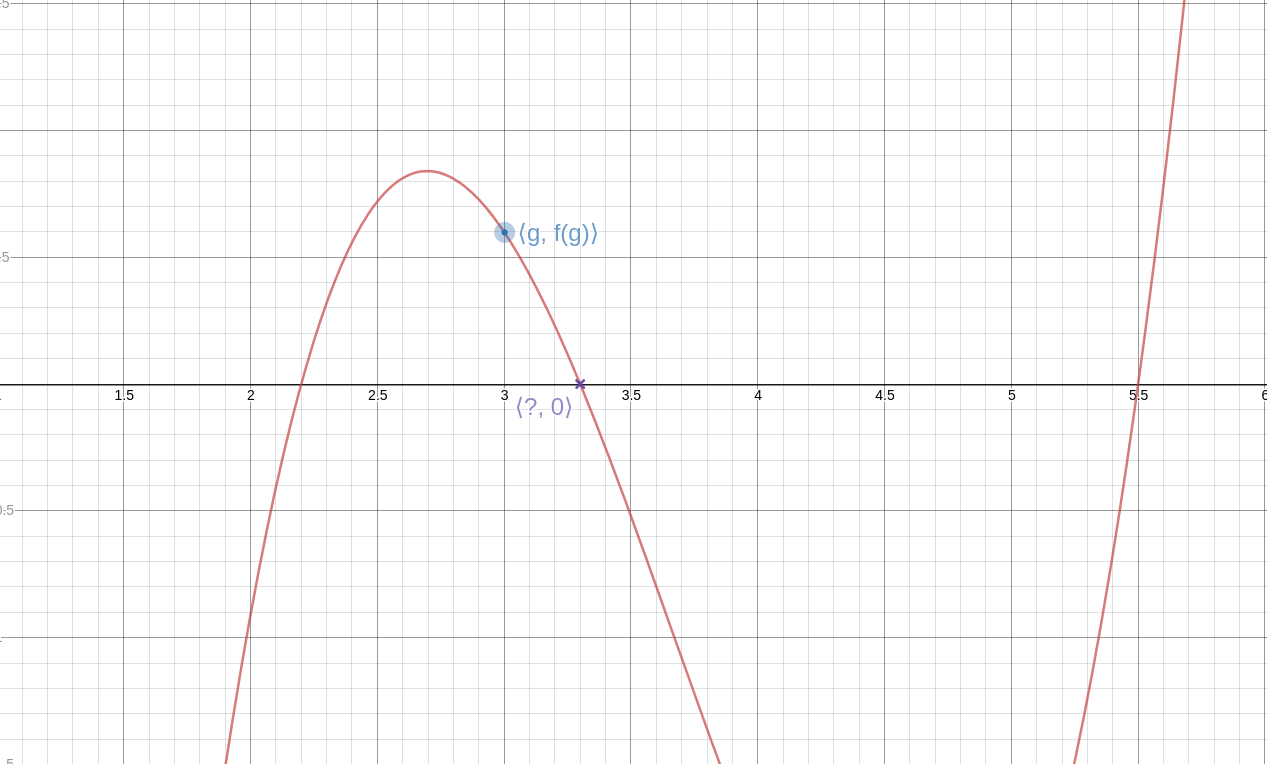
Then we calculate the line !!T!! tangent to !!f!! through the point !!\langle g, f(g)\rangle!!. This line intersects the !!x!!-axis at some new point !!\langle \hat g, 0\rangle!!, and this new value, !!\hat g!!, is a better approximation to the value we're seeking.
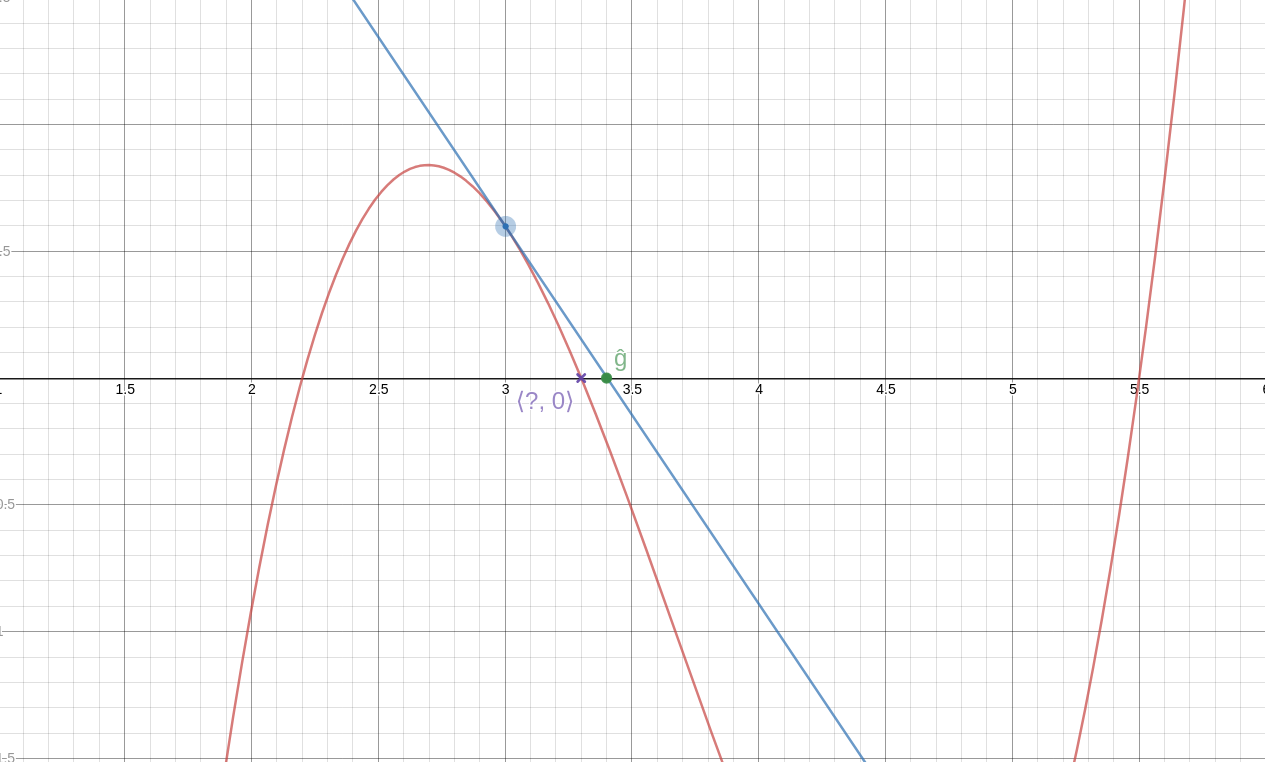
Analytically, we have:
$$\hat g = g - \frac{f(g)}{f'(g)}$$
where !!f'(g)!! is the derivative of !!f!! at !!g!!.
We can repeat the process if we like, getting better and better approximations to the solution. (See detail at left; click to enlarge. Again, the blue line is the tangent, this time at !!\langle \hat g, f(\hat g)\rangle!!. As you can see, it intersects the axis very close to the actual solution.)
In general, this requires calculus or something like it, but in any particular case you can avoid the calculus. Suppose we would like to find the square root of 2. This amounts to solving the equation $$x^2-2 = 0.$$ The function !!f!! here is !!x^2-2!!, and !!f'!! is !!2x!!. Once we know (or guess) !!f'!!, no further calculus is needed. The method then becomes: Guess !!g!!, then calculate $$\hat g = g - \frac{g^2-2}{2g}.$$ For example, if our initial guess is !!g = 1.5!!, then the formula above tells us that a better guess is !!\hat g = 1.5 - \frac{2.25 - 2}{3} = 1.4166\ldots!!, and repeating the process with !!\hat g!! produces !!1.41421\mathbf{5686}!!, which is very close to the correct result !!1.41421\mathbf{3562}!!. If we want the square root of a different number !!n!! we just substitute it for the !!2!! in the numerator.
This method for extracting square roots works well and requires no calculus. It's called the Babylonian method and while there's no evidence that it was actually known to the Babylonians, it is quite ancient; it was first recorded by Hero of Alexandria about 2000 years ago.
How might this have been discovered if you didn't have calculus? It's actually quite easy. Here's a picture of the number line. Zero is at one end, !!n!! is at the other, and somewhere in between is !!\sqrt n!!, which we want to find.
Also somewhere in between is our guess !!g!!. Say we guessed too low, so !!0 \lt g < \sqrt n!!. Now consider !!\frac ng!!. Since !!g!! is too small to be !!\sqrt n!! exactly, !!\frac ng!! must be too large. (If !!g!! and !!\frac ng!! were both smaller than !!\sqrt n!!, then their product would be smaller than !!n!!, and it isn't.)
Similarly, if the guess !!g!! is too large, so that !!\sqrt n < g!!, then !!\frac ng!! must be less than !!\sqrt n!!. The important point is that !!\sqrt n!! is between !!g!! and !!\frac ng!!. We have narrowed down the interval in which !!\sqrt n!! lies, just by guessing.
Since !!\sqrt n!! lies in the interval between !!g!! and !!\frac ng!! our next guess should be somewhere in this smaller interval. The most obvious thing we can do is to pick the point halfway in the middle of !!g!! and !!\frac ng!!, So if we guess the average, $$\frac12\left(g + \frac ng\right),$$ this will probably be much closer to !!\sqrt n!! than !!g!! was:
This average is exactly what Newton's method would have calculated, because $$\frac12\left(g + \frac ng\right) = g - \frac{g^2-n}{2g}.$$
But we were able to arrive at the same computation with no calculus at all — which is why this method could have been, and was, discovered 1700 years before Newton's method itself.
If we're dealing with rational numbers then we might write !!g=\frac ab!!, and then instead of replacing our guess !!g!! with a better guess !!\frac12\left(g + \frac ng\right)!!, we could think of it as replacing our guess !!\frac ab!! with a better guess !!\frac12\left(\frac ab + \frac n{\frac ab}\right)!!. This simplifies to
$$\frac ab \Rightarrow \frac{a^2 + nb^2}{2ab}$$
so that for example, if we are calculating !!\sqrt 2!!, and we start with the guess !!g=\frac32!!, the next guess is $$\frac{3^2 + 2\cdot2^2}{2\cdot3\cdot 2} = \frac{17}{12} = 1.4166\ldots$$ as we saw before. The approximation after that is !!\frac{289+288}{2\cdot17\cdot12} = \frac{577}{408} = 1.41421568\ldots!!. Used this way, the method requires only integer calculations, and converges very quickly.
But the numerators and denominators increase rapidly, which is good in one sense (it means you get to the accurate approximations quickly) but can also be troublesome because the numbers get big and also because you have to multiply, and multiplication is hard.
But remember how we figured out to do this calculation in the first place: all we're really trying to do is find a number in between !!g!! and !!\frac ng!!. We did that the first way that came to mind, by averaging. But perhaps there's a simpler operation that we could use instead, something even easier to compute?
Indeed there is! We can calculate the mediant. The mediant of !!\frac ab!! and !!\frac cd!! is simply $$\frac{a+c}{b+d}$$ and it is very easy to show that it lies between !!\frac ab!! and !!\frac cd!!, as we want.
So instead of the relatively complicated $$\frac ab \Rightarrow \frac{a^2 + nb^2}{2ab}$$ operation, we can try the very simple and quick $$\frac ab \Rightarrow \operatorname{mediant}\left(\frac ab, \frac{nb}{a}\right) = \frac{a+nb}{b+a}$$ operation.
Taking !!n=2!! as before, and starting with !!\frac 32!!, this produces:
$$ \frac 32 \Rightarrow\frac{ 7 }{ 5 } \Rightarrow\frac{ 17 }{ 12 } \Rightarrow\frac{ 41 }{ 29 } \Rightarrow\frac{ 99 }{ 70 } \Rightarrow\frac{ 239 }{ 169 } \Rightarrow\frac{ 577 }{ 408 } \Rightarrow\cdots$$
which you may recognize as the convergents of !!\sqrt2!!. These are actually the rational approximations of !!\sqrt 2!! that are optimally accurate relative to the sizes of their denominators. Notice that !!\frac{17}{12}!! and !!\frac{577}{408}!! are in there as they were before, although it takes longer to get to them.
I think it's cool that you can view it as a highly-simplified version of Newton's method.
[ Addendum: An earlier version of the last paragraph claimed:
None of this is a big surprise, because it's well-known that you can get the convergents of !!\sqrt n!! by applying the transformation !!\frac ab\Rightarrow \frac{a+nb}{a+b}!!, starting with !!\frac11!!.
Simon Tatham pointed out that this was mistaken. It's true when !!n=2!!, but not in general. The sequence of fractions that you get does indeed converge to !!\sqrt n!!, but it's not usually the convergents, or even in lowest terms. When !!n=3!!, for example, the numerators and denominators are all even. ]
[ Addendum: Newton's method as I described it, with the crucial !!g → g - \frac{f(g)}{f'(g)}!! transformation, was actually invented in 1740 by Thomas Simpson. Both Isaac Newton and Thomas Raphson had earlier described only special cases, as had several Asian mathematicians, including Seki Kōwa. ]
[ Previous discussion of convergents: Archimedes and the square root of 3; 60-degree angles on a lattice. A different variation on the Babylonian method. ]
[ Note to self: Take a look at what the AM-GM inequality has to say about the behavior of !!\hat g!!. ]
[ Addendum 20201018: A while back I discussed the general method of picking a function !!f!! that has !!\sqrt 2!! as a fixed point, and iterating !!f!!. This is yet another example of such a function. ]
[Other articles in category /math] permanent link
Wed, 23 Sep 2020
The mystery of the malformed command-line flags
Today a user came to tell me that their command
greenlight submit branch-name --require-review-by skordokott
failed, saying:
**
** unexpected extra argument 'branch-name' to 'submit' command
**
This is surprising. The command looks correct. The branch name is
required. The --require-review-by option can be supplied any
number of times (including none) and each must have a value provided.
Here it is given once and the provided value appears to be
skordocott.
The greenlight command is a crappy shell script that pre-validates
the arguments before sending them over the network to the real server.
I guessed that the crappy shell script parser wanted the branch name
last, even though the server itself would have been happy to take the
arguments in either order. I suggested that the user try:
greenlight submit --require-review-by skordokott branch-name
But it still didn't work:
**
** unexpected extra argument '--require-review-by' to 'submit' command
**
I dug in to the script and discovered the problem, which was not actually a programming error. The crappy shell script was behaving correctly!
I had written up release notes for the --require-review-by feature.
The user had clipboard-copied the option string out of
the release notes and pasted it into the shell. So why didn't it work?
In an earlier draft of the release notes, when they were displayed as an HTML page, there would be bad line breaks:
blah blah blah be sure to use the
-
-require-review-byoption…
or:
blah blah blah the new
--
require-review-byfeature is…
No problem, I can fix it! I just changed the pair of hyphens (- U+002D)
at the beginning of --require-review-by to Unicode nonbreaking
hyphens (‑ U+2011). Bad line breaks begone!
But then this hapless user clipboard-copied the option string out of
the release notes, including its U+2011 characters. The parser in the
script was (correctly) looking for U+002D characters, and didn't
recognize --require-review-by as an option flag.
One lesson learned: people will copy-paste stuff out of documentation, and I should be prepared for that.
There are several places to address this. I made the error message more transparent; formerly it would complain only about the first argument, which was confusing because it was the one argument that wasn't superfluous. Now it will say something like
**
** extra branch name '--require-review-by' in 'submit' command
**
**
** extra branch name 'skordokott' in 'submit' command
**
which is more descriptive of what it actually doesn't like.
I could change the nonbreaking hyphens in the release notes back to regular hyphens and just accept the bad line breaks. But I don't want to. Typography is important.
One idea I'm toying with is to have the shell script silently replace all nonbreaking hyphens with regular ones before any further processing. It's a hack, but it seems like it might be a harmless one.
So many weird things can go wrong. This computer stuff is really complicated. I don't know how anyone get anything done.
[ Addendum: A reader suggests that I could have fixed the line breaks with CSS. But the release notes were being presented as a Slack “Post”, which is essentially a WYSIWYG editor for creating shared documents. It presents the document in a canned HTML style, and as far as I know there's no way to change the CSS it uses. Similarly, there's no way to insert raw HTML elements, so no way to change the style per-element. ]
[Other articles in category /prog/bug] permanent link
Sun, 13 Sep 2020The front page of NPR.org today has this headline:
It contains this annoying phrase:
The race for Joni Ernst's seat could help determine control of the Senate.
Someone has really committed to hedging.
I would have said that the race would certainly help determine control of the Senate, or that it could determine control of the Senate. The statement as written makes an extremely weak claim.
The article itself doesn't include this phrase. This is why reporters hate headline-writers.
[Other articles in category /lang] permanent link
Fri, 11 Sep 2020
Historical diffusion of words for “eggplant”
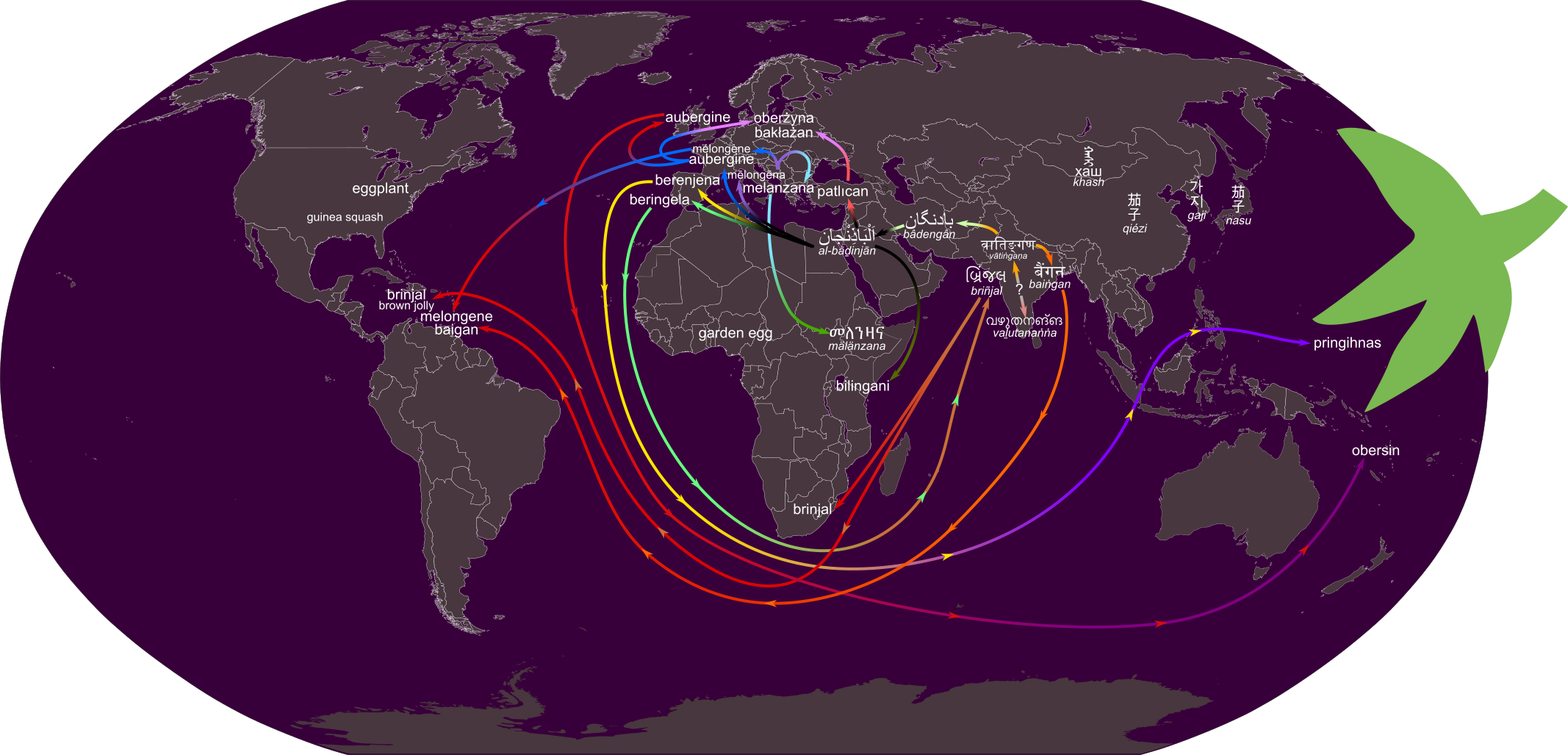
In reply to my recent article about the history of words for “eggplant”, a reader, Lydia, sent me this incredible map they had made that depicts the history and the diffusion of the terms:
Lydia kindly gave me permission to share their map with you. You can see the early Dravidian term vaḻutanaṅṅa in India, and then the arrows show it travelling westward across Persia and, Arabia, from there to East Africa and Europe, and from there to the rest of the world, eventually making its way back to India as brinjal before setting out again on yet more voyages.
Thank you very much, Lydia! And Happy Diada Nacional de Catalunya, everyone!
[Other articles in category /lang/etym] permanent link
A maxim for conference speakers
The only thing worse than re-writing your talk the night before is writing your talk the night before.
[Other articles in category /talk] permanent link
Fri, 28 Aug 2020This morning Katara asked me why we call these vegetables “zucchini” and “eggplant” but the British call them “courgette” and “aubergine”.
I have only partial answers, and the more I look, the more complicated they get.
Zucchini
The zucchini is a kind of squash, which means that in Europe it is a post-Columbian import from the Americas.
“Squash” itself is from Narragansett, and is not related to the verb “to squash”. So I speculate that what happened here was:
American colonists had some name for the zucchini, perhaps derived from an Narragansett or another Algonquian language, or perhaps just “green squash” or “little gourd” or something like that. A squash is not exactly a gourd, but it's not exactly not a gourd either, and the Europeans seem to have accepted it as a gourd (see below).
When the vegetable arrived in France, the French named it courgette, which means “little gourd”. (Courge = “gourd”.) Then the Brits borrowed “courgette” from the French.
Sometime much later, the Americans changed the name to “zucchini”, which also means “little gourd”, this time in Italian. (Zucca = “gourd”.)
The Big Dictionary has citations for “zucchini” only back to 1929, and “courgette” to 1931. What was this vegetable called before that? Why did the Americans start calling it “zucchini” instead of whatever they called it before, and why “zucchini” and not “courgette”? If it was brought in by Italian immigrants, one might expect to the word to have appeared earlier; the mass immigration of Italians into the U.S. was over by 1920.
Following up on this thought, I found a mention of it in Cuniberti, J. Lovejoy., Herndon, J. B. (1918). Practical Italian recipes for American kitchens, p. 18: “Zucchini are a kind of small squash for sale in groceries and markets of the Italian neighborhoods of our large cities.” Note that Cuniberti explains what a zucchini is, rather than saying something like “the zucchini is sometimes known as a green summer squash” or whatever, which suggests that she thinks it will not already be familiar to the readers. It looks as though the story is: Colonial Europeans in North America stopped eating the zucchini at some point, and forgot about it, until it was re-introduced in the early 20th century by Italian immigrants.
When did the French start calling it courgette? When did the Italians start calling it zucchini? Is the Italian term a calque of the French, or vice versa? Or neither? And since courge (and gourd) are evidently descended from Latin cucurbita, where did the Italians get zucca?
So many mysteries.
Eggplant
Here I was able to get better answers. Unlike squash, the eggplant is native to Eurasia and has been cultivated in western Asia for thousands of years.
The puzzling name “eggplant” is because the fruit, in some varieties, is round, white, and egg-sized.

The term “eggplant” was then adopted for other varieties of the same plant where the fruit is entirely un-egglike.
“Eggplant” in English goes back only to 1767. What was it called before that? Here the OED was more help. It gives this quotation, from 1785:
When this [sc. its fruit] is white, it has the name of Egg-Plant.
I inferred that the preceding text described it under a better-known name, so, thanks to the Wonders of the Internet, I looked up the original source:
Melongena or Mad Apple is also of this genus [solanum]; it is cultivated as a curiosity for the largeness and shape of its fruit; and when this is white, it has the name of Egg Plant; and indeed it then perfectly resembles a hen's egg in size, shape, and colour.
(Jean-Jacques Rosseau, Letters on the Elements of Botany, tr. Thos. Martyn 1785. Page 202. (Wikipedia))
The most common term I've found that was used before “egg-plant” itself is “mad apple”. The OED has cites from the late 1500s that also refer to it as a “rage apple”, which is a calque of French pomme de rage. I don't know how long it was called that in French. I also found “Malum Insanam” in the 1736 Lexicon technicum of John Harris, entry “Bacciferous Plants”.
Melongena was used as a scientific genus name around 1700 and later adopted by Linnaeus in 1753. I can't find any sign that it was used in English colloquial, non-scientific writing. Its etymology is a whirlwind trip across the globe. Here's what the OED says about it:
The neo-Latin scientific term is from medieval Latin melongena
Latin melongena is from medieval Greek μελιντζάνα (/melintzána/), a variant of Byzantine Greek ματιζάνιον (/matizánion/) probably inspired by the common Greek prefix μελανο- (/melano-/) “dark-colored”. (Akin to “melanin” for example.)
Greek ματιζάνιον is from Arabic bāḏinjān (بَاذِنْجَان). (The -ιον suffix is a diminutive.)
Arabic bāḏinjān is from Persian bādingān (بادنگان)
Persian bādingān is from Sanskrit and Pali vātiṅgaṇa (भण्टाकी)
Sanskrit vātiṅgaṇa is from Dravidian (for example, Malayalam is vaḻutana (വഴുതന); the OED says “compare… Tamil vaṟutuṇai”, which I could not verify.)
Wowzers.
Okay, now how do we get to “aubergine”? The list above includes Arabic bāḏinjān, and this, like many Arabic words was borrowed into Spanish, as berengena or alberingena. (The “al-” prefix is Arabic for “the” and is attached to many such borrowings, for example “alcohol” and “alcove”.)
From alberingena it's a short step to French aubergine. The OED entry for aubergine doesn't mention this. It claims that aubergine is from “Spanish alberchigo, alverchiga, ‘an apricocke’”. I think it's clear that the OED blew it here, and I think this must be the first time I've ever been confident enough to say that. Even the OED itself supports me on this: the note at the entry for brinjal says: “cognate with the Spanish alberengena is the French aubergine”. Okay then. (Brinjal, of course, is a contraction of berengena, via Portuguese bringella.)
Sanskrit vātiṅgaṇa is also the ultimate source of modern Hindi baingan, as in baingan bharta.
(Wasn't there a classical Latin word for eggplant? If so, what was it? Didn't the Romans eat eggplant? How do you conquer the world without any eggplants?)
[ Addendum: My search for antedatings of “zucchini” turned up some surprises. For example, I found what seemed to be many mentions in an 1896 history of Sicily. These turned out not to be about zucchini at all, but rather the computer's pathetic attempts at recognizing the word Σικελίαν. ]
[ Addendum 20200831: Another surprise: Google Books and Hathi Trust report that “zucchini” appears in the 1905 Collier Modern Eclectic Dictionary of the English Langauge, but it's an incredible OCR failure for the word “acclamation”. ]
[ Addendum 20200911: A reader, Lydia, sent me a beautiful map showing the evolution of the many words for ‘eggplant’. Check it out. ]
[ Addendum 20231021: The Japanese kabocha squash (カボチャ) is probably so-called because it was brought by the Portuguese from Camboja, Cambodia. ]
[ Addendum 20231127: A while back I looked into the question of whether the Romans had eggplants, and it seems that consensus was that they did not! Incredible. How much longer their empire would have lasted if they had been able to draw in the power of the eggplant? This probably goes some way to explaining why the Byzantine Empire lasted so much longer than the Western Empire. ]
[Other articles in category /lang/etym] permanent link
Mon, 24 Aug 2020Ripta Pasay brought to my attention the English cookbook Liber Cure Cocorum, published sometime between 1420 and 1440. The recipes are conveyed as poems:
Conyngus in gravé.
Sethe welle þy conyngus in water clere,
After, in water colde þou wasshe hom sere,
Take mylke of almondes, lay hit anone
With myed bred or amydone;
Fors hit with cloves or gode gyngere;
Boyle hit over þo fyre,
Hew þo conyngus, do hom þer to,
Seson hit with wyn or sugur þo.
(Original plus translation by Cindy Renfrow)
“Conyngus” is a rabbit; English has the cognate “coney”.
If you have read my article on how to read Middle English you won't have much trouble with this. There are a few obsolete words: sere means “separately”; myed bread is bread crumbs, and amydone is starch.
I translate it (very freely) as follows:
Rabbit in gravy.
Boil well your rabbits in clear water,
then wash them separately in cold water.
Take almond milk, put it on them
with grated bread or starch;
stuff them with cloves or good ginger;
boil them over the fire,
cut them up,
and season with wine or sugar.
Thanks, Ripta!
[Other articles in category /food] permanent link
Fri, 21 Aug 2020
Mixed-radix fractions in Bengali
[ Previously, Base-4 fractions in Telugu. ]
I was really not expecting to revisit this topic, but a couple of weeks ago, looking for something else, I happened upon the following curiously-named Unicode characters:
U+09F4 (e0 a7 b4): BENGALI CURRENCY NUMERATOR ONE [৴]
U+09F5 (e0 a7 b5): BENGALI CURRENCY NUMERATOR TWO [৵]
U+09F6 (e0 a7 b6): BENGALI CURRENCY NUMERATOR THREE [৶]
U+09F7 (e0 a7 b7): BENGALI CURRENCY NUMERATOR FOUR [৷]
U+09F8 (e0 a7 b8): BENGALI CURRENCY NUMERATOR ONE LESS THAN THE DENOMINATOR [৸]
U+09F9 (e0 a7 b9): BENGALI CURRENCY DENOMINATOR SIXTEEN [৹]
Oh boy, more base-four fractions! What on earth does “NUMERATOR ONE LESS THAN THE DENOMINATOR” mean and how is it used?
An explanation appears in the Unicode proposal to add the related “ganda” sign:
U+09FB (e0 a7 bb): BENGALI GANDA MARK [৻]
(Anshuman Pandey, “Proposal to Encode the Ganda Currency Mark for Bengali in the BMP of the UCS”, 2007.)
Pandey explains: prior to decimalization, the Bengali rupee (rupayā) was divided into sixteen ānā. Standard Bengali numerals were used to write rupee amounts, but there was a special notation for ānā. The sign ৹ always appears, and means sixteenths. Then. Prefixed to this is a numerator symbol, which goes ৴, ৵, ৶, ৷ for 1, 2, 3, 4. So for example, 3 ānā is written ৶৹, which means !!\frac3{16}!!.
The larger fractions are made by adding the numerators, grouping by 4's:
| ৴ | ৵ | ৶ | 1, 2, 3 | |
| ৷ | ৷৴ | ৷৵ | ৷৶ | 4, 5, 6, 7 |
| ৷৷ | ৷৷৴ | ৷৷৵ | ৷৷৶ | 8, 9, 10, 11 |
| ৸ | ৸৴ | ৸৵ | ৸৶ | 12, 13, 14, 15 |
except that three fours (৷৷৷) is too many, and is abbreviated by the intriguing NUMERATOR ONE LESS THAN THE DENOMINATOR sign ৸ when more than 11 ānā are being written.
Historically, the ānā was divided into 20 gaṇḍā; the gaṇḍā amounts are written with standard (Benagli decimal) numerals instead of the special-purpose base-4 numerals just described. The gaṇḍā sign ৻ precedes the numeral, so 4 gaṇḍā (!!\frac15!! ānā) is wrtten as ৻৪. (The ৪ is not an 8, it is a four.)
What if you want to write 17 rupees plus !!9\frac15!! ānā? That is 17 rupees plus 9 ānā plus 4 gaṇḍā. If I am reading this report correctly, you write it this way:
১৭৷৷৴৻৪
This breaks down into three parts as ১৭ ৷৷৴ ৻৪. The ১৭ is a 17, for 17 rupees; the ৷৷৴ means 9 ānā (the denominator ৹ is left implicit) and the ৻৪ means 4 gaṇḍā, as before. There is no separator between the rupees and the ānā. But there doesn't need to be, because different numerals are used! An analogous imaginary system in Latin script would be to write the amount as
17dda¢4
where the ‘17’ means 17 rupees, the ‘dda’ means 4+4+1=9 ānā, and the ¢4 means 4 gaṇḍā. There is no trouble seeing where the ‘17’ ends and the ‘dda’ begins.
Pandey says there was an even smaller unit, the kaṛi. It was worth ¼ of a gaṇḍā and was again written with the special base-4 numerals, but as if the gaṇḍā had been divided into 16. A complete amount might be written with decimal numerals for the rupees, base-4 numerals for the ānā, decimal numerals again for the gaṇḍā, and base-4 numerals again for the kaṛi. No separators are needed, because each section is written symbols that are different from the ones in the adjoining sections.
[Other articles in category /math] permanent link
Thu, 06 Aug 2020
Recommended reading: Matt Levine’s Money Stuff
Lately my favorite read has been Matt Levine’s Money Stuff articles from Bloomberg News. Bloomberg's web site requires a subscription but you can also get the Money Stuff articles as an occasional email. It arrives at most once per day.
Almost every issue teaches me something interesting I didn't know, and almost every issue makes me laugh.
Example of something interesting: a while back it was all over the news that oil prices were negative. Levine was there to explain what was really going on and why. Some people manage index funds. They are not trying to beat the market, they are trying to match the index. So they buy derivatives that give them the right to buy oil futures contracts at whatever the day's closing price is. But say they already own a bunch of oil contracts. If they can get the close-of-day price to dip, then their buy-at-the-end-of-the-day contracts will all be worth more because the counterparties have contracted to buy at the dip price. How can you get the price to dip by the end of the day? Easy, unload 20% of your contracts at a bizarre low price, to make the value of the other 80% spike… it makes my head swim.
But there are weird second- and third-order effects too. Normally if you invest fifty million dollars in oil futures speculation, there is a worst-case: the price of oil goes to zero and you lose your fifty million dollars. But for these derivative futures, the price could in theory become negative, and for short time in April, it did:
If the ETF’s oil futures go to -$37.63 a barrel, as some futures did recently, the ETF investors lose $20—their entire investment—and, uh, oops? The ETF runs out of money when the futures hit zero; someone else has to come up with the other $37.63 per barrel.
One article I particularly remember discussed the kerfuffle a while back concerning whether Kelly Loeffler improperly traded stocks on classified coronavirus-related intelligence that she received in her capacity as a U.S. senator. I found Levine's argument persuasive:
“I didn’t dump stocks, I am a well-advised rich person, someone else manages my stocks, and they dumped stocks without any input from me” … is a good defense! It’s not insider trading if you don’t trade; if your investment manager sold your stocks without input from you then you’re fine. Of course they could be lying, but in context the defense seems pretty plausible. (Kelly Loeffler, for instance, controversially dumped about 0.6% of her portfolio at around the same time, which sure seems like the sort of thing an investment adviser would do without any input from her? You could call your adviser and say “a disaster is coming, sell everything!,” but calling them to say “a disaster is coming, sell a tiny bit!” seems pointless.)
He contrasted this case with that of Richard Burr, who, unlike Loeffler, remains under investigation. The discussion was factual and informative, unlike what you would get from, say, Twitter, or even Metafilter, where the response was mostly limited to variations on “string them up” and “eat the rich”.
Money Stuff is also very funny. Today’s letter discusses a disclosure filed recently by Nikola Corporation:
More impressive is that Nikola’s revenue for the second quarter was very small, just $36,000. Most impressive, though, is how they earned that revenue:
During the three months ended June 30, 2020 and 2019 the Company recorded solar revenues of $0.03 million and $0.04 million, respectively, for the provision of solar installation services to the Executive Chairman, which are billed on time and materials basis. …
“Solar installation projects are not related to our primary operations and are expected to be discontinued,” says Nikola, but I guess they are doing one last job, specifically installing solar panels at founder and executive chairman Trevor Milton’s house? It is a $13 billion company whose only business so far is doing odd jobs around its founder’s house.
A couple of recent articles that cracked me up discussed clueless day-traders pushing up the price of Hertz stock after Hertz had declared bankruptcy, and how Hertz diffidently attempted to get the SEC to approve a new stock issue to cater to these idiots. (The SEC said no.)
One recurring theme in the newsletter is “Everything is Securities Fraud”. This week, Levine asks:
Is it securities fraud for a public company to pay bribes to public officials in exchange for lucrative public benefits?
Of course you'd expect that the executives would be criminally charged, as they have been. But is there a cause for the company’s shareholders to sue? If you follow the newsletter, you know what the answer will be:
Oh absolutely…
because Everything is Securities Fraud.
Still it is a little weird. Paying bribes to get public benefits is, you might think, the sort of activity that benefits shareholders. Sure they were deceived, and sure the stock price was too high because investors thought the company’s good performance was more legitimate and sustainable than it was, etc., but the shareholders are strange victims. In effect, executives broke the law in order to steal money for the shareholders, and when the shareholders found out they sued? It seems a little ungrateful?
I recommend it.
Levine also has a Twitter account but it is mostly just links to his newsletter articles.
[ Addendum 20200821: Unfortunately, just a few days after I posted this, Matt Levine announced that his newletter would be on hiatus for a few months, as he would be on paternity leave. Sorry! ]
[ Addendum 20210207: Money Stuff is back. ]
[ Addendum 20221204: This article about the balance sheet circulated by FTX in the hours before its bankruptcy may be my favorite of all time. ]
[Other articles in category /ref] permanent link
Wed, 05 Aug 2020
A maybe-interesting number trick?
I'm not sure if this is interesting, trivial, or both. You decide.
Let's divide the numbers from 1 to 30 into the following six groups:
| A | 1 | 2 | 4 | 8 | 16 |
| B | 3 | 6 | 12 | 17 | 24 |
| C | 5 | 9 | 10 | 18 | 20 |
| D | 7 | 14 | 19 | 25 | 28 |
| E | 11 | 13 | 21 | 22 | 26 |
| F | 15 | 23 | 27 | 29 | 30 |
Choose any two rows. Chose a number from each row, and multiply them mod 31. (That is, multiply them, and if the product is 31 or larger, divide it by 31 and keep the remainder.)
Regardless of which two numbers you chose, the result will always be in the same row. For example, any two numbers chosen from rows B and D will multiply to yield a number in row E. If both numbers are chosen from row F, their product will always appear in row A.
[Other articles in category /math] permanent link
Sun, 02 Aug 2020Gulliver's Travels (1726), Part III, chapter 2:
I observed, here and there, many in the habit of servants, with a blown bladder, fastened like a flail to the end of a stick, which they carried in their hands. In each bladder was a small quantity of dried peas, or little pebbles, as I was afterwards informed. With these bladders, they now and then flapped the mouths and ears of those who stood near them, of which practice I could not then conceive the meaning. It seems the minds of these people are so taken up with intense speculations, that they neither can speak, nor attend to the discourses of others, without being roused by some external action upon the organs of speech and hearing… . This flapper is likewise employed diligently to attend his master in his walks, and upon occasion to give him a soft flap on his eyes; because he is always so wrapped up in cogitation, that he is in manifest danger of falling down every precipice, and bouncing his head against every post; and in the streets, of justling others, or being justled himself into the kennel.
When I first told Katara about this, several years ago, instead of “the minds of these people are so taken up with intense speculations” I said they were obsessed with their phones.
Now the phones themselves have become the flappers:
Y. Tung and K. G. Shin, "Use of Phone Sensors to Enhance Distracted Pedestrians’ Safety," in IEEE Transactions on Mobile Computing, vol. 17, no. 6, pp. 1469–1482, 1 June 2018, doi: 10.1109/TMC.2017.2764909.
Our minds are not even taken up with intense speculations, but with Instagram. Dean Swift would no doubt be disgusted.
[Other articles in category /book] permanent link
Sat, 01 Aug 2020
How are finite fields constructed?
Here's another recent Math Stack Exchange answer I'm pleased with.
I know this question has been asked many times and there is good information out there which has clarified a lot for me but I still do not understand how the addition and multiplication tables for !!GF(4)!! is constructed?
I've seen [links] but none explicity explain the construction and I'm too new to be told "its an extension of !!GF(2)!!"
The only “reasonable” answer here is “get an undergraduate abstract algebra text and read the chapter on finite fields”. Because come on, you can't expect some random stranger to appear and write up a detailed but short explanation at your exact level of knowledge.
But sometimes Internet Magic Lightning strikes and that's what you do get! And OP set themselves up to be struck by magic lightning, because you can't get a detailed but short explanation at your exact level of knowledge if you don't provide a detailed but short explanation of your exact level of knowledge — and this person did just that. They understand finite fields of prime order, but not how to construct the extension fields. No problem, I can explain that!
I had special fun writing this answer because I just love constructing extensions of finite fields. (Previously: [1] [2])
For any given !!n!!, there is at most one field with !!n!! elements: only one, if !!n!! is a power of a prime number (!!2, 3, 2^2, 5, 7, 2^3, 3^2, 11, 13, \ldots!!) and none otherwise (!!6, 10, 12, 14\ldots!!). This field with !!n!! elements is written as !!\Bbb F_n!! or as !!GF(n)!!.
Suppose we want to construct !!\Bbb F_n!! where !!n=p^k!!. When !!k=1!!, this is easy-peasy: take the !!n!! elements to be the integers !!0, 1, 2\ldots p-1!!, and the addition and multiplication are done modulo !!n!!.
When !!k>1!! it is more interesting. One possible construction goes like this:
The elements of !!\Bbb F_{p^k}!! are the polynomials $$a_{k-1}x^{k-1} + a_{k-2}x^{k-2} + \ldots + a_1x+a_0$$ where the coefficients !!a_i!! are elements of !!\Bbb F_p!!. That is, the coefficients are just integers in !!{0, 1, \ldots p-1}!!, but with the understanding that the addition and multiplication will be done modulo !!p!!. Note that there are !!p^k!! of these polynomials in total.
Addition of polynomials is done exactly as usual: combine like terms, but remember that the coefficients are added modulo !!p!! because they are elements of !!\Bbb F_p!!.
Multiplication is more interesting:
a. Pick an irreducible polynomial !!P!! of degree !!k!!. “Irreducible” means that it does not factor into a product of smaller polynomials. How to actually locate an irreducible polynomial is an interesting question; here we will mostly ignore it.
b. To multiply two elements, multiply them normally, remembering that the coefficients are in !!\Bbb F_p!!. Divide the product by !!P!! and keep the remainder. Since !!P!! has degree !!k!!, the remainder must have degree at most !!k-1!!, and this is your answer.
Now we will see an example: we will construct !!\Bbb F_{2^2}!!. Here !!k=2!! and !!p=2!!. The elements will be polynomials of degree at most 1, with coefficients in !!\Bbb F_2!!. There are four elements: !!0x+0, 0x+1, 1x+0, !! and !!1x+1!!. As usual we will write these as !!0, 1, x, x+1!!. This will not be misleading.
Addition is straightforward: combine like terms, remembering that !!1+1=0!! because the coefficients are in !!\Bbb F_2!!:
$$\begin{array}{c|cccc} + & 0 & 1 & x & x+1 \\ \hline 0 & 0 & 1 & x & x+1 \\ 1 & 1 & 0 & x+1 & x \\ x & x & x+1 & 0 & 1 \\ x+1 & x+1 & x & 1 & 0 \end{array} $$
The multiplication as always is more interesting. We need to find an irreducible polynomial !!P!!. It so happens that !!P=x^2+x+1!! is the only one that works. (If you didn't know this, you could find out easily: a reducible polynomial of degree 2 factors into two linear factors. So the reducible polynomials are !!x^2, x·(x+1) = x^2+x!!, and !!(x+1)^2 = x^2+2x+1 = x^2+1!!. That leaves only !!x^2+x+1!!.)
To multiply two polynomials, we multiply them normally, then divide by !!x^2+x+1!! and keep the remainder. For example, what is !!(x+1)(x+1)!!? It's !!x^2+2x+1 = x^2 + 1!!. There is a theorem from elementary algebra (the “division theorem”) that we can find a unique quotient !!Q!! and remainder !!R!!, with the degree of !!R!! less than 2, such that !!PQ+R = x^2+1!!. In this case, !!Q=1, R=x!! works. (You should check this.) Since !!R=x!! this is our answer: !!(x+1)(x+1) = x!!.
Let's try !!x·x = x^2!!. We want !!PQ+R = x^2!!, and it happens that !!Q=1, R=x+1!! works. So !!x·x = x+1!!.
I strongly recommend that you calculate the multiplication table yourself. But here it is if you want to check:
$$\begin{array}{c|cccc} · & 0 & 1 & x & x+1 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & x & x+1 \\ x & 0 & x & x+1 & 1 \\ x+1 & 0 & x+1 & 1 & x \end{array} $$
To calculate the unique field !!\Bbb F_{2^3}!! of order 8, you let the elements be the 8 second-degree polynomials !!0, 1, x, \ldots, x^2+x, x^2+x+1!! and instead of reducing by !!x^2+x+1!!, you reduce by !!x^3+x+1!!. (Not by !!x^3+x^2+x+1!!, because that factors as !!(x^2+1)(x+1)!!.) To calculate the unique field !!\Bbb F_{3^2}!! of order 27, you start with the 27 third-degree polynomials with coefficients in !!{0,1,2}!!, and you reduce by !!x^3+2x+1!! (I think).
The special notation !!\Bbb F_p[x]!! means the ring of all polynomials with coefficients from !!\Bbb F_p!!. !!\langle P \rangle!! means the ring of all multiples of polynomial !!P!!. (A ring is a set with an addition, subtraction, and multiplication defined.)
When we write !!\Bbb F_p[x] / \langle P\rangle!! we are constructing a thing called a “quotient” structure. This is a generalization of the process that turns the ordinary integers !!\Bbb Z!! into the modular-arithmetic integers we have been calling !!\Bbb F_p!!. To construct !!\Bbb F_p!!, we start with !!\Bbb Z!! and then agree that two elements of !!\Bbb Z!! will be considered equivalent if they differ by a multiple of !!p!!.
To get !!\Bbb F_p[x] / \langle P \rangle!! we start with !!\Bbb F_p[x]!!, and then agree that elements of !!\Bbb F_p[x]!! will be considered equivalent if they differ by a multiple of !!P!!. The division theorem guarantees that of all the equivalent polynomials in a class, exactly one of them will have degree less than that of !!P!!, and that is the one we choose as a representative of its class and write into the multiplication table. This is what we are doing when we “divide by !!P!! and keep the remainder”.
A particularly important example of this construction is !!\Bbb R[x] / \langle x^2 + 1\rangle!!. That is, we take the set of polynomials with real coefficients, but we consider two polynomials equivalent if they differ by a multiple of !!x^2 + 1!!. By the division theorem, each polynomial is then equivalent to some first-degree polynomial !!ax+b!!.
Let's multiply $$(ax+b)(cx+d).$$ As usual we obtain $$acx^2 + (ad+bc)x + bd.$$ From this we can subtract !!ac(x^2 + 1)!! to obtain the equivalent first-degree polynomial $$(ad+bc) x + (bd-ac).$$
Now recall that in the complex numbers, !!(b+ai)(d + ci) = (bd-ac) + (ad+bc)i!!. We have just constructed the complex numbers,with the polynomial !!x!! playing the role of !!i!!.
[ Note to self: maybe write a separate article about what makes this a good answer, and how it is structured. ]
[Other articles in category /math/se] permanent link
Fri, 31 Jul 2020
What does it mean to expand a function “in powers of x-1”?
A recent Math Stack Excahnge post was asked to expand the function !!e^{2x}!! in powers of !!(x-1)!! and was confused about what that meant, and what the point of it was. I wrote an answer I liked, which I am reproducing here.
You asked:
I don't understand what are we doing in this whole process
which is a fair question. I didn't understand this either when I first learned it. But it's important for practical engineering reasons as well as for theoretical mathematical ones.
Before we go on, let's see that your proposal is the wrong answer to this question, because it is the correct answer, but to a different question. You suggested: $$e^{2x}\approx1+2\left(x-1\right)+2\left(x-1\right)^2+\frac{4}{3}\left(x-1\right)^3$$
Taking !!x=1!! we get !!e^2 \approx 1!!, which is just wrong, since actually !!e^2\approx 7.39!!. As a comment pointed out, the series you have above is for !!e^{2(x-1)}!!. But we wanted a series that adds up to !!e^{2x}!!.
As you know, the Maclaurin series works here:
$$e^{2x} \approx 1+2x+2x^2+\frac{4}{3}x^3$$
so why don't we just use it? Let's try !!x=1!!. We get $$e^2\approx 1 + 2 + 2 + \frac43$$
This adds to !!6+\frac13!!, but the correct answer is actually around !!7.39!! as we saw before. That is not a very accurate approximation. Maybe we need more terms? Let's try ten:
$$e^{2x} \approx 1+2x+2x^2+\frac{4}{3}x^3 + \ldots + \frac{8}{2835}x^9$$
If we do this we get !!7.3887!!, which isn't too far off. But it was a lot of work! And we find that as !!x!! gets farther away from zero, the series above gets less and less accurate. For example, take !!x=3.1!!, the formula with four terms gives us !!66.14!!, which is dead wrong. Even if we use ten terms, we get !!444.3!!, which is still way off. The right answer is actually !!492.7!!.
What do we do about this? Just add more terms? That could be a lot of work and it might not get us where we need to go. (Some Maclaurin series just stop working at all too far from zero, and no amount of terms will make them work.) Instead we use a different technique.
Expanding the Taylor series “around !!x=a!!” gets us a different series, one that works best when !!x!! is close to !!a!! instead of when !!x!! is close to zero. Your homework is to expand it around !!x=1!!, and I don't want to give away the answer, so I'll do a different example. We'll expand !!e^{2x}!! around !!x=3!!. The general formula is $$e^{2x} \approx \sum \frac{f^{(i)}(3)}{i!} (x-3)^i\tag{$\star$}\ \qquad \text{(when $x$ is close to $3$)}$$
The !!f^{(i)}(x)!! is the !!i!!'th derivative of !! e^{2x}!! , which is !!2^ie^{2x}!!, so the first few terms of the series above are:
$$\begin{eqnarray} e^{2x} & \approx& e^6 + \frac{2e^6}1 (x-3) + \frac{4e^6}{2}(x-3)^2 + \frac{8e^6}{6}(x-3)^3\\ & = & e^6\left(1+ 2(x-3) + 2(x-3)^2 + \frac34(x-3)^3\right)\\ & & \qquad \text{(when $x$ is close to $3$)} \end{eqnarray} $$
The first thing to notice here is that when !!x!! is exactly !!3!!, this series is perfectly correct; we get !!e^6 = e^6!! exactly, even when we add up only the first term, and ignore the rest. That's a kind of useless answer because we already knew that !!e^6 = e^6!!. But that's not what this series is for. The whole point of this series is to tell us how different !!e^{2x}!! is from !!e^6!! when !!x!! is close to, but not equal to !!3!!.
Let's see what it does at !!x=3.1!!. With only four terms we get $$\begin{eqnarray} e^{6.2} & \approx& e^6(1 + 2(0.1) + 2(0.1)^2 + \frac34(0.1)^3)\\ & = & e^6 \cdot 1.22075 \\ & \approx & 492.486 \end{eqnarray}$$
which is very close to the correct answer, which is !!492.7!!. And that's with only four terms. Even if we didn't know an exact value for !!e^6!!, we could find out that !!e^{6.2}!! is about !!22.075\%!! larger, with hardly any calculation.
Why did this work so well? If you look at the expression !!(\star)!! you can see: The terms of the series all have factors of the form !!(x-3)^i!!. When !!x=3.1!!, these are !!(0.1)^i!!, which becomes very small very quickly as !!i!! increases. Because the later terms of the series are very small, they don't affect the final sum, and if we leave them out, we won't mess up the answer too much. So the series works well, producing accurate results from only a few terms, when !!x!! is close to !!3!!.
But in the Maclaurin series, which is around !!x=0!!, those !!(x-3)^i!! terms are !!x^i!! terms intead, and when !!x=3.1!!, they are not small, they're very large! They get bigger as !!i!! increases, and very quickly. (The !! i! !! in the denominator wins, eventually, but that doesn't happen for many terms.) If we leave out these many large terms, we get the wrong results.
The short answer to your question is:
Maclaurin series are only good for calculating functions when !!x!! is close to !!0!!, and become inaccurate as !!x!! moves away from zero. But a Taylor series around !!a!! has its “center” near !!a!! and is most accurate when !!x!! is close to !!a!!.
[Other articles in category /math/se] permanent link
Wed, 29 Jul 2020Toph left the cap off one of her fancy art markers and it dried out, so I went to get her a replacement. The marker costs $5.85, plus tax, and the web site wanted a $5.95 shipping fee. Disgusted, I resolved to take my business elsewhere.
On Wednesday I drove over to a local art-supply store to get the marker. After taxes the marker was somehow around $8.50, but I also had to pay $1.90 for parking. So if there was a win there, it was a very small one.
But also, I messed up the parking payment app, which has maybe the worst UI of any phone app I've ever used. The result was a $36 parking ticket.
Lesson learned. I hope.
[Other articles in category /oops] permanent link
Today I learned:
There is a genus of ankylosaurs named Zuul after “demon and demi-god Zuul, the Gatekeeper of Gozer, featured in the 1984 film Ghostbusters”.
The type species of Zuul is Zuul crurivastator, which means “Zuul, destroyer of shins”. Wikipedia says:
The epithet … refers to a presumed defensive tactic of ankylosaurids, smashing the lower legs of attacking predatory theropods with their tail clubs.
My eight-year-old self is gratified that the ankylosaurids are believed to attack their enemies’ ankles.
The original specimen of Z. crurivastator, unusually-well preserved, was nicknamed “Sherman”.
Here is a video of Dan Aykroyd discussing the name, with Sherman.
[Other articles in category /bio] permanent link
Wed, 15 Jul 2020
More trivia about megafauna and poisonous plants
A couple of people expressed disappointment with yesterday's article, which asked were giant ground sloths immune to poison ivy?, but then failed to deliver on the implied promise. I hope today's article will make up for that.
Elephants
I said:
Mangoes are tropical fruit and I haven't been able to find any examples of Pleistocene megafauna that lived in the tropics…
David Formosa points out what should have been obvious: elephants are megafauna, elephants live where mangoes grow (both in Africa and in India), elephants love eating mangoes [1] [2] [3], and, not obvious at all…
Elephants are immune to poison ivy!
Captive elephants have been known to eat poison ivy, not just a little bite, but devouring entire vines, leaves and even digging up the roots. To most people this would have cause a horrific rash … To the elephants, there was no rash and no ill effect at all…
It's sad that we no longer have megatherium. But we do have elephants, which is pretty awesome.
Idiot fruit
The idiot fruit is just another one of those legendarily awful creatures that seem to infest every corner of Australia (see also: box jellyfish, stonefish, gympie gympie, etc.); Wikipedia says:
The seeds are so toxic that most animals cannot eat them without being severely poisoned.
At present the seeds are mostly dispersed by gravity. The plant is believed to be an evolutionary anachronism. What Pleistocene megafauna formerly dispersed the poisonous seeds of the idiot fruit?
A wombat. A six-foot-tall wombat.
I am speechless with delight.
[Other articles in category /bio] permanent link
Tue, 14 Jul 2020
Were giant ground sloths immune to poison ivy?
The skin of the mango fruit contains urushiol, the same irritating chemical that is found in poison ivy. But why? From the mango's point of view, the whole point of the mango fruit is to get someone to come along and eat it, so that they will leave the seed somewhere else. Posioning the skin seems counterproductive.
An analogous case is the chili pepper, which contains an irritating chemical, capsaicin. I think the answer here is believed to be that while capsaicin irritates mammals, birds are unaffected. The chili's intended target is birds; you can tell from the small seeds, which are the right size to be pooped out by birds. So chilis have a chemical that encourages mammals to leave the fruit in place for birds.
What's the intended target for the mango fruit? Who's going to poop out a seed the size of a mango pit? You'd need a very large animal, large enough to swallow a whole mango. There aren't many of these now, but that's because they became extinct at the end of the Pleistocene epoch: woolly mammoths and rhinoceroses, huge crocodiles, giant ground sloths, and so on. We may have eaten the animals themselves, but we seem to have quite a lot of fruits around that evolved to have their seeds dispersed by Pleistocene megafauna that are now extinct. So my first thought was, maybe the mango is expecting to be gobbled up by a giant gound sloth, and have its giant seed pooped out elsewhere. And perhaps its urushiol-laden skin makes it unpalatable to smaller animals that might not disperse the seeds as widely, but the giant ground sloth is immune. (Similarly, I'm told that goats are immune to urushiol, and devour poison ivy as they do everything else.)
Well, maybe this theory is partly correct, but even if so, the animal definitely wasn't a giant ground sloth, because those lived only in South America, whereas the mango is native to South Asia. Ground slots and avocados, yes; mangos no.
Still the theory seems reasonable, except that mangoes are tropical fruit and I haven't been able to find any examples of Pleistocene megafauna that lived in the tropics. Still I didn't look very hard.
Wikipedia has an article on evolutionary anachronisms that lists a great many plants, but not the mango.
[ Addendum: I've eaten many mangoes but never noticed any irritation from the peel. I speculate that cultivated mangoes are varieties that have been bred to contain little or no urushiol, or that there is a post-harvest process that removes or inactivates the urushiol, or both. ]
[ Addendum 20200715: I know this article was a little disappointing and that it does not resolve the question in the title. Sorry. But I wrote a followup that you might enjoy anyway. ]
[Other articles in category /bio] permanent link
Wed, 08 Jul 2020Ron Graham has died. He had a good run. When I check out I will probably not be as accomplished or as missed as Graham, even if I make it to 84.
I met Graham once and he was very nice to me, as he apparently was to everyone. I was planning to write up a reminiscence of the time, but I find I've already done it so you can read that if you care.
Graham's little book Rudiments of Ramsey Theory made a big impression on me when I was an undergraduate. Chapter 1, if I remember correctly, is a large collection of examples, which suited me fine. Chapter 2 begins by introducing a certain notation of Erdős and Rado: !!\left[{\Bbb N\atop k}\right]!! is the family of subsets of !!\Bbb N!! of size !!k!!, and
$$\left[{\Bbb N\atop k}\right] \to \left[{\Bbb N\atop k}\right]_r$$
is an abbreviation of the statement that for any !!r!!-coloring of members of !!\left[{\Bbb N\atop k}\right]!! there is always an infinite subset !!S\subset \Bbb N!! for which every member of !!\left[{S\atop k}\right]!! is the same color. I still do not find this notation perspicuous, and at the time, with much less experience, I was boggled. In the midst of my bogglement I was hit with the next sentence, which completely derailed me:
After this I could no longer think about the mathematics, but only about the sentence.
Outside the mathematical community Graham is probably best-known for juggling, or for Graham's number, which Wikipedia describes:
At the time of its introduction, it was the largest specific positive integer ever to have been used in a published mathematical proof.
One of my better Math Stack Exchange posts was in answer to the question Graham's Number : Why so big?. I love the phrasing of this question! And that, even with the strange phrasing, there is an answer! This type of huge number is quite typical in proofs of Ramsey theory, and I answered in detail.
The sense of humor that led Graham to write “danger of no confusion” is very much on display in the paper that gave us Graham's number. If you are wondering about Graham's number, check out my post.
[Other articles in category /math] permanent link
Addendum to “Weirdos during the Depression”
[ Previously ]
Ran Prieur had a take on this that I thought was insightful:
I would frame it like this: If you break rules that other people are following, you have to pretend to be unhappy, or they'll get really mad, because they don't want to face the grief that they could have been breaking the rules themselves all this time.
[Other articles in category /addenda] permanent link
Mon, 06 Jul 2020
Weird constants in math problems
Michael Lugo recently considered a problem involving the allocation of swimmers to swim lanes at random, ending with:
If we compute this for large !!n!! we get !!f(n) \sim 0.4323n!!, which agrees with the Monte Carlo simulations… The constant !!0.4323!! is $$\frac{(1-e^{-2})}2.$$
I love when stuff like this happens. The computer is great at doing a quick random simulation and getting you some weird number, and you have no idea what it really means. But mathematical technique can unmask the weird number and learn its true identity. (“It was Old Man Haskins all along!”)
A couple of years back Math Stack Exchange had Expected Number and Size of Contiguously Filled Bins, and although it wasn't exactly what was asked, I ended up looking into this question: We take !!n!! balls and throw them at random into !!n!! bins that are lined up in a row. A maximal contiguous sequence of all-empty or all-nonempty bins is called a “cluster”. For example, here we have 13 balls that I placed randomly into 13 bins:
In this example, there are 8 clusters, of sizes 1, 1, 1, 1, 4, 1, 3, 1. Is this typical? What's the expected cluster size?
It's easy to use Monte Carlo methods and find that when !!n!! is large, the average cluster size is approximately !!2.15013!!. Do you recognize this number? I didn't.
But it's not hard to do the calculation analytically and discover that that the reason it's approximately !!2.15013!! is that the actual answer is $$\frac1{2(e^{-1} - e^{-2})}$$ which is approximately !!2.15013!!.
Math is awesome and wonderful.
(Incidentally, I tried the Inverse Symbolic Calculator just now, but it was no help. It's also not in Plouffe's Miscellaneous Mathematical Constants)
[ Addendum 20200707: WolframAlpha does correctly identify the !!2.15013!! constant. ]
[Other articles in category /math] permanent link
Useful and informative article about privately funded border wall
The Philadelphia Inquirer's daily email newsletter referred me to this excellent article, by Jeremy Schwartz and Perla Trevizo.
Wow!” I said. “This is way better than the Inquirer's usual reporting. I wonder what that means?” Turns out it meant that the Inquirer was not responsible for the article. But thanks for the pointer, Inquirer folks!
The article is full of legal, political, and engineering details about why it's harder to build a border wall than I would have expected. I learned a lot! I had known about the issue that most of the land is privately owned. But I hadn't considered that there are international water-use treaties that come into play if the wall is built too close to the Rio Grande, or that the wall would be on the river's floodplain. (Or that the Rio Grande even had a floodplain.)
He built a privately funded border wall. It's already at risk of falling down if not fixed, courtesy of The Texas Tribune and ProPublica.
[Other articles in category /tech] permanent link
Wed, 24 Jun 2020
Geeking out over arbitrary boundaries
Reddit today had this delightful map, drawn by Peter Klumpenhower, of “the largest city in each 10-by-10 degree area of latitude-longitude in the world”:
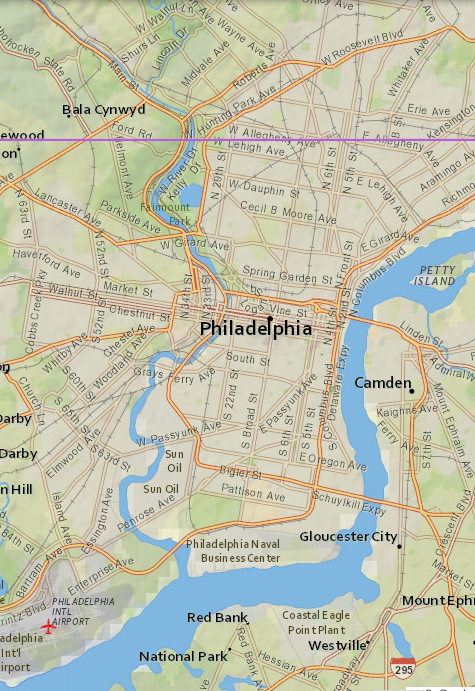
Almost every square is a kind of puzzle! Perhaps it is surprising that Philadelphia is there? Clearly New York dominates its square, but Philadelphia is just barely across the border in the next square south: the 40th parallel runs right through North Philadelphia. (See map at right.) Philadelphia City Hall (the black dot on the map) is at 39.9524 north latitude.
This reminds me of the time I was visiting Tom Christiansen in Boulder, Colorado. We were driving on Baseline Road and he remarked that it was so named because it runs exactly along the 40th parallel. Then he said “that's rather farther south than where you live”. And I said no, the 40th parallel also runs through Philadelphia! Other noteworthy cities at this latitude include Madrid, Ankara, Yerevan, and Beijing.
Anyway speaking of Boulder, the appearance of Fort Collins was the first puzzle I noticed. If you look at the U.S. cities that appear on the map, you see most of the Usual Suspects: New York, Philadelphia, Chicago, Los Angeles, Seattle, Dallas, Houston. And then you have Fort Collins.
“Fort Collins?” I said. “Why not Denver? Or even Boulder?”
Boulder, it turns out, is smaller than Fort Collins. (I did not know this.) And Denver, being on the other side of Baseline Road, doesn't compete with Fort Collins. Everything south of Baseline Road, including Denver, is shut out by Ciudad Juárez, México (population 1.5 million).
There is a Chinese version of this. The Chinese cities on the map include the big Chinese cities: Shanghai, Beijing, Chongqing, Shenzhen, Chengdu. Shenyang. A couple of cities in Inner Mongolia, analogous to the appearance of Boise on the U.S. map. And…
Wenchang. What the heck is Wenchang?
It's the county seat of Wenchang County, in Hainan, not even as important as Fort Collins. China has 352 cities with populations over 125,000. Wenchang isn't one of them. According to the list I found, Wenchang is the 379th-largest city in China. (Fort Collins, by the way, is 159th-largest in the United States. For the 379th, think of Sugar Land, Texas or Cicero, Illinois.)
Since we're in China, please notice how close Beijing is to the 40th parallel. Ten kilometers farther north and it would have displaced Boise — sorry, I meant Hohhot — and ceded its box to Tianjin (pop. 15.6 million). Similarly (but in reverse), had Philadelphia been a bit farther north, it would have disappeared into New York's box, and yielded its own box to Baltimore or Washington or some other hamlet.
Opposite to the “what the heck is?" puzzles are there “what the heck
happened to?” puzzles. Some are easier than others. It's obvious
what happened to Seoul: it's in the same box as Shanghai. The largest
missing U.S. city is Phoenix, which you can probably guess is in the same box as Los Angeles.
But what the heck happened to Nairobi? (Nairobi is the ninth-largest city in Africa. Dar Es Salaam is the sixth-largest and is in the same box.)
What the heck happened to St. Petersburg? (at 59.938N, 30.309E, it is just barely inside the same box as Moscow. The map is quite distorted in this region.)
What the heck happened to Tashkent? (It's right where it should be. I just missed it somehow.)
 There are some boxes where there just isn't much
space for cities. Some of these are obvious: most of Micronesia;
notoriously isolated places like Easter Island, Tristan Da Cunha, and
St. Helena; other islands like Ni‘ihau, Saipan, and Bermuda. But some
are less obvious. We saw Wenchang already. Most of West Falkland
Island is in the same box as
Río Gallegos, Argentina (pop.
98,000). But the capital, Stanley,
(pop. 2,460) is on the East Island, in the next box over.
There are some boxes where there just isn't much
space for cities. Some of these are obvious: most of Micronesia;
notoriously isolated places like Easter Island, Tristan Da Cunha, and
St. Helena; other islands like Ni‘ihau, Saipan, and Bermuda. But some
are less obvious. We saw Wenchang already. Most of West Falkland
Island is in the same box as
Río Gallegos, Argentina (pop.
98,000). But the capital, Stanley,
(pop. 2,460) is on the East Island, in the next box over.
 Okay, enough islands. Some of those little
towns, alone in their boxes, are on the mainland and (unlike, say, Ittoqqortoormiit) in places where
people actually live. But they just happened to get lucky and be the only town in
their box. Gabon isn't a big part of Africa.
Port-Gentil (pop. 136,462) isn't the largest city
in Gabon. But it's on the mainland of Africa and it's the largest city in its box.
Okay, enough islands. Some of those little
towns, alone in their boxes, are on the mainland and (unlike, say, Ittoqqortoormiit) in places where
people actually live. But they just happened to get lucky and be the only town in
their box. Gabon isn't a big part of Africa.
Port-Gentil (pop. 136,462) isn't the largest city
in Gabon. But it's on the mainland of Africa and it's the largest city in its box.
 I think my favorite oddity so far is that Maputo (population 2.7 million) would have won in its box,
if Durban (population 3.7 million) were 13 kilometers farther south.
But Durban is at 29.9°S, and that means that the largest settlement
in Africa east of 30°E that is also south of 30°S is
Port Shepstone (pop. 35,633).
I think my favorite oddity so far is that Maputo (population 2.7 million) would have won in its box,
if Durban (population 3.7 million) were 13 kilometers farther south.
But Durban is at 29.9°S, and that means that the largest settlement
in Africa east of 30°E that is also south of 30°S is
Port Shepstone (pop. 35,633).
[ Addendum: Reddit discussion has pointed out that Clifden (pop. 1,597) , in western Ireland, is not the largest settlement in its box. There are two slivers of Ireland in that box, and Dingle, four hours away in County Kerry, has a population of 2,050. The Reddit discussion has a few other corrections. The most important is probably that Caracas should beat out Santo Domingo. M. Klumpenhower says that they will send me a revised version of the map. ]
[ Thanks to Hacker News user oefrha for pointing out that Hohhot and Baotou are in China, not Mongolia as I originally said. ]
[ Addendum 20200627: M. Klumpenhower has sent me a revised map, which now appears in place of the old one. It corrects the errors mentioned above. Here's a graphic that shows the differences. But Walt Mankowski pointed out another possible error: The box with Kochi (southern India) should probably be owned by Colombo. ]
[Other articles in category /geo] permanent link
Thu, 11 Jun 2020
Malicious trojan horse code hidden in large patches
This article isn't going to be fun to write but I'm going to push through it because I think it's genuinely important. How often have you heard me say that?
A couple of weeks ago the Insurrection Act of 1807 was in the news. I noticed that the Wikipedia article about it contained this very strange-seeming claim:
A secret amendment was made to the Insurrection Act by an unknown Congressional sponsor, allowing such intervention against the will of state governors.
“What the heck is a ‘secret amendment’?” I asked myself. “Secret from whom? Sounds like Wikipedia crackpottery.” But there was a citation, so I could look to see what it said.
The citation is Hoffmeister, Thaddeus (2010). "An Insurrection Act for the Twenty-First Century". Stetson Law Review. 39: 898.
Sometimes Wikipedia claims will be accompanied by an authoritative-seeming citation — often lacking a page number, as this one did at the time — that doesn't actually support the claim. So I checked. But Hoffmeister did indeed make that disturbing claim:
Once finalized, the Enforcement Act was quietly tucked into a large defense authorization bill: the John Warner Defense Authorization Act of 2007. Very few people, including many members of Congress who voted on the larger defense bill, actually knew they were also voting to modify the Insurrection Act. The secrecy surrounding the Enforcement Act was so pervasive that the actual sponsor of the new legislation remains unknown to this day.
I had sometimes wondered if large, complex acts such as HIPAA or the omnibus budget acts sometimes contained provisions that were smuggled into law without anyone noticing. I hoped that someone somewhere was paying attention, so that it couldn't happen.
But apparently the answer is that it does.
[Other articles in category /law] permanent link
Wed, 10 Jun 2020
Middle English fonts and orthography
In case you're interested, here's what the Caxton “eggys” anecdote looked like originally:

2
3
4
5
6
7
8
9
10
11
12
In my dayes happened that
certain marchaȗtes were in a ship in tamyse for to haue
sayled ouer the see into zelande / and for lacke of wynde thei
taryed atte forlond. and wente to lande for to refreshe them
And one of theym named Sheffelde a mercer cam in to an
hows and axed for mete. and specyally he axyd after eggys
And the goode wyf answerde.that she coude speke no fren-
she. And the marchaȗt was angry. For he also coude speke
no frenshe. But wolde haue hadde egges / and she understode
hym not/ And thenne at laste a nother sayd he wolde
haue eyren/ then the good wyf sayd that she understod hym
wel/
It takes a while to get used to the dense black-letter font, and I think it will help to know the following:
Except at the end of a word, the letter ‘s’ is always written as the “long s”
 , ‘ſ’, which is easy
to confuse with ‘f’
, ‘ſ’, which is easy
to confuse with ‘f’  .
.Compare the ‘f’ and ‘s’ in “frenshe”
 (line 9) or “wyf sayd”
(line 9) or “wyf sayd”  (line 11).
(line 11).Some of the ‘r’s are the “rounded r”, ‘ꝛ’,
 . which looks like a ‘2’. But it
is not a ‘2’, it is an ‘r’.
. which looks like a ‘2’. But it
is not a ‘2’, it is an ‘r’.Examples include “for”
 (line 2) and “after”
(line 2) and “after”
 (line 6).
(line 6).In “marchaȗtes”
 (line 2), the mark above the ‘ȗ’ is an abbreviation for letter ‘n’ (it's
actually a tiny ‘n’), so this word is actually “marchauntes”.
Similarly “marchaȗt” in line 8 is an abbreviation for “marchaunt”.
I have written about this kind of abbreviation before:
Abbreviations in medieval manuscripts.
(line 2), the mark above the ‘ȗ’ is an abbreviation for letter ‘n’ (it's
actually a tiny ‘n’), so this word is actually “marchauntes”.
Similarly “marchaȗt” in line 8 is an abbreviation for “marchaunt”.
I have written about this kind of abbreviation before:
Abbreviations in medieval manuscripts.
[Other articles in category /IT/typo] permanent link
Tue, 09 Jun 2020
The two-bit huckster in medieval Italy
The eighth story on the seventh day of the Decameron concerns a Monna Sismonda, a young gentlewoman who is married to a merchant. She contrives to cheat on him, and then when her husband Arriguccio catches her, she manages to deflect the blame through a cunning series of lies. Arriguccio summons Sismonda's mother and brothers to witness her misbehavior, but when Sismonda seems to refute his claims, they heap abuse on him. Sismonda's mother rants about merchants with noble pretensions who marry above their station. My English translation (by G.H. McWilliam, 1972) included this striking phrase:
‘Have you heard how your poor sister is treated by this precious brother-in-law of yours? He’s a tuppenny-ha’penny pedlar, that's what he is!’
“Tuppeny-ha’penny” seemed rather odd in the context of medieval Florentines. It put me in mind of Douglas Hofstadter's complaint about an English translation of Crime and Punishment that rendered “S[toliarny] Pereulok” as “Carpenter’s Lane”:
So now we might imagine ourselves in London, … and in the midst of a situation invented by Dickens… . Is that what we want?
Intrigued by McWilliam's choice, I went to look at the other translation I had handy, John Payne's of 1886, as adapted by Cormac Ó Cuilleanáin in 2004:
‘Have you heard how your fine brother-in-law here, this two-bit huckster, is treating your sister?’
This seemed even more jarring, because Payne was English and Ó Cuilleanáin is Irish, but “two-bit” is 100% American. I wondered what the original had said.
Brown University has the Italian text online, so I didn't even have to go into the house to find out the answer:
‘Avete voi udito come il buono vostro cognato tratta la sirocchia vostra, mercatantuolo di quattro denari che egli è?’
In the coinage of the time, the denier or denarius was the penny, equal in value (at least notionally) to !!\frac1{240}!! of a pound (lira) of silver. It is the reason that pre-decimal British currency wrote fourpence as “4d.”. I think ‘-uolo’ is a diminutive suffix, so that Sismonda's mother is calling Arriguccio a fourpenny merchantling.
McWilliam’s and Ó Cuilleanáin’s translations are looking pretty good! I judged them too hastily.
While writing this up I was bothered by something else. I decided it was impossible that John Payne, in England in 1886, had ever written the words “two-bit huckster”. So I hunted up the original Payne translation from which Ó Cuilleanáin had adapted his version. I was only half right:
‘Have you heard how your fine brother-in-law here entreateth your sister? Four-farthing huckster that he is!’
“Four-farthing” is a quite literal translation of the original Italian, a farthing being an old-style English coin worth one-fourth of a penny. I was surprised to see “huckster”, which I would have guessed was 19th-century American slang. But my guess was completely wrong: “Huckster” is Middle English, going back at least to the 14th century.
In the Payne edition, there's a footnote attached to “four-farthing” that explains:
Or, in modern parlance, ‘twopenny-halfpenny.’
which is what McWilliam had. I don't know if the footnote is Payne's or belongs to the 1925 editor.
The Internet Archive's copy of the Payne translation was published in 1925, with naughty illustrations by Clara Tice. Wikipedia says “According to herself and the New York Times, in 1908 Tice was the first woman in Greenwich Village to bob her hair.”
[ Addendum 20210331: It took me until now to realize that -uolo is probably akin to the -ole suffix one finds in French words like casserole and profiterole, and derived from the Latin diminutive suffix -ulus that one finds in calculus and annulus. ]
[Other articles in category /lang] permanent link
Mon, 08 Jun 2020
More about Middle English and related issues
Quite a few people wrote me delightful letters about my recent article about how to read Middle English.
Corrections
Paul Bolle pointed out that in my map, I had put the “Zeeland” label in Belgium. Here's the corrected map:
I was so glad I had done the map in SVG! Moving the label was trivial.
I had said:
The printing press was introduced in the late 15th century, and at that point, because most books were published in or around London, the Midlands dialect used there became the standard, and the other dialects started to disappear.
But Derek Cotter pointed out the obvious fact that London is not in the Midlands; it is in the south. Whoooops. M. Cotter elaborates:
You rightly say modern English comes largely from the Midlands dialect, but London isn't in the Midlands, as your map shows; it's in the South. And the South dialects were among the losers in the standardisation of English, as your Caxton story shows: we now say Northern "eggs", not Southern "eyren". William Tyndale from Gloucestershire, Shakespeare from Warwickshire, and Dr Johnson from Staffordshire were influential in the development of modern English, along with hundreds of aristocrats, thousands of prosperous middle class, and millions of migrating workers.
I had been puzzled about schuleth, saying:
“Schuleth” goes with ‘ye’ so it ought to be ‘schulest’. I don't know what's up with that.
Derek Cotter explained my mistake: the -st suffix is only for singular thou, but ye here is plural. For comparison, consider the analogous -t in “Thou shalt not kill”. I knew this, and felt a little silly that I did not remember it.
Regarding Old English / Anglo-Saxon
- Jarkko Hietaniemi advises me to check out Simon Roper's Youtube channel for Old English, and the langfocus guy for Frisian.
Regarding Dutch
brian d foy pointed me to this video of a person trying to buy a cow from a Frisian farmer, by speaking in Old English. Friesland is up the coast from Zeeland, and approximately the original home of the Anglo-Saxon language. The attempt was successful! And the person is Eddie Izzard, who pops up in the oddest places.
I had mentioned a couple of common Middle English words that are no longer in use, and M. Bolle informed me that several are current in Modern Dutch:
Middle English eke (“almost”) is spelled ook and pronounced /oke/ in Dutch.
Wyf (“woman”) persists in Dutch as wijf, pronounced like Modern English “wife”. In Dutch this term is insulting, approximately “bitch”. (German cognates are weib (“woman”) and weibliche (“female”).)
Eyren (“eggs”). In Dutch this is eieren. (In German, one egg is ei and several is eier.) We aren't sure what the -en suffix is doing there but I speculated that it's the same plural suffix you still see only in “oxen”. (And, as Tony Finch pointed out to me, in “brethren” and “children”.) M. Bolle informs me that it is still common in Dutch.
Regarding German
My original article was about schuleþ, an old form of “shall, should”. Aristotle Pagaltzis informed me that in Modern German the word is spelled schulden, but the /d/ is very reduced, “merely hinted at in the transition between syllables”.
One trick I didn't mention in the article was that if a Middle English word doesn't seem to make sense as English, try reading it as German instead and see if that works better. I didn't bring it up because it didn't seem as helpful as the other tricks, partly because it doesn't come up that often, and mainly because you actually have to know something. I didn't want to be saying “look how easy it is to read Middle English, you just have to know German”.
Tobias Boege and I had a long discussion about the intermutations of ‘ȝ’, ‘y’, ‘g’, and ‘gh’ in English and German. M. Boege tells me:
I would just like to mention, although I suppose unrelated to the development in England, that in the Berlin/Brandenburg region close to where I live, the dialect often turns "g" into "y" sounds, for example "gestern" into "yestern".
This somewhat spreads into Saxony-Anhalt, too. While first letter "g"s turn into "y"/"j", internal ones tend to become a soft "ch". The local pronunciation of my hometown Magdeburg is close to "Mach-tte-burch".
and also brought to my attention this amusing remark about the pronounciation of ‘G’ in Magdeburg:
Man sagt, die Magdeburger sprechen das G auf fünf verschiedene Arten, aber G ist nicht dabei!
(“It is said, that the Magdeburgers pronounce the ‘G’ in five different ways, but none of them is /g/!”)
The Wikipedia article provides more details, so check it out if you read German.
It occurs to me now that the ‘G’ in Dutch is pronounced in many cases not at all as /g/, but as /ɣ/. We don't really have this sound in English, but if we did we might write it as ‘gh’, so it is yet another example of this intermutation. Dutch words with this ‘g’ include gouda and the first ‘G’ in Van Gogh.
Aristotle Pagaltzis pointed out that the singular / plural thou / ye distinction persists in Modern German. The German second person singular du is cognate with the Middle English singular thou, but the German plural is ihr.
Final note
The previous article about weirdos during the Depression hit #1 on Hacker News and was viewed 60,000 times. But I consider the Middle English article much more successful, because I very much prefer receiving interesting and thoughtful messages from six Gentle Readers to any amount of attention from Hacker News. Thanks to everyone who wrote, and also to everyone who read without writing.
[Other articles in category /lang] permanent link
Fri, 05 Jun 2020
You can learn to read Middle English
In a recent article I quoted this bit of Middle English:
Ȝelde ȝe to alle men ȝoure dettes: to hym þat ȝe schuleþ trybut, trybut.
and I said:
As often with Middle English, this is easier than it looks at first. In fact this one is so much easier than it looks that it might become my go-to example. The only strange word is schuleþ itself…
Yup! If you can read English, you can learn to read Middle English. It looks like a foreign language, but it's not. Not entirely foreign, anyway. There are tricks you can pick up. The tricks get you maybe 90 or 95% of the way there, at least for later texts, say after 1350 or so.
Disclaimer: I have never studied Middle English. This is just stuff I've picked up on my own. Any factual claims in this article might be 100% wrong. Nevertheless I have pretty good success reading Middle English, and this is how I do it.
Some quick historical notes
It helps to understand why Middle English is the way it is.
English started out as German. Old English, also called Anglo-Saxon, really is a foreign language, and requires serious study. I don't think an anglophone can learn to read it with mere tricks.
Over the centuries Old English diverged from German. In 1066 the Normans invaded England and the English language got a thick layer of French applied on top. Middle English is that mashup of English and French. It's still German underneath, but a lot of the spelling and vocabulary is Frenchified. This is good, because a lot of that Frenchification is still in Modern English, so it will be familiar.
For a long time each little bit of England had its own little dialect. The printing press was introduced in the late 15th century, and at that point, because most books were published in or around London, the Midlands dialect used there became the standard, and the other dialects started to disappear.
[ Addendum 20200606: The part about Midlands dialect is right. The part about London is wrong. London is not in the Midlands. ]
With the introduction of printing, the spelling, which had been fluid and do-as-you-please, became frozen. Unfortunately, during the 15th century, the Midlands dialect had been undergoing a change in pronunciation now called the Great Vowel Shift and many words froze with spelling and pronunciations that didn't match. This is why English vowel spellings are such a mess. For example, why are “meat” and “meet” spelled differently but pronounced the same? Why are “read” (present tense) and “read” (past tense) pronounced differently but spelled the same? In Old English, it made more sense. Modern English is a snapshot of the moment in the middle of a move when half your stuff is sitting in boxes on the sidewalk.
By the end of the 17th century things had settled down to the spelling mess that is Modern English.
The letters are a little funny
Depending on when it was written and by whom, you might see some of these obsolete letters:
Ȝ — This letter is called yogh. It's usually a ‘y’ sound, but if the word it's in doesn't make sense with a ‘y’ try pretending that it's a ‘g’ or ‘gh’ instead and see if the meaning becomes clearer. (It was originally more like a “gh-” sound. German words like gestern and garden change to yesterday and yard when they turn into English. This is also why we have words like ‘night’ that are still spelled with a ‘gh’ but is now pronounced with a ‘y’.)
þ — This is a thorn. It represents the sound we now write as th.
ð — This is an edh. This is usually also a th, but it might be a d. Originally þ and ð represented different sounds (“thin” and “this” respectively) but in Middle English they're kinda interchangeable. The uppercase version looks like Đ.
Some familiar letters behave a little differently:
u, v — Letters ‘u’ and ‘v’ are sometimes interchangeable. If there's a ‘u’ in a funny place, try reading it as a ‘v’ instead and see if it makes more sense. For example, what's the exotic-looking "haue”? When you know the trick, you see it's just the totally ordinary word “have”, wearing a funny hat.
w — When w is used as a vowel, Middle English just uses a ‘u’. For example, the word for “law” is often spelled “laue”.
y — Where Middle English uses ‘y’, we often use ‘i’. Also sometimes vice-versa.
The quotation I discussed in the earlier article looks like this:
Ȝelde ȝe to alle men ȝoure dettes: to hym þat ȝe schuleþ trybut, trybut.
Daunting, right? But it's not as bad as it looks. Let's get rid of the yoghs and thorns:
Yelde ye to alle men youre dettes: to hym that ye schuleth trybut, trybut.
The spelling is a little funny
Here's the big secret of reading Middle English: it sounds better than it looks. If you're not sure what a word is, try reading it aloud. For example, what's “alle men”? Oh, it's just “all men”, that was easy. What's “youre dettes”? It turns out it's “your debts”. That's not much of a disguise! It would be a stretch to call this “translation”.
Yelde ye to all men your debts: to him that ye schuleth trybut, trybut.
“Yelde” and “trybut” are a little trickier. As languages change, vowels nearly always change faster than consonants. Vowels in Middle English can be rather different from their modern counterparts; consonants less so. So if you can't figure out a word, try mashing on the vowels a little. For example, “much” is usually spelled “moche”.
With a little squinting you might be able to turn “trybut” into “tribute”, which is what it is. The first “tribute” is a noun, the second a verb. The construction is analogous to “if you have a drink, drink!”
I had to look up “yelde”, but after I had I felt a little silly, because it's “yield”.
Yield ye to all men your debts: to him that ye schuleth tribute, tribute.
We'll deal with “schuleth” a little later.
The word order is pretty much the same
That's because the basic grammar of English is still mostly the same as German. One thing English now does differently from German is that we no longer put the main verb at the end of the sentence. If a Middle English sentence has a verb hanging at the end, it's probably the main verb. Just interpret it as if you had heard it from Yoda.
The words are a little bit old-fashioned
… but many of them are old-fashioned in a way you might be familiar with. For example, you probably know what “ye” means: it's “you”, like in “hear ye, hear ye!” or “o ye of little faith!”.
Verbs in second person singular end in ‘-st’; in third person singular, ‘-th’. So for example:
- I read
- Thou readst
- He readeth
- I drink
- Thou drinkst
- She drinketh
In particular, the forms of “do” are: I do, thou dost, he doth.
Some words that were common in Middle English are just gone. You'll probably need to consult a dictionary at some point. The Oxford English Dictionary is great if you have a subscription. The University of Michigan has a dictionary of Middle English that you can use for free.
Here are a couple of common words that come to mind:
- eke — “also”
- wyf — “woman”
Verbs change form to indicate tense
In German (and the proto-language from which German descended), verb tense is indicated by a change in the vowel. Sometimes this persists in modern English. For example, it's why we have “drink, drank, drunk” and “sleep, slept”. In Modern German this is more common than in Modern English, and in Middle English it's also more common than it is now.
Past tense usually gets an ‘-ed’ on the end, like in Modern English.
The last mystery word here is “schuleth”:
Yield ye to all men your debts: to him that ye schuleth tribute, tribute.
This is the hard word here.
The first thing to know is that “sch-” is always pronounced “sh-” as it still is in German, never with a hard sound like “school” or “schedule”.
What's “schuleth” then? Maybe something do to with schools? It turns out not. This is a form of “shall, should” but in this context it has its old meaning, now lost, of “owe”. If I hadn't run across this while researching the history of the word “should”, I wouldn't have known what it was, and would have had to look it up.
But notice that it does follow a typical Middle English pattern: the consonants ‘sh-’ and ‘-l-’ stayed the same, while the vowels changed. In the modern word “should” we have a version of “schulen” with the past tense indicated by ‘-d’ just like usual.
“Schuleth” goes with ‘ye’ so it ought to be ‘schulest’. I don't know what's up with that.
[ Addendum 20200608: “ye” is plural, and ‘-st’ only goes on singular verbs. ]
Prose example
Let's try Wycliffe's Bible, which was written around 1380ish. This is Matthew 6:1:
Takith hede, that ye do not youre riytwisnesse bifor men, to be seyn of hem, ellis ye schulen haue no meede at youre fadir that is in heuenes.
Most of this reads right off:
Take heed, that you do not your riytwisnesse before men, to be seen of them, else you shall have no meede at your father that is in heaven.
“Take heed” is a bit archaic but still good English; it means “Be careful”.
Reading “riytwisnesse” aloud we can guess that it is actually “righteousness”. (Remember that that ‘y’ started out as a ‘gh’.)
“Schulen“ we've already seen; here it just means “shall”.
I had to look up “meede”, which seems to have disappeared since 1380. It meant “reward”, and that's exactly how the NIV translates it:
Be careful not to practice your righteousness in front of others to be seen by them. If you do, you will have no reward from your Father in heaven.
That was fun, let's do another:
Therfore whanne thou doist almes, nyle thou trumpe tofore thee, as ypocritis doon in synagogis and stretis, that thei be worschipid of men; sotheli Y seie to you, they han resseyued her meede.
The same tricks work for most of this. “Whanne” is “when”. We still have the word “almes”, now spelled “alms”: it's the handout you give to beggars. The “sch” in “worschipid” is pronounced like ‘sh’ so it's “worshipped”.
“Resseyued” looks hard, but if you remember to try reading the ‘u’ as a ‘v’ and the ‘y’ as an ‘i’, you get “resseived” which is just one letter off of “received”. “Meede” we just learned. So this is:
Therefore when you do alms, nyle thou trumpe before you, as hypocrites do in synagogues and streets, that they be worshipped by men; sotheli I say to you, they have received their reward.
Now we have the general meaning and some of the other words become clearer. What's “trumpe”? It's “trumpeting”. When you give to the needy, don't you trumpet before you, as the hypocrites do. So even though I don't know what “nyle” is exactly, the context makes it clear that it's something like “do not”. Negative words often began with ‘n’ just as they do now (no, nor, not, never, neither, nothing, etc.). Looking it up, I find that it's more usually spelled “nill”. This word is no longer used; it means the opposite of “will”. (It still appears in the phrase “willy-nilly”, which means “whether you want to or not”.)
“Sothely” means “truly”. “Soth” or “sooth” is an archaic word for truth, like in “soothsayer”, a truth-speaker.
Here's the NIV translation:
So when you give to the needy, do not announce it with trumpets, as the hypocrites do in the synagogues and on the streets, to be honored by others. Truly I tell you, they have received their reward in full.
Poetic example
Let's try something a little harder, a random sentence from The Canterbury Tales, written around 1390. Wish me luck!
We olde men, I drede, so fare we:
Til we be roten, kan we nat be rype;
We hoppen alwey whil that the world wol pype.
The main difficulty is that it's poetic language, which might be a bit obscure even in Modern English. But first let's fix the spelling of the obvious parts:
We old men, I dread, so fare we:
Til we be rotten, can we not be ripe?
We hoppen alwey whil that the world will pipe.
The University of Michigan dictionary can be a bit tricky to use. For example, if you look up “meede” it won't find it; it's listed under “mede”. If you don't find the word you want as a headword, try doing full-text search.
Anyway, hoppen is in there. It can mean “hopping”, but in this poetic context it means dancing.
We old men, I dread, so fare we:
Til we be rotten, can we not be ripe?
We dance always while the world will pipe.
“Pipe” is a verb here, it means (even now) to play the pipes.
You try!
William Caxton is thought to have been the first person to print and sell books in England. This anecdote of his is one of my favorites. He wrote it the late 1490s, at the very tail end of Middle English:
In my dayes happened that certayn marchauntes were in a shippe in Tamyse, for to haue sayled ouer the see into zelande, and for lacke of wynde thei taryed atte Forlond, and wente to lande for to refreshe them; And one of theym named Sheffelde, a mercer, cam in-to an hows and axed for mete; and specyally he axyed after eggys; and the goode wyf answerde, that she coude speke no frenshe, And the marchaunt was angry, for he also coude speke no frenshe, but wolde haue hadde ‘egges’ and she understode hym not. And theene at laste another sayd that he wolde haue ‘eyren’ then the good wyf sayd that she vnderstod hym wel.
A “mercer” is a merchant, and “taryed“ is now spelled “tarried”, which is now uncommon and means to stay somewhere temporarily.
I think the only other part of this that doesn't succumb to the tricks in this article is the place names:
- Tamyse — River Thames
- Zelande — Zeeland
- Forlond — Foreland, Kent
Caxton is bemoaning the difficulties of translating into “English” in 1490, at a time when English was still a collection of local dialects. He ends the anecdote by asking:
Loo, what sholde a man in thyse dayes now wryte, ‘egges’ or ‘eyren’?
Thanks to Caxton and those that followed him, we can answer: definitely “egges”.
[ Addenda 20200608: More about Middle English. ]
[ Addendum 20211027: An extended example of “half your stuff is sitting on the sidewalk” ]
[ Addendum 20211028: More about “eke” ]
[Other articles in category /lang] permanent link
Wed, 03 Jun 2020Lately I've been rereading To Kill a Mockingbird. There's an episode in which the kids meet Mr. Dolphus Raymond, who is drunk all the time, and who lives with his black spouse and their mixed-race kids. The ⸢respectable⸣ white folks won't associate with him. Scout and Jem see him ride into town so drunk he can barely sit on his horse. He is noted for always carrying around a paper bag with a coke bottle filled with moonshine.
At one point Mr. Dolphus Raymond offers Dill a drink out of his coke bottle, and Dill is surprised to discover that it actually contains Coke.
Mr. Raymond explains he is not actually a drunk, he only pretends to be one so that the ⸢respectable⸣ people will write him off, stay off his back about his black spouse and kids, and leave him alone. If they think it's because he's an alcoholic they can fit it into their worldview and let it go, which they wouldn't do if they suspected the truth, which is that it's his choice.
There's a whole chapter in Cannery Row on the same theme! Doc has a beard, and people are always asking him why he has a beard. Doc learned a long time ago that it makes people angry and suspicious if he tells the truth, which is he has a beard because he likes having a beard. So he's in the habit of explaining that the beard covers up an ugly scar. Then people are okay with it and even sympathetic. (There is no scar.)
Doc has a whim to try drinking a beer milkshake, and when he orders one the waitress is suspicious and wary until he explains to her that he has a stomach ulcer, and his doctor has ordered him to drink beer milkshakes daily. Then she is sympathetic. She says it's a shame about the ulcer, and gets him the milkshake, instead of kicking him out for being a weirdo.
Both books are set at the same time. Cannery Row was published in 1945 but is set during the Depression; To Kill a Mockingbird was published in 1960, and its main events take place in 1935.
I think it must be a lot easier to be a weird misfit now than it was in 1935.
[ Sort of related. ]
[ 20200708: Addendum ]
[Other articles in category /book] permanent link
Sun, 31 May 2020
Reordering git commits (not patches) with interactive rebase
This is the third article in a series. ([1] [2]) You may want to reread the earlier ones, which were in 2015. I'll try to summarize.
The original issue considered the implementation of some program feature X. In commit A, the feature had not yet been implemented. In the next commit C it had been implemented, and was enabled. Then there was a third commit, B, that left feature X implemented but disabled it:
no X X on X off
A ------ C ------ B
but what I wanted was to have the commits in this order:
no X X off X on
A ------ B ------ C
so that when X first appeared in the history, it was disabled, and then a following commit enabled it.
The first article in the series began:
I know, you want to say “Why didn't you just use
git-rebase?” Becausegit-rebasewouldn't work here, that's why.
Using interactive rebase here “to reorder B and C” will not work
because git-rebase reorders patches, not commits. It will attempt
to apply the B→C diff as a patch to A, and will fail, because
the patch is attempting to disable a feature that isn't implemented in
commit A.
My original articles described a way around this, using the plumbing
command git-commit-tree to construct the desired commits with the
desired parents. I also proposed that one could write a
git-reorder-commits command to automate the process, but my proposal
gave it a clumsy and bizarre argument convention.
Recently, Curtis Dunham wrote to me with a much better idea that uses the
interactive rebase UI to accomplish the same thing much more cleanly.
If we had B checked out and we tried git rebase -i A, we would get a
little menu like this:
pick ccccccc implement feature X
pick bbbbbbb disable feature X
As I said before, just switching the order of these two pick
commands doesn't work, because the bbbbbbb diff can't be applied on
the base commit A.
M. Dunham's suggestion is to use git-rebase -i as usual, but instead
of simply reversing the order of the two pick commands, which
doesn't work, also change them to exec git snap:
exec git snap bbbbbbb disable feature X
exec git snap ccccccc implement feature X
But what's git snap? Whereas pick means
run
git showto construct a patch from the next commit,
then apply that patch to the current tree
git snap means:
get the complete tree from the next commit,
and commit it unchanged
That is, “take a snapshot of that commit”.
It's simple to implement:
# read the tree from the some commit and store it in the index
git read-tree $SHA^{tree}
# then commit the index, re-using the old commit message
git commit -C $SHA
There needs to be a bit of cleanup to get the working tree back into
sync with the new index.
M. Dunham's actual implementation
does this with git-reset (which I'm not sure is quite sufficient),
and has some argument checking, but that's the main idea.
I hadn't know about the exec command in a git-rebase script, but
it seems like it could do all sorts of useful things. The
git-rebase man page suggests
inserting exec make at points in your script, to check that your
reordering hasn't broken the build along the way.
Thank you again, M. Dunham!
[Other articles in category /prog] permanent link
Sat, 30 May 2020Rob Hoelz mentioned that (one of?) the Nenets languages has different verb moods for concepts that in English are both indicated by “should” and “ought”:
"this is the state of the world as I assume it" vs "this is the state of the world as it currently isn't, but it would be ideal"
Examples of the former being:
- That pie should be ready to come out of the oven
- If you leave now, you should be able to catch the 8:15 to Casablanca
and of the latter:
- People should be kinder to one another
- They should manufacture these bags with stronger handles
I have often wished that English were clearer about distinguishing these. For example, someone will say to me
Using
git splurchshould fix that
and it is not always clear whether they are advising me how to fix the problem, or lamenting that it won't.
A similar issue applies to the phrase “ought to”. As far as I can tell the two phrases are completely interchangeable, and both share the same ambiguities. I want to suggest that everyone start using “should” for the deontic version (“you should go now”) and “ought to” for the predictive verion (“you ought to be able to see the lighthouse from here”) and never vice versa, but that's obviously a lost cause.
I think the original meaning of both forms is more deontic. Both words originally meant monetary debts or obligations. With ought this is obvious, at least once it's pointed out, because it's so similar in spelling and pronunciation to owed. (Compare pass, passed, past with owe, owed, ought.)
For shall, the Big Dictionary has several citations, none later than 1425 CE. One is a Middle English version of Romans 13:7:
Ȝelde ȝe to alle men ȝoure dettes: to hym þat ȝe schuleþ trybut, trybut.
As often with Middle English, this is easier than it looks at first. In fact this one is so much easier than it looks that it might become my go-to example. The only strange word is schuleþ itself. Here's my almost word-for-word translation:
Yield ye to all men your debts: to him that ye oweth tribute, pay tribute.
The NIV translates it like this:
Give to everyone what you owe them: If you owe taxes, pay taxes
Anyway, this is a digression. I wanted to talk about different kinds of should. The Big Dictionary distinguishes two types but mixes them together in its listing, saying:
In statements of duty, obligation, or propriety. Also, in statements of expectation, likelihood, prediction, etc.
The first of these seems to correspond to what I was calling the deontic form (“people should be kinder”) and the second (“you should be able to catch that train”.) But their quotations reveal several other shades of meaning that don't seem exactly like either of these:
Some men should have been women
This is not any of duty, obligation, propriety, expectation, likelihood, or prediction. But it is exactly M. Hoelz’ “state of the world as it currently isn't”.
Similarly:
I should have gotten out while I had the chance
Again, this isn't (necessarily) duty, obligation, or propriety. It's just a wish contrary to fact.
The OED does give several other related shades of “should” which are not always easy to distinguish. For example, its definition 18b says
ought according to appearances to be, presumably is
and gives as an example
That should be Barbados..unless my reckoning is far out.
Compare “We should be able to see Barbados from here”.
Its 18c is “you should have seen that fight!” which again is of the wish-contrary-to-fact type; they even gloss it as “I wish you could have…”.
Another distinction I would like to have in English is between “should” used for mere suggestion in contrast with the deontic use. For example
It's sunny out, we should go swimming!
(suggestion) versus
You should finish your homework before you play ball.
(obligation).
Say this distinction was marked in English. Then your mom might say to you in the morning
You should¹ wash the dishes now, before they get crusty
and later, when you still haven't washed the dishes:
You should² wash the dishes before you go out
meaning that you'll be in trouble if you fail in your dish washing duties.
When my kids were small I started to notice how poorly this sort of thing was communicated by many parents. They would regularly say things like
- You should be quiet now
- I need you to be quiet now
- You need to be quiet now
- You want to be quiet now
(the second one in particular) when what they really meant, it seemed to me, was “I want you to be quiet now”.
[ I didn't mean to end the article there, but after accidentally publishing it I decided it was as good a place as any to stop. ]
[Other articles in category /lang] permanent link
[ Previously ]
John Gleeson points out that my optical illusion (below left) appears to be a variation on the classic Poggendorff illusion (below right):
|
|
[Other articles in category /brain] permanent link
Fri, 29 May 2020
Infinite zeroes with one on the end
I recently complained about people who claim:
you can't have a 1 after an infinite sequence of zeroes, because an infinite sequence of zeroes goes on forever.
When I read something like this, the first thing that usually comes to mind is the ordinal number !!\omega+1!!, which is a canonical representative of this type of ordering. But I think in the future I'll bring up this much more elementary example:
$$ S = \biggl\{-1, -\frac12, -\frac13, -\frac14, \ldots, 0\biggr\} $$
Even a middle school student can understand this, and I doubt they'd be able to argue seriously that it doesn't have an infinite sequence of elements that is followed by yet another final element.
Then we could define the supposedly problematic !!0, 0, 0, \ldots, 1!! thingy as a map from !!S!!, just as an ordinary sequence is defined as a map from !!\Bbb N!!.
[ Related: A familiar set with an unexpected order type. ]
[Other articles in category /math] permanent link
A couple of years ago I wrote an article about a topological counterexample, which included this illustration:
Since then, every time I have looked at this illustration, I have noticed that the blue segment is drawn wrong. It is intended to be a portion of a radius, so if I extend it toward the center of the circle it ought to intersect the center point. But clearly, the slope is too high and the extension passes significantly below the center.
Or so it appears. I have checked the original SVG, using Inkscape to extend the blue segment: the extension passes through the center of the circle. I have also checked the rendered version of the illustration, by holding a straightedge up to the screen. The segment is pointing in the correct direction.
So I know it's right, but still I'm jarred every time I see it, because to me it looks so clearly wrong.
[ Addendum 20200530: John Gleeson has pointed out the similarity to the Poggendorff illusion. ]
[Other articles in category /brain] permanent link
Thu, 21 May 2020There have been several reports of the theft of catalytic converters in our neighborhood, the thieves going under the car and cutting the whole thing out. The catalytic converter contains a few grams of some precious metal, typically platinum, and this can be recycled by a sufficiently crooked junk dealer.
Why weren't these being stolen before? I have a theory. The catalytic converter contains only a few grams of platinum, worth around $30. Crawling under a car to cut one out is a lot of trouble and risk to go to for $30. I think the stay-at-home order has put a lot of burglars and housebreakers out of work. People aren't leaving their houses and in particular they aren't going on vacations. So thieves have to steal what they can get.
[ Addendum 20200522: An initial glance at the official crime statistics suggests that my theory is wrong. I'll try to make a report over the weekend. ]
[Other articles in category /misc] permanent link
Thu, 07 May 2020Yesterday I went through the last few months of web server logs, used them to correct some bad links in my blog articles.
Today I checked the logs again and all the "page not found" errors are caused by people attacking my WordPress and PHP installations. So, um, yay, I guess?
[Other articles in category /meta] permanent link
Tue, 05 May 2020
Article explodes at the last moment
I wrote a really great blog post over the last couple of days. Last year I posted about the difference between !!\frac10!! and !!\frac00!! and this was going to be a followup. I had a great example from linear regression, where the answer comes out as !!\frac10!! in situations where the slope of computed line is infinite (and you can fix it, by going into projective space and doing everything in homogeneous coordinates), and as !!\frac00!! in situations where the line is completely indeterminite, and you can't fix it, but instead you can just pick any slope you want and proceed from there.
Except no, it never does come out !!\frac10!!. It always comes out !!\frac00!!, even in the situations I said were !!\frac10!!.
I think maybe I can fix it though, I hope, maybe. If so, then I will be able to write a third article.
Maybe.
It could have been worse. I almost published the thing, and only noticed my huge mistake because I was going to tack on an extra section at the end that it didn't really need. When I ran into difficulties with the extra section, I was tempted to go ahead and publish without it.
[Other articles in category /oops] permanent link
Fri, 01 May 2020
More about Sir Thomas Urquhart
I don't have much to add at this point, but when I looked into Sir Thomas Urquhart a bit more, I found this amazing article by Denton Fox in London Review of Books. It's a review of a new edition of Urquhart's 1652 book The Jewel (Ekskybalauron), published in 1984. The whole article is worth reading. It begins:
Sir Thomas Urquhart … must have been a most peculiar man.
and then oh boy, does it deliver. So much of this article is quotable that I'm not sure what to quote. But let's start with:
The little we know about Urquhart’s early life comes mostly from his own pen, and is therefore not likely to be true.
Some excerpts will follow. You may enjoy reading the whole thing.
Trissotetras
I spent much way more time on this than I expected. Fox says:
In 1645 he brought out the Trissotetras … . Urquhart’s biographer, Willcock, says that ‘no one is known to have read it or to have been able to read it,’ …
Thanks to the Wonders of the Internet, a copy is available, and I have been able to glance at it. Urquhart has invented a microlanguage along the lines of Wilkins’ philosophical language, in which the words are constructed systematically. But the language of Trissotetras has a very limited focus: it is intended only for expressing statements of trigonometry. Urquhart says:
The novelty of these words I know will seeme strange to some, and to the eares of illiterate hearers sound like termes of Conjuration: yet seeing that since the very infancie of learning, such inventions have beene made use of, and new words coyned, …
The sentence continues for another 118 words but I think the point is made: the idea is not obviously terrible.
Here is an example of Urquhart's trigonometric language in action:
The second axiom is Eproso, that is, the sides are proportionall to one another as the sines of their opposite angles…
A person skilled in the art might be able to infer the meaning of this axiom from its name:
- E — a side
- Pro – proportional
- S – the sine
- O – the opposite angle
That is, a side (of a triangle) is proportional to the sine of the opposite angle. This principle is currently known as the law of sines.
Urquhart's idea of constructing mnemonic nonsense words for basic laws was not a new one. There was a long-established tradition of referring to forms of syllogistic reasoning with constructed mnemonics. For example a syllogism in “Darii” is a deduction of this form:
- All mammals have hair
- Some animals are mammals
- Therefore some animals have hair.
The ‘A’ in “Darii” is a mnemonic for the “all” clause and the ‘I’s for the “some” clauses. By memorizing a list of 24 names, one could remember which of the 256 possible deductions were valid.
Urquhart is following this well-trodden path and borrows some of its terminology. But the way he develops it is rather daunting:
The Directory of this second Axiome is Pubkegdaxesh, which declareth that there are seven Enodandas grounded on it, to wit, foure Rectangular, Upalem, Ubeman, Ekarul, Egalem, and three Obliquangular, Danarele, Xemenoro, and Shenerolem.
I think that ‘Pubkegdaxesh’ is compounded from the initial syllables of the seven enodandas, with p from upalem, ub from ubamen, k from ekarul, eg from egalem, and so on. I haven't been able to decipher any of these, although I didn't try very hard. There are many difficulties. Sometimes the language is obscure because it's obsolete and sometimes because Urquhart makes up his own words. (What does “enodandas” mean?)
Let's just take “Upalem”. Here are Urquhart's glosses:
- U – the Subtendent side
- P – Opposite, whether Angle or side
- A — an angle
- L — the secant
- E — a side
- M — A tangent complement
I believe “a tangent complement” is exactly what we would now call a cotangent; that is, the tangent of the complementary angle. But how these six items relate to one another, I do not know.
Here's another difficulty: I'm not sure that ‘al’ is one component or two. It might be one:
- U – the Subtendent side
- P – Opposite, whether Angle or side
- Al — half
- E — a side
- M — A tangent complement
Either way I'm not sure what is meant. Wait, there is a helpful diagram, and an explanation of it:
The first figure, Vale, hath but one mood, and therefore of as great extent as it selfe, which is Upalem; whose nature is to let us know, when a plane right angled triangle is given us to resolve, who subtendent and one of the obliques is proposed, and one of the ambients required, that we must have recourse unto its resolver, which being Rad—U—Sapy ☞ Yr sheweth, that if we joyne the artificiall sine of the angle opposite to the side demanded with the Logarithm of the subtendent, the summe searched in the canon of absolute numbers will afford us the Logarithm of the side required.
This is unclear but tantalizing. Urquhart is solving a problem of elementary plane trigonometry. Some of the sides and angles are known, and we are to find one of the unknown ones. I think if if I read the book from the beginning I think I might be able to make out better what Urquhart was getting at. Tempting as it is I am going to abandon it here.
Trissotetras is dedicated to Urquhart's mother. In the introduction, he laments that
Trigonometry … hath beene hitherto exposed to the world in a method whose intricacy deterreth many from adventuring on it…
He must have been an admirer of Alexander Rosse, because the front matter ends with a little poem attributed to Rosse.
Pantochronachanon
Fox again:
Urquhart, with many others, was taken to London as a prisoner, where, apparently, he determined to recover his freedom and his estates by using his pen. His first effort was a genealogy in which he names and describes his ancestors, going back to Adam. … A modern reader might think this Urquhart’s clever trick to prove that he was not guilty by reason of insanity …
This is Pantochronachanon, which Wikipedia says “has been the subject of ridicule since the time of its first publication, though it was likely an elaborate joke”, with no citation given.
Fox mentions that Urquhart claims Alcibiades as one of his ancestors. He also claims the Queen of Sheba.
According to Pantochronachanon the world was created in 3948 BC (Ussher puts it in 4004), and Sir Thomas belonged to the 153rd generation of mankind.
The Jewel
Denton Fox:
Urquhart found it necessary to try again with the Jewel, or, to to give it its full title, which in some sense describes it accurately…
EKSKUBALAURON [Εκσκυβαλαυρον]: OR, The Discovery of A most exquisite Jewel, more precious then Diamonds inchased in Gold, the like whereof was never seen in any age; found in the kennel [gutter] of Worcester-streets, the day after the Fight, and six before the Autumnal Aequinox, anno 1651. Serving in this place, To frontal a Vindication of the honour of SCOTLAND, from that Infamy, whereinto the Rigid Presbyterian party of that Nation, out of their Covetousness and ambition, most dissembledly hath involved it.
Wowzers.
Fox claims that the title Εκσκυβαλαυρον means “from dung, gold” but I do not understand why he says this. λαύρα might be a sewer or privy, and I think the word σκυβα means garden herbs. (Addendum: the explanation.)
[The book] relates how… Urquhart’s lodgings were plundered, and over 3200 sheets of his writings, in three portmanteaux, were taken.… One should remember that there is not likely to be the slightest bit of truth in this story: it speaks well for the morality of modern scholars that so many of them should have speculated why Urquhart took all his manuscripts to war with him.
Fox says that in spite of the general interest in universal languages, “parts of his prospectus must have seemed absurd even then”, quoting this item:
Three and twentiethly, every word in this language signifieth as well backward as forward; and how ever you invert the letters, still shall you fall upon significant words, whereby a wonderful facility is obtained in making of anagrams.
Urquhart boasts that where other, presumably inferior languages have only five or six cases, his language has ten “besides the nominative”. I think Finnish has fourteen but I am not sure even the Finns would be so sure that more was better. Verbs in Urquhart's language have one of ten tenses, seven moods, and four voices. In addition to singular and plural, his language has dual (like Ancient Greek) and also ‘redual’ numbers. Nouns may have one of eleven genders. It's like a language designed by the Oglaf Dwarves.
A later item states:
This language affordeth so concise words for numbering, that the number for setting down, whereof would require in vulgar arithmetick more figures in a row then there might be grains of sand containable from the center of the earth to the highest heavens, is in it expressed by two letters.
and another item claims that a word of one syllable is capable of expressing an exact date and time down to the “half quarter of the hour”. Sir Thomas, I believe that Entropia, the goddess of Information Theory, would like a word with you about that.
Wrapping up
One final quote from Fox:
In 1658, when he must have been in his late forties, he sent a long and ornately abusive letter to his cousin, challenging him to a duel at a place Urquhart would later name,
quhich shall not be aboue ane hunderethe – fourtie leagues distant from Scotland.
If the cousin would neither make amends or accept the challenge, Urquhart proposed to disperse copies of his letter
over all whole the kingdome off Scotland with ane incitment to Scullions, hogge rubbers [sheep-stealers], kenell rakers [gutter-scavengers] – all others off the meanist sorte of rascallitie, to spit in yor face, kicke yow in the breach to tred on yor mushtashes ...
Fox says “Nothing much came of this, either.”.
I really wish I had made a note of what I had planned to say about Urquhart in 2008.
[ Addendum 20200502: Brent Yorgey has explained Εκσκυβαλαυρον for me. Σκύβαλα (‘skubala’) is dung, garbage, or refuse; it appears in the original Greek text of Philippians 3:8:
What is more, I consider everything a loss because of the surpassing worth of knowing Christ Jesus my Lord, for whose sake I have lost all things. I consider them garbage, that I may gain Christ…
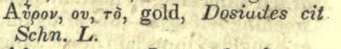
And while the usual Greek word for gold is χρῡσός (‘chrysos’), the word αύρον (‘auron’, probably akin to Latin aurum) is also gold. The screenshot at right is from the 8th edition of Liddell and Scott. Thank you, M. Yorgey! ]
[Other articles in category /book] permanent link
Thu, 30 Apr 2020
Geeky boasting about dictionaries
Yesterday Katara and I were talking about words for ‘song’. Where did ‘song’ come from? Obviously from German, because sing, song, sang, sung is maybe the perfect example of ablaut in Germanic languages. (In fact, I looked it up in Wikipedia just now and that's the example they actually used in the lede.)
But the German word I'm familiar with is Lied. So what happened there? Do they still have something like Song? I checked the Oxford English Dictionary but it was typically unhelpful. “It just says it's from Old German Sang, meaning ‘song’. To find out what happened, we'd need to look in the Oxford German Dictionary.”
Katara considered. “Is that really a thing?”
“I think so, except it's written in German, and obviously not published by Oxford.”
“What's it called?”
I paused and frowned, then said “Deutsches Wörterbuch.”
“Did you just happen to know that?”
“Well, I might be totally wrong, but yeah.” But I looked. Yeah, it's called Deutsches Wörterbuch:
The Deutsches Wörterbuch … is the largest and most comprehensive dictionary of the German language in existence. … The dictionary's historical linguistics approach … makes it to German what the Oxford English Dictionary is to English.
So, yes, I just happened to know that. Yay me!
Deutsches Wörterbuch was begun by Wilhelm and Jakob Grimm (yes, those Brothers Grimm) although the project was much too big to be finished in their lifetimes. Wilhelm did the letter ‘D’. Jakob lived longer, and was able to finish ‘A’, ‘B’, ‘C’, and ‘E’. Wikipedia mentions the detail that he died “while working on the entry for ‘Frucht’ (fruit)”.
Wikipedia says “the work … proceeded very slowly”:
Hermann Wunderlich, Hildebrand's successor, only finished Gestüme to Gezwang after 20 years of work …
(This isn't as ridiculous as it seems; German has a lot of words that begin with ‘ge-’.)
The project came to an end in 2016, after 178 years of effort. The revision of the Grimms’ original work on A–F, planned since the 1950s, is complete, and there are no current plans to revise the other letters.
[Other articles in category /lang] permanent link
Tue, 28 Apr 2020
Urquhart, Rosse, and Browne
[ Warning: I abandoned this article in 2008 and forgot that it
existed. I ran across it today and decided that what I did write was
worth publishing, although it breaks off suddenly. ]
A couple of years ago, not long before I started this blog, I read some of the works of Sir Thomas Browne. I forget exactly why: there was some footnote I read somewhere that said that something in one of Jorge Luis Borges' stories had been inspired by something he read in Browne's book The Urn Burial, which was a favorite of Borges'. I wish I could remember the details! I don't think I even remembered them at the time. But Thomas Browne turned out to be wonderful. He is witty, and learned, and wise, and humane, and to read his books is to feel that you are in the company of this witty, learned, wise, humane man, one of the best men that the English Renaissance has to offer, and that you are profiting thereby.
The book of Browne's that made the biggest impression on me was Pseudodoxia Epidemica (1646), which is a compendium of erroneous beliefs that people held at the time, with discussion. For example, is it true that chameleons eat nothing but air? ("Thus much is in plain terms affirmed by Solinus, Pliny, and others...") Browne thinks not. He cites various evidence against this hypothesis: contemporary reports of the consumption of various insects by chameleons; the presence of teeth, tongues, stomachs and guts in dissected chameleons; the presence of semi-digested insects in the stomachs of dissected chameleons. There's more; he attacks the whole idea that an animal could be nourished by air. Maybe all this seems obvious, but in 1672 it was still a matter for discussion. And Browne's discussion is so insightful, so pithy, so clear, that it is a delight to read.
Browne's list of topics is fascinating in itself. Some of the many issues he deals with are:
- That Crystall is nothing else but Ice strongly congealed;
- That a Diamond is made soft, or broke by the blood of a Goate;
- That Misseltoe is bred upon trees, from seeds which birds let fall thereon;
- That an Elephant hath no joints;
- That Snayles have two eyes, and at the end of their hornes;
- That men weigh heavier dead then alive;
- Of the pictures of Adam and Eve With Navels [a classic question, that; Saint Augustine took it up in City of God];
- Of the pictures of our Saviour with long haire;
- Of the falling of salt;
- That Children would naturally speak Hebrew [another question of perennial interest. I have heard that Frederick the Great actually made the experiment and raised children in isolation to see if they would learn Hebrew];
- Of the blacknesse of Negroes;
- That a man hath one Rib lesse then a woman;
- Of Crassus that never laughed but once;
- Of the wandring Jew;
- Of Milo, who by daylie lifting a Calfe, attained an ability to carry it being a Bull.
Well, I digress. To return to that list of topics I quoted, you might see "of the blacknesse of Negroes", and feel your heart sink a little. What racist jackass thing is the 1646 Englishman going to say about the blackness of negroes?
Actually, though, Browne comes out of it extremely well, not only much better than one would fear, but quite well even by modern standards. It is one of the more extensive discourses in Pseudodoxia Epidemica, occupying several chapters. He starts by rebutting two popular explanations: that they are burnt black by the heat of the sun, and that they are marked black because of the curse of Ham as described in Genesis 9:20–26.
Regarding the latter, Browne begins by addressing the Biblical issue directly, and on its own terms, and finds against it. But then he takes up the larger question of whether black skin can be considered to be a curse at all. Browne thinks not. He spends some time rejecting this notion: "to inferr this as a curse, or to reason it as a deformity, is no way reasonable". He points out that the people who have it don't seem to mind, and that "Beauty is determined by opinion, and seems to have no essence that holds one notion with all; that seeming beauteous unto one, which hath no favour with another; and that unto every one, according as custome hath made it natural, or sympathy and conformity of minds shall make it seem agreeable."
Finally, he ends by complaining that "It is a very injurious method unto Philosophy, and a perpetual promotion of Ignorance, in points of obscurity, ... to fall upon a present refuge unto Miracles; or recurr unto immediate contrivance, from the insearchable hands of God." I wish more of my contemporaries agreed.
Another reason I love this book is that Browne is nearly always right. If you were having doubts that one could arrive at correct notions by thoughtful examination of theory and evidence, Pseudodoxia Epidemica might help dispel them, because Browne's record of coming to the correct conclusions is marvelous.
Some time afterward, I learned that there was a rebuttal to Pseudodoxia Epidemica, written by a Dr. Alexander Rosse. (Arcana Microcosmi, ... with A Refutation of Doctor Brown's VULGAR ERRORS... (1652).) And holy cow, Rosse is an incredible knucklehead. Watching him try to argue with Browne reminded me of watching an argument on Usenet (a sort of pre-Internet distributed BBS) where one person is right about everything, and is being flamed point by point by some jackass who is wrong about everything, and everyone but the jackass knows it. I have seen this many, many times on Usenet, but never as far back as 1652.
This is the point at which I stopped writing the article in 2008. I had mentioned the blockheaded Mr. Rosse in an earlier article. But I have no idea what else I had planned to say about him here.
Additional notes (April 2020)
- I mentioned “the table of contents from Richard Waller's
Posthumous Works of Robert Hooke”. I had mentioned Waller
previously, in connection with Hooke's measurement of the rate at
which a fly beats its wings. The Waller book is
available on the Internet Archive, but
it does not have a table of contents! I realize I had actually been
thinking of Hooke’s Philosophical Experiments and
Observations, edited by William Derham, which in some editions, does have a table
of contents. The Derham book made a couple of other appearances
in this blog in the early days.
- I no longer have any idea who Urquhart was, or what I had planned to
say about him. Searching for him in conjunction with Browne I find he was Sir Thomas Urquhart, a contemporary of
Browne's. There is a Wikipedia
article about Urquhart. Like his better-known contemporary John
Wilkins, he tried to design a universal language in which the meaning
of a word could be inferred from its spelling.
- I learned that Rosse was
the target of sarcastic mockery in Samuel Butler's Hudibras:
There was an ancient sage philosopher
It seems that Rosse was a noted dumbass even in his own lifetime.
Who had read Alexander Ross over. - John Willcock's biography of Urquhart says “Ross himself is now only
known to most of us from the mention made of him in
Hudibras”, and that was in 1899.
- Thomas Browne is the source of the often-quoted suggestion that:
What song the Sirens sang, or what name Achilles assumed when he hid himself among women, though puzzling questions, are not beyond all conjecture.
(It appears in his book Hydrotaphia, or Urn Buriall.) This hopeful talisman has inspired many people over the centuries to continue their pursuit of such puzzling questions, sometimes when faced with what seems like a featureless wall of lost history. - A few years later I revisited Milo, who by daylie lifting a Calfe, attained an ability to carry it being a Bull.
[Other articles in category /book] permanent link
Sun, 26 Apr 2020I ran into this album by Jools Holland:

What do you see when you look at this? If you're me, you spend a few minutes wondering why there is a map of Delaware.
[ Addendum 20250203: Another example, this time a little closer to home. ]
[Other articles in category /misc] permanent link
Fri, 24 Apr 2020
Tiers of answers to half-baked questions
[ This article is itself somewhat half-baked. ]
There's this thing that happens on Stack Exchange sometimes. A somewhat-clueless person will show up and ask a half-baked question about something they are thinking about. Their question is groping toward something sensible but won't be all the way there, and then several people will reply saying no, that is not sensible, your idea is silly, without ever admitting that there is anything to the idea at all.
I have three examples of this handy, and I'm sure I could find many more.
One recent one concerns chirality (handedness) in topology. OP showed up to ask why a donut seems to be achiral while a coffee cup is chiral (because the handle is on one side and not the other). Some people told them that the coffee cup is actually achiral and some others people told them that topology doesn't distinguish between left- and right-handed objects, because reflection is a continuous transformation. (“From a topological point of view, no object is distinguishable from its mirror image”.) I've seen many similar discussions play out the same way in the past.
But nobody (other than me) told them that there is a whole branch of topology, knot theory, where the difference between left- and right-handed objects is a major concern. Everyone else was just acting like this was a nonissue.
This category theory example is somewhat more obscure.
In category theory one can always turn any construction backward to make a “dual” construction, and the “dual” construction is different but usually no less interesting than the original. For example, there is a category-theoretic construction of “product objects”, which generalizes cartesian products of sets, topological product spaces, the direct product of groups, and so on. The dual construction is “coproduct objects” which corresponds to the disjoint union of sets and topological spaces, and to the free product of groups.
There is a standard notion of an “exponential object” and OP wanted to know about the dual notion of a “co-exponential object”. They gave a proposed definition of such an object, but got their proposal a little bit wrong, so that what they had defined was not the actual co-exponential object but instead was trivial. Two other users pointed out in detail why their proposed construction was uninteresting. Neither one pointed out that there is a co-exponential object, and that it is interesting, if you perform the dualization correctly.
(The exponential object concerns a certain property of a mapping !!f :A×B\to C!!. OP asked insead about !!f : C\to A× B!!. Such a mapping can always be factored into a product !!(f_1: C\to A)×(f_2: C\to B)!! and then the two factors can be treated independently. The correct dual construction concerns a property of a mapping !!f : C\to A\sqcup B!!, where !!\sqcup!! is the coproduct. This admits no corresponding simplification.)
A frequently-asked question is (some half-baked variation on) whether there is a smallest positive real number. Often this is motivated by the surprising fact that !!0.9999\ldots = 1!!, and in an effort to capture their intuitive notion of the difference, sometimes OP will suggest that there should be a number !!0.000\ldots 1!!, with “an infinite number of zeroes before the 1”.
There is no such real number, but the question is a reasonable one to ask and to investigate. Often people will dismiss the question claiming that it does not make any sense at all, using some formula like “you can't have a 1 after an infinite sequence of zeroes, because an infinite sequence of zeroes goes on forever.”. Mathematically, this response is complete bullshit because mathematicians are perfectly comfortable with the idea of an infinite sequence that has one item (or more) appended after the others. (Such an object is said to “have order type !!\omega + 1!!”, and is completely legitimate.) The problem isn't with the proposed object itself, but with the results of the attempt to incorporate it into the arithmetic of real numbers: what would you get, for example, if you tried to multiply it by !!10!!?
Or sometimes one sees answers that go no further than “no, because the definition of a real number is…”. But a better engagement with the question would recognize that OP is probably interested in alternative definitions of real numbers.
In a recent blog article I proposed a classification of answers to certain half-baked software questions (“Is it possible to do X?”):
- It surely could, but nobody has done it yet
- It perhaps could, but nobody is quite sure how
- It maybe could, but what you want is not as clear as you think
- It can't, because that is impossible
- I am not able rightly to apprehend the kind of confusion of ideas that could provoke such a question
and I said:
Often, engineers will go straight to #5, when actually the answer is in a higher tier. Or they go to #4 without asking if maybe, once the desiderata are clarified a bit, it will move from “impossible” to merely “difficult”. These are bad habits.
These mathematically half-baked questions also deserve better answers. A similar classification of answers to “can we do this” might look like this:
- Yes, that is exactly what we do, only more formally. You can find out more about the details in this source…
- Yes, we do something very much like that, but there are some significant differences to address points you have not considered…
- Yes, we might like to do something along those lines, but to make it work we need to make some major changes…
- That seems at first like a reasonable thing to try, but if you look more deeply you find that it can't be made to work, because…
- I am not able rightly to apprehend the kind of confusion of ideas that could provoke such a question
The category theory answer was from tier 4, but should have been from tier 2. People asking about !!0.0000…1!! often receive answers from tier 5, but ought to get answers from tier 4, or even tier 3, if you wanted to get into nonstandard analysis à la Robinson.
There is a similar hierarchy for questions of the type “can we model this concept mathematically”, ranging from “yes, all the time” through “nobody has figured that out yet” and “it seems unlikely, because”, to “what would that even mean?”. The topological chirality question was of this type and the answers given were from the “no we can't and we don't” tiers, when they could have been from a much higher tier: “yes, it's more complicated than that but there is an entire subfield devoted to dealing with it.”
This is a sort of refinement of the opposition of “yes, and…” versus “no, but…”, with the tiers something like:
- Yes, and…
- Yes, but…
- Perhaps, if…
- No, but…
- No, because…
- I am embarrassed for you
When formulating the answer to a question, aiming for the upper tiers usually produces more helpful, more useful, and more interesting results.
[ Addendum 20200525: Here's a typical dismissal of the !!0.\bar01!! suggestion: “This is confusing because !!0.\bar01!! seems to indicate a decimal with ‘infinite zeros and then a one at the end.’ Which, of course, is absurd.” ]
[ Addendum 20230421: Another example, concerning “almost orthogonal” unit vectors ]
[Other articles in category /misc] permanent link
Wed, 22 Apr 2020This morning I got spam with this subject:
Subject: yaxşı xəbər
Now what language is that? The ‘şı’ looks Turkish, but I don't think Turkish has a letter ‘ə’. It took me a little while to find out the answer.
Bonus trivia: The official Unicode name of ‘ƣ’ is
LATIN SMALL LETTER OI.
Unicode Technical Note #27 says:
These should have been called letter GHA. They are neither pronounced 'oi' nor based on the letters 'o' and 'i'.
[ Addendum 20210215: I was pleased to discover today that I have not yet forgotten what Azeri looks like. ]
[ Addendum 20230731: Another mystery language sample. ]
[Other articles in category /lang] permanent link
Dave Turner pointed me to the 1939 Russian-language retelling of The Wizard of Oz, titled The Wizard of the Emerald City. In Russian the original title was Волшебник Изумрудного Города. It's fun to try to figure these things out. Often Russian words are borrowed from English or are at least related to things I know but this one was tricky. I didn't recognize any of the words. But from the word order I'd expect that Волшебник was the wizard. -ого is a possessive ending so maybe Изумрудного is “of emeralds”? But Изумрудного didn't look anything like emeralds… until it did.
Изумрудного is pronounced (approximately) “izumrudnogo”. But “emerald” used to have an ‘s’ in it, “esmerald”. (That's where we get the name “Esmeralda”.) So the “izumrud” is not that far off from “esmerad” and there they are!
[Other articles in category /lang] permanent link
Fri, 17 Apr 2020In my previous article I claimed
the oldest known metaphorical use of “dumpster fire” is in reference to the movie Shrek the Third.
However, this is mistaken. Eric Harley has brought to my attention that the phrase was used as early as 2003 to describe The Texas Chainsaw Massacre. According to this Salt Lake Tribune article:
One early use found by Oxford Dictionaries' Jeff Sherwood was a 2003 movie review by the Arizona Republic's Bill Muller that referred to that year's remake of "The Texas Chainsaw Massacre" as "the cinematic equivalent of a dumpster fire — stinky but insignificant."
If Sherwood is affiliated with Oxford Dictionaries, I wonder why this citation hasn't gotten into the Big Dictionary. The Tribune also pointed me to Claire Fallon's 2016 discussion of the phrase.
Thank you, M. Harley.
[Other articles in category /lang] permanent link
Thu, 16 Apr 2020Today I learned that the oldest known metaphorical use of “dumpster fire” (to mean “a chaotic or disastrously mishandled situation”) is in reference to the movie Shrek the Third.
The OED's earliest citation is from
a 2008 Usenet post,
oddly in rec.sport.pro-wrestling. I looked in Google Book search
for an earlier one, but everything I found was about literal
dumpster fires.
I missed the movie, and now that I know it was the original Dumpster Fire, I feel lucky.
[ Addendum 20200417: More about this. ]
[Other articles in category /lang] permanent link
Tue, 07 Apr 2020
Fern motif experts on the Internet
I live near Woodlands Cemetery and by far the largest monument there, a thirty-foot obelisk, belongs to Thomas W. Evans, who is an interesting person. In his life he was a world-famous dentist, whose clients included many crowned heads of Europe. He was born in Philadelphia, and land to the University of Pennsylvania to found a dental school, which to this day is located at the site of Evans’ former family home at 40th and Spruce Street.
A few days ago my family went to visit the cemetery and I insisted on visting the Evans memorial.
The obelisk has this interesting ornament:
The thing around the middle is evidently a wreath of pine branches, but what is the thing in the middle? Some sort of leaf, or frond perhaps? Or is it a feather? If Evans had been a writer I would have assumed it was a quill pen, but he was a dentist. Thanks to the Wonders of the Internet, I was able to find out.
First I took the question to Reddit's /r/whatisthisthing forum. Reddit didn't have the answer, but Reddit user @hangeryyy had something better: they observed that there was a fad for fern decorations, called pteridomania, in the second half of the 19th century. Maybe the thing was a fern.
I was nerdsniped by pteridomania and found out that a book on pteridomania had been written by Dr. Sarah Whittingham, who goes by the encouraging Twitter name of @DrFrond.
Dr. Whittingham's opinion is that this is not a fern frond, but a palm frond. The question has been answered to my full and complete satisfaction.
My thanks to Dr. Whittingham, @hangeryyy, and the /r/whatisthisthing community.
[Other articles in category /art] permanent link
Mon, 06 Apr 2020
Anglo-Saxon and Hawai‘ian Wikipedias
Yesterday browsing the list of Wikipedias I learned there is an Anglo-Saxon Wikipedia. This seems really strange to me for several reasons: Who is writing it? And why?
And there is a vocabulary problem. Not just because Anglo-Saxon is dead, and one wouldn't expect it to have any words for anything not invented in the last 900 years or so. But also, there are very few extant Anglo-Saxon manuscripts, so we don't have a lot of vocabulary, even for things that had been invented beore the language died.
Helene Hanff said:
I have these guilts about never having read Chaucer but I was talked out of learning Early Anglo-Saxon / Middle English by a friend who had to take it for her Ph.D. They told her to write an essay in Early Anglo-Saxon on any-subject-of-her-own-choosing. “Which is all very well,” she said bitterly, “but the only essay subject you can find enough Early Anglo-Saxon words for is ‘How to Slaughter a Thousand Men in a Mead Hall’.”
I don't read Anglo-Saxon but if you want to investigate, you might look at the Anglo-Saxon article about the Maybach Exelero (a hēahfremmende sportƿægn), Barack Obama, or taekwondo. I am pre-committing to not getting sucked into this, but sportƿægn is evidently intended to mean “sportscar” (the ƿ is an obsolete letter called wynn and is approximately a W, so that ƿægn is “wagon”) and I think that fremmende is “foreign” and hēah is something like "high" or "very". But I'm really not sure.
Anyway Wikipedia reports that the Anglo-Saxon Wikipedia has 3,197 articles (although most are very short) and around 30 active users. In contrast, the Hawai‘ian Wikipedia has 3,919 articles and only around 14 active users, and that is a language that people actually speak.
[Other articles in category /lang] permanent link
Caricatures of Nazis and the number four in Russian
[ Warning: this article is kinda all over the place. ]
I was looking at this awesome poster of D. Moor (Д. Моор), one of Russia's most famous political poster artists:
(original source at Artchive.RU)
This is interesting for a couple of reasons. First, in Russian, “Himmler”, “Göring”, “Hitler”, and “Goebbels” all begin with the same letter, ‘Г’, which is homologous to ‘G’. (Similarly, Harry Potter in Russian is Га́рри, ‘Garri’.)
I also love the pictures, and especially Goebbels. These four men were so ugly, each in his own distinctively loathsome way. The artist has done such a marvelous job of depicting them, highlighting their various hideousness. It's exaggerated, and yet not unfair, these are really good likenesses! It's as if D. Moor had drawn a map of all the ways in which these men were ugly.
My all-time favorite depiction of Goebbels is this one, by Boris Yefimov (Бори́с Ефи́мов):
For comparison, here's the actual Goebbels:
Looking at pictures of Goebbels, I had often thought “That is one ugly guy,” but never been able to put my finger on what specifically was wrong with his face. But since seeing the Yefimov picture, I have never been able to look at a picture of Goebbels without thinking of a rat. D. Moor has also drawn Goebbels as a tiny rat, scurrying around the baseboards of his poster.
Anyway, that was not what I had planned to write about. The right-hand side of D. Moor's poster imagines the initial ‘Г’ of the four Nazis’ names as the four bent arms of the swastika. The captions underneath mean “first Г”, “second Г” and so on.
[ Addendum: Darrin Edwards explains the meaning here that had escaped me:
One of the Russian words for shit is "govno" (говно). A euphemism for this is to just use the initial g; so "something na g" is roughly equivalent to saying "a crappy something". So the title "vse na g" (all on g) is literally "they all start with g" but pretty blatantly means "they're all crap" or "what a bunch of crap". I believe the trick of constructing the swastika out of four g's is meant to extend this association from the four men to the entire movement…
Thank you, M. Edwards! ]
Looking at the fourth one, четвертое /chetvyertoye/, I had a sudden brainwave. “Aha,” I thought, “I bet this is akin to Greek “tetra”, and the /t/ turned into /ch/ in Russian.”
Well, now that I'm writing it down it doesn't seem that exciting. I now remember that all the other Russian number words are clearly derived from PIE just as Greek, Latin, and German are:
| English | German | Latin | Greek | Russian |
|---|---|---|---|---|
| one | ein | unum | εἷς (eis) | оди́н (odeen) |
| two | zwei | duo | δύο (dyo) | два (dva) |
| three | drei | trēs | τρεῖς (treis) | три (tri) |
| four | vier | quattuor | τέτταρες (tettares) | четы́ре (chyetirye) |
| five | fünf | quinque | πέντε (pente) | пять (pyat’) |
In Latin that /t/ turned into a /k/ and we get /quadra/ instead of /tetra/. The Russian Ч /ch/ is more like a /t/ than it is like a /k/.
The change from /t/ to /f/ in English and /v/ in German is a bit weird. (The Big Dictionary says it “presents anomalies of which the explanation is still disputed”.) The change from the /p/ of ‘pente’ to the /f/ of ‘five’ is much more typical. (Consider Latin ‘pater’, ‘piscum’, ‘ped’ and the corresponding English ‘father’, ‘fish’, ‘foot’.) This is called Grimm's Law, yeah, after that Grimm.
The change from /q/ in quinque to /p/ in pente is also not unusual. (The ancestral form in PIE is believed to have been more like the /q/.) There's a classification of Celtic lanugages into P-Celtic and Q-Celtic that's similar, exemplified by the change from the Irish patronymic prefix Mac- into the Welsh patronymic map or ap.
I could probably write a whole article comparing the numbers from one to ten in these languages. (And Sanskrit. Wouldn't want to leave out Sanskrit.) The line for ‘two’ would be a great place to begin because all those words are basically the same, with only minor and typical variations in the spelling and pronunciation. Maybe someday.
Addendum 20250215
I don't know much Polish, but having written this article I could read one word of this remark, enough to get the overall sense!
[Other articles in category /lang/etym] permanent link
Sun, 05 Apr 2020
Screensharing your talk slides is skeuomorphic
Back when the Web was much newer, and people hadn't really figured it out yet, there was an attempt to bring a dictionary to the web. Like a paper dictionary, its text was set in a barely-readable tiny font, and there were page breaks in arbitrary places. That is a skeuomorph: it's an incidental feature of an object that persists even in a new medium where the incidental feature no longer makes sense.
Anyway, I was scheduled to give a talk to the local Linux user group last week, and because of current conditions we tried doing it as a videoconference. I thought this went well!
We used Jitsi Meet, which I thought worked quite well, and which I recommend.
The usual procedure is for the speaker to have some sort of presentation materials, anachronistically called “slides”, which they display one at a time to the audience. In the Victorian age these were glass plates, and the image was projected on a screen with a slide projector. Later developments replaced the glass with celluloid or other transparent plastic, and then with digital projectors. In videoconferences, the slides are presented by displaying them on the speaker's screen, and then sharing the screen image to the audience.
This last development is skeuomorphic. When the audience is together in a big room, it might make sense to project the slide images on a shared screen. But when everyone is looking at the talk on their own separate screen anyway, why make them all use the exact same copy?
Instead, I published the slides on my website ahead of time, and sent the link to the attendees. They had the option to follow along on the web site, or to download a copy and follow along in their own local copy.
This has several advantages:
Each audience person can adjust the monitor size, font size, colors to suit their own viewing preferences.
With the screenshare, everyone is stuck with whatever I have chosen. If my font is too small for one person to read, they are out of luck.
The audience can see the speaker. Instead of using my outgoing video feed to share the slides, I could share my face as I spoke. I'm not sure how common this is, but I hate attending lectures given by disembodied voices. And I hate even more being the disembodied voice. Giving a talk to people I can't see is creepy. My one condition to the Linux people was that I had to be able to see at least part of the audience.
With the slides under their control, audience members can go back to refer to earlier material, or skip ahead if they want. Haven't you had the experience of having the presenter skip ahead to the next slide before you had finished reading the one you were looking at? With this technique, that can't happen.
Some co-workers suggested the drawback that it might be annoying to try to stay synchronized with the speaker. It didn't take me long to get in the habit of saying “Next slide, #18” or whatever as I moved through the talk. If you try this, be sure to put numbers on the slides! (This is a good practice anyway, I have found.) I don't know if my audience found it annoying.
The whole idea only works if you can be sure that everyone will have suitable display software for your presentation materials. If you require WalSoft AwesomePresent version 18.3, it will be a problem. But for the past 25 years I have made my presentation materials in HTML, so this wasn't an issue.
If you're giving a talk over videoconference, consider trying this technique.
[ Addendum: I should write an article about all the many ways in which the HTML has been a good choice. ]
[ Addendum 20201102: I implemented a little software system,
page-turner, that
addresses my co-workers’ objections that it might be annoying to try
to stay synchronized with the speaker. The little system
automatically keeps the pages synchronized with the presenter, except
when attendee doesn't want that. I wrote a followup blog post about
page-turner. ]
[Other articles in category /talk] permanent link
Fri, 27 Mar 2020Last week Pierre-Françoys Brousseau and I invented a nice chess variant that I've never seen before. The main idea is: two pieces can be on the same square. Sometimes when you try to make a drastic change to the rules, what you get fails completely. This one seemed to work okay. We played a game and it was fun.
Specfically, our rules say:
All pieces move and capture the same as in standard chess, except:
Up to two pieces may occupy the same square.
A piece may move into an occupied square, but not through it.
A piece moving into a square occupied by a piece of the opposite color has the option to capture it or to share the square.
Pieces of opposite colors sharing a square do not threaten one another.
A piece moving into a square occupied by two pieces of the opposite color may capture either, but not both.
Castling is permitted, but only under the same circumstances as standard chess. Pieces moved during castling must move to empty squares.
Miscellaneous notes
Pierre-Françoys says he wishes that more than two pieces could share a square. I think it could be confusing. (Also, with the chess set we had, more than two did not really fit within the physical confines of the squares.)
Similarly, I proposed the castling rule because I thought it would be less confusing. And I did not like the idea that you could castle on the first move of the game.
The role of pawns is very different than in standard chess. In this variant, you cannot stop a pawn from advancing by blocking it with another pawn.
Usually when you have the chance to capture an enemy piece that is alone on its square you will want to do that, rather than move your own piece into its square to share space. But it is not hard to imagine that in rare circumstances you might want to pick a nonviolent approach, perhaps to avoid a stalemate.
Some discussion of similar variants is on Chess Stack Exchange.
The name “Pauli Chess”, is inspired by the Pauli exclusion principle, which says that no more than two electrons can occupy the same atomic orbital.
[Other articles in category /games] permanent link
Tue, 24 Mar 2020
git log --author=... confused me
Today I was looking for recent commits by co worker Fred Flooney,
address fflooney@example.com, so I did
git log --author=ffloo
but nothing came up. I couldn't remember if --author would do a
substring search, so I tried
git log --author=fflooney
git log --author=fflooney@example.com
and still nothing came up. “Okay,” I said, “probably I have Fred's address wrong.” Then I did
git log --format=%ae | grep ffloo
The --format=%ae means to just print out commit author email
addresses, instead of the usual information. This command did
produce many commits with the author address
fflooney@example.com.
I changed this to
git log --format='%H %ae' | grep ffloo
which also prints out the full hash of the matching commits. The first one was 542ab72c92c2692d223bfca4470cf2c0f2339441.
Then I had a perplexity. When I did
git log -1 --format='%H %ae' 542ab72c92c2692d223bfca4470cf2c0f2339441
it told me the author email address was
fflooney@example.com. But when I did
git show 542ab72c92c2692d223bfca4470cf2c0f2339441
the address displayed was fredf@example.com.
The answer is, the repository might have a file in its root named
.mailmap that says “If you see this name and address, pretend you
saw this other name and address instead.” Some of the commits really
had been created with the address I was looking for, fflooney. But
the .mailmap said that the canonical version of that address was
fredf@. Nearly all Git operations use the canonical address. The
git-log --author option searches the canonical address, and
git-show and git-log, by default, display the canonical address.
But my --format=%ae overrides the default behavior; %ae explicitly
requests the actual address. To display the canonical address, I
should have used --format=%aE instead.
Also, I learned that --author= does not only a substring search but
a regex search. I asked it for --author=d* and was puzzled when
it produced commits written by people with no d. This is a beginner
mistake: d* matches zero or more instances of d, and every name
contains zero or more instances of d. (I had thought that the *
would be like a shell glob.)
Also, I learned that --author=d+ matches only authors that contain
the literal characters d+. If you want the + to mean “one or
more” you need --author=d\+.
Thanks to Cees Hek, Gerald Burns, and Val Kalesnik for helping me get to the bottom of this.
The .mailmap thing is documented in
git-check-mailmap.
[ Addendum: I could also have used git-log --no-use-mailmap ...,
had I known about this beforehand. ]
[Other articles in category /prog] permanent link
Sun, 16 Feb 2020Over on the other blog I said “Midichlorians predated The Phantom Menace.” No, the bacterium was named years after the movie was released.
Thanks to Eyal Joseph Minsky-Fenick and Shreevatsa R. for (almost simultaneously) pointing out this mistake.
[Other articles in category /oops] permanent link
Thu, 13 Feb 2020
Gentzen's rules for natural deduction
Here is Gerhard Gentzen's original statement of the rules of Natural Deduction (“ein Kalkül für ‘natürliche’, intuitionistische Herleitungen”):
Natural deduction looks pretty much exactly the same as it does today, although the symbols are a little different. But only a little! Gentzen has not yet invented !!\land!! for logical and, and is still using !!\&!!. But he has invented !!\forall!!. The style of the !!\lnot!! symbol is a little different from what we use now, and he has that tent thingy !!⋏!! where we would now use !!\bot!!. I suppose !!⋏!! didn't catch on because it looks too much like !!\land!!. (He similarly used !!⋎!! to mean !!\top!!, but as usual, that doesn't appear in the deduction rules.)
We still use Gentzen's system for naming the rules. The notations “UE” and “OB” for example, stand for “und-Einführung” and “oder-Beseitigung”, which mean “and-introduction” and “or-elimination”.
Gentzen says (footnote 4, page 178) that he got the !!\lor, \supset, \exists!! signs from Russell, but he didn't want to use Russell's signs !!\cdot, \equiv, \sim, ()!! because they already had other meanings in mathematics. He took the !!\&!! from Hilbert, but Gentzen disliked his other symbols. Gentzen objected especially to the “uncomfortable” overbar that Hilbert used to indicate negation (“[Es] stellt eine Abweichung von der linearen Anordnung der Zeichen dar”). He attributes his symbols for logical equivalence (!!\supset\subset!!) and negation to Heyting, and explains that his new !!\forall!! symbol is analogous to !!\exists!!. I find it remarkable how quickly this caught on. Gentzen also later replaced !!\&!! with !!\land!!. Of the rest, the only one that didn't stick was !!\supset\subset!! in place of !!\equiv!!. But !!\equiv!! is much less important than the others, being merely an abbreviation.
Gentzen died at age 35, a casualty of the World War.
Source: Gerhard Gentzen, “Untersuchungen über das logische Schließen I”, pp. 176–210 Mathematische Zeitschrift v. 39, Springer, 1935. The display above appears on page 186.
[ Addendum 20200214: Thanks to Andreas Fuchs for correcting my German grammar. ]
[Other articles in category /math/logic] permanent link
Thu, 06 Feb 2020
Major screwups in mathematics: example 3
[ Previously: “Cases in which some statement S was considered to be proved, and later turned out to be false”. ]
In 1905, Henri Lebesgue claimed to have proved that if !!B!! is a subset of !!\Bbb R^2!! with the Borel property, then its projection onto a line (the !!x!!-axis, say) is a Borel subset of the line. This is false. The mistake was apparently noticed some years later by Andrei Souslin. In 1912 Souslin and Luzin defined an analytic set as the projection of a Borel set. All Borel sets are analytic, but, contrary to Lebesgue's claim, the converse is false. These sets are counterexamples to the plausible-seeming conjecture that all measurable sets are Borel.
I would like to track down more details about this. This Math Overflow post summarizes Lebesgue's error:
It came down to his claim that if !!{A_n}!! is a decreasing sequence of subsets in the plane with intersection !!A!!, the projected sets in the line intersect to the projection of !!A!!. Of course this is nonsense. Lebesgue knew projection didn't commute with countable intersections, but apparently thought that by requiring the sets to be decreasing this would work.
[Other articles in category /math] permanent link
Tue, 28 Jan 2020Today I learned that James Blaine (U.S. Speaker of the House, senator, perennial presidential candidate, and Secretary of State under Presidents Cleveland, Garfield, and Arthur; previously) was the namesake of the notorious “Blaine Amendments”. These are still an ongoing legal issue!
The Blaine Amendment was a proposed U.S. constitutional amendment rooted in anti-Catholic, anti-immigrant sentiment, at a time when the scary immigrant bogeymen were Irish and Italian Catholics.
The amendment would have prevented the U.S. federal government from providing aid to any educational institution with a religious affiliation; the specific intention was to make Catholic parochial schools ineligible for federal education funds. The federal amendment failed, but many states adopted it and still have it in their state constitutions.
Here we are 150 years later and this is still an issue! It was the subject of the 2017 Supreme Court case Trinity Lutheran Church of Columbia, Inc. v. Comer. My quick summary is:
The Missouri state Department of Natural Resources had a program offering grants to licensed daycare facilities to resurface their playgrounds with shredded tires.
In 2012, a daycare facility operated by Trinity Lutheran church ranked fifth out of 44 applicants according to the department’s criteria.
14 of the 44 applicants received grants, but Trinity Lutheran's daycare was denied, because the Missouri constitution has a Blaine Amendment.
The Court found (7–2) that denying the grant to an otherwise qualified daycare just because of its religious affiliation was a violation of the Constitution's promises of free exercise of religion. (Full opinion)
It's interesting to me that now that Blaine is someone I recognize, he keeps turning up. He was really important, a major player in national politics for thirty years. But who remembers him now?
[Other articles in category /law] permanent link
Fri, 17 Jan 2020As Middle English goes, Pylgremage of the Sowle (unknown author, 1413) is much easier to read than Chaucer:
He hath iourneyed by the perylous pas of Pryde, by the malycious montayne of Wrethe and Enuye, he hath waltred hym self and wesshen in the lothely lake of cursyd Lechery, he hath ben encombred in the golf of Glotony. Also he hath mysgouerned hym in the contre of Couetyse, and often tyme taken his rest whan tyme was best to trauayle, slepyng and slomeryng in the bed of Slouthe.
I initially misread “Enuye” as “ennui”, understanding it as sloth. But when sloth showed up at the end, I realized that it was simpler than I thought, it's just “envy”.
[Other articles in category /book] permanent link
Thu, 16 Jan 2020
A serious proposal to exploit the loophole in the U.S. Constitution
In 2007 I described an impractical scheme to turn the U.S. into a dictatorship, or to make any other desired change to the Constitution, by having Congress admit a large number of very small states, which could then ratify any constitutional amendments deemed desirable.
An anonymous writer (probably a third-year law student) has independently discovered my scheme, and has proposed it as a way to “fix” the problems that they perceive with the current political and electoral structure. The proposal has been published in the Harvard Law Review in an article that does not appear to be an April Fools’ prank.
The article points out that admission of new states has sometimes been done as a political hack. It says:
Republicans in Congress were worried about Lincoln’s reelection chances and short the votes necessary to pass the Thirteenth Amendment. So notwithstanding the traditional population requirements for statehood, they turned the territory of Nevada — population 6,857 — into a state, adding Republican votes to Congress and the Electoral College.
Specifically, the proposal is that the new states should be allocated out of territory currently in the District of Columbia (which will help ensure that they are politically aligned in the way the author prefers), and that a suitable number of new states might be one hundred and twenty-seven.
[Other articles in category /law] permanent link
Tue, 14 Jan 2020
More about triple border points
[ Previously ]
A couple of readers wrote to discuss tripoints, which are places where three states or other regions share a common border point.
Doug Orleans told me about the Tri-States Monument near Port Jervis, New York. This marks the approximate location of the Pennsylvania - New Jersey - New York border. (The actual tripoint, as I mentioned, is at the bottom of the river.)
I had independently been thinking about taking a drive around the entire border of Pennsylvania, and this is just one more reason to do that. (Also, I would drive through the Delaware Water Gap, which is lovely.) Looking into this I learned about the small town of North East, so-named because it's in the northeast corner of Erie County. It's also the northernmost point in Pennsylvania.
(I got onto a tangent about whether it was the northeastmost point in Pennsylvania, and I'm really not sure. It is certainly an extreme northeast point in the sense that you can't travel north, east, or northeast from it without leaving the state. But it would be a very strange choice, since Erie County is at the very western end of the state.)
My putative circumnavigation of Pennsylvanias would take me as close as possible to Pennsylvania's only international boundary, with Ontario; there are Pennsylvania - Ontario tripoints with New York and with Ohio. Unfortunately, both of them are in Lake Erie. The only really accessible Pennsylvania tripoints are the one with West Virginia and Maryland (near Morgantown) and Maryland and Delaware (near Newark).
These points do tend to be marked, with surveyors’ markers if nothing else. Loren Spice sent me a picture of themselves standing at the tripoint of Kansas, Missouri, and Oklahoma, not too far from Joplin, Missouri.
While looking into this, I discovered the Kentucky Bend, which is an exclave of Kentucky, embedded between Tennessee and Missouri:
The “bubble” here is part of Fulton County, Kentucky. North, across the river, is New Madrid County, Missouri. The land border of the bubble is with Lake County, Tennessee.
It appears that what happened here is that the border between Kentucky and Missouri is the river, with Kentucky getting the territory on the left bank, here the south side. And the border between Kentucky and Tennessee is a straight line, following roughly the 36.5 parallel, with Kentucky getting the territory north of the line. The bubble is south of the river but north of the line.
So these three states have not one tripoint, but three, all only a few miles apart!

Finally, I must mention the Lakes of Wada, which are not real lakes, but rather are three connected subsets of the unit disc which have the property that every point on their boundaries is a tripoint.
[Other articles in category /misc] permanent link
Thu, 09 Jan 2020I'm a fan of geographic oddities, and a few years back when I took a road trip to circumnavigate Chesapeake Bay, I planned its official start in New Castle, DE, which is noted for being the center of the only circular state boundary in the U.S.:
The red blob is New Castle. Supposedly an early treaty allotted to Delaware all points west of the river that were within twelve miles of the State House in New Castle.
I drove to New Castle, made a short visit to the State House, and then began my road trip in earnest. This is a little bit silly, because the border is completely invisible, whether you are up close or twelve miles away, and the State House is just another building, and would be exactly the same even if the border were actually a semicubic parabola with its focus at the second-tallest building in Wilmington.
Whatever, I like going places, so I went to New Castle to check it out. Perhaps it was silly, but I enjoyed going out of my way to visit a point of purely geometric significance. The continuing popularity of Four Corners as a tourist destination shows that I'm not the only one. I don't have any plans to visit Four Corners, because it's far away, kinda in the middle of nowhere, and seems like rather a tourist trap. (Not that I begrudge the Navajo Nation whatever they can get from it.)
Four Corners is famously the only point in the U.S. where four state borders coincide. But a couple of weeks ago as I was falling asleep, I had the thought that there are many triple-border points, and it might be fun to visit some. In particular, I live in southeastern Pennsylvania, so the Pennsylvania-New Jersey-Delaware triple point must be somewhere nearby. I sat up and got my phone so I could look at the map, and felt foolish:
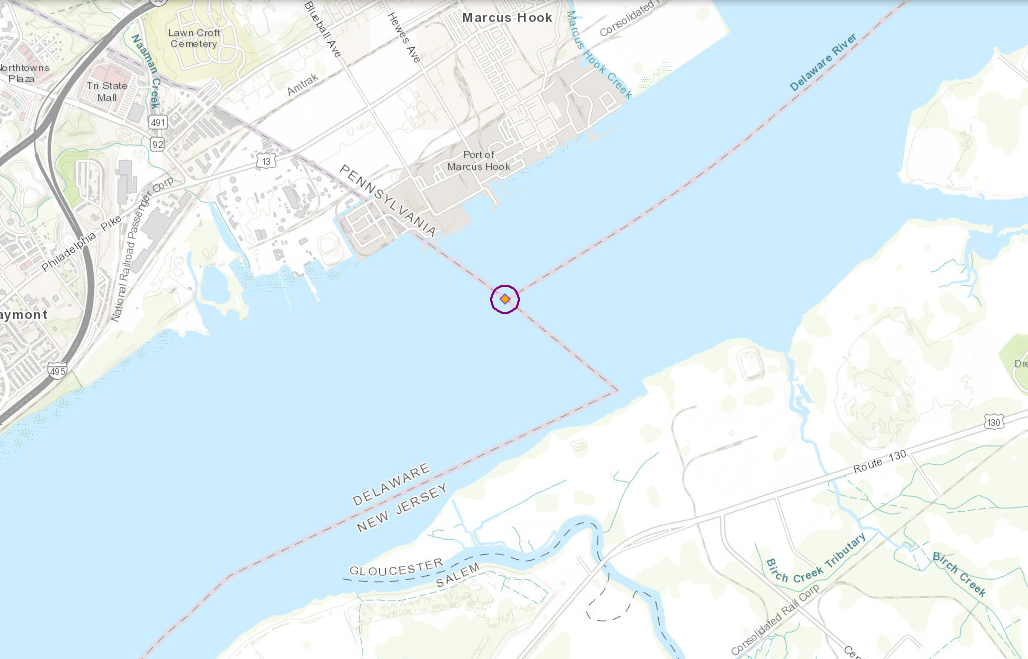
As you can see, the triple point is in the middle of the Delaware River, as of course it must be; the entire border between Pennsylvania and New Jersey, all the hundreds of miles from its northernmost point (near Port Jervis) to its southernmost (shown above), runs right down the middle of the Delaware.
I briefly considered making a trip to get as close as possible, and photographing the point from land. That would not be too inconvenient. Nearby Marcus Hook is served by commuter rail. But Marcus Hook is not very attractive as a destination. Having been to Marcus Hook, it is hard for me to work up much enthusiasm for a return visit.
But I may look into this further. I usually like going places and being places, and I like being surprised when I get there, so visting arbitrarily-chosen places has often worked out well for me. I see that the Pennsylvania-Delaware-Maryland triple border is near White Clay Creek State Park, outside of Newark, DE. That sounds nice, so perhaps I will stop by and take a look, and see if there really is white clay in the creek.
Who knows, I may even go back to Marcus Hook one day.
Addenda
20190114
More about nearby tripoints and related matters.
20201209
I visited the tripoint marker in White Clay Creek State Park.
20220422
More about how visting arbitrarily-chosen places has often worked out well for me. I have a superstitious belief in the power of Fate to bring me to where I am supposed to be, but rationally I understand that the true explanation is that random walks are likely to bring me to an interesting destination simply because I am easily interested and so find most destinations interesting.
20240831
I have now gone back to Marcus Hook to view the tripoint.
20250215
I somehow forgot to mention that back in August 2022 I made the drive up to Port Jervis to visit the NJ-NY-PA tripoint. It's in the river, of course, but there is a marker nearby on a tiny island that is used as a support for the I84 crossing of the Delaware River. As I recall, I saw a flock of geese.
I don't have the photos handy but I did at least save these screenshots:
The marker is not as hard to get to as it might appear. The rest of the little island is a graveyard, and has a footpath from which you can easily reach the marker. The marker itself is a stone column about four feet high.
[Other articles in category /misc] permanent link
Wed, 08 Jan 2020
Unix bc command and its -l flag
In a recent article about Unix utilities, I wrote:
We need the
-lflag onbcbecause otherwise it stupidly does integer arithmetic.
This is wrong, as was kindly pointed out to me by Luke Shumaker. The
behavior of bc is rather more complicated than I said, and less
stupid. In the application I was discussing, the input was a string
like 0.25+0.37, and it's easy to verify that bc produces the
correct answer even without -l:
$ echo 0.25+0.37 | bc
.62
In bc, each number is
represented internally as !!m·10^{-s}!!, where !!m!! is in base 10 and
!!s!! is called the “scale”, essentially the number of digits after
the decimal point. For addition, subtraction, and multiplication, bc
produces a result with the correct scale for an exact result. For
example, when multiplying two numbers with scales a and b, the
result always has scale a + b, so the operation is performed with
exact precision.
But for division, bc doesn't know what scale it should use for the
result. The result of !!23÷7!! can't
be represented exactly, regardless of the scale used. So how should
bc choose how many digits to retain? It can't retain all of them,
and it doesn't know how many you
will want. The answer is: you tell it, by setting a special variable,
called scale. If you set scale=3 then !!23÷7!! will produce the
result !!3.285!!.
Unfortunately, if you don't set it — this is the stupid part — scale defaults to zero. Then
bc will discard everything after the decimal point, and tell you that
!!23÷7 = 3!!.
Long, long ago I was in the habit of manually entering scale=20 at
the start of every bc session. I eventually learned about -l,
which, among other things, sets the default scale to 20 instead of 0.
And I have used -l habitually ever since, even in cases like this,
where it isn't needed.
Many thanks to Luke Shumaker for pointing this out. M. Shumaker adds:
I think the mis-recollection/understanding of
-lsays something about your "memorized trivia" point, but I'm not quite sure what.
Yeah, same.
[Other articles in category /oops] permanent link
Tue, 07 Jan 2020
Social classes identified by letters
Looking up the letter E in the Big Dictionary, I learned that British sociologists were dividing social classes into lettered strata long before Aldous Huxley did it in Brave New World (1932). The OED quoted F. G. D’Aeth, “Present Tendencies of Class Differentiation”, The Sociological Review, vol 3 no 4, October, 1910:
The present class structure is based upon different standards of life…
A. The Loafer
B. Low-skilled labour
C. Artizan
D. Smaller Shopkeeper and clerk
E. Smaller Business Class
F. Professional and Administrative Class
G. The Rich
The OED doesn't quote further, but D’Aeth goes on to explain:
A. represents the refuse of a race; C. is a solid, independent and valuable class in society. … E. possesses the elements of refinement; provincialisms in speech are avoided, its sons are selected as clerks, etc., in good class businesses, e.g., banking, insurance.
Notice that in D’Aeth's classification, the later letters are higher classes. According to the OED this was typical; they also quote a similar classification from 1887 in which A was the lowest class. But the OED labels this sort of classification, with A at the bottom, as “obsolete”.
In Brave New World, you will recall, it is the in the other direction, with the Alphas (administrators and specialists), at the top, and the Epsilons (menial workers with artificially-induced fetal alcohol syndrome) at the bottom.
The OED's later quotations, from 1950–2014, all follow Huxley in putting class A at the top and E at the bottom. They also follow Huxley in having only five classes instead of seven or eight. (One has six classes, but two of them are C1 and C2.)
I wonder how much influence Brave New World had on this sort of classification. Was anyone before Huxley dividing British society into five lettered classes with A at the top?
[ By the way, I have been informed that this paper, which I have linked above, is “Copyright © 2020 by The Sociological Review Publication Limited. All rights are reserved.” This is a bald lie. Sociological Review Publication Limited should be ashamed of themselves. ]
[Other articles in category /lang] permanent link
Fri, 03 Jan 2020
Benchmarking shell pipelines and the Unix “tools” philosophy
Sometimes I look through the HTTP referrer logs to see if anyone is
talking about my blog. I use the f 11 command to extract the
referrer field from the log files, count up the number of occurrences
of each referring URL, then discard the ones that are internal
referrers from elsewhere on my blog. It looks like this:
f 11 access.2020-01-0* | count | grep -v plover
(I've discussed f before. The f 11 just
prints the eleventh field of each line. It is
essentially shorthand for awk '{print $11}' or perl -lane 'print
$F[10]'. The count utility is even simpler; it counts the number
of occurrences of each distinct line in its input, and emits a report
sorted from least to most frequent, essentially a trivial wrapper
around sort | uniq -c | sort -n. Civilization advances by extending the number of
important operations which we can perform without thinking about
them.)
This has obvious defects, but it works well enough. But every time I
used it, I wondered: is it faster to do the grep before the count,
or after? I didn't ever notice a difference. But I still wanted to
know.
After years of idly wondering this, I have finally looked into it. The point of this article is that the investigation produced the following pipeline, which I think is a great example of the Unix “tools” philosophy:
for i in $(seq 20); do
TIME="%U+%S" time \
sh -c 'f 11 access.2020-01-0* | grep -v plover | count > /dev/null' \
2>&1 | bc -l ;
done | addup
I typed this on the command line, with no backslashes or newlines, so it actually looked like this:
for i in $(seq 20); do TIME="%U+%S" time sh -c 'f 11 access.2020-01-0* | grep -v plover |count > /dev/null' 2>&1 | bc -l ; done | addup
Okay, what's going on here? The pipeline I actually want to analyze,
with f | grep| count, is
there in the middle, and I've already explained it, so let's elide it:
for i in $(seq 20); do
TIME="%U+%S" time \
sh -c '¿SOMETHING? > /dev/null' 2>&1 | bc -l ;
done | addup
Continuing to work from inside to out, we're going to use time to
actually do the timings. The time command is standard. It runs a
program, asks the kernel how long the program took, then prints
a report.
The time command will only time a single process (plus its
subprocesses, a crucial fact that is inexplicably omitted from the man
page). The ¿SOMETHING? includes a pipeline, which must be set up by
the shell, so we're actually timing a shell command sh -c '...'
which tells time to run the shell and instruct it to run the pipeline we're
interested in. We tell the shell to throw away the output of
the pipeline, with > /dev/null, so that the output doesn't get mixed
up with time's own report.
The default format for the report printed by time is intended for human consumption. We can
supply an alternative format in the $TIME variable. The format I'm using here is %U+%S, which comes out as something
like 0.25+0.37, where 0.25 is the user CPU time and 0.37 is the
system CPU time. I didn't see a format specifier that would emit the
sum of these directly. So instead I had it emit them with a + in
between, and then piped the result through the bc command, which performs the requested arithmetic
and emits the result. We need the -l flag on bc
because otherwise it stupidly does integer arithmetic. The time command emits its report to
standard error, so I use 2>&1
to redirect the standard error into the pipe.
[ Addendum 20200108: We don't actually need -l here; I was mistaken. ]
Collapsing the details I just discussed, we have:
for i in $(seq 20); do
(run once and emit the total CPU time)
done | addup
seq is a utility I invented no later than 1993 which has since
become standard in most Unix systems. (As with
netcat, I am not claiming to be the
first or only person to have invented this, only to have invented it
independently.) There are many variations of seq, but
the main use case is that seq 20 prints
1
2
3
…
19
20
Here we don't actually care about the output (we never actually use
$i) but it's a convenient way to get the for loop to run twenty
times. The output of the for loop is the twenty total CPU
times that were emitted by the twenty invocations of bc. (Did you know that
you can pipe the output of a loop?) These twenty lines of output are
passed into addup, which I wrote no later than 2011. (Why did it
take me so long to do this?) It reads a list of numbers and prints the
sum.
All together, the command runs and prints a single number like 5.17,
indicating that the twenty runs of the pipeline took 5.17 CPU-seconds
total. I can do this a few times for the original pipeline, with
count before grep, get times between 4.77 and 5.78, and then try
again with the grep before the count, producing times between 4.32
and 5.14. The difference is large enough to detect but too small to
notice.
(To do this right we also need to test a null command, say
sh -c 'sleep 0.1 < /dev/null'
because we might learn that 95% of the reported time is spent in running the shell, so the actual difference between the two pipelines is twenty times as large as we thought. I did this; it turns out that the time spent to run the shell is insignificant.)
What to learn from all this? On the one hand, Unix wins: it's
supposed to be quick and easy to assemble small tools to do whatever it is
you're trying to do. When time wouldn't do the arithmetic I needed
it to, I sent its output to a generic arithmetic-doing utility. When
I needed to count to twenty, I had a utility for doing that; if I
hadn't there are any number of easy workarounds. The
shell provided the I/O redirection and control flow I needed.
On the other hand, gosh, what a weird mishmash of stuff I had to
remember or look up. The -l flag for bc. The fact that I needed
bc at all because time won't report total CPU time. The $TIME
variable that controls its report format. The bizarro 2>&1 syntax
for redirecting standard error into a pipe. The sh -c trick to get
time to execute a pipeline. The missing documentation of the core
functionality of time.
Was it a win overall? What if Unix had less compositionality but I could use it with less memorized trivia? Would that be an improvement?
I don't know. I rather suspect that there's no way to actually reach that hypothetical universe. The bizarre mishmash of weirdness exists because so many different people invented so many tools over such a long period. And they wouldn't have done any of that inventing if the compositionality hadn't been there. I think we don't actually get to make a choice between an incoherent mess of composable paraphernalia and a coherent, well-designed but noncompositional system. Rather, we get a choice between a incoherent but useful mess and an incomplete, limited noncompositional system.
(Notes to self: (1) In connection with Parse::RecDescent, you once wrote
about open versus closed systems. This is another point in that
discussion. (2) Open systems tend to evolve into messes. But closed
systems tend not to evolve at all, and die. (3) Closed systems are
centralized and hierarchical; open systems, when they succeed, are
decentralized and organic. (4) If you are looking for another
example of a successful incoherent mess of composable paraphernalia,
consider Git.)
[ Addendum: Add this to the list of “weird mishmash of trivia”: There are two
time commands. One, which I discussed above, is a separate
executable, usually in /usr/bin/time. The other is built into the
shell. They are incompatible. Which was I actually using? I would
have been pretty confused if I had accidentally gotten the built-in
one, which ignores $TIME and uses a $TIMEFORMAT that is
interpreted in a completely different way. I was fortunate, and got
the one I intended to get. But it took me quite a while to understand
why I had! The appearance of the TIME=… assignment at the start of
the shell command disabled the shell's special builtin treatment of the
keyword time, so it really did use /usr/bin/time. This computer stuff
is amazingly complicated. I don't know how anyone gets anything done. ]
[ Addenda 20200104: (1) Perl's module ecosystem is another example of a
successful incoherent mess of composable paraphernalia. (2) Of the
seven trivia I included in my “weird mishmash”, five were related to
the time command. Is this a reflection on time, or is it just
because time was central to this particular example? ]
[ Addendum 20200104: And, of course, this is exactly what Richard Gabriel was thinking about in Worse is Better. Like Gabriel, I'm not sure. ]
[Other articles in category /Unix] permanent link
Thu, 02 Jan 2020
A sticky problem that evaporated
Back in early 1995, I worked on an incredibly early e-commerce site.
The folks there were used to producing shopping catalogs for
distribution in airplane seat-back pockets and such like, and they
were going to try bringing a catalog to this World-Wide Web thing
that people were all of a sudden talking about.
One of their clients was Eddie Bauer. They wanted to put up a product catalog with a page for each product, say a sweatshirt, and the page should show color swatches for each possible sweatshirt color.
“Sure, I can do that,” I said. “But you have to understand that the user may not see the color swatches exactly as you expect them to.” Nobody would need to have this explained now, but in early 1995 I wasn't sure the catalog folks would understand. When you have a physical catalog you can leaf through a few samples to make sure that the printer didn't mess up the colors.
But what if two months down the line the Eddie Bauer people were shocked by how many complaints customers had about things being not quite the right color, “Hey I ordered mulberry but this is more like maroonish.” Having absolutely no way to solve the problem, I didn't want to to land in my lap, I wanted to be able to say I had warned them ahead of time. So I asked “Will it be okay that there will be variations in how each customer sees the color swatches?”
The catalog people were concerned. Why wouldn't the colors be the same? And I struggled to explain: the customer will see the swatches on their monitor, and we have no idea how old or crappy it might be, we have no idea how the monitor settings are adjusted, the colors could be completely off, it might be a monochrome monitor, or maybe the green part of their RGB video cable is badly seated and the monitor is displaying everything in red, blue, and purple, blah blah blah… I completely failed to get the point across in a way that the catalog people could understand.
They looked more and more puzzled, but then one of them brightened up suddenly and said “Oh, just like on TV!”
“Yes!” I cried in relief. “Just like that!”
“Oh sure, that's no problem.” Clearly, that was what I should have said in the first place, but I hadn't thought of it.
I no longer have any idea who it was that suddenly figured out what Geek Boy's actual point was, but I'm really grateful that they did.
[Other articles in category /tech] permanent link