Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 30 Oct 2019
Russian names in English and English names in Russian
One day I was surprised to find that Michael Jordan's name in Russian is “Майкл” (‘mai-kl’), and not “Михаи́л” (‘Mikhail’, the Russian translation of Michael.) Which is just what I should have expected; we don't refer to Mikhail Gorbachev or Baryshnikov as “Michael”, and it would be just as odd, in the other direction, if the Russians referred to the famous basketball player “Mikhail” Jordan.
When I was taking high school Russian we were assigned Russian versions of our names and I was disappointed to receive “Марк” (“Mark”) rather than anything more interesting. My friend Jeremy was stiffed in a different way. Apparently there is no direct Russian analog of “Jeremy” so the teacher opted for “Юрий” (Yuri). Yuri is not in any way a correct translation of Jeremy; it is the Russian version of “George”. Looking into it now, I wish she had thought to use “Иереми́я” (Jeremiah), or perhaps “Иерони́м” (Jerome).

It's funny how sometimes these names can be so easy to translate and sometimes so difficult. Mark is Mark, Aleksandr is Alexander, Viktor is Victor, Ivan is John, Yuri is George, Yakov is Jacob (or maybe James), Fyedor is Theodore, nothing is William, and Igor is nothing.
Italian Maria is obviously English “Mary” but how do you translate Mario? English has no male version of “Mary”.
(Side note: it is so bizarre that James and Jacob are somehow the same name, that when you turn Iacobus / Jacques / Iago (Latin / French / Spanish) into English it somehow turns into James. Another: What knucklehead decided to translate Frère Jacques as Brother John?)
[ Addendum: My previous article discussed the Korean translation of 邓小平, the name of Chinese leader Deng Xiaoping. Brian Lee points out that the usual Korean translation of Chinese小 (“small”) is 소 (pronounced, roughly, as /shoo/), but, just as in my Michael-Jordan examples above, the Koreans have chosen to translate the name so as to preserve the foreign pronunciation, 샤오 (/shya-oh/). Thanks! ]
[ Addendum: Dmitry Ivanov points out that there is a second Russian version of George, less common but closer to the English version: Георгий (“Georgy”). He also drew my attention to another Russian version of Jeremy, Ерёма (“Yerema”). This led me to discover that Russian Wikipedia has an entire page about Jeremy-related names, and mentions at least the following:
- Еремей
- Ереми́й
- Ерене́й
- Ерёма
- Иереме́й
- Иереми́й
- Иереми́я
- Ириме́й
- Ярёма
Clearly, my high school Russian teacher blew it. ]
[Other articles in category /lang] permanent link
Tue, 29 Oct 2019Something I've been wondering about for a while: there's this vowel in Mandarin which is usually written as ‘e’, for example in Deng (Xiaoping, 邓小平) or in feng shui (風水). But it's not pronounced like the ‘e’ in English “bed” or “pen”. It seems to my untrained ear to be more like the Korean vowel ‘ㅓ’, which is sort of between English “bought” and “but”. So I had wanted for a while to look up how Deng's name was spelled in Korean to see if they used ‘ㅓ’ or some other vowel. Partial success. Sure enough, Deng is spelled with ‘ㅓ’ in Korean: 덩(샤오핑).
“Feng shui” is spelled differently in Korean, with a different vowel: 풍수. But that's not too surprising, since the term “feng shui” presumably entered the Korean language centuries ago, and not only was the Chinese pronunciation probably different then, the Korean pronunciation would have changed over time after the adoption. In contrast, Deng's name presumably wasn't translated into Korean until sometime in the 20th century.
I was surprised that “Xiaoping” turns into three syllables in Korean. But Korean doesn't have that /aʊ/ dipthong, so that's the best it can do. This reminds me now of how amused I was by Corn Flakes boxes in Korea: in Korean, “Flake” is a four-syllable word. (플레이크).
[Other articles in category /lang] permanent link
Mon, 28 Oct 2019
A solution in search of a problem
I don't remember right now what inspired this, but I got to thinking last week, what if I were to start writing the English letter ‘C’ in two forms, to distinguish its two pronunçiations? Speçifically, when ‘C’ gets the soft /s/ sound, we'll write it with a çedilla, and when it gets the hard /k/ sound we'll write it as usual.
Many improvements have been proposed to English spelling, and why not? Almost any change would be an improvement. But most orthographic innovations produçe barbaric or bizarre spellings. For example, “enuff” is still just wrong and may remain so for a long time. “Thru” and “donut” have been in common use long enough that not everyone thinks they look entirely bizarre, and I think only the Brits still object to “catalog” in plaçe of “catalogue”. But my ‘ç’ suggestion seems to me to be less violent. All the words are still spelled the same way. Nobody would have to deal with the shock of new spellings like “sirkular” or “klearanse”. I think the difficulty of adjusting to “çircular” and “clearançe” seems quite low.
On the other hand, the benefit also seems quite low. There aren't that many C’s to begin with. And who does this help, exactly? Foreigners who might otherwise have trouble deçiding how to pronounçe a particular ‘C’? Are there any people who actually have trouble reading “circle” and would be helped if it were spelled çircle”? And if there are, isn't c-vs-ç the least of their problems?
(Also, as Katara points out, ‘C’ is nearly superfluous in English as it is. You can almost always replaçe it with ‘S’ or ‘K’, accordingly. Although she did point out a counterexample: spelling “mace” as “mase” could be misleading. My proposal of “maçe”, though, is quite clear.)
I wonder, though, if this doesn't point the way toward a more general intervention that might be more generally helpful. The “ough” cluster gets a bad rap, but the real problems in English orthography are mostly in the totally inconsistent vowel spellings. Some diacritical marks might be a big help. For example, consider “bread” and “bead”. What if the close vowel in “bead” were indicated by spelling it “bēad”? Then it becomes easy to distinguish between “rēad” (/ɹid/, present tense) and “read” (/ɹɛd/, past tense), similarly “lēad” and “lead”. Native Anglophones will quickly learn to ignore the diacritical marks. A similar tactic might even help with the notorious “ough”. I don't really know what to do about words like “precious” or “ocean”, though. We can't leave them as they were, because that would unambiguously indicate the wrong pronunçiation “prekious”, “okean”. But to spell them “preçious” or “oçean” would be misleading. “Prećious”, maybe?
(I suppose someone wants to suggest “preşious” and “oşean”, but this is exactly what I'm trying to avoid. If you're going to do that you might as well go whole hog and use “preshus” and “oshun”.)
If you follow this path too far (and in the wrong direction) you end up with Unifon. I think this is a better direction and could end in a better plaçe. Maybe not better enough to be worth doing, though.
Peaçe out.
[Other articles in category /lang] permanent link
Fri, 25 Oct 2019Wikipedia's article on the etymology of gringo is quite good, well-cited, and I did not detect any fishy smells. I had previously tried to look up gringo in the Big Dictionary, but it only informed me that it was from Mexican Spanish, which is not really helpful. (I know that's because their jurisdiction stops at the English border, and they aren't responsible for anything outside, but really, OED folks? Nothing else?)
Anyway Wikipedia helped me out. I had gotten onto this gringos thing because yesterday I learned about gringas, which are white flour tortillas. I immediately wondered: are they called gringas because (like gringos) they're made of white paste? Or is it because they're eaten by gringos, who don't care for corn tortillas? The answer seems to be: both explanations are current, but nobody knows if either is correct.
On the way to gringo I spent a while reading about yanqui, which Latin Americans use to refer to northerners.
So do people in the USA for that matter. Southerners will angrily deny being “yanqui”. They reserve that term to mean anyone from the north, such as myself. But folks like me from the Mid-Atlantic states also deny being Yankees and will tell you that it only means people from New England. Many New Englanders will disclaim being truly Yankee and say that to meet true Yankees you need to go to Maine or maybe New Hampshire. And I suppose people in Maine use it to mean one particular old Yankee farmer who lives up near the Canadian border.
Anyway, I wonder: in Latin America, does “yanqui” always mean specifically USA-ians, or would it also include Canadians? Would a typical Mexican or Guatemalan person refer casually to Canadians as yanquis? Or, if they were drinking beer with a Canadian, and the Canadian refered to themselves as yanqui, would they correct them? (“You're not a yanqui, you're Canadian! Not the same thing at all!”)
If Mexicans do consider Canadians to be a species of yanqui, what do they make of the Québécois? Also yanqui? Or do Francophones get a pass? (What about the Cajuns for that matter?)
[ Addendum 20250202: Teri Kanefield writes about how “there are no Yankees here”, using it as a metaphor for authoritarianism: “There are no authoritarians here. The authoritarians are on the other side.”
[Other articles in category /lang/etym] permanent link
Fri, 11 Oct 2019In a recent article about fair cake division, I said:
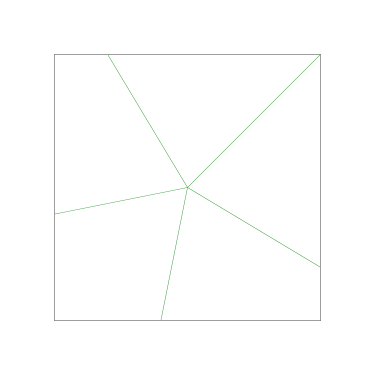
Grandma can use the same method … to divide a regular 17-gonal cake into 23 equally-iced equal pieces.
I got to wondering what that would look like, and the answer is, not very interesting. A regular 17-gon is pretty close to a circle, and the 23 pieces, which are quite narrow, look very much like equal wedges of a circle:
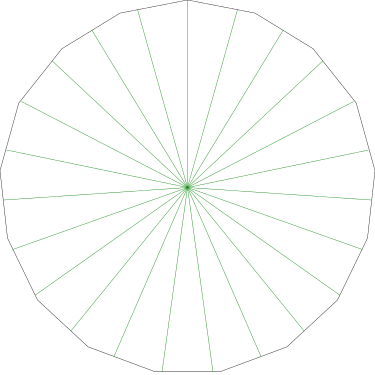
This is generally true, and it becomes more nearly so both as the number of sides of the polygon increases (it becomes more nearly circular) and as the number of pieces increases (the very small amount of perimeter included in each piece is not very different from a short circular arc).
Recall my observation
from last time that even in the nearly extreme case of 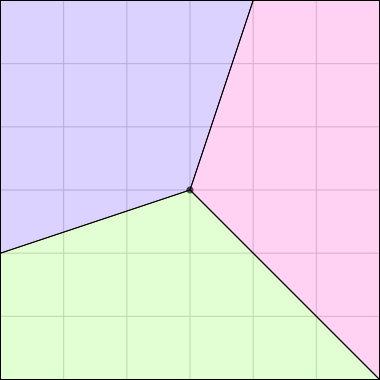 , the central angles deviate from equality by
only a few percent.
, the central angles deviate from equality by
only a few percent.
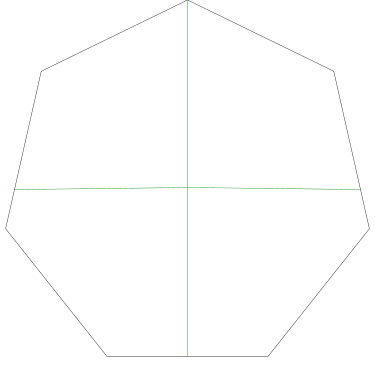
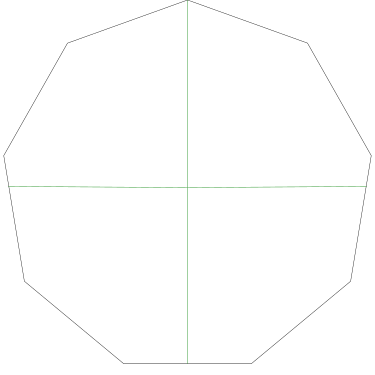
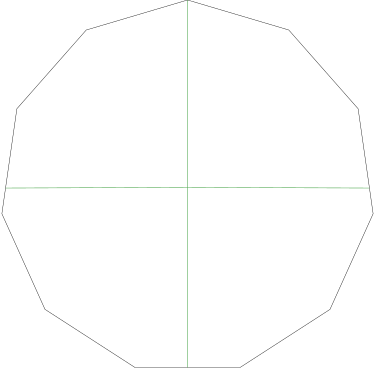
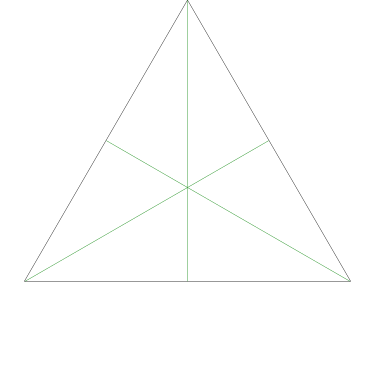
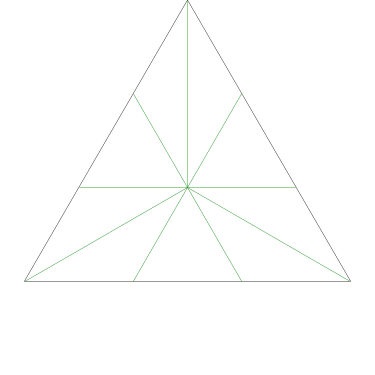
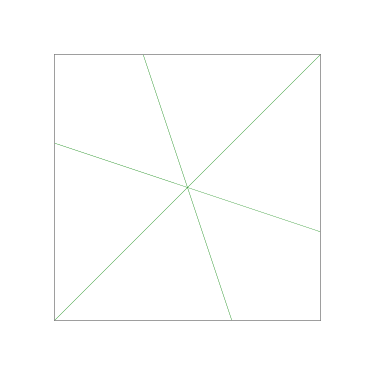
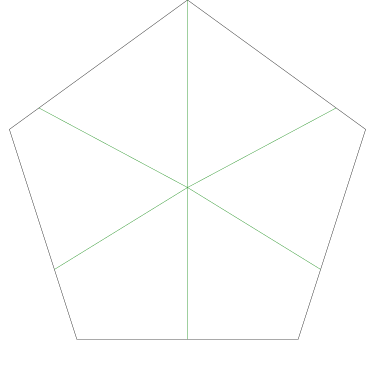
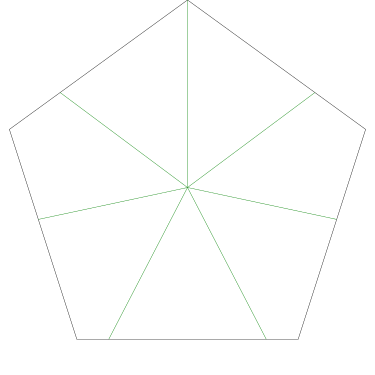
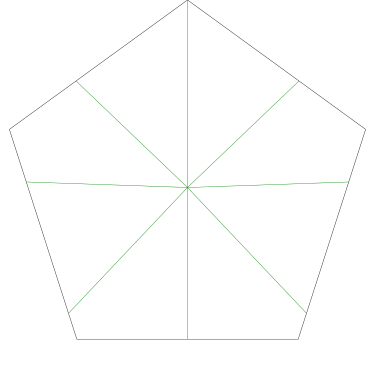
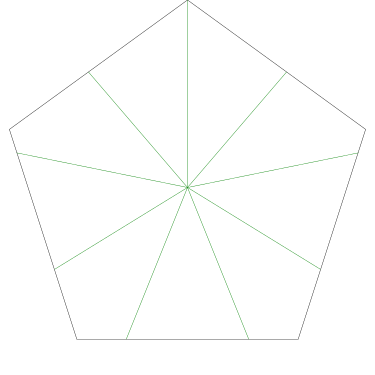
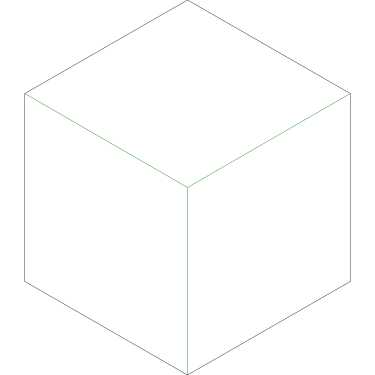
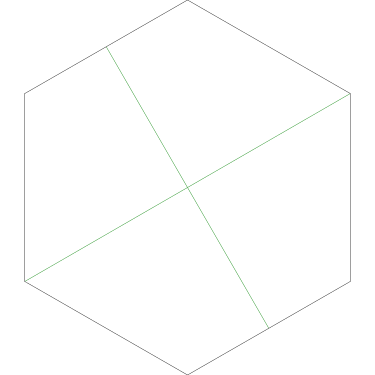
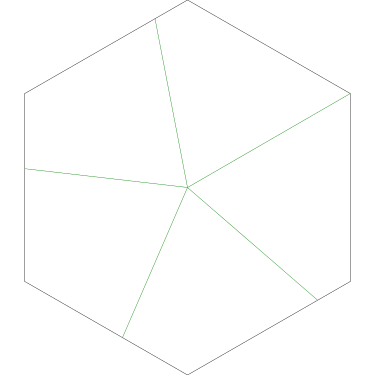
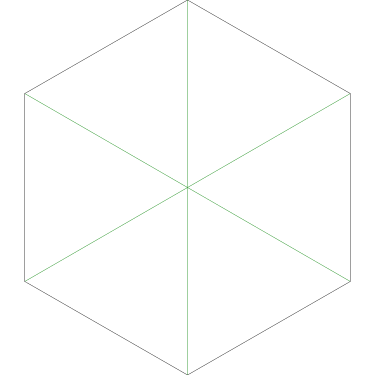
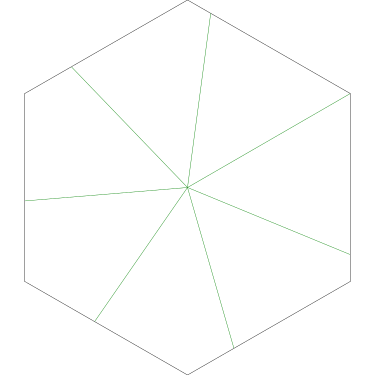
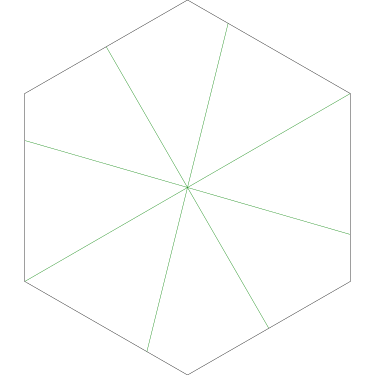
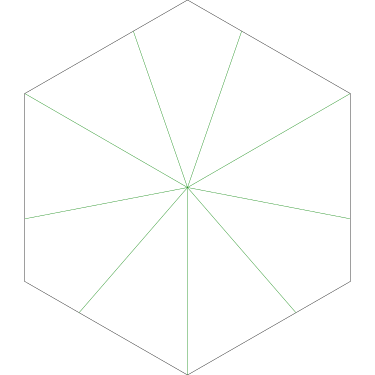
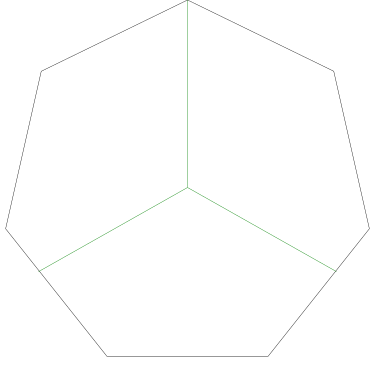
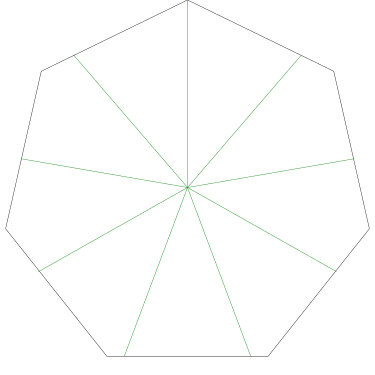
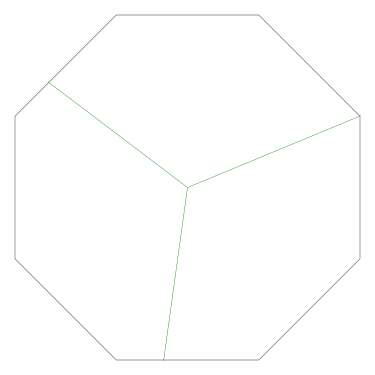
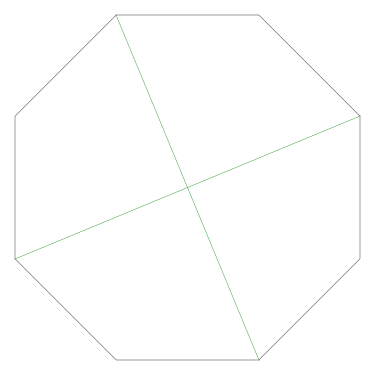
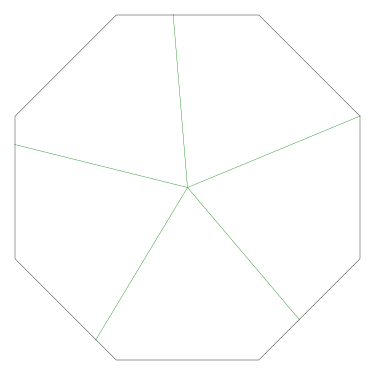
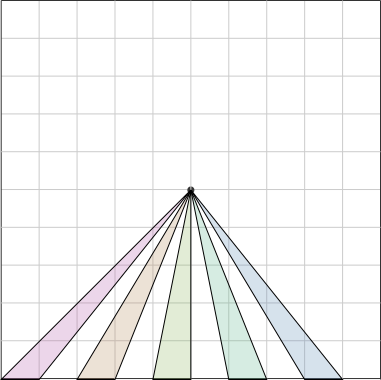
Of particular interest to me is this series of demonstrations of how to cut four pieces from a cake with an odd number of sides:
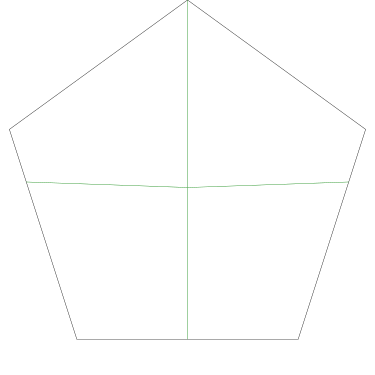
| 
| 
| 
|
I think this shows that the whole question is a little bit silly: if you just cut the cake into equiangular wedges, the resulting slices are very close in volume and in frosting. If the nearly-horizontal cuts in the pentagon above had been perfectly straight and along the !!y!!-axis, they would have intersected the pentagon only 3% of a radius-length lower than they should have.
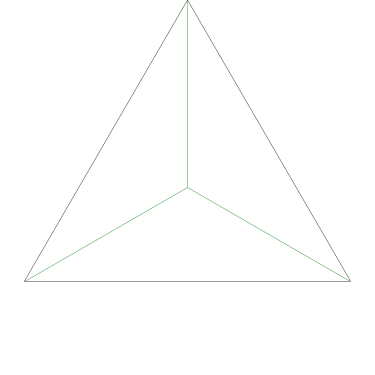
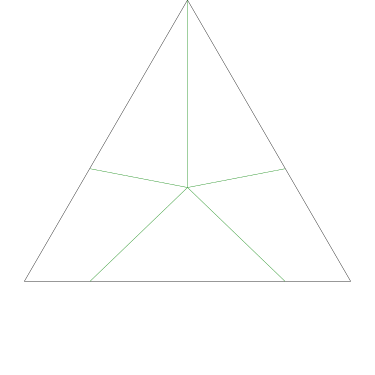
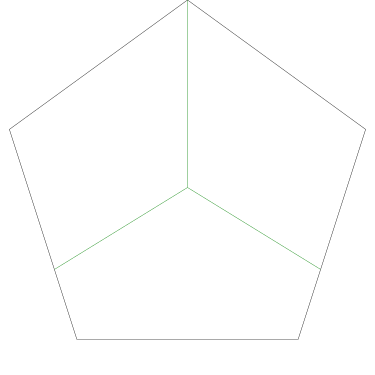
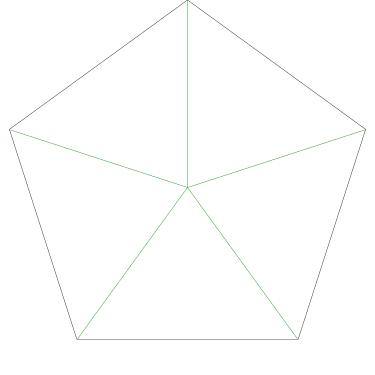
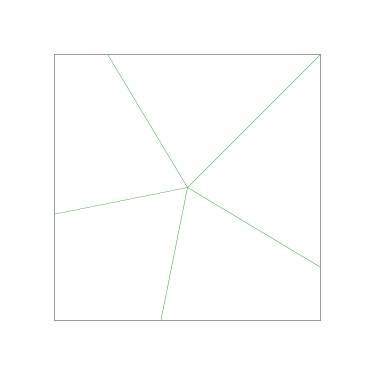
Some of the simpler divisions of simpler cakes are interesting. A solution to the original problem (of dividing a square cake into nine pieces) is highlighted.
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
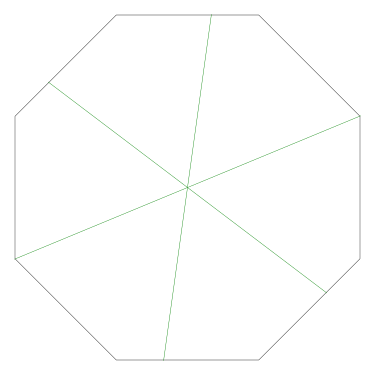
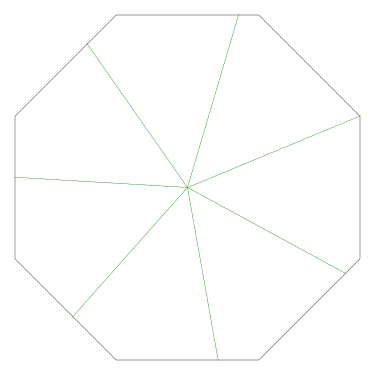
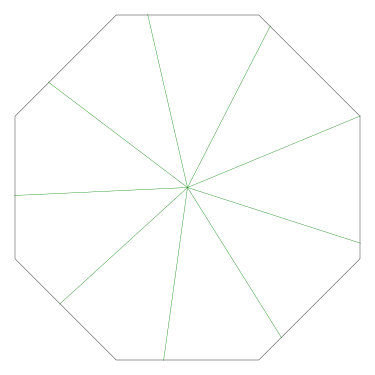
The method as given works regardless of where you make the first cut. But the results do not look very different in any case:
| 
| 
| 
|
The original SVG files are also available, as is the program that wrote them.
[Other articles in category /math] permanent link
Thu, 10 Oct 2019
Incenters of chocolate-iced cakes
A MathOverflow post asks:
Puzzle 1: Grandma made a cake whose base was a square of size 30 by 30 cm and the height was 10 cm. She wanted to divide the cake fairly among her 9 grandchildren. How should she cut the cake?
Okay, this is obvious.
Puzzle 2: Grandma made a cake whose base was a square of size 30 by 30 cm and the height was 10 cm. She put chocolate icing on top of the cake and on the sides, but not on the bottom. She wanted to divide the cake fairly among her 9 grandchildren so that each child would get an equal amount of the cake and the icing. How should she cut the cake?
This one stumped me; the best I could do was to cut the cake into 27 slabs, each !!\frac{10}3×10×10!! cm, and each with between 1 and 5 units of icing. Then we can give three slabs to each grandkid, taking care that each kid's slabs have a total of 7 units of icing. This seems like it might work for an actual cake, but I suspected that it wasn't the solution that was wanted, because the problem seems like a geometry problem and my solution is essentially combinatorial.
Indeed, there is a geometric solution, which is more interesting, and which cuts the cake into only 9 pieces.
I eventually gave up and looked at the answer, which I will discuss below. Sometimes when I give up I feel that if I had had thought a little harder or given up a little later, I would have gotten the answer, but not this time. It depends on an elementary property of squares that I had been completely unaware of.
This is your last chance to avoid spoilers.
The solution given is this: Divide the perimeter of the square cake into 9 equal-length segments, each of length !!\frac{120}{9}!! cm. Some of these will be straight and others may have right angles; it does not matter. Cut from the center of the cake to the endpoints of these segments; the resulting pieces will satisfy the requirements.
“Wat.” I said. “If the perimeter lengths are equal, then the areas are equal? How can that be?”
This is obviously true for two pieces; if you cut the square from the center into two pieces into two parts that divide the perimeter equally, then of course they are the same size and shape. But surely that is not the case for three pieces?
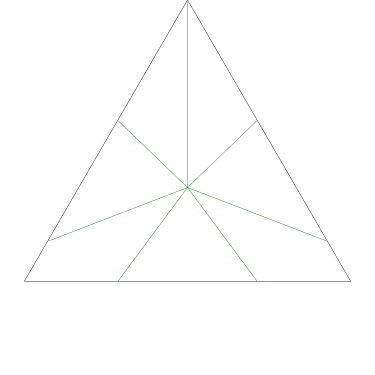
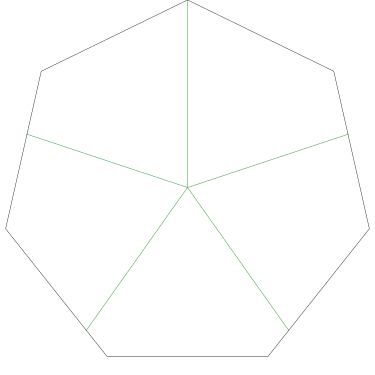
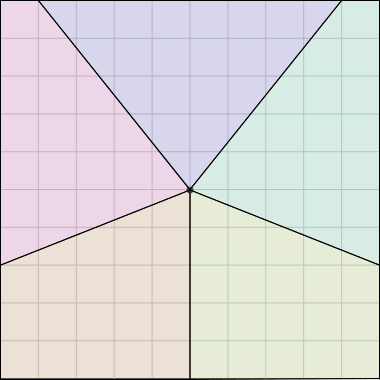
I could not believe it until I got home and drew some pictures on graph paper. Here Grandma has cut her cake into three pieces in the prescribed way:

The three pieces are not the same shape! But each one contains one-third of the square's outer perimeter, and each has an area of 12 square units. (Note, by the way, that although the central angles may appear equal, they are not; the blue one is around 126.9° and the pink and green ones are only 116.6°.)
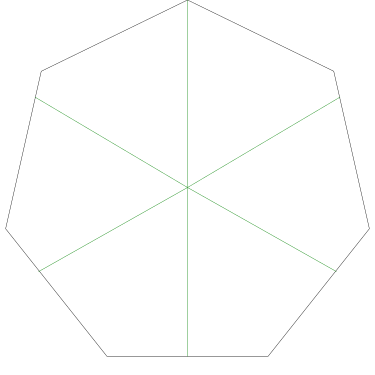
And indeed, any piece cut by Grandma from the center that includes one-third of the square's perimeter will have an area of one-third of the whole square:


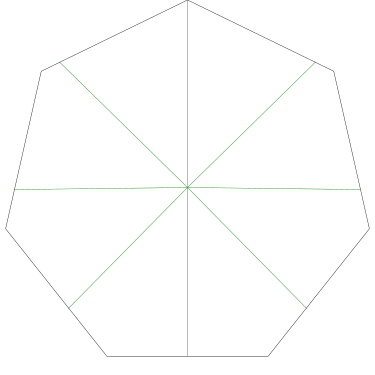
The proof that this works is actually quite easy. Consider a triangle !!OAB!! where !!O!! is the center of the square and !!A!! and !!B!! are points on one of the square's edges.
The triangle's area is half its height times its base. The base is of course the length of the segment !!AB!!, and the height is the length of the perpendicular from !!O!! to the edge of the square. So for any such triangle, its area is proportional to the length of !!AB!!.
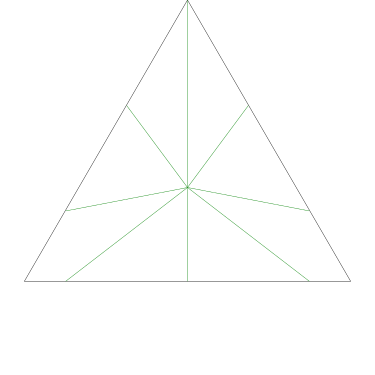
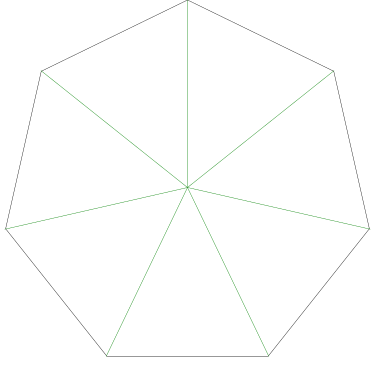
No two of the five triangles below are congruent, but each has the same base and height, and so each has the same area.
Since the center of the square is the same distance from each of the four edges, the same is true for any two triangles, regardless of which edge they arise from: the area of each triangle is proportional to the length of the square's perimeter at its base. Any piece Grandma cuts in this way, from the center of the cake to the edge, is a disjoint union of triangular pieces of this type, so the total area of any such piece is also proportional to the length of the square's perimeter that it includes.
That's the crucial property of the square that I had not known before: if you make cuts from the center of a square, the area of the piece you get is proportional to the length of the perimeter that it contains. Awesome!
Here Grandma has used the same method to cut a pair of square cakes into ten equal-sized pieces that all the have same amount of icing.
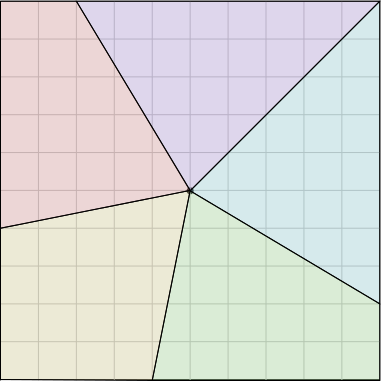
The crucial property here was that the square’s center is the same distance from each of its four edges. This is really obvious, but not every polygon has an analogous point. The center of a regular polygon always has this property, and every triangle has a unique point, called its incenter, which enjoys this property. So Grandma can use the same method to divide a triangular cake into 7 equally-iced equal pieces, if she can find its incenter, or to divide a regular 17-gonal cake into 23 equally-iced equal pieces.
Not every polygon does have an incenter, though. Rhombuses and kites always do, but rectangles do not, except when they are square. If Grandma tries this method with a rectangular sheet cake, someone will get shortchanged. I learned today that polygons that have incenters are known as tangential polygons. They are the only polygons in which can one inscribe a single circle that is tangent to every side of the polygon. This property is easy to detect: these are exactly the polygons in which all the angle bisectors meet at a single point. Grandma should be able to fairly divide the cake and icing for any tangential polygon.
I have probably thought about this before, perhaps in high-school geometry but perhaps not since. Suppose you have two lines, !!m!! and !!n!!, that cross at an acute angle at !!P!!, and you consider the set of points that are equidistant from both !!m!! and !!n!!. Let !!\ell!! be a line through !!P!! which bisects the angle between !!m!! and !!n!!; clearly any point on !!\ell!! will be equidistant from !!m!! and !!n!! by a straightforward argument involving congruent triangles.
Now consider a triangle !!△ABC!!. Let !!P!! be the intersection of the angle bisectors of angles !!∠ A!! and !!∠ B!!.
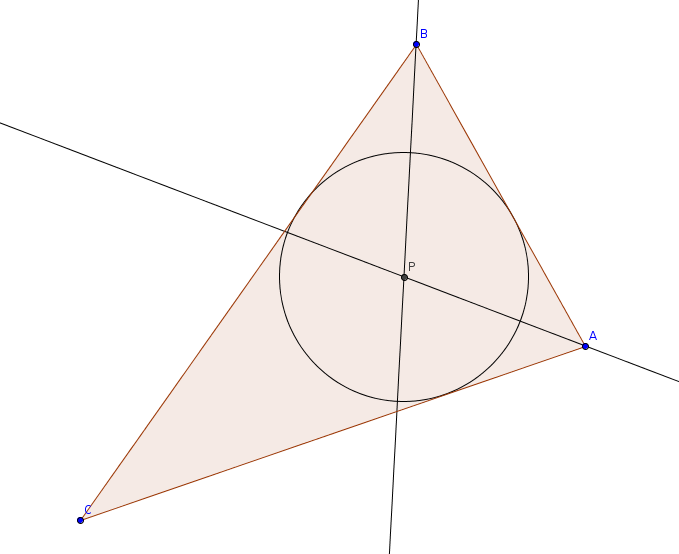
!!P!! is the same distance from both !!AB!! and !!AC!! because it is on the angle bisector of !!∠ A!!, and similarly it is the same distance from both !!AB!! and !!BC!! because it is on the angle bisector of !!∠ B!!.
So therefore !!P!! is the same distance from both !!AC!! and !!BC!! and it must be on the angle bisector of angle !!∠ C!! also. We have just shown that a triangle's three angle bisectors are concurrent! I knew this before, but I don't think I knew a proof.
[ Addendum 20191011: Many illustrated examples. ]
[Other articles in category /math] permanent link
Fri, 04 Oct 2019
Addenda to recent articles 201910
Several people have written in with helpful remarks about recent posts:
Regarding online tracking of legislation:
- Ed Davies directed my attention to www.legislation.gov.uk, an official organ of the British government, which says:
The aim is to publish legislation on this site simultaneously, or at least within 24 hours, of its publication in printed form.
M. Davies is impressed. So am I. Here is the European Union (Withdrawal) Act 2018.
Nik Clayton showed me the @unitedstates project, whcih among other things has a program that attempts to parse the United States Code and produce a tree-structured output.
Twitter user
@sunk818pointed out How I changed the law with a GitHub pull request. The title oversells what actually happened: the codified law contained a minor technical error, which could be corrected without requiring any actual legislation. But the takeaway is that the District of Columbia officially publishes its law to a Github repo.
This then led me to Standardizing the World’s Legislative Information — One hackathon at a time on the LII's VOXPOPULII blog.
(Reminder to readers: I do not normally read Twitter, and it is not a reliable way to contact me.)
Regarding the mysteriously wide letter ‘O’ on the Yeadon firehouse. I had I had guessed that it was not in the same family as the others, perhaps because the original one had been damaged. I asked Jonathan Hoefler, a noted font expert; he agreed.
But one reader, Steve Nicholson, pointed out that it is quite common, in Art Deco fonts, for the ‘O’ to be circular even when that makes it much wider than the other letters. He provided ten examples, such as Haute Corniche.
I suggested this to M. Hoefler, but he rejected the theory decisively:
True; it's a Deco mannerism to have 'modulated capitals'… . But this isn't a deco font, or a deco building, and in any case it would have been HIGHLY unlikely for a municipal sign shop to spec something like this for any purpose, let alone a firehouse. It's a wrong sort O, probably installed from the outset.
(The letter spacing suggests that this is the original ‘O’.)
Several people wrote to me about the problem of taking half a pill every day, in which I overlooked that the solution was simply the harmonic numbers.
Robin Houston linked to this YouTube video, “the frog problem”, which has the same solution, and observed that the two problems are isomorphic, proceeding essentially as Jonathan Dushoff does below.
Shreevatsa R. wrote a long blog article detailing their thoughts about the solution. I have not yet read the whole thing carefully but knowing M. Shreevatsa, it is well worth reading. M. Shreevatsa concludes, as I did, that a Markov chain approach is unlikely to be fruitful, but then finds an interesting approach to the problem using probability generating functions, and then another reformulating it as a balls-in-bins problem.
Jonathan Dushoff sent me a very clear and elegant solution and kindly gave me permission to publish it here:
The first key to my solution is the fact that you can add expectations even when variables are not independent.
In this case, that means that each time we break a pill we can calculate the probability that the half pill we produce will "survive" to be counted at the endpoint. That's the same as the expectation of the number of half-pills that pill will contribute to the final total. We can then just add these expectations to get the answer! A little counter-intuitive, but absolutely solid.
The next key is symmetry. If I break a half pill and there are !!j!! whole pills left, the only question for that half pill is the relative order in which I pick those !!j+1!! objects. In particular, any other half pills that exist or might be generated can be ignored for the purpose of this part of the question. By symmetry, any of these !!j+1!! objects is equally likely to be last, so the survival probability is !!\frac1{j+1}!!.
If I start with !!n!! pills and break one, I have !!n-1!! whole pills left, so the probability of that pill surviving is !!\frac1n!!. Going through to the end we get the answer:
$$\frac1n + \frac1{n-1} + \ldots + 1.$$
I have gotten feedback from several people about my Haskell type constructor clutter, which I will write up separately, probably, once I digest it.
Thanks to everyone who wrote in, even people I forgot to mention above, and even to the Twitter person who didn't actually write in.
[Other articles in category /addenda] permanent link
Thu, 03 Oct 2019I recently mentioned a citation listing on one of the pages of the United States Code at LII. It said:
(Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904; Pub. L. 86–342, title I, § 106, Sept. 21, 1959, 73 Stat. 612; Pub. L. 87–61, title I, § 106, June 29, 1961, 75 Stat. 123; Pub. L. 88–157, § 5, Oct. 24, 1963, 77 Stat. 277; Pub. L. 89–285, title I, § 101, Oct. 22, 1965, 79 Stat. 1028; Pub. L. 89–574, § 8(a), Sept. 13, 1966, 80 Stat. 768; Pub. L. 90–495, § 6(a)–(d), Aug. 23, 1968, 82 Stat. 817; Pub. L. 91–605, title I, § 122(a), Dec. 31, 1970, 84 Stat. 1726; Pub. L. 93–643, § 109, Jan. 4, 1975, 88 Stat. 2284; Pub. L. 94–280, title I, § 122, May 5, 1976, 90 Stat. 438; Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701; Pub. L. 96–106, § 6, Nov. 9, 1979, 93 Stat. 797; Pub. L. 102–240, title I, § 1046(a)–(c), Dec. 18, 1991, 105 Stat. 1995, 1996; Pub. L. 102–302, § 104, June 22, 1992, 106 Stat. 253; Pub. L. 104–59, title III, § 314, Nov. 28, 1995, 109 Stat. 586; Pub. L. 105–178, title I, § 1212(a)(2)(A), June 9, 1998, 112 Stat. 193; Pub. L. 112–141, div. A, title I, §§ 1519(c)(6), formerly 1519(c)(7), 1539(b), July 6, 2012, 126 Stat. 576, 587, renumbered § 1519(c)(6), Pub. L. 114–94, div. A, title I, § 1446(d)(5)(B), Dec. 4, 2015, 129 Stat. 1438.)
My comment was “Whew”.
But this wouldn't have been so awful if LII had made even a minimal effort to clean it up:
- Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904
- Pub. L. 86–342, title I, § 106, Sept. 21, 1959, 73 Stat. 612
- Pub. L. 87–61, title I, § 106, June 29, 1961, 75 Stat. 123
- Pub. L. 88–157, § 5, Oct. 24, 1963, 77 Stat. 277
- Pub. L. 89–285, title I, § 101, Oct. 22, 1965, 79 Stat. 1028
- Pub. L. 89–574, § 8(a), Sept. 13, 1966, 80 Stat. 768
- Pub. L. 90–495, § 6(a)–(d), Aug. 23, 1968, 82 Stat. 817
- Pub. L. 91–605, title I, § 122(a), Dec. 31, 1970, 84 Stat. 1726
- Pub. L. 93–643, § 109, Jan. 4, 1975, 88 Stat. 2284
- Pub. L. 94–280, title I, § 122, May 5, 1976, 90 Stat. 438
- Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701
- Pub. L. 96–106, § 6, Nov. 9, 1979, 93 Stat. 797
- Pub. L. 102–240, title I, § 1046(a)–(c), Dec. 18, 1991, 105 Stat. 1995, 1996
- Pub. L. 102–302, § 104, June 22, 1992, 106 Stat. 253
- Pub. L. 104–59, title III, § 314, Nov. 28, 1995, 109 Stat. 586
- Pub. L. 105–178, title I, § 1212(a)(2)(A), June 9, 1998, 112 Stat. 193
- Pub. L. 112–141, div. A, title I, §§ 1519(c)(6), formerly 1519(c)(7), 1539(b), July 6, 2012, 126 Stat. 576, 587, renumbered § 1519(c)(6), Pub. L. 114–94, div. A, title I, § 1446(d)(5)(B), Dec. 4, 2015, 129 Stat. 1438.
That's the result of s/; /<li>/g, nothing more.
(I wonder if that long citation at the end is actually two citations.)
[Other articles in category /IT] permanent link
The pain of tracking down changes in U.S. law
Last month when I was researching my article about the free coffee provision in U.S. federal highway law, I spent a great deal of time writing this fragment:
I knew that the provision was in 23 USC §131, but I should explain what this means.
The body of U.S. statutory law can be considered a single giant document, which is "codified" as the United States Code, or USC for short. USC is divided into fifty or sixty “titles” or subject areas, of which the relevant one here, title 23, concerns “Highways”. The titles are then divided into sections (the free coffee is in section 131), paragraphs, sub-paragraphs, and so on, each with an identifying letter. The free coffee is 23 USC §131 (c)(5).
But this didn't tell me when the coffee exception was introduced or in what legislation. Most of Title 23 dates from 1958, but the coffee sign exception was added later. When Congress amends a law, they do it by specifying a patch to the existing code. My use of the programmer jargon term “patch” here is not an analogy. The portion of the Federal-Aid Highway Act of 1978 that enacted the “free coffee” exception reads as follows:
ADVERTISING BY NONPROFIT ORGANIZATIONS
Sec. 121. Section 131(c) of title 23, United States Code, is amended—
(1) by striking out “and (4)” and inserting in lieu thereof “(4)”; and
(2) by striking out the period at the end thereof and inserting in lieu thereof a comma and the following: “and (5) signs, displays, and devices advertising the distribution of nonprofit organizations of free coffee […]”.
(The “[…]” is my elision. The Act includes the complete text that was to be inserted.)
The act is not phrased as a high-level functional description, such as “extend the list of exceptions to include: ... ”. It says to replace the text ‘and (4)’ with the text ‘(4)’; then replace the period with a comma; then …”, just as if Congress were preparing a patch in a version control system.
Unfortunately, the lack of an actual version control system makes it quite hard to find out when any particular change was introduced. The code page I read is provided by the Legal Information Institute at Cornell University. At the bottom of the page, there is a listing of the changes that went into this particular section:
(Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904; Pub. L. 86–342, title I, § 106, Sept. 21, 1959, 73 Stat. 612; Pub. L. 87–61, title I, § 106, June 29, 1961, 75 Stat. 123; Pub. L. 88–157, § 5, Oct. 24, 1963, 77 Stat. 277; Pub. L. 89–285, title I, § 101, Oct. 22, 1965, 79 Stat. 1028; Pub. L. 89–574, § 8(a), Sept. 13, 1966, 80 Stat. 768; Pub. L. 90–495, § 6(a)–(d), Aug. 23, 1968, 82 Stat. 817; Pub. L. 91–605, title I, § 122(a), Dec. 31, 1970, 84 Stat. 1726; Pub. L. 93–643, § 109, Jan. 4, 1975, 88 Stat. 2284; Pub. L. 94–280, title I, § 122, May 5, 1976, 90 Stat. 438; Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701; Pub. L. 96–106, § 6, Nov. 9, 1979, 93 Stat. 797; Pub. L. 102–240, title I, § 1046(a)–(c), Dec. 18, 1991, 105 Stat. 1995, 1996; Pub. L. 102–302, § 104, June 22, 1992, 106 Stat. 253; Pub. L. 104–59, title III, § 314, Nov. 28, 1995, 109 Stat. 586; Pub. L. 105–178, title I, § 1212(a)(2)(A), June 9, 1998, 112 Stat. 193; Pub. L. 112–141, div. A, title I, §§ 1519(c)(6), formerly 1519(c)(7), 1539(b), July 6, 2012, 126 Stat. 576, 587, renumbered § 1519(c)(6), Pub. L. 114–94, div. A, title I, § 1446(d)(5)(B), Dec. 4, 2015, 129 Stat. 1438.)
Whew.
Each of these is a citation of a particular Act of Congress. For example, the first one
Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904
refers to “Public law 85–767”, the 767th law enacted by the 85th Congress, which met during the Eisenhower administration, from 1957–1959. The U.S. Congress has a useful web site that contains a list of all the public laws, with links — but it only goes back to the 93rd Congress of 1973–1974.
And anyway, just knowing that it is Public law 85–767 is not (or was not formerly) enough to tell you how to look up its text. The laws must be published somewhere before they are codified, and scans of these publications, the United States Statutes at Large, are online back to the 82nd Congress. That is what the “72 Stat. 904” means: the publication was in volume 72 of the Statutes at Large, page 904. This citation style was obviously designed at a time when the best (or only) way to find the statute was to go down to the library and pull volume 72 off the shelf. It is well-designed for that purpose. Now, not so much.
Here's a screengrab of the relevant portion of the relevant part of the 1978 act:

The citation for this was:
Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701
(Note that “title I, §§ 121, 122” here refers to the sections of the act itself, not the section of the US Code that was being amended; that was title 23, §131, remember.)
To track this down, I had no choice but to grovel over each of the links to the Statutes at Large, download each scan, and search over each one looking for the coffee provision. I kept written notes so that I wouldn't mix up the congressional term numbers with the Statutes volume numbers.
It ought to be possible, at least in principle, to put the entire U.S. Code into a version control system, with each Act of Congress represented as one or more commits, maybe as a merged topic branch. The commit message could contain the citation, something like this:
commit a4e2b2a1ca2d5245c275ddef55bf8169d72580df
Merge: 6829b2dd986 836108c2ba0
Author: ... <...>
Date: Mon Nov 6 00:00:00 1978 -0400
Surface Transportation Assistance Act of 1978
P.L. 95–599
92 Stat. 2689–2762
H.R. 11733
Merge branch `pl-95-599` to `master`
commit 836108c2ba0d5245c275ddef55bf8169d72580df
Author: ... <...>
Date: Mon Nov 6 00:00:00 1978 -0400
Federal-Aid Highway Act of 1978 (section 121)
(Surface Transportation Assistance Act of 1978, title I)
P.L. 95–599
92 Stat. 2689–2762
H.R. 11733
Signs advertising free coffee are no longer prohibited
within 660 feet of a federal highway.
diff --git a/USC/title23.md b/USC/title23.md
index 084bfc2..caa5a53 100644
--- a/USC/title23.md
+++ b/USC/title23.md
@@ -20565,11 +20565,16 @@ 23 U.S. Code § 131. Control of outdoor advertising
be changed at reasonable intervals by electronic process or by remote
control, advertising activities conducted on the property on which
-they are located, and (4) signs lawfully in existence on October 22,
+they are located, (4) signs lawfully in existence on October 22,
1965, determined by the State, subject to the approval of the
Secretary, to be landmark signs, including signs on farm structures or
natural surfaces, or historic or artistic significance the
preservation of which would be consistent with the purposes of this
-section.
+section, and (5) signs, displays, and devices advertising the
+distribution by nonprofit organizations of free coffee to individuals
+traveling on the Interstate System or the primary system. For the
+purposes of this subsection, the term “free coffee” shall include
+coffee for which a donation may be made, but is not required.
+
*(d)* In order to promote the reasonable, orderly and effective
Or maybe the titles would be directories and the sections would be numbered files in those directories. Whatever. If this existed, I would be able to do something like:
git log -Scoffee -p -- USC/title23.md
and the Act that I wanted would pop right out.
Preparing a version history of the United States Code would be a dauntingly large undertaking, but gosh, so useful. A good VCS enables you to answer questions that you previously wouldn't have even thought of asking.

This article started as a lament about how hard it was for me to track down the provenance of the coffee exception. But it occurs to me that this is the response of someone who has been spoiled by plenty. A generation ago it would have been unthinkable for me even to try to track this down. I would have had to start by reading a book about legal citations and learning what “79 Stat. 1028” meant, instead of just picking it up on the fly. Then I would have had to locate a library with a set of the Statutes at Large and travel to it. And here I am complaining about how I had to click 18 links and do an (automated!) text search on 18 short, relevant excerpts of the Statutes at Large, all while sitting in my chair.
My kids can't quite process the fact that in my childhood, you simply didn't know what the law was and you had no good way to find out. You could go down to the library, take the pertinent volumes of the USC off the shelf, and hope you had looked in all the appropriate places for the relevant statutes, but you could never be sure you hadn't overlooked something. OK, well, you still can't be sure, but now you can do keyword search, and you can at least read what it does say without having to get on a train.
Truly, we live in an age of marvels.
[ Addendum 20191004: More about this ]
[Other articles in category /law] permanent link
Wed, 02 Oct 2019Last month I mentioned that, while federal law generally prohibits signs and billboards about signs within ⅛ mile of a federal highway, signs offering free coffee are allowed.
Vilhelm Sjöberg brought to my attention the 2015 U.S. Supreme Court decision in Reed v. Town of Gilbert. Under the Reed logic, the exemption for free coffee may actually be unconsitutional. The majority's opinion states, in part:
The Sign Code is content based on its face. It defines the categories of temporary, political, and ideological signs on the basis of their messages and then subjects each category to different restrictions. The restrictions applied thus depend entirely on the sign’s communicative content.
The court concluded that the Sign Code (of the town of Gilbert, AZ) was therefore subject to the very restrictive standard of strict scrutiny, which required that it be struck down unless the government could demonstrate both that it was necessary to a “compelling state interest” and that it be “narrowly tailored” to achieving that interest. The Gilbert Sign Code did not survive this analysis.
Although the court unanimously struck down the Sign Code, a concurrence, written by Justice Kagan and joined by Ginsburg and Breyer, faulted the majority's reasoning:
On the majority’s view, courts would have to determine that a town has a compelling interest in informing passersby where George Washington slept. And likewise, courts would have to find that a town has no other way to prevent hidden-driveway mishaps than by specially treating hidden-driveway signs. (Well-placed speed bumps? Lower speed limits? Or how about just a ban on hidden driveways?)
Kagan specifically mentioned the “free coffee” exception as being one of many that would be imperiled by the court's reasoning in this case.
Thanks very much to M. Sjöberg for pointing this out.
[Other articles in category /law] permanent link
Tue, 01 Oct 2019
How do I keep type constructors from overrunning my Haskell program?
Here's a little function I wrote over the weekend as part of a suite for investigating Yahtzee:
type DiceChoice = [ Bool ]
type DiceVals = [ Integer ]
type DiceState = (DiceVals, Integer)
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls [] ([], n) = [ ([], n-1) ]
allRolls [] _ = undefined
allRolls (chosen:choices) (v:vs, n) =
allRolls choices (vs,n-1) >>=
\(roll,_) -> [ (d:roll, n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
I don't claim this code is any good; I was just hacking around exploring the problem space. But it does do what I wanted.
The allRolls function takes a current game state, something like
( [ 6, 4, 4, 3, 1 ], 2 )
which means that we have two rolls remaining in the round, and the most recent roll of the five dice showed 6, 4, 4, 3, and 1, respectively. It also takes a choice of which dice to keep: The list
[ False, True, True, False, False ]
means to keep the 4's and reroll the 6, the 3, and the 1.
The allRolls function then produces a list of the possible resulting
dice states, in this case 216 items:
[ ( [ 1, 4, 4, 1, 1 ], 1 ) ,
( [ 1, 4, 4, 1, 2 ], 1 ) ,
( [ 1, 4, 4, 1, 3 ], 1 ) ,
…
( [ 6, 4, 4, 6, 6 ], 1 ) ]
This function was not hard to write and it did work adequately.
But I wasn't satisfied. What if I have some unrelated integer list
and I pass it to a function that is expecting a DiceVals, or vice
versa? Haskell type checking is supposed to prevent this from
happening, and by using type aliases I am forgoing this advantage.
No problem, I can easily make DiceVals and the others into datatypes:
data DiceChoice = DiceChoice [ Bool ]
data DiceVals = DiceVals [ Integer ]
data DiceState = DiceState (DiceVals, Integer)
The declared type of allRolls is the same:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
But now I need to rewrite allRolls, and a straightforward
translation is unreadable:
allRolls (DiceChoice []) (DiceState (DiceVals [], n)) = [ DiceState(DiceVals [], n-1) ]
allRolls (DiceChoice []) _ = undefined
allRolls (DiceChoice (chosen:choices)) (DiceState (DiceVals (v:vs), n)) =
allRolls (DiceChoice choices) (DiceState (DiceVals vs,n-1)) >>=
\(DiceState(DiceVals roll, _)) -> [ DiceState (DiceVals (d:roll), n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
This still compiles and it still produces the results I want. And it
has the type checking I want. I can no longer pass a raw integer
list, or any other isomorphic type, to allRolls. But it's
unmaintainable.
I could rename allRolls to something similar, say allRolls__, and
then have allRolls itself be just a type-checking front end to
allRolls__, say like this:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls (DiceChoice dc) (DiceState ((DiceVals dv), n)) =
allRolls__ dc dv n
allRolls__ [] [] n = [ DiceState (DiceVals [], n-1) ]
allRolls__ [] _ _ = undefined
allRolls__ (chosen:choices) (v:vs) n =
allRolls__ choices vs n >>=
\(DiceState(DiceVals roll,_)) -> [ DiceState (DiceVals (d:roll), n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
And I can do something similar on the output side also:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls (DiceChoice dc) (DiceState ((DiceVals dv), n)) =
map wrap $ allRolls__ dc dv n
where wrap (dv, n) = DiceState (DiceVals dv, n)
allRolls__ [] [] n = [ ([], n-1) ]
allRolls__ [] _ _ = undefined
allRolls__ (chosen:choices) (v:vs) n =
allRolls__ choices vs n >>=
\(roll,_) -> [ (d:roll, n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
This is not unreasonably longer or more cluttered than the original
code. It does forgo type checking inside of allRolls__,
unfortunately. (Suppose that the choices and vs arguments had the
same type, and imagine that in the recursive call I put them in the
wrong order.)
Is this considered The Thing To Do? And if so, where could I have learned this, so that I wouldn't have had to invent it? (Or, if not, where could I have learned whatever is The Thing To Do?)
I find most Haskell instruction on the Internet to be either too elementary
pet the nice monad, don't be scared, just approach it very slowly and it won't bite
or too advanced
here we've enabled the
{-# SemispatulatedTypes #-}pragma so we can introduce an overloaded contravariant quasimorphism in the slice category
with very little practical advice about how to write, you know, an actual program. Where can I find some?
[Other articles in category /prog/haskell] permanent link


