Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 04 Dec 2018
I figured out that context manager bug!
A couple of days ago I described a strange bug in my “Greenlight” project that was causing Git to fail unpredictably, saying:
fatal: this operation must be run in a work tree
The problem seemed to go away when I changed
with env_var("GIT_DIR", self.repo_dir):
with env_var("GIT_WORK_TREE", self.work_dir):
result = subprocess.run(command, ...)
to
with env_var("GIT_DIR", self.repo_dir, "GIT_WORK_TREE", self.work_dir):
result = subprocess.run(command, ...)
but I didn't understand why. I said:
This was so unexpected that I wondered if the real problem was nondeterministic and if some of the debugging messages had somehow perturbed it. But I removed everything but the context manager change and ran another test, which succeeded. By then I was five and half hours into the debugging and I didn't have any energy left to actually understand what the problem had been. I still don't know.
The problem re-manifested again today, and this time I was able to track it down and fix it. The context manager code I mentioned above was not the issue.
That subprocess.run call is made inside a git_util object which,
as you can see in the tiny excerpt above, has a self.work_dir
attribute that tells it where to find the working tree. Just before
running a Git command, the git_util object installs self.work_dir
into the environment to tell Git where the working tree is.
The git_util object is originally manufactured by Greenlight itself,
which sets the work_dir attribute to a path that contains the
current process ID number. Just before the process exits, Greenlight
destroys the working tree. This way, concurrent processes never try
to use the same working tree, which would be a mess.
When Greenlight needs to operate on the repository, it uses its
git_util object directly. It also creates a submission object to
represent the submitted branch, and it installs the git_util object
into the submission object, so that the submission object can also
operate on the repository. For example, the submission object may ask
its git_util object if it needs to be rebased onto some other
branch, and if so to please do it. So:
- Greenlight has a
submission. submission.gitis thegit_utilobject that deals with Git.submission.git.work_diris the path to the per-process temporary working tree.
Greenlight's main purpose is to track these submission objects, and it has a database of them. To save time when writing the initial implementation, instead of using a real database, I had Greenlight use Python's “pickle” feature to pickle the list of submissions.
Someone would submit a branch, and Greenlight would pickle the
submission. The submission contained its git_util object, and that
got pickled along with the rest. Then Greenlight would exit and, just
before doing so, it would destroy its temporary working tree.
Then later, when someone else wanted to approve the submission for
publication, Greenlight would set up a different working tree with its
new process ID, and unpickle the submission. But the submission's
git.work_dir had been pickled with the old path, which no longer
existed.
The context manager was working just fine. It was setting
GIT_WORK_TREE to the work_dir value in the git_util object. But
the object was obsolete and its work_dir value pointed to a
directory that had been destroyed!
Adding to the confusion:
Greenlight's own
git_utilobject was always fresh and had the right path in it, so Git commands run directly by Greenlight all worked properly.Any new
submissionobjects created by Greenlight would have the right path, so Git commands run by fresh submissions also worked properly.Greenlight doesn't always destroy the working tree when it exits. If it exits abnormally, it leaves the working tree intact, for a later autopsy. And the unpickled submission would work perfectly if the working tree still existed, and it would be impossible to reproduce the problem!
Toward the end of the previous article, I said:
I suspect I'm being sabotaged somewhere by Python's weird implicit ideas of scope and variable duration, but I don't know. Yet.
For the record, then: The issue was indeed one of variable duration. But Python's weird implicit ideas were, in this instance, completely blameless. Instead the issue was caused by a software component even more complex and more poorly understood: “Dominus”.
This computer stuff is amazingly complicated. I don't know how anyone gets anything done.
[Other articles in category /prog/bug] permanent link
Sun, 02 Dec 2018There are combinatorial objects called necklaces and bracelets and I can never remember which is which.
Both are finite sequences of things (typically symbols) where the
start point is not important. So the bracelet ABCDE is considered
to be the same as the bracelets BCDEA, CDEAB, DEABC, and
EABCD.
One of the two also disregards the direction you go, so that
ABCDE is also considered the same as EDCBA (and so also DCBAE,
etc.). But which? I have to look it up every time.
I have finally thought of a mnemonic. In a necklace, the direction is important, because to reverse an actual necklace you have to pull it off over the wearer's head, turn it over, and put it back on. But in a bracelet the direction is not important, because it could be on either wrist, and a bracelet on the left wrist is the same as the reversed bracelet on the right wrist.
Okay, silly, maybe, but I think it's going to work.
[Other articles in category /math] permanent link
Another day, another bug. No, four bugs.
I'm working on a large and wonderful project called “Greenlight”. It's a Git branch merging service that implements the following workflow:
- Submitter submits a branch to Greenlight (
greenlight submit my-topic-branch) - Greenlight analyzes the branch to decide if it changes anything that requires review and signoff
- If so, it contacts the authorized reviewers, who then inform
Greenlight that they approve the changes (
greenlight approve 03a46dc1) - Greenlight merges the branch to
masterand publishes the result to the central repository
Of course, there are many details elided here.
Multiple instances of Greenlight share a local repository, but to avoid
confusion each has its own working tree. In Git you can configure
these by setting GIT_DIR and GIT_WORK_TREE environment variables,
respectively. When Greenlight needs to run a Git command, it does so
like this:
with env_var("GIT_DIR", self.repo_dir):
with env_var("GIT_WORK_TREE", self.work_dir):
result = subprocess.run(command, ...)
The env_var here is a Python context manager that saves the old
environment, sets the new environment variable, and then when the body
of the block is complete, it restores the environment to the way it
was. This worked in testing every time.
But the first time a beta tester ran the approve command, Greenlight
threw a fatal exception. It was trying to run git checkout --quiet
--detach, and this was failing, with Git saying
fatal: this operation must be run in a work tree
Where was the GIT_WORK_TREE setting going? I still don't know. But
in the course of trying to track the problem down, I changed the code
above to:
with env_var("GIT_DIR", self.repo_dir, "GIT_WORK_TREE", self.work_dir):
result = subprocess.run(command, ...)
and the problem, whatever it was, no longer manifested.
But this revealed a second bug: Greenlight no longer failed in the
approval phase. It went ahead and merged the branch, and then tried
to publish the merge with git push origin .... But the push was
rejected.
This is because the origin repository had an update hook that ran
on every push, which performed the same review analysis that Greenlight
was performing; one of Greenlight's main purposes is to be a
replacement for this hook. To avoid tying up the main repository for
too long, this hook had a two-minute timeout, after which it would die
and reject the push. This had only happened very rarely in the past,
usually when someone was inadvertently trying to push a malformed
branch. For example, they might have rebased all of master onto
their topic branch. In this case, however, the branch really was
legitimately enormous; it contained over 2900 commits.
“Oh, right,” I said. “I forgot to add the exception to the hook that tells it that it can immediately approve anything pushed by Greenlight.” The hook can assume that if the push comes from Greenlight, it has already been checked and authorized.
Pushes are happening via SSH, and Greenlight has its own SSH identity,
which is passed to the hook itself in the GL_USERNAME variable.
Modifying the hook was easy: I just added:
if environ["GL_USERNAME"] == 'greenlight':
exit(0)
This didn't work. My first idea was that Greenlight's public SSH key
had not been installed in the authorized_keys file in the right
place. When I grepped for greenlight in the authorized_keys file,
there were no matches. The key was actually there, but in Gitlab the
authorized_keys file doesn't have actual usernames in it. It has
internal userids, which are then mapped to GL_USERNAME variables by
some other entity. So I chased that wild goose for a while.
Eventually I determined that the key was in the right place, but
that the name of the Greenlight identity on the receiving side was not
greenlight but bot-greenlight, which I had forgotten.
So I changed the exception to say:
if environ["GL_USERNAME"] == 'bot-greenlight':
exit(0)
and it still didn't work. I eventually discovered that when
Greenlight did the push, the GL_USERNAME was actually set to mjd.
“Oh, right,” I said. “I forgot to have Greenlight use its own
SSH credentials in the ssh connection.”
The way you do this is to write a little wrapper program that obtains
the correct credentials and runs ssh, and then you set GIT_SSH to
point to the wrapper. It looks like this:
#!/usr/bin/env bash
export -n SSH_CLIENT SSH_TTY SSH_AUTH_SOCK SSH_CONNECTION
exec /usr/bin/ssh -i $HOME/.ssh/identity "$@"
But wait, why hadn't I noticed this before? Because, apparently,
every single person who had alpha-tested Greenlight had had their own
credentials stored in ssh-agent, and every single one had had
agent-forwarding enabled, so that when Greenlight tried to use ssh
to connect to the Git repository, SSH duly forwarded their credentials
along and the pushes succeeded. Amazing.
With these changes, the publication went through. I committed the changes to the SSH credential stuff, and some other unrelated changes, and I looked at what was left to see what had actually fixed the original bug. Every change but one was to add diagnostic messages and logging. The fix for the original bug had been to replace the nested context managers with a single context manager. This was so unexpected that I wondered if the real problem was nondeterministic and if some of the debugging messages had somehow perturbed it. But I removed everything but the context manager change and ran another test, which succeeded. By then I was five and half hours into the debugging and I didn't have any energy left to actually understand what the problem had been. I still don't know.
If you'd like to play along at home, the context manager looks like this, and did not change during the debugging process:
from contextlib import contextmanager
@contextmanager
def env_var(*args):
# Save old values of environment variables in `old`
# A saved value of `None` means that the variable was not there before
old = {}
for i in range(len(args)//2):
(key, value) = (args[2*i : 2*i+2])
old[key] = None
if key in os.environ:
old[key] = os.environ[str(key)]
if value is None: os.environ.pop(str(key), "dummy")
else:
os.environ[str(key)] = str(value)
yield
# Undo changes from versions saved in `old`
for (key, value) in old.items():
if value is None: os.environ.pop(str(key), "dummy")
else: os.environ[str(key)] = value
I suspect I'm being sabotaged somewhere by Python's weird implicit ideas of scope and variable duration, but I don't know. Yet.
This computer stuff is amazingly complicated. I don't know how anyone gets anything done.
[ Addendum 20181204: I figured it out. ]
[Other articles in category /prog/bug] permanent link
Thu, 29 Nov 2018
How many kinds of polygonal loops? (part 2)
And I said I thought there were nine analogous figures with six points.
Rahul Narain referred me to a recent discussion of almost this exact question on Math Stackexchange. (Note that the discussion there considers two figures different if they are reflections of one another; I consider them the same.) The answer turns out to be OEIS A000940. I had said:
… for !!N=6!!, I found it hard to enumerate. I think there are nine shapes but I might have missed one, because I know I kept making mistakes in the enumeration …
I missed three. The nine I got were:
And the three I missed are:
I had tried to break them down by the arrangement of the outside ring of edges, which can be described by a composition. The first two of these have type !!1+1+1+1+2!! (which I missed completely; I thought there were none of this type) and the other has type !!1+2+1+2!!, the same as the !!015342!! one in the lower right of the previous diagram.
I had ended by saying:
I would certainly not trust myself to hand-enumerate the !!N=7!! shapes.
Good call, Mr. Dominus! I considered filing this under “oops” but I decided that although I had gotten the wrong answer, my confidence in it had been adequately low. On one level it was a mistake, but on a higher and more important level, I did better.
I am going to try the (Cauchy-Frobenius-)Burnside-(Redfield-)Pólya lemma on it next and see if I can get the right answer.
Thanks again to Rahul Narain for bringing this to my attention.
[Other articles in category /math] permanent link
How many kinds of polygonal loops?
Take !!N!! equally-spaced points on a circle. Now connect them in a loop: each point should be connected to exactly two others, and each point should be reachable from the others. How many geometrically distinct shapes can be formed?
For example, when !!N=5!!, these four shapes can be formed:
(I phrased this like a geometry problem, but it should be clear it's actually a combinatorics problem. But it's much easier to express as a geometry problem; to talk about the combinatorics I have to ask you to consider a permutation !!P!! where !!P(i±1)≠P(i)±1!! blah blah blah…)
For !!N<5!! it's easy. When !!N=3!! it is always a triangle. When !!N=4!! there are only two shapes: a square and a bow tie.
But for !!N=6!!, I found it hard to enumerate. I think there are nine shapes but I might have missed one, because I know I kept making mistakes in the enumeration, and I am not sure they are all corrected:
It seems like it ought not to be hard to generate and count these, but so far I haven't gotten a good handle on it. I produced the !!N=6!! display above by considering the compositions of the number !!6!!:
| Composition | How many loops? |
|---|---|
| 6 | 1 |
| 1+5 | — |
| 2+4 | 1 |
| 3+3 | 1 |
| 1+1+4 | — |
| 1+2+3 | 1 |
| 2+2+2 | 2 |
| 1+1+1+3 | — |
| 1+1+2+2 | 1 |
| 1+2+1+1 | 1 |
| 1+1+1+1+2 | — |
| 1+1+1+1+1+1 | 1 |
| Total | 9 (?) |
(Actually it's the compositions, modulo bracelet symmetries — that is, modulo the action of the dihedral group.)
But this is fraught with opportunities for mistakes in both directions. I would certainly not trust myself to hand-enumerate the !!N=7!! shapes.
[ Addendum: For !!N=6!! there are 12 figures, not 9. For !!N=7!!, there are 39. Further details. ]
[Other articles in category /math] permanent link
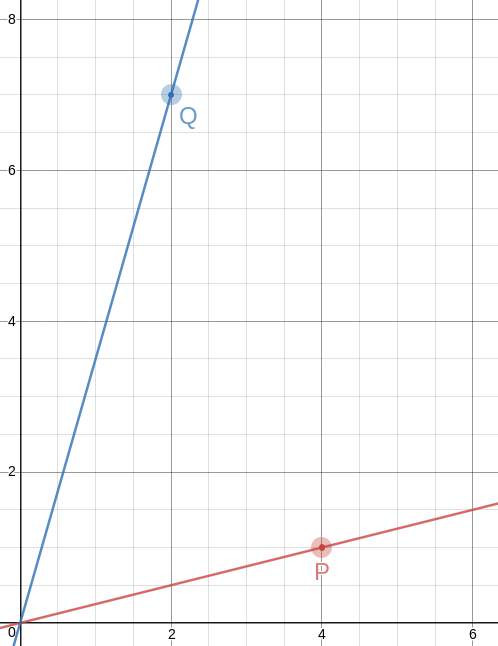
Sun, 25 Nov 2018A couple of years back I was thinking about how to draw a good approximation to an equilateral triangle on a piece of graph paper. There are no lattice points that are exactly the vertices of an equilateral triangle, but you can come close, and one way to do it is to find integers !!a!! and !!b!! with !!\frac ba\approx \sqrt 3!!, and then !!\langle 0, 0\rangle, \langle 2a, 0\rangle,!! and !!\langle a, b\rangle!! are almost an equilateral triangle.
But today I came back to it for some reason and I wondered if it would be possible to get an angle closer to 60°, or numbers that were simpler, or both, by not making one of the sides of the triangle perfectly horizontal as in that example.
So okay, we want to find !!P = \langle a, b\rangle!! and !!Q = \langle c,d\rangle!! so that the angle !!\alpha!! between the rays !!\overrightarrow{OP}!! and !!\overrightarrow{OQ}!! is as close as possible to !!\frac\pi 3!!.
The first thing I thought of was that the dot product !!P\cdot Q = |P||Q|\cos\alpha!!, and !!P\cdot Q!! is super-easy to calculate, it's just !!ac+bd!!. So we want $$\frac{ad+bc}{|P||Q|} = \cos\alpha \approx \frac12,$$ and everything is simple, except that !!|P||Q| = \sqrt{a^2+b^2}\sqrt{c^2+d^2}!!, which is not so great.
Then I tried something else, using high-school trigonometry. Let !!\alpha_P!! and !!\alpha_Q!! be the angles that the rays make with the !!x!!-axis. Then !!\alpha = \alpha_Q - \alpha_P = \tan^{-1} \frac dc - \tan^{-1} \frac ba!!, which we want close to !!\frac\pi3!!.
Taking the tangent of both sides and applying the formula $$\tan(q-p) = \frac{\tan q - \tan p}{1 + \tan q \tan p}$$ we get $$ \frac{\frac dc - \frac ba}{1 + \frac dc\frac ba} \approx \sqrt3.$$ Or simplifying a bit, the super-simple $$\frac{ad-bc}{ac+bd} \approx \sqrt3.$$
After I got there I realized that my dot product idea had almost worked. To get rid of the troublesome !!|P||Q|!! you should consider the cross product also. Observe that the magnitude of !!P\times Q!! is !!|P||Q|\sin\alpha!!, and is also $$\begin{vmatrix} a & b & 0 \\ c & d & 0 \\ 1 & 1 & 1 \end{vmatrix} = ad - bc$$ so that !!\sin\alpha = \frac{ad-bc}{|P||Q|}!!. Then if we divide, the !!|P||Q|!! things cancel out nicely: $$\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = \frac{ad-bc}{ac+bd}$$ which we want to be as close as possible to !!\sqrt 3!!.
Okay, that's fine. Now we need to find some integers !!a,b,c,d!! that do what we want. The usual trick, “see what happens if !!a=0!!”, is already used up, since that's what the previous article was about. So let's look under the next-closest lamppost, and let !!a=1!!. Actually we'll let !!b=1!! instead to keep things more horizonal. Then, taking !!\frac74!! as our approximation for !!\sqrt3!!, we want
$$\frac{ad-c}{ac+d} = \frac74$$
or equivalently $$\frac dc = \frac{7a+4}{4a-7}.$$
Now we just tabulate !!7a+4!! and !!4a-7!! looking for nice fractions:
| !!a!! | !!d =!! !!7a+4!! | !!c=!! !!4a-7!! |
|---|---|---|
| 2 | 18 | 1 |
| 3 | 25 | 5 |
| 4 | 32 | 9 |
| 5 | 39 | 13 |
| 6 | 46 | 17 |
| 7 | 53 | 21 |
| 8 | 60 | 25 |
| 9 | 67 | 29 |
| 10 | 74 | 33 |
| 11 | 81 | 37 |
| 12 | 88 | 41 |
| 13 | 95 | 45 |
| 14 | 102 | 49 |
| 15 | 109 | 53 |
| 16 | 116 | 57 |
| 17 | 123 | 61 |
| 18 | 130 | 65 |
| 19 | 137 | 69 |
| 20 | 144 | 73 |
Each of these gives us a !!\langle c,d\rangle!! point, but some are much better than others. For example, in line 3, we have take !!\langle 5,25\rangle!! but we can use !!\langle 1,5\rangle!! which gives the same !!\frac dc!! but is simpler. We still get !!\frac{ad-bc}{ac+bd} = \frac 74!! as we want.
Doing this gives us the two points !!P=\langle 3,1\rangle!! and !!Q=\langle 1, 5\rangle!!. The angle between !!\overrightarrow{OP}!! and !!\overrightarrow{OQ}!! is then !!60.255°!!. This is exactly the same as in the approximately equilateral !!\langle 0, 0\rangle, \langle 8, 0\rangle,!! and !!\langle 4, 7\rangle!! triangle I mentioned before, but the numbers could not possibly be easier to remember. So the method is a success: I wanted simpler numbers or a better approximation, and I got the same approximation with simpler numbers.
To draw a 60° angle on graph paper, mark !!P=\langle 3,1\rangle!! and !!Q=\langle 1, 5\rangle!!, draw lines to them from the origin with a straightedge, and there is your 60° angle, to better than a half a percent.
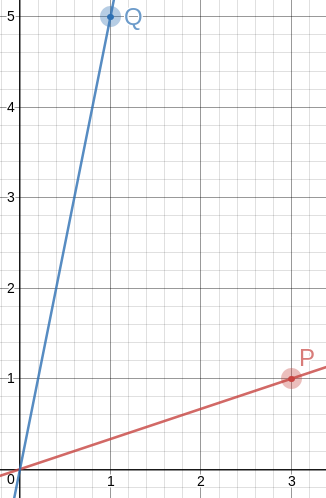
There are some other items in the table (for example row 18 gives !!P=\langle 18,1\rangle!! and !!Q=\langle 1, 2\rangle!!) but because of the way we constructed the table, every row is going to give us the same angle of !!60.225°!!, because we approximated !!\sqrt3\approx\frac74!! and !!60.225° = \tan^{-1}\frac74!!. And the chance of finding numbers better than !!\langle 3,1\rangle!! and !!\langle 1, 5\rangle!! seems slim. So now let's see if we can get the angle closer to exactly !!60°!! by using a better approximation to !!\sqrt3!! than !!\frac 74!!.
The next convergents to !!\sqrt 3!! are !!\frac{19}{11}!! and !!\frac{26}{15}!!. I tried the same procedure for !!\frac{19}{11}!! and it was a bust. But !!\frac{26}{15}!! hit the jackpot: !!a=4!! gives us !!15a-26 = 34!! and !!26a-15=119!!, both of which are multiples of 17. So the points are !!P=\langle 4,1\rangle!! and !!Q=\langle 2, 7\rangle!!, and this time the angle between the rays is !!\tan^{-1}\frac{26}{15} = 60.018°!!. This is as accurate as anyone drawing on graph paper could possibly need; on a circle with a one-mile radius it is an error of 20 inches.
Of course, the triangles you get are no longer equilateral, not even close. That first one has sides of !!\sqrt{10}, \sqrt{20}, !! and !!\sqrt{26}!!, and the second one has sides of !!\sqrt{17}, \sqrt{40}, !! and !!\sqrt{53}!!. But! The slopes of the lines are so simple, it's easy to construct equilateral triangles with a straightedge and a bit of easy measuring. Let's do it on the !!60.018°!! angle and see how it looks.
!!\overrightarrow{OP}!! has slope !!\frac14!!, so the perpendicular to it has slope !!-4!!, which means that you can draw the perpendicular by placing the straightedge between !!P!! and some point !!P+x\langle -1, 4\rangle!!, say !!\langle 2, 9\rangle!! as in the picture. The straightedge should have slope !!-4!!, which is very easy to arrange: just imagine the little squares grouped into stacks of four, and have the straightedge go through opposite corners of each stack. The line won't necessarily intersect !!\overrightarrow{OQ}!! anywhere great, but it doesn't need to, because we can just mark the intersection, wherever it is:
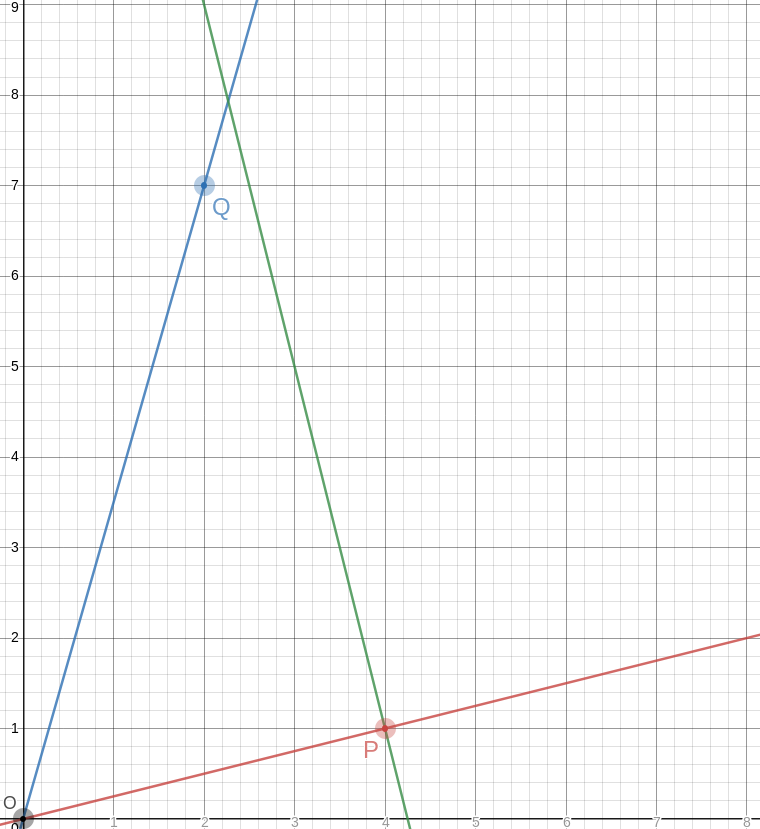
Let's call that intersection !!A!! for “apex”.
The point opposite to !!O!! on the other side of !!P!! is even easier; it's just !!P'=2P =\langle 8, 2\rangle!!. And the segment !!P'A!! is the third side of our equilateral triangle:
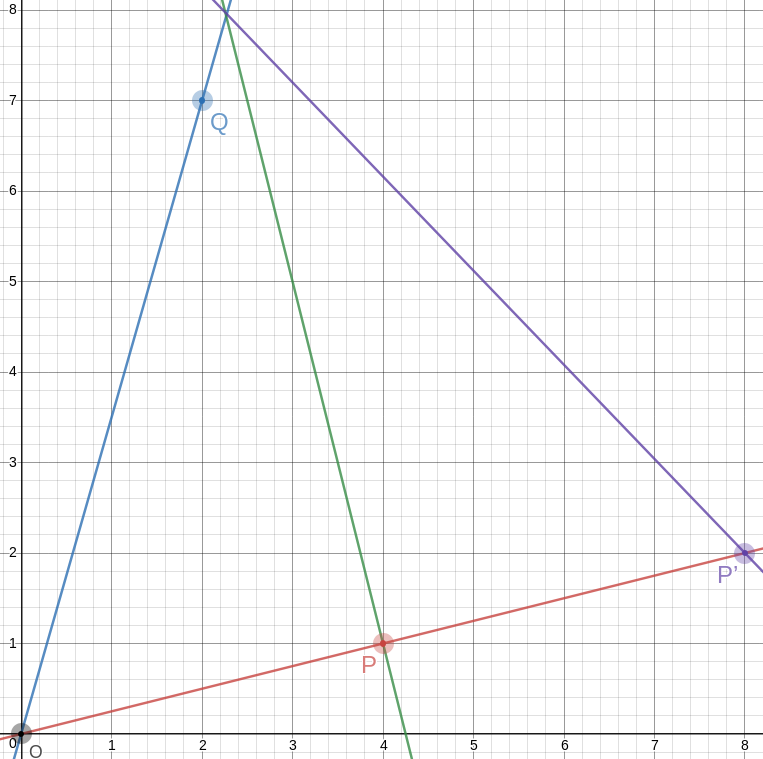
This triangle is geometrically similar to a triangle with vertices at !!\langle 0, 0\rangle, \langle 30, 0\rangle,!! and !!\langle 15, 26\rangle!!, and the angles are just close to 60°, but it is much smaller.
Woot!
[Other articles in category /math] permanent link
Mon, 19 Nov 2018I think I forgot to mention that I was looking recently at hamiltonian cycles on a dodecahedron. The dodecahedron has 30 edges and 20 vertices, so a hamiltonian path contains 20 edges and omits 10. It turns out that it is possible to color the edges of the dodecahedron in three colors so that:
- Every vertex is incident to one edge of each color
- The edges of any two of the three colors form a hamiltonian cycle
Marvelous!
(In this presentation, I have taken one of the vertices and sent it away to infinity. The three edges with arrowheads are all attached to that vertex, off at infinity, and the three faces incident to it have been stretched out to cover the rest of the plane.)
Every face has five edges and there are only three colors, so the colors can't be distributed evenly around a face. Each face is surrounded by two edges of one color, two of a second color, and only one of the last color. This naturally divides the 12 faces into three classes, depending on which color is assigned to only one edge of that face.
Each class contains two pairs of two adjacent pentagons, and each adjacent pair is adjacent to the four pairs in the other classes but not to the other pair in its own class.
Each pair shares a single edge, which we might call its “hinge”. Each pair has 8 vertices, of which two are on its hinge, four are adjacent to the hinge, and two are not near of the hinge. These last two vertices are always part of the hinges of the pairs of a different class.
I could think about this for a long time, and probably will. There is plenty more to be seen, but I think there is something else I was supposed to be doing today, let me think…. Oh yes! My “job”! So I will leave you to go on from here on your own.
[ Addendum 20181203: David Eppstein has written a much longer and more detailed article about triply-Hamiltonian edge colorings, using this example as a jumping-off point. ]
[Other articles in category /math] permanent link
Sat, 17 Nov 2018
How do you make a stella octangula?
Yesterday Katara asked me out of nowhere “When you make a stella octangula, do you build it up from an octahedron or a tetrahedron?” Stella octangula was her favorite polyhedron eight years ago.
“Uh,” I said. “Both?”
Then she had to make one to see what I meant. You can start with a regular octahedron:
Then you erect spikes onto four of the octahedron's faces; this produces a regular tetrahedron:
Then you erect spikes onto the other four of the octahedron's faces. Now you have a stella octangula.
So yeah, both. Or instead of starting with a unit octahedron and erecting eight spikes of size 1, you can start with a unit tetrahedron and erect four spikes of size ½. It's both at once.
[Other articles in category /math] permanent link
Tue, 13 Nov 2018
Counting paths through polyhedra
A while back someone asked on math stack exchange how many paths there were of length !!N!! from one vertex of a dodecahedron to the opposite vertex. The vertices are distance 5 apart, so for !!N<5!! the answer is zero, but the paths need not be simple, so the number grows rapidly with !!N!!; there are 58 million paths of length 19.
This is the kind of thing that the computer answers easily, so that's where I started, and unfortunately that's also where I finished, saying:
I'm still working out a combinatorial method of calculating the answer, and I may not be successful.
Another user reminded me of this and I took another whack at it. I couldn't remember what my idea had been last year, but my idea this time around was to think of the dodecahedron as the Cayley graph for a group, and then the paths are expressions that multiply out to a particular group element.
I started by looking at a tetrahedron instead of at a dodecahedron, to see how it would work out. Here's a tetrahedron.
Let's say we're counting paths from the center vertex to one of the others, say the one at the top. (Tetrahedra don't have opposite vertices, but that's not an important part of the problem.) A path is just a list of edges, and each edge is labeled with a letter !!a!!, !!b!!, or !!c!!. Since each vertex has exactly one edge with each label, every sequence of !!a!!'s, !!b!!'s, and !!c!!'s represents a distinct path from the center to somewhere else, although not necessarily to the place we want to go. Which of these paths end at the bottom vertex?
The edge labeling I chose here lets us play a wonderful trick. First, since any edge has the same label at both ends, the path !!x!! always ends at the same place as !!xaa!!, because the first !!a!! goes somewhere else and then the second !!a!! comes back again, and similarly !!xbb!! and !!xcc!! also go to the same place. So if we have a path that ends where we want, we can insert any number of pairs !!aa, bb, !! or !!cc!! and the new path will end at the same place.
But there's an even better trick available. For any starting point, and any letters !!x!! and !!y!!, the path !!xy!! always ends at the same place as !!yx!!. For example, if we start at the middle and follow edge !!b!!, then !!c!!, we end at the lower left; similarly if we follow edge !!c!! and then !!b!! we end at the same place, although by a different path.
Now suppose we want to find all the paths of length 7 from the middle to the top. Such a path is a sequence of a's, b's, and c's of length 7. Every such sequence specifies a different path out of the middle vertex, but how can we recognize which sequences end at the top vertex?
Since !!xy!! always goes to the same place as !!yx!!, the order of the
seven letters doesn't matter.
A complicated-seeming path like abacbcb must go to the same place
as !!aabbbcc!!, the same path with the letters in alphabetical order.
And since !!xx!! always goes back to
where it came from, the path !!aabbbcc!! goes to the same place as !!b!!
Since the paths we want are those that go to the same place as the trivial path !!c!!, we want paths that have an even number of !!a!!s and !!b!!s and an odd number of !!c!!s. Any path fitting that description will go to same place as !!c!!, which is the top vertex. It's easy to enumerate such paths:
| Prototypical path | How many? |
|---|---|
| ccccccc | 1 |
| cccccaa | 21 |
| cccccbb | 21 |
| cccaaaa | 35 |
| cccaabb | 210 |
| cccbbbb | 35 |
| caaaaaa | 7 |
| caaaabb | 105 |
| caabbbb | 105 |
| cbbbbbb | 7 |
| Total | 547 |
Here something like “cccbbbb” stands for all the paths that have three c's and four b's, in some order; there are !!\frac{7!}{4!3!} = 35!! possible orders, so 35 paths of this type. If we wanted to consider paths of arbitrary length, we could use Burnside's lemma, but I consider the tetrahedron to have been sufficiently well solved by the observations above (we counted 547 paths by hand in under 60 seconds) and I don't want to belabor the point.
Okay! Easy-peasy!
Now let's try cubes:
Here we'll consider paths between two antipodal vertices in the upper left and the lower right, which I've colored much darker gray than the other six vertices.
The same magic happens as in the tetrahedron. No matter where we
start, and no matter what !!x!! and !!y!! are, the path !!xy!! always
gets us to the same place as !!yx!!. So again, if some complicated
path gets us where we want to go, we can permute its components into
any order and get a different path of the same length to the same
place. For example, starting from the upper left, bcba, abcb, and
abbc all go to the same place.
And again, because !!xx!! always make a trip along one edge and then
back along the same edge, it never goes anywhere. So the three paths
in the previous paragraph also go to the same place as ac and ca
and also aa bcba bb aa aa aa aa bb cc cc cc bb.
We want to count paths from one dark vertex to the other. Obviously
abc is one such, and so too must be bac, cba, acb, and so
forth. There are six paths of length 3.
To get paths of length 5, we must insert a pair of matching letters
into one of the paths of length 3. Without loss of generality we can
assume that we are inserting aa. There are 20 possible orders for
aaabc, and three choices about which pair to insert, for a total of
60 paths.
To get paths of length 7, we must insert two pairs. If the two pairs are the same, there are !!\frac{7!}{5!} = 42!! possible orders and 3 choices about which letters to insert, for a total of 126. If the two pairs are different, there are !!\frac{7!}{3!3!} = 140!! possible orders and again 3 choices about which pairs to insert, for a total of 420, and a grand total of !!420+126 = 546!! paths of length 7. Counting the paths of length 9 is almost as easy. For the general case, again we could use Burnside's lemma, or at this point we could look up the unusual sequence !!6, 60, 546!! in OEIS and find that the number of paths of length !!2n+1!! is already known to be !!\frac34(9^n-1)!!.
So far this technique has worked undeservedly well. The original problem wanted to use it to study paths on a dodecahedron. Where, unfortunately, the magic property !!xy=yx!! doesn't hold. It is possible to label the edges of the dodecahedron so that every sequence of labels determines a unique path:
but there's nothing like !!xy=yx!!. Well, nothing exactly like it. !!xy=yx!! is equivalent to !!(xy)^2=1!!, and here instead we have !!(xy)^{10}=1!!. I'm not sure that helps. I will probably need another idea.
The method fails similarly for the octahedron — which is good, because I can use the octahedron as a test platform to try to figure out a new idea. On an octahedron we need to use four kinds of labels because each vertex has four edges emerging from it:
Here again we don't have !!(xy)^2=1!! but we do have !!(xy)^3 = 1!!. So it's possible that if I figure out a good way to enumerate paths on the octahedron I may be able to adapt the technique to the dodecahedron. But the octahedron will be !!\frac{10}3!! times easier.
Viewed as groups, by the way, these path groups are all examples of Coxeter groups. I'm not sure this is actually a useful observation, but I've been wanting to learn about Coxeter groups for a long time and this might be a good enough excuse.
[Other articles in category /math] permanent link
A puzzle about representing numbers as a sum of 3-smooth numbers
I think this would be fun for a suitably-minded bright kid of maybe 12–15 years old.
Consider the following table of numbers of the form !!2^i3^j!!:
| 1 | 3 | 9 | 27 | 81 | 243 |
| 2 | 6 | 18 | 54 | 162 | … |
| 4 | 12 | 36 | 108 | … | … |
| 8 | 24 | 72 | 216 | … | … |
| 16 | 48 | 144 | … | … | … |
| 32 | 96 | … | … | … | … |
| 64 | 192 | … | … | … | … |
| 128 | … | … | … | … | … |
Given a number !!n!!, it is possible to represent !!n!! as a sum of entries from the table, with the following constraints:
- No more than one entry from any column
- An entry may only be used if it is in a strictly higher row than any entry to its left.
For example, one may not represent !!23 = 2 + 12 + 9!!, because the !!12!! is in a lower row than the !!2!! to its left.
| 1 | 3 | 9 | 27 |
| 2 | 6 | 18 | 54 |
| 4 | 12 | 36 | 108 |
But !!23 = 8 + 6 + 9!! is acceptable, because 6 is higher than 8, and 9 is higher than 6.
| 1 | 3 | 9 | 27 |
| 2 | 6 | 18 | 54 |
| 4 | 12 | 36 | 108 |
| 8 | 24 | 72 | 216 |
Or, put another way: can we represent any number !!n!! in the form $$n = \sum_i 2^{a_i}3^{b_i}$$ where the !!a_i!! are strictly decreasing and the !!b_i!! are strictly increasing?
Spoiler:
maxpow3 1 = 1
maxpow3 2 = 1
maxpow3 n = 3 * maxpow3 (n `div` 3)
rep :: Integer -> [Integer]
rep 0 = []
rep n = if even n then map (* 2) (rep (n `div` 2))
else (rep (n - mp3)) ++ [mp3] where mp3 = maxpow3 n
Sadly, the representation is not unique. For example, !!8+3 = 2+9!!, and !!32+24+9 = 32+6+27 = 8+12=18+27!!.
[Other articles in category /math] permanent link
Fri, 09 Nov 2018
Why I never finish my Haskell programs (part 3 of ∞)
I'm doing more work on matrix functions. A matrix represents a
relation, and I am representing a matrix as a [[Integer]]. Then
matrix addition is simply liftA2 (liftA2 (+)). Except no, that's
not right, and this is not a complaint, it's certainly my mistake.
The overloading for liftA2 for lists does not do what I want, which
is to apply the operation to each pair of correponding elements. I want
liftA2 (+) [1,2,3] [10,20,30] to be [11,22,33] but it is not.
Instead liftA2 lifts an operation to apply to each possible pair of
elements, producing [11,21,31,12,22,32,13,23,33].
And the twice-lifted version is
similarly not what I want:
$$ \require{enclose} \begin{pmatrix}1&2\\3&4\end{pmatrix}\enclose{circle}{\oplus} \begin{pmatrix}10&20\\30&40\end{pmatrix}= \begin{pmatrix} 11 & 21 & 12 & 22 \\ 31 & 41 & 32 & 42 \\ 13 & 23 & 14 & 24 \\ 33 & 43 & 34 & 44 \end{pmatrix} $$
No problem, this is what ZipList is for. ZipLists are just regular
lists that have a label on them that advises liftA2 to lift an
operation to the element-by-element version I want instead of the
each-one-by-every-other-one version that is the default. For instance
liftA2 (+) (ZipList [1,2,3]) (ZipList [10,20,30])
gives ZipList [11,22,33], as desired. The getZipList function
turns a ZipList back into a regular list.
But my matrices are nested lists, so I need to apply the ZipList
marker twice, once to the outer list, and once to each of the inner
lists, because I want the element-by-element behavior at both
levels. That's easy enough:
matrix :: [[a]] -> ZipList (ZipList a)
matrix m = ZipList (fmap ZipList m)
(The fmap here is actually being specialized to map, but that's
okay.)
Now
(liftA2 . liftA2) (+) (matrix [[1,2],[3,4]]) (matrix [[10,20],[30, 40]])
does indeed produce the result I want, except that the type markers are still in there: instead of
[[11,22],[33,44]]
I get
ZipList [ ZipList [11, 22], ZipList [33, 44] ]
No problem, I'll just use getZipList to turn them back again:
unmatrix :: ZipList (ZipList a) -> [[a]]
unmatrix m = getZipList (fmap getZipList m)
And now matrix addition is finished:
matrixplus :: [[a]] -> [[a]] -> [[a]]
matrixplus m n = unmatrix $ (liftA2 . liftA2) (+) (matrix m) (matrix n)
This works perfectly.
But the matrix and unmatrix pair bugs me a little. This business
of changing labels at both levels has happened twice already and
I am likely to need it again. So I will turn the two functions
into a single higher-order function by abstracting over ZipList.
This turns this
matrix m = ZipList (fmap ZipList m)
into this:
twice zl m = zl (fmap zl m)
with the idea that I will now have matrix = twice ZipList and
unmatrix = twice getZipList.
The first sign that something is going wrong is that twice does not
have the type I wanted. It is:
twice :: Functor f => (f a -> a) -> f (f a) -> a
where I was hoping for something more like this:
twice :: (Functor f, Functor g) => (f a -> g a) -> f (f a) -> g (g a)
which is not reasonable to expect: how can Haskell be expected to
figure out I wanted two diferent functors in there when there is only one
fmap? And indeed twice does not work; my desired matrix = twice
ZipList does not even type-check:
<interactive>:19:7: error:
• Occurs check: cannot construct the infinite type: a ~ ZipList a
Expected type: [ZipList a] -> ZipList a
Actual type: [a] -> ZipList a
• In the first argument of ‘twice’, namely ‘ZipList’
In the expression: twice ZipList
In an equation for ‘matrix’: matrix = twice ZipList
• Relevant bindings include
matrix :: [[ZipList a]] -> ZipList a (bound at <interactive>:20:5)
Telling GHC explicitly what type I want for twice doesn't work
either, so I decide it's time to go to lunch. I take paper with me,
and while I am eating my roast pork hoagie with sharp provolone and
spinach (a popular local delicacy) I work out the results of the type
unification algorithm on paper for both cases to see what goes wrong.
I get the same answers that Haskell got, but I can't see where the difference was coming from.
So now, instead of defining matrix operations, I am looking into the
type unification algorithm and trying to figure out why twice
doesn't work.
And that is yet another reason why I never finish my Haskell programs. (“What do you mean, λ-abstraction didn't work?”)
[Other articles in category /prog/haskell] permanent link
Thu, 08 Nov 2018
Haskell type checker complaint 184 of 698
I want to build an adjacency matrix for the vertices of a cube; this
is a matrix that has m[a][b] = 1 exactly when vertices a and b
share an edge. We can enumerate the vertices arbitrarily but a
convenient way to do it is to assign them the numbers 0 through 7 and
then say that vertices !!a!! and !!b!! are adjacent if, regarded as
binary numerals, they differ in exactly one bit, so:
import Data.Bits
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
This compiles and GHC infers the type
adj :: (Bits a, Num a, Num t) => a -> a -> t
Fine.

Now I want to build the adjacency matrix, which is completely straightforward:
cube = [ [a `adj` b | b <- [0 .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Ha ha, no it isn't; in Haskell nothing is straightforward. This
produces 106 lines of type whining, followed by a failed compilation.
Apparently this is because because 0 and 7 are overloaded, and
could mean some weird values in some freakish instance of Num, and
then 0 .. 7 might generate an infinite list of 1-graded torsion
rings or something.
To fix this I have to say explicitly what I mean by 0. “Oh, yeah,
by the way, that there zero is intended to denote the integer zero,
and not the 1-graded torsion ring with no elements.”
cube = [ [a `adj` b | b <- [0 :: Integer .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Here's another way I could accomplish this:
zero_i_really_mean_it = 0 :: Integer
cube = [ [a `adj` b | b <- [zero_i_really_mean_it .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Or how about this?
cube = [ [a `adj` b | b <- numbers_dammit [0 .. 7] ] | a <- [0 .. 7] ] where
p `adj` q = if (elem (xor p q) [1, 2, 4]) then 1 else 0
numbers_dammit = id :: [Integer] -> [Integer]
I think there must be something really wrong with the language design here. I don't know exactly what it is, but I think someone must have made the wrong tradeoff at some point.
[Other articles in category /prog/haskell] permanent link
How not to reconfigure your sshd
Yesterday I wanted to reconfigure the sshd on a remote machine.
Although I'd never done sshd itself, I've done this kind of thing
a zillion times before. It looks like this: there is a configuration
file (in this case /etc/ssh/sshd-config) that you modify. But this
doesn't change the running server; you have to notify the server that
it should reread the file. One way would be by killing the server and
starting a new one. This would interrupt service, so instead you can
send the server a different signal (in this case SIGHUP) that tells
it to reload its configuration without exiting. Simple enough.
Except, it didn't work. I added:
Match User mjd
ForceCommand echo "I like pie!"
and signalled the server, then made a new connection to see if it
would print I like pie! instead of starting a shell. It started a
shell. Okay, I've never used Match or ForceCommand before, maybe
I don't understand how they work, I'll try something simpler. I
added:
PrintMotd yes
which seemed straightforward enough, and I put some text into
/etc/motd, but when I connected it didn't print the motd.
I tried a couple of other things but none of them seemed to work.
Okay, maybe the sshd is not getting the signal, or something? I
hunted up the logs, but there was a report like what I expected:
sshd[1210]: Received SIGHUP; restarting.
This was a head-scratcher. Was I modifying the wrong file? It semed
hardly possible, but I don't administer this machine so who knows? I
tried lsof -p 1210 to see if maybe sshd had some other config file
open, but it doesn't keep the file open after it reads it, so that was
no help.
Eventually I hit upon the answer, and I wish I had some useful piece of advice here for my future self about how to figure this out. But I don't because the answer just struck me all of a sudden.
(It's nice when that happens, but I feel a bit cheated afterward: I solved the problem this time, but I didn't learn anything, so how does it help me for next time? I put in the toil, but I didn't get the full payoff.)
“Aha,” I said. “I bet it's because my connection is multiplexed.”
Normally when you make an ssh connection to a remote machine, it
calls up the server, exchanges credentials, each side authenticates
the other, and they negotiate an encryption key. Then the server
forks, the child starts up a login shell and mediates between the
shell and the network, encrypting in one direction and decrypting in
the other. All that negotiation and authentication takes time.
There is a “multiplexing” option you can use instead. The handshaking
process still occurs as usual for the first connection. But once the
connection succeeds, there's no need to start all over again to make a
second connection. You can tell ssh to multiplex several virtual
connections over its one real connection. To make a new virtual
connection, you run ssh in the same way, but instead of contacting
the remote server as before, it contacts the local ssh client that's
already running and requests a new virtual connection. The client,
already connected to the remote server, tells the server to allocate a
new virtual connection and to start up a new shell session for it.
The server doesn't even have to fork; it just has to allocate another
pseudo-tty and run a shell in it. This is a lot faster.
I had my local ssh client configured to use a virtual connection if
that was possible. So my subsequent ssh commands weren't going
through the reconfigured parent server. They were all going through
the child server that had been forked hours before when I started my
first connection. It wasn't affected by reconfiguration of the parent
server, from which it was now separate.
I verified this by telling ssh to make a new connection without
trying to reuse the existing virtual connection:
ssh -o ControlPath=none -o ControlMaster=no ...
This time I saw the MOTD and when I reinstated that Match command I
got I like pie! instead of a shell.
(It occurs to me now that I could have tried to SIGHUP the child server process that my connections were going through, and that would probably have reconfigured any future virtual connections through that process, but I didn't think of it at the time.)
Then I went home for the day, feeling pretty darn clever, right up
until I discovered, partway through writing this article, that I can't
log in because all I get is I like pie! instead of a shell.
[Other articles in category /Unix] permanent link
Fri, 02 Nov 2018
Another trivial utility: git-q
One of my favorite programs is a super simple Git utility called
git-vee
that I just love, and I use fifty times a day. It displays a very
simple graph that shows where two branches diverged. For example, my
push of master was refused because it was not a
fast-forward. So I
used git-vee to investigate, and saw:
* a41d493 (HEAD -> master) new article: Migraine
* 2825a71 message headers are now beyond parody
| * fa2ae34 (origin/master) message headers are now beyond parody
|/
o 142c68a a bit more information
The current head (master) and its upstream (origin/master) are
displayed by default. Here the nearest common ancestor is 142c68a,
and I can see the two commits after that on master that are
different from the commit on origin/master. The command is called
git-vee because the graph is (usually) V-shaped, and I want to find
out where the point of the V is and what is on its two arms.
From this V, it appears that what happened was: I pushed fa2ae34,
then amended it to produce 2825a71, but I have not yet force-pushed
the amendment. Okay! I should simply do the force-push now…
Except wait, what if that's not what happened? What if what
happened was, 2825a71 was the original commit, and I pushed it, then
fetched it on a different machine, amended it to produce fa2ae34,
and force-pushed that? If so, then force-pushing 2825a71 now would
overwrite the amendments. How can I tell what I should do?
Formerly I would have used diff and studied the differences, but now
I have an easier way to find the answer. I run:
git q HEAD^ origin/master
and it produces the dates on which each commit was created:
2825a71 Fri Nov 2 02:30:06 2018 +0000
fa2ae34 Fri Nov 2 02:25:29 2018 +0000
Aha, it was as I originally thought: 2825a71 is five minutes newer.
The force-push is the right thing to do this time.
Although the commit date is the default output, the git-q
command can
produce any of the information known to git-log, using the usual
escape sequences.
For example, git q %s ... produces subject lines:
% git q %s HEAD origin/master 142c68a
a41d493 new article: Migraine
fa2ae34 message headers are now beyond parody
142c68a a bit more information
and git q '%an <%ae>' tells you who made the commits:
a41d493 Mark Jason Dominus (陶敏修) <mjd@plover.com>
fa2ae34 Mark Jason Dominus (陶敏修) <mjd@plover.com>
142c68a Mark Jason Dominus (陶敏修) <mjd@plover.com>
The program is in my personal git-util repository but it's totally simple and should be easy to customize the way you want:
#!/usr/bin/python3
from sys import argv, stderr
import subprocess
if len(argv) < 3: usage()
if argv[1].startswith('%'):
item = argv[1]
ids = argv[2:]
else:
item='%cd'
ids = argv[1:]
for id in ids:
subprocess.run([ "git", "--no-pager",
"log", "-1", "--format=%h " + item, id])
[Other articles in category /prog] permanent link
Mon, 29 Oct 2018Warning: Long and possibly dull.
I spent a big chunk of today fixing a bug that should have been easy but that just went deeper and deeper. If you look over in the left sidebar there you'll se a sub-menu titled “subtopics” with a per-category count of the number of articles in each section of this blog. (Unless you're using a small display, where the whole sidebar is suppressed.) That menu was at least a year out of date. I wanted to fix it.
The blog software I use is the wonderfully terrible
Blosxom. It has a plugin system,
and the topic menu was generated by a plugin that I wrote some time
ago. When the topic plugin starts up it opens two Berkeley
DB files. Each is a simple
key-value mapping. One maps topic names to article counts. The other
is just a set of article IDs for the articles that have already been
counted. These key-value mappings are exposed in Perl as hash
variables.
When I regenerate the static site, the topic plugin has a
subroutine, story, that is called for each article in each generated
page. The business end of the subroutine looks something like this:
sub story {
# ... acquire arguments ..
if ( $Seen{ $article_id } ) {
return;
} else {
$topic_count{ $article_topic }++;
$Seen{ $article_id } = 1;
}
}
The reason the menu wasn't being updated is that at some point in the
past, I changed the way story plugins were called. Out of the box,
Blosxom passes story a list of five arguments, like this:
my ($pkg, $path, $filename, $story_ref, $title_ref) = @_;
Over the years I had extended this to eight or nine, and I felt it was getting unwieldy, so at some point I changed it to pass a hash, like this:
my %args = (
category => $path, # directory of this story
filename => $fn, # filename of story, without suffix
...
)
$entries = $plugin->story(\%args);
When I made this conversion, I had to convert all the plugins. I
missed converting topic. So instead of getting the eight or nine
arguments it expected, it got two: the plugin itself, and the hash.
Then it used the hash as the key into the databases, which by now
were full of thousands of entries for things like HASH(0x436c1d)
because that is what Perl silently and uselessly does if you try to
use a hash as if it were a string.
Anyway, this was easily fixed, or should have been easily fixed. All I needed to do was convert the plugin to use the new calling convention. Ha!
One thing all my plugins do when they start up is write a diagnostic log, something like this:
sub start {
open F, ">", "/tmp/topic.$>";
print F "Writing to $blosxom::plugin_state_dir/topics\n";
}
Then whenever the plugin has something to announce it just does
print F. For example, when the plugin increments the count for a
topic, it inserts a message like this:
print F "'$article_id' is item $topic_count{$article_topic} in topic $article_topic.\n";
If the article has already been seen, it remains silent.
Later I can look in /tmp/topic.119 or whatever to see what it said.
When I'm debugging a plugin, I can open an Emacs buffer on this file
and put it in auto-revert mode so that Emacs always displays the
current contents of the file.
Blosxom has an option to generate pages on demand for a web browser,
and I use this for testing. https://blog.plover.com/PATH is the
static version of the article, served from a pre-generated static
file. But https://blog.plover.com/test/PATH calls Blosxom as a CGI
script to generate the article on the fly and send it to the browser.
So I visited https://blog.plover.com/test/2018/, which should
generate a page with all the articles from 2018, to see what the
plugin put in the file. I should have seen it inserting a lot of
HASH(0x436c1d) garbage:
'lang/etym/Arabic-2' is article 1 in topic HASH(0x22c501b)
'addenda/200801' is article 1 in topic HASH(0x5300aa2)
'games/poker-24' is article 1 in topic HASH(0x4634a79)
'brain/pills' is article 1 in topic HASH(0x1a9f6ab)
'lang/long-s' is article 1 in topic HASH(0x29489be)
'google-roundup/200602' is article 1 in topic HASH(0x360e6f5)
'prog/van-der-waerden-1' is article 1 in topic HASH(0x3f2a6dd)
'math/math-se-gods' is article 1 in topic HASH(0x412b105)
'math/pow-sqrt-2' is article 1 in topic HASH(0x23ebfe4)
'aliens/dd/p22' is article 1 in topic HASH(0x878748)
I didn't see this. I saw the startup message and nothing else. I did
a bunch of very typical debugging, such as having the plugin print a
message every time story was called:
sub story {
print F "Calling 'story' (@_)\n";
...
}
Nothing. But I knew that story was being called. Was I maybe
editing the wrong file on disk? No, because I could introduce a
syntax error and the browser would happily report the resulting 500
Server Error. Fortunately, somewhere along the way I changed
open F, ">", "/tmp/topic.$>";
to
open F, ">>", "/tmp/topic.$>";
and discovered that each time I loaded the page, the plugin was run
exactly twice. When I had had >, the second run would immediately
overwrite the diagnostics from the first run.
But why was the plugin being run twice? This took quite a while to track down. At first I suspected that Blosxom was doing it, either on purpose or by accident. My instance of Blosxom is a hideous Frankenstein monster that has been cut up and reassembled and hacked and patched dozens of times since 2006 and it is full of unpleasant surprises. But the problem turned out to be quite different. Looking at the Apache server logs I saw that the browser was actually making two requests, not one:
100.14.199.174 - mjd [28/Oct/2018:18:00:49 +0000] "GET /test/2018/ HTTP/1.1" 200 213417 "-" ...
100.14.199.174 - mjd [28/Oct/2018:18:00:57 +0000] "GET /test/2018/BLOGIMGREF/horseshoe-curve-small.mp4 HTTP/1.1" 200 623 ...
Since the second request was for a nonexistent article, the story
callback wasn't invoked in the second run. So I would see the startup
message, but I didn't see any messages from the story callback.
They had been there in the first run for the first request, but that
output was immediately overwritten on the second request.
BLOGIMGREF is a tag that I include in image URLs, that expands to
whatever is the appropriate URL for the images for the particular
article it's in. This expansion is done by a different plugin, called
path2, and apparently in this case it wasn't being expanded. The
place it was being used was easy enough to find; it looked like this:
<video width="480" height="270" controls>
<source src="BLOGIMGREF/horseshoe-curve-small.mp4" type="video/mp4">
</video>
So I dug down into the path2 plugin to find out why BLOGIMGREF
wasn't being replaced by the correct URL prefix, which should have
been in a different domain entirely.
This took a very long time to track down, and I think it was totally
not my fault. When I first wrote path2 I just had it do a straight
text substitution. But at some point I had improved this to use a real
HTML parser, supplied by the Perl HTML::TreeBuilder module. This
would parse the article body and return a tree of HTML::Element
objects, which the plugin would then filter, looking for img and a
elements. The plugin would look for the magic tags and replace them
with the right URLs.
This magic tag was not in an img or an a element, so the plugin
wasn't finding it. I needed to tell the plugin to look in source
elements also. Easy fix! Except it didn't work.
Then began a tedious ten-year odyssey through the HTML::TreeBuilder
and HTML::Element modules to find out why it hadn't worked. It took
a long time because I'm good at debugging. When you lose your wallet,
you look in the most likely places first, and I know from many years
of experience what the most likely places are — usually in my
misunderstanding of the calling convention of some library I didn't
write, or my misunderstanding of what it was supposed to do; sometimes
in my own code. The downside of this is that when the wallet is in
an unlikely place it takes a really long time to find it.
The end result this time was that it wasn't in any of the usual
places. It was 100% not my fault: HTML::TreeBuilder has a bug in
its parser. For
some reason it completely ignores source elements:
perl -MHTML::TreeBuilder -e '$z = q{<source src="/media/horseshoe-curve-small.mp4" type="video/mp4"/>}; HTML::TreeBuilder->new->parse($z)->eof->elementify()->dump(\*STDERR)'
The output is:
<html> @0 (IMPLICIT)
<head> @0.0 (IMPLICIT)
<body> @0.1 (IMPLICIT)
No trace of the source element. I reported the bug, commented out
the source element in the article, and moved on. (The article was
unpublished, in part because I could never get the video to play
properly in the browser. I had been tearing my hair about over it,
but now I knew why! The BLOGIMGREF in the URL was not being
replaced! Because of a bug in the HTML parser!)
With that fixed I went back to finish the work on the topic plugin.
Now that the diagnostics were no longer being overwritten by the bogus
request for /test/2018/BLOGIMGREF/horseshoe-curve-small.mp4, I
expected to see the HASH(0x436c1d) garbage. I did, and I fixed
that. Then I expected the 'article' is article 17 in topic prog
lines to go away. They were only printed for new articles that hadn't
been seen before, and by this time every article should have been in
the %Seen database.
But no, every article on the page, every article from 2018, was being processed every time I rebuilt the page. And the topic counts were going up, up, up.
This also took a long time to track down, because again the cause was so unlikely. I must have been desperate because I finally found it by doing something like this:
if ( $Seen{ $article_id } ) {
return;
} else {
$topic_count{ $article_topic }++;
$Seen{ $article_id } = 1;
die "WTF!!" unless $Seen{ $article_id };
}
Yep, it died. Either Berkeley DB, or Perl's BerkeleyDB module, was
just flat-out not working. Both of them are ancient, and this kind of
shocking bug should have been shaken out 20 years go. WTF, indeed,
I fixed this by discarding the entire database and rebuilding it. I
needed to clean out the HASH(0x436c1d) crap anyway.
I am sick of DB files. I am never using them again. I have been bitten too many times. From now on I am doing the smart thing, by which I mean the dumb thing, the worse-is-better thing: I will read a plain text file into memory, modify it, and write out the modified version whem I am done. It will be simple to debug the code and simple to modify the database.
Well, that sucked. Usually this sort of thing is all my fault, but this time I was only maybe 10% responsible.
At least it's working again.
[ Addendum: I learned that discarding the source element is a
⸢feature⸣ of HTML::Parser. It has a list of valid HTML4 tags and by
default it ignores any element that isn't one. The maintainer won't
change the default to HTML5 because that might break backward
compatibility for people who are depending on this behavior. ]
[Other articles in category /prog/bug] permanent link
Sun, 28 Oct 2018
More about auto-generated switch-cases
Yesterday I described what I thought was a cool hack I had seen in
rsync, to try several
possible methods and then remember which one worked so as to skip the
others on future attempts. This was abetted by a different hack, for
automatically generating the case labels for the switch, which I
thought was less cool.
Simon Tatham wrote to me with a technique for compile-time generation
of case labels that I liked better. Recall that the context is:
int set_the_mtime(...) {
static int switch_step = 0;
switch (switch_step) {
#ifdef METHOD_1_MIGHT_WORK
case ???:
if (method_1_works(...))
break;
switch_step++;
/* FALLTHROUGH */
#endif
#ifdef METHOD_2_MIGHT_WORK
case ???:
if (method_2_works(...))
break;
switch_step++;
/* FALLTHROUGH */
#endif
... etc. ...
}
return 1;
}
M. Tatham suggested this:
#define NEXT_CASE switch_step = __LINE__; case __LINE__
You use it like this:
int set_the_mtime(...) {
static int switch_step = 0;
switch (switch_step) {
default:
#ifdef METHOD_1_MIGHT_WORK
NEXT_CASE:
if (method_1_works(...))
break;
/* FALLTHROUGH */
#endif
#ifdef METHOD_2_MIGHT_WORK
NEXT_CASE:
if (method_2_works(...))
break;
/* FALLTHROUGH */
#endif
... etc. ...
}
return 1;
}
The case labels are no longer consecutive, but that doesn't matter;
all that is needed is for them to be distinct. Nobody is ever going
to see them except the compiler. M. Tatham called this
“the case __LINE__ trick”, which suggested to me that it was
generally known. But it was new to me.
One possible drawback of this method is that if the file contains more
than 255 lines, the case labels will not fit in a single byte. The
ultimate effect of this depends on how the compiler handles switch.
It might be compiled into a jump table with !!2^{16}!! entries, which
would only be a problem if you had to run your program in 1986. Or it
might be compiled to an if-else tree, or something else we don't want.
Still, it seems like a reasonable bet.
You could use case 0: at the beginning instead of default:, but
that's not as much fun. M. Tatham observes that it's one of very few
situations in which it makes sense not to put default: last. He
says this is the only other one he knows:
switch (month) {
case SEPTEMBER:
case APRIL:
case JUNE:
case NOVEMBER:
days = 30;
break;
default:
days = 31;
break;
case FEBRUARY:
days = 28;
if (leap_year)
days = 29;
break;
}
Addendum 20181029: Several people have asked for an explanation of why
the default is in the middle of the last switch. It follows the
pattern of a very well-known mnemonic
poem that goes
Thirty days has September,
April, June and November.
All the rest have thirty-one
Except February, it's a different one:
It has 28 days clear,
and 29 each leap year.
Wikipedia says:
[The poem has] been called “one of the most popular and oft-repeated verses in the English language” and “probably the only sixteenth-century poem most ordinary citizens know by heart”.
[Other articles in category /prog] permanent link
Sat, 27 Oct 2018
A fun optimization trick from rsync
I was looking at the rsync source code today and I saw a neat trick
I'd never seen before. It wants to try to set the mtime on a file,
and there are several methods that might work, but it doesn't know
which. So it tries them in sequence, and then it remembers which one
worked and uses that method on subsequent calls:
int set_the_mtime(...) {
static int switch_step = 0;
switch (switch_step) {
case 0:
if (method_0_works(...))
break;
switch_step++;
/* FALLTHROUGH */
case 1:
if (method_1_works(...))
break;
switch_step++;
/* FALLTHROUGH */
case 2:
...
case 17:
if (method_17_works(...))
break;
return -1; /* ultimate failure */
}
return 0; /* success */
}
The key item here is the static switch_step variable. The first
time the function is called, its value is 0 and the switch starts at
case 0. If methods 0 through 7 all fail and method 8 succeeds,
switch_step will have been set to 8, and on subsequent calls to the
function the switch will jump immediately to case 8.
The actual code is a little more sophisticated than this. The list of
cases is built depending on the setting of several compile-time config
flags, so that the code that is compiled only includes the methods
that are actually callable. Calling one of the methods can produce
three distinguishable results: success, real failure (because of
permission problems or some such), or a sort of fake failure
(ENOSYS) that only means that the underlying syscall is
unimplemented. This third type of result is the one where it makes
sense to try another method. So the cases actually look like this:
case 7:
if (method_7_works(...))
break;
if (errno != ENOSYS)
return -1; /* real failure */
switch_step++;
/* FALLTHROUGH */
On top of this there's another trick: since the various cases are
conditionally compiled depending on the config flags, we don't know
ahead of time which ones will be included. So the case labels
themselves are generated at compile time this way:
#include "case_N.h"
if (method_7_works(...))
break;
...
#include "case_N.h"
if (method_8_works(...))
break;
...
The first time we #include "case_N.h", it turns into case 0:; the
second time, it turns into case 1:, and so on:
#if !defined CASE_N_STATE_0
#define CASE_N_STATE_0
case 0:
#elif !defined CASE_N_STATE_1
#define CASE_N_STATE_1
case 1:
...
#else
#error Need to add more case statements!
#endif
Unfortunately you can only use this trick one switch per file.
Although I suppose if you really wanted to reuse it you could make a
reset_case_N.h file which would contain
#undef CASE_N_STATE_0
#undef CASE_N_STATE_1
...
[ Addendum 20181028: Simon Tatham brought up a technique for
generating the case labels that we agree is
better than what rsync did. ]
[Other articles in category /prog] permanent link
Fri, 26 Oct 2018
A snide addendum about implicit typeclass instances
In an earlier article I demanded:
Maybe someone can explain to me why this is a useful behavior, and then explain why it is so useful that it should happen automatically …
“This” being that instead of raising a type error, Haskell quietly accepts this nonsense:
fmap ("super"++) (++"weasel")
but it clutches its pearls and faints in horror when confronted with this expression:
fmap ("super"++) "weasel"
Nobody did explain this.
But I imagined
someone earnestly explaining: “Okay, but in the first case, the
(++"weasel") is interpreted as a value in the environment functor,
so fmap is resolved to its the environment instance, which is (.).
That doesn't happen in the second example.”
Yeah, yeah, I know that. Hey, you know what else is a functor? The
identity functor. If fmap can be quietly demoted to its (->) e
instance, why can't it also be quietly demoted to its Id instance,
which is ($), so that fmap ("super"++) "weasel" can quietly
produce "superweasel"?
I understand this is a terrible idea. To be clear, what I want is for it to collapse on the divan for both expressions. Pearl-clutching is Haskell's finest feature and greatest strength, and it should do it whenever possible.
[Other articles in category /prog/haskell] permanent link
Tue, 23 Oct 2018A few years back I asked on history stackexchange:
Wikipedia's article on the Halifax Gibbet says, with several citations:
…ancient custom and law gave the Lord of the Manor the authority to execute summarily by decapitation any thief caught with stolen goods to the value of 13½d or more…
My question being: why 13½ pence?
This immediately attracted an answer that was no good at all. The author began by giving up:
This question is historically unanswerable.
I've met this guy and probably you have too: he knows everything worth knowing, and therefore what he doesn't know must be completely beyond the reach of mortal ken. But that doesn't mean he will shrug and leave it at that, oh no. Having said nobody could possibly know, he will nevertheless ramble for six or seven decreasingly relevant paragraphs, as he did here.
45 months later, however, a concise and pertinent answer was given by Aaron Brick:
13½d is a historical value called a loonslate. According to William Hone, it has a Scottish origin, being two-thirds of the Scottish pound, as the mark was two-thirds of the English pound. The same value was proposed as coinage for South Carolina in 1700.
This answer makes me happy in several ways, most of them positive. I'm glad to have a lead for where the 13½ pence comes from. I'm glad to learn the odd word “loonslate”. And I'm glad to be introduced to the bizarre world of pre-union Scottish currency, which, in addition to the loonslate, includes the bawbee, the unicorn, the hardhead, the bodle, and the plack.
My pleasure has a bit of evil spice in it too. That fatuous claim that the question was “historically unanswerable” had been bothering me for years, and M. Brick's slam-dunk put it right where it deserved.
I'm still not completely satisfied. The Scottish mark was worth ⅔ of a pound Scots, and the pound Scots, like the English one, was divided not into 12 pence but into 20 shillings of 12 pence each, so that a Scottish mark was worth 160d, not 13½d. Brick cites William Hone, who claims that the pound Scots was divided into twelve pence, rather than twenty shillings, so that a mark was worth 13⅔ pence, but I can't find any other source that agrees with him. Confusing the issue is that starting under the reign of James VI and I in 1606, the Scottish pound was converted to the English at a rate of twelve-to-one, so that a Scottish mark would indeed have been convertible to 13⅔ English pence, except that the English didn't denominate pence in thirds, so perhaps it was legally rounded down to 13½ pence. But this would all have been long after the establishment of the 13½d in the Halifax gibbet law and so unrelated to it.
Or would it? Maybe the 13½d entered popular consciousness in the 17th century, acquired the evocative slang name “hangman’s wages”, and then an urban legend arose about it being the cutoff amount for the Halifax gibbet, long after the gibbet itself was dismantled arond 1650. I haven't found any really convincing connection between the 13½d and the gibbet that dates earlier than 1712. The appearance of the 13½d in the gibbet law could be entirely the invention of Samuel Midgley.
I may dig into this some more. The 1771 Encyclopædia Britannica has a 16-page article on “Money” that I can look at. I may not find out what I want to know, but I will probably find out something.
[Other articles in category /history] permanent link
Getting Applicatives from Monads and “>>=” from “join”
I complained recently about GHC not being able to infer an
Applicative instance from a type that already has a Monad
instance, and there is a related complaint that the Monad instance
must define >>=. In some type classes, you get a choice about
what to define, and then the rest of the functions are built from the
ones you provided. To take a particular simple example, with Eq
you have the choice of defining == or /=, and if you omit one
Haskell will construct the other for you. It could do this with >>=
and join, but it doesn't, for technical reasons I don't
understand
[1]
[2]
[3].
But both of these problems can be worked around. If I have a Monad instance, it seems to work just fine if I say:
instance Applicative Tree where
pure = return
fs <*> xs = do
f <- fs
x <- xs
return (f x)
Where this code is completely canned, the same for every Monad.
And if I know join but not >>=, it seems to work just fine if I say:
instance Monad Tree where
return = ...
x >>= f = join (fmap f x) where
join tt = ...
I suppose these might faul foul of whatever problem is being described in the documents I linked above. But I'll either find out, or I won't, and either way is a good outcome.
[ Addendum: Vaibhav Sagar points out that my definition of <*> above
is identical to that of Control.Monad.ap, so that instead of
defining <*> from scratch, I could have imported ap and then
written <*> = ap. ]
[ Addendum 20221021: There are actually two definitions of <*> that will work. [1] [2] ]
[Other articles in category /prog/haskell] permanent link
Mon, 22 Oct 2018While I was writing up last week's long article about Traversable, I wrote this stuff about Applicative also. It's part of the story but I wasn't sure how to work it into the other narrative, so I took it out and left a remark that “maybe I'll publish a writeup of that later”. This is a disorganized collection of loosely-related paragraphs on that topic.
It concerns my attempts to create various class instance definitions for the following type:
data Tree a = Con a | Add (Tree a) (Tree a)
deriving (Eq, Show)
which notionally represents a type of very simple expression tree over values of type a.
I need some function for making Trees that isn't too
simple or too complicated, and I went with:
h n | n < 2 = Con n
h n = if even n then Add (h (n `div` 2)) (h (n `div` 2))
else Add (Con 1) (h (n - 1))
which builds trees like these:
2 = 1 + 1
3 = 1 + (1 + 1)
4 = (1 + 1) + (1 + 1)
5 = 1 + ((1 + 1) + (1 + 1))
6 = (1 + (1 + 1)) + (1 + (1 + 1))
7 = 1 + (1 + (1 + 1)) + (1 + (1 + 1))
8 = ((1 + 1) + (1 + 1)) + ((1 + 1) + (1 + 1))
Now I wanted to traverse h [1,2,3] but I couldn't do that because I
didn't have an Applicative instance for Tree. I had been putting off
dealing with this, but since Traversable doesn't really make sense without
Applicative I thought the day of reckoning would come. Here it was. Now is
when I learn how to fix all my broken monads.
To define an Applicative instance for Tree I needed to define pure, which
is obvious (it's just Con) and <*> which would apply a tree of
functions to a tree of inputs to get a tree of results. What the hell
does that mean?
Well, I can kinda make sense of it. If I apply one function to a
tree of inputs, that's straightforward, it's just fmap, and I get a
tree of results. Suppose I have a tree of functions, and I replace
the function at each leaf with the tree of its function's results.
Then I have a tree of trees. But a tree that has trees at its leaves
is just a tree. So I could write some tree-flattening function that
builds the tree of trees, then flattens out the type. In fact this is just
join that I already know from Monad world.
The corresponding operation for lists takes a list of lists
and flattens them into a single list.) Flattening a tree is quite easy to do:
join (Con ta) = ta
join (Add ttx tty) = Add (join ttx) (join tty)
and since this is enough to define a Monad instance for Tree I
suppose it is enough to get an Applicative instance also, since every Monad
is an Applicative. Haskell makes this a pain. It should be able to infer
the Applicative from this, and I wasn't clever enough to do it myself. And
there ought to be some formulaic way to get <*> from >>= and
join and fmap, the way you can get join from >>=:
join = (>>= id)
but I couldn't find out what it was. This gets back to my original
complaint: Haskell now wants every Monad instance to be an instance
of Applicative, but if I give it the fmap and the join and the return
it ought to be able to figure out the Applicative instance itself instead of
refusing to compile my program. Okay, fine, whatever. Haskell's
gonna Hask.
(I later realized that building <*> when you have a Monad instance
is easy once you know the recipe; it's just:
fs <*> xs = do
f <- fs
x <- xs
return (f x)
So again, why can't GHC infer <*> from my Monad instance, maybe
with a nonfatal warning?
Warning: No Applicative instance provided for Tree; deriving one from Monad
This is not a rhetorical question.)
(Side note: it seems like there ought to be a nice short abbreviation
of the (<*>) function above, the way one can write join = (>>=
id). I sought one but did not find any. One can eliminate the do
notation to obtain the expression:
fs <*> xs = fs >>= \f -> xs >>= \x -> return (f x)
but that is not any help unless we can simplify the expression with
the usual tricks, such as combinatory logic and η-conversion. I was
not able to do this, and the automatic pointfree
converter produced
(. ((. (return .)) . (>>=))) . (>>=) ARGH MY EYES.)
Anyway I did eventually figure out my <*> function for trees by
breaking the left side into cases. When the tree of functions is Con
f it's a single function and we can just use fmap to map it over
the input tree:
(Con f) <*> tv = fmap f tv
And when it's bigger than that we can break it up recursively:
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
Once this is written it seemed a little embarrassing that it took me so long to figure out what it meant but this kind of thing always seems easier from the far side of the fence. It's hard to understand until you understand it.
Actually that wasn't quite the <*> I wanted. Say we have a tree of
functions and a tree of arguments.

Add (Con (* 10))
(Con (* 100))
Add (Add (Con 3) (Con 4)) (Con 5)I can map the whole tree of functions over each single leaf on the right, like this:
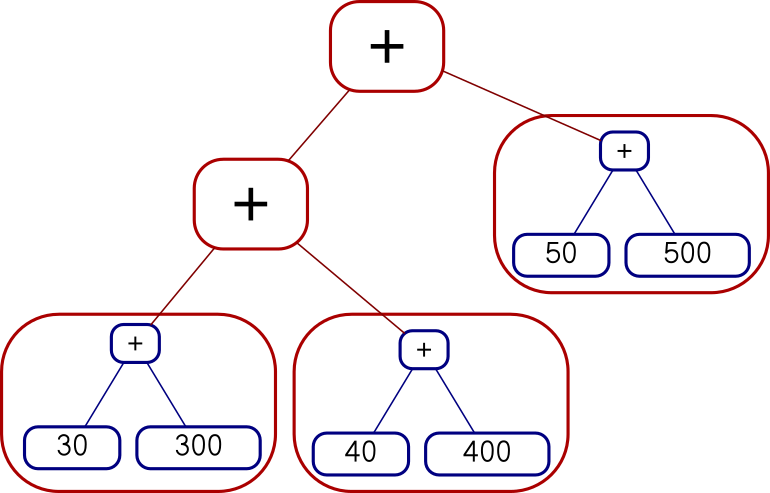
Add (Add (Add (Con 30) (Con 300))
(Add (Con 40) (Con 400)))
(Add (Con 50) (Con 500))
or I can map each function over the whole tree on the right, like this:
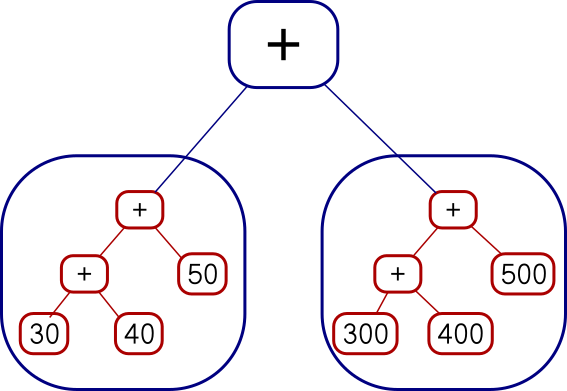
Add
(Add (Add (Con 30) (Con 40)) (Con 50))
(Add (Add (Con 300) (Con 400)) (Con 500))The code I showed earlier does the second of those. You can see it from
the fmap f tv expression, which takes a single function and maps it over a whole
tree of values. I had actually wanted the other one, but there isn't
anything quite like fmap for that. I was busy trying to
understand Applicative and I was afraid if I got distracted trying to invent
a reverse fmap I might lose the thread. This happens to me a lot
with Haskell. I did eventually go back and figure it out. The
reverse fmap is
pamf fs v = fmap ($ v) fs -- good
or
pamf = flip (fmap . flip id) -- yuck
Now there's a simple answer to this which occurs to me now that I
didn't think of before, but I'm going to proceed with how I planned to
do it before, with pamf. The <*> that I didn't want looked like this:
(Con f) <*> tv = fmap f tv
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
I need to do the main recursion on the values argument instead of on the functions argument:
tf <*> (Con v) = pamf tf v
where pamf fs v = fmap ($ v) fs
tf <*> (Add lv rv) = Add (tf <*> lv) (tf <*> rv)
(This is an interesting example: usually the base case is trivial and the recursive clause is harder to write, but this time it's the base case that's not perfectly straightforward.)
Anyway, this worked, but there was an easier solution at hand. The difference between the first version and the second is exactly the same as the difference between
fs <*> xs = do
f <- fs
x <- xs
return (f x)
and
fs <*> xs = do
x <- xs
f <- fs
return (f x)
Digging deeper into why this worked this way was interesting, but it's bed time, so I'm going to cut the scroll here.
[ Addendum 20221021: More about the two versions of <*> and a third version that doesn't work. ]
[Other articles in category /prog/haskell] permanent link
Sat, 20 Oct 2018
I struggle to understand Traversable
Haskell evolved a lot since the last time I seriously wrote any
Haskell code, so much so that all my old programs broke. My Monad
instances don't compile any more because I'm no longer allowed to
have a monad which isn't also an instance of Applicative. Last time I used
Haskell, Applicative wasn't even a thing. I had read the McBride and
Paterson paper that introduced applicative functors, but that was
years ago, and I didn't remember any of the details. (In fact, while
writing this article, I realized that the paper I read was a preprint,
and I probably read it before it was published, in 2008.) So to
resuscitate my old code I had to implement a bunch of <*> functions
and since I didn't really understand what it was supposed to be doing
I couldn't do that. It was a very annoying experience.
Anyway I got that more or less under control (maybe I'll publish a
writeup of that later) and moved on to Traversable which, I hadn't realized
before, was also introduced in that same paper. (In the
prepublication version, Traversable had been given the unmemorable name
IFunctor.) I had casually looked into this several times in the
last few years but I never found anything enlightening. A Traversable is a
functor (which must also implement Foldable, but let's pass over that
for now, no pun intended) that implements a traverse method with the
following signature:
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
The traversable functor itself here is t. The f thing is an
appurtenance. Often one looks at the type of some function and says “Oh, that's what
that does”, but I did not get any understanding from this signature.
The first thing to try here is to make it less abstract. I was thinking about Traversable this time because I thought I might want it for a certain type of tree structure I was working with. So I defined an even simpler tree structure:
data Tree a = Con a | Add (Tree a) (Tree a)
deriving (Eq, Show)
Defining a bunch of other cases wouldn't add anything to my understanding, and it would make it take longer to try stuff, so I really want to use the simplest possible example here. And this is it: one base case, one recursive case.
Then I tried to make this type it into a Traversable instance. First we need it to be a Functor, which is totally straightforward:
instance Functor Tree where
fmap f (Con a) = Con (f a)
fmap f (Add x y) = Add (fmap f x) (fmap f y)
Then we need it to be a Foldable, which means it needs to provide a
version of foldr. The old-fashioned foldr was
foldr :: (a -> b -> b) -> b -> [a] -> b
but these days the list functor in the third place has been generalized:
foldr :: Foldable f => (a -> b -> b) -> b -> f a -> b
The idea is that foldr fn collapses a list of as into a single b
value by feeding in the as one at a time. Each time, foldr takes
the previous b and the current a and constructs a new b. The
second argument is the initial value of b.
Another way to think about it is that every list has the form
e1 : e2 : .... : []
and foldr fn b applied to this list replaces the (:) calls with fn
and the trailing [] with b, giving me
e1 `f` e2 `f` .... `f` b
The canonical examples for lists are:
sum = foldr (+) 0
(add up the elements, starting with zero) and
length = foldr (\_ -> (+ 1)) 0
(ignore the elements, adding 1 to the total each time, starting with
zero). Also foldr (:) [] is the identity function for lists because
it replaces the (:) calls with (:) and the trailing [] with [].
Anyway for Tree it looks like this:
instance Foldable Tree where
foldr f b (Con a) = f a b
foldr f b (Add x y) = (foldr f) (foldr f b x) y
The Con clause says to take the constant value and combine it with
the default total. The Add clause says to first fold up the
left-side subtree x to a single value, then use that as the initial
value for folding up the right-side subtree y, so everything gets
all folded up together. (We could of course do the right subtree
before the left; the results would be different but just as good.)
I didn't write this off the top of my head, I got it by following the types, like this:
In the first clause
foldr f b (Con a) = ???we have a function
fthat wants anavalue and abvalue, and we have both anaand ab, so put the tabs in the slots.In the second clause
foldr f b (Add x y) = ???fneeds anavalue and none is available, so we can't usefby itself. We can only use it recursively viafoldr. So forgetf, we will only be dealing only withfoldr f, which has typeb -> Tree a -> b. We need to apply this to abvalue and the only one we have isb, and then we need to apply that to one of the subtrees, sayx, and thus we have synthesized thefoldr f b xsubexpression. Then pretty much the same process gets us the rest of it: we need aband the only one we have now isfoldr f b x, and then we need another tree and the only one we haven't used isy.
It turns out it is easier and more straightforward to write foldMap
instead, but I didn't know that at the time. I won't go into it
further because I have already digressed enough. The preliminaries
are done, we can finally get on to the thing I wanted, the Traversable:
instance Traversable Tree where
traverse = ....
and here I was stumped. What is this supposed to actually do?
For our Tree functor it has this signature:
traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
Okay, a function a -> f b I understand, it turns each tree leaf
value into a list or something, so at each point of the tree it gets
out a list of bs, and it potentially has one of those for each item
in the input tree. But how the hell do I turn a tree of lists into
a single list of Tree b? (The answer is that the secret sauce is
in the Applicative, but I didn't understand that yet.)
I scratched my head and read a bunch of different explanations and none of them helped. All the descriptions I found were in either prose or mathematics and I still couldn't figure out what it was for. Finally I just wrote a bunch of examples and at last the light came on. I'm going to show you the examples and maybe the light will come on for you too.
We need two Traversable functors to use as examples. We don't have a Traversable
implementation for Tree yet so we can't use that. When I think of
functors, the first two I always think of are List and Maybe, so
we'll use those.
> traverse (\n -> [1..n]) Nothing
[Nothing]
> traverse (\n -> [1..n]) (Just 3)
[Just 1,Just 2,Just 3]
Okay, I think I could have guessed that just from the types. And
going the other way is not very interesting because the output, being
a Maybe, does not have that much information in it.
> let f x = if even x then Just (x `div` 2) else Nothing
If the !!x!! is even then the result is just half of !!x!!, and otherwise the division by 2 “fails” and the result is nothing. Now:
> traverse f [ 1, 2, 3, 4 ]
Nothing
> traverse f [ 10, 4, 18 ]
Just [5,2,9]
It took me a few examples to figure out what was going on here: When
all the list elements are even, the result is Just a list of half of
each. But if any of the elements is odd, that spoils the whole result
and we get Nothing. (traverse f [] is Just [] as one would
expect.)
That pretty much exhausts what can be done with lists and maybes. Now
I have two choices about where to go next: I could try making both
functors List, or I could use a different functor entirely. (Making
both Maybe seemed like a nonstarter.) Using List twice seemed
confusing, and when I tried it I could kinda see what it was doing but
I didn't understand why. So I took a third choice: I worked up a Traversable
instance for Tree just by following the types even though I didn't
understand what it ought to be doing. I thought I'd at least see if I
could get the easy clause:
traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
instance Traversable Tree where
traverse fn (Con a) = ...
In the ... I have fn :: a -> f b and I have at hand a single a. I need to
construct a Tree b. The only way to get a b is to apply fn to
it, but this gets me an f b and I need f (Tree b). How do I get the
Tree in there? Well, that's what Con is for, getting Tree in
there, it turns a t into Tree t. But how do I do that inside of
f? I tinkered around a little bit and eventually found
traverse fn (Con a) = Con <$> (fn a)
which not only type checks but looks like it could even be correct.
So now I have a motto for what <$> is about: if I have some
function, but I want to use it inside of some applicative functor
f, I can apply it with <$> instead of with $.
Which, now that I have said it myself, I realize it is exactly what
everyone else was trying to tell me all along: normal function
application takes an a -> b and applies to to an a giving a b.
Applicative application takes an f (a -> b) and applies it to an f a
giving an f b. That's what applicative functors are all about,
doing stuff inside of f.
Okay, I can listen all day to an explanation of what an electric drill does, but until I hold it in my hand and drill some holes I don't really understand.
Encouraged, I tried the hard clause:
traverse fn (Add x y) = ...
and this time I had a roadmap to follow:
traverse fn (Add x y) = Add <$> ...
The Con clause had fn a at that point to produce an f b but that won't
work here because we don't have an a, we have a whole Tree a, and we
don't need an f b, we need an f (Tree b). Oh, no problem,
traverse fn supposedly turns a Tree a into an f (Tree b), which
is just what we want.
And it makes sense to have a recursive call to traverse because this is the
recursive part of the recursive data structure:
traverse fn (Add x y) = Add <$> (traverse fn x) ...
Clearly traverse fn y is going to have to get in there somehow, and
since the pattern for all the applicative functor stuff is
f <$> ... <*> ... <*> ...
let's try that:
traverse fn (Add x y) = Add <$> (traverse fn x) <*> (traverse fn y)
This looks plausible. It compiles, so it must be doing something.
Partial victory! But what is it doing? We can run it and see, which
was the whole point of an exercise: work up a Traversable instance for Tree
so that I can figure out what Traversable is about.
Here are some example trees:
t1 = Con 3 -- 3
t2 = Add (Con 3) (Con 4) -- 3 + 4
t3 = Add (Add (Con 3) (Con 4)) (Con 2) -- (3 + 4) + 2
(I also tried Add (Con 3) (Add (Con 4) (Con 2)) but it did not
contribute any new insights so I will leave it out of this article.)
First we'll try Maybe. We still have that f function from before:
f x = if even x then Just (x `div` 2) else Nothing
but traverse f t1, traverse f t2, and traverse f t3 only produce
Nothing, presumably because of the odd numbers in the trees. One
odd number spoils the whole thing, just like in a list.
So try:
traverse f (Add (Add (Con 10) (Con 4)) (Con 18))
which yields:
Just (Add (Add (Con 5) (Con 2)) (Con 9))
It keeps the existing structure, and applies f at each value
point, just like fmap, except that if f ever returns Nothing
the whole computation is spoiled and we get Nothing. This is
just like what traverse f was doing on lists.
But where does that spoilage behavior come from exactly? It comes
from the overloaded behavior of <*> in the Applicative instance of Maybe:
(Just f) <*> (Just x) = Just (f x)
Nothing <*> _ = Nothing
_ <*> Nothing = Nothing
Once we get a Nothing in there at any point, the Nothing takes
over and we can't get rid of it again.
I think that's one way to think of traverse: it transforms each
value in some container, just like fmap, except that where fmap
makes all its transformations independently, and reassembles the exact
same structure, with traverse the reassembly is done with the
special Applicative semantics. For Maybe that means “oh, and if at any
point you get Nothing, just give up”.
Now let's try the next-simplest Applicative, which is List. Say,
g n = [ 1 .. n ]
Now traverse g (Con 3) is [Con 1,Con 2,Con 3] which is not exactly
a surprise but traverse g (Add (Con 3) (Con 4)) is something that
required thinking about:
[Add (Con 1) (Con 1),
Add (Con 1) (Con 2),
Add (Con 1) (Con 3),
Add (Con 1) (Con 4),
Add (Con 2) (Con 1),
Add (Con 2) (Con 2),
Add (Con 2) (Con 3),
Add (Con 2) (Con 4),
Add (Con 3) (Con 1),
Add (Con 3) (Con 2),
Add (Con 3) (Con 3),
Add (Con 3) (Con 4)]
This is where the light finally went on for me. Instead of thinking
of lists as lists, I should be thinking of them as choices. A list
like [ "soup", "salad" ] means that I can choose soup or salad, but
not both. A function g :: a -> [b] says, in restaurant a, what
bs are on the menu.
The g function says what is on the menu at each node. If a node has
the number 4, I am allowed to choose any of [1,2,3,4], but if it has
the number 3 then the choice 4 is off the menu and I can choose only
from [1,2,3].
Traversing g over a Tree means, at each leaf, I am handed a menu,
and I make a choice for what goes at that leaf. Then the result of
traverse g is a complete menu of all the possible complete trees I
could construct.
Now I finally understand how the t and the f switch places in
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
I asked “how the hell do I turn a tree of lists into a single list
of Tree b”? And that's the answer: each list is a local menu of
dishes available at one leaf, and the result list is the global menu
of the complete dinners available over the entire tree.
Okay! And indeed traverse g (Add (Add (Con 3) (Con 4)) (Con 2)) has
24 items, starting
Add (Add (Con 1) (Con 1)) (Con 1)
Add (Add (Con 1) (Con 1)) (Con 2)
Add (Add (Con 1) (Con 2)) (Con 1)
...
and ending
Add (Add (Con 3) (Con 4)) (Con 1)
Add (Add (Con 3) (Con 4)) (Con 2)
That was traversing a list function over a Tree. What if I go the
other way? I would need an Applicative instance for Tree and I didn't
really understand Applicative yet so that wasn't going to happen for a
while. I know I can't really understand Traversable without understanding
Applicative first but I wanted to postpone the day of reckoning as long as
possible.
What other functors do I know? One easy one is the functor that takes
type a and turns it into type (String, a). Haskell even has a
built-in Applicative instance for this, so I tried it:
> traverse (\x -> ("foo", x)) [1..3]
("foofoofoo",[1,2,3])
> traverse (\x -> ("foo", x*x)) [1,5,2,3]
("foofoofoofoo",[1,25,4,9])
Huh, I don't know what I was expecting but I think that wouldn't have
been it. But I figured out what was going on: the built-in Applicative
instance for the a -> (String, a) functor just concatenates the
strings. In general it is defined on a -> (m, b) whenever m is a
monoid, and it does fmap on the right component and uses monoid
concatenation on the left component. So I can use integers instead of
strings, and it will add the integers instead of concatenating the
strings. Except no, it won't, because there are several ways to make
integers into a monoid, but each type can only have one kind of
Monoid operations, and if one was wired in it might not be the one I
want. So instead they define a bunch of types that are all integers
in obvious disguises, just labels stuck on them that say “I am not an
integer, I am a duck”; “I am not an integer, I am a potato”. Then
they define different overloadings for “ducks” and “potatoes”. Then
if I want the integers to get added up I can put duck labels on my
integers and if I want them to be multiplied I can stick potato labels
on instead. It looks like this:
import Data.Monoid
h n = (Sum 1, n*10)
Sum is the duck label. When it needs to combine two
ducks, it will add the integers:
> traverse h [5,29,83]
(Sum {getSum = 3},[50,290,830])
But if we wanted it to multiply instead we could use the potato label,
which is called Data.Monoid.Product:
> traverse (\n -> (Data.Monoid.Product 7, 10*n)) [5,29,83]
(Product {getProduct = 343}, [50,290,830])
There are three leaves, so we multiply three sevens and get 343.
Or we could do the same sort of thing on a Tree:
> traverse (\n -> (Data.Monoid.Product n, 10*n)) (Add (Con 2) (Add (Con 3) (Con 4)))
(Product {getProduct = 24}, Add (Con 20) (Add (Con 30) (Con 40)))
Here instead of multiplying together a bunch of sevens we multiply together the leaf values themselves.
The McBride and Paterson paper spends a couple of pages talking about
traversals over monoids, and when I saw the example above it started
to make more sense to me. And their ZipList example became clearer
too. Remember when we had a function that gave us a menu at every
leaf of a tree, and traverse-ing that function over a tree gave us a
menu of possible trees?
> traverse (\n -> [1,n,n*n]) (Add (Con 2) (Con 3))
[Add (Con 1) (Con 1),
Add (Con 1) (Con 3),
Add (Con 1) (Con 9),
Add (Con 2) (Con 1),
Add (Con 2) (Con 3),
Add (Con 2) (Con 9),
Add (Con 4) (Con 1),
Add (Con 4) (Con 3),
Add (Con 4) (Con 9)]
There's another useful way to traverse a list function. Instead of taking each choice at each leaf we make a single choice ahead of time about whether we'll take the first, second, or third menu item, and then we take that item every time:
> traverse (\n -> Control.Applicative.ZipList [1,n,n*n]) (Add (Con 2) (Con 3))
ZipList {getZipList = [Add (Con 1) (Con 1),
Add (Con 2) (Con 3),
Add (Con 4) (Con 9)]}
There's a built-in instance for Either a b also. It's a lot like
Maybe. Right is like Just and Left is like Nothing. If all
the sub-results are Right y then it rebuilds the structure with all
the ys and gives back Right (structure). But if any of the
sub-results is Left x then the computation is spoiled and it gives
back the first Left x. For example:
> traverse (\x -> if even x then Left (x `div` 2) else Right (x * 10)) [3,17,23,9]
Right [30,170,230,90]
> traverse (\x -> if even x then Left (x `div` 2) else Right (x * 10)) [3,17,22,9]
Left 11
Okay, I think I got it.
Now I just have to drill some more holes.
[Other articles in category /prog/haskell] permanent link
Tue, 16 Oct 2018
I redesign the LA Times’ Hurricane Maria chart
This could have been a great chart, but I think it has a big problem:
It appears that the death toll started increasing in early August, even though the hurricane didn't hit until 20 September. According to this chart, the hurricane was shortly followed by a drastic decrease in the death rate.
What's actually going on is that the August value is a total for all of August and is typically low, the September value is a total for all of September and is atypically high, and the chart designer has drawn a straight line between the August and September values, implying a linear increase over the course of August. The data for August is at the mark “A” on the chart, which seems reasonable, except that one has to understand that “A” as marking the end of August instead of the beginning, which is the opposite of the usual convention.
I think a bar chart would have been a better choice here. The lines imply continuous streams of data, but the reality is that each line represents only twelve data points. Maybe something like this instead?
I'm not sure the historical range bars are really adding much.
If I were designing this from scratch I think I might replace the blue bars with brackets (although maybe the LA Times knows that their readership finds those confusing?). Or maybe plot the difference between the 2017 data and ths historical average. But I think you get the point.
[Other articles in category /IT] permanent link
Mon, 15 Oct 2018
'The' reader monad does not exist
Reading over my recent article complaining about the environment functor I realized there's yet another terminology problem that makes the discussion unnecessarily confusing. “The” environment functor isn't unique. There is a family of environment functors, one for each possible environment type e. If g is the environment functor at type e, a value of type g t is a function e → t. But e could be anything and if g and h are environment functors at two different types e and e’ they are of course different functors.
This is even obvious from the definition:
data Environ e t = Env (e -> t)
instance Functor (Environ e) where
fmap f (Env x) = Env $ \e -> f (x e)
The functor isn't Environ, it's Environ e, and the functor
instance declaration, as it says on line 2. (It seems to me that the
notation is missing a universal quantifier somewhere, but I'm not
going to open that issue.)
We should speak of Environ e as an environment functor, not
the environment functor. So for example instead of:
When operating in the environment functor,
fmaphas the type(a -> b) -> g a -> g b
I should have said:
When operating in an environment functor,
fmaphas the type(a -> b) -> g a -> g b
And instead of:
A function
p -> qis aqparcel in the environment functor
I should have said:
A function
p -> qis aqparcel in an environment functor
or
A function
p -> qis aqparcel in the environment functor atp
although I'm not sure I like the way the prepositions are proliferating there.
The same issue affects ⸢the⸣ reader monad, ⸢the⸣ state monad, and many others.
I'm beginning to find remarkable how much basic terminology Haskell is missing or gets wrong. Mathematicians have a very keen appreciation of the importance of specific and precise terminology, and you'd think this would have filtered into the Haskell world. People are forever complaining that Haskell uses unfamiliar terms like “functor”, and the community's response is (properly, I think) that these terms are pre-existing and there is no point to inventing a new term that will be just as unfamiliar, or, worse, lure people into thinking that the know what it means when they don't. You don't want to call a functor a “container”, says the argument, because many functors (environment functors for example) are nothing at all like containers. I think this is wise.
But having planted their flag on that hill, the Haskell folks don't
then use their own terminology correctly. I complained years
ago that the term
“monad” was used interchangeably for four subtly different concepts,
and here we actually have a fifth. I pointed out that in the case of
Environment e t, common usage refers to both Environment e and
Environment e t as monads, and only the first is correct. But when
people say “the environment monad” they mean that Environment itself
is a monad, which it is not.
[Other articles in category /prog/haskell] permanent link
Thu, 11 Oct 2018Is there any good terminology for a value of type
f awhenfis an arbitrary functor? I will try calling anf tvalue a “tparcel” and see how that works.
The more I think about “parcel” the happier I am with it. It strongly
suggests container types, of course, so that a t parcel might be a
boxful of ts. But it also hints at some other possible situations:
- You might open the parcel and find it empty. (
Maybe t) - You might open the parcel and find, instead of the
tyou expected, a surprising prank snake. (Either ErrorMessage t) - You might open the parcel and find that your
thas been shipped with assembly required. (env -> t) - The parcel might explode when you open it. (
IO t) - And, of course, a burrito is a sort of parcel of meat and beans.
I coined “parcel” thinking that one would want different terminology
for values of type f t depending on whether f was a functor
(“parcel”) or also a monad (“mote”). Of course every mote is a
parcel, but not always vice versa. Now I'm not sure that both terms
are needed. Non-monadic functors are unusual, and non-applicative
functors rare, so perhaps one term will do for all three.
[Other articles in category /prog/haskell] permanent link
I hate the environment functor
Here we have the well-known fmap function:
fmap :: Functor f => (a -> b) -> f a -> f b
It takes a single function and a (collection of input values / decorated input value / something something input value) and produces a (collection of output values / decorated output value / something something output value).
Yow, that's not going to work. Is there any good terminology for a
value of type f a when f is an arbitrary functor? A while back I
discussed a similar
problem and suggested
the term “mote” for a value in a monadic type. I will try calling an
f t value a “t parcel and see how that works. So
[t], Maybe t, and IO t are all examples of t parcels, in
various functors.
Starting over then. Here we have the well-known fmap function:
fmap :: Functor f => (a -> b) -> f a -> f b
It takes a single function, and an a parcel, and produces a b
parcel, by applying the function independently to the a values in
the parcel.
Here is a sort of reversed version of fmap that I call pamf:
pamf :: Functor f => f (a -> b) -> a -> f b
It takes a parcel of functions, and a single input and produces a
parcel of outputs, by applying each function in the parcel
independently to the single a value. It can be defined in terms of
fmap:
pamf fs a = fmap ($ a) fs
So far so good. Now I ask you to predict the type of
pamf fmap
Certainly it should start out with
pamf fmap :: (Functor f, Functor g) => ...
because the pamf and the fmap might be operating in two different
functors, right? Indeed, if I compose the functions the other way
around, fmap pamf, the type does begin this way; it is:
(Functor f, Functor g) => f (g (a -> b)) -> f (a -> g b)
The f here is the functor in which fmap operates, and the g is
the functor in which pamf is operating. In general fmap takes an
arbitrary function
a -> b
and lifts it to a new function that operates in the f functor:
f a -> f b
Here it has taken pamf, which is a function
g (a -> b) -> (a -> g b)
and lifted it to a new function that operates in the f functor:
f (g (a -> b)) -> f (a -> g b)
This is complicated but straightforward. Okay, that was fmap pamf.
What about pamf fmap though? The computed type is
pamf fmap :: Functor f => f a -> (a -> b) -> f b
and when I saw this I said “What. Where did g go? What happened to
g?”
Then I paused and for a while and said “… I bet it's that goddamn environment thing again.” Yep, that's what it was. It's the environment functor, always turning up where I don't want it and least expect it, like that one guy we all went to college with. The environment functor, by the way, is yet another one of those things that Haskell ought to have a standard name for, but doesn't. The phrase “the reader monad” is fairly common, but here I only want the functor part of the monad. And people variously say “reader monad”, “environment monad”, and “evaluation monad” to mean the same thing. In this article, it will be the environment functor.
Here's what happened. Here are fmap and pamf again:
fmap :: Functor f => (p -> q) -> f p -> f q
pamf :: Functor g => g (a -> b) -> a -> g b
The first argument to pamf should be a parcel in the g functor.
But fmap is not a parcel, so pamf fmap will be a type error,
right? Wrong! If you are committed enough, there is a way to
construe any function as a parcel. A function p -> q is a q
parcel in the environment functor. Say that g denotes an
environment functor. In this functor, a parcel of type g t is a
function which consults an “environment” of type e and yields a
result of type t. That is, $$g\ t \equiv e \to t.$$
When operating in the environment functor, fmap has the type (a ->
b) -> g a -> g b, which is shorthand for (a -> b) -> (e -> a) -> (e
-> b). This instance of fmap is defined this way:
fmap f x = \e -> f (x e)
or shorter and more mysteriously
fmap = (.)
which follows by η-reduction, something Haskell enthusiasts never seem to get enough of.
In fmap f x, the x isn't the actual value to give to f; instead
it's a parcel, as it always is with fmap. In the context of the
environment functor, x is a function that consults the environment
e and returns an a. The result of fmap f x is a new parcel: it
uses x to consult the supplied environment for a value of type a,
which it then feeds to f to get the required value of type b.
In the application pamf fmap, the left side pamf wants fmap to
be a parcel. But it's not a parcel, it's a function. So, type error,
right? No! Any function is a parcel if you want it to be, it's a
parcel in the environment functor! And fmap is a function:
fmap :: Functor f => (p -> q) -> f p -> f q
so it can be understood as a parcel in the environment functor, where
the environment e has type p -> q. Then pamf is operating in
this environment functor, so $$g\ t = (p \to q) \to t.$$ A g t parcel
is a function that consults an “environment” of type p -> q and
somehow produces a t value. (Haskell folks, who are obsessed with
currying all the things, will write this as the
nearly unreadable g = ((->) (p -> q)).)
We wanted pamf to have this type:
pamf :: Functor g => g (a -> b) -> a -> g b
and since Haskell has decided that g must be the environment functor
with !!g\ x \equiv (p \to q) \to x!!,
this is an abbreviation for:
pamf :: ((p -> q) -> (a -> b)) -> a -> ((p -> q) -> b)
To apply this to fmap, we have to unify the type of pamf's
argument, which is (p -> q) -> (a -> b), and the type of fmap,
which is (p -> q) -> (f p -> f q). Then !!a\equiv f\ p!! and !!b
\equiv f\ q!!, so the result of pamf fmap is
pamf fmap :: Functor f => f p -> ((p -> q) -> f q)
Where did g go? It was specialized to mean the environment functor
((->) (p -> q)), so it's gone.
The funny thing about the type of pamf fmap is that it is exactly
the type of flip fmap, which is fmap with the order of its two
arguments reversed:
(flip fmap) x f ≡ fmap f x
and indeed, by some theorem or other, because the types are identical,
the functions themselves must be identical also! (There are some side
conditions, all of which hold here.) The two functions pamf fmap and
flip fmap are identical. Analogous to the way fmap, restricted
to the environment functor, is identical to (.), pamf, when
similarly restricted, is exactly
flip. You can even see this from its type:
pamf :: ((p -> q) -> (a -> b)) -> a -> ((p -> q) -> b)
Or, cleaning up some superfluous parentheses and inserting some new ones:
pamf :: ((p -> q) -> a -> b) -> (a -> (p -> q) -> b)
And putting !!c = p\to q!!:
pamf :: (c -> a -> b) -> (a -> c -> b)
flip :: ( the same )
Honestly, I would have preferred a type error: “Hey, dummy, fmap has
the wrong type to be an argument to pamf, which wants a functorial
value.” Instead I got “Okay, if you want functions to be a kind of
functor I can do that, also wouldn't it be simpler if the universe was
two-dimensional and there were only three kinds of quarks? Here you
go, no need to thank me!” Maybe someone can explain to me why this is
a useful behavior, and then explain why it is so useful that it should
happen automatically and implicitly instead of being triggered
by some lexical marker like:
newtype Environment e a = Environment (e -> a)
instance Functor (Environment e) where
fmap f (Environment x) = Environment $ \e -> f (x e)
I mean, seriously, suppose you wrote a + b where b was
accidentally a function instead of a number. What if when you did
that, instead of a type error, Haskell would silently shift into some
restricted domain in which it could implicitly interpret b as a
number in some weird way and give you something totally bizarre?
Isn't the whole point of Haskell supposed to be that it doesn't
implicitly convert things that way?
[ Addendum 20181111: Apparently, everyone else hates it too. ]
[Other articles in category /prog/haskell] permanent link
Wed, 10 Oct 2018Minecraft makes maps in-game, and until now I would hold up the map in the game, take a screenshot, print it out, and annotate the printout.
Now I can do better. I have a utility that takes multiple the map files direcly from the Minecraft data directory and joins them together into a single PNG image that I can then do whatever with. Here's a sample, made by automatically processing the 124(!) maps that exist in my current Minecraft world.

Notice how different part of the result are at different resolutions. That is because Minecraft maps are in five different resolutions, from !!2^{14}!! to !!2^{22}!! square meters in area, and these have been stitched together properly. My current base of operations is a little comma-shaped thingy about halfway down in the middle of the ocean, and on my largest ocean map it is completely invisible. But here it has been interpolated into the correct tiny scrap of that big blue map.
Bonus: If your in-game map is lost or destroyed, the data file still hangs around, and you can recover the map from it.
Source code is on Github. It needs some work:
- You have to manually decompress the map files
- It doesn't show banners or other markers
- I got bored typing in the color table and didn't finish
- Invoking it is kind of heinous
./dumpmap $(./sortbyscale map_*) | pnmtopng > result.png
Patches welcome!
[Other articles in category /games] permanent link
Mon, 08 Oct 2018
Notes on using git-replace to get rid of giant objects
A couple of years ago someone accidentally committed a 350 megabyte
file to our Git repository. Now it's baked in. I wanted to get rid
of it. I thought that I might be able to work out a partial but
lightweight solution using git-replace.
Summary: It didn't work.
Details
In 2016 a programmer commited a 350 megabyte file to my employer's repo, then in the following commit they removed it again. Of course it's still in there, because someone might check out the one commit where it existed. Everyone who clones the repo gets a copy of the big file. Every copy of the repo takes up an extra 350 megabytes on disk.
The usual way to fix this is onerous:
Use
git-filter-branchto rebuild all the repository history after the bad commit.Update all the existing refs to point to the analogous rebuilt objects.
Get everyone in the company to update all the refs in their local copies of the repo.
I thought I'd tinker around with git-replace to see if there was
some way around this, maybe something that someone could do locally on
their own repo without requiring everyone else to go along with it.
The git-replace command annotates the Git repository to say that
whenever object A is wanted, object B should be used instead. Say
that the 350 MB file has an ID of
ffff9999ffff9999ffff9999ffff9999ffff9999. I can create a small file
that says
This is a replacement object. It replaces a very large file
that was committed by mistake. To see the commit as it really
was, use
git --no-replace-objects show 183a5c7e90b2d4f6183a5c7e90b2d4f6183a5c7e
git --no-replace-objects checkout 183a5c7e90b2d4f6183a5c7e90b2d4f6183a5c7e
or similarly. To see the file itself, use
git --no-replace-objects show ffff9999ffff9999ffff9999ffff9999ffff9999
I can turn this small file into an object with git-add; say the new
small object has ID 1111333311113333111133331111333311113333. I
then run:
git replace ffff9999ffff9999ffff9999ffff9999ffff9999 1111333311113333111133331111333311113333
This creates
.git/refs/replace/ffff9999ffff9999ffff9999ffff9999ffff9999, which
contains the text 1111333311113333111133331111333311113333.
thenceforward, any Git command that tries to access the original
object ffff9999 will silently behave as if it were 11113333
instead. For example, git show 183a5c7e will show the diff between
that commit and the previous, as if the user had committed my small
file back in 2016 instead of their large one. And checking out that
commit will check out the small file instead of the large one.
So far this doesn't help much. The checkout is smaller, but nobody was likely to have that commit checked out anyway. The large file is still in the repository, and clones and transfers still clone and transfer it.
The first thing I tried was a wan hope: will git gc discard the
replaced object? No, of course not. The ref in refs/replace/
counts as a reference to it, and it will never be garbage-collected.
If it had been, you would no longer be able to examine it with the
--no-replace-objects commands. So much for following the rules!
Now comes the hacking part: I am going to destroy the actual object. Say for example, what if:
cp /dev/null .git/objects/ff/ff9999ffff9999ffff9999ffff9999ffff9999
Now the repository is smaller! And maybe Git won't notice, as long as
I do not use --no-replace-objects?
Indeed, much normal Git usage doesn't notice. For example, I can make
new commits with no trouble, and of course any other operation that
doesn't go back as far as 2016 doesn't notice the change. And
git-log works just fine even past the bad commit; it only looks at
the replacement object and never notices that the bad object is
missing.
But some things become wonky. You get an error message when you clone
the repo because an object is missing. The replacement refs are local
to the repo, and don't get cloned, so clone doesn't know to use the
replacement object anyway. In the clone, you can use git replace -f
.... to reinstate the replacement, and then all is well unless
something tries to look at the missing object. So maybe a user could
apply this hack on their own local copy if they are willing to
tolerate a little wonkiness…?
No. Unfortunately, there is a show-stopper: git-gc no longer
works in either the parent repo or in the clone:
fatal: unable to read ffff9999ffff9999ffff9999ffff9999ffff9999
error: failed to run repack
and it doesn't create the pack files. It dies, and leaves behind a
.git/objects/pack/tmp_pack_XxXxXx that has to be cleaned up by hand.
I think I've reached the end of this road. Oh well, it was worth a look.
[ Addendum 20181009: A lot of people have unfortunately missed the point of this article, and have suggested that I use BFG or reposurgeon. I have a small problem and a large problem. The small problem is how to remove some files from the repository. This is straightforward, and the tools mentioned will help with it. But because of the way Git works, the result is effectively a new repository. The tools will not help with the much larger problem I would have then: How to get 350 developers to migrate to the new repository at the same time. The approach I investigated in this article was an attempt to work around this second, much larger problem. ]
[Other articles in category /prog] permanent link
Sat, 06 Oct 2018Last week we visited Toph's school and I saw a big map of Pennsylvania. I was struck by something I had never noticed before. Here's a detail of central Pennsylvania, an area roughly 100 miles (160 km) square:
As you can see, a great many lines on this map start in the lower left, proceed in roughly parallel tracks north-by-northeast, then bend to the right, ending in the upper right corner. Many of the lines represent roads, but some represent county borders, and some represent natural features such as forests and rivers.
When something like this happens, it is almost always for some topographic reason. For example, here's a map of two adjacent communities in Los Angeles:
You can see just from the pattern of the streets that these two places must have different topography. The streets in Santa Monica are a nice rectangular grid. The streets in Pacific Palisades are in groups of concentric squiggles. This is because Pacific Palisades is hilly, and the roads go in level curves around the hills, whereas Santa Monica is as flat as a squid.
I had never noticed before that all the lines in central Pennsylvania go in the same direction. From looking at the map, one might guess that central Pennsylvania was folded into many long parallel wrinkles, and that the roads, forests, and rivers mostly lay in the valleys between the wrinkles. This is indeed the case. This part of Pennsylvania is part of the Ridge-and-Valley Appalachians, and the pattern of ridges and valleys extends far beyond Pennsylvania.
The wrinkling occurred over a long period, ending around 260 million years ago, in an event called the Alleghanian orogeny. North America and Africa (then part of the supercontinents Euramerica and Gondwana, respectively) collided with one another, and that whole part of North America crumpled up like a sheet of aluminum foil. People in Harrisburg and State College are living in the crumples.
[Other articles in category /misc] permanent link
Mon, 24 Sep 2018A long time ago, I wrote up a blog article about how to derive the linear regression formulas from first principles. Then I decided it was not of general interest, so I didn't publish it. (Sometime later I posted it to math stack exchange, so the effort wasn't wasted.)
The basic idea is, you have some points !!(x_i, y_i)!!, and you assume that they can be approximated by a line !!y=mx+b!!. You let the error be a function of !!m!! and !!b!!: $$\varepsilon(m, b) = \sum (mx_i + b - y_i)^2$$ and you use basic calculus to find !!m!! and !!b!! for which !!\varepsilon!! is minimal. Bing bang boom.
I knew this for a long time but it didn't occur to me until a few months ago that you could use basically the same technique to fit any other sort of curve. For example, suppose you think your data is not a line but a parabola of the type !!y=ax^2+bx+c!!. Then let the error be a function of !!a, b, !! and !!c!!:
$$\varepsilon(a,b,c) = \sum (ax_i^2 + bx_i + c - y_i)^2$$
and again minimize !!\varepsilon!!. You can even get a closed form as you can with ordinary linear regression.
I especially wanted to try fitting hyperbolas to data that I expected to have a Zipfian distribution. For example, take the hundred most popular names for girl babies in Illinois in 2017. Is there a simple formula which, given an ordinal number like 27, tells us approximately how many girls were given the 27th most popular name that year? (“Scarlett”? Seriously?)
I first tried fitting a hyperbola of the form !!y = c + \frac ax!!. We could, of course, take !!y_i' = \frac 1{y_i}!! and then try to fit a line to the points !!\langle x_i, y_i'\rangle!! instead. But this will distort the measurement of the error. It will tolerate gross errors in the points with large !!y!!-coordinates, and it will be extremely intolerant of errors in points close to the !!x!!-axis. This may not be what we want, and it wasn't what I wanted. So I went ahead and figured out the Zipfian regression formulas:
$$ \begin{align} a & = \frac{HY-NQ}D \\ c & = \frac{HQ-JY}D \end{align} $$
Where:
$$\begin{align} H & = \sum x_i^{-1} \\ J & = \sum x_i^{-2} \\ N & = \sum 1\\ Q & = \sum y_ix_i^{-1} \\ Y & = \sum y_i \\ D & = H^2 - NJ \end{align} $$
When I tried to fit this to some known hyperbolic data, it worked just fine. For example, given the four points !!\langle1, 1\rangle, \langle2, 0.5\rangle, \langle3, 0.333\rangle, \langle4, 0.25\rangle!!, it produces the hyperbola $$y = \frac{1.00018461538462}{x} - 0.000179487179486797.$$ This is close enough to !!y=\frac1x!! to confirm that the formulas work; the slight error in the coefficients is because we used !!\bigl\langle3, \frac{333}{1000}\bigr\rangle!! rather than !!\bigl\langle3, \frac13\bigr\rangle!!.
Unfortunately these formulas don't work for the Illinois baby data. Or rather, the hyperbola fits very badly. The regression produces !!y = \frac{892.765272442475}{x} + 182.128894972025:!!
I think maybe I need to be using some hyperbola with more parameters, maybe something like !!y = \frac a{x-b} + c!!.
In the meantime, here's a trivial script for fitting !!y = \frac ax + c!! hyperbolas to your data:
while (<>) {
chomp;
my ($x, $y) = split;
($x, $y) = ($., $x) if not defined $y;
$H += 1/$x;
$J += 1/($x*$x);
$N += 1;
$Q += $y/$x;
$Y += $y;
}
my $D = $H*$H - $J*$N;
my $c = ($Q*$H - $J*$Y)/$D;
my $a = ($Y*$H - $Q*$N)/$D;
print "y = $a / x + $c\n";
[ Addendum 20180925: Shreevatsa R. asked a related question on StackOverflow and summarized the answers. The problem is more complex than it might first appear. Check it out. ]
[Other articles in category /math] permanent link
Fri, 14 Sep 2018
How not to remember the prime numbers under 1,000
A while back I said I wanted to memorize all the prime numbers under 1,000, because I am tired of getting some number like 851 or 857, or even 307, and then not knowing whether it is prime.
The straightforward way to deal with this is: just memorize the list. There are only 168 of them, and I have the first 25 or so memorized anyway.
But I had a different idea also. Say that a set of numbers from !!10n!! to !!10n+9!! is a “decade”. Each decade contains at most 4 primes, so 4 bits are enough to describe the primes in a single decade. Assign a consonant to each of the 16 possible patterns, say “b” when none of the four numbers is a prime, “d” when only !!10n+1!! is prime, “f” when only !!10n+3!! is, and so on.
Now memorizing the primes in the 90 decades is reduced to memorizing 90 consonants. Inserting vowels wherever convenient, we have now turned the problem into one of memorizing around 45 words. A word like “potato” would encode the constellation of primes in three consecutive decades. 45 words is only a few sentences, so perhaps we could reduce the list of primes to a short and easily-remembered paragraph. If so, memorizing a few sentences should be much easier than memorizing the original list of primes.
The method has several clear drawbacks. We would have to memorize the mapping from consonants to bit patterns, but this is short and maybe not too difficult.
More significant is that if we're trying to decide if, say, 637 is prime, we have to remember which consonant in which word represents the 63rd decade. This can be fixed, maybe, by selecting words and sentences of standard length. Say there are three sentences and each contains 30 consonants. Maybe we can arrange that words always appear in patterns, say four words with 1 or 2 consonants each that together total 7 consonants, followed by a single long word with three consonants. Then each sentence can contain three of these five-word groups and it will be relatively easy to locate the 23rd consonant in a sentence: it is early in the third group.
Katara and I tried this, with not much success. But I'm not ready to give up on the idea quite yet. A problem we encountered early on is that we remember consonants not be how words are spelled but by how they sound. So we don't want a word like “hammer” to represent the consonant pattern h-m-m but rather just h-m.
Another problem is that some constellations of primes are much more common than others. We initially assigned consonants to constellations in order. This assigned letter “b” to the decades that contain no primes. But this is the most common situation, so the letter “b” tended to predominate in the words we needed for our mnemonic. We need to be careful to assign the most common constellations to the best letters.
Some consonants in English like to appear in clusters, and it's not trivial to match these up with the common constellations. The mapping from prime constellations to consonants must be carefully chosen to work with English. We initially assigned “s” to the constellation “☆•☆☆” (where !!10n+1, 10n+7,!! and !!10n+9!! are prime but !!10n+3!! is not) and “t” to the constellation “☆☆••” (where !!10n+1!! and !!10n+3!! are prime but !!10n+7!! and !!10n+9!! are not) but these constellations cannot appear consecutively, since at least one of !!10n+7, 10n+9, 10n+11!! is composite. So any word with “s” and “t” with no intervening consonants was out of play. This eliminated a significant fraction of the entire dictionary!
I still think it could be made to work, maybe. If you're interested
in playing around with this, the programs I wrote are available on
Github. The mapping
from decade constellations to consonant clusters is in
select_words.py.
[Other articles in category /math] permanent link
Wed, 12 Sep 2018
Perils of hacking on mature software
Yesterday I wrote up an interesting bug in git-log --follow's
handling of empty files. Afterward
I thought I'd see if I could fix it.
People complain that the trouble of working on mature software like Git is to understand the way the code is structured, its conventions, the accumulated layers of cruft, and where everything is. I think this is a relatively minor difficulty. The hard part is no so much doing what you want, as knowing what you want to do.
My original idea for the fix was this: I can give git log a new
option, say --follow-size-threshhold=n. This would disable all
copy and rename detection for any files of size less than n bytes.
If not specified or configured, n would default to 1, so that the
default behavior would disable copy and rename detection of empty
files but not of anything else. I was concerned that an integer
option was unnecessarily delicate. It might have been sufficient to
have a boolean --follow-empty-files flag. But either way the
programming would be almost the same and it would be easy to simplify
the option later if the Git maintainers wanted it that way
I excavated the code and found where the change needed to go. It's
not actually in git-log itself. Git has an internal system for
diffing pairs of files, and git-log --follow uses this to decide
when two blobs are similar enough for it to switch from following one
to the other. So the flag actually needed to be added to git-diff,
where I called it --rename-size-threshhold. Then git-log would
set that option internally before using the Git diff system to detect
renames.
But then I ran into a roadblock. Diff already has an undocumented
flag called --rename-empty that tells it to report on renames of
empty files in certain contexts — not the context I was interested in
unfortunately. The flag is set by default, but it is cleared internally
when git-merge is resolving conflicts. The issue it addresses is
this: Suppose the merge base has some empty file X. Somewhere along
the line X has been removed. In one branch, an unrelated empty file
Y has been created, and in the other branch a different unrelated
empty file Z has been created. When merging these two branches, Git
will detect a merge conflict: was file X moved to location Y or to
location Z? This ⸢conflict⸣ is almost certainly spurious, and is is
very unlikely that the user will thank us for demanding that they
resolve it manually. So git-merge sets --no-rename-empty
internally and Git resolves the ⸢conflict⸣ automatically.
(See this commit for further details.)
The roadblock is: how does --rename-empty fit together with my
proposed --rename-size-threshhold flag? Should they be the same
thing? Or should they be separate options? There appear to be at
least three subsystems in Git that try to decide if two similar or
identical files (which might have different names, or the same name in
different directories) are “the same file” for various purposes. Do
we want to control the behavior of these subsystems separately or in
unison?
If they should be controlled in unison, should
--rename-size-threshhold be demoted to a boolean, or should
--rename-empty be promoted to an integer? And if they should be the
same, what are the implications for backward compatibility? Should
the existing --rename-empty be documented?
If we add new options, how do they interact with the existing and
already non-orthogonal flags that do something like this? They
include at least the following options of git-diff, git-log, and
git-show:
--follow
--find-renames=n
--find-copies
--find-copies-harder
-l
Only git-log has --follow and my new feature was conceived as a
modification of it, which is why I named it
--follow-size-threshhold. But git-log wouldn't be implementing
this itself, except to pass the flag into the diff system. Calling it
--follow-size-threshhold in git-diff didn't make sense because
git-diff doesn't have a --follow option. It needs a different
name. But if I do that, then we have git-diff and git-log options
with different names that nevertheless do exactly the same thing.
Confusing!
Now suppose you would like to configure a default for this option in
your .gitconfig. Does it make sense to have both
diff.renameSizeThreshhold and log.followSizeThreshhold options?
Not really. It would never be useful to set one but not the other.
So eliminate log.followSizeThreshhold. But now someone like me who
wants to change the behavior of git-log --follow will not know to
look in the right place for the option they need.
The thing to do at this point is to come up with some
reasonable-seeming proposal and send it to Jeff King, who created the
undocumented --rename-empty feature, and who is also a good person
to work with. But coming up with a good solution entirely on my own
is unlikely.
Doing any particular thing would not be too hard. The hard part is deciding what particular thing to do.
[Other articles in category /prog] permanent link
Language fluency in speech and print
Long ago I worked among the graduate students at the University of Pennsylvania department of Computer and Information Sciences. Among other things, I did system and software support for them, and being about the same age and with many common interests, I socialized with them also.
There was one Chinese-Malaysian graduate student who I thought of as having poor English. But one day, reading one of his emailed support requests, I was struck by how clear and well-composed it was. I suddenly realized I had been wrong. His English was excellent. It was his pronunciation that was not so good. When speaking to him in person, this was all I had perceived. In email, his accent vanished and he spoke English like a well-educated native. When I next met him in person I paid more careful attention and I realized that, indeed, I had not seen past the surface: he spoke the way he wrote, but his accent had blinded me to his excellent grammar and diction.
Once I picked up on this, I started to notice better. There were many examples of the same phenomenon, and also the opposite phenomenon, where someone spoke poorly but I hadn't noticed because their pronunciation was good. But then they would send email and the veil would be lifted. This was even true of native speakers, who can get away with all sorts of mistakes because their pronunciation is so perfect. (I don't mean perfect in the sense of pronouncing things the way the book says you should; I mean in the sense of pronouncing things the way a native speaker does.) I didn't notice this unless I was making an effort to look for it.
I'm not sure I have anything else to say about this, except that it seems to me that when learning a foreign language, one ought to consider whether one will be using it primarily for speech or primarily for writing, and optimize one's study time accordingly. For speech, concentrate on good pronunciation; for writing, focus on grammar and diction.
Hmm, put that way it seems obvious. Also, the sky is sometimes blue.
[Other articles in category /lang] permanent link
Mon, 10 Sep 2018
Why hooks and forks in the J language?
I don't know why [Ken] Iverson thought the hook was the thing to embed in the [J] language.
And I think I now recall that the name of the language itself, J, is intended to showcase the hook, so he must have thought it was pretty wonderful.
A helpful Hacker News
comment pointed me to
the explanation. Here Iverson explains why the “hook”
feature: it is actually the
S combinator in disguise. Recall that
$${\bf S} x y z = x z (y z).$$ This is exactly what J's hook computes
when you write (x y) z. For instance, if I understand correctly, in
J (+ !) means the one-place operation that takes an argument !!z!!
to !!z + z! !!.
As McBride and Paterson point
out, S
is also the same as the <*> operator in the Reader instance of
Applicative.
Since in J the only possible inputs to a hook are functions, it is
operating in the Reader idiom and in that context its hook is doing
the same thing as Haskell's <*>. Similarly, J's “fork” feature can
be understood as essentially the same as the Reader insance of
Haskell's liftA2.
[Other articles in category /prog] permanent link
git log --follow enthusiastically tracks empty files
This bug I just found in git log --follow is impressively massive.
Until I worked out what was going on I was really perplexed, and even
considered that my repository might have become corrupted.
I knew I'd written a draft of a blog article about the Watchmen movie, and I went to find out how long it had been sitting around:
% git log -- movie/Watchmen.blog
commit 934961428feff98fa3cb085e04a0d594b083f597
Author: Mark Dominus <mjd@plover.com>
Date: Fri Feb 3 16:32:25 2012 -0500
link to Mad Watchmen parody
also recategorize under movie instead of under book
The log stopped there, and the commit message says clearly that the
article was moved from elsewhere, so I used git-log --follow --stat
to find out how old it really was. The result was spectacularly
weird. It began in the right place:
commit 934961428feff98fa3cb085e04a0d594b083f597
Author: Mark Dominus <mjd@plover.com>
Date: Fri Feb 3 16:32:25 2012 -0500
link to Mad Watchmen parody
also recategorize under movie instead of under book
{book => movie}/Watchmen.blog | 8 +++++++-
1 file changed, 7 insertions(+), 1 deletion(-)
Okay, it was moved, with slight modifications, from book to movie,
as the message says.
commit 5bf6e946f66e290fc6abf044aa26b9f7cfaaedc4
Author: Mark Jason Dominus (陶敏修) <mjd@plover.com>
Date: Tue Jan 17 20:36:27 2012 -0500
finally started article about Watchment movie
book/Watchmen.blog | 40 ++++++++++++++++++++++++++++++++++++++++
1 file changed, 40 insertions(+)
Okay, the previous month I added some text to it.
Then I skipped to the bottom to see when it first appeared, and the bottom was completely weird, mentioning a series of completely unrelated articles:
commit e6779efdc9510374510705b4beb0b4c4b5853a93
Author: mjd <mjd>
Date: Thu May 4 15:21:57 2006 +0000
First chunk of linear regression article
prog/maxims/paste-code.notyet => math/linear-regression.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
commit 9d9038a3358a82616a159493c6bdc91dd03d03f4
Author: mjd <mjd>
Date: Tue May 2 14:16:24 2006 +0000
maxims directory reorganization
tech/mercury.notyet => prog/maxims/paste-code.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
commit 1273c618ed6efa4df75ce97255204251678d04d3
Author: mjd <mjd>
Date: Tue Apr 4 15:32:00 2006 +0000
Thingy about propagation delay and mercury delay lines
tech/mercury.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
(The complete output is available for your perusal.)
The log is showing unrelated files being moved to totally unrelated
places. And also, the log messages do not seem to match up. “First
chunk of linear regression article” should be on some commit that adds
text to math/linear-regression.notyet or
math/linear-regression.blog. But according to the output above,
that file is still empty after that commit. Maybe I added the text in
a later commit? “Maxims directory reorganization” suggests that I
reorganized the contents of prog/maxims, but the stat says
otherwise.
My first thought was: when I imported my blog from CVS to Git, many years ago, I made a series of mistakes, and mismatched the log messages to the commits, or worse, and I might have to do it over again. Despair!
But no, it turns out that git-log is just intensely confused.
Let's look at one of the puzzling commits. Here it is as reported by
git log --follow --stat:
commit 9d9038a3358a82616a159493c6bdc91dd03d03f4
Author: mjd <mjd>
Date: Tue May 2 14:16:24 2006 +0000
maxims directory reorganization
tech/mercury.notyet => prog/maxims/paste-code.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
But if I do git show --stat 9d9038a3, I get a very different
picture, one that makes sense:
% git show --stat 9d9038a3
commit 9d9038a3358a82616a159493c6bdc91dd03d03f4
Author: mjd <mjd>
Date: Tue May 2 14:16:24 2006 +0000
maxims directory reorganization
prog/maxims.notyet | 226 -------------------------------------------
prog/maxims/maxims.notyet | 95 ++++++++++++++++++
prog/maxims/paste-code.blog | 134 +++++++++++++++++++++++++
prog/maxims/paste-code.notyet | 0
4 files changed, 229 insertions(+), 226 deletions(-)
This is easy to understand. The commit message was correct: the
maxims are being reorganized. But git-log --stat, in conjunction
with --follow, has produced a stat that has only a tenuous
connection with reality.
I believe what happened here is this: In 2012 I “finally started article”. But I didn't create the file at that time. Rather, I had created the file in 2009 with the intention of putting something into it later:
% git show --stat 5c8c5e66
commit 5c8c5e66bcd1b5485576348cb5bbca20c37bd330
Author: mjd <mjd>
Date: Tue Jun 23 18:42:31 2009 +0000
empty file
book/Watchmen.blog | 0
book/Watchmen.notyet | 0
2 files changed, 0 insertions(+), 0 deletions(-)
This commit does appear in the git-log --follow output, but it
looks like this:
commit 5c8c5e66bcd1b5485576348cb5bbca20c37bd330
Author: mjd <mjd>
Date: Tue Jun 23 18:42:31 2009 +0000
empty file
wikipedia/mega.notyet => book/Watchmen.blog | 0
1 file changed, 0 insertions(+), 0 deletions(-)
It appears that Git, having detected that book/Watchmen.blog was
moved to movie/Watchmen.blog in Febraury 2012, is now following
book/Watchmen.blog backward in time. It sees that in January 2012
the file was modified, and was formerly empty, and after that it sees
that in June 2009 the empty file was created. At that time there was
another empty file, wikipedia/mega.notyet. And git-log decides that the
empty file book/Watchmen.blog was copied from the other empty
file.
At this point it has gone completely off the rails, because it is now
following the unrelated empty file wikipedia/mega.notyet. It then
makes more mistakes of the same type. At one point there was an empty
wikipedia/mega.blog file, but commit ff0d744d5 added some text to it
and also created an empty wikipedia/mega.notyet alongside it. The
git-log --follow command has interpreted this as the empty
wikipedia/mega.blog being moved to wikipedia/mega.notyet and a
new wikipedia/mega.blog being created alongside it. It is now following
wikipedia/mega.blog.
Commit ff398402 created the empty file wikipedia/mega.blog fresh,
but git-log --follow interprets the commit as copying
wikipedia/mega.blog from the already-existing empty file
tech/mercury.notyet. Commit 1273c618 created tech/mercury.notyet,
and after that the trail comes to an end, because that was shortly
after I started keeping my blog in revision control; there were no
empty files before that. I suppose that attempting to follow the
history of any file that started out empty is going to lead to the
same place, tech/mercury.notyet.
On a different machine with a different copy of the repository, the
git-log --follow on this file threads its way through ten
irrelvant files before winding up at tech/mercury.notyet.
There is a --find-renames=... flag to tell Git how conservative to
be when guessing that a file might have been renamed and modified at
the same time. The default is 50%. But even turning it up to 100%
doesn't help with this problem, because in this case the false
positives are files that are actually identical.
As far as I can tell there is no option to set an absolute threshhold
on when two files are considered the same by --follow. Perhaps it
would be enough to tell Git that it should simply not try to follow
files whose size is less than !!n!! bytes, for some small !!n!!, perhaps
even !!n=1!!.
The part I don't fully understand is how git-log --follow is
generating its stat outputs. Certainly it's not doing it in the
same way that git show is. Instead it is trying to do something
clever, to highlight the copies and renames it thinks it has found,
and in this case it goes badly wrong.
The problem appears in Git 1.7.11, 2.7.4, and 2.13.0.
[ Addendum 20180912: A followup about my work on a fix for this. ]
[Other articles in category /prog] permanent link
Sun, 09 Sep 2018I very recently suggested a mathematical operation that does this:
$$\begin{align} \left((\sqrt\bullet) \cdot x + \left(\frac1\bullet\right) \cdot 1 \right) ⊛ (9x+4) & = \sqrt9 x^2 + \sqrt4 x + \frac19 x + \frac14 \\ & = 3x^2 + \frac{19}{9} x + \frac 14 \end{align}$$
Here the left-hand argument is like a polynomial, except that the coefficients are functions. The right-hand argument is an ordinary polynomial.
It occurs to me that the APL progamming lanaguage (invented around 1966) actually has something almost like this, in its generalized matrix product.
In APL, if ? and ! are any binary operators, you can write ?.!
to combine them into a matrix operator. Like ordinary matrix
multiplication, the new operator combines an !!m×n!! and an !!n×r!! matrix
into an !!m×r!! matrix. Ordinary matrix multiplication is defined like
this:
$$c_{ij} = a_{i1} \cdot b_{1j} +
a_{i2} \cdot b_{2j} + \ldots +
a_{in} \cdot b_{nj} $$
The APL ?.! operator replaces the addition with ? and the
multiplication with !, so that +.× is exactly the standard matrix
multiplication. Several other combined operations of this type are,
if not common, at least idiomatic. For example, I have seen, and
perhaps used, ∨.∧, +.∧, and ⌈.⌊. (⌈ and ⌊ are APL's
two-argument minimum and maximum operators.)
With this feature, the ⊛ operator I proposed above would be something
like +.∘, where ∘ means function composition. To make it work you
need to interpret the coefficients of an ordinary polynomial as
constant functions, but that is not much of a stretch. APL doesn't
actually have a function composition operator.
APL does have a ∘ symbol, but it doesn't mean function composition,
and also the !.? notation is special cased, in typically APL style,
so that ∘.? does something sort of related but rather different.
Observe also that if !!a!! and !!b!! are !!1×n!! and !!n×1!! matrices,
respectively, then !!a +.× b!! ought to be dot product of !!a!! and !!b!!:
it is a !!1×1!! matrix whose sole entry is:
$$c_{11} = a_{11} \cdot b_{11} +
a_{12} \cdot b_{21} + \ldots +
a_{1n} \cdot b_{n1} $$
and similarly if !!a!! is !!n×1!! and !!b!! is !!1×m!! then !!a +.× b!! is the
outer product, the !!n×m!! matrix whose !!c_{ij} = a_i × b_j!!. But I
think APL doesn't distinguish between a !!1×n!! matrix and a vector,
though, and always considers them to be vectors, so that in such cases
!!a +.× b!! always gets you the dot product, if !!a!! and !!b!! are the same
length, and an error otherwise. If you want the outer product of two
vectors you use a ∘.× b instead. a ∘.+ b would be the outer
product matrix with !!c_{ij} = a_i + b_j!!. APL is really strange.
I applied for an APL job once; I went to a job fair (late 1980s maybe?) and some Delaware bank was looking for APL programmers to help maintain their legacy APL software. I was quite excited at the idea of programming APL professionally, but I had no professional APL experience so they passed me over. I think they made a mistake, because there are not that many people with professional APL experience anyway, and how many twenty-year-olds are there who know APL and come knocking on your door looking for a job? But whatever, it's probably better that I didn't take that route.
The +.× thing exemplifies my biggest complaint about APL semantics:
it was groping toward the idea of functional programming without quite
getting there, never quite general enough. You could use !/, where
! was any built-in binary operator, and this was quite like a fold.
But you couldn't fold a user-defined function of two arguments! And
you couldn't write a higher-order fold function either.
I was pleased to find out that Iverson had designed a successor language, J, and then quickly disappointed when I saw how little it added. For example, it has an implicit “hook” construction, which is a special case in the language for handling one special case of function composition. In Haskell it would be:
hook f g x = x `f` (g x)
but in J the hook itself is implicit. If you would rather use (g x) `f` x
instead, you are out of luck because that is not built-in. I don't
know why Iverson thought the hook was the thing to embed in the
language. (J also has an implicit “fork” which is fork f g h x =
(f x) `g` (h x).)
[ Addendum 20180910: The explanation. ]
Meanwhile the awful APL notation has gotten much more awful in J, and
you get little in return. You even lose all the fun of the little
squiggles. Haskell is a much better J than J ever was. Haskell's
notation can be pretty awful too ((.) . (.)?), but at least you are
are getting your money's worth.
I thought I'd see about implementing APL's !.? thing in Haskell to
see what it would look like. I decided to do it by implementing a
regular matrix product and then generalizing. Let's do the simplest
thing that could possibly work and represent a matrix as a list of
rows, each of which is a list of entries.
For a regular matrix product, !!C = AB!! means that !!c_{ij}!! is the dot product of the !!i!!th row of !!A!! and the !!j!!th column of !!B!!, so I implemented a dot product function:
dot_product :: Num b => [b] -> [b] -> b
dot_product a b = foldr (+) 0 $ zipWith (*) a b
OK, that was straightforward.
The rows of !!A!! are right there, but we also need the columns from !!B!!, so here's a function to get those:
transpose ([]:_) = []
transpose x = (map head x) : transpose (map tail x)
Also straightforward.
After that I toiled for a very long time over the matrix product itself. My first idea was to turn !!A!! into a list of functions, each of which would dot-product one of the rows of !!A!! by a given vector. Then I would map each of these functions over the columns of !!B!!.
Turning !!A!! into a list of functions was easy:
map dot_product a :: [ [x] -> x ]
and getting the columns of !!B!! I had already done:
transpose b :: [[x]]
and now I just need to apply each row of functions in the first part to each column in the second part and collect the results:
??? (map dot_product a) (transpose b)
I don't know why this turned out to be so damn hard. This is the sort of thing that ought to be really, really easy in Haskell. But I had many difficulties.
First I wasted a bunch of time trying to get <*> to work, because it
does do something like that.
But the thing
I wanted has signature
??? :: [a -> b] -> [a] -> [[b]]
whereas <*> flattens the result:
<*> :: [a -> b] -> [a] -> [b]
and I needed to keep that extra structure. I tried all sorts of
tinkering with <*> and <$> but never found what I wanted.
Another part of the problem was I didn't know any primitive for “map a list of functions over a single argument”. Although it's not hard to write, I had some trouble thinking about it after I wrote it:
pamf fs b = fmap ($ b) fs
Then the “map each function over each list of arguments” is map . pamf, so I got
(map . pamf) (map dot_product a) (transpose b)
and this almost works, except it produces the columns of the results
instead of the rows. There is an easy fix and a better fix. The easy
fix is to just transpose the final result. I never did find the
better fix. I thought I'd be able to replace map . pamf with pamf
. map but the latter doesn't even type check.
Anyway this did work:
matrix_product a b =
transpose $ (map . pamf) (map dot_product a) (transpose b)
but that transpose on the front kept bothering me and I couldn't
leave it alone.
So then I went down a rabbit hole and wrote nine more versions of
???:
fs `op` as = do
f <- fs
return $ fmap f as
fs `op2` as = fs >>= (\f -> return $ fmap f as)
fs `op3` as = fs >>= (return . flip fmap as )
fs `op4` as = fmap ( flip fmap as ) fs
op5 as = fmap ( flip fmap as )
op6 :: [a -> b] -> [a] -> [[b]]
op6 = flip $ fmap . (flip fmap)
fs `op7` as = map (\f -> [ f a | a <- as ]) fs
fs `op8` as = map (\f -> (map f as)) fs
fs `op9` as = map (flip map as) fs
I finally settled on op6, except it takes the arguments in the
“wrong” order, with the list of functions second and their arguments
first. But I used it anyway:
matrix_product a b = (map . flip map) (transpose b) (map dot_product a)
The result was okay, but it took me so long to get there.
Now I have matrix_product and I can generalize it to uses two
arbitrary operations instead of addition and multiplication. And
hey, I don't have to touch matrix_product! I only need to change
dot_product because that's where the arithmetic is. Instead of
dot_product a b = foldr (+) 0 $ zipWith (*) a b
just use:
inner_product u v = foldr add 0 $ zipWith mul u v
Except uh oh, that 0 is wrong. It might not be the identity for
whatever weird operation add is; it might be min and then we need
the 0 to be minus infinity.
I tinkered a bit with requiring a Monoid instance for the matrix
entries, which seemed interesting at least, but to do that I would
need to switch monoids in the middle of the computation and I didn't
want to think about how to do that. So instead I wrote a version of
foldr that doesn't need an identity element:
foldr' f (a:as) = foldr f a as
This fails on empty lists, which is just fine, since I wasn't planning on multiplying any empty matrices.
Then I have the final answer:
general_matrix_product add mul a b =
(map . flip map) (transpose b) (map inner_product a) where
inner_product u v = foldr' add $ zipWith mul u v
It's nice and short, but on the other hand it has that mysterious map
. flip map in there. If I hadn't written that myself I would see it
and ask what on earth it was doing. In fact I did write it myself
and I although I do know what it is doing I don't really understand
why.
As for the shortness, let's see what it looks like in a more conventional language:
def transpose(m):
return list(zip(*m))
Wow, that was amazingly easy.
def matrix_product(a, b):
def dot_product(u, v):
total = 0
for pair in zip(u, v):
total += pair[0] * pair[1]
return total
bT = transpose(b)
c = []
for i in range(len(a)):
c.append([])
for j in range(len(bT)):
c[-1].append(None)
c[i][j] = dot_product(a[i], bT[j])
return c
Okay, that was kind of a mess. The dot_product should be shorter
because Python has a nice built-in sum function but how do I build
the list of products I want to sum? It doesn't have map because it
doesn't have lambdas. I know, I know, someone is going to insist that
Python has lambdas. It does, sort of, but they suck.
I think the standard Python answer to this is that you don't need
map because you're supposed to use list comprehension instead:
def dot_product(u, v):
return sum([ x*y for (x, y) in zip(u, v) ])
I don't know how I feel about that argument in general but in this case the result was lovely. I have no complaints.
While I was writing the Python program I got a weird bug that turned
out to be related to mutability: I had initialized c with
c = [[None] * len(bT)] * len(a)
But this makes the rows of c the same mutable object, and then
installing values in each row overwrites the entries we stored in the
previous rows. So definitely score one point for Haskell there.
A lot of the mess in the code is because Python is so obstinate about extending lists when you need them extended, you have to say pretty please every time. Maybe I can get rid of that by using more list comprehensions?
def matrix_product2(a, b):
def dot_product(u, v):
return sum([ x*y for (x, y) in zip(u, v) ])
return [ [ dot_product(u, v) for v in transpose(b) ] for u in a ]
Python's list comprehensions usually make me long for Haskell's, which are so much nicer, but this time they were fine. Python totally wins here. No wait, that's not fair: maybe I should have been using list comprehensions in Haskell also?
matrix_product = [ [ dot_product row col | col <- transpose b ] | row <- a ]
Yeah, okay. All that map . flip map stuff was for the birds. Guido
thinks that map is a bad idea, and I thought he was being silly, but
maybe he has a point. If I did want the ??? thing that applies a
list of functions to a list of arguments, the list comprehension
solves that too:
[ f x | f <- fs, x <- xs ]
Well, lesson learned.
I really wish I could write Haskell faster. In the mid-1990s I wrote thousands of lines of SML code and despite (or perhaps because of) SML's limitations I was usually able to get my programs to do what I wanted. But when I try to write programs in Haskell it takes me a really long time to get anywhere.
Apropos of nothing, today is the 77th birthday of Dennis M. Ritchie.
[ Addendum: It took me until now to realize that, after all that, the operation I wanted for polynomials is not matrix multiplication. Not at all! It is actually a convolution:
$$ c_k = \sum_{i+j=k} a_ib_j $$
or, for my weird functional version, replace the multiplication !!a_ib_j!! with function composition !!a_i ∘ b_j!!. I may implement this later, for practice. And it's also tempting to try to do it in APL, even though that would most likely be a terrible waste of time… ]
[ Addendum 20180909: Vaibhav Sagar points out that my foldr' is the
standard Prelude function
foldr1.
But as I said in the previous
article, one of the
problems I have is that faced with a need for something like foldr1,
instead of taking one minute to write it, I will waste fifteen minutes
looking for it in Hoogle. This time I opted to not do that. In
hindsight it was a mistake, perhaps, but I don't regret the choice.
It is not easy to predict what is worth looking for. To see the
downside risk, consider pamf. A Hoogle search for
pamf
produces nothing like what I want, and, indeed, it doesn't seem to
exist. ]
[Other articles in category /prog] permanent link
Sat, 08 Sep 2018
Why I never finish my Haskell programs (part 2 of ∞)
Here's something else that often goes wrong when I am writing a Haskell program. It's related to the problem in the previous article but not the same.
Let's say I'm building a module for managing polynomials. Say
Polynomial a is the type of (univariate) polynomials over some
number-like set of coefficients a.
Now clearly this is going to be a functor, so I define the Functor instance, which is totally straightforward:
instance Functor Polynomial where
fmap f (Poly a) = Poly $ map f a
Then I ask myself if it is also going to be an Applicative.
Certainly the pure function makes sense; it just lifts a number to
be a constant polynomial:
pure a = Poly [a]
But what about <*>? This would have the
type:
(Polynomial (a -> b)) -> Polynomial a -> Polynomial b
The first argument there is a polynomial whose coefficients are functions. This is not something we normally deal with. That ought to be the end of the matter.
But instead I pursue it just a little farther. Suppose we did have such an object. What would it mean to apply a functional polynomial and an ordinary polynomial? Do we apply the functions on the left to the coefficients on the right and then collect like terms? Say for example
$$\begin{align} \left((\sqrt\bullet) \cdot x + \left(\frac1\bullet\right) \cdot 1 \right) ⊛ (9x+4) & = \sqrt9 x^2 + \sqrt4 x + \frac19 x + \frac14 \\ & = 3x^2 + \frac{19}{9} x + \frac 14 \end{align}$$
Well, this is kinda interesting. And it would mean that the pure
definition wouldn't be what I said; instead it would lift a number to
a constant function:
pure a = Poly [λ_ -> a]
Then the ⊛ can be understood to be just like polynomial
multiplication, except that coefficients are combined with function
composition instead of with multiplication. The operation is
associative, as one would hope and expect, and even though the ⊛
operation is not commutative, it has a two-sided identity element,
which is Poly [id]. Then I start to wonder if it's useful for anything, and
how ⊛ interacts with ordinary multiplication, and so forth.
This is different from the failure mode of the previous article because in that example I was going down a Haskell rabbit hole of more and more unnecessary programming. This time the programming is all trivial. Instead, I've discovered a new kind of mathematical operation and I abandon the programming entirely and go off chasing a mathematical wild goose.
[ Addendum 20181109: Another one of these. ]
[Other articles in category /prog/haskell] permanent link
Mon, 03 Sep 2018
Why I never finish my Haskell programs (part 1 of ∞)
Whenever I try to program in Haskell, the same thing always goes wrong. Here is an example.
I am writing a module to operate on polynomials. The polynomial !!x^3 - 3x + 1!! is represented as
Poly [1, -3, 0, 1]
[ Addendum 20180904: This is not an error. The !!x^3!! term is last, not first. Much easier that way. Fun fact: two separate people on Reddit both commented that I was a dummy for not doing it the easy way, which is the way I did do it. Fuckin' Reddit, man. ]
I want to add two polynomials. To do this I just add the corresponding coefficients, so it's just
(Poly a) + (Poly b) = Poly $ zipWith (+) a b
Except no, that's wrong, because it stops too soon. When the lists
are different lengths, zipWith discards the extra, so for example it
says that !!(x^2 + x + 1) + (2x + 2) = 3x + 3!!, because it has
discarded the extra !!x^2!! term. But I want it to keep the extra, as
if the short list was extended with enough zeroes. This would be a
correct implementation:
(Poly a) + (Poly b) = Poly $ addup a b where
addup [] b = b
addup a [] = a
addup (a:as) (b:bs) = (a+b):(addup as bs)
and I can write this off the top of my head.
But do I? No, this is where things go off the rails. “I ought to be
able to generalize this,” I say. “I can define a function like
zipWith that is defined over any Monoid, it will combine the
elements pairwise with mplus, and when one of the lists
runs out, it will pretend that that one has some memptys stuck on the
end.” Here I am thinking of something like ffff :: Monoid a => [a] ->
[a] -> [a], and then the (+) above would just be
(Poly a) + (Poly b) = Poly (ffff a b)
as long as there is a suitable Monoid instance for the as and bs.
I could write ffff in two minutes, but instead I spend fifteen
minutes looking around in Hoogle to see if there is already an ffff,
and I find mzip, and waste time being confused by mzip, until I
notice that I was only confused because mzip is for Monad, not
for Monoid, and is not what I wanted at all.
So do I write ffff and get on with my life? No, I'm still not done.
It gets worse. “I ought to be able to generalize this,” I say. “It
makes sense not just for lists, but for any Traversable… Hmm, or
does it?” Then I start thinking about trees and how it should decide
when to recurse and when to give up and use mempty, and then I start
thinking about the Maybe version of it.
Then I open a new file and start writing
mzip :: (Traversable f, Monoid a) => f a -> f a -> f a
mzip as bs = …
And I go father and farther down the rabbit hole and I never come back
to what I was actually working on. Maybe the next step in this
descent into madness is that I start thinking about how to perform
unification of arbitrary algebraic data structures, I abandon mzip
and open a new file for defining class Unifiable…
Actually when I try to program in Haskell there a lot of things that go wrong and this is only one of them, but it seems like this one might be more amenable to a quick fix than some of the other things.
[ Addendum 20180904: A lobste.rs
user
points out that I don't need Monoid, but only Semigroup, since
I don't need mempty. True that! I didn't know there was a
Semigroup class. ]
[ Addendum 20181109: More articles in this series: [2] [3] ]
[Other articles in category /prog/haskell] permanent link
Wed, 29 Aug 2018On long road trips I spend a lot of time listening to music and even more time talking to myself. My recent road trip was longer than usual and I eventually grew tired of these amusements. I got the happy idea that I might listen to an audiobook, something I've never done before. Usually the thought of sitting and listening to someone droning out a book for 14 hours makes me want to dig my heart out with a spoon (“You say a word. Then I think for a long time. Then you say another word.”) but I had a long drive and I was not going anywhere anyway, so thought it might be a good way to pass the time.
The first thing I thought to try was Ann Leckie's Ancillary Justice, which everyone says is excellent, and which I had wanted to read. I was delighted to learn that I could listen to the first hour or so before paying anything, so I downloaded the sample.
It was intolerable. The voice actor they chose (Celeste Ciulla) was hilariously inappropriate, so much so that, had I not gotten the book from the most unimpeachable source, I would have suspected I was being pranked. Ancillary Justice is a hard-boiled military story in which the protagonist is some sort of world-weary slave or robot, or at least so I gather from the first half of the first chapter. Everything that appears in the first chapter is terrible: the people, the situation, the weather. It opens with these words:
The body lay naked and facedown, a deathly gray, spatters of blood staining the snow around it. It was minus fifteen degrees Celsius and a storm had passed just hours before.
But Ms. Ciulla's voice… there's nothing wrong with it, maybe — but for some other book. I can imagine listening to her reading What Katy Did or Eight Cousins or some other 19th-century girl story.
I found myself mockingly repeating Ciulla's pronunciation. And about twelve minutes in I gave up and turned it off. Here's a sample of that point. It ends with:
Is Ciulla even capable of growling? Unclear.
I figured that the book was probably good, and I was afraid Ciulla would ruin it for me permanently.
Spotify had a recording of Sir Christopher Lee reading Dr. Jekyll and Mr. Hyde, so I listened to that instead.
I think I could do a better job reading than most of the audiobook actors I sampled, and I might give it a try later. I think I might start with The 13 Clocks. Or maybe something by C.A. Stephens, which is in the public domain.
[Other articles in category /book] permanent link
Tue, 28 Aug 2018Yogi, accompanied by his constant companion Boo-Boo Bear, would often try to steal picnic baskets from campers in the park, much to the displeasure of Park Ranger Smith.

[Other articles in category /misc] permanent link
How quickly did dentists start trying to use X-rays?
I had dental x-rays today and I wondered how much time elapsed between the discovery of x-rays and their use by dentists.
About two weeks, it turns out. Roentgen's original publication was in late 1895. Dr. Otto Walkhoff made the first x-ray picture of teeth 14 days later. The exposure took 25 minutes.
Despite the long exposure time, dentists had already begun using x-rays in their practices in the next two years. Dr. William J. Morton presented the new technology to the New York Odontological Society in April 1896, and his dental radiography, depicting a molar with an artificial crown clearly visible, was published in a dental journal later that year.
Morton's subject had been a dried skull. The first dental x-ray of a living human in the United States was made by Charles Edmund Kells in April or May of 1896. In July at the annual meeting of the Southern Dental Association he presented a dental clinic in which he demonstrated the use of his x-ray equipment on live patients. The practice seems to have rapidly become routine.
The following story about Morton is not dental-related but I didn't want to leave it out:
In March 1896, strongman Eugene Sandow, considered the father of modern bodybuilding, turned to Morton in an effort to locate the source of a frustrating pain he was experiencing in his foot. Apparently Sandow had stepped on some broken glass, but even his personal physician could not specify the location of the glass in his foot. The potential for the x-ray must have seemed obvious, and Sandow reached out specifically to Morton to see if he could be of help. Morton was eager to oblige. He turned the x-rays on Sandow’s foot and located the shard of glass disturbing Sandow’s equanimity. A surgeon subsequently operated and removed the glass, and the story made national news.
(Daniel S. Goldberg, “The Early Days of the X-Ray”)
The first dental x-ray machine was manufactured in 1923 by Victor X-ray Company, which later became part of General Electric.
In preparing this article I was fortunate to have access to B. Martinez, In a New Light: Early X-Ray Technology in Dentistry, 1890–1955, Arizona State University, 2013.
[Other articles in category /tech] permanent link
Mon, 27 Aug 2018
Linear mappings of projective space
[ Epistemic status: uninformed musings; anything and everything in here might be wrong or ill-conceived. ]
Suppose !!V!! is some vector space, and let !!V_n!! be the family of all !!n!!-dimensional subspaces of !!V!!. In particular !!V_1!! is the family of all one-dimensional subspaces of !!V!!. When !!V!! is euclidean space, !!V_1!! is the corresponding projective space.
if !!L!! is a nonsingular linear mapping !!V\to V!!, then !!L!! induces a mapping !!L_n!! from !!V_n\to V_n!!. (It does not make sense to ask at this point if the induced mapping is linear because we do not have any obvious linear structure on the projective space. Or maybe there is but I have not heard of it.)
The eigenspaces of !!V!! are precisely the fixed points of !!L_n!!.
(Wrong! Any subspace generated by an !!n!!-set of eigenvectors is a fixed point of !!L_n!!. But such a subspace is not in general an eigenspace. (Note this includes the entire space as a special case.) The converse, however, does hold, since any eigenspace is generated by a subset of eigenvectors.)
Now it is an interesting and useful fact that for typical mappings, say from !!\Bbb R\to\Bbb R!!, fixed points tend to be attractors or repellers. (For example, see this earlier article.) This is true of !!L_1!! also. One-dimensional eigenspaces whose eigenvalues are larger than !!1!! are attractors of !!L_1!!, and those whose eigenvalues are smaller than !!1!! are repellers, and this is one reason why the eigenspaces are important: if !!L!! represents the evolution of state space, then vectors in !!V!! will tend to evolve toward being eigenvectors.
So consider, say, the projective plane !!\Bbb P^2!!, under the induced mapping of some linear operator on !!\Bbb R^3!!. There will be (typically) three special points in !!\Bbb P^2!! and other points will typically tend to gravitate towards one or more of these. Isn't this interesting? Is the three-dimensional situation more interesting than the two-dimensional one? What if a point attracts in one dimension and repels in the other? What can the orbits look like?
Or consider the Grassmanian space !!Gr(2, \Bbb R^3)!! of all planes in !!\Bbb R^3!!. Does a linear operator on !!\Bbb R^3!! tend to drive points in !!Gr(2, \Bbb R^3)!! toward three fixed points? (In general, I suppose !!Gr(k, \Bbb R^n)!! will have !!n\choose k!! fixed points, some of which might attract and some repel.) Is there any geometric intuition for this?
I have been wanting to think about Grassmanian spaces more for a long time now.
[Other articles in category /math] permanent link
Sat, 25 Aug 2018
A software archaeology screwup
This week I switched from using the konsole terminal program to using gnome-terminal,
because the former gets all sorts of font widths and heights wrong for
high-bit characters like ⇒ and ③, making it very difficult to edit
such text, and the latter, I discovered doesn't. Here's how konsole
displays the text ☆☆★★★ “Good” as I move the cursor rightwards
through it:






Uggggggh. Why did I put up with this bullshit for so long?
(I know, someone is going to write in and say the problem isn't in konsole,
it's in the settings for the KooKooFont 3.7.1 package, and I can
easily fix this by adding, removing, or adjusting the appropriate
directives in
/usr/share/config/fontk/config/fontulator-compat.d/04-spatulation,
and… I don't care, gnome-terminal works and konsole doesn't.)
So I switched terminals, but this introduced a new problem: konsole would
detect when a shell command had been run, and automatically retitle
the tab it was run in, until the command exited. I didn't realize until this
feature went away how much I had been depending on it to tell the tabs
apart. Under gnome-terminal all the tabs just said Terminal.
Reaching back into my memory, to a time even before there were tabs, I
recalled that there used to be a simple utility I could run on the
command line to set a terminal title. I did remember xsetname,
which sets the X window title, but I didn't want that in this
case. I looked around through the manual and my bin directory and
didn't find it, so I decided to write it fresh.
It's not hard. There's an escape sequence which, if received by the terminal, should cause it to retitle itself. If the terminal receives
ESC ] 0 ; pyrzqxgl \cG
it will change its title to pyrzqxgl. (Spaces in the display above
are for clarity only and should be ignored.)
It didn't take long to write the program:
#!/usr/bin/python3
from sys import argv, stderr
if len(argv) != 2:
print("Usage: title 'new title'", file=stderr)
exit(-2)
print("\033]0;{}\a".format(argv[1]), end="")
The only important part here is the last line. I named the program
title, installed it in ~/bin, and began using it
immediately.
A few minutes later I was looking for the tab that had an SSH session
to the machine plover.com, and since the title was still Terminal,
once I found it, I ran title plover, which worked. Then I stopped
and frowned. I had not yet copied the program to Plover. What just
happened?
Plover already had a ~/bin/title that I wrote no less than
14½ years ago:
-rwxr-xr-x 1 mjd mjd 138 Feb 11 2004 /home/mjd/bin/title
Here it is:
#!/usr/bin/perl
my $title = join " ", @ARGV;
$title = qx{hostname -s || hostname} if $title eq "";
chomp $title;
print "\e]0;$title\cG";
Why didn't I find that before I wrote the other one?
The old program is better-written too. Instead of wasting code to print a usage message if I didn't use it right, I had spent that code in having it do something useful instead.
This is not the first time I have done something like this.
Oh well, at least I can reacquire the better UI now that I know about it.
[ Addendum 20220127: I did it again ]
[Other articles in category /oops] permanent link
Thu, 23 Aug 2018
Frank Baum's uncomfortable relationship with Oz
L. Frank Baum's The Wonderful Wizard of Oz was a runaway success, and he wrote thirteen sequels. It's clear that he didn't want to write 13 more Oz books. He wanted to write fantasy adventure generally. And he did pretty well at this. His non-Oz books like Zixi of Ix and John Dough and the Cherub are considerably above average, but were not as commercially successful.
In the sequel to The Wonderful Wizard, titled The Marvelous Land of Oz, he brought back the Scarecrow, the Tin Woodman, and Glinda, with the other characters being new. But the fans demanded Dorothy (who returned in every book thereafter) and the Wizard (from book 4 onward).
Book 3, Ozma of Oz, is excellent, definitely my favorite. It introduces the malevolent Nome King, whom Baum seems to have loved, as he returned over and over. Ozma of Oz has a superb plot with building dramatic tension involving a frightening magical competition. But by the fourth book, Dorothy and the Wizard in Oz, Baum had gone too many times to the well. The new characters (a workhorse, a farmhand, and a pink kitten) are forgettable and forgotten. There is no plot, just visits to a series of peculiar locations, terminating in the characters’ arrival in Oz. Steve Parker, whose summary review of the Oz books has stuck with me for many years, said:
The Oz books fall into two categories: Icky-cute twee travelogues (characters go from icky-cute place to icky-cute place. Nothing happens) and darned good stories (key feature: they have conflict).
Signs of this are already in The Wonderful Wizard itself. The original book is roughly in three phases: Dorothy and her associates journey to the Emerald City, where they confront the Wizard. The Wizard demands that they destroy the Wicked Witch of the West, which they do, but then abandons Dorothy. And then there is a third part in which they travel south to ask Glinda to help send Dorothy home.
In the 1939 MGM movie, which otherwise sticks closely to the plot of the book, the third part was omitted entirely. Glinda arrives immediately after the Wizard absconds and wraps up the story. As a small child I was incensed by this omission. But if I were making a movie of The Wizard of Oz I would do exactly the same. The third part of the book is superfluous. The four companions visit a country where everyone is a decorative china figure (nothing happens), a forest where the trees refuse to admit them (the Woodman chops them), another forest where the denizens are being terrorized by a monster (the Lion kills the monster), and a hill guarded by surly armless men whose heads fly off like corks from popguns (they fly over). Having bypassed these obstacles, they arrive at Glinda's palace and the story can get moving again.
But it isn't until Dorothy and the Wizard in Oz that the “twee travelogue” mode really gets going, and it continues in the fifth book, The Road to Oz.
By the sixth book, The Emerald City of Oz, it was clear that Baum was sick of the whole thing. The story is in two parts that alternate chapters. In one set of chapters, Dorothy and her uncle and aunt go on a pointless carriage tour of twee locations in Oz, completely unaware that in the intervening chapters, the wicked General Guph is gathering armies of malevolent beings to tunnel under the desert, destroy Oz, and enslave the Oz people. These chapters with Guph are really good, some of the best writing Baum ever did. Guph is easily the most interesting person in the book and Baum is certainly more interested in him than in Dorothy's visit to the town where everything is made of biscuits, the town where everything is made of paper, the town where everyone is made of jigsaw puzzles, and the town where everyone is a rabbit. But Baum couldn't really go through with his plan to destroy Oz. At the end of the book Guph's plan is foiled.
Baum nevertheless tried to throw Holmes down Reichenbach Falls. Glinda casts a powerful magic spell to seal off Oz from the rest of the world entirely:
The writer of these Oz stories has received a little note from Princess Dorothy of Oz which, for a time, has made him feel rather discontented. The note was written on a broad white feather from a stork's wing, and it said:
You will never hear anything more about Oz, because we are now cut off forever from all the rest of the world. But Toto and I will always love you and all the other children who love us.
DOROTHY GALE.
But as for Conan Doyle, it didn't work. The public demanded more, and just as Holmes came back from the grave, so did Oz. After a delay of three years, the seventh book, The Patchwork Girl of Oz, appeared. By this time Baum had had an inspiration. This book is the sort of magical fantasy he wanted to write. People only wanted to read about Oz, so Baum has set it in the Oz continuity. Ojo and his uncle supposedly live in the Munchkin country, but must flee their home in search of food, despite the fact that nobody in Oz ever has to do that. They visit the magician Dr. Pipt. He is is stated to be the same as the anonymous one mentioned in passing in The Marvelous Land of Oz, but this is not a plot point. Until the second half there is no significant connection to the rest of the series. The characters are all new (the Patchwork Girl, the Glass Cat, and the Woozy) and go on a quest to restore Ojo's uncle, who has been accidentally turned to stone. (Dorothy and other familiar characters do eventually join the proceedings.)
Baum apparently felt this was an acceptable compromise, because he repeatedly used this tactic of grafting Oz bits onto an otherwise unrelated fantasy adventure. The following book, Tik-Tok of Oz, takes the pattern quite far. Its main characters are Queen Ann and her subjects. Ann is Queen of Oogaboo, which is part of Oz, except, ha ha, fooled you, it isn't:
Away up in the mountains, in a far corner of the beautiful fairyland of Oz, lies a small valley which is named Oogaboo … the simple folk of Oogaboo never visited Ozma.
Oogaboo is separated from the rest of Oz by a mountain pass, and when Ann and her army try to reach Oz through this pass, it is magically twisted around by Glinda (who does not otherwise appear in the book) and they come out somewhere else entirely. A variety of other characters join them, including Polychrome and the Shaggy Man (from the awful Road to Oz), and Tik-Tok (from Ozma) and they struggle with the perennially villainous Nome King, of whom Baum seemingly never tired. But there is no other connection to Oz until the plot has been completely wrapped up, around the end of chapter 23. Then Ozma and Dorothy appear from nowhere and bring everyone to Oz for two unbearably sentimental final chapters.
The ninth book, The Scarecrow of Oz, often cited as the best of the series, follows exactly the same pattern. The main characters of this one are Trot, Cap'n Bill, and the Ork, who had appeared before in two of Baum's non-Oz novels, which did not sell well. No problem, Baum can bring them to Oz, where they may find more popularity among readers. So he has them find their way to Oogaboo. Excuse me, to Jinxland.
“I'm sorry to say that Jinxland is separated from the rest of the Quadling Country by that row of high mountains you see yonder, which have such steep sides that no one can cross them. So we live here all by ourselves, and are ruled by our own King, instead of by Ozma of Oz.”
The main plot takes place entirely in Jinxland, and concerns the struggles of Pon, the gardener's boy, to marry the Princess Gloria against the wishes of King Krewl. The Scarecrow is dispatched to Jinxland to assist, but none of the other Oz people plays an important part, and once the plot is wrapped up in chapter 20 Ozma and Dorothy arrange to bring everyone back to the Emerald City for a party at which Baum drops the names of all the characters who did not otherwise appear in the book.
The excellent tenth book, Rinkitink in Oz, repeats the pattern. In fact, Rinkitink was written much earlier, around 1907, but Baum couldn't get it published. So in 1916 he appended a couple of chapters in which Dorothy and the Wizard appear from nowhere to resolve the plot, and then in chapter 22 Ozma brings everyone back to the Emerald City for a party at which Baum drops the names of all the characters who did not otherwise appear in the book.
Well, you get the idea. The last few books are pretty good when they are in the "not really Oz but let's say it is" mode of The Scarecrow or Rinkitink, and pretty awful when they are in "twee travelogue" mode of The Road to Oz:
The Lost Princess of Oz has a good plot with a new set of characters from Oogaboo (excuse me — I mean from the Yip Country) searching for a stolen magical dishpan, and a travelogue plot with Dorothy etc. searching for Ozma. The characters meet up at the end and defeat the evil shoemaker who has stolen both, and Baum recycles his “the enchanted person was in the little boy's pocket the whole time” trope from Ozma of Oz. Probably they all go back to the Emerald City for a name-dropping party, but I forget.
The Tin Woodman of Oz, generally considered one of the worst of the books, is almost entirely travelogue. There are no new characters of note.
The Magic of Oz sees the return (again!) of the Nome King and a new scheme to destroy Oz. Again, it takes place in Oogaboo. Excuse me, in Gugu Forest:
In the central western part of the Gillikin Country is a great tangle of trees called Gugu Forest … home of most of the wild beasts that inhabit Oz. These are seldom disturbed in their leafy haunts because there is no reason why Oz people should go there, except on rare occasions, and most parts of the forest have never been seen by any eyes but the eyes of the beasts who make their home there.
Dorothy and the Wizard do play an important part. The plot is wrapped up with the same device as in The Emerald City.
Oh, and the book ends with a literal birthday party at which the omitted characters are mentioned by name.
Glinda of Oz, like the several that precede it, takes place in Oogaboo, this time called the Skeezer country. Ozma says:
The Skeezer Country is 'way at the upper edge of the Gillikin Country, with the sandy, impassable desert on one side and the mountains of Oogaboo on another side. That is a part of the Land of Oz of which I know very little.
Glinda, Dorothy, Ozma, and the Wizard do appear, but spend much of the book trapped in the underwater city of the Skeezers. Meanwhile the interesting part of the story concerns Ervic, a Skeezer who schemes and dissembles in order to persuade a recalcitrant witch to disenchant three Adepts of Magic who have been transformed into fish. For variety, the scene with every previous character sitting around a table is at the beginning instead of at the end.
Glinda was published posthumously, and Baum, who had died in 1919, was free of Oz at last.
[Other articles in category /book] permanent link
Mon, 20 Aug 2018
Miscellaneous addenda about Catholic priest sex abuse
I hope and expect this will be my last post on this loathsome subject.
Diocesan vs. religious priests
In the previous article, I said:
let us say that there are currently around 1620 priests total in the other six dioceses. (This seems on the high side, since my hand-count of Pittsburgh priests contains only about 200. I don't know what to make of this.)
Later I added a guess about why:
I wonder if it is because my hand counts, taken from diocesan directory pages, include only diocesan priests, where the total of 2500 also includes the religious priests. I should look into this.
I think this is probably correct. The list of Pittsburgh priests has a section at the bottom headed “Religious Priests Serving in the Diocese”, but it is empty.
Kennedy's Catholic Directory
While attempting to get better estimates for the total number of active priests, I located part of The Official Catholic Directory of P.J. Kennedy & Sons for the year 1980, available on the Internet Archive. It appears that this is only one volume of many, and unfortunately IA does not seem to have the others. Luckily, though, this happens to be the volume that includes information for Philadelphia, Pittsburgh, and Scranton. It reports:
| Philadelphia | Pittsburgh | Scranton | |
|---|---|---|---|
| (p. 695) | (p. 715) | (p. 892) | |
| Priests: diocesian active in diocese | 831 | 547 | 374 |
| Priests: active outside diocese | 33 | 29 | 13 |
| Priests: retired, sick or absent: | 121 | 60 | 52 |
| Diocesan Priests in foreign missions | 2 | 2 | 26 |
| Religious Priests resident in diocese | 553 | 243 | 107 |
| Religious Priests from diocese in foreign missions: | 93 | 78 | 26 |
| Total Priests in Diocese | 1631 | 957 | 572 |
I have no idea how authoritative this is, or what is the precise meaning of “official” in the title. The front matter would probably explain, but it does not appear in the one volume I have. The cover also advises “Important: see explanatory notes, pp. vi–viii”, which I have not seen.
The Directory also includes information for the Ukrainian Catholic Archepathy of Philadelphia, which, being part of a separate (but still Catholic) church is separate from the Philadelphia Roman Catholic dioceses. (It reports 127 total priests.) It's not clear whether to absorb this into my estimate because I'm not sure if it was part of the total number I got from the Pennsylvania Catholic Conference.
But I am not going back to check because I feel there is no point in trying to push on in this way. An authoritative and accurate answer is available from the official census, and my next step, should I care to take one, should be to go to the library and look at it, rather than continuing to pile up inaccurate guesses based on incomplete information.
Sipe's earlier estimate
Jonathan Segal points out that A.W. Richard Sipe, a famous expert on clergy sexual abuse, had estimated in 1990 that about 6% of U.S. priests has sexually abused children. This is close to my own estimate of 6.1% for the six Pennsylvania dioceses. Most of this agreement should be ascribed to luck.
Final remark
In 1992, Sinéad O'Connor became infamous for protesting systematic Catholic sex abuse by tearing up a photograph of John Paul II on live American television. She was almost universally condemned. (The Wikipedia article has a few of the details.)
This week, America: The Jesuit Review, which claims to be “the leading Catholic journal of opinion in the United States”, reported:
Pope Francis issued a letter to Catholics around the world Monday condemning the "crime" of priestly sexual abuse and its cover-up and demanding accountability…
The Vatican issued the three-page letter ahead of Francis' trip this weekend to Ireland, a once staunchly Roman Catholic country where the church's credibility has been damaged by years of revelations that priests raped and molested children with impunity and their superiors covered up for them.
(“Pope Francis issues new letter on sex abuse: ‘We showed no care for the little ones’”.)
A lot of people owe Sinéad O'Connor a humble apology.
[ Update 20230726: Sinéad O'Connor has died, probably without having received an apology from most of those people. ]
[Other articles in category /religion] permanent link
Fri, 17 Aug 2018
What fraction of Pennsylvania Catholic priests were child molesters?
The grand jury report on Catholic clergy sexual abuse has been released and I have been poring over it. The great majority of it is details about the church's handling of the 301 “predator priests” that the grand jury identified.
I have seen several places the suggestion that this is one-third of a total of 900. This is certainly not the case. There may be 900 priests there now, but the report covers all the abuse that the grand jury found in examining official records from the past seventy years or so. Taking a random example, pages 367–368 of the report concern the Reverend J. Pascal Sabas, who abused a 14-year-old boy starting in 1964. Sabas was ordained in 1954 and died in 1996.
I tried to get a good estimate of the total number of priests over the period covered by the report. Information was rather sketchy. The Vatican does do an annual census of priests, the Annuarium Statisticum Ecclesiae, but I could not find it online and hardcopies sell for around €48. Summary information by continent is reported elsewhere [2], but the census unfortunately aggregates North and South America as a single continent. I did not think it reasonable to try to extrapolate from the aggregate to the number of priests in the U.S. alone, much less to Pennsylvania.
Still we might get a very rough estimate as follows. The Pennsylvania Catholic Conference says that there were a total of just about 2500 priests in Pennsylvania in 2017 or 2016. The Philadelphia Archdiocese and the Altoona-Johnstown Diocese are not discussed in the grand jury report, having been the subject of previous investigations. The official websites of these two dioceses contain lists of priests and I counted 792 in the Philadelphia directory and 80 in the Altoona-Johnstown directory, so let us say that there are currently around 1620 priests total in the other six dioceses. (This seems on the high side, since my hand-count of Pittsburgh priests contains only about 200. I don't know what to make of this.)
[ Addendum 20180820: I wonder if it is because my hand counts, taken from diocesan directory pages, include only diocesan priests, where the total of 2500 also includes the religious priests. I should look into this. ]
Suppose that in 1950 there were somewhat more, say 2160. The average age of ordination is around 35 years; say that a typical priestly career lasts around 40 years further. So say that each decade, around one-quarter of the priesthood retires. If around 84% of the retirees are replaced, the replacement brings the total number back up to 96% of its previous level, so that after 70 years about 75% remain. Then the annual populations might be approximately:
$$\begin{array}{rrrrr} \text{year} & \text{total population} & \text{retirements} & \text{new arrivals} & \\ 1950 & 2160 & 540 & 453 \\ 1960 & 2073 & 518 & 434 \\ 1970 & 1989 & 497 & 417 \\ 1980 & 1909 & 477 & 400 \\ 1990 & 1832 & 458 & 384 \\ 2000 & 1758 & 439 & 368 \\ 2010 & 1687 & 421 & 354 \\ \hline \text{(total)} & & 3350 & 2810 \\ \end{array}$$
From the guesses above we might estimate a total number of individual priests serving between 1950 and 2018 as !!2160 + 2810 - 70 = 4900!!. (That's 2160 priests who were active in 1950, plus 2810 new arrivals since then, except minus !!354\cdot20\% \approx 70!! because it's only 2018 and 20% of the new arrivals for 2010–2020 haven't happened yet.)
So the 301 predator priests don't represent one-third of the population, they probably represent “only” around !!\frac{301}{4900} \approx 6.1\%!!.
The church's offical response is availble.
[ Addenda: An earlier version of this article estimated around 900 current priests instead of 1620; I believe that this was substantially too low. Also, that earlier version incorrectly assumed that ordinations equalled new priests, which is certainly untrue, since ordained priests can and do arrive in Pennsylvania from elsewhere. ]
[ Addendum 20180820: Some followup notes. ]
[Other articles in category /religion] permanent link
Tue, 14 Aug 2018A few years ago Katara was very puzzled by traffic jams and any time we were in a traffic slowdown she would ask questions about it. For example, why is traffic still moving, and why does your car eventually get through even though the traffic jam is still there? Why do they persist even after the original cause is repaired? But she seemed unsatisfied with my answers. Eventually in a flash of inspiration I improvised the following example, which seemed to satisfy her, and I still think it's a good explanation.
Suppose you have a four-lane highway where each lane can carry up to 25 cars per minute. Right now only 80 cars per minute are going by so the road is well under capacity.
But then there is a collision or some other problem that blocks one of the lanes. Now only three lanes are open and they have a capacity of 75 cars per minute. 80 cars per minute are arriving, but only 75 per minute can get past the blockage. What happens now? Five cars more are arriving every minute than can leave, and they will accumulate at the blocked point. After two hours, 600 cars have piled up.
But it's not always the same 600 cars! 75 cars per minute are still leaving from the front of the traffic jam. But as they do, 80 cars have arrived at the back to replace them. If you are at the back, there are 600 cars in front of you waiting to leave. After a minute, the 75 at the front have left and there are only 525 cars in front of you; meanwhile 80 more cars have joined the line. After 8 minutes all the cars in front of you have left and you are at the front and can move on. Meanwhile, the traffic jam has gotten bigger.
Suppose that after two hours the blockage is cleared. The road again has a capacity of 100 cars per minute. But cars are still arriving at 80 per minute, so each minute 20 more cars can leave than arrived. There are 600 waiting, so it takes another 30 minutes for the entire traffic jam to disperse.
This leaves out some important second-order (and third-order) effects. For example, traffic travels more slowly on congested roads; maximum safe speed decreases with following distance. But as a first explanation I think it really nails the phenomenon.
[Other articles in category /tech] permanent link
Wed, 08 Aug 2018In my original article, I said:
I was fairly confident I had seen something like this somewhere before, and that it was not original to me.
Jeremy Yallop brought up an example that I had definitely seen before.
In 2008 Conor McBride and Ross Paterson wrote an influential paper, “Idioms: applicative programming with effects” that introduced the idea of an applicative functor, a sort of intermediate point between functors and monads. It has since made its way into standard Haskell and was deemed sufficiently important to be worth breaking backward compatibility.
McBride and Paterson used several notations for operations in an
applicative functor. Their primary notation was !!\iota!! for what is
now known as pure and !!\circledast!! for what has since come to be written
as <*>. But the construction
$$\iota f \circledast is_1 \circledast \ldots \circledast is_n$$
came up so often they wanted a less cluttered notation for it:
We therefore find it convenient, at least within this paper, to write this form using a special notation
$$ [\![ f is_1 \ldots is_n ]\!] $$
The brackets indicate a shift into an idiom where a pure function is applied to a sequence of computations. Our intention is to provide a sufficient indication that effects are present without compromising the readability of the code.
On page 5, they suggested an exercise:
… show how to replace !![\![!! and !!]\!]!! by identifiers
iIandIiwhose computational behaviour delivers the above expansion.
They give a hint, intended to lead the reader to the solution, which
involves a function named iI that does some legerdemain on the front
end and then a singleton type data Ii = Ii that terminates the legerdemain on
the back end. The upshot is that one can write
iI f x y Ii
and have it mean
(pure f) <*> x <*> y
The haskell wiki has details, written by Don Stewart when the McBride-Paterson paper was still in preprint. The wiki goes somewhat further, also defining
data J = J
so that
iI f x y J z Ii
now does a join on the result of f x y before applying the result
to z.
I have certainly read this paper more than once, and I was groping for this example while I was writing the original article, but I couldn't quite put my finger on it. Thank you, M. Yallop!
[ By the way, I am a little bit disappointed that the haskell wiki is not called “Hicki”. ]
[Other articles in category /prog/haskell] permanent link
In the previous article I described a rather odd abuse of the Haskell type system to use a singleton type as a sort of pseudo-keyword, and asked if anyone had seen this done elsewhere.
Joachim Breitner reported having seen this before. Most recently in
LiquidHaskell, which defines a QED singleton
type:
data QED = QED
infixl 2 ***
(***) :: a -> QED -> Proof
_ *** _ = ()
so that they can end every proof with *** QED:
singletonP x
= reverse [x]
==. reverse [] ++ [x]
==. [] ++ [x]
==. [x]
*** QED
This example is from Vazou et al., Functional Pearl: Theorem Proving
for All, p. 3. The authors
explain: “The QED argument serves a purely aesthetic purpose,
allowing us to conclude proofs with *** QED.”.
Or see the examples from the bottom of the LH splash
page, proving the
associative law for ++.
I looked in the rest of the LiquidHaskell distribution but did not find any other uses of the singleton-type trick. I would still be interested to see more examples.
[ Addendum: Another example. ]
[Other articles in category /prog/haskell] permanent link
Is this weird Haskell technique something I made up?
A friend asked me the other day about techniques in Haskell to pretend
to make up keywords. For example, suppose we want something like a
(monadic) while loop, say like this:
while cond act =
cond >>= \b -> if b then act >> while cond act
else return ()
This uses a condition cond (which might be stateful or
exception-throwing or whatever, but which must yield a boolean value)
and an action act (likewise, but its value is ignored) and it
repeates the action over and over until the condition is false.
Now suppose for whatever reason we don't like writing it as while
condition action and we want instead to write while condition do
action or something of that sort. (This is a maximally simple
example, but the point should be clear even though it is silly.) My
first suggestion was somewhat gross:
while c _ a = ...
Now we can write
while condition "do" action
and the "do" will be ignored. Unfortunately we can also write
while condition "wombat" action and you know how programmers are
when you give them enough rope.
But then I had a surprising idea. We can define it this way:
data Do = Do
while c Do a = ...
Now we write
while condition
Do action
and if we omit or misspell the Do we get a compile-time type error
that is not even too obscure.
For a less trivial (but perhaps sillier) example, consider:
data Exception a = OK a | Exception String
instance Monad Exception where ...
data Catch = Catch
data OnSuccess = OnSuccess
data AndThen = AndThen
try computation Catch handler OnSuccess success AndThen continuation =
case computation of OK a -> success >> (OK a) >>= continuation
Exception e -> (handler e) >>= continuation
The idea here is that we want to try a computation, and do one thing
if it succeeds and another if it throws an exception. The point is
not the usefulness of this particular and somewhat contrived exception
handling construct, it's the syntactic sugar of the Catch,
OnSuccess, and AndThen:
try (evaluate some_expression)
Catch (\error -> case error of "Divison by zero" -> ...
... )
OnSuccess ...
AndThen ...
I was fairly confident I had seen something like this somewhere before, and that it was not original to me. But I've asked several Haskell experts and nobody has said it was familar. I thought perhaps I had seen it somewhere in Brent Yorgey's code, but he vehemently denied it.
So my question is, did I make up this technique of using a one-element type as a pretend keyword?
[ Addendum: At least one example of this trick appears in LiquidHaskell. I would be interested to hear about other places it has been used. ]
[ Addendum: Jeremy Yallop points out that a similar trick was hinted at in McBride and Paterson “Idioms: applicative programming with effects” (2008), with which I am familiar, although their trick is both more useful and more complex. So this might have been what I was thinking of. ]
[Other articles in category /prog/haskell] permanent link
Thu, 02 Aug 2018
How to explain infinity to kids
A professor of mine once said to me that all teaching was a process of lying, and then of replacing the lies with successively better approximations of the truth. “I say it's like this,” he said, “and then later I say, well, it's not actually like that, it's more like this, because the real story is too complicated to explain all at once.” I wouldn't have phrased it like this, but I agree with him in principle. One of the most important issues in pedagogical practice is deciding what to leave out, and for how long.
Kids inevitably want to ask about numerical infinity, and many adults will fumble the question, mumbling out some vague or mystical blather. Mathematics is prepared to offer a coherent and carefully-considered answer. Unfortunately, many mathematically-trained people also fumble the question, because mathematics is prepared to offer too many answers. So the mathematical adult will often say something like “well, it's a lot of things…” which for this purpose is exactly not what is wanted. When explaining the concept for the very first time, it is better to give a clear and accurate partial explanation than a vague and imprecise overview. This article suggests an answer that is short, to the point, and also technically correct.
In mathematics “infinity” names a whole collection of not always closely related concepts from analysis, geometry, and set theory. Some of the concepts that come under this heading are:
The !!+\infty!! and !!-\infty!! one meets in real analysis, which can be seen either as a convenient fiction (with “as !!x!! goes to infinity” being only a conventional rephrasing of “as !!x!! increases without bound”) or as the endpoints in the two-point compactification of !!\Bbb R!!.
The !!\infty!! one meets in complex analysis, which is a single point one adds to compactify the complex plane into the Riemann sphere.
The real version of the preceding, the “point at infinity” on the real projective line.
The entire “line at infinity” that bounds the real projective plane.
The vast family of set-theoretic infinite cardinals !!\aleph_0, \aleph_1, \ldots!!.
The vast family of set-theoretic infinite ordinals, !!\omega, \omega+1, \ldots, \epsilon_0, \ldots, \Omega, \ldots!!.
I made a decision ahead of time that when my kids first asked what infinity was, I would at first adopt the stance that “infinity” referred specifically to the set-theoretic ordinal !!\omega!!, and that the two terms were interchangeable. I could provide more details later on. But my first answer to “what is infinity” was:
It's the smallest number you can't count to.
As an explanation of !!\omega!! for kids, I think this is flawless. It's brief and it's understandable. It phrases the idea in familiar terms: counting. And it is technically unimpeachable. !!\omega!! is, in fact, precisely the unique smallest number you can't count to.
How can there be a number that you can't count to? Kids who ask about infinity are already quite familiar with the idea that the sequence of natural numbers is unending, and that they can count on and on without bound. “Imagine taking all the numbers that you could reach by counting,” I said. “Then add one more, after all of them. That is infinity.” This is a bit mind-boggling, but again it is technically unimpeachable, and the mind-bogglyness of it is nothing more than the intrinsic mind-bogglyness of the concept of infinity itself. None has been added by vagueness or imprecise metaphor. When you grapple with this notion, you are grappling with the essence of the problem of the completed infinity.

In my experience all kids make the same move at this point, which is to ask “what comes after infinity?” By taking “infinity” to mean !!\omega!!, we set ourselves up for an answer that is much better than the perplexing usual one “nothing comes after infinity”, which, if infinity is to be considered a number, is simply false. Instead we can decisively say that there is another number after infinity, which is called “infinity plus one”. This suggests further questions. “What comes after infinity plus one?” is obvious, but a bright kid will infer the existence of !!\omega\cdot 2!!. A different bright kid might ask about !!\omega-1!!, which opens a different but fruitful line of discussion: !!\omega!! is not a successor ordinal, it is a limit ordinal.
Or the kid might ask if infinity plus one isn't equal to infinity, in which case you can discuss the non-commutativity of ordinal addition: if you add the “plus one” at the beginning, it is the same (except for !!\omega!! itself, the picture has just been shifted over on the page):

But if you add the new item at the other end, it is a different picture:

Before there was only one extra item on the right, and now there are two. The first picture exemplifies the Dedekind property, which is an essential feature of infinity. But the existence of an injection from !!\omega+1!! to !!\omega!! does not mean that every such map is injective.
Just use !!\omega!!. Later on the kid may ask questions that will need to be answered with “Earlier, I did not tell you the whole story.” That is all right. At that point you can reveal the next thing.
[ Addendum 20220226: Joel D. Hamkins wrote a Math Stack Exchange post in which he made the same suggestion: “In my experience with children, one of the easiest-to-grasp concepts of infinity is provided by the transfinite ordinals…”. ]
[Other articles in category /math] permanent link
Mon, 30 Jul 2018
Lost and found authors: The Poppy Seed Cakes
As a very small child, I loved The Poppy Seed Cakes (1924), by Margery Clark. Later I read it to my own kids. Toph never cared for it, but it was by far Katara's favorite book when she was three. The illustrations are by Maud and Miska Petersham, who later won the Caldecott Medal.
(At left, the protagonist, Andrewshek, meeting Auntie Katushka's new white goat, who has run home from the market without her. He is swinging on the gate, which his Autie Katushka has specifically told him not to do, or the chickens will run out into the road. At right, Auntie Katushka arriving from the Old Country. Depicted are the fine feather bed, the umbrella with the crooked handle, and probably the bag of poppy seeds, all of which are plot points.)
As an adult I wanted to know if Margery Clark had written anything else. And the answer was, yes! Margery Clark, I learned, was a pseudonym for the two authors, Margery Closey Quigley and Mary E. Clark, who were librarians in Endicott, New York. The town was full of Russian and Polish immigrants who came there to make shoes, and Andrewshek and his Auntie Katushka were no doubt inspired by real library patrons. I looked up maps of Endicott in 1924 and found the little park with the stream where Andrewshek's picnic was nearly stolen by a swan. I spent way too much time trying to find out if Andrewshek was more likely to be Russian or Polish by poring over census data.
And Quigley had written another book! After Endicott she became a librarian in Montclair, New Jersey and wrote Portrait of a Library (1936) about how the Montclair Public Library was run. I found it fascinating and compelling. One detail I remember is that when automobiles became common, they started to offer a pickup and delivery service, which the citizens loved:
Delivery of books has been added to the borrowing system. Delivery is made by parcel-post, by Postal Telegraph, by the library messenger, and by the A. & P. delivery man. A messenger who spends one day a week following up overdue books was added in the fall of 1930.
She mentions that in 1934, over 3,000 books were delivered via Western Union messenger, with the borrower paying the 10¢ delivery fee. I think it's pretty awesome that they were able to press the A&P guy into library service.
My favorite detail, though, concerned a major renovation to the library building. They took the opportunity to reorganize the layout of the sections and shelves:
… the confusion and the press of work upon assistants and the criticisms from the public about overcrowding at the library came much too thick and fast. At this point an offer of professional services came from one of Montclair's citizens who is an efficiency engineer. Simultaneously government-subsidized workers were assigned to the library.
The findings made by the library staff under the direction of the efficiency engineer became the beginning of a complete physical rearrangement of the main library and of a redistribution of duties among the staff.
“Oh, wow!” I said. “I know who that was!” That was a fun moment.
(But I see now that I was wrong! Montclair was home to two world-famous efficiency engineers, but one of them had died in 1924, and the library renovation was done in 1931–1932. Quigley's efficiency engineer was surely Lillian Moller Gilbreth. Ooops!)
Regrettably, the Internet Archive has only an abridged version of The Poppy Seed Cakes, with only three of the eight stories. I may have it professionally scanned.
[Other articles in category /book] permanent link
Sat, 28 Jul 2018When I was a kid I enjoyed a story called George Washington's Breakfast, which I have since learned was written in 1969 by Jean Fritz. The protagonist is a boy named George Washington Allen who is fascinated by all things related to his namesake. One morning at breakfast he wonders what George Washington ate for his own breakfast. He has read all the books in his school library about George Washington, but does not know this important detail. His grandmother promises him that when he finds out what George Washington had for breakfast, she will cook it for him, whatever it is.
This launches the whole family on an odyssey that takes them as far as Mount Vernon, but even the people at Mount Vernon don't know. In the end George gets lucky: he finds an old book in the attic that authoritatively states that George Washington
breakfasts about seven o'clock on three small Indian hoecakes, and as many dishes of tea.
George is thrilled, and, having looked up hoecake in the dictionary to find out what it is (a corn cake cooked in the fireplace, on a hoe), jumps up from the table. His grandmother asks him where he is going, and of course he is going to the basement to get the hoe. Grandma refuses to cook on a hoe; George objects.
“When you were in George Washington's kitchen in Mount Vernon, did you see any hoes?”
“Well no, but…”
“Did you see any black iron griddles?”
“Yes.”
“Then that's what I'll use.”
This stuck with me for many years, and thinking back on it one day as an adult, I was suddenly certain that George Allen and his family were black, notwithstanding the plump white kid in the illustrations. At some point I even looked up the original publication to see if the kid was black in the 1969 illustrations. Nope, they are by Paul Galdone and he has made George white. A new edition was published in 1998 with new illustrations by Tomie dePaola, again with a white kid. Ms. Fritz died last year at the age of 102, so it is too late to ask her what she had in mind. But it doesn't matter to me; I am sure George is black. There was a trend in the 1960s for white authors of children’s books to make an effort to depict black kids. (For example: The Snowy Day (1962) and its sequels (through 1968); Corduroy (1968); and many others less well-known.)
Anyway, chalk this up as another story that could not happen in 2018. George's family would search on the Internet, and immediately find out about the hoecakes. I don't recall exactly what book it was that George found in the attic, but in a minute’s searching I was able to find out that it was probably Paul Leicester Ford’s George Washington (1896), and the authoritative statement about Washington's hoecake-and-tea breakfast, on page 193, is quoted from Samuel Stearns, a contemporary of Washington's.
The Stearns quotation definitely appeared in Fritz's story; I remember the wording, and even Samuel Stearns rings a bell now that I see his name again.
For oddballs like me and George Washington Allen, who become obsessed by trivial questions, the Internet is a magnificent and glorious boon. I often think that for me, one of the best results of the rise of the Internet is that I can now track down all the books from my childhood that I liked but only half-remember, find out who wrote them and read them again.
[ Addendum 20230807: The “hoe” in hoecake is apparently not a literal garden hoe, but a regional Virginia term for a skillet, as George's grandmother surmised. It was sometimes called a “bread hoe” to distinguish it from a garden hoe. ]
[Other articles in category /book] permanent link
Thu, 26 Jul 2018There are well-known tests if a number (represented as a base-10 numeral) is divisible by 2, 3, 5, 9, or 11. What about 7?
Let's look at where the divisibility-by-9 test comes from. We add up the digits of our number !!n!!. The sum !!s(n)!! is divisible by !!9!! if and only if !!n!! is. Why is that?
Say that !!d_nd_{n-1}\ldots d_0!! are the digits of our number !!n!!. Then
$$n = \sum 10^id_i.$$
The sum of the digits is
$$s(n) = \sum d_i$$
which differs from !!n!! by $$\sum (10^i-1)d_i.$$ Since !!10^i-1!! is a multiple of !!9!! for every !!i!!, every term in the last sum is a multiple of !!9!!. So by passing from !!n!! to its digit sum, we have subtracted some multiple of !!9!!, and the residue mod 9 is unchanged. Put another way:
$$\begin{align} n &= \sum 10^id_i \\ &\equiv \sum 1^id_i \pmod 9 \qquad\text{(because $10 \equiv 1\pmod 9$)} \\ &= \sum d_i \end{align} $$
The same argument works for the divisibility-by-3 test.
For !!11!! the analysis is similar. We add up the digits !!d_0+d_2+\ldots!! and !!d_1+d_3+\ldots!! and check if the sums are equal mod 11. Why alternating digits? It's because !!10\equiv -1\pmod{11}!!, so $$n\equiv \sum (-1)^id_i \pmod{11}$$
and the sum is zero only if the sum of the positive terms is equal to the sum of the negative terms.
The same type of analysis works similarly for !!2, 4, 5, !! and !!8!!. For !!4!! we observe that !!10^i\equiv 0\pmod 4!! for all !!i>1!!, so all but two terms of the sum vanish, leaving us with the rule that !!n!! is a multiple of !!4!! if and only if !!10d_1+d_0!! is. We could simplify this a bit: !!10\equiv 2\pmod 4!! so !!10d_1+d_0 \equiv 2d_1+d_0\pmod 4!!, but we don't usually bother. Say we are investigating !!571496!!; the rule tells us to just consider !!96!!. The "simplified" rule says to consider !!2\cdot9+6 = 24!! instead. It's not clear that that is actually easier.
This approach works badly for divisibility by 7, because !!10^i\bmod 7!! is not simple. It repeats with period 6.
$$\begin{array}{c|cccccc|ccc} i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\ %10^i & 1 & 10 & 100 & 1000 & 10000 & \ldots \\ 10^i\bmod 7 & 1 & 3 & 2 & 6 & 4 & 5 & 1 & 3 & 2 & 6 & 4 &\ldots \\ \end{array} $$
The rule we get from this is:
Take the units digit. Add three times the ones digit, twice the hundreds digit, six times the thousands digit… (blah blah blah) and the original number is a multiple of !!7!! if and only if the sum is also.
For example, considering !!12345678!! we must calculate $$\begin{align} 12345678 & \Rightarrow & 3\cdot1 + 1\cdot 2 + 5\cdot 3 + 4\cdot 4 + 6\cdot 5 + 2\cdot6 + 3\cdot 7 + 1\cdot 8 & = & 107 \\\\ 107 & \Rightarrow & 2\cdot1 + 3\cdot 0 + 1\cdot7 & = & 9 \end{align} $$ and indeed !!12345678\equiv 107\equiv 9\pmod 7!!.
My kids were taught the practical divisibility tests in school, or perhaps learned them from YouTube or something like that. Katara was impressed by my ability to test large numbers for divisibility by 7 and asked how I did it. At first I didn't think about my answer enough, and just said “Oh, it's not hard, just divide by 7 and look at the remainder.” (“Just count the legs and divide by 4.”) But I realized later that there are several tricks I was using that are not obvious. First, she had never learned short division. When I was in school I had been tormented extensively with long division, which looks like this:
Another one of the tricks I was using that wasn't obvious to Katara was: we don't care about the quotient anyway, only the remainder. So when I did this in my head, I discarded the parts of the calculation that were about the quotient, and only kept the steps that pertained to the remainder. The way I was actually doing this sounded like this in my mind:
7 into 12 leaves 5. 7 into 53 leaves 4. 7 into 44 leaves 2. 7 into 25 leaves 4. 7 into 46 leaves 4. 7 into 57 leaves 5. 7 into 58 leaves 9. The answer is 9.
At each step, we consider only the leftmost part of the number, starting with !!12!!. !!12\div 7 !! has a remainder of 5, and to this 5 we append the next digit of the dividend, 3, giving 53. Then we continue in the same way: !!53\div 7!! has a remainder of 4, and to this 4 we append the next digit, giving 44. We never calculate the quotient at all.
I explained the idea with a smaller example, like this:
Suppose you want to see if 1234 is divisible by 7. It's 1200-something, so take away 700, which leaves 500-something. 500-what? 530-something. So take away 490, leaving 40-something. 40-what? 44. Now take away 42, leaving 2. That's not 0, so 1234 is not divisible by 7.
This is how I actually do it. For me this works reasonably well up to 13, and after that it gets progressively more difficult until by 37 I can't effectively do it at all. A crucial element is having the multiples of the divisor memorized. If you're thinking about the mod-13 residue of 680-something, it is a big help to know immediately that you can subtract 650.
A year or two ago I discovered a different method, which I'm sure must be ancient, but is interesting because it's quite different from the other methods I described.
Suppose that the final digit of !!n!! is !!b!!, so that !!n=10a+b!!. Then !!-2n = -20a-2b!!, and this is a multiple of !!7!! if and only if !!n!! is. But !!-20a\equiv a\pmod7 !!, so !!a-2b!! is a multiple of !!7!! if and only if !!n!! is. This gives us the rule:
To check if !!n!! is a multiple of 7, chop off the last digit, double it, and subtract it from the rest of the number. Repeat until the answer becomes obvious.
For !!1234!! we first chop off the !!4!! and subtract !!2\cdot4!! from !!123!! leaving !!115!!. Then we chop off the !!5!! and subtract !!2\cdot5!! from !!11!!, leaving !!1!!. This is not a multiple of !!7!!, so neither is !!1234!!. But with !!1239!!, which is a multiple of !!7!!, we get !!123-2\cdot 9 = 105!! and then !!10-2\cdot5 = 0!!, and we win.
In contrast to the other methods in this article, this method does not tell you the remainder on dividing because it does not preserve the residue mod 7. When we started with !!1234!! we ended with !!1!!. But !!1234\not\equiv 1\pmod 7!!; rather !!1234\equiv 2!!. Each step in this method multiplies the residue by -2, or, if you prefer, by 5. The original residue was 2, so the final residue is !!2\cdot-2\cdot-2 = 8 \equiv 1\pmod 7!!. (Or, if you prefer, !!2\cdot 5\cdot 5= 50 \equiv 1\pmod 7!!.) But if we only care about whether the residue is zero, multiplying it by !!-2!! doesn't matter.
There are some shortcuts in this method too. If the final digit is !!7!!, then rather than doubling it and subtracting 14 you can just chop it off and throw it away, going directly from !!10a+7!! to !!a!!. If your number is !!10a+8!! you can subtract !!7!! from it to make it easier to work with, getting !!10a+1!! and then going to !!a-2!! instead of to !!a-16!!. Similarly when your number ends in !!9!! you can go to !!a-4!! instead of to !!a-18!!. And on the other side, if it ends in !!4!! it is easier to go to !!a-1!! instead of to !!a-8!!.
But even with these tricks it's not clear that this is faster or easier than just doing the short division. It's the same number of steps, and it seems like each step is about the same amount of work.
Finally, I once wowed Katara on an airplane ride by showing her this:

To check !!1429!! using this device, you start at ⓪. The first digit is !!1!!, so you follow one black arrow, to ①, and then a blue arrow, to ③. The next digit is !!4!!, so you follow four black arrows, back to ⓪, and then a blue arrow which loops around to ⓪ again. The next digit is !!2!!, so you follow two black arrows to ② and then a blue arrow to ⑥. And the last digit is 9 so you then follow 9 black arrows to ① and then stop. If you end where you started, at ⓪, the number is divisible by 7. This time we ended at ①, so !!1429!! is not divisible by 7. But if the last digit had been !!1!! instead, then in the last step we would have followed only one black arrow from ⑥ to ⓪, before we stopped, so !!1421!! is a multiple of 7.
This probably isn't useful for mental calculations, but I can imagine that if you were stuck on a long plane ride with no calculator and you needed to compute a lot of mod-7 residues for some reason, it could be quicker than the short division method. The chart is easy to construct and need not be memorized. The black arrows obviously point from !!n!! to !!n+1!!, and the blue arrows all point from !!n!! to !!10n!!.
I made up a whole set of these diagrams and I think it's fun to see how the conventional divisibility rules turn up in them. For example, the rule for divisibility by 3 that says just add up the digits:
Or the rule for divisibility by 5 that says to ignore everything but the last digit:
[ Addendum 20201122: Testing for divisibility by 19. ]
[ Addendum 20220106: Another test for divisibility by 7. ]
[Other articles in category /math] permanent link
Wed, 25 Jul 2018In my email today I found a note I sent to myself on 24 June 2015 that says only:
Self-warming sake bottle
which would be useful, if you don't drink your sake so quickly that it is gone before it has cooled.
As far as I know, these are not common and perhaps do not exist at all. Why not? Is this a billion-dollar idea?
A few problems come to mind. If the bottle has a cord, it will be hard to pour and will be easily upset. Maybe the best choice here would be a special power supply with relatively high voltage and a thin cord such as is used for earbuds. But this might be dangerous, or impractical for other reasons I am not thinking of.
I think battery power is also probably impractical. Heating requires a lot of energy and batteries don't supply enough. They would need to be frequently replaced, which gets expensive.
Also temperature control might be troublesome. You would need some sort of thermostat in the bottle. Typical inexpensive heating containers and immersion heaters are for bringing water to a boil, which is much simpler than warming sake to the right temperature: just dump in as much heat as possible, as quickly as possible, and perhaps also arrange to have the heat shut off if the heating element gets up to 100°C. This is much too hot for sake.
I think a more practical solution would be a tabletop hot water bath with a bottle-shaped depression in it. The hot water bath could have the thermostat and be permanently attached to a wall outlet. You insert the bottle in its bath to keep it warm when you are not pouring.
This seems practical enough that I imagine it already exists. In fact it occurs to me that I owned a similar sort of warmer at one point, for warming baby bottles. But a quick perusal of available sake warmers suggests that this approach is not common. What gives?
[Other articles in category /food] permanent link
Mon, 23 Jul 2018
Operations that are not quite associative
The paper “Verification of Identities” (1997) of Rajagopalan and Schulman discusses fast ways to test whether a binary operation on a finite set is associative. In general, there is no method that is faster than the naïve algorithm of simply checking whether $$a\ast(b\ast c) = (a\ast b)\ast c$$ for all triples !!\langle a, b, c\rangle!!. This is because:
For every !!n≥3!!, there exists an operation with just one nonassociative triple.
(Page 3.)
But R&S do not give an example. I now have a very nice example, and I think the process that led me to it is a good example of Lower Mathematics at work.
Let's say that an operation !!\ast!! is “good” if it is associative except in exactly one case. We want to find a “good” operation. My first idea was that if we could find a primitive good operation on a set of 3 elements, we could probably extend it to give a good operation on a larger set. Say the set is !!\{a_0, a_1, a_2, b_0, b_1, \ldots, b_{n-4}\}!!. We just need to define the extended operation so that if either of the operands is !!b_i!!, it is associative, and if both operands are !!a_i!! then it is the same as the primitive good operation we already found. The former part is easy: just make it constant, say !!x\ast y = b_0!! except when !!x,y\in\{a_0, a_1, a_2\}!!.
So now all we need to do is find a single good primitive operation, and I did not expend any thought on this at all. There are only !!3^9=19683!! binary operations, and we could quite easily write a program to check them all. In fact, we can do better: generate a binary operation at random and check it. If it's not the primitive good operation we want, just throw it away and try again. This could take longer to run than the exhaustive search, if there happen to be very few good operations and if the program is unlucky, but the program is easier to write, and the run time will be utterly insignificant either way.
I wrote the program, which instantly produced:
$$ \begin{array}{c|ccc} \ast & 0 & 1 & 2 \\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 2 & 0 & 1 & 2 \end{array} $$
This is associative except for the case !!1\ast(2\ast 1) \ne (1\ast 2)\ast 1!!. This solves the problem. But confirming that this is a good operation requires manually checking 27 cases, or a perhaps not-immediately-obvious case analysis.
But on a later run of the program, I got lucky and it found a simpler operation, which I can explain without a table:
!!a\ast b = 0!!, except !!2\ast 1=2!!.
Now we don't have to check 27 cases. The operation is simpler, so the proof is too: We know !!b\ast c\ne 1!!, so !!a\ast(b\ast c) !! must be !!0!!. And the only way !!(a \ast b)\ast c \ne 0!! can occur is when !!a\ast b=2!! and !!c=1!!, so !!a=2, b=1, c=1!!.
Now we can even dispense with the construction that extended the operation from !!3!! to !!n!! elements, because the description of the extended operation is the same. We wanted to extend it to be constant whenever !!a!! or !!b!! was larger than !!2!!, and that's what the description already says!
So that reduces the whole thing to about two sentences, which explain the example and why it works. But when reduced in that way, you see how the example works but not how you might go about finding it. I think the interesting part is to see how to get there, and quite a lot of mathematical education tends to over-emphasize analysis (“how can we show this is a good operation?”) at the expense of synthesis (“how can we find a good operation?”).
The exhaustive search would probably have produced the simple operation early on in its run, so there is something to be said for that approach too.
[Other articles in category /math] permanent link
Fri, 20 Jul 2018Volume was way down in May and June, mainly because of giant work crises that ate all my energy. I will try to get back on track now.
May
- The imperative mood [1] [2] [3] [4]
- An anti-lipogrammatic precommitment
- Non-transitive relations
- Cranial nerves
- I found lipograms hard to put down
- Seen…
- One of the weirdest conversations I have ever had…
- A lipogrammatic warning
- Blog article spam
- A riddle!
- Butterer
- Another missing word
- Mysterious markings on my Water-Pik
- Well okay then!
- Spruce hats
- Philadelphia street tree streets
- Cautionary tale about pseudonyms
- Today in Internet advertising
- App update schedule
June
In the past I have boldfaced posts that seemed more likely to be of general interest. None of these seem likely to be of general interest.
Also, I think it is time to stop posting these roundups. By now everyone who wants to know about shitpost.plover.com is aware of it and can follow along without prompting. So I expect this will be the last of these posts. Shitposting will continue, but without these summaries.
[Other articles in category /meta/shitpost] permanent link
Mon, 16 Jul 2018[ I wrote this in 2007 and it seems I forgot to publish it. Enjoy! ]
I eat pretty much everything. Except ketchup. I can't stand ketchup. When I went to Taiwan a couple of years ago my hosts asked if there were any foods I didn't eat. I said no, except for ketchup.
"Ketchup? You mean that red stuff?"
Right. Yes, it's strange.
When I was thirteen my grandparents took me to Greece, and for some reason I ate hardly anything but souvlaki the whole time. When I got home, I felt like a complete ass. I swore that I would never squander another such opportunity, and that if I ever went abroad again I would eat absolutely everything that was put before me.
This is a good policy not just because it exposes me to a lot of delicious and interesting food, and not just because it prevents me from feeling like a complete ass, but also because I don't have to worry that perhaps my hosts will be insulted or disappointed that I won't eat the food they get for me.
On my second trip to Taiwan, I ate at a hot pot buffet restaurant. They give you a pot of soup, and then you go to the buffet and load up with raw meat and vegetables and things, and cook them at your table in the soup. It's fun. In my soup there were some dark reddish-brown cubes that had approximately the same texture as soft tofu. I didn't know what it was, but I ate it and tried to figure it out.
The next day I took the bus to Lishan (梨山), and through good fortune was invited to eat dinner with a Taiwanese professor of criminology and his family. The soup had those red chunks in it again, and I said "I had these for lunch yesterday! What are they?" I then sucked one down quickly, because sometimes people interpret that kind of question as a criticism, and I didn't want to offend the professor.
Actually it's much easier to ask about food in China than it is in, say, Korea. Koreans are defensive about their cuisine. They get jumpy if you ask what something is, and are likely to answer "It's good. Just eat it!". They are afraid that the next words out of your mouth will be something about how bad it smells. This is because the Japanese, champion sneerers, made about one billion insulting remarks about smelly Korean food while they were occupying the country between 1911 and 1945. So if you are in Korea and you don't like the food, the Koreans will take it very personally.
Chinese people, on the other hand, know that they have the best food in the world, and that everyone loves Chinese food. If you don't like it, they will not get offended. They will just conclude that you are a barbarian or an idiot, and eat it themselves.
Anyway, it turns out that the reddish-brown stuff was congealed duck's blood. Okay. Hey, I had congealed duck blood soup twice in two days! No way am I going home from this trip feeling like an ass.
So the eat-absolutely-everything policy has worked out well for me, and although I haven't liked everything, at least I don't feel like I wasted my time.
The only time I've regretted the policy was on my first trip to Taiwan. I was taken out to dinner and one of the dishes turned out to be pieces of steamed squid. That's not my favorite food, but I can live with it. But the steamed squid was buried under a big, quivering mound of sugared mayonnaise.
I remembered my policy, and took a bite. I'm sure I turned green.
So that's the food that I couldn't eat.
[ Some of this 2007 article duplicates stuff I have said since; for example I cut out the chicken knuckles story, which would have been a repeat. Also previously; also previously; and another one ]
[Other articles in category /food] permanent link
Wed, 11 Jul 2018Here is another bit of Perl code:
sub function {
my ($self, $cookie) = @_;
$cookie = ref $cookie && $cookie->can('value') ? $cookie->value : $cookie;
...
}
The idea here is that we are expecting $cookie to be either a
string, passed directly, or some sort of cookie object with a value
method that will produce the desired string.
The ref … && … condition
distinguishes the two situations.
A relatively minor problem is that if someone passes an object with no
value method, $cookie will be set to that object instead of to a
string, with mysterious results later on.
But the real problem here is that the function's interface is not simple enough. The function needs the string. It should insist on being passed the string. If the caller has the string, it can pass the string. If the caller has a cookie object, it should extract the string and pass the string. If the caller has some other object that contains the string, it should extract the string and pass the string. It is not the job of this function to know how to extract cookie strings from every possible kind of object.
I have seen code in which this obsequiousness has escalated to
absurdity. I recently saw a function whose job was to send an email.
It needs an EmailClass object, which encapsulates the message
template and some of the headers. Here is how it obtains that object:
12 my $stash = $args{stash} || {};
…
16 my $emailclass_obj = delete $args{emailclass_obj}; # isn't being passed here
17 my $emailclass = $args{emailclass_name} || $args{emailclass} || $stash->{emailclass} || '';
18 $emailclass = $emailclass->emailclass_name if $emailclass && ref($emailclass);
…
60 $emailclass_obj //= $args{schema}->resultset('EmailClass')->find_by_name($emailclass);
Here the function needs an EmailClass object. The caller can pass
one in $args{emailclass_obj}. But maybe the caller doesn't have
one, and only knows the name of the emailclass it wants to use. Very
well, we will allow it to pass the string and look it up later.
But that string could be passed in any of $args{emailclass_name}, or
$args{emailclass}, or $args{stash}{emailclass} at the caller's
whim and we have to rummage around hoping to find it.
Oh, and by the way, that string might not be a string! It might be the actual object, so there are actually seven possibilities:
$args{emailclass}
$args{emailclass_obj}
$args{emailclass_name}
$args{stash}{emailclass}
$args{emailclass}->emailclass_name
$args{emailclass_name}->emailclass_name
$args{stash}{emailclass}->emailclass_name
Notice that if $args{emailclass_name} is actually an emailclass
object, the name will be extracted from that object on line 18, and
then, 42 lines later, the name may be used to perform a database
lookup to recover the original object again.
We hope by the end of this rigamarole that $emailclass_obj will
contain an EmailClass object, and $emailclass will contain its
name. But can you find any combinations of arguments where this turns
out not to be true? (There are several.) Does the existing code
exercise any of these cases? (I don't know. This function is called
in 133 places.)
All this because this function was not prepared to insist firmly that its arguments be passed in a simple and unambiguous format, say like this:
my $emailclass = $args->{emailclass}
|| $self->look_up_emailclass($args->{emailclass_name})
|| croak "one of emailclass or emailclass_name is required";
I am not certain why programmers think it is a good idea to have functions communicate their arguments by way of a round of Charades. But here's my current theory: some programmers think it is discreditable for their function to throw an exception. “It doesn't have to die there,” they say to themselves. “It would be more convenient for the caller if we just accepted either form and did what they meant.” This is a good way to think about user interfaces! But a function's calling convention is not a user interface. If a function is called with the wrong arguments, the best thing it can do is to drop dead immediately, pausing only long enough to gasp out a message explaining what is wrong, and incriminating its caller. Humans are deserving of mercy; calling functions are not.
Allowing an argument to be passed in seven different ways may be
convenient for the programmer writing the call, who can save a few
seconds looking up the correct spelling of emailclass_name, but
debugging what happens when elaborate and inconsistent arguments are
misinterpreted will eat up the gains many times over. Code is
written once, and read many times, so we should be willing to spend
more time writing it if it will save trouble reading it again later.
Novice programmers may ask “But what if this is business-critical code? A failure here could be catastrophic!”
Perhaps a failure here could be catastrophic. But if it is a catastrophe to throw an exception, when we know the caller is so confused that it is failing to pass the required arguments, then how much more catastrophic to pretend nothing is wrong and to continue onward when we are surely ignorant of the caller's intentions? And that catastrophe may not be detected until long afterward, or at all.
There is such a thing as being too accommodating.
[Other articles in category /prog/perl] permanent link
Fri, 06 Jul 2018[ This article has undergone major revisions since it was first published yesterday. ]
Here is a line of Perl code:
if ($self->fidget && blessed $self->fidget eq 'Widget::Fidget') {
This looks to see if $self has anything in its fidget slot, and if
so it checks to see if the value there is an instance of the class
Widget::Fidget. If both are true, it runs the following block.
That blessed check is bad practice for several reasons.
It duplicates the declaration of the
fidgetmember data:has fidget => ( is => 'rw', isa => 'Widget::Fidget', init_arg => undef, );So the
fidgetslot can't contain anything other than aWidget::Fidget, because the OOP system is already enforcing that. That means that theblessed…eqtest is not doing anything — unless someone comes along later and changes the declared type, in which case the test will then be checking the wrong condition.Actually, that has already happened! The declaration, as written, allows
fidgetto be an instance not just ofWidget::Fidgetbut of any class derived from it. But theblessed…eqcheck prevents this. This reneges on a major promise of OOP, that if a class doesn't have the behavior you need, you can subclass it and modify or extend it, and then use objects from the subclass instead. But if you try that here, theblessed…eqcheck will foil you.So this is a prime example of “… in which case the test will be checking the wrong condition” above. The test does not match the declaration, so it is checking the wrong condition. The
blessed…eqcheck breaks the ability of the class to work with derived classes ofWidget::Fidget.Similarly, the check prevents someone from changing the declared type to something more permissive, such as
“either
Widget::FidgetorGidget::Fidget”or
“any object that supports
wiggleandwagglemethods”or
“any object that adheres to the specification of
Widget::Interface”and then inserting a different object that supports the same interface. But the whole point of object-oriented programming is that as long as an object conforms to the required interface, you shouldn't care about its internal implementation.
In particular, the check above prevents someone from creating a mock
Widget::Fidgetobject and injecting it for testing purposes.We have traded away many of the modularity and interoperability guarantees that OOP was trying to preserve for us. What did we get in return? What are the purported advantages of the
blessed…eqcheck? I suppose it is intended to detect an anomalous situation in which some completely wrong object is somehow stored into theself.fidgetmember. The member declaration will prevent this (that is what it is for), but let's imagine that it has happened anyway. This could be a very serious problem. What will happen next?With the check in place, the bug will go unnoticed because the function will simply continue as if it had no fidget. This could cause a much more subtle failure much farther down the road. Someone trying to debug this will be mystified: At best “it's behaving as though it had no fidget, but I know that one was set earlier”, and at worst “why is there two years of inconsistent data in the database?” This could take a very long time to track down. Even worse, it might never be noticed, and the method might quietly do the wrong thing every time it was used.
Without the extra check, the situation is much better: the function will throw an exception as soon as it tries to call a fidget method on the non-fidget object. The exception will point a big fat finger right at the problem: “hey, on line 2389 you tried to call the
rotatemethod on aSkunk::Stinkyobject, but that class has no such method`. Someone trying to debug this will immediately ask the right question: “Who put a skunk in there instead of a widget?”
It's easy to get this right. Instead of
if ($self->fidget && blessed $self->fidget eq 'Widget::Fidget') {
one can simply use:
if ($self->fidget) {
Moral of the story: programmers write too much code.
I am reminded of something chess master Aron Nimzovitch once said, maybe in Chess Praxis, that amateur chess players are always trying to be Doing Something.
[Other articles in category /prog/perl] permanent link
In which, to my surprise, I find myself belonging to a group
My employer ZipRecruiter had a giant crisis at last month, of a scale that I have never seen at this company, and indeed, have never seen at any well-run company before. A great many of us, all the way up to the CTO, made a heroic effort for a month and got it sorted out.
It reminded me a bit of when Toph was three days old and I got a call from the hospital to bring her into the emergency room immediately. She had jaundice, which is not unusual in newborn babies. It is easy to treat, but if untreated it can cause permanent brain damage. So Toph and I went to the hospital, where she underwent the treatment, which was to have very bright lights shined directly on her skin for thirty-six hours. (Strange but true!)
The nurses in the hospital told me they had everything under control, and they would take care of Toph while I went home, but I did not go. I wanted to be sure that Toph was fed immediately and that her diapers were changed timely. The nurses have other people to take care of, and there was no reason to make her wait to eat and sleep when I could be there tending to her. It was not as if I had something else to do that I felt was more important. So I stayed in the room with Toph until it was time for us to go home, feeding her and taking care of her and just being with her.
It could have been a very stressful time, but I don't remember it that way. I remember it as a calm and happy time. Toph was in no real danger. The path forward was clear. I had my job, to help Toph get better, and I was able to do it undistracted. The hospital (Children's Hospital of Philadelphia) was wonderful, and gave me all the support I needed to do my job. When I got there they showed me the closet where the bedding was and the other closet where the snacks were and told me to help myself. They gave me the number to call at mealtimes to order meals to be sent up to my room. They had wi-fi so I could work quietly when Toph was asleep. Everything went smoothly, Toph got better, and we went home.
This was something like that. It wasn't calm; it was alarming and disquieting. But not in an entirely bad way; it was also exciting and engaging. It was hard work, but it was work I enjoyed and that I felt was worth doing. I love working and programming and thinking about things, and doing that extra-intensely for a few weeks was fun. Stressful, but fun.
And I was not alone. So many of the people I work with are so good at their jobs. I had all the support I needed. I could focus on my part of the work and feel confident that the other parts I was ignoring were being handled by competent and reasonable people who were at least as dedicated as I was. The higher-up management was coordinating things from the top, connecting technical and business concerns, and I felt secure that the overall design of the new system would make sense even if I couldn't always understand why. I didn't want to think about business concerns, I wanted someone else to do it for me and tell me what to do, and they did. Other teams working on different components that my components would interface with would deliver what they promised and it would work.
And the other programmers in my group were outstanding. We were scattered all over the globe, but handed off tasks to one another without any mishaps. I would come into work in the morning and the guys in Europe would be getting ready to go to bed and would tell me what they were up to and the other east-coasters and I could help pick up where they left off. The earth turned and the west-coasters appeared and as the end of the day came I would tell them what I had done and they could continue with it.
I am almost pathologically averse to belonging to groups. It makes me uncomfortable and even in groups that I have been associated with for years I feel out of place and like my membership is only provisional and temporary. I always want to go my own way and if everyone around me is going the same way I am suspicious and contrarian. When other people feel group loyalty I wonder what is wrong with them.
The up-side of this is that I am more willing than most people to cross group boundaries. People in a close-knit community often read all the same books and know all the same techniques for solving problems. This means that when a problem comes along that one of them can't solve, none of the rest can solve it either. I am sometimes the person who can find the solution because I have spent time in a different tribe and I know different things. This is a role I enjoy.
Higher-Order Perl exemplifies this. To write Higher-Order Perl I visited functional programming communities and tried to learn techniques that those communities understood that people outside those communities could use. Then I came back to the Perl community with the loot I had gathered.
But it's not all good. I have sometimes been able to make my non-belonging work out well. But it is not a choice; it's the way I am made, and I can't control it. When I am asked to be part of a team, I immediately become wary and wonder what the scam is. I can be loyal to people personally, but I have hardly any group loyalty. Sometimes this can lead to ugly situations.
But in fixing this crisis I felt proud to be part of the team. It is a really good team and I think it says something good about me that I can work well with the rest of them. And I felt proud to be part of this company, which is so functional, so well-run, so full of kind and talented people. Have I ever had this feeling before? If I have it was a long, long time ago.
G.H. Hardy once wrote that when he found himself forced to listen to pompous people, he would console himself by thinking:
Well, I have done one thing you could never have done, and that is to have collaborated with Littlewood and Ramanujan on something like equal terms.
Well, I was at ZipRecruiter during the great crisis of June 2018 and I was able to do my part and to collaborate with those people on equal terms, and that is something to be proud of.
[Other articles in category /brain] permanent link
Wed, 04 Jul 2018
Jackson and Gregg on optimization
Today Brendan Gregg's blog has an article Evaluating the Evaluation: Benchmarking Checklist that begins:
A co-worker introduced me to Craig Hanson and Pat Crain's performance mantras, which neatly summarize much of what we do in performance analysis and tuning. They are:
Performance mantras
- Don't do it
- Do it, but don't do it again
- Do it less
- Do it later
- Do it when they're not looking
- Do it concurrently
- Do it cheaper
I found this striking because I took it to be an obvious reference Michael A. Jackson's advice in his brilliant 1975 book Principles of Program Design. Jackson said:
We follow two rules in the matter of optimization:
Rule 1: Don't do it.
Rule 2 (for experts only). Don't do it yet.
The intent of the two passages is completely different. Hanson and Crain are offering advice about what to optimize. “Don't do it” means that to make a program run faster, eliminate some of the things it does. “Do it, but don't do it again” means that to make a program run faster, have it avoid repeating work it has already done, say by caching results. And so on.
Jackson's advice is of a very different nature. It is only indirectly about improving the program's behavior. Instead it is addressing the programmer's behavior: stop trying to optimize all the damn time! It is not about what to optimize but whether, and Jackson says that to a first approximation, the answer is no.
Here are Jackson's rules with more complete context. The quotation is from the preface (page vii) and is discussing the style of the examples in his book:
Above all, optimization is avoided. We follow two rules in the matter of optimization:
Rule 1. Don't do it.
Rule 2 (for experts only). Don't do it yet — that is, not until you have a perfectly clear and unoptimized solution.Most programmers do too much optimization, and virtually all do it too early. This book tries to act as an antidote. Of course, there are systems which must be highly optimized if they are to be economically useful, and Chapter 12 discusses some relevant techniques. But two points should always be remembered: first, optimization makes a system less reliable and harder to maintain, and therefore more expensive to build and operate; second, because optimization obscures structure it is difficult to improve the efficiency of a system which is already partly optimized.
Here's some code I dealt with this month:
my $emailclass = $args->{emailclass};
if (!$emailclass && $args->{emailclass_name} ) {
# do some caching so if we're called on the same object over and over we don't have to do another find.
my $last_emailclass = $self->{__LAST_EMAILCLASS__};
if ( $last_emailclass && $last_emailclass->{name} eq $args->{emailclass_name} ) {
$emailclass = $last_emailclass->{emailclass};
} else {
$emailclass = $self->schema->resultset('EmailClass')
->find_by_name($args->{emailclass_name});
$self->{__LAST_EMAILCLASS__} = {
name => $args->{emailclass_name},
emailclass => $emailclass,
};
}
}
Holy cow, this is wrong in so many ways. 8 lines of this mess, for
what? To cache a single database lookup (the ->find_by_name call),
in a single object, if it happens to be looking for the same name as
last time. If caching was actually wanted, it should have been
addressed in the ->find_by_name call, which could do the caching
more generally, and which has some hope of knowing something about
when the cache entries should be expired. Even stipulating that
caching was wanted and for some reason should have been put here, why
such an elaborate mechanism, all to cache just the last lookup? It
could have been:
$emailclass = $self->emailclass_for_name($args->{emailclass_name});
...
sub emailclass_for_name {
my ($self, $name) = @_;
$self->{emailclass}{$name} //=
$self->schema->resultset('EmailClass')->find_by_name($name);
return $self->{emailclass}{$name};
}
I was able to do a bit better than this, and replaced the code with:
$emailclass = $self->schema->resultset('EmailClass')
->find_by_name($args->{emailclass_name});
My first thought was that the original caching code had been written by a very inexperienced programmer, someone who with more maturity might learn to do their job with less wasted effort. I was wrong; it had been written by a senior developer, someone who with more maturity might learn to do their job with less wasted effort.
The tragedy did not end there. Two years after the original code was written a more junior programmer duplicated the same unnecessary code elsewhere in the same module, saying:
I figured they must have had a reason to do it that way…
Thus is the iniquity of the fathers visited on the children.
In a nearby piece of code, an object A, on the first call to a certain method, constructed object B and cached it:
B->new(
base_path => ...
schema => $self->schema,
retry => ...,
);
Then on subsequent calls, it reused B from the cache.
But the cache was shared among many instances of A, not all of which
had the same ->schema member. So some of those instances of A
would ask B a question and get the answer from the wrong database.
A co-worker spent hours and hours in the middle of the night last
month tracking this down. Again, the cache was not only broken but
completely unnecesary. What was being saved? A single object
construction, probably a few hundred bytes and a few hundred
microseconds at most. And again, the code was perpetrated by a senior
developer who should have known better. My co-worker replaced 13
lines of broken code with four that worked.
Brendan Gregg is unusually clever, and an exceptional case. Most programmers are not Brendan Gregg, and should take Jackson's advice and stop trying to be so clever all the time.
[Other articles in category /prog] permanent link
Mon, 18 Jun 2018Yesterday I presented as a counterexample the topology induced by the following metric:
I asked:
It seems like this example could be useful in other circumstances too. Does it have a name?
Several Gentle Readers have written in to tell me that that this metric is variously known as the British Rail metric, French Metro metric, or SNCF metric. (SNCF = Société nationale des chemins de fer français, the French national railway company). In all cases the conceit is the same (up to isomorphism): to travel to a destination on another railway line one must change trains in London / Paris, where all the lines converge.
Wikipedia claims this is called the post office metric, again I suppose because all the mail comes to the central post office for sorting. I have not seen it called the FedEx metric, but it could have been, with the center of the disc in Memphis.
[ Addendum 20180621: Thanks for Brent Yorgey for correcting my claim that the FedEx super hub is in Nashville. It is in Memphis ]
[Other articles in category /math] permanent link
Sun, 17 Jun 2018
Bounded does not imply totally bounded
I somehow managed to miss the notion of totally bounded when I was learning topology, and it popped up on stack exchange recently. It is a stronger version of boundedness for metric spaces: a space !!M!! is totally bounded if, for any chosen !!\epsilon!!, !!M!! can be covered by a finite family of balls of radius !!\epsilon!!.
This is a strictly stronger property than ordinary boundedness, so the question immediately comes up: what is an example of a space that is bounded but not totally bounded. Many examples are well-known. For example, the infinite-dimensional unit ball is bounded but not totally bounded. But I didn't think of this right away.
Instead I thought of the following rather odd example: Let !!S!! be the closed unit disc and assign each point a polar coordinate !!\langle r,\theta\rangle!! as usual. Now consider the following metric:
$$ d(\langle r_1, \theta_1\rangle, \langle r_2, \theta_2\rangle) = \begin{cases} r_1, & \qquad \text{ if $r_2 = 0$} \\ \lvert r_1 - r_2 \rvert, & \qquad\text{ if $\theta_1 = \theta_2$} \\ r_1 + r_2 & \qquad\text{ otherwise} \\ \end{cases} $$
The idea is this: you can travel between points only along the radii of the disc. To get from !!p_1!! to !!p_2!! that are on different radii, you must go through the origin:
Now clearly when !!\epsilon < \frac12!!, the !!\epsilon!!-ball that covers each point point !!\left\langle 1, \theta\right\rangle!! lies entirely within one of the radii, and so an uncountable number of such balls are required to cover the disc.
It seems like this example could be useful in other circumstances too. Does it have a name?
[ Addendum 2018-07-18: Several Gentle Readers have informed me that this metric has not just one name, but several. ]
[Other articles in category /math] permanent link
Mon, 21 May 2018
More about disabling standard I/O buffering
In yesterday's article I described a simple and useful feature that could have been added to the standard I/O library, to allow an environment variable to override the default buffering behavior. This would allow the invoker of a program to request that the program change its buffering behavior even if the program itself didn't provide an option specifically for doing that.
Simon Tatham directed me to the GNU Coreutils stdbuf
command
which does something of this sort. It is rather like the
pseudo-tty-pipe program I described, but instead of using the
pseudo-tty hack I suggested, it works by forcing the child program to
dynamically
load
a custom replacement for
stdio.
There appears to be a very similar command in FreeBSD.
[ Addendum 20240820: This description is not accurate; see below. ]
Roderick Schertler pointed out that Dan Bernstein wrote a utility
program, pty, in 1990, atop which my pseudo-tty-pipe program could
easily be built; or maybe its ptybandage utility is exactly what I
wanted. Jonathan de Boyne Pollard has a page explaining it in
detail, and related
packages.
A later version of pty is still
available.
Here's M. Bernstein's blurb about it:
ptygetis a universal pseudo-terminal interface. It is designed to be used by any program that needs a pty.
ptygetcan also serve as a wrapper to improve the behavior of existing programs. For example,ptybandage telnetis liketelnetbut can be put into a pipeline.nobuf grepis likegrepbut won't block-buffer if it's redirected.Previous pty-allocating programs —
rlogind,telnetd,sshd,xterm,screen,emacs,expect, etc. — have caused dozens of security problems. There are two fundamental reasons for this. First, these programs are installed setuid root so that they can allocate ptys; this turns every little bug in hundreds of thousands of lines of code into a potential security hole. Second, these programs are not careful enough to protect the pty from access by other users.
ptygetsolves both of these problems. All the privileged code is in one tiny program. This program guarantees that one user can't touch another user's pty.
ptygetis a complete rewrite ofpty4.0, my previous pty-allocating package.pty4.0's session management features have been split off into a separate package,sess.
Leonardo Taccari informed me that NetBSD's stdio actually
has the environment variable feature I was asking for! Christos
Zoulas suggested adding stdbuf similar to the GNU and FreeBSD
implementations, but the NetBSD people observed, as I did, that it
would be simpler to just control stdio directly with an environment
variable, and did it. Here's the relevant part of the NetBSD setbuf(3) man
page:
The default buffer settings can be overwritten per descriptor (
STDBUFn) where n is the numeric value of the file descriptor represented by the stream, or for all descriptors (STDBUF). The environment variable value is a letter followed by an optional numeric value indicating the size of the buffer. Valid sizes range from 0B to 1MB. Valid letters are:
Uunbuffered
Lline buffered
Ffully buffered
Here's the discussion from the NetBSD tech-userlevel mailing
list.
The actual patch looks almost exactly the way I imagined it would.
Finally, Mariusz Ceier pointed out that there is an ancient bug report in
glibc
suggesting essentially the same environment variable mechanism that I
suggested and that was adopted in NetBSD. The suggestion was firmly
and summarily rejected. (“Hell, no … this is a terrible idea.”)
Interesting wrinkle: the bug report was submitted by Pádraig Brady,
who subsequently wrote the stdbuf command I described above.
Thank you, Gentle Readers!
Addenda
20240820
nabijaczleweli has pointed out that my explanation of the GNU stdbuf
command above is not accurate. I said "it works by forcing the child
program to dynamically load a custom replacement for stdio". It's
less heavyweight than that. Instead, it arranges to load
a dynamic library
that runs before the rest of the program starts, examines the
environment, and simply calls setvbuf as needed on the three
standard streams.
[Other articles in category /Unix] permanent link
Sun, 20 May 2018
Proposal for turning off standard I/O buffering
Some Unix commands, such as grep, will have a command-line flag to
say that you want to turn off the buffering that is normally done in
the standard I/O library. Some just try to guess what you probably
want. Every command is a little different and if the command you want
doesn't have the flag you need, you are basically out of luck.
Maybe I should explain the putative use case here. You have some
command (or pipeline) X that will produce dribbles of data at
uncertain intervals. If you run it at the terminal, you see each
dribble timely, as it appears. But if you put X into a pipeline,
say with
X | tee ...
or
X | grep ...
then the dribbles are buffered and only come out of X when an entire
block is ready to be written, and the dribbles could be very old
before the downstream part of the pipeline, including yourself, sees
them. Because this is happening in user space inside of X, there is
not a damn thing anyone farther downstream can do about it. The only
escape is if X has some mode in which it turns off standard I/O
buffering. Since standard I/O buffering is on by default, there is a
good chance that the author of X did not think to affirmatively add
this feature.
Note that adding the --unbuffered flag to the downstream grep does
not solve the problem; grep will produce its own output timely, but
it's still getting its input from X after a long delay.
One could imagine a program which would interpose a pseudo-tty, and
make X think it is writing to a terminal, and then the standard I/O
library would stay in line-buffered mode by default. Instead of
running
X | tee some-file | ...
or whatever, one would do
pseudo-tty-pipe -c X | tee some-file | ...
which allocates a pseudo-tty device, attaches standard output to it,
and forks. The child runs X, which dribbles timely into the
pseudo-tty while the parent runs a read loop to remove dribbles from
the master end of the TTY and copy them timely into the pipe. This
would work. Although tee itself also has no --unbuffered flag
so you might even have to:
pseudo-tty-pipe -c X | pseudo-tty-pipe -c 'tee some-file' | ...
I don't think such a program exists, and anyway, this is all
ridiculous, a ridiculous abuse of the standard I/O library's buffering
behavior: we want line buffering, the library will only give it to us
if the process is attached to a TTY device, so we fake up a TTY just
to fool stdio into giving us what we want. And why? Simply because
stdio has no way to explicitly say what we want.
But it could easily expose this behavior as a controllable feature. Currently there is a branch in the library that says how to set up a buffering mode when a stream is opened for the first time:
if the stream is for writing, and is attached to descriptor 2, it should be unbuffered; otherwise …
if the stream is for writing, and connects descriptor 1 to a terminal device, it should be line-buffered; otherwise …
if the moon is waxing …
…
otherwise, the stream should be block-buffered
To this, I propose a simple change, to be inserted right at the beginning:
If the environment variable
STDIO_BUFis set to"line", streams default to line buffering. If it's set to"none", streams default to no buffering. If it's set to"block", streams default to block buffered. If it's anything else, or unset, it is ignored.
Now instead of this:
pseudo-tty-pipe --from X | tee some-file | ...
you write this:
STDIO_BUF=line X | tee some-file | ...
Problem solved.
Or maybe you would like to do this:
export STDIO_BUF=line
which then it affects every program in every pipeline in the rest of the session:
X | tee some-file | ...
Control is global if you want it, and per-process if you want it.
This feature would cost around 20 lines of C code in the standard I/O
library and would impose only an insigificant run-time cost. It would
effectively add an --unbuffered flag to every program in the
universe, retroactively, and the flag would be the same for every
program. You would not have to remember that in mysql the magic
option is -n and that in GNU grep it is --line-buffered and that
for jq is is --unbuffered and that Python scripts can be
unbuffered by supplying the -u flag and that in tee you are just
SOL, etc. Setting STDIO_BUF=line would Just Work.
Programming languages would all get this for free also. Python
already has PYTHONUNBUFFERED but in other languages
you have to do something or other; in Perl you use some
horrible Perl-4-ism like
{ my $ofh = select OUTPUT; $|++; select $ofh }
This proposal would fix every programming language everywhere. The Perl code would become:
$ENV{STDIO_BUF} = 'line';
and every other language would be similarly simple:
/* In C */
putenv("STDIO_BUF=line");
[ Addendum 20180521: Mariusz Ceier corrects me, pointing out that this will not work for the process’ own standard streams, as they are pre-opened before the process gets a chance to set the variable. ]
It's easy to think of elaborations on this: STDIO_BUF=1:line might
mean that only standard output gets line-buffering by default,
everything else is up to the library.
This is an easy thing to do. I have wanted this for twenty years. How is it possible that it hasn't been in the GNU/Linux standard library for that long?
[ Addendum 20180521: it turns out there is quite a lot to say about the state of the art here. In particular, NetBSD has the feature very much as I described it. ]
[Other articles in category /Unix] permanent link
Mon, 07 May 2018
Katara constructs finite projective planes
This weekend I got a very exciting text message from Katara:
I have a math question for you
Oh boy! I hope it's one I can answer.
Okay
there's this game called spot it where you have cards with 8 symbols on them like soand the goal is to find the one matching symbol on your card and the one in the middle
how is it possible that given any pair of cards, there is exactly one matching symbol
Well, whatever my failings as a dad, this is one problem I can solve. I went a little of overboard in my reply:
You need a particular kind of structure called a projective plane.
They only exist for certain numbers of symbols
A simpler example has 7 cards with 3 symbols each.
One thing that's cool about it is that the symbols and the cards are "dual": say you give each round card a name. Then make up a new deck of square cards. There's one square card for each symbol. So there's a square"Ladybug" card. The Ladybug card has on it the names of the round cards that have the Ladybug. Now you can play Spot with the square cards instead of the round ones: each two square cards have exactly one name in common.
In a geometric plane any two points lie on exactly one common line and any two lines intersect in exactly one common point. This is a sort of finite model of that, with cards playing the role of lines and symbols playing the role of points. Or vice versa, it doesn't matter.
More than you wanted to know 😂
ah thank you, I'm pretty sure I understand, sorry for not responding, my phone was charging
I still couldn't shut up about the finite projective planes:
No problem! No response necessary.
It is known that all finite projective planes have n²+n+1 points for some n. So I guess the Spot deck has either 31, 57, or 73 cards and the same number of symbols. Is 57 correct?
Must be 57 because I see from your picture that each card has 8 symbols.
Katara was very patient:
I guess, I would like to talk about this some more when i get home if that's okay
Any time.
Anyway this evening I cut up some index cards, and found a bunch of stickers in a drawer, and made Katara a projective plane of order 3. This has 13 cards, each with 4 different stickers, and again, every two cards share exactly one sticker. She was very pleased and wanted to know how to make them herself.
Each set of cards has an order, which is a non-negative integer. Then there must be !!n^2 + n + 1!! cards, each with !!n+1!! stickers or symbols. When !!n!! is a prime power, you can use field theory to construct a set of cards from the structure of the (unique) field of order !!n!!.
Fields to projective planes
Order 2
I'll describe the procedure using the plane of order !!n=2!!, which is unusually simple. There will be !!2^2+2+1 = 7!! cards, each with !!3!! of the !!7!! symbols.
Here is the finite field of order 2, called !!GF(2)!!:
|
|
The stickers correspond to ordered triples of elements of !!GF(2)!!, except that !!\langle 0,0,0\rangle!! is always omitted. So they are:
$$\require{cancel}\begin{array}{cc} \cancel{\langle 0,0,0\rangle} & \langle 1,0,0\rangle \\ \langle 0,0,1\rangle & \langle 1,0,1\rangle \\ \langle 0,1,0\rangle & \langle 1,1,0\rangle \\ \langle 0,1,1\rangle & \langle 1,1,1\rangle \\ \end{array} $$
Of course, you probably do not want to use these symbols exactly. You might decide that !!\langle 1,0,0\rangle!! is a sticker with a picture of a fish, and !!\langle 0,1,0\rangle!! is a sticker with a ladybug.
Each card will have !!n+1 = 3!! stickers. To generate a card, pick any two stickers that haven't appeared together before and put them on the card. Say these stickers correspond to the triples !!\langle a,b,c\rangle!! and !!\langle x,y,z\rangle!!. To find the triple for the third sticker on the card, just add the first two triples componentwise, obtaining !!\langle a+x,b+y,c+z\rangle!!. Remember that the addition must be done according to the !!GF(2)!! addition table above! So for example if a card has !!\langle 1,0,1\rangle!! and !!\langle 0,1,1\rangle!!, its third triple will be
$$\begin{align} \langle 1,0,1 \rangle + \langle 0,1,1 \rangle & = \\ \langle 1+0,0+1,1+1 \rangle & = \\ \langle 1,1,0 \rangle \end{align} $$
Observe that it doesn't matter which two triples you add; you always get the third one!
Okay, well, that was simple.
Larger order
After Katara did the order 2 case, which has 7 cards, each with 3 of the 7 kinds of stickers, she was ready to move on to something bigger. I had already done the order 3 deck so she decided to do order 4. This has !!4^2+4+1 = 21!! cards each with 5 of the 21 kinds of stickers. The arithmetic is more complicated too; it's !!GF(2^2)!! instead of !!GF(2)!!:
|
|
When the order !!n!! is larger than 2, there is another wrinkle. There are !!4^3 = 64!! possible triples, and we are throwing away !!\langle 0,0,0\rangle!! as usual, so we have 63. But we need !!4^2+4+1 = 21!!, not !!63!!.
Each sticker is represented not by one triple, but by three. The triples !!\langle a,b,c\rangle, \langle 2a,2b,2c\rangle,!! and !!\langle 3a,3b,3c\rangle!! must be understood to represent the same sticker, all the multiplications being done according to the table above. Then each group of three triples corresponds to a sticker, and we have 21 as we wanted.
Each triple must have a leftmost non-zero entry, and in each group of three similar triples, there will be one where this leftmost non-zero entry is a !!1!!; we will take this as the canonical representative of its class, and it can wear a costume or a disguise that makes it appear to begin with a !!2!! or a !!3!!.
We might assign stickers to triples like this:
$$ \begin{array}{rl} \cancel{\langle 0,0,0\rangle} & \\ \langle 0,0,1 \rangle & \text{apple} \\ \hline \langle 0,1,0 \rangle & \text{bicycle} \\ \langle 0,1,1 \rangle & \text{carrot} \\ \langle 0,1,2 \rangle & \text{dice} \\ \langle 0,1,3 \rangle & \text{elephant} \\ \hline \langle 1,0,0 \rangle & \text{frog} \\ \langle 1,0,1 \rangle & \text{goat} \\ \langle 1,0,2 \rangle & \text{hat} \\ \langle 1,0,3 \rangle & \text{igloo} \\ \langle 1,1,0 \rangle & \text{jellyfish} \\ \langle 1,1,1 \rangle & \text{kite} \\ \langle 1,1,2 \rangle & \text{ladybug} \\ \langle 1,1,3 \rangle & \text{mermaid} \\ \langle 1,2,0 \rangle & \text{nose} \\ \langle 1,2,1 \rangle & \text{octopus} \\ \langle 1,2,2 \rangle & \text{piano} \\ \langle 1,2,3 \rangle & \text{queen} \\ \langle 1,3,0 \rangle & \text{rainbow} \\ \langle 1,3,1 \rangle & \text{shoe} \\ \langle 1,3,2 \rangle & \text{trombone} \\ \langle 1,3,3 \rangle & \text{umbrella} \\ \end{array} $$
We can stop there, because everything after !!\langle 1,3,3 \rangle!! begins with a !!2!! or a !!3!!, and so is some other triple in disguise. For example what sticker goes with !!\langle 0,2,3 \rangle!!? That's actually !!\langle 0,1,2 \rangle!! in disguise, it's !!2·\langle 0,1,2 \rangle!!, which is “dice”. Okay, how about !!\langle 3,3,1 \rangle!!? That's the same as !!3\cdot\langle 1,1,2 \rangle!!, which is “ladybug”. There are !!21!!, as we wanted. Note that the !!21!! naturally breaks down as !!1+4+4^2!!, depending on how many zeroes are at the beginning; that's where that comes from.
Now, just like before, to make a card, we pick two triples that have not yet gone together, say !!\langle 0,0,1 \rangle!! and !!\langle 0,1,0 \rangle!!. We start adding these together as before, obtaining !!\langle 0,1,1 \rangle!!. But we must also add together the disguised versions of these triples, !!\langle 0,0,2 \rangle!! and !!\langle 0,0,3 \rangle!! for the first, and !!\langle 0,2,0 \rangle!! and !! \langle 0,3,0 \rangle!! for the second. This gets us two additional sums, !!\langle 0,2,3 \rangle!!, which is !!\langle 0,1,2 \rangle!! in disguise, and !!\langle 0,3,2 \rangle!!, which is !!\langle 0,1,3 \rangle!! in disguise.
It might seem like it also gets us !!\langle 0,2,2 \rangle!! and !!\langle 0,3,3 \rangle!!, but these are just !!\langle 0,1,1 \rangle!! again, in disguise. Since there are three disguises for !!\langle 0,0,1 \rangle!! and three for !!\langle 0,1,0 \rangle!!, we have nine possible sums, but it turns out that the nine sums are only three different triples, each in three different disguises. So our nine sums get us three additional triples, and, including the two we started with, that makes five, which is exactly how many we need for the first card. The first card gets the stickers for triples !!\langle 0,0,1 \rangle, \langle 0,1,0 \rangle \langle 0,1,1 \rangle \langle 0,1,2 \rangle,!! and !!\langle 0,1,3 \rangle,!! which are apple, bicycle, carrot, dice, and elephant.
That was anticlimactic. Let's do one more. We don't have a card yet with ladybug and trombone. These are !!\langle 1,1,2 \rangle!! and !!\langle 1,3,2 \rangle!!, and we must add them together, and also the disguised versions:
$$\begin{array}{c|ccc} & \langle 1,1,2 \rangle & \langle 2,2,3 \rangle & \langle 3,3,1 \rangle \\ \hline \langle 1,3,2 \rangle & \langle 0,2,0 \rangle & \langle 3,1,1 \rangle & \langle 2,0,3 \rangle \\ \langle 2,1,3 \rangle & \langle 3,0,1 \rangle & \langle 0,3,0 \rangle & \langle 1,2,2 \rangle \\ \langle 3,2,1 \rangle & \langle 2,3,3 \rangle & \langle 1,0,2 \rangle & \langle 0,1,0 \rangle \\ \end{array}$$
These nine results do indeed pick out three triples in three disguises each, and it's easy to select the three of these that are canonical: they have a 1 in the leftmost nonzero position, so the three sums are !!\langle 0,1,0 \rangle,!! !!\langle 1,0,2 \rangle,!! and !!\langle 1,2,2 \rangle!!, which are bicycle, hat, and piano. So the one card that has a ladybug and a trombone also has a bicycle, a hat, and a piano, which should not seem obvious. Note that this card does have the required single overlap with the other card we constructed: both have bicycles.
Well, that was fun. Katara did hers with colored dots instead of stickers:
The ABCDE card is in the upper left; the bicycle-hat-ladybug-piano-trombone one is the second row from the bottom, second column from the left. The colors look bad in this picture; the light is too yellow and so all the blues and purples look black.
After I took this picture, we checked these cards and found a couple of calculation errors, which we corrected. A correct set of cards is:
$$ \begin{array}{ccc} \text{abcde} & \text{bhlpt} & \text{dgmpr} \\ \text{afghi} & \text{bimqu} & \text{dhjou} \\ \text{ajklm} & \text{cfkpu} & \text{diknt} \\ \text{anopq} & \text{cgjqt} & \text{efmot} \\ \text{arstu} & \text{chmns} & \text{eglnu} \\ \text{bfjnr} & \text{cilor} & \text{ehkqr} \\ \text{bgkos} & \text{dflqs} & \text{eijps} \\ \end{array} $$
Fun facts about finite projective planes:
This construction always turns a finite field of order !!n!! into a finite projective plane of order !!n!!.
A finite field of order !!n!! exists exactly when !!n!! is a prime power and then there is exactly one finite field. So this construction gives us finite projective planes of orders !!1,2,3,4,5,7,8,9,11,13,16!!, but not of orders !!6,10,12,14,15!!. Do finite projective planes of those latter orders exist?
- 6: No, proven by R.C. Bose in 1938
- 10: No, proven by Clement Lam in 1991 with a very large computer search
- 12, 15: Nobody knows.
- 14: No, by the Bruck-Ryser theorem (1949).
Is this method the only way to construct a finite projective plane? Yes, when !!n<9!!. But there are four non-isomorphic projective planes of order !!9!!, and this only constructs one of them.
What about for !!n≥11!!? Nobody knows.
[Other articles in category /math] permanent link
Sun, 06 May 2018Last month I regretted making only 22 posts but I promised:
April will be better; I'm on pace to break the previous volume record, and I've also been doing a good job of promoting better posts to the major leagues.
I blew it! I tied the previous volume record. But I also think I did do a decent job promoting the better posts. Usually I look over the previous month's posts and pick out two or three that seem to be of more interest than the others. Not this month! They are all shit, except the one ghostwritten by Anette Gordon-Reed. If this keeps up, I will stop doing these monthly roundup posts.
- Hotel classification jargon
- I'm missing !!Con this year
- Camptown
- Sigils in Perl and PILOT
- Birthday greetings from my stalker
- Yuca frita
- Intriguing trending hashtags
- On the preferred numbers of the One God
- Chitin
- History of the Unicode “byte order mark”; addendum
- 'Abd al-Karim
- One of everything in the universe
- Ruby improvement
- My hero Kurt Schwitters
- The hardest question ever asked on Math StackExchange
- Friday the 13th
- September 12 activities
- The National Day of Catalonia
- Melilla
- Beware…
- The joy of Dada [1] [2]
- FGSFDS
- Why we itch
- Why we have little hairs on our arms
- Minoxidil
- Ulcers
- Things English fails to distinguish
- Today I learned… [2] [3] [4] [5]
- Xiangtan
- Mealworm frass
- Free-range organically fed flies
- Not the worst job in the world
- Bug squeamishness
- Gordon-Reed on Andrew Johnson
- People suck
- Plagiarism, plagiarism, baked beans, and plagiarism
- I learned a new word!
- Phagocytization
- Lipogrammatic Math Stackexchange posts
- Hegel and the Seven Planets
- Philosophical duh
- Headline of the Month
- Why do people hate?
- Software sucks
- Comment of the day
[Other articles in category /meta/shitpost] permanent link
Wed, 02 May 2018
Addenda to recent articles 201804
Andrew Rodland and Adam Vartanian explained ramp metering. Here's M. Rodland's explanation:
ramp metering is the practice of installing signals on freeway onramps that only allow one car every few seconds, so that cars enter the freeway at evenly-spaced intervals instead of in bunches and don't cause as many problems merging.
He added that it was widely used in California. McCain is headquartered in California, and mentions frequently on their web site that their equipment conforms to Caltrans standards.
M. Vartanian and Richard Soderberg also suggested an explanation for why the traffic control system might also control sprinklers and pumps. M. Soderberg says:
DOTs in California and presumably elsewhere often have a need for erosion control on the steep inclines of earth surrounding their highway ramps. So any time you see a 45-degree incline covered in greenery, chances are it has a sprinkler system attached and carefully maintained by the DOT. Those same sprinklers are often within a few feet of the ramp's metering lights…
That makes perfect sense! I had been imagining fire sprinklers, and then I was puzzled: why would you need fire sprinklers at an intersection?
Several readers suggested explanations for why soldier fly larvae are more expensive than pork chops. I rejected several explanations:
Hogs are kept in poor and inhumane conditions (often true, but their accommodations must still be much more expensive than the flies’)
Hog farmers are exempted from paying for the negative externalities of their occupation such as environmental degradation and antibiotic resistance (often true, but the fly farmers cannot be paying that much to offset externalities)
Slaughterhouse waste and rotten fruit are more expensive than the corn and soy on which hogs are fed (I think slaughterhouse waste and waste fruit are available essentially free to anyone who wants to haul them away)
The drying process is difficult and expensive (but the listed price for undried maggots is twice as high)
But I find Marcel Fourné's suggestion much more plausible: the pork price is artificially depressed by enormous government subsidies.
I started looking into the numbers on this, and got completely sidetracked on something only peripherally related:
According to the USDA Census of Agriculture for 2012, in 2012 U.S. farms reported an inventory of 66 million pigs and hogs, and sales of 193 million pigs and hogs. (Table 20, page 22.)
When I first saw this, I thought I must be misunderstanding the numbers. I said to myself:
!!\frac{193}{66}\approx 3!!, so the inventory must be turning over three times a year. But that means that the average hog goes to market when it is four months old. That can't be right.
Of course it isn't right, it isn't even close, it's complete nonsense. I wrote up my mistake but did not publish it, and while I was doing that I forgot to finish working on the subsidy numbers.
James Kushner directed my attention to the MUTCD news feed and in particular this amusing item:
the FHWA issued Official Interpretation 4(09)-64 to clarify that the flash rate for traffic control signals and beacons is a single repetitive flash rate of approximately once per second, and that a combination of faster and slower flash rates that result in 50 to 60 flashes per minute is not compliant…
James writes:
I imagined a beacon that flashed once every ten seconds; after five such iterations, there was one iteration where the beacon would flash fifty times in a second. "But it flashes 55 times every minute, so, you know, it, uh, conforms to the standard..."
But the Official Interpretation also says
You asked whether the FHWA would be willing to consider experimentation with alternative flash rates for warning beacons. Any requests for experimentation would be evaluated on their merits and would be addressed separately from this official ruling.
so there is still hope for James’ scheme.
Two readers suggested musical jokes. Jordan Fultz asks:
Q: How does Lady Gaga like her steak?
A: Raw, raw, raw-raw-raw!(This is Bad Romance)
And betaveros asks:
Q. What kind of overalls does Mario wear?
A. Denim denim denim.(This is the Super Mario Bros. Underworld Theme)
I feel like we might be hitting the bottom of the barrel.
Thanks to all readers who wrote to me, and also to all readers who did not write to me.
[Other articles in category /addenda] permanent link
Tue, 01 May 2018
What's in those mysterious cabinets?
Last Monday some folks were working on this thing on Walnut Street. I didn't remember having seen the inside of one before, so I took some pictures of it to look at later.
Thanks to the Wonders of the Internet, it didn't take long to figure out what it is for. It is a controller for the traffic lights at the intersection.
In particular, the top module in the right-hand picture is a Model 170 ATC HC11 Controller manufactured by McCain Inc, a thirty-year old manufacturer of traffic control devices. The controller runs software developed and supported by McCain, and the cabinet is also made by McCain.
The descriptions of the controllers are written in a dense traffic control jargon that I find fascinating but opaque. For example, the 170 controller's product description reads:
The McCain 170E, 170E HC11, and 170 ATC HC11 controllers’ primary design function is to operate eight-phase dual ring intersections. Based on the software control package utilized, the 170’s control applications can expand to include: ramp metering, variable message signs, sprinklers, pumps, and changeable lane control.
I think I understand what variable message signs are, and I can guess at changeable lane control, but what are the sprinklers and pumps for? What is ramp metering?
[ Addendum 20180502: readers explain ]
The eight-phase dual ring intersection, which I had never heard of before, is an important topic in the traffic control world. I gather that it is a four-way intersection with a four-way traffic light that also has a left-turn-only green arrow portion. The eight “phases” refer to different traffic paths through the intersections that must be separately controlled: even numbers for the four paths through the intersection, and odd numbers 1,3,5,7 for the left-turn-only paths that do not pass through. Some phases conflict; for example phase 5 (left-turning in some direction, say from south to east), conflicts with phase 6 (through-passing heading in the opposite direction) but not with phase 1 (left-turning from north to west).

There's plenty of detailed information about this available. For example, the U.S. Federal Highway Administration publishes their Traffic Signal Timing Manual. (Published in 2008, it has since been superseded.) Unfortunately, this seems to be too advanced for me! Section 4.2.1 (“Definitions and Terminology”) is the first place in the document that mentions the dual-ring layout, and it does so without explanation — apparently this is so elementary that anyone reading the Traffic Signal Timing Manual will already be familiar with it:
Over the years, the description of the “individual movements” of the dual-ring 8-movement controller as “phases” has blurred into common communicated terminology of “movement number” being synonymous as “phase number”.
But these helpful notes explain in more detail: a “ring” is “a sequence of phases that are not compatible and that must time sequentially”.
Then we measure the demand for each phase, and there is an interesting and complex design problem: how long should each phase last to optimize traffic flow through the intersection for safety and efficiency? See chapter 3a for more details of how this is done.
I love when I discover there is an entire technical domain that I never even suspected existed. If you like this kind of thing, you may enjoy geeking out over the Manual of Uniform Traffic Control Devices, which explains what traffic signs should look like and what each one means. Have you ever noticed that the green guide signs on the highway have up-pointing and down-pointing arrows that are totally different shapes?
That's because they have different meanings: the up-pointing arrows mean “go this way” and the down-pointing arrows mean “use this lane”. The MUTCD says what the arrows should look like, how big they should be, and when each one should be used.
The MUTCD is the source of one of my favorite quotations:
Regulatory and warning signs should be used conservatively because these signs, if used to excess, tend to lose their effectiveness.
Words to live by! Programmers in particular should keep this in mind when designing error messages. You could spend your life studying this 864-page manual, and I think some people do.
Related geekery: Geometric highway design: how sharply can the Interstate curve and still be safe, and how much do the curves need to be banked? How do you design an interchange between two major highways? How about a highway exit?
Here's a highway off-ramp, exit 346A on Pennsylvania I-76 West:
Did you know that the long pointy triangle thing is called a “gore”?
What happens if you can't make up your mind whether to stay on the highway or take the exit, you drive over the gore, and then smack into the thing beyond it where the road divides? Well, you might survive, because there is a thing there that is designed to crush when you hit it. It might be a QuadGuard Elite Crash Cushion System, manufactured by Energy Absorption Systems, Inc..
It's such a big world out there, so much to know.
[Other articles in category /tech] permanent link
Sun, 29 Apr 2018In August 2011, on a particular famous discussion forum (brought up on this blog again and again) an individual A, notorious for such acts, posts a quasi-philosophical inquiry, incurring unpopularity, antagonism, and many bad marks, although also a surprising quantity of rational discussion, including a thoughtful solution or two.
Many months forward, a distinct party B puts up a substantial bounty on this inquiry, saying:
I would like a complete answer to this question which does not use the letter "e" at any point.
(My apology for any anguish you may go through at this point in my story on account of this quotation and its obvious and blatant faults. My wrongdoing was involuntary, but I had no way to avoid it and still maintain full accuracy.)
By and by, a valiant third individual constructs a brilliant disquisition satisfying this surprising condition and thus obtains B's award.
Now, this month, in our group's accompanying policy board, a fourth collaborator, a guy (or gal, for all I know) I shall call D, and who I think may lack a minimal inclination for fun, finds fault with A's original post and particularly with C's bounty, and complains as follows:
Should we discourage bounties that encourage “clever” but unclear answers?
(Again, I must ask you for absolution. This is a word-for-word quotation.)
A thorough dismissal of OP's complaint, from a fifth author, adds a fully satisfactory finish to our affair.
[Other articles in category /lang] permanent link
Fri, 20 Apr 2018Here is a list of March's shitposts. I don't recall what my excuse was for there being only 22, but in my defense, I will add that they were almost all terrible. There was one decent math post I maybe should have promoted.
(And also Nancy and Squid, which was awesome, and also 100% Grade A shitpost. I thought when I posted it a crowd of people would burst into the room and carry me off on their shoulders. Instead, nobody seems to have noticed.)
April will be better; I'm on pace to break the previous volume record, and I've also been doing a good job of promoting better posts to the major leagues.
- Today I learned…
- Soot
- Seedless fruit
- I'm so old…
- Whether to get donations via Patreon
- Nancy and Squid
- Today I learned…
- Poor phrasing of the day…
- W and V
- Executive departments
- Stuff my brain came up with this morning
- Browning
- The opposite of vegan soup
- Cantonese style non-vegan soup
- Israeli chicken sandwich
- Names that begin with an 'X', and don't
- Ear care tips
- Icelandic butt
- Peddler's Pantry
- Chaise LONGUE
- Hotel ritual
- Things English fails to distinguish
[Other articles in category /meta/shitpost] permanent link
Thu, 19 Apr 2018
Soldier fly protein: why so expensive?

There have been recurring news stories about the use of dried maggots as protein supplement in animal feed. For example Insects could feed the animals of tomorrow’s meat industry (maggots fed on slaughterhouse waste, particularly blood) or Insect farms gear up to feed soaring global protein demand (maggots fed on rotten fruit). Then they dry the larvae and either use them whole or grind them into meal. In particular the fly meal can be used as a replacement for fish meal, which is ground dried fish that is used as feed for fish in fish farms. (Yep, we grind up fish we don't like, to feed to other, better fish.)
I was referred to that second article by Metafilter and The Google, in its infinite wisdom, decided to show me an advertisement for dried fly larvae. The ad was for NaturesPeck, which sells bagged fly larvae and fly meal for use as poultry feed or wild bird feed. They have a special “value pack” that contains 16 pounds of dried larvae for $88. That is $5.50 a pound! Holy cow, WTF? How can that even be possible when my local grocery store is selling boneless center cut pork chops for $2.50 per pound?
Okay, I thought maybe NaturesPeck was some sort of boutique operation, charging a high markup for small quantities, maybe they claim to have sustainably-harvested fly meal from free-range organically-fed flies or something. So I went looking for an industrial wholesaler of bulk fly meal and quickly found Haocheng Mealworms Inc. in Xiangtan, China. This is definitely what I was looking for; they will be glad to sell you a standard 40-foot shipping container full of dried maggots or other larvae. The quoted price for dried mealworm larvae is $8400 per metric tonne, plus shipping ($170–200 per tonne).
Prices, converted to U.S. dollars per pound, are as follows:
| Dried soldier fly maggots | $2.49 |
| Powdered soldier fly maggots | 2.81 |
| Dried mealworms | 3.81 |
| Powdered mealworms | 4.22 |
| Live mealworms | 5.67 |
| Canned fresh mealworms | 7.08 |
| Dried superworms | 4.76 |
| Live superworms | 8.30 |
| Canned fresh superworms | 7.71 |
So it wasn't just that NaturesPeck was marking them up. Even the least expensive product costs as much as retail pork chops.
I don't get it. There must be some important aspect of this that I am missing, because a market failure of this magnitude is impossible.
BTW, Haocheng recommends that:
As a source of high protein additive, put [mealworms] into the bread, flour, instant noodle, pastry, biscuit, candy, condiment, and direct into the dishes on the dining table like the foodstuff, and process into the health care nourishment to improve the human body immunity ability.
Not at those prices, buddy.
[ Addendum 20180502: Some possible explanations ]
[Other articles in category /food] permanent link
Wed, 18 Apr 2018
Lower mathematics solves an easy problem
[ Warning: this article is mathematically uninteresting. ]
I woke up in the middle of the night last night and while I was waiting to go back to sleep, I browsed math Stack Exchange. At four in the morning I am not at my best, but sometimes I can learn something and sometimes I can even contribute.
The question that grabbed my attention this time was Arithmetic sequence where every term is prime?. OP wants to know if the arithmetic sequence $$d\mapsto a+d b$$ contains composite elements for every fixed positive integers !!a,b!!.
Now of course the answer is yes, or the counterexample would give us a quick and simple method for constructing prime numbers, and finding such has been an open problem for thousands of years. OP was certainly aware of this, but had not been able to find a simple proof. Their searching was confounded by more advanced matters relating to the Green-Tao theorem and such like, which, being more interesting, are much more widely discussed.
There are a couple of remarkable things about the answers that were given. First, even though the problem is easy, the first two answers posted were actually wrong, and another (quickly deleted) was so complicated that I couldn't tell if it was right or not.
One user immediately commented:
What happens if !!d=a!!?
which is very much to the point; when !!d=a!! then the element of the sequence is !!a+ab!! which is necessarily composite…
…unless !!a=1!!. So the comment does not quite take care of the whole question. A second user posted an answer with this same omission, and had to correct it later.
I might not have picked up on this case either, during the daytime. But at 4 AM I was not immediately certain that !!a+ab!! was composite and I had to think about it. I factored it to get !!a(1+b)!! and then I saw that if !!a=1!! or !!1+b=1!! then we lose. (!!1+b=1!! is impossible. !!a+ab!! might of course be composite even if !!a=1!!, but further argumentation is needed.)
So I did pick up on this, and gave a complete answer, of which the important part is:
Just take !!d=kb+k+a!! for any !!k!! whatever. Then the element is $$kb^2+(k+a)b+a = (kb+a)(b+a)$$ which is composite.
Okay, fine. But OP asked how I came up with that and if it was pure “insight”, so I thought I'd try to reconstruct how I got there at 4 AM. The problem is simple enough that I think I can remember most of how I got to the answer.
As I've mentioned before, I am not a pure insight kind of person. While better mathematicians are flitting swiftly from peak to peak, I plod along in the dark and gloomy valleys. I did not get !!d=kb+k+a!! in a brilliant flash of inspiration.
Instead, my thought process, as well as I can remember it, went like this:
“That doesn't work when !!a=1!!. But there must be composite numbers in sequences of the form !!d b+1!!. I wonder what they look like?”
“I guess I'll try an example. How about !!4d+1!!?”
“Hmm, it starts at 5, 5 is composite… No it isn't.”
“But it's increasing by 4 each time so it must hit each mod-5 residue class in some order.”
I should cut in at this point to add that my thinking was nowhere near this articulate or even verbal. The thing about the sequence hitting all the residue classes was more like a feeling in my body, like when I am recognizing a familiar place. When !!a!! and !!b!! are relatively prime, that means that when you are taking steps of size !!b!!, you hit all the !!a!!'s and don't skip any; that's what relatively prime is all about.
So maybe that counts as “insight”? Or “intuition about relative primality”? I think that description makes it sound much more impressive than it really is. I do not want a lot of credit for this. Maybe a better way to describe it is that I had been in this familiar place many times before, and I recognized it again.
Anyway I continued something like this:
- “If it hits every residue class over and over in sequence it must hit residue class !!0!! infinitely often. How does that go? It hits !!5!!, so it hits !!5+4·5 = 25!! also.”
That was good enough for me; I did not even consider the next hit, !!45!!, perhaps because that number was too big for me to calculate at that moment.
I didn't use the phrase “residue class” either. That's just my verbal translation of my 4AM nonverbal thinking. At the time it was more like: there are some good things to hit and some bad ones, and the good ones are evenly spaced out, so if we hit each position in the even spacing-ness we must periodically hit some of the good things.
- “Okay, then the first element of !!1+d b!! is !!1+b!!, and then every !!1+b!! steps after that it hits another multiple of !!1+b!!, so we want every !!1+b!! elements, so take !!d = 1 + k(1+b)!!.”
Then I posted the answer, saying that when !!a=1!! you take !!d=1+k(1+b)!! and the sequence element is !!1+b+kb+kb^2 = (1+b)(1+kb)!!.
Then I realized that I had the same feeling in my body even when !!a≠1!!, because it only depended on the way the residue classes repeated, and changing !!a!! doesn't affect that, it just slides everything left or right by a constant amount. So I went back to edit the !!1+k(1+b)!! to be !!a+k(1+b)!! instead.
I have no particular conclusion to draw about this.
[Other articles in category /math] permanent link
Mon, 16 Apr 2018
A familiar set with an unexpected order type
I dreamed this one up in high school and I recommend it as an exercise for kids at an appropriate level.
Consider the set of all Roman numerals
$${ \text{I}, \text{II}, \text{III}, \text{IV}, \text{V}, \ldots, \text{XIII}, \text{XIV}, \text{XV}, \text{XVI}, \ldots, \\ \text{XXXVIII}, \text{XXXIX}, \text{XL}, \text{XLI}, \ldots, \text{XLIX}, \text{L},\ldots,\\ \text{C}, \ldots , \text{D}, \ldots, \text{M}, \ldots, \text{MM}, \ldots, \text{MMM}, \ldots, \text{MMMM}, \ldots, \text{MMMMM}, \ldots }$$
where we allow an arbitrarily large number of M's on the front, so that every number has a unique representation. For example the number 10,067 is represented by !!\text{MMMMMMMMMMLXVII}!!.
Now sort the list into alphabetical order.
It is easy to show that it begins with !!\text{C}, \text{CC}, \text{CCC}, \text{CCCI}, \ldots!! and ends !!\text{XXXVII}, \text{XXXVIII}!!. But it's still an infinite list! Instead of being infinite at one end or the other, or even both, like most infinite lists, it's infinite in the middle.
Of course once you have the idea it's easy to think of more examples (!!\left\{ \frac1n\mid n\in\Bbb Z, n\ne 0\right\}!! for instance) but I hadn't seen anything like this before and I was quite pleased.
[Other articles in category /math] permanent link
Sun, 15 Apr 2018
On the smallest natural number
The earliest known mathematics book printed in Europe is an untitled arithmetic text published in Treviso in 1478, Originally written in Venetian dialect.
The Treviso Arithmetic states unequivocally:
Number is a multitude brought together or assembled from several units, and always from two at least, as in the case of 2, which is the first and the smallest number.
And a little later:
Of [the digits] the first figure, 1, is not called a number but the source of number.
(English translations are from David Eugene Smith, A Source Book in Mathematics (1959). A complete translation appears in Frank J. Swetz, Capitalism and Arithmetic The New Math of the Fifteenth Century (1987).)
By the way, today is the 311th birthday of Leonhard Euler.
[Other articles in category /math] permanent link
Sat, 14 Apr 2018
Colored blobs on electric wires
The high-voltage power lines run along the New Jersey Turnpike for a long way, and there is this one short stretch of road where the wires have red, white, and yellow blobs on them. Google's Street View shot shows them quite clearly.
A thousand feet or so farther down the road, no more blobs.
I did Internet searches to find out what the blobs were about, and everyone seemed to agree that they were to make the wires more visible to low-flying aircraft. Which seemed reasonable, but puzzling, because as far as I knew there was no airport in the vicinity. And anyway, why blobs only on that one short stretch of wire?
Last week I drove Katara up to New York and when I saw the blobs coming I asked her to photograph them and email me the pictures. She did, and as I hoped, there in the EXIF data in the images was the exact location at which the pictures had been taken: !!(40.2106, -74.57726675)!!. I handed the coordinates to Google and it gave me the answer to my question:
The wires with blobs are exactly in line with the runway of nearby Trenton-Robbinsville Airport. Mystery solved!
(It is not surprising that I didn't guess this. I had no idea there was a nearby airport. Trenton itself is about ten miles west of there, and its main airport, Trenton-Mercer Airport, is another five miles beyond that.)
I have been wondering for years why those blobs were in that exact place, and I am really glad to have it cleared up. Thank you, Google!
Dear vision-impaired readers: I wanted to add a description of the
view in the iframed Google Street View picture above. Iframes do not
support an alt attribute, and MDN says that longdesc is “not
helpful for non-visual
browsers”.
I was not sure what to do.
In the future, is there a better place to put a description of an iframed image? Thanks.
[Other articles in category /tech] permanent link
Fri, 13 Apr 2018As an undergraduate I wondered and wondered about how manifolds and things are classified in algebraic topology, but I couldn't find any way into the subject. All the presentations I found were too abstract and I never came out of it with any concrete idea of how you would actually calculate any specific fundamental groups. I knew that the fundamental group of the circle was !!\Bbb Z!! and the group of the torus was !!\Bbb Z^2!! and I understood basically why, but I didn't know how you would figure this out without geometric intuition.
This was fixed for me in the very last undergrad math class I took, at Columbia University with Johan Tysk. That was the lowest point of my adult life, but the algebraic topology was the one bright spot in it. I don't know what might have happened to me if I hadn't had that class to sustain my spirit. And I learned how to calculate homotopy groups!
(We used Professor Tysk's course notes, supplemented by William Massey's introduction to algebraic topology. I didn't buy a copy of Massey and I haven't read it all, but I think I can recommend it for this purpose. The parts I have read seemed clear and direct.)
Anyway there things stood for a long time. Over the next few decades I made a couple of superficial attempts to find out about homology groups, but again the presentations were too abstract. I had been told that the homology approach was preferred to the homotopy approach because the groups were easier to actually calculate. But none of the sources I found seemed to tell me how to actually calculate anything concrete.
Then a few days ago I was in the coffee shop working on a geometry problem involving an icosi-dodecahedron, and the woman next to me asked me what I was doing. Usually when someone asks me this in a coffee shop, they do not want to hear the answer, and I do not want to give it, because if I do their eyes will glaze over and then they will make some comment that I have heard before and do not want to hear again. But it transpired that this woman was a math postdoc at Penn, and an algebraic topologist, so I could launch into an explanation of what I was doing, comfortable in the knowledge that if I said something she didn't understand she would just stop me and ask a question. Yay, fun!
Her research is in “persistent homology”, which I had never heard of. So I looked that up and didn't get very far, also because I still didn't know anything about homology. (Also, as she says, the Wikipedia article is kinda crappy.) But I ran into her again a couple of days later and she explained the persistent part, and I know enough about what homology is that the explanation made sense.
Her research involves actually calculating actual homology groups of actual manifolds on an actual computer, so I was inspired to take another crack at understanding homology groups. I did a couple of web searches and when I searched for “betti number tutorial” I hit paydirt: these notes titled “persistent homology tutorial” by Xiaojin Zhu of the University of Wisconsin at Madison. They're only 37 slides long, and I could skip the first 15. Then slide 23 gives the magic key. Okay! I have not yet calculated any actual homology groups, so this post might be premature, but I expect I'll finish the slides in a couple of days and try my hand at the calculations and be more or less successful. And the instructions seem clear enough that I can imagine implementing a computer algorithm to calculate the homology groups for a big ugly complex, as this math postdoc does.
I had heard before that the advantage of the homology approach over the homotopy approach is that the homologies are easier to actually calculate with, and now I see why. I could have programmed a computer to do homotopy group calculations, but the output would in general have been some quotient of a free group given by a group presentation, and this is basically useless as far as further computation goes. For example the question of whether two differently-presented groups are isomorphic is undecidable, and I think similar sorts of questions, such as whether the group is abelian, or whether it is infinite, are similarly undecidable.
Sometimes you get a nice group, but usually you don't. For example the homotopy group of the Klein bottle is the quotient of the free group on two generators under the smallest equivalence relation in which !!aba = b!!; that is:
$$\langle a, b\mid abab^{-1}\rangle$$
which is not anything I have seen in any other context. Even the question of whether two given group elements are equal is in general undecidable. So you get an answer, but then you can't actually do anything with it once you have it. (“You're in a balloon!”) The homology approach throws away a lot of information, enough to render the results comprehensible, but it also leaves enough to do something with.
[Other articles in category /math] permanent link
Tue, 10 Apr 2018
Inconceivable things and non-contingent facts
Philosophy makes a distinguish between necessary and contingent facts, but I'm not exactly sure what it is. I think they would say that the election of Al Gore in 2000 is contingent because it's easy to imagine a universe in which it went the other way and the other guy won. But that seems to depend on our powers of imagination, which doesn't seem very rigorous. Is the mass of the electron necessary or contingent? What about the fine-structure constant?
What facts are necessary? Often in this context people fall back on mathematical truths, for example !!1+1=2!!, which does seem hard to assail. But I recently thought of something even farther down the scale, which seems to me even harder to argue.
Mathematics deals with many sorts of objects which are more or less like the ordinary numbers. Some are more complicated, and ordinary numbers are special cases, for example functions and matrices. Some are simpler, and are special cases themselves. Mathematicians can and do define !!2!! in many different ways. There are mathematical systems with !!1!! and !!+!! in which there is no !!2!!, and instead of !!1+1=2!! we have !!1+1=0!!. Well, not quite; there is !!2!!, but !!2=0!!. So one can say that !!1+1=2!! still, but the !!2!! is not very much like the !!2!! that we usually mean when we say !!1+1=2!!. Anyway certainly there is such a system, and I can certainly conceive of it, so there might be a philosophical argument that could be made that !!1+1=2!! is a contingent fact about how numbers happen to work in the universe in which we happen to find ourselves: we are not living in a universe where numbers form a field of characteristic 2.
But here's a fact that I think is unassailably necessary: rubies are red. Why? By definition! A ruby is a kind of gemstone, a type of aluminum oxide called a corundum, that has a deep red color. There are non-red corundums, but they are sapphires, not rubies, because a ruby is a red corundum. There is no such thing as a blue or a green ruby; a blue or green ruby is not a ruby at all, but a sapphire.
How about over in Narnia, where rubies are blue? Well, maybe the Narnians people call hats “avocadoes”, but whether those things are hats or avocadoes depends not on what the Narnians call them but on their properties. If those things are made of felt and the Narnians wear them on their heads, they are hats, regardless of what the Narnians call them; they are avocadoes only if they are globular and can be eaten on toast. Narnians might put actual avocadoes on their heads and then there might be an argument that these things were hats, but if the avocado is a hat it is only because it is customarily worn on the head.
And so too the Narnians can call !!2!! an avocado and say that !!1+1=\text{avocado}!! but that doesn't mean that !!1+1!! is an avocado, even in Narnia. Maybe the Narnians call avocadoes “rubies”, but they're still avocadoes, not rubies. And maybe the Narnians call blue corundums “rubies”, but they're still sapphires, not rubies, because rubies are red.
So I think it might be conceivable that !!1+1=2!! is contingent, and it's certainly easy to conceive of a universe with no rubies at all, but I can't conceive of any way that a ruby could be other than red.
[Other articles in category /misc/philosophy] permanent link
Wed, 04 Apr 2018
Genealogy of the Saudi royal family
[ Note: None of this is a joke, nothing here is intended humorously, and certainly none of it should be taken as mockery or disparagement. The naming conventions of Saudi royalty are not for me to judge or criticize, and if they cause problems for me, the problems are my own. It is, however, a serious lament. ]
The following innocuous claim appears in Wikipedia's article on Abdullah bin Abdul-Rahman:
He was the seventh son of the Emir of the Second Saudi State, Abdul Rahman bin Faisal.
Yesterday I tried to verify this claim and I was not able to do it.
Somewhere there must be a complete and authoritative pedigree of the entire Saudi royal family, but I could not find it online, perhaps because it is very big. There is a Saudi royal family official web site, and when I found that it does have a page about the family tree, I rejoiced, thinking my search was over. But the tree only lists the descendants of King Abdulaziz Ibn Saud, founder of the modern Saudi state. Abdullah was his half-brother and does not appear there.
Well, no problem, just Google the name, right? Ha!
Problem 1: These princes all have at least twenty kids each. No, seriously. The Wikipedia article on Ibn Saud himself lists twenty-one wives and then gives up, ending with an exhausted “Possibly other wives”. There is a separate article on his descendants that lists 72 children of various sexes, and the following section on grandchildren begins:
Due to the Islamic traditions of polygyny and easy divorce (on the male side), King Abdul Aziz [Ibn Saud] has approximately a thousand grandchildren.
Problem 2: They reuse many of the names. Because of course they do; if wife #12 wants to name her first son the same as the sixth son of wife #2, why not? They don't live in the same house. So among the children of Ibn Saud there are two Abdullahs (“servant of God”), two Badrs (“full moon”), two Fahds (“leopard”), two each of Majid (“majestic”), Mishari (I dunno), Talal (dunno), and Turki (“handsome”). There are three sons named Khalid (“eternal”). There is a Sa'ad and a Saad, which I think are the exact same name (“success”) as spelled by two different Wikipedia editors.
And then they reuse the names intergenerationally. Among Ibn Saud's numerous patrilineal grandsons there are at least six more Fahds, the sons respectively of Mohammed, Badr (the second one), Sultan, Turki (also the second one), Muqrin, and Salman. Abdulaziz Ibn Saud has a grandson also named Abdulaziz, whose name is therefore Abdulaziz bin Talal bin Abdulaziz Al Saud. (The “bin” means “son of”; the feminine form is “bint”.) It appears that the House of Saud does not name sons after their fathers, for which I am grateful.
Ibn Saud's father was Abdul Rahman (this is the Abdul Rahman of Abdullah bin Abdul-Rahman, who is the subject of this article. Remember him?) One of Ibn Saud's sons is also Abdul Rahman, I think probably the first one to be born after the death of his grandfather, and at least two of his patrilineal grandsons are also.
Problem 3: Romanization of Arabic names is done very inconsistently. I mentioned “Saad” and “Sa'ad” before. I find the name Abdul Rahman spelled variously “Abdul Rahman”, “Abdulrahman”, “Abdul-Rahman”, and “Abd al-Rahman”. This makes text searches difficult and unreliable. (The name, by the way, means "Servant of the gracious one”, referring to God.)
Problem 4: None of these people has a surname. Instead they are all patronymics. Ibn Saud has six grandsons named Fahd; how do you tell them apart? No problem, their fathers all have different names, so they are Fahd bin Mohammed, Fahd bin Badr, Fahd bin Sultan, Fahd bin Turki, Fahd bin Muqrin, and Fahd bin Salman. But again this confuses text searches terribly.
You can search for “Abdullah bin Abdul-Rahman” but many of the results will be about his descendants Fahd bin Abdullah bin Abdul Rahman, Fahd bin Khalid bin Abdullah bin Abdul Rahman, Fahd bin Muhammad bin Abdullah bin Abdul Rahman, Abdullah bin Bandar bin Abdullah bin Abdul Rahman, Faisal bin Abdullah bin Abdul Rahman, Faisal bin Abdul Rahman bin Abdullah bin Abdul Rahman, etc.
In combination with the reuse of the same few names, the result is even more confusing. There is Bandar bin Khalid, and Khalid bin Bandar; Fahad bin Khalid and Khalid bin Fahd.
There is Mohammed al Saud (Mohammed of (the house of) Saud) and Mohammed bin Saud (Mohammed the son of Saud).
There are grandsons named Saad bin Faisal, Faisal bin Bandar, Bandar bin Sultan, Sultan bin Fahd, Fahd bin Turki, Turki bin Talal, Talal bin Mansour, Mansour bin Mutaib, Mutaib bin Abdullah, and Abdullah bin Saad. I swear I am not making this up.
Perhaps Abdullah was the seventh son of Abdul Rahman.
Perhaps not.
I surrender.
Addendum 20250211
Today I became aware of a comparably confusing European tradition. Since the 13th century, every male in the House of Reuss has been named “Heinrich”.
[Other articles in category /lang] permanent link
Sat, 24 Mar 2018Today I went to see The Death of Stalin. If someone is going to go to the trouble of making a comedy about the death of Stalin, that seems like a worthy attempt, and I will do them the courtesy of going to watch it. At least I can be sure it will not be the same old shit.
I was interested to see if it was possible to make a comedy about the death of Stalin, and if so, would it would be funny? I got my answer: no, you can't, and it isn't.
It was worth a shot, I guess, and I give the writers and director top marks for audacity. The cast was great. The acting was great. I thought Jason Isaacs as Marshal Zhukov stole every scene he was in. But yeah, it's hard to be funny when Lavrenty Beria is raping a bunch of fourteen-year-old girls, and the movie didn't work for me.
There's a long and solid tradition of comedy about completely loathsome people, but I think most of it follows pretty much the same pattern: terrible stuff happens to the loathsome people and it is funny because the people are so loathsome and because they so richly deserve all the terrible stuff that happens to them. It can be fun to see a horrible person sabotage themselves with their own horribleness.
(Examples off the top of my head: Fawlty Towers. Otto in A Fish Called Wanda. Jack Vance's Cugel books. Married With Children. I think this might have been the main attraction of Seinfeld, although if it is I didn't get the joke until after the series was over.)
Unfortunately this movie, being historical fiction, has to stick to the history: Malenkov gets swept under a rug. Khrushchev seizes power. Molotov keeps on doing what he does. Beria is murdered, but there is nothing funny about it, and I found it unsatisfying. Indeed, all of these horrible people are suffering because of the horrible world they have created for themselves, but I found no fun in it because there were another 170 million people suffering much worse from the same horrible crap. The coyote's look of dismay as he falls of the cliff loses all its savor if he has the road runner's broken body in his jaws when it happens.
So, eh. Sorry, Iannucci. I wanted to like your movie.
[ Odd trivium: I started writing articles in the “movies” section of this blog back in 2007, but this is the first one that has seen publication. ]
[Other articles in category /movie] permanent link
Addenda to recent articles 201803
It's been a while since we had one of these. But gosh, people have sent me quite a lot of really interesting mail lately.
I related my childhood disappointment at the limited number of cool coordinate systems. Norman Yarvin directed me to prolate spheroidal coordinates which are themselves a three-dimensional version of elliptic coordinates which are a system of exactly the sort I escribed in the article, this time parametrized by a family of ellipses and a family of hyperbolas, all of which share the same two foci; this article links in turn to parabolic coordinates in which the two families are curves are up-facing and down-facing parabolas that all share a focus. (Hmm, this seems like a special case of the ellipses, where one focus goes to infinity.)
Walt Mankowski also referred me to the Smith chart, shown at right, which is definitely relevant. It is a sort of nomogram, and parametrizes certain points by their position on circles from two families
$$\begin{align} F_1(c): && (x- c)^2 & + y^2 & =c^2 \\ F_2(c): && x^2 & + (y- c)^2 & =c^2 \\ \end{align} $$
Electrical engineers use this for some sort of electrical engineer calculation. They use the letter !!j!! instead of !!i!! for the imaginary unit because they had already used !!i!! to stand for electrical current, which is totally reasonable because “electrical current” does after all start with the letter !!i!!. (In French! The French word is courant. Now do you understand? Stop asking questions!)
Regarding what part of the body Skaði was looking at when the Norse text says fótr, which is probably something like the foot, Alexander Gurney and Brent Yorgey reminded me that Biblical Hebrew often uses the foot as a euphemism for the genitals. One example that comes immediately to mind is important in the book of Ruth:
And when Boaz had eaten and drunk, and his heart was merry, he went to lie down at the end of the heap of corn: and she came softly, and uncovered his feet, and laid her down. (Ruth 3:7)
M. Gurney suggested Isaiah 6:2. (“Above him were seraphim, each with six wings: With two wings they covered their faces, with two they covered their feet, and with two they were flying.”) I think Ezekiel 16:25 is also of this type.
I mentioned to Brent that I don't think Skaði was looking at the Æsir's genitals, because it wouldn't fit the tone of the story.
Alexander Gurney sent me a lot of other interesting material. I had translated the Old Icelandic hreðjar as “scrotum”, following Zoëga. But M. Gurney pointed out that the modern Icelandic for “radish” is hreðka. Coincidence? Or was hreðjar a euphemism even then? Zoëga doesn't mention it, but he doesn't say what word was used for “radish”, so I don't know.
He also pointed me to Parts of the body in older Germanic and Scandinavian by Torild Washington Arnoldson. As in English, there are many words for the scrotum and testicles; some related to bags, some to balls, etc. Arnoldson does mention hreðjar in the section about words that are bag-derived but doesn't say why. Still if Arnoldson is right it is not about radishes.
I should add that the Skáldskaparmál itself has a section about parts of the body listing suitable words and phrases for use by skálds:
Hönd, fótr.
… Á fæti heitir lær, kné, kálfi, bein, leggr, rist, jarki, il, tá. …
(… The parts of the legs are called thigh, knee, calf, lower leg, upper leg, instep, arch, sole, toe … [ Brodeur ])
I think Brodeur's phrase “of the legs” here is an interpolation. Then he glosses lær as “thigh”, kné as “knee”, kálfi as “calf”, and so on. This passage is what I was thinking of when I said
Many of the words seem to match, which is sometimes helpful but also can be misleading, because many don't.
I could disappear down this rabbit hole for a long time.
Regarding mental estimation of the number of primes less than 1,000, which the Prime Number Theorem says is approximately !!\frac{1000}{\ln 1000}!!, several people pointed out that if I had memorized !!\ln 10\approx 2.3!! then I would have had that there are around !!\frac{1000}{3·2.3}!! primes under 1,000.
Now it happens that I do have memorized !!\ln 10\approx 2.3!! and although I didn't happen come up with it while driving that day, I did come up with it a couple of days later in the parking lot of a Wawa where I stopped to get coffee before my piano lesson. The next step, if you are in a parking lot, is to approximate the division as !!\frac{1000}{6.9} \approx \frac{1000}7 = 142.857\ldots!! (because you have !!\frac17=0.\overline{142857}!! memorized, don't you?) and that gives you an estimate of around 145 primes.
Which, perhaps surprisingly, is worse than what I did the first time around; it is 14% too low instead of 8% too high. (The right answer is 168 and my original estimate was 182.)
The explanation is that for small !!n!!, the approximation !!\pi(N)\sim\frac{N}{\ln N}!! is not actually very good, and I think the interpolation I did, using actual low-value counts, takes better account of the low-value error.
[Other articles in category /addenda] permanent link
Fri, 23 Mar 2018Here is a list of February's shitposts, later than usual, but who cares? Boldface indicates the articles that may (may) be of more general interest (ha). I think that I did a better job of noticing when a post wasn't shitty enough and promoting it, pre-publication, to this blog, so you will have seen all the better stuff already.
I'm pleased, volume over January is slightly up, and quality is definitely down, especially in the last half of the month. But I posted on only 21 of 28 days; I'll have to work on that.
- Gitignore patterns
- Grook
- English orthography
- Uncountable tilings of the line
- Cork flakes
- Non compote mentis
- Oaken tokens
- The sinister bag strap
- Puzzle Zapper Blog
- CNS
- Andy Lee's higgledy-piggledy
- The fickle gods of math Stackexchange
- Woo Philadelphia Eagles 2018 Super Bowl champs!!1!
- The remainder of a square root
- Ear piercing
- Eagles-related property damage
- Mathematicians with the same name
- Only
- My current favorite puncutation mark
- Qihui
- Qen
- Best practices for cache management
- “Obvious” in mathematics
- SVG images rendered at different scales
- Tom Waits
- Weighted reservoir sampling
- More reservoir sampling [1] [2] [3]
- People who are only photographed in black and white
- Reservoids
- Dumbest math.se question this week
- The duties of John von Neumann's assistant
- Calculate the Taylor expansion… OR DIE
- I'm so old… [4] [5]
- Pizza delivery failure
- Scorpion and Felix
- Google flubs a spelling correction
- Thus!
- Public service announcement about spamming
- The Platonic thing
- A peculiar genre of joke
- Michael Jordan and Charles Barkley
- Historical followup
- Another joke in this peculiar genre
- Calculus
- Imbricated
- French is verbose
- Stuff I wanted to say but didn't
- Today I learned…
[Other articles in category /meta/shitpost] permanent link
Thu, 22 Mar 2018
Does Skaði choose the husband with the best butt?
(Warning: I do not know anything about Old Norse, so everything I say about it should be understood as ill-informed speculation. I welcome corrections.)
In one of my favorite episodes from Norse mythology, the Æsir owe a payment to the Jötunn Skaði in compensation for killing her father. But they know she is very wealthy, and offer her an alternative compensation: one of their men in marriage.
Skaði wants to marry Baldr, because he is extremely handsome. But Baldr is already married. Odin proposes a compromise: the Æsir will line up behind a short curtain, and Skaði will choose her husband. She will marry whomever she picks; if she can pick out Baldr by his legs, she can have him. Skaði agrees, assuming that the beautiful Baldr will have the best legs.
(She chooses wrong. Njörðr has the best legs.)
Thinking on this as an adult, I said to myself “Aha, this is like that horn full of milk that was actually mead. I bet this was also cleaned up in the version I read, and that in the original material, Skaði was actually choosing the husband with the best butt.”
I went to check, and I was wrong. The sources say she was looking only at their feet.
I was going to just quote this:
she should choose for herself a husband from among the Æsir and choose by the feet only, seeing no more of him.
But then I got worried. This is of course not the original source but an English translation; what if it is inaccurate?
Well, there was nothing else to do but ask Snorri about it. He says:
En æsir buðu henni sætt ok yfirbætr ok it fyrsta, at hon skal kjósa sér mann af ásum ok kjósa at fótum ok sjá ekki fleira af.
(Sætt is recompense or settlement; yfirbætr similarly. (Bætr is a cure, as in “I was sick, but I got better”.) The first (fyrsta) part of the settlement is that she “shall choose a man for herself” (skal kjósa sér mann) but choose by the feet (kjósa at fótum) seeing nothing else (sjá ekki fleira af).)
The crucial word here is fótum, which certainly looks like “foot”. (It is the dative form of fótr.) Could it possibly mean the buttocks? I don't think so. It's hard to be 100% certain, because it could be a euphemism — anything could be a euphemism for the buttocks if you paused before saying it and raised one eyebrow. (Did the Norse bards ever do this?) Also the Norse seem to have divided up the leg differently than we do. Many of the words seem to match, which is sometimes helpful but also can be misleading, because many don't. For example, I think leggr, despite its appearance, means just the shank. And I think fótum may not be just the foot itself, but some part of the leg that includes the foot.
But I'm pretty sure fótum is not the butt, at least not canonically. To do this right I would look at all the other instances of fótr to see what I could glean from the usage, but I have other work to do today. So anyway, Skaði probably was looking at their feet, and not at their butts. Oh well.
However! the other part of Skaði's settlement is that the Æsir must make her laugh. In the version I first read, Loki achieves this by tying his beard to a goat's. Nope!
Þá gerði Loki þat, at hann batt um skegg geitar nökkurrar ok öðrum enda um hreðjar sér, ok létu þau ýmsi eftir ok skrækði hvárt tveggja hátt.
Skegg geitar nökkurar is indeed some goat's beard. But hann batt … ok öðrum enda um hreðjar sér is “he tied … the other end to his own scrotum”.
Useful resources:
- Skáldskaparmál, English translation of Arthur Gilchrist Brodeur (1916)
- Skáldskaparmál, original Old Icelandic (1220-ish)
- Zoëga's Concise Dictionary of Old Icelandic (1910)
Addendum 20240712
Toph has asked an excellent question about this.
[Other articles in category /lang] permanent link
Wed, 21 Mar 2018A couple of years ago I was reading Wikipedia's article about the the 1943 Bengal famine, and I was startled by the following claim:
"If food is so scarce, why hasn’t Gandhi died yet?"
Winston Churchill's response to an urgent request to release food stocks for India.
It was cited, but also marked with the “not in citation” tag, which is supposed to mean that someone checked the reference and found that it did not actually support the claim.
It sounded like it might be the sort of scurrilous lie that is widely repeated but not actually supportable, so I went to follow it up. It turned out that although the quotation was not quite exact, it was not misleadingly altered, and not a scurrilous lie at all. The attributed source (Tharoor, Shashi "The Ugly Briton". Time, (29 November 2010).) claimed:
Churchill's only response to a telegram from the government in Delhi about people perishing in the famine was to ask why Gandhi hadn't died yet.
I removed the “not in citation” tag, which I felt was very misleading.
Still, I felt that anything this shocking should be as well-supported as possible. It cited Tharoor, but Tharoor could have been mistaken. So I put in some effort and dug up the original source. It is from the journal entry of Archibald Wavell, then Viceroy of India, of 5 July 1944:
Winston sent me a peevish telegram to ask why Gandhi hadn't died yet! He has never answered my telegram about food.
This appears in the published version of Lord Wavell's journals. (Wavell, Archibald Percival. Wavell: The Viceroy's journal, p. 78. Moon, Penderel, ed. Oxford University Press, 1973.) This is the most reliable testimony one could hope for. The 1973 edition is available from the Internet Archive.
A few months later, the entire article was massively overhauled by a group of anglophiles and Churchill-rehabilitators. Having failed to remove the quotation for being uncited, and then having failed to mendaciously discredit the cited source, they removed the quotation in a typical episode of Wikipedia chicanery. In a 5,000-word article, one sentence quoting the views of the then-current British Prime Minister was deemed “undue weight”, and a failure to “fairly represent all significant viewpoints that have been published by reliable sources”.
Further reading: In Winston Churchill, Hollywood rewards a mass murderer. (Tharoor again, in last week's Washington Post.)
[Other articles in category /wikipedia] permanent link
Mon, 19 Mar 2018In English we can sometimes turn an adjective into a verb by suffixing “-en”. For example:
black → blacken
red → redden
white → whiten
wide → widen
But not
blue → bluen*
green → greenen*
yellow → yellowen*
long → longen*
(Note that I am only looking at -en verbs that are adjective-derived present tenses. This post is not concerned with the many -en verbs that are past participles, such as “smitten” (past participle of “smite”), “spoken” (“speak”), “molten” (“melt”), “sodden” (“seethe”), etc.)
I asked some linguist about this once and they were sure it was purely morphological, something like: black, red, and white end in stop consonants, and blue, green, and yellow don't.
Well, let's see:
| Morphology | Good | Bad |
|---|---|---|
| Stop |
Blacken Brighten Broaden Cheapen Darken Deaden Embolden Fatten Flatten Gladden Golden Harden Hearten Heighten Louden Madden Open (?) Quicken Quieten Redden Ripen Sadden Sharpen Shorten Sicken Slacken Smarten Straighten Straiten Sweeten Thicken Tighten Weaken Whiten Widen |
Biggen |
| Fricative |
Coarsen Deafen Enlargen Enliven Fasten Freshen Hasten Leaven Lengthen Lessen Loosen Moisten Roughen Soften Stiffen Strengthen Toughen Worsen |
Largen Smoothen |
| Nasal |
Cleanen Dimmen Dumben Finen Greenen Longen Slimmen Strongen Thinnen | |
| Vowel |
Angrien Bluen Dirtien Dryen Grayen Highen Lowen Narrowen Noisien Saltien Slowen Yellowen | |
| Nasalized stop |
Dampen Pinken | Blunten |
| Glide |
Betteren Bitteren Dullen Faren Greateren Moren Nearen Smallen Souren Stalen |
There are some fine points:
- “Biggen” used to exist but has fallen out of use
- Perhaps I should have ommitted “strengthen” and “hasten”, which are derived from nouns, not from adjectives
- I'm not sure whether “closen”, “hotten” and “wetten” are good or bad so I left them off
- “moisten” and “soften” might belong with the stops instead of the fricatives
- etc.
but clearly the morphological explanation wins. I'm convinced.
[ Addendum: Wiktionary discusses this suffix, distinguishing it from the etymologically distinct participial “-en”, and says “it is not currently very productive in forming new words, being mostly restricted to monosyllabic bases which end in an obstruent”. ]
[Other articles in category /lang] permanent link
I had a fun idea this morning. As a kid I was really interested in polar coordinates and kind of disappointed that there didn't seem to be any other coordinate systems to tinker with. But this morning I realized there were a lot.
Let !!F(c)!! be some parametrized family of curves that partition the plane, or almost all of the plane, say except for a finite number of exceptions. If you have two such families !!F_1(c)!! and !!F_2(c)!!, and if each curve in !!F_1!! intersects each curve in !!F_2!! in exactly one point (again with maybe a few exceptions) then you have a coordinate system: almost every point !!P!! lies on !!F_1(a)!! and !!F_2(b)!! for some unique choice of !!\langle a, b\rangle!!, and these are its coordinates in the !!F_1–F_2!! system.
For example, when !!F_1(c)!! is the family of lines !!x=c!! and !!F_2(c)!! is the family of lines !!y=c!! then you get ordinary Cartesian coordinates, and when !!F_1(c)!! is the family of circles !!x^2+y^2=c!! and !!F_2(c)!! is the family !!y=cx!! (plus also !!x=0!!) you get standard polar coordinates, which don't quite work because the origin is in every member of !!F_2!!, but it's the only weird exception.
But there are many other families that work. To take a particularly simple example you can pick some constant !!k!! and then take
$$\begin{align} F_1(c): && x & =c \\ F_2(c): && y & =kx+c. \end{align} $$
This is like Cartesian coordinates except the axes are skewed. I did know about this when I was a kid but I considered it not sufficiently interesting.
For a more interesting example, try
$$\begin{align} F_1(c): && x^2-y^2 & =c \\ F_2(c): && xy & =c \end{align} $$
which looks like this:
 The hyperbolas
!!x^2-y^2 = c!! (in blue) and !!xy=c!! (in red)
The hyperbolas
!!x^2-y^2 = c!! (in blue) and !!xy=c!! (in red)
I've seen that illustration before but I don't think I thought of using it as a coordinate system. Well, okay, every pair of hyperbolas intersects in two points, not one. So it's a parametrization of the boundary of real projective space or something, fine. Still fun!
In the very nice cases (such as the hyperbolas) each pair of curves is orthogonal at their point of intersection, but that's not a requirement, as with the skew Cartesian system. I'm pretty sure that if you have one family !!F!! you can construct a dual family !!F'!! that is orthogonal to it everywhere by letting !!F'!! be the paths of gradient descent or something. I'm not sure what the orthogonality is going to be important for but I bet it's sometimes useful.
You can also mix and match families, so for example take:
$$\begin{align} F_1(c): && x & =c \\ F_2(c): && xy & =c \end{align} $$
Some examples work better than others. The !!xy=c!! hyperbolas are kind of a mess when !!c=0!!, and they don't go together with the !!x^2+y^2=c!! circles in the right way at all: each circle intersects each hyperbola in four points. But it occurs to me that as with the projective plane thingy, we don't have to let that be a problem. Take !!S!! to be the quotient space of the plane where two points are identified if their !!F_1–F_2!!-coordinates are the same and then investigate !!S!!. Or maybe go more directly and take !!S = F_1 \times F_2!! (literally the Cartesian product), and then topologize !!S!! in some reasonably natural way. Maybe just give it the product topology. I dunno, I have to think about it.
(I was a bit worried about how to draw the hyperbola picture, but I tried Google Image search for “families of orthogonal hyperbolas”, and got just what I needed. Truly, we live in an age of marvels!)
[Other articles in category /math] permanent link
Sun, 11 Mar 2018
Quick and dirty prime counting
I've been thinking for a while that I probably ought to get around to memorizing all the prime numbers under 1,000, so that I don't have to wonder about things like 893 all the time, and last night in the car I started thinking about it again, and wondered how hard it would be. There are 25 primes under 100, so presumably fewer than 250 under 1,000, which is not excessive. But I wondered if I could get a better estimate.
The prime number theorem tells us that the number of primes less than !!n!! is !!O(\frac n{\log n})!! and I think the logarithm is a natural one, but maybe there is some constant factor in there or something, I forget and I did not want to think about it too hard because I was driving. Anyway I cannot do natural logarithms in my head.
Be we don't need to do any actual logarithms. Let's estimate the fraction of primes up to !!n!! as !!\frac 1{c\log n}!! where !!c!! is unknown and the base of the logarithm is then unimportant. The denominator scales linearly with the power of !!n!!, so the difference between the denominators for !!n=10!! and !!n=100!! is the same as the difference between the denominators for !!n=100!! and !!n=1000!!.
There are 4 primes less than 10, or !!\frac25!!, so the denominator is 2.5. And there are 25 primes less than 100, so the denominator here is 4. The difference is 1.5, so the denominator for !!n=1000!! ought to be around 5.5, and that means that about !!\frac2{11}!! of the numbers up to 1000 are prime. This yields an estimate of 182.
I found out later that the correct number is 186, so I felt pretty good about that.
[ Addendum: The correct number is 168, not 186, so I wasn't as close as I thought. ]
[Other articles in category /math] permanent link
Mon, 19 Feb 2018
Composition of utility pole ID tags
In a recent article discussing utility poles, and the metal ID plates they carry, I wondered what the plates were made of:
Steel would rust; and I thought even stainless steel wouldn't last as long as these tags need to. Aluminum is expensive. Tin degrades at low temperatures. … I will go test the tags with a magnet to see if they are ferrous.
They are not ferrous. Probably they are aluminum. My idea that aluminum is too expensive to use for the plates was ridiculous. The pole itself costs a lot of money. The sophisticated electrical equipment on the pole costs thousands of dollars. The insulated wire strung from the pole is made of copper. Compared with all this, a ten-centimeter oval of stamped aluminum is not a big deal.
1.8mm aluminum sheet costs $100 per square meter even if you don't buy it in great quantity. Those aluminum tags probably cost no more than fifty cents each.
[Other articles in category /oops] permanent link
Wed, 14 Feb 2018I am almost always interested in utility infrastructure. I see it every day, and often don't think about it. The electric power distribution grid is a gigantic machine, one of the biggest devices ever built, and people spend their whole lives becoming experts on just one part of it. What is it all for, how does it work? What goes wrong, and how do you fix it? Who makes the parts, and how much do they cost? Every day I go outside and see things like these big cylinders:
and I wonder what they are. In this case from clues in the environment I was able to guess they were electrical power transformers. Power is distributed on these poles at about seven thousand volts, which is called “medium voltage”. But you do not want 7000-volt power in your house because it would come squirting out of the electric outlets in awesome lightnings and burn everything up. Also most household uses do not want three-phase power, they want single-phase power. So between the pole and the house there is a transformer to change the shape of the electricity to 120V, and that's what these things are. They turn out to be called “distribution transformers” and they are manufactured by — guess who? — General Electric, and they cost a few thousand bucks each. And because of the Wonders of the Internet, I can find out quite a lot about them. The cans are full of mineral oil, or sometimes vegetable oil! (Why are they full of oil? I don't know; I guess for insulation. But I could probably find out.) There are three because that is one way to change the three-phase power to single-phase, something I wish I understood better. Truly, we live in an age of marvels.
Anyway, I was having dinner with a friend recently and for some reason we got to talking about the ID plates on utility poles. The poles around here all carry ID numbers, and I imagine that back at the electric company there are giant books listing, for each pole ID number, where the pole is. Probably they computerized this back in the seventies, and the books are moldering in a closet somewhere.
As I discussed recently, some of those poles are a hundred years old, and the style of the ID tags has changed over that time:
It looks to me like the original style was those oval plates that you see on the left, and that at some point some of the plates started to wear out and were replaced by the yellow digit tags in the middle picture. The most recent poles don't have tags: the identifier is burnt into the pole.
Poles in my neighborhood tend to have consecutive numbers. I don't think this was carefully planned. I guess how this happened is: when they sent the poles out on the truck to be installed, they also sent out a bunch of ID plates, perhaps already attached to the poles, or perhaps to be attached onsite. The plates would already have the numbers on them, and when you grab a bunch of them out of the stack they will naturally tend to have consecutive numbers, as in the pictures above, because that's how they were manufactured. So the poles in a vicinity will tend to have numbers that are close together, until they don't, because at that point the truck had to go back for more poles. So although you might find poles 79518–79604 in my neighborhood, poles 79605–79923 might be in a completely different part of the city.
Later on someone was inspecting pole 79557 (middle picture) and noticed that the number plate was wearing out. So they pried it off and replaced it with the yellow digit tag, which is much newer than the pole itself. The inspector will have a bunch of empty frames and a box full of digits, so they put up a new tag with the old ID number.
But sometime more recently they switched to these new-style poles with numbers burnt into them at the factory, in a different format than before. I have tried to imagine what the number-burning device looks like, but I'm not at all sure. Is it like a heated printing press, or perhaps a sort of configurable branding iron? Or is it more like a big soldering iron that is on a computer-controlled axis and writes the numbers on like a pen?
I wonder what the old plates are made of. They have to last a long time. For a while I was puzzled. Steel would rust; and I thought even stainless steel wouldn't last as long as these tags need to. Aluminum is expensive. Tin degrades at low temperatures. But thanks to the Wonders of the Internet, I have learned that, properly made, stainless steel tags can indeed last long enough; the web site of the British Stainless Steel Association advises me that even in rough conditions, stainless steel with the right composition can last 85 years outdoors. I will do what I should have done in the first place, and go test the tags with a magnet to see if they are ferrous.
Here's where some knucklehead in the Streets Department decided to nail a No Parking sign right over the ID tag:
Another thing you can see on these poles is inspection tags:
Without the Internet I would just have to wonder what these were and what OSMOSE meant. It is the name of the company that PECO has hired to inspect and maintain the poles. They specialize in this kind of work. This old pole was inspected in 2001 and again in 2013. The dated inspection tag from the previous inspection is lost but we can see a pie-shaped tag that says WOODFUME. You may recall from my previous article that the main killer of wood poles is fungal infection. Woodfume is an inexpensive fumigant that retards pole decay. It propagates into the pole and decomposes into MITC (methyl isothiocyanate). By 2001 PECO had switched to using MITC-FUME, which impregnates the pole directly with MITC. Osmose will be glad to tell you all about it.
(Warning: Probably at least 30% of the surmise in this article is wrong.)
Addendum 20250306
After they cut out those little metal rectangles with the numbers on them, what do they do with the leftover bit?
They nail it to the bottom of the pole to make it easier to see.
[Other articles in category /tech] permanent link
Tue, 13 Feb 2018(If you already know about reservoir sampling, just skip to the good part.)
The basic reservoir sampling algorithm asks us to select a random item from a list, easy peasy, except:
- Each item must be selected with equal probability
- We don't know ahead of time how big the list is
- We may only make one pass over the list
- We may use only constant memory
Maybe the items are being read from a pipe or some other lazy data structure. There might be zillions of them, so we can't simply load them into an array. Obviously something like this doesn't work:
# Python
from random import random
selected = inputs.next()
for item in inputs:
if random() < 0.5:
selected = item
because it doesn't select the items with equal probability. Far from it! The last item is selected as often as all the preceding items put together.
The requirements may seem at first impossible to satisfy, but it can be done and it's not even difficult:
from random import random
n = 0
selected = None
for item in inputs:
n += 1
if random() < 1/n:
selected = item
The inputs here is some sort of generator that presents the list of
items, one at a time. After the loop completes, the selected item is
in selected. A proof that this selects each item equiprobably is
left as an easy exercise, or see this math StackExchange
post. A variation
for selecting !!k!! items instead of only one is quite easy.
The good part
Last week I thought of a different simple variation. Suppose each item !!s_i!! is presented along with an arbitrary non-negative weight !!w_i!!, measuring the relative likelihood of its being selected for the output. For example, an item with weight 6 should be selected twice as often as an item with weight 3, and three times as often as an item with weight 2.
The total weight is !!W = \sum w_i!! and at the end, whenever that is, we want to have selected each item !!s_i!! with probability !!\frac{w_i}{W}!!:
total_weight = 0
selected = None
for item, weight in inputs:
if weight == 0: continue
total += weight
if random() < weight/total:
selected = item
The correctness proof is almost the same. Clearly this reduces to the standard algorithm when all the weights are equal.
This isn't a major change, but it seems useful and I hadn't seen it before.
[Other articles in category /prog] permanent link
Mon, 12 Feb 2018
Philadelphia sports fans behaving badly
Philadelphia sports fans have a bad reputation. For example, we are famous for booing Santa Claus and hitting him with snowballs. I wasn't around for that; it happened in 1968. When the Santa died in 2015, he got an obituary in the Phildelphia Inquirer:
Frank Olivo, the Santa Claus who got pelted with snowballs at the Eagles game that winter day in 1968, died Thursday, April 30…
The most famous story of this type is about Ed Rendell (after he was Philadelphia District Attorney, but before he was Mayor) betting a Eagles fan that they could not throw snowballs all the way from their upper-deck seat onto the field. This was originally reported in 1989 by Steve Lopez in the Inquirer.
(Lopez's story is a blast. He called up Rendell, who denied the claim, and referred Lopez to a friend who had been there with him. Lopez left a message for the friend. Then Rendell called back to confess. Later Rendell's friend called back to deny the story. Lopez wrote:
Was former D.A. Ed Rendell's worst mistake to (A) bet a drunken hooligan he couldn't reach the field, (B) lie about it, (C) confess, or (D) take his friend down with him?
My vote is C. Too honest. Why do you think he can't win an election?
A few years later Rendell was elected Mayor of Philadelphia, and later, Governor of Pennsylvania. Anyway, I digress.)
I don't attend football games, and baseball games are not held in snowy weather, so we have to find other things to throw on the field. I am too young to remember Bat Day, where each attending ticket-holder was presented with a miniature souvenir baseball bat; that was eliminated long ago because too many bats were thrown at the visiting players. (I do remember when those bats stopped being sold at the concession stands, for the same reason.) Over the years, all the larger and harder premiums were eliminated, one by one, but we are an adaptable people and once, to protest a bad call by the umpire, we delayed the game by wadding up our free promotional sport socks and throwing them onto the field. That was the end of Sock Day.
On one memorable occasion, two very fat gentlemen down by the third-base line ran out of patience during an excessively long rain delay and climbed over the fence, ran out and belly-flopped onto the infield, sliding on the wet tarpaulin all the way to the first-base side. Confronted there by security, they evaded capture by turning around and sliding back. These heroes were eventually run down, but only after livening up what had been a very trying evening.
The main point of this note is to shore up a less well-known story of this type. I have seen it reported that Phillies fans once booed Miss Pennsylvania, and I have also seen people suggest that this never really happened. On my honor, it did happen. We not only booed Miss Pennsylvania, we booed her for singing the national anthem. I was at that game, in 1993. The Star-Spangled Banner has a lot of problems that the singer must solve one way or another, and there are a lot of ways to interpret it. But it has a melody, and the singer's interpretation is not permitted to stray so far from the standard that they are singing a different song that happens to have the same words. I booed too, and I'm not ashamed to admit it.
[Other articles in category /games] permanent link
Wed, 07 Feb 2018
The many faces of the Petersen graph
(Actually the Petersen graph cannot really be said to have faces, as it is nonplanar. HA! HA! I MAKE JOKE!!1!)
This article was going to be about how GraphViz renders the Petersen graph, but instead it turned out to be about how GraphViz doesn't render the Petersen graph. The GraphViz stuff will be along later.
Here we have the Petersen graph, which, according to Donald Knuth, “serves as a counterexample to many optimistic predictions about what might be true for graphs in general.” It is not that the Petersen graph is stubborn! But it marches to the beat of a different drummer. If you have not met it before, prepare to be delighted.
This is the basic structure: a blue 5-cycle, and a red 5-cycle. Corresponding vertices in the two cycles are connected by five purple edges. But there is a twist! Notice that the vertices in the red cycle are connected in the order 1–3–5–2–4.
There are different ways to lay out the Petersen graph that showcase its many interesting properties. For example, the standard presentation, above, demonstrates that the Petersen graph is nonplanar, since it obviously contracts to !!K_5!!. The presentation below obscures this, but it is good for seeing that the graph has diameter only 2:
Wait, what? Where did the pentagons go?
Try this instead:

Again the red vertices are connected in the order 1–3–5–2–4.
Okay, that is indeed the Petersen graph, but how does it help us see that the graph has diameter 2? Color the nodes by how far down they are from the root:
Obviously, the root node (black) has distance at most 2 to every other node, because the tree has only depth 2.
Each of the three second-level nodes (red) is distance 2 from the other two, via a path through the root.
The six third-level nodes (blue) are linked in a 6-cycle (dotted lines), so that each third-level node is at most two steps away along the cycle from the others, except for the one furthest away, but that is its sibling in the tree, and it has a path of length 2 through their common parent.
And since each third-level node (say, the one with the red ring) is connected by a dotted edge (orange) to cousins in both of the other branches of the tree, it's only distance 2 from both of its red uncle nodes.
Looking at the pentagonal version, you would not suspect the Petersen graph of also having a sixfold symmetry, but it does. We'll get there in two steps. Again, here's a version where it's not so easy to see that it's actually the Petersen graph, but whatever it is, it is at least clear that it has an automorphism of order six (give it a one-sixth turn):
The 
Let's pull apart the three vertices




Here is the same drawing, recolored to match the tree diagram from before; the outer hexagon is just the 6-cycle formed by the six blue leaf nodes:

| 
|
But maybe it's easier to see if we look for red and blue pentagons. There are a couple of ways to do that:

| 
|
As always, the red vertices are connected in the order 1–3–5–2–4.
Finally, here's a presentation you don't often see. It demonstrates that the Petersen graph also has fourfold symmetry:

Again, 

The pentagons are deeply hidden here. Can you find them? (Spoiler)
Even though this article was supposed to be about GraphViz, I found it impossible to get it to render the diagrams I wanted it to, and I had to fall back on Inkscape. Fortunately Inkscape is a ton of fun.
[Other articles in category /math] permanent link
Thu, 01 Feb 2018As I may have mentioned, I have started another
blog, called Content-type:
text/shitpost.
Last month I said:
The shitposts have been suffering quality creep and I am making an effort to lower my standards. I will keep you posted about how this develops.
I think I am doing better. I will continue my efforts to emphasize quantity over quality, with a multi-pronged approach:
- Faster production with lower production standards
- Less filtering of possible topics for relevance, general interest, or almost anything else
- Promote insufficiently shitty posts to The Universe of Discourse
It will be a struggle, but I resolve to do my best!
Here is a list of January's shitposts. Boldface indicates the articles that may (may) be of more general interest (ha). There are fewer of these than last month because I promoted several of the better ones, so you have seen them already.
- Cartesian Demon
- Ukulele scams
- Vacation in Florida
- The statistics package
- Dysphonia
- Sourtoe brand expansion
- Great Falls
- Software Archaeology
- More shuffling commands
- Disaster narrowly averted
- How to seed a pomegranate
- Google Docs detects a spelling error!
- Software vendor pomegranate video
- Equatorial countries
- Computers suck: episode 17817 of 31279
- Scientists who died young
- Mozart the prodigy
- The Seebeck effect
- Abort
- ABEND
- Coincidence? Or Conspiracy?
- More life goals
- The Carrot Cake Man
- No, it's fine!
- Public Service Announcment: Fuchsia
- Morea vuvuzela fail
- The most Santa Monica thing ever
- My world is turned upside down
- A little algebraic thingy
- Pork stew
- The Liver of Piacenza
- Pouring piss out of a boot
- I'm so old…: [1] [2] [3]
- James Macpherson and Samuel Johnson
- Trump and the golden toilet
- I am a mathematician
- My blog and Planet Haskell
- An atheist reads the Bible
- The universal remote
- Marvels of modern technology
- The cobbler at court
- Differing philosophies of Python and PHP
- Plant pest survey
- Grayeeuts
[Other articles in category /meta/shitpost] permanent link
Tue, 30 Jan 2018Sapporo restaurant, on West 49th Street in New York, closed yesterday. There are 24,000 restaurants in New York, and for many, many years, Sapporo was my favorite.
Sapporo was a ramen restaurant, probably the first in New York. I remember first hearing the word “ramen” in the early 1980s, when the Larmen Dosanko appeared near Lincoln Center. But Sapporo opened in 1975. I started going there around 1984. I didn't discover it on my own; I think my dad and I happened in one day when we were in the neighborhood. But it made a big impression on me, and I would regularly stop in whenever I was nearby, and sometimes I would walk downtown (about 45 minutes) just to eat there.
When I was fifteen years old, I did something fifteen-year-old boys often do: I grew six inches and added thirty pounds in one year. I ate all the time. I spent so much time eating that it wasn't enjoyable any more, and I complained that I was tired of it and didn't have enough time to do anything else. I would come home from school and eat a double-decker sandwich (sliced muenster with mayonnaise was my favorite), half a pound of feta cheese, three yogurts, and whatever leftovers I could find in the fridge, and then two hours later when my parents got home I would ask “What's for dinner? I'm starving.” I fell in love with Sapporo because it was the only restaurant where I could afford to order as much food as I could eat. I would come out of Sapporo full. Sometimes when I left Sapporo there was still some rice or noodles in my bowl, and I would stop thinking about food for an hour or two.
On the table were three intriguing bottles, one brown, one pale yellow, and one bright red. The brown one was obviously soy sauce, but what were the others? I learned that the pale yellow one was vinegar and the bright red one was hot oil and had great fun trying them out in different combinations. I had never thought of using vinegar as a condiment, and I loved it.
Sapporo was where I first had agedashi dofu, which is delectable cubes of soft tofu, dusted in flour or starch, fried brown and crisp, and served in savory broth. It is ephemeral: you have to eat it right away, before it gets cold and soggy.
My favorite dish was the pork cutlet donburi. (They didn't call it “katsudon”; I didn't learn that until later.) The cutlet was embedded, with onions, in a fried egg that covered and adhered to the top of the rice, and I can still remember how it tasted with the soy sauce and vinegar, and the texture of it. It was tricky to pick up the cutlet, with its attached fried egg, with chopsticks. I now use chopsticks as well as I use a fork, automatically and unconsciously, and I think Sapporo was probably where I learned to do it.
Because of Sapporo, I became so enamored of vinegar that I started to put it on everything. I didn't like mustard, I thought, but one day I learned that the principal ingredient in mustard, other than the mustard itself, was vinegar. This put a new light on things and I immediately decided I had better give mustard another try. I discovered that I did indeed like mustard (like vinegar, but with extra flavor!) and I have liked it ever since.
(Around the same time of my life, I was learning about beer, and I eagerly tried Sapporo beer, which they feature, hoping that it would be as wonderful as Sapporo restaurant. I was disappointed.)
I deeply regret that I missed my last chance to eat there. I was staying in Midtown with Toph last summer and suggested that we eat dinner there, but she chose to go somewhere else. It didn't occur to me that Sapporo might not always be there, or I would have insisted.
Goodbye, Sapporo. I love you and I will miss you.
[Other articles in category /food] permanent link
Mon, 29 Jan 2018
The rubber duck explains coherence spaces
I've spent a chunk of the past week, at least, trying to understand the idea of a coherence space (or coherent space). This appears in Jean-Yves Girard's Proofs and Types, and it's a model of a data type. For example, the type of integers and the type of booleans can be modeled as coherence spaces.
The definition is one of those simple but bafflingly abstract ones that you often meet in mathematics: There is a set !!\lvert \mathcal{A}\rvert!! of tokens, and the points of the coherence space !!\mathcal{A}!! (“cliques”) are sets of tokens. The cliques are required to satisfy two properties:
- If !!a!! is a clique, and !!a'\subset a!!, then !!a'!! is also a clique.
- Suppose !!\mathcal M!! is some family of cliques such that !!a\cup a'!! is a clique for each !!a, a'\in \mathcal M!!. Then !!\bigcup {\mathcal M}!! is also a clique.
To beginning math students it often seems like these sorts of definitions are generated at random. Okay, today we're going to study Eulerian preorders with no maximum element that are closed under finite unions; tomorrow we're going to study semispatulated coalgebras with countably infinite signatures and the weak Cosell property. Whatever, man.
I have a long article about this in progress, but I'll summarize: they are never generated at random. The properties are carefully chosen because we have something in mind that we are trying to model, and until you understand what that thing is, and why someone thinks those properties are the important ones, you are not going to get anywhere.
So when I see something like this I must stop immediately and ask ‘wat’. I can try to come up with the explanation myself, or I can read on hoping for an explanation, or I can do some of each, but I am not going to progress very far until I understand what it is about. And I'm not sure anyone short of Alexander Grothendieck would have any more success trying to move on with the definition itself and nothing else.
Girard explains shortly after:
The aim is to interpret a type by a coherence space !!\mathcal{A}!!, and a term of this type as a point [clique] of !!\mathcal{A}!!, infinite in general…
Okay, fine. I understand the point of the project, although not why the definition is what it is. I know a fair amount about types. And Girard has given two examples: booleans and integers. But these examples are unusually simple, because none of the cliques has more than one element, and so the examples are not as illuminating as they might be.
Some of the ways I tried to press onward were:
Read ahead and see if there is more explanation. I tried this but I still wasn't getting it. The next section seemed clear: the cliques define a “coherence” relation on the tokens, from which the cliques can be recovered. Consider a graph, where the vertices are tokens and there is an edge !!a—b!! exactly when !!\{a, b\}!! is a clique; we say that !!a!! and !!b!! are coherent. Then the cliques of the coherence space are exactly the cliques of the graph; hence the name. The graph is called the web of the space, and from the web one can recover the original space.
But after that part came stable functions, which I couldn't figure out, and I got stuck again.
Read ahead and see if there is a more complicated specific example. There wasn't.
Read ahead and see if any of the derived concepts are familiar, and if so then work backward. For instance, if I had been able to recognize that I already knew what stable functions were, I might have been able to leverage that into an understanding of what was going on with the coherence spaces. But for me they were just another problem of the same sort: what is a stable function supposed to be modeling?
Read someone else's explanation instead. I tried several without much success. They all seemed to be written for someone who already had a clue what was going on. (That is a large part of the reason I have written up this long and clueless explanation.)
Try to construct some examples and see if they make sense in the context of what comes later. For example, I know what the coherence space of booleans looks like because Girard showed me. Can I figure out the structure of the coherence space for the type of “wrapped booleans”?
-- (Haskell) data WrappedBoolean = W BoolCan I figure it out for the type of pairs of booleans?
-- (Haskell) type BooleanPair = (Bool, Bool)
None of this was working. I had several different ideas about what the coherence spaces might look like for other types, but none of them seemed to fit with what Girard was doing. I couldn't come up with any consistent story.
So I prepared to ask on StackExchange, and I spent about an hour writing up my question, explaining all the things I had tried and what the problems were with each one. And as I drew near to the end of this, the clouds parted! I never had to post the question. I was in the middle of composing this paragraph:
In section 8.4 Girard defines a direct product of coherence spaces, but it doesn't look like the direct product I need to get a product type; it looks more like a disjoint union type. If the coherence space for
Pairboolis the square of the coherence space for !!{{\mathcal B}ool}!!, how? It has 4 2-cliques, but if those are the total elements of !!{{\mathcal B}ool}^2!!, then what are do the 1-cliques mean?
I decided I hadn't made enough of an effort to understand the direct product. So even though I couldn't see how it could possibly give me anything like what I wanted, I followed its definition for !!{{\mathcal B}ool}^2!! — and the light came on.
Here's the puzzling coproduct-like definition of the product of two coherence spaces, from page 61:
If !!{\mathcal A}!! and !!{\mathcal B}!! are two coherence spaces, we define !!{\mathcal A}\&{\mathcal B}!! by:
!!|{\mathcal A}\&{\mathcal B}| = |{\mathcal A}| + |{\mathcal B}| = \{1\}×|{\mathcal A}| \cup \{2\}×|{\mathcal B}|!!
That is, the tokens in the product space are literally the disjoint union of the tokens in the component spaces.
And the edges in the product's web are whatever they were in !!{\mathcal A}!!'s web (except lifted from !!|{\mathcal A}|!! to !!\{1\}×|{\mathcal A}|!!), whatever they were in !!{\mathcal B}!!'s web (similarly), and also there is an edge between every !!\langle1, {\mathcal A}\rangle!! and each !!\langle2, {\mathcal B}\rangle!!. For !!{{\mathcal B}ool}^2!! the web looks like this:
There is no edge between !!\langle 1, \text{True}\rangle!! and !!\langle 1, \text{False}\rangle!! because in !!{{\mathcal B}ool}!! there is no edge between !!\text{True}!! and !!\text{False}!!.
This graph has nine cliques. Here they are ordered by set inclusion:
(In this second diagram I have abbreviated the pair !!\langle1, \text{True}\rangle!! to just !!1T!!. The top nodes in the diagram are each labeled with a set of two ordered pairs.)
What does this mean? The ordered pairs of booleans are being represented by functions. The boolean pair !!\langle x, y\rangle!! is represented by the function that takes as its argument a number, either 1 or 2, and then returns the corresponding component of the pair: the first component !!x!! if the argument was 1, and the second component !!y!! if the argument was 2.
The nodes in the bottom diagram represent functions. The top row are fully-defined functions. For example, !!\{1F, 2T\}!! is the function with !!f(1) = \text{False}!! and !!f(2) = \text{True}!!, representing the boolean pair !!\langle\text{False}, \text{True}\rangle!!. Similarly if we were looking at a space of infinite lists, we could consider it a function from !!\Bbb N!! to whatever the type of the lists elements was. Then the top row of nodes in the coherence space would be infinite sets of pairs of the form !!\langle n, \text{(list element)}\rangle!!.
The lower nodes are still functions, but they are functions about which we have only incomplete information. The node !!\{2T\}!! is a function for which !!f(2) = \text{True}!!. But we don't yet know what !!f(1)!! is because we haven't yet tried to compute it. And the bottommost node !!\varnothing!! is a function where we don't know anything at all — yet. As we test the function on various arguments, we move up the graph, always following the edges. The lower nodes are approximations to the upper ones, made on the basis of incomplete information about what is higher up.
Now the importance of finite approximants on page 56 becomes clearer. !!{{\mathcal B}ool}^2!! is already finite. But in general the space is infinite because the type is functions on an infinite domain, or infinite lists, or something of that sort. In such a space we can't get all the way to the top row of nodes because to do that we would have to call the function on all its possible arguments, or examine every element of the list, which is impossible. Girard says “Above all, there are enough finite approximants to a.” I didn't understand what he meant by “enough”. But what he means is that each clique !!a!! is the union of its finite approximants: each bit of information in the function !!a!! is obtainable from some finite approximation of !!a!!. The “stable functions” of section 8.3 start to become less nebulous also.
I had been thinking that the !!\varnothing!! node was somehow like the
!!\bot!! element in a Scott domain, and then I struggled to
identify anything like !!\langle \text{False}, \bot\rangle!!.
It looks at first
like you can do it somehow, because there are the right number of
nodes at the middle level.
Trouble arises in other coherence
spaces.
For the WrappedBoolean type, for example, the type has
four elements: !!
W\ \text{True},
W\ \text{False},
W\ \bot,!! and !!\bot!!. I think the coherence space for WrappedBoolean is just like the one
for !!{{\mathcal B}ool}!!:
Presented with a value from WrappedBoolean, you don't initially know
what it is. Then you examine it, and you know whether it is
!!W\ \text{True}!! or !!W\ \text{False}!!. You are now done.
I think there isn't anything like !!\bot!! or !!W\ \bot!! in the coherence space. Or maybe they they are there but sharing the !!\varnothing!! node. But I think more likely partial objects will appear in some other way.
Whew! Now I can move along.
(If you don't understand why “rubber duck”, Wikipedia explains:
Many programmers have had the experience of explaining a problem to someone else, possibly even to someone who knows nothing about programming, and then hitting upon the solution in the process of explaining the problem.
[“Rubber duck”] is a reference to a story in the book The Pragmatic Programmer in which a programmer would carry around a rubber duck and debug their code by forcing themselves to explain it, line-by-line, to the duck.
I spent a week on this but didn't figure it out until I tried formulating my question for StackExchange. The draft question, never completed, is here if for some reason you want to see what it looked like.)
[Other articles in category /math/logic] permanent link
Thu, 25 Jan 2018For me, a little of Samuel Johnson goes a long way, because he was a tremendous asshole, and the draught is too strong for me to take much at once. But he is at his best when he is in opposition to someone who is an even bigger asshole, in this case James Macpherson.
Macpherson was a Scottish poet who perpetrated a major hoax for his own literary benefit. He claimed to have discovered and translated a collection of 3rd-century Gaelic manuscripts, written by a bard named Ossian, which he then published, with great commercial and critical success.
Thomas Bailey Saunders, in The Life and Letters of James Macpherson (1894), writes:
[Macpherson] was six-and-twenty, and flattered to the top of his bent. What happened with him was only what happens with most literary adventurers whose success is immediate and greater than their strict deserts; he contracted the foolish temper in which a man regards all criticism as ignorant and impertinent, and declines to take advice from any one.
Ossian and Macpherson did receive a great deal of criticism. Much of it was rooted in anti-Scottish bigotry, but many people at the time correctly suspected that Macpherson had written the "translations” himself, from scratch or nearly so. There was a great controversy, in which nobody participated more forcefully (or impolitely) than Johnson, a noted anti-Scottish bigot, who said that not only was the poems’ claimed history fraudulent, but that the poems themselves were rubbish.
The argument raged for some time. Johnson took up the matter in Journey to the Western Islands of Scotland (1775), in which he said:
I believe [the poems] never existed in any other form than that which we have seen. The editor, or author, never could shew the original; nor can it be shewn by any other; to revenge reasonable incredulity, by refusing evidence, is a degree of insolence, with which the world is not yet acquainted; and stubborn audacity is the last refuge of guilt. It would be easy to shew it if he had it; but whence could it be had?
Macpherson was furious to learn, before it was published, what Journey to the Western Islands would say, and attempted to prevent the passage from appearing in the book at all. When he discovered he was too late for this, he suggested that a slip of paper be inserted into the printed copies, apologizing and withdrawing the paragraph. This suggestion was ignored, and Johnson's book was published with no alteration.
Macpherson then challenged Johnson to a duel, and then, Johnson having declined, sent him a final letter, now lost, which a contemporary described as telling Johnson:
as he had declined to withdraw from his book the injurious expressions reflecting on Mr. Macpherson's private character, his age and infirmities alone protected him from the treatment due to an infamous liar and traducer.
(John Clark, An Answer to Mr. [William] Shaw's Inquiry, p. 51. Reprinted in Works of Ossian, vol. 1, 1783.)
Johnson's famous reply to this letter, quoted by Boswell, was:
MR. JAMES MACPHERSON.
I RECEIVED your foolish and impudent letter. Any violence offered me I shall do my best to repel; and what I cannot do for myself, the law shall do for me. I hope I shall never be deterred from detecting what I think a cheat, by the menaces of a ruffian.
What would you have me retract? I thought your book an imposture; I think it an imposture still. For this opinion I have given my reasons to the publick, which I here dare you to refute. Your rage I defy. Your abilities, since your Homer, are not so formidable; and what I hear of your morals inclines me to pay regard not to what you shall say, but to what you shall prove. You may print this if you will.
SAM. Johnson.
Both Macpherson and Johnson are buried in Westminster Abbey. Some say Macpherson bought his way in.
[Other articles in category /book] permanent link
Mon, 22 Jan 2018
The gods of Stackexchange karma are fickle
A few years ago an se.math user asked why their undistinguished answer to some humdrum question had gotten so many upvotes. I replied:
It's the gods of Stackexchange Karma evening your score for that really clever answer you posted two weeks ago that still has 0 upvotes.
If you're going to do Stack Exchange, I think it's important not to stress out about the whys of the votes, and particularly important not to take them personally. The karma gods do not always show the most refined taste. As Brandon Tartikoff once said, “All hits are flukes”.
Today I got an unusually flukey hit. But first, here are some nice examples in the opposite direction, posts that I put a lot of trouble and effort into, which were clear and useful, helpful to the querent, and which received no upvotes at all.
Here the querent asked, suppose I have several nonstandard dice with various labeling on the faces. Player A rolls some of the dice, and Player B rolls a different set of dice. How do I calculate things like “Player A has an X% chance of rolling a higher total”?
Mathematicians are not really the right people to ask this to, because many of them will reply obtusely, informing you that it depends on how many dice are rolled and on how their faces are actually labeled, and that the question did not specify these, but that if it had, the problem would be trivial. (I thought there were comments to that effect on this question, but if there were they have been deleted. In any case nobody else answered.) But this person was writing a computer game and wanted to understand how to implement a computer algorithm for doing the calculation. There is a lot one can do to help this person. I posted an answer that I thought was very nice. The querent liked it, but it got zero upvotes. This happens quite often. Which is fine, because the fun of doing it and the satisfaction of helping someone are reward enough.
Like that one, many of these questions are ignored because they aren't mathematically interesting. Or sometimes the mathematics is simple but the computer implementation is not.
Sometimes I do them just because I want to know the particular answer. (How much of an advantage does Player A get from being allowed to add 1 to their total?)
Sometimes there's an interesting pedagogical problem, such as: how do I give a hint that will point in the right direction without giving away the whole secret? Or: how do I wade through this person's confused explanation and understand what they are really asking, or what they are really confused about? That last person was given a proof that glossed over six or seven steps in the reasoning, focusing instead on the technically interesting induction proof in the middle. The six or seven steps are straightforward, if you already have enough practice with logical reasoning about quantified statements. But this querent didn't follow the reasoning that led up to the induction, so they didn't understand why the induction was useful or what it was for.
Some people are just confused about what the question is. That person has a complicated-seeming homework exercise about the behavior of the logistic map, and need helps interpreting it from someone who has a better idea what is going on. The answer didn't require any research effort, and it's mathematically uninteresting, but it did require attention from someone who has a better idea of what is going on. The querent was happy, I was happy, and nobody else noticed.
I never take the voting personally, because the gods of Stackexchange karma are so fickle, and today I got a reminder of that. Today's runaway hit was for a complete triviality that I knocked off in two minutes. It currently has 94 upvotes and seems likely to get a gold medal. (That gold medal, plus $4.25, will get me a free latte at Starbuck's!)
The question asks how to find a prime factor of 7,999,973 without using a calculator.
It's one of those easy-if-you-happen-to-know-the-trick things, and I just happened to get there before one of the (many) other people who happens to know the trick.
As we used to say in the system administration biz, some days you're an idiot if you can't explain how to do real-time robot arm control in Unix, other days you're a genius if you fix their terminal by plugging it in.
[ Addendum 20180123: I got the gold medal. Woo-hoo, free latte! ]
[Other articles in category /math] permanent link
Sat, 20 Jan 2018
I forgot there are party conventions
Yesterday I made a huge mistake in my article about California's bill requiring presidential candidates to disclose their tax returns. I asked:
Did I miss anything?
Yes, yes I did. I forgot that party nominees are picked not by per-state primary elections, but by national conventions. Even had Ronnie won the California Republican primary election, rather than Trump, that would not be enough the get him on the ballot in the general election.
In the corrected version of my scenario, California sends many Ronnie supporters to the Republican National Convention, where the other delegates overwhelmingly nominate Trump anyway. Trump then becomes the Republican party candidate and appears on the California general election ballot in November. Whoops.
I had concluded that conceding California couldn't hurt Trump, and it could actually a huge benefit to him. After correcting my mistake, most of the benefit evaporates.
I wonder if Trump might blow off California in 2020 anyway. The upside would be that he could spend the resources in places that might give him some electoral votes. (One reader pointed out that Trump didn't blow off California in the 2016 election, but of course the situation was completely different. In 2016 he was not the incumbent, he was in a crowded field, and he did not yet know that he was going to lose California by 30%.)
Traditionally, candidates campaign even in states they expect to lose. One reason is to show support for candidates in local elections. I can imagine many California Republican candidates would prefer that Trump didn't show up. Another reason is to preserve at least a pretense that they are representatives of the whole people. Newly-elected Presidents have often upheld the dignity of the office by stating the need for unity after a national election and promising (however implausibly) to work for all Americans. I don't care to write the rest of this paragraph.
The major downside that I can think of (for Trump) is that Republican voters in California would be infuriated, and while they can't directly affect the outcome of the presidential election, they can make it politically impossible for their congressional representatives to work with Trump once he is elected. A California-led anti-Trump bloc in Congress would probably cause huge problems for him.
Wild times we live in.
[Other articles in category /oops] permanent link
Fri, 19 Jan 2018
Presidential tax return disclosure
The California state legislature passed a bill that would require presidential candidates to disclose their past five tax returns in order to qualify for California primary elections. The bill was vetoed by Governor Brown, but what if it had become law?
Suppose Donald Trump ran for re-election in 2020, as seems likely, barring his death or expulsion. And suppose he declined once again to disclose his tax returns, and was excluded from the California Republican primary election. I don't see how this could possibly hurt Trump, and it could benefit him.
It doesn't matter to Trump whether he enters the primary or wins the primary. Trump lost California by 30% in 2016. Either way he would be just as certain to get the same number of electors: zero. So he would have no incentive to comply with the law by releasing his tax returns.
Most candidates would do it anyway, because they try to maintain a pretense of representing the entire country they are campaigning to lead, but Trump is really different in this way. I can easily imagine he might simply refuse to campaign in California, instead dismissing the entire state with some vulgar comment. If there is a downside for Trump, I don't see what it could be.
Someone else (call them “Ronnie”) would then win the California Republican primary. Certainly Ronnie is better-qualified and more competent than Trump, and most likely Ronnie is much more attractive to the California electorate.
Ronnie might even be more attractive than the Democratic candidate, and might defeat them in the general election, depriving Trump's challenger of 55 electoral votes and swinging the election heavily in Trump's favor.
Did I miss anything?
[ Addendum 20180120: Yeah, I forgot that after the primary there is a convention that nominates a national party candidate. Whooops. Further discussion. ]
[ Addendum 20191123: The tax return disclosure law passed, but the California Supreme Court recently found it to be in conflict with the California state constitution. ]
[Other articles in category /politics] permanent link
Thu, 18 Jan 2018In autumn 2014 I paid for something and got $15.33 in change. I thought I'd take the hint from the Universe and read Wikipedia's article on the year 1533. This turned out unexpectedly exciting. 1533 was a big year in English history. Here are the highlights:
- January 25: King Henry VIII marries Anne Boleyn
- March 30: Thomas Cranmer becomes Archbishop of Canterbury
- May 23: Cranmer annuls Henry's marriage to Catherine of Aragon
- June 1: Boleyn crowned queen consort by Cranmer
- July 11: Henry excommunicated by Pope Clement VII
- September 7: Princess Elizabeth, later Queen Elizabeth I, is born to Boleyn
A story clearly emerges here, the story of Henry's frantic response to Anne Boleyn's surprise pregnancy.
The first thing to notice is that Elizabeth was born only seven months after Henry married Boleyn. The next thing to notice is that Henry was still married to Catherine when he married Boleyn. He had to get Cranmer to annul the marriage, issuing a retroactive decree that not only was Henry not married to Catherine, but he had never been married to her.
In 2014 I imagined that Henry appointed Cranmer to be Archbishop on condition that he get the annulment, and eventually decided that was not the case. Looking at it now, I'm not sure why I decided that.
While Cranmer was following Charles through Italy, he received a royal letter dated 1 October 1532 informing him that he had been appointed the new Archbishop of Canterbury, following the death of archbishop William Warham [on 22 August]. Cranmer was ordered to return to England. The appointment had been secured by the family of Anne Boleyn, who was being courted by Henry.
Cranmer had been working on that annulment since at least 1527. In 1532 he was ambassador to Charles V, the Holy Roman Emperor, who was the nephew of Henry's current wife Catherine. I suppose a large part of Cranmer's job was trying to persuade Charles to support the annulment. (He was unsuccessful.) When Charles conveniently went to Rome (what for? Wikipedia doesn't say) Cranmer followed him and tried to drum up support there for the annulment. (He was unsuccessful in that too.)
Fortunately there was a convenient vacancy, and Henry called him back to fill it, and got his annulment that way. In 2014 I thought Warham's death was just a little too convenient, but I decided that he died too early for it to have been arranged by Henry. Now I'm less sure — Henry was certainly capable of such cold-blooded planning — but I can't find any mention of foul play, and The Divorce of Henry VIII: The Untold Story from Inside the Vatican describes the death as “convenient though entirely natural”.
[ Addendum: This article used to say that Elizabeth was born “less than seven months” after Henry and Boleyn's marriage. Daniel Holtz has pointed out that this was wrong. The exact amount is 225 days, or 32 weeks plus one day. The management regrets the error. ]
[Other articles in category /history] permanent link
Tue, 16 Jan 2018In an earlier article, I said:
If I were in charge of keeping plutonium out of the wrong hands, I would still worry about [people extracting it from plutonium-fueled pacemakers].
This turns out to be no worry at all. The isotope in the pacemaker batteries is Pu-238, which is entirely unsuitable for making weapons. Pu-238 is very dangerous, being both radioactive and highly poisonous, but it is not fissile. In a fission chain reaction, an already-unstable atomic nucleus is hit by a high-energy neutron, which causes it to fragment into two lighter nuclei. This releases a large amount of nuclear binding energy, and more neutrons which continue the reaction. The only nuclei that are unstable enough for this to work have an odd number of neutrons (for reasons I do not understand), and Pu-238 does not fit the bill (Z=94, N=144). Plutonium fission weapons are made from Pu-241 (N=147), and this must be carefully separated from the Pu-238, which tends to impede the chain reaction. Similarly, uranium weapons are made from U-235, and this must be painstakingly extracted from the vastly more common U-238 with high-powered centrifuges.
But I did not know this when I spent part of the weekend thinking about the difficulties of collecting plutonium from pacemakers, and discussing it with a correspondent. It was an interesting exercise, so I will publish it anyway.
While mulling it over I tried to identify the biggest real risks, and what would be the most effective defenses against them. An exercise one does when considering security problems is to switch hats: if I were the bad guy, what would I try? What problems would I have to overcome, and what measures would most effectively frustrate me? So I put on my Black Hat and tried to think about it from the viewpoint of someone, let's call him George, who wants to build a nuclear weapon from pacemaker batteries.
I calculated (I hope correctly) that a pacemaker had around 0.165 mg of plutonium, and learned online that one needs 4–6 kg to make a plutonium bomb. With skill and experience one can supposedly get this down to 2 kg, but let's take 25,000 pacemakers as the number George would need. How could he get this much plutonium?
(Please bear in mind that the following discussion is entirely theoretical, and takes place in an imaginary world in which plutonium-powered pacemakers are common. In the real world, they were never common, and the last ones were manufactured in 1974. And this imaginary world exists in an imaginary universe in which plutonium-238 can sustain a chain reaction.)
Obviously, George's top target would be the factory where the pacemakers are made. Best of all is to steal the plutonium before it is encapsulated, say just after it has been delivered to the factory. But equally obviously, this is where the security will be the most concentrated. The factory is not as juicy a target as it might seem at first. Plutonium is radioactive and toxic, so they do not want to have to store a lot of it on-site. They will have it delivered as late as possible, in amounts as small as possible, and use it up as quickly as possible. The chances of George getting a big haul of plutonium by hitting the factory seem poor.
Second-best is for George to steal the capsules in bulk before they are turned into pacemakers. Third-best is for him to steal cartons of pacemakers from the factory or from the hospitals they are delivered to. But bulk theft is not something George can pull off over and over. The authorities will quickly realize that someone is going after pacemakers. And after George's first heist, everyone will be looking for him.
If the project gets to the point of retrieving pacemakers after they are implanted, George's problems multiply enormously. It is impractical to remove a pacemaker from a living subject. George would need to steal them from funeral homes or crematoria. These places are required to collect the capsules for return to Oak Ridge, and conceivably might sometimes have more than one on hand at a time, but probably not more than a few. It's going to be a long slog, and it beggars belief that George would be able to get enough pacemakers this way without someone noticing that something was up.
The last resort is for George to locate people with pacemakers, murder, and dissect them. Even if George somehow knows whom to kill, he'd have to be Merlin to arrange the murder of 25,000 people without getting caught. Merlin doesn't need plutonium; he can create nuclear fireballs just by waving his magic wand.
If George does manage to collect the 25,000 capsules, his problems get even worse. He has to open the titanium capsules, already difficult because they are carefully made to be hard to open — you wouldn't want the plutonium getting out, would you? He has to open them without spilling the plutonium, or inhaling it, or making any sort of mess while extracting it. He has to do this 25,000 times without messing up, and without ingesting the tiniest speck of plutonium, or he is dead.
He has to find a way to safely store the plutonium while he is accumulating it. He has to keep it hidden not only from people actively looking for him — and they will be, with great yearning — but also from every Joe Blow who happens to be checking background radiation levels in the vicinity.
And George cannot afford to take his time and be cautious. He is racing against the clock, because every 464 days, 1% of his accumulated stock, however much that is, will turn into U-234 and be useless. The more he accumulates, the harder it is to keep up. If George has 25,000 pacemakers in a warehouse, ready for processing, one pacemaker-worth of Pu-238 will be going bad every two days.
In connection with this, my correspondent brought up the famous case of the Radioactive Boy Scout, which I had had in mind. (The RBS gathered a recklessly large amount of americium-241 from common household smoke detectors.) Ignoring again the unsuitability of americium for fission weapons (an even number of neutrons again), the project is obviously much easier. At the very least, you can try calling up a manufacturer of smoke alarms, telling them you are building an apartment complex in Seoul, and that you need to bulk-order 2,000 units or whatever. You can rob the warehouse at Home Depot. You can even buy them online.
[Other articles in category /tech] permanent link
Sat, 13 Jan 2018
How do plutonium-powered pacemakers work?
I woke up in the middle of the night wondering: Some people have implanted medical devices, such as pacemakers, that are plutonium-powered. How the hell does that work? The plutonium gets hot, but what then? You need electricity. Surely there is not a tiny turbine generator in there!
There is not, and the answer turns out to be really interesting, and to involve a bunch of physics I didn't know.
If one end of a wire is hotter than the other, electrons tend to diffuse from the hot end to the cold end; the amount of diffusion depends on the material and the temperature. Take two wires of different metals and join them into a loop. (This is called a thermocouple.) Make one of the joints hotter than the other. Electrons will diffuse from the hot joint to the cold joint. If there were only one metal, this would not be very interesting. But the electrons diffuse better through one wire (say wire A) than through the other (B), and this means that there will be net electron flow from the hot side down through wire A and then back up through B, creating an electric current. This is called the Seebeck effect. The potential difference between the joints is proportional to the temperature difference, on the order of a few hundred microvolts per kelvin. Because of this simple proportionality, the main use of the thermocouple is to measure the temperature difference by measuring the voltage or current induced in the wire. But if you don't need a lot of power, the thermocouple can be used as a current source.
In practice they don't use a single loop, but rather a long loop of alternating metals, with many junctions:
This is called a thermopile; when the heat source is radioactive material, as here, the device is called a radioisotope thermoelectric generator (RTG). The illustration shows the thermocouples strung out in a long line, but in an actual RTG you put the plutonium in a capsule and put the thermocouples in the wall of the capsule, with the outside joints attached to heat sinks. The plutonium heats up the inside joints to generate the current.
RTGs are more commonly used to power spacecraft, but there are a few dozen people still in the U.S. with plutonium-powered thermopile batteries in their pacemakers.
In pacemakers, the plutonium was sealed inside a titanium capsule, which was strong enough to survive an accident (such as a bullet impact or auto collision) or cremation. But Wikipedia says the technique was abandoned because of worries that the capsule wouldn't be absolutely certain to survive a cremation. (Cremation temperatures go up to around 1000°C; titanium melts at 1668°C.) Loose plutonium in the environment would be Very Bad.
(I wondered if there wasn't also worry about plutonium being recovered for weapons use, but the risk seems much smaller: you need several kilograms of plutonium to make a bomb, and a pacemaker has only around 135 mg, if I did the conversion from curies correctly. Even so, if I were in charge of keeping plutonium out of the wrong hands, I would still worry about this. It does not seem totally out of the realm of possibility that someone could collect 25,000 pacemakers. Opening 25,000 titanium capsules does sound rather tedious.)
Earlier a completely different nuclear-powered pacemaker was tried, based on promethium-powered betavoltaics. This is not a heat-conversion process. Instead, a semiconductor does some quantum physics magic with the electrons produced by radioactive beta decay. This was first demonstrated by Henry Moseley in 1913. Moseley is better-known for discovering that atoms have an atomic number, thus explaining the periodic table. The periodic table had previously been formulated in terms of atomic mass, which put some of the elements in the wrong order. Scientists guessed they were in the wrong order, because the periodicity didn't work, but they weren't sure why. Moseley was able to compute the electric charge of the atomic nucleus from spectrographic observations. I have often wondered what else Moseley would have done if he had not been killed in the European war at the age of 27.
It took a while to gather the information about this. Several of Wikipedia's articles on the topic are not up to their usual standards. The one about the radioisotope thermoelectric generator is excellent, though.
Thermopile illustration is by FluxTeq (Own work) CC BY-SA 4.0, via Wikimedia Commons.
[ Addendum 20180115: Commenters on Hacker News have pointed out that my concern about the use of plutonium in fission weapons is easily satisfied: the fuel in the batteries is Pu-238, which is not fissile. The plutonium to use in bombs is Pu-241, and indeed, when building a plutonium bomb you need to remove as much Pu-238 as possible, to prevent its non-fissile nuclei from interfering with the chain reaction. Interestingly, you can tell this from looking at the numbers: atomic nuclei with an odd number of neutrons are much more fissile than those with an even number. Plutonium is atomic number 94, so Pu-238 has an even number of neutrons and is not usable. The other isotope commonly used in fission is U-235, with 143 neutrons. I had planned to publish a long article today detailing the difficulties of gathering enough plutonium from pacemakers to make a bomb, but now I think I might have to rewrite it as a comedy. ]
[ Addendum 20170116: I published it anyway, with some editing. ]
[Other articles in category /tech] permanent link
Sun, 07 Jan 2018Well, yesterday I wrote an article about the drinking contest in the Gylfaginning and specifically about what was in the horn. I was very pleased with it. In the article, I said several times:
Obviously, the horn was full of mead.
A couple of my Gentle Readers have gently pointed out that I was wrong, wrong, wrong. I am deeply embarrassed.
The punch line of the story is that the end of the horn is attached to the ocean, and Thor cannot empty it, because he is trying to drink the ocean. The horn is therefore not filled with mead; it is filled with seawater.
How could I make such a dumb mistake? As I mentioned, the version I read first as a child stated that the horn was full of milk. And as a child I wondered: how could the horn be full of milk if it was attached to the sea? I decided that whatever enchantment connected the horn to the sea also changed the water to milk as it came into the horn. Later, when I realized that the milk was a falsehood, I retained my idea that there was an enchantment turning the seawater into something else.
But there is nothing in the text to support this. The jötunns don't tell Thor that the horn is full of mead. Adam Sjøgren pointed out that if they had, Thor would have known immediately that something was wrong. But as the story is, they bring the horn, they say that even wimps can empty it in three draughts, and they leave it at that. Wouldn't Thor notice that he is not drinking mead (or milk)? I think certainly, and perhaps he is initially surprised. But he is in a drinking contest and this is what they have brought him to drink, so he drinks it. The alternative is to put down the horn and complain, which would be completely out of character.
And the narrator doesn't say, and mustn't, that the horn was full of mead, because it wasn't; that would be in impermissible deceit of the audience. (“Hey, wait, you told us before that the horn was full of mead!”)
I wrote:
The story does not say what was in the horn. Because why would they bother to say what was in the horn? It was obviously mead.
No, it's not. It's because the narrator wants us to assume it is obviously mead, and then to spring the surprise on us as it was sprung on Thor: it was actually the ocean. The way it is told is a clever piece of misdirection. The two translators I quoted picked up on this, and I completely misunderstood it.
I have mixed feelings about Neil Gaiman, but Veit Heller pointed out that Gaiman understood this perfectly. In his Norse Mythology he tells the story this way:
He raised the brimming horn to his lips and began to drink. The mead of the giants was cold and salty…
In yesterday's article I presented a fantasy of Marion French, the author of my childhood “milk” version, hearing Snorri tell the story:
“Utgarða-Loki called his skutilsveinn, and requested him to bring the penalty-horn that his hirðmen were wont to drink from…”
“Excuse me! Excuse me, Mr. Sturluson! Just what were they wont to drink from it?”
“Eh, what's that?”
”What beverage was in the horn?”
“Why, mead, of course. What did you think it was, milk?”
But this couldn't have been how it went down. I now imagine it was more like this:
“Excuse me! Excuse me, Mr. Sturluson! Just what were they wont to drink from it?”
“Shhh! I'm getting to that! Stop interrupting!”
Thanks again to Adam Sjøgren and Veit Heller for pointing out my error, and especially for not wounding my pride any more than they had to.
[Other articles in category /oops] permanent link
Sat, 06 Jan 2018When I was a kid I had a book of “Myths and Legends of the Ages”, by Marion N. French. One of the myths was the story of Thor's ill-fated visit to Utgard. The jötunns of Utgard challenge Thor and Loki to various contests and defeat them all through a combination of talent and guile. In one of these contests, Thor is given a drinking horn and told that even the wimpiest of the jötunns is able to empty it of its contents in three drinks. (The jötunns are lying. The pointy end of the horn has been invisibly connected to the ocean.)
The book specified that the horn was full of milk, and as a sweet and innocent kiddie I did not question this. Decades later it hit me suddenly: no way was the horn filled with milk. When the mighty jötunns of Utgard are sitting around in their hall, they do not hold contests to see who can drink the most milk. Obviously, the horn was full of mead.
The next sentence I wrote in the draft version of this article was:
In the canonical source material (poetic edda maybe?) the horn is full of *mead*. Of course it is.
In my drafts, I often write this sort of bald statement of fact, intending to go back later and check it, and perhaps produce a citation. As the quotation above betrays, I was absolutely certain that when I hunted down the original source it would contradict Ms. French and say mead. But I have now hunted down the canonical source material (in the Prose Edda, it turns out, not the Poetic one) and as far as I can tell it does not say mead!
Here is an extract of an 1880 translation by Rasmus Björn Anderson, provided by WikiSource:
He went into the hall, called his cup-bearer, and requested him to take the sconce-horn that his thanes were wont to drink from. The cup-bearer immediately brought forward the horn and handed it to Thor. Said Utgard-Loke: From this horn it is thought to be well drunk if it is emptied in one draught, some men empty it in two draughts, but there is no drinker so wretched that he cannot exhaust it in three.
For comparison, here is the 1916 translation of Arthur Gilchrist Brodeur, provided by sacred-texts.com:
He went into the hall and called his serving-boy, and bade him bring the sconce-horn which the henchmen were wont to drink off. Straightway the serving-lad came forward with the horn and put it into Thor's hand. Then said Útgarda-Loki: 'It is held that this horn is well drained if it is drunk off in one drink, but some drink it off in two; but no one is so poor a man at drinking that it fails to drain off in three.'
In both cases the following text details Thor's unsuccessful attempts to drain the horn, and Utgard-Loki's patronizing mockery of him after. But neither one mentions at any point what was in the horn.
I thought it would be fun to take a look at the original Old Norse to see if the translators had elided this detail, and if it would look interesting. It was fun and it did look interesting. Here it is, courtesy of Heimskringla.NO:
Útgarða-Loki segir, at þat má vel vera, ok gengr inn í höllina ok kallar skutilsvein sinn, biðr, at hann taki vítishorn þat, er hirðmenn eru vanir at drekka af. Því næst kemr fram skutilsveinn með horninu ok fær Þór í hönd. Þá mælti Útgarða-Loki: "Af horni þessu þykkir þá vel drukkit, ef í einum drykk gengr af, en sumir menn drekka af í tveim drykkjum, en engi er svá lítill drykkjumaðr, at eigi gangi af í þrimr."
This was written in Old Norse around 1220, and I was astounded at how much of it is recognizable, at least when you already know what it is going to say. However, the following examples are all ill-informed speculation, and at least one of my confident claims is likely to be wrong. I hope that some of my Gentle Readers are Icelanders and can correct my more ridiculous errors.
“Höllina” is the hall. “Kallar” is to call in. The horn appears three times, as ‘horninu’, ‘horni’, and in ‘vítishorn’, which is a compound that specifies what kind of horn it is. “Þór í hönd” is “in Thor's hand”. (The ‘Þ’ is pronounced like the /th/ of “Thor”.) “Drekka”, “drukkit”, “drykk”, “drykkjum”, and “drykkjumaðr” are about drinking or draughts; “vel drukkit” is “well-drunk”. You can see the one-two-three in there as “einum-tveim-þrimr”. (Remember that the “þ” is a /th/.) One can almost see English in:
sumir menn drekka af í tveim drykkjum
which says “some men drink it in two drinks”. And “lítill drykkjumaðr” is a little-drinking-person, which I translated above as “wimp”.
It might be tempting to guess that “með horninu” is a mead-horn, but I'm pretty sure it is not; mead is “mjað” or “mjöð”. I'm not sure, but I think “með” here is just “with”, akin to modern German “mit”, so that:
næst kemr fram skutilsveinn með horninu
is something like “next, the skutilsveinn came with the horn”. (The skutilsveinn is something we don't have in English; compare trying to translate “designated hitter” into Old Norse.)
For a laugh, I tried putting this into Google Translate, and I was impressed with the results. It makes a heroic effort, and produces something that does capture some of the sense of the passage. It identifies the language as Icelandic, which while not correct, isn't entirely incorrect either. (The author, Snorri Sturluson, was in fact Icelandic.) Google somehow mistakes the horn for a corner, and it completely fails to get the obsolete term “hirðmenn” (roughly, “henchmen”), mistaking it for herdsmen. The skutilsveinn is one of the hirðmenn.
Anyway there is no mead here, and none in the rest of the story, which details Thor's unsuccessful attempts to drink the ocean. Nor is there any milk, which would be “mjólk”.
So where does that leave us? The jötunns challenge Thor to a drinking contest, and bring him a horn, and even though it was obviously mead, the story does not say what was in the horn.
Because why would they bother to say what was in the horn? It was obviously mead. When the boys crack open a cold one, you do not have to specify what it was that was cold, and nobody should suppose that it was a cold bottle of milk.
I imagine Marion N. French sitting by the fire, listening while Snorri tells the story of Thor and the enchanted drinking horn of Utgard:
“Utgarða-Loki called his skutilsveinn, and requested him to bring the penalty-horn that his hirðmen were wont to drink from…”
“Excuse me! Excuse me, Mr. Sturluson! Just what were they wont to drink from it?”
“Eh, what's that?”
”What beverage was in the horn?”
“Why, mead, of course. What did you think it was, milk?”
(Merriment ensues, liberally seasoned with patronizing mockery.)
(In preparing this article, I found it helpful to consult Zoëga's Concise Dictionary of Old Icelandic of 1910.)
[ Addendum 2018-01-17: Holy cow, I was so wrong. It was so obviously not mead. I was so, so wrong. Amazingly, unbelievably wrong. ]
[ Addendum 2018-03-22: A followup in which I investigate what organs Skaði looked at when choosing her husband, and what two things Loki tied together to make her laugh. ]
[Other articles in category /lang] permanent link
Fri, 05 Jan 2018Last month I wrote about the Turkish analog of “Joe Blow”. I got email from Gaal Yahas, who said
I bet you'll get plenty of replies on your last post about translating "John Doe" to different languages.
Sadly no. But M. Yahas did tell me in detail about the Hebrew version, and I did a little additional research.
The Hebrew version of “Joe Blow” / “John Doe” is unequivocally “Ploni Almoni” (”פלוני אלמוני“, I think). This usage goes back at least to the Book of Ruth, approximately 2500 years ago. Ruth's husband has died without leaving an heir, and custom demands that a close relative of her father-in-law should marry her, to keep the property in the family. Boaz takes on this duty, but first meets with another man, who is a closer relative than he:
Then went Boaz up to the gate, and sat him down there: and, behold, the kinsman of whom Boaz spake came by; unto whom he said, Ho, such a one! turn aside, sit down here. And he turned aside, and sat down.
(Ruth 4:1, KJV)
This other relative declines to marry Ruth. He is not named, and is referred to in the Hebrew version as Ploni Almoni, translated here as “such a one”. This article in The Jewish Chronicle discusses the possible etymology of these words, glossing “ploni” as akin to “covered” or “hidden” and “almoni” as akin to “silenced” or “muted”.
Ploni Almoni also appears in the book of Samuel, probably even older than Ruth:
David answered Ahimelek the priest, “The king sent me on a mission and said to me, 'No one is to know anything about the mission I am sending you on.' As for my men, I have told them to meet me at a certain place.”
(1 Samuel 21:2, NIV)
The mission is secret, so David does not reveal the meeting place to Ahimelek. Instead, he refers to it as Ploni Almoni. There is a similar usage at 2 Kings 6:8.
Apparently the use of “Ploni” in Hebrew to mean “some guy” continues through the Talmud and up to the present day. M. Yahas also alerted me to two small but storied streets in Tel Aviv. According to this article from Haaretz:
A wealthy American businessman was buying up chunks of real estate in Tel Aviv. He purchased the two alleyways with the intention of naming them after himself and his wife, even going so far as to put up temporary shingles with the streets’ new names. But he had christened the streets without official permission from the city council.
The mayor was so incensed by the businessman’s chutzpah that he decided to temporarily name the alleyways Simta Almonit and Simta Plonit.
And so they remain, 95 years later.
(M. Yahas explains that “Simta” means “alley” and is feminine, so that Ploni and Almoni take the feminine ‘-it’ ending to agree with it.)
Wikipedia has not one but many articles on this topic and related ones:
- List of placeholder names by
language
discusses not only Ploni Almoni and the yellow-booted Mehmet
Ağa, but many others as well and related matters, for example the
Latin word res (“thing”, “matter”, or “affair”).
- Oddly, the precursor of the featureless English word “thing” was much more specific, and in Icelandic and other northern Germanic languages it has retained some of this specificity.
- Placeholder name mainly concerns English, but more generally than just unspecified persons. For example, “widget” as a placeholder for an unspecified manufactured article.
- Indefinite and fictitious numbers such as “umpteen” and “zillions”, which I have discussed here before.
- Multiple-use name. For example, “Alan Smithee”.
- Another Hebrew version, this one more analogous to “John Smith”, is Israel Israeli.
- Hebrew Wikipedia has an article on פלוני
- An international
list of terms related to an average
person,
and many individual articles about specific examples such as:
- Joe Bloggs
- Jane Doe
- John Doe
- J. Random Hacker
- John Q. Public
- Joe Schmoe
- Tom, Dick, and Harry
- Note that the “Roe” of the famous 1973 Roe v. Wade Supreme Court case refers to “Jane Roe”, a variation on “Jane Doe”. Roe's actual name was McCovey.
My own tiny contribution in this area: my in-laws live in a rather distant and undeveloped neighborhood on the periphery of Seoul, and I once referred to it as 아무데도동 (/amudedo-dong/), approximately “nowhereville”. This is not standard in Korean, but I believe the meaning is clear.
[ Addendum 20230423: Every time I reread this article, I am startled by Haaretz's use of the word “christened” in this context. ]
[Other articles in category /lang] permanent link
Tue, 02 Jan 2018As I mentioned before, I have started another
blog, called Content-type:
text/shitpost.
The shitposts have been suffering quality creep and I am making an effort to lower my standards. I will keep you posted about how this develops. (I don't think the quality creep was the cause of lower volume this month; rather, I was on vacation for a week.)
Here is a list of last month's shitposts. I have added a short blurb to those that may be of more general interest.
- Drat, I messed up a shitpost
- Лох-Несского
- Bitcoin
- Mmm, sandalwood
- “Oh, you ate that?”
- My rule about eating everything
- Shitpost academy
- Life in the 21st Century
- Hey, that's not how that is meant to be used!
- Mmmm baked potatoes: Making a good baked potato takes a lot of time. It doesn't require skill or attention, just patience.
- Vegan dominatrix supplies
- Fiona sings Frosty
- Lesbians on my desktop
- Mathematical ladders
- A non-coincidence
- Jingle Bell Rock
- Stuff the kids know and stuff they don't
- Non-straight ladders
- Computers suck: episode 17787 of 31279: My epic journey into the wild and uncharted jungles of the Linux keyboard system. Or should I say systems.
- Testing for divisibility by 99
- More mathematical shitposting
- The Physical Layer: Two programmers discuss the OSI network model.
- Metonymy
- Too many suffixes
- Alphabet game: One of the games that Toph and I sometimes play in the car is the “Alphabet Game”: You try to spot the letter ‘A’, then ‘B’, and so on, and get through to ‘Z’ before you reach your destination.
- The spelling of “Dominus”
- Hot sake
- The Physical Layer: Alternative punch line
- Comparing heaps of beans
- Petits fours
- Fornax
I plan to continue to post monthly summaries here.
[Other articles in category /meta/shitpost] permanent link
Mon, 01 Jan 2018
Converting Google Docs to Markdown
I was on vacation last week and I didn't bring my computer, which has been a good choice in the past. But I did bring my phone, and I spent some quiet time writing various parts of around 20 blog posts on the phone. I composed these in my phone's Google Docs app, which seemed at the time like a reasonable choice.
But when I got back I found that it wasn't as easy as I had expected
to get the documents back out. What I really wanted was Markdown.
HTML would have been acceptable, since Blosxom accepts that also. I
could download a single document in one of several formats, including
HTML and ODF, but I had twenty and didn't want to do them one at a
time. Google has a bulk download feature, to download a zip file of
an entire folder, but upon unzipping I found that all twenty documents
had been converted to Microsoft's docx format and I didn't know a
good way to handle these. I could not find an option for a bulk
download in any other format.
Several tools will compose in Markdown and then export to Google docs, but the only option I found for translating from Google docs to Markdown was Renato Mangini's Google Apps script. I would have had to add the script to each of the 20 files, then run it, and the output appears in email, so for this task, it was even less like what I wanted.
The right answer turned out to be: Accept Google's bulk download of
docx files and then use Pandoc to convert the
docx to Markdown:
for i in *.docx; do
echo -n "$i ? ";
read j; mv -i "$i" $j.docx;
pandoc --extract-media . -t markdown -o "$(suf "$j" mkdn)" "$j.docx";
done
The read is because I had given the files Unix-unfriendly names like
Polyominoes as orthogonal polygons.docx and I wanted to give them
shorter names like orthogonal-polyominoes.docx.
The suf command is a little utility that performs the very common
task of removing or changing the suffix of a filename. The suf "$j"
mkdn command means that if $j is something like foo.docx it
should turn into foo.mkdn. Here's the tiny source code:
#!/usr/bin/perl
#
# Usage: suf FILENAME [suffix]
#
# If filename ends with a suffix, the suffix is replaced with the given suffix
# otheriswe, the given suffix is appended
#
# For example:
# suf foo.bar baz => foo.baz
# suf foo baz => foo.baz
# suf foo.bar => foo
# suf foo => foo
@ARGV == 2 or @ARGV == 1 or usage();
my ($file, $suf) = @ARGV;
$file =~ s/\.[^.]*$//;
if (defined $suf) {
print "$file.$suf\n";
} else {
print "$file\n";
}
sub usage {
print STDERR "Usage: suf filename [newsuffix]\n";
exit 1;
}
Often, I feel that I have written too much code, but not this time.
Some people might be tempted to add bells and whistles to this: what
if the suffix is not delimited by a dot character? What if I only
want to change certain suffixes? What if my foot swells up? What if
the moon falls out of the sky? Blah blah blah. No, for that we can
break out sed.
Next time I go on vacation I will know better and I will not use Google Docs. I don't know yet what instead. StackEdit maybe.
[ Addendum 20180108: Eric Roode pointed out that the program above has
a genuine bug: if given a filename like a.b/c.d it truncates the
entire b/c.d instead of just the d. The current version fixes
this. ]
[Other articles in category /Unix] permanent link