Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Early warning signs of shitty software |
| My big mistake about dense sets |
| Snow White in German |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 31 Jan 2021
Early warning signs of shitty software
Here's a screenshot of menu on the documentation page of a package I'm using. You can see right away that the software is going to be crappy:
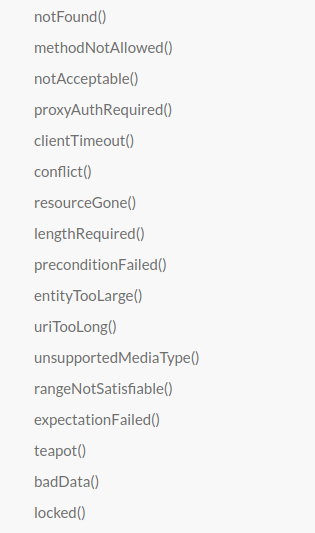
Major warning sign: The items are not in alphabetical order. (They are in numeric order, but the numbers are not displayed.)
- Was alphabetization too hard for these people?
Or did they simply not think for one second about who would want to use this menu and how?
If you are looking up a particular function to find out what it does, you have to do linear search on the list to find the one you want.
Yes, you could do full-text search on the whole page, but then what is the menu for?
Minor warning sign: But at least they included an API function to
generate the frequently-used HTTP 418 I'm a teapot status.
<sarcasm>Clearly a lot of thought here about what really matters.</sarcasm>
[Other articles in category /prog] permanent link
Sun, 03 Jan 2021Tonight I was thinking of
Mirror, mirror, on the wall
Who is the fairest of them all?
I remembered that the original was in German and wondered whether it had always rhymed. It turns out that it had:
Spieglein, Spieglein an der Wand,
Wer ist die Schönste im ganzen Land?
The English is a pretty literal translation.
When the wunderbare Spiegel gives the Queen the bad news, it says:
Frau Königin, Ihr seid die Schönste hier,
Aber Schneewittchen ist tausendmal schöner als Ihr.
(“Queen, you are the fairest one here, but Little Snow White is a thousand times as fair as you.”)
When the dwarfs see Snow White in one of their beds, they cry
Ei, du mein Gott!
which is German for “zOMG”.
Later the Queen returns to the mirror, expecting a better answer, but she gets this:
Frau Königin, Ihr seid die Schönste hier,
Aber Schneewittchen über den Bergen
Bei den sieben Zwergen
Ist noch tausendmal schöner als Ihr.
(“Queen, you are the fairest here, but Little Snow White up on the mountain with the seven dwarfs is still a thousand times as fair as you.”)
I like the way this poem here interpolates the earlier version, turning the A-A rhyme into A-B-B-A. The English version I have has “in the glen / little men” in place of “über den Bergen / sieben Zwergen”. The original is much better, but I am not sure English has any good rhymes for “dwarfs”. Except “wharfs”, but putting the dwarfs by the wharfs is much worse than putting them in the glen.
[ Thanks to Gaal Yahas for correcting my translation of noch and to Mario Lang for correcting my German grammar. ]
[ Addendum 20200115: Was the mirror magical? ]
[Other articles in category /lang] permanent link
Fri, 01 Jan 2021
My big mistake about dense sets
I made a big mistake in a Math Stack Exchange answer this week. It turned out that I believed something that was completely wrong.
Here's the question, are terminating decimals dense in the reals?. It asks if the terminating decimals (that is, the rational numbers of the form !!\frac m{10^n}!!) are dense in the reals. “Dense in the reals” means that if an adversary names a real number !!r!! and a small distance !!d!!, and challenges us to find a terminating decimal !!t!! that is closer than !!d!! to point !!r!!, we can always do it. For example, is there a terminating decimal !!t!! that is within !!0.0000001!! of !!\sqrt 2!!? There is: !!\frac{14142135}{10^7} = 1.4142135!! is closer than that; the difference is less than !!0.00000007!!.
The answer to the question is ‘yes’ and the example shows why: every real number has a decimal expansion, and if you truncate that expansion far enough out, you get a terminating decimal that is as close as you like to the original number. This is the obvious and straightforward way to prove it, and it's just what the top-scoring answer did.
I thought I'd go another way, though. I said that it's enough to show that for any two terminating decimals, !!a!! and !!b!!, there is another one that lies between them. I remember my grandfather telling me long ago that this was a sufficient condition for a set to be dense in the reals, and I believed him. But it isn't sufficient, as Noah Schweber kindly pointed out.
(It is, of course, necessary, since if !!S!! is a subset of !!\Bbb R!!, and !!a,b\in S!! but no element of !!S!! between these, then there is no element of !!S!! that is less than distance !!\frac{b-a}2!! of !!\frac{a+b}2!!. Both !!a!! and !!b!! are at that distance, and no other point of !!S!! is closer.)
The counterexample that M. Schweber pointed out can be explained quickly if you know what the Cantor middle-thirds set is: construct the Cantor set, and consider the set of midpoints of the deleted intervals; this set of midpoints has the property that between any two there is another, but it is not dense in the reals. I was going to do a whole thing with diagrams for people who don't know the Cantor set, but I think what follows will be simpler.
Consider the set of real numbers between 0 and 1. These can of course be represented as decimals, some terminating and some not. Our counterexample will consist of all the terminating decimals that end with !!5!!, and before that final !!5!! have nothing but zeroes and nines. So, for example, !!0.5!!. To the left and right of !!0.5!!, respectively, are !!0.05!! and !!0.95!!.
In between (and around) these three are: $$\begin{array}{l} \color{darkblue}{ 0.005 }\\ 0.05 \\ \color{darkblue}{ 0.095 }\\ 0.5 \\ \color{darkblue}{ 0.905 }\\ 0.95 \\ \color{darkblue}{ 0.995 }\\ \end{array}$$
(Dark blue are the new ones we added.)
And in between and around these are:
$$\begin{array}{l} \color{darkblue}{ 0.0005 }\\ 0.005 \\ \color{darkblue}{ 0.0095 }\\ 0.05 \\ \color{darkblue}{ 0.0905 }\\ 0.095 \\ \color{darkblue}{ 0.0995 }\\ 0.5 \\ \color{darkblue}{ 0.9005 }\\ 0.905 \\ \color{darkblue}{ 0.9095 }\\ 0.95 \\ \color{darkblue}{ 0.9905 }\\ 0.995 \\ \color{darkblue}{ 0.9995 }\\ \end{array}$$
Clearly, between any two of these there is another one, because around !!0.????5!! we've added !!0.????05!! before and !!0.????95!! after, which will lie between !!0.????5!! and any decimal with fewer !!?!! digits before it terminates. So this set does have the between-each-two-is-another property that I was depending on.
But it should also be clear that this set is not dense in the reals, because, for example, there is obviously no number of this type that is near !!0.7!!.
(This isn't the midpoints of the middle-thirds set, it's the midpoints of the middle-four-fifths set, but the idea is exactly the same.)
Happy New Year, everyone!
[Other articles in category /math] permanent link


