Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 27 Sep 2019
Typographical mysteries of Yeadon
Here are some pictures I took of the firehouse in Yeadon, PA.
Every time I drive past this, I wonder: is that the original letter “O”? Or was there originally a narrow “O” that was lost or damaged, and which couldn't be replaced with a matching letter?
Here's the Google Street View version, from November 2016. The letters are painted green, but the “O” is still the circular one.
[ Addendum 20191004: More about this ]
[Other articles in category /IT/typo] permanent link
Wed, 25 Sep 2019A couple of months ago I asked why the disco ball had to wait until the 20th century:
The 17th century could produce mirrors by gluing metal foil to the back of a piece of glass, so I wonder why they didn't. They wouldn't have been able to spotlight it, but they certainly could have hung it under an orbiculum. Was there a technological limitation, or did nobody happen to think of it?
I think the lighting issue is the show-stopper. To make good use of a disco ball you really do need a dark room and a spotlight. You can get reflections by hanging the ball under an orbiculum, but then the room will be lit by the orbiculum, and the reflections will be pale and washed out, at best.
Long ago I attended a series of lectures by Atsushi Akera on the hidden prerequisites for technological adoption. For example, you can't have practical skyscrapers without also inventing elevators, and you can't have practical automobiles without also inventing windshield wipers. (And windshields. And tires. And … )
This is an amusing example of the same sort. You can't have practical disco balls without also inventing spotlights.
But now I kinda wonder about the possibility of wowing theatre-goers in 1850 with a disco ball, lit by a sort of large hooded lantern containing a limelight and a (lighthouse-style) Fresnel lens.
[ Addendum: Apparently, nobody but me has ever used the word “orbiculum”. I don't know how I started using it, but it seems that the correct word for what I meant is oculus. ]
[ Addendum 20241218: I wondered what had become of Akera, and thanks to the Wonders of the Internet I was able to find out the delightful answer. She had had a career at Rensselaer in Troy, New York. Then she opened a café nearby, owned and run cooperatively by several transgender and non-gender-conforming people, presumably including herself. (She was male-preesnting when I knew her in the 1990s.) It gives me a warm feeling, seeing that the world is finding more ways to let people be themselves, and that because of the Internet I can sometimes share their joyful stories. ]
[Other articles in category /tech] permanent link
Yesterday Katara asked me about impeachment, and in mentioning the impeachment of Andrew Johnson, I realized that I didn't know who would have assumed the presidency, had Johnson been convicted. Who was Johnson's vice president?
Well, I couldn't remember because he didn't have one. Until the ratification of the 25th Amendment in 1967, there was no provision for the replacement of a vice-president except through a normal election.
Under the Presidential Succession Act of 1792, next in line was the President Pro Tempore of the Senate. This is a largely ceremonial position, filled by a senator, and elected by the Senate. The President Pro Tempore in 1868 was Benjamin Wade, senator from Ohio. Wade, as a senator, would be voting on Johnson's conviction and therefore had an enormous conflict of interest: if Johnson was removed, Wade would assume the presidency.
There were calls for Wade to abstain from voting. Which he did. Not! Ha ha, of course he didn't. He voted to convict.
The conviction, famously, fell short by one vote: it went 35–19 in favor of conviction, but they needed 36 votes to convict. Suppose it had gone 36-18, with Wade's vote being the 36th, and Wade taking over the presidency as a result? Wikipedia claims (with plausible citation) that at Wade told at least one other senator what cabinet position he could expect to receive in exchange for his vote to convict.
How could those 1792 folks not have foreseen this? Sheesh.
Government is hard. Really, really hard.
Thinking about the Civil War era of U.S. history, I always have ambivalent feelings. First, hope and relief: “Our current situation could be much worse than it is”, followed by dread: “Our current situation might get much worse than it is”.
[ Maybe I should also mention that many sources suggest that Johnson would have been removed had his successor been someone less divisive than Wade. ]
[Other articles in category /politics] permanent link
Tue, 17 Sep 2019Suppose you have a bottle that contains !!N!! whole pills. Each day you select a pill at random from the bottle. If it is a whole pill you eat half and put the other half back in the bottle. If it is a half pill, you eat it. How many half-pills can you expect to have in the bottle the day after you break the last whole pill?
Let's write !!H(N)!! for the expected number of half-pills left, if you start with !!N!!. It's easily seen that !!H(N) = 0, 1, \frac32!! for !!N=0,1,2!!, and it's not hard to calculate that !!H(3) = \frac{11}{6}!!.
For larger !!N!! it's easy to use Monte Carlo simulation, and find that !!H(30)!! is almost exactly !!4!!. But it's also easy to use dynamic programming and compute that $$H(30) = \frac{9304682830147}{2329089562800}$$ exactly, which is a bit less than 4, only !!3.994987!!. Similarly, the dynamic programming approach tells us that $$H(100) = \frac{14466636279520351160221518043104131447711}{2788815009188499086581352357412492142272}$$ which is about !!5.187!!.
(I hate the term “dynamic programming”. It sounds so cool, but then you find out that all it means is “I memoized the results in a table”. Ho hum.)
As you'd expect for a distribution with a small mean, you're much more likely to end with a small number of half-pills than a large number. In this graph, the red line shows the probability of ending with various numbers of half-pills for an initial bottle of 100 whole pills; the blue line for an initial bottle of 30 whole pills, and the orange line for an initial bottle of 5 whole pills. The data were generated by this program.
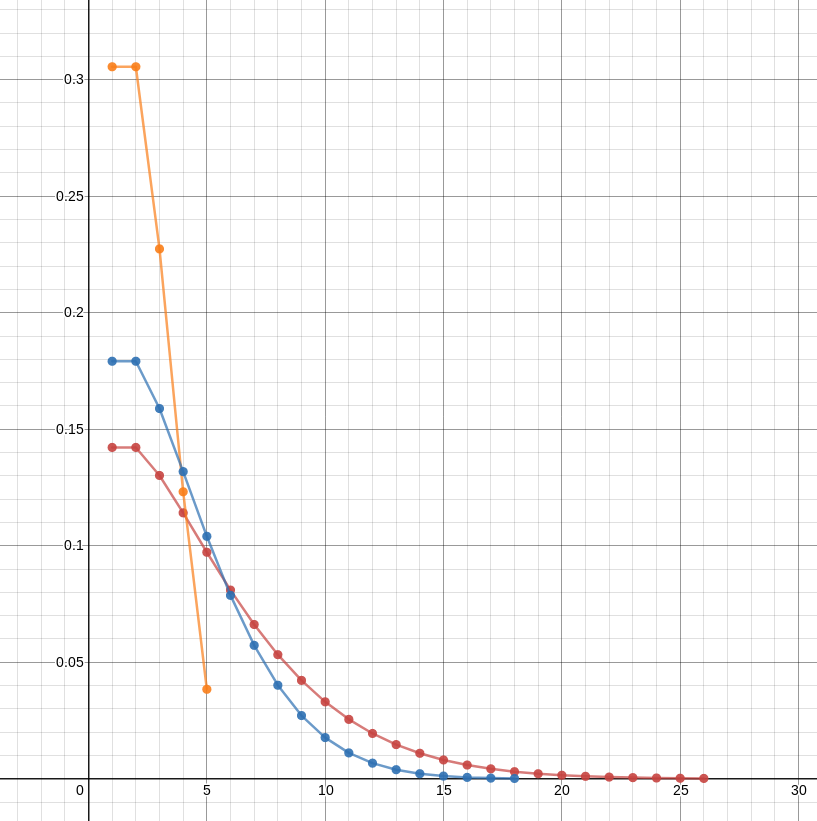
The !!E!! function appears to increase approximately logarithmically. It first exceeds !!2!! at !!N=4!!, !!3!! at !!N=11!!, !!4!! at !!N=31!!, and !!5!! at !!N=83!!. The successive ratios of these !!N!!-values are !!2.75, 2.81,!! and !!2.68!!. So we might guess that !!H(N)!! first exceeds 6 around !!N=228!! or so, and indeed !!H(226) < 6 < H(227)!!. So based on purely empirical considerations, we might guess that $$H(N) \approx \frac{\log{\frac{15}{22}N}}{\log 2.75}.$$
(The !!\frac{15}{22}!! is a fudge factor to get the curves to line up properly.)
I don't have any theoretical justification for this, but I think it might be possible to get a bound.
I don't think modeling this as a Markov process would work well. There are too many states, and it is not ergodic.
[ Addendum 20190919: Ben Handley informs me that !!H(n)!! is simply the harmonic numbers, !!H(n) = \sum_1^n \frac1n!!. I feel a little foolish that I did not notice that the first four terms matched. The appearance of !!H(3)=\frac{11}6!! should have tipped me off. Thank you, M. Handley. ]
[ Addendum 20190920: I was so fried when I wrote this that I also didn't notice that the denominator I guessed, !!2.75!!, is almost exactly !!e!!. (The correct value is !!e!!.) I also suspect that the !!\frac{15}{22}!! is just plain wrong, and ought to be !!e^\gamma!! or something like that, but I need to take a closer look. ]
[ Addendum 20191004: More about this ]
[Other articles in category /math] permanent link
Today it occurred to me that in the many comedy duos that feature a “straight man” and a “comedian”, the straight man is invariably named first. The central example, of course, is Abbott and Costello. But we also have:
- Laurel and Hardy
- Burns and Allen
- Rowan and Martin
- Martin and Lewis
- Bert and Ernie
and this even extends to entirely fictitious pairs such as Jeeves and Wooster, Harold and Kumar, or Sam and Max, Freelance Police. Also, if you are a mathematician, Smothers and Smothers. This is why people hate mathematicians.
I did Google search for "Kermit and Fozzie" (hits outnumber "Fozzie and Kermit" by around three-to-one) and "Kermit and Miss Piggy" (hits outnumber "Miss Piggy and Kermit", although only by about 60%.)
Wikipedia says this is no accident!
In vaudeville, effective straight men were much less common than comedians. The straight man's name usually appeared first and he usually received 60% of the take.
But my co-worker Jeff Culverhouse found a counterexample: Silent Bob is certainly the straight man of Jay and Silent Bob.
Wikipedia also has a list of American Comedy Duos. Not all of them follow the straight man / comedian pattern, and I don't recognize many of those that do. More research is needed.
Addenda
I wanted to find a gender-neutral term for "straight man", but failed.
20220623
I thought of another counterexample: Wallace and Gromit.
20230221
Google search hits for “Tom and Dick Smothers” outnumber those for “Dick and Tom Smothers” to more than 7 to 1. (20600 to 2670.) Dick was the straight man.
20250508
Michel Dingler points out that R2-D2 and C-3PO are another counterexample:
Popular consensus in my Mastodon timeline seems to agree.
I haven't seen it, but I suppose that in the action comedy series B.J. and the Bear, B.J. (played by Greg Evigan) is the straight man to the Bear (played by some monkey).
[Other articles in category /misc] permanent link
According to the New York Times of 10 March 1982:
In 1970, for example, President Nixon and Vice President Agnew did a piano duet built around their so-called ''Southern Strategy.'' No matter what song Mr. Nixon played, Mr. Agnew cut in with ''Dixie.'' The audience found it uproariously funny, as they did the spectacle of the Vice President clicking his heels, saluting and telling Mr. Nixon, ''Yes suh, Mr. President, ah agree with you completely on yoah Southern strategy.''
And yet the cruel earth refused to open and swallow everyone involved.
[Other articles in category /politics] permanent link
Mon, 16 Sep 201923 USC §131 controls the display of billboards and other signs within 660 feet of a federal interstate highway. As originally enacted in 1965, there were a few exceptions, such as directional signs, and signs advertising events taking place on the property on which they stood, or the sale or lease of that property.
Today I learned that under the Federal-Aid Highway Act of 1978, the list of exceptions was extended to include:
signs, displays, and devices advertising the distribution by nonprofit organizations of free coffee to individuals traveling on the Interstate System or the primary system.
There is no exception for free tea.
[ Addendum 20191002: A 2015 Supreme Court decision imperils the free coffee exception, according to three of the justices. I've written a detailed followup. ]
[Other articles in category /law] permanent link
Sat, 14 Sep 2019[ (Previously) ]
Wikipedia has an animation that shows the convergence of the Maclaurin series for the exponential function:
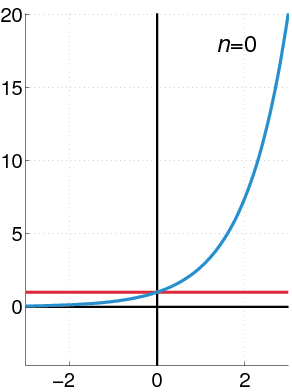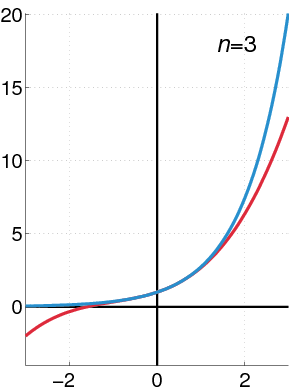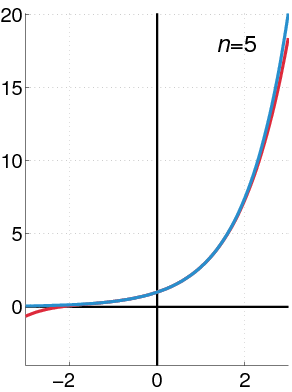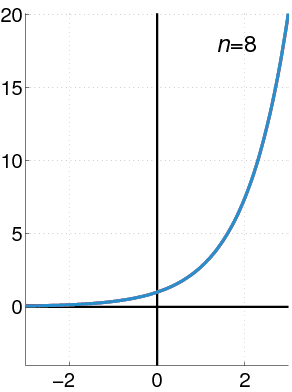
This makes it look a lot better-behaved than it is. First, because it only shows a narrow region around the center of convergence. But also, it emphasizes the right-hand quadrant, where the convergence is monotone.
If you focus on the left-hand side instead, you see the appoximations thrashing back and forth like a screen door in a hurricane:
This is the same as Wikipedia's animation, just focused on a slightly different region of the plane. But how different it looks!
(Individual frames are available)
[Other articles in category /math] permanent link
Fare-dodging insurance businesses
A recent article described a business that insured transit riders against being fined for fare-dodging, and asked:
Does anyone remember this? Can someone point me to a reference?
Florian Ilgenfritz wrote to tell me that they had heard of such a system in Berlin, and this let them to the German Wikipedia article on Schwarzfahrerversicherung, which is precisely what I was looking for. (“Schwarzfahrer“ is fare-dodging, literally “blackriding”, and “versicherung” is insurance.) The article mentions similar systems in Paris and Stockholm, and also one run by the student union of the University of Hanover, which had to shut down because increased fare enforcement on the Hanover metro depleted the benefits pool.
One Paris version, as described at this archived page, was amusingly called le Réseau pour l’Abolition des Transports Payants. (Its initials, RATP, are the same as those of the state-owned public transportation operator). Each RATP group was an insurance cooperative. Would-be fare-dodgers would meet at the beginning of the month and contribute to a pool, from which fines would be reimbursed.
The page says:
- a group will have 10–30 members
- each member will put 6–7 Euros into the kitty
- “even a very unlucky person cannot be fined more than 4 or 5 times a year”
Each member is putting in €72–84 per year. Even if every member is maximally unlucky, this is enough to cover a fine of €16–17, and two or three times that much of not everyone is caught so frequently.
NPR reported on the Stockholm version as recently as 2015, and the Paris version in 2010. There is a German-language article from Der Spiegel from around the same time. This article claims that in one Berlin association, only 50% of the members’ €11 monthly premium had to be paid out in benefits, leaving a €33,000 profit. No word on what happened to the profit. Perhaps it was reinvested for the benefit pool, or perhaps the least scrupulous of the fund organizers embezzled it.
Most Philadelphia public transit is guarded by turnstiles, making fare-dodging more troublesome. The exception is on the regional rail system, where the passenger can board, with or without a ticket, and the conductor comes around to punch tickets, or sell higher-priced on-train tickets to people without any. This is well enough enforced that a fare dodger would be caught almost every time and have to pay the higher price, so the insurance scheme would not be practical. But I remember back in the 1990s it would sometimes be worth while to ride regional rail for a couple of stops in Center City, rather than the subway. The on-board regional rail fare was substantially higher than the subway fare, but the chance of getting off the crowded train without having to buy a ticket was good.
A recent article in the Philadelphia Inquirer describes a different fare-dodging scheme. SEPTA will sell a weekly pass, good for up to 56 rides, for $25.50, or 45.5¢ per ride. The cash fare is $2.50. The fare-dodgers will buy a weekly pass, and then stand at the turnstile offering to let cash-fare riders use it for $2 cash. The cash-fare rider is ahead by $0.50 and the entrepreneur can earn a return of up to 449% on their $22.50 investment.
Exercise for the reader: where is the extra value here and why doesn't SEPTA capture it? Are the entrepreneurs increasing or depleting the public good?
Thanks to M. Ilgenfritz for the initial references, which provided enough for me to get started following up the details on my own.
[Other articles in category /misc] permanent link
Tue, 10 Sep 2019
Chicken-fondling discouraged by the CDC
This week, according to the Washington Post, Kissing chickens is bad for your health, CDC warns. (The story was also reported by Newsweek last week. )
Specifically, the CDC Investigation Notice advises:
Don’t kiss backyard poultry or snuggle them and then touch your face or mouth.
This isn't quite clear. Is it:
Don’t ((kiss backyard poultry)
or
((snuggle them) and (then touch your (face or mouth))))
or is it rather
Don’t (((kiss backyard poultry) or (snuggle them))
and (then touch your (face or mouth)))
I think they mean the former? But if it's the latter, then the Post has it wrong, and it's okay to kiss backyard poultry, as long as you don't then touch your face or mouth.
But is this really a pressing issue? Apparently so! Kissing chickens, according to the CDC research, is disturbingly common:
Among respondents with baby poultry exposure … 13% (53/400) reported kissing baby birds.
No word on how many of the 53 chicken-kissers tried to use their tongues.

[ Addendum 20210520: This has come around again:
The CDC reports that 163 people have contracted salmonella from backyard poultry, and again implores people not to kiss or snuggle them. ]
[ Addendum 20210523: The blonde lady, I have learned, is Tiara Soleim, who, when she was a contestant on The Bachelor, was also identified as a “chicken enthusiast”. The Tucker Carlson segment contains footage of her demonstrating how to snuggle and kiss chickens. ]
[Other articles in category /misc] permanent link
Sun, 08 Sep 2019
The exponential function is a miracle
The Maclaurin series for the exponential function converges for every complex number !!x!!: $$1 - x + \frac{x^2}{2} - \frac{x^3}{6} + \frac{x^4}{24} - \ldots = e^{-x} $$
Say that !!x!! is any reasonably large number, such as 5. Then !!e^{-x}!! is close to zero, But the terms of the series are not close to zero. For !!x=5!! we have: $$ 1 - 5 + 12.5 - 20.83 + 26.04 - 26.04 + 21.7 - 15.5 + 9.69 - 5.38 + \ldots \approx {\Large 0}$$
Somehow all these largish random numbers manage to cancel out almost completely. And the larger we make !!x!!, the more of these largish random numbers there are, the larger they are, and yet the more exactly they cancel out. For even as small an argument as !!x=20!!, the series begins with 52 terms that vary between 1 and forty-three million, and these somehow cancel out almost entirely. The sum of these 52 numbers is !!-0.4!!.
In this graph, the red lines are the various partial sums (!!1-x, 1-x+\frac{x^2}2, !! etc.) and the blue line is the total sum !!e^{-x}!!.
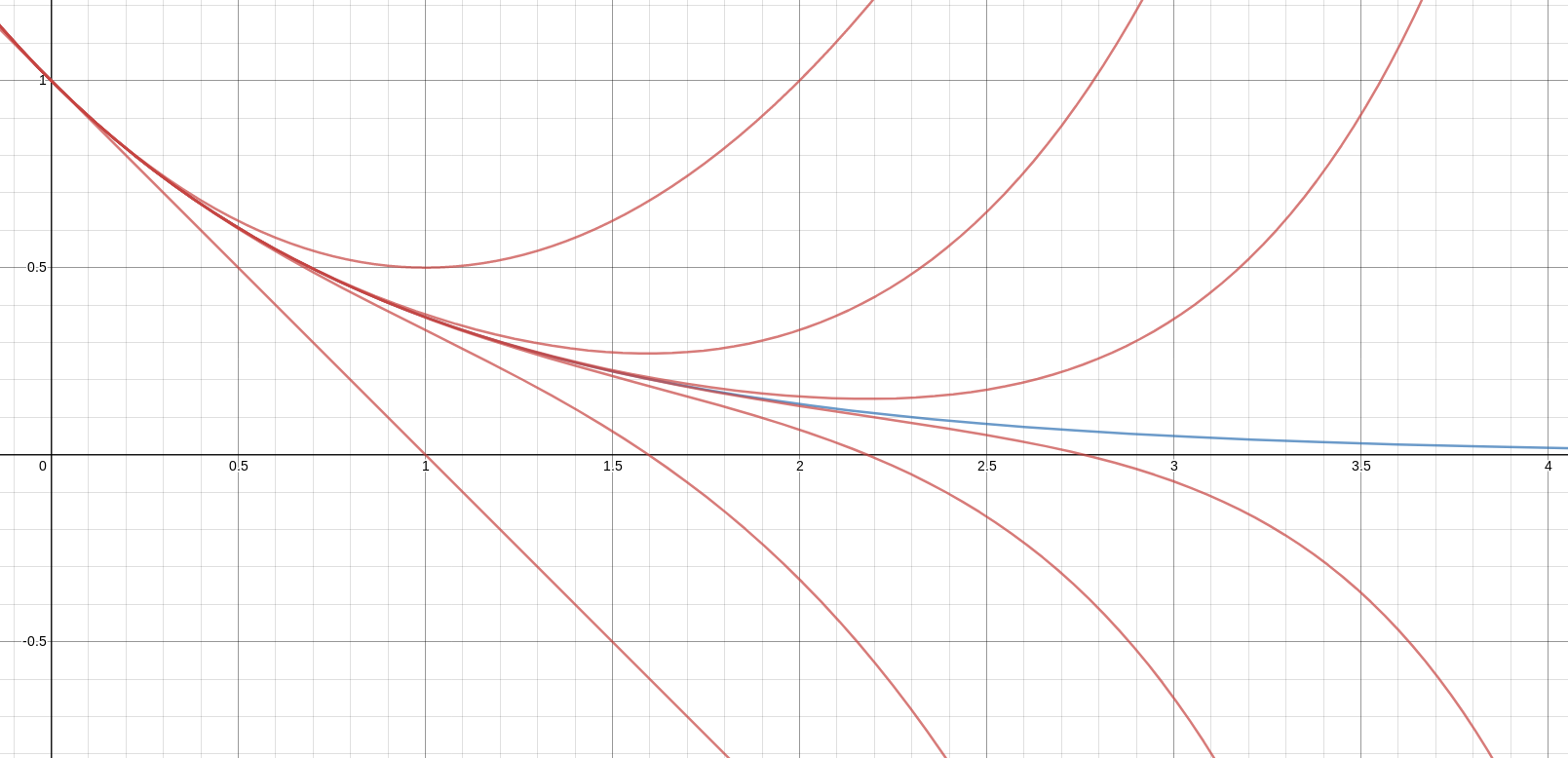
As you can see, each red line is a very bad approximation to the blue one, except within a rather narrow region. And yet somehow, it all works out in the end.
[ (Addendum) ]
[Other articles in category /math] permanent link
Mon, 02 Sep 2019I think a disco ball would not be out of place at Versailles.
This got me thinking about what if all of Versailles had been tricked out in awesome 1970's disco style? I could easily picture Louis XIV in a white leisure suit, open to the navel, with gold chains and bell-bottom trousers, his platform shoes glittering with real diamonds. (Surely you didn't think le Roi Soleil would wear rhinestones?)
I have been enjoying this mental picture for some time now, but part of it is wrong: the bell-bottoms. Louis didn't have a pretty face. But he had great legs, he knew it, and he never missed an opportunity to show them off:
Notice the recurring theme: skin-tight trousers or tights. Fancy garters. When he's wearing heavy state robes, they're cut away or swept back to expose his legs, and he always stands sideways or sticks them out so that you can see them.
(In that last picture, the diamond studded platform shoes, just as I said. Nailed it!)
Here Louis is fancifully depicted as Alexander the Great. He surely did not dress up in costume for the portrait. But the unknown painter knew what Louis liked and made him bare-legged, with a diaphanous blue tunic:
This is not a man who is going to wear bell-bottoms.
[ Addendum 20190903: “Louis loved ballet and frequently danced in court ballets during the early half of his reign. In general, Louis was an eager dancer who performed 80 roles in 40 major ballets.” Thanks to Akiva Leffert from bringing this to my attention. ]
[Other articles in category /misc] permanent link










-th.jpg)


