Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Basterma |
| Benjamin Franklin and the Exercises of Ignatius |
| Master of the Pecos River |
| The corner of Pennsylvania |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 30 Dec 2020
Benjamin Franklin and the Exercises of Ignatius
Recently I learned of the Spiritual Exercises of St. Ignatius. Wikipedia says (or quotes, it's not clear):
Morning, afternoon, and evening will be times of the examinations. The morning is to guard against a particular sin or fault, the afternoon is a fuller examination of the same sin or defect. There will be a visual record with a tally of the frequency of sins or defects during each day. In it, the letter 'g' will indicate days, with 'G' for Sunday. Three kinds of thoughts: "my own" and two from outside, one from the "good spirit" and the other from the "bad spirit".
This reminded me very strongly of Chapter 9 of Benjamin Franklin's Autobiography, in which he presents “A Plan for Attaining Moral Perfection”:
My intention being to acquire the habitude of all these virtues, I judg'd it would be well not to distract my attention by attempting the whole at once, but to fix it on one of them at a time… Conceiving then, that, agreeably to the advice of Pythagoras in his Golden Verses, daily examination would be necessary, I contrived the following method for conducting that examination.
I made a little book, in which I allotted a page for each of the virtues. I rul'd each page with red ink, so as to have seven columns, one for each day of the week, marking each column with a letter for the day. I cross'd these columns with thirteen red lines, marking the beginning of each line with the first letter of one of the virtues, on which line, and in its proper column, I might mark, by a little black spot, every fault I found upon examination to have been committed respecting that virtue upon that day.
I determined to give a week's strict attention to each of the virtues successively. Thus, in the first week, my great guard was to avoid every the least offense against Temperance, leaving the other virtues to their ordinary chance, only marking every evening the faults of the day.
So I wondered: was Franklin influenced by the Exercises? I don't know, but it's possible. Wondering about this I consulted the Mighty Internet, and found two items in the Woodstock Letters, a 19th-century Jesuit periodical, wondering the same thing:
The following extract from Franklin’s Autobiography will prove of interest to students of the Exercises: … Did Franklin learn of our method of Particular Examen from some of the old members of the Suppressed Society?
(“Woodstock Letters” Volume XXXIV #2 (Sep 1905) p.311–313)
I can't guess at the main question, but I can correct one small detail: although this part of the Autobiography was written around 1784, the time of which Franklin was writing, when he actually made his little book, was around 1730, well before the suppression of the Society.
The following issue takes up the matter again:
Another proof that Franklin was acquainted with the Exercises is shown from a letter he wrote to Joseph Priestley from London in 1772, where he gives the method of election of the Exercises. …
(“Woodstock Letters” Volume XXXIV #3 (Dec 1905) p.459–461)
Franklin describes making a decision by listing, on a divided sheet of paper, the reasons for and against the proposed action. And then a variation I hadn't seen: balance arguments for and arguments against, and cross out equally-balanced sets of arguments. Franklin even suggests evaluations as fine as matching two arguments for with three slightly weaker arguments against and crossing out all five together.
I don't know what this resembles in the Exercises but it certainly was striking.
[Other articles in category /book] permanent link
Sat, 26 Dec 2020This tweet from Raffi Melkonian describes the appetizer plate at his house on Christmas. One item jumped out at me:
basterma (err, spicy beef prosciutto)
I wondered what that was like, and then I realized I do have some idea, because I recognized the word. Basterma is not an originally Armenian word, it's a Turkish loanword, I think canonically spelled pastırma. And from Turkish it made a long journey through Romanian and Yiddish to arrive in English as… pastrami…
For which “spicy beef prosciutto” isn't a bad description at all.
[Other articles in category /lang/etym] permanent link
Tue, 15 Dec 2020The world is so complicated! It has so many things in it that I could not even have imagined.
Yesterday I learned that since 1949 there has been a compact between New Mexico and Texas about how to divide up the water in the Pecos River, which flows from New Mexico to Texas, and then into the Rio Grande.
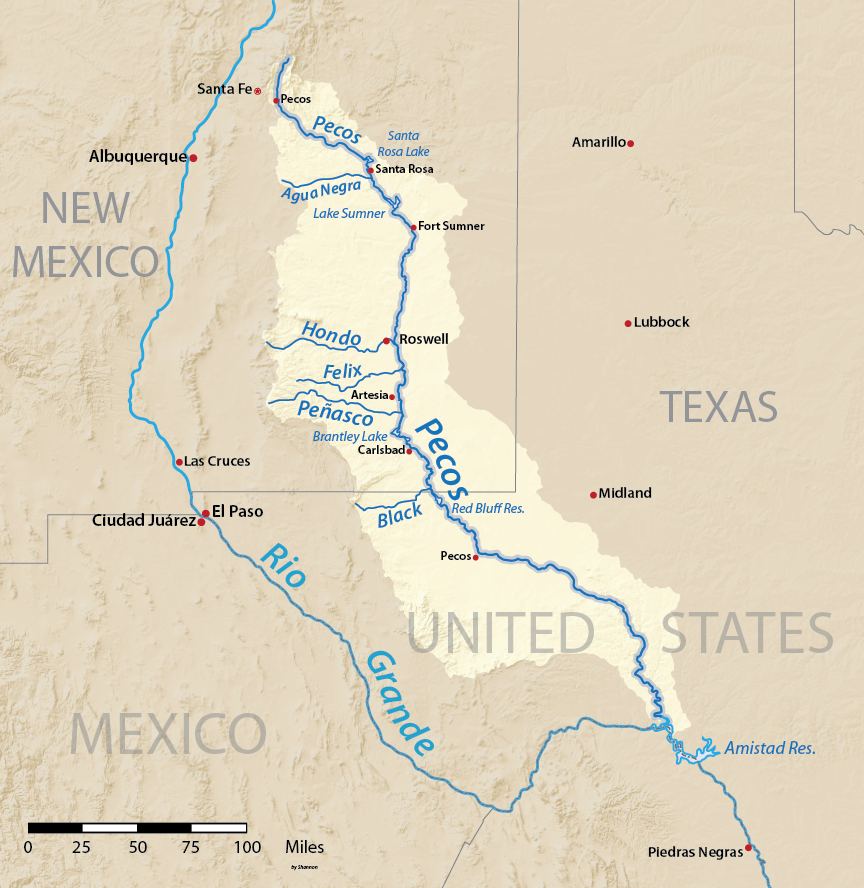
New Mexico is not allowed to use all the water before it gets to Texas. Texas is entitled to receive a certain amount.
There have been disputes about this in the past (the Supreme Court case has been active since 1974), so in 1988 the Supreme Court appointed Neil S. Grigg, a hydraulic engineer and water management expert from Colorado, to be “River Master of the Pecos River”, to mediate the disputes and account for the water. The River Master has a rulebook, which you can read online. I don't know how much Dr. Grigg is paid for this.
In 2014, Tropical Storm Odile dumped a lot of rain on the U.S. Southwest. The Pecos River was flooding, so Texas asked NM to hold onto the Texas share of the water until later. (The rulebook says they can do this.) New Mexico arranged for the water that was owed to Texas to be stored in the Brantley Reservoir.
A few months later Texas wanted their water. "OK," said New Mexico. “But while we were holding it for you in our reservoir, some of it evaporated. We will give you what is left.”
“No,” said Texas, “we are entitled to a certain amount of water from you. We want it all.”
But the rule book says that even though the water was in New Mexico's reservoir, it was Texas's water that evaporated. (Section C5, “Texas Water Stored in New Mexico Reservoirs”.)
[ Addendum 20230528: To my amazement this case has come to my attention again, because legal blogger Adam Unikowsky cited it as one of “the [ten] least significant cases of the decade”. I wrote a brief followup about why I enjoy Unikowsky's Legal Newsletter. ]
[Other articles in category /law] permanent link
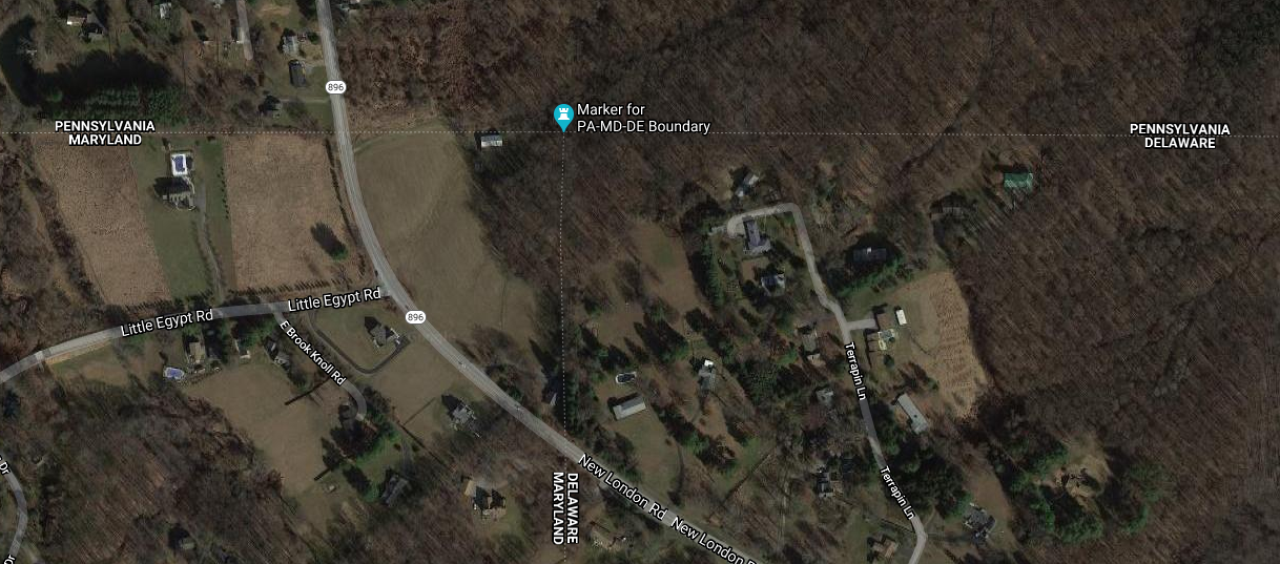
Thu, 10 Dec 2020I see that the Pennsylvania-Delaware-Maryland triple border is near White Clay Creek State Park, outside of Newark, DE. That sounds nice, so perhaps I will stop by and take a look, and see if there really is white clay in the creek.
I had some free time yesterday, so that is what I did. The creek is pretty. I did not see anything that appeared to be white clay. Of course I did not investigate extensively, or even closely, because the weather was too cold for wading. But the park was beautiful.
There is a walking trail in the park that reaches the tripoint itself. I didn't walk the whole trail. The park entrance is at the other end of the park from the tripoint. After wandering around in the park for a while, I went back to the car, drove to the Maryland end of the park, and left the car on the side of the Maryland Route 896 (or maybe Pennsylvania Route 896, it's hard to be sure). Then I cut across private property to the marker.
The marker itself looks like this:
As you see, the Pennsylvania sides of the monument are marked with ‘P’ and the Maryland side with ‘M’. The other ‘M’ is actually in Delaware. This Newark Post article explains why there is no ‘D’:
The marker lists only Maryland and Pennsylvania, not Delaware, because in 1765, Delaware was part of Pennsylvania.
This does not explain the whole thing. The point was first marked in 1765 by Mason and Dixon and at that time Delaware was indeed part of Pennsylvania. But as you see the stone marker was placed in 1849, by which time Delaware had been there for some time. Perhaps the people who installed the new marker were trying to pretend that Delaware did not exist.
[ Addendum 20201218: Daniel Wagner points out that even if the 1849 people were trying to depict things as they were in 1765, the marker is still wrong; it should have three ‘P’ and one ‘M’, not two of each. I did read that the surveyors who originally placed the 1849 marker put it in the wrong spot, and it had to be moved later, so perhaps they were just not careful people. ]
Theron Stanford notes that this point is also the northwestern corner of the Wedge. This sliver of land was east of the Maryland border, but outside the Twelve-Mile Circle and so formed an odd prodtrusion from Pennsylvania. Pennsylvania only reliquinshed claims to it in 1921 and it is now agreed to be part of Delaware. Were the Wedge still part of Pennsylvania, the tripoint would have been at its southernmost point.
Looking at the map now I see that to get to the marker, I must have driven within a hundred yards of the westmost point of the Twelve-Mile Circle itself, and there is a (somewhat more impressive) marker there. Had I realized at the time I probably would have tried to stop off.
I have some other pictures of the marker if you are not tired of this yet.
[ Addendum 20201211: Tim Heany asks “Is there no sign at the border on 896?” There probably is, and this observation is a strong argument that I parked the car in Maryland. ]
[ Addendum 20201211: Yes, ‘prodtrusion’ was a typo, but it is a gift from the Gods of Dada and should be treasured, not thrown in the trash. ]
[Other articles in category /misc] permanent link