Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 31 May 2020
Reordering git commits (not patches) with interactive rebase
This is the third article in a series. ([1] [2]) You may want to reread the earlier ones, which were in 2015. I'll try to summarize.
The original issue considered the implementation of some program feature X. In commit A, the feature had not yet been implemented. In the next commit C it had been implemented, and was enabled. Then there was a third commit, B, that left feature X implemented but disabled it:
no X X on X off
A ------ C ------ B
but what I wanted was to have the commits in this order:
no X X off X on
A ------ B ------ C
so that when X first appeared in the history, it was disabled, and then a following commit enabled it.
The first article in the series began:
I know, you want to say “Why didn't you just use
git-rebase?” Becausegit-rebasewouldn't work here, that's why.
Using interactive rebase here “to reorder B and C” will not work
because git-rebase reorders patches, not commits. It will attempt
to apply the B→C diff as a patch to A, and will fail, because
the patch is attempting to disable a feature that isn't implemented in
commit A.
My original articles described a way around this, using the plumbing
command git-commit-tree to construct the desired commits with the
desired parents. I also proposed that one could write a
git-reorder-commits command to automate the process, but my proposal
gave it a clumsy and bizarre argument convention.
Recently, Curtis Dunham wrote to me with a much better idea that uses the
interactive rebase UI to accomplish the same thing much more cleanly.
If we had B checked out and we tried git rebase -i A, we would get a
little menu like this:
pick ccccccc implement feature X
pick bbbbbbb disable feature X
As I said before, just switching the order of these two pick
commands doesn't work, because the bbbbbbb diff can't be applied on
the base commit A.
M. Dunham's suggestion is to use git-rebase -i as usual, but instead
of simply reversing the order of the two pick commands, which
doesn't work, also change them to exec git snap:
exec git snap bbbbbbb disable feature X
exec git snap ccccccc implement feature X
But what's git snap? Whereas pick means
run
git showto construct a patch from the next commit,
then apply that patch to the current tree
git snap means:
get the complete tree from the next commit,
and commit it unchanged
That is, “take a snapshot of that commit”.
It's simple to implement:
# read the tree from the some commit and store it in the index
git read-tree $SHA^{tree}
# then commit the index, re-using the old commit message
git commit -C $SHA
There needs to be a bit of cleanup to get the working tree back into
sync with the new index.
M. Dunham's actual implementation
does this with git-reset (which I'm not sure is quite sufficient),
and has some argument checking, but that's the main idea.
I hadn't know about the exec command in a git-rebase script, but
it seems like it could do all sorts of useful things. The
git-rebase man page suggests
inserting exec make at points in your script, to check that your
reordering hasn't broken the build along the way.
Thank you again, M. Dunham!
[Other articles in category /prog] permanent link
Sat, 30 May 2020Rob Hoelz mentioned that (one of?) the Nenets languages has different verb moods for concepts that in English are both indicated by “should” and “ought”:
"this is the state of the world as I assume it" vs "this is the state of the world as it currently isn't, but it would be ideal"
Examples of the former being:
- That pie should be ready to come out of the oven
- If you leave now, you should be able to catch the 8:15 to Casablanca
and of the latter:
- People should be kinder to one another
- They should manufacture these bags with stronger handles
I have often wished that English were clearer about distinguishing these. For example, someone will say to me
Using
git splurchshould fix that
and it is not always clear whether they are advising me how to fix the problem, or lamenting that it won't.
A similar issue applies to the phrase “ought to”. As far as I can tell the two phrases are completely interchangeable, and both share the same ambiguities. I want to suggest that everyone start using “should” for the deontic version (“you should go now”) and “ought to” for the predictive verion (“you ought to be able to see the lighthouse from here”) and never vice versa, but that's obviously a lost cause.
I think the original meaning of both forms is more deontic. Both words originally meant monetary debts or obligations. With ought this is obvious, at least once it's pointed out, because it's so similar in spelling and pronunciation to owed. (Compare pass, passed, past with owe, owed, ought.)
For shall, the Big Dictionary has several citations, none later than 1425 CE. One is a Middle English version of Romans 13:7:
Ȝelde ȝe to alle men ȝoure dettes: to hym þat ȝe schuleþ trybut, trybut.
As often with Middle English, this is easier than it looks at first. In fact this one is so much easier than it looks that it might become my go-to example. The only strange word is schuleþ itself. Here's my almost word-for-word translation:
Yield ye to all men your debts: to him that ye oweth tribute, pay tribute.
The NIV translates it like this:
Give to everyone what you owe them: If you owe taxes, pay taxes
Anyway, this is a digression. I wanted to talk about different kinds of should. The Big Dictionary distinguishes two types but mixes them together in its listing, saying:
In statements of duty, obligation, or propriety. Also, in statements of expectation, likelihood, prediction, etc.
The first of these seems to correspond to what I was calling the deontic form (“people should be kinder”) and the second (“you should be able to catch that train”.) But their quotations reveal several other shades of meaning that don't seem exactly like either of these:
Some men should have been women
This is not any of duty, obligation, propriety, expectation, likelihood, or prediction. But it is exactly M. Hoelz’ “state of the world as it currently isn't”.
Similarly:
I should have gotten out while I had the chance
Again, this isn't (necessarily) duty, obligation, or propriety. It's just a wish contrary to fact.
The OED does give several other related shades of “should” which are not always easy to distinguish. For example, its definition 18b says
ought according to appearances to be, presumably is
and gives as an example
That should be Barbados..unless my reckoning is far out.
Compare “We should be able to see Barbados from here”.
Its 18c is “you should have seen that fight!” which again is of the wish-contrary-to-fact type; they even gloss it as “I wish you could have…”.
Another distinction I would like to have in English is between “should” used for mere suggestion in contrast with the deontic use. For example
It's sunny out, we should go swimming!
(suggestion) versus
You should finish your homework before you play ball.
(obligation).
Say this distinction was marked in English. Then your mom might say to you in the morning
You should¹ wash the dishes now, before they get crusty
and later, when you still haven't washed the dishes:
You should² wash the dishes before you go out
meaning that you'll be in trouble if you fail in your dish washing duties.
When my kids were small I started to notice how poorly this sort of thing was communicated by many parents. They would regularly say things like
- You should be quiet now
- I need you to be quiet now
- You need to be quiet now
- You want to be quiet now
(the second one in particular) when what they really meant, it seemed to me, was “I want you to be quiet now”.
[ I didn't mean to end the article there, but after accidentally publishing it I decided it was as good a place as any to stop. ]
[Other articles in category /lang] permanent link
[ Previously ]
John Gleeson points out that my optical illusion (below left) appears to be a variation on the classic Poggendorff illusion (below right):
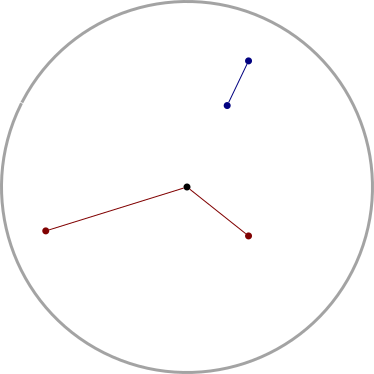
|
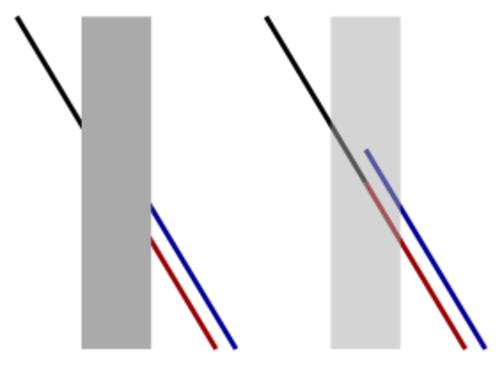
|
[Other articles in category /brain] permanent link
Fri, 29 May 2020
Infinite zeroes with one on the end
I recently complained about people who claim:
you can't have a 1 after an infinite sequence of zeroes, because an infinite sequence of zeroes goes on forever.
When I read something like this, the first thing that usually comes to mind is the ordinal number !!\omega+1!!, which is a canonical representative of this type of ordering. But I think in the future I'll bring up this much more elementary example:
$$ S = \biggl\{-1, -\frac12, -\frac13, -\frac14, \ldots, 0\biggr\} $$
Even a middle school student can understand this, and I doubt they'd be able to argue seriously that it doesn't have an infinite sequence of elements that is followed by yet another final element.
Then we could define the supposedly problematic !!0, 0, 0, \ldots, 1!! thingy as a map from !!S!!, just as an ordinary sequence is defined as a map from !!\Bbb N!!.
[ Related: A familiar set with an unexpected order type. ]
[Other articles in category /math] permanent link
A couple of years ago I wrote an article about a topological counterexample, which included this illustration:
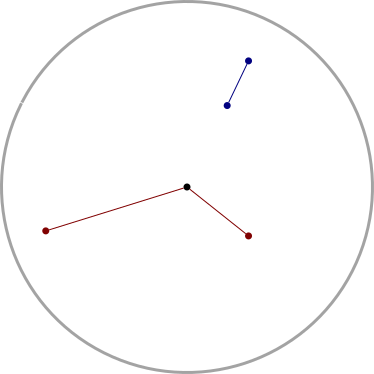
Since then, every time I have looked at this illustration, I have noticed that the blue segment is drawn wrong. It is intended to be a portion of a radius, so if I extend it toward the center of the circle it ought to intersect the center point. But clearly, the slope is too high and the extension passes significantly below the center.
Or so it appears. I have checked the original SVG, using Inkscape to extend the blue segment: the extension passes through the center of the circle. I have also checked the rendered version of the illustration, by holding a straightedge up to the screen. The segment is pointing in the correct direction.
So I know it's right, but still I'm jarred every time I see it, because to me it looks so clearly wrong.
[ Addendum 20200530: John Gleeson has pointed out the similarity to the Poggendorff illusion. ]
[Other articles in category /brain] permanent link
Thu, 21 May 2020There have been several reports of the theft of catalytic converters in our neighborhood, the thieves going under the car and cutting the whole thing out. The catalytic converter contains a few grams of some precious metal, typically platinum, and this can be recycled by a sufficiently crooked junk dealer.
Why weren't these being stolen before? I have a theory. The catalytic converter contains only a few grams of platinum, worth around $30. Crawling under a car to cut one out is a lot of trouble and risk to go to for $30. I think the stay-at-home order has put a lot of burglars and housebreakers out of work. People aren't leaving their houses and in particular they aren't going on vacations. So thieves have to steal what they can get.
[ Addendum 20200522: An initial glance at the official crime statistics suggests that my theory is wrong. I'll try to make a report over the weekend. ]
[Other articles in category /misc] permanent link
Thu, 07 May 2020Yesterday I went through the last few months of web server logs, used them to correct some bad links in my blog articles.
Today I checked the logs again and all the "page not found" errors are caused by people attacking my WordPress and PHP installations. So, um, yay, I guess?
[Other articles in category /meta] permanent link
Tue, 05 May 2020
Article explodes at the last moment
I wrote a really great blog post over the last couple of days. Last year I posted about the difference between !!\frac10!! and !!\frac00!! and this was going to be a followup. I had a great example from linear regression, where the answer comes out as !!\frac10!! in situations where the slope of computed line is infinite (and you can fix it, by going into projective space and doing everything in homogeneous coordinates), and as !!\frac00!! in situations where the line is completely indeterminite, and you can't fix it, but instead you can just pick any slope you want and proceed from there.
Except no, it never does come out !!\frac10!!. It always comes out !!\frac00!!, even in the situations I said were !!\frac10!!.
I think maybe I can fix it though, I hope, maybe. If so, then I will be able to write a third article.
Maybe.
It could have been worse. I almost published the thing, and only noticed my huge mistake because I was going to tack on an extra section at the end that it didn't really need. When I ran into difficulties with the extra section, I was tempted to go ahead and publish without it.
[Other articles in category /oops] permanent link
Fri, 01 May 2020
More about Sir Thomas Urquhart
I don't have much to add at this point, but when I looked into Sir Thomas Urquhart a bit more, I found this amazing article by Denton Fox in London Review of Books. It's a review of a new edition of Urquhart's 1652 book The Jewel (Ekskybalauron), published in 1984. The whole article is worth reading. It begins:
Sir Thomas Urquhart … must have been a most peculiar man.
and then oh boy, does it deliver. So much of this article is quotable that I'm not sure what to quote. But let's start with:
The little we know about Urquhart’s early life comes mostly from his own pen, and is therefore not likely to be true.
Some excerpts will follow. You may enjoy reading the whole thing.
Trissotetras
I spent much way more time on this than I expected. Fox says:
In 1645 he brought out the Trissotetras … . Urquhart’s biographer, Willcock, says that ‘no one is known to have read it or to have been able to read it,’ …
Thanks to the Wonders of the Internet, a copy is available, and I have been able to glance at it. Urquhart has invented a microlanguage along the lines of Wilkins’ philosophical language, in which the words are constructed systematically. But the language of Trissotetras has a very limited focus: it is intended only for expressing statements of trigonometry. Urquhart says:
The novelty of these words I know will seeme strange to some, and to the eares of illiterate hearers sound like termes of Conjuration: yet seeing that since the very infancie of learning, such inventions have beene made use of, and new words coyned, …
The sentence continues for another 118 words but I think the point is made: the idea is not obviously terrible.
Here is an example of Urquhart's trigonometric language in action:
The second axiom is Eproso, that is, the sides are proportionall to one another as the sines of their opposite angles…
A person skilled in the art might be able to infer the meaning of this axiom from its name:
- E — a side
- Pro – proportional
- S – the sine
- O – the opposite angle
That is, a side (of a triangle) is proportional to the sine of the opposite angle. This principle is currently known as the law of sines.
Urquhart's idea of constructing mnemonic nonsense words for basic laws was not a new one. There was a long-established tradition of referring to forms of syllogistic reasoning with constructed mnemonics. For example a syllogism in “Darii” is a deduction of this form:
- All mammals have hair
- Some animals are mammals
- Therefore some animals have hair.
The ‘A’ in “Darii” is a mnemonic for the “all” clause and the ‘I’s for the “some” clauses. By memorizing a list of 24 names, one could remember which of the 256 possible deductions were valid.
Urquhart is following this well-trodden path and borrows some of its terminology. But the way he develops it is rather daunting:
The Directory of this second Axiome is Pubkegdaxesh, which declareth that there are seven Enodandas grounded on it, to wit, foure Rectangular, Upalem, Ubeman, Ekarul, Egalem, and three Obliquangular, Danarele, Xemenoro, and Shenerolem.
I think that ‘Pubkegdaxesh’ is compounded from the initial syllables of the seven enodandas, with p from upalem, ub from ubamen, k from ekarul, eg from egalem, and so on. I haven't been able to decipher any of these, although I didn't try very hard. There are many difficulties. Sometimes the language is obscure because it's obsolete and sometimes because Urquhart makes up his own words. (What does “enodandas” mean?)
Let's just take “Upalem”. Here are Urquhart's glosses:
- U – the Subtendent side
- P – Opposite, whether Angle or side
- A — an angle
- L — the secant
- E — a side
- M — A tangent complement
I believe “a tangent complement” is exactly what we would now call a cotangent; that is, the tangent of the complementary angle. But how these six items relate to one another, I do not know.
Here's another difficulty: I'm not sure that ‘al’ is one component or two. It might be one:
- U – the Subtendent side
- P – Opposite, whether Angle or side
- Al — half
- E — a side
- M — A tangent complement
Either way I'm not sure what is meant. Wait, there is a helpful diagram, and an explanation of it:
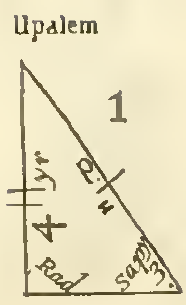
The first figure, Vale, hath but one mood, and therefore of as great extent as it selfe, which is Upalem; whose nature is to let us know, when a plane right angled triangle is given us to resolve, who subtendent and one of the obliques is proposed, and one of the ambients required, that we must have recourse unto its resolver, which being Rad—U—Sapy ☞ Yr sheweth, that if we joyne the artificiall sine of the angle opposite to the side demanded with the Logarithm of the subtendent, the summe searched in the canon of absolute numbers will afford us the Logarithm of the side required.
This is unclear but tantalizing. Urquhart is solving a problem of elementary plane trigonometry. Some of the sides and angles are known, and we are to find one of the unknown ones. I think if if I read the book from the beginning I think I might be able to make out better what Urquhart was getting at. Tempting as it is I am going to abandon it here.
Trissotetras is dedicated to Urquhart's mother. In the introduction, he laments that
Trigonometry … hath beene hitherto exposed to the world in a method whose intricacy deterreth many from adventuring on it…
He must have been an admirer of Alexander Rosse, because the front matter ends with a little poem attributed to Rosse.
Pantochronachanon
Fox again:
Urquhart, with many others, was taken to London as a prisoner, where, apparently, he determined to recover his freedom and his estates by using his pen. His first effort was a genealogy in which he names and describes his ancestors, going back to Adam. … A modern reader might think this Urquhart’s clever trick to prove that he was not guilty by reason of insanity …
This is Pantochronachanon, which Wikipedia says “has been the subject of ridicule since the time of its first publication, though it was likely an elaborate joke”, with no citation given.
Fox mentions that Urquhart claims Alcibiades as one of his ancestors. He also claims the Queen of Sheba.
According to Pantochronachanon the world was created in 3948 BC (Ussher puts it in 4004), and Sir Thomas belonged to the 153rd generation of mankind.
The Jewel
Denton Fox:
Urquhart found it necessary to try again with the Jewel, or, to to give it its full title, which in some sense describes it accurately…
EKSKUBALAURON [Εκσκυβαλαυρον]: OR, The Discovery of A most exquisite Jewel, more precious then Diamonds inchased in Gold, the like whereof was never seen in any age; found in the kennel [gutter] of Worcester-streets, the day after the Fight, and six before the Autumnal Aequinox, anno 1651. Serving in this place, To frontal a Vindication of the honour of SCOTLAND, from that Infamy, whereinto the Rigid Presbyterian party of that Nation, out of their Covetousness and ambition, most dissembledly hath involved it.
Wowzers.
Fox claims that the title Εκσκυβαλαυρον means “from dung, gold” but I do not understand why he says this. λαύρα might be a sewer or privy, and I think the word σκυβα means garden herbs. (Addendum: the explanation.)
[The book] relates how… Urquhart’s lodgings were plundered, and over 3200 sheets of his writings, in three portmanteaux, were taken.… One should remember that there is not likely to be the slightest bit of truth in this story: it speaks well for the morality of modern scholars that so many of them should have speculated why Urquhart took all his manuscripts to war with him.
Fox says that in spite of the general interest in universal languages, “parts of his prospectus must have seemed absurd even then”, quoting this item:
Three and twentiethly, every word in this language signifieth as well backward as forward; and how ever you invert the letters, still shall you fall upon significant words, whereby a wonderful facility is obtained in making of anagrams.
Urquhart boasts that where other, presumably inferior languages have only five or six cases, his language has ten “besides the nominative”. I think Finnish has fourteen but I am not sure even the Finns would be so sure that more was better. Verbs in Urquhart's language have one of ten tenses, seven moods, and four voices. In addition to singular and plural, his language has dual (like Ancient Greek) and also ‘redual’ numbers. Nouns may have one of eleven genders. It's like a language designed by the Oglaf Dwarves.
A later item states:
This language affordeth so concise words for numbering, that the number for setting down, whereof would require in vulgar arithmetick more figures in a row then there might be grains of sand containable from the center of the earth to the highest heavens, is in it expressed by two letters.
and another item claims that a word of one syllable is capable of expressing an exact date and time down to the “half quarter of the hour”. Sir Thomas, I believe that Entropia, the goddess of Information Theory, would like a word with you about that.
Wrapping up
One final quote from Fox:
In 1658, when he must have been in his late forties, he sent a long and ornately abusive letter to his cousin, challenging him to a duel at a place Urquhart would later name,
quhich shall not be aboue ane hunderethe – fourtie leagues distant from Scotland.
If the cousin would neither make amends or accept the challenge, Urquhart proposed to disperse copies of his letter
over all whole the kingdome off Scotland with ane incitment to Scullions, hogge rubbers [sheep-stealers], kenell rakers [gutter-scavengers] – all others off the meanist sorte of rascallitie, to spit in yor face, kicke yow in the breach to tred on yor mushtashes ...
Fox says “Nothing much came of this, either.”.
I really wish I had made a note of what I had planned to say about Urquhart in 2008.
[ Addendum 20200502: Brent Yorgey has explained Εκσκυβαλαυρον for me. Σκύβαλα (‘skubala’) is dung, garbage, or refuse; it appears in the original Greek text of Philippians 3:8:
What is more, I consider everything a loss because of the surpassing worth of knowing Christ Jesus my Lord, for whose sake I have lost all things. I consider them garbage, that I may gain Christ…
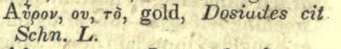
And while the usual Greek word for gold is χρῡσός (‘chrysos’), the word αύρον (‘auron’, probably akin to Latin aurum) is also gold. The screenshot at right is from the 8th edition of Liddell and Scott. Thank you, M. Yorgey! ]
[Other articles in category /book] permanent link



