Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 21 Dec 2015
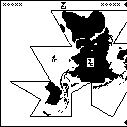
A message to the aliens, part 23/23 (wat)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry) Page 18 (cell respiration and division) Pages 19-20 (map of the Earth) Page 21 (the message) Page 22 (cosmology)
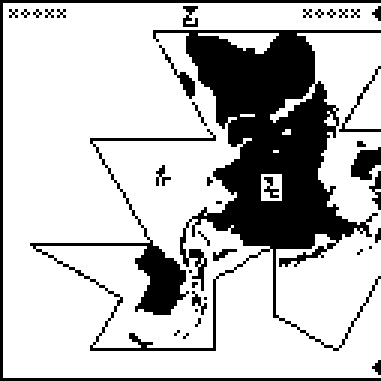
This is page 23 (the last) of the Cosmic Call message. An explanation follows.

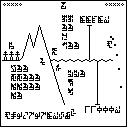
This page is a series of questions for the recipients of the message.
It is labeled with the glyph  , which heretofore
appeared only on page 4 in the context
of solving of algebraic equations. So we might interpret it as
meaning a solution or a desire to solve or understand. I have chosen to translate
it as “wat”.
, which heretofore
appeared only on page 4 in the context
of solving of algebraic equations. So we might interpret it as
meaning a solution or a desire to solve or understand. I have chosen to translate
it as “wat”.
I find this page irritating in its vagueness and confusion. Its
layout is disorganized. Glyphs are used inconsistent with their uses
elsewhere on the page and elsewhere in the message.
For example, the mysterious glyph
 , which
has something to do with the recipients of the message, and which
appeared only on page 21 is used here to
ask about both the recipients themselves and also about their planet.
, which
has something to do with the recipients of the message, and which
appeared only on page 21 is used here to
ask about both the recipients themselves and also about their planet.
The questions are arranged in groups. For easy identification, I have color-coded the groups.
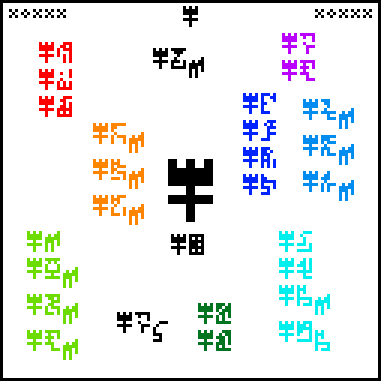
Starting from the upper-left corner, and proceeding counterclockwise, we have:
 Kilograms, meters, and seconds, wat. I would have used the glyphs for
abstract mass, distance, and time,
Kilograms, meters, and seconds, wat. I would have used the glyphs for
abstract mass, distance, and time,

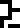 and
and 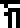 ,
since that seems to be closer to the intended meaning.
,
since that seems to be closer to the intended meaning.
 Alien mathematics, physics, and biology, wat. Note that this asks
specifically about the recipients’ version of the sciences.
None of these three glyphs has been subscripted before. Will the
meaning be clear to the recipients? One also wonders why the message
doesn't express a desire to understand human science, or science
generally. One might argue that it does not make sense to ask the
recipients about the human versions of mathematics and physics. But a
later group expresses a desire to understand males and females, and the
recipients don't know anything about that either.
Alien mathematics, physics, and biology, wat. Note that this asks
specifically about the recipients’ version of the sciences.
None of these three glyphs has been subscripted before. Will the
meaning be clear to the recipients? One also wonders why the message
doesn't express a desire to understand human science, or science
generally. One might argue that it does not make sense to ask the
recipients about the human versions of mathematics and physics. But a
later group expresses a desire to understand males and females, and the
recipients don't know anything about that either.
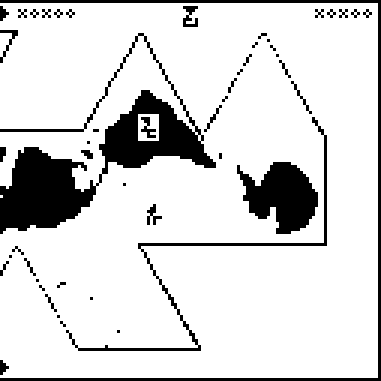
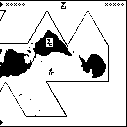
 Aliens wat. Alien [planet] mass, radius, acceleration wat.
The meaning of
Aliens wat. Alien [planet] mass, radius, acceleration wat.
The meaning of
 shifts here from meaning the recipients themselves to the recipients’
planet. “Acceleration”
shifts here from meaning the recipients themselves to the recipients’
planet. “Acceleration”
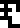 is intended to refer to the planet's gravitational acceleration as
on page 14. What if the recipients
don't live on a planet? I suppose they will be familiar with planets
generally and with the fact that we live on a planet, which explained
back on pages 11–13, and will get the idea.
is intended to refer to the planet's gravitational acceleration as
on page 14. What if the recipients
don't live on a planet? I suppose they will be familiar with planets
generally and with the fact that we live on a planet, which explained
back on pages 11–13, and will get the idea.
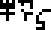 Fucking speed of light, how does it work?
Fucking speed of light, how does it work?
 Planck's constant, wat. Universal gravitation constant, wat?
Planck's constant, wat. Universal gravitation constant, wat?
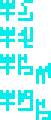 Males and females, wat. Alien people, wat. Age of people,
wat. This group seems to be about our desire to understand ourselves,
except that the third item relates to the aliens. I'm not quite sure
what is going on. Perhaps “males and females” is intended to refer to
the recipients? But the glyphs are not subscripted, and there is no
strong reason to believe that the aliens have the same sexuality.
Males and females, wat. Alien people, wat. Age of people,
wat. This group seems to be about our desire to understand ourselves,
except that the third item relates to the aliens. I'm not quite sure
what is going on. Perhaps “males and females” is intended to refer to
the recipients? But the glyphs are not subscripted, and there is no
strong reason to believe that the aliens have the same sexuality.
The glyph
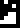 , already used
both to mean the age of the Earth and the typical human lifespan, is
even less clear here. Does it mean we want to understand the reasons
for human life expectancy? Or is it intended to continue the inquiry
from the previous line and is asking about the recipients’ history or
lifespan?
, already used
both to mean the age of the Earth and the typical human lifespan, is
even less clear here. Does it mean we want to understand the reasons
for human life expectancy? Or is it intended to continue the inquiry
from the previous line and is asking about the recipients’ history or
lifespan?
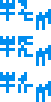 Land, water, and atmosphere of the recipients’ planet, wat.
Land, water, and atmosphere of the recipients’ planet, wat.
 Energy, force, pressure, power, wat. The usage here is
inconsistent from the first group, which asked not about mass,
distance, and time but about kilograms, meters, and seconds specifically.
Energy, force, pressure, power, wat. The usage here is
inconsistent from the first group, which asked not about mass,
distance, and time but about kilograms, meters, and seconds specifically.
 Velocity and acceleration, wat. I wonder why these are in a
separate group, instead of being clustered with the previous group or
the first group. I also worry about the equivocation in
Velocity and acceleration, wat. I wonder why these are in a
separate group, instead of being clustered with the previous group or
the first group. I also worry about the equivocation in
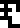 acceleration,
which is sometimes used to mean the Earth's gravitational acceleration
and sometimes acceleration generally. We already said we want to
understand
mass
acceleration,
which is sometimes used to mean the Earth's gravitational acceleration
and sometimes acceleration generally. We already said we want to
understand
mass 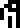 ,
!!G!!
,
!!G!! 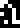 ,
and the size of the Earth. The Earth's surface gravity can be
straightforwardly calculated from these, so there's nothing else to
understand about that.
,
and the size of the Earth. The Earth's surface gravity can be
straightforwardly calculated from these, so there's nothing else to
understand about that.
 Alien planet, wat.
The glyph
Alien planet, wat.
The glyph
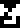 has
heretofore been used only to refer to the planet Earth. It does not mean planets
generally, because it was not used in connection with Jupiter
has
heretofore been used only to refer to the planet Earth. It does not mean planets
generally, because it was not used in connection with Jupiter
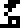 .
Here, however, it
seems to refer to the recipients’ planet.
.
Here, however, it
seems to refer to the recipients’ planet.
 The universe, wat. HUH???
The universe, wat. HUH???
That was the last page. Thanks for your kind attention.
[ Many thanks to Anna Gundlach, without whose timely email I might not have found the motivation to finish this series. ]
[Other articles in category /aliens/dd] permanent link
Fri, 18 Dec 2015I only posted three answers in August, but two of them were interesting.
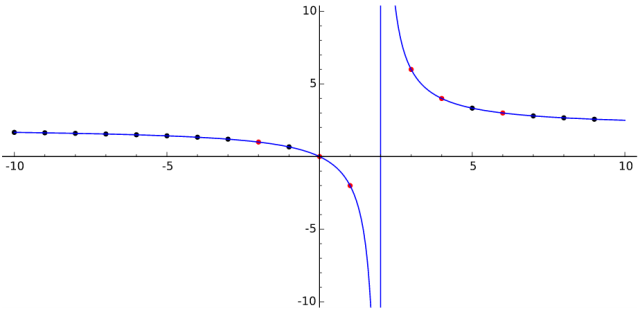
In why this !!\sigma\pi\sigma^{-1}!! keeps apearing in my group theory book? (cycle decomposition) the querent asked about the “conjugation” operation that keeps cropping up in group theory. Why is it important? I sympathize with this; it wasn't adequately explained when I took group theory, and I had to figure it out a long time later. Unfortunately I don't think I picked the right example to explain it, so I am going to try again now.
Consider the eight symmetries of the square. They are of five types:
- Rotation clockwise or counterclockwise by 90°.
- Rotation by 180°.
- Horizontal or vertical reflection
- Diagonal reflection
- The trivial (identity) symmetry
What is meant when I say that a horizontal and a vertical reflection are of the same ‘type’? Informally, it is that the horizontal reflection looks just like the vertical reflection, if you turn your head ninety degrees. We can formalize this by observing that if we rotate the square 90°, then give it a horizontal flip, then rotate it back, the effect is exactly to give it a vertical flip. In notation, we might represent the horizontal flip by !!H!!, the vertical flip by !!V!!, the clockwise rotation by !!\rho!!, and the counterclockwise rotation by !!\rho^{-1}!!; then we have
$$ \rho H \rho^{-1} = V$$
and similarly
$$ \rho V \rho^{-1} = H.$$
Vertical flips do not look like diagonal flips—the diagonal flip leaves two of the corners in the same place, and the vertical flip does not—and indeed there is no analogous formula with !!H!! replaced with one of the diagonal flips. However, if !!D_1!! and !!D_2!! are the two diagonal flips, then we do have
$$ \rho D_1 \rho^{-1} = D_2.$$
In general, When !!a!! and !!b!! are two symmetries, and there is some symmetry !!x!! for which
$$xax^{-1} = b$$
we say that !!a!! is conjugate to !!b!!. One can show that conjugacy is an equivalence relation, which means that the symmetries of any object can be divided into separate “conjugacy classes” such that two symmetries are conjugate if and only if they are in the same class. For the square, the conjugacy classes are the five I listed earlier.
This conjugacy thing is important for telling when two symmetries are group-theoretically “the same”, and have the same group-theoretic properties. For example, the fact that the horizontal and vertical flips move all four vertices, while the diagonal flips do not. Another example is that a horizontal flip is self-inverse (if you do it again, it cancels itself out), but a 90° rotation is not (you have to do it four times before it cancels out.) But the horizontal flip shares all its properties with the vertical flip, because it is the same if you just turn your head.
Identifying this sameness makes certain kinds of arguments much simpler. For example, in counting squares, I wanted to count the number of ways of coloring the faces of a cube, and instead of dealing with the 24 symmetries of the cube, I only needed to deal with their 5 conjugacy classes.
The example I gave in my math.se answer was maybe less perspicuous. I considered the symmetries of a sphere, and talked about how two rotations of the sphere by 17° are conjugate, regardless of what axis one rotates around. I thought of the square at the end, and threw it in, but I wish I had started with it.
How to convert a decimal to a fraction easily? was the month's big winner. OP wanted to know how to take a decimal like !!0.3760683761!! and discover that it can be written as !!\frac{44}{117}!!. The right answer to this is of course to use continued fraction theory, but I did not want to write a long treatise on continued fractions, so I stripped down the theory to obtain an algorithm that is slower, but much easier to understand.
The algorithm is just binary search, but with a twist. If you are looking for a fraction for !!x!!, and you know !!\frac ab < x < \frac cd!!, then you construct the mediant !!\frac{a+c}{b+d}!! and compare it with !!x!!. This gives you a smaller interval in which to search for !!x!!, and the reason you use the mediant instead of using !!\frac12\left(\frac ab + \frac cd\right)!! as usual is that if you use the mediant you are guaranteed to exactly nail all the best rational approximations of !!x!!. This is the algorithm I described a few years ago in your age as a fraction, again; there the binary search proceeds down the branches of the Stern-Brocot tree to find a fraction close to !!0.368!!.
I did ask a question this month: I was looking for a simpler version of the dogbone space construction. The dogbone space is a very peculiar counterexample of general topology, originally constructed by R.H. Bing. I mentioned it here in 2007, and said, at the time:
[The paper] is on my desk, but I have not read this yet, and I may never.
I did try to read it, but I did not try very hard, and I did not understand it. So my question this month was if there was a simpler example of the same type. I did not receive an answer, just a followup comment that no, there is no such example.
[Other articles in category /math/se] permanent link
Sat, 12 Dec 2015
A message to the aliens, part 22/23 (cosmology)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry) Page 18 (cell respiration and division) Pages 19-20 (map of the Earth) Page 21 (the message)
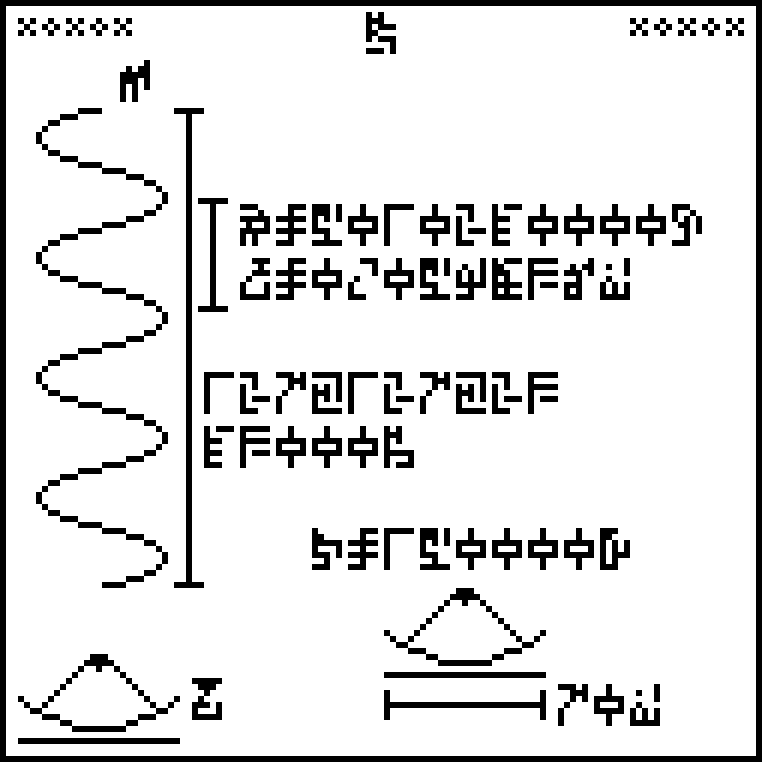
This is page 22 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 | 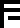 3 |  4 | 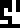 5 |  6 | 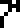 7 | 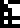 8 | 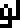 9 |
This page discusses properties of the entire universe. It is labeled
with a new glyph,
 ,
which denotes the universe or the cosmos. On this page I am on
uncertain ground, because I know very little about cosmology. My
explanation here could be completely wrong without my realizing it.
,
which denotes the universe or the cosmos. On this page I am on
uncertain ground, because I know very little about cosmology. My
explanation here could be completely wrong without my realizing it.
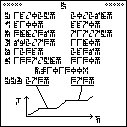
The page contains only five lines of text. In order, they state:
The Friedmann equation which is the current model for the expansion of the universe. This expansion is believed to be uniform everywhere, but even if it isn't, the recipients are so close by that they will see exactly the same expansion we do. If they have noticed the expansion, they may well have come to the same theoretical conclusions about it. The equation is:
$$H^2 = \frac{8\pi G}3\rho + \frac{\Lambda c^2 }3$$
where !!H!! is the Hubble parameter (which describes how quickly the universe is expanding), !!G!! is the universal gravitation constant
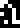 (introduced on page 9),
!!\rho!! is the density of the universe
(introduced on page 9),
!!\rho!! is the density of the universe
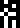
 (given on the next line),
and !!\Lambda c^2!! (
(given on the next line),
and !!\Lambda c^2!! ( )
is one of the forms of the
cosmological constant (given on the following line).
)
is one of the forms of the
cosmological constant (given on the following line).The average density
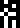 of the universe
of the universe  ,
given as !!2.76\times 10^{-27} \mathrm{kg}
~\mathrm{m}^{-3}!!. The “density” glyph would have been more at home
with the other physics definitions of page
9, but it wasn't needed until now, and
that page was full.
,
given as !!2.76\times 10^{-27} \mathrm{kg}
~\mathrm{m}^{-3}!!. The “density” glyph would have been more at home
with the other physics definitions of page
9, but it wasn't needed until now, and
that page was full.The cosmological constant !!\Lambda!! is about !!10^{-52} \mathrm{m}^{-2}!!. The related value given here, !!\Lambda c^2!!, is !!1.08\cdot 10^{-35} \mathrm{s}^{-2}!!.
The calculated value of the Hubble parameter !!H!!
 is given here in
the rather strange form !!\frac1{14000000000}\mathrm{year}^{-1}!!.
The reason it is phrased this way is that (assuming that !!H!! were
constant) !!\frac1H!! would be the age of the universe, approximately
14,000,000,000 years. So this line not only communicates our
estimate for the current value of the Hubble parameter, it
expresses it in units that may make clear our beliefs about the age
of the universe. It is regrettable that this wasn't stated more
explicitly, using the glyph
is given here in
the rather strange form !!\frac1{14000000000}\mathrm{year}^{-1}!!.
The reason it is phrased this way is that (assuming that !!H!! were
constant) !!\frac1H!! would be the age of the universe, approximately
14,000,000,000 years. So this line not only communicates our
estimate for the current value of the Hubble parameter, it
expresses it in units that may make clear our beliefs about the age
of the universe. It is regrettable that this wasn't stated more
explicitly, using the glyph  that was already used for the age of the Earth on page
13. There
was plenty of extra space, so perhaps the senders didn't think of it.
that was already used for the age of the Earth on page
13. There
was plenty of extra space, so perhaps the senders didn't think of it.The average temperature
 of the universe, about 2.736 kelvins. This is based on measurements of the cosmic microwave background radiation, which is the same in every direction, so if the recipients have noticed it at all, they have seen the same CMB that we have.
of the universe, about 2.736 kelvins. This is based on measurements of the cosmic microwave background radiation, which is the same in every direction, so if the recipients have noticed it at all, they have seen the same CMB that we have.
[Other articles in category /aliens/dd] permanent link
Sun, 06 Dec 2015
A message to the aliens, part 21/23 (the message)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry) Page 18 (cell respiration and division) Pages 19-20 (map of the Earth)
This is page 21 of the Cosmic Call message. An explanation follows.
The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 | 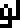 9 |
This page discusses the message itself. It is headed with the glyph
for “physics” 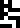 .
.
 The
leftmost part of the page has a cartoon of the Yevpatoria RT-70 radio
telescope
that was used to send the message, labeled “Earth”
The
leftmost part of the page has a cartoon of the Yevpatoria RT-70 radio
telescope
that was used to send the message, labeled “Earth” 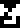 . Coming out the
the telescope is a stylized depiction of a radio wave. Two rulers
measure the radio wave. The smaller one measures a single wavelength,
and is labeled “frequency
. Coming out the
the telescope is a stylized depiction of a radio wave. Two rulers
measure the radio wave. The smaller one measures a single wavelength,
and is labeled “frequency 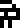 =
5,010,240,000 Hz
=
5,010,240,000 Hz 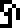 ” and “wavelength
” and “wavelength
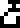 =
0.059836 meters
=
0.059836 meters 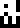 ”; these are the
frequency and the wavelength of the radio waves used to send the
message. The longer ruler has the notation “127×127×23”, describing
the format of the message itself, 23 pages of 127×127 bitmaps, and
also “43000 people
”; these are the
frequency and the wavelength of the radio waves used to send the
message. The longer ruler has the notation “127×127×23”, describing
the format of the message itself, 23 pages of 127×127 bitmaps, and
also “43000 people 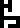 ”, which I do not
understand at all. Were 43,000 people somehow involved with sending
the message? That seems far too many. Were there 43,000 people in
Yevpatoria in 1999? That seems far too few; the current population is
over 100,000. I am mystified.
”, which I do not
understand at all. Were 43,000 people somehow involved with sending
the message? That seems far too many. Were there 43,000 people in
Yevpatoria in 1999? That seems far too few; the current population is
over 100,000. I am mystified.
At the other end of the radio wave is
the glyph  , which is
hard to decipher, because it appears only on this page and on the
unhelpful page 23. I guess it is intended to refer to the
recipients of the message.
, which is
hard to decipher, because it appears only on this page and on the
unhelpful page 23. I guess it is intended to refer to the
recipients of the message.
[ Addendum 20151219: Having reviewed page 23, I am still in the
dark.
References to the mass and radius of
 suggest that it refers to the recipients’ planet, but references to the mathematics, physics, and biology of
suggest that it refers to the recipients’ planet, but references to the mathematics, physics, and biology of
 suggests that it refers to the recipients themselves. ]
suggests that it refers to the recipients themselves. ]
In the lower-right corner of the page is another cartoon of the RT-70, this time with a ruler underneath showing its diameter, 70 meters. Above the cartoon is the power output of the telescope, 150 kilowatts.
The next article will discuss page 22, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link
Fri, 27 Nov 2015
A message to the aliens, part 19/23 (map of the Earth)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry) Page 18 (cell respiration and division)
These are pages 19–20 of the Cosmic Call message. An explanation follows.
These two pages are a map of the surface of the Earth. Every other page in the document is surrounded by a one-pixel-wide frame, to separate the page from its neighbors, but the two pages that comprise the map are missing part of their borders to show that the two pages are part of a whole. Assembled correctly, the two pages are surrounded by a single border. The matching sides of the map pages have diamond-shaped registration marks to show how to align the two pages.
The map projection used here is R. Buckminster Fuller's Dymaxion projection, in which the spherical surface of the Earth is first projected onto a regular icosahedron, which is then unfolded into a flat net. This offers a good compromise between directional distortion and size distortion. Each twentieth of the map is distorted only enough to turn it into a triangle, and the interruptions between the triangles can be arranged to occur at uninteresting parts of the map.
Both pages are labeled with
the glyph 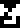 for “Earth”.
On each page, the land parts of the map are labeled with
for “Earth”.
On each page, the land parts of the map are labeled with
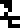 and the water parts with
and the water parts with
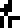 , as on
page 14, since the recipients
wouldn't otherwise be able to tell which was which.
, as on
page 14, since the recipients
wouldn't otherwise be able to tell which was which.
[Other articles in category /aliens/dd] permanent link
Mon, 02 Nov 2015
A message to the aliens, part 18/23 (cell respiration and division)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry)
This is page 18 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 | 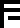 3 |  4 | 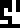 5 |  6 | 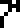 7 | 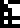 8 | 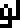 9 |
This page depicts the best way to fry eggs. The optimal fried egg is shown at left. Ha ha, just kidding. The left half of the page explains cellular respiration. The fried egg is actually a cell, with a DNA molecule in its nucleus. Will the aliens be familiar enough with the structure of DNA to recognize that the highly abbreviated picture of the DNA molecule is related to the nucleobases on the previous page? Perhaps, if their genetic biochemistry is similar to ours, but we really have no reason to think that it is.
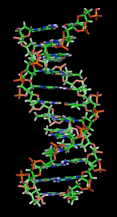 The illustration of the DNA molecule is subtly wrong. It shows a
symmetric molecule. In reality, one of the two grooves between the
strands is about twice as big as the other, as shown at right.
The illustration of the DNA molecule is subtly wrong. It shows a
symmetric molecule. In reality, one of the two grooves between the
strands is about twice as big as the other, as shown at right.
The top formula says that C6H12O6 and
O2 go into the cell; the bottom formula says that CO2 comes
out. (Energy comes out also; I wonder why this wasn't mentioned.)
The notation for chemical compounds here is different from that used
on
page 14: there, O2 was written as
 ;
here it is written as
;
here it is written as


 (“2×O”).
(“2×O”).
The glyph near the left margin 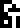 does not appear elsewhere,
but I think it is supposed to mean “cell”. Supposing that is correct,
the text at the bottom says that the number of cells in a man or woman
is !!10^{13}!!. The number of cells in a human is not known, except
very approximately, but !!10^{13}!! is probably the right order of
magnitude. (A
2013 paper from Annals of Human Biology estimates
!!3.72\cdot 10^{13}!!.)
does not appear elsewhere,
but I think it is supposed to mean “cell”. Supposing that is correct,
the text at the bottom says that the number of cells in a man or woman
is !!10^{13}!!. The number of cells in a human is not known, except
very approximately, but !!10^{13}!! is probably the right order of
magnitude. (A
2013 paper from Annals of Human Biology estimates
!!3.72\cdot 10^{13}!!.)
Next to the cell is a ruler labeled !!10^{-5}!! meters, which is a typical size for a eukaryotic cell.
The illustration on the right of the page, annotated with the glyphs
for the four nucleobases from the previous page 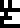
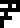
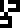
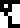 , depicts the
duplication of genetic material during cellular division. The DNA
molecule splits down the middle like a zipper. The cell then
constructs a new mate for each half of the zipper, and when it
divides, each daughter cell gets one complete zipper.
, depicts the
duplication of genetic material during cellular division. The DNA
molecule splits down the middle like a zipper. The cell then
constructs a new mate for each half of the zipper, and when it
divides, each daughter cell gets one complete zipper.
[Other articles in category /aliens/dd] permanent link
Fri, 02 Oct 2015
A message to the aliens, part 17/23 (DNA chemistry)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics)
This is page 17 of the Cosmic Call message. An explanation follows.
The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 | 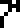 7 | 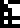 8 | 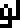 9 |
This page depicts the chemical structures of the four
nucleobases that make up
the information-carrying part of the DNA molecule. Clockwise from top
left, they are thymine 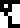 , adenine
, adenine  , guanine
, guanine  , and cytosine
, and cytosine
 .
.
The deoxyribose and phosphate components of the nucleotides, shown at right, are not depicted. These form the spiral backbone of the DNA and are crucial to its structure. Will the recipients understand why the nucleobases are important enough for us to have mentioned them?
The next article will discuss page 18, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link
Wed, 30 Sep 2015
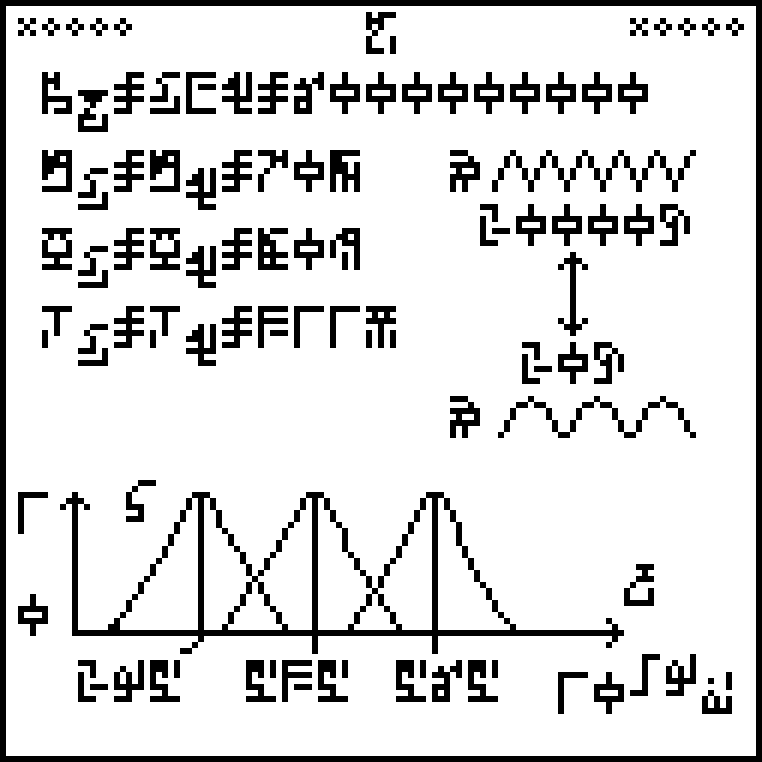
A message to the aliens, part 16/23 (vital statistics)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy)
This is page 16 of the Cosmic Call message. An explanation follows.
The 10 digits are:
 0 |  1 |  2 |  3 |  4 | 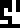 5 |  6 | 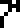 7 | 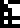 8 | 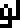 9 |
This page, about human vital statistics and senses, is in three
sections. The text in the top left explains the population of the
Earth: around 6,000,000,000 people at the time the message was sent.
The three following lines give the life expectancy (70 years), mass
(80 kg), and body temperature (311K) of humans. In each case it is
stated explicitly that the value for men and for women is the same,
which is not really true.
The glyph used for life expectancy 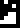 is the same one used
to denote the age of the Earth back on page 13 even though the
two notions are not really the same.
And why 311K when the commonly-accepted value is 310K?
is the same one used
to denote the age of the Earth back on page 13 even though the
two notions are not really the same.
And why 311K when the commonly-accepted value is 310K?
The diagram at right attempts to explain the human sense of hearing,
showing a high-frequency wave at top and a low frequency one at
bottom, annotated with the glyph for frequency 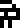 and the upper
and lower frequency limits of human hearing, 20,000 Hz and 20 Hz
respectively. I found this extremely puzzling the first time I
deciphered the message, so much so that it was one of the few parts of
the document that left me completely mystified, even with the advantage
of knowing already what humans are like. A significant part of the
problem here is that the illustration is just flat out wrong. It
depicts transverse waves:
and the upper
and lower frequency limits of human hearing, 20,000 Hz and 20 Hz
respectively. I found this extremely puzzling the first time I
deciphered the message, so much so that it was one of the few parts of
the document that left me completely mystified, even with the advantage
of knowing already what humans are like. A significant part of the
problem here is that the illustration is just flat out wrong. It
depicts transverse waves:
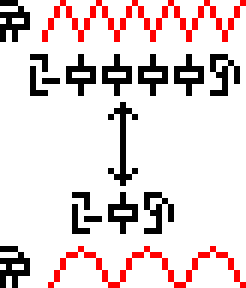
but sound waves are not transverse, they are compression waves. The aliens are going to think we don't understand compression waves. (To see the difference, think of water waves, which are transverse: the water molecules move up and down—think of a bobbing cork—but the wave itself travels in a perpendicular direction, not vertically but toward the shore, where it eventually crashes on the beach. Sound waves are not like this. The air molecules move back and forth, parallel to the direction the sound is moving.)
I'm not sure what would be better; I tried generating some random compression waves to fit in the same space. (I also tried doing a cartoon of a non-random, neatly periodic compression wave, but I couldn't get anything I thought looked good.) I think the compression waves are better in some ways, but perhaps very confusing:
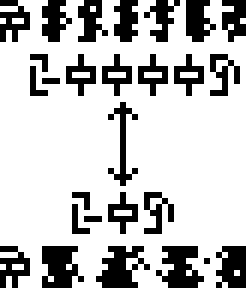
On the one hand, I think they express the intended meaning more
clearly; on the other hand, I think they're too easy to confuse with
glyphs, since they happen to be on almost the same scale. I think
the message might be clearer if a little more space were allotted for
them. Also, they could be annotated with the glyph for pressure 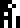 , maybe something like this:
, maybe something like this:
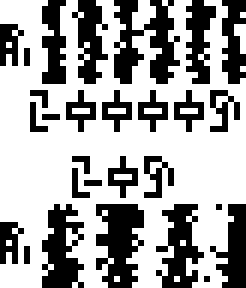
This also gets rid of the meaningless double-headed arrow. I'm not sure I buy the argument that the aliens won't know about arrows; they may not have arrows but it's hard to imagine they don't know about any sort of pointy projectile, and of course the whole purpose of a pointy projectile (the whole point, one might say) is that the point is on the front end. But the arrows here don't communicate motion or direction or anything like that; even as a human I'm not sure what they are supposed to communicate.
The bottom third of the diagram is more sensible. It is a diagram
showing the wavelengths of light 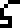 to which the human
visual system is most sensitive. The x-axis is labeled with
“wavelength”
to which the human
visual system is most sensitive. The x-axis is labeled with
“wavelength”  and the
y-axis with a range from 0 to 1. The three peaks have their centers
at 295 nm (blue), 535 nm (green), and 565 nm (often called “red”, but
actually yellow). These correspond to the three types of cone cells
in the retina, and the existence of three different types is why we
perceive the color space as being three-dimensional. (I discussed
this at greater
length a few
years ago.) Isn't it interesting that the “red” and green
sensitivities are so close together? This is why we have red-green
color blindness.
and the
y-axis with a range from 0 to 1. The three peaks have their centers
at 295 nm (blue), 535 nm (green), and 565 nm (often called “red”, but
actually yellow). These correspond to the three types of cone cells
in the retina, and the existence of three different types is why we
perceive the color space as being three-dimensional. (I discussed
this at greater
length a few
years ago.) Isn't it interesting that the “red” and green
sensitivities are so close together? This is why we have red-green
color blindness.
[Other articles in category /aliens/dd] permanent link
Mon, 28 Sep 2015
A message to the aliens, part 15/23 (human anatomy)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain)
This is page 15 of the Cosmic Call message. An explanation follows.
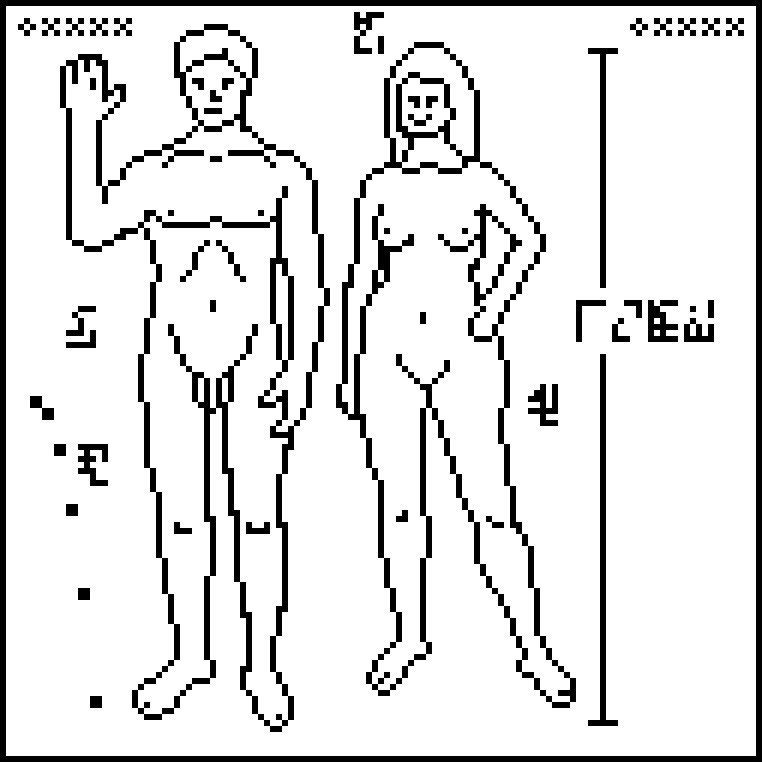
The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 | 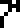 7 | 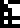 8 | 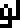 9 |
This page starts a new section of the document, each page headed with the glyph for “biology”
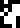 . The illustration
is adapted from the Pioneer
plaque; the relevant
portion is shown below.
. The illustration
is adapted from the Pioneer
plaque; the relevant
portion is shown below.
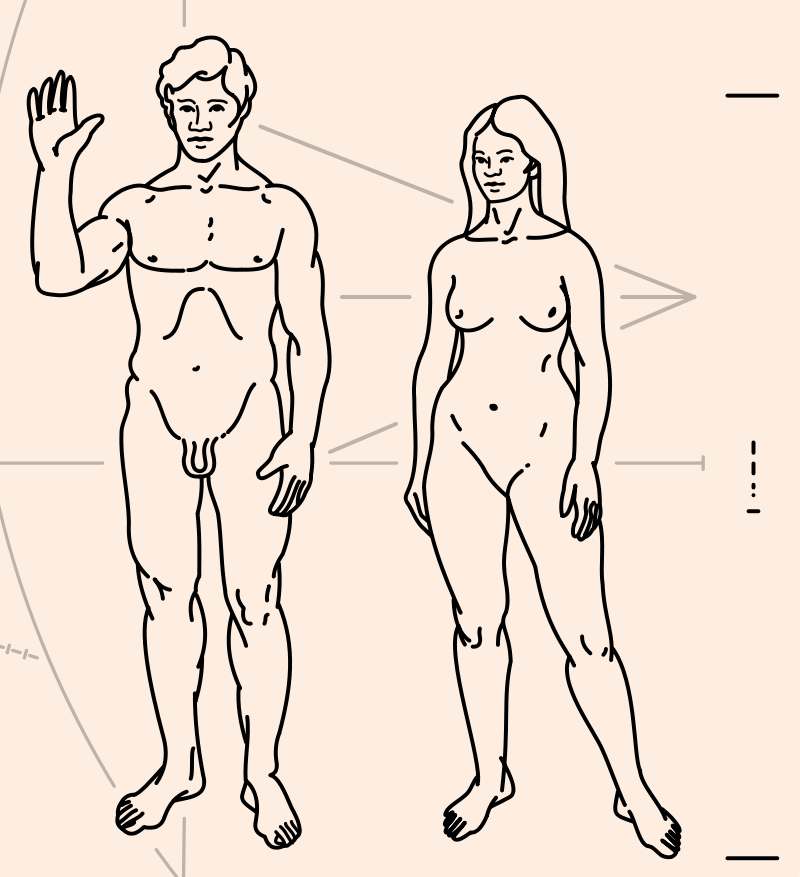
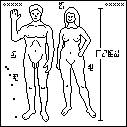
Copies of the plaque were placed on the 1972 and 1973 Pioneer spacecraft. The Pioneer image has been widely discussed and criticized; see the Wikipedia article for some of the history here. The illustration suffers considerably from its translation to a low-resolution bitmap. The original picture omits the woman's vulva; the senders have not seen fit to correct this bit of prudery.
The man and the woman are labeled with the glyphs 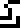 and
and 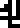 , respectively.
The glyph for “people”
, respectively.
The glyph for “people” 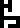 , which identified
the stick figures on the previous page, is inexplicably omitted here.
, which identified
the stick figures on the previous page, is inexplicably omitted here.
 The ruler on the right somewhat puzzlingly goes from a bit above the man's toe
to a bit below the top of the woman's head; it does not measure either of the
two figures. It is labeled 1.8 meters, a typical height for men. The
original Pioneer plaque spanned the woman exactly and gave her height
as 168 cm, which is conveniently an integer multiple of the basic measuring unit (21 cm) defined on the plaque.
The ruler on the right somewhat puzzlingly goes from a bit above the man's toe
to a bit below the top of the woman's head; it does not measure either of the
two figures. It is labeled 1.8 meters, a typical height for men. The
original Pioneer plaque spanned the woman exactly and gave her height
as 168 cm, which is conveniently an integer multiple of the basic measuring unit (21 cm) defined on the plaque.
To prevent the recipients from getting confused about which end of the
body is the top, a parabolic figure (shown here at left), annotated with the glyph
for “acceleration”, shows the direction of gravitational acceleration
as on the previous page.
[Other articles in category /aliens/dd] permanent link
Fri, 25 Sep 2015
A message to the aliens, part 14/23 (terrain)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years)
This is page 14 of the Cosmic Call message. An explanation follows.
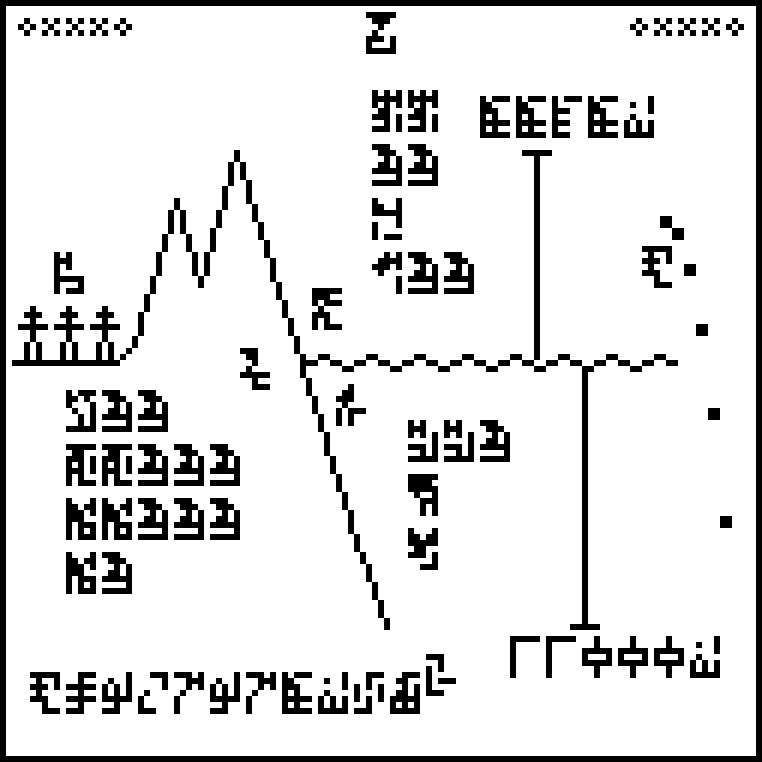
The 10 digits are:
 0 |  1 |  2 | 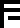 3 |  4 | 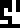 5 |  6 | 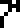 7 |  8 |  9 |
This is my favorite page: there is a lot of varied information and the
illustration is ingenious. The page heading says 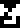 to match up with
the corresponding labels on the previous three pages. The page
depicts the overall terrain of the Earth. The main feature is a large
illustration of some mountains (yellow in my highlighted illustration below)
plunging into the sea (blue).
to match up with
the corresponding labels on the previous three pages. The page
depicts the overall terrain of the Earth. The main feature is a large
illustration of some mountains (yellow in my highlighted illustration below)
plunging into the sea (blue).
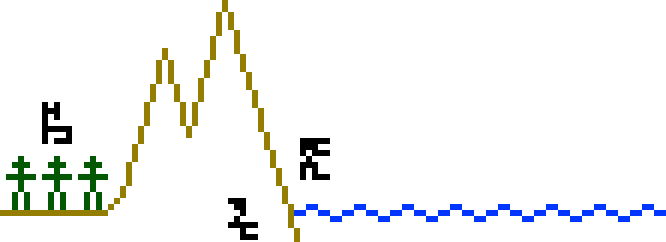
The land part is labeled 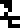 , the air part
, the air part 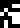 , and the water part
, and the water part
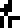 . Over on the
left of the land part are little stick figures, labeled people
. Over on the
left of the land part are little stick figures, labeled people 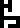 . This is to show
that people live on the land part of the Earth, not under water or in
the air. The stick figures may not be clear to the recipients, but
they are explained in more detail on the next page.
. This is to show
that people live on the land part of the Earth, not under water or in
the air. The stick figures may not be clear to the recipients, but
they are explained in more detail on the next page.
Each of the three main divisions is annotated with its general chemical composition, with compounds listed in order of prevalence., All the chemical element symbols were introduced earlier, on pages 6 and 7:
The lithosphere 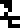 :
silicon dioxide (SiO2)
:
silicon dioxide (SiO2)
![]()
 ;
aluminium oxide (Al2O3)
;
aluminium oxide (Al2O3)


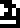
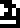 ;
iron(III) oxide (Fe2O3)
;
iron(III) oxide (Fe2O3)
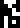
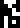
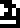
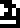
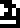 ;
iron(II) oxide (FeO)
;
iron(II) oxide (FeO)
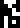
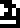 . Wikipedia and other sources dispute this listing, giving instead:
SiO2, MgO, FeO,
Al2O3,
CaO, Na2O,
Fe2O3 in that order.
. Wikipedia and other sources dispute this listing, giving instead:
SiO2, MgO, FeO,
Al2O3,
CaO, Na2O,
Fe2O3 in that order.
The atmosphere 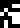 :
nitrogen gas (N2)
:
nitrogen gas (N2)
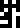
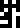 ;
oxygen gas (O2)
;
oxygen gas (O2)
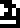
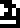 ;
argon (Ar)
;
argon (Ar)
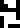 ;
carbon dioxide (CO2)
;
carbon dioxide (CO2)
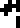
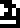
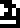 .
.
The hydrosphere 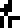 :
water (H2O)
:
water (H2O)
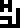
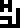
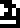 ;
sodium (Na)
;
sodium (Na)
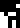 ;
chlorine (Cl)
;
chlorine (Cl)
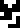 .
.
There are rulers extending upward from the surface of the water to the height of top of the mountain and downward to the bottom of the ocean. The height ruler is labeled 8838 meters, which is the height the peak of Mount Everest, the point highest above sea level. The depth ruler is labeled 11000 meters, which is the depth of the Challenger Deep in the Mariana Trench, the deepest part of the ocean. The two rulers have the correct sizes relative to one another. The human figures at left are not to scale (they would be about 1.7 miles high), but the next page will explain how big they really are.
I don't think the message contains anything to tell the recipients the temperature of the Earth, so it may not be clear that the hydrosphere is liquid water. But perhaps the wavy line here will suggest that. The practice of measuring the height of the mountains and depth of the ocean from the surface may also be suggestive of a liquid ocean, since it would not otherwise have a flat surface to provide a global standard.
 There is a potential problem with this picture: how will the
recipients know which edge is the top? What if they hold it
upside-down, and think the human figures are pointing down into the
earth, heads downwards?
There is a potential problem with this picture: how will the
recipients know which edge is the top? What if they hold it
upside-down, and think the human figures are pointing down into the
earth, heads downwards?
This problem is solved in a clever way: the dots at the right of the
page depict an object accelerating under the influence of gravity,
falling in a characteristic parabolic path. To make the point clear,
the dots are labeled with the glyph 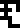 for
acceleration.
for
acceleration.
Finally, the lower left of the page states the 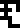 acceleration due to gravity at the Earth's surface, 9.7978
m/s2. The recipients can calculate this value from the
mass and radius of the Earth given earlier. Linked with the other
appearance of acceleration on the page, this should suggest that the
dots depict an object falling under the influence of gravity toward
the bottom of the page.
acceleration due to gravity at the Earth's surface, 9.7978
m/s2. The recipients can calculate this value from the
mass and radius of the Earth given earlier. Linked with the other
appearance of acceleration on the page, this should suggest that the
dots depict an object falling under the influence of gravity toward
the bottom of the page.
[Other articles in category /aliens/dd] permanent link
Wed, 23 Sep 2015
A message to the aliens, part 13/23 (days, months, and years)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system)
This is page 13 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 | 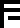 3 |  4 | 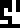 5 |  6 | 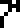 7 | 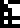 8 | 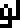 9 |
There are three diagrams on this page, each depicting something going around. Although the direction is ambiguous (unless you understand arrows) it should at least should be clear that all three rotations are in the same direction. This is all you can reasonably say anyhow, because the rotations would all appear to be going the other way if you looked at them from the other side.
 The upper left diagram depicts the Earth
The upper left diagram depicts the Earth 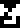 going around the
Sun
going around the
Sun 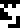 and
underneath is a note that says that the time
and
underneath is a note that says that the time 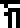 is equal to
315569268 seconds, and is also equal to one year
is equal to
315569268 seconds, and is also equal to one year  . This defines the
year.
. This defines the
year.
 The upper-right
diagram depicts the Moon
The upper-right
diagram depicts the Moon 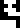 going around the
Earth
going around the
Earth 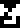 ; the
notation says that this takes 2360591 seconds, or around 27⅓
days. This is not the 29½ days that one might naïvely expect, because
it is the sidereal month rather than the synodic month. Suppose the
phase of the Moon is new, so that the Moon lies exactly between the
Earth and the Sun. 27⅓ days later the Moon has made a complete trip around
the Earth, but because the Earth has moved, the Moon is not yet again
on the line between the Earth and the Sun; the line is in a different
direction. The Earth has moved about !!\frac1{13}!! of the way around
the sun, so it takes about another !!\frac1{12}\cdot 27\frac13!! days
before the moon is again between Earth and Sun and so a total of about
29½ days between new moons.
; the
notation says that this takes 2360591 seconds, or around 27⅓
days. This is not the 29½ days that one might naïvely expect, because
it is the sidereal month rather than the synodic month. Suppose the
phase of the Moon is new, so that the Moon lies exactly between the
Earth and the Sun. 27⅓ days later the Moon has made a complete trip around
the Earth, but because the Earth has moved, the Moon is not yet again
on the line between the Earth and the Sun; the line is in a different
direction. The Earth has moved about !!\frac1{13}!! of the way around
the sun, so it takes about another !!\frac1{12}\cdot 27\frac13!! days
before the moon is again between Earth and Sun and so a total of about
29½ days between new moons.
 The lower-right diagram depicts the rotation of the Earth, giving a time of
86163 seconds for the day. Again, this is not the 86400 seconds one
would expect, because it is the sidereal day rather than the solar
day; the issue is the same as in the previous paragraph.
The lower-right diagram depicts the rotation of the Earth, giving a time of
86163 seconds for the day. Again, this is not the 86400 seconds one
would expect, because it is the sidereal day rather than the solar
day; the issue is the same as in the previous paragraph.
None of the three circles appears to be circular. The first one is nearly circular, but it looks worse than it is because the Sun has been placed off-center. The curve representing the Moon's orbit is decidedly noncircular. This is reasonable, because the Moon's orbit is elliptical to approximately the same degree. In the third diagram, the curve is intended to represent the surface of the Earth, so its eccentricity is indefensible. The ellipse is not the same as the one used for the Moon's orbit, so it wasn't just a copying mistake.
The last two lines state that the ages of the Sun and the Earth are each
4550000000 years. This is the first appearance of the glyph
 for “age”.
for “age”.
[Other articles in category /aliens/dd] permanent link
Mon, 21 Sep 2015
A message to the aliens, part 12/23 (earth-moon system)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system)
This is page 12 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 | 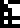 8 | 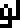 9 |
Page 12, begins a new section of the document, with pages headed with
the glyph 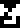 “Earth”, describing the Earth and its environs. This will help the recipients locate our planet, should they come to visit.
“Earth”, describing the Earth and its environs. This will help the recipients locate our planet, should they come to visit.
The top of the page
has a diagram of the Earth 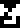 -Moon
-Moon 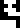 system and a ruler
labeled with the distance between them, !!3844\cdot 10^5!! meters. Since the distance between Earth and Moon varies (the orbit is elliptical) an average value is given.
system and a ruler
labeled with the distance between them, !!3844\cdot 10^5!! meters. Since the distance between Earth and Moon varies (the orbit is elliptical) an average value is given.

The glyph used here for distance, 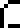 , is different
from the one defined on page 9
, is different
from the one defined on page 9 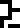 . Neither
appears elsewhere in the message, so this is probably a mistake.
. Neither
appears elsewhere in the message, so this is probably a mistake.
The following five lines give the mass  and radius
and radius 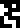 of the Moon and the Earth, and also the distance from the Earth to the Sun. The latter would have been better on the previous page, which discussed the solar system, but was omitted from there for some reason.
of the Moon and the Earth, and also the distance from the Earth to the Sun. The latter would have been better on the previous page, which discussed the solar system, but was omitted from there for some reason.
[Other articles in category /aliens/dd] permanent link
Fri, 18 Sep 2015
A message to the aliens, part 11/23 (solar system)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature)
This is page 11 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 | 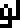 9 |
Page 11, headed with the glyph for “physics” 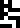 is evidently a
chart of the solar system, with the Sun
is evidently a
chart of the solar system, with the Sun 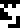 at left. The Earth
at left. The Earth
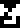 is also
labeled, as is Jupiter
is also
labeled, as is Jupiter 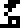 , the planet most
likely to be visible to the recipients. The “Jupiter” glyph does not appear again.
Pluto is included, as it was still considered a planet in 1999. (Pluto's
status as only one of many similar trans-Neptunian objects was not
well appreciated in 1999 when the message was composed, the second TNO
having only been discovered in 1992.)
To the extent permitted by the low resolution of the image,
The diameters of the planets and
the Sun are to scale,
but not their relative positions; the page is
much too small for that. Saturn's rings are not shown, as they are in
the Pioneer plaque; by
this time it was appreciated that ring systems may be common around large
planets.
, the planet most
likely to be visible to the recipients. The “Jupiter” glyph does not appear again.
Pluto is included, as it was still considered a planet in 1999. (Pluto's
status as only one of many similar trans-Neptunian objects was not
well appreciated in 1999 when the message was composed, the second TNO
having only been discovered in 1992.)
To the extent permitted by the low resolution of the image,
The diameters of the planets and
the Sun are to scale,
but not their relative positions; the page is
much too small for that. Saturn's rings are not shown, as they are in
the Pioneer plaque; by
this time it was appreciated that ring systems may be common around large
planets.
The masses
 and radii
and radii
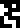 of Jupiter and the Sun are given, Jupiter above
the illustration and the Sun below. The (external) temperature
of Jupiter and the Sun are given, Jupiter above
the illustration and the Sun below. The (external) temperature 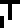 of the Sun
is also given, 5763 kelvins. This should be visible to the aliens
because the Sun is a blackbody emitter and the spectrum of blackbody
radiation is a clear indicator of its temperature. This data should
allow the aliens to locate us, should they be so inclined: they know
which way the message came from, and can look for a star with the
right size and temperature in that direction. When they get closer,
Jupiter and the sizes of the planets will provide a confirmation that
they are in the right place. Later pages explain that we live on the
Earth, so the aliens will know where to point their fusion cannon in
order to obliterate our planet.
of the Sun
is also given, 5763 kelvins. This should be visible to the aliens
because the Sun is a blackbody emitter and the spectrum of blackbody
radiation is a clear indicator of its temperature. This data should
allow the aliens to locate us, should they be so inclined: they know
which way the message came from, and can look for a star with the
right size and temperature in that direction. When they get closer,
Jupiter and the sizes of the planets will provide a confirmation that
they are in the right place. Later pages explain that we live on the
Earth, so the aliens will know where to point their fusion cannon in
order to obliterate our planet.
[Other articles in category /aliens/dd] permanent link
Wed, 16 Sep 2015
A message to the aliens, part 10/23 (temperature)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units)
This is page 10 of the Cosmic Call message. An explanation follows.
The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 | 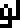 9 |
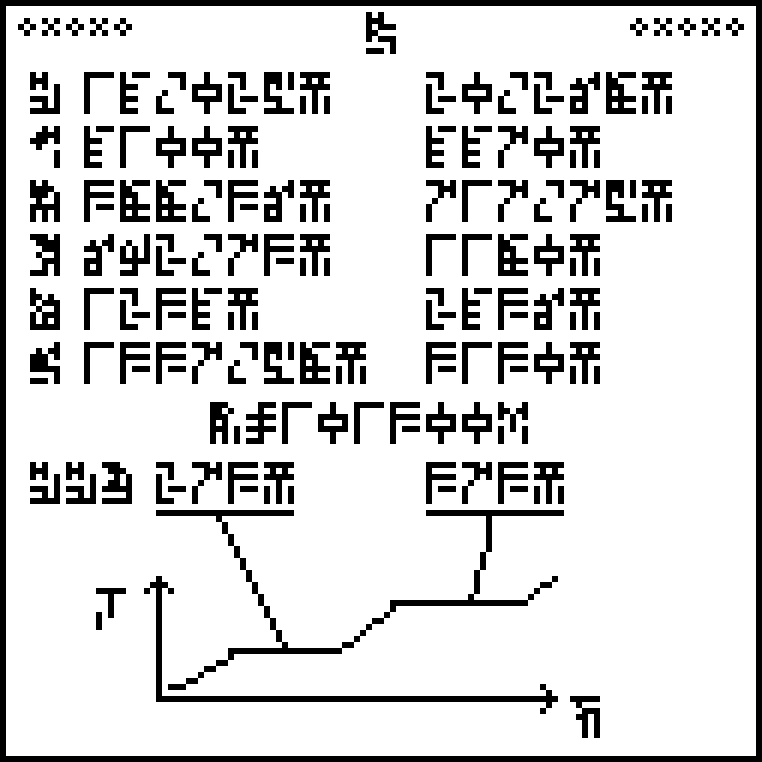
The top half of this page is a table of melting points (on the left)
and boiling points (on the right) for various substances: hydrogen
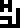 , carbon
, carbon
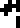 , sulfur
, sulfur
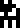 , zinc
, zinc 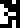 , silver
, silver 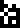 , and gold
, and gold 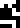 . The temperatures
are given in kelvins
. The temperatures
are given in kelvins  .
.
The boiling points depend on pressure, so there is a notation at the
bottom of the list that the pressure 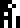 should be
101300 pascals
should be
101300 pascals  . This is one standard atmosphere, so it may tell the aliens a
little more about our planet.
. This is one standard atmosphere, so it may tell the aliens a
little more about our planet.
To help calibrate the kelvins, the bottom of the page is a chart
of the temperature
increase of water
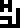
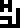
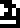 , showing how the temperature stops increasing at the
melting point (273K) and the boiling point (373K). This introduces the
glyph for temperature
, showing how the temperature stops increasing at the
melting point (273K) and the boiling point (373K). This introduces the
glyph for temperature 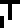 , which will recur later.
, which will recur later.
There are two
regrettable things about this chart. One is that the horizontal axis
is labeled “time”
 . Why is the
temperature of the water increasing with time? It should be energy.
. Why is the
temperature of the water increasing with time? It should be energy.
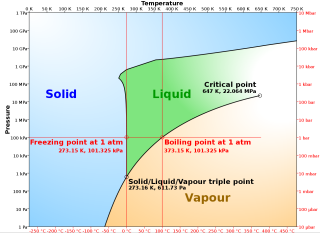
But a more serious complaint, I think, it that this is the wrong
chart. It depends crucially on the (Earth-)standard atmospheric pressure,
with which the recipients may not be familiar. And the kelvin is not defined
in terms of standard pressure anyway. It is defined in terms of the
triple point of water, the unique, universal temperature and pressure at which
all three states of water can coexist. Why not a temperature and
pressure chart with the triple point labeled? This is something one
might more reasonably expect the aliens to have studied.
[Other articles in category /aliens/dd] permanent link
Mon, 14 Sep 2015
A message to the aliens, part 9/23 (physical units)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space)
This is page 9 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 | 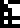 8 | 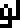 9 |
The previous two pages defined fundamental units of mass, distance, and time. This page adds some derived notions: force, energy, pressure, and power; velocity and acceleration.
The first four lines are in two parts each. The left part defines an
abstract quantity like force or energy; the right part defines a unit
of that quantity like newtons or joules. For example, the second line defines energy and units of energy. The left side says that energy
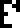 is equal to mass
is equal to mass
 times distance
times distance
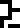 squared divided by time
squared divided by time 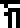 squared. (This is the first appearance of the glyphs for distance and time.)
The right side says that a joule
squared. (This is the first appearance of the glyphs for distance and time.)
The right side says that a joule
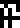 of energy is !!1\frac{\mathrm{kg}\,\mathrm{m}^2}{\mathrm{s}^2}!!.
of energy is !!1\frac{\mathrm{kg}\,\mathrm{m}^2}{\mathrm{s}^2}!!.
The two following lines define the abstract concepts of velocity 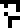 (which has
appeared before in connection with the speed of light) and
acceleration
(which has
appeared before in connection with the speed of light) and
acceleration 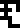 (which is
new). There are no units given for these.
(which is
new). There are no units given for these.
| Concept | 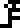 force | 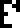 energy | 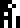 pressure | 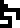 power | 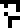 velocity | 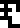 acceleration |
|---|---|---|---|---|---|---|
| Unit | 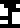 newton | 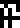 joule |  pascal | 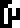 watt | (none) | (none) |
The newton and the joule won't appear again. Force won't appear again except on the last page, which asks “force WTF?”.
The final part of the page is the most interesting. It mentions the
Planck constant !!h!!
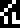 (not the related !!\hbar!!) which is
!!6.6260755\cdot 10^{{}^-34}!! joule-seconds and the universal gravitation constant !!G!!
(not the related !!\hbar!!) which is
!!6.6260755\cdot 10^{{}^-34}!! joule-seconds and the universal gravitation constant !!G!!
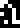 which is !!6.67259\cdot 10^{{}^-11}\; \mathrm{m}^3\;
\mathrm{kg}^{{}^-1}\; \mathrm{s}^{{}^-2}!!.
which is !!6.67259\cdot 10^{{}^-11}\; \mathrm{m}^3\;
\mathrm{kg}^{{}^-1}\; \mathrm{s}^{{}^-2}!!.
It's quite possible that the recipients won't recognize the gravitational constant, which is tricky to measure directly. Newton's law of universal gravitation was known on Earth for hundreds of years before the value of !!G!! was worked out. But if the recipients don't know it, they will be able to work it out from the later statements about the mass and radius of the Earth and the gravitational force at its surface, This would in turn allow them to calculate the mass of their own planet.
Note that on this page some inverse units are written with a division sign and some with a negative exponent. Will this inconsistency puzzle the aliens? My coworker Jeff Ober suggests that it communicates the important personal information that humans are confused and inconsistent.
The next article will discuss page 10, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link
Thu, 10 Sep 2015
A message to the aliens, part 8/23 (time and space)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass)
This is page 8 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 |  3 |  4 | 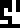 5 |  6 | 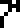 7 | 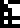 8 | 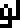 9 |

The main feature of this page is a diagram of the electron energy
levels for a hydrogen atom, annotated at the top with the glyph for
hydrogen 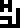 and at the bottom with the glyph for energy
and at the bottom with the glyph for energy 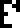 . The four lowest
levels are shown, with the lowest level (the ground state) at the
bottom. Above these is a thicker bar representing the way the higher
energy levels all pile up into a smear. If the bottom level is at 0
and the smear is at 1, then the three intermediate levels are
shown at approximately their exact values of !!\frac34, \frac89, !! and !!\frac{15}{16}!!; these are
given by the Rydberg
formula.
. The four lowest
levels are shown, with the lowest level (the ground state) at the
bottom. Above these is a thicker bar representing the way the higher
energy levels all pile up into a smear. If the bottom level is at 0
and the smear is at 1, then the three intermediate levels are
shown at approximately their exact values of !!\frac34, \frac89, !! and !!\frac{15}{16}!!; these are
given by the Rydberg
formula.
The aliens should be familiar with hydrogen. Normally a hydrogen atom's sole electron is in the ground state. If a photon couples with the electron, say because starlight is falling on the atom, or someone has applied an electric current to it, the electron may jump up to a higher quantum state. (This is the only correct use of the phrase "quantum leap".) When it drops back down, it will emit a photon. But the energy of the emitted photon must be one of a few particular values, corresponding to the difference between the old and the new energy level; the electron never drops down partway to the next level. An incandescent cloud of hydrogen gas will not typically glow in every possible color; it will emit light in only a few particular, characteristic wavelengths, and these colors can be separated with a spectroscope. The wavelengths of these characteristic colors of light, visible everywhere the message is likely to reach, provide a basis for defining the meter.
For example, the second pair of numbers labels the transition from the !!n=3!! to the !!n=2!! state, and an electron transiting between these two states will always emit a photon with a wavelength of 656.2852 nanometers and a frequency of 456.8021 terahertz, and these are the two numbers in the pair. The product of the two numbers in each pair is a constant, which should further confirm to the recipients that they have the right interpretation. The constant product is close to 299792458, which is the speed of light in meters per second. This defines four glyphs, for wavelength and frequency, and meters and hertz.
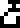 wavelength | 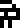 frequency | 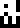 meters | 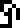 hertz | 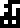 seconds |
The following item
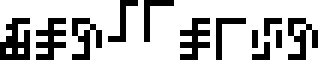
defines the second 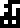 as the inverse of
the hertz (written as !!\mathrm{Hz}^{{}^-1}!! and as
!!1\div\mathrm{Hz}!!).
as the inverse of
the hertz (written as !!\mathrm{Hz}^{{}^-1}!! and as
!!1\div\mathrm{Hz}!!).
Finally, the speed 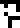 of light
of light 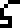 is given, first
theoretically, as the product of wavelength and frequency
is given, first
theoretically, as the product of wavelength and frequency 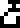

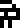 and then
numerically, as 299792458 meters per second
and then
numerically, as 299792458 meters per second 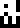
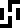
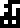 .
.
Try to figure it out before then.
[Other articles in category /aliens/dd] permanent link
Wed, 09 Sep 2015
A message to the aliens, part 7/23 (mass)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry)
This is page 7 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 | 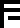 3 |  4 | 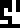 5 |  6 | 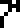 7 | 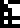 8 | 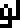 9 |
Page 7 discusses mass and defines the kilogram.
The top section of the page continues the table of chemical elements
from the previous page, giving the number of protons and neutrons.
For example, gold 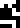 is described as having 79 protons
is described as having 79 protons 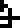 and 117 neutrons
and 117 neutrons
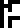 .
.
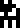 Sulfur | 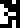 Zinc | 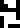 Argon | 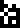 Silver | 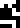 Gold |  Uranium | 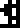 Copernicium |
Copernicium, element 112, had been discovered but not named at the time the document was written.
There is a major error here.
Uranium
 is given as having 92 protons and 116
neutrons. There is no such substance. It should have said 146
neutrons.
is given as having 92 protons and 116
neutrons. There is no such substance. It should have said 146
neutrons.

I sometimes imagine the aliens, having received the message, come to visit us. “We weren't going to bother,” they say, “but we had to know about the uranium-208.” And then we will have to tell them that we messed up. Ouch. (It could be an error for lead-208 or bismuth-208 instead; one can't be sure because the glyph does not appear elsewhere in the document.)
I'd been planning to write that paragraph about uranium-208 for more
than ten years, but it wasn't until just now that I realized there is
a much more serious mistake two lines down, so that the uranium is no longer
the most serious error that I know of in the entire document. The
line after the table of elements says that the mass of a carbon atom is the mass of six
protons plus the mass of six neutrons plus “energy”, 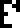 , by which I think
they mean the binding energy in the nucleus. This is the first
appearance of the glyph for energy, which will recur later. And then
the following line commits a really horrible boner, one that has the
potential to spoil the whole message.
, by which I think
they mean the binding energy in the nucleus. This is the first
appearance of the glyph for energy, which will recur later. And then
the following line commits a really horrible boner, one that has the
potential to spoil the whole message.
With the mass of the carbon nucleus pinned down, the authors want to
define the kilogram 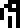 : the document
says that 12 kilograms is the mass of !!6022137\cdot 10^{19} !!
carbon-12 atoms. That !!6022137\cdot 10^{19} !! is Avogadro's number.
Except it's not. Avogadro's number is usually given as
!!6.022137\cdot 10^{23} !!, and this number is 100 times that big.
But it should be 1000 times that big.
: the document
says that 12 kilograms is the mass of !!6022137\cdot 10^{19} !!
carbon-12 atoms. That !!6022137\cdot 10^{19} !! is Avogadro's number.
Except it's not. Avogadro's number is usually given as
!!6.022137\cdot 10^{23} !!, and this number is 100 times that big.
But it should be 1000 times that big.
Normally, one would say that !!6.022137\cdot 10^{23} !! carbon atoms mass 12 grams, but there are two confusing factors here. One is that the authors have written !!6022137!! instead of !!6.022137!! and the other is that they are defining 12 kilograms instead of 12 grams. But it should be that !!6.022137\cdot 10^{23} = 6022137\cdot 10^{17}!! atoms is 12 grams so that !!6022137\cdot 10^{20}!! atoms is 12 kilograms, and the number written is instead !!6022137 10^{19}!! atoms, making the kilogram 90% smaller than it should have been.

It's possible that the aliens can figure this out, because it is detectably inconsistent with the following statements about the masses of the fundamental particles in kilograms. But it may not be clear to the recipients which of the two definitions of the kilogram is the correct one. Especially given the—I really hate to report this—the typo in the second statement.
The three following lines give the masses of the proton, neutron, and electron in kilograms. These are all more or less correct (although the book values have changed since the message were written) and I think the value for the neutron has a typo; it says !!1.6739286\cdot 10^{{}^-34}!! kg but it probably should have been !!1.67{\mathit 4}9286\cdot 10^{{}^-34}!! kg which would agree with the current book value of !!1.674927351\cdot 10^{{}^-34}!! kg.

Since we're going over the errors on this page, here is yet another
oddity. The number of neutrons in a gold atom
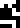 is given at the top of
the page as 117. Unlike uranium-208., the isotope gold-196 actually exists. But it is radioactive,
breaking down into platinum or mercury after about a week. One would
expect the listing to be for gold-197 instead, which is the only
stable isotope and so is the only isotope occurring in naturally-found
gold. (Thanks to Peter Annema for bringing this to my attention.)
A similar oddity occurs in the listing for zinc
is given at the top of
the page as 117. Unlike uranium-208., the isotope gold-196 actually exists. But it is radioactive,
breaking down into platinum or mercury after about a week. One would
expect the listing to be for gold-197 instead, which is the only
stable isotope and so is the only isotope occurring in naturally-found
gold. (Thanks to Peter Annema for bringing this to my attention.)
A similar oddity occurs in the listing for zinc
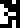 :
zinc-65 is given instead of the stable zinc-64 or zinc-66.
The
other isotopes listed here (sulfur-32, argon-40, silver-107) are more
plausible.
:
zinc-65 is given instead of the stable zinc-64 or zinc-66.
The
other isotopes listed here (sulfur-32, argon-40, silver-107) are more
plausible.
[Other articles in category /aliens/dd] permanent link
Fri, 21 Aug 2015
A message to the aliens, part 6/23 (chemistry)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry)
This is page 6 of the Cosmic Call message. An explanation follows.

The 10 digits again:
 0 |  1 |  2 | 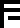 3 |  4 | 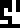 5 |  6 | 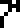 7 | 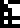 8 | 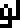 9 |
Page 6 discusses fundamental particles of matter, the structure of the hydrogen and helium atoms, and defines glyphs for the most important chemical elements.
Depicted at top left is the hydrogen atom, with a proton 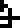 in the center and
an electron
in the center and
an electron 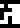 circulating
around the outside. This diagram is equated to the glyph
circulating
around the outside. This diagram is equated to the glyph 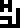 for hydrogen.
for hydrogen.
The diagram for helium 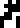 is similar but has two electrons, and its nucleus has two protons and
also two
is similar but has two electrons, and its nucleus has two protons and
also two
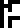 neutrons.
neutrons.
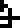 Proton | 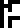 Neutron | 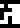 Electron |
The illustrations may puzzle the aliens, depending on how they think of atoms. (Feynman once said that this idea of atoms as little solar systems, with the electrons traveling around the nucleus like planets, was a hundred years old and out of date.) But the accompanying mass and charge data should help clear things up. The first formula says

!!M_p = 1836\cdot M_e!!
the mass of the proton is 1836 times the mass of the electron, and that 1836, independent of the units used and believed to be a universal and fundamental constant, ought to be a dead giveaway about what is being discussed here.
If you want to communicate fundamental constants, you have a bit of a problem. You can't tell the aliens that the speed of light is !!1.8\cdot10^{12}!! furlongs per fortnight without first explaining furlongs and fortnights (as is actually done on a later page). But the proton-electron mass ratio is dimensionless; it's 1836 in every system of units. (Although the value is actually known to be 1836.15267; I don't know why a more accurate value wasn't given.)
This is the first use of subscripts in the document. It also takes
care of introducing the symbol  for mass. The
following formula does the same for charge
for mass. The
following formula does the same for charge 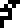 : !!Q_p = -Q_e!!.
: !!Q_p = -Q_e!!.
The next two formulas, accompanying the illustration of the helium
atom, describe the mass (1.00138 protons) and charge (zero) of the
neutron. I wonder why the authors went for the number 1.00138 here
instead of writing the neutron-electron mass ratio of 1838 for
consistency with the previous ratio. I also worry that this won't be
enough for the aliens to be sure about the meaning of 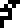 . The 1836 is as
clear as anything can be, but the 0 and -1 of the corresponding charge
ratios could in principle be a lot of other things. Will the context
be enough to make clear what is being discussed? I suppose it has to; charge, unlike mass, comes in discrete units and there is nothing like the 1836.
. The 1836 is as
clear as anything can be, but the 0 and -1 of the corresponding charge
ratios could in principle be a lot of other things. Will the context
be enough to make clear what is being discussed? I suppose it has to; charge, unlike mass, comes in discrete units and there is nothing like the 1836.
The second half of the page reiterates the symbols for hydrogen and
helium and defines symbols for eight other chemical elements. Some of
these appear in organic compounds that will be discussed later; others
are important constituents of the Earth. It also
introduces symbol for “union” or “and”:  . For example,
sodium is described as having 11 protons and 12 neutrons.
. For example,
sodium is described as having 11 protons and 12 neutrons.
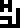 Hydrogen | 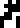 Helium | 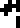 Carbon | 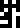 Nitrogen | 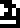 Oxygen |  Aluminium | Silicon | 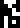 Iron | 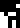 Sodium |  Chlorine |
Most of these new glyphs are not especially mnemonic, except for hydrogen—and aluminium, which is spectacular.
The blog is going on hiatus until early September. When it returns, the next article will discuss page 7, shown at right. It has three errors. Can you find them? (Click to enlarge.)[Other articles in category /aliens/dd] permanent link
Wed, 19 Aug 2015
A message to the aliens, part 5/23 (geometry)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra)
This is page 5 of the Cosmic Call message. An explanation follows.
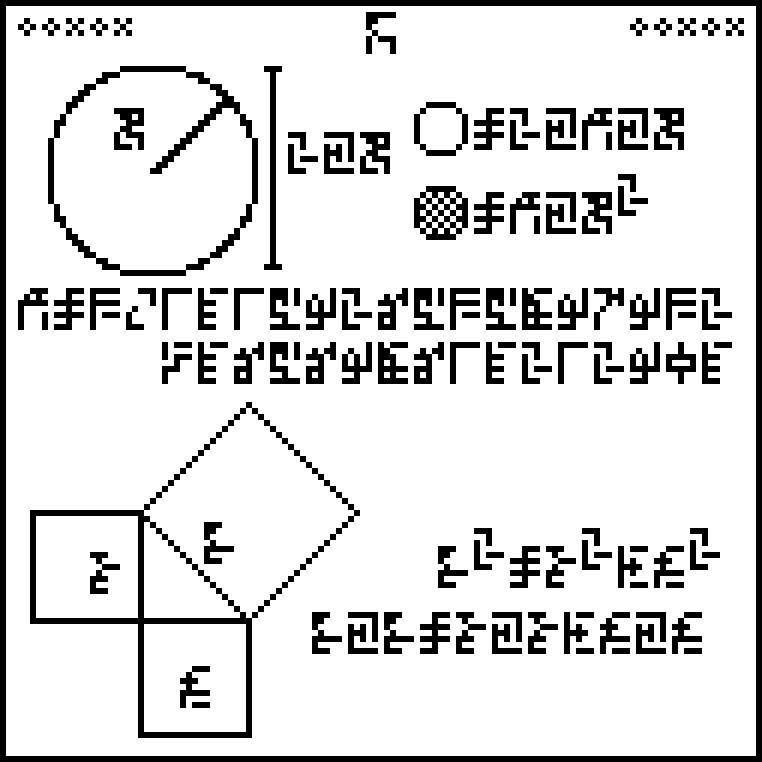
The 10 digits again:
 0 |  1 |  2 |  3 |  4 |  5 |  6 | 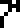 7 | 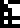 8 | 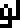 9 |
Page 5 discusses two basic notions of geometry. The top half concerns
circles and introduces !!\pi!!. There is a large circle with its
radius labeled  :
:
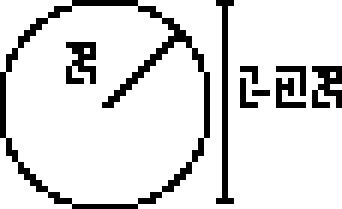
The outer
diameter is then 

 which is !!2\cdot r!!.
which is !!2\cdot r!!.
The perimeter
 is twice
is twice
 times the radius
times the radius
 ,
and the area
,
and the area
 is
is
 times the square of the radius
times the square of the radius  . What is
. What is  ? It's !!\pi!! of
course, as the next line explains, giving !!\pi =
3.1415926545697932…365698614212904!!, which gives enough digits on the
front to make clear what is being communicated. The trailing digits
are around the 51 billionth places and communicate part of the state
of our knowledge of !!\pi!!. I almost wish the authors had included
a sequence of fifteen random digits at this point, just to keep the aliens
wondering.
? It's !!\pi!! of
course, as the next line explains, giving !!\pi =
3.1415926545697932…365698614212904!!, which gives enough digits on the
front to make clear what is being communicated. The trailing digits
are around the 51 billionth places and communicate part of the state
of our knowledge of !!\pi!!. I almost wish the authors had included
a sequence of fifteen random digits at this point, just to keep the aliens
wondering.
The bottom half of the page is about the pythagorean theorem. Here
there's a rather strange feature. Instead of using the three variables
from the previous page,
 ,
the authors changed the second one and used
,
the authors changed the second one and used
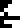 instead. This new
instead. This new  glyph does not
appear anywhere else. A mistake, or did they do it on purpose?
glyph does not
appear anywhere else. A mistake, or did they do it on purpose?
In any case, the pythagorean formula is repeated twice, once with exponents and once without, as both !!z^2=x^2+b^2!! and !!z\cdot z = x\cdot x + b\cdot b!!. I think they threw this in just in case the exponentiation on the previous pages wasn't sufficiently clear. I don't know why the authors chose to use an isosceles right triangle; why not a 3–4–5 or some other scalene triangle, for maximum generality? (What if the aliens think we think the pythagorean theorem applies only for isosceles triangles?) But perhaps they were worried about accurately representing any funny angles on their pixel grid. I wanted to see if it would fit, and it does. You have to make the diagram smaller, but I think it's still clear:
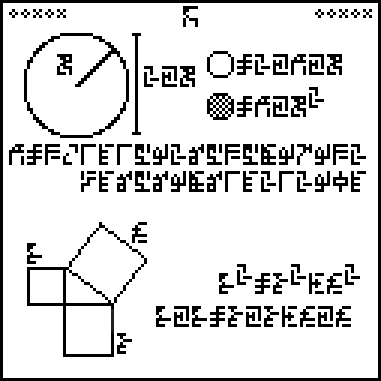
(I made it smaller than it needed to be and then didn't want to redo it.)
I hope this section will be sufficiently unmistakable that the aliens will see past the oddities.
The next article will discuss page 6, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link
Mon, 17 Aug 2015
A message to the aliens, part 4/23 (algebra)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents)
This is page 4 of the Cosmic Call message. An explanation follows.
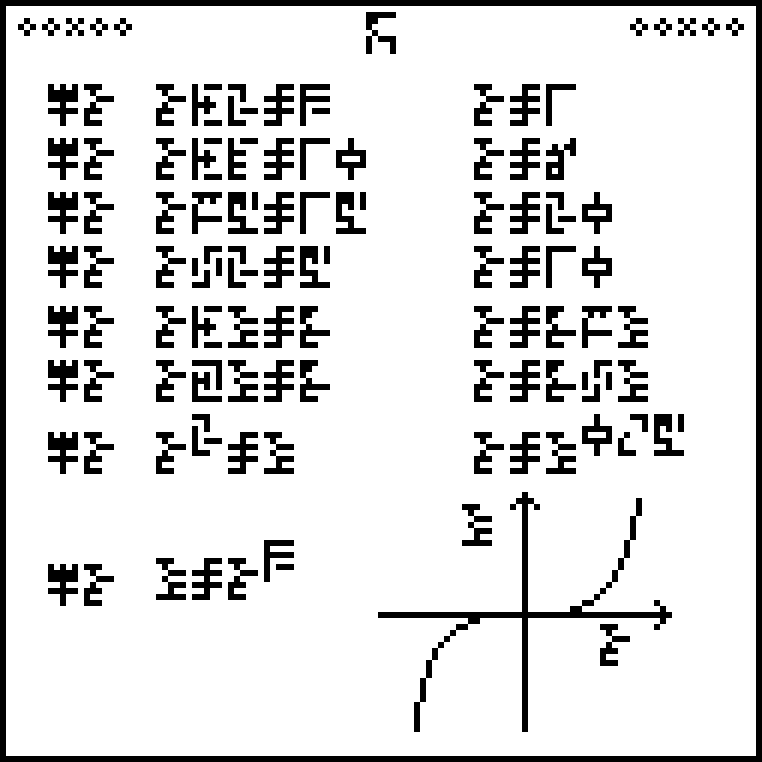
Reminder: page 1 explained the ten digits:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 | 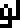 9 |
And the equal sign  .
Page 2 explained the four basic arithmetic operations and some associated notions:
.
Page 2 explained the four basic arithmetic operations and some associated notions:
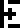 addition | 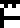 subtraction |  multiplication | 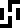 division |  negation |  ellipsis (…) |  decimal point |  indeterminate |
This page, headed with the glyph for “mathematics”  , describes the solution of simple algebraic equations and defines glyphs for three variables, which we may as well call !!x,y,!! and !!z!!:
, describes the solution of simple algebraic equations and defines glyphs for three variables, which we may as well call !!x,y,!! and !!z!!:
 x |  y |  z |
Each equation is introduced by the locution 
 which means “solve
for !!x!!”. This somewhat peculiar “solve” glyph will not appear
again until page 23.
which means “solve
for !!x!!”. This somewhat peculiar “solve” glyph will not appear
again until page 23.
For example the second equation is !!x+4=10!!:
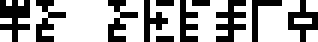
Solve for !!x!!: !!x+4=10!!
The solution, 6, is given over on the right:
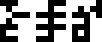
!!x=6!!
After the fourth line, the equations to be solved change from simple numerical equations in one variable to more abstract algebraic relations between three variables. For example, if

Solve for !!x!!: !!x\cdot y=z!!
then
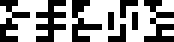
!!x=z\div y!!.
The next-to-last line uses a decimal fraction in the exponent,
!!0.5!!:
 . On the previous page, the rational fraction !!1\div 2!! was
used. Had the same style been followed, it would have looked like this:
. On the previous page, the rational fraction !!1\div 2!! was
used. Had the same style been followed, it would have looked like this:
 .
.
Finally, the last line defines !!x=y^3!! and then, instead of an algebraic solution, gives a graph of the resulting relation, with axes labeled. The scale on the axes is not the same; the !!x!!-coordinate increases from 0 to 20 pixels, but the !!y!!-coordinate increases from 0 to 8000 pixels because !!20^3 = 8000!!. If axes were to the same scale, the curve would go up by 8,000 pixels. Notice that the curve does not peek above the !!x!!-axis until around !!x=8, y=512!! or so. The authors could have stated that this was the graph of !!y=x^3\div 400!!, but chose not to.
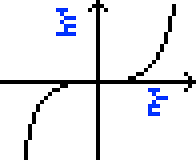
I also wonder what the aliens will make of the arrows on the axes. I think the authors want to show that our coordinates increase going up and to the left, but this seems like a strange and opaque way to do that. A better choice would have been to use a function with an asymmetric graph, such as !!y=2^x!!.
(After I wrote that I learned that similar concerns were voiced about the use of a directional arrow in the Pioneer plaque.
(Wikipedia says: “An article in Scientific American criticized the use of an arrow because arrows are an artifact of hunter-gatherer societies like those on Earth; finders with a different cultural heritage may find the arrow symbol meaningless.”)
The next article will discuss page 5, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link
Sun, 16 Aug 2015My overall SE posting volume was down this month, and not only did I post relatively few interesting items, I've already written a whole article about the most interesting one. So this will be a short report.
I already wrote up Building a box from smaller boxes on the blog here. But maybe I have a couple of extra remarks. First, the other guy's proposed solution is awful. It's long and complicated, which is forgivable if it had answered the question, but it doesn't. And the key point is “blah blah blah therefore code a solver which visits all configurations of the search space”. Well heck, if this post had just been one sentence that ended with “code a solver which visits all configurations of the search space” I would not have any complaints about that.
As an undergraduate I once gave a talk on this topic. One of my examples was the problem of packing 31 dominoes into a chessboard from which two squares have been deleted. There is a simple combinatorial argument why this is impossible if the two deleted squares are the same color, say if they are opposite corners: each domino must cover one square of each color. But if you don't take time to think about the combinatorial argument you could waste a lot of time on computer search learning that there is no solution in that case, and completely miss the deeper understanding that it brings you. So this has been on my mind for a long time.
I wrote a few posts this month where I thought I gave good hints. In How to scale an unit vector !!u!! in such way that !!a u\cdot u=1!! where !!a!! is a scalar I think I did a good job identifying the original author's confusion; he was conflating his original unit vector !!u!! and the scaled, leading him to write !!au\cdot u=1!!. This is sure to lead to confusion. So I led him to the point of writing !!a(bv)\cdot(bv)=1!! and let him take it from there. The other proposed solution is much more rote and mechanical. (“Divide this by that…”)
In Find numbers !!\overline{abcd}!! so that !!\overline{abcd}+\overline{bcd}+\overline{cd}+d+1=\overline{dcba}!! the OP got stuck partway through and I specifically addressed the stuckness; other people solved the problem from the beginning. I think that's the way to go, if the original proposal was never going to work, especially if you stop and say why it was never going to work, but this time OP's original suggestion was perfectly good and she just didn't know how to get to the next step. By the way, the notation !!\overline{abcd}!! here means the number !!1000a+100b+10c+d!!.
In Help finding the limit of this series !!\frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \cdots!! it would have been really easy to say “use the formula” or to analyze the series de novo, but I think I almost hit the nail on the head here: it's just like !!1+\frac12 + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \cdots!!, which I bet OP already knows, except a little different. But I pointed out the wrong difference: I observed that the first sequence is one-fourth the second one (which it is) but it would have been simpler to observe that it's just the second one without the !!1+\frac12!!. I had to review it just now to give the simpler explanation, but I sure wish I'd thought of it at the time. Nobody else pointed it out either. Best of all, would have been to mention both methods. If you can notice both of them you can solve the problem without the advance knowledge of the value of !!1+\frac12+\frac14+\ldots!!, because you have !!4S = 1+\frac12 + S!! and then solve for !!S!!.
In Visualization of Rhombus made of Radii and Chords it seemed that OP just needed to see a diagram (“I really really don't see how two circles can form a rhombus?”), so I drew one.
[Other articles in category /math/se] permanent link
Fri, 14 Aug 2015
A message to the aliens, part 3/23 (exponentiation)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic)
This is page 3 of the Cosmic Call message. An explanation follows.

Reminder: page 1 explained the ten digits:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 | 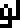 9 |
And the equal sign  .
Page 2 explained the four basic arithmetic operations and some associated notions:
.
Page 2 explained the four basic arithmetic operations and some associated notions:
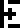 addition | 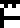 subtraction |  multiplication | 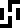 division |  negation |  ellipsis (…) |  decimal point |  indeterminate |
This page, headed with the glyph for “mathematics”  , explains
notations for exponentiation and scientific notation. (This notation
was first used on page 1 in the mersenne prime
, explains
notations for exponentiation and scientific notation. (This notation
was first used on page 1 in the mersenne prime  .)
.)
Exponentiation could be represented by an operator, but instead the authors have chosen to represent it by a superscripted position on the page, as is done in conventional mathematical notation. This saves space.
The top section of the page has small examples of exponentiation, including for example !!5^3=125!!:

!!5^3=125!!
There is a section that follows with powers of 10: !!10^1=10, 10^2=100, 10^3=1000, !! and more interestingly !!10^{{}^-2} = 0.01!!:
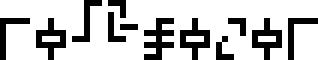
!!10^{{}^-2} = 0.01!!
This is a lead-in to the next section, which expresses various quantities in scientific notation, which will recur frequently later on. For example, !!0.045!! can be written as !!45\times 10^{{}^-2}!!:
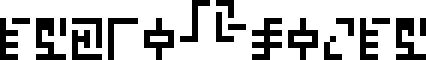
!!45\times10^{{}^-2} = 0.45!!
Finally, there is an offhand remark about the approximate value of the square root of 2:

!!2^{1\div 2} = 1.41421356…!!
[Other articles in category /aliens/dd] permanent link
Wed, 12 Aug 2015
Another solution to Tuesday's git problem
On Tuesday I discussed an interesting solution to the problem of turning this:
no X X on
A --------------- C
into this:
no X X off X on
A ------ B ------ C
Dave Du Cros has suggested an alternative solution: Make the changes required to turn off feature X, and commit them as B, as in my solution:
no X X on X off
A ------ C ------ B
Then use git-revert to revert the changes, making a new C commit in
the right place:
no X X on X off X on
A ------ C ------ B ------ C'
C' and C have identical trees.
Then use git-rebase to squash together C and B:
no X X off X on
A --------------- B ------ C'
This has the benefit of not requiring anything strange. I think my solution is more general, but it's also weird, and it's not clear that the increased generality is useful.
However, what if there were a git-reorder-commits command? Then my
solution would seem much less weird. It would look like this: create
B, as before, and do:
git reorder-commits 0 1
This last command would mean that the previous two commits, normally
HEAD~1 and HEAD~0, should switch places. This might be a useful
standard tool. Or similarly to turn
B -- 3 -- 2 -- 1 -- 0
into
B -- 2 -- 0 -- 3 -- 1
one would use
git reorder-commits 2 0 3 1
I think git-reorder-commits would be easy to implement, as a loop
atop git-commit-tree, as in the previous article.
[ Addendum 20200531: Curtis Dunham suggested a much better interface to this functionality
than my git-reorder-commits proposal. ]
[Other articles in category /prog] permanent link
A message to the aliens, part 1/23 (numbers)
Earlier articles: Introduction Common features
This is page 1 of the Cosmic Call message. An explanation follows.

This page, headed with the glyph for “mathematics”  , explains
the numeral symbols that will be used throughout the rest of the
document. I should warn you that these first few pages are a little
dull, establishing basic mathematical notions. The good stuff comes a
little later.
, explains
the numeral symbols that will be used throughout the rest of the
document. I should warn you that these first few pages are a little
dull, establishing basic mathematical notions. The good stuff comes a
little later.
The page is in three sections. The first section explains the individual digit symbols. A typical portion looks like this:
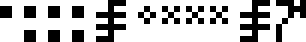
•••• ••• = 0111 = 7
Here the number 7 is written in three ways: first, as seven dots,
probably unmistakable. Second, as a 4-bit binary number, using the
same bit symbols that are used in the page numbers. The three forms
are separated by the glyph  , which means “equals”.
The ten digits, in order from 0 to 9, are represented by the glyphs
, which means “equals”.
The ten digits, in order from 0 to 9, are represented by the glyphs
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 |  9 |
The authors did a great job selecting glyphs that resemble the numerals they represent. All have some resemblance except for 4, which has 4 horizontal strokes. Watch out for 4; it's easy to confuse with 3.
The second section serves two purposes. It confirms the meaning of the ten digits, and it also informs the aliens that the rest of the message will write numerals in base ten. For example, the number 14:

••••• ••••• •••• = 14
Again, there are 14 dots, an equal sign, and the numeral 14, this time
written with the two glyphs  (1) and
(1) and  (4). The base-2
version is omitted this time, to save space. The aliens know from this
that we are using base 10; had it been, say, base 8, the glyphs would
have been
(4). The base-2
version is omitted this time, to save space. The aliens know from this
that we are using base 10; had it been, say, base 8, the glyphs would
have been 
 .
.
People often ask why the numbers are written in base 10, rather than say in base 2. One good answer is: why not? We write numbers in base 10; is there a reason to hide that from the aliens? The whole point of the message is to tell the aliens a little bit about ourselves, so why disguise the fact that we use base-10 numerals? Another reason is that base-10 numbers are easier to proofread for the humans sending the message.
The third section of the page is a list of prime numbers from 2 to 89:
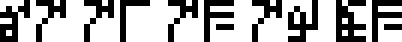
67, 71, 73, 79, 83
and finally the number !!2^{3021377}-1!!
 ,
,
!!2^{3021377}-1!!
I often wonder what the aliens will think of the !!2^{3021377}-1!!. Will they laugh at how cute we are, boasting about the sweet little prime number we found? Or will they be astounded and wonder why we think we know that such a big number is prime?
The next article, to appear 2015-08-12, will discuss page 2, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link
A message to the aliens, part 2/23 (arithmetic)
Earlier articles: Introduction Common features Page 1 (numerals)
This is page 2 of the Cosmic Call message. An explanation follows.

Reminder: the previous page explained the ten digits:
 0 |  1 |  2 |  3 |  4 |  5 |  6 | 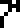 7 | 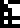 8 | 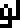 9 |
This page, headed with the glyph for “mathematics” 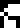 , explains the arithmetic operations on numbers.
, explains the arithmetic operations on numbers.
The page is in five sections, three on top and two below.
The first four sections explain
addition 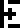 ,
subtraction
,
subtraction 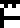 ,
multiplication
,
multiplication  , and
division
, and
division  . Each is explained with a series of five typical arithmetic equalities. For example, !!4\times 3= 12!!:
. Each is explained with a series of five typical arithmetic equalities. For example, !!4\times 3= 12!!:

The subtraction sign actually appeared back on page 1
in the Mersenne prime !!2^{3021377}-1!!  .
.
The negative sign  is introduced in
connection with subtraction, since !!1-2={}^-1!!:
is introduced in
connection with subtraction, since !!1-2={}^-1!!:

Note that the negative-number sign is not the same as the subtraction sign.
The decimal point 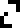 is
introduced in connection with division. For example, !!3\div 2 =
1.5!!:
is
introduced in connection with division. For example, !!3\div 2 =
1.5!!:
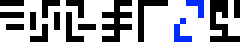
There is also an attempt to divide by zero:

It's not clear what the authors mean by this; the mysterious glyph
 does
not appear anywhere else in the document. What did they think it
meant? Infinity? Indeterminate? Well, I found out later they
published a cheat sheet, which assigns the meaning “undetermined” to
this glyph. Not a great choice, in my opinion, because !!1÷0!! is not
numerically equal to anything.
does
not appear anywhere else in the document. What did they think it
meant? Infinity? Indeterminate? Well, I found out later they
published a cheat sheet, which assigns the meaning “undetermined” to
this glyph. Not a great choice, in my opinion, because !!1÷0!! is not
numerically equal to anything.
For some reason, perhaps because of space limitations, the authors have stuck the equation !!0-1 = {}^-1!! at the bottom of the division section.
The fifth section, at lower right, displays some nonterminating decimal fractions and introduces
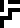 the ellipsis or ‘…’ symbol. For example, !!1\div 9 = 0.1111\ldots!!:
the ellipsis or ‘…’ symbol. For example, !!1\div 9 = 0.1111\ldots!!:
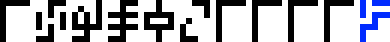
I would have put !!2÷27 = 0.0740…!! here instead of !!2\div 3!!, which I think is too similar to the other examples.
The next article, to appear 2015-08-14, will discuss page 3, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link
Tue, 11 Aug 2015
Reordering git commits with git-commit-tree
I know, you want to say “Why didn't you just use git-rebase?”
Because git-rebase wouldn't work here, that's why. Let me back up.
Say I have commit A, in which feature X does not exist yet. Then in commit C, I implement feature X.
But I realize what I really wanted was to have A, then B, in which feature X was implemented but disabled, and then C in which feature X was enabled. The C I want is just like the C that I have, but I don't have the intervening B.
I have:
no X X on
A --------------- C
I want:
no X X off X on
A ------ B ------ C
One way to do this is to use git-rebase in edit mode to split C into
B and C. To do this I would pause while rebasing C, edit C to disable
feature X, commit the result, which is B, then undo the previous edits
to re-enable X, and continue the rebase, creating C. That's two sets
of edits. I could backup the files before the first edit and then
copy them back for the second edit, but that's the SVN way, so I'm not
going to do that.
Now someone wants me to use git-rebase to “reorder the commits”.
Their idea is: I have C. Edit C to disable feature X and commit the
result as B':
no X X on X off
A ------ C ------ B'
Now use interactive git-rebase to reorder B and C. But this will
not work. git-rebase will construct a patch for turning C into B'
and will try to apply it to A. This will fail completely, because a
patch for turning C into B' is a patch for turning off feature X once
it is implemented. Feature X is not in A and you can't turn something
off that isn't there. So the rebase will fail to apply the
patch.
What I did instead was rather bizarre, using a plumbing command, but worked well. I wrote the code to disable X, and committed it as B, obtaining this:
no X X on X off
A ------ C ------ B
Now B and C have the files I want in them, but their parents are wrong. That is, the history is in the wrong order, but if the parent of C was B and the parent of B was A, eveything would be perfect.
But we can't just change the parents; we have to create a new commit, say B', which has the same files as B but whose parent is A instead of C, and we have to create a new commit C' which has the same files as C but whose parent is B' instead of A.
This is what git-commit-tree does. You give it a tree object
containing the files you want, a list of parents, and a commit
message, and it creates the commit you asked for and prints its SHA1.
When we use git-commit, it first turns the index into a tree, with
git-write-tree, then creates the commit, with git-commit-tree, and
then moves the current head ref up to the new commit. Here we will
use git-commit-tree directly.
So I did:
% git checkout -b XX A
Switched to a new branch 'XX'
% git commit-tree -p HEAD B^{tree}
10ddf433039fd3cbc5bec0c64970a45add15482e
% git reset --hard 10ddf433039fd3cbc5bec0c64970a45add15482e
% git commit-tree -p HEAD C^{tree}
ce46beb90d4aa4e2c9fe0e2e3d22eea256edceac
% git reset --hard ce46beb90d4aa4e2c9fe0e2e3d22eea256edceac
The first git-commit-tree
% git commit-tree -p HEAD B^{tree}
says to make a commit whose tree is the same as B's, and whose parent
is the current HEAD, which is A. (B^{tree} is a special notation
that means to get the tree from commit B.) Git pauses here to read the
commit message from standard input (not shown), and prints the SHA of
the new commit on the terminal. I then use git-reset to move the
current head ref, XX, up to the new commit. Normally git-commit
would do this for us, but we're not using git-commit today.
Then I do the same thing with C:
% git commit-tree -p HEAD C^{tree}
makes a new commit whose tree is the same as C's, and whose parent is
the current head, which looks just like B. Again it reads a commit
message from standard input, and prints the SHA of the new commit on
the terminal, and again I use git-reset to move XX up to the new
commit.
Now I have what I want and I only had to edit the files once. To
complete the task I just reset the head of my working branch to
wherever XX is now, discarding the old A-C-B branch in favor of the
new A-B-C branch. If there's an easier way to do this, I don't know
it.
It seems to me that there have been a number of times in the past
when I wanted to do something like reordering commits, and
git-rebase did not do what I wanted because it reorders patches
and not commits. I should keep my eyes open, and see if this comes up
again, and if it is worth automating.
[ Thanks to Jeremy Leader for suggesting I write this up and to Jeremy Leader and Rik Signes for advance editing. ]
[ Addendum 20150813: a followup article ]
[ Addendum 20200531: a better way to accomplish the same thing ]
[Other articles in category /prog] permanent link
Sun, 09 Aug 2015
A message to the aliens, part 0/23 (framing)
Earlier articles: Introduction
(At left is page 1 of the Cosmic Call message. For an enlarged version of the image, click it.)
First, some notes about the general format of each page. The Cosmic Call message was structured as 23 pages, each a 127×127 bitmap. The entire message was therefore 127×127×23 bits, and this would hopefully be suggestive to the aliens: they could try decoding it as 127 pages of 127×23-bit images, which would produce garbage, or as 23 pages of 127×127-bit images, which is correct. Or they might try decoding it as a single 127×2921-bit image, which would also work. But the choices are quite limited and it shouldn't take long to figure out which one makes sense.
 To
assist in the framing, each page of the message is surrounded by a
border of black pixels and then a second smaller border of white
pixels. If the recipient misinterpreted the framing of the bit sequence,
say by supposing that the message was made of lines of 23 pixels, it
would be immediately apparent that something was wrong, as at right.
At the very least the regular appearance of the black border pixels
every 127 positions, and the fact that the message began with 128
black pixels, would suggest that there was something significant about
that number. If the aliens fourier-transform the message, there
should be a nice big spike at the 127 mark.
To
assist in the framing, each page of the message is surrounded by a
border of black pixels and then a second smaller border of white
pixels. If the recipient misinterpreted the framing of the bit sequence,
say by supposing that the message was made of lines of 23 pixels, it
would be immediately apparent that something was wrong, as at right.
At the very least the regular appearance of the black border pixels
every 127 positions, and the fact that the message began with 128
black pixels, would suggest that there was something significant about
that number. If the aliens fourier-transform the message, there
should be a nice big spike at the 127 mark.
Most of the message is encoded as a series of 5×7-pixel glyphs. The glyphs were generated at random and then subject to later filtering: candidate glyphs were discarded unless they differed from previous glyphs in enough bit positions. This was to help the recipients reconstruct the glyphs if some of the bits were corrupted in transmission, as is likely.
The experimenters then eyeballed the glyphs and tried to match glyphs
with their meanings in a way that would be easy for humans to
remember, to aid in proofreading. For example, the glyph they chose
to represent the digit 7 was 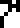 .
.
People frequently ask why the message uses strange glyphs instead of standard hindu-arabic numerals. This is explained by the need to have the glyphs be as different as possible. Communication with other stars is very lossy. Imagine trying to see a tiny flickering light against the background of a star at a distance of several light years. In between you and the flickering light are variable dust and gas clouds. Many of the pixels are likely to be corrupted in transmission. The message needs to survive this corruption. So glyphs are 35 bits each. Each one differs from the other glyphs in many positions, whereas a change of only a few pixels could change a standard 6 into an 8 or vice versa. A glyph is spread across multiple lines of the image, which makes it more resistant to burst errors: even if an entire line of pixels is destroyed in transit, no entire glyph will be lost.
At the top left and top right of each page are page numbers. For
example, page number 1:  The page numbers
are written in binary, most significant bit first, with
The page numbers
are written in binary, most significant bit first, with
 representing a 1 bit and
representing a 1 bit and  representing a 0 bit. These bit
shapes were chosen to be resistant to data corruption; you can change
any 4 of the 9 pixels in either shape and the recipient can still
recover the entire bit unambiguously. There is an ambiguity about
whether the numerals are written right to left or left to right—is
representing a 0 bit. These bit
shapes were chosen to be resistant to data corruption; you can change
any 4 of the 9 pixels in either shape and the recipient can still
recover the entire bit unambiguously. There is an ambiguity about
whether the numerals are written right to left or left to right—is
 the number 1
or the number 16?—but the aliens should be able to figure it out by
comparing page numbers on consecutive pages; this in turn will help
them when time comes for them to figure out the digit symbols.
the number 1
or the number 16?—but the aliens should be able to figure it out by
comparing page numbers on consecutive pages; this in turn will help
them when time comes for them to figure out the digit symbols.
Every page has a topic header, in this case 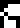 , which roughly means
“mathematics”. The topics of the following pages are something like:
, which roughly means
“mathematics”. The topics of the following pages are something like:
- 1–5 Mathematics
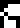
- 6–11,21 Physics
- 12–14,19–20 The Earth
- 15–18 Human anatomy and biochemistry
- 22 Cosmology

- 23 Questions

In the next article I'll explain the contents of page 1. Each following article will appear two or three days later and will explain another page.
To follow the whole series of articles in your feed reader, subscribe to: RSS Atom
(Next article, to appear 2015-08-10: page 1)
[Other articles in category /aliens/dd] permanent link
Thu, 06 Aug 2015
A message to the aliens (introduction)
In 1999, two Canadian astrophysicists, Stéphane Dumas and
Yvan Dutil, composed and sent a message into space. The message
was composed of twenty-three pages of bitmapped data, and was sent
from the RT-70
radio telescope in Yevpatoria, Ukraine, as part of a set of
messages called Cosmic
Call.
The message images themselves are extremely compelling. I saw the first one in the book Beyond Contact by Brian McConnell:

Sometimes when I gave conference talks, I would put this image on the screen during break, to give people something to think about before the class started up again. I like to say that it's fun to see if you're as smart as an alien, or at least if as smart as the Canadian astrophysicists thought the aliens would be.
I invite you to try to understand what is going on in the first image, above. In a day or two I will post a full explanation, along with the second image. Over the next few weeks I hope to write a series of blog articles about the 23 pages, explaining the details of each.
If you can't wait that long for the full set, you can browse them here, or download a zip file.
Addendum 20151223: The series is now complete. The full set of articles is:
- Common features
- Page 1 (numerals)
- Page 2 (arithmetic)
- Page 3 (exponents)
- Page 4 (algebra)
- Page 5 (geometry)
- Page 6 (chemistry)
- Page 7 (mass)
- Page 8 (time and space)
- Page 9 (physical units)
- Page 10 (temperature)
- Page 11 (solar system)
- Page 12 (Earth-Moon system)
- Page 13 (days, months, and years)
- Page 14 (terrain)
- Page 15 (human anatomy)
- Page 16 (vital statistics)
- Page 17 (DNA chemistry)
- Page 18 (cell respiration and division)
- Pages 19-20 (map of the Earth)
- Page 21 (the message)
- Page 22 (cosmology)
- Page 23 (wat)
[Other articles in category /aliens/dd] permanent link
Tue, 04 Aug 2015
The list monad in Perl and Python
A few months ago I wrote an article about using Haskell's list monad to do exhaustive search, with the running example of solving this cryptarithm puzzle:
S E N D
+ M O R E
-----------
M O N E Y
(This means that we want to map the letters S, E, N, D, M,
O, R, Y to distinct digits 0 through 9 to produce a five-digit
and two four-digit numerals which, when added in the indicated way,
produce the indicated sum.)
At the end, I said:
It would be an interesting and pleasant exercise to try to implement the same underlying machinery in another language. I tried this in Perl once, and I found that although it worked perfectly well, between the lack of the do-notation's syntactic sugar and Perl's clumsy notation for lambda functions (
sub { my ($s) = @_; … }instead of\s -> …)the result was completely unreadable and therefore unusable. However, I suspect it would be even worse in Python because of semantic limitations of that language. I would be interested to hear about this if anyone tries it.
I was specifically worried about Python's peculiar local variable binding. But I did receive the following quite clear solution from Peter De Wachter, who has kindly allowed me to reprint it:
digits = set(range(10))
def to_number(*digits):
n = 0
for d in digits:
n = n * 10 + d
return n
def let(x, f):
return f(x)
def unit(x):
return [x]
def bind(xs, f):
ys = []
for x in xs:
ys += f(x)
return ys
def guard(b, f):
return f() if b else []
after which the complete solution looks like:
def solutions():
return bind(digits - {0}, lambda s:
bind(digits - {s}, lambda e:
bind(digits - {s,e}, lambda n:
bind(digits - {s,e,n}, lambda d:
let(to_number(s,e,n,d), lambda send:
bind(digits - {0,s,e,n,d}, lambda m:
bind(digits - {s,e,n,d,m}, lambda o:
bind(digits - {s,e,n,d,m,o}, lambda r:
let(to_number(m,o,r,e), lambda more:
bind(digits - {s,e,n,d,m,o,r}, lambda y:
let(to_number(m,o,n,e,y), lambda money:
guard(send + more == money, lambda:
unit((send, more, money))))))))))))))
print(solutions())
I think this shows that my fears were unfounded. This code produces the correct answer in about 1.8 seconds on my laptop.
Thus inspired, I tried doing it again in Perl, and it was not as bad as I remembered:
sub bd { my ($ls, $f) = @_;
[ map @{$f->($_)}, @$ls ] # Yow
}
sub guard { $_[0] ? [undef] : [] }
I opted to omit unit/return since an idiomatic solution doesn't
really need it. We can't name the bind function bind because that
is reserved for a built-in function; I named it bd instead. We
could use Perl's operator overloading to represent binding with the
>> operator, but that would require turning all the lists into
objects, and it didn't seem worth doing.
We don't need to_number, because Perl does it implicitly, but we do
need a set subtraction function, because Perl has no built-in set
operators:
sub remove {
my ($b, $a) = @_;
my %h = map { $_ => 1 } @$a;
delete $h{$_} for @$b;
return [ keys %h ];
}
After which the solution, although cluttered by Perl's verbose notation for lambda functions, is not too bad:
my $digits = [0..9];
my $solutions =
bd remove([0], $digits) => sub { my ($s) = @_;
bd remove([$s], $digits) => sub { my ($e) = @_;
bd remove([$s,$e], $digits) => sub { my ($n) = @_;
bd remove([$s,$e,$n], $digits) => sub { my ($d) = @_;
my $send = "$s$e$n$d";
bd remove([0,$s,$e,$n,$d], $digits) => sub { my ($m) = @_;
bd remove([$s,$e,$n,$d,$m], $digits) => sub { my ($o) = @_;
bd remove([$s,$e,$n,$d,$m,$o], $digits) => sub { my ($r) = @_;
my $more = "$m$o$r$e";
bd remove([$s,$e,$n,$d,$m,$o,$r], $digits) => sub { my ($y) = @_;
my $money = "$m$o$n$e$y";
bd guard($send + $more == $money) => sub { [[$send, $more, $money]] }}}}}}}}};
for my $s (@$solutions) {
print "@$s\n";
}
This runs in about 5.5 seconds on my laptop. I guess, but am not sure,
that remove is mainly at fault for this poor performance.
An earlier version of this article claimed, incorrectly, that the Python version had lazy semantics. It does not; it is strict.
[ Addendum: Aaron Crane has done some benchmarking of the Perl
version. A better implementation of remove (using an array instead
of a hash) does speed up the calculation somewhat, but contrary to my
guess, the largest part of the run time is bd itself, apparently
becuse Perl function calls are relatively slow.
HN user masklinn tried a translation of the Python code into a
version that returns a lazy
iterator; I gather the
changes were minor. ]
Addendum 20241010
There is a discussion on StackOverflow about doing this in Elixr.
[Other articles in category /prog] permanent link
Tue, 28 Jul 2015A few months ago I wrote an article here called an ounce of theory is worth a pound of search and I have a nice followup.
When I went looking for that article I couldn't find it, because I thought it was about how an ounce of search is worth a pound of theory, and that I was writing a counterexample. I am quite surprised to discover that that I have several times discussed how a little theory can replace a lot of searching, and not vice versa, but perhaps that is because the search is my default.
Anyway, the question came up on math StackExchange today:
John has 77 boxes each having dimensions 3×3×1. Is it possible for John to build one big box with dimensions 7×9×11?
OP opined no, but had no argument. The first answer that appeared was somewhat elaborate and outlined a computer search strategy which claimed to reduce the search space to only 14,553 items. (I think the analysis is wrong, but I agree that the search space is not too large.)
I almost wrote the search program. I have a program around that is something like what would be needed, although it is optimized to deal with a few oddly-shaped tiles instead of many similar tiles, and would need some work. Fortunately, I paused to think a little before diving in to the programming.
For there is an easy answer. Suppose John solved the problem. Look at just one of the 7×11 faces of the big box. It is a 7×11 rectangle that is completely filled by 1×3 and 3×3 rectangles. But 7×11 is not a multiple of 3. So there can be no solution.
Now how did I think of this? It was a very geometric line of reasoning. I imagined a 7×11×9 carton and imagined putting the small boxes into the carton. There can be no leftover space; every one of the 693 cells must be filled. So in particular, we must fill up the bottom 7×11 layer. I started considering how to pack the bottommost 7×11×1 slice with just the bottom parts of the small boxes and quickly realized it couldn't be done; there is always an empty cell left over somewhere, usually in the corner. The argument about considering just one face of the large box came later; I decided it was clearer than what I actually came up with.
I think this is a nice example of the Pólya strategy “solve a simpler problem” from How to Solve It, but I was not thinking of that specifically when I came up with the solution.
For a more interesting problem of the same sort, suppose you have six 2×2x1 slabs and three extra 1×1×1 cubes. Can you pack the nine pieces into a 3×3x3 box?
[Other articles in category /math] permanent link
Thu, 23 Jul 2015
Mystery of the misaligned lowercase ‘p’
I've seen this ad on the subway at least a hundred times, but I never noticed this oddity before:

Specifically, check out the vertical alignment of those ‘p’s:

Notice that it is not simply an unusual font. The height of the ‘p’ matches the other lowercase letters exactly. Here's how it ought to look:

At first I thought the designer was going for a playful, informal logotype. Some of the other lawyers who advertise in the subway go for a playful, informal look. But it seemed odd in the context of the rest of the sign.
As I wondered what happened here, a whole story unfolded in my mind. Here's how I imagine it went down:
The ‘p’, in proper position, collided with the edge of the light-colored box, or overlapped it entirely, causing the serif to disappear into the black area.
The designer (Spivack's nephew) suggested enlarging the box, but there was not enough room. The sign must fit a standard subway car frame, so its size is prescribed.
The designer then suggested eliminating “LAW OFFICES OF”, or eliminating some of the following copy, or reducing its size, but Spivack refused to cede even a single line. “Millions for defense,” cried Spivack, “but not one cent for tribute!”
Spivack found the obvious solution: “Just move the up the ‘p’ so it doesn't bump into the edge, stupid!” Spivack's nephew complied. “Looks great!” said Spivack. “Print it!”
I have no real reason to believe that most of this is true, but I find it all so very plausible.
[ Addendum: Noted typographic expert Jonathan Hoefler says “I'm certain you are correct.” ]
[Other articles in category /IT/typo] permanent link
Sat, 18 Jul 2015[ Notice: I originally published this report at the wrong URL. I moved it so that I could publish the June 2015 report at that URL instead. If you're seeing this for the second time, you might want to read the June article instead. ]
A lot of the stuff I've written in the past couple of years has been on Mathematics StackExchange. Some of it is pretty mundane, but some is interesting. I thought I might have a little meta-discussion in the blog and see how that goes. These are the noteworthy posts I made in April 2015.
Languages and their relation : help is pretty mundane, but interesting for one reason: OP was confused about a statement in a textbook, and provided a reference, which OPs don't always do. The text used the symbol !!\subset_\ne!!. OP had interpreted it as meaning !!\not\subseteq!!, but I think what was meant was !!\subsetneq!!.
I dug up a copy of the text and groveled over it looking for the explanation of !!\subset_\ne!!, which is not standard. There was none that I could find. The book even had a section with a glossary of notation, which didn't mention !!\subset_\ne!!. Math professors can be assholes sometimes.
Is there an operation that takes !!a^b!! and !!a^c!!, and returns !!a^{bc}!! is more interesting. First off, why is this even a reasonable question? Why should there be such an operation? But note that there is an operation that takes !!a^b!! and !!a^c!! and returns !!a^{b+c}!!, namely, multiplication, so it's plausible that the operation that OP wants might also exist.
But it's easy to see that there is no operation that takes !!a^b!! and !!a^c!! and returns !!a^{bc}!!: just observe that although !!4^2=2^4!!, the putative operation (call it !!f!!) should take !!f(2^4, 2^4)!! and yield !!2^{4\cdot4} = 2^{16} = 65536!!, but it should also take !!f(4^2, 4^2)!! and yield !!4^{2\cdot2} = 2^4 = 256!!. So the operation is not well-defined. And you can take this even further: !!2^4!! can be written as !!e^{4\log 2}!!, so !!f!! should also take !!f(e^{2\log 4}, e^{2\log 4})!! and yield !!e^{4(\log 4)^2} \approx 2180.37!!.
They key point is that the representation of a number, or even an integer, in the form !!a^b!! is not unique. (Jargon: "exponentiation is not injective".) You can raise !!a^b!!, but having done so you cannot look at the result and know what !!a!! and !!b!! were, which is what !!f!! needs to do.
But if !!f!! can't do it, how can multiplication do it when it multiplies !!a^b!! and !!a^c!! and gets !!a^{b+c}!!? Does it somehow know what !!a!! is? No, it turns out that it doesn't need !!a!! in this case. There is something magical going on there, ultimately related to the fact that if some quantity is increasing by a factor of !!x!! every !!t!! units of time, then there is some !!t_2!! for which it is exactly doubling every !!t_2!! units of time. Because of this there is a marvelous group homomophism $$\log : \langle \Bbb R^+, \times\rangle \to \langle \Bbb R ,+\rangle$$ which can change multiplication into addition without knowing what the base numbers are.
In that thread I had a brief argument with someone who thinks that operators apply to expressions rather than to numbers. Well, you can say this, but it makes the question trivial: you can certainly have an "operator" that takes expressions !!a^b!! and !!a^c!! and yields the expression !!a^{bc}!!. You just can't expect to apply it to numbers, such as !!16!! and !!16!!, because those numbers are not expressions in the form !!a^b!!. I remembered the argument going on longer than it did; I originally ended this paragraph with a lament that I wasted more than two comments on this guy, but looking at the record, it seems that I didn't. Good work, Mr. Dominus.
how 1/0.5 is equal to 2? wants a simple explanation. Very likely OP is a primary school student. The question reminds me of a similar question, asking why the long division algorithm is the way it is. Each of these is a failure of education to explain what division is actually doing. The long division answer is that long division is an optimization for repeated subtraction; to divide !!450\div 3!! you want to know how many shares of three cookies each you can get from !!450!! cookies. Long division is simply a notation for keeping track of removing !!100!! shares, leaving !!150!! cookies, then !!5\cdot 10!! further shares, leaving none.
In this question there was a similar answer. !!1/0.5!! is !!2!! because if you have one cookie, and want to give each kid a share of !!0.5!! cookies, you can get out two shares. Simple enough.
I like division examples that involve giving cookies to kids, because cookies are easy to focus on, and because the motivation for equal shares is intuitively understood by everyone who has kids, or who has been one.
There is a general pedagogical principle that an ounce of examples are worth a pound of theory. My answer here is a good example of that. When you explain the theory, you're telling the student how to understand it. When you give an example, though, if it's the right example, the student can't help but understand it, and when they do they'll understand it in their own way, which is better than if you told them how.
How to read a cycle graph? is interesting because hapless OP is asking for an explanation of a particularly strange diagram from Wikipedia. I'm familiar with the eccentric Wikipedian who drew this, and I was glad that I was around to say "The other stuff in this diagram is nonstandard stuff that the somewhat eccentric author made up. Don't worry if it's not clear; this author is notorious for that."
In Expected number of die tosses to get something less than 5, OP calculated as follows: The first die roll is a winner !!\frac23!! of the time. The second roll is the first winner !!\frac13\cdot\frac23!! of the time. The third roll is the first winner !!\frac13\cdot\frac13\cdot\frac23!! of the time. Summing the series !!\sum_n \frac23\left(\frac13\right)^nn!! we eventually obtain the answer, !!\frac32!!. The accepted answer does it this way also.
But there's a much easier way to solve this problem. What we really want to know is: how many rolls before we expect to have seen one good one? And the answer is: the expected number of winners per die roll is !!\frac23!!, expectations are additive, so the expected number of winners per !!n!! die rolls is !!\frac23n!!, and so we need !!n=\frac32!! rolls to expect one winner. Problem solved!
I first discovered this when I was around fifteen, and wrote about it here a few years ago.
As I've mentioned before, this is one of the best things about mathematics: not that it works, but that you can do it by whatever method that occurs to you and you get the same answer. This is where mathematics pedagogy goes wrong most often: it proscribes that you must get the answer by method X, rather than that you must get the answer by hook or by crook. If the student uses method Y, and it works (and if it is correct) that should be worth full credit.
Bad instructors always say "Well, we need to test to see if the student knows method X." No, we should be testing to see if the student can solve problem P. If we are testing for method X, that is a failure of the test or of the curriculum. Because if method X is useful, it is useful because for some problems, it is the only method that works. It is the instructor's job to find one of these problems and put it on the test. If there is no such problem, then X is useless and it is the instructor's job to omit it from the curriculum. If Y always works, but X is faster, it is the instructor's job to explain this, and then to assign a problem for the test where Y would take more time than is available.
I see now I wrote the same thing in 2006. It bears repeating. I also said it again a couple of years ago on math.se itself in reply to a similar comment by Brian Scott:
If the goal is to teach students how to write proofs by induction, the instructor should damned well come up with problems for which induction is the best approach. And if even then a student comes up with a different approach, the instructor should be pleased. ... The directions should not begin [with "prove by induction"]. I consider it a failure on the part of the instructor if he or she has to specify a technique in order to give students practice in applying it.
[Other articles in category /math/se] permanent link
Fri, 03 Jul 2015
The annoying boxes puzzle: solution
I presented this logic puzzle on Wednesday:
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."It's not too late to try to solve this before reading on. If you want, you can submit your answer here:Can you figure out which box contains the treasure?
Results
There were 506 total responses up to Fri Jul 3 11:09:52 2015 UTC; I kept only the first response from each IP address, leaving 451. I read all the "something else" submissions and where it seemed clear I recoded them as votes for "red", for "not enough information", or as spam. (Several people had the right answer but submitted "other" so they could explain themselves.) There was also one post attempted to attack my (nonexistent) SQL database. Sorry, Charlie; I'm not as stupid as I look.
66.52% 300 red 25.72 116 not-enough-info 3.55 16 green 2.00 9 other 1.55 7 spam 0.44 2 red-with-qualification 0.22 1 attack 100.00 451 TOTAL
What?
Let me show you. I stated:
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."
The labels are as I said. Everything I told you was literally true.
The treasure is definitely not in the red box.
No, it is actually in the green box.
(It's hard to see, but one of the items in the green box is the gold and diamond ring made in Vienna by my great-grandfather, which is unquestionably a real treasure.)
So if you said the treasure must be in the red box, you were simply mistaken. If you had a logical argument why the treasure had to be in the red box, your argument was fallacious, and you should pause and try to figure out what was wrong with it.
I will discuss it in detail below.
Solution
The treasure is undeniably in the green box. However, correct answer to the puzzle is "no, you cannot figure out which box contains the treasure". There is not enough information given. (Notice that the question was not “Where is the treasure?” but “Can you figure out…?”)
(Fallacious) Argument A
Many people erroneously conclude that the treasure is in the red box, using reasoning something like the following:
- Suppose the red label is true. Then exactly one label is true, and since the red label is true, the green label is false. Since it says that the treasure is in the green box, the treasure must really be in the red box.
- Now suppose that the red label is false. Then the green label must also be false. So again, the treasure is in the red box.
- Since both cases lead to the conclusion that the treasure is in the red box, that must be where it is.
What's wrong with argument A?
Here are some responses people commonly have when I tell them that argument A is fallacious:
"If the treasure is in the green box, the red label is lying."
Not quite, but argument A explicitly considers the possibility that the red label was false, so what's the problem?
"If the treasure is in the green box, the red label is inconsistent."
It could be. Nothing in the puzzle statement ruled this out. But actually it's not inconsistent, it's just irrelevant.
"If the treasure is in the green box, the red label is meaningless."
Nonsense. The meaning is plain: it says “exactly one of these labels is true”, and the meaning is that exactly one of the labels is true. Anyone presenting argument A must have understood the label to mean that, and it is incoherent to understand it that way and then to turn around and say that it is meaningless! (I discussed this point in more detail in 2007.)
"But the treasure could have been in the red box."
True! But it is not, as you can see in the pictures. The puzzle does not give enough information to solve the problem. If you said that there was not enough information, then congratulations, you have the right answer. The answer produced by argument A is incontestably wrong, since it asserts that the treasure is in the red box, when it is not.
"The conditions supplied by the puzzle statement are inconsistent."
They certainly are not. Inconsistent systems do not have models, and in particular cannot exist in the real world. The photographs above demonstrate a real-world model that satisfies every condition posed by the puzzle, and so proves that it is consistent.
"But that's not fair! You could have made up any random garbage at all, and then told me afterwards that you had been lying."
Had I done that, it would have been an unfair puzzle. For example, suppose I opened the boxes at the end to reveal that there was no treasure at all. That would have directly contradicted my assertion that "One [box] contains a treasure". That would have been cheating, and I would deserve a kick in the ass.But I did not do that. As the photograph shows, the boxes, their colors, their labels, and the disposition of the treasure are all exactly as I said. I did not make up a lie to trick you; I described a real situation, and asked whether people they could diagnose the location of the treasure.
(Two respondents accused me of making up lies. One said:
There is no treasure. Both labels are lying. Look at those boxes. Do you really think someone put a treasure in one of them just for this logic puzzle?What can I say? I did put a treasure in a box just for this logic puzzle. Some of us just have higher standards.)
"But what about the labels?"
Indeed! What about the labels?
The labels are worthless
The labels are red herrings; the provide no information. Consider the following version of the puzzle:
There are two boxes on a table, one red and one green. One contains a treasure.Obviously, the problem cannot be solved from the information given.Which box contains the treasure?
Now consider this version:
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "gcoadd atniy fnck z fbi c rirpx hrfyrom". The green box is labelled "ofurb rz bzbsgtuuocxl ckddwdfiwzjwe ydtd."One is similarly at a loss here.Which box contains the treasure?
(By the way, people who said one label was meaningless: this is what a meaningless label looks like.)
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."The point being that in the absence of additional information, there is no reason to believe that the labels give any information about the contents of the boxes, or about labels, or about anything at all. This should not come as a surprise to anyone. It is true not just in annoying puzzles, but in the world in general. A box labeled “fresh figs” might contain fresh figs, or spoiled figs, or angry hornets, or nothing at all.But then the janitor happens by. "Don't be confused by those labels," he says. "They were stuck on there by the previous owner of the boxes, who was an illiterate shoemaker who only spoke Serbian. I think he cut them out of a magazine because he liked the frilly borders."
Which box contains the treasure?
Why doesn't every logic puzzle fall afoul of this problem?
I said as part of the puzzle conditions that there was a treasure in one box. For a fair puzzle, I am required to tell the truth about the puzzle conditions. Otherwise I'm just being a jerk.Typically the truth or falsity of the labels is part of the puzzle conditions. Here's a typical example, which I took from Raymond Smullyan's What is the name of this book? (problem 67a):
… She had the following inscriptions put on the caskets:Notice that the problem condition gives the suitor a certification about the truth of the labels, on which he may rely. In the quotation above, the certification is in boldface.Portia explained to the suitor that of the three statements, at most one was true.
Gold Silver Lead THE PORTRAIT IS IN THIS CASKET THE PORTRAIT IS NOT IN THIS CASKET THE PORTRAIT IS NOT IN THE GOLD CASKET Which casket should the suitor choose [to find the portrait]?
A well-constructed puzzle will always contain such a certification, something like “one label is true and one is false” or “on this island, each person always lies, or always tells the truth”. I went to What is the Name of this Book? to get the example above, and found more than I had bargained for: problem 70 is exactly the annoying boxes problem! Smullyan says:
Good heavens, I can take any number of caskets that I please and put an object in one of them and then write any inscriptions at all on the lids; these sentences won't convey any information whatsoever.(Page 65)
Had I known ahead of time that Smullyan had treated the exact same topic with the exact same example, I doubt I would have written this post at all.
But why is this so surprising?
I don't know.
Final notes
16 people correctly said that the treasure was in the green box. This has to be counted as a lucky guess, unacceptable as a solution to a logic puzzle.One respondent referred me to a similar post on lesswrong.
I did warn you all that the puzzle was annoying.
I started writing this post in October 2007, and then it sat on the shelf until I got around to finding and photographing the boxes. A triumph of procrastination!
Addendum 2015091
Steven Mazie has written a blog article about this topic, A Logic Puzzle That Teaches a Life Lesson.
Addendum 20240628
It seems that the Lesswrongers call this The Parable of the Dagger. Here's their version of the payoff:
The jester opened the second box, and found a dagger.“How?!” cried the jester in horror, as he was dragged away. “It’s logically impossible!”
“It is entirely possible,” replied the king. “I merely wrote those inscriptions on two boxes, and then I put the dagger in the second one.”
[Other articles in category /math/logic] permanent link
Wed, 01 Jul 2015
The annoying boxes puzzle
Here is a logic puzzle. I will present the solution on Friday.
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."Starting on 2015-07-03, the solution will be here.Can you figure out which box contains the treasure?
[Other articles in category /math/logic] permanent link
Mon, 22 Jun 2015In late April I served a residency at Recurse Center, formerly known as Hacker School. I want to write up what I did before I forget.
Recurse Center bills itself as being like a writer's retreat, but for programming. Recursers get better at programming four days a week for three months. There are some full-time instructors there to help, and periodically a resident, usually someone notable, shows up for a week. It's free to students: RC partners with companies that then pay it a fee if they hire a Recurser.
I got onto the RC chat system and BBS a few weeks ahead and immediately realized that it was going to be great. I am really wary about belonging to groups, but I felt like I fit right in at RC, in a way that I hadn't felt since I went off to math camp at age 14. Recurse Center isn't that different from math camp now that I think about it.
The only prescribed duty of a resident is to give a half-hour talk on Monday night, preferably on a technical topic. I gave mine on the history and internals of lightweight hash structures in programming languages like Python and Perl. (You can read all about that if you want to.)
Here's what else I did:
I gave a bunch of other talks: two on Git, one on calculating with continued fractions, one on how the Haskell type inferencer works, one on the topology of data types, one on the Unix process model, one on Alien Horrors from the Dawn of Unix. This was too many talks. I didn't have enough energy and time to prepare all of them properly. On the other hand, a lot of people were very complimentary about the talks and said they were very glad that I gave so many. Also, giving talks is a great way to get people familiar with you so that they won't be shy about talking to you or asking you to work with them. But I think I'll cut it down to one per day next time.
Alex Taipale was inspired by my hash talk to implement hashes synthetically in Python, and I paired with her on that for the first part and reviewed her code a couple of times after. It was really fun to see how she went about it.
Libby Horacek showed me around the text adventure game she wrote in Haskell. I had the first of several strokes of luck here. Libby had defined an input format to specify the room layout and the objects, and I observed that it was very similar to Asherah, a project that another Recurser, Michelle Steigerwalt, had done a couple of years before. I found this out because I read everyone's self-posted bio ahead of time and browsed the interesting-sounding links.
Aditya Mukerjee was implementing Git in Go. He wanted help deciphering the delta format. Later I paired with Aditya again and we debugged his implementation of the code that expanded the deltas back into complete files. I hadn't known any Go but it's easy to pick up.
Geoffrey Gilmore had read my ancient article on how to write a regex matcher. He had written his own implementation in Scala and wanted to show it to me. I didn't know any Scala but the code was very clear. Geoffrey had worked out a clever way to visualize the resulting finite automaton: his automaton object had a method that would dump out its graph in the "dot" language, and he could feed that to Graphviz to get it to draw the graph.
I had a conference with Ahmed Abdalla and Joel Burget about SML. The main question they wanted me to answer: Why might they want to look at SML instead of Haskell? This was a stroke of luck: I was unusually well-prepared to answer this question, having written many thousands of lines of SML since about 1993. My answer was unequivocally that there was no reason, SML was obsolete, because it had big problems which had never been solved, and Haskell had been introduced in part to solve, avoid, or finesse these problems.
For example, nobody knows how to incorporate references into a Hindley-Milner type system. SML has tried at least three methods for doing this over the years. They all suck, and none of them work right. Haskell avoids the whole issue: no references. If you want something like references, you can build a monad that simulates it locally.
I could probably write a whole blog article about this, so maybe another time.
[ Addendum 20220425: The article is written! ]
Libby wanted to pair with me again. She offered me a choice: she was building an e-reader, controlled by a Raspberry Pi, and mounted inside an antique book that she had hollowed out. I would have been willing to try this, although I didn't know anything about Raspberry Pi. But my other choice was very attractive: she was reviving KiSS, an ancient Windows paper-doll app that had been current in the 1990s. people had designed hundreds or thousands of dolls and costumes, which were all languishing because nobody wanted to run the app any more. She wanted to reimplement the dress-up program in Javascript, and port the doll and clothing cels to PNG files. Here I had another stroke of luck. I was already familiar with the program, and I think I have even been into its source code at some point.
Libby had found that Gimp could load a KiSS cel, so we looked at the Gimp source code to figure out the file format. She had been planning to use
libpngto turn the cel into a PNG, but I showed her a better way: convert it into a PPM file and feed to toppmtopng. This saved a lot of trouble! (I have written a little bit about this approach in the past.) Libby hacked in the Gimp code, grafting her PPM file writing code into the Gimp cel reading code in place of Gimp's internal pixmap operations. It worked!I talked to Chris Ball about his GitTorrent project. Chris wants to make a decentralized github that doesn't depend on the GitHub company or on their technical infrastructure. He spent a long time trying to make me understand why he wanted to do the project at all and what it was for. I think I eventually got it. It also transpired that Chris knows way more about BitTorrent than I do. I don't think I was much help to Chris.
Jesse Chen paired with me to fix the layout problems that have been troubling my blog for years. We redid the ancient table-based layout that I had inherited from Blosxom ten years ago, converting it mostly to CSS, and fixed a bunch of scrolling problems. We also fixed it to be legible on a phone display, which it previously wasn't. Thanks Jesse!
I had a discussion with Michelle Steigerwalt about big-O notation and how you figure out what an algorithm's big-O-ness is, either from counting lines in the source code or the pseudocode, or from running the algorithm on different-size inputs and timing it. It's fun that you can do the static analysis and then run the program and see it produce the results you predicted.
There was a lot of other stuff. I met or at least spoke with around 90% of the seventy or so Recursers who were there with me. I attended the daily stand-up status meetings with a different group each time. I ate lunch and dinner with many people and had many conversations. I went out drinking with Recursers at least once. The RC principals kindly rescheduled the usual Thursday lightning talks to Monday so I could attend. I met Erik Osheim for lunch one day. And I baked cookies for our cookie-decorating party!
It was a great time, definitely a high point in my life. A thousand thanks to RC, to Rachel Vincent and Dave Albert for essential support while I was there, and to the facilitators, principals, and especially to the other Recursers.
[Other articles in category /misc] permanent link
Thu, 18 Jun 2015A lot of the stuff I've written in the past couple of years has been on math.StackExchange. Some of it is pretty mundane, but some is interesting. My summary of April's interesting posts was well-received, so here are the noteworthy posts I made in May 2015.
What matrix transforms !!(1,0)!! into !!(2,6)!! and tranforms !!(0,1)!! into !!(4,8)!!? was a little funny because the answer is $$\begin{pmatrix}2 & 4 \\ 6 & 8 \end{pmatrix}$$ and yeah, it works exactly like it appears to, there's no trick. But if I just told the guy that, he might feel unnecessarily foolish. I gave him a method for solving the problem and figured that when he saw what answer he came up with, he might learn the thing that the exercise was designed to teach him.
Is a “network topology'” a topological space? is interesting because several people showed up right away to say no, it is an abuse of terminology, and that network topology really has nothing to do with mathematical topology. Most of those comments have since been deleted. My answer was essentially: it is topological, because just as in mathematical topology you care about which computers are connected to which, and not about where any of the computers actually are.
Nobody constructing a token ring network thinks that it has to be a geometrically circular ring. No, it only has to be a topologically circular ring. A square is fine; so is a triangle; topologically they are equivalent, both in networking and in mathematics. The wires can cross, as long as they don't connect at the crossings. But if you use something that isn't topologically a ring, like say a line or a star or a tree, the network doesn't work.
The term “topological” is a little funny. “Topos” means “place” (like in “topography” or “toponym”) but in topology you don't care about places.
Is there a standard term for this generalization of the Euler totient function? was asked by me. I don't include all my answers in these posts, but I think maybe I should have a policy of including all my questions. This one concerned a simple concept from number theory which I was surprised had no name: I wanted !!\phi_k(n)!! to be the number of integers !!m!! that are no larger than !!n!! for which !!\gcd(m,n) = k!!. For !!k=1!! this is the famous Euler totient function, written !!\varphi(n)!!.
But then I realized that the reason it has no name is that it's simply !!\phi_k(n) = \varphi\left(\frac n k\right)!! so there's no need for a name or a special notation.
As often happens, I found the answer myself shortly after I asked the question. I wonder if the reason for this is that my time to come up with the answer is Poisson-distributed. Then if I set a time threshold for how long I'll work on the problem before asking about it, I am likely to find the answer to almost any question that exceeds the threshold shortly after I exceed the threshold. But if I set the threshold higher, this would still be true, so there is no way to win this particular game. Good feature of this theory: I am off the hook for asking questions I could have answered myself. Bad feature: no real empirical support.
how many ways can you divide 24 people into groups of two? displays a few oddities, and I think I didn't understand what was going on at that time. OP has calculated the first few special cases:
1:1 2:1 3:3 4:3 5:12 6:15
which I think means that there is one way to divide 2 people into groups of 2, 3 ways to divide 4 people, and 15 ways to divide 6 people. This is all correct! But what could the 1:1, 3:3, 5:12 terms mean? You simply can't divide 5 people into groups of 2. Well, maybe OP was counting the extra odd person left over as a sort of group on their own? Then odd values would be correct; I didn't appreciate this at the time.
But having calculated 6 special cases correctly, why can't OP calculate the seventh? Perhaps they were using brute force: the next value is 48, hard to brute-force correctly if you don't have a enough experience with combinatorics.
I tried to suggest a general strategy: look at special cases, and not by brute force, but try to analyze them so that you can come up with a method for solving them. The method is unnecessary for the small cases, where brute force enumeration suffices, but you can use the brute force enumeration to check that the method is working. And then for the larger cases, where brute force is impractical, you use your method.
It seems that OP couldn't understand my method, and when they tried to apply it, got wrong answers. Oh well, you can lead a horse to water, etc.
The other pathology here is:
I think I did what you said and I got 1.585times 10 to the 21
for the !!n=24!! case. The correct answer is $$23\cdot21\cdot19\cdot17\cdot15\cdot13\cdot11\cdot9\cdot7\cdot5\cdot3\cdot1 = 316234143225 \approx 3.16\cdot 10^{11}.$$ OP didn't explain how they got !!1.585\cdot10^{21}!! so there's not much hope of correcting their weird error.
This is someone who probably could have been helped in person, but on the Internet it's hopeless. Their problems are Internet communication problems.
Lambda calculus typing isn't especially noteworthy, but I wrote a fairly detailed explanation of the algorithm that Haskell or SML uses to find the type of an expression, and that might be interesting to someone.
I think Special representation of a number is the standout post of the month. OP speculates that, among numbers of the form !!pq+rs!! (where !!p,q,r,s!! are prime), the choice of !!p,q,r,s!! is unique. That is, the mapping !!\langle p,q,r,s\rangle \to pq+rs!! is reversible.
I was able to guess that this was not the case within a couple of minutes, replied pretty much immediately:
I would bet money against this representation being unique.
I was sure that a simple computer search would find counterexamples. In fact, the smallest is !!11\cdot13 + 19\cdot 29 = 11\cdot 43 + 13\cdot 17 = 694!! which is small enough that you could find it without the computer if you are patient.
The obvious lesson to learn from this is that many elementary conjectures of this type can be easily disproved by a trivial computer search, and I frequently wonder why more amateur mathematicians don't learn enough computer programming to investigate this sort of thing. (I wrote recently on the topic of An ounce of theory is worth a pound of search , and this is an interesting counterpoint to that.)
But the most interesting thing here is how I was able to instantly guess the answer. I explained in some detail in the post. But the basic line of reasoning goes like this.
Additive properties of the primes are always distributed more or less at random unless there is some obvious reason why they can't be. For example, let !!p!! be prime and consider !!2p+1!!. This must have exactly one of the three forms !!3n-1, 3n,!! or !!3n+1!! for some integer !!n!!. It obviously has the form !!3n+1!! almost never (the only exception is !!p=3!!). But of the other two forms there is no obvious reason to prefer one over the other, and indeed of the primes up to 10,000, 611 are of the type !!3n!! and and 616 are of the type !!3n-1!!.
So we should expect the value !!pq+rs!! to be distributed more or less randomly over the set of outputs, because there's no obvious reason why it couldn't be, except for simple stuff, like that it's obviously almost always even.
So we are throwing a bunch of balls at random into bins, and the claim is that no bin should contain more than one ball. For that to happen, there must be vastly more bins than balls. But the bins are numbers, and primes are not at all uncommon among numbers, so the number of bins isn't vastly larger, and there ought to be at least some collisions.
In fact, a more careful analysis, which I wrote up on the site, shows that the number of balls is vastly larger—to have them be roughly the same, you would need primes to be roughly as common as perfect squares, but they are far more abundant than that—so as you take larger and larger primes, the number of collisions increases enormously and it's easy to find twenty or more quadruples of primes that all map to the same result. But I was able to predict this after a couple of minutes of thought, from completely elementary considerations, so I think it's a good example of Lower Mathematics at work.
This is an example of a fairly common pathology of math.se questions: OP makes a conjecture that !!X!! never occurs or that there are no examples with property !!X!!, when actually !!X!! almost always occurs or every example has property !!X!!.
I don't know what causes this. Rik Signes speculates that it's just wishful thinking: OP is doing some project where it would be useful to have !!pq+rs!! be unique, so posts in hope that someone will tell them that it is. But there was nothing more to it than baseless hope. Rik might be right.
[ Addendum 20150619: A previous version of this article included the delightful typo “mathemativicians”. ]
[Other articles in category /math/se] permanent link
Sun, 14 Jun 2015[ This page originally held the report for April 2015, which has moved. It now contains the report for June 2015. ]
Is “smarter than” a transitive relationship? concerns a hypothetical "is smarter than" relation with the following paradoxical-seeming property:
most X's are smarter than most Y's, but most Y's are such that it is not the case that most X's are smarter than it.
That is, if !!\mathsf Mx.\Phi(x)!! means that most !!x!! have property !!\Phi!!, then we want both $$\mathsf Mx.\mathsf My.S(x, y)$$ and also $$\mathsf My.\mathsf Mx.\lnot S(x, y).$$
“Most” is a little funny here: what does it mean? But we can pin it down by supposing that there are an infinite number of !!x!!es and !!y!!s, and agreeing that most !!x!! have property !!P!! if there are only a finite number of exceptions. For example, everyone should agree that most positive integers are larger than 7 and that most prime numbers are odd. The jargon word here is that we are saying that a subset contains “most of” the elements of a larger set if it is cofinite.
There is a model of this property, and OP reports that they asked the prof if this was because the "smarter than" relation !!S(x,y)!! could be antitransitive, so that one might have !!S(x,y), S(y,z)!! but also !!S(z,x)!!. The prof said no, it's not because of that, but the OP want so argue that it's that anyway. But no, it's not because of that; there is a model that uses a perfectly simple transitive relation, and the nontransitive thing nothing but a distraction. (The model maps the !!x!!es and !!y!!s onto numbers, and says !!x!! is smarter than !!y!! if its number is bigger.) Despite this OP couldn't give up the idea that the model exists because of intransitive relations. It's funny how sometimes people get stuck on one idea and can't let go of it.
How to generate a random number between 1 and 10 with a six-sided die? was a lot of fun and attracted several very good answers. Top-scoring is Jack D'Aurizio's, which proposes a completely straightforward method: roll once to generate a bit that selects !!N=0!! or !!N=5!!, and then roll again until you get !!M\ne 6!!, and the result is !!N+M!!.
But several other answers were suggested, including two by me, one explaining the general technique of arithmetic coding, which I'll probably refer back to in the future when people ask similar questions. Don't miss NovaDenizen's clever simplification of arithmetic coding, which I want to think about more, or D'Aurizio's suggestion that if you threw the die into a V-shaped trough, it would land with one edge pointing up and thus select a random number from 1 to 12 in a single throw.
Interesting question: Is there an easy-to-remember mapping from edges to numbers from 1–12? Each edge is naturally identified by a pair of distinct integers from 1–6 that do not add to 7.
The oddly-phrased Category theory with objects as logical expressions over !!{\vee,\wedge,\neg}!! and morphisms as? asks if there is a standard way to turn logical expressions into a category, which there is: you put an arrow from !!A\to B!! for each proof that !!A!! implies !!B!!; composition of arrows is concatenation of proofs, and identity arrows are empty proofs. The categorial product, coproduct, and exponential then correspond to !!\land, \lor, !! and !!\to!!.
This got me thinking though. Proofs are properly not lists, they are trees, so it's not entirely clear what the concatenation operation is. For example, suppose proof !!X!! concludes !!A!! at its root and proof !!Y!! assumes !!A!! in more than one leaf. When you concatenate !!X!! and !!Y!! do you join all the !!A!!'s, or what? I really need to study this more. Maybe the Lambek and Scott book talks about it, or maybe the Goldblatt Topoi book, which I actually own. I somehow skipped most of the Cartesian closed category stuff, which is an oversight I ought to correct.
In Why is the Ramsey`s theorem a generalization of the Pigeonhole principle I gave what I thought was a terrific answer, showing how Ramsey's graph theorem and the pigeonhole principle are both special cases of Ramsey's hypergraph theorem. This might be my favorite answer of the month. It got several upvotes, but OP preferred a different answer, with fewer details.
There was a thread a while back about theorems which are generalizations of other theorems in non-obvious ways. I pointed out the Yoneda lemma was a generalization of Cayley's theorem from group theory. I see that nobody mentioned the Ramsey hypergraph theorem being a generalization of the pigeonhole principle, but it's closed now, so it's too late to add it.
In Why does the Deduction Theorem use Union? I explained that the English word and actually has multiple meanings. I know I've seen this discussed in elementary logic texts but I don't remember where.
Finally, Which is the largest power of natural number that can be evaluated by computers? asks if it's possible for a computer to calculate !!7^{120000000000}!!. The answer is yes, but it's nontrivial and you need to use some tricks. You have to use the multiplying-by-squaring trick, and for the squarings you probably want to do the multiplication with DFT. OP was dissatistifed with the answer, and seemed to have some axe to grind, but I couldn't figure out what it was.
[Other articles in category /math/se] permanent link
Wed, 13 May 2015
Want to work with me on one of these projects?
I did a residency at the Recurse Center last month. I made a profile page on their web site, which asked me to list some projects I was interested in working on while there. Nobody took me up on any of the projects, but I'm still interested. So if you think any of these projects sounds interesting, drop me a note and maybe we can get something together.
They are listed roughly in order of their nearness to completion, with the most developed ideas first and the vaporware at the bottom. I am generally language-agnostic, except I refuse to work in C++.
Or if you don't want to work with me, feel free to swipe any of these ideas yourself. Share and enjoy.
Linogram
Linogram is a constraint-based diagram-drawing language that I think
will be better than prior languages (like pic, Metapost, or, god
forbid, raw postscript or SVG) and very different from WYSIWYG drawing
programs like Inkscape or Omnigraffle. I described it in detail in
chapter 9 of Higher-Order
Perl
and it's missing only one or two important features that I can't quite
figure out how to do. It also needs an SVG output module, which I
think should be pretty simple.
Most of the code for this already exists, in Perl.
I have discussed Linogram previously in this blog.
Orthogonal polygons
Each angle of an orthogonal polygon is either 90° or 270°. All 4-sided orthogonal polygons are rectangles. All 6-sided orthogonal polygons are similar-looking letter Ls. There are essentially only four different kinds of 8-sided orthogonal polygons. There are 8 kinds of 10-sided orthogonal polygons:
There are 29 kinds of 12-sided orthogonal polygons. I want to efficiently count the number of orthogonal polygons with N sides, and have the computer draw exemplars of each type.
I have a nice method for systematically generating descriptions of all simple orthogonal polygons, and although it doesn't scale to polygons with many sides I think I have an idea to fix that, making use of group-theoretic (mathematical) techniques. (These would not be hard for anyone to learn quickly; my ten-year-old daughter picked them right up. Teaching the computer would be somewhat trickier.) For making the pictures, I only have half the ideas I need, and I haven't done the programming yet.
The little code I have is written in Perl, but it would be no trouble to switch to a different language.
[ Addendum 20150607: the orthogonal polygon sequence is now in OEIS! ]
Simple Android app
I want to learn to build Android apps for my Android phone. I think a
good first project would be a utility where you put in a sequence of
letters, say FBS, and it displays all the words that contain those
letters in order. (For FBS the list contains "afterburners",
"chlorofluorocarbons", "fables", "fabricates", …, "surfboards".) I
play this game often with my kid (the letters are supplied by license
plates we pass) and we want a way to cheat when we are stumped.
My biggest problem with Android development in the past has been getting the immense Android SDK set up.
The project would need to be done in Java, because that is what Android uses.
gi
Git is great, but its user interface is awful. The command set is obscure and non-orthogonal. Error messages are confusing. gi is a thinnish layer that tries to present a more intuitive and uniform command set, with better error messages and clearer advice, without removing any of git's power.
There's no code written yet, and we could do it in any language. Perl or Python would be good choices. The programming is probably easy; the hard part of this project is (a) design and (b) user testing.
I have a bunch of design notes written up about this already.
Twingler
Twingler takes an example of an input data structure and and output data structure, and writes code in your favorite language for transforming the input into the output. Or maybe it takes some sort of simplified description of what is wanted and writes the code from that. The description would be declarative, not procedural. I'm really not at all sure what it should do or how it should work, but I have a lot of notes, and if we could make it happen a lot of people would love it.
No code is written; we could do this in your favorite language. Haskell maybe?
Bonus: Whatever your favorite language is, I bet it needs something like this.
Crapspad
I want a simple library that can render simple pixel graphics and detect and respond to mouse events. I want people to be able to learn to use it in ten minutes. It should be as easy as programming graphics on an Apple II and easier than a Commodore 64. It should not be a gigantic object-oriented windowing system with widgets and all that stuff. It should be possible to whip up a simple doodling program in Crapspad in 15 minutes.
I hope to get Perl bindings for this, because I want to use it from Perl programs, but we could design it to have a language-independent interface without too much trouble.
Git GUI
There are about 17 GUIs for Git and they all suck in exactly the same way: they essentially provide a menu for running all the same Git commands that you would run at the command line, obscuring what is going on without actually making Git any easier to use. Let's fix this.
For example, why can't you click on a branch and drag it elsewhere to rebase it, or shift-drag it to create a new branch and rebase that? Why can't you drag diff hunks from one commit to another?
I'm not saying this stuff would be easy, but it should be possible. Although I'm not convinced I really want to put ion the amount of effort that would be required. Maybe we could just submit new features to someone else's already-written Git GUI? Or if they don't like our features, fork their project?
I have no code yet, and I don't even know what would be good to use.
[Other articles in category /prog] permanent link
Fri, 24 Apr 2015
Easy exhaustive search with the list monad
(Haskell people may want to skip this article about Haskell, because the technique is well-known in the Haskell community.)
Suppose you would like to perform an exhaustive search. Let's say for concreteness that we would like to solve this cryptarithm puzzle:
S E N D
+ M O R E
-----------
M O N E Y
This means that we want to map the letters S, E, N, D, M,
O, R, Y to distinct digits 0 through 9 to produce a five-digit
and two four-digit numerals which, when added in the indicated way,
produce the indicated sum.
(This is not an especially difficult example; my 10-year-old daughter Katara was able to solve it, with some assistance, in about 30 minutes.)
If I were doing this in Perl, I would write up either a recursive descent search or a solution based on a stack or queue of partial solutions which the program would progressively try to expand to a full solution, as per the techniques of chapter 5 of Higher-Order Perl. In Haskell, we can use the list monad to hide all the searching machinery under the surface. First a few utility functions:
import Control.Monad (guard)
digits = [0..9]
to_number = foldl (\a -> \b -> a*10 + b) 0
remove rs ls = foldl remove' ls rs
where remove' ls x = filter (/= x) ls
to_number takes a list of digits like [1,4,3] and produces the
number they represent, 143. remove takes two lists and returns all
the things in the second list that are not in the first list. There
is probably a standard library function for this but I don't remember
what it is. This version is !!O(n^2)!!, but who cares.
Now the solution to the problem is:
-- S E N D
-- + M O R E
-- ---------
-- M O N E Y
solutions = do
s <- remove [0] digits
e <- remove [s] digits
n <- remove [s,e] digits
d <- remove [s,e,n] digits
let send = to_number [s,e,n,d]
m <- remove [0,s,e,n,d] digits
o <- remove [s,e,n,d,m] digits
r <- remove [s,e,n,d,m,o] digits
let more = to_number [m,o,r,e]
y <- remove [s,e,n,d,m,o,r] digits
let money = to_number [m,o,n,e,y]
guard $ send + more == money
return (send, more, money)
Let's look at just the first line of this:
solutions = do
s <- remove [0] digits
…
The do notation is syntactic sugar for
(remove [0] digits) >>= \s -> …
where “…” is the rest of the block. To expand this further, we need
to look at the overloading for >>= which is implemented differently
for every type. The mote on the left of >>= is a list value, and
the definition of >>= for lists is:
concat $ map (\s -> …) (remove [0] digits)
where “…” is the rest of the block.
So the variable s is bound to each of 1,2,3,4,5,6,7,8,9 in turn, the
rest of the block is evaluated for each of these nine possible
bindings of s, and the nine returned lists of solutions are combined
(by concat) into a single list.
The next line is the same:
e <- remove [s] digits
for each of the nine possible values for s, we loop over nine value
for e (this time including 0 but not including whatever we chose for
s) and evaluate the rest of the block. The nine resulting lists of
solutions are concatenated into a single list and returned to the
previous map call.
n <- remove [s,e] digits
d <- remove [s,e,n] digits
This is two more nested loops.
let send = to_number [s,e,n,d]
At this point the value of send is determined, so we compute and
save it so that we don't have to repeatedly compute it each time
through the following 300 loop executions.
m <- remove [0,s,e,n,d] digits
o <- remove [s,e,n,d,m] digits
r <- remove [s,e,n,d,m,o] digits
let more = to_number [m,o,r,e]
Three more nested loops and another computation.
y <- remove [s,e,n,d,m,o,r] digits
let money = to_number [m,o,n,e,y]
Yet another nested loop and a final computation.
guard $ send + more == money
return (send, more, money)
This is the business end. I find guard a little tricky so let's
look at it slowly. There is no binding (<-) in the first line, so
these two lines are composed with >> instead of >>=:
(guard $ send + more == money) >> (return (send, more, money))
which is equivalent to:
(guard $ send + more == money) >>= (\_ -> return (send, more, money))
which means that the values in the list returned by guard will be
discarded before the return is evaluated.
If send + more == money is true, the guard expression yields
[()], a list of one useless item, and then the following >>= loops
over this one useless item, discards it, and returns yields a list
containing the tuple (send, more, money) instead.
But if send + more == money is false, the guard expression yields
[], a list of zero useless items, and then the following >>= loops
over these zero useless items, never runs return at all, and yields
an empty list.
The result is that if we have found a solution at this point, a list
containing it is returned, to be concatenated into the list of all
solutions that is being constructed by the nested concats. But if
the sum adds up wrong, an empty list is returned and concated
instead.
After a few seconds, Haskell generates and tests 1.36 million choices for the eight bindings, and produces the unique solution:
[(9567,1085,10652)]
That is:
S E N D 9 5 6 7
+ M O R E + 1 0 8 5
----------- -----------
M O N E Y 1 0 6 5 2
It would be an interesting and pleasant exercise to try to implement
the same underlying machinery in another language. I tried this in
Perl once, and I found that although it worked perfectly well, between
the lack of the do-notation's syntactic sugar and Perl's clumsy
notation for lambda functions (sub { my ($s) = @_; … } instead of
\s -> …) the result was completely unreadable and therefore
unusable. However, I suspect it would be even worse in Python
because of semantic limitations of that language. I would be
interested to hear about this if anyone tries it.
[ Addendum: Thanks to Tony Finch for pointing out the η-reduction I missed while writing this at 3 AM. ]
[ Addendum: Several people so far have misunderstood the question
about Python in the last paragraph. The question was not to implement
an exhaustive search in Python; I had no doubt that it could be done
in a simple and clean way, as it can in Perl. The question was to
implement the same underlying machinery, including the list monad
and its bind operator, and to find the solution using the list
monad.
[ Peter De Wachter has written in with a Python solution that clearly demonstrates that the problems I was worried about will not arise, at least for this task. I hope to post his solution in the next few days. ]
[ Addendum 20150803: De Wachter's solution and one in Perl ]
[Other articles in category /prog/haskell] permanent link
Tue, 21 Apr 2015
Another use for strace (isatty)
(This is a followup to an earlier article describing an interesting use of strace.)
A while back I was writing a talk about Unix internals and I wanted to
discuss how the ls command does a different display when talking to
a terminal than otherwise:
ls to a terminal

ls not to a terminal

How does ls know when it is talking to a terminal? I expect that is
uses the standard POSIX function isatty. But how does isatty find
out?
I had written down my guess. Had I been programming in C, without
isatty, I would have written something like this:
@statinfo = stat STDOUT;
if ( $statinfo[2] & 0060000 == 0020000
&& ($statinfo[6] & 0xff) == 5) { say "Terminal" }
else { say "Not a terminal" }
(This is Perl, written as if it were C.) It uses fstat (exposed in
Perl as stat) to get the mode bits ($statinfo[2]) of the inode
attached to STDOUT, and then it masks out the bits the determine if
the inode is a character device file. If so, $statinfo[6] is the
major and minor device numbers; if the major number (low byte) is
equal to the magic number 5, the device is a terminal device. On my
current computers the magic number is actually 136. Obviously this
magic number is nonportable. You may hear people claim that those bit
operations are also nonportable. I believe that claim is mistaken.
The analogous code using isatty is:
use POSIX 'isatty';
if (isatty(STDOUT)) { say "Terminal" }
else { say "Not a terminal" }
Is isatty doing what I wrote above? Or something else?
Let's use strace to find out. Here's our test script:
% perl -MPOSIX=isatty -le 'print STDERR isatty(STDOUT) ? "terminal" : "nonterminal"'
terminal
% perl -MPOSIX=isatty -le 'print STDERR isatty(STDOUT) ? "terminal" : "nonterminal"' > /dev/null
nonterminal
Now we use strace:
% strace -o /tmp/isatty perl -MPOSIX=isatty -le 'print STDERR isatty(STDOUT) ? "terminal" : "nonterminal"' > /dev/null
nonterminal
% less /tmp/isatty
We expect to see a long startup as Perl gets loaded and initialized,
then whatever isatty is doing, the write of nonterminal, and then
a short teardown, so we start searching at the end and quickly
discover, a couple of screens up:
ioctl(1, SNDCTL_TMR_TIMEBASE or TCGETS, 0x7ffea6840a58) = -1 ENOTTY (Inappropriate ioctl for device)
write(2, "nonterminal", 11) = 11
write(2, "\n", 1) = 1
My guess about fstat was totally wrong! The actual method is that
isatty makes an ioctl call; this is a device-driver-specific
command. The TCGETS parameter says what command is, in this case
“get the terminal configuration”. If you do this on a non-device, or
a non-terminal device, the call fails with the error ENOTTY. When
the ioctl call fails, you know you don't have a terminal. If you do
have a terminal, the TCGETS command has no effects, because it is a
passive read of the terminal state. Here's the successful call:
ioctl(1, SNDCTL_TMR_TIMEBASE or TCGETS, {B38400 opost isig icanon echo ...}) = 0
write(2, "terminal", 8) = 8
write(2, "\n", 1) = 1
The B38400 opost… stuff is the terminal configuration; 38400 is the baud rate.
(In the past the explanatory text for ENOTTY was the mystifying “Not
a typewriter”, even more mystifying because it tended to pop up when
you didn't expect it. Apparently Linux has revised the message to the
possibly less mystifying “Inappropriate ioctl for device”.)
(SNDCTL_TMR_TIMEBASE is mentioned because apparently someone decided
to give their SNDCTL_TMR_TIMEBASE operation, whatever that is, the
same numeric code as TCGETS, and strace isn't sure which one is
being requested. It's possible that if we figured out which device was
expecting SNDCTL_TMR_TIMEBASE, and redirected standard output to
that device, that isatty would erroneously claim that it was a
terminal.)
[ Addendum 20150415: Paul Bolle has found that the
SNDCTL_TMR_TIMEBASE pertains to the old and possibly deprecated OSS
(Open Sound System)
It is conceivable that isatty would yield the wrong answer when
pointed at the OSS /dev/dsp or /dev/audio device or similar. If
anyone is running OSS and willing to give it a try, please contact me at mjd@plover.com. ]
[ Addendum 20191201: Thanks to Hacker News user
jwilk for pointing
out that strace is
now able to distinguish TCGETS from SNDCTL_TMR_TIMEBASE. ]
[Other articles in category /Unix] permanent link
Sun, 19 Apr 2015
Another use for strace (groff)
The marvelous Julia Evans is always looking for ways to express her
love of strace and now has written a zine about
it. I don't use
strace that often (not as often as I should, perhaps) but every once
in a while a problem comes up for which it's not only just the right
thing to use but the only thing to use. This was one of those
times.
I sometimes use the ancient Unix drawing language
pic. Pic has many
good features, but is unfortunately coupled too closely to the Roff
family of formatters (troff, nroff, and the GNU project version,
groff). It only produces Roff output, and not anything more
generally useful like SVG or even a bitmap. I need raw images to
inline into my HTML pages. In the past I have produced these with a
jury-rigged pipeline of groff, to produce PostScript, and then GNU
Ghostscript (gs) to translate the PostScript to a PPM
bitmap, some PPM utilities to crop and
scale the result, and finally ppmtogif or whatever. This has some
drawbacks. For example, gs requires that I set a paper size, and
its largest paper size is A0. This means that large drawings go off
the edge of the “paper” and gs discards the out-of-bounds portions.
So yesterday I looked into eliminating gs. Specifically I wanted to
see if I could get groff to produce the bitmap directly.
GNU groff has a -Tdevice option that specifies the "output"
device; some choices are -Tps for postscript output and -Tpdf for
PDF output. So I thought perhaps there would be a -Tppm or
something like that. A search of the manual did not suggest anything
so useful, but did mention -TX100, which had something to do with
100-DPI X window system graphics. But when I tried this groff only said:
groff: can't find `DESC' file
groff:fatal error: invalid device `X100`
The groff -h command said only -Tdev use device dev. So what
devices are actually available?
strace to the rescue! I did:
% strace -o /tmp/gr groff -Tfpuzhpx
and then a search for fpuzhpx in the output file tells me exactly
where groff is searching for device definitions:
% grep fpuzhpx /tmp/gr
execve("/usr/bin/groff", ["groff", "-Tfpuzhpx"], [/* 80 vars */]) = 0
open("/usr/share/groff/site-font/devfpuzhpx/DESC", O_RDONLY) = -1 ENOENT (No such file or directory)
open("/usr/share/groff/1.22.2/font/devfpuzhpx/DESC", O_RDONLY) = -1 ENOENT (No such file or directory)
open("/usr/lib/font/devfpuzhpx/DESC", O_RDONLY) = -1 ENOENT (No such file or directory)
I could then examine those three directories to see if they existed, and if so find out what was in them.
Without strace here, I would be reduced to groveling over the
source, which in this case is likely to mean trawling through the
autoconf output, and that is something that nobody wants to do.
Addendum 20150421: another article about strace. ]
[ Addendum 20150424: I did figure out how to prevent gs from
cropping my output. You can use the flag -p-P48i,48i to groff to
set the page size to 48 inches (48i) by 48 inches. The flag is
passed to grops, and then resulting PostScript file contains
%%DocumentMedia: Default 3456 3456 0 () ()
which instructs gs to pretend the paper size is that big. If it's
not big enough, increase 48i to 120i or whatever. ]
[Other articles in category /Unix] permanent link
Tue, 14 Apr 2015This week I introduced myself to Recurse Center, where I will be in residence later this month, and mentioned:
I have worked as a professional programmer for a long time so I sometimes know strange historical stuff because I lived through it.
Ms. Nikki Bee said she wanted to hear more. Once I got started I had trouble stopping.
I got interested in programming from watching my mom do it. I first programmed before video terminals were common. I still remember the smell of the greasy paper and the terminal's lubricating oil. When you typed control-G, the ASCII BEL character, a little metal hammer hit an actual metal bell that went "ding!".
I remember when there was a dedicated computer just for word processing; that's all it did. I remember when hard disks were the size of washing machines. I remember when you could buy magnetic cores on Canal Street, not far from where Recurse Center is now. Computer memory is still sometimes called “core”, and on Unix your program still dumps a core file if it segfaults. I've worked with programmers who were debugging core dumps printed on greenbar paper, although I've never had to do it myself.
I frequented dialup
BBSes before
there was an Internet. I remember when the domain name system was
rolled out. Until then email addresses looked like yuri@kremvax,
with no dots; you didn't need dots because each mail host had a unique
name. I read the GNU
Manifesto in its
original publication in Dr. Dobb's. I remember the day the Morris
Worm hit.
I complained to Laurence Canter after he and his wife perpetrated the first large scale commercial spamming of the Internet. He replied:
People in your group are interested. Why do you wish to deprive them of what they consider to be important information??
which is the same excuse used by every spammer since.
I know the secret history of the Java compiler, why Java 5.0 had generics even though Sun didn't want them, and why they couldn't get rid of them. I remember when the inventors of LiveScript changed its name to JavaScript in a craven attempt to borrow some of Java's buzz.
I once worked with Ted Nelson.
I remember when Sun decided they would start charging extra to ship C compilers with their hardware, and how the whole Internet got together to fund an improved version of the GNU C compiler that would be be free and much better than the old Sun compiler ever was.
I remember when NCSA had a web page, updated daily, called “What's New on the World Wide Web”. I think I was the first person to have a guest book page on the Web. I remember the great land rush of 1996 when every company woke up at the same time and realized it needed a web site.
I remember when if you were going to speak at a conference, you would mail a paper copy of your slides to the conference people a month before so they could print it into books to hand out to the attendees. Then you would photocopy the slides onto plastic sheets so you could display them on the projector when you got there. God help you if you spilled the stack of plastic right before the talk.
tl;dr i've been around a while.
However, I have never programmed in COBOL.
[ Addendum 20150609: I'm so old, I once attended a meeting at which Adobe was pitching their new portable document format. ]
(I'm not actually very old, but I got started very young.)
[Other articles in category /IT] permanent link
Wed, 01 Apr 2015
Your kids will love a cookie-decorating party
We had a party last week for Toph's 7th birthday, at an indoor rock-climbing gym, same as last year. Last year at least two of the guests showed up and didn't want to climb, so Lorrie asked me to help think of something for them to do if the same thing happened this year. After thinking about it, I decided we should have cookie decorating.
This is easy to set up and kids love it. I baked some plain sugar cookies, bought chocolate, vanilla, and strawberry frosting, several tubes of edible gel, and I mixed up five kinds of colored sugar. We had some colored sprinkles and little gold dragées and things like that. I laid the ingredients out on the table in the gym's side room with some plastic knives and paintbrushes, and the kids who didn't want to climb, or who wanted a break from climbing, decorated cookies. It was a great success. Toph's older sister Katara had hurt her leg, and couldn't climb, so she helped the littler kids with cookies. Even the tiny two-year-old sister of one of the guests was able to participate, and enjoyed playing with the dragées.
(It's easy to vary the project depending on how much trouble you want to take. I made the cookies from scratch, which is pretty easy, but realized later I could have bought prefabricated cookie batter, which would have been even easier. The store sold colored sugar for $3.29 for four ounces, which is offensive, so I went home and made my own. You put one drop of food coloring per two ounces of sugar in a sealed container and shake it up for a minute, for a total cost of close to zero; Toph helped with this. I bought my frosting, but when my grandmother used to do it she'd make a simple white frosting from confectioners' sugar and then color it with food coloring.)
I was really pleased with the outcome, and not just because the guests liked it, but also because it is a violation of gender norms for a man to plan a cookie-decorating activity and then bake the cookies and prepare the pastel-colored sugar and so forth. (And of course I decorated some cookies myself.) These gender norms are insidious and pervasive, and to my mind no opportunity to interfere with them should be wasted. Messing with the gender norms is setting a good example for the kids and a good example for other dads and for the rest of the world.
I am bisexual, and sometimes I feel that it doesn't affect my life very much. The sexual part is mostly irrelevant now; I fell in love with a woman twenty years ago and married her and now we have kids. I probably won't ever have sex with another man. Whatever! In life you make choices. My life could have swung another way, but it didn't.
But there's one part of being bisexual that has never stopped paying dividends for me, and that is that when I came out as queer, it suddenly became apparent to me that I had abandoned the entire gigantic structure of how men are supposed to behave. And good riddance! This structure belongs in the trash; it completely sucks. So many straight men spend a huge amount of time terrified that other straight men will mock them for being insufficiently manly, or mocking other straight men for not being sufficiently manly. They're constantly wondering "if I do this will the other guys think it's gay?" But I've already ceded that argument. The horse is out of the barn, and I don't have to think about it any more. If people think what I'm doing is gay, that's a pill I swallowed when I came out in 1984. If they say I'm acting gay I'll say "close, but actually, I'm bi, and go choke on a bag of eels, jackass."
You don't have to be queer to opt out of straight-guy bullshit, and I think I would eventually have done it anyway, but being queer made opting out unavoidable. When I was first figuring out being queer I spent a lot of time rethinking my relationship to society and its gender constructions, and I felt that I was going to have to construct my own gender from now and that I no longer had the option of taking the default. I wasn't ever going to follow Rule Number One of Being a Man (“do not under any circumstances touch, look at, mention, or think about any dick other than your own”), so what rules was I going to follow? Whenever someone tried to pull “men don't” on me, (or whenever I tried to pull it on myself) I'd immediately think of all the Rule Number One stuff I did that “men don't” and it would all go in the same trash bin. Where (did I say this already?) it belongs.
Opting out frees up a lot of mental energy that I might otherwise waste worrying about what other people think of stuff that is none of their business, leaving me more space to think about how I feel about it and whether I think it's morally or ethically right and whether it's what I want. It means that if someone is puzzled or startled by my pink sneakers, I don't have to care, except I might congratulate myself a little for making them think about gender construction for a moment. Or the same if people find out I have a favorite flower (CROCUSES YEAH!) or if I wash the dishes or if I play with my daughters or watch the ‘wrong’ TV programs or cry or apologize for something I did wrong or whatever bullshit they're uncomfortable about this time.
Opting out frees me up to be a feminist; I don't have to worry that a bunch of men think I'm betraying The Team, because I was never on their lousy team in the first place.
And it frees me up to bake cookies for my kid's birthday party, to make a lot of little kids happy, and to know that that can only add to, not subtract from, my identity. I'm Dominus, who loves programming and mathematics and practicing the piano and playing with toy octopuses and decorating cookies with a bunch of delightful girls.
This doesn't have to be a big deal. Nobody is likely to be shocked or even much startled by Dad baking cookies. But these tiny actions, chipping away at these vile rules, are one way we take tiny steps toward a better world. Every kid at that party will know, if they didn't before, that men can and do decorate cookies.
And perhaps I can give someone else courage to ignore some of that same bullshit that prevents all of us from being as great as we could and should be, all those rules about stuff men aren't supposed to do and other stuff women aren't supposed to do, that make everyone less. I decided about twenty years ago that that was the best reason for coming out at all. People are afraid to be different. If I can be different, maybe I can give other people courage and comfort when they need to be different too. As a smart guy once said, you can be a light to the world, like a city on a hilltop that cannot be hidden.
And to anyone who doesn't like it, I say:
[Other articles in category /misc] permanent link
Sat, 21 Mar 2015
Examples of contracts you should not sign
Shortly after I posted A public service announcement about contracts Steve Bogart asked me on on Twitter for examples of dealbreaker clauses. Some general types I thought of immediately were:
Any nonspecific non-disclosure agreement with a horizon more than three years off, because after three years you are not going to remember what it was that you were not supposed to disclose.
Any contract in which you give up your right to sue the other party if they were to cheat you.
Most contracts in which you permanently relinquish your right to disparage or publicly criticize the other party.
Any contract that leaves you on the hook for the other party's losses if the project is unsuccessful.
Any contract that would require you to do something immoral or unethical.
Addendum 20150401: Chas. Owens suggests, and I agree, that you not sign a contract that gives the other party ownership of everything you produce, even including things you created on your own time with your own equipment.
A couple of recent specific examples:
Comcast is negotiating a contract with our homeowner's association to bring cable Internet to our village; the proposed agreement included a clause in which we promised not to buy Internet service from any other company for the next ten years. I refused to sign. The guy on our side who was negotiating the agreement was annoyed with me. If too many people refuse to sign, maybe Comcast will back out. “Do you think you're going to get FIOS in here in the next ten years?” he asked sarcastically. “No,” I said. “But I might move.”
Or, you know, I might get sick of Comcast and want to go back to whatever I was using before. Or my satellite TV provider might start delivering satellite Internet. Or the municipal wireless might suddenly improve. Or Google might park a crazy Internet Balloon over my house. Or some company that doesn't exist yet might do something we can't even imagine. Google itself is barely ten years old! The iPhone is only eight!
In 2013 I was on a job interview at company X and was asked to sign an NDA that enjoined me from disclosing anything I learned that day for the next ten years. I explained that I could not sign such an agreement because I would not be able to honor it. I insisted on changing it to three years, which is also too long, but I am not completely unwilling to compromise. It's now two years later and I have completely forgotten what we discussed that day; I might be violating the NDA right now for all I know. Had they insisted on ten years, would I have walked out? You bet I would. You don't let your mouth write checks that your ass can't cash.
[ Addendum 20191107: Our FIOS was installed in January of 2018. Lucky I hadn't signed that ten-year contract, huh? ]
[ Addendum 20220420: More about why it's important to push back ]
[Other articles in category /law] permanent link
Fri, 20 Mar 2015
A public service announcement about contracts
Every so often, when I am called upon to sign some contract or other, I have a conversation that goes like this:
Me: I can't sign this contract; clause 14(a) gives you the right to chop off my hand.
Them: Oh, the lawyers made us put that in. Don't worry about it; of course we would never exercise that clause.
There is only one response you should make to this line of argument:
Well, my lawyer says I can't agree to that, and since you say that you would never exercise that clause, I'm sure you will have no problem removing it from the contract.
Because if the lawyers made them put in there, that is for a reason. And there is only one possible reason, which is that the lawyers do, in fact, envision that they might one day exercise that clause and chop off your hand.
The other party may proceed further with the same argument: “Look, I have been in this business twenty years, and I swear to you that we have never chopped off anyone's hand.” You must remember the one response, and repeat it:
Great! Since you say that you have never chopped off anyone's hand, then you will have no problem removing that clause from the contract.
You must repeat this over and over until it works. The other party is lazy. They just want the contract signed. They don't want to deal with their lawyers. They may sincerely believe that they would never chop off anyone's hand. They are just looking for the easiest way forward. You must make them understand that there is no easier way forward than to remove the hand-chopping clause.
They will say “The deadline is looming! If we don't get this contract executed soon it will be TOO LATE!” They are trying to blame you for the blown deadline. You should put the blame back where it belongs:
As I've made quite clear, I can't sign this contract with the hand-chopping clause. If you want to get this executed soon, you must strike out that clause before it is TOO LATE.
And if the other party would prefer to walk away from the deal rather than abandon their hand-chopping rights, what does that tell you about the value they put on the hand-chopping clause? They claim that they don't care about it and they have never exercised it, but they would prefer to give up on the whole project, rather than abandon hand-chopping? That is a situation that is well worth walking away from, and you can congratulate yourself on your clean escape.
[ Addendum: Steve Bogart asked on Twitter for examples of unacceptable contract demands; I thought of so many that I put them in a separate article. ]
[ Addendum 20150401: Chas. Owens points out that you don't have to argue about it; you can just cross out the hand-chopping clause, add your initials and date in the margin. I do this also, but then I bring the modification it to the other party's attention, because that is the honest and just thing to do. ]
[ Addendum 20220420: More and more, contracts are moving online and getting electronic signatures. This removes the option to modify the contract before signing: you can sign it intact, or not at all. Don't ever forget that the Man is always trying to get his foot on your neck. ]
[ Addendum 20220420: More about why it's important to push back ]
[Other articles in category /law] permanent link
Rectangles with equal area and perimeter
Wednesday while my 10-year-old daughter Katara was doing her math homework, she observed with pleasure that a !!6×3!! rectangle has a perimeter of 18 units and also an area of 18 square units. I mentioned that there was an infinite family of such rectangles, and, after a small amount of tinkering, that the only other such rectangle with integer sides is a !!4×4!! square, so in a sense she had found the single interesting example. She was very interested in how I knew this, and I promised to show her how to figure it out once she finished her homework. She didn't finish before bedtime, so we came back to it the following evening.
This is just one of many examples of how she has way too much homework, and how it interferes with her education.
She had already remarked that she knew how to write an equation expressing the condition she wanted, so I asked her to do that; she wrote $$(L×W) = ([L+W]×2).$$ I remember being her age and using all different shapes of parentheses too. I suggested that she should solve the equation for !!W!!, getting !!W!! on one side and a bunch of stuff involving !!L!! on the other, but she wasn't sure how to do it, so I offered suggestions while she moved the symbols around, eventually obtaining $$W = 2L\div (L-2).$$ I would have written it as a fraction, but getting the right answer is important, and using the same notation I would use is much less so, so I didn't say anything.
I asked her to plug in !!L=3!! and observe that !!W=6!! popped right out, and then similarly that !!L=6!! yields !!W=3!!, and then I asked her to try the other example she knew. Then I suggested that she see what !!L=5!! did: it gives !!W=\frac{10}3!!, This was new, so she checked it by calculating the area and the perimeter, both !!\frac{50}3!!. She was very excited by this time. As I have mentioned earlier, algebra is magical in its ability to mechanically yield answers to all sorts of questions. Even after thirty years I find it astonishing and delightful. You set up the equations, push the symbols around, and all sorts of stuff pops out like magic. Calculus is somehow much less astonishing; the machinery is all explicit. But how does algebra work? I've been thinking about this on and off for a long time and I'm still not sure.
At that point I took over because I didn't think I would be able to guide her through the next part of the problem without a demonstration; I wanted to graph the function !!W=2L\div(L-2)!! and she does not have much experience with that. She put in the five points we already knew, which already lie on a nice little curve, and then she asked an incisive question: does it level off, or does it keep going down, or what? We discussed what happens when !!L!! gets close to 2; then !!W!! shoots up to infinity. And when !!L!! gets big, say a million, you can see from the algebra that !!W!! is a hair more than 2. So I drew in the asymptotes on the hyperbola.
Katara is not yet familiar with hyperbolas. (She has known about parabolas since she was tiny. I have a very fond memory of visiting Portland with her when she was almost two, and we entered Holladay park, which has fountains that squirt out of the ground. Seeing the water arching up before her, she cried delightedly “parabolas!”)
Once you know how the graph behaves, it is a simple matter to see that there are no integer solutions other than !!\langle 3,6\rangle, \langle 4,4\rangle,!! and !!\langle6,3\rangle!!. We know that !!L=5!! does not work. For !!L>6!! the value of !!W!! is always strictly between !!2!! and !!3!!. For !!L=2!! there is no value of !!W!! that works at all. For !!0\lt L\lt 2!! the formula says that !!W!! is negative, on the other branch of the hyperbola, which is a perfectly good numerical solution (for example, !!L=1, W=-2!!) but makes no sense as the width of a rectangle. So it was a good lesson about how mathematical modeling sometimes introduces solutions that are wrong, and how you have to translate the solutions back to the original problem to see if they make sense.
[ Addendum 20150330: Thanks to Steve Hastings for his plot of the hyperbola, which is in the public domain. ]
[Other articles in category /math] permanent link
Thu, 19 Mar 2015
An ounce of theory is worth a pound of search
The computer is really awesome at doing quick searches for numbers with weird properties, and people with an amateur interest in recreational mathematics would do well to learn some simple programming. People appear on math.stackexchange quite often with questions about tic-tac-toe, but there are only 5,478 total positions, so any question you want to ask can be instantaneously answered by an exhaustive search. An amateur showed up last fall asking “Is it true that no prime larger than 241 can be made by either adding or subtracting 2 coprime numbers made up out of the prime factors 2,3, and 5?” and, once you dig through the jargon, the question is easily answered by the computer, which quickly finds many counterexamples, such as !!162+625=787!! and !!2^{19}+3^4=524369!!.
But sometimes the search appears too large to be practical, and then you need to apply theory. Sometimes you can deploy a lot of theory and solve the problem completely, avoiding the search. But theory is expensive, and not always available. A hybrid approach often works, which uses a tiny amount of theory to restrict the search space to the point where the search is easy.
One of these I wrote up on this blog back in 2006:
A number !!n!! is excellent if it has an even number of digits, and if when you chop it into a front half !!a!! and a back half !!b!!, you have !!b^2 - a^2 = n!!. For example, !!48!! is excellent, because !!8^2 - 4^2 = 48!!, and !!3468!! is excellent, because !!68^2 - 34^2 = 4624 - 1156 = 3468!!.
The programmer who gave me thie problem had tried a brute-force search over all numbers, but to find all 10-digit excellent numbers, this required an infeasible search of 9,000,000,000 candidates. With the application of a tiny amount of algebra, one finds that !!a(10^k+a) = b^2+b!! and it's not hard to quickly test candidates for !!a!! to see if !!a(10^k+a)!! has this form and if so to find the corresponding value of !!b!!. (Details are in the other post.) This reduces the search space for 10-digit excellent numbers from 9,000,000,000 candidates to 90,000, which could be done in under a minute even with last-century technology, and is pretty nearly instantaneous on modern equipment.
But anyway, the real point of this note is to discuss a different problem entirely. A recreational mathematician on stackexchange wanted to find distinct integers !!a,b,c,d!! for which !!a^2+b^2, b^2+c^2, c^2+d^2, !! and !!d^2+a^2!! were all perfect squares. You can search over all possible quadruples of numbers, but this takes a long time. The querent indicated later that he had tried such a search but lost patience before it yielded anything.
Instead, observe that if !!a^2+b^2!! is a perfect square then !!a!! and !!b!! are the legs of a right triangle with integer sides; they are terms in what is known as a Pythagorean triple. The prototypical example is !!3^2 + 4^2 = 5^2!!, and !!\langle 3,4,5\rangle!! is the Pythagorean triple. (The querent was quite aware that he was asking for Pythagorean triples, and mentioned them specifically.)
Here's the key point: It has been known since ancient times that if !!\langle a,b,c\rangle!! is a Pythagorean triple, then there exist integers !!m!! and !!n!! such that: $$\begin{align} \require{align} a & = n^2-m^2 \\ b & = 2mn \\ c & = n^2 + m^2 \end{align}$$
So you don't have to search for Pythagorean triples; you can just generate them with no searching:
for my $m (1 .. 200) {
for my $n ($m+1 .. 200) {
my $a = $n*$n-$m*$m;
my $b = 2 * $n * $m;
$trip{$a}{$b} = 1;
$trip{$b}{$a} = 1;
}
}
This builds a hash table, %trip, with two important properties:
$trip{$a}is a sub-table whose keys are all the numbers that can form a triple with !!a!!. For example,$trip{20}is a hash with three keys: 21, 48, and 99, because !!20^2+21^2 = 29^2, 20^2+48^2= 52^2, !! and !!20^2 + 99^2 = 101^2!!, but 20 is not a participant in any other triples.$trip{$a}{$b}is true if and only if !!a^2+b^2!! is a perfect square, and false otherwise.
The table has only around 40,000 entries. Having constructed it, we now search it:
for my $a (keys %trip) {
for my $b (keys %{$trip{$a}}) {
for my $c (keys %{$trip{$b}}) {
next if $c == $a;
for my $d (keys %{$trip{$c}}) {
next if $d == $b;
print "$a $b $c $d\n" if $trip{$d}{$a};
}
}
}
}
The outer loop runs over each !!a!! that is known to be a member of a Pythagorean triple. (Actually the !!m,n!! formulas show that every number bigger than 2 is a member of some triple, but we may as well skip the ones that are only in triples we didn't tabulate.) Then the next loop runs over every !!b!! that can possibly form a triple with !!a!!; that is, every !!b!! for which !!a^2+b^2!! is a perfect square. We don't have to search for them; we have them tabulated ahead of time. Then for each such !!b!! (and there aren't very many) we run over every !!c!! that forms a triple with !!b!!, and again there is no searching and very few candidates. Then then similarly !!d!!, and if the !!d!! we try forms a triple with !!a!!, we have a winner.
The next if $c == $a and next if $d == $b tests are to rule out
trivial solutions like !!a=c=3, b=d=4!!, which the querent wasn't
interested in anyway. We don't have to test for equality of any of
ther other pairs because no number can form a Pythagorean triple with
itself (because !!\sqrt2!! is irrational).
This runs in less than a second on so-so hardware and produces 11 solutions:
3472 7296 10400 2175
4312 23520 12008 465
6512 9984 800 6375
12312 666 1288 8415
14592 6944 4350 20800
16830 2576 1332 24624
19968 13024 12750 1600
25500 26048 39936 3200
30192 6175 2400 9856
41600 29184 13888 8700
47040 8624 930 24016
Only five of these are really different. For example, the last one is the same as the second, with every element multiplied by 2; the third, seventh, and eighth are similarly the same. In general if !!\langle a,b,c,d\rangle!! is a solution, so is !!\langle ka, kb,kc,kd\rangle!! for any !!k!!. A slightly improved version would require that the four numbers not have any common factor greater than 1; there are few enough solutions that the cost of this test would be completely negligible.
The only other thing wrong with the program is that it produces each solution 8 times; if !!\langle a,b,c,d\rangle!! is a solution, then so are !!\langle b,c,d,a\rangle, \langle d,c,b,a\rangle,!! and so on. This is easily fixed with a little post-filtering; pipe the output through
perl -nle '$k = join " ", sort { $a <=> $b } split; print unless $seen{$k}++ '
or something of that sort.
The corresponding run with !!m!! and !!n!! up to 2,000 instead of only 200 takes 5 minutes and finds 445 solutions, of which 101 are distinct, including !!\langle 3614220, 618192, 2080820, 574461\rangle!!. It would take a very long time to find this with a naïve search.
[ For a much larger and more complex example of the same sort of thing, see When do !!n!! and !!2n!! have the same digits?. I took a seemingly-intractable problem and analyzed it mathematically. I used considerably more than an ounce of theory in this case, and while the theory was not enough to solve the problem, it was enough to reduce the pool of candates to the point that a computer search was feasible. ]
[ Addendum 20150728: Another example ]
[Other articles in category /math] permanent link