Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 04 Nov 2022
A map of Haskell's numeric types
I keep getting lost in the maze of Haskell's numeric types. Here's the map I drew to help myself out. (I think there might have been something like this in the original Haskell 1998 report.)
Ovals are typeclasses. Rectangles are types. Black mostly-straight arrows show instance relationships. Most of the defined functions have straightforward types like !!\alpha\to\alpha!! or !!\alpha\to\alpha\to\alpha!! or !!\alpha\to\alpha\to\text{Bool}!!. The few exceptions are shown by wiggly colored arrows.
Basic plan
After I had meditated for a while on this picture I began to understand the underlying organization. All numbers support !!=!! and !!\neq!!. And there are three important properties numbers might additionally have:
Ord: ordered; supports !!\lt\leqslant\geqslant\gt!! etc.Fractional: supports divisionEnum: supports ‘pred’ and ‘succ’
Integral types are both Ord and Enum, but they are not
Fractional because integers aren't closed under division.
Floating-point and rational types are Ord and Fractional but not
Enum because there's no notion of the ‘next’ or ‘previous’ rational
number.
Complex numbers are numbers but not Ord because they don't admit a
total ordering. That's why Num plus Ord is called Real: it's
‘real’ as constrasted with ‘complex’.
More stuff
That's the basic scheme. There are some less-important elaborations:
Real plus Fractional is called RealFrac.
Fractional numbers can be represented as exact rationals or as
floating point. In the latter case they are instances of
Floating. The Floating types are required to support a large
family of functions like !!\log, \sin,!! and π.
You can construct a Ratio a type for any a; that's a fraction
whose numerators and denominators are values of type a. If you do this, the
Ratio a that you get is a Fractional, even if a wasn't one. In particular,
Ratio Integer is called Rational and is (of course) Fractional.
Shuff that don't work so good
Complex Int and Complex Rational look like they should exist, but
they don't really. Complex a is only an instance of Num when a
is floating-point. This means you can't even do 3 :: Complex
Int — there's no definition of fromInteger.
You can construct values of type Complex Int, but you can't do
anything with them, not even addition and subtraction. I think the
root of the problem is that Num requires an abs
function, and for complex numbers you need the sqrt function to be
able to compute abs.
Complex Int could in principle support most of the functions
required by Integral (such as div and mod) but Haskell
forecloses this too because its definition of Integral requires
Real as a prerequisite.
You are only allowed to construct Ratio a if a is integral.
Mathematically this is a bit odd. There is a generic construction,
called the field of quotients, which takes
a ring and turns it into a field, essentially by considering all the
formal fractions !!\frac ab!! (where !!b\ne 0!!), and with !!\frac ab!!
considered equivalent to !!\frac{a'}{b'}!! exactly when !!ab' = a'b!!.
If you do this with the integers, you get the rational numbers; if you
do it with a ring of polynomials, you get a field of rational functions, and
so on. If you do it to a ring that's already a field, it still
works, and the field you get is trivially isomorphic to the original
one. But Haskell doesn't allow it.
I had another couple of pages written about yet more ways in which the numeric class hierarchy is a mess (the draft title of this article was "Haskell's numbers are a hot mess") but I'm going to cut the scroll here and leave the hot mess for another time.
[ Addendum: Updated SVG and PNG to version 1.1. ]
[Other articles in category /prog/haskell] permanent link
Fri, 21 Oct 2022
More notes on deriving Applicative from Monad
A year or two ago I wrote about what you do if you already have a Monad and you need to define an Applicative instance for it. This comes up in converting old code that predates the incorporation of Applicative into the language: it has these monad instance declarations, and newer compilers will refuse to compile them because you are no longer allowed to define a Monad instance for something that is not an Applicative. I complained that the compiler should be able to infer this automatically, but it does not.
My current job involves Haskell programming and I ran into this issue again in August, because I understood monads but at that point I was still shaky about applicatives. This is a rough edit of the notes I made at the time about how to define the Applicative instance if you already understand the Monad instance.
pure is easy: it is identical to return.
Now suppose we
have >>=: how can we get <*>? As I eventually figured out last
time this came up, there is a simple solution:
fc <*> vc = do
f <- fc
v <- vc
return $ f v
or equivalently:
fc <*> vc = fc >>= \f -> vc >>= \v -> return $ f v
And in fact there is at least one other way to define it is just as good:
fc <*> vc = do
v <- vc
f <- fc
return $ f v
(Control.Applicative.Backwards
provides a Backwards constructor that reverses the order of the
effects in <*>.)
I had run into this previously
and written a blog post about it.
At that time I had wanted the second <*>, not the first.
The issue came up again in August because, as an exercise, I was trying to
implement the StateT state transformer monad constructor from scratch. (I found
this very educational. I had written State before, but StateT was
an order of magnitude harder.)
I had written this weird piece of code:
instance Applicative f => Applicative (StateT s f) where
pure a = StateT $ \s -> pure (s, a)
stf <*> stv = StateT $
\s -> let apf = run stf s
apv = run stv s
in liftA2 comb apf apv where
comb = \(s1, f) (s2, v) -> (s1, f v) -- s1? s2?
It may not be obvious why this is weird. Normally the definition of
<*> would look something like this:
stf <*> stv = StateT $
\s0 -> let (s1, f) = run stf s0
let (s2, v) = run stv s1
in (s2, f v)
This runs stf on the initial state, yielding f and a new state
s1, then runs stv on the new state, yielding v and a final state
s2. The end result is f v and the final state s2.
Or one could just as well run the two state-changing computations in the opposite order:
stf <*> stv = StateT $
\s0 -> let (s1, v) = run stv s0
let (s2, f) = run stf s1
in (s2, f v)
which lets stv mutate the state first and gives stf the result
from that.
I had been unsure of whether I wanted to run stf or stv first. I
was familiar with monads, in which the question does not come up. In
v >>= f you must run v first because you will pass its value
to the function f. In an Applicative there is no such dependency, so I
wasn't sure what I neeeded to do. I tried to avoid the question by
running the two computations ⸢simultaneously⸣ on the initial state
s0:
stf <*> stv = StateT $
\s0 -> let (sf, f) = run stf s0
let (sv, v) = run stv s0
in (sf, f v)
Trying to sneak around the problem, I was caught immediately, like a
small child hoping to exit a room unseen but only getting to the
doorway. I could run the computations ⸢simultaneously⸣ but on the
very next line I still had to say what the final state was in the end:
the one resulting from computation stf or the one resulting from
computation stv. And whichever I chose, I would be discarding the
effect of the other computation.
My co-worker Brandon Chinn
opined that this must
violate one of the
applicative functor laws.
I wasn't sure, but he was correct.
This implementation of <*> violates the applicative ”interchange”
law that requires:
f <*> pure x == pure ($ x) <*> f
Suppose f updates the state from !!s_0!! to !!s_f!!. pure x and
pure ($ x), being pure, leave it unchanged.
My proposed implementation of <*> above runs the two
computations and then updates the state to whatever was the result of
the left-hand operand, sf discarding any updates performed by the right-hand
one. In the case of f <*> pure x the update from f is accepted
and the final state is !!s_f!!.
But in the case of pure ($ x) <*> f the left-hand operand doesn't do
an update, and the update from f is discarded, so the final state is
!!s_0!!, not !!s_f!!. The interchange law is violated by this implementation.
(Of course we can't rescue this by yielding (sv, f v) in place of
(sf, f v); the problem is the same. The final state is now the
state resulting from the right-hand operand alone, !!s_0!! on the
left side of the law and !!s_f!! on the right-hand side.)
Stack Overflow discussion
I worked for a while to compose a question about this for Stack Overflow, but it has been discussed there at length, so I didn't need to post anything:
<**>is a variant of<*>with the arguments reversed. What does "reversed" mean?- How arbitrary is the "ap" implementation for monads?
- To what extent are Applicative/Monad instances uniquely determined?
That first thread contains this enlightening comment:
Functors are generalized loops
[ f x | x <- xs];Applicatives are generalized nested loops
[ (x,y) | x <- xs, y <- ys];Monads are generalized dynamically created nested loops
[ (x,y) | x <- xs, y <- k x].
That middle dictum provides another way to understand why my idea of running the effects ⸢simultaneously⸣ was doomed: one of the loops has to be innermost.
The second thread above (“How arbitrary is the ap implementation for
monads?”) is close to what I was aiming for in my question, and
includes a wonderful answer by Conor McBride (one of the inventors of
Applicative). Among other things, McBride points out that there are at least
four reasonable Applicative instances consistent with the monad
definition for nonempty lists.
(There is a hint in his answer here.)
Another answer there sketches a proof that if the applicative
”interchange” law holds for some applicative functor f, it holds for
the corresponding functor which is the same except that its <*>
sequences effects in the reverse order.
[Other articles in category /prog/haskell] permanent link
Tue, 18 Oct 2022In Perl I would often write a generic tree search function:
# Perl
sub search {
my ($is_good, $children_of, $root) = @_;
my @queue = ($root);
return sub {
while (1) {
return unless @queue;
my $node = shift @queue;
push @queue, $children_of->($node);
return $node if $is_good->($node);
}
}
}
For example, see Higher-Order Perl, section 5.3.
To use this, we provide two callback functions. $is_good checks
whether the current item has the properties we were searching for.
$children_of takes an item and returns its children in the tree.
The search function returns an iterator object, which, each time it is
called, returns a single item satisfying the $is_good predicate, or
undef if none remains. For example, this searches the space of all
strings over abc for palindromic strings:
# Perl
my $it = search(sub { $_[0] eq reverse $_[0] },
sub { return map "$_[0]$_" => ("a", "b", "c") },
"");
while (my $pal = $it->()) {
print $pal, "\n";
}
Many variations of this are possible. For example, replacing push
with unshift changes the search from breadth-first to depth-first.
Higher-Order Perl shows how to modify it to do heuristically-guided search.
I wanted to do this in Haskell, and my first try didn’t work at all:
-- Haskell
search1 :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search1 isGood childrenOf root =
s [root]
where
s nodes = do
n <- nodes
filter isGood (s $ childrenOf n)
There are two problems with this. First, the filter is in the wrong
place. It says that the search should proceed downward only from the
good nodes, and stop when it reaches a not-good node.
To see what's wrong with this, consider a search for palindromes. Th
string ab isn't a palindrome, so the search would be cut off
at ab, and never proceed downward to find aba or abccbccba.
It should be up to childrenOf to decide how to
continue the search. If the search should be pruned at a particular
node, childrenOf should return an empty list of children. The
$isGood callback has no role here.
But the larger problem is that in most cases this function will compute
forever without producing any output at all, because the call to s
recurses before it returns even one list element.
Here’s the palindrome example in Haskell:
palindromes = search isPalindrome extend ""
where
isPalindrome s = (s == reverse s)
extend s = map (s ++) ["a", "b", "c"]
This yields a big fat !!\huge \bot!!: it does nothing, until memory is exhausted, and then it crashes.
My next attempt looked something like this:
search2 :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search2 isGood childrenOf root = filter isGood $ s [root]
where
s nodes = do
n <- nodes
n : (s $ childrenOf n)
The filter has moved outward, into a single final pass over the
generated tree. And s now returns a list that at least has the node
n on the front, before it recurses. If one doesn’t look at the nodes
after n, the program doesn’t make the recursive call.
The palindromes program still isn’t right though. take 20
palindromes produces:
["","a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa",
"aaaaaaaaa", "aaaaaaaaaa","aaaaaaaaaaa","aaaaaaaaaaaa",
"aaaaaaaaaaaaa","aaaaaaaaaaaaaa", "aaaaaaaaaaaaaaa",
"aaaaaaaaaaaaaaaa","aaaaaaaaaaaaaaaaa", "aaaaaaaaaaaaaaaaaa",
"aaaaaaaaaaaaaaaaaaa"]
It’s doing a depth-first search, charging down the leftmost branch to
infinity. That’s because the list returned from s (a:b:rest) starts
with a, then has the descendants of a, before continuing with b
and b's descendants. So we get all the palindromes beginning with
“a” before any of the ones beginning with "b", and similarly all
the ones beginning with "aa" before any of the ones beginning with
"ab", and so on.
I needed to convert the search to breadth-first, which is memory-expensive but at least visits all the nodes, even when the tree is infinite:
search3 :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search3 isGood childrenOf root = filter isGood $ s [root]
where
s nodes = nodes ++ (s $ concat (map childrenOf nodes))
This worked. I got a little lucky here, in that I had already had the
idea to make s :: [n] -> [n] rather than the more obvious s :: n ->
[n]. I had done that because I wanted to do the n <- nodes thing,
which is no longer present in this version. But it’s just what we need, because we
want s to return a list that has all the nodes at the current
level (nodes) before it recurses to compute the nodes farther down.
Now take 20 palindromes produces the answer I wanted:
["","a","b","c","aa","bb","cc","aaa","aba","aca","bab","bbb","bcb",
"cac", "cbc","ccc","aaaa","abba","acca","baab"]
While I was writing this version I vaguely wondered if there was something that combines concat and map, but I didn’t follow up on it until just now. It turns out there is and it’s called concatMap. 😛
search3' :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search3' isGood childrenOf root = filter isGood $ s [root]
where
s nodes = nodes ++ (s $ concatMap childrenOf nodes)
So this worked, and I was going to move on. But then a brainwave hit me: Haskell is a lazy language. I don’t have to generate and filter the tree at the same time. I can generate the entire (infinite) tree and filter it later:
-- breadth-first tree search
bfsTree :: (n -> [n]) -> [n] -> [n]
bfsTree childrenOf nodes =
nodes ++ bfsTree childrenOf (concatMap childrenOf nodes)
search4 isGood childrenOf root =
filter isGood $ bfsTree childrenOf [root]
This is much better because it breaks the generation and filtering into independent components, and also makes clear that searching is nothing more than filtering the list of nodes. The interesting part of this program is the breadth-first tree traversal, and the tree traversal part now has only two arguments instead of three; the filter operation afterwards is trivial. Tree search in Haskell is mostly tree, and hardly any search!
With this refactoring we might well decide to get rid of search entirely:
palindromes4 = filter isPalindrome allStrings
where
isPalindrome s = (s == reverse s)
allStrings = bfsTree (\s -> map (s ++) ["a", "b", "c"]) [""]
And then I remembered something I hadn’t thought about in a long, long time:
[Lazy evaluation] makes it practical to modularize a program as a generator that constructs a large number of possible answers, and a selector that chooses the appropriate one.
That's exactly what I was doing and what I should have been doing all along. And it ends:
Lazy evaluation is perhaps the most powerful tool for modularization … the most powerful glue functional programmers possess.
(”Why Functional Programming Matters”, John Hughes, 1990.)
I felt a little bit silly, because I wrote a book about lazy functional programming and yet somehow, it’s not the glue I reach for first when I need glue.
[ Addendum 20221023: somewhere along the way I dropped the idea of
using the list monad for the list construction, instead using explicit
map and concat. But it could be put back. For example:
s nodes = (nodes ++) . s $ do
n <- nodes
childrenOf n
I don't think this is an improvement on just using concatMap. ]
[Other articles in category /prog/haskell] permanent link
Tue, 26 Apr 2022[ I hope this article won't be too controversial. My sense is that SML is moribund at this point and serious ML projects that still exist are carried on in OCaml. But I do observe that there was a new SML/NJ version released only six months ago, so perhaps I am mistaken. ]
It was apparent that SML had some major problems. When I encountered Haskell around 1998 it seemed that Haskell at least had a story for how these problems might be fixed.
A reader wrote to ask:
I was curious what the major problems you saw with SML were.
I actually have notes about this that I made while I was writing the first article, and was luckily able to restrain myself from writing up at the time, because it would have been a huge digression. But I think the criticism is technically interesting and may provide some interesting historical context about what things looked like in 1995.
I had three main items in mind. Every language has problems, but these three seemed to me be the deep ones where a drastically different direction was needed.
Notation for types and expressions in this article will be a mishmash of SML, Haskell, and pseudocode. I can only hope that the examples will all be simple enough that the meaning is clear.
Mutation
Reference type soundness
It seems easy to write down the rules for type inference in the presence of references. This turns out not to be the case.
The naïve idea was: for each type α there is a corresponding
type ref α, the type of memory cells containing a value of type
α. You can create a cell with an initialized value by using the
ref function: If v has type α, then ref v has type ref α
and its value is a cell that has been initialized to contain the value
v. (SML actually calls the type α ref, but the meaning is the same.)
The reverse of this is the operator ! which takes a reference of
type ref α and returns the referenced value of type α.
And finally,
if m is a reference, then you can overwrite the value stored in its
its memory cell by saying with m := v. For example:
m = ref 4 -- m is a cell containing 4
m := 1 + !m -- overwrite contents with 1+4
print (2 * !m) -- prints 10
The type rules seem very straightforward:
ref :: α → ref α
(!) :: ref α → α
(:=) :: ref α × α → unit
(Translated into Haskellese, that last one would look more like (ref α, α) → ()
or perhaps ref α → α → () because Haskell loves currying.)
This all seems clear, but it is not sound. The prototypical example is:
m = ref (fn x ⇒ x)
Here m is a reference to the identity function. The identity
function has type α → α, so variable m has type ref(α → α).
m := not
Now we assign the Boolean negation operator to m. not has type
bool → bool, so the types can be unified: m has type ref(α →
α). The type elaborator sees := here and says okay, the first
argument has type
ref(α → α), the second has type bool → bool, I can unify that, I
get α = bool, everything is fine.
Then we do
print ((!m) 23)
and again the type checker is happy. It says:
mhas typeref(α → α)!mhas typeα → α23has typeint
and that unifies, with α = int, so the result will have type
int. Then the runtime blithely invokes the boolean not
function on the argument 23. OOOOOPS.
SML's reference type variables
A little before the time I got into SML, this problem had been discovered and a patch
put in place to prevent it. Basically, some type variables were
ordinary variables, other types (distinguished by having names that began
with an underscore) were special “reference type variables”. The ref
function didn't have type α → ref α, it had type _α → ref _α.
The type elaboration algorithm was stricter when specializing
reference types than when specializing ordinary types. It was
complicated, clearly a hack, and I no longer remember the details.
At the time I got out of SML, this hack been replaced with a more complicated hack, in which the variables still had annotations to say how they related to references, but instead of a flag the annotation was now a number. I never understood it. For details, see this section of the SML '97 documentation, which begins “The interaction between polymorphism and side-effects has always been a troublesome problem for ML.”
After this article was published, Akiva Leffert reminded me that SML later settled on a third fix to this problem, the “value restriction”, which you can read about in the document linked previously. (I thought I remembered there being three different systems, but then decided that I was being silly, and I must have been remembering wrong. I wasn't.)
Haskell's primary solution to this is to burn it all to the ground. Mutation doesn't cause any type problems because there isn't any.
If you want something like ref which will break purity, you
encapsulate it inside the State monad or something like it, or else
you throw up your hands and do it in the IO monad, depending on what
you're trying to accomplish.
Scala has a very different solution to this problem, called covariant and contravariant traits.
Impure features more generally
More generally I found it hard to program in SML because I didn't understand the evaluation model. Consider a very simple example:
map print [1..1000]
Does it print the values in forward or reverse order? One could implement it either way. Or perhaps it prints them in random order, or concurrently. Issues of normal-order versus applicative-order evaluation become important. SML has exceptions, and I often found myself surprised by the timing of exceptions. It has mutation, and I often found that mutations didn't occur in the order I expected.
Haskell's solution to this again is monads. In general it promises
nothing at all about execution order, and if you want to force
something to happen in a particular sequence, you use the monadic bind
operator >>=. Peyton-Jones’ paper
“Tackling the Awkward Squad”
discusses the monadic approach to impure features.
Combining computations that require different effects (say, state
and IO and exceptions) is very badly handled by Haskell. The
standard answer is to use a stacked monadic type like IO ExceptionT a
(State b) with monad transformers. This requires explicit liftings
of computations into the appropriate monad. It's confusing and
nonorthogonal. Monad composition is non-commutative so that IO
(Error a) is subtly different from Error (IO a), and you may find
you have the one when you need the other, and you need to rewrite a
large chunks of your program when you realize that you stacked your
monads in the wrong order.
My favorite solution to this so far is algebraic effect systems. Pretnar's 2015 paper “An Introduction to Algebraic Effects and Handlers” is excellent. I see that Alexis King is working on an algebraic effect system for Haskell but I haven't tried it and don't know how well it works.
Overloading and ad-hoc polymorphism
Arithmetic types
Every language has to solve the problem of 3 + 0.5. The left
argument is an integer, the right argument is something else, let's
call it a float. This issue is baked into the hardware, which has two
representations for numbers and two sets of machine instructions for
adding them.
Dynamically-typed languages have an easy answer: at run time, discover that the left argument is an integer, convert it to a float, add the numbers as floats, and yield a float result. Languages such as C do something similar but at compile time.
Hindley-Milner type languages like ML have a deeper problem: What is the type of the addition function? Tough question.
I understand that OCaml punts on this. There are two addition
functions with different names. One, +, has type int × int → int. The other,
+., has type float × float → float. The expression 3 + 0.5 is
ill-typed because its right-hand argument is not an integer. You
should have written something like int_to_float 3 +. 0.5.
SML didn't do things this way. It was a little less inconvenient and a
little less conceptually simple. The + function claimed to
have type α × α → α, but this was actually a lie. At compile
time it would be resolved to either int × int → int
or to float × float → float. The problem expression above was still
illegal. You needed to write int_to_float 3 + 0.5, but at least
there was only one symbol for addition and you were still writing +
with no adornments. The explicit
calls to int_to_float and similar conversions still cluttered up the
code, sometimes severely
The overloading of + was a special case in the compiler.
Nothing like it was available to the programmer. If you wanted to
create your own numeric type, say a complex number, you could not overload
+ to operate on it. You would have to use |+| or some other
identifier. And you couldn't define anything like this:
def dot_product (a, b) (c, d) = a*c + b*d -- won't work
because SML wouldn't know which multiplication and addition to use;
you'd have to put in an explicit type annotation and have two versions
of dot_product:
def dot_product_int (a : int, b) (c, d) = a*c + b*d
def dot_product_float (a : float, b) (c, d) = a*c + b*d
Notice that the right-hand sides are identical. That's how you can tell that the language is doing something stupid.
That only gets you so far. If you might want to compute the dot product of an int vector and a float vector, you would need four functions:
def dot_product_ii (a : int, b) (c, d) = a*c + b*d
def dot_product_ff (a : float, b) (c, d) = a*c + b*d
def dot_product_if (a, b) (c, d) = (int_to_float a) * c + (int_to_float b)*d
def dot_product_fi (a, b) (c, d) = a * (int_to_float c) + b * (int_to_float d)
Oh, you wanted your vectors to maybe have components of different types? I guess you need to manually define 16 functions then…
Equality types
A similar problem comes up in connection with equality. You can write
3 = 4 and 3.0 = 4.0 but not 3 = 4.0; you need to say int_to_float 3
= 4.0. At least the type of = is clearer here; it really is
α × α → bool because you can compare not only numbers but also
strings, booleans, lists, and so forth. Anything, really, as
indicated by the free variable α.
Ha ha, I lied, you can't actually compare functions. (If you could, you could
solve the halting problem.) So the α in the type of = is not
completely free; it mustn't be replaced by a function type. (It is also
questionable whether it should work for real numbers, and I think SML
changed its mind about this at one point.)
Here, OCaml's +. trick was unworkable. You cannot have a different
identifier for equality comparisons at every different type. SML's
solution was a further epicycle on the type system. Some type
variables were designated “equality type variables”. The type of =
was not
α × α → bool
but
''α × ''α → bool
where ''α means that the α can be instantiated only for an
“equality type” that admits equality comparisons. Integers were an
equality type, but functions (and, in some versions, reals) were not.
Again, this
mechanism was not available to the programmer. If your type was a
structure, it would be an equality type if and only if all its members
were equality types. Otherwise you would have to write your own
synthetic equality function and name it === or something. If !!t!!
is an equality type, then so too is “list of !!t!!”, but this sort of
inheritance, beautifully handled in general by Haskell's type subclass
feature, was available in SML only as a couple of hardwired special cases.
Type classes
Haskell dealt with all these issues reasonably well with type classes,
proposed in Wadler and Blott's 1988 paper
“How to make ad-hoc polymorphism less ad hoc”.
In Haskell, the addition function now has type Num a ⇒ a → a → a
and the equality function has type Eq a ⇒ a → a → Bool. Anyone can
define their own instance of Num and define an addition function for
it. You need an explicit conversion if you want to add it to an
integer:
some_int + myNumericValue -- No
toMyNumericType some_int + myNumericValue -- Yes
but at least it can be done. And you can define a type class and overload toMyNumericType so that
one identifier serves for every type you can convert to your type. Also, a
special hack takes care of lexical constants with no explicit conversion:
23 + myNumericValue -- Yes
-- (actually uses overloaded fromInteger 23 instead)
As far as I know Haskell still doesn't have a complete solution to the
problem of how to make numeric types interoperate smoothly. Maybe
nobody does. Most dynamic languages with ad-hoc polymorphism will
treat a + b differently from b + a, and can give you spooky action
at a distance problems. If type B isn't overloaded, b + a will
invoke the overloaded addition for type A, but then if someone defines
an overloaded addition operator for B, in a different module, the
meaning of every b + a in the program changes completely because it
now calls the overloaded addition for B instead of the one for A.
In Structure and Interpretation of Computer Programs, Abelson and Sussman describe an arithmetic system in which the arithmetic types form an explicit lattice. Every type comes with a “promotion” function to promote it to a type higher up in the lattice. When values of different types are added, each value is promoted, perhaps repeatedly, until the two values are the same type, which is the lattice join of the two original types. I've never used anything like this and don't know how well it works in practice, but it seems like a plausible approach, one which works the way we usually think about numbers, and understands that it can add a float to a Gaussian integer by construing both of them as complex numbers.
[ Addendum 20220430: Phil Eaton informs me that my sense of SML's moribundity is exaggerated: “Standard ML variations are in fact quite alive and the number of variations is growing at the moment”, they said, and provided a link to their summary of the state of Standard ML in 2020, which ends with a recommendation of SML's “small but definitely, surprisingly, not dead community.” Thanks, M. Eaton! ]
[ Addendum 20221108: On the other hand, the Haskell Weekly News annual survey this year includes a question that asks “Which programming languages other than Haskell are you fluent in?” and the offered choices include C#, Ocaml, Scala, and even Perl, but not SML. ]
[Other articles in category /prog/haskell] permanent link
Tue, 01 Oct 2019
How do I keep type constructors from overrunning my Haskell program?
Here's a little function I wrote over the weekend as part of a suite for investigating Yahtzee:
type DiceChoice = [ Bool ]
type DiceVals = [ Integer ]
type DiceState = (DiceVals, Integer)
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls [] ([], n) = [ ([], n-1) ]
allRolls [] _ = undefined
allRolls (chosen:choices) (v:vs, n) =
allRolls choices (vs,n-1) >>=
\(roll,_) -> [ (d:roll, n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
I don't claim this code is any good; I was just hacking around exploring the problem space. But it does do what I wanted.
The allRolls function takes a current game state, something like
( [ 6, 4, 4, 3, 1 ], 2 )
which means that we have two rolls remaining in the round, and the most recent roll of the five dice showed 6, 4, 4, 3, and 1, respectively. It also takes a choice of which dice to keep: The list
[ False, True, True, False, False ]
means to keep the 4's and reroll the 6, the 3, and the 1.
The allRolls function then produces a list of the possible resulting
dice states, in this case 216 items:
[ ( [ 1, 4, 4, 1, 1 ], 1 ) ,
( [ 1, 4, 4, 1, 2 ], 1 ) ,
( [ 1, 4, 4, 1, 3 ], 1 ) ,
…
( [ 6, 4, 4, 6, 6 ], 1 ) ]
This function was not hard to write and it did work adequately.
But I wasn't satisfied. What if I have some unrelated integer list
and I pass it to a function that is expecting a DiceVals, or vice
versa? Haskell type checking is supposed to prevent this from
happening, and by using type aliases I am forgoing this advantage.
No problem, I can easily make DiceVals and the others into datatypes:
data DiceChoice = DiceChoice [ Bool ]
data DiceVals = DiceVals [ Integer ]
data DiceState = DiceState (DiceVals, Integer)
The declared type of allRolls is the same:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
But now I need to rewrite allRolls, and a straightforward
translation is unreadable:
allRolls (DiceChoice []) (DiceState (DiceVals [], n)) = [ DiceState(DiceVals [], n-1) ]
allRolls (DiceChoice []) _ = undefined
allRolls (DiceChoice (chosen:choices)) (DiceState (DiceVals (v:vs), n)) =
allRolls (DiceChoice choices) (DiceState (DiceVals vs,n-1)) >>=
\(DiceState(DiceVals roll, _)) -> [ DiceState (DiceVals (d:roll), n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
This still compiles and it still produces the results I want. And it
has the type checking I want. I can no longer pass a raw integer
list, or any other isomorphic type, to allRolls. But it's
unmaintainable.
I could rename allRolls to something similar, say allRolls__, and
then have allRolls itself be just a type-checking front end to
allRolls__, say like this:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls (DiceChoice dc) (DiceState ((DiceVals dv), n)) =
allRolls__ dc dv n
allRolls__ [] [] n = [ DiceState (DiceVals [], n-1) ]
allRolls__ [] _ _ = undefined
allRolls__ (chosen:choices) (v:vs) n =
allRolls__ choices vs n >>=
\(DiceState(DiceVals roll,_)) -> [ DiceState (DiceVals (d:roll), n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
And I can do something similar on the output side also:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls (DiceChoice dc) (DiceState ((DiceVals dv), n)) =
map wrap $ allRolls__ dc dv n
where wrap (dv, n) = DiceState (DiceVals dv, n)
allRolls__ [] [] n = [ ([], n-1) ]
allRolls__ [] _ _ = undefined
allRolls__ (chosen:choices) (v:vs) n =
allRolls__ choices vs n >>=
\(roll,_) -> [ (d:roll, n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
This is not unreasonably longer or more cluttered than the original
code. It does forgo type checking inside of allRolls__,
unfortunately. (Suppose that the choices and vs arguments had the
same type, and imagine that in the recursive call I put them in the
wrong order.)
Is this considered The Thing To Do? And if so, where could I have learned this, so that I wouldn't have had to invent it? (Or, if not, where could I have learned whatever is The Thing To Do?)
I find most Haskell instruction on the Internet to be either too elementary
pet the nice monad, don't be scared, just approach it very slowly and it won't bite
or too advanced
here we've enabled the
{-# SemispatulatedTypes #-}pragma so we can introduce an overloaded contravariant quasimorphism in the slice category
with very little practical advice about how to write, you know, an actual program. Where can I find some?
[Other articles in category /prog/haskell] permanent link
Fri, 09 Nov 2018
Why I never finish my Haskell programs (part 3 of ∞)
I'm doing more work on matrix functions. A matrix represents a
relation, and I am representing a matrix as a [[Integer]]. Then
matrix addition is simply liftA2 (liftA2 (+)). Except no, that's
not right, and this is not a complaint, it's certainly my mistake.
The overloading for liftA2 for lists does not do what I want, which
is to apply the operation to each pair of correponding elements. I want
liftA2 (+) [1,2,3] [10,20,30] to be [11,22,33] but it is not.
Instead liftA2 lifts an operation to apply to each possible pair of
elements, producing [11,21,31,12,22,32,13,23,33].
And the twice-lifted version is
similarly not what I want:
$$ \require{enclose} \begin{pmatrix}1&2\\3&4\end{pmatrix}\enclose{circle}{\oplus} \begin{pmatrix}10&20\\30&40\end{pmatrix}= \begin{pmatrix} 11 & 21 & 12 & 22 \\ 31 & 41 & 32 & 42 \\ 13 & 23 & 14 & 24 \\ 33 & 43 & 34 & 44 \end{pmatrix} $$
No problem, this is what ZipList is for. ZipLists are just regular
lists that have a label on them that advises liftA2 to lift an
operation to the element-by-element version I want instead of the
each-one-by-every-other-one version that is the default. For instance
liftA2 (+) (ZipList [1,2,3]) (ZipList [10,20,30])
gives ZipList [11,22,33], as desired. The getZipList function
turns a ZipList back into a regular list.
But my matrices are nested lists, so I need to apply the ZipList
marker twice, once to the outer list, and once to each of the inner
lists, because I want the element-by-element behavior at both
levels. That's easy enough:
matrix :: [[a]] -> ZipList (ZipList a)
matrix m = ZipList (fmap ZipList m)
(The fmap here is actually being specialized to map, but that's
okay.)
Now
(liftA2 . liftA2) (+) (matrix [[1,2],[3,4]]) (matrix [[10,20],[30, 40]])
does indeed produce the result I want, except that the type markers are still in there: instead of
[[11,22],[33,44]]
I get
ZipList [ ZipList [11, 22], ZipList [33, 44] ]
No problem, I'll just use getZipList to turn them back again:
unmatrix :: ZipList (ZipList a) -> [[a]]
unmatrix m = getZipList (fmap getZipList m)
And now matrix addition is finished:
matrixplus :: [[a]] -> [[a]] -> [[a]]
matrixplus m n = unmatrix $ (liftA2 . liftA2) (+) (matrix m) (matrix n)
This works perfectly.
But the matrix and unmatrix pair bugs me a little. This business
of changing labels at both levels has happened twice already and
I am likely to need it again. So I will turn the two functions
into a single higher-order function by abstracting over ZipList.
This turns this
matrix m = ZipList (fmap ZipList m)
into this:
twice zl m = zl (fmap zl m)
with the idea that I will now have matrix = twice ZipList and
unmatrix = twice getZipList.
The first sign that something is going wrong is that twice does not
have the type I wanted. It is:
twice :: Functor f => (f a -> a) -> f (f a) -> a
where I was hoping for something more like this:
twice :: (Functor f, Functor g) => (f a -> g a) -> f (f a) -> g (g a)
which is not reasonable to expect: how can Haskell be expected to
figure out I wanted two diferent functors in there when there is only one
fmap? And indeed twice does not work; my desired matrix = twice
ZipList does not even type-check:
<interactive>:19:7: error:
• Occurs check: cannot construct the infinite type: a ~ ZipList a
Expected type: [ZipList a] -> ZipList a
Actual type: [a] -> ZipList a
• In the first argument of ‘twice’, namely ‘ZipList’
In the expression: twice ZipList
In an equation for ‘matrix’: matrix = twice ZipList
• Relevant bindings include
matrix :: [[ZipList a]] -> ZipList a (bound at <interactive>:20:5)
Telling GHC explicitly what type I want for twice doesn't work
either, so I decide it's time to go to lunch. I take paper with me,
and while I am eating my roast pork hoagie with sharp provolone and
spinach (a popular local delicacy) I work out the results of the type
unification algorithm on paper for both cases to see what goes wrong.
I get the same answers that Haskell got, but I can't see where the difference was coming from.
So now, instead of defining matrix operations, I am looking into the
type unification algorithm and trying to figure out why twice
doesn't work.
And that is yet another reason why I never finish my Haskell programs. (“What do you mean, λ-abstraction didn't work?”)
[Other articles in category /prog/haskell] permanent link
Thu, 08 Nov 2018
Haskell type checker complaint 184 of 698
I want to build an adjacency matrix for the vertices of a cube; this
is a matrix that has m[a][b] = 1 exactly when vertices a and b
share an edge. We can enumerate the vertices arbitrarily but a
convenient way to do it is to assign them the numbers 0 through 7 and
then say that vertices !!a!! and !!b!! are adjacent if, regarded as
binary numerals, they differ in exactly one bit, so:
import Data.Bits
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
This compiles and GHC infers the type
adj :: (Bits a, Num a, Num t) => a -> a -> t
Fine.

Now I want to build the adjacency matrix, which is completely straightforward:
cube = [ [a `adj` b | b <- [0 .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Ha ha, no it isn't; in Haskell nothing is straightforward. This
produces 106 lines of type whining, followed by a failed compilation.
Apparently this is because because 0 and 7 are overloaded, and
could mean some weird values in some freakish instance of Num, and
then 0 .. 7 might generate an infinite list of 1-graded torsion
rings or something.
To fix this I have to say explicitly what I mean by 0. “Oh, yeah,
by the way, that there zero is intended to denote the integer zero,
and not the 1-graded torsion ring with no elements.”
cube = [ [a `adj` b | b <- [0 :: Integer .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Here's another way I could accomplish this:
zero_i_really_mean_it = 0 :: Integer
cube = [ [a `adj` b | b <- [zero_i_really_mean_it .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Or how about this?
cube = [ [a `adj` b | b <- numbers_dammit [0 .. 7] ] | a <- [0 .. 7] ] where
p `adj` q = if (elem (xor p q) [1, 2, 4]) then 1 else 0
numbers_dammit = id :: [Integer] -> [Integer]
I think there must be something really wrong with the language design here. I don't know exactly what it is, but I think someone must have made the wrong tradeoff at some point.
[Other articles in category /prog/haskell] permanent link
Fri, 26 Oct 2018
A snide addendum about implicit typeclass instances
In an earlier article I demanded:
Maybe someone can explain to me why this is a useful behavior, and then explain why it is so useful that it should happen automatically …
“This” being that instead of raising a type error, Haskell quietly accepts this nonsense:
fmap ("super"++) (++"weasel")
but it clutches its pearls and faints in horror when confronted with this expression:
fmap ("super"++) "weasel"
Nobody did explain this.
But I imagined
someone earnestly explaining: “Okay, but in the first case, the
(++"weasel") is interpreted as a value in the environment functor,
so fmap is resolved to its the environment instance, which is (.).
That doesn't happen in the second example.”
Yeah, yeah, I know that. Hey, you know what else is a functor? The
identity functor. If fmap can be quietly demoted to its (->) e
instance, why can't it also be quietly demoted to its Id instance,
which is ($), so that fmap ("super"++) "weasel" can quietly
produce "superweasel"?
I understand this is a terrible idea. To be clear, what I want is for it to collapse on the divan for both expressions. Pearl-clutching is Haskell's finest feature and greatest strength, and it should do it whenever possible.
[Other articles in category /prog/haskell] permanent link
Tue, 23 Oct 2018
Getting Applicatives from Monads and “>>=” from “join”
I complained recently about GHC not being able to infer an
Applicative instance from a type that already has a Monad
instance, and there is a related complaint that the Monad instance
must define >>=. In some type classes, you get a choice about
what to define, and then the rest of the functions are built from the
ones you provided. To take a particular simple example, with Eq
you have the choice of defining == or /=, and if you omit one
Haskell will construct the other for you. It could do this with >>=
and join, but it doesn't, for technical reasons I don't
understand
[1]
[2]
[3].
But both of these problems can be worked around. If I have a Monad instance, it seems to work just fine if I say:
instance Applicative Tree where
pure = return
fs <*> xs = do
f <- fs
x <- xs
return (f x)
Where this code is completely canned, the same for every Monad.
And if I know join but not >>=, it seems to work just fine if I say:
instance Monad Tree where
return = ...
x >>= f = join (fmap f x) where
join tt = ...
I suppose these might faul foul of whatever problem is being described in the documents I linked above. But I'll either find out, or I won't, and either way is a good outcome.
[ Addendum: Vaibhav Sagar points out that my definition of <*> above
is identical to that of Control.Monad.ap, so that instead of
defining <*> from scratch, I could have imported ap and then
written <*> = ap. ]
[ Addendum 20221021: There are actually two definitions of <*> that will work. [1] [2] ]
[Other articles in category /prog/haskell] permanent link
Mon, 22 Oct 2018While I was writing up last week's long article about Traversable, I wrote this stuff about Applicative also. It's part of the story but I wasn't sure how to work it into the other narrative, so I took it out and left a remark that “maybe I'll publish a writeup of that later”. This is a disorganized collection of loosely-related paragraphs on that topic.
It concerns my attempts to create various class instance definitions for the following type:
data Tree a = Con a | Add (Tree a) (Tree a)
deriving (Eq, Show)
which notionally represents a type of very simple expression tree over values of type a.
I need some function for making Trees that isn't too
simple or too complicated, and I went with:
h n | n < 2 = Con n
h n = if even n then Add (h (n `div` 2)) (h (n `div` 2))
else Add (Con 1) (h (n - 1))
which builds trees like these:
2 = 1 + 1
3 = 1 + (1 + 1)
4 = (1 + 1) + (1 + 1)
5 = 1 + ((1 + 1) + (1 + 1))
6 = (1 + (1 + 1)) + (1 + (1 + 1))
7 = 1 + (1 + (1 + 1)) + (1 + (1 + 1))
8 = ((1 + 1) + (1 + 1)) + ((1 + 1) + (1 + 1))
Now I wanted to traverse h [1,2,3] but I couldn't do that because I
didn't have an Applicative instance for Tree. I had been putting off
dealing with this, but since Traversable doesn't really make sense without
Applicative I thought the day of reckoning would come. Here it was. Now is
when I learn how to fix all my broken monads.
To define an Applicative instance for Tree I needed to define pure, which
is obvious (it's just Con) and <*> which would apply a tree of
functions to a tree of inputs to get a tree of results. What the hell
does that mean?
Well, I can kinda make sense of it. If I apply one function to a
tree of inputs, that's straightforward, it's just fmap, and I get a
tree of results. Suppose I have a tree of functions, and I replace
the function at each leaf with the tree of its function's results.
Then I have a tree of trees. But a tree that has trees at its leaves
is just a tree. So I could write some tree-flattening function that
builds the tree of trees, then flattens out the type. In fact this is just
join that I already know from Monad world.
The corresponding operation for lists takes a list of lists
and flattens them into a single list.) Flattening a tree is quite easy to do:
join (Con ta) = ta
join (Add ttx tty) = Add (join ttx) (join tty)
and since this is enough to define a Monad instance for Tree I
suppose it is enough to get an Applicative instance also, since every Monad
is an Applicative. Haskell makes this a pain. It should be able to infer
the Applicative from this, and I wasn't clever enough to do it myself. And
there ought to be some formulaic way to get <*> from >>= and
join and fmap, the way you can get join from >>=:
join = (>>= id)
but I couldn't find out what it was. This gets back to my original
complaint: Haskell now wants every Monad instance to be an instance
of Applicative, but if I give it the fmap and the join and the return
it ought to be able to figure out the Applicative instance itself instead of
refusing to compile my program. Okay, fine, whatever. Haskell's
gonna Hask.
(I later realized that building <*> when you have a Monad instance
is easy once you know the recipe; it's just:
fs <*> xs = do
f <- fs
x <- xs
return (f x)
So again, why can't GHC infer <*> from my Monad instance, maybe
with a nonfatal warning?
Warning: No Applicative instance provided for Tree; deriving one from Monad
This is not a rhetorical question.)
(Side note: it seems like there ought to be a nice short abbreviation
of the (<*>) function above, the way one can write join = (>>=
id). I sought one but did not find any. One can eliminate the do
notation to obtain the expression:
fs <*> xs = fs >>= \f -> xs >>= \x -> return (f x)
but that is not any help unless we can simplify the expression with
the usual tricks, such as combinatory logic and η-conversion. I was
not able to do this, and the automatic pointfree
converter produced
(. ((. (return .)) . (>>=))) . (>>=) ARGH MY EYES.)
Anyway I did eventually figure out my <*> function for trees by
breaking the left side into cases. When the tree of functions is Con
f it's a single function and we can just use fmap to map it over
the input tree:
(Con f) <*> tv = fmap f tv
And when it's bigger than that we can break it up recursively:
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
Once this is written it seemed a little embarrassing that it took me so long to figure out what it meant but this kind of thing always seems easier from the far side of the fence. It's hard to understand until you understand it.
Actually that wasn't quite the <*> I wanted. Say we have a tree of
functions and a tree of arguments.

Add (Con (* 10))
(Con (* 100))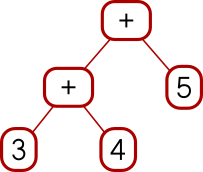
Add (Add (Con 3) (Con 4)) (Con 5)I can map the whole tree of functions over each single leaf on the right, like this:
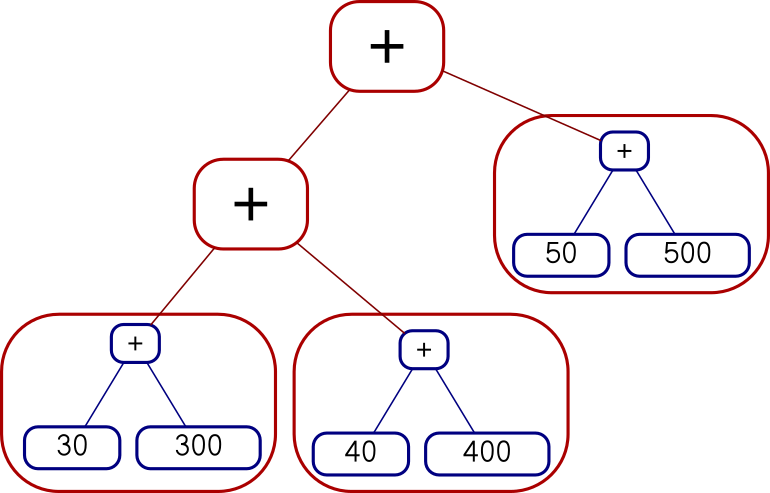
Add (Add (Add (Con 30) (Con 300))
(Add (Con 40) (Con 400)))
(Add (Con 50) (Con 500))
or I can map each function over the whole tree on the right, like this:
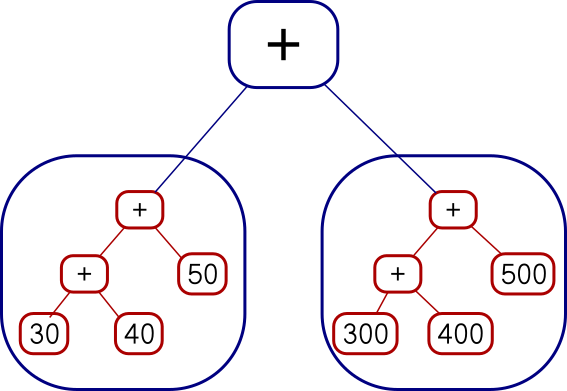
Add
(Add (Add (Con 30) (Con 40)) (Con 50))
(Add (Add (Con 300) (Con 400)) (Con 500))The code I showed earlier does the second of those. You can see it from
the fmap f tv expression, which takes a single function and maps it over a whole
tree of values. I had actually wanted the other one, but there isn't
anything quite like fmap for that. I was busy trying to
understand Applicative and I was afraid if I got distracted trying to invent
a reverse fmap I might lose the thread. This happens to me a lot
with Haskell. I did eventually go back and figure it out. The
reverse fmap is
pamf fs v = fmap ($ v) fs -- good
or
pamf = flip (fmap . flip id) -- yuck
Now there's a simple answer to this which occurs to me now that I
didn't think of before, but I'm going to proceed with how I planned to
do it before, with pamf. The <*> that I didn't want looked like this:
(Con f) <*> tv = fmap f tv
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
I need to do the main recursion on the values argument instead of on the functions argument:
tf <*> (Con v) = pamf tf v
where pamf fs v = fmap ($ v) fs
tf <*> (Add lv rv) = Add (tf <*> lv) (tf <*> rv)
(This is an interesting example: usually the base case is trivial and the recursive clause is harder to write, but this time it's the base case that's not perfectly straightforward.)
Anyway, this worked, but there was an easier solution at hand. The difference between the first version and the second is exactly the same as the difference between
fs <*> xs = do
f <- fs
x <- xs
return (f x)
and
fs <*> xs = do
x <- xs
f <- fs
return (f x)
Digging deeper into why this worked this way was interesting, but it's bed time, so I'm going to cut the scroll here.
[ Addendum 20221021: More about the two versions of <*> and a third version that doesn't work. ]
[Other articles in category /prog/haskell] permanent link
Sat, 20 Oct 2018
I struggle to understand Traversable
Haskell evolved a lot since the last time I seriously wrote any
Haskell code, so much so that all my old programs broke. My Monad
instances don't compile any more because I'm no longer allowed to
have a monad which isn't also an instance of Applicative. Last time I used
Haskell, Applicative wasn't even a thing. I had read the McBride and
Paterson paper that introduced applicative functors, but that was
years ago, and I didn't remember any of the details. (In fact, while
writing this article, I realized that the paper I read was a preprint,
and I probably read it before it was published, in 2008.) So to
resuscitate my old code I had to implement a bunch of <*> functions
and since I didn't really understand what it was supposed to be doing
I couldn't do that. It was a very annoying experience.
Anyway I got that more or less under control (maybe I'll publish a
writeup of that later) and moved on to Traversable which, I hadn't realized
before, was also introduced in that same paper. (In the
prepublication version, Traversable had been given the unmemorable name
IFunctor.) I had casually looked into this several times in the
last few years but I never found anything enlightening. A Traversable is a
functor (which must also implement Foldable, but let's pass over that
for now, no pun intended) that implements a traverse method with the
following signature:
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
The traversable functor itself here is t. The f thing is an
appurtenance. Often one looks at the type of some function and says “Oh, that's what
that does”, but I did not get any understanding from this signature.
The first thing to try here is to make it less abstract. I was thinking about Traversable this time because I thought I might want it for a certain type of tree structure I was working with. So I defined an even simpler tree structure:
data Tree a = Con a | Add (Tree a) (Tree a)
deriving (Eq, Show)
Defining a bunch of other cases wouldn't add anything to my understanding, and it would make it take longer to try stuff, so I really want to use the simplest possible example here. And this is it: one base case, one recursive case.
Then I tried to make this type it into a Traversable instance. First we need it to be a Functor, which is totally straightforward:
instance Functor Tree where
fmap f (Con a) = Con (f a)
fmap f (Add x y) = Add (fmap f x) (fmap f y)
Then we need it to be a Foldable, which means it needs to provide a
version of foldr. The old-fashioned foldr was
foldr :: (a -> b -> b) -> b -> [a] -> b
but these days the list functor in the third place has been generalized:
foldr :: Foldable f => (a -> b -> b) -> b -> f a -> b
The idea is that foldr fn collapses a list of as into a single b
value by feeding in the as one at a time. Each time, foldr takes
the previous b and the current a and constructs a new b. The
second argument is the initial value of b.
Another way to think about it is that every list has the form
e1 : e2 : .... : []
and foldr fn b applied to this list replaces the (:) calls with fn
and the trailing [] with b, giving me
e1 `f` e2 `f` .... `f` b
The canonical examples for lists are:
sum = foldr (+) 0
(add up the elements, starting with zero) and
length = foldr (\_ -> (+ 1)) 0
(ignore the elements, adding 1 to the total each time, starting with
zero). Also foldr (:) [] is the identity function for lists because
it replaces the (:) calls with (:) and the trailing [] with [].
Anyway for Tree it looks like this:
instance Foldable Tree where
foldr f b (Con a) = f a b
foldr f b (Add x y) = (foldr f) (foldr f b x) y
The Con clause says to take the constant value and combine it with
the default total. The Add clause says to first fold up the
left-side subtree x to a single value, then use that as the initial
value for folding up the right-side subtree y, so everything gets
all folded up together. (We could of course do the right subtree
before the left; the results would be different but just as good.)
I didn't write this off the top of my head, I got it by following the types, like this:
In the first clause
foldr f b (Con a) = ???we have a function
fthat wants anavalue and abvalue, and we have both anaand ab, so put the tabs in the slots.In the second clause
foldr f b (Add x y) = ???fneeds anavalue and none is available, so we can't usefby itself. We can only use it recursively viafoldr. So forgetf, we will only be dealing only withfoldr f, which has typeb -> Tree a -> b. We need to apply this to abvalue and the only one we have isb, and then we need to apply that to one of the subtrees, sayx, and thus we have synthesized thefoldr f b xsubexpression. Then pretty much the same process gets us the rest of it: we need aband the only one we have now isfoldr f b x, and then we need another tree and the only one we haven't used isy.
It turns out it is easier and more straightforward to write foldMap
instead, but I didn't know that at the time. I won't go into it
further because I have already digressed enough. The preliminaries
are done, we can finally get on to the thing I wanted, the Traversable:
instance Traversable Tree where
traverse = ....
and here I was stumped. What is this supposed to actually do?
For our Tree functor it has this signature:
traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
Okay, a function a -> f b I understand, it turns each tree leaf
value into a list or something, so at each point of the tree it gets
out a list of bs, and it potentially has one of those for each item
in the input tree. But how the hell do I turn a tree of lists into
a single list of Tree b? (The answer is that the secret sauce is
in the Applicative, but I didn't understand that yet.)
I scratched my head and read a bunch of different explanations and none of them helped. All the descriptions I found were in either prose or mathematics and I still couldn't figure out what it was for. Finally I just wrote a bunch of examples and at last the light came on. I'm going to show you the examples and maybe the light will come on for you too.
We need two Traversable functors to use as examples. We don't have a Traversable
implementation for Tree yet so we can't use that. When I think of
functors, the first two I always think of are List and Maybe, so
we'll use those.
> traverse (\n -> [1..n]) Nothing
[Nothing]
> traverse (\n -> [1..n]) (Just 3)
[Just 1,Just 2,Just 3]
Okay, I think I could have guessed that just from the types. And
going the other way is not very interesting because the output, being
a Maybe, does not have that much information in it.
> let f x = if even x then Just (x `div` 2) else Nothing
If the !!x!! is even then the result is just half of !!x!!, and otherwise the division by 2 “fails” and the result is nothing. Now:
> traverse f [ 1, 2, 3, 4 ]
Nothing
> traverse f [ 10, 4, 18 ]
Just [5,2,9]
It took me a few examples to figure out what was going on here: When
all the list elements are even, the result is Just a list of half of
each. But if any of the elements is odd, that spoils the whole result
and we get Nothing. (traverse f [] is Just [] as one would
expect.)
That pretty much exhausts what can be done with lists and maybes. Now
I have two choices about where to go next: I could try making both
functors List, or I could use a different functor entirely. (Making
both Maybe seemed like a nonstarter.) Using List twice seemed
confusing, and when I tried it I could kinda see what it was doing but
I didn't understand why. So I took a third choice: I worked up a Traversable
instance for Tree just by following the types even though I didn't
understand what it ought to be doing. I thought I'd at least see if I
could get the easy clause:
traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
instance Traversable Tree where
traverse fn (Con a) = ...
In the ... I have fn :: a -> f b and I have at hand a single a. I need to
construct a Tree b. The only way to get a b is to apply fn to
it, but this gets me an f b and I need f (Tree b). How do I get the
Tree in there? Well, that's what Con is for, getting Tree in
there, it turns a t into Tree t. But how do I do that inside of
f? I tinkered around a little bit and eventually found
traverse fn (Con a) = Con <$> (fn a)
which not only type checks but looks like it could even be correct.
So now I have a motto for what <$> is about: if I have some
function, but I want to use it inside of some applicative functor
f, I can apply it with <$> instead of with $.
Which, now that I have said it myself, I realize it is exactly what
everyone else was trying to tell me all along: normal function
application takes an a -> b and applies to to an a giving a b.
Applicative application takes an f (a -> b) and applies it to an f a
giving an f b. That's what applicative functors are all about,
doing stuff inside of f.
Okay, I can listen all day to an explanation of what an electric drill does, but until I hold it in my hand and drill some holes I don't really understand.
Encouraged, I tried the hard clause:
traverse fn (Add x y) = ...
and this time I had a roadmap to follow:
traverse fn (Add x y) = Add <$> ...
The Con clause had fn a at that point to produce an f b but that won't
work here because we don't have an a, we have a whole Tree a, and we
don't need an f b, we need an f (Tree b). Oh, no problem,
traverse fn supposedly turns a Tree a into an f (Tree b), which
is just what we want.
And it makes sense to have a recursive call to traverse because this is the
recursive part of the recursive data structure:
traverse fn (Add x y) = Add <$> (traverse fn x) ...
Clearly traverse fn y is going to have to get in there somehow, and
since the pattern for all the applicative functor stuff is
f <$> ... <*> ... <*> ...
let's try that:
traverse fn (Add x y) = Add <$> (traverse fn x) <*> (traverse fn y)
This looks plausible. It compiles, so it must be doing something.
Partial victory! But what is it doing? We can run it and see, which
was the whole point of an exercise: work up a Traversable instance for Tree
so that I can figure out what Traversable is about.
Here are some example trees:
t1 = Con 3 -- 3
t2 = Add (Con 3) (Con 4) -- 3 + 4
t3 = Add (Add (Con 3) (Con 4)) (Con 2) -- (3 + 4) + 2
(I also tried Add (Con 3) (Add (Con 4) (Con 2)) but it did not
contribute any new insights so I will leave it out of this article.)
First we'll try Maybe. We still have that f function from before:
f x = if even x then Just (x `div` 2) else Nothing
but traverse f t1, traverse f t2, and traverse f t3 only produce
Nothing, presumably because of the odd numbers in the trees. One
odd number spoils the whole thing, just like in a list.
So try:
traverse f (Add (Add (Con 10) (Con 4)) (Con 18))
which yields:
Just (Add (Add (Con 5) (Con 2)) (Con 9))
It keeps the existing structure, and applies f at each value
point, just like fmap, except that if f ever returns Nothing
the whole computation is spoiled and we get Nothing. This is
just like what traverse f was doing on lists.
But where does that spoilage behavior come from exactly? It comes
from the overloaded behavior of <*> in the Applicative instance of Maybe:
(Just f) <*> (Just x) = Just (f x)
Nothing <*> _ = Nothing
_ <*> Nothing = Nothing
Once we get a Nothing in there at any point, the Nothing takes
over and we can't get rid of it again.
I think that's one way to think of traverse: it transforms each
value in some container, just like fmap, except that where fmap
makes all its transformations independently, and reassembles the exact
same structure, with traverse the reassembly is done with the
special Applicative semantics. For Maybe that means “oh, and if at any
point you get Nothing, just give up”.
Now let's try the next-simplest Applicative, which is List. Say,
g n = [ 1 .. n ]
Now traverse g (Con 3) is [Con 1,Con 2,Con 3] which is not exactly
a surprise but traverse g (Add (Con 3) (Con 4)) is something that
required thinking about:
[Add (Con 1) (Con 1),
Add (Con 1) (Con 2),
Add (Con 1) (Con 3),
Add (Con 1) (Con 4),
Add (Con 2) (Con 1),
Add (Con 2) (Con 2),
Add (Con 2) (Con 3),
Add (Con 2) (Con 4),
Add (Con 3) (Con 1),
Add (Con 3) (Con 2),
Add (Con 3) (Con 3),
Add (Con 3) (Con 4)]
This is where the light finally went on for me. Instead of thinking
of lists as lists, I should be thinking of them as choices. A list
like [ "soup", "salad" ] means that I can choose soup or salad, but
not both. A function g :: a -> [b] says, in restaurant a, what
bs are on the menu.
The g function says what is on the menu at each node. If a node has
the number 4, I am allowed to choose any of [1,2,3,4], but if it has
the number 3 then the choice 4 is off the menu and I can choose only
from [1,2,3].
Traversing g over a Tree means, at each leaf, I am handed a menu,
and I make a choice for what goes at that leaf. Then the result of
traverse g is a complete menu of all the possible complete trees I
could construct.
Now I finally understand how the t and the f switch places in
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
I asked “how the hell do I turn a tree of lists into a single list
of Tree b”? And that's the answer: each list is a local menu of
dishes available at one leaf, and the result list is the global menu
of the complete dinners available over the entire tree.
Okay! And indeed traverse g (Add (Add (Con 3) (Con 4)) (Con 2)) has
24 items, starting
Add (Add (Con 1) (Con 1)) (Con 1)
Add (Add (Con 1) (Con 1)) (Con 2)
Add (Add (Con 1) (Con 2)) (Con 1)
...
and ending
Add (Add (Con 3) (Con 4)) (Con 1)
Add (Add (Con 3) (Con 4)) (Con 2)
That was traversing a list function over a Tree. What if I go the
other way? I would need an Applicative instance for Tree and I didn't
really understand Applicative yet so that wasn't going to happen for a
while. I know I can't really understand Traversable without understanding
Applicative first but I wanted to postpone the day of reckoning as long as
possible.
What other functors do I know? One easy one is the functor that takes
type a and turns it into type (String, a). Haskell even has a
built-in Applicative instance for this, so I tried it:
> traverse (\x -> ("foo", x)) [1..3]
("foofoofoo",[1,2,3])
> traverse (\x -> ("foo", x*x)) [1,5,2,3]
("foofoofoofoo",[1,25,4,9])
Huh, I don't know what I was expecting but I think that wouldn't have
been it. But I figured out what was going on: the built-in Applicative
instance for the a -> (String, a) functor just concatenates the
strings. In general it is defined on a -> (m, b) whenever m is a
monoid, and it does fmap on the right component and uses monoid
concatenation on the left component. So I can use integers instead of
strings, and it will add the integers instead of concatenating the
strings. Except no, it won't, because there are several ways to make
integers into a monoid, but each type can only have one kind of
Monoid operations, and if one was wired in it might not be the one I
want. So instead they define a bunch of types that are all integers
in obvious disguises, just labels stuck on them that say “I am not an
integer, I am a duck”; “I am not an integer, I am a potato”. Then
they define different overloadings for “ducks” and “potatoes”. Then
if I want the integers to get added up I can put duck labels on my
integers and if I want them to be multiplied I can stick potato labels
on instead. It looks like this:
import Data.Monoid
h n = (Sum 1, n*10)
Sum is the duck label. When it needs to combine two
ducks, it will add the integers:
> traverse h [5,29,83]
(Sum {getSum = 3},[50,290,830])
But if we wanted it to multiply instead we could use the potato label,
which is called Data.Monoid.Product:
> traverse (\n -> (Data.Monoid.Product 7, 10*n)) [5,29,83]
(Product {getProduct = 343}, [50,290,830])
There are three leaves, so we multiply three sevens and get 343.
Or we could do the same sort of thing on a Tree:
> traverse (\n -> (Data.Monoid.Product n, 10*n)) (Add (Con 2) (Add (Con 3) (Con 4)))
(Product {getProduct = 24}, Add (Con 20) (Add (Con 30) (Con 40)))
Here instead of multiplying together a bunch of sevens we multiply together the leaf values themselves.
The McBride and Paterson paper spends a couple of pages talking about
traversals over monoids, and when I saw the example above it started
to make more sense to me. And their ZipList example became clearer
too. Remember when we had a function that gave us a menu at every
leaf of a tree, and traverse-ing that function over a tree gave us a
menu of possible trees?
> traverse (\n -> [1,n,n*n]) (Add (Con 2) (Con 3))
[Add (Con 1) (Con 1),
Add (Con 1) (Con 3),
Add (Con 1) (Con 9),
Add (Con 2) (Con 1),
Add (Con 2) (Con 3),
Add (Con 2) (Con 9),
Add (Con 4) (Con 1),
Add (Con 4) (Con 3),
Add (Con 4) (Con 9)]
There's another useful way to traverse a list function. Instead of taking each choice at each leaf we make a single choice ahead of time about whether we'll take the first, second, or third menu item, and then we take that item every time:
> traverse (\n -> Control.Applicative.ZipList [1,n,n*n]) (Add (Con 2) (Con 3))
ZipList {getZipList = [Add (Con 1) (Con 1),
Add (Con 2) (Con 3),
Add (Con 4) (Con 9)]}
There's a built-in instance for Either a b also. It's a lot like
Maybe. Right is like Just and Left is like Nothing. If all
the sub-results are Right y then it rebuilds the structure with all
the ys and gives back Right (structure). But if any of the
sub-results is Left x then the computation is spoiled and it gives
back the first Left x. For example:
> traverse (\x -> if even x then Left (x `div` 2) else Right (x * 10)) [3,17,23,9]
Right [30,170,230,90]
> traverse (\x -> if even x then Left (x `div` 2) else Right (x * 10)) [3,17,22,9]
Left 11
Okay, I think I got it.
Now I just have to drill some more holes.
[Other articles in category /prog/haskell] permanent link
Mon, 15 Oct 2018
'The' reader monad does not exist
Reading over my recent article complaining about the environment functor I realized there's yet another terminology problem that makes the discussion unnecessarily confusing. “The” environment functor isn't unique. There is a family of environment functors, one for each possible environment type e. If g is the environment functor at type e, a value of type g t is a function e → t. But e could be anything and if g and h are environment functors at two different types e and e’ they are of course different functors.
This is even obvious from the definition:
data Environ e t = Env (e -> t)
instance Functor (Environ e) where
fmap f (Env x) = Env $ \e -> f (x e)
The functor isn't Environ, it's Environ e, and the functor
instance declaration, as it says on line 2. (It seems to me that the
notation is missing a universal quantifier somewhere, but I'm not
going to open that issue.)
We should speak of Environ e as an environment functor, not
the environment functor. So for example instead of:
When operating in the environment functor,
fmaphas the type(a -> b) -> g a -> g b
I should have said:
When operating in an environment functor,
fmaphas the type(a -> b) -> g a -> g b
And instead of:
A function
p -> qis aqparcel in the environment functor
I should have said:
A function
p -> qis aqparcel in an environment functor
or
A function
p -> qis aqparcel in the environment functor atp
although I'm not sure I like the way the prepositions are proliferating there.
The same issue affects ⸢the⸣ reader monad, ⸢the⸣ state monad, and many others.
I'm beginning to find remarkable how much basic terminology Haskell is missing or gets wrong. Mathematicians have a very keen appreciation of the importance of specific and precise terminology, and you'd think this would have filtered into the Haskell world. People are forever complaining that Haskell uses unfamiliar terms like “functor”, and the community's response is (properly, I think) that these terms are pre-existing and there is no point to inventing a new term that will be just as unfamiliar, or, worse, lure people into thinking that the know what it means when they don't. You don't want to call a functor a “container”, says the argument, because many functors (environment functors for example) are nothing at all like containers. I think this is wise.
But having planted their flag on that hill, the Haskell folks don't
then use their own terminology correctly. I complained years
ago that the term
“monad” was used interchangeably for four subtly different concepts,
and here we actually have a fifth. I pointed out that in the case of
Environment e t, common usage refers to both Environment e and
Environment e t as monads, and only the first is correct. But when
people say “the environment monad” they mean that Environment itself
is a monad, which it is not.
[Other articles in category /prog/haskell] permanent link
Thu, 11 Oct 2018Is there any good terminology for a value of type
f awhenfis an arbitrary functor? I will try calling anf tvalue a “tparcel” and see how that works.
The more I think about “parcel” the happier I am with it. It strongly
suggests container types, of course, so that a t parcel might be a
boxful of ts. But it also hints at some other possible situations:
- You might open the parcel and find it empty. (
Maybe t) - You might open the parcel and find, instead of the
tyou expected, a surprising prank snake. (Either ErrorMessage t) - You might open the parcel and find that your
thas been shipped with assembly required. (env -> t) - The parcel might explode when you open it. (
IO t) - And, of course, a burrito is a sort of parcel of meat and beans.
I coined “parcel” thinking that one would want different terminology
for values of type f t depending on whether f was a functor
(“parcel”) or also a monad (“mote”). Of course every mote is a
parcel, but not always vice versa. Now I'm not sure that both terms
are needed. Non-monadic functors are unusual, and non-applicative
functors rare, so perhaps one term will do for all three.
[Other articles in category /prog/haskell] permanent link
I hate the environment functor
Here we have the well-known fmap function:
fmap :: Functor f => (a -> b) -> f a -> f b
It takes a single function and a (collection of input values / decorated input value / something something input value) and produces a (collection of output values / decorated output value / something something output value).
Yow, that's not going to work. Is there any good terminology for a
value of type f a when f is an arbitrary functor? A while back I
discussed a similar
problem and suggested
the term “mote” for a value in a monadic type. I will try calling an
f t value a “t parcel and see how that works. So
[t], Maybe t, and IO t are all examples of t parcels, in
various functors.
Starting over then. Here we have the well-known fmap function:
fmap :: Functor f => (a -> b) -> f a -> f b
It takes a single function, and an a parcel, and produces a b
parcel, by applying the function independently to the a values in
the parcel.
Here is a sort of reversed version of fmap that I call pamf:
pamf :: Functor f => f (a -> b) -> a -> f b
It takes a parcel of functions, and a single input and produces a
parcel of outputs, by applying each function in the parcel
independently to the single a value. It can be defined in terms of
fmap:
pamf fs a = fmap ($ a) fs
So far so good. Now I ask you to predict the type of
pamf fmap
Certainly it should start out with
pamf fmap :: (Functor f, Functor g) => ...
because the pamf and the fmap might be operating in two different
functors, right? Indeed, if I compose the functions the other way
around, fmap pamf, the type does begin this way; it is:
(Functor f, Functor g) => f (g (a -> b)) -> f (a -> g b)
The f here is the functor in which fmap operates, and the g is
the functor in which pamf is operating. In general fmap takes an
arbitrary function
a -> b
and lifts it to a new function that operates in the f functor:
f a -> f b
Here it has taken pamf, which is a function
g (a -> b) -> (a -> g b)
and lifted it to a new function that operates in the f functor:
f (g (a -> b)) -> f (a -> g b)
This is complicated but straightforward. Okay, that was fmap pamf.
What about pamf fmap though? The computed type is
pamf fmap :: Functor f => f a -> (a -> b) -> f b
and when I saw this I said “What. Where did g go? What happened to
g?”
Then I paused and for a while and said “… I bet it's that goddamn environment thing again.” Yep, that's what it was. It's the environment functor, always turning up where I don't want it and least expect it, like that one guy we all went to college with. The environment functor, by the way, is yet another one of those things that Haskell ought to have a standard name for, but doesn't. The phrase “the reader monad” is fairly common, but here I only want the functor part of the monad. And people variously say “reader monad”, “environment monad”, and “evaluation monad” to mean the same thing. In this article, it will be the environment functor.
Here's what happened. Here are fmap and pamf again:
fmap :: Functor f => (p -> q) -> f p -> f q
pamf :: Functor g => g (a -> b) -> a -> g b
The first argument to pamf should be a parcel in the g functor.
But fmap is not a parcel, so pamf fmap will be a type error,
right? Wrong! If you are committed enough, there is a way to
construe any function as a parcel. A function p -> q is a q
parcel in the environment functor. Say that g denotes an
environment functor. In this functor, a parcel of type g t is a
function which consults an “environment” of type e and yields a
result of type t. That is, $$g\ t \equiv e \to t.$$
When operating in the environment functor, fmap has the type (a ->
b) -> g a -> g b, which is shorthand for (a -> b) -> (e -> a) -> (e
-> b). This instance of fmap is defined this way:
fmap f x = \e -> f (x e)
or shorter and more mysteriously
fmap = (.)
which follows by η-reduction, something Haskell enthusiasts never seem to get enough of.
In fmap f x, the x isn't the actual value to give to f; instead
it's a parcel, as it always is with fmap. In the context of the
environment functor, x is a function that consults the environment
e and returns an a. The result of fmap f x is a new parcel: it
uses x to consult the supplied environment for a value of type a,
which it then feeds to f to get the required value of type b.
In the application pamf fmap, the left side pamf wants fmap to
be a parcel. But it's not a parcel, it's a function. So, type error,
right? No! Any function is a parcel if you want it to be, it's a
parcel in the environment functor! And fmap is a function:
fmap :: Functor f => (p -> q) -> f p -> f q
so it can be understood as a parcel in the environment functor, where
the environment e has type p -> q. Then pamf is operating in
this environment functor, so $$g\ t = (p \to q) \to t.$$ A g t parcel
is a function that consults an “environment” of type p -> q and
somehow produces a t value. (Haskell folks, who are obsessed with
currying all the things, will write this as the
nearly unreadable g = ((->) (p -> q)).)
We wanted pamf to have this type:
pamf :: Functor g => g (a -> b) -> a -> g b
and since Haskell has decided that g must be the environment functor
with !!g\ x \equiv (p \to q) \to x!!,
this is an abbreviation for:
pamf :: ((p -> q) -> (a -> b)) -> a -> ((p -> q) -> b)
To apply this to fmap, we have to unify the type of pamf's
argument, which is (p -> q) -> (a -> b), and the type of fmap,
which is (p -> q) -> (f p -> f q). Then !!a\equiv f\ p!! and !!b
\equiv f\ q!!, so the result of pamf fmap is
pamf fmap :: Functor f => f p -> ((p -> q) -> f q)
Where did g go? It was specialized to mean the environment functor
((->) (p -> q)), so it's gone.
The funny thing about the type of pamf fmap is that it is exactly
the type of flip fmap, which is fmap with the order of its two
arguments reversed:
(flip fmap) x f ≡ fmap f x
and indeed, by some theorem or other, because the types are identical,
the functions themselves must be identical also! (There are some side
conditions, all of which hold here.) The two functions pamf fmap and
flip fmap are identical. Analogous to the way fmap, restricted
to the environment functor, is identical to (.), pamf, when
similarly restricted, is exactly
flip. You can even see this from its type:
pamf :: ((p -> q) -> (a -> b)) -> a -> ((p -> q) -> b)
Or, cleaning up some superfluous parentheses and inserting some new ones:
pamf :: ((p -> q) -> a -> b) -> (a -> (p -> q) -> b)
And putting !!c = p\to q!!:
pamf :: (c -> a -> b) -> (a -> c -> b)
flip :: ( the same )
Honestly, I would have preferred a type error: “Hey, dummy, fmap has
the wrong type to be an argument to pamf, which wants a functorial
value.” Instead I got “Okay, if you want functions to be a kind of
functor I can do that, also wouldn't it be simpler if the universe was
two-dimensional and there were only three kinds of quarks? Here you
go, no need to thank me!” Maybe someone can explain to me why this is
a useful behavior, and then explain why it is so useful that it should
happen automatically and implicitly instead of being triggered
by some lexical marker like:
newtype Environment e a = Environment (e -> a)
instance Functor (Environment e) where
fmap f (Environment x) = Environment $ \e -> f (x e)
I mean, seriously, suppose you wrote a + b where b was
accidentally a function instead of a number. What if when you did
that, instead of a type error, Haskell would silently shift into some
restricted domain in which it could implicitly interpret b as a
number in some weird way and give you something totally bizarre?
Isn't the whole point of Haskell supposed to be that it doesn't
implicitly convert things that way?
[ Addendum 20181111: Apparently, everyone else hates it too. ]
[Other articles in category /prog/haskell] permanent link
Sat, 08 Sep 2018
Why I never finish my Haskell programs (part 2 of ∞)
Here's something else that often goes wrong when I am writing a Haskell program. It's related to the problem in the previous article but not the same.
Let's say I'm building a module for managing polynomials. Say
Polynomial a is the type of (univariate) polynomials over some
number-like set of coefficients a.
Now clearly this is going to be a functor, so I define the Functor instance, which is totally straightforward:
instance Functor Polynomial where
fmap f (Poly a) = Poly $ map f a
Then I ask myself if it is also going to be an Applicative.
Certainly the pure function makes sense; it just lifts a number to
be a constant polynomial:
pure a = Poly [a]
But what about <*>? This would have the
type:
(Polynomial (a -> b)) -> Polynomial a -> Polynomial b
The first argument there is a polynomial whose coefficients are functions. This is not something we normally deal with. That ought to be the end of the matter.
But instead I pursue it just a little farther. Suppose we did have such an object. What would it mean to apply a functional polynomial and an ordinary polynomial? Do we apply the functions on the left to the coefficients on the right and then collect like terms? Say for example
$$\begin{align} \left((\sqrt\bullet) \cdot x + \left(\frac1\bullet\right) \cdot 1 \right) ⊛ (9x+4) & = \sqrt9 x^2 + \sqrt4 x + \frac19 x + \frac14 \\ & = 3x^2 + \frac{19}{9} x + \frac 14 \end{align}$$
Well, this is kinda interesting. And it would mean that the pure
definition wouldn't be what I said; instead it would lift a number to
a constant function:
pure a = Poly [λ_ -> a]
Then the ⊛ can be understood to be just like polynomial
multiplication, except that coefficients are combined with function
composition instead of with multiplication. The operation is
associative, as one would hope and expect, and even though the ⊛
operation is not commutative, it has a two-sided identity element,
which is Poly [id]. Then I start to wonder if it's useful for anything, and
how ⊛ interacts with ordinary multiplication, and so forth.
This is different from the failure mode of the previous article because in that example I was going down a Haskell rabbit hole of more and more unnecessary programming. This time the programming is all trivial. Instead, I've discovered a new kind of mathematical operation and I abandon the programming entirely and go off chasing a mathematical wild goose.
[ Addendum 20181109: Another one of these. ]
[Other articles in category /prog/haskell] permanent link
Mon, 03 Sep 2018
Why I never finish my Haskell programs (part 1 of ∞)
Whenever I try to program in Haskell, the same thing always goes wrong. Here is an example.
I am writing a module to operate on polynomials. The polynomial !!x^3 - 3x + 1!! is represented as
Poly [1, -3, 0, 1]
[ Addendum 20180904: This is not an error. The !!x^3!! term is last, not first. Much easier that way. Fun fact: two separate people on Reddit both commented that I was a dummy for not doing it the easy way, which is the way I did do it. Fuckin' Reddit, man. ]
I want to add two polynomials. To do this I just add the corresponding coefficients, so it's just
(Poly a) + (Poly b) = Poly $ zipWith (+) a b
Except no, that's wrong, because it stops too soon. When the lists
are different lengths, zipWith discards the extra, so for example it
says that !!(x^2 + x + 1) + (2x + 2) = 3x + 3!!, because it has
discarded the extra !!x^2!! term. But I want it to keep the extra, as
if the short list was extended with enough zeroes. This would be a
correct implementation:
(Poly a) + (Poly b) = Poly $ addup a b where
addup [] b = b
addup a [] = a
addup (a:as) (b:bs) = (a+b):(addup as bs)
and I can write this off the top of my head.
But do I? No, this is where things go off the rails. “I ought to be
able to generalize this,” I say. “I can define a function like
zipWith that is defined over any Monoid, it will combine the
elements pairwise with mplus, and when one of the lists
runs out, it will pretend that that one has some memptys stuck on the
end.” Here I am thinking of something like ffff :: Monoid a => [a] ->
[a] -> [a], and then the (+) above would just be
(Poly a) + (Poly b) = Poly (ffff a b)
as long as there is a suitable Monoid instance for the as and bs.
I could write ffff in two minutes, but instead I spend fifteen
minutes looking around in Hoogle to see if there is already an ffff,
and I find mzip, and waste time being confused by mzip, until I
notice that I was only confused because mzip is for Monad, not
for Monoid, and is not what I wanted at all.
So do I write ffff and get on with my life? No, I'm still not done.
It gets worse. “I ought to be able to generalize this,” I say. “It
makes sense not just for lists, but for any Traversable… Hmm, or
does it?” Then I start thinking about trees and how it should decide
when to recurse and when to give up and use mempty, and then I start
thinking about the Maybe version of it.
Then I open a new file and start writing
mzip :: (Traversable f, Monoid a) => f a -> f a -> f a
mzip as bs = …
And I go father and farther down the rabbit hole and I never come back
to what I was actually working on. Maybe the next step in this
descent into madness is that I start thinking about how to perform
unification of arbitrary algebraic data structures, I abandon mzip
and open a new file for defining class Unifiable…
Actually when I try to program in Haskell there a lot of things that go wrong and this is only one of them, but it seems like this one might be more amenable to a quick fix than some of the other things.
[ Addendum 20180904: A lobste.rs
user
points out that I don't need Monoid, but only Semigroup, since
I don't need mempty. True that! I didn't know there was a
Semigroup class. ]
[ Addendum 20181109: More articles in this series: [2] [3] ]
[Other articles in category /prog/haskell] permanent link
Wed, 08 Aug 2018In my original article, I said:
I was fairly confident I had seen something like this somewhere before, and that it was not original to me.
Jeremy Yallop brought up an example that I had definitely seen before.
In 2008 Conor McBride and Ross Paterson wrote an influential paper, “Idioms: applicative programming with effects” that introduced the idea of an applicative functor, a sort of intermediate point between functors and monads. It has since made its way into standard Haskell and was deemed sufficiently important to be worth breaking backward compatibility.
McBride and Paterson used several notations for operations in an
applicative functor. Their primary notation was !!\iota!! for what is
now known as pure and !!\circledast!! for what has since come to be written
as <*>. But the construction
$$\iota f \circledast is_1 \circledast \ldots \circledast is_n$$
came up so often they wanted a less cluttered notation for it:
We therefore find it convenient, at least within this paper, to write this form using a special notation
$$ [\![ f is_1 \ldots is_n ]\!] $$
The brackets indicate a shift into an idiom where a pure function is applied to a sequence of computations. Our intention is to provide a sufficient indication that effects are present without compromising the readability of the code.
On page 5, they suggested an exercise:
… show how to replace !![\![!! and !!]\!]!! by identifiers
iIandIiwhose computational behaviour delivers the above expansion.
They give a hint, intended to lead the reader to the solution, which
involves a function named iI that does some legerdemain on the front
end and then a singleton type data Ii = Ii that terminates the legerdemain on
the back end. The upshot is that one can write
iI f x y Ii
and have it mean
(pure f) <*> x <*> y
The haskell wiki has details, written by Don Stewart when the McBride-Paterson paper was still in preprint. The wiki goes somewhat further, also defining
data J = J
so that
iI f x y J z Ii
now does a join on the result of f x y before applying the result
to z.
I have certainly read this paper more than once, and I was groping for this example while I was writing the original article, but I couldn't quite put my finger on it. Thank you, M. Yallop!
[ By the way, I am a little bit disappointed that the haskell wiki is not called “Hicki”. ]
[Other articles in category /prog/haskell] permanent link
In the previous article I described a rather odd abuse of the Haskell type system to use a singleton type as a sort of pseudo-keyword, and asked if anyone had seen this done elsewhere.
Joachim Breitner reported having seen this before. Most recently in
LiquidHaskell, which defines a QED singleton
type:
data QED = QED
infixl 2 ***
(***) :: a -> QED -> Proof
_ *** _ = ()
so that they can end every proof with *** QED:
singletonP x
= reverse [x]
==. reverse [] ++ [x]
==. [] ++ [x]
==. [x]
*** QED
This example is from Vazou et al., Functional Pearl: Theorem Proving
for All, p. 3. The authors
explain: “The QED argument serves a purely aesthetic purpose,
allowing us to conclude proofs with *** QED.”.
Or see the examples from the bottom of the LH splash
page, proving the
associative law for ++.
I looked in the rest of the LiquidHaskell distribution but did not find any other uses of the singleton-type trick. I would still be interested to see more examples.
[ Addendum: Another example. ]
[Other articles in category /prog/haskell] permanent link
Is this weird Haskell technique something I made up?
A friend asked me the other day about techniques in Haskell to pretend
to make up keywords. For example, suppose we want something like a
(monadic) while loop, say like this:
while cond act =
cond >>= \b -> if b then act >> while cond act
else return ()
This uses a condition cond (which might be stateful or
exception-throwing or whatever, but which must yield a boolean value)
and an action act (likewise, but its value is ignored) and it
repeates the action over and over until the condition is false.
Now suppose for whatever reason we don't like writing it as while
condition action and we want instead to write while condition do
action or something of that sort. (This is a maximally simple
example, but the point should be clear even though it is silly.) My
first suggestion was somewhat gross:
while c _ a = ...
Now we can write
while condition "do" action
and the "do" will be ignored. Unfortunately we can also write
while condition "wombat" action and you know how programmers are
when you give them enough rope.
But then I had a surprising idea. We can define it this way:
data Do = Do
while c Do a = ...
Now we write
while condition
Do action
and if we omit or misspell the Do we get a compile-time type error
that is not even too obscure.
For a less trivial (but perhaps sillier) example, consider:
data Exception a = OK a | Exception String
instance Monad Exception where ...
data Catch = Catch
data OnSuccess = OnSuccess
data AndThen = AndThen
try computation Catch handler OnSuccess success AndThen continuation =
case computation of OK a -> success >> (OK a) >>= continuation
Exception e -> (handler e) >>= continuation
The idea here is that we want to try a computation, and do one thing
if it succeeds and another if it throws an exception. The point is
not the usefulness of this particular and somewhat contrived exception
handling construct, it's the syntactic sugar of the Catch,
OnSuccess, and AndThen:
try (evaluate some_expression)
Catch (\error -> case error of "Divison by zero" -> ...
... )
OnSuccess ...
AndThen ...
I was fairly confident I had seen something like this somewhere before, and that it was not original to me. But I've asked several Haskell experts and nobody has said it was familar. I thought perhaps I had seen it somewhere in Brent Yorgey's code, but he vehemently denied it.
So my question is, did I make up this technique of using a one-element type as a pretend keyword?
[ Addendum: At least one example of this trick appears in LiquidHaskell. I would be interested to hear about other places it has been used. ]
[ Addendum: Jeremy Yallop points out that a similar trick was hinted at in McBride and Paterson “Idioms: applicative programming with effects” (2008), with which I am familiar, although their trick is both more useful and more complex. So this might have been what I was thinking of. ]
[Other articles in category /prog/haskell] permanent link
Fri, 24 Apr 2015
Easy exhaustive search with the list monad
(Haskell people may want to skip this article about Haskell, because the technique is well-known in the Haskell community.)
Suppose you would like to perform an exhaustive search. Let's say for concreteness that we would like to solve this cryptarithm puzzle:
S E N D
+ M O R E
-----------
M O N E Y
This means that we want to map the letters S, E, N, D, M,
O, R, Y to distinct digits 0 through 9 to produce a five-digit
and two four-digit numerals which, when added in the indicated way,
produce the indicated sum.
(This is not an especially difficult example; my 10-year-old daughter Katara was able to solve it, with some assistance, in about 30 minutes.)
If I were doing this in Perl, I would write up either a recursive descent search or a solution based on a stack or queue of partial solutions which the program would progressively try to expand to a full solution, as per the techniques of chapter 5 of Higher-Order Perl. In Haskell, we can use the list monad to hide all the searching machinery under the surface. First a few utility functions:
import Control.Monad (guard)
digits = [0..9]
to_number = foldl (\a -> \b -> a*10 + b) 0
remove rs ls = foldl remove' ls rs
where remove' ls x = filter (/= x) ls
to_number takes a list of digits like [1,4,3] and produces the
number they represent, 143. remove takes two lists and returns all
the things in the second list that are not in the first list. There
is probably a standard library function for this but I don't remember
what it is. This version is !!O(n^2)!!, but who cares.
Now the solution to the problem is:
-- S E N D
-- + M O R E
-- ---------
-- M O N E Y
solutions = do
s <- remove [0] digits
e <- remove [s] digits
n <- remove [s,e] digits
d <- remove [s,e,n] digits
let send = to_number [s,e,n,d]
m <- remove [0,s,e,n,d] digits
o <- remove [s,e,n,d,m] digits
r <- remove [s,e,n,d,m,o] digits
let more = to_number [m,o,r,e]
y <- remove [s,e,n,d,m,o,r] digits
let money = to_number [m,o,n,e,y]
guard $ send + more == money
return (send, more, money)
Let's look at just the first line of this:
solutions = do
s <- remove [0] digits
…
The do notation is syntactic sugar for
(remove [0] digits) >>= \s -> …
where “…” is the rest of the block. To expand this further, we need
to look at the overloading for >>= which is implemented differently
for every type. The mote on the left of >>= is a list value, and
the definition of >>= for lists is:
concat $ map (\s -> …) (remove [0] digits)
where “…” is the rest of the block.
So the variable s is bound to each of 1,2,3,4,5,6,7,8,9 in turn, the
rest of the block is evaluated for each of these nine possible
bindings of s, and the nine returned lists of solutions are combined
(by concat) into a single list.
The next line is the same:
e <- remove [s] digits
for each of the nine possible values for s, we loop over nine value
for e (this time including 0 but not including whatever we chose for
s) and evaluate the rest of the block. The nine resulting lists of
solutions are concatenated into a single list and returned to the
previous map call.
n <- remove [s,e] digits
d <- remove [s,e,n] digits
This is two more nested loops.
let send = to_number [s,e,n,d]
At this point the value of send is determined, so we compute and
save it so that we don't have to repeatedly compute it each time
through the following 300 loop executions.
m <- remove [0,s,e,n,d] digits
o <- remove [s,e,n,d,m] digits
r <- remove [s,e,n,d,m,o] digits
let more = to_number [m,o,r,e]
Three more nested loops and another computation.
y <- remove [s,e,n,d,m,o,r] digits
let money = to_number [m,o,n,e,y]
Yet another nested loop and a final computation.
guard $ send + more == money
return (send, more, money)
This is the business end. I find guard a little tricky so let's
look at it slowly. There is no binding (<-) in the first line, so
these two lines are composed with >> instead of >>=:
(guard $ send + more == money) >> (return (send, more, money))
which is equivalent to:
(guard $ send + more == money) >>= (\_ -> return (send, more, money))
which means that the values in the list returned by guard will be
discarded before the return is evaluated.
If send + more == money is true, the guard expression yields
[()], a list of one useless item, and then the following >>= loops
over this one useless item, discards it, and returns yields a list
containing the tuple (send, more, money) instead.
But if send + more == money is false, the guard expression yields
[], a list of zero useless items, and then the following >>= loops
over these zero useless items, never runs return at all, and yields
an empty list.
The result is that if we have found a solution at this point, a list
containing it is returned, to be concatenated into the list of all
solutions that is being constructed by the nested concats. But if
the sum adds up wrong, an empty list is returned and concated
instead.
After a few seconds, Haskell generates and tests 1.36 million choices for the eight bindings, and produces the unique solution:
[(9567,1085,10652)]
That is:
S E N D 9 5 6 7
+ M O R E + 1 0 8 5
----------- -----------
M O N E Y 1 0 6 5 2
It would be an interesting and pleasant exercise to try to implement
the same underlying machinery in another language. I tried this in
Perl once, and I found that although it worked perfectly well, between
the lack of the do-notation's syntactic sugar and Perl's clumsy
notation for lambda functions (sub { my ($s) = @_; … } instead of
\s -> …) the result was completely unreadable and therefore
unusable. However, I suspect it would be even worse in Python
because of semantic limitations of that language. I would be
interested to hear about this if anyone tries it.
[ Addendum: Thanks to Tony Finch for pointing out the η-reduction I missed while writing this at 3 AM. ]
[ Addendum: Several people so far have misunderstood the question
about Python in the last paragraph. The question was not to implement
an exhaustive search in Python; I had no doubt that it could be done
in a simple and clean way, as it can in Perl. The question was to
implement the same underlying machinery, including the list monad
and its bind operator, and to find the solution using the list
monad.
[ Peter De Wachter has written in with a Python solution that clearly demonstrates that the problems I was worried about will not arise, at least for this task. I hope to post his solution in the next few days. ]
[ Addendum 20150803: De Wachter's solution and one in Perl ]
[Other articles in category /prog/haskell] permanent link
Thu, 26 Aug 2010
Monad terminology problem
I think one problem (of many) that beginners might have with Haskell
monads is the confusing terminology. The word "monad" can refer to
four related but different things:
- The Monad typeclass itself.
- When a type constructor T of kind ∗ → ∗ is an
instance of Monad we say that T "is a monad".
For example, "Tree is a monad"; "((→) a) is
a monad". This is the only usage that is strictly corrrect.
- Types resulting from the application of monadic type constructors
(#2) are sometimes referred to as monads. For example, "[Integer]
is a monad".
- Individual values of monadic types (#3) are often referred to as
monads. For example, the "All
About Monads" tutorial says "A
list is also a monad".
The most serious problem here is #4, that people refer to individual values of monadic types as "monads". Even when they don't do this, they are hampered by the lack of a good term for it. As I know no good alternative has been proposed. People often say "monadic value" (I think), which is accurate, but something of a mouthful.
One thing I have discovered in my writing life is that the clarity of a confusing document can sometimes be improved merely by replacing a polysyllabic noun phrase with a monosyllable. For example, chapter 3 of Higher-Order Perl discussed the technique of memoizing a function by generating an anonymous replacement for it that maintains a cache and calls the real function on a cache miss. Early drafts were hard to understand, and improved greatly when I replaced the phrase "anonymous replacement function" with "stub". The Perl documentation was significantly improved merely by replacing "associative array" everywhere with "hash" and "funny punctuation character" with "sigil".
I think a monosyllabic replacement for "monadic value" would be a similar boon to discussion of monads, not just for beginners but for everyone else too. The drawback, of introducing yet another jargon term, would in this case be outweighed by the benefits. Jargon can obscure, but sometimes it can clarify.
The replacement word should be euphonious, clear but not overly specific, and not easily confused with similar jargon words. It would probably be good for it to begin with the letter "m". I suggest:
So return takes a value and returns a mote. The >>= function similarly lifts a function on pure values to a function on motes; when the mote is a container one may think of >>= as applying the function to the values in the container. [] is a monad, so lists are motes. The expression on the right-hand side of a var ← expr in a do-block must have mote type; it binds the mote on the right to the name on the left, using the >>= operator.
I have been using this term privately for several months, and it has been a small but noticeable success. Writing and debugging monadic programs is easier because I have a simple name for the motes that the program manipulates, which I can use when I mumble to myself: "What is the type error here? Oh, commit should be returning a mote." And then I insert return in the right place.
I'm don't want to oversell the importance of this invention. But there is clearly a gap in the current terminology, and I think it is well-filled by "mote".
(While this article was in progress I discovered that What a Monad is not uses the nonceword "mobit". I still prefer "mote".)
[Other articles in category /prog/haskell] permanent link
Sun, 03 Jan 2010
A short bibliography of probability monads
Several people helpfully wrote to me to provide references to earlier
work on probability
distribution monads. Here is a summary:
- Material related to Martin Erwig and Steve Kollmansberger's
probability library:
- Probabilistic Functional Programming in Haskell, their 2006 paper
- the package, described in the paper, and specifically its probability distribution monad
- Some
commentary on this library, by someone who doesn't put their name
on their blog.
- Some stuff from Dan Piponi's blog:
- Eric Kidd's blog: "What would a programming language look like if Bayes’ rule were as simple as an if statement?"
I did not imagine that my idea was a new one. I arrived at it by thinking about List as a representation of non-deterministic computation. But if you think of it that way, the natural interpretation is that every list element represents an equally likely outcome, and so annotating the list elements with probabilities is the obvious next step. So the existence of the Erwig library was not a big surprise.
A little more surprising though, were the references in the Erwig paper. Specifically, the idea dates back to at least 1981; Erwig cites a paper that describes the probability monad in a pure-mathematics context.
Nobody responded to my taunting complaint about Haskell's failure to provide support a good monad of sets. It may be that this is because they all agree with me. (For example, the documentation of the Erwig package says "Unfortunately we cannot use a more efficient data structure because the key type must be of class Ord, but the Monad class does not allow constraints for result types.") But a number of years ago I said that the C++ macro processor blows goat dick. I would not have put it so strongly had I not naïvely believed that this was a universally-held opinion. But no, plenty of hapless C++ programmers wrote me indignant messages defending their macro system. So my being right is no guarantee that language partisans will not dispute with me, and the Haskell community's failure to do so in this case reflects well on them, I think.
[Other articles in category /prog/haskell] permanent link
Thu, 31 Dec 2009
A monad for probability and provenance
I don't quite remember how I arrived at this, but it occurred to me
last week that probability distributions form a monad. This is the
first time I've invented a new monad that I hadn't seen before; then I
implemented it and it behaved pretty much the way I thought it would.
So I feel like I've finally arrived, monadwise.
Suppose a monad value represents all the possible outcomes of an event, each with a probability of occurrence. For concreteness, let's suppose all our probability distributions are discrete. Then we might have:
data ProbDist p a = ProbDist [(a,p)] deriving (Eq, Show) unpd (ProbDist ps) = psEach a is an outcome, and each p is the probability of that outcome occurring. For example, biased and unbiased coins:
unbiasedCoin = ProbDist [ ("heads", 0.5),
("tails", 0.5) ];
biasedCoin = ProbDist [ ("heads", 0.6),
("tails", 0.4) ];
Or a couple of simple functions for making dice:
import Data.Ratio
d sides = ProbDist [(i, 1 % sides) | i <- [1 .. sides]]
die = d 6
d n is an n-sided die.
The Functor instance is straightforward:
instance Functor (ProbDist p) where
fmap f (ProbDist pas) = ProbDist $ map (\(a,p) -> (f a, p)) pas
The Monad instance requires return and
>>=. The return function merely takes an event and
turns it into a distribution where that event occurs with probability
1. I find join easier to think about than >>=.
The join function takes a nested distribution, where each
outcome of the outer distribution specifies an inner distribution for
the actual events, and collapses it into a regular, overall
distribution. For example, suppose you put a biased coin and an
unbiased coin in a bag, then pull one out and flip it:
bag :: ProbDist Double (ProbDist Double String)
bag = ProbDist [ (biasedCoin, 0.5),
(unbiasedCoin, 0.5) ]
The join operator collapses this into a single ProbDist
Double String:
ProbDist [("heads",0.3),
("tails",0.2),
("heads",0.25),
("tails",0.25)]
It would be nice if join could combine the duplicate
heads into a single ("heads", 0.55) entry. But that
would force an Eq a constraint on the event type, which isn't
allowed, because (>>=) must work for all data types, not
just for instances of Eq. This is a problem with Haskell,
not with the monad itself. It's the same problem that prevents one
from making a good set monad in Haskell, even though categorially sets
are a perfectly good monad. (The return function constructs
singletons, and the join function is simply set union.)
Maybe in the next language.Perhaps someone else will find the >>= operator easier to understand than join? I don't know. Anyway, it's simple enough to derive once you understand join; here's the code:
instance (Num p) => Monad (ProbDist p) where return a = ProbDist [(a, 1)] (ProbDist pas) >>= f = ProbDist $ do (a, p) <- pas let (ProbDist pbs) = f a (b, q) <- pbs return (b, p*q)So now we can do some straightforward experiments:
liftM2 (+) (d 6) (d 6) ProbDist [(2,1 % 36),(3,1 % 36),(4,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(3,1 % 36),(4,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(4,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(10,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(10,1 % 36),(11,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(10,1 % 36),(11,1 % 36),(12,1 % 36)]This is nasty-looking; we really need to merge the multiple listings of the same event. Here is a function to do that:
agglomerate :: (Num p, Eq b) => (a -> b) -> ProbDist p a -> ProbDist p b
agglomerate f pd = ProbDist $ foldr insert [] (unpd (fmap f pd)) where
insert (k, p) [] = [(k, p)]
insert (k, p) ((k', p'):kps) | k == k' = (k, p+p'):kps
| otherwise = (k', p'):(insert (k,p) kps)
agg :: (Num p, Eq a) => ProbDist p a -> ProbDist p a
agg = agglomerate id
Then agg $ liftM2 (+) (d 6) (d 6) produces:
ProbDist [(12,1 % 36),(11,1 % 18),(10,1 % 12),(9,1 % 9),
(8,5 % 36),(7,1 % 6),(6,5 % 36),(5,1 % 9),
(4,1 % 12),(3,1 % 18),(2,1 % 36)]
Hey, that's correct.There must be a shorter way to write insert. It really bothers me, because it looks look it should be possible to do it as a fold. But I couldn't make it look any better.
You are not limited to calculating probabilities. The monad actually will count things. For example, let us throw three dice and count how many ways there are to throw various numbers of sixes:
eq6 n = if n == 6 then 1 else 0
agg $ liftM3 (\a b c -> eq6 a + eq6 b + eq6 c) die die die
ProbDist [(3,1),(2,15),(1,75),(0,125)]
There is one way to throw three sixes, 15 ways to throw two sixes, 75
ways to throw one six, and 125 ways to throw no sixes. So
ProbDist is a misnomer. It's easy to convert counts to probabilities:
probMap :: (p -> q) -> ProbDist p a -> ProbDist q a probMap f (ProbDist pds) = ProbDist $ (map (\(a,p) -> (a, f p))) pds normalize :: (Fractional p) => ProbDist p a -> ProbDist p a normalize pd@(ProbDist pas) = probMap (/ total) pd where total = sum . (map snd) $ pas normalize $ agg $ probMap toRational $ liftM3 (\a b c -> eq6 a + eq6 b + eq6 c) die die die ProbDist [(3,1 % 216),(2,5 % 72),(1,25 % 72),(0,125 % 216)]I think this is the first time I've gotten to write die die die in a computer program.
The do notation is very nice. Here we calculate the distribution where we roll four dice and discard the smallest:
stat = do
a <- d 6
b <- d 6
c <- d 6
d <- d 6
return (a+b+c+d - minimum [a,b,c,d])
probMap fromRational $ agg stat
ProbDist [(18,1.6203703703703703e-2),
(17,4.1666666666666664e-2), (16,7.253086419753087e-2),
(15,0.10108024691358025), (14,0.12345679012345678),
(13,0.13271604938271606), (12,0.12885802469135801),
(11,0.11419753086419752), (10,9.41358024691358e-2),
(9,7.021604938271606e-2), (8,4.7839506172839504e-2),
(7,2.9320987654320986e-2), (6,1.6203703703703703e-2),
(5,7.716049382716049e-3), (4,3.0864197530864196e-3),
(3,7.716049382716049e-4)]
One thing I was hoping to get didn't work out. I had this idea that
I'd be able to calculate the outcome of a game of craps like this:
dice = liftM2 (+) (d 6) (d 6) point n = do roll <- dice case roll of 7 -> return "lose" _ | roll == n = "win" _ | otherwise = point n craps = do roll <- dice case roll of 2 -> return "lose" 3 -> return "lose" 4 -> point 4 5 -> point 5 6 -> point 6 7 -> return "win" 8 -> point 8 9 -> point 9 10 -> point 10 11 -> return "win" 12 -> return "lose"This doesn't work at all; point is an infinite loop because the first value of dice, namely 2, causes a recursive call. I might be able to do something about this, but I'll have to think about it more.
It also occurred to me that the use of * in the definition of >>= / join could be generalized. A couple of years back I mentioned a paper of Green, Karvounarakis, and Tannen that discusses "provenance semirings". The idea is that each item in a database is annotated with some "provenance" information about why it is there, and you want to calculate the provenance for items in tables that are computed from table joins. My earlier explanation is here.
One special case of provenance information is that the provenances are probabilities that the database information is correct, and then the probabilities are calculated correctly for the joins, by multiplication and addition of probabilities. But in the general case the provenances are opaque symbols, and the multiplication and addition construct regular expressions over these symbols. One could generalize ProbDist similarly, and the ProbDist monad (even more of a misnomer this time) would calculate the provenance automatically. It occurs to me now that there's probably a natural way to view a database table join as a sort of Kleisli composition, but this article has gone on too long already.
Happy new year, everyone.
[ Addendum 20100103: unsurprisingly, this is not a new idea. Several readers wrote in with references to previous discussion of this monad, and related monads. It turns out that the idea goes back at least to 1981. ]
[ Addendum 20220522: The article begins “I don't quite remember how I arrived at this”, but I just remembered how I arrived at it! I was thinking about how List can be interpreted as the monad that captures the idea of nondeterministic computation. A function that yields a list [a, b, c] represents a nondeterministic computation that might yield any of a, b, or c. (This idea goes back at least as far as Moggi's 1989 monads paper.) I was thinking about an extension to this idea: what if the outcomes were annotated with probabilities to indicate how often each was the result. ]
My thanks to Graham Hunter for his donation.
[Other articles in category /prog/haskell] permanent link
Tue, 16 Jun 2009
Haskell logo fail
The Haskell folks have chosen a new logo.


[Other articles in category /prog/haskell] permanent link
Thu, 03 Jan 2008
Note on point-free programming style
This old
comp.lang.functional article by Albert Y. C. Lai, makes
the point that Unix shell pipeline programming is done in an
essentially "point-free" style, using the shell example:
grep '^X-Spam-Level' | sort | uniq | wc -l
and the analogous Haskell code:
length . nub . sort . filter (isPrefixOf "X-Spam-Level")
Neither one explicitly mentions its argument, which is why this is
"point-free". In "point-free" programming, instead of defining a
function in terms of its effect on its arguments, one defines it by
composing the component functions themselves, directly, with
higher-order operators. For example, instead of:
foo x y = 2 * x + yone has, in point-free style:
foo = (+) . (2 *)where (2 *) is the function that doubles its argument, and (+) is the (curried) addition function. The two definitions of foo are entirely equivalent.
As the two examples should make clear, point-free style is sometimes natural, and sometimes not, and the example chosen by M. Lai was carefully selected to bias the argument in favor of point-free style.
Often, after writing a function in pointful style, I get the computer to convert it automatically to point-free style, just to see what it looks like. This is usually educational, and sometimes I use the computed point-free definition instead. As I get better at understanding point-free programming style in Haskell, I am more and more likely to write certain functions point-free in the first place. For example, I recently wrote:
soln = int 1 (srt (add one (neg (sqr soln))))
and then scratched my head, erased it, and replaced it with the equivalent:
soln = int 1 ((srt . (add one) . neg . sqr) soln)
I could have factored out the int 1 too:
soln = (int 1 . srt . add one . neg . sqr) soln
I could even have removed soln from the right-hand side:
soln = fix (int 1 . srt . add one . neg . sqr)
but I am not yet a perfect sage.Sometimes I opt for an intermediate form, one in which some of the arguments are explicit and some are implicit. For example, as an exercise I wrote a function numOccurrences which takes a value and a list and counts the number of times the value occurs in the list. A straightforward and conventional implementation is:
numOccurrences x [] = 0
numOccurrences x (y:ys) =
if (x == y) then 1 + rest
else rest
where rest = numOccurrences x ys
but the partially point-free version I wrote was much better:
numOccurrences x = length . filter (== x)
Once you see this, it's easy to go back to a fully pointful
version:
numOccurrences x y = length (filter (== x) y)
Or you can go the other way, to a point-free version:
numOccurrences = (length .) . filter . (==)
which I find confusing.Anyway, the point of this note is not to argue that the point-free style is better or worse than the pointful style. Sometimes I use the one, and sometimes the other. I just want to point out that the argument made by M. Lai is deceptive, because of the choice of examples. As an equally biased counterexample, consider:
bar x = x*x + 2*x + 1
which the automatic converter informs me can be written in point-free
style as:
bar = (1 +) . ap ((+) . join (*)) (2 *)
Perusal of this example will reveal much to the attentive reader,
including the definitions of join and ap. But I
don't think many people would argue that it is an improvement on the
original. (Maybe I'm wrong, and people would argue that it was an
improvement. I won't know for sure until I have more experience.)For some sort of balance, here is another example where I think the point-free version is at least as good as the pointful version: a recent comment on Reddit suggested a >>> operator that composes functions just like the . operator, but in the other order, so that:
f >>> g = g . f
or, if you prefer:
(>>>) f g x = g(f(x))
The point-free definition of >>> is:
(>>>) = flip (.)
where the flip operator takes a function of two arguments and
makes a new function that does the same thing, but with the arguments
in the opposite order. Whatever your feelings about point-free style,
it is undeniable that the point-free definition makes perfectly clear
that >>> is nothing but . with its arguments in
reverse order.
[Other articles in category /prog/haskell] permanent link



