Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 21 May 2018
More about disabling standard I/O buffering
In yesterday's article I described a simple and useful feature that could have been added to the standard I/O library, to allow an environment variable to override the default buffering behavior. This would allow the invoker of a program to request that the program change its buffering behavior even if the program itself didn't provide an option specifically for doing that.
Simon Tatham directed me to the GNU Coreutils stdbuf
command
which does something of this sort. It is rather like the
pseudo-tty-pipe program I described, but instead of using the
pseudo-tty hack I suggested, it works by forcing the child program to
dynamically
load
a custom replacement for
stdio.
There appears to be a very similar command in FreeBSD.
[ Addendum 20240820: This description is not accurate; see below. ]
Roderick Schertler pointed out that Dan Bernstein wrote a utility
program, pty, in 1990, atop which my pseudo-tty-pipe program could
easily be built; or maybe its ptybandage utility is exactly what I
wanted. Jonathan de Boyne Pollard has a page explaining it in
detail, and related
packages.
A later version of pty is still
available.
Here's M. Bernstein's blurb about it:
ptygetis a universal pseudo-terminal interface. It is designed to be used by any program that needs a pty.
ptygetcan also serve as a wrapper to improve the behavior of existing programs. For example,ptybandage telnetis liketelnetbut can be put into a pipeline.nobuf grepis likegrepbut won't block-buffer if it's redirected.Previous pty-allocating programs —
rlogind,telnetd,sshd,xterm,screen,emacs,expect, etc. — have caused dozens of security problems. There are two fundamental reasons for this. First, these programs are installed setuid root so that they can allocate ptys; this turns every little bug in hundreds of thousands of lines of code into a potential security hole. Second, these programs are not careful enough to protect the pty from access by other users.
ptygetsolves both of these problems. All the privileged code is in one tiny program. This program guarantees that one user can't touch another user's pty.
ptygetis a complete rewrite ofpty4.0, my previous pty-allocating package.pty4.0's session management features have been split off into a separate package,sess.
Leonardo Taccari informed me that NetBSD's stdio actually
has the environment variable feature I was asking for! Christos
Zoulas suggested adding stdbuf similar to the GNU and FreeBSD
implementations, but the NetBSD people observed, as I did, that it
would be simpler to just control stdio directly with an environment
variable, and did it. Here's the relevant part of the NetBSD setbuf(3) man
page:
The default buffer settings can be overwritten per descriptor (
STDBUFn) where n is the numeric value of the file descriptor represented by the stream, or for all descriptors (STDBUF). The environment variable value is a letter followed by an optional numeric value indicating the size of the buffer. Valid sizes range from 0B to 1MB. Valid letters are:
Uunbuffered
Lline buffered
Ffully buffered
Here's the discussion from the NetBSD tech-userlevel mailing
list.
The actual patch looks almost exactly the way I imagined it would.
Finally, Mariusz Ceier pointed out that there is an ancient bug report in
glibc
suggesting essentially the same environment variable mechanism that I
suggested and that was adopted in NetBSD. The suggestion was firmly
and summarily rejected. (“Hell, no … this is a terrible idea.”)
Interesting wrinkle: the bug report was submitted by Pádraig Brady,
who subsequently wrote the stdbuf command I described above.
Thank you, Gentle Readers!
Addenda
20240820
nabijaczleweli has pointed out that my explanation of the GNU stdbuf
command above is not accurate. I said "it works by forcing the child
program to dynamically load a custom replacement for stdio". It's
less heavyweight than that. Instead, it arranges to load
a dynamic library
that runs before the rest of the program starts, examines the
environment, and simply calls setvbuf as needed on the three
standard streams.
[Other articles in category /Unix] permanent link
Sun, 20 May 2018
Proposal for turning off standard I/O buffering
Some Unix commands, such as grep, will have a command-line flag to
say that you want to turn off the buffering that is normally done in
the standard I/O library. Some just try to guess what you probably
want. Every command is a little different and if the command you want
doesn't have the flag you need, you are basically out of luck.
Maybe I should explain the putative use case here. You have some
command (or pipeline) X that will produce dribbles of data at
uncertain intervals. If you run it at the terminal, you see each
dribble timely, as it appears. But if you put X into a pipeline,
say with
X | tee ...
or
X | grep ...
then the dribbles are buffered and only come out of X when an entire
block is ready to be written, and the dribbles could be very old
before the downstream part of the pipeline, including yourself, sees
them. Because this is happening in user space inside of X, there is
not a damn thing anyone farther downstream can do about it. The only
escape is if X has some mode in which it turns off standard I/O
buffering. Since standard I/O buffering is on by default, there is a
good chance that the author of X did not think to affirmatively add
this feature.
Note that adding the --unbuffered flag to the downstream grep does
not solve the problem; grep will produce its own output timely, but
it's still getting its input from X after a long delay.
One could imagine a program which would interpose a pseudo-tty, and
make X think it is writing to a terminal, and then the standard I/O
library would stay in line-buffered mode by default. Instead of
running
X | tee some-file | ...
or whatever, one would do
pseudo-tty-pipe -c X | tee some-file | ...
which allocates a pseudo-tty device, attaches standard output to it,
and forks. The child runs X, which dribbles timely into the
pseudo-tty while the parent runs a read loop to remove dribbles from
the master end of the TTY and copy them timely into the pipe. This
would work. Although tee itself also has no --unbuffered flag
so you might even have to:
pseudo-tty-pipe -c X | pseudo-tty-pipe -c 'tee some-file' | ...
I don't think such a program exists, and anyway, this is all
ridiculous, a ridiculous abuse of the standard I/O library's buffering
behavior: we want line buffering, the library will only give it to us
if the process is attached to a TTY device, so we fake up a TTY just
to fool stdio into giving us what we want. And why? Simply because
stdio has no way to explicitly say what we want.
But it could easily expose this behavior as a controllable feature. Currently there is a branch in the library that says how to set up a buffering mode when a stream is opened for the first time:
if the stream is for writing, and is attached to descriptor 2, it should be unbuffered; otherwise …
if the stream is for writing, and connects descriptor 1 to a terminal device, it should be line-buffered; otherwise …
if the moon is waxing …
…
otherwise, the stream should be block-buffered
To this, I propose a simple change, to be inserted right at the beginning:
If the environment variable
STDIO_BUFis set to"line", streams default to line buffering. If it's set to"none", streams default to no buffering. If it's set to"block", streams default to block buffered. If it's anything else, or unset, it is ignored.
Now instead of this:
pseudo-tty-pipe --from X | tee some-file | ...
you write this:
STDIO_BUF=line X | tee some-file | ...
Problem solved.
Or maybe you would like to do this:
export STDIO_BUF=line
which then it affects every program in every pipeline in the rest of the session:
X | tee some-file | ...
Control is global if you want it, and per-process if you want it.
This feature would cost around 20 lines of C code in the standard I/O
library and would impose only an insigificant run-time cost. It would
effectively add an --unbuffered flag to every program in the
universe, retroactively, and the flag would be the same for every
program. You would not have to remember that in mysql the magic
option is -n and that in GNU grep it is --line-buffered and that
for jq is is --unbuffered and that Python scripts can be
unbuffered by supplying the -u flag and that in tee you are just
SOL, etc. Setting STDIO_BUF=line would Just Work.
Programming languages would all get this for free also. Python
already has PYTHONUNBUFFERED but in other languages
you have to do something or other; in Perl you use some
horrible Perl-4-ism like
{ my $ofh = select OUTPUT; $|++; select $ofh }
This proposal would fix every programming language everywhere. The Perl code would become:
$ENV{STDIO_BUF} = 'line';
and every other language would be similarly simple:
/* In C */
putenv("STDIO_BUF=line");
[ Addendum 20180521: Mariusz Ceier corrects me, pointing out that this will not work for the process’ own standard streams, as they are pre-opened before the process gets a chance to set the variable. ]
It's easy to think of elaborations on this: STDIO_BUF=1:line might
mean that only standard output gets line-buffering by default,
everything else is up to the library.
This is an easy thing to do. I have wanted this for twenty years. How is it possible that it hasn't been in the GNU/Linux standard library for that long?
[ Addendum 20180521: it turns out there is quite a lot to say about the state of the art here. In particular, NetBSD has the feature very much as I described it. ]
[Other articles in category /Unix] permanent link
Mon, 07 May 2018
Katara constructs finite projective planes
This weekend I got a very exciting text message from Katara:
I have a math question for you
Oh boy! I hope it's one I can answer.
Okay
there's this game called spot it where you have cards with 8 symbols on them like soand the goal is to find the one matching symbol on your card and the one in the middle
how is it possible that given any pair of cards, there is exactly one matching symbol
Well, whatever my failings as a dad, this is one problem I can solve. I went a little of overboard in my reply:
You need a particular kind of structure called a projective plane.
They only exist for certain numbers of symbols
A simpler example has 7 cards with 3 symbols each.
One thing that's cool about it is that the symbols and the cards are "dual": say you give each round card a name. Then make up a new deck of square cards. There's one square card for each symbol. So there's a square"Ladybug" card. The Ladybug card has on it the names of the round cards that have the Ladybug. Now you can play Spot with the square cards instead of the round ones: each two square cards have exactly one name in common.
In a geometric plane any two points lie on exactly one common line and any two lines intersect in exactly one common point. This is a sort of finite model of that, with cards playing the role of lines and symbols playing the role of points. Or vice versa, it doesn't matter.
More than you wanted to know 😂
ah thank you, I'm pretty sure I understand, sorry for not responding, my phone was charging
I still couldn't shut up about the finite projective planes:
No problem! No response necessary.
It is known that all finite projective planes have n²+n+1 points for some n. So I guess the Spot deck has either 31, 57, or 73 cards and the same number of symbols. Is 57 correct?
Must be 57 because I see from your picture that each card has 8 symbols.
Katara was very patient:
I guess, I would like to talk about this some more when i get home if that's okay
Any time.
Anyway this evening I cut up some index cards, and found a bunch of stickers in a drawer, and made Katara a projective plane of order 3. This has 13 cards, each with 4 different stickers, and again, every two cards share exactly one sticker. She was very pleased and wanted to know how to make them herself.
Each set of cards has an order, which is a non-negative integer. Then there must be !!n^2 + n + 1!! cards, each with !!n+1!! stickers or symbols. When !!n!! is a prime power, you can use field theory to construct a set of cards from the structure of the (unique) field of order !!n!!.
Fields to projective planes
Order 2
I'll describe the procedure using the plane of order !!n=2!!, which is unusually simple. There will be !!2^2+2+1 = 7!! cards, each with !!3!! of the !!7!! symbols.
Here is the finite field of order 2, called !!GF(2)!!:
|
|
The stickers correspond to ordered triples of elements of !!GF(2)!!, except that !!\langle 0,0,0\rangle!! is always omitted. So they are:
$$\require{cancel}\begin{array}{cc} \cancel{\langle 0,0,0\rangle} & \langle 1,0,0\rangle \\ \langle 0,0,1\rangle & \langle 1,0,1\rangle \\ \langle 0,1,0\rangle & \langle 1,1,0\rangle \\ \langle 0,1,1\rangle & \langle 1,1,1\rangle \\ \end{array} $$
Of course, you probably do not want to use these symbols exactly. You might decide that !!\langle 1,0,0\rangle!! is a sticker with a picture of a fish, and !!\langle 0,1,0\rangle!! is a sticker with a ladybug.
Each card will have !!n+1 = 3!! stickers. To generate a card, pick any two stickers that haven't appeared together before and put them on the card. Say these stickers correspond to the triples !!\langle a,b,c\rangle!! and !!\langle x,y,z\rangle!!. To find the triple for the third sticker on the card, just add the first two triples componentwise, obtaining !!\langle a+x,b+y,c+z\rangle!!. Remember that the addition must be done according to the !!GF(2)!! addition table above! So for example if a card has !!\langle 1,0,1\rangle!! and !!\langle 0,1,1\rangle!!, its third triple will be
$$\begin{align} \langle 1,0,1 \rangle + \langle 0,1,1 \rangle & = \\ \langle 1+0,0+1,1+1 \rangle & = \\ \langle 1,1,0 \rangle \end{align} $$
Observe that it doesn't matter which two triples you add; you always get the third one!
Okay, well, that was simple.
Larger order
After Katara did the order 2 case, which has 7 cards, each with 3 of the 7 kinds of stickers, she was ready to move on to something bigger. I had already done the order 3 deck so she decided to do order 4. This has !!4^2+4+1 = 21!! cards each with 5 of the 21 kinds of stickers. The arithmetic is more complicated too; it's !!GF(2^2)!! instead of !!GF(2)!!:
|
|
When the order !!n!! is larger than 2, there is another wrinkle. There are !!4^3 = 64!! possible triples, and we are throwing away !!\langle 0,0,0\rangle!! as usual, so we have 63. But we need !!4^2+4+1 = 21!!, not !!63!!.
Each sticker is represented not by one triple, but by three. The triples !!\langle a,b,c\rangle, \langle 2a,2b,2c\rangle,!! and !!\langle 3a,3b,3c\rangle!! must be understood to represent the same sticker, all the multiplications being done according to the table above. Then each group of three triples corresponds to a sticker, and we have 21 as we wanted.
Each triple must have a leftmost non-zero entry, and in each group of three similar triples, there will be one where this leftmost non-zero entry is a !!1!!; we will take this as the canonical representative of its class, and it can wear a costume or a disguise that makes it appear to begin with a !!2!! or a !!3!!.
We might assign stickers to triples like this:
$$ \begin{array}{rl} \cancel{\langle 0,0,0\rangle} & \\ \langle 0,0,1 \rangle & \text{apple} \\ \hline \langle 0,1,0 \rangle & \text{bicycle} \\ \langle 0,1,1 \rangle & \text{carrot} \\ \langle 0,1,2 \rangle & \text{dice} \\ \langle 0,1,3 \rangle & \text{elephant} \\ \hline \langle 1,0,0 \rangle & \text{frog} \\ \langle 1,0,1 \rangle & \text{goat} \\ \langle 1,0,2 \rangle & \text{hat} \\ \langle 1,0,3 \rangle & \text{igloo} \\ \langle 1,1,0 \rangle & \text{jellyfish} \\ \langle 1,1,1 \rangle & \text{kite} \\ \langle 1,1,2 \rangle & \text{ladybug} \\ \langle 1,1,3 \rangle & \text{mermaid} \\ \langle 1,2,0 \rangle & \text{nose} \\ \langle 1,2,1 \rangle & \text{octopus} \\ \langle 1,2,2 \rangle & \text{piano} \\ \langle 1,2,3 \rangle & \text{queen} \\ \langle 1,3,0 \rangle & \text{rainbow} \\ \langle 1,3,1 \rangle & \text{shoe} \\ \langle 1,3,2 \rangle & \text{trombone} \\ \langle 1,3,3 \rangle & \text{umbrella} \\ \end{array} $$
We can stop there, because everything after !!\langle 1,3,3 \rangle!! begins with a !!2!! or a !!3!!, and so is some other triple in disguise. For example what sticker goes with !!\langle 0,2,3 \rangle!!? That's actually !!\langle 0,1,2 \rangle!! in disguise, it's !!2·\langle 0,1,2 \rangle!!, which is “dice”. Okay, how about !!\langle 3,3,1 \rangle!!? That's the same as !!3\cdot\langle 1,1,2 \rangle!!, which is “ladybug”. There are !!21!!, as we wanted. Note that the !!21!! naturally breaks down as !!1+4+4^2!!, depending on how many zeroes are at the beginning; that's where that comes from.
Now, just like before, to make a card, we pick two triples that have not yet gone together, say !!\langle 0,0,1 \rangle!! and !!\langle 0,1,0 \rangle!!. We start adding these together as before, obtaining !!\langle 0,1,1 \rangle!!. But we must also add together the disguised versions of these triples, !!\langle 0,0,2 \rangle!! and !!\langle 0,0,3 \rangle!! for the first, and !!\langle 0,2,0 \rangle!! and !! \langle 0,3,0 \rangle!! for the second. This gets us two additional sums, !!\langle 0,2,3 \rangle!!, which is !!\langle 0,1,2 \rangle!! in disguise, and !!\langle 0,3,2 \rangle!!, which is !!\langle 0,1,3 \rangle!! in disguise.
It might seem like it also gets us !!\langle 0,2,2 \rangle!! and !!\langle 0,3,3 \rangle!!, but these are just !!\langle 0,1,1 \rangle!! again, in disguise. Since there are three disguises for !!\langle 0,0,1 \rangle!! and three for !!\langle 0,1,0 \rangle!!, we have nine possible sums, but it turns out that the nine sums are only three different triples, each in three different disguises. So our nine sums get us three additional triples, and, including the two we started with, that makes five, which is exactly how many we need for the first card. The first card gets the stickers for triples !!\langle 0,0,1 \rangle, \langle 0,1,0 \rangle \langle 0,1,1 \rangle \langle 0,1,2 \rangle,!! and !!\langle 0,1,3 \rangle,!! which are apple, bicycle, carrot, dice, and elephant.
That was anticlimactic. Let's do one more. We don't have a card yet with ladybug and trombone. These are !!\langle 1,1,2 \rangle!! and !!\langle 1,3,2 \rangle!!, and we must add them together, and also the disguised versions:
$$\begin{array}{c|ccc} & \langle 1,1,2 \rangle & \langle 2,2,3 \rangle & \langle 3,3,1 \rangle \\ \hline \langle 1,3,2 \rangle & \langle 0,2,0 \rangle & \langle 3,1,1 \rangle & \langle 2,0,3 \rangle \\ \langle 2,1,3 \rangle & \langle 3,0,1 \rangle & \langle 0,3,0 \rangle & \langle 1,2,2 \rangle \\ \langle 3,2,1 \rangle & \langle 2,3,3 \rangle & \langle 1,0,2 \rangle & \langle 0,1,0 \rangle \\ \end{array}$$
These nine results do indeed pick out three triples in three disguises each, and it's easy to select the three of these that are canonical: they have a 1 in the leftmost nonzero position, so the three sums are !!\langle 0,1,0 \rangle,!! !!\langle 1,0,2 \rangle,!! and !!\langle 1,2,2 \rangle!!, which are bicycle, hat, and piano. So the one card that has a ladybug and a trombone also has a bicycle, a hat, and a piano, which should not seem obvious. Note that this card does have the required single overlap with the other card we constructed: both have bicycles.
Well, that was fun. Katara did hers with colored dots instead of stickers:
The ABCDE card is in the upper left; the bicycle-hat-ladybug-piano-trombone one is the second row from the bottom, second column from the left. The colors look bad in this picture; the light is too yellow and so all the blues and purples look black.
After I took this picture, we checked these cards and found a couple of calculation errors, which we corrected. A correct set of cards is:
$$ \begin{array}{ccc} \text{abcde} & \text{bhlpt} & \text{dgmpr} \\ \text{afghi} & \text{bimqu} & \text{dhjou} \\ \text{ajklm} & \text{cfkpu} & \text{diknt} \\ \text{anopq} & \text{cgjqt} & \text{efmot} \\ \text{arstu} & \text{chmns} & \text{eglnu} \\ \text{bfjnr} & \text{cilor} & \text{ehkqr} \\ \text{bgkos} & \text{dflqs} & \text{eijps} \\ \end{array} $$
Fun facts about finite projective planes:
This construction always turns a finite field of order !!n!! into a finite projective plane of order !!n!!.
A finite field of order !!n!! exists exactly when !!n!! is a prime power and then there is exactly one finite field. So this construction gives us finite projective planes of orders !!1,2,3,4,5,7,8,9,11,13,16!!, but not of orders !!6,10,12,14,15!!. Do finite projective planes of those latter orders exist?
- 6: No, proven by R.C. Bose in 1938
- 10: No, proven by Clement Lam in 1991 with a very large computer search
- 12, 15: Nobody knows.
- 14: No, by the Bruck-Ryser theorem (1949).
Is this method the only way to construct a finite projective plane? Yes, when !!n<9!!. But there are four non-isomorphic projective planes of order !!9!!, and this only constructs one of them.
What about for !!n≥11!!? Nobody knows.
[Other articles in category /math] permanent link
Sun, 06 May 2018Last month I regretted making only 22 posts but I promised:
April will be better; I'm on pace to break the previous volume record, and I've also been doing a good job of promoting better posts to the major leagues.
I blew it! I tied the previous volume record. But I also think I did do a decent job promoting the better posts. Usually I look over the previous month's posts and pick out two or three that seem to be of more interest than the others. Not this month! They are all shit, except the one ghostwritten by Anette Gordon-Reed. If this keeps up, I will stop doing these monthly roundup posts.
- Hotel classification jargon
- I'm missing !!Con this year
- Camptown
- Sigils in Perl and PILOT
- Birthday greetings from my stalker
- Yuca frita
- Intriguing trending hashtags
- On the preferred numbers of the One God
- Chitin
- History of the Unicode “byte order mark”; addendum
- 'Abd al-Karim
- One of everything in the universe
- Ruby improvement
- My hero Kurt Schwitters
- The hardest question ever asked on Math StackExchange
- Friday the 13th
- September 12 activities
- The National Day of Catalonia
- Melilla
- Beware…
- The joy of Dada [1] [2]
- FGSFDS
- Why we itch
- Why we have little hairs on our arms
- Minoxidil
- Ulcers
- Things English fails to distinguish
- Today I learned… [2] [3] [4] [5]
- Xiangtan
- Mealworm frass
- Free-range organically fed flies
- Not the worst job in the world
- Bug squeamishness
- Gordon-Reed on Andrew Johnson
- People suck
- Plagiarism, plagiarism, baked beans, and plagiarism
- I learned a new word!
- Phagocytization
- Lipogrammatic Math Stackexchange posts
- Hegel and the Seven Planets
- Philosophical duh
- Headline of the Month
- Why do people hate?
- Software sucks
- Comment of the day
[Other articles in category /meta/shitpost] permanent link
Wed, 02 May 2018
Addenda to recent articles 201804
Andrew Rodland and Adam Vartanian explained ramp metering. Here's M. Rodland's explanation:
ramp metering is the practice of installing signals on freeway onramps that only allow one car every few seconds, so that cars enter the freeway at evenly-spaced intervals instead of in bunches and don't cause as many problems merging.
He added that it was widely used in California. McCain is headquartered in California, and mentions frequently on their web site that their equipment conforms to Caltrans standards.
M. Vartanian and Richard Soderberg also suggested an explanation for why the traffic control system might also control sprinklers and pumps. M. Soderberg says:
DOTs in California and presumably elsewhere often have a need for erosion control on the steep inclines of earth surrounding their highway ramps. So any time you see a 45-degree incline covered in greenery, chances are it has a sprinkler system attached and carefully maintained by the DOT. Those same sprinklers are often within a few feet of the ramp's metering lights…
That makes perfect sense! I had been imagining fire sprinklers, and then I was puzzled: why would you need fire sprinklers at an intersection?
Several readers suggested explanations for why soldier fly larvae are more expensive than pork chops. I rejected several explanations:
Hogs are kept in poor and inhumane conditions (often true, but their accommodations must still be much more expensive than the flies’)
Hog farmers are exempted from paying for the negative externalities of their occupation such as environmental degradation and antibiotic resistance (often true, but the fly farmers cannot be paying that much to offset externalities)
Slaughterhouse waste and rotten fruit are more expensive than the corn and soy on which hogs are fed (I think slaughterhouse waste and waste fruit are available essentially free to anyone who wants to haul them away)
The drying process is difficult and expensive (but the listed price for undried maggots is twice as high)
But I find Marcel Fourné's suggestion much more plausible: the pork price is artificially depressed by enormous government subsidies.
I started looking into the numbers on this, and got completely sidetracked on something only peripherally related:
According to the USDA Census of Agriculture for 2012, in 2012 U.S. farms reported an inventory of 66 million pigs and hogs, and sales of 193 million pigs and hogs. (Table 20, page 22.)
When I first saw this, I thought I must be misunderstanding the numbers. I said to myself:
!!\frac{193}{66}\approx 3!!, so the inventory must be turning over three times a year. But that means that the average hog goes to market when it is four months old. That can't be right.
Of course it isn't right, it isn't even close, it's complete nonsense. I wrote up my mistake but did not publish it, and while I was doing that I forgot to finish working on the subsidy numbers.
James Kushner directed my attention to the MUTCD news feed and in particular this amusing item:
the FHWA issued Official Interpretation 4(09)-64 to clarify that the flash rate for traffic control signals and beacons is a single repetitive flash rate of approximately once per second, and that a combination of faster and slower flash rates that result in 50 to 60 flashes per minute is not compliant…
James writes:
I imagined a beacon that flashed once every ten seconds; after five such iterations, there was one iteration where the beacon would flash fifty times in a second. "But it flashes 55 times every minute, so, you know, it, uh, conforms to the standard..."
But the Official Interpretation also says
You asked whether the FHWA would be willing to consider experimentation with alternative flash rates for warning beacons. Any requests for experimentation would be evaluated on their merits and would be addressed separately from this official ruling.
so there is still hope for James’ scheme.
Two readers suggested musical jokes. Jordan Fultz asks:
Q: How does Lady Gaga like her steak?
A: Raw, raw, raw-raw-raw!(This is Bad Romance)
And betaveros asks:
Q. What kind of overalls does Mario wear?
A. Denim denim denim.(This is the Super Mario Bros. Underworld Theme)
I feel like we might be hitting the bottom of the barrel.
Thanks to all readers who wrote to me, and also to all readers who did not write to me.
[Other articles in category /addenda] permanent link
Tue, 01 May 2018
What's in those mysterious cabinets?
Last Monday some folks were working on this thing on Walnut Street. I didn't remember having seen the inside of one before, so I took some pictures of it to look at later.
Thanks to the Wonders of the Internet, it didn't take long to figure out what it is for. It is a controller for the traffic lights at the intersection.
In particular, the top module in the right-hand picture is a Model 170 ATC HC11 Controller manufactured by McCain Inc, a thirty-year old manufacturer of traffic control devices. The controller runs software developed and supported by McCain, and the cabinet is also made by McCain.
The descriptions of the controllers are written in a dense traffic control jargon that I find fascinating but opaque. For example, the 170 controller's product description reads:
The McCain 170E, 170E HC11, and 170 ATC HC11 controllers’ primary design function is to operate eight-phase dual ring intersections. Based on the software control package utilized, the 170’s control applications can expand to include: ramp metering, variable message signs, sprinklers, pumps, and changeable lane control.
I think I understand what variable message signs are, and I can guess at changeable lane control, but what are the sprinklers and pumps for? What is ramp metering?
[ Addendum 20180502: readers explain ]
The eight-phase dual ring intersection, which I had never heard of before, is an important topic in the traffic control world. I gather that it is a four-way intersection with a four-way traffic light that also has a left-turn-only green arrow portion. The eight “phases” refer to different traffic paths through the intersections that must be separately controlled: even numbers for the four paths through the intersection, and odd numbers 1,3,5,7 for the left-turn-only paths that do not pass through. Some phases conflict; for example phase 5 (left-turning in some direction, say from south to east), conflicts with phase 6 (through-passing heading in the opposite direction) but not with phase 1 (left-turning from north to west).

There's plenty of detailed information about this available. For example, the U.S. Federal Highway Administration publishes their Traffic Signal Timing Manual. (Published in 2008, it has since been superseded.) Unfortunately, this seems to be too advanced for me! Section 4.2.1 (“Definitions and Terminology”) is the first place in the document that mentions the dual-ring layout, and it does so without explanation — apparently this is so elementary that anyone reading the Traffic Signal Timing Manual will already be familiar with it:
Over the years, the description of the “individual movements” of the dual-ring 8-movement controller as “phases” has blurred into common communicated terminology of “movement number” being synonymous as “phase number”.
But these helpful notes explain in more detail: a “ring” is “a sequence of phases that are not compatible and that must time sequentially”.
Then we measure the demand for each phase, and there is an interesting and complex design problem: how long should each phase last to optimize traffic flow through the intersection for safety and efficiency? See chapter 3a for more details of how this is done.
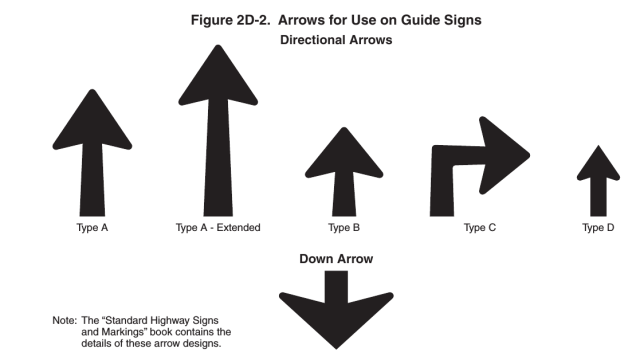
I love when I discover there is an entire technical domain that I never even suspected existed. If you like this kind of thing, you may enjoy geeking out over the Manual of Uniform Traffic Control Devices, which explains what traffic signs should look like and what each one means. Have you ever noticed that the green guide signs on the highway have up-pointing and down-pointing arrows that are totally different shapes?
That's because they have different meanings: the up-pointing arrows mean “go this way” and the down-pointing arrows mean “use this lane”. The MUTCD says what the arrows should look like, how big they should be, and when each one should be used.
The MUTCD is the source of one of my favorite quotations:
Regulatory and warning signs should be used conservatively because these signs, if used to excess, tend to lose their effectiveness.
Words to live by! Programmers in particular should keep this in mind when designing error messages. You could spend your life studying this 864-page manual, and I think some people do.
Related geekery: Geometric highway design: how sharply can the Interstate curve and still be safe, and how much do the curves need to be banked? How do you design an interchange between two major highways? How about a highway exit?
Here's a highway off-ramp, exit 346A on Pennsylvania I-76 West:
Did you know that the long pointy triangle thing is called a “gore”?
What happens if you can't make up your mind whether to stay on the highway or take the exit, you drive over the gore, and then smack into the thing beyond it where the road divides? Well, you might survive, because there is a thing there that is designed to crush when you hit it. It might be a QuadGuard Elite Crash Cushion System, manufactured by Energy Absorption Systems, Inc..
It's such a big world out there, so much to know.
[Other articles in category /tech] permanent link