Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 31 Jan 2006
Petard
A petard is a Renaissance-era bomb, basically a big firecracker: a box
or small barrel of gunpowder with a fuse attached. Those hissing
black exploding spheres that you see in Daffy Duck cartoons are
petards. Outside of cartoons, you are most likely to encounter the
petard in the phrase "hoist with his own petard", which is from
Hamlet. Rosencrantz and Guildenstern are being sent to
England with the warrant for Hamlet's death; Hamlet alters the warrant
to contain R&G's names instead of his own. "Hoist", of course,
means "raised", and Hamlet is saying that it is amusing to see someone
screw up his own petard and blow himself sky-high with it.
This morning I read in On Food in Cooking that there's a kind of fried choux pastry called pets de soeurs ("nuns' farts") because they're so light and delicate. That brought to mind Le Pétomane, the world-famous theatrical fartmaster. Then there was a link on reddit titled "Xmas Petard (cool gif video!)" which got me thinking about petards, and it occurred to me that "petard" was probably akin to pets, because it makes a bang like a fart. And hey, I was right; how delightful.
Another fart-related word is "partridge", so named because its call sounds like a fart.
[ Update 20260202: Some corrections ]
[Other articles in category /lang/etym] permanent link
Mon, 30 Jan 2006
Google query roundup
Now that I have a reasonably-sized body of blog posts, my blog is
starting to attract Google queries. It's really exciting when someone
visits one of my pages looking for something incredibly specific and
obscure and I can tell from their query in the referrer log that I
have unknowingly written exactly the document they were hoping to
find. That's one of the wonders of the Internet thingy.
For example:
1 monkey rope banana weight 1 "how long is the banana" 3 monkey's mother problem 1 "basil brown" carrot juice 1 story about diophantus,how old was diophantus when he got married(Numbers indicate the number of hits on my pages that were referred by the indicated query.)
And this visitor got rather more than they wanted:
1 what pennsylvanian can we thank for daylight savings timeI imagine a middle-schooler, working on her homework. The middle-schooler is now going to have to go back to her teacher and tell her that she was wrong, and that Franklin did not invent DST, and a lot of other stuff that middle-school teachers usually do not want to be bothereed with. I hope it works out well. Or perhaps the middle-schooler will just write down "Benjamin Franklin" and leave it at that, which would be cynical but effective.
Although you'd think that by now the middle schooler would have figured out that questions that start with "What Pennsylvanian can we thank for..." are about Benjamin Franklin with extremely high probability.
I think this person was probably fairly happy:
3 franklin "restoration of life by sun rays"The referenced page includes the title of a book that contains the relevant essay, with a link to the bookseller. The only way the searcher could be happier is if they found the text of the essay itself.
Similarly, I imagine that this person was pleased:
1 monarch-like butterflyPerhaps they couldn't remember the name of the Viceroy butterfly, and my article reminded them.
Some of the queries are intriguing. I wonder what this person was looking for?
1 spanish armada & monkeyI'd love to know the story of the Monkey and the Spanish Armada. if there isn't one already, someone should invent one.
1 there is a cabinet with 12 drawers. each drawer is opened only once. in each drawer are about 30 compartments, with only 7 names.This one was so weird that I had to do the search myself. It's a puzzle on a page described as "Quick Riddles: Easy puzzles, riddles and brainteasers you can solve on sight"; the question was "what is it?" Presumably it's some sort of calendrical object, containing pills or some other item to be dispensed daily. I looked at the answer on the web page, which is just "the calendar". I have not seen any calendars with drawers and compartments, so I suppose they were meant metaphorically. I think it's a pretty crappy riddle.
Sometimes I know that the searches did not find what they were looking for.
1 eliminate debt using linear mathI don't know what this was, but it reminds me of when I was teaching math at the Johns Hopkins CTY program. One of my fellow instructors told me sadly that he had a student whose uncle had invented a brilliant secret system for making millions of dollars in the stock market. The student had been sent to math camp to learn trigonometry so that he would be able to execute the system for his uncle. Kids get sent to math camp for a lot of bad reasons, but I think that one was the winner.
1 armonica how many people can properly use itThis one is a complete miss. The armonica (or "glass harmonica") is a kind of musical instrument. (Who can guess what Pennsylvanian we have to thank for it?) As all ill-behaved children know, you can make a water glass sing by rubbing its edge with a damp fingertip. The armonica is a souped-up version of this. There is a series of glass bowls in graduated sizes, mounted on a revolving spindle. The operator touches the rims of the revolving bowls with his fingers; this makes them vibrate. The smaller bowls produce higher tones. The sound is very ethereal, not like any other instrument.
I had the good fortune to attend an armonica recital by Dean Shostak as part of the Philadelphia Fringe Festival a few years ago. Mr. Shostak is one of very few living armonica players. (He says that there are seven others.) The armonica is not popular because it is bulky, hard to manufacture, and difficult to play. The bowls must be constructed precisely, by a skilled glassblower, to almost the right pitch, and then carefully filed down until they are exactly right. If you overfile one, it is junk. If a bowl goes out of tune, it must be replaced; this requires that all the other bowls be unmounted from the spindle. The bowls are fragile and break easily.
The operator's hands must be perfectly clean, because the slightest amount of lubrication prevents the operator from setting the glass vibrating. The operator must keep his fingertips damp at all times, continually wetting them from a convenient bowl of water. By the end of a concert, his fingers are all pruney and have been continually rubbed against the rotating bowls; this limits the amount of time the instrument can be played.
Shostak's web site has some samples that you can listen to. Unfortunately, it does not also have any videos of him playing the instrument.
1 want did an wang inventThis one was also a miss; the poor querent found my page about medieval Chinese type management instead.
An Wang invented the magnetic core memory that was the principal high-speed memory for computers through the 1950s and 1960s. In this memory technology, each bit was stored in a little ferrite doughnut, called a "core". If the magnetic field went one way through the doughnut, it represented a 0; the other way was a 1. Thousands of these cores would be strung on wire grids. Each core was on one vertical and one horizontal wire. The computer could modify the value of the bit by sending current on the core's horizontal wire and vertical wire simultaneously. The two currents individually were too small to modify the other bits in the same row and column. If the bit was actually changed, the resulting effect on the current could be detected; this is how bits were read: You'd try to write a 1, and see if that caused a change in the bit value. Then if it turned out to have been a 0, you'd put it back the way it was.
The cores themselves were cheap and easy to manufacture. You mix powdered iron with ceramic, stamp it into the desired shape in a mold, and bake it in a kiln. Stringing cores into grids was more expensive. and was done by hand.
As the technology improved, the cores themselves got smaller and the grids held more and more of them. Cores from the 1950s were about a quarter-inch in diameter; cores from the late 1960s were about one-quarter that size. They were finally obsoleted in the 1970s by integrated circuits.
When I was in high school in New York in the 1980s, it was still possible to obtain ferrite cores by the pound from the surplus-electronics stores on Canal Street. By the 1990s, the cores were gone. You can still buy them online.
An Wang got very rich from the invention and was able to found Wang computers. Around 1980 my mother's employer had a Wang word-processing system. It was a marvel that took up a large space and cost $15,000. ($35,000 in 2006 dollars.) She sometimes brought me in on weekends so that I could play with it. Such systems, the first word processors, were tremendously popular between 1976 and 1981. They invented the form, which, as I recall, was not significantly different from the word processors we have today. Of course, these systems were doomed, replaced by cheap general-purpose machines within a few years.
The undergraduate dormitories at Harvard University are named mostly for Harvard's presidents: Mather House, Dunster House, Eliot House, and so on. One exception was North House. A legend says Harvard refused an immense donation from Wang, whose successful company was based in Cambridge, because it came with the condition that North house be renamed after him. (Similarly, one sometimes hears it said that the Houses are named for all the first presidents of Harvard, except for president number 3, Leonard Hoar, who was skipped. It's not true; numbers 2, 4, and 5 were skipped also.)
[Other articles in category /google-roundup] permanent link
Rotten code in a ProFTPD plugin module
One of my work colleagues asked me to look at a piece of C source code
today. He was tracking down a bug in the FTP server. He thought he
had traced it to this spot, and wanted to know if I concurred and if I
agreed with his suggested change.
Here's the (exceptionally putrid) (relevant portion of the) code:
static int gss_netio_write_cb(pr_netio_stream_t *nstrm, char *buf,size_t buflen) {
int count=0;
int total_count=0;
char *p;
OM_uint32 maj_stat, min_stat;
OM_uint32 max_buf_size;
...
/* max_buf_size = maximal input buffer size */
p=buf;
while ( buflen > total_count ) {
/* */
if ( buflen - total_count > max_buf_size ) {
if ((count = gss_write(nstrm,p,max_buf_size)) != max_buf_size )
return -1;
} else {
if ((count = gss_write(nstrm,p,buflen-total_count)) != buflen-total_count )
return -1;
}
total_count = buflen - total_count > max_buf_size ? total_count + max_buf_size : buflen;
p=p+total_count;
}
return buflen;
}
(You know there's something wrong when the comment says "maximal input
buffer size", but the buffer is for performing output. I have not
looked at any of the other code in this module, which is 2,800 lines
long, so I do not know if this chunk is typical.)
Mr. Colleague suggested that p=p+total_count was wrong, and
should be replaced with p=p+max_buf_size. I agreed that it
was wrong, and that his change would fix the problem, although I
suggested that p += count would be a better change.
Mr. Colleague's change, although it would no longer manifest the bug,
was still "wrong" in the sense that it would leave p pointing
to a garbage location (and incidentally invokes behavior not defined
by the C language standard) whereas my change would leave p
pointing to the end of the buffer, as one would expect.Since this is a maintenance programming task, I recommended that we not touch anything not directly related to fixing the bug at hand. But I couldn't stop myself from pointing out that the code here is remarkably badly written. Did I say "exceptionally putrid" yet? Oh, I did.
Good. It stinks like a week-old fish.
The first thing to notice is that the expression buflen - total_count appears four times in only nine lines of code—five if you count the buflen > total_count comparison. This strongly suggests that the algorithm would be more clearly expressed in terms of whatever buflen - total_count really is. Since buflen is the total number of characters to be written, and total_count is the number of characters that have been written, buflen - total_count is just the number of characters remaining. Rather than computing the same expression four times, we should rewrite the loop in terms of the number of characters remaining.
size_t left_to_write = buflen;
while ( left_to_write > 0 ) {
/* */
if ( left_to_write > max_buf_size ) {
if ((count = gss_write(nstrm,p,max_buf_size)) != max_buf_size )
return -1;
} else {
if ((count = gss_write(nstrm,p,left_to_write)) != left_to_write )
return -1;
}
total_count = left_to_write > max_buf_size ? total_count + max_buf_size : buflen;
p=p+total_count;
left_to_write -= count;
}
Now we should notice that the two calls to gss_write are
almost exactly the same. Duplicated code like this can almost always
be eliminated, and eliminating it almost always produces a favorable
result. In this case, it's just a matter of introducing an auxiliary
variable to record the amount that should be written:
size_t left_to_write = buflen, write_size;
while ( left_to_write > 0 ) {
write_size = left_to_write > max_buf_size ? max_buf_size : left_to_write;
if ((count = gss_write(nstrm,p,write_size)) != write_size )
return -1;
total_count = left_to_write > max_buf_size ? total_count + max_buf_size : buflen;
p=p+total_count;
left_to_write -= count;
}
At this point we can see that write_size is going to be
max_buf_size for every write except possibly the last one, so
we can simplify the logic the maintains it:
size_t left_to_write = buflen, write_size = max_buf_size;
while ( left_to_write > 0 ) {
if (left_to_write < max_buf_size)
write_size = left_to_write;
if ((count = gss_write(nstrm,p,write_size)) != write_size )
return -1;
total_count = left_to_write > max_buf_size ? total_count + max_buf_size : buflen;
p=p+total_count;
left_to_write -= count;
}
Even if we weren't here to fix a bug, we might notice something fishy:
left_to_write is being decremented by count, but
p, the buffer position, is being incremented by
total_count instead. In fact, this is exactly the bug that
was discovered by Mr. Colleague. Let's fix it:
size_t left_to_write = buflen, write_size = max_buf_size;
while ( left_to_write > 0 ) {
if (left_to_write < max_buf_size)
write_size = left_to_write;
if ((count = gss_write(nstrm,p,write_size)) != write_size )
return -1;
total_count = left_to_write > max_buf_size ? total_count + max_buf_size : buflen;
p += count;
left_to_write -= count;
}
We could fix up the line the maintains the total_count
variable so that it would be correct, but since total_count
isn't used anywhere else, let's just delete it.
size_t left_to_write = buflen, write_size = max_buf_size;
while ( left_to_write > 0 ) {
if (left_to_write < max_buf_size)
write_size = left_to_write;
if ((count = gss_write(nstrm,p,write_size)) != write_size )
return -1;
p += count;
left_to_write -= count;
}
Finally, if we change the != write_size test to <
0, the function will correctly handle partial writes, should
gss_write be modified in the future to perform them:
size_t left_to_write = buflen, write_size = max_buf_size;
while ( left_to_write > 0 ) {
if (left_to_write < max_buf_size)
write_size = left_to_write;
if ((count = gss_write(nstrm,p,write_size)) < 0 )
return -1;
p += count;
left_to_write -= count;
}
We could trim one more line of code and one more state change by
eliminating the modification of p:
size_t left_to_write = buflen, write_size = max_buf_size;
while ( left_to_write > 0 ) {
if (left_to_write < max_buf_size)
write_size = left_to_write;
if ((count = gss_write(nstrm,p+buflen-left_to_write,write_size)) < 0 )
return -1;
left_to_write -= count;
}
I'm not sure I think that is an improvement. (My idea is that if we
do this, it would be better to create a p_end variable up
front, set to p+buflen, and then use p_end -
left_to_write in place of p+buflen-left_to_write. But
that adds back another variable, although it's a constant one, and the
backward logic in the calculation might be more confusing than the
thing we were replacing. Like I said, I'm not sure. What do you
think?)Anyway, I am sure that the final code is a big improvement on the original in every way. It has fewer bugs, both active and latent. It has the same number of variables. It has six lines of logic instead of eight, and they are simpler lines. I suspect that it will be a bit more efficient, since it's doing the same thing in the same way but without the redundant computations, although you never know what the compiler will be able to optimize away.
Right now I'm engaged in writing a book about this sort of cleanup and renovation for Perl programs. I've long suspected that the same sort of processes could be applied to C programs, but this is the first time I've actually done it.
The funny thing about this code is that it's performing a task that I thought every C programmer would already have known how to do: block-writing of a bufferfull of data. Examples of the right way to do this are all over the place. I first saw it done in Marc J. Rochkind's superb book Advanced Unix Programming around 1989. (I learned from the first edition, but the link to the right is for the much-expanded second edition that came out in 2004.) I'm sure it must pop up all over the Stevens books.
But the really exciting thing I've learned about code like this is that it doesn't matter if you don't already know how to do it right, because you can turn the wrong code into the right code, as we did here, by noticing a few common problems, like duplicate tests and repeated subexpressions, and applying a few simple refactorizations to get rid of them. That's what my book will be about.
(I am also very pleased that it has taken me 37 blog entries to work around to discussing any programming-related matters.)
[Other articles in category /prog] permanent link
Sun, 29 Jan 2006
G.H. Hardy on analytic number theory and other matters
| Buy Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work from Bookshop.org (with kickback) (without kickback) |
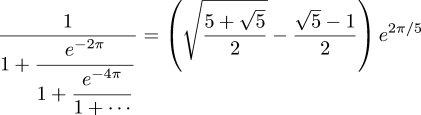
But anyway, the main point of this note is to present the following quotation from Hardy. He is discussing analytic number theory:
The fact remains that hardly any of Ramanujan's work in this field had any permanent value. The analytic theory of numbers is one of those exceptional branches of mathematics in which proof really is everything and nothing short of absolute rigour counts. The achievement of the mathematicians who found the Prime Number Theorem was quite a small thing compared with that of those who found the proof. It is not merely that in this theory (as Littlewood's theorem shows) you can never be quite sure of the facts without the proof, though this is important enough. The whole history of the Prime Number Theorem, and the other big theorems of the subject, shows that you cannot reach any real understanding of the structure and meaning of the theory, or have any sound instincts to guide you in further research, until you have mastered the proofs. It is comparatively easy to make clever guesses; indeed there are theorems like "Goldbach's Theorem", which have never been proved and which any fool could have guessed.(G.H. Hardy, Ramanujan.)
Some notes about this:
- Notice that this implies that in most branches of
mathematics, you can get away with less than absolute rigor. I think
that Hardy is quite correct here. (This is a rather arrogant remark,
since Hardy is much more qualified than I am to be telling you what
counts as worthwhile mathematics and what it is like. But this is my
blog.) In most branches of mathematics, the difficult part is
understanding the objects you are studying. If you understand them
well enough to come up with a plausible conjecture, you are doing
well. And in some mathematical pursuits, the proof may even be
secondary. Consider, for example, linear programming problems. The
point of the theory is to come up with good numerical solutions to the
problems. If you can do that, your understanding of the mathematics
is in some sense unimportant. If you invent a good algorithm that
reliably produces good answers reasonably efficiently, proving that
the algorithm is always efficient is of rather less value. In
fact, there is such an algorithm—the "simplex
algorithm"—and it is known to have exponential time in the worst
case, a fact which is of decidedly limited practical interest.
In analytic number theory, however, two facts weigh in favor of rigor. First, the objects you are studying are the positive integers. You already have as much intuitive understanding of them as you are ever going to have; you are not, through years of study and analysis, going to come to a clearer intuition of the number 3. And second, analytic number theory is much more inward-looking than most mathematics. The applications to the rest of mathematics are somewhat limited, and to the wider world even more limited. So a guessed or conjectured theorem is unlikely to have much value; the value is in understanding the theorem itself, and if you don't have a rigorous proof, you don't really understand the theorem.
Hardy's example of the Goldbach conjecture is a good one. In the 18th Century, Christian Goldbach, who was nobody in particular, conjectured that every even number is the sum of two primes. Nobody doubts that this is true. It's certainly true for all small even numbers, and for large ones, you have lots and lots of primes to choose from. No proof, however, is in view. (The primes are all about multiplication. Proving things about their additive properties is swimming upstream.) And nobody particularly cares whether the conjecture is true or not. So what if every even number is the sum of two primes? But a proof would involve startling mathematics, deep understanding of something not even guessed at now, powerful techniques not currently devised. The proof itself would have value, but the result doesn't.
Fermat's theorem (the one about an + bn = cn) is another example of this type. Not that Fermat was in any sense a fool to have conjectured it. But the result itself is of almost no interest. Again, all the value is in the proof, and the techniques that were required to carry it through.
- The Prime Number Theorem that Hardy mentions is the theorem about
the average density of the prime numbers. The Greeks knew that there
were an infinite number of primes. So the next question to ask is
what fraction of integers are prime. Are the primes sparse, like the
squares? Or are they common, like multiples of 7? The answer turns
out to be somewhere in between.
Of the integers 1–10, four (2, 3, 5, 7) are prime, or 40%. Of the integers 1–100, 25% are prime. Of the integers 1–1000, 16.8% are prime. What's the relationship?
The relationship turns out to be amazing: Of the integers 1–n, about 1/log(n) are prime. Here's a graph: the red line is the fraction of the numbers 1–n that are prime; the green line is 1/log(n):
It's not hard to conjecture this, and I think it's not hard to come up with offhand arguments why it should be so. But, as Hardy says, proving it is another matter, and that's where the real value is, because to prove it requires powerful understanding and sophisticated technique, and the understanding and technique will be applicable to other problems.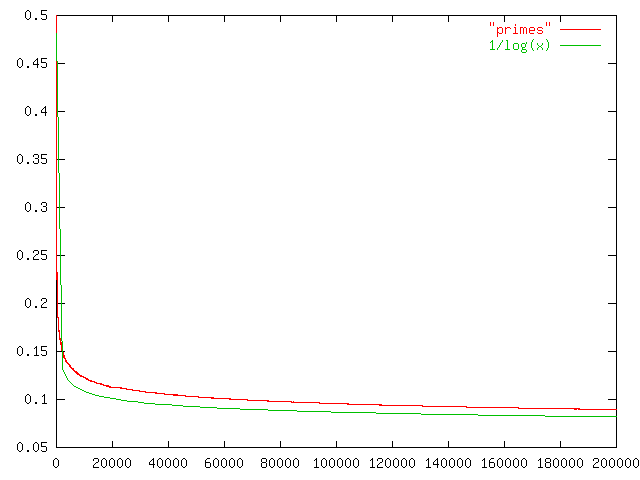
The theorem of Littlewood that Hardy refers to is a related matter.
A man who sets out to justify his existence and his activities has to distinguish two different questions. The first is whether the work which he does is worth doing; and the second is why he does it, whatever its value may be, The first question is often very difficult, and the answer very discouraging, but most people will find the second easy enough even then. Their answers, if they are honest, will usually take one or another of two forms . . . the first . . . is the only answer which we need consider seriously.And that, ultimately, is why I didn't become a mathematician. I don't have the talent for it. I have no doubt that I could have become a quite competent second-rate mathematician, with a secure appointment at some second-rate college, and a series of second-rate published papers. But as I entered my mid-twenties, it became clear that although I wouldn't ever be a first-rate mathematician, I could be a first-rate computer programmer and teacher of computer programming. I don't think the world is any worse off for the lack of my mediocre mathematical contributions. But by teaching I've been able to give entertainment and skill to a lot of people.(1) 'I do what I do because it is the one and only thing I can do at all well. . . . I agree that it might be better to be a poet or a mathematician, but unfortunately I have no talents for such pursuits.'
I am not suggesting that this is a defence which can be made by most people, since most people can do nothing at all well. But it is impregnable when it can be made without absurdity. . . It is a tiny minority who can do anything really well, and the number of men who can do two things well is negligible. If a man has any genuine talent, he should be ready to make almost any sacrifice in order to cultivate it to the full.
When I teach classes, I sometimes come back from the mid-class break and ask if there are any questions about anything at all. Not infrequently, some wag in the audience asks why the sky is blue, or what the meaning of life is. If you're going to do something as risky as asking for unconstrained questions, you need to be ready with answers. When people ask why the sky is blue, I reply "because it reflects the sea." And the first time I got the question about the meaning of life, I was glad that I had thought about this beforehand and so had an answer ready. "Find out what your work is," I said, "and then do it as well as you can." I am sure that this idea owes a lot to Hardy. I wouldn't want to say that's the meaning of life for everyone, but it seems to me to be a good answer, so if you are looking for a meaning of life, you might try that one and see how you like it.
(Incidentally, I'm not sure it makes sense to buy a copy of this book, since it's really just a long essay. My copy, which is the same as the one I've linked above, ekes it out to book length by setting it in a very large font with very large margins, and by prepending a fifty-page(!) introduction by C.P. Snow.)
[ Addendum 20210727: regarding theorems “which have never been proved and which any fool could have guessed” Vladimir Arnol'd once said something similar: “There is a general principle that a stupid man can ask such questions to which one hundred wise men would not be able to answer.” ]
Addendum 20230810
I was quoting from memory above. Hardy's exact words were:[Formulas] (1.10)–(1.12) defeated me completely; I had never seen anything in the least like them before. A single look at them is enough to show that they could only be written down by a mathematician of the highest class. They must be true because, if they were not true, no one would have had the imagination to invent them. Finally… the writer must be completely honest, because great mathematicians are commoner than thieves or humbugs of such incredible skill.This is from page 9 of Ramanujan: Twelve Lectures on Subjects Suggested by his Life and Work, Cambridge University Press, 1940. The two relevant pages may be downloaded here, and the entire book is available in the Internet Archive.
[Other articles in category /math] permanent link
Sat, 28 Jan 2006
An unusually badly designed bit of software
I am inaugurating this new
section of my blog, which will contain articles detailing things I
have screwed up.
Back on 19 January, I decided that readers might find it convenient if, when I mentioned a book, there was a link to buy the book. I was planning to write a lot about what books I was reading, and perhaps if I was convincing enough about how interesting they were, people would want their own copies.
The obvious way to do this is just to embed the HTML for the book link directly into each entry in the appropriate place. But that is a pain in the butt, and if you want to change the format of the book link, there is no good way to do it. So I decided to write a Blosxom plugin module that would translate some sort of escape code into the appropriate HTML. The escape code would only need to contain one bit of information about the book, say its ISBN, and then the plugin could fetch the other information, such as the title and price, from a database.
The initial implementation allowed me to put <book>1558607013</book> tags into an entry, and the plugin would translate this to the appropriate HTML. (There's an example on the right.
) The 1558607013 was the ISBN. The plugin would look up this key in a Berkeley DB database, where it would find the book title and Barnes and Noble image URL. Then it would replace the <book> element with the appropriate HTML. I did a really bad job with this plugin and had to rewrite it.Since Berkeley DB only maps string keys to single string values, I had stored the title and image URL as a single string, with a colon character in between. That was my first dumb mistake, since book titles frequently include colons. I ran into this right away, with Voyages and Discoveries: Selections from Hakluyt's Principal Navigations.
This, however, was a minor error. I had made two major errors. One was that the <book>1558607013</book> tags were unintelligible. There was no way to look at one and know what book was being linked without consulting the database.
But even this wouldn't have been a disaster without the other big mistake, which was to use Berkeley DB. Berkeley DB is a great package. It provides fast keyed lookup even if you have millions of records. I don't have millions of records. I will never have millions of records. Right now, I have 15 records. In a year, I might have 200.
[ Addendum 20180201: Twelve years later, I have 122. ] The price I paid for fast access to the millions of records I don't have is that the database is not a text file. If it were a text file, I could look up <book>1558607013</book> by using grep. Instead, I need a special tool to dump out the database in text form, and pipe the output through grep. I can't use my text editor to add a record to the database; I had to write a special tool to do that. If I use the wrong ISBN by mistake, I can't just correct it; I have to write a special tool to delete an item from the database and then I have to insert the new record.
When I decided to change the field separator from colon to \x22, I couldn't just M-x replace-string; I had to write a special tool. If I later decided to add another field to the database, I wouldn't be able to enter the new data by hand; I'd have to write a special tool.
On top of all that, for my database, Berkeley DB was probably slower than the flat text file would have been. The Berkeley DB file was 12,288 bytes long. It has an index, which Berkeley DB must consult first, before it can fetch the data. Loading the Berkeley DB module takes time too. The text file is 845 bytes long and can be read entirely into memory. Doing so requires only builtin functions and only a single trip to the disk.
I redid the plugin module to use a flat text file with tab-separated columns:
HOP 1558607013 Higher-Order Perl 9072008
DDI 068482471X Darwin's Dangerous Idea 1363778
Autobiog 0760768617 Franklin's Autobiography 9101737
VoyDD 0486434915 The Voyages of Doctor Dolittle 7969205
Brainstorms 0262540371 Brainstorms 1163594
Liber Abaci 0387954198 Liber Abaci 6934973
Perl Medic 0201795264 Perl Medic 7254439
Perl Debugged 0201700549 Perl Debugged 3942025
CLTL2 1555580416 Common Lisp: The Language 3851403
Frege 0631194452 The Frege Reader 8619273
Ingenious Franklin 0812210670 Ingenious Dr. Franklin 977000
The columns are a nickname ("HOP" for Higher-Order Perl,
for example), the ISBN, the full title, and the image URL. The plugin
will accept either <book>1558607013</book> or
<book>HOP</book> to designate Higher-Order
Perl. I only use the nicknames now, but I let it accept ISBNs
for backward compatibility so I wouldn't have to go around changing
all the <book> elements I had already done.Now I'm going to go off and write "just use a text file, fool!" a hundred times.
[Other articles in category /oops] permanent link
Fri, 27 Jan 2006
Travels of Mirza Abu Taleb Khan
In a
couple of recent posts, I talked about the lucky finds you can
have when you browse at random in strange libraries. Sometimes the
finds don't turn out so well.
I'm an employee of the University of Pennsylvania, and one of the best fringe benefits of the job is that I get unrestricted access to the library and generous borrowing privileges. A few weeks ago I was up there, and found my way somehow into the section with the travel books. I grabbed a bunch, one of which was the source for my discussion of the dot product in 1580. Another was Travels of Mirza Abu Taleb Khan, written around 1806, and translated into English and published in English in 1814.
Travels is the account of a Persian nobleman who fell upon hard times in India and decided to take a leave of absence and travel to Europe. His travels lasted from 1799 through August 1803, and when he got back to Calcutta, he wrote up an account of his journey for popular consumption.
Wow, what a find, I thought, when I discovered it in the library. How could such a book fail to be fascinating? But if you take that as a real question, not as a rhetorical one, an answer comes to mind immediately: Mirza Abu Taleb does not have very much to say!
A large portion of the book drops the names of the many people that Mirza Abu Taleb met with, had dinner with, went riding with, went drinking with, or attended a party at the house of. Opening the book at random, for example, I find:
The Duke of Leinster, the first of the nobles of this kingdom honoured me with an invitation; his house is the most superb of any in Dublin, and contains a very numerous and valuable collection of statues and paintings. His grace is distinguished for the dignity of his manners, and the urbanity of his disposition. He is blessed with several angelic daughters.There you see how to use sixty-two words to communicate nothing. How fascinating it might have been to hear about the superbities of the Duke's house. How marvelous to have seen even one of the numerous and valuable statues. How delightful to meet one of his several angelic daughters. How unfortunate that Abu Taleb's powers of description have been exhausted and that we don't get to do any of those things. "Dude, I saw the awesomest house yesterday! I can't really describe it, but it was really really awesome!"
Here's another:
[In Paris] I also had the pleasure of again meeting my friend Colonel Wombell, from whom I experienced so much civility in Dublin. He was rejoiced to see me, and accompanied me to all the public places. From Mr. and Miss Ogilvy I received the most marked attention.I could quote another fifty paragraphs like those, but I'll spare you.
Even when Abu Taleb has something to say, he usually doesn't say it:
I was much entertained by an exhibition of Horsemanship, by Mr. Astley and his company. They have an established house in London, but come over to Dublin for four or five months in every year, to gratify the Irish, by displaying their skill in this science, which far surpasses any thing I ever saw in India.Oh boy! I can't wait to hear about the surpassing horsemanship. Did they do tricks? How many were in the company? Was it men only, or both men and women? Did they wear glittery costumes? What were the horses like? Was the exhibition indoors or out? Was the crowd pleased? Did anything go wrong?
I don't know. That's all there is about Mr. Astley and his company.
Almost the whole book is like this. Abu Taleb is simply not a good observer. Good writers in any language can make you feel that you were there at the same place and the same time, seeing what they saw and hearing what they heard. Abu Taleb doesn't understand that one good specific story is worth a pound of vague, obscure generalities. This defect spoils nearly every part of the book in one degree or another:
[The Irish] are not so intolerant as the English, neither have they austerity and bigotry of the Scotch. In bravery and determination, hospitality, and prodigality, freedom of speech and open-heartedness, they surpass the English and the Scotch, but are deficient in prudence and sound judgement: they are nevertheless witty, and quick of comprehension.But every once in a while you come upon an anecdote or some other specific. I found the next passage interesting:
Thus my land lady and her children soon comprehended my broken English; and what I could not explain by language, they understood by signs. . . . When I was about to leave them, and proceed on my journey, many of my friends appeared much affected, and said: "With your little knowledge of the language, you will suffer much distress in England; for the people there will not give themselves any trouble to comprehend your meaning, or to make themselves useful to you." In fact, after I had resided for a whole year in England, and could speak the language a hundred times better than on my first arrival, I found much more difficulty in obtaining what I wanted, than I did in Ireland.Aha, so that's what he meant by "quick of comprehension". Thanks, Mirza.
Here's another passage I liked:
In this country and all through Europe, but especially in France and in Italy, statues of stone and marble are held in high estimation, approaching to idolatry. Once in my presence, in London, a figure which had lost its head, arms, and legs, and of which, in short, nothing but the trunk remained, was sold for 40,000 rupees (£5000). It is really astonishing that people possessing so much knowledge and good sense, and who reproach the nobility of Hindoostan with wearing gold and silver ornaments like women, whould be thus tempted by Satan to throw away their money upon useless blocks. There is a great variety of these figures, and they seem to have appropriate statues for every situation. . .Oh no—he isn't going to stop there, is he? No! We're saved!
. . . thus, at the doors or gates, they have huge janitors; in the interior they have figures of women dancing with tambourines and other musical instruments; over the chimney-pieces they place some of the heathen deities of Greece; in the burying grounds they have the statues of the deceased; and in the gardens they put up devils, tigers, or wolves in pursuit of a fox, in hopes that animals, on beholding these figures will be frightened, and not come into the garden.If more of the book were like that, it would be a treasure. But you have to wait a long time between such paragraphs.
| Buy Personal Narrative of a Pilgrimage to Al Madinah and Meccah, Vol. 1  from Bookshop.org (with kickback) (without kickback) |
Another similarly good travel book is Sir Richard Francis Burton's 1853 account of his pilgimage to Mecca. Infidels were not allowed in the holy city of Mecca. Burton disguised himself as an Afghan and snuck in. I expect I'll have something to say about this book in a future article.
[ Addendum 20171024: On rereading this, I discovered that I have since
learned who Mr. Astley was:
he invented the circus, in its modern form, and is quite famous. So
the questions I asked about Mr. Astley's surpassing horsemanship can
at least be answered, despite Mirza Abu Taleb's failure to do
so. ]
[Other articles in category /book] permanent link
Thu, 26 Jan 2006
The octopus and the creation of the cosmos
In
an earlier post, I mentioned the lucky finds you sometimes make
when you're wandering at random in a library. Here's another such.
In 2001 I was in Boston with my wife, who was attending the United
States Figure Skating Championships. Instead of attending the Junior
Dance Compulsories, I went to the Boston Public Library, where I
serendipitously unearthed the following treasure:
Although we have the source of all things from chaos, it is a chaos which is simply the wreck and ruin of an earlier world....The drama of creation, according to The Hawaiian account, is divided into a series of stages, and in the very first of these life springs from the shadowy abyss and dark night...At first the lowly zoophytes and corals come into being, and these are followed by worms and shellfish, each type being declared to conquer and destroy its predecessor, a struggle for existence in which the strongest survive....As type follows type, the accumulating slime of their decay raises land above the waters, in which, as spectator of all, swims the octopus, the lone survivor of an earlier world.(Mythology of All Races, vol. ix ("Oceanic"), R.B. Dixon. Thanks to the wonders of the Internet, you can now read the complete text online.)
Everyone, it seems, recognizes the octopus as a weird alien, unique in our universe.
[Other articles in category /bio/octopus] permanent link
The square root of 2 is irrational
I heard some story that the Pythagoreans tried to cover this up by
drowning the guy who discovered it, but I don't know if it's true and
probably nobody else does either.
The usual proof goes like this. Suppose that √2 is rational; then there are integers a and b with a / b = √2, where a / b is in lowest terms. Then a2 / b2 = 2, and a2 = 2b2. Since the right-hand side is even, so too must the left-hand side be, and since a2 is even, a must also be even. Then a = 2k for some integer k, and we have 4k2 = 2b2, and so 2k2 = b2. But then since the left-hand side is even, so too must the right-hand side be, and since b2 is even, b must also be even. But since a and b are both even, a / b was not in lowest terms, a contradiction. So no such a and b can exist, and √2 is irrational.
There are some subtle points that are glossed over here, but that's OK; the proof is correct.
A number of years ago, a different proof occurred to me. It goes like this:
Suppose that √2 is rational; then there are integers a and b with a / b = √2, where a / b is in lowest terms. Since a and b have no common factors, nor do a2 and b2, and a2 / b2 = 2 is also in lowest terms. Since the representation of rational numbers by fractions in lowest terms is unique, and a2 / b2 = 2/1, we have a2 = 2. But there is no such integer a, a contradiction. So no such a and b can exist, and √2 is irrational.
This also glosses over some subtle points, but it also seems to be correct.
I've been pondering this off and on for several years now, and it seems to me that it seems simpler in some ways and more complex in others. These are all hidden in the subtle points I alluded to.
For example, consider fact that both proofs should go through just as well for 3 as for 2. They do. And both should fail for 4, since √4 is rational. Where do these failures occur? The first proof concludes that since a2 is even, a must be also. This is simple. And this is the step that fails if you replace 2 with 4: the corresponding deduction is that since a2 is a multiple of 4, a must be also. This is false. Fine.
You would also like the proof to go through successfully for 12, because √12 is irrational. But instead it fails, because the crucial step is that since a2 is divisible by 12, a must be also—and this step is false.
You can fix this, but you have to get tricky. To make it go through for 12, you have to say that a2 is divisible by 3, and so a must be also. To do it in general for √n requires some fussing.
The second proof, however, works whenever it should and fails whenever it shouldn't. The failure for √4 is in the final step, and it is totally transparent: "we have a2 = 4," it says, "but there is no such integer....oops, yes there is." And, unlike the first proof, it works just fine for 12, with no required fussery: "we have a2 = 12. But there is no such integer, a contradiction."
The second proof depends on the (unproved) fact that lowest-term fractions are unique. This is actually a very strong theorem. It is true in the integers, but not in general domains. (More about this in the future, probably.) Is this a defect? I'm not sure. On the one hand, one could be seen as pulling the wool over the readers' eyes, or using a heavy theorem to prove a light one. On the other hand, this is a very interesting connection, and raises the question of whether the corresponding theorems are true in general domains. The first proof also does some wool-pulling, and it's rather more complicated-looking than the second. And whereas the first one appears simple, and is actually more complex than it seems, the point of complexity in the second proof is right out in the open, inviting question.
The really interesting thing here is that you always see the first proof quoted, never the second. When I first discovered the second proof I pulled a few books off the shelf at random to see how the proof went; it was invariably the first one. For a while I wondered if perhaps the second proof had some subtle mistake I was missing, but I'm pretty sure it doesn't.
[ Addendum 20070220: a later article discusses an awesome geometric proof by Tom M. Apostol. Check it out. ]
[Other articles in category /math] permanent link
More irrational numbers
Gaal Yahas has written in with a delightfully simple proof that a
particular number is irrational. Let x =
log2 3; that is, such that 2x = 3. If
x is rational, then we have 2a/b = 3
and 2a = 3b, where a and
b are integers. But the left side is even and the right side
is odd, so there are no such integers, and x must be
irrational.
As long as I am on the subject, undergraduates are sometimes asked whether there are irrational numbers a and b such that ab is rational. It's easy to prove that there are. First, consider a = b = √2. If √2√2 is rational, then we are done. Otherwise, take a = √2√2 and b = √2. Both are irrational, but ab = 2.
This is also a standard example of a non-constructive proof: it demonstrates conclusively that the numbers in question exist, but it does not tell you which of the two constructed pairs is actually the one that is wanted. Pinning down the real answer is tricky. The Gelfond-Schneider theorem establishes that it is in fact the second pair, as one would expect.
[Other articles in category /math] permanent link
"Farther" vs. "further"
People mostly use "farther" and "further" interchangeably. What's the
difference?
I looked it up in the dictionary, and it turns out it's simple. "Farther" means "more far". "Further" means "more forward".
"Further" does often connote "farther", because something that is further out is usually farther away, and so in many cases the two are interchangeable. For example, "Hitherto shalt thou come, but no further" (Job 38:11.)
But now when I see people write things like China Steps Further Back From Democracy (The New York Times, 26 November 1995) or, even worse, Big Pension Plans Fall Further Behind (Washington Post, 7 June 2005) it freaks me out.
Google finds 3.2 million citations for "further back", and 9.5 million for "further behind", so common usage is strongly in favor of this. But a quick check of the OED does not reveal much historical confusion between these two. Of the citations there, I can only find one that rings my alarm bell. ("1821 J. BAILLIE Metr. Leg., Wallace lvi, In the further rear.")
[Other articles in category /lang] permanent link
Wed, 25 Jan 2006
Morphogenetic puzzles
In a recent
post, I briefly discussed puzzling issues of morphogenesis: when a
caterpillar pupates, how do its cells know how to reorganize into a
butterfly? When the blastocyst grows inside a mammal, how do its
cells know what shape to take? I said it was all a big mystery.
A reader, who goes by the name of Omar, wrote to remind me of the "Hox" (short for "homeobox") genes discussed by Richard Dawkins in The Ancestor's Tale. (No "buy this" link; I only do that for books I've actually read and recommend.) These genes are certainly part of the story, just not the part I was wondering about.
The Hox genes seem to be the master controls for notifying developing cells of their body locations. The proteins they manufacture bind with DNA and enable or disable other genes, which in turn manufacture proteins that enable still other genes, and so on. A mutation to the Hox genes, therefore, results in a major change to the animal's body plan. Inserting an additional copy of a Hox gene into an invertebrate can cause its offspring to have duplicated body segements; transposing the order of the genes can mix up the segments. One such mutation, occurring in fruit flies, is called antennapedia, and causes the flies' antennae to be replaced by fully-formed legs!
So it's clear that these genes play an important part in the overall body layout.
But the question I'm most interested in right now is how the small details are implemented. That's why I specifically brought up the example of a ring finger.
Or consider that part of the ring finger turns into a fingernail bed and the rest doesn't. The nail bed is distally located, but the most distal part of the finger nevertheless decides not to be a nail bed. And the ventral part of the finger at the same distance also decides not to be a nail bed.
Meanwhile, the ear is growing into a very complicated but specific shape with a helix and an antihelix and a tragus and an antitragus. How does that happen? How do the growing parts communicate between each other so as to produce that exact shape? (Sometimes, of course, they get confused; look up accessory tragus for example.)
In computer science there are a series of related problems called "firing squad problems". In the basic problem, you have a line of soldiers. You can communicate with the guy at one end, and other than that each soldier can only communicate with the two standing next to him. The idea is to give the soldiers a protocol that allows them to synchronize so that they all fire their guns simultaneously.
It seems to me that the embryonic cells have a much more difficult problem of the same type. Now you need the soldiers to get into an extremely elaborate formation, even though each soldier can only see and talk to the soldiers next to him.
Omar suggested that the Hox genes contain the answer to how the fetal cells "know" whether to be a finger and not a kneecap. But I think that's the wrong way to look at the problem, and one that glosses over the part I find so interesting. No cell "becomes a finger". There is no such thing as a "finger cell". Some cells turn into hair follicles and some turn into bone and some turn into nail bed and some turn into nerves and some turn into oil glands and some turn into fat, and yet you somehow end up with all the cells in the right places turning into the right things so that you have a finger! And the finger has hair on the first knuckle but not the second. How do the cells know which knuckle they are part of? At the end of the finger, the oil glands are in the grooves and not on the ridges. How do the cells know whether they will be at the ridges or the grooves? And the fat pad is on the underside of the distal knuckle and not all spread around. How do the cells know that they are in the middle of the ventral surface of the distal knuckle, but not too close to the surface?
Somehow the fat pad arises in just the right place, and decides to stop growing when it gets big enough. The hair cells arise only on the dorsal side and the oil glands only on the ventral side.
How do they know all these things? How does the cell decide that it's in the right place to differentiate into an oil gland cell? How does the skin decide to grow in that funny pattern of ridges and grooves? And having decided that, how do the skin cells know whether they're positioned at the appropriate place for a ridge or a groove? Is there a master control that tells all the cells everything at once? I bet not; I imagine that the cells conduct chemical arguments with their neighbors about who will do which job.
One example of this kind of communication is phyllotaxis, the way plants decide how to distribute their leaves around the stem. Under certain simple assumptions, there is an optimal way to do this: you want to go around the stem, putting each leaf about 360°/φ farther than the previous one, where φ is ½(1+√5). (More about this in some future post.) And in fact many plants do grow in just this pattern. How does the plant do such an elaborate calculation? It turns out to be simple: Suppose leafing is controlled by the buildup of some chemical, and a leaf comes out when the chemical concentration is high. But when a leaf comes out, it also depletes the concentration of the chemical in its vicinity, so that the next leaf is more likely to come out somewhere else. Then the plant does in fact get leaves with very close to optimal placement. Each leaf, when it comes out, warns the nearby cells not to turn into a leaf themselves---not until the rest of the stem is full, anyway. I imagine that the shape of the ear is constructed through a more complicated control system of the same sort.
[Other articles in category /bio] permanent link
Red Flags world tour: New York City
My wife came up with a brilliant plan to help me make regular progress
on my current book.
The idea of the book is that I show how to take typical programs and
repair and refurbish them. The result usually has between one-third
and one-half less code, is usually a little faster, and sometimes has
fewer bugs. Lorrie's idea was that I should schedule a series of talks for
Perl Mongers groups. Before each talk, I would solicit groups to
send me code to review; then I'd write up and deliver the talk, and
then afterward I could turn the talk notes into a book chapter. The
talks provide built-in, inflexible deadlines, and I love giving talks,
so the plan will help keep me happy while writing the book.
The first of these talks was on Monday, in my home town of New York.
'It makes no odds whether a man has a thousand pound, or nothing, there. Particular in New York, I'm told, where Ned landed.'(Charles Dickens, Martin Chuzzlewit, about which more in some future entry, perhaps.)'New York, was it?' asked Martin, thoughtfully.
'Yes,' said Bill. 'New York. I know that, because he sent word home that it brought Old York to his mind, quite wivid, in consequence of being so exactly unlike it in every respect.'
The New Yorkers gave me a wonderful welcome, and generously paid my expenses afterward. The only major hitch was that I accidentally wrote my talk about a submission that had come from London. Oops! I must be more careful in the future.
Each time I look at a new program it teaches me something new. Some people, perhaps, seem to be able to reason from general principles to specifics: if you tell them that common code in both branches of a conditional can be factored out, they will immediately see what you mean. Or so they would have you believe; I have my doubts. Anyway, whether they are telling the truth or not, I have almost none of that ability myself. I frequently tell people that I have very little capacity for abstract thought. They sometimes think I'm joking, but I'm not. What I mean is that I can't identify, remember, or understand general principles except as generalizations of specific examples. Whenever I want to study some problem, my approach is always to select a few typical-seeming examples and study them minutely to try to understand what they might have in common. Some people seem to be able to go from abstract properties to conclusions; I can only go from examples.
So my approach to understanding how to improve programs is to collect a bunch of programs, repair them, take notes, and see what sorts of repairs come up frequently, what techniques seem to apply to multiple programs, what techniques work on one program and fail on another, and why, and so on. Probably someone smarter than me would come up with a brilliant general theory about what makes bad programs bad, but that's not how my brain works. My brain is good at coming up with a body of technique. It's a limitation, but it's not all bad.
The goal of generalization had become so fashionable that a generation of mathematicians had become unable to relish beauty in the particular, to enjoy the challenge of solving quantitative problems, or to appreciate the value of technique.(Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics.)
So anyway, here's something I learned from this program. I have this idea now that you should generally avoid the Perl . (string concatenation) operator, because there's almost always a better alternative. The typical use of the . operator looks like this:
$html = "<a href='".$url."'>".$hot_text."</a>";
It's hard to see here what is code and what is data. You
pretty much have to run the Perl lexer algorithm in your head. But
Perl has another notation for concatenating strings: "$a$b"
concatenates strings $a and $b. If you use this
interpolation notation to rewrite the example above, it gets much
easier to read:
$html = "<a href='$url'>$hot_text</a>";
So when I do these classes, I always suggest that whenever you're
going to use the . operator, you try writing it as an
interpolation too and see which you like better.This frequently brings on a question about what to do in cases like this:
$tmpfilealrt = "alert_$daynum" . "_$day" . "_$mon.log" ;
Here you can't eliminate the . operators in this way, because
you would get:
$tmpfilealrt = "alert_$daynum_$day_$mon.log" ;
This fails because it wants to interpolate $daynum_ and
$day_, rather than $daynum and $day. Perl
has an escape hatch for this situation:
$tmpfilealrt = "alert_${daynum}_${day}_$mon.log" ;
But it's not clear to me that that is an improvement on the version
that used the . operator. The punctuation is only slightly
reduced, and you've used an obscure notation that a lot of people
won't recognize and that is visually similar to, but entirely
unconnected with, hash notation.Anyway, when this question would come up, I'd discuss it, and say that yeah, in that case it didn't seem to me that the . operator was inferior to the alternatives. But since my review of the program I talked about in New York on Monday, I know a better alternative. The author of that program wrote it like this:
$tmpfilealrt = "alert_$daynum\_$day\_$mon.log" ;
When I saw it, I said "Duh! Why didn't I think of that?"
[Other articles in category /prs] permanent link
In an earlier post I remarked that "The liver of arctic animals . . . has a toxically high concentration of vitamin D". Dennis Taylor has pointed out that this is mistaken; I meant to say "vitamin A". Thanks, Dennis.B and C vitamins are not toxic in large doses; they are water-soluble so that excess quantities are easily excreted. Vitamins A and D are not water-soluble, so excess quantities are harder to get rid of. Apparently, though, the liver is capable of storing very large quantities of vitamin D, so that vitamin D poisoning is extremely rare.
The only cases of vitamin A poisoning I've heard of concerned either people who ate the livers of polar bears, walruses, sled dogs, or other arctic animals, or else health food nuts who consumed enormous quantities of pure vitamin A in a misguided effort to prove how healthy it is. In On Food and Cooking, Harold McGee writes:
In the space of 10 days in February of 1974, an English health food enthusiast named Basil Brown took about 10,000 times the recommended requirement of vitamin A, and drank about 10 gallons of carrot juice, whose pigment is a precursor of vitamin A. At the end of those ten days, he was dead of severe liver damage. His skin was bright yellow.(First edition, p. 536.)
There was a period in my life in which I was eating very large quantities of carrots. (Not for any policy reason; just because I like carrots.) I started to worry that I might hurt myself, so I did a little research. The carrots themselves don't contain vitamin A; they contain beta-carotene, which the body converts internally to vitamin A. The beta-carotene itself is harmless, and excess is easily eliminated. So eat all the carrots you want! You might turn orange, but it probably won't kill you.
[Other articles in category /bio] permanent link
Tue, 24 Jan 2006
Butterflies
Yesterday I visited the American Museum of Natural History in New York
City, for the first time in many years. They have a special exhibit
of butterflies. They get pupae shipped in from farms, and pin the
pupae to wooden racks; when the adults emerge, they get to flutter
around in a heated room that is furnished with plants, ponds of
nectar, and cut fruit.
The really interesting thing I learned was that chrysalises are not featureless lumps. You can see something of the shape of the animal in them. (See, for example, this Wikipedia illustration.) The caterpillar has an exoskeleton, which it molts several times as it grows. When time comes to pupate, the chrysalis is in fact the final exoskeleton, part of the animal itself. This is in contrast to a cocoon, which is different. A cocoon is a case made of silk or leaves that is not part of the animal; the animal builds it and lives inside. When you think of a featureless round lump, you're thinking of a cocoon.
Until recently, I had the idea that the larva's legs get longer, wings sprout, and so forth, but it's not like that at all. Instead, inside the chrysalis, almost the entire animal breaks down into a liquid! The metamorphosis then reorganizes this soup into an adult. I asked the explainer at the Museum if the individual cells retained their identities, or if they were broken down into component chemicals. She didn't know, unfortunately. I hope to find this out in coming weeks.
How does the animal reorganize itself during metamorphosis? How does its body know what new shape to grow into? It's all a big mystery. It's nice that we still have big mysteries. Not all mysteries have survived the scientific revolution. What makes the rain fall and the lightning strike? Solved problems. What happens to the food we eat, and why do we breathe? Well-understood. How does the butterfly reorganize itself from caterpillar soup? It's a big puzzle.
A related puzzle is how a single cell turns into a human baby during gestation. For a while, the thing doubles, then doubles again, and again, becoming roughly spherical, as you'd expect. But then stuff starts to happen: it dimples, and folds over; three layers form, a miracle occurs, and eventually you get a small but perfectly-formed human being. How do the cells in the fingers decide to turn into fingers? How does the cells in the fourth finger know they're one finger from one side of the hand and three fingers from the other side? Maybe the formation of the adult insect inside the chrysalis uses a similar mechanism. Or maybe it's completely different. Both possibilities are mind-boggling.
This is nowhere near being the biggest pending mystery; I think we at least have some idea of where to start looking for the answer. Contrast this with the question of how it is we are conscious, where nobody even has a good idea of what the question is.
Other caterpillar news: chrysalides are so named because they often have a bright golden sheen, or golden features. (Greek "khrusos" is "gold".) The Wikipedia picture of this is excellent too. The "gold" is a yellow pigmented area covered with a shiny coating. The explainer said that some people speculate that it helps break up the outlines of the pupa and camouflage it.
I asked if the chrysalis of the viceroy butterfly, which, as an adult, resembles the poisonous monarch butterfly, also resembled the monarch's chrysalis. The answer: no, they look completely different. Isn't that interesting? You'd think that the pupa would get at least as much benefit from mimicry as the adult. One possible explanation why not: most pupae don't make it to adulthood anyway, so the marginal benefit to the species from mimicry in the pupal stage is small compared with the benefit in the adult stage. Another: the pupa's main defense, which is not available to the adult, is to be difficult to see; beyond that it doesn't matter much what happens if it is seen. Which is correct? I don't know.
For a long time folks thought that the monarch was poisonous and the viceroy was not, and that the viceroy's monarch-like coloring tricked predators into avoiding it unnecessarily. It's now believed that both speciies are poisonous and bad-tasting, and that their similar coloring therefore protects both species. A predator who eats one will avoid both in the future. The former kind of mimicry is called Batesian; the latter, Müllerian.
The monarch butterfly does not manufacture its toxic and bad-tasting chemicals itself. It is poisonous because it ingests poisonous chemicals in its food, which I think is milkweed plants. Plant chemistry is very weird. Think of all the poisonous foods you've ever heard of. Very few of them are animals. (The only poisonous meat I can think of offhand is the liver of arctic animals, which has a toxically high concentration of vitamin D.) If you're stuck on a desert island, you're a lot safer eating strange animals than you are eating strange berries.
[Other articles in category /bio] permanent link
Franklin and Daylight Saving Time
You often hear it asserted that Benjamin Franklin was the inventor of
daylight saving time. But it's really not true.
The essential feature of DST is that there is an official change to the civil calendar to move back all the real times by one hour. Events that were scheduled to occur at noon now occur at 11 AM, because all the clocks say noon when it's really 11 AM.
The proposal by Franklin that's cited as evidence that he invented DST doesn't propose any such thing. It's a letter to the editors of The Journal of Paris, originally sent in 1784. There are two things you should know about this letter: First, it's obviously a joke. And second, what it actually proposes is just that people should get up earlier!
I went home, and to bed, three or four hours after midnight. . . . An accidental sudden noise waked me about six in the morning, when I was surprised to find my room filled with light. . . I got up and looked out to see what might be the occasion of it, when I saw the sun just rising above the horizon, from whence he poured his rays plentifully into my chamber. . .Franklin then follows with a calculation of the number of candles that would be saved if everyone in Paris got up at six in the morning instead of at noon, and how much money would be saved thereby. He then proposes four measures to encourage this: that windows be taxed if they have shutters; that "guards be placed in the shops of the wax and tallow chandlers, and no family be permitted to be supplied with more than one pound of candles per week", that travelling by coach after sundown be forbidden, and that church bells be rung and cannon fired in the street every day at dawn.. . . still thinking it something extraordinary that the sun should rise so early, I looked into the almanac, where I found it to be the hour given for his rising on that day. . . . Your readers, who with me have never seen any signs of sunshine before noon, and seldom regard the astronomical part of the almanac, will be as much astonished as I was, when they hear of his rising so early; and especially when I assure them, that he gives light as soon as he rises. I am convinced of this. I am certain of my fact. One cannot be more certain of any fact. I saw it with my own eyes. And, having repeated this observation the three following mornings, I found always precisely the same result.
I considered that, if I had not been awakened so early in the morning, I should have slept six hours longer by the light of the sun, and in exchange have lived six hours the following night by candle-light; and, the latter being a much more expensive light than the former, my love of economy induced me to muster up what little arithmetic I was master of, and to make some calculations. . .
Franklin finishes by offering his brilliant insight to the world free of charge or reward:
I expect only to have the honour of it. And yet I know there are little, envious minds, who will, as usual, deny me this and say, that my invention was known to the ancients, and perhaps they may bring passages out of the old books in proof of it. I will not dispute with these people, that the ancients knew not the sun would rise at certain hours; they possibly had, as we have, almanacs that predicted it; but it does not follow thence, that they knew he gave light as soon as he rose. This is what I claim as my discovery.As usual, the complete text is available online.
OK, I'm not done yet. I think the story of how I happened to find this out might be instructive.
I used to live at 9th and Pine streets, across from Pennsylvania Hospital. (It's the oldest hospital in the U.S.) Sometimes I would get tired of working at home and would go across the street to the hospital to read or think. Hospitals in general are good for that: they are well-equipped with lounges, waiting rooms, comfortable chairs, sofas, coffee carts, cafeterias, and bathrooms. They are open around the clock. The staff do not check at the door to make sure that you actually have business there. Most of the people who work in the hospital are too busy to notice if you have been hanging around for hours on end, and if they do notice they will not think it is unusual; people do that all the time. A hospital is a great place to work unmolested.
Pennsylvania Hospital is an unusually pleasant hospital. The original building is still standing, and you can go see the cornerstone that was laid in 1755 by Franklin himself. It has a beautful flower garden, with azaleas and wisteria, and a medicinal herb garden. Inside, the building is decorated with exhibits of art and urban archaeology, including a fire engine that the hospital acquired in 1780, and a massive painting of Christ healing the sick, originally painted by Benjamin West so that the hospital could raise funds by charging people a fee to come look at it. You can visit the 19th-century surgical amphitheatre, with its observation gallery. Even the food in the cafeteria is way above average. (I realize that that is not saying much, since it is, after all, a hospital cafeteria. But it was sufficiently palatable to induce me to eat lunch there from time to time.)
Having found so many reasons to like Pennsylvania Hospital, I went to visit their web site to see what else I could find out. I discovered that the hospital's clinical library, adjacent to the surgical amphitheatre, was open to the public. So I went to visit a few times and browsed the stacks.
Mostly, as you would expect, they had a lot of medical texts. But on one of these visits I happened to notice a copy of Ingenious Dr. Franklin: Selected Scientific Letters of Benjamin Franklin on the shelf. This caught my interest, so I sat down with it. It contained all sorts of good stuff, including Franklin's letter on "Daylight Saving". Here is the table of contents:
PrefaceI'm sure that anyone who bothers to read my blog would find at least some of those items appealing. I certainly did.
The Ingenious Dr. Franklin
Daylight Saving
Treatment for Gout
Cold Air Bath
Electrical Treatment for Paralysis
Lead Poisoning
Rules of Health and Long Life
The Art of Procuring Pleasant Dreams
Learning to Swim
On Swimming
Choosing Eye-Glasses
Bifocals
Lightning Rods
Advantage of Pointed Conductors
Pennsylvanian Fireplaces
Slaughtering by Electricity
Canal Transportation
Indian Corn
The Armonica
First Hydrogen Balloon
A Hot-Air Balloon
First Aerial Voyage by Man
Second Aerial Voyage by Man
A Prophecy on Aerial Navigation
Magic Squares
Early Electrical Experiments
Electrical Experiments
The Kite
The Course and Effect of Lightning
Character of Clouds
Musical Sounds
Locating the Gulf Stream
Charting the Gulf Stream
Depth of Water and Speed of Boats
Distillation of Salt Water
Behavior of Oil on Water
Earliest Account of Marsh Gas
Smallpox and Cancer
Restoration of Life by Sun Rays
Cause of Colds
Definition of a Cold
Heat and Cold
Cold by Evaporation
On Springs
Tides and Rivers
Direction of Rivers
Salt and Salt Water
Origin of Northeast Storms
Effect of Oil on Water
Spouts and Whirlwinds
Sun Spots
Conductors and Non-Conductors
Queries on Electricity
Magnetism and the Theory of the Earth
Nature of Lightning
Sound
Prehistoric Animals of the Ohio
Toads Found in Stone
Checklist of Letters and Papers
List of Correspondents
List of a Few Additional Letters
Anyway, the moral of the story, as I see it, is: If you make your way into strange libraries and browse through the stacks, sometimes you find some good stuff, so go do that once in a while.
[ Addendum 20181026: The Franklin Institute agrees. ]
[Other articles in category /calendar] permanent link
Mon, 23 Jan 2006
The Bowdlerization of Dr. Dolittle
The 1988 reprinting contains an afterword by Christopher Lofting, the son of Hugh Lofting, and explains why the changes were made:
When it was decided to reissue the Doctor Dolittle books, we were faced with a challenging opportunity and decision. In some of the books there were certain incidents depicted that, in light of today's sensitivities, were considered by some to be disrespectful to ethnic minorities and, therefore, perhaps inappropriate for today's young reader. In these centenary editions, this issue is addressed.This note will summarize some of the changes to The Voyages of Doctor Dolittle. I have not examined the text exhaustively. I worked from memory, reading the Centenary Edition, and when I thought I noticed a change, I crosschecked the text against the Project Gutenberg version of the original text. So this does not purport to be a complete listing of all the changes that were made. But I do think it is comprehensive enough to give a sense of what was changed.. . . After much soul-searching the consensus was that changes should be made. The deciding factor was the strong belief that the author himself would have immediately approved of making the alterations. Hugh Lofting would have been appalled at the suggestion that any part of his work could give offense and would have been the first to have made the changes himself. In any case, the alterations are minor enough not to interfere with the style and spirit of the original.
Many of the changes concern Prince Bumpo, a character who first appeared in The Story of Doctor Dolittle. Bumpo is a black African prince, who, at the beginning of Voyages, is in England, attending school at Oxford. Bumpo is a highly sympathetic character, but also a comic one. In Voyages his speech is sprinkled with inappropriate "Oxford" words: he refers to "the college quadrilateral", and later says "I feel I am about to weep from sediment", for example. Studying algebra makes his head hurt, but he says "I think Cicero's fine—so simultaneous. By the way, they tell me his son is rowing for our college next year—charming fellow." None of this humor at Bumpo's expense has been removed from the Centenary Edition.
Bumpo's first appearance in the book, however, has been substantially cut:
The Doctor had no sooner gone below to stow away his note-books than another visitor appeared upon the gang-plank. This was a most extraordinary-looking black man. The only other negroes I had seen had been in circuses, where they wore feathers and bone necklaces and things like that. But this one was dressed in a fashionable frock coat with an enormous bright red cravat. On his head was a straw hat with a gay band; and over this he held a large green umbrella. He was very smart in every respect except his feet. He wore no shoes or socks.In the revised edition, this is abridged to:
The Doctor had no sooner gone below to stow away his note-books than another visitor appeared upon the gang-plank. This was a black man, very fashionably dressed. (p. 128)I think it's interesting that they excised the part about Bumpo being barefooted, because the explanation of his now unmentioned barefootedness still appears on the following page. (The shoes hurt his feet, and he threw them over the wall of "the college quadrilateral" earlier that morning.) Bumpo's feet make another appearance later on:
I very soon grew to be quite fond of our funny black friend Bumpo, with his grand way of speaking and his enormous feet which some one was always stepping on or falling over.The only change to this in the revised version is the omission of the word 'black'. (p.139)
This is typical. Most of the changes are excisions of rather ordinary references to the skin color of the characters. For example, the original:
It is quite possible we shall be the first white men to land there. But I daresay we shall have some difficulty in finding it first."The bowdlerized version omits 'white men'. (p.120.)
Another typical cut:
"Great Red-Skin," he said in the fierce screams and short grunts that the big birds use, "never have I been so glad in all my life as I am to-day to find you still alive."(Long Arrow has been buried alive for several months in a cave.) The revised edition replaces "Great Red-Skin" with "Great Long Arrow", and "Mighty White Man" with "Mighty Friend". (p.223)In a flash Long Arrow's stony face lit up with a smile of understanding; and back came the answer in eagle-tongue.
"Mighty White Man, I owe my life to you. For the remainder of my days I am your servant to command."
Another, larger change of this type, where apparently value-neutral references to skin color have been excised, is in the poem "The Song of the Terrible Three" at the end of part V, chapter 5. The complete poem is:
THE SONG OF THE TERRIBLE THREEThe ten lines in boldface have been excised in the revised version. Also in this vicinity, the phrase "the strength and weight of those three men of different lands and colors" has been changed to omit "and colors". (pp. 242-243)
Oh hear ye the Song of the Terrible Three
And the fight that they fought by the edge of the sea.
Down from the mountains, the rocks and the crags,
Swarming like wasps, came the Bag-jagderags.
Surrounding our village, our walls they broke down.
Oh, sad was the plight of our men and our town!
But Heaven determined our land to set free
And sent us the help of the Terrible Three.
One was a Black—he was dark as the night;
One was a Red-skin, a mountain of height;
But the chief was a White Man, round like a bee;
And all in a row stood the Terrible Three.
Shoulder to shoulder, they hammered and hit.
Like demons of fury they kicked and they bit.
Like a wall of destruction they stood in a row,
Flattening enemies, six at a blow.
Oh, strong was the Red-skin fierce was the Black.
Bag-jagderags trembled and tried to turn back.
But 'twas of the White Man they shouted, "Beware!
He throws men in handfuls, straight up in the air!"
Long shall they frighten bad children at night
With tales of the Red and the Black and the White.
And long shall we sing of the Terrible Three
And the fight that they fought by the edge of the sea.
Here's an interesting change:
Long Arrow said they were apologizing and trying to tell the Doctor how sorry they were that they had seemed unfriendly to him at the beach. They had never seen a white man before and had really been afraid of him—especially when they saw him conversing with the porpoises. They had thought he was the Devil, they said.The revised edition changes 'a white man' to 'a man like him' (which seems rather vague) and makes 'devil' lower-case.
In some cases the changes seem completely bizarre. When I first heard that the books had been purged of racism I immediately thought of this passage, in which the protagonists discover that a sailor has stowed away on their boat and eaten all their salt beef (p. 142):
"I don't know what the mischief we're going to do now," I heard her whisper to Bumpo. "We've no money to buy any more; and that salt beef was the most important part of the stores."I was expecting major changes to this passage, or its complete removal. I would never have guessed the changes that were actually made. Here is the revised version of the passage, with the changed part marked in boldface:"Would it not be good political economy," Bumpo whispered back, "if we salted the able seaman and ate him instead? I should judge that he would weigh more than a hundred and twenty pounds."
"How often must I tell you that we are not in Jolliginki," snapped Polynesia. "Those things are not done on white men's ships—Still," she murmured after a moment's thought, "it's an awfully bright idea. I don't suppose anybody saw him come on to the ship—Oh, but Heavens! we haven't got enough salt. Besides, he'd be sure to taste of tobacco."
"I don't know what the mischief we're going to do now," I heard her whisper to Bumpo. "We've no money to buy any more; and that salt beef was the most important part of the stores."The reference to 'white men' has been removed, but rest of passage, which I would consider to be among the most potentially offensive of the entire book, with its association of Bumpo with cannibalism, is otherwise unchanged. I was amazed. It is interesting to notice that the references to cannibalism have been excised from a passage on page 30:"Would it not be good political economy," Bumpo whispered back, "if we salted the able seaman and ate him instead? I should judge that he would weigh more than a hundred and twenty pounds."
"Don't be silly," snapped Polynesia. "Those things are not done anymore.—Still," she murmured after a moment's thought, "it's an awfully bright idea. I don't suppose anybody saw him come on to the ship—Oh, but Heavens! we haven't got enough salt. Besides, he'd be sure to taste of tobacco."
"There were great doings in Jolliginki when he left. He was scared to death to come. He was the first man from that country to go abroad. He thought he was going to be eaten by white cannibals or something.The revised edition cuts the sentence about white cannibals. The rest of the paragraph continues:
"You know what those niggers are—that ignorant! Well!—But his father made him come. He said that all the black kings were sending their sons to Oxford now. It was the fashion, and he would have to go. Bumpo wanted to bring his six wives with him. But the king wouldn't let him do that either. Poor Bumpo went off in tears—and everybody in the palace was crying too. You never heard such a hullabaloo."The revised version reads:
"But his father made him come. He said that all the African kings were sending their sons to Oxford now. It was the fashion, and he would have to go. Poor Bumpo went off in tears—and everybody in the palace was crying too. You never heard such a hullabaloo."The six paragraphs that follow this, which refer to the Sleeping Beauty subplot from the previous book, The Story of Doctor Dolittle, have been excised. (More about this later.)
There are some apparently trivial changes:
"Listen," said Polynesia, "I've been breaking my head trying to think up some way we can get money to buy those stores with; and at last I've got it."The revised edition omits 'stupid'. (p.155) On page 230:"The money?" said Bumpo.
"No, stupid. The idea—to make the money with."
"Poor perishing heathens!" muttered Bumpo. "No wonder the old chief died of cold!"becomes
"No wonder the old chief died of cold!" muttered Bumpo.I gather from other people's remarks that the changes to The Story of Doctor Dolittle were much more extensive. In Story (in which Bumpo first appears) there is a subplot that concerns Bumpo wanting to be made into a white prince. The doctor agrees to do this in return for help escaping from jail.
When I found out this had been excised, I thought it was unfortunate. It seems to me that it was easy to view the original plot as a commentary on the cultural appropriation and racism that accompanies colonialism. (Bumpo wants to be a white prince because he has become obsessed with European fairy tales, Sleeping Beauty in particular.) Perhaps had the book been left intact it might have sparked discussion of these issues. I'm told that this subplot was replaced with one in which Bumpo wants the Doctor to turn him into a lion.
[Other articles in category /book] permanent link
Fri, 20 Jan 2006
Franklin is indeed 300 years old
I can now happily report that
my
determination that Benjamin Franklin is only 299 years
old this year was mistaken. To my relief, Franklin is really 300
years old after all.
After hearing an alternative analysis from Corprew Reed, I double-checked with Daniel K. Richter, a Professor of History at the University of Pennsylvania, and director of the new McNeil Center for Early American Studies.
Richter confirms Reed's analysis: By the 18th century, nearly everyone was reckoning years to start on 1 January except certain official legal documents. The official change of New Year's day was only to bring the legal documents into conformance with what everyone was already doing. So when Franklin's birthdate is reported as 6 January 1706, it means 1706 according to modern reckoning (that is, January 300 years ago) and not 1706 in the "official" reckoning (which would have been only 299 years ago).
Deke Kassabian also wrote in with a helpful reference, referring me to an article that appeared Wednesday in Slate. The relevant part says:
. . . according to documents from Boston's city registrar, he actually came into the world on the old-style Jan. 6, 1705. So, this year's tricentennial is right on time.So the matter is cleared up, and in the best possible way. Many thanks to Deke, Corprew, and Professor Richter.
[Other articles in category /calendar] permanent link
Thu, 19 Jan 2006
Franklin is probably 300 years old after all
In a
recent post, I surmised that Benjamin Franklin is only 299 years
old this year, not 300, because of rejiggering of the start of the
calendar year in England and its colonies in 1751/1752.
However, Corprew Reed writes to suggest that I am mistaken. Reed points out that although the legal start of the year prior to 1752 was 25 March, the common usage was to cite 1 January as the start of the year. The the British Calendar Act of 1751 even says as much:
WHEREAS the legal Supputation of the Year . . . according to which the Year beginneth on the 25th Day of March, hath been found by Experience to be attended with divers Inconveniencies, . . . as it differs . . . from the common Usage throughout the whole Kingdom. . .So Reed suggests that when Franklin (and others) report his birthdate as being 6 January 1706, they are referring to "common usage", the winter of the official, legal year 1705, and thus that Franklin really was born exactly 300 years ago as of Tuesday.
If so, this would be a great relief to me. It was really bothering me that everyone might be celebrating Franklin's 300th birthday a year early without realizing it.
I'm going to try to see who here at Penn I can bother about it to find out for sure one way or the other. Thanks for the suggestion, Corprew!
[ Addendum: Yes. ]
[Other articles in category /calendar] permanent link
Benjamin Franklin and the Quakers
In one story, the firefighting company was considering contributing money to the drive to buy guns for the defense of Philadelphia against the English. A majority of board members was required, but twenty-two of the thirty board members were Quakers, who would presumably oppose such an outlay. But when the meeting time came, twenty-one of the Quakers were mysteriously absent from the meeting! Franklin and his friends agreed to wait a while to see if any more would arrive, but instead, a waiter came to report to him that eight of the Quakers were awaiting in a nearby tavern, willing to come vote in favor of the guns if necessary, but that they would prefer to remain absent if it wouldn't affect the vote, "as their voting for such a measure might embroil them with their elders and friends."
Franklin follows this story with a long discourse on the subterfuges used by Quakers to pretend that they were not violating their pacifist principles:
And a similar story, about a request to the Pennsylvania Assembly for money to buy gunpowder:My being many years in the Assembly. . . gave me frequent opportunities of seeing the embarrassment given them by their principle against war, whenever application was made to them, by order of the crown, to grant aids for military purposes. . . . The common mode at last was, to grant money under the phrase of its being "for the king's use," and never to inquire how it was applied.
And Franklin repeats an anecdote about William Penn himself:. . . they could not grant money to buy powder, because that was an ingredient of war; but they voted an aid to New England of three thousand pounds, to he put into the hands of the governor, and appropriated it for the purchasing of bread, flour, wheat, or other grain. Some of the council, desirous of giving the House still further embarrassment, advis'd the governor not to accept provision, as not being the thing he had demanded; but he reply'd, "I shall take the money, for I understand very well their meaning; other grain is gunpowder," which he accordingly bought, and they never objected to it.
The honorable and learned Mr. Logan, who had always been of that sect . . . told me the following anecdote of his old master, William Penn, respecting defense. It was war-time, and their ship was chas'd by an armed vessel, suppos'd to be an enemy. Their captain prepar'd for defense; but told William Penn and his company of Quakers, that he did not expect their assistance, and they might retire into the cabin, which they did, except James Logan, who chose to stay upon deck, and was quarter'd to a gun. The suppos'd enemy prov'd a friend, so there was no fighting; but when [Logan] went down to communicate the intelligence, William Penn rebuk'd him severely for staying upon deck, and undertaking to assist in defending the vessel, contrary to the principles of Friends, especially as it had not been required by the captain. This reproof, being before all the company, piqu'd [Mr. Logan], who answer'd, "I being thy servant, why did thee not order me to come down? But thee was willing enough that I should stay and help to fight the ship when thee thought there was danger."
[Other articles in category /religion] permanent link
Wed, 18 Jan 2006
Why 3–13 September?
In an
earlier post about the British adjustment from the Julian to the
Gregorian calendar, I pointed out that the calendar dates were
synchronized with those in use in the rest of Europe by the deletion
of 3 September through 13 September, so that Wednesday, 2 September
1752 was followed immediately by Thursday, 14 September 1752. I asked:
Why September 3-13? I don't know, although I would love to find out.Clinton Pierce has provided information which, if true, is probably the answer:
The reason for deleting the 3rd - 13th of September is that in that span there are no significant Holy Days on the Anglican calendar (at least that I can tell). September 8th's "Birth of the Blessed Virgin Mary" is actually an alternate to August 14th. It's also one of the few places on the 1752 calendar where this empty span occurs beginning at midweek.If I have time, I will try to dig up an authoritative ecclesiastical calendar for 1752. The ones I have found online show several other similar gaps; for example, it seems that 12 January could have been followed by 24 January, or 14 June followed by 26 June. But these calendars may not be historically accurate — that is, they may simply be anachronistically projecting the current practices back to 1752.This would also allow the autumnal equinox (one of the significant events mentioned in the Act) to fall properly on the 21st of September whereas doing the adjustment in October (the other late 1752 span of no Holy Days) wouldn't permit that.
[Other articles in category /calendar] permanent link
Daniel Dennett is a philosopher of mind and consciousness. The first work of his that came to my attention was his essay "Why You Can't Build a Computer That Can Feel Pain". This is just the sort of topic that college sophomores love to argue about at midnight in the dorm lounge, the kind of argument that drives me away, screaming "Shut up! Shut up! Shut up!"But to my lasting surprise, this essay really had something to say. Dennett marshaled an impressive amount of factual evidence for his point of view, and found arguments that I wouldn't have thought of. At the end, I felt as though I really knew something about this topic, whereas before I read the essay, I wouldn't have imagined that there was anything to know about it. Since then, I've tried hard to read everything I can find that Dennett has written.
A teleological explanation is one the explains the existence or occurrence of something by citing a goal or purpose that is served by the thing. Artifacts are the most obvious cases; the goal or purpose of an artifact is the function it was designed to serve by its creator. There is no controversy about the telos of a hammer: it is for hammering in and pulling out nails. The telos of more complicated artifacts, such as camcorders or tow trucks or CT scanners, is if anything more obvious. But even in simple cases, a problem can be seen to loom in the background:(Darwin's Dangerous Idea, pp. 24–25.)
"Why are you sawing that board?"
"To make a door."
"And what is the door for?"
"To secure my house."
"And why do you want a secure house?"
"So I can sleep nights."
"And why do you want to sleep nights?"
"Go run along and stop asking such silly questions."This exchange reveals one of the troubles with teleology: where does it all stop? What final cause can be cited to bring this hierarchy of reasons to a close? Aristotle had an answer: God, the Prime Mover, the for-which to end all for-whiches. The idea, which is taken up by the Christian, Jewish, and Islamic traditions, is that all our purposes are ultimately God's purposes. . . . But what are God's purposes? That is something of a mystery.
. . . One of Darwin's fundamental contributions is showing us a new way to make sense of "why" questions. Like it or not, Darwin's idea offers one way—a clear, cogent, surprisingly versatile way—of dissolving these old conundrums. It takes some getting used to, and is often misapplied, even by its staunchest friends. Gradually exposing and clarifying this way of thinking is a central project of the present book. Darwinian thinking must be carefully distinguished from some oversimplified and all-too-popular impostors, and this will take us into some technicalities, but it is worth it. The prize is, for the first time, a stable system of explanation that does not go round and round in circles or spiral off in an infinite regress of mysteries. Some people would very much prefer the infinite regress of mysteries, apparently, but in this day and age the cost is prohibitive: you have to get yourself deceived. You can either deceive yourself or let others do the dirty work, but there is no intellectually defensible way of rebuilding the mighty barriers to comprehension that Darwin smashed.
Anyway, there's one place in this otherwise excellent book where Dennett really blew it. First he quotes from a 1988 Boston Globe article by Chet Raymo, "Mysterious Sleep":
University of Chicago sleep researcher Allan Rechtshaffen asks "how could natural selection with its irrevocable logic have 'permitted' the animal kingdom to pay the price of sleep for no good reason? Sleep is so apparently maladaptive that it is hard to understand why some other condition did not evolve to satisfy whatever need it is that sleep satisfies.And then Dennett argues:
But why does sleep need a "clear biological function" at all? It is being awake that needs an explanation, and presumably its explanation is obvious. Animals—unlike plants—need to be awake at least part of the time in order to search for food and procreate, as Raymo notes. But once you've headed down this path of leading an active existence, the cost-benefit analysis of the options that arise is far from obvious. Being awake is relatively costly, compared with lying dormant. So presumably Mother Nature economizes where she can. . . . But surely we animals are at greater risk from predators while we sleep? Not necessarily. Leaving the den is risky, too, and if we're going to minimize that risky phase, we might as well keep the metabolism idling while we bide our time, conserving energy for the main business of replicating.(Darwin's Dangerous Idea, pp. 339–340, or see index under "Sleep, function of".)
This is a terrible argument, because Dennett has apparently missed the really interesting question here. The question isn't why we sleep; it's why we need to sleep. Let's consider another important function, eating. There's no question about why we eat. We eat because we need to eat, and there's no question about why we need to eat either. Sure, eating might be maladaptive: you have to leave the den and expose yourself to danger. It would be very convenient not to have to eat. But just as clearly, not eating won't work, because you need to eat. You have to get energy from somewhere; you simply cannot run your physiology without eating something once in a while. Fine.
But suppose you are in your den, and you are hungry, and need to go out to find food. But there is a predator sniffing around the door, waiting for you. You have a choice: you can stay in and go hungry, using up the reserves that were stored either in your body or in your den. When you run out of food, you can still go without, even though the consequences to your health of this choice may be terrible. In the final extremity, you have the option of starving to death, and that might, under certain circumstances, be a better strategy than going out to be immediately mauled by the predator.
With sleep, you have no such options. If you're treed by a panther, and you need to stay awake to balance on your branch, you have no options. You cannot use up your stored reserves of sleep. You do not have the option to go without sleep in the hope that the panther will get bored and depart. You cannot postpone sleep and suffer the physical consequences. You cannot choose to die from lack of sleep rather than give up and fall out of the tree. Sooner or later you will sleep, whether you choose to or not, and when you sleep you will fall out of the tree and die.
People can and do go on hunger strikes, refuse to eat, and starve to death. Nobody goes on sleep strikes. They can't. Why not? Because they can't. But why can't they? I don't think anyone knows.
The question isn't about the maladaptivity of sleeping itself; it's about the maladaptivity of being unable to prevent or even to delay sleep. Sleep is not merely a strategy to keep us conveniently out of trouble. If that were all it was, we would need to sleep only when it was safe, and we would be able to forgo it when we were in trouble. Sleep, even more than food, must serve some vital physiological role. The role must be so essential that it is impossible to run a mammalian physiology without it, even for as long as three days. Otherwise, there would be adaptive value in being able to postpone sleep for three days, rather than to fall asleep involuntarily and be at the mercy of one's enemies.
Given that, it is indeed a puzzle that we have not been able to identify the vital physiological role of sleep, and Rechtshaffen's puzzlement above makes sense.
[Other articles in category /bio] permanent link
Tue, 17 Jan 2006
An adjustment to Franklin's birthday
Thanks to the wonders of the Internet, the
text of the British Calendar Act of 1751 is available. (Should
you read the Act, it may be helpful to know that the obscure word
"supputation" just means "calculation".) This is the act that
adjusted the calendar from Julian to Gregorian and fixed the 11-day
discrepancy that had accumulated since the Nicean Council in 325 CE,
by deleting September 3-13, so that the month of September 1752 had
only 19 days:
| September 1752 | ||||||
| Sun | Mon | Tue | Wed | Thu | Fri | Sat |
| 1 | 2 | 14 | 15 | 16 | ||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
And why September? Had I been writing the Act, I think I would have preferred to delete a chunk of February; nobody likes February anyway.
Anyway, the effect of this was to make the year 1752 only 355 days long, instead of the usual 366.
I hadn't remembered, however, that this act was also the one that moved the beginning of the year from 25 March to 1 January. Since 1752 was the first civil year to begin on 1 January, that meant that 1751 was only 282 days long, running from 25 March through 31 December. I used to think that the authors of the Unix cal program were very clever for getting September 1752 correct:
% cal 1752
1752
January February March
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 1 1 2 3 4 5 6 7
5 6 7 8 9 10 11 2 3 4 5 6 7 8 8 9 10 11 12 13 14
12 13 14 15 16 17 18 9 10 11 12 13 14 15 15 16 17 18 19 20 21
19 20 21 22 23 24 25 16 17 18 19 20 21 22 22 23 24 25 26 27 28
26 27 28 29 30 31 23 24 25 26 27 28 29 29 30 31
April May June
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 1 2 1 2 3 4 5 6
5 6 7 8 9 10 11 3 4 5 6 7 8 9 7 8 9 10 11 12 13
12 13 14 15 16 17 18 10 11 12 13 14 15 16 14 15 16 17 18 19 20
19 20 21 22 23 24 25 17 18 19 20 21 22 23 21 22 23 24 25 26 27
26 27 28 29 30 24 25 26 27 28 29 30 28 29 30
31
July August September
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 1 1 2 14 15 16
5 6 7 8 9 10 11 2 3 4 5 6 7 8 17 18 19 20 21 22 23
12 13 14 15 16 17 18 9 10 11 12 13 14 15 24 25 26 27 28 29 30
19 20 21 22 23 24 25 16 17 18 19 20 21 22
26 27 28 29 30 31 23 24 25 26 27 28 29
30 31
October November December
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 5 6 7 1 2 3 4 1 2
8 9 10 11 12 13 14 5 6 7 8 9 10 11 3 4 5 6 7 8 9
15 16 17 18 19 20 21 12 13 14 15 16 17 18 10 11 12 13 14 15 16
22 23 24 25 26 27 28 19 20 21 22 23 24 25 17 18 19 20 21 22 23
29 30 31 26 27 28 29 30 24 25 26 27 28 29 30
31
But now I realize that they weren't clever enough to get 1751
right too:
% cal 1751
1751
January February March
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 5 1 2 1 2
6 7 8 9 10 11 12 3 4 5 6 7 8 9 3 4 5 6 7 8 9
13 14 15 16 17 18 19 10 11 12 13 14 15 16 10 11 12 13 14 15 16
20 21 22 23 24 25 26 17 18 19 20 21 22 23 17 18 19 20 21 22 23
27 28 29 30 31 24 25 26 27 28 24 25 26 27 28 29 30
31
April May June
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 5 6 1 2 3 4 1
7 8 9 10 11 12 13 5 6 7 8 9 10 11 2 3 4 5 6 7 8
14 15 16 17 18 19 20 12 13 14 15 16 17 18 9 10 11 12 13 14 15
21 22 23 24 25 26 27 19 20 21 22 23 24 25 16 17 18 19 20 21 22
28 29 30 26 27 28 29 30 31 23 24 25 26 27 28 29
30
July August September
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 5 6 1 2 3 1 2 3 4 5 6 7
7 8 9 10 11 12 13 4 5 6 7 8 9 10 8 9 10 11 12 13 14
14 15 16 17 18 19 20 11 12 13 14 15 16 17 15 16 17 18 19 20 21
21 22 23 24 25 26 27 18 19 20 21 22 23 24 22 23 24 25 26 27 28
28 29 30 31 25 26 27 28 29 30 31 29 30
October November December
Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa
1 2 3 4 5 1 2 1 2 3 4 5 6 7
6 7 8 9 10 11 12 3 4 5 6 7 8 9 8 9 10 11 12 13 14
13 14 15 16 17 18 19 10 11 12 13 14 15 16 15 16 17 18 19 20 21
20 21 22 23 24 25 26 17 18 19 20 21 22 23 22 23 24 25 26 27 28
27 28 29 30 31 24 25 26 27 28 29 30 29 30 31
This is quite wrong, since 1751 started on March 25, and there was no
such thing as January 1751 or February 1751. When you excise eleven days from the calendar, you have a lot of puzzles. For any event that was previously scheduled to occur on or after 14 September, 1752, you now need to ask the question: should you leave its nominal date unchanged, so that the event actually occurs 11 days sooner than it would have, or do you advance its nominal date 11 days forward? The Calendar Act deals with this in some detail. Certain court dates and ecclesiastical feasts, including corporate elections, are moved forward by 11 real days, so that their nominal dates remain the same; other events are adjusted so that the occur at the same real times as they would have without the tamperings of the calendar act. Private functions are not addressed; I suppose the details were left up to the convenience of the participants.
Historians of that period have to suffer all sorts of annoyances in dealing with the dates, since, for example, you find English accounts of the Battle of Gravelines occurring on 28 July, but Spanish accounts that their Armada wasn't even in sight of Cornwall until 29 July. Sometimes the histories will use a notation like "11/21 July" to mean that it was the day known as 11 July in England and 21 July in Spain. I find this clear, but the historians mostly seem to hate this notation. ("Fractions! If I wanted to deal in fractions, I would have become a grocer, not a historian!")
You sometimes hear that there were riots by tenants, angry to be paying a full month's rent for only 19 days of tenancy in September 1752. I think this is a myth. The act says quite clearly:
. . . nothing in this present Act contained shall extend, or be construed to extend, to accelerate or anticipate the Time of Payment of any Rent or Rents, Annuity or Annuities, or Sum or Sums of Money whatsoever. . . or the Time of doing any Matter or Thing directed or required by any such Act or Acts of Parliament to be done in relation thereto; or to accelerate the Payment of, or increase the Interest of, any such Sum of Money which shall become payable as aforesaid; or to accelerate the Time of the Delivery of any Goods, Chattles, Wares, Merchandize or other Things whatsoever . . .It goes on in that vein for quite a while, and in particular, it says that "all and every such Rent and Rents. . . shall remain and continue to be due and payable; at and upon the same respective natural Days and Times, as the same should and ought to have been payable or made, or would have happened, in case this Act had not been made. . . ". It also specifies that interest payments are to be reckoned according to the natural number of days elapsed, not according to the calendar dates. There is also a special clause asserting that no person shall be deemed to have reached the age of twenty-one years until they are actually twenty-one years old, calendrical trickery notwithstanding.
I first brought this up in connection with Benjamin Franklin's 300th birthday, saying that although Franklin had been born on 6 January, 1706, his birthday had been moved up 11 days by the Act. But things seem less clear to me now that I have reread the act. I thought there was a clause that specifically moved birthdays forward, but there isn't. There is the clause that says that Franklin cannot be said to be 300 years old until 17 January, and it also says that dates of delivery of merchandise should remain on the same real days. If you had contracted for flowers and cake to be delivered to a birthday party to be held on 6 January 2006, the date of delivery is advanced so that the florist and the baker have the same real amount of time to make delivery, and are now required to deliver on 17 January 2006.
But there is the additional confusion I had forgotten, which is that Franklin was born on 6 January 1706, and there was no 6 January 1751. What would have been 6 January 1751 was renominated to be 6 January 1752 instead, and then the old 6 January 1752 was renominated as 17 January 1753.
To make the problem more explicit, consider John Smith, born 1 January 1750. The previous day was 31 December 1750, not 1749, because 1749 ended nine months earlier, on March 24. Similarly, 1751 will not begin until 25 March, when John is 84 days old. 1751 is an oddity, and ends on December 31, when John is 364 days old. The following day is 1 January 1752, and John is now one year old. Did you catch that? John was born on 1 January 1750, but he is one year old on 1 January 1752. Similarly, he is two years old on 1 January 1753.
The same thing happens with Benjamin Franklin. Franklin was born on 6 January 1706, so he will be 300 years old (that is, 365 × 300 + 73 = 109573 days old) on 17 January 2007.
So I conclude that the cake and flowers for Franklin's 300th birthday celebration are being delivered a year early!
[ Addendum: Why it was 3–13 September. ] [ Addendum: 2006 is the correct year for Franklin's 300th birthday. [1] [2] ]
[Other articles in category /calendar] permanent link
Happy Birthday Benjamin Franklin!
Today is Benjamin Franklin's 300th birthday.
Franklin was born on 6 January, 1706. When they switched to the Gregorian calendar in 1752, everyone had their birthday moved forward eleven days, so Franklin's moved up to 17 January. (You need to do this so that, for example, someone who is entitled to receive a trust fund when he is thirty years old does not get access to it eleven days before he should. This adjustment is also why George Washington's birthday is on 22 February even though he was born 11 February 1732.)
(You sometimes hear claims that there were riots when the calendar was changed, from tenants who were angry at paying a month's rent for only 19 days of tenancy. It's not true. The English weren't stupid. The law that adjusted the calendar specified that monthly rents and such like would be pro-rated for the actual number of days.)
Since I live in Philadelphia, Franklin is often in my thoughts. In the 18th century, Franklin was Philadelphia's most important citizen. (When I first moved here, my girlfriend of the time sourly observed that he was still Philadelphia's most important citizen. Philadelphia's importance has faded since the 18th century, leaving it with a forlorn nostalgia for Colonial days.) When you read Franklin's Autobiography, you hear him discussing places in the city that are still there:
So not considering or knowing the difference of money, and the greater cheapness nor the names of his bread, I made him give me three-penny worth of any sort. He gave me, accordingly, three great puffy rolls. I was surpriz'd at the quantity, but took it, and, having no room in my pockets, walk'd off with a roll under each arm, and eating the other.
Thus I went up Market-street as far as Fourth-street, passing by the door of Mr. Read, my future wife's father; when she, standing at the door, saw me, and thought I made, as I certainly did, a most awkward, ridiculous appearance.
Heck, I was down at Fourth and Market just last month.
Franklin's personality comes across so clearly in his Autobiography and other writings that it's easy to imagine what he might have been like to talk to. I sometimes like to pretend that Franklin and I are walking around Philadelphia together. Wouldn't he be surprised at what Philadelphia looks like, 250 years on! What questions does Franklin have? I spend a lot of time explaining to Franklin how the technology works. (People who pass me in the street probably think I'm insane, or else that I'm on the phone.) Some of the explaining is easy, some less so. Explaining how cars work is easy. Explaining how cell phones work is much harder.
Here's my favorite quotation from Franklin:
I believe I have omitted mentioning that, in my first voyage from Boston, being becalm'd off Block Island, our people set about catching cod, and hauled up a great many. Hitherto I had stuck to my resolution of not eating animal food, and on this occasion consider'd, with my master Tryon, the taking every fish as a kind of unprovoked murder, since none of them had, or ever could do us any injury that might justify the slaughter. All this seemed very reasonable. But I had formerly been a great lover of fish, and, when this came hot out of the frying-pan, it smelt admirably well. I balanc'd some time between principle and inclination, till I recollected that, when the fish were opened, I saw smaller fish taken out of their stomachs; then thought I, "If you eat one another, I don't see why we mayn't eat you." So I din'd upon cod very heartily, and continued to eat with other people, returning only now and then occasionally to a vegetable diet. So convenient a thing it is to be a reasonable creature, since it enables one to find or make a reason for everything one has a mind to do.
Happy birthday, Dr. Franklin.
[Other articles in category /anniversary] permanent link
Mon, 16 Jan 2006It's with some trepidation that I'm starting this section of my blog, because I really don't understand physics very well. Most of it, I suspect, will be about how little I understand. But I'm going to give it a whirl.
Sometime this summer it occurred to me that the phenomenon of transparency is more more complex than one might initially think, and more so than most people realize. I went around asking people with more physics education than I had if they could explain to me why things like glass and water are transparent, and it seemed to me that not only did they not understand it any better than I did, but they didn't realize that they didn't understand it.
A common response, for example, was that media like glass and water are transparent because the light passes through them unimpeded. This is clearly wrong. We can see that it's wrong because both glass and water have a tendency to refract incident light. Unimpeded photons always travel in straight lines. If light is refracted by a medium, it is because the photons couple with electrons in the medium, are absorbed, and then new photons are emitted later, going in a different direction. So the photons are being absorbed; they are not passing through the water unimpeded. (Similarly, light passes more slowly though glass and water than it does through vacuum, because of the time taken up by the interactions between the photons and the electrons. If the photons were unimpeded by electromagnetic effects, they would pass through with speed c.)
Sometimes the physics students tell me that some of the photons interact, but the rest pass through unimpeded. This is not the case either. If some of the photons were unimpeded when passing through water or glass, then you would see two images of the other side: one refracted, and one not. But you don't; you see only one image. (Some photons are reflected completely, so you do see two images: a reflected one, and a transmitted one. But if photons were refracted internally as well as being transmitted unimpeded, there would be two transmitted images.) This demonstrates that all the photons are interacting with the medium.
The no-interference explanation is correct for a vacuum, of course. Vacuum is transparent because the photons pass through it with no interaction. So there are actually two separate phenomena that both go by the name of "transparency". The way in which vacuum is transparent is physically different from the way in which glass is transparent. I don't know which of these phenomena is responsible for the transparency of air.
Now, here is the thing that was really puzzling me about glass and water. For transparency, you need the photons to come out of the medium going in the same direction as they went in. If photons are scattered in all different directions, you get a translucent or opaque medium. Transparency is only achieved when the photons that come out have the same velocity and frequency as those going in, or at least when the outgoing velocity depends in some simple fashion on the incoming velocity, as with a lens.
Since the photon that comes out of glass is going in the exact same direction as the photon that went in, something very interesting is happening inside the glass. The photon reaches the glass and is immediately absorbed by an electron. Sometime later, the electron emits a new photon. The new photon is travelling in exactly the same direction as the old photon. The new photon is absorbed by the next electron, which later emits another photon, again travelling in the exact same direction. This process repeats billions of times until the final photon is ejected on the other side of the glass, still in the exact same direction, and goes on its way.
Even a tiny amount of random scattering of the photons would disrupt the transparency completely. So, I thought, I would expect to find transparency in media that have a very rigid crystalline structure, so that the electromagnetic interactions would be exactly the same at each step. But in fact we find transparency not in crystalline substances, such as metals, but rather in amorphous ones, like glass and water! This was the big puzzle for me. How can it be that the photon always comes out in the same direction that it went in, even though it was wandering about inside of glass or water, which have random internal structures?
Nobody has been able to give me a convincing explanation of this. After much pondering, I have decided that it is probably due to conservation of relativistic momentum. Because of quantum constraints, the electron can only emit a new photon of the same energy as the incoming photon. Because the electron is bound in an atom, its own momentum cannot change, so conservation of momentum requires that the outgoing photon have the same velocity as the incoming one.
I would like to have this confirmed by someone who really understands physics. So far, though, I haven't met anyone like that! I'm thinking that I should start attending physics colloquia at the University of Pennsylvania and see if I can buttonhole a couple of solid-state physics professors. Even if I don't buttonhole anyone, going to the colloquia might be useful and interesting. I should write a blog post about why it's easier to learn stuff from a colloquium than from a book.
[ Update 20231128: Jez Humble posted (in 2007) [an answer to this](https://jezhumble.net/2007/01/07/the-nature-of-transparency.html). If I understand it correctly, the answer is, in fact, because of the conservation of momentum as I guessed above. See the next-to-last paragraph of M. Humble's explanation. ][Other articles in category /physics] permanent link
Sat, 14 Jan 2006
Happy Birthday Universe of Discourse
Today is the 12th anniversary of my web site. Early attractions
included a CGI
version of the venerable "Guess-the-Animal" game and what I
believe was the first "guestbook" application on the web.
It's been a wild ride! I hope the next twelve years are as much fun.
[Other articles in category /anniversary] permanent link
Thu, 12 Jan 2006
Medieval Chinese typesetting technique
One of my longtime fantasies has been to write a book called
Quipus and Abacuses: Digital Information Processing Before
1946. The point being that digital information processing did
exist well before 1946, when large-scale general-purpose electronic
digital computers first appeared. (Abacuses you already know about,
and a future blog posting may discuss the use of abacuses in Roman
times and in medieval Europe. Quipus are bunches of knotted cords
used in Peru to record numbers.)
There are all sorts of interesting questions to be answered. For
instance, who first invented alphabetization? (Answer: the scribes at
the Great Library in Alexandria, around 200 CE.) And how did they do
it? (Answer to come in a future blog posting.) How were secret
messages sent? (Answer: lots of steganography.) How did people do
simple arithmetic with crappy Roman numerals? (Answer: abacuses.)
How were large quantities of records kept, indexed, and searched? How
were receipts made when the recipients were illiterate?
Here's a nice example. You may have heard that the Koreans and the Chinese had printing presses with movable type before Gutenberg invented it in Europe. How did they organize the types?
In Europe, there is no problem to solve. You have 26 different types for capital letters and 26 for small letters, so you make two type cases, each divided into 26 compartments. You put the capital letter types in the upper case and the small letter types in the lower case. (Hence the names "uppercase letter" and "lowercase letter".) You put some extra compartments into the cases for digits, punctuation symbols, and blank spaces. When you break down a page, you sort the types into the appropriate compartments. There are only about 100 different types, so whatever you do will be pretty easy.
However, if you are typesetting Chinese, you have a much bigger problem on your hands. You need to prepare several thousand types just for the common characters. You need to store them somehow, and when you are making up a page to be printed you need to find the required types efficiently. The page may require some rare characters, and you either need to have up to 30,000 rarely-used types made up in advance or some way to quickly make new types as needed. And you need a way to sort out the types and put them away in order when the page is complete.
(I'm sure some reader is itching to point out that Korean is written with a phonetic alphabet, hangul, which avoids the problem by having only 28 letters. But in fact that is wrong for two reasons. First, the layout of Korean writing requires that a type be made for each two- or three-letter syllable. And second, perhaps more to the point, moveable type presses were used in Korea before the invention of hangul, before Korean even had a written form. Movable type was invented in Korea around 1234 CE; hangul was first promulgated by Sejong the Great in 1443 or 1444. The first Korean moveable type presses were used to typeset documents in Chinese, which was the language of scholarship and culture in Korea until the 19th century.)
In fact, several different solutions were adopted. The earliest movable types in China were made of clay mixed with glue. These had the benefit of being cheap. Copper types were made later, but had two serious disadvantages. First, they were very expensive. And second, since much of their value could be recovered by melting them down, the government was always tempted to destroy them to recover the copper, which did indeed happen.
Wang Chen (王禎), in 1313, writes that the types were organized as follows: There were two circular bamboo tables, each seven feet across and with one leg in the middle; the tabletops were mounted on the legs so that they could rotate. One table was for common types and the other for the rare, one-off types. The top of each table was divided into eight sections, and in each section, types were arranged in their numerical order according to their listing in the Book of Rhymes, an early Chinese dictionary that organized the characters by their sounds.
To set the type for a page, the compositors would go through the proof and number each character with a code indicating its code number from the Book of Rhymes. One compositor would then read from the list of numbers while the other, perched on a seat between the two rotating tables, would select the types from the tables. Wang doesn't say, but one supposes that the compositors would first put the code numbers into increasing order before starting the search for the right types. This would have two benefits: First, it would enable a single pass to be made over the two tables, and second, if a certain character appeared multiple times on the page, it would allow all the types needed for that character to be picked up at once.
The types would then be inserted into the composition frame. If a character was needed for which there was no type, one was made on the spot. Wang Chen's types were made of wood. The character was carefully written on very thin paper, which was then pasted upside-down onto a blank type slug. A wood carver with a delicate chisel would then cut around the character into the wood.
(Source: Invention of printing in China and its spread westward. Thomas Francis Carter, 1925.)
In 1776 a great printing project was overseen by Jian Jin (Chin Ch'ien), also using wooden types. Jin left detailed instructions about how the whole thing was accomplished. By this time the Book of Rhymes had been superseded.
The Imperial K'ang Hsi Dictionary (K'ang-hsi tzu-tien or Kāngxī Zìdiǎn, 康熙字典), written between 1710 and 1716, was the gold standard for Chinese dictionaries at the time, and to some extent, still is, since it set the pattern for the organization of Chinese characters that is still followed today. If you go into a store and buy a Chinese dictionary (or a Chinese-English dictionary) that was published last week, its organization will be essentially the same as that of the Imperial K'ang Hsi Dictionary. Since readers may be unfamiliar with the organization of Chinese dictionaries, I will try to explain.
Characters are organized primarily by a "classifier", more usually called a "radical" today. The typical Chinese character incorporates some subcharacters. For example, the character for "bright" is clearly made up of the characters for "sun" and "moon"; the character for "sweat" is made up of "water" and "shield". (The "shield" part is not because of anything relating to a shield, but because it sounds like the word for "shield".) Part of each character is designated its radical. For "sweat", the radical is "water"; for "bright" it is "sun". How do you know that the radical for "bright" is "sun" and not "moon"? You just have to know.
What about characters that are not so clearly divisible? They have radicals too, some of which were arbitrarily designated long ago, and some of which were designated based on incorrect theories of etymology. So some of it is arbitrary. But all ordering of words is arbitrary to some extent or another. Why does "D" come before "N"? No reason; you just have to know. And if you have ever seen a first-grader trying to look up "scissors" in the dictionary, you know how difficult it can be. How do you know it has a "c"? You just have to know.
Anyway, a character has a radical, which you can usually guess in at most two or three tries if you don't already know it. There are probably a couple of hundred radicals in all, and they are ordered first by number of strokes, and then in an arbitrary but standard order among the ones with the same number of strokes. The characters in the dictionary are listed in order by their radical. Then, among all the characters with a particular radical, the characters are ordered by the number of strokes used in writing them, from least to most. This you can tell just by looking at the characters. Finally, among characters with the same number of strokes and the same radical, the order is arbitrary. But it is still standardized, because it is the order used by the Imperial K'ang Hsi Dictionary.
So if you want to look up some character like "sweat", you first identify the radical, which is "water", and has four strokes. You look in the radical index among the four-stroke radicals, of which there are no more than a couple dozen, until you find "water", and this refers you to the section of the dictionary where all the characters with the "water" radical are listed. You turn to this section, and look through it for the subsection for characters that have seven strokes. Among these characters, you search until you find the one you want.
This is the solution to the problem of devising an ordering for the characters in the dictionary. Since this ordering was (and is) well-known, Jin used it to organize his type cases. He writes:
Label and arrange twelve wooden cabinets according to the names of the twelve divisions of the Imperial K'ang Hsi Dictionary. The cabinets are 5'7" high, 5'1" wide, 2'2" deep with legs 1'5" high. Before each one place a wooden bench of the same height as the cabinet's legs; they are convenient to stand on when selecting type. Each case has 200 sliding drawers, and each drawer is divided into eight large and eight small compartments, each containing four large or four small type. Write the characters, with their classifiers and number of strokes, on labels on the front of each drawer.(Source: A Chinese Printing Manual, 1776. Translated by Richard C. Rudolph, 1954.)When selecting type, first examine the make-up of the character for its corresponding classifier, and then you will know in which case it is stored. Next, count the number of strokes, and then you will know in which drawer it is. If one is experienced in this method, the hand will not err in its movements.
There are some rare characters that are seldom used, and for which few type will have been prepared. Arrange small separate cabinets for them, according to the twelve divisions mentioned above, and place them on top of each type case where they may be seen at a glance.
The size measurements here are misleading. The translator says that the "inch" used here is the Chinese inch of the time, which is about 32.5 mm, not the 25.4 mm of the modern inch. He does not say what is meant by "foot"; I assume 12 inches. That means that the type cases are actually 7'2" high, 6'6" wide, 2'9" deep, (218 cm × 198 cm × 84 cm) with legs 1'10" high (55 cm), in modern units.
(Addendum 20060116: The quote doesn't say, but the illustration in Jin's book shows that the cabinets have 20 rows of 10 drawers each.)
One puzzle I have not resolved is that there do not appear to be enough type drawers. Jin writes that there are twelve cabinets with 200 drawers each; each drawer contains 16 compartments, and each compartment four type. This is enough space for 153,600 types (remember that you need multiples of the common characters), but Jin reports that 250,000 types were cut for his project. Still, it seems clear that the technique is feasible.
Another puzzle is that I still don't know what the "twelve divisions" of the Imperial K'ang Hsi Dictionary are. I examined a copy in the library and I didn't see any twelve divisions. Perhaps some reader can enlighten me.
As in Wang's project, one compositor would first go over the proof page, making a list of which types needed to be selected, and how many; new types were cut from wood as needed. Then compositors would visit the appropriate cases to select the types as necessary; another compositor would set the type, and then the page would be printed, and the type broken down. These activities were always going on in parallel, so that page n was being printed while page n+1 was being typeset, the types for page n+2 were being selected, and page n-1 was being broken down and its types returned to the cabinet.
[Other articles in category /IT] permanent link
Wed, 11 Jan 2006Since I mentioned the book Liber Abaci, written in 1202 by Leonardo Pisano (better known as Fibonacci) in an earlier post, I may as well quote you its most famous passage:
A certain man had one pair of rabbits together in a certain enclosed place, and one wishes to know how many are created from the pair in one year when it is the nature of them in a single month to bear another pair, and in the second month those born to bear also.This passage is the reason that the Fibonacci numbers are so called.Because the abovewritten pair in the first month bore, you will double it; there will be two pairs in one month. One of these, namely the first, bears in the second month, and thus there are in the second month 3 pairs; of these in on month two are pregnant, and in the third month 2 pairs of rabbits are born, and thus there are 5 pairs in the month...
You can indeed see in the margin how we operated, namely that we added the first number to the second, namely the 1 to the 2, and the second to the third, and the third to the fourth, and the fourth to the fifth, and thus one after another until we added the tenth to the eleventh, namely the 144 to the 233, and we had the abovewritten sum of rabbits, namely 377, and thus you can in order find it for an unending number of months.
Much of Liber Abaci is incredibly dull, with pages and pages of stuff of the form "Then because three from five is two, you put a two under the three, and then because eight is less than six you take the four that is next to the six and make forty-six, and take eight from forty-six and that is thirty-eight, so you put the eight from the thirty-eight under the six...". And oh, gosh, it's just deadly. I had hoped I might learn something interesting about the way people did arithmetic in 1202, but it turns out it's almost exactly the same as the way we do it today.
But there's some fun stuff too. In the section just before the one about the famous rabbits, he presents (without proof) the formula 2n-1 · (2n -1) for perfect numbers. Euler proved in the 18th century that all even perfect numbers have this form. It's still unknown whether there are any odd perfect numbers.
Elsewhere, Leonardo considers a problem in which seven men are going to Rome, and each has seven sacks, each of which contains seven loaves of bread, each of which is pierced with seven knives, each of which has seven scabbards, and asks for the total amount of stuff going to Rome.
Negative numbers weren't widely used in Europe until the 16th century, but Liber Abaci does consider several problems whose solution requires the use of negative numbers, and Leonardo seems to fully appreciate their behavior.
Some sources say that Leonardo was only able to understand negative numbers as a financial loss; for example Dr. Math says:
Fibonacci, about 1200, allowed negative solutions in financial problems where they could be interpreted as a loss rather than a gain.
This, however, is untrue. Understanding a negative number as a loss; that is, as a relative decrease from one value to another over time, is a much less subtle idea than to understand a negative number as an absolute quantity in itself, and it is in the latter way that Leonardo seems to have understood negative numbers.
In Liber Abaci, Leonardo considers the solution of the following system of simultaneous equations:
A + P = 2(B + C)
B + P = 3(C + D)
C + P = 4(D + A)
D + P = 5(A + B)
(Note that although there are only four equations for the five unknowns, the four equations do determine the relative proportions of the five unknowns, and so the problem makes sense because all the solutions are equivalent under a change of units.)
Leonardo presents the problem as follows:
Also there are four men; the first with the purse has double the second and third, the second with the purse has triple the third and fourth; the third with the purse has quadruple the fourth and first. The fourth similarly with the purse has quintuple the first and second;
and then asserts (correctly) that the problem cannot be solved with positive numbers only:
this problem is not solvable unless it is conceded that the first man can have a debit,
and then presents the solution:
and thus in smallest numbers the second has 4, the third 1, the fourth 4, and the purse 11, and the debit of the first man is 1;
That is, the solution has B=4, C=1, D=4, P=11, and A= -1.
Leonardo also demonstrates understanding of how negative numbers participate in arithmetic operations:
and thus the first with the purse has 10, namely double the second and third;
That is, -1 + 11 = 2 · (1 + 4);
also the second with the purse has 15, namely triple the third and fourth; and the third with the purse has quadruple the fourth and the first, because if from the 4 that the fourth man has is subtracted the debit of the first, then there will remain 3, and this many is said to be had between the fourth and first men.
The explanation of the problem goes on at considerable length, at least two full pages in the original, including such observations as:
Therefore the second's denari and the fourth's denari are the sum of the denari of the four men; this is inconsistent unless one of the others, namely the first or third has a debit which will be equal to the capital of the other, because their capital is added to the second and fourth's denari; and from this sum is subtracted the debit of the other, undoubtedly there will remain the sum of the second and fourth's denari, that is the sum of the denari of the four men."
That is, he reasons that A + B + C + D = B + D, and so therefore A = -C.
Quotations are from Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation, L. E. Sigler. Springer, 2002. pp. 484-486.
[Other articles in category /math] permanent link
Tue, 10 Jan 2006
Typographic conventions in computer books
At OSCON this summer I was talking to Peter Scott (author of Perl Debugged, Perl Medic, and other books I wanted to write but didn't), and he observed that the preface of HOP did not contain a section that explained that the prose text was on proportional font and the code was all in monospaced font.
I don't remember what (if any) conclusion Peter drew from this, but I was struck by it, because I had been thinking about that myself for a couple of days. Really, what is this section for? Does anyone really need it? Here, for example, is the corresponding section from Mastering Algorithms with Perl, because it is the first book I pulled off my shelf:
Conventions Used in This Book
- Italic
- Used for filenames, directory names, URLs, and occasional emphasis.
- Constant width
- Used for elements of programming languages, text manipulated by programs, code examples, and output.
- Constant width bold
- Used for use input and for emphasis in code
- Constant width italic
- Used for replaceable values
Several questions came to my mind as I transcribed that, even though it was 4 AM.
First, does anyone really read this section and pay attention to it, making a careful note that italic font is used for filenames, directory names, URLs, and occasional emphasis? Does anyone, reading the book, and encountering italic text, say to themselves "I wonder what the funny font is about? Oh! I remember that note in the preface that italic font would be used for filenames, directory names, URLs, and occasional emphasis. I guess this must be one of those."
Second, does anyone really need such an explanation? Wouldn't absolutely everyone be able to identify filenames, directory names, URLs, and occasonal emphasis, since these are in italics, without the explicit directions?
I wonder, if anyone really needed these instructions, wouldn't they be confused by the reference to "constant-width italic", which isn't italic at all? (It's slanted, not italic.)
Even if someone needs to be told that constant-width fonts are used for code, do they really need to be told that constant-width bold fonts are used for emphasis in code? If so, shouldn't they also be told that bold roman fonts are used for emphasis in running text?
Some books, like Common Lisp: The Language, have extensive introductions explaining their complex notational conventions. For example, pages 4--11 include the following notices:
The symbol "⇒" is used in examples to indicate evaluation. For example,
(+ 4 5) ⇒ 9means "the result of evaluating the code (+ 4 5) is (or would be, or would have been) 9."The symbol "→" is used in examples to indicate macro expansions. ...
Explanation of this sort of unusual notation does seem to me to be
valuable. But really the explanations in most computer books make me
think of long-playing record albums that have a recorded voice at the
end of the first side that instructs the listener "Now turn the record
over and listen to the other side."
I don't think omitted this section from HOP on purpose; it simply never occurred to me to put one in. Had MK asked me about it, I don't know what I would have said; they didn't ask.
HOP does have at least one unusual typographic convention: when two versions of the same code are shown, the code in the second version that was modified or changed has been set in boldface. I had been wondering for a couple of weeks before OSCON if I had actually explained that; after running into Peter I finally remembed to check. The answer: no, there is no explanation. And I don't think it's a common convention.
But of all the people who have seen it, including a bunch of official technical reviewers, a few hundred casual readers on the mailing list, and now a few thousand customers, nobody suggested than an explanation was needed, and nobody has reported being puzzled. People seem to understand it right away.
I don't know what to conclude from this yet, although I suspect it will be something like:
(a) the typographic conventions in typical computer books are sufficiently well-established, sufficiently obvious, or both, that you don't have to bother explaining them unles they're really bizarre,
or:
(b) readers are smarter and more resilient than a lot of people give them credit for.
Explanation (b) reminds me of a related topic, which is that conference tutorial attendees are smarter and more resilient than a lot of conference tutorial speakers give them credit for. I suppose that is a topic for a future blog entry.
(Consensus on my mailing list, where this was originally posted, was that the ubiquitous explanations of typographic conventions are not useful. Of course, people for whom they would have been useful were unlikely to be subscribers to my mailing list, so I'm not sure we can conclude anything useful from this.)
[Other articles in category /book] permanent link
Foundations of Mathematics in the early 20th Century
Last fall I read a bunch of books on logic and foundations of mathematics that had been written around the end of the 19th and beginning of the 20th centuries. I also read some later commentary on this work, by people like W. V. O. Quine. What follows are some notes I wrote up afterwards.
The following are only my vague and uninformed impressions. They should not be construed as statements of fact. They are also poorly edited.
1. Frege and Peano were the pioneers of modern mathematical logic. All the work before Peano has a distinctly medieval flavor. Even transitionary figures like Boole seem to belong more to the old traditions than to the new. The notation we use today was all invented by Frege and Peano. Frege and Peano were the first to recognize that one must distinguish between x and {x}.
(Added later: I finally realized today what this reminds me of. In physics, there is a fairly sharp demarcation between classical physics (pre-1900, approximately) and modern physics (post-1900). There was a series of major advances in physics around this time, in which the old ideas, old outlooks, and old approaches were swept away and replaced with the new quantum theories of Planck and Einstein, leaving the field completely different than it was before. Peano and Frege are the Planck and Einstein of mathematical logic.)
2. Russell's paradox has become trite, but I think we may have forgotten how shocked and horrified everyone was when it first appeared. Some of the stories about it are hair-raising. For example, Frege had published volume I of his Grundgesetze der Arithmetik ("Basic Laws of Arithmetic"). Russell sent him a letter as volume II was in press, pointing out that Frege's axioms were inconsistent. Frege was able to add an appendix to volume II, including a heartbreaking note:
"Hardly anything more unwelcome can befall a scientific writer than that one of the foundations of his edifice be shaken after the work is finished. I have been placed in this position by a letter of Mr Bertrand Russell just as the printing of the second volume was nearing completion..."
I hope nothing like this ever happens to any of my dear readers.
The struggle to figure out Russell's paradox took years. It's so tempting to think that the paradox is just a fluke or a wart. Frege, for example, first tried to fix his axioms by simply forbidding (x ∈ x). This, of course, is insufficient, and the Russell paradox runs extremely deep, infecting not just set theory, but any system that attempts to deal with properties and descriptions of things. (Expect a future blog post about this.)
3. Straightening out Russell's paradox went in several different directions. Russell, famously, invented the so-called "Theory of Types", presented as an appendix to Principia Mathematica. The theory of types is noted for being complicated and obscure, and there were several later simplifications. Another direction was Zermelo's, which suffers from different defects: all of Zermelo's classes are small, there aren't very many of them, and they aren't very interesting. A third direction is von Neumann's: any sets that would cause paradoxes are blackballed and forbidden from being elements of other sets.
To someone like me, who grew up on Zermelo-Fraenkel, a term like "(z = complement({w}))" is weird and slightly uncanny.
(Addendum 20060110: Quine's "New Foundations" program is yet another technique, sort of a simplified and streamlined version of the theory of types. Yet another technique, quite different from the others, is to forbid the use of the ∼ ("not") operator in set comprehensions. This last is very unusual.)
4. Notation seems to have undergone several revisions since the first half of the 20th Century. Principia Mathematica and other works use a "dots" notation instead of or in additional to using parentheses for grouping. For example, instead of writing "((a + b) × c) + ((e + f) × g)", one would write "a + b .× c :+: e + f .× g". (This notation was invented by—guess who?—Peano.) This takes some getting used to when you have not seen it before. The dot notation seems to have fallen completely out of use. Last week, I thought it had technical advantages over parentheses; now I am not sure.
The upside-down-A (∀) symbol meaning "for each" is of more recent invention than is the upside-down-E (∃) symbol meaning "there exists". Early C20 would write "∃z:P(z)" as "(∃z)P(z)" but would write "∀z: P(z)" as simply "(z)P(z)".
The turnstile symbol $$\vdash$$ is Russell and Whitehead's abbreviation of the elaborate notation of Frege's Begriffschrift. The Begriffschrift notation was essentially annotated abstract syntax trees. The root of the tree was decorated with a vertical bar to indicate that the statement was asserted to be true. When you throw away the tree, leaving only the root with its bar, you get a turnstile symbol.
The ∨ symbol is used for disjunction, but its conjunctive counterpart, the ∧, is not used. Early C20 logicians use a dot for conjunction. I have been told that the ∨ was chosen by Russell and Whitehead as an abbreviation for the Latin vel = "or". Quine says that the $$\sim$$ denotes logical negation because of its resemblance to the letter "N" (for "not"). Incidentally, Quine also says that the ↓ that is sometimes used to mean logical nor is simply the ∨ with a vertical slash through it, analogous to ≠.
An ι is prepended to an expression x to denote the set that we would write today as {x}. The set { u : P(u) } of all u such that P(u) is true is written as ûP. Peter Norvig says (in Paradigms of Artificial Intelligence Programming) that this circumflex is the ultimate source of the use of "lambda" for function abstraction in Lisp and elsewhere.
5. (Addendum 20060110: Everyone always talks about Russell and Whitehead's Principia Mathematica, but it isn't; it's Whitehead and Russell's. Addendum 20070913: In a later article, I asked how and when Whitehead lost top billing in casual citation; my conclusion was that it occurred on 10 December, 1950.)
6. (Addendum 20060116: The ¬ symbol is probably an abbreviated version of Frege's notation for logical negation, which is to attach a little stem to the underside of the branch of the abstract syntax tree that is to be negated. The universal quantifier notation current in Principia Mathematica, to write (x)P(x) to mean that P(x) is true for all x, may also be an adaptation of Frege's notation, which is to put a little cup in the branch of the tree to the left of P(x) and write x in the cup.
[Other articles in category /math] permanent link
Mon, 09 Jan 2006[I sent this out to my book discussion mailing list back in November, but it seems like it might be of general interest, so I'm reposting it. - MJD]
People I talk to often don't understand how authors get paid. It's interesting, so I thought I'd send out a note about it.
Basically, the deal is that you get a percentage of the publisher's net revenues. This percentage is called "royalties". So you're getting a percentage of every book sold. Typical royalties seem to be around 15%. O'Reilly's are usually closer to 10%. If there are multiple authors, they split the royalty between them.
Every three or six months your publisher will send you a statement that says how many copies sold and at what price, and what your royalties are. If the publisher owes you money, the statement will be accompanied by a check.
The 15% royalty is a percentage of the net receipts. The publisher never sees a lot of the money you pay for the book in a store. Say you buy a book for $60 in a bookstore. About half of that goes to the store and the book distributor. The publisher gets the other half. So the publisher has sold the book to the distributor for $30, and the distributor sold it to the store for perhaps $45. This is why companies like Amazon can offer such a large discount: there's no store and no distributor.
So let's apply this information to a practical example and snoop into someone else's finances. Perl Cookbook sells for $50. Of that $50, O'Reilly probably sees about $25. Of that $25, about $2.50 is authors' royalties. Assuming that Tom and Nat split the royalties evenly (which perhaps they didn't; Tom was more important than Nat) each of them gets about $1.25 per copy sold. Since O'Reilly claims to have sold 150,000 copies of this book, we can guess that Tom has made around $187,500 from this book. Maybe. It might be more (if Tom got more than 50%) and it might be less (that 150,000 might include foreign sales, for which the royalty might be different, or bulk sales, for which the publisher might discount the cover price; also, a lot of those 150,000 copies were the first edition, and I forget the price of that.) But we can figure that Tom and Nat did pretty well from this book. On the other hand, if $187,500 sounds like a lot, recall that that's the total for 8 years, averaging about $23,500 per year, and also recall that, as Nat says, writing a book involves staring at the blank page until blood starts to ooze from your pores.
Here's a more complicated example. The book Best of The Perl Journal vol. 1 is a collection of articles by many people. The deal these people were offered was that if they contributed less than X amount, they would get a flat $150, and if they contributed more than X amount, they would get royalties in proportion to the number of pages they contributed. (I forget what X was.) I was by far the contributor of the largest number of pages, about 14% of the entire book. The book has a cover price of $40, so O'Reilly's net revenues are about $20 per copy and the royalties are about $2 per copy. Of that $2, I get about 14%, or $0.28 per copy. But for Best of the Perl Journal, vol. 2, I contributed only one article and got the flat $150. Which one was worth more for me? I think it was probably volume 1, but it's closer than you might think. There was a biggish check of a hundred and some dollars when the book was first published, and then a smaller check, and by now the checks are coming in amounts like $20.55 and $12.83.
The author only gets the 15% on the publisher's net receipts. If the books in the stores aren't selling, the bookstore gets to return them to the publisher for a credit. The publisher subtracts these copies from the number of copies sold to arrive at the royalty. If more copies come back than are sold, the author ends up owing the publisher money! Sometimes when the book is a mass-market paperback, the publisher doesn't want the returned copies; in this case the store is supposed to destroy the books, tear off the covers, and send the covers back to the publisher to prove that the copies didn't sell. This saves on postage and trouble. Sometimes you see these coverless books appear for sale anyway.
When you sign the contract to write the book, you usually get an "advance". This is a chunk of money that the publisher pays you in advance to help support you while you're writing. When you hear about authors like Stephen King getting a one-million-dollar advance, this is what they are talking about. But the advance is really a loan; you pay it back out of your royalties, and until the advance is repaid, you don't see any royalty checks. If you write the book and then it doesn't sell, you don't get any royalties, but you still get to keep the advance. But if you don't write the book, you usually have to return the advance, or most of the advance. I've known authors who declined to take an advance, but it seems to me that there is no downside to getting as big an advance as possible. In the worst case, the book doesn't sell, and then you have more money than you would have gotten from the royalties. If the book does sell, you have the same amount of money, but you have it sooner. I got a big advance for HOP. My advance will be paid back after 4,836 copies are sold. Exercise: estimate the size of my advance. (Actually, the 4,836 is not quite correct, because of variations in revenues from overseas sales, discounted copies, and such like. When the publisher sells a copy of the book from their web site, it costs the buyer $51 instead of $60, but the publisher gets the whole $51, and pays royalties on the full amount.)
If the publisher manages to exploit the book in other ways, the author gets various percentages. If Morgan Kaufmann produces a Chinese translation of HOP, I get 5% of the revenues for each copy; if instead they sell to a Chinese publisher the rights to produce and sell a Chinese translation, I get 50% of whatever the Chinese publisher paid them. If Universal pictures were to pay my publisher a million dollars for the rights to make HOP into a movie starring Kevin Bacon, I would get $50,000 of that. (Wouldn't it be cool to live in that universe? I hear that 119 is a prime number over there.)
If you find this kind of thing interesting, O'Reilly has an annotated version of their standard publishing contract online.
[ Addendum 20060109: I was inspired to repost this by the arrival in the mail today of my O'Reilly quarterly royalty statement. I thought I'd share the numbers. Since the last statement, 31 copies of Computer Science & Perl Programming were sold: 16 copies domestically and 15 foreign. The cover price is $39.95, so we would expect that O'Reilly's revenues would be close to $619.22; in fact, they reported revenues of $602.89. My royalty is 1.704 percent. The statement was therefore accompanied by a check for $10.27. Who says writing doesn't pay? ]
[ Addendum 20140428: The original source of Nat's remark about writing is from Gene Fowler, who said “Writing is easy. All you do is stare at a blank sheet of paper until drops of blood form on your forehead.” ]
[Other articles in category /book] permanent link
Mixed fractions in Liber Abaci
Leonardo Pisano has an interesting notation for fractions. He often uses mixed-base systems. In general, he writes:
where a, b, c, p, q, r, x are integers. This represents the number:
which may seem odd at first. But the notation is a good one, and here's why. Suppose your currency is pounds, and there are 20 soldi in a pound and 12 denari in a soldo. This is the ancient Roman system, used throughout Europe in the middle ages, and in England up through the 1970s. You have 6 pounds, 7 soldi, and 4 denari. To convert this to pounds requires no arithmetic whatsooever; the answer is simply
And in general, L pounds, S soldi and D denari can be written
Now similarly you have a distance of 3 miles, 6 furlongs, 42 yards, 2 feet, and 7 inches. You want to calculate something having to do with miles, so you need to know how many miles that is. No problem; it's just
We tend to do this sort of thing either in decimals (which is inconvenient unless all the units are powers of 10) or else we reduce everything to a single denominator, in which case the numbers get quite large. If you have many mixed units, as medieval merchants did, Leonardo's notation is very convenient.
One operation that comes up all the time is as follows. Suppose you have
and you wish that the denominator were s instead of b. It is easy to convert. You calculate the quotient q and remainder r of dividing a·s by b. Then the equivalent fraction with denominator s is just:
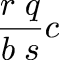
(Here we have replaced c + a/b with c + q/s + r/bs, which we can do since q and r were chosen so that qb + r = as.)
Why would you want to convert a denominator in this way? Here is a typical example. Suppose you have 24 pounds and you want to split it 11 ways. Well, clearly each share is worth
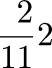
pounds; we can get that far without medieval arithmetic tricks. But how much is 2/11 pounds? Now you want to convert the 2/11 to soldi; there are 20 soldi in a pound. So you multiply 2/11 by 20 and get 40/11; the quotient is 3 and the remainder 7, so that each share is really worth
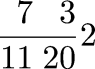
pounds. That is, each share is worth 2 pounds, plus 3 and 7/11 soldi.
But maybe you want to convert the 7/11 soldi to denari; there are 12 denari in a soldo. So you multiply 7/11 by 12 and get 84/11; the quotient is 7 and the remainder 7 also, so that each share is
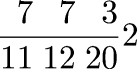
so each share is worth precisely 2 pounds, 3 soldi, and 7 7/11 denari.
Note that this system subsumes the usual decimal system, since you can always write something like
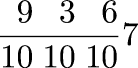
when you mean the number 7.639. And in fact Leanardo does do exactly this when it makes sense in problems concerning decimal currencies and other decimal matters. For example, in Chapter 12 of Liber Abaci, Leonardo says that there is a man with 100 bezants, who travels through 12 cities, giving away 1/10 of his money in each city. (A bezant was a medieval coin minted in Constantinople. Unlike the European money, it was a decimal currency, divided into 10 parts.) The problem is clearly to calculate (9/10)12 × 100, and Leonardo indeed gives the answer as
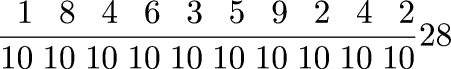
He then asks how much money was given away, subtracting the previous compound fraction from 100, getting
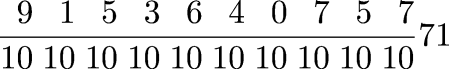
(Leonardo's extensive discussion of this problem appears on pp. 439–443 of L. E. Sigler Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation.)
The flexibility of the notation appears in many places. In a problem "On a Soldier Receiving Three Hundred Bezants for His Fief" (p. 392) Leonardo must consider the fraction
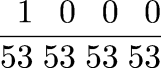
(That is, 1/534) which he multiplies by 2050601250 to get the final answer in beautiful base-53 decimals:
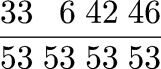
Post scriptum: The Roman names for pound, soldo, and denaro are librum ("pound"), solidus, and denarius. The names survived into Renaissance French (livre, sou, denier) and almost survived into modern English. Until the currency was decimalized, British money amounts were written in the form "£3 4s. 2d." even though the English names of the units are "pound", "shilling", "penny", because "£" stands for "libra", "s" for "solidi", and "d" for "denarii". In small amounts one would write simply "10/6" instead of "10s. 6d.", and thus the "/" symbol came to be known as a "solidus", and still is.
The Spanish word for money, dinero, means denarii. The Arabic word dinar, which is the name of the currency in Algeria, Bahrain, Iraq, Jordan, Kuwait, Libya, Sudan, and Tunisia, means denarii.
Soldiers are so called after the solidi with which they were paid.
[Other articles in category /math] permanent link
Sun, 08 Jan 2006| Buy Voyages and Discoveries: Selections from Hakluyt's Principal Navigations from Bookshop.org (with kickback) (without kickback) |
The Principal Navigations, Voyages, Traffiques, & Discoveries of the English Nation was published in 1589, a collection of essays, letters, and journals written mostly by English persons about their experiences in the great sea voyages of discovery of the latter half of the 16th century.
One important concern of the English at this time was to find an alternate route to Asia and the spice islands, since the Portuguese monopolized the sea route around the coast of Africa. So many of the selections concern the search for a Northwest or Northeast passage, routes around North America or Siberia, respectively. Other items concern military battles, including the defeat of the Spanish Armada; proper outfitting of whaling ships, and an account of a sailor who was shipwrecked in the West Indies and made his way home at last sixteen years later.
One item, titled "Experiences and reasons of the Sphere, to proove all partes of the worlde habitable, and thereby to confute the position of the five Zones," contains the following sentence:
First you are to understand that the Sunne doeth worke his more or lesse heat in these lower parts by two meanes, the one is by the kinde of Angle that the Sunne beames doe make with the earth, as in all Torrida Zona it maketh perpendicularly right Angles in some place or other at noone, and towards the two Poles very oblique and uneven Angles.
This explanation is quite correct. (The second explanation, which I omitted, is that the sun might spend more or less time above the horizon, and is also correct.) This was the point at which I happened to set down the book before I went to sleep.
But over the next couple of days I realized that there was something deeply puzzling about it: This explanation should not be accessible to an Englishman of 1580, when this item was written.
In 2006, I would explain that the sun's rays are a directed radiant energy field in direction E, and that the energy received by a surface S is the dot product of the energy vector E and the surface normal vector n. If E and n are parallel, you get the greatest amount of energy; as E and n become perpendicular, less and less energy is incident on S.
Englishmen in 1580 do not have a notion of the dot product of two vectors, or of vectors themselves for that matter. Analytic geometry will not be invented until 1637. You can explain the weakness of oblique rays without invoking vectors, by appeal to the law of conservation of energy, but the Englishmen do not have the idea of an energy field, or of conservation of energy, or of energy at all. They do not have any notion of the amount of radiant energy per unit area. Galileo's idea of mathematical expression of physical law will not be published until 1638.
So how do they have the idea that perpendicular sun is more intense than oblique? How did they think this up? And what is their argument for it?
(Try to guess before you read the answer.)
In fact, the author is completely wrong about the reason. Here's what he says the answer is:
... the perpendicular beames reflect and reverberate in themselves, so that the heat is doubled, every beam striking twice, & by uniting are multiplied, and continued strong in forme of a Columne. But in our Latitude of 50. and 60. degrees, the Sunne beames descend oblique and slanting wise, and so strike but once and depart, and therefore our heat is the lesse for any effect that the Angle of the Sunne beames make.
Did you get that? Perpendicular sun is warmer because the beams get you twice, once on the way down and once on the way back up. But oblique beams "strike but once and depart."
[Other articles in category /math] permanent link
Mark Dominus:
One of the types of problems that al-Khwarizmi treats extensively in his book is the problem of computing inheritances under Islamic law.Well, these examples are getting sillier and sillier, but
... but maybe they're not silly enough:
A rope over the top of a fence has the same length on each side and weighs one-third of a pound per foot. On one end of the rope hangs a monkey holding a banana, and on the other end a weight equal to the weight of the monkey. The banana weighs 2 ounces per inch. The length of the rope in feet is the same as the age of the monkey, and the weight of the monkey in ounces is as much as the age of the monkey's mother. The combined ages of the monkey and its mother is 30 years. One-half the weight of the monkey plus the weight of the banana is one-fourth the sum of the weights of the rope and the weight. The monkey's mother is one-half as old as the monkey will be when it is three times as old as its mother was when she was one-half as old as the monkey will be when it is as old as its mother will be when she is four times as old as the monkey was when it was twice as old as its mother was when she was one-third as old as the monkey was when it was as old as its mother was when she was three times as old as the monkey was when it was one-fourth as old as its is now. How long is the banana?
(Spoiler solution using, guess what, Linogram....)
define object {
param number density;
number length, weight;
constraints { density * length = weight; }
draw { &dump_all; }
}
object banana(density = 24/16), rope(density = 1/3);
number monkey_age, mother_age;
number monkey_weight, weight_weight;
constraints {
monkey_weight * 16 = mother_age;
monkey_age + mother_age = 30;
rope.length = monkey_age;
monkey_weight / 2 + banana.weight =
1/4 * (rope.weight + weight_weight);
mother_age = 1/2 * 3 * 1/2 * 4 * 2 * 1/3 * 3 * 1/4 * monkey_age;
monkey_weight = weight_weight;
}
draw { banana; }
__END__
use Data::Dumper;
sub dump_all {
my $h = shift;
print Dumper($h);
# for my $var (sort keys %$h) {
# print "$var = $h->{$var}\n";
# }
}
OK, seriously, how often do you get to write a program that includes the directive draw { banana; }?
The output is:
$VAR1 = bless( {
'length' => '0.479166666666667',
'weight' => '0.71875',
'density' => '1.5'
}, 'Environment' );
So the length of the banana is 0.479166666666667 feet, which is 5.75 inches.
[Other articles in category /linogram] permanent link
Tue, 03 Jan 2006
Islamic inheritance law
Since Linogram
incorporates a generic linear equation solver, it can be used to solve
problems that have nothing to do with geometry. I don't claim that
the following problem is a "practical application" of
Linogram or of the techniques of HOP. But I did find it
interesting.
An early and extremely influential book on algebra was Kitab al-jabr wa l-muqabala ("Book of Restoring and Balancing"), written around 850 by Muhammad ibn Musa al-Khwarizmi. In fact, this book was so influential in Europe that it gave us the word "algebra", from the "al-jabr" in the title. The word "algorithm" itself is a corrupted version of "al-Khwarizmi".
One of the types of problems that al-Khwarizmi treats extensively in his book is the problem of computing inheritances under Islamic law. Here's a simple example:
A woman dies, leaving her husband, a son, and three daughters.
Under the law of the time, the husband is entitled to 1/4 of the woman's estate, daughters to equal shares of the remainder, and sons to shares that are twice the daughters'. So a little arithmetic will find that the son receives 30%, and the three daughters 15% each. No algebra is required for this simple problem.
Here's another simple example, one I made up:
A man dies, leaving two sons. His estate consists of ten dirhams of ready cash and ten dirhams as a claim against one of the sons, to whom he has loaned the money.
There is more than one way to look at this, depending on the prevailing law and customs. For example, you might say that the death cancels the debt, and the two sons each get half of the cash, or 5 dirhams. But this is not the solution chosen by al-Khwarismi's society. (Nor by ours.)
Instead, the estate is considered to have 20 dirhams in assets, which are split evenly between the sons. Son #1 gets half, or 10 dirhams, in cash; son #2, who owes the debt, gets 10 dirhams, which cancels his debt and leaves him at zero.
This is the fairest method of allocation because it is the only one that gives the debtor son neither an incentive nor a disincentive to pay back the money. He won't be withholding cash from his dying father in hopes that dad will die and leave him free; nor will he be out borrowing from his friends in a desparate last-minute push to pay back the debt before dad kicks the bucket.
However, here is a more complicated example:
A man dies, leaving two sons and bequeathing one-third of his estate to a stranger. His estate consists of ten dirhams of ready cash and ten dirhams as a claim against one of the sons, to whom he has loaned the money.
According to the Islamic law of the time, if son #2's share of the estate is not large enough to enable him to pay back the debt completely, the remainder is written off as uncollectable. But the stranger gets to collect his legacy before the shares of the rest of the estate is computed.
We need to know son #2's share to calculate the writeoff. But we need to know the writeoff to calculate the value of the estate, we need the value of the estate to calculate the bequest to the stranger, and the need to know the size of the bequest to calculate the size of the shares. So this is a problem in algebra.
In Linogram, we write:
number estate, writeoff, share, stranger, cash = 10, debt = 10;
Then the laws introduce the following constraints: The total estate is the cash on hand, plus the collectible part of the debt:
constraints {
estate = cash + (debt - writeoff);
Son #2 pays back part of his debt with his share of the estate; the rest of the debt is written off:
debt - share = writeoff;
The stranger gets 1/3 of the total estate:
stranger = estate / 3;
Each son gets a share consisting of half of the value of the estate after the stranger is paid off:
share = (estate - stranger) / 2;
}
Linogram will solve the equations and try to "draw" the result. We'll tell Linogram that the way to "draw" this "picture" is just to print out the solutions of the equations:
draw { &dump_all; }
__END__
use Data::Dumper;
sub dump_all {
my $h = shift;
print Dumper($h);
}
And now we can get the answer by running Linogram on this file:
% perl linogram.pl inherit1
$VAR1 = bless( {
'estate' => 15,
'debt' => 10,
'share' => '5',
'writeoff' => 5,
'stranger' => 5,
'cash' => 10
}, 'Environment' );
Here's the solution found by Linogram: Of the 10 dirham debt owed by son #2, 5 dirhams are written off. The estate then consists of 10 dirhams in cash and the 5 dirham debt, totalling 15. The stranger gets one-third, or 5. The two sons each get half of the remainder, or 5 each. That means that the rest of the cash, 5 dirhams, goes to son #1, and son #2's inheritance is to have the other half of his debt cancelled.
OK, that was a simple example. Suppose the stranger was only supposed to get 1/4 of the estate instead of 1/3? Then the algebra works out differently:
$VAR1 = bless( {
'estate' => 16,
'debt' => 10,
'share' => 6,
'writeoff' => 4,
'stranger' => 4,
'cash' => 10
}, 'Environment' );
Here only 4 dirhams of son #2's debt is forgiven. This leaves an estate of 16 dirhams. 1/4 of the estate, or 4 dirhams, is given to the stranger, leaving 12. Son #1 receives 6 dirhams cash; son #2's 6 dirham debt is cancelled.
(Notice that the rules always cancel the debt; they never leave anyone owing money to either their family or to strangers after the original creditor is dead.)
These examples are both quite simple, and you can solve them in your head with a little tinkering, once you understand the rules. But here is one that al-Khwarizmi treats that I could not do in my head; this is the one that inspired me to pull out Linogram. It is as before, but this time the bequest to the stranger is 1/5 of the estate plus one extra dirham. The Linogram specification is:
number estate, writeoff, share, stranger, cash = 10, debt = 10;
constraints {
estate = cash + debt - writeoff;
debt = share + writeoff;
stranger = estate / 5 + 1;
share = (estate - stranger)/2;
}
draw { &dump_all; }
__END__
use Data::Dumper;
sub dump_all {
my $h = shift;
print Dumper($h);
}
The solution:
$VAR1 = bless( {
'estate' => '15.8333333333333',
'debt' => 10,
'share' => '5.83333333333333',
'writeoff' => '4.16666666666667',
'stranger' => '4.16666666666667',
'cash' => 10
}, 'Environment' );
Son #2 has 4 1/6 dirhams of his debt forgiven. He now owes the estate 5 5/6 dirhams. This amount, plus the cash, makes 15 5/6 dirhams. The stranger receives 1/5 of this, or 3 1/6 dirhams, plus 1. This leaves 11 2/3 dirhams to divide equally between the two sons. Son #1 gets the remaining 5 5/6 dirhams cash; son #2's remaining 5 5/6 dirham debt is cancelled.
(Examples in this message, except the one I made up, were taken from Episodes in the Mathematics of Medieval Islam, by J.L. Berggren (Springer, 1983). Thanks to Walt Mankowski for lending this to me.
[Other articles in category /linogram] permanent link
Mark Dominus:
One of the types of problems that al-Khwarizmi treats extensively in his book is the problem of computing inheritances under Islamic law.
Well, these examples are getting sillier and sillier, but I still think they're kind of fun. I was thinking about the Islamic estate law stuff, and I remembered that there's a famous problem, perhaps invented about 1500 years ago, that says of the Greek mathematician Diophantus:
He was a boy for one-sixth of his life. After one-twelfth more, he acquired a beard. After another one-seventh, he married. In the fifth year after his marriage his son was born. The son lived half as many as his father. Diophantus died 4 years after his son. How old was Diophantus when he died?
So let's haul out Linogram again:
number birth, eo_boyhood, beard, marriage, son, son_dies, death, life;
constraints {
eo_boyhood - birth = life / 6;
beard = eo_boyhood + life / 12;
marriage = beard + life / 7;
son = marriage + 5;
(son_dies - son) = life / 2;
death = son_dies + 4;
life = death - birth;
}
draw { &dump_all; }
__END__
use Data::Dumper;
sub dump_all {
my $h = shift;
print Dumper($h);
}
And the output is:
$VAR1 = bless( {
'life' => '83.9999999999999'
}, 'Environment' );
84 years is indeed the correct solution. (That is a really annoying roundoff error. Gosh, how I hate floating-point numbers! The next version of Linogram is going to use rationals everywhere.)
Note that because all the variables except for "life" are absolute dates rather than durations, they are all indeterminate. If we add the equation "birth = 211" for example, then we get an output that lists the years in which all the other events occurred.
[Other articles in category /linogram] permanent link






