Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 25 Nov 2018
A couple of years back I was thinking about how to draw a good approximation to an equilateral triangle on a piece of graph paper. There are no lattice points that are exactly the vertices of an equilateral triangle, but you can come close, and one way to do it is to find integers !!a!! and !!b!! with !!\frac ba\approx \sqrt 3!!, and then !!\langle 0, 0\rangle, \langle 2a, 0\rangle,!! and !!\langle a, b\rangle!! are almost an equilateral triangle.
But today I came back to it for some reason and I wondered if it would be possible to get an angle closer to 60°, or numbers that were simpler, or both, by not making one of the sides of the triangle perfectly horizontal as in that example.
So okay, we want to find !!P = \langle a, b\rangle!! and !!Q = \langle c,d\rangle!! so that the angle !!\alpha!! between the rays !!\overrightarrow{OP}!! and !!\overrightarrow{OQ}!! is as close as possible to !!\frac\pi 3!!.
The first thing I thought of was that the dot product !!P\cdot Q = |P||Q|\cos\alpha!!, and !!P\cdot Q!! is super-easy to calculate, it's just !!ac+bd!!. So we want $$\frac{ad+bc}{|P||Q|} = \cos\alpha \approx \frac12,$$ and everything is simple, except that !!|P||Q| = \sqrt{a^2+b^2}\sqrt{c^2+d^2}!!, which is not so great.
Then I tried something else, using high-school trigonometry. Let !!\alpha_P!! and !!\alpha_Q!! be the angles that the rays make with the !!x!!-axis. Then !!\alpha = \alpha_Q - \alpha_P = \tan^{-1} \frac dc - \tan^{-1} \frac ba!!, which we want close to !!\frac\pi3!!.
Taking the tangent of both sides and applying the formula $$\tan(q-p) = \frac{\tan q - \tan p}{1 + \tan q \tan p}$$ we get $$ \frac{\frac dc - \frac ba}{1 + \frac dc\frac ba} \approx \sqrt3.$$ Or simplifying a bit, the super-simple $$\frac{ad-bc}{ac+bd} \approx \sqrt3.$$
After I got there I realized that my dot product idea had almost worked. To get rid of the troublesome !!|P||Q|!! you should consider the cross product also. Observe that the magnitude of !!P\times Q!! is !!|P||Q|\sin\alpha!!, and is also $$\begin{vmatrix} a & b & 0 \\ c & d & 0 \\ 1 & 1 & 1 \end{vmatrix} = ad - bc$$ so that !!\sin\alpha = \frac{ad-bc}{|P||Q|}!!. Then if we divide, the !!|P||Q|!! things cancel out nicely: $$\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = \frac{ad-bc}{ac+bd}$$ which we want to be as close as possible to !!\sqrt 3!!.
Okay, that's fine. Now we need to find some integers !!a,b,c,d!! that do what we want. The usual trick, “see what happens if !!a=0!!”, is already used up, since that's what the previous article was about. So let's look under the next-closest lamppost, and let !!a=1!!. Actually we'll let !!b=1!! instead to keep things more horizonal. Then, taking !!\frac74!! as our approximation for !!\sqrt3!!, we want
$$\frac{ad-c}{ac+d} = \frac74$$
or equivalently $$\frac dc = \frac{7a+4}{4a-7}.$$
Now we just tabulate !!7a+4!! and !!4a-7!! looking for nice fractions:
| !!a!! | !!d =!! !!7a+4!! | !!c=!! !!4a-7!! |
|---|---|---|
| 2 | 18 | 1 |
| 3 | 25 | 5 |
| 4 | 32 | 9 |
| 5 | 39 | 13 |
| 6 | 46 | 17 |
| 7 | 53 | 21 |
| 8 | 60 | 25 |
| 9 | 67 | 29 |
| 10 | 74 | 33 |
| 11 | 81 | 37 |
| 12 | 88 | 41 |
| 13 | 95 | 45 |
| 14 | 102 | 49 |
| 15 | 109 | 53 |
| 16 | 116 | 57 |
| 17 | 123 | 61 |
| 18 | 130 | 65 |
| 19 | 137 | 69 |
| 20 | 144 | 73 |
Each of these gives us a !!\langle c,d\rangle!! point, but some are much better than others. For example, in line 3, we have take !!\langle 5,25\rangle!! but we can use !!\langle 1,5\rangle!! which gives the same !!\frac dc!! but is simpler. We still get !!\frac{ad-bc}{ac+bd} = \frac 74!! as we want.
Doing this gives us the two points !!P=\langle 3,1\rangle!! and !!Q=\langle 1, 5\rangle!!. The angle between !!\overrightarrow{OP}!! and !!\overrightarrow{OQ}!! is then !!60.255°!!. This is exactly the same as in the approximately equilateral !!\langle 0, 0\rangle, \langle 8, 0\rangle,!! and !!\langle 4, 7\rangle!! triangle I mentioned before, but the numbers could not possibly be easier to remember. So the method is a success: I wanted simpler numbers or a better approximation, and I got the same approximation with simpler numbers.
To draw a 60° angle on graph paper, mark !!P=\langle 3,1\rangle!! and !!Q=\langle 1, 5\rangle!!, draw lines to them from the origin with a straightedge, and there is your 60° angle, to better than a half a percent.
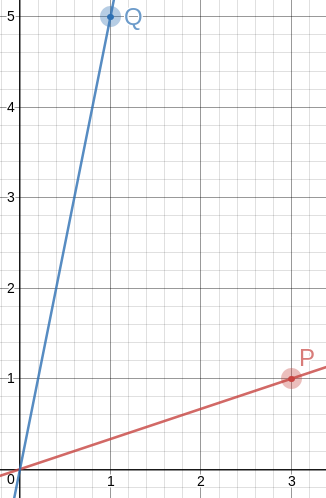
There are some other items in the table (for example row 18 gives !!P=\langle 18,1\rangle!! and !!Q=\langle 1, 2\rangle!!) but because of the way we constructed the table, every row is going to give us the same angle of !!60.225°!!, because we approximated !!\sqrt3\approx\frac74!! and !!60.225° = \tan^{-1}\frac74!!. And the chance of finding numbers better than !!\langle 3,1\rangle!! and !!\langle 1, 5\rangle!! seems slim. So now let's see if we can get the angle closer to exactly !!60°!! by using a better approximation to !!\sqrt3!! than !!\frac 74!!.
The next convergents to !!\sqrt 3!! are !!\frac{19}{11}!! and !!\frac{26}{15}!!. I tried the same procedure for !!\frac{19}{11}!! and it was a bust. But !!\frac{26}{15}!! hit the jackpot: !!a=4!! gives us !!15a-26 = 34!! and !!26a-15=119!!, both of which are multiples of 17. So the points are !!P=\langle 4,1\rangle!! and !!Q=\langle 2, 7\rangle!!, and this time the angle between the rays is !!\tan^{-1}\frac{26}{15} = 60.018°!!. This is as accurate as anyone drawing on graph paper could possibly need; on a circle with a one-mile radius it is an error of 20 inches.
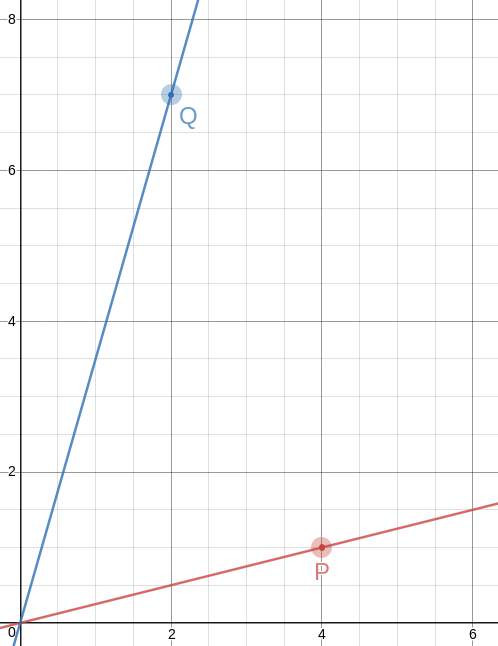
Of course, the triangles you get are no longer equilateral, not even close. That first one has sides of !!\sqrt{10}, \sqrt{20}, !! and !!\sqrt{26}!!, and the second one has sides of !!\sqrt{17}, \sqrt{40}, !! and !!\sqrt{53}!!. But! The slopes of the lines are so simple, it's easy to construct equilateral triangles with a straightedge and a bit of easy measuring. Let's do it on the !!60.018°!! angle and see how it looks.
!!\overrightarrow{OP}!! has slope !!\frac14!!, so the perpendicular to it has slope !!-4!!, which means that you can draw the perpendicular by placing the straightedge between !!P!! and some point !!P+x\langle -1, 4\rangle!!, say !!\langle 2, 9\rangle!! as in the picture. The straightedge should have slope !!-4!!, which is very easy to arrange: just imagine the little squares grouped into stacks of four, and have the straightedge go through opposite corners of each stack. The line won't necessarily intersect !!\overrightarrow{OQ}!! anywhere great, but it doesn't need to, because we can just mark the intersection, wherever it is:
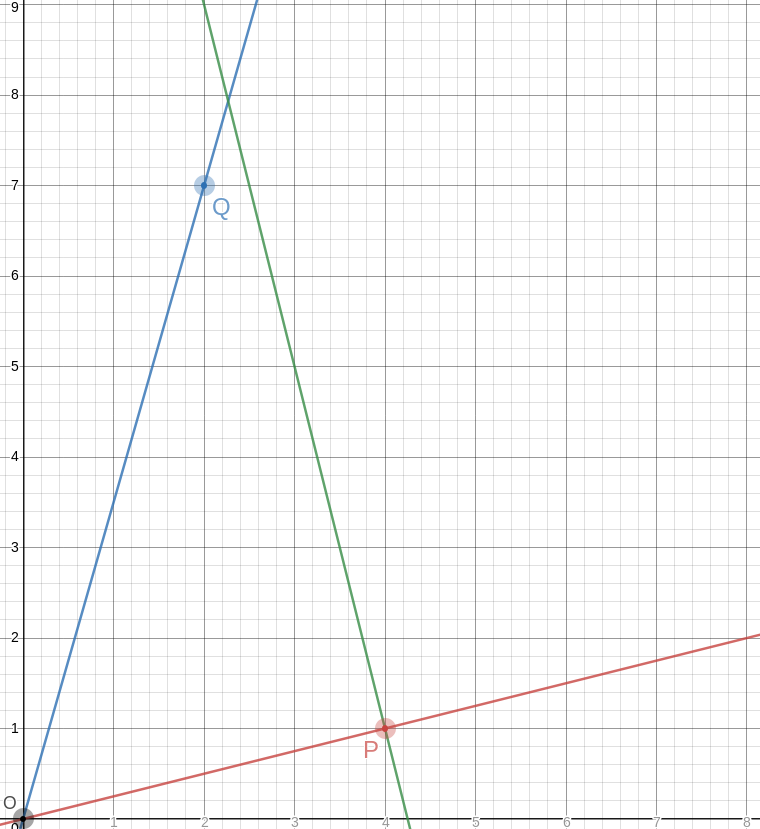
Let's call that intersection !!A!! for “apex”.
The point opposite to !!O!! on the other side of !!P!! is even easier; it's just !!P'=2P =\langle 8, 2\rangle!!. And the segment !!P'A!! is the third side of our equilateral triangle:
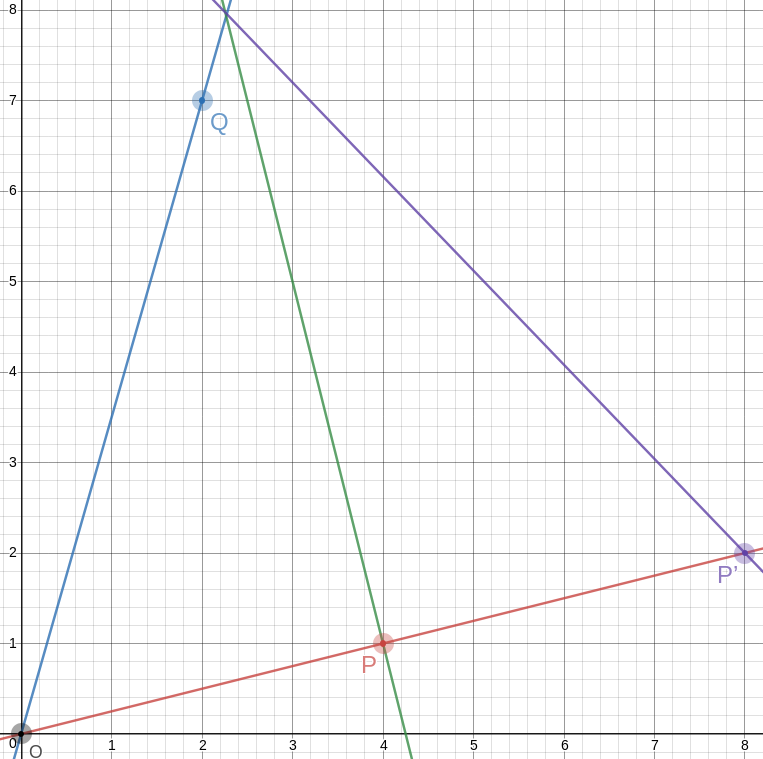
This triangle is geometrically similar to a triangle with vertices at !!\langle 0, 0\rangle, \langle 30, 0\rangle,!! and !!\langle 15, 26\rangle!!, and the angles are just close to 60°, but it is much smaller.
Woot!
[Other articles in category /math] permanent link


