Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 30 Jul 2018
Lost and found authors: The Poppy Seed Cakes
As a very small child, I loved The Poppy Seed Cakes (1924), by Margery Clark. Later I read it to my own kids. Toph never cared for it, but it was by far Katara's favorite book when she was three. The illustrations are by Maud and Miska Petersham, who later won the Caldecott Medal.
(At left, the protagonist, Andrewshek, meeting Auntie Katushka's new white goat, who has run home from the market without her. He is swinging on the gate, which his Autie Katushka has specifically told him not to do, or the chickens will run out into the road. At right, Auntie Katushka arriving from the Old Country. Depicted are the fine feather bed, the umbrella with the crooked handle, and probably the bag of poppy seeds, all of which are plot points.)
As an adult I wanted to know if Margery Clark had written anything else. And the answer was, yes! Margery Clark, I learned, was a pseudonym for the two authors, Margery Closey Quigley and Mary E. Clark, who were librarians in Endicott, New York. The town was full of Russian and Polish immigrants who came there to make shoes, and Andrewshek and his Auntie Katushka were no doubt inspired by real library patrons. I looked up maps of Endicott in 1924 and found the little park with the stream where Andrewshek's picnic was nearly stolen by a swan. I spent way too much time trying to find out if Andrewshek was more likely to be Russian or Polish by poring over census data.
And Quigley had written another book! After Endicott she became a librarian in Montclair, New Jersey and wrote Portrait of a Library (1936) about how the Montclair Public Library was run. I found it fascinating and compelling. One detail I remember is that when automobiles became common, they started to offer a pickup and delivery service, which the citizens loved:
Delivery of books has been added to the borrowing system. Delivery is made by parcel-post, by Postal Telegraph, by the library messenger, and by the A. & P. delivery man. A messenger who spends one day a week following up overdue books was added in the fall of 1930.
She mentions that in 1934, over 3,000 books were delivered via Western Union messenger, with the borrower paying the 10¢ delivery fee. I think it's pretty awesome that they were able to press the A&P guy into library service.
My favorite detail, though, concerned a major renovation to the library building. They took the opportunity to reorganize the layout of the sections and shelves:
… the confusion and the press of work upon assistants and the criticisms from the public about overcrowding at the library came much too thick and fast. At this point an offer of professional services came from one of Montclair's citizens who is an efficiency engineer. Simultaneously government-subsidized workers were assigned to the library.
The findings made by the library staff under the direction of the efficiency engineer became the beginning of a complete physical rearrangement of the main library and of a redistribution of duties among the staff.
“Oh, wow!” I said. “I know who that was!” That was a fun moment.
(But I see now that I was wrong! Montclair was home to two world-famous efficiency engineers, but one of them had died in 1924, and the library renovation was done in 1931–1932. Quigley's efficiency engineer was surely Lillian Moller Gilbreth. Ooops!)
Regrettably, the Internet Archive has only an abridged version of The Poppy Seed Cakes, with only three of the eight stories. I may have it professionally scanned.
[Other articles in category /book] permanent link
Sat, 28 Jul 2018When I was a kid I enjoyed a story called George Washington's Breakfast, which I have since learned was written in 1969 by Jean Fritz. The protagonist is a boy named George Washington Allen who is fascinated by all things related to his namesake. One morning at breakfast he wonders what George Washington ate for his own breakfast. He has read all the books in his school library about George Washington, but does not know this important detail. His grandmother promises him that when he finds out what George Washington had for breakfast, she will cook it for him, whatever it is.
This launches the whole family on an odyssey that takes them as far as Mount Vernon, but even the people at Mount Vernon don't know. In the end George gets lucky: he finds an old book in the attic that authoritatively states that George Washington
breakfasts about seven o'clock on three small Indian hoecakes, and as many dishes of tea.
George is thrilled, and, having looked up hoecake in the dictionary to find out what it is (a corn cake cooked in the fireplace, on a hoe), jumps up from the table. His grandmother asks him where he is going, and of course he is going to the basement to get the hoe. Grandma refuses to cook on a hoe; George objects.
“When you were in George Washington's kitchen in Mount Vernon, did you see any hoes?”
“Well no, but…”
“Did you see any black iron griddles?”
“Yes.”
“Then that's what I'll use.”
This stuck with me for many years, and thinking back on it one day as an adult, I was suddenly certain that George Allen and his family were black, notwithstanding the plump white kid in the illustrations. At some point I even looked up the original publication to see if the kid was black in the 1969 illustrations. Nope, they are by Paul Galdone and he has made George white. A new edition was published in 1998 with new illustrations by Tomie dePaola, again with a white kid. Ms. Fritz died last year at the age of 102, so it is too late to ask her what she had in mind. But it doesn't matter to me; I am sure George is black. There was a trend in the 1960s for white authors of children’s books to make an effort to depict black kids. (For example: The Snowy Day (1962) and its sequels (through 1968); Corduroy (1968); and many others less well-known.)
Anyway, chalk this up as another story that could not happen in 2018. George's family would search on the Internet, and immediately find out about the hoecakes. I don't recall exactly what book it was that George found in the attic, but in a minute’s searching I was able to find out that it was probably Paul Leicester Ford’s George Washington (1896), and the authoritative statement about Washington's hoecake-and-tea breakfast, on page 193, is quoted from Samuel Stearns, a contemporary of Washington's.
The Stearns quotation definitely appeared in Fritz's story; I remember the wording, and even Samuel Stearns rings a bell now that I see his name again.
For oddballs like me and George Washington Allen, who become obsessed by trivial questions, the Internet is a magnificent and glorious boon. I often think that for me, one of the best results of the rise of the Internet is that I can now track down all the books from my childhood that I liked but only half-remember, find out who wrote them and read them again.
[ Addendum 20230807: The “hoe” in hoecake is apparently not a literal garden hoe, but a regional Virginia term for a skillet, as George's grandmother surmised. It was sometimes called a “bread hoe” to distinguish it from a garden hoe. ]
[Other articles in category /book] permanent link
Thu, 26 Jul 2018There are well-known tests if a number (represented as a base-10 numeral) is divisible by 2, 3, 5, 9, or 11. What about 7?
Let's look at where the divisibility-by-9 test comes from. We add up the digits of our number !!n!!. The sum !!s(n)!! is divisible by !!9!! if and only if !!n!! is. Why is that?
Say that !!d_nd_{n-1}\ldots d_0!! are the digits of our number !!n!!. Then
$$n = \sum 10^id_i.$$
The sum of the digits is
$$s(n) = \sum d_i$$
which differs from !!n!! by $$\sum (10^i-1)d_i.$$ Since !!10^i-1!! is a multiple of !!9!! for every !!i!!, every term in the last sum is a multiple of !!9!!. So by passing from !!n!! to its digit sum, we have subtracted some multiple of !!9!!, and the residue mod 9 is unchanged. Put another way:
$$\begin{align} n &= \sum 10^id_i \\ &\equiv \sum 1^id_i \pmod 9 \qquad\text{(because $10 \equiv 1\pmod 9$)} \\ &= \sum d_i \end{align} $$
The same argument works for the divisibility-by-3 test.
For !!11!! the analysis is similar. We add up the digits !!d_0+d_2+\ldots!! and !!d_1+d_3+\ldots!! and check if the sums are equal mod 11. Why alternating digits? It's because !!10\equiv -1\pmod{11}!!, so $$n\equiv \sum (-1)^id_i \pmod{11}$$
and the sum is zero only if the sum of the positive terms is equal to the sum of the negative terms.
The same type of analysis works similarly for !!2, 4, 5, !! and !!8!!. For !!4!! we observe that !!10^i\equiv 0\pmod 4!! for all !!i>1!!, so all but two terms of the sum vanish, leaving us with the rule that !!n!! is a multiple of !!4!! if and only if !!10d_1+d_0!! is. We could simplify this a bit: !!10\equiv 2\pmod 4!! so !!10d_1+d_0 \equiv 2d_1+d_0\pmod 4!!, but we don't usually bother. Say we are investigating !!571496!!; the rule tells us to just consider !!96!!. The "simplified" rule says to consider !!2\cdot9+6 = 24!! instead. It's not clear that that is actually easier.
This approach works badly for divisibility by 7, because !!10^i\bmod 7!! is not simple. It repeats with period 6.
$$\begin{array}{c|cccccc|ccc} i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\ %10^i & 1 & 10 & 100 & 1000 & 10000 & \ldots \\ 10^i\bmod 7 & 1 & 3 & 2 & 6 & 4 & 5 & 1 & 3 & 2 & 6 & 4 &\ldots \\ \end{array} $$
The rule we get from this is:
Take the units digit. Add three times the ones digit, twice the hundreds digit, six times the thousands digit… (blah blah blah) and the original number is a multiple of !!7!! if and only if the sum is also.
For example, considering !!12345678!! we must calculate $$\begin{align} 12345678 & \Rightarrow & 3\cdot1 + 1\cdot 2 + 5\cdot 3 + 4\cdot 4 + 6\cdot 5 + 2\cdot6 + 3\cdot 7 + 1\cdot 8 & = & 107 \\\\ 107 & \Rightarrow & 2\cdot1 + 3\cdot 0 + 1\cdot7 & = & 9 \end{align} $$ and indeed !!12345678\equiv 107\equiv 9\pmod 7!!.
My kids were taught the practical divisibility tests in school, or perhaps learned them from YouTube or something like that. Katara was impressed by my ability to test large numbers for divisibility by 7 and asked how I did it. At first I didn't think about my answer enough, and just said “Oh, it's not hard, just divide by 7 and look at the remainder.” (“Just count the legs and divide by 4.”) But I realized later that there are several tricks I was using that are not obvious. First, she had never learned short division. When I was in school I had been tormented extensively with long division, which looks like this:
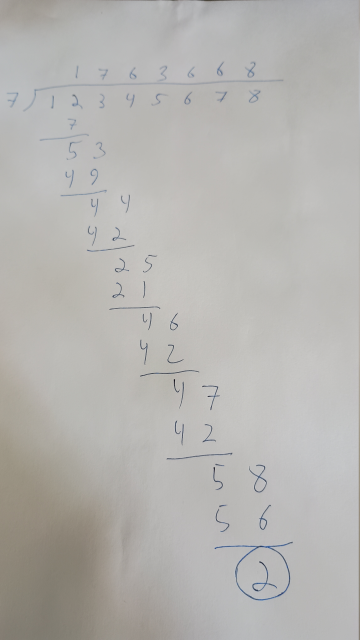
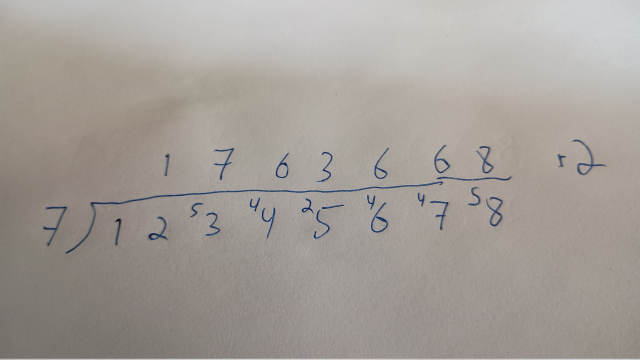
Another one of the tricks I was using that wasn't obvious to Katara was: we don't care about the quotient anyway, only the remainder. So when I did this in my head, I discarded the parts of the calculation that were about the quotient, and only kept the steps that pertained to the remainder. The way I was actually doing this sounded like this in my mind:
7 into 12 leaves 5. 7 into 53 leaves 4. 7 into 44 leaves 2. 7 into 25 leaves 4. 7 into 46 leaves 4. 7 into 57 leaves 5. 7 into 58 leaves 9. The answer is 9.
At each step, we consider only the leftmost part of the number, starting with !!12!!. !!12\div 7 !! has a remainder of 5, and to this 5 we append the next digit of the dividend, 3, giving 53. Then we continue in the same way: !!53\div 7!! has a remainder of 4, and to this 4 we append the next digit, giving 44. We never calculate the quotient at all.
I explained the idea with a smaller example, like this:
Suppose you want to see if 1234 is divisible by 7. It's 1200-something, so take away 700, which leaves 500-something. 500-what? 530-something. So take away 490, leaving 40-something. 40-what? 44. Now take away 42, leaving 2. That's not 0, so 1234 is not divisible by 7.
This is how I actually do it. For me this works reasonably well up to 13, and after that it gets progressively more difficult until by 37 I can't effectively do it at all. A crucial element is having the multiples of the divisor memorized. If you're thinking about the mod-13 residue of 680-something, it is a big help to know immediately that you can subtract 650.
A year or two ago I discovered a different method, which I'm sure must be ancient, but is interesting because it's quite different from the other methods I described.
Suppose that the final digit of !!n!! is !!b!!, so that !!n=10a+b!!. Then !!-2n = -20a-2b!!, and this is a multiple of !!7!! if and only if !!n!! is. But !!-20a\equiv a\pmod7 !!, so !!a-2b!! is a multiple of !!7!! if and only if !!n!! is. This gives us the rule:
To check if !!n!! is a multiple of 7, chop off the last digit, double it, and subtract it from the rest of the number. Repeat until the answer becomes obvious.
For !!1234!! we first chop off the !!4!! and subtract !!2\cdot4!! from !!123!! leaving !!115!!. Then we chop off the !!5!! and subtract !!2\cdot5!! from !!11!!, leaving !!1!!. This is not a multiple of !!7!!, so neither is !!1234!!. But with !!1239!!, which is a multiple of !!7!!, we get !!123-2\cdot 9 = 105!! and then !!10-2\cdot5 = 0!!, and we win.
In contrast to the other methods in this article, this method does not tell you the remainder on dividing because it does not preserve the residue mod 7. When we started with !!1234!! we ended with !!1!!. But !!1234\not\equiv 1\pmod 7!!; rather !!1234\equiv 2!!. Each step in this method multiplies the residue by -2, or, if you prefer, by 5. The original residue was 2, so the final residue is !!2\cdot-2\cdot-2 = 8 \equiv 1\pmod 7!!. (Or, if you prefer, !!2\cdot 5\cdot 5= 50 \equiv 1\pmod 7!!.) But if we only care about whether the residue is zero, multiplying it by !!-2!! doesn't matter.
There are some shortcuts in this method too. If the final digit is !!7!!, then rather than doubling it and subtracting 14 you can just chop it off and throw it away, going directly from !!10a+7!! to !!a!!. If your number is !!10a+8!! you can subtract !!7!! from it to make it easier to work with, getting !!10a+1!! and then going to !!a-2!! instead of to !!a-16!!. Similarly when your number ends in !!9!! you can go to !!a-4!! instead of to !!a-18!!. And on the other side, if it ends in !!4!! it is easier to go to !!a-1!! instead of to !!a-8!!.
But even with these tricks it's not clear that this is faster or easier than just doing the short division. It's the same number of steps, and it seems like each step is about the same amount of work.
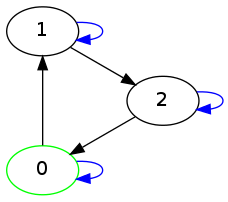
Finally, I once wowed Katara on an airplane ride by showing her this:

To check !!1429!! using this device, you start at ⓪. The first digit is !!1!!, so you follow one black arrow, to ①, and then a blue arrow, to ③. The next digit is !!4!!, so you follow four black arrows, back to ⓪, and then a blue arrow which loops around to ⓪ again. The next digit is !!2!!, so you follow two black arrows to ② and then a blue arrow to ⑥. And the last digit is 9 so you then follow 9 black arrows to ① and then stop. If you end where you started, at ⓪, the number is divisible by 7. This time we ended at ①, so !!1429!! is not divisible by 7. But if the last digit had been !!1!! instead, then in the last step we would have followed only one black arrow from ⑥ to ⓪, before we stopped, so !!1421!! is a multiple of 7.
This probably isn't useful for mental calculations, but I can imagine that if you were stuck on a long plane ride with no calculator and you needed to compute a lot of mod-7 residues for some reason, it could be quicker than the short division method. The chart is easy to construct and need not be memorized. The black arrows obviously point from !!n!! to !!n+1!!, and the blue arrows all point from !!n!! to !!10n!!.
I made up a whole set of these diagrams and I think it's fun to see how the conventional divisibility rules turn up in them. For example, the rule for divisibility by 3 that says just add up the digits:
Or the rule for divisibility by 5 that says to ignore everything but the last digit:
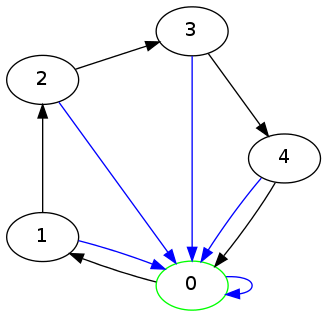
[ Addendum 20201122: Testing for divisibility by 19. ]
[ Addendum 20220106: Another test for divisibility by 7. ]
[Other articles in category /math] permanent link
Wed, 25 Jul 2018In my email today I found a note I sent to myself on 24 June 2015 that says only:
Self-warming sake bottle
which would be useful, if you don't drink your sake so quickly that it is gone before it has cooled.
As far as I know, these are not common and perhaps do not exist at all. Why not? Is this a billion-dollar idea?
A few problems come to mind. If the bottle has a cord, it will be hard to pour and will be easily upset. Maybe the best choice here would be a special power supply with relatively high voltage and a thin cord such as is used for earbuds. But this might be dangerous, or impractical for other reasons I am not thinking of.
I think battery power is also probably impractical. Heating requires a lot of energy and batteries don't supply enough. They would need to be frequently replaced, which gets expensive.
Also temperature control might be troublesome. You would need some sort of thermostat in the bottle. Typical inexpensive heating containers and immersion heaters are for bringing water to a boil, which is much simpler than warming sake to the right temperature: just dump in as much heat as possible, as quickly as possible, and perhaps also arrange to have the heat shut off if the heating element gets up to 100°C. This is much too hot for sake.
I think a more practical solution would be a tabletop hot water bath with a bottle-shaped depression in it. The hot water bath could have the thermostat and be permanently attached to a wall outlet. You insert the bottle in its bath to keep it warm when you are not pouring.
This seems practical enough that I imagine it already exists. In fact it occurs to me that I owned a similar sort of warmer at one point, for warming baby bottles. But a quick perusal of available sake warmers suggests that this approach is not common. What gives?
[Other articles in category /food] permanent link
Mon, 23 Jul 2018
Operations that are not quite associative
The paper “Verification of Identities” (1997) of Rajagopalan and Schulman discusses fast ways to test whether a binary operation on a finite set is associative. In general, there is no method that is faster than the naïve algorithm of simply checking whether $$a\ast(b\ast c) = (a\ast b)\ast c$$ for all triples !!\langle a, b, c\rangle!!. This is because:
For every !!n≥3!!, there exists an operation with just one nonassociative triple.
(Page 3.)
But R&S do not give an example. I now have a very nice example, and I think the process that led me to it is a good example of Lower Mathematics at work.
Let's say that an operation !!\ast!! is “good” if it is associative except in exactly one case. We want to find a “good” operation. My first idea was that if we could find a primitive good operation on a set of 3 elements, we could probably extend it to give a good operation on a larger set. Say the set is !!\{a_0, a_1, a_2, b_0, b_1, \ldots, b_{n-4}\}!!. We just need to define the extended operation so that if either of the operands is !!b_i!!, it is associative, and if both operands are !!a_i!! then it is the same as the primitive good operation we already found. The former part is easy: just make it constant, say !!x\ast y = b_0!! except when !!x,y\in\{a_0, a_1, a_2\}!!.
So now all we need to do is find a single good primitive operation, and I did not expend any thought on this at all. There are only !!3^9=19683!! binary operations, and we could quite easily write a program to check them all. In fact, we can do better: generate a binary operation at random and check it. If it's not the primitive good operation we want, just throw it away and try again. This could take longer to run than the exhaustive search, if there happen to be very few good operations and if the program is unlucky, but the program is easier to write, and the run time will be utterly insignificant either way.
I wrote the program, which instantly produced:
$$ \begin{array}{c|ccc} \ast & 0 & 1 & 2 \\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 2 & 0 & 1 & 2 \end{array} $$
This is associative except for the case !!1\ast(2\ast 1) \ne (1\ast 2)\ast 1!!. This solves the problem. But confirming that this is a good operation requires manually checking 27 cases, or a perhaps not-immediately-obvious case analysis.
But on a later run of the program, I got lucky and it found a simpler operation, which I can explain without a table:
!!a\ast b = 0!!, except !!2\ast 1=2!!.
Now we don't have to check 27 cases. The operation is simpler, so the proof is too: We know !!b\ast c\ne 1!!, so !!a\ast(b\ast c) !! must be !!0!!. And the only way !!(a \ast b)\ast c \ne 0!! can occur is when !!a\ast b=2!! and !!c=1!!, so !!a=2, b=1, c=1!!.
Now we can even dispense with the construction that extended the operation from !!3!! to !!n!! elements, because the description of the extended operation is the same. We wanted to extend it to be constant whenever !!a!! or !!b!! was larger than !!2!!, and that's what the description already says!
So that reduces the whole thing to about two sentences, which explain the example and why it works. But when reduced in that way, you see how the example works but not how you might go about finding it. I think the interesting part is to see how to get there, and quite a lot of mathematical education tends to over-emphasize analysis (“how can we show this is a good operation?”) at the expense of synthesis (“how can we find a good operation?”).
The exhaustive search would probably have produced the simple operation early on in its run, so there is something to be said for that approach too.
[Other articles in category /math] permanent link
Fri, 20 Jul 2018Volume was way down in May and June, mainly because of giant work crises that ate all my energy. I will try to get back on track now.
May
- The imperative mood [1] [2] [3] [4]
- An anti-lipogrammatic precommitment
- Non-transitive relations
- Cranial nerves
- I found lipograms hard to put down
- Seen…
- One of the weirdest conversations I have ever had…
- A lipogrammatic warning
- Blog article spam
- A riddle!
- Butterer
- Another missing word
- Mysterious markings on my Water-Pik
- Well okay then!
- Spruce hats
- Philadelphia street tree streets
- Cautionary tale about pseudonyms
- Today in Internet advertising
- App update schedule
June
In the past I have boldfaced posts that seemed more likely to be of general interest. None of these seem likely to be of general interest.
Also, I think it is time to stop posting these roundups. By now everyone who wants to know about shitpost.plover.com is aware of it and can follow along without prompting. So I expect this will be the last of these posts. Shitposting will continue, but without these summaries.
[Other articles in category /meta/shitpost] permanent link
Mon, 16 Jul 2018[ I wrote this in 2007 and it seems I forgot to publish it. Enjoy! ]
I eat pretty much everything. Except ketchup. I can't stand ketchup. When I went to Taiwan a couple of years ago my hosts asked if there were any foods I didn't eat. I said no, except for ketchup.
"Ketchup? You mean that red stuff?"
Right. Yes, it's strange.
When I was thirteen my grandparents took me to Greece, and for some reason I ate hardly anything but souvlaki the whole time. When I got home, I felt like a complete ass. I swore that I would never squander another such opportunity, and that if I ever went abroad again I would eat absolutely everything that was put before me.
This is a good policy not just because it exposes me to a lot of delicious and interesting food, and not just because it prevents me from feeling like a complete ass, but also because I don't have to worry that perhaps my hosts will be insulted or disappointed that I won't eat the food they get for me.
On my second trip to Taiwan, I ate at a hot pot buffet restaurant. They give you a pot of soup, and then you go to the buffet and load up with raw meat and vegetables and things, and cook them at your table in the soup. It's fun. In my soup there were some dark reddish-brown cubes that had approximately the same texture as soft tofu. I didn't know what it was, but I ate it and tried to figure it out.
The next day I took the bus to Lishan (梨山), and through good fortune was invited to eat dinner with a Taiwanese professor of criminology and his family. The soup had those red chunks in it again, and I said "I had these for lunch yesterday! What are they?" I then sucked one down quickly, because sometimes people interpret that kind of question as a criticism, and I didn't want to offend the professor.
Actually it's much easier to ask about food in China than it is in, say, Korea. Koreans are defensive about their cuisine. They get jumpy if you ask what something is, and are likely to answer "It's good. Just eat it!". They are afraid that the next words out of your mouth will be something about how bad it smells. This is because the Japanese, champion sneerers, made about one billion insulting remarks about smelly Korean food while they were occupying the country between 1911 and 1945. So if you are in Korea and you don't like the food, the Koreans will take it very personally.
Chinese people, on the other hand, know that they have the best food in the world, and that everyone loves Chinese food. If you don't like it, they will not get offended. They will just conclude that you are a barbarian or an idiot, and eat it themselves.
Anyway, it turns out that the reddish-brown stuff was congealed duck's blood. Okay. Hey, I had congealed duck blood soup twice in two days! No way am I going home from this trip feeling like an ass.
So the eat-absolutely-everything policy has worked out well for me, and although I haven't liked everything, at least I don't feel like I wasted my time.
The only time I've regretted the policy was on my first trip to Taiwan. I was taken out to dinner and one of the dishes turned out to be pieces of steamed squid. That's not my favorite food, but I can live with it. But the steamed squid was buried under a big, quivering mound of sugared mayonnaise.
I remembered my policy, and took a bite. I'm sure I turned green.
So that's the food that I couldn't eat.
[ Some of this 2007 article duplicates stuff I have said since; for example I cut out the chicken knuckles story, which would have been a repeat. Also previously; also previously; and another one ]
[Other articles in category /food] permanent link
Wed, 11 Jul 2018Here is another bit of Perl code:
sub function {
my ($self, $cookie) = @_;
$cookie = ref $cookie && $cookie->can('value') ? $cookie->value : $cookie;
...
}
The idea here is that we are expecting $cookie to be either a
string, passed directly, or some sort of cookie object with a value
method that will produce the desired string.
The ref … && … condition
distinguishes the two situations.
A relatively minor problem is that if someone passes an object with no
value method, $cookie will be set to that object instead of to a
string, with mysterious results later on.
But the real problem here is that the function's interface is not simple enough. The function needs the string. It should insist on being passed the string. If the caller has the string, it can pass the string. If the caller has a cookie object, it should extract the string and pass the string. If the caller has some other object that contains the string, it should extract the string and pass the string. It is not the job of this function to know how to extract cookie strings from every possible kind of object.
I have seen code in which this obsequiousness has escalated to
absurdity. I recently saw a function whose job was to send an email.
It needs an EmailClass object, which encapsulates the message
template and some of the headers. Here is how it obtains that object:
12 my $stash = $args{stash} || {};
…
16 my $emailclass_obj = delete $args{emailclass_obj}; # isn't being passed here
17 my $emailclass = $args{emailclass_name} || $args{emailclass} || $stash->{emailclass} || '';
18 $emailclass = $emailclass->emailclass_name if $emailclass && ref($emailclass);
…
60 $emailclass_obj //= $args{schema}->resultset('EmailClass')->find_by_name($emailclass);
Here the function needs an EmailClass object. The caller can pass
one in $args{emailclass_obj}. But maybe the caller doesn't have
one, and only knows the name of the emailclass it wants to use. Very
well, we will allow it to pass the string and look it up later.
But that string could be passed in any of $args{emailclass_name}, or
$args{emailclass}, or $args{stash}{emailclass} at the caller's
whim and we have to rummage around hoping to find it.
Oh, and by the way, that string might not be a string! It might be the actual object, so there are actually seven possibilities:
$args{emailclass}
$args{emailclass_obj}
$args{emailclass_name}
$args{stash}{emailclass}
$args{emailclass}->emailclass_name
$args{emailclass_name}->emailclass_name
$args{stash}{emailclass}->emailclass_name
Notice that if $args{emailclass_name} is actually an emailclass
object, the name will be extracted from that object on line 18, and
then, 42 lines later, the name may be used to perform a database
lookup to recover the original object again.
We hope by the end of this rigamarole that $emailclass_obj will
contain an EmailClass object, and $emailclass will contain its
name. But can you find any combinations of arguments where this turns
out not to be true? (There are several.) Does the existing code
exercise any of these cases? (I don't know. This function is called
in 133 places.)
All this because this function was not prepared to insist firmly that its arguments be passed in a simple and unambiguous format, say like this:
my $emailclass = $args->{emailclass}
|| $self->look_up_emailclass($args->{emailclass_name})
|| croak "one of emailclass or emailclass_name is required";
I am not certain why programmers think it is a good idea to have functions communicate their arguments by way of a round of Charades. But here's my current theory: some programmers think it is discreditable for their function to throw an exception. “It doesn't have to die there,” they say to themselves. “It would be more convenient for the caller if we just accepted either form and did what they meant.” This is a good way to think about user interfaces! But a function's calling convention is not a user interface. If a function is called with the wrong arguments, the best thing it can do is to drop dead immediately, pausing only long enough to gasp out a message explaining what is wrong, and incriminating its caller. Humans are deserving of mercy; calling functions are not.
Allowing an argument to be passed in seven different ways may be
convenient for the programmer writing the call, who can save a few
seconds looking up the correct spelling of emailclass_name, but
debugging what happens when elaborate and inconsistent arguments are
misinterpreted will eat up the gains many times over. Code is
written once, and read many times, so we should be willing to spend
more time writing it if it will save trouble reading it again later.
Novice programmers may ask “But what if this is business-critical code? A failure here could be catastrophic!”
Perhaps a failure here could be catastrophic. But if it is a catastrophe to throw an exception, when we know the caller is so confused that it is failing to pass the required arguments, then how much more catastrophic to pretend nothing is wrong and to continue onward when we are surely ignorant of the caller's intentions? And that catastrophe may not be detected until long afterward, or at all.
There is such a thing as being too accommodating.
[Other articles in category /prog/perl] permanent link
Fri, 06 Jul 2018[ This article has undergone major revisions since it was first published yesterday. ]
Here is a line of Perl code:
if ($self->fidget && blessed $self->fidget eq 'Widget::Fidget') {
This looks to see if $self has anything in its fidget slot, and if
so it checks to see if the value there is an instance of the class
Widget::Fidget. If both are true, it runs the following block.
That blessed check is bad practice for several reasons.
It duplicates the declaration of the
fidgetmember data:has fidget => ( is => 'rw', isa => 'Widget::Fidget', init_arg => undef, );So the
fidgetslot can't contain anything other than aWidget::Fidget, because the OOP system is already enforcing that. That means that theblessed…eqtest is not doing anything — unless someone comes along later and changes the declared type, in which case the test will then be checking the wrong condition.Actually, that has already happened! The declaration, as written, allows
fidgetto be an instance not just ofWidget::Fidgetbut of any class derived from it. But theblessed…eqcheck prevents this. This reneges on a major promise of OOP, that if a class doesn't have the behavior you need, you can subclass it and modify or extend it, and then use objects from the subclass instead. But if you try that here, theblessed…eqcheck will foil you.So this is a prime example of “… in which case the test will be checking the wrong condition” above. The test does not match the declaration, so it is checking the wrong condition. The
blessed…eqcheck breaks the ability of the class to work with derived classes ofWidget::Fidget.Similarly, the check prevents someone from changing the declared type to something more permissive, such as
“either
Widget::FidgetorGidget::Fidget”or
“any object that supports
wiggleandwagglemethods”or
“any object that adheres to the specification of
Widget::Interface”and then inserting a different object that supports the same interface. But the whole point of object-oriented programming is that as long as an object conforms to the required interface, you shouldn't care about its internal implementation.
In particular, the check above prevents someone from creating a mock
Widget::Fidgetobject and injecting it for testing purposes.We have traded away many of the modularity and interoperability guarantees that OOP was trying to preserve for us. What did we get in return? What are the purported advantages of the
blessed…eqcheck? I suppose it is intended to detect an anomalous situation in which some completely wrong object is somehow stored into theself.fidgetmember. The member declaration will prevent this (that is what it is for), but let's imagine that it has happened anyway. This could be a very serious problem. What will happen next?With the check in place, the bug will go unnoticed because the function will simply continue as if it had no fidget. This could cause a much more subtle failure much farther down the road. Someone trying to debug this will be mystified: At best “it's behaving as though it had no fidget, but I know that one was set earlier”, and at worst “why is there two years of inconsistent data in the database?” This could take a very long time to track down. Even worse, it might never be noticed, and the method might quietly do the wrong thing every time it was used.
Without the extra check, the situation is much better: the function will throw an exception as soon as it tries to call a fidget method on the non-fidget object. The exception will point a big fat finger right at the problem: “hey, on line 2389 you tried to call the
rotatemethod on aSkunk::Stinkyobject, but that class has no such method`. Someone trying to debug this will immediately ask the right question: “Who put a skunk in there instead of a widget?”
It's easy to get this right. Instead of
if ($self->fidget && blessed $self->fidget eq 'Widget::Fidget') {
one can simply use:
if ($self->fidget) {
Moral of the story: programmers write too much code.
I am reminded of something chess master Aron Nimzovitch once said, maybe in Chess Praxis, that amateur chess players are always trying to be Doing Something.
[Other articles in category /prog/perl] permanent link
In which, to my surprise, I find myself belonging to a group
My employer ZipRecruiter had a giant crisis at last month, of a scale that I have never seen at this company, and indeed, have never seen at any well-run company before. A great many of us, all the way up to the CTO, made a heroic effort for a month and got it sorted out.
It reminded me a bit of when Toph was three days old and I got a call from the hospital to bring her into the emergency room immediately. She had jaundice, which is not unusual in newborn babies. It is easy to treat, but if untreated it can cause permanent brain damage. So Toph and I went to the hospital, where she underwent the treatment, which was to have very bright lights shined directly on her skin for thirty-six hours. (Strange but true!)
The nurses in the hospital told me they had everything under control, and they would take care of Toph while I went home, but I did not go. I wanted to be sure that Toph was fed immediately and that her diapers were changed timely. The nurses have other people to take care of, and there was no reason to make her wait to eat and sleep when I could be there tending to her. It was not as if I had something else to do that I felt was more important. So I stayed in the room with Toph until it was time for us to go home, feeding her and taking care of her and just being with her.
It could have been a very stressful time, but I don't remember it that way. I remember it as a calm and happy time. Toph was in no real danger. The path forward was clear. I had my job, to help Toph get better, and I was able to do it undistracted. The hospital (Children's Hospital of Philadelphia) was wonderful, and gave me all the support I needed to do my job. When I got there they showed me the closet where the bedding was and the other closet where the snacks were and told me to help myself. They gave me the number to call at mealtimes to order meals to be sent up to my room. They had wi-fi so I could work quietly when Toph was asleep. Everything went smoothly, Toph got better, and we went home.
This was something like that. It wasn't calm; it was alarming and disquieting. But not in an entirely bad way; it was also exciting and engaging. It was hard work, but it was work I enjoyed and that I felt was worth doing. I love working and programming and thinking about things, and doing that extra-intensely for a few weeks was fun. Stressful, but fun.
And I was not alone. So many of the people I work with are so good at their jobs. I had all the support I needed. I could focus on my part of the work and feel confident that the other parts I was ignoring were being handled by competent and reasonable people who were at least as dedicated as I was. The higher-up management was coordinating things from the top, connecting technical and business concerns, and I felt secure that the overall design of the new system would make sense even if I couldn't always understand why. I didn't want to think about business concerns, I wanted someone else to do it for me and tell me what to do, and they did. Other teams working on different components that my components would interface with would deliver what they promised and it would work.
And the other programmers in my group were outstanding. We were scattered all over the globe, but handed off tasks to one another without any mishaps. I would come into work in the morning and the guys in Europe would be getting ready to go to bed and would tell me what they were up to and the other east-coasters and I could help pick up where they left off. The earth turned and the west-coasters appeared and as the end of the day came I would tell them what I had done and they could continue with it.
I am almost pathologically averse to belonging to groups. It makes me uncomfortable and even in groups that I have been associated with for years I feel out of place and like my membership is only provisional and temporary. I always want to go my own way and if everyone around me is going the same way I am suspicious and contrarian. When other people feel group loyalty I wonder what is wrong with them.
The up-side of this is that I am more willing than most people to cross group boundaries. People in a close-knit community often read all the same books and know all the same techniques for solving problems. This means that when a problem comes along that one of them can't solve, none of the rest can solve it either. I am sometimes the person who can find the solution because I have spent time in a different tribe and I know different things. This is a role I enjoy.
Higher-Order Perl exemplifies this. To write Higher-Order Perl I visited functional programming communities and tried to learn techniques that those communities understood that people outside those communities could use. Then I came back to the Perl community with the loot I had gathered.
But it's not all good. I have sometimes been able to make my non-belonging work out well. But it is not a choice; it's the way I am made, and I can't control it. When I am asked to be part of a team, I immediately become wary and wonder what the scam is. I can be loyal to people personally, but I have hardly any group loyalty. Sometimes this can lead to ugly situations.
But in fixing this crisis I felt proud to be part of the team. It is a really good team and I think it says something good about me that I can work well with the rest of them. And I felt proud to be part of this company, which is so functional, so well-run, so full of kind and talented people. Have I ever had this feeling before? If I have it was a long, long time ago.
G.H. Hardy once wrote that when he found himself forced to listen to pompous people, he would console himself by thinking:
Well, I have done one thing you could never have done, and that is to have collaborated with Littlewood and Ramanujan on something like equal terms.
Well, I was at ZipRecruiter during the great crisis of June 2018 and I was able to do my part and to collaborate with those people on equal terms, and that is something to be proud of.
[Other articles in category /brain] permanent link
Wed, 04 Jul 2018
Jackson and Gregg on optimization
Today Brendan Gregg's blog has an article Evaluating the Evaluation: Benchmarking Checklist that begins:
A co-worker introduced me to Craig Hanson and Pat Crain's performance mantras, which neatly summarize much of what we do in performance analysis and tuning. They are:
Performance mantras
- Don't do it
- Do it, but don't do it again
- Do it less
- Do it later
- Do it when they're not looking
- Do it concurrently
- Do it cheaper
I found this striking because I took it to be an obvious reference Michael A. Jackson's advice in his brilliant 1975 book Principles of Program Design. Jackson said:
We follow two rules in the matter of optimization:
Rule 1: Don't do it.
Rule 2 (for experts only). Don't do it yet.
The intent of the two passages is completely different. Hanson and Crain are offering advice about what to optimize. “Don't do it” means that to make a program run faster, eliminate some of the things it does. “Do it, but don't do it again” means that to make a program run faster, have it avoid repeating work it has already done, say by caching results. And so on.
Jackson's advice is of a very different nature. It is only indirectly about improving the program's behavior. Instead it is addressing the programmer's behavior: stop trying to optimize all the damn time! It is not about what to optimize but whether, and Jackson says that to a first approximation, the answer is no.
Here are Jackson's rules with more complete context. The quotation is from the preface (page vii) and is discussing the style of the examples in his book:
Above all, optimization is avoided. We follow two rules in the matter of optimization:
Rule 1. Don't do it.
Rule 2 (for experts only). Don't do it yet — that is, not until you have a perfectly clear and unoptimized solution.Most programmers do too much optimization, and virtually all do it too early. This book tries to act as an antidote. Of course, there are systems which must be highly optimized if they are to be economically useful, and Chapter 12 discusses some relevant techniques. But two points should always be remembered: first, optimization makes a system less reliable and harder to maintain, and therefore more expensive to build and operate; second, because optimization obscures structure it is difficult to improve the efficiency of a system which is already partly optimized.
Here's some code I dealt with this month:
my $emailclass = $args->{emailclass};
if (!$emailclass && $args->{emailclass_name} ) {
# do some caching so if we're called on the same object over and over we don't have to do another find.
my $last_emailclass = $self->{__LAST_EMAILCLASS__};
if ( $last_emailclass && $last_emailclass->{name} eq $args->{emailclass_name} ) {
$emailclass = $last_emailclass->{emailclass};
} else {
$emailclass = $self->schema->resultset('EmailClass')
->find_by_name($args->{emailclass_name});
$self->{__LAST_EMAILCLASS__} = {
name => $args->{emailclass_name},
emailclass => $emailclass,
};
}
}
Holy cow, this is wrong in so many ways. 8 lines of this mess, for
what? To cache a single database lookup (the ->find_by_name call),
in a single object, if it happens to be looking for the same name as
last time. If caching was actually wanted, it should have been
addressed in the ->find_by_name call, which could do the caching
more generally, and which has some hope of knowing something about
when the cache entries should be expired. Even stipulating that
caching was wanted and for some reason should have been put here, why
such an elaborate mechanism, all to cache just the last lookup? It
could have been:
$emailclass = $self->emailclass_for_name($args->{emailclass_name});
...
sub emailclass_for_name {
my ($self, $name) = @_;
$self->{emailclass}{$name} //=
$self->schema->resultset('EmailClass')->find_by_name($name);
return $self->{emailclass}{$name};
}
I was able to do a bit better than this, and replaced the code with:
$emailclass = $self->schema->resultset('EmailClass')
->find_by_name($args->{emailclass_name});
My first thought was that the original caching code had been written by a very inexperienced programmer, someone who with more maturity might learn to do their job with less wasted effort. I was wrong; it had been written by a senior developer, someone who with more maturity might learn to do their job with less wasted effort.
The tragedy did not end there. Two years after the original code was written a more junior programmer duplicated the same unnecessary code elsewhere in the same module, saying:
I figured they must have had a reason to do it that way…
Thus is the iniquity of the fathers visited on the children.
In a nearby piece of code, an object A, on the first call to a certain method, constructed object B and cached it:
B->new(
base_path => ...
schema => $self->schema,
retry => ...,
);
Then on subsequent calls, it reused B from the cache.
But the cache was shared among many instances of A, not all of which
had the same ->schema member. So some of those instances of A
would ask B a question and get the answer from the wrong database.
A co-worker spent hours and hours in the middle of the night last
month tracking this down. Again, the cache was not only broken but
completely unnecesary. What was being saved? A single object
construction, probably a few hundred bytes and a few hundred
microseconds at most. And again, the code was perpetrated by a senior
developer who should have known better. My co-worker replaced 13
lines of broken code with four that worked.
Brendan Gregg is unusually clever, and an exceptional case. Most programmers are not Brendan Gregg, and should take Jackson's advice and stop trying to be so clever all the time.
[Other articles in category /prog] permanent link





