Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Thu, 29 Nov 2018
How many kinds of polygonal loops? (part 2)
And I said I thought there were nine analogous figures with six points.
Rahul Narain referred me to a recent discussion of almost this exact question on Math Stackexchange. (Note that the discussion there considers two figures different if they are reflections of one another; I consider them the same.) The answer turns out to be OEIS A000940. I had said:
… for !!N=6!!, I found it hard to enumerate. I think there are nine shapes but I might have missed one, because I know I kept making mistakes in the enumeration …
I missed three. The nine I got were:
And the three I missed are:
I had tried to break them down by the arrangement of the outside ring of edges, which can be described by a composition. The first two of these have type !!1+1+1+1+2!! (which I missed completely; I thought there were none of this type) and the other has type !!1+2+1+2!!, the same as the !!015342!! one in the lower right of the previous diagram.
I had ended by saying:
I would certainly not trust myself to hand-enumerate the !!N=7!! shapes.
Good call, Mr. Dominus! I considered filing this under “oops” but I decided that although I had gotten the wrong answer, my confidence in it had been adequately low. On one level it was a mistake, but on a higher and more important level, I did better.
I am going to try the (Cauchy-Frobenius-)Burnside-(Redfield-)Pólya lemma on it next and see if I can get the right answer.
Thanks again to Rahul Narain for bringing this to my attention.
[Other articles in category /math] permanent link
How many kinds of polygonal loops?
Take !!N!! equally-spaced points on a circle. Now connect them in a loop: each point should be connected to exactly two others, and each point should be reachable from the others. How many geometrically distinct shapes can be formed?
For example, when !!N=5!!, these four shapes can be formed:
(I phrased this like a geometry problem, but it should be clear it's actually a combinatorics problem. But it's much easier to express as a geometry problem; to talk about the combinatorics I have to ask you to consider a permutation !!P!! where !!P(i±1)≠P(i)±1!! blah blah blah…)
For !!N<5!! it's easy. When !!N=3!! it is always a triangle. When !!N=4!! there are only two shapes: a square and a bow tie.
But for !!N=6!!, I found it hard to enumerate. I think there are nine shapes but I might have missed one, because I know I kept making mistakes in the enumeration, and I am not sure they are all corrected:
It seems like it ought not to be hard to generate and count these, but so far I haven't gotten a good handle on it. I produced the !!N=6!! display above by considering the compositions of the number !!6!!:
| Composition | How many loops? |
|---|---|
| 6 | 1 |
| 1+5 | — |
| 2+4 | 1 |
| 3+3 | 1 |
| 1+1+4 | — |
| 1+2+3 | 1 |
| 2+2+2 | 2 |
| 1+1+1+3 | — |
| 1+1+2+2 | 1 |
| 1+2+1+1 | 1 |
| 1+1+1+1+2 | — |
| 1+1+1+1+1+1 | 1 |
| Total | 9 (?) |
(Actually it's the compositions, modulo bracelet symmetries — that is, modulo the action of the dihedral group.)
But this is fraught with opportunities for mistakes in both directions. I would certainly not trust myself to hand-enumerate the !!N=7!! shapes.
[ Addendum: For !!N=6!! there are 12 figures, not 9. For !!N=7!!, there are 39. Further details. ]
[Other articles in category /math] permanent link
Sun, 25 Nov 2018A couple of years back I was thinking about how to draw a good approximation to an equilateral triangle on a piece of graph paper. There are no lattice points that are exactly the vertices of an equilateral triangle, but you can come close, and one way to do it is to find integers !!a!! and !!b!! with !!\frac ba\approx \sqrt 3!!, and then !!\langle 0, 0\rangle, \langle 2a, 0\rangle,!! and !!\langle a, b\rangle!! are almost an equilateral triangle.
But today I came back to it for some reason and I wondered if it would be possible to get an angle closer to 60°, or numbers that were simpler, or both, by not making one of the sides of the triangle perfectly horizontal as in that example.
So okay, we want to find !!P = \langle a, b\rangle!! and !!Q = \langle c,d\rangle!! so that the angle !!\alpha!! between the rays !!\overrightarrow{OP}!! and !!\overrightarrow{OQ}!! is as close as possible to !!\frac\pi 3!!.
The first thing I thought of was that the dot product !!P\cdot Q = |P||Q|\cos\alpha!!, and !!P\cdot Q!! is super-easy to calculate, it's just !!ac+bd!!. So we want $$\frac{ad+bc}{|P||Q|} = \cos\alpha \approx \frac12,$$ and everything is simple, except that !!|P||Q| = \sqrt{a^2+b^2}\sqrt{c^2+d^2}!!, which is not so great.
Then I tried something else, using high-school trigonometry. Let !!\alpha_P!! and !!\alpha_Q!! be the angles that the rays make with the !!x!!-axis. Then !!\alpha = \alpha_Q - \alpha_P = \tan^{-1} \frac dc - \tan^{-1} \frac ba!!, which we want close to !!\frac\pi3!!.
Taking the tangent of both sides and applying the formula $$\tan(q-p) = \frac{\tan q - \tan p}{1 + \tan q \tan p}$$ we get $$ \frac{\frac dc - \frac ba}{1 + \frac dc\frac ba} \approx \sqrt3.$$ Or simplifying a bit, the super-simple $$\frac{ad-bc}{ac+bd} \approx \sqrt3.$$
After I got there I realized that my dot product idea had almost worked. To get rid of the troublesome !!|P||Q|!! you should consider the cross product also. Observe that the magnitude of !!P\times Q!! is !!|P||Q|\sin\alpha!!, and is also $$\begin{vmatrix} a & b & 0 \\ c & d & 0 \\ 1 & 1 & 1 \end{vmatrix} = ad - bc$$ so that !!\sin\alpha = \frac{ad-bc}{|P||Q|}!!. Then if we divide, the !!|P||Q|!! things cancel out nicely: $$\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = \frac{ad-bc}{ac+bd}$$ which we want to be as close as possible to !!\sqrt 3!!.
Okay, that's fine. Now we need to find some integers !!a,b,c,d!! that do what we want. The usual trick, “see what happens if !!a=0!!”, is already used up, since that's what the previous article was about. So let's look under the next-closest lamppost, and let !!a=1!!. Actually we'll let !!b=1!! instead to keep things more horizonal. Then, taking !!\frac74!! as our approximation for !!\sqrt3!!, we want
$$\frac{ad-c}{ac+d} = \frac74$$
or equivalently $$\frac dc = \frac{7a+4}{4a-7}.$$
Now we just tabulate !!7a+4!! and !!4a-7!! looking for nice fractions:
| !!a!! | !!d =!! !!7a+4!! | !!c=!! !!4a-7!! |
|---|---|---|
| 2 | 18 | 1 |
| 3 | 25 | 5 |
| 4 | 32 | 9 |
| 5 | 39 | 13 |
| 6 | 46 | 17 |
| 7 | 53 | 21 |
| 8 | 60 | 25 |
| 9 | 67 | 29 |
| 10 | 74 | 33 |
| 11 | 81 | 37 |
| 12 | 88 | 41 |
| 13 | 95 | 45 |
| 14 | 102 | 49 |
| 15 | 109 | 53 |
| 16 | 116 | 57 |
| 17 | 123 | 61 |
| 18 | 130 | 65 |
| 19 | 137 | 69 |
| 20 | 144 | 73 |
Each of these gives us a !!\langle c,d\rangle!! point, but some are much better than others. For example, in line 3, we have take !!\langle 5,25\rangle!! but we can use !!\langle 1,5\rangle!! which gives the same !!\frac dc!! but is simpler. We still get !!\frac{ad-bc}{ac+bd} = \frac 74!! as we want.
Doing this gives us the two points !!P=\langle 3,1\rangle!! and !!Q=\langle 1, 5\rangle!!. The angle between !!\overrightarrow{OP}!! and !!\overrightarrow{OQ}!! is then !!60.255°!!. This is exactly the same as in the approximately equilateral !!\langle 0, 0\rangle, \langle 8, 0\rangle,!! and !!\langle 4, 7\rangle!! triangle I mentioned before, but the numbers could not possibly be easier to remember. So the method is a success: I wanted simpler numbers or a better approximation, and I got the same approximation with simpler numbers.
To draw a 60° angle on graph paper, mark !!P=\langle 3,1\rangle!! and !!Q=\langle 1, 5\rangle!!, draw lines to them from the origin with a straightedge, and there is your 60° angle, to better than a half a percent.
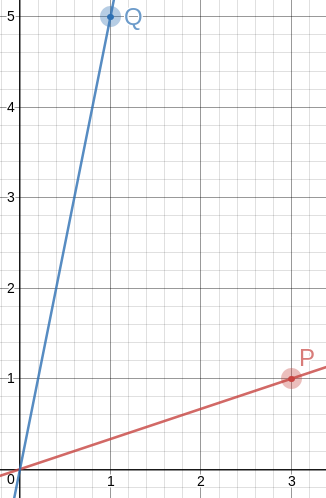
There are some other items in the table (for example row 18 gives !!P=\langle 18,1\rangle!! and !!Q=\langle 1, 2\rangle!!) but because of the way we constructed the table, every row is going to give us the same angle of !!60.225°!!, because we approximated !!\sqrt3\approx\frac74!! and !!60.225° = \tan^{-1}\frac74!!. And the chance of finding numbers better than !!\langle 3,1\rangle!! and !!\langle 1, 5\rangle!! seems slim. So now let's see if we can get the angle closer to exactly !!60°!! by using a better approximation to !!\sqrt3!! than !!\frac 74!!.
The next convergents to !!\sqrt 3!! are !!\frac{19}{11}!! and !!\frac{26}{15}!!. I tried the same procedure for !!\frac{19}{11}!! and it was a bust. But !!\frac{26}{15}!! hit the jackpot: !!a=4!! gives us !!15a-26 = 34!! and !!26a-15=119!!, both of which are multiples of 17. So the points are !!P=\langle 4,1\rangle!! and !!Q=\langle 2, 7\rangle!!, and this time the angle between the rays is !!\tan^{-1}\frac{26}{15} = 60.018°!!. This is as accurate as anyone drawing on graph paper could possibly need; on a circle with a one-mile radius it is an error of 20 inches.
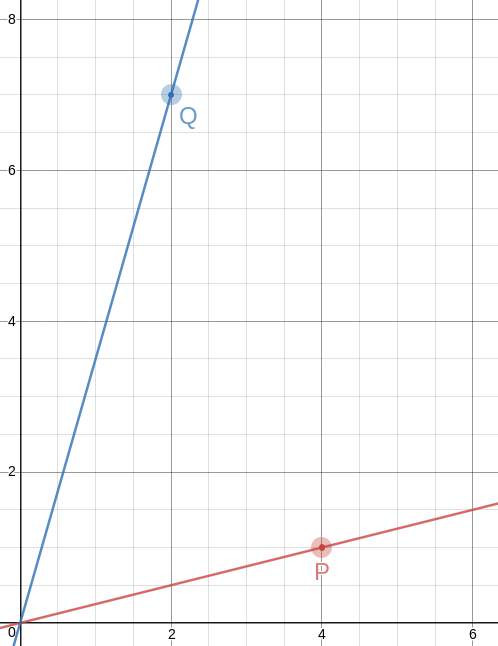
Of course, the triangles you get are no longer equilateral, not even close. That first one has sides of !!\sqrt{10}, \sqrt{20}, !! and !!\sqrt{26}!!, and the second one has sides of !!\sqrt{17}, \sqrt{40}, !! and !!\sqrt{53}!!. But! The slopes of the lines are so simple, it's easy to construct equilateral triangles with a straightedge and a bit of easy measuring. Let's do it on the !!60.018°!! angle and see how it looks.
!!\overrightarrow{OP}!! has slope !!\frac14!!, so the perpendicular to it has slope !!-4!!, which means that you can draw the perpendicular by placing the straightedge between !!P!! and some point !!P+x\langle -1, 4\rangle!!, say !!\langle 2, 9\rangle!! as in the picture. The straightedge should have slope !!-4!!, which is very easy to arrange: just imagine the little squares grouped into stacks of four, and have the straightedge go through opposite corners of each stack. The line won't necessarily intersect !!\overrightarrow{OQ}!! anywhere great, but it doesn't need to, because we can just mark the intersection, wherever it is:
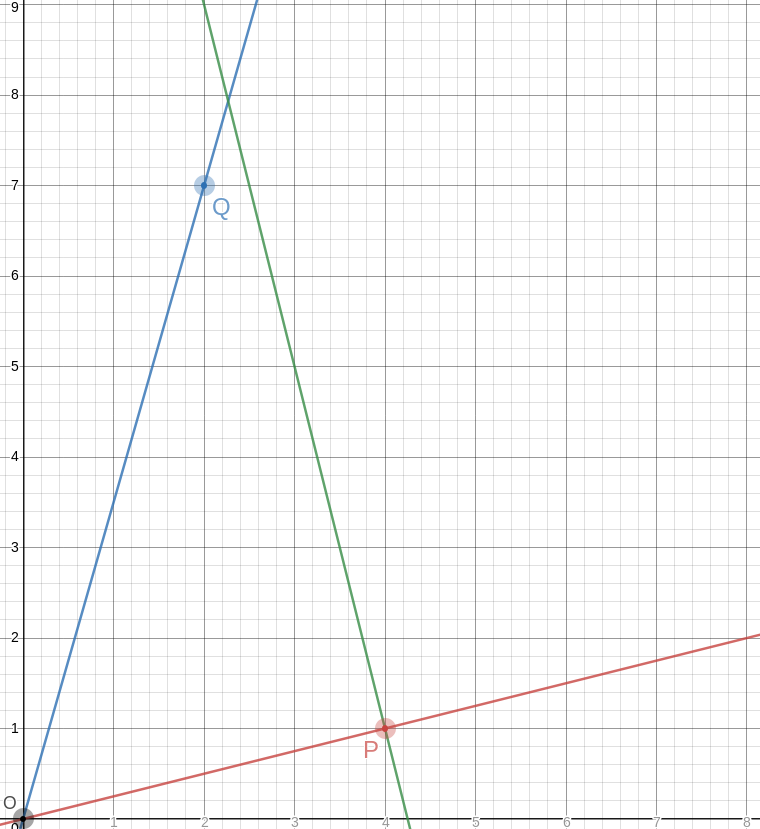
Let's call that intersection !!A!! for “apex”.
The point opposite to !!O!! on the other side of !!P!! is even easier; it's just !!P'=2P =\langle 8, 2\rangle!!. And the segment !!P'A!! is the third side of our equilateral triangle:
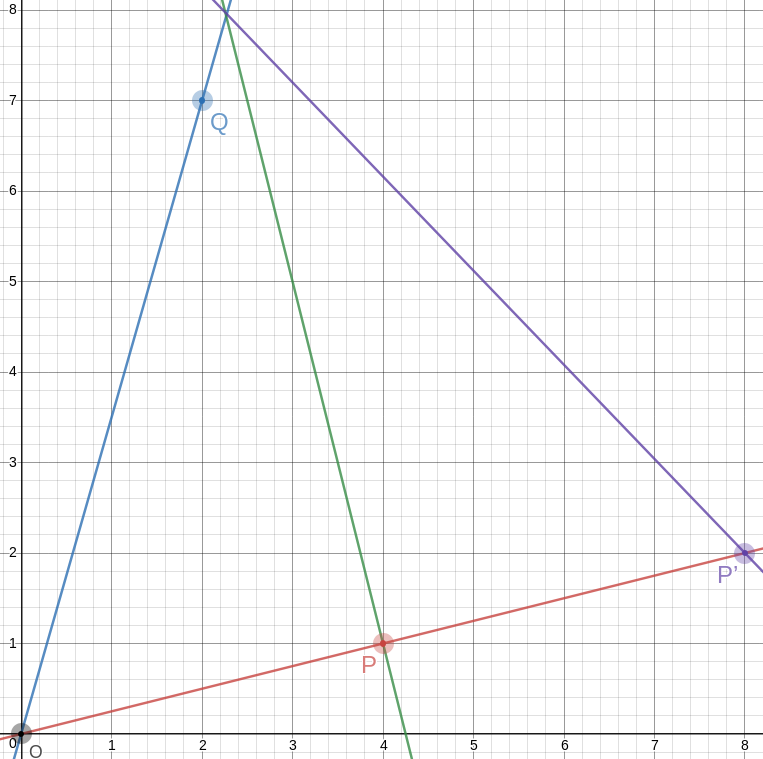
This triangle is geometrically similar to a triangle with vertices at !!\langle 0, 0\rangle, \langle 30, 0\rangle,!! and !!\langle 15, 26\rangle!!, and the angles are just close to 60°, but it is much smaller.
Woot!
[Other articles in category /math] permanent link
Mon, 19 Nov 2018I think I forgot to mention that I was looking recently at hamiltonian cycles on a dodecahedron. The dodecahedron has 30 edges and 20 vertices, so a hamiltonian path contains 20 edges and omits 10. It turns out that it is possible to color the edges of the dodecahedron in three colors so that:
- Every vertex is incident to one edge of each color
- The edges of any two of the three colors form a hamiltonian cycle
Marvelous!
(In this presentation, I have taken one of the vertices and sent it away to infinity. The three edges with arrowheads are all attached to that vertex, off at infinity, and the three faces incident to it have been stretched out to cover the rest of the plane.)
Every face has five edges and there are only three colors, so the colors can't be distributed evenly around a face. Each face is surrounded by two edges of one color, two of a second color, and only one of the last color. This naturally divides the 12 faces into three classes, depending on which color is assigned to only one edge of that face.
Each class contains two pairs of two adjacent pentagons, and each adjacent pair is adjacent to the four pairs in the other classes but not to the other pair in its own class.
Each pair shares a single edge, which we might call its “hinge”. Each pair has 8 vertices, of which two are on its hinge, four are adjacent to the hinge, and two are not near of the hinge. These last two vertices are always part of the hinges of the pairs of a different class.
I could think about this for a long time, and probably will. There is plenty more to be seen, but I think there is something else I was supposed to be doing today, let me think…. Oh yes! My “job”! So I will leave you to go on from here on your own.
[ Addendum 20181203: David Eppstein has written a much longer and more detailed article about triply-Hamiltonian edge colorings, using this example as a jumping-off point. ]
[Other articles in category /math] permanent link
Sat, 17 Nov 2018
How do you make a stella octangula?
Yesterday Katara asked me out of nowhere “When you make a stella octangula, do you build it up from an octahedron or a tetrahedron?” Stella octangula was her favorite polyhedron eight years ago.
“Uh,” I said. “Both?”
Then she had to make one to see what I meant. You can start with a regular octahedron:
Then you erect spikes onto four of the octahedron's faces; this produces a regular tetrahedron:
Then you erect spikes onto the other four of the octahedron's faces. Now you have a stella octangula.
So yeah, both. Or instead of starting with a unit octahedron and erecting eight spikes of size 1, you can start with a unit tetrahedron and erect four spikes of size ½. It's both at once.
[Other articles in category /math] permanent link
Tue, 13 Nov 2018
Counting paths through polyhedra
A while back someone asked on math stack exchange how many paths there were of length !!N!! from one vertex of a dodecahedron to the opposite vertex. The vertices are distance 5 apart, so for !!N<5!! the answer is zero, but the paths need not be simple, so the number grows rapidly with !!N!!; there are 58 million paths of length 19.
This is the kind of thing that the computer answers easily, so that's where I started, and unfortunately that's also where I finished, saying:
I'm still working out a combinatorial method of calculating the answer, and I may not be successful.
Another user reminded me of this and I took another whack at it. I couldn't remember what my idea had been last year, but my idea this time around was to think of the dodecahedron as the Cayley graph for a group, and then the paths are expressions that multiply out to a particular group element.
I started by looking at a tetrahedron instead of at a dodecahedron, to see how it would work out. Here's a tetrahedron.
Let's say we're counting paths from the center vertex to one of the others, say the one at the top. (Tetrahedra don't have opposite vertices, but that's not an important part of the problem.) A path is just a list of edges, and each edge is labeled with a letter !!a!!, !!b!!, or !!c!!. Since each vertex has exactly one edge with each label, every sequence of !!a!!'s, !!b!!'s, and !!c!!'s represents a distinct path from the center to somewhere else, although not necessarily to the place we want to go. Which of these paths end at the bottom vertex?
The edge labeling I chose here lets us play a wonderful trick. First, since any edge has the same label at both ends, the path !!x!! always ends at the same place as !!xaa!!, because the first !!a!! goes somewhere else and then the second !!a!! comes back again, and similarly !!xbb!! and !!xcc!! also go to the same place. So if we have a path that ends where we want, we can insert any number of pairs !!aa, bb, !! or !!cc!! and the new path will end at the same place.
But there's an even better trick available. For any starting point, and any letters !!x!! and !!y!!, the path !!xy!! always ends at the same place as !!yx!!. For example, if we start at the middle and follow edge !!b!!, then !!c!!, we end at the lower left; similarly if we follow edge !!c!! and then !!b!! we end at the same place, although by a different path.
Now suppose we want to find all the paths of length 7 from the middle to the top. Such a path is a sequence of a's, b's, and c's of length 7. Every such sequence specifies a different path out of the middle vertex, but how can we recognize which sequences end at the top vertex?
Since !!xy!! always goes to the same place as !!yx!!, the order of the
seven letters doesn't matter.
A complicated-seeming path like abacbcb must go to the same place
as !!aabbbcc!!, the same path with the letters in alphabetical order.
And since !!xx!! always goes back to
where it came from, the path !!aabbbcc!! goes to the same place as !!b!!
Since the paths we want are those that go to the same place as the trivial path !!c!!, we want paths that have an even number of !!a!!s and !!b!!s and an odd number of !!c!!s. Any path fitting that description will go to same place as !!c!!, which is the top vertex. It's easy to enumerate such paths:
| Prototypical path | How many? |
|---|---|
| ccccccc | 1 |
| cccccaa | 21 |
| cccccbb | 21 |
| cccaaaa | 35 |
| cccaabb | 210 |
| cccbbbb | 35 |
| caaaaaa | 7 |
| caaaabb | 105 |
| caabbbb | 105 |
| cbbbbbb | 7 |
| Total | 547 |
Here something like “cccbbbb” stands for all the paths that have three c's and four b's, in some order; there are !!\frac{7!}{4!3!} = 35!! possible orders, so 35 paths of this type. If we wanted to consider paths of arbitrary length, we could use Burnside's lemma, but I consider the tetrahedron to have been sufficiently well solved by the observations above (we counted 547 paths by hand in under 60 seconds) and I don't want to belabor the point.
Okay! Easy-peasy!
Now let's try cubes:
Here we'll consider paths between two antipodal vertices in the upper left and the lower right, which I've colored much darker gray than the other six vertices.
The same magic happens as in the tetrahedron. No matter where we
start, and no matter what !!x!! and !!y!! are, the path !!xy!! always
gets us to the same place as !!yx!!. So again, if some complicated
path gets us where we want to go, we can permute its components into
any order and get a different path of the same length to the same
place. For example, starting from the upper left, bcba, abcb, and
abbc all go to the same place.
And again, because !!xx!! always make a trip along one edge and then
back along the same edge, it never goes anywhere. So the three paths
in the previous paragraph also go to the same place as ac and ca
and also aa bcba bb aa aa aa aa bb cc cc cc bb.
We want to count paths from one dark vertex to the other. Obviously
abc is one such, and so too must be bac, cba, acb, and so
forth. There are six paths of length 3.
To get paths of length 5, we must insert a pair of matching letters
into one of the paths of length 3. Without loss of generality we can
assume that we are inserting aa. There are 20 possible orders for
aaabc, and three choices about which pair to insert, for a total of
60 paths.
To get paths of length 7, we must insert two pairs. If the two pairs are the same, there are !!\frac{7!}{5!} = 42!! possible orders and 3 choices about which letters to insert, for a total of 126. If the two pairs are different, there are !!\frac{7!}{3!3!} = 140!! possible orders and again 3 choices about which pairs to insert, for a total of 420, and a grand total of !!420+126 = 546!! paths of length 7. Counting the paths of length 9 is almost as easy. For the general case, again we could use Burnside's lemma, or at this point we could look up the unusual sequence !!6, 60, 546!! in OEIS and find that the number of paths of length !!2n+1!! is already known to be !!\frac34(9^n-1)!!.
So far this technique has worked undeservedly well. The original problem wanted to use it to study paths on a dodecahedron. Where, unfortunately, the magic property !!xy=yx!! doesn't hold. It is possible to label the edges of the dodecahedron so that every sequence of labels determines a unique path:
but there's nothing like !!xy=yx!!. Well, nothing exactly like it. !!xy=yx!! is equivalent to !!(xy)^2=1!!, and here instead we have !!(xy)^{10}=1!!. I'm not sure that helps. I will probably need another idea.
The method fails similarly for the octahedron — which is good, because I can use the octahedron as a test platform to try to figure out a new idea. On an octahedron we need to use four kinds of labels because each vertex has four edges emerging from it:
Here again we don't have !!(xy)^2=1!! but we do have !!(xy)^3 = 1!!. So it's possible that if I figure out a good way to enumerate paths on the octahedron I may be able to adapt the technique to the dodecahedron. But the octahedron will be !!\frac{10}3!! times easier.
Viewed as groups, by the way, these path groups are all examples of Coxeter groups. I'm not sure this is actually a useful observation, but I've been wanting to learn about Coxeter groups for a long time and this might be a good enough excuse.
[Other articles in category /math] permanent link
A puzzle about representing numbers as a sum of 3-smooth numbers
I think this would be fun for a suitably-minded bright kid of maybe 12–15 years old.
Consider the following table of numbers of the form !!2^i3^j!!:
| 1 | 3 | 9 | 27 | 81 | 243 |
| 2 | 6 | 18 | 54 | 162 | … |
| 4 | 12 | 36 | 108 | … | … |
| 8 | 24 | 72 | 216 | … | … |
| 16 | 48 | 144 | … | … | … |
| 32 | 96 | … | … | … | … |
| 64 | 192 | … | … | … | … |
| 128 | … | … | … | … | … |
Given a number !!n!!, it is possible to represent !!n!! as a sum of entries from the table, with the following constraints:
- No more than one entry from any column
- An entry may only be used if it is in a strictly higher row than any entry to its left.
For example, one may not represent !!23 = 2 + 12 + 9!!, because the !!12!! is in a lower row than the !!2!! to its left.
| 1 | 3 | 9 | 27 |
| 2 | 6 | 18 | 54 |
| 4 | 12 | 36 | 108 |
But !!23 = 8 + 6 + 9!! is acceptable, because 6 is higher than 8, and 9 is higher than 6.
| 1 | 3 | 9 | 27 |
| 2 | 6 | 18 | 54 |
| 4 | 12 | 36 | 108 |
| 8 | 24 | 72 | 216 |
Or, put another way: can we represent any number !!n!! in the form $$n = \sum_i 2^{a_i}3^{b_i}$$ where the !!a_i!! are strictly decreasing and the !!b_i!! are strictly increasing?
Spoiler:
maxpow3 1 = 1
maxpow3 2 = 1
maxpow3 n = 3 * maxpow3 (n `div` 3)
rep :: Integer -> [Integer]
rep 0 = []
rep n = if even n then map (* 2) (rep (n `div` 2))
else (rep (n - mp3)) ++ [mp3] where mp3 = maxpow3 n
Sadly, the representation is not unique. For example, !!8+3 = 2+9!!, and !!32+24+9 = 32+6+27 = 8+12=18+27!!.
[Other articles in category /math] permanent link
Fri, 09 Nov 2018
Why I never finish my Haskell programs (part 3 of ∞)
I'm doing more work on matrix functions. A matrix represents a
relation, and I am representing a matrix as a [[Integer]]. Then
matrix addition is simply liftA2 (liftA2 (+)). Except no, that's
not right, and this is not a complaint, it's certainly my mistake.
The overloading for liftA2 for lists does not do what I want, which
is to apply the operation to each pair of correponding elements. I want
liftA2 (+) [1,2,3] [10,20,30] to be [11,22,33] but it is not.
Instead liftA2 lifts an operation to apply to each possible pair of
elements, producing [11,21,31,12,22,32,13,23,33].
And the twice-lifted version is
similarly not what I want:
$$ \require{enclose} \begin{pmatrix}1&2\\3&4\end{pmatrix}\enclose{circle}{\oplus} \begin{pmatrix}10&20\\30&40\end{pmatrix}= \begin{pmatrix} 11 & 21 & 12 & 22 \\ 31 & 41 & 32 & 42 \\ 13 & 23 & 14 & 24 \\ 33 & 43 & 34 & 44 \end{pmatrix} $$
No problem, this is what ZipList is for. ZipLists are just regular
lists that have a label on them that advises liftA2 to lift an
operation to the element-by-element version I want instead of the
each-one-by-every-other-one version that is the default. For instance
liftA2 (+) (ZipList [1,2,3]) (ZipList [10,20,30])
gives ZipList [11,22,33], as desired. The getZipList function
turns a ZipList back into a regular list.
But my matrices are nested lists, so I need to apply the ZipList
marker twice, once to the outer list, and once to each of the inner
lists, because I want the element-by-element behavior at both
levels. That's easy enough:
matrix :: [[a]] -> ZipList (ZipList a)
matrix m = ZipList (fmap ZipList m)
(The fmap here is actually being specialized to map, but that's
okay.)
Now
(liftA2 . liftA2) (+) (matrix [[1,2],[3,4]]) (matrix [[10,20],[30, 40]])
does indeed produce the result I want, except that the type markers are still in there: instead of
[[11,22],[33,44]]
I get
ZipList [ ZipList [11, 22], ZipList [33, 44] ]
No problem, I'll just use getZipList to turn them back again:
unmatrix :: ZipList (ZipList a) -> [[a]]
unmatrix m = getZipList (fmap getZipList m)
And now matrix addition is finished:
matrixplus :: [[a]] -> [[a]] -> [[a]]
matrixplus m n = unmatrix $ (liftA2 . liftA2) (+) (matrix m) (matrix n)
This works perfectly.
But the matrix and unmatrix pair bugs me a little. This business
of changing labels at both levels has happened twice already and
I am likely to need it again. So I will turn the two functions
into a single higher-order function by abstracting over ZipList.
This turns this
matrix m = ZipList (fmap ZipList m)
into this:
twice zl m = zl (fmap zl m)
with the idea that I will now have matrix = twice ZipList and
unmatrix = twice getZipList.
The first sign that something is going wrong is that twice does not
have the type I wanted. It is:
twice :: Functor f => (f a -> a) -> f (f a) -> a
where I was hoping for something more like this:
twice :: (Functor f, Functor g) => (f a -> g a) -> f (f a) -> g (g a)
which is not reasonable to expect: how can Haskell be expected to
figure out I wanted two diferent functors in there when there is only one
fmap? And indeed twice does not work; my desired matrix = twice
ZipList does not even type-check:
<interactive>:19:7: error:
• Occurs check: cannot construct the infinite type: a ~ ZipList a
Expected type: [ZipList a] -> ZipList a
Actual type: [a] -> ZipList a
• In the first argument of ‘twice’, namely ‘ZipList’
In the expression: twice ZipList
In an equation for ‘matrix’: matrix = twice ZipList
• Relevant bindings include
matrix :: [[ZipList a]] -> ZipList a (bound at <interactive>:20:5)
Telling GHC explicitly what type I want for twice doesn't work
either, so I decide it's time to go to lunch. I take paper with me,
and while I am eating my roast pork hoagie with sharp provolone and
spinach (a popular local delicacy) I work out the results of the type
unification algorithm on paper for both cases to see what goes wrong.
I get the same answers that Haskell got, but I can't see where the difference was coming from.
So now, instead of defining matrix operations, I am looking into the
type unification algorithm and trying to figure out why twice
doesn't work.
And that is yet another reason why I never finish my Haskell programs. (“What do you mean, λ-abstraction didn't work?”)
[Other articles in category /prog/haskell] permanent link
Thu, 08 Nov 2018
Haskell type checker complaint 184 of 698
I want to build an adjacency matrix for the vertices of a cube; this
is a matrix that has m[a][b] = 1 exactly when vertices a and b
share an edge. We can enumerate the vertices arbitrarily but a
convenient way to do it is to assign them the numbers 0 through 7 and
then say that vertices !!a!! and !!b!! are adjacent if, regarded as
binary numerals, they differ in exactly one bit, so:
import Data.Bits
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
This compiles and GHC infers the type
adj :: (Bits a, Num a, Num t) => a -> a -> t
Fine.

Now I want to build the adjacency matrix, which is completely straightforward:
cube = [ [a `adj` b | b <- [0 .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Ha ha, no it isn't; in Haskell nothing is straightforward. This
produces 106 lines of type whining, followed by a failed compilation.
Apparently this is because because 0 and 7 are overloaded, and
could mean some weird values in some freakish instance of Num, and
then 0 .. 7 might generate an infinite list of 1-graded torsion
rings or something.
To fix this I have to say explicitly what I mean by 0. “Oh, yeah,
by the way, that there zero is intended to denote the integer zero,
and not the 1-graded torsion ring with no elements.”
cube = [ [a `adj` b | b <- [0 :: Integer .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Here's another way I could accomplish this:
zero_i_really_mean_it = 0 :: Integer
cube = [ [a `adj` b | b <- [zero_i_really_mean_it .. 7] ] | a <- [0 .. 7] ] where
a `adj` b = if (elem (xor a b) [1, 2, 4]) then 1 else 0
Or how about this?
cube = [ [a `adj` b | b <- numbers_dammit [0 .. 7] ] | a <- [0 .. 7] ] where
p `adj` q = if (elem (xor p q) [1, 2, 4]) then 1 else 0
numbers_dammit = id :: [Integer] -> [Integer]
I think there must be something really wrong with the language design here. I don't know exactly what it is, but I think someone must have made the wrong tradeoff at some point.
[Other articles in category /prog/haskell] permanent link
How not to reconfigure your sshd
Yesterday I wanted to reconfigure the sshd on a remote machine.
Although I'd never done sshd itself, I've done this kind of thing
a zillion times before. It looks like this: there is a configuration
file (in this case /etc/ssh/sshd-config) that you modify. But this
doesn't change the running server; you have to notify the server that
it should reread the file. One way would be by killing the server and
starting a new one. This would interrupt service, so instead you can
send the server a different signal (in this case SIGHUP) that tells
it to reload its configuration without exiting. Simple enough.
Except, it didn't work. I added:
Match User mjd
ForceCommand echo "I like pie!"
and signalled the server, then made a new connection to see if it
would print I like pie! instead of starting a shell. It started a
shell. Okay, I've never used Match or ForceCommand before, maybe
I don't understand how they work, I'll try something simpler. I
added:
PrintMotd yes
which seemed straightforward enough, and I put some text into
/etc/motd, but when I connected it didn't print the motd.
I tried a couple of other things but none of them seemed to work.
Okay, maybe the sshd is not getting the signal, or something? I
hunted up the logs, but there was a report like what I expected:
sshd[1210]: Received SIGHUP; restarting.
This was a head-scratcher. Was I modifying the wrong file? It semed
hardly possible, but I don't administer this machine so who knows? I
tried lsof -p 1210 to see if maybe sshd had some other config file
open, but it doesn't keep the file open after it reads it, so that was
no help.
Eventually I hit upon the answer, and I wish I had some useful piece of advice here for my future self about how to figure this out. But I don't because the answer just struck me all of a sudden.
(It's nice when that happens, but I feel a bit cheated afterward: I solved the problem this time, but I didn't learn anything, so how does it help me for next time? I put in the toil, but I didn't get the full payoff.)
“Aha,” I said. “I bet it's because my connection is multiplexed.”
Normally when you make an ssh connection to a remote machine, it
calls up the server, exchanges credentials, each side authenticates
the other, and they negotiate an encryption key. Then the server
forks, the child starts up a login shell and mediates between the
shell and the network, encrypting in one direction and decrypting in
the other. All that negotiation and authentication takes time.
There is a “multiplexing” option you can use instead. The handshaking
process still occurs as usual for the first connection. But once the
connection succeeds, there's no need to start all over again to make a
second connection. You can tell ssh to multiplex several virtual
connections over its one real connection. To make a new virtual
connection, you run ssh in the same way, but instead of contacting
the remote server as before, it contacts the local ssh client that's
already running and requests a new virtual connection. The client,
already connected to the remote server, tells the server to allocate a
new virtual connection and to start up a new shell session for it.
The server doesn't even have to fork; it just has to allocate another
pseudo-tty and run a shell in it. This is a lot faster.
I had my local ssh client configured to use a virtual connection if
that was possible. So my subsequent ssh commands weren't going
through the reconfigured parent server. They were all going through
the child server that had been forked hours before when I started my
first connection. It wasn't affected by reconfiguration of the parent
server, from which it was now separate.
I verified this by telling ssh to make a new connection without
trying to reuse the existing virtual connection:
ssh -o ControlPath=none -o ControlMaster=no ...
This time I saw the MOTD and when I reinstated that Match command I
got I like pie! instead of a shell.
(It occurs to me now that I could have tried to SIGHUP the child server process that my connections were going through, and that would probably have reconfigured any future virtual connections through that process, but I didn't think of it at the time.)
Then I went home for the day, feeling pretty darn clever, right up
until I discovered, partway through writing this article, that I can't
log in because all I get is I like pie! instead of a shell.
[Other articles in category /Unix] permanent link
Fri, 02 Nov 2018
Another trivial utility: git-q
One of my favorite programs is a super simple Git utility called
git-vee
that I just love, and I use fifty times a day. It displays a very
simple graph that shows where two branches diverged. For example, my
push of master was refused because it was not a
fast-forward. So I
used git-vee to investigate, and saw:
* a41d493 (HEAD -> master) new article: Migraine
* 2825a71 message headers are now beyond parody
| * fa2ae34 (origin/master) message headers are now beyond parody
|/
o 142c68a a bit more information
The current head (master) and its upstream (origin/master) are
displayed by default. Here the nearest common ancestor is 142c68a,
and I can see the two commits after that on master that are
different from the commit on origin/master. The command is called
git-vee because the graph is (usually) V-shaped, and I want to find
out where the point of the V is and what is on its two arms.
From this V, it appears that what happened was: I pushed fa2ae34,
then amended it to produce 2825a71, but I have not yet force-pushed
the amendment. Okay! I should simply do the force-push now…
Except wait, what if that's not what happened? What if what
happened was, 2825a71 was the original commit, and I pushed it, then
fetched it on a different machine, amended it to produce fa2ae34,
and force-pushed that? If so, then force-pushing 2825a71 now would
overwrite the amendments. How can I tell what I should do?
Formerly I would have used diff and studied the differences, but now
I have an easier way to find the answer. I run:
git q HEAD^ origin/master
and it produces the dates on which each commit was created:
2825a71 Fri Nov 2 02:30:06 2018 +0000
fa2ae34 Fri Nov 2 02:25:29 2018 +0000
Aha, it was as I originally thought: 2825a71 is five minutes newer.
The force-push is the right thing to do this time.
Although the commit date is the default output, the git-q
command can
produce any of the information known to git-log, using the usual
escape sequences.
For example, git q %s ... produces subject lines:
% git q %s HEAD origin/master 142c68a
a41d493 new article: Migraine
fa2ae34 message headers are now beyond parody
142c68a a bit more information
and git q '%an <%ae>' tells you who made the commits:
a41d493 Mark Jason Dominus (陶敏修) <mjd@plover.com>
fa2ae34 Mark Jason Dominus (陶敏修) <mjd@plover.com>
142c68a Mark Jason Dominus (陶敏修) <mjd@plover.com>
The program is in my personal git-util repository but it's totally simple and should be easy to customize the way you want:
#!/usr/bin/python3
from sys import argv, stderr
import subprocess
if len(argv) < 3: usage()
if argv[1].startswith('%'):
item = argv[1]
ids = argv[2:]
else:
item='%cd'
ids = argv[1:]
for id in ids:
subprocess.run([ "git", "--no-pager",
"log", "-1", "--format=%h " + item, id])
[Other articles in category /prog] permanent link
















