Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Thu, 31 Dec 2009
A monad for probability and provenance
I don't quite remember how I arrived at this, but it occurred to me
last week that probability distributions form a monad. This is the
first time I've invented a new monad that I hadn't seen before; then I
implemented it and it behaved pretty much the way I thought it would.
So I feel like I've finally arrived, monadwise.
Suppose a monad value represents all the possible outcomes of an event, each with a probability of occurrence. For concreteness, let's suppose all our probability distributions are discrete. Then we might have:
data ProbDist p a = ProbDist [(a,p)] deriving (Eq, Show) unpd (ProbDist ps) = psEach a is an outcome, and each p is the probability of that outcome occurring. For example, biased and unbiased coins:
unbiasedCoin = ProbDist [ ("heads", 0.5),
("tails", 0.5) ];
biasedCoin = ProbDist [ ("heads", 0.6),
("tails", 0.4) ];
Or a couple of simple functions for making dice:
import Data.Ratio
d sides = ProbDist [(i, 1 % sides) | i <- [1 .. sides]]
die = d 6
d n is an n-sided die.
The Functor instance is straightforward:
instance Functor (ProbDist p) where
fmap f (ProbDist pas) = ProbDist $ map (\(a,p) -> (f a, p)) pas
The Monad instance requires return and
>>=. The return function merely takes an event and
turns it into a distribution where that event occurs with probability
1. I find join easier to think about than >>=.
The join function takes a nested distribution, where each
outcome of the outer distribution specifies an inner distribution for
the actual events, and collapses it into a regular, overall
distribution. For example, suppose you put a biased coin and an
unbiased coin in a bag, then pull one out and flip it:
bag :: ProbDist Double (ProbDist Double String)
bag = ProbDist [ (biasedCoin, 0.5),
(unbiasedCoin, 0.5) ]
The join operator collapses this into a single ProbDist
Double String:
ProbDist [("heads",0.3),
("tails",0.2),
("heads",0.25),
("tails",0.25)]
It would be nice if join could combine the duplicate
heads into a single ("heads", 0.55) entry. But that
would force an Eq a constraint on the event type, which isn't
allowed, because (>>=) must work for all data types, not
just for instances of Eq. This is a problem with Haskell,
not with the monad itself. It's the same problem that prevents one
from making a good set monad in Haskell, even though categorially sets
are a perfectly good monad. (The return function constructs
singletons, and the join function is simply set union.)
Maybe in the next language.Perhaps someone else will find the >>= operator easier to understand than join? I don't know. Anyway, it's simple enough to derive once you understand join; here's the code:
instance (Num p) => Monad (ProbDist p) where return a = ProbDist [(a, 1)] (ProbDist pas) >>= f = ProbDist $ do (a, p) <- pas let (ProbDist pbs) = f a (b, q) <- pbs return (b, p*q)So now we can do some straightforward experiments:
liftM2 (+) (d 6) (d 6) ProbDist [(2,1 % 36),(3,1 % 36),(4,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(3,1 % 36),(4,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(4,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(5,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(10,1 % 36),(6,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(10,1 % 36),(11,1 % 36),(7,1 % 36),(8,1 % 36),(9,1 % 36),(10,1 % 36),(11,1 % 36),(12,1 % 36)]This is nasty-looking; we really need to merge the multiple listings of the same event. Here is a function to do that:
agglomerate :: (Num p, Eq b) => (a -> b) -> ProbDist p a -> ProbDist p b
agglomerate f pd = ProbDist $ foldr insert [] (unpd (fmap f pd)) where
insert (k, p) [] = [(k, p)]
insert (k, p) ((k', p'):kps) | k == k' = (k, p+p'):kps
| otherwise = (k', p'):(insert (k,p) kps)
agg :: (Num p, Eq a) => ProbDist p a -> ProbDist p a
agg = agglomerate id
Then agg $ liftM2 (+) (d 6) (d 6) produces:
ProbDist [(12,1 % 36),(11,1 % 18),(10,1 % 12),(9,1 % 9),
(8,5 % 36),(7,1 % 6),(6,5 % 36),(5,1 % 9),
(4,1 % 12),(3,1 % 18),(2,1 % 36)]
Hey, that's correct.There must be a shorter way to write insert. It really bothers me, because it looks look it should be possible to do it as a fold. But I couldn't make it look any better.
You are not limited to calculating probabilities. The monad actually will count things. For example, let us throw three dice and count how many ways there are to throw various numbers of sixes:
eq6 n = if n == 6 then 1 else 0
agg $ liftM3 (\a b c -> eq6 a + eq6 b + eq6 c) die die die
ProbDist [(3,1),(2,15),(1,75),(0,125)]
There is one way to throw three sixes, 15 ways to throw two sixes, 75
ways to throw one six, and 125 ways to throw no sixes. So
ProbDist is a misnomer. It's easy to convert counts to probabilities:
probMap :: (p -> q) -> ProbDist p a -> ProbDist q a probMap f (ProbDist pds) = ProbDist $ (map (\(a,p) -> (a, f p))) pds normalize :: (Fractional p) => ProbDist p a -> ProbDist p a normalize pd@(ProbDist pas) = probMap (/ total) pd where total = sum . (map snd) $ pas normalize $ agg $ probMap toRational $ liftM3 (\a b c -> eq6 a + eq6 b + eq6 c) die die die ProbDist [(3,1 % 216),(2,5 % 72),(1,25 % 72),(0,125 % 216)]I think this is the first time I've gotten to write die die die in a computer program.
The do notation is very nice. Here we calculate the distribution where we roll four dice and discard the smallest:
stat = do
a <- d 6
b <- d 6
c <- d 6
d <- d 6
return (a+b+c+d - minimum [a,b,c,d])
probMap fromRational $ agg stat
ProbDist [(18,1.6203703703703703e-2),
(17,4.1666666666666664e-2), (16,7.253086419753087e-2),
(15,0.10108024691358025), (14,0.12345679012345678),
(13,0.13271604938271606), (12,0.12885802469135801),
(11,0.11419753086419752), (10,9.41358024691358e-2),
(9,7.021604938271606e-2), (8,4.7839506172839504e-2),
(7,2.9320987654320986e-2), (6,1.6203703703703703e-2),
(5,7.716049382716049e-3), (4,3.0864197530864196e-3),
(3,7.716049382716049e-4)]
One thing I was hoping to get didn't work out. I had this idea that
I'd be able to calculate the outcome of a game of craps like this:
dice = liftM2 (+) (d 6) (d 6) point n = do roll <- dice case roll of 7 -> return "lose" _ | roll == n = "win" _ | otherwise = point n craps = do roll <- dice case roll of 2 -> return "lose" 3 -> return "lose" 4 -> point 4 5 -> point 5 6 -> point 6 7 -> return "win" 8 -> point 8 9 -> point 9 10 -> point 10 11 -> return "win" 12 -> return "lose"This doesn't work at all; point is an infinite loop because the first value of dice, namely 2, causes a recursive call. I might be able to do something about this, but I'll have to think about it more.
It also occurred to me that the use of * in the definition of >>= / join could be generalized. A couple of years back I mentioned a paper of Green, Karvounarakis, and Tannen that discusses "provenance semirings". The idea is that each item in a database is annotated with some "provenance" information about why it is there, and you want to calculate the provenance for items in tables that are computed from table joins. My earlier explanation is here.
One special case of provenance information is that the provenances are probabilities that the database information is correct, and then the probabilities are calculated correctly for the joins, by multiplication and addition of probabilities. But in the general case the provenances are opaque symbols, and the multiplication and addition construct regular expressions over these symbols. One could generalize ProbDist similarly, and the ProbDist monad (even more of a misnomer this time) would calculate the provenance automatically. It occurs to me now that there's probably a natural way to view a database table join as a sort of Kleisli composition, but this article has gone on too long already.
Happy new year, everyone.
[ Addendum 20100103: unsurprisingly, this is not a new idea. Several readers wrote in with references to previous discussion of this monad, and related monads. It turns out that the idea goes back at least to 1981. ]
[ Addendum 20220522: The article begins “I don't quite remember how I arrived at this”, but I just remembered how I arrived at it! I was thinking about how List can be interpreted as the monad that captures the idea of nondeterministic computation. A function that yields a list [a, b, c] represents a nondeterministic computation that might yield any of a, b, or c. (This idea goes back at least as far as Moggi's 1989 monads paper.) I was thinking about an extension to this idea: what if the outcomes were annotated with probabilities to indicate how often each was the result. ]
My thanks to Graham Hunter for his donation.
[Other articles in category /prog/haskell] permanent link
Tue, 15 Dec 2009
Monads are like burritos
A few months ago Brent
Yorgey complained about a certain class of tutorials which present
monads by explaining how monads are like burritos.
At first I thought the choice of burritos was only a facetious reference to the peculiar and sometimes strained analogies these tutorials make. But then I realized that monads are like burritos.
I will explain.
A monad is a special kind of a functor. A functor F takes each type T and maps it to a new type FT. A burrito is like a functor: it takes a type, like meat or beans, and turns it into a new type, like beef burrito or bean burrito.
A functor must also be equipped with a map function that lifts functions over the original type into functions over the new type. For example, you can add chopped jalapeños or shredded cheese to any type, like meat or beans; the lifted version of this function adds chopped jalapeños or shredded cheese to the corresponding burrito.
A monad must also possess a unit function that takes a regular value, such as a particular batch of meat, and turns it into a burrito. The unit function for burritos is obviously a tortilla.
Finally, a monad must possess a join function that takes a ridiculous burrito of burritos and turns them into a regular burrito. Here the obvious join function is to remove the outer tortilla, then unwrap the inner burritos and transfer their fillings into the outer tortilla, and throw away the inner wrappings.
The map, join, and unit functions must satisfy certain laws. For example, if B is already a burrito, and not merely a filling for a burrito, then join(unit(B)) must be the same as B. This means that if you have a burrito, and you wrap it in a second tortilla, and then unwrap the contents into the outer tortilla, the result is the same as what you started with.
This is true because tortillas are indistinguishable.
I know you are going to point out that some tortillas have the face of Jesus. But those have been toasted, and so are unsuitable for burrito-making, and do not concern us here.
So monads are indeed like burritos.
I asked Brent if this was actually what he had in mind when he first suggested the idea of tutorials explaining monads in terms of burritos, and if everyone else had understood this right away.
But he said no, I was the lone genius.
[ Addendum 20120106: Chris Done has presented this theory in cartoon form. ]
[ Addendum 20201025: Eugenia Cheng tweets this page! But the last word, “stupid”, is inexplicably misspelled. ]
[Other articles in category /prog] permanent link
Mon, 14 Dec 2009
Another short explanation of Gödel's theorem
In yesterday's article, I
said:
A while back I started writing up an article titled "World's shortest explanation of Gödel's theorem". But I didn't finish it...
I went and had a look to see what was wrong with it, and to my surprise, there seemed to be hardly anything wrong with it. Perhaps I just forgot to post it. So if you disliked yesterday's brief explanation of Gödel's theorem—and many people did—you'll probably dislike this one even more. Enjoy!
A reader wrote to question my characterization of Gödel's theorem in the previous article. But I think I characterized it correctly; I said:
The only systems of mathematical axioms strong enough to prove all true statements of arithmetic, are those that are so strong that they also prove all the false statements of arithmetic.I'm going to explain how this works.
You start by choosing some system of mathematics that has some machinery in it for making statements about things like numbers and for constructing proofs of theorems like 1+1=2. Many such systems exist. Let's call the one we have chosen M, for "mathematics".
Gödel shows that if M has enough mathematical machinery in it to actually do arithmetic, then it is possible to produce a statement S whose meaning is essentially "Statement S cannot be proved in system M."
It is not at all obvious that this is possible, or how it can be done, and I am not going to get into the details here. Gödel's contribution was seeing that it was possible to do this.
So here's S again:
S: Statement S cannot be proved in system M.
Now there are two possibilities. Either S is in fact provable in system M, or it is not. One of these must hold.
If S is provable in system M, then it is false, and so it is a false statement that can be proved in system M. M therefore proves some false statements of arithmetic.
If S is not provable in system M, then it is true, and so it is a true statement that cannot be proved in system M. M therefore fails to prove some true statements of arithmetic.
So something goes wrong with M: either it fails to prove some true statements, or else it succeeds in proving some false statements.
List of topics I deliberately omitted from this article, that mathematicians should not write to me about with corrections: Presburger arithmetic. Dialetheism. Inexhaustibility. ω-incompleteness. Non-RE sets of axioms.
| Buy Godel's Theorem: An Incomplete Guide to Its Use and Abuse  from Bookshop.org (with kickback) (without kickback) |
If you liked this post, you may enjoy Torkel Franzén's books Godel's Theorem: An Incomplete Guide to Its Use and Abuse and Inexhaustibility: A Non-Exhaustive Treatment. If you disliked this post, you are even more likely to enjoy them.
Many thanks to Robert Bond for his contribution.
[Other articles in category /math] permanent link
Sun, 13 Dec 2009
World's shortest explanation of Gödel's theorem
A while back I started writing up an article titled "World's shortest
explanation of Gödel's theorem". But I didn't finish it, and
later I encountered Raymond Smullyan's version, which is much shorter
anyway. So here, shamelessly stolen from Smullyan, is the World's
shortest explanation of Gödel's theorem.
We have some sort of machine that prints out statements in some sort of language. It needn't be a statement-printing machine exactly; it could be some sort of technique for taking statements and deciding if they are true. But let's think of it as a machine that prints out statements.
In particular, some of the statements that the machine might (or might not) print look like these:
| P*x | (which means that | the machine will print x) |
| NP*x | (which means that | the machine will never print x) |
| PR*x | (which means that | the machine will print xx) |
| NPR*x | (which means that | the machine will never print xx) |
For example, NPR*FOO means that the machine will never print FOOFOO. NP*FOOFOO means the same thing. So far, so good.
Now, let's consider the statement NPR*NPR*. This statement asserts that the machine will never print NPR*NPR*.
Either the machine prints NPR*NPR*, or it never prints NPR*NPR*.
If the machine prints NPR*NPR*, it has printed a false statement. But if the machine never prints NPR*NPR*, then NPR*NPR* is a true statement that the machine never prints.
So either the machine sometimes prints false statements, or there are true statements that it never prints.
So any machine that prints only true statements must fail to print some true statements.
Or conversely, any machine that prints every possible true statement must print some false statements too.
The proof of Gödel's theorem shows that there are statements of pure arithmetic that essentially express NPR*NPR*; the trick is to find some way to express NPR*NPR* as a statement about arithmetic, and most of the technical details (and cleverness!) of Gödel's theorem are concerned with this trick. But once the trick is done, the argument can be applied to any machine or other method for producing statements about arithmetic.
The conclusion then translates directly: any machine or method that produces statements about arithmetic either sometimes produces false statements, or else there are true statements about arithmetic that it never produces. Because if it produces something like NPR*NPR* then it is wrong, but if it fails to produce NPR*NPR*, then that is a true statement that it has failed to produce.
So any machine or other method that produces only true statements about arithmetic must fail to produce some true statements.
Hope this helps!
(This explanation appears in Smullyan's book 5000 BC and Other Philosophical Fantasies, chapter 3, section 65, which is where I saw it. He discusses it at considerable length in Chapter 16 of The Lady or the Tiger?, "Machines that Talk About Themselves". It also appears in The Mystery of Scheherezade.)
I gratefully acknowledge Charles Colht for his generous donation to this blog.
[ Addendum 20091214: Another article on the same topic. ]
[ Addendum 20150403: Reddit user cafe_anon has formalized this argument as a Coq proof. ]
[ Addendum 20150406: Reddit user TezlaKoil has formalized this argument as an Agda proof. (Unformatted version) ]
[Other articles in category /math] permanent link
Fri, 11 Dec 2009
On failing open
An axiom of security analysis is that nearly all security mechanisms
must fail closed. What this means is that if there is an uncertainty
about whether to grant or to deny access, the right choice is nearly
always to deny access.
For example, consider a login component that accepts a username and a password and then queries a remote authentication server to find out if the password is correct. If the connection to the authentication server fails, or if the authentication server is down, the login component must decide whether to grant or deny access, in the absence of correct information from the server. The correct design is almost certainly to "fail closed", and to deny access.
I used to teach security classes, and I would point out that programs sometimes have bugs, and do the wrong thing. If your program has failed closed, and if this is a bug, then you have an irate user. The user might call you up and chew you out, or might chew you out to your boss, and they might even miss a crucial deadline because your software denied them access when it should have granted access. But these are relatively small problems. If your program has failed open, and if this is a bug, then the user might abscond with the entire payroll and flee to Brazil.
(I was once teaching one of these classes in Lisbon, and I reached the "flee to Brazil" example without having realized ahead of time that this had greater potential to offend the Portuguese than many other people. So I apologized. But my hosts very kindly told me that they would have put it the same way, and that in fact the Mayor of Lisbon had done precisely what I described a few years before. The moral of the story is to read over the slides ahead of time before giving the talk.)
But I digress. One can find many examples in the history of security that failed the wrong way.
However, the issue is on my mind because I was at a job interview a few weeks ago with giant media corporation XYZ. At the interview, we spent about an hour talking about an architectural problem they were trying to solve. XYZ operates a web site where people can watch movies and TV programs online. Thy would like to extend the service so that people who subscribe to premium cable services, such as HBO, can authenticate themselves to the web site and watch HBO programs there; HBO non-subscribers should get only free TV content. The problem in this case was that the authentication data was held on an underpowered legacy system that could serve only a small fraction of the requests that came in.
The solution was to cache the authentication data on a better system, and gather and merge change information from the slow legacy system as possible.
I observed during the discussion that this was a striking example of the rare situation in which one wants the authentication system to fail open instead of closed. For suppose one grants access that should not be granted. Then someone on the Internet gets to watch a movie or an episode of The Sopranos for free, which is not worth getting excited about and which happens a zillion times a day anyhow.
But suppose the software denies access that should have been granted. Then there is a legitimate paying customer who has paid to watch The Sopranos, and we told them no. Now they are a legitimately irate customer, which is bad, and they may call the support desk, costing XYZ Corp a significant amount of money, which is also bad. So all other things being equal, one should err on the side of lenity: when in doubt, grant access.
I would like to thank Andrew Lenards for his gift.
[Other articles in category /tech] permanent link
Wed, 09 Sep 2009
You think you're All That, but you're not!
I have long been interested in term rewriting systems, and one of my
long-term goals is to implement the Knuth-Bendix completion algorithm,
described by Knuth and Bendix in their famous paper "Word Problems in
Universal Algebras". This paper grabbed my attention around 1988; I
found it in an anthology edited by John Leech (of Leech lattice fame)
that I was probably looking into because it also contained an
enumeration by J.H. Conway of all knots with at most eleven
crossings. I found the Knuth-Bendix paper very hard to read, but the
examples at the end were extremely compelling. I still find the paper
very hard to read, but fortunately better explanations are now
available. (For
example, this one by A.J.J. Dick.) One of the also-ran
topics for Higher-Order Perl was a structured drawing
system based on Wm Leler's "Bertrand" term-rewriting system.
So I was delighted to discover that there was a new book out called Term Rewriting and All That. The "...and All That" suffix is a reference to the tongue-in-cheek classic of British history, 1066 and All That, and promised a casual, accessible, and possibly humorous treatment.
Unfortunately the promise was not kept. The book is very good, but it is not casual or humorous. Nor is it especially accessible. It is a solid slab of term rewriting, one of those books that make me think "I would not want to drop it on my foot." That is not a bad thing; the Barendregt book is superb, an enormous superb slab of lambda calculus that you would not want to drop on your foot. But it is not titled "Lambda Calculus and All That".
So why the title? I don't know. The authors are Germans, so perhaps they don't understand the joke?
[ Addendum: There's exactly one review of this book on Amazon, and it says the same thing I do. It begins: "My main criticism of this book is its title." ]
[Other articles in category /book] permanent link
Fri, 31 Jul 2009
Dijkstra was not insane
Recently, a reader on the Higher-Order Perl
discussion mailing list made a remark about Edsger Dijkstra and
his well-known opposition to the break construction (in Perl,
last) that escapes prematurely from a loop. People often use
this as an example to show that Dijkstra was excessively doctrinaire,
and out of touch with the reality of programming[1], but usually it's
because they don't know what his argument was.
I wrote a response, explaining where Dijkstra was coming from, and I am very happy with how it came out, so I'm reposting it here.
The list subscriber said, in part:
On a side note, I never read anything by Dijkstra that wasn't noticeably out of touch with the reality of programming, which qualifies them as screeds to me.A lot of people bring up the premature-loop-exit prohibition without understanding why Dijkstra suggested it; it wasn't just that he was a tightassed Dutchman.And I say that as a former Pascal programmer, and as one who has read, and bought into, things like Kernighan's "Why Pascal is Not My Favorite Programming Language" and the valid rants about how some form of breaking out of a loop without having to proceed to the end is very useful, without destroying structure (except by Dijkstra's definition of structure)...
Dijkstra's idea was this: suppose you want to prove, mathematically, that your program does what it is supposed to do. Please, everyone, suspend your judgment of this issue for a few paragraphs, and bear with me. Let's really suppose that we want to do this.
Dijkstra's idea is that the program is essentially a concatenation of blocks, each of which is trying to accomplish something or other, and each of which does not make sense to run unless some part of the program state is set up for it ahead of time. For example, the program might be to print a sorted list of links from a web page. Then the obvious blocks are:
- A
- get the web page and store it in a variable
- B
- extract the links from the text in the variable into an array
- C
- sort the array
- D
- print out the array contents
We say that the "precondition" for C is that the array be populated with URLs, and the "postcondition" is that the array be in sorted order. What you would want to prove about C is that if the precondition holds—that is, if the array is properly populated before C begins—then the postcondition will hold too—that is, the array will be in sorted order when C completes.
It occurs to me that calling this a "proof" is probably biasing everyone's thinking. Let's forget about mathematical proofs and just think about ordinary programmers trying to understand if the program is correct. If the intern in the next cubicle handed you his code for this program, and you were looking it over, you would probably think in very much this way: you would identify block C (maybe it's a subroutine, or maybe not) and then you would try to understand if C, given an array of URLs, would produce a properly sorted array by the time it was done.
C itself might depend on some sub-blocks or subroutines that performed sub-parts of the task; you could try to understand them similarly.
Having proved (or convinced yourself) that C will produce the postcondition "array contains sorted list of URLs", you are in an excellent position to prove (or convince yourself) that block D prints out a sorted array of URLs, which is what you want. Without that belief about C, you are building on sand; you have almost nothing to go on, and you can conclude hardly anything useful about the behavior of D.
Now consider a more complex block, one of the form:
if (q) { E; }
else { F; }
Suppose you believe that code E, given precondition x, is
guaranteed to produce postcondition y. And suppose you believe
the same thing about F. Then you can conclude the same thing about
the entire if-else block: if x was true before it began
executing, then y will be true when it is done.[2] So you can build up proofs (or beliefs)
about small bits of code into proofs (or beliefs) about larger ones.We can understand while loops similarly. Suppose we know that condition p is true prior to the commencement of some loop, and that if p is true before G executes, then p will also be true when G finishes. Then what can we say about this loop?
while (q) { G; }
We can conclude that if p was true before the loop began, then p will
still be true, and q will be false, when the loop ends.BUT BUT BUT BUT if your language has break, then that guarantee goes out the window and you can conclude nothing. Or at the very least your conclusions will become much more difficult. You can no longer treat G atomically; you have to understand its contents in detail.
So this is where Dijkstra is coming from: features like break[3] tend to sabotage the benefits of structured programming, and prevent the programmer from understanding the program as a composition of independent units. The other subscriber made a seemingly disparaging reference to "Dijkstra's idea of structure", but I hope it is clear that it was not an arbitrary idea. Dijkstra's idea of structure is what will allow you to understand a large program as a collection of modules.
Regardless of your opinion about formal verification methods, or correctness proofs, or the practicality of omitting break from your language, it should at least be clear that Dijkstra was not being doctrinaire just for the sake of doctrine.
Some additional notes
Here are some interesting peripheral points that I left out of my main discussion because I wanted to stick to the main point, which was: "Dijkstra was not insane".
- I said in an earlier post that "I often find
Dijkstra's innumerable screeds very tiresome in their unkind,
unforgiving, and unrealistic attitudes toward programmers." But
despite this, I believe he was a brilliant thinker, and almost every
time he opened his mouth it was to make a carefully-considered
argument. You may not like him, and you may not agree with him, but
you'll be better off listening to him.
An archive of Dijkstra's miscellaneous notes and essays (a pre-blogging blog, if you like) is maintained at the University of Texas. I recommend it.
- I said:
Actually, your job is slightly easier. Let's write this:if (q) { E; } else { F; }Suppose you believe that code E, given precondition x, is guaranteed to produce postcondition y. And suppose you believe the same thing about F. Then you can conclude the same thing about the entire if-else block.[x] E [y]
to mean that code E, given precondition x, produces postcondition y. That is, if we know that x is true when E begins execution, then we know that y is true when E finishes. Then my quoted paragraph above says that from these:[x] E [y]
we can conclude this:
[x] F [y][x] if (q) {E} else {F} [y]
But actually we can make a somewhat stronger statement. We can make the same conclusion from weaker assumptions. If we believe these:[x and q] E [y]
then we can conclude this:
[x and not q] F [y][x] if (q) {E} else {F} [y]
In fact this precisely expresses the complete semantics of the if-else construction. Why do we use if-else blocks anyway? This is the reason: we want to be able to write code to guarantee something like this:[x] BLAH [y]
but we only know how to guarantee[x and q] FOO [y]
and[x and not q] BAR [y]
for some q. So we write two blocks of code, each of which accomplishes y under some circumstances, and use if-else to make sure that the right one is selected under the right circumstances. - Similar to break (but worse), in the presence of goto you are on very shaky ground in trying to conclude anything about whether the program is correct. Suppose you know that C is correct if its precondition (an array of URLs) is satisfied. And you know that B will set up that precondition (that is, the array) if its precondition is satisfied, so it seems like you are all right. But no, because block W somewhere else might have goto C; and transfer control to C without setting up the precondition, and then C could cause winged demons to fly out of your nose.
Further reading
-
For a quick overview, see the Wikipedia article
on Hoare logic. Hoare logic is the
[x] E [y] notation I used above, and a set of
rules saying how to reason with claims of that form. For example,
one rule of Hoare logic defines the meaning of the null statement: if ; is the null
statement, then [p] ; [p] for all conditions
p.
Hoare logic was invented by Tony Hoare, who also invented the Quicksort algorithm.
-
For further details, see Dijkstra's book "A Discipline of
Programming". Dijkstra introduces a function called wp for
"weakest precondition".
Given a piece of code C and a desired postcondition
q, wp(C, q) is the weakest precondition
that is sufficient for code C to accomplish q. That
is, it's the minimum prerequisite for C to accomplish
q. Most of the book is about how to figure out what these
weakest preconditions are, and, once you know them, how they can
guide you to through the implementation of your program.
I have an idea that the Dijkstra book might be easier to follow after having read this introduction than without it.
- No discussion of structured programming and goto is
complete without a mention of Donald Knuth's wonderful paper
Stuctured Programming with go to Statements.
This is my single all-time favorite computer science paper. Download it here.
- Software Tools in Pascal is a book by Kernighan and
Plauger that tries to translate the tool suite of their earlier
Software Tools book into Pascal. They were repeatedly
screwed by deficiencies in the Pascal language, and this was the
inspiration for Kernighan's famous "Why Pascal is not my Favorite
Programming Language" paper. In effect, Software Tools in
Pascal is a book-length case study of the deficiencies of
Pascal for practical programming tasks.
[Other articles in category /prog] permanent link
Sun, 21 Jun 2009
Gray code at the pediatrician's office

 Last week we took Katara to the pediatrician for a checkup, during which
they weighed, measured, and inoculated her. The measuring device,
which I later learned is called a stadiometer, had a bracket on a slider that went up and down on a
post. Katara stood against the post and the nurse adjusted the bracket
to exactly the top of her head. Then she read off Katara's height from
an attached display.
Last week we took Katara to the pediatrician for a checkup, during which
they weighed, measured, and inoculated her. The measuring device,
which I later learned is called a stadiometer, had a bracket on a slider that went up and down on a
post. Katara stood against the post and the nurse adjusted the bracket
to exactly the top of her head. Then she read off Katara's height from
an attached display.
How did the bracket know exactly what height to report? This was done in a way I hadn't seen before. It had a photosensor looking at the post, which was printed with this pattern:
 (Click to view the other pictures I took of the post.)
(Click to view the other pictures I took of the post.)
The pattern is binary numerals. Each numeral is a certain fraction of a centimeter high, say 1/4 centimeter. If the sensor reads the number 433, that means that the bracket is 433/4 = 108.25 cm off the ground, and so that Katara is 108.25 cm tall.
The patterned strip in the left margin of this article is a straightforward translation of binary numerals to black and white boxes, with black representing 1 and white representing 0:
0000000000If you are paying attention, you will notice that although the strip at left is similar to the pattern in the doctor's office, it is not the same. That is because the numbers on the post are Gray-coded.
0000000001
0000000010
0000000011
0000000100
0000000101
0000000101
...
1111101000
1111101001
...
1111111111
Gray codes solve the following problem with raw binary numbers. Suppose Katara is close to 104 = 416/4 cm tall, so that the photosensor is in the following region of the post:
...But suppose that the sensor (or the post) is slightly mis-aligned, so that instead of properly reading the (416) row, it reads the first half of the (416) row and last half of the (415) row. That makes 0110111111, which is 447 = 111.75 cm, an error of almost 7.5%. (That's three inches, for my American and Burmese readers.) Or the error could go the other way: if the sensor reads the first half of the (415) and the second half of the (416) row, it will see 0110000000 = 384 = 96 cm.
0110100001 (417)
0110100000 (416)
0110011111 (415)
0110011110 (414)
...
Gray code is a method for encoding numbers in binary so that each numeral differs from the adjacent ones in only one position:
0000000000This is the pattern from the post, which you can also see at the right of this article.
0000000001
0000000011
0000000010
0000000110
0000000111
0000000101
0000000100
0000001100
...
1000011100
1000011101
...
1000000000
Now suppose that the mis-aligned sensor reads part of the (416) line and part of the (417) line. With ordinary binary coding, this could result in an error of up to 7.75 cm. (And worse errors for children of other heights.) But with Gray coding no error results from the misreading:
...No matter what parts of 0101110000 and 0101110001 are stitched together, the result is always either 416 or 417.
0101110000 (417)
0101010000 (416)
0101010001 (415)
0101010011 (414)
...
Converting from Gray code to standard binary is easy: take the binary expansion, and invert every bit that is immediately to the right of a 1 bit. For example, in 1111101000, each red bit is to the right of a 1, and so is inverted to obtain the Gray code 1000011100.
Converting back is also easy: Flip any bit that is anywhere to the right of an odd number of 1 bits, and leave alone the bits that are to the right of an even number of 1 bits. For example, Gray code 1000011100 contains four 1's, and the bits to the right of the first (00001) and third (1), but not the second or fourth, get flipped to 11110 and 0, to give 1111101000.
[ Addendum 20110525: Every so often someone asks why the stadiometer is so sophisticated. Here is the answer. ]
[Other articles in category /math] permanent link
Tue, 16 Jun 2009
Haskell logo fail
The Haskell folks have chosen a new logo.


[Other articles in category /prog/haskell] permanent link
Fri, 22 May 2009
A child is bitten by a dog every 0.07 seconds...
I read in the
newspaper today that letter carriers were bitten by dogs 3,000
times last year. (Curiously, this is not a round number; it
is exact.) The article then continued: "children ... are 900
times more likely to be bitten than letter carriers."
This is obviously nonsense, because suppose the post office employs half a million letter carriers. (The actual number is actually about half that, but we are doing a back-of-the-envelope estimate of plausibility.) Then the bite rate is six bites per thousand letter carriers per year, and if children are 900 times more likely to be bitten, they are getting bitten at a rate of 5,400 bites per thousand children per year, or 5.4 bites per child. Insert your own joke here, or use the prefabricated joke framework in the title of this article.
I wrote to the reporter, who attributed the claim to the Postal Bulletin 22258 of 7 May 2009. It does indeed appear there. I am trying to track down the ultimate source, but I suspect I will not get any farther. I have discovered that the "900 times" figure appears in the Post Office's annual announcements of Dog Bite Prevention Month as far back as 2004, but not as far back as 2002.
Meantime, what are the correct numbers?
The Centers for Disease Control and Prevention have a superb on-line database of injury data. It immediately delivers the correct numbers for dog bite rate among children:
| Age | Number of injuries | Population | Rate per 100,000 |
|---|---|---|---|
| 0 | 2,302 | 4,257,020 | 54.08 |
| 1 | 7,100 | 4,182,171 | 169.77 |
| 2 | 10,049 | 4,110,458 | 244.47 |
| 3 | 10,355 | 4,111,354 | 251.86 |
| 4 | 9,920 | 4,063,122 | 244.15 |
| 5 | 7,915 | 4,031,709 | 196.32 |
| 6 | 8,829 | 4,089,126 | 215.91 |
| 7 | 6,404 | 3,935,663 | 162.72 |
| 8 | 8,464 | 3,891,755 | 217.48 |
| 9 | 8,090 | 3,901,375 | 207.36 |
| 10 | 7,388 | 3,927,298 | 188.11 |
| 11 | 6,501 | 4,010,171 | 162.11 |
| 12 | 7,640 | 4,074,587 | 187.49 |
| 13 | 5,876 | 4,108,962 | 142.99 |
| 14 | 4,720 | 4,193,291 | 112.56 |
| 15 | 5,477 | 4,264,883 | 128.42 |
| 16 | 4,379 | 4,334,265 | 101.03 |
| 17 | 4,459 | 4,414,523 | 101.01 |
| Total | 133,560 | 82,361,752 | 162.16 |
According to the USPS 2008 Annual Report, in 2008 the USPS employed 211,661 city delivery carriers and 68,900 full-time rural delivery carriers, a total of 280,561. Since these 280,561 carriers received 3,000 dog bites, the rate per 100,000 carriers per year is 1069.29 bites.
So the correct statistic is not that children are 900 times more likely than carriers to be bitten, but rather that carriers are 6.6 times as likely as children to be bitten, 5.6 times if you consider only children under 13. Incidentally, your toddler's chance of being bitten in the course of a year is only about a quarter of a percent, ceteris paribus.
Where did 900 come from? I have no idea.
There are 293 times as many children as there are letter carriers, and they received a total of 44.5 times as many bites. The "900" figure is all over the Internet, despite being utterly wrong. Even with extensive searching, I was not able to find this factoid in the brochures or reports of any other reputable organization, including the American Veterinary Medical Association, the American Academy of Pediatrics, the Centers for Disease Control and Prevention, or the Humane Society of the Uniited States. It appears to be the invention of the USPS.
Also in the same newspaper, the new Indian restaurant on Baltimore avenue was advertising that they "specialize in vegetarian and non-vegetarian food". It's just a cornucopia of stupidity today, isn't it?
[Other articles in category /math] permanent link
Thu, 21 May 2009| The number of crank dissertations |
| dealing with the effects of sunspots |
| on political and economic events |
| peaks every eleven years. |
[Other articles in category /misc] permanent link
Wed, 20 May 2009
No flimping
Advance disclaimer: I am not a linguist, have never studied
linguistics, and am sure to get some of the details wrong in this
article. Caveat lector.
There is a standard example in linguistics that is attached to the word "flimp". The idea it labels is that certain grammatical operations are restricted in the way they behave, and cannot reach deeply into grammatical structures and rearrange them.
For instance, you can ask "What did you use to see the girl on the hill in the blue dress?" and I can reply "I used a telescope to see the girl on the hill in the blue dress". Here "the girl on the hill in the blue dress" is operating as a single component, which could, in principle, be arbitrarily long. ("The girl on the hill that was fought over in the war between the two countries that have been at war since the time your mother saw that monkey climb the steeple of the church...") This component can be extracted whole from one sentence and made the object of a new sentence, or the subject of some other sentence.
But certain other structures are not transportable. For example, in "Bill left all his money to Fred and someone", one can reach down as far as "Fred and someone" and ask "What did Bill leave to Fred and someone?" but one cannot reach all the way down to "someone" and ask "Who did Bill leave all his money to Fred and"?
Under certain linguistic theories of syntax, analogous constraints rule out the existence of certain words. "Flimped" is the hypothetical nonexistent word which, under these theories, cannot exist. To flimp is to kiss a girl who is allergic to. For example, to flimp coconuts is to kiss a girl who is allergic to coconuts. (The grammatical failure in the last sentence but one illustrates the syntactic problem that supposedly rules out the word "flimped".
I am not making this up; for more details (from someone who, unlike me, may know what he is talking about) See Word meaning and Montague grammar by David Dowty, p. 236. Dowty cites the earlier sources, from 1969–1973 who proposed this theory in the first place. The "flimped" example above is exactly the same as Dowty's, and I believe it is the standard one.
Dowty provides a similar, but different example: there is not, and under this theory there cannot be, a verb "to thork" which means "to lend your uncle and", so that "John thorked Harry ten dollars" would mean "John lent his uncle and Harry ten dollars".
I had these examples knocking around in my head for many years. I used to work for the University of Pennsylvania Computer and Information Sciences department, and from my frequent contacts with various cognitive-science types I acquired a lot of odds and ends of linguistic and computational folklore. Michael Niv told me this one sometime around 1992.
The "flimp" thing rattled around my head, surfacing every few months or so, until last week, when I thought of a counterexample: Wank.
The verb "to wank to" means "to rub one's genitals while considering", and so seems to provide a countexample to the theory that says that verbs of this type are illegal in English.
When I went to investigate, I found that the theory had pretty much been refuted anyway. The Dowty book (published 1979) produced another example: "to cuckold" is "to have sexual intercourse with the woman who is married to".
Some Reddit person recently complained that one of my blog posts had no point. Eat this, Reddit person.
[Other articles in category /lang] permanent link
Sun, 17 May 2009
Bipartite matching and same-sex marriage
My use of the identifiers husband and wife in Thursday's example code
should not be taken as any sort of political statement against
same-sex marriage. The function was written as part of a program to
solve the stable bipartite
matching problem. In this problem, which has historically been
presented as concerning "marriage", there are two disjoint
equinumerous sets, which we may call "men" and "women". Each man
ranks the women in preference order, and each woman ranks the men in
preference order. Men are then matched to women. A matching is
"stable" if there is no man m and no woman w such that
m and w both prefer each other to their current
partners. A theorem of Gale and Shapley guarantees the existence of a
stable matching and provides an algorithm to construct one.
However, if same-sex marriages are permitted, there may not be a stable matching, so the character of the problem changes significantly.
A minimal counterexample is:
| A prefers: | B | C | X |
| B prefers: | C | A | X |
| C prefers: | A | B | X |
| X prefers: | A | B | C |
Suppose we match A–B, C–X. Then since B prefers C to A, and C prefers B to X, B and C divorce their mates and marry each other, yielding B–C, A–X.
But now C can improve her situation further by divorcing B in favor of A, who is only too glad to dump the miserable X. The marriages are now A–C, B–X.
B now realizes that his first divorce was a bad idea, since he thought he was trading up from A to C, but has gotten stuck with X instead. So he reconciles with A, who regards the fickle B as superior to her current mate C. The marriages are now A–B, C–X, and we are back where we started, having gone through every possible matching.
This should not be taken as an argument against same-sex marriage. The model fails to generate the following obvious real-world solution: A, B, and C should all move in together and live in joyous tripartite depravity, and X should jump off a bridge.
[Other articles in category /math] permanent link
Fri, 15 May 2009
"Known to Man" and the advent of the space aliens
Last week I wrote about how I
was systematically changing the phrase "known to man" to just "known"
in Wikipedia articles.
Two people so far have written to warn me that I would regret this once the space aliens come, and I have to go around undoing all my changes. But even completely leaving aside Wikipedia's "Wikipedia is not a crystal ball" policy, which completely absolves me from having to worry about this eventuality, I think these people have not analyzed the situation correctly. Here is how it seems to me.
Consider these example sentences:
- Diamond is the hardest substance known to man.
- Diamond is the hardest substance known.
There are four possible outcomes for the future:
- Aliens reveal superhardium, a substance harder than diamond.
- Aliens exist, but do not know about superhardium.
- The aliens do not turn up, but humans discover superhardium on their own.
- No aliens and no superhardium.
In cases (1) and (3), both sentences require revision.
In case (4), neither sentence requires revision.
But in case (2), sentence (a) requires revision, while (b) does not. So my change is a potential improvement in a way I had not appreciated.
Also in last week's article, I said it would be nice to find a case where a Wikipedia article's use of "known to man" actually intended a contrast with divine or feminine knowledge, rather than being a piece of inept blather. I did eventually find such a case: the article on runic alphabet says, in part:
In the Poetic Edda poem Rígþula another origin is related of how the runic alphabet became known to man. The poem relates how Ríg, identified as Heimdall in the introduction, ...
I gratefully acknowledge the gift of Thomas Guest. Thank you!
[Other articles in category /aliens] permanent link
Thu, 14 May 2009
Product types in Java
Recently I wanted a Java function that would return two Person
objects. Java functions return only a single value. I could, of
course, make a class that encapsulates two Persons:
class Persons2 {
Person personA, personB;
Persons2(Person a, Person b) {
personA = a; personB = b;
}
Person getPersonA() { return personA; }
...
}
Java is loathsome in its verbosity, and this sort of monkey code is
Java's verbosity at its most loathsome. So I did not do this.Haskell functions return only one value also, but this is no limitation, because Haskell has product types. And starting in Java 5, the Java type system is a sort of dented, bolted-on version of the type systems that eventually evolved into the Haskell type system. But product types are pretty simple. I can make a generic product type in Java:
class Pair<A,B> {
A a; B b;
Pair(A a, B b) { this.a = a; this.b = b; }
A fst() { return a; }
B snd() { return b; }
}
Then I can declare my function to return a
Pair<Person,Person>:
Pair<Person,Person> findMatch() {
...
return new Pair(husband, wife);
}
Okay, that worked just fine. The
boilerplate is still there, but you only have to do it once. This
trick seems sufficiently useful that I can imagine that I will use it
again, and that someone else reading this will want to use it too.I've been saying for a while that up through version 1.4, Java was a throwback to the languages of the 1970s, but that with the introduction of generics in Java 5, it took a giant step forward into the 1980s. I think this is a point of evidence in favor of that claim.
I wonder why this class isn't in the standard library. I was not the first person to think of doing this; web search turns up several others, who also wonder why this class isn't in the standard library.
I wrote a long, irrelevant coda regarding my use of the identifiers husband and wife in the example, but, contrary to my usual practice, I will publish it another day.
[ Addendum 20090517: Here's the long, irrelevant coda. ]
I gratefully acknowledge the gift of Petr Kiryakov. Thank you!
[Other articles in category /prog/java] permanent link
Fri, 08 May 2009
Most annoying phrase known to man?
I have been wasting time, those precious minutes of my life that will
never return, by eliminating the odious phrase "known to man" from
Wikipedia articles. It is satisfying, in much the same way as doing
the crossword puzzle, or popping bubble wrap.
In the past I have gone on search-and-destroy missions against certain specific phrases, for example "It should be noted that...", which can nearly always be replaced with "" with no loss of meaning. But "known to man" is more fun.
One pleasant property of this phrase is that one can sidestep the issue of whether "man" is gender-neutral. People on both sides of this argument can still agree that "known to man" is best replaced with "known". For example:
- The only albino gorilla known to man...
- The most reactive and electronegative substance known to man...
- Copper and iron were known to man well before the copper age and iron age...
As a pleonasm and a cliché, "known to man" is a signpost to prose that has been written by someone who was not thinking about what they were saying, and so one often finds it amid other prose that is pleonastic and clichéd. For example:
Diamond ... is one of the hardest naturally occurring material known (another harder substance known today is the man-made substance aggregated diamond nanorods which is still not the hardest substance known to man).Which I trimmed to say:
Diamond ... is one of the hardest naturally-occurring materials known. (Some artificial substances, such as aggregated diamond nanorods, are harder.)Many people ridicule Strunk and White's fatuous advice to "omit needless words"—if you knew which words were needless, you wouldn't need the advice—but all editors know that beginning writers will use ten words where five will do. The passage above is a good example.
Can "known to man" always be improved by replacement with "known"? I might have said so yesterday, but I mentioned the issue to Yaakov Sloman, who pointed out that the original use was meant to suggest a contrast not with female knowledge but with divine knowledge, an important point that completely escaped my atheist self. In light of this observation, it was easy to come up with a counterexample: "His acts descended to a depth of evil previously unknown to man" partakes of the theological connotations very nicely, I think, and so loses some of its force if it is truncated to "... previously unknown". I suppose that many similar examples appear in the work of H. P. Lovecraft.
It would be nice if some of the Wikipedia examples were of this type, but so far I haven't found any. The only cases so far that I haven't changed are all direct quotations, including several from the introductory narration of The Twilight Zone, which asserts that "There is a fifth dimension beyond that which is known to man...". I like when things turn out better than I expected, but this wasn't one of those times. Instead, there was one example that was even worse than I expected. Bad writing it may be, but the wrongness of "known to man" is at least arguable in most cases. (An argument I don't want to make today, although if I did, I might suggest that "titanium dioxide is the best whitening agent known to man" be rewritten as "titanium dioxide is the best whitening agent known to persons of both sexes with at least nine and a half inches of savage, throbbing cockmeat.") But one of the examples I corrected was risibly inept, in an unusual way:
Wonder Woman's Amazon training also gave her limited telepathy, profound scientific knowledge, and the ability to speak every language known to man.I have difficulty imagining that the training imparted to Diana, crown princess of the exclusively female population of Paradise Island, would be limited to languages known to man.
Earle Martin drew my attention to the Wikipedia article on "The hardest metal known to man". I did not dare to change this.
[ Addendum 20090515: There is a followup article. ]
[Other articles in category /lang] permanent link
Sun, 22 Mar 2009
Worst error messages this month
This month's winner is:
Line 319 in XML document from class path resource [applicationContext-standalone.xml] is invalid; nested exception is org.xml.sax.SAXParseException: cvc-complex-type.2.3: Element 'beans' cannot have character [children], because the type's content type is element-only.Experienced technicians will of course want to look at line 319. Silly! If looking at line 319 were any help, this would not be this month's lucky winner. Line 319 is the last line of the document, and says, in whole, "</beans>".
What this actually means is that there is a stray plus sign at the end of line 54.
Well, that is the ultimate cause. The Fregean Bedeutung, as it were.
What it really means (the Sinn) is that the <beans>...</beans> element is allowed to contain sub-elements, but not naked text ("content type is element-only") and the stray plus sign is naked text.
The mixture of weird jargon ("cvc-complex-type.2.3") and obscure anaphora ("character [children]" for "plus sign") got this message nominated for the competition. The totally wrong line number is a bonus. But what won this message the prize is that even if you somehow understand what it means, it doesn't help you find the actual problem! You get to grovel over the 319-line XML file line-by-line, looking for the extra character.
Come on, folks, it's a SAX parser, so how hard is it to complain about the plus sign as soon as it shows up?
What do we have for the lucky winner, Johnny?
You'll be flown to lovely Centralia, Pennsylvania, where you'll enjoy four days and three nights of solitude in an abandoned coal mine being flogged with holly branches and CAT-5 ethernet cable by the cast of "The Hills"!Thank you, Johnny. And there is a runner-up! The badblocks utility that is distributed as part of the Linux e2fsprogs package, produces the following extremely useful error message:
% badblocks /home badblocks: invalid starting block (0): must be less than 0Apparently this is Linux-speak for "This program needs the name of a device file, and the programmer was too lazy to have it detect that you supplied the name of the mount point instead".
Happy spring, everyone!
[Other articles in category /prog] permanent link
Tue, 17 Feb 2009
Second-largest cities
A while back I was in the local coffee shop and mentioned that my wife
had been born in Rochester, New York. "Ah," said the server. "The
third-largest city in New York." Really? I would not have guessed
that. (She was right, by the way.) As a native of the first-largest
city in New York, the one they named the state after, I have spent
very little time thinking about the lesser cities of New York. I
have, of course, heard that there are some. But I have hardly any
idea what they are called, or where they are.
 It appears that the
second-largest city in New York state is some place called (get this)
"Buffalo". Okay, whatever. But that got me wondering if New York was
the state with the greatest disparity between its largest and
second-largest city.
Since I had the census data lying around from a related project (and a
good thing too, since the Census Bureau website moved the file) I
decided to find out.
It appears that the
second-largest city in New York state is some place called (get this)
"Buffalo". Okay, whatever. But that got me wondering if New York was
the state with the greatest disparity between its largest and
second-largest city.
Since I had the census data lying around from a related project (and a
good thing too, since the Census Bureau website moved the file) I
decided to find out.
The answer is no. New York state has only one major city, since its next-largest settlement is Buffalo, with 1.1 million people. (Estimated, as of 2006.) But the second-largest city in Illinois is Peoria, which is actually the punchline of jokes. (Not merely because of its small size; compare Dubuque, Iowa, a joke, with Davenport, Iowa, not a joke.) The population of Peoria is around 370,000, less than one twenty-fifth that of Chicago.
But if you want to count weird exceptions, Rhode Island has everyone else beat. You cannot compare the sizes of the largest and second-largest cities in Rhode Island at all. Rhode Island is so small that it has only one city, Seriously. No, stop laughing! Rhode Island is no laughing matter.
The Articles of Confederation required unanimous consent to amend, and Rhode Island kept screwing everyone else up, by withholding consent, so the rest of the states had to junk the Articles in favor of the current United States Constitution. Rhode Island refused to ratify the new Constitution, insisting to the very end that the other states had no right to secede from the Confederation, until well after all of the other twelve had done it, and they finally realized that the future of their teeny one-state Confederation as an enclave of the United States of America was rather iffy. Even then, their vote to join the United States went 34–32.
But I digress.
Actually, for many years I have said that you can impress a Rhode Islander by asking where they live, and then—regardless of what they say—remarking "Oh, that's near Providence, isn't it?" They are always pleased. "Yes, that's right!" The census data proves that this is guaranteed to work. (Unless they live in Providence, of course.)
Here's a joke for mathematicians. Q: What is Rhode Island? A: The topological closure of Providence.
Okay, I am finally done ragging on Rhode Island.
Here is the complete data, ordered by size disparity. I wasn't sure whether to put Rhode Island at the top or the bottom, so I listed it twice, just like in the Senate.
| State | Largest city and its Population | Second-largest city and its population | Quotient | |||
|---|---|---|---|---|---|---|
| Rhode Island | Providence-New Bedford-Fall River | 1,612,989 | — | |||
| Illinois | Chicago-Naperville-Joliet | 9,505,748 | Peoria | 370,194 | 25 | .68 |
| New York | New York-Northern New Jersey-Long Island | 18,818,536 | Buffalo-Niagara Falls | 1,137,520 | 16 | .54 |
| Minnesota | Minneapolis-St. Paul-Bloomington | 3,175,041 | Duluth | 274,244 | 11 | .58 |
| Maryland | Baltimore-Towson | 2,658,405 | Hagerstown-Martinsburg | 257,619 | 10 | .32 |
| Georgia | Atlanta-Sandy Springs-Marietta | 5,138,223 | Augusta-Richmond County | 523,249 | 9 | .82 |
| Washington | Seattle-Tacoma-Bellevue | 3,263,497 | Spokane | 446,706 | 7 | .31 |
| Michigan | Detroit-Warren-Livonia | 4,468,966 | Grand Rapids-Wyoming | 774,084 | 5 | .77 |
| Massachusetts | Boston-Cambridge-Quincy | 4,455,217 | Worcester | 784,992 | 5 | .68 |
| Oregon | Portland-Vancouver-Beaverton | 2,137,565 | Salem | 384,600 | 5 | .56 |
| Hawaii | Honolulu | 909,863 | Hilo | 171,191 | 5 | .31 |
| Nevada | Las Vegas-Paradise | 1,777,539 | Reno-Sparks | 400,560 | 4 | .44 |
| Idaho | Boise City-Nampa | 567,640 | Coeur d'Alene | 131,507 | 4 | .32 |
| Arizona | Phoenix-Mesa-Scottsdale | 4,039,182 | Tucson | 946,362 | 4 | .27 |
| New Mexico | Albuquerque | 816,811 | Las Cruces | 193,888 | 4 | .21 |
| Alaska | Anchorage | 359,180 | Fairbanks | 86,754 | 4 | .14 |
| Indiana | Indianapolis-Carmel | 1,666,032 | Fort Wayne | 408,071 | 4 | .08 |
| Colorado | Denver-Aurora | 2,408,750 | Colorado Springs | 599,127 | 4 | .02 |
| Maine | Portland-South Portland-Biddeford | 513,667 | Bangor | 147,180 | 3 | .49 |
| Vermont | Burlington-South Burlington | 206,007 | Rutland | 63,641 | 3 | .24 |
| California | Los Angeles-Long Beach-Santa Ana | 12,950,129 | San Francisco-Oakland-Fremont | 4,180,027 | 3 | .10 |
| Nebraska | Omaha-Council Bluffs | 822,549 | Lincoln | 283,970 | 2 | .90 |
| Kentucky | Louisville-Jefferson County | 1,222,216 | Lexington-Fayette | 436,684 | 2 | .80 |
| Wisconsin | Milwaukee-Waukesha-West Allis | 1,509,981 | Madison | 543,022 | 2 | .78 |
| Alabama | Birmingham-Hoover | 1,100,019 | Mobile | 404,157 | 2 | .72 |
| Kansas | Wichita | 592,126 | Topeka | 228,894 | 2 | .59 |
| Pennsylvania | Philadelphia-Camden-Wilmington | 5,826,742 | Pittsburgh | 2,370,776 | 2 | .46 |
| New Hampshire | Manchester-Nashua | 402,789 | Lebanon | 172,429 | 2 | .34 |
| Mississippi | Jackson | 529,456 | Gulfport-Biloxi | 227,904 | 2 | .32 |
| Utah | Salt Lake City | 1,067,722 | Ogden-Clearfield | 497,640 | 2 | .15 |
| Florida | Miami-Fort Lauderdale-Miami Beach | 5,463,857 | Tampa-St. Petersburg-Clearwater | 2,697,731 | 2 | .03 |
| North Dakota | Fargo | 187,001 | Bismarck | 101,138 | 1 | .85 |
| South Dakota | Sioux Falls | 212,911 | Rapid City | 118,763 | 1 | .79 |
| North Carolina | Charlotte-Gastonia-Concord | 1,583,016 | Raleigh-Cary | 994,551 | 1 | .59 |
| Arkansas | Little Rock-North Little Rock | 652,834 | Fayetteville-Springdale-Rogers | 420,876 | 1 | .55 |
| Montana | Billings | 148,116 | Missoula | 101,417 | 1 | .46 |
| Missouri | St. Louis | 2,796,368 | Kansas City | 1,967,405 | 1 | .42 |
| Iowa | Des Moines-West Des Moines | 534,230 | Davenport-Moline-Rock Island | 377,291 | 1 | .42 |
| Virginia | Virginia Beach-Norfolk-Newport News | 1,649,457 | Richmond | 1,194,008 | 1 | .38 |
| New Jersey | Trenton-Ewing | 367,605 | Atlantic City | 271,620 | 1 | .35 |
| Louisiana | New Orleans-Metairie-Kenner | 1,024,678 | Baton Rouge | 766,514 | 1 | .34 |
| Connecticut | Hartford-West Hartford-East Hartford | 1,188,841 | Bridgeport-Stamford-Norwalk | 900,440 | 1 | .32 |
| Oklahoma | Oklahoma City | 1,172,339 | Tulsa | 897,752 | 1 | .31 |
| Delaware | Seaford | 180,288 | Dover | 147,601 | 1 | .22 |
| Wyoming | Cheyenne | 85,384 | Casper | 70,401 | 1 | .21 |
| South Carolina | Columbia | 703,771 | Charleston-North Charleston | 603,178 | 1 | .17 |
| Tennessee | Nashville-Davidson--Murfreesboro | 1,455,097 | Memphis | 1,274,704 | 1 | .14 |
| Texas | Dallas-Fort Worth-Arlington | 6,003,967 | Houston-Sugar Land-Baytown | 5,539,949 | 1 | .08 |
| West Virginia | Charleston | 305,526 | Huntington-Ashland | 285,475 | 1 | .07 |
| Ohio | Cleveland-Elyria-Mentor | 2,114,155 | Cincinnati-Middletown | 2,104,218 | 1 | .00 |
| Rhode Island | Providence-New Bedford-Fall River | 1,612,989 | — | |||
Some of this data is rather odd because of the way the census bureau aggregates cities. For example, the largest city in New Jersey is Newark. But Newark is counted as part of the New York City metropolitan area, so doesn't count separately. If it did, New Jersey's quotient would be 5.86 instead of 1.35. I should probably rerun the data without the aggregation. But you get oddities that way also.
I also made a scatter plot. The x-axis is the population of the largest city, and the y-axis is the population of the second-largest city. Both axes are log-scale:
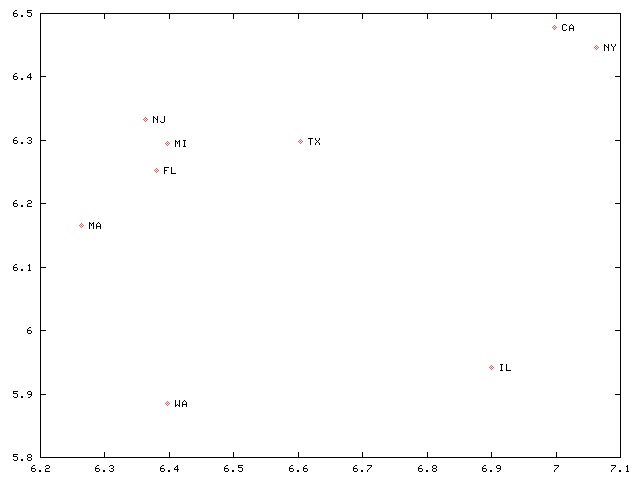
I gratefully acknowledge the gift of Tim McKenzie. Thank you!
[Other articles in category /misc] permanent link
Sun, 15 Feb 2009
Milo of Croton and the sometimes failure of inductive proofs
Ranjit Bhatnagar once told me the following story: A young boy, upon
hearing the legend of Milo of Croton,
determined to do the same. There was a calf in the barn, born that
very morning, and the boy resolved to lift up the calf each day. As the
calf grew, so would his strength, day by day, until the calf was grown
and he was able to lift a bull.
"Did it work?" I asked.
"No," said Ranjit. "A newborn calf already weighs like a hundred pounds."
Usually you expect the induction step to fail, but sometimes it's the base case that gets you.
[Other articles in category /misc] permanent link
Stupid crap, presented by Plato
Yesterday I posted:
"She is not 'your' girlfriend," said this knucklehead. "She does not belong to you."Through pure happenstance, I discovered last night that there is an account of this same bit of equivocation in Plato's Euthydemus. In this dialogue, Socrates tells of a sophist named Dionysodorus, who is so clever that he can refute any proposition, whether true or false. Here Dionysodorus demonstrates that Ctesippus's father is a dog:
You say that you have a dog.So my knuckleheaded interlocutor was not even being original.Yes, a villain of a one, said Ctesippus.
And he has puppies?
Yes, and they are very like himself.
And the dog is the father of them?
Yes, he said, I certainly saw him and the mother of the puppies come together.
And is he not yours?
To be sure he is.
Then he is a father, and he is yours; ergo, he is your father, and the puppies are your brothers.
I gratefully acknowledge the gift of Thomas Guest. Thank you very much!
[Other articles in category /lang] permanent link
Sat, 14 Feb 2009
The junk heap of (blog) history
A couple of years ago, I said:
I have an idea that I might inaugurate a new section of the blog, called "junkheap", where unfinished articles would appear after aging in the cellar for three years, regardless what sort of crappy condition they are in.Some of the stuff in the cellar is in pretty good shape. Some is really trash. I don't want to publish any of it on the main blog, for various reasons; if I did, I would have already. But some of it might have some interest for someone, or I wouldn't be revisiting it at all.
Here's a summary of the cellared items from February-April 2006, with the reasons why each was abandoned:
- Two different ways to find a number n so that if you
remove the final digit of n and append it to the front, the
resulting numeral represents 2n. (Nothing wrong with this one;
I just don't care for it for some reason.)
- The first part in a series on Perl's little-used features:
single-argument bless (Introduction too long, I couldn't figure out what my point
was, I never finished writing the article, and the problems with single-argument bless are
well-publicized anyway.)
- A version of my
article about Baroque writing style, but with all the s's replaced
by ſ's. (Do I need to explain?)
- Frequently-asked questions about my blog. (Too self-indulgent.)
- The use of mercury in acoustic-delay computer
memories of the 1950's. (Interesting, but needs more research. I
pulled a lot of details out of my butt, intending to follow them up
later. But didn't.)
- Thoughts on the purpose and motivation for the set of real
numbers. Putatively article #2 in a series explaining topology.
(Unfinished; I just couldn't quite get it together, although I tried repeatedly.)
I invite your suggestions for what to do with this stuff. Mailing list? Post brief descriptions in the blog and let people request them by mail? Post them on a wiki and let people hack on them? Stop pretending that my every passing thought is so fascinating that even my failures are worth reading?
The last one is the default, and I apologize for taking up your valuable time with this nonsense.
[Other articles in category /meta] permanent link
Fri, 13 Feb 2009
Stupid crap
This is a short compendium of some of the dumbest arguments I've ever
heard. Why? I think it's because they were so egregiously stupid
that they've been bugging me ever since.
Anyway, it's been on my to-do list for about three years, so what the hell.
Around 1986, I heard it claimed that Ronald Reagan did not have practical qualifications for the presidency, because he had not been a lawyer or a general or anything like that, but rather an actor. "An actor?" said this person. "How does being an actor prepare you to be President?"
I pointed out that he had also been the Governor of California.
"Oh, yeah."
But it doesn't even stop there. Who says some actor is qualified to govern California? Well, he had previously been president of the Screen Actors' Guild, which seems like a reasonable thing for the Governor of California to have done.
Around 1992, I was talking to a woman who claimed that the presidency was not open to the disabled, because the President was commander-in-chief of the army, he had to satisfy the army's physical criteria, and they got to disqualify him if he couldn't complete basic training, or something like that. I asked how her theory accommodated Ronald Reagan, who had been elected at the age of 68 or whatever. Then I asked how the theory accommodated Franklin Roosevelt, who could not walk, or even stand without assistance, and who traveled in a wheelchair.
"Huh."
I was once harangued by someone for using the phrase "my girlfriend." "She is not 'your' girlfriend," said this knucklehead. "She does not belong to you."
Sometimes you can't think of the right thing to say at the right time, but this time I did think of the right thing. "My father," I said. "My brother. My husband. My doctor. My boss. My congressman."
"Oh yeah."
My notes also suggest a long article about dumb theories in general. For example, I once read about someone who theorized that people were not actually smaller in the Middle Ages than they are today. We only think they were, says this theory, because we have a lot of leftover suits of armor around that are too small to fit on modern adults. But, according to the theory, the full-sized armor got chopped up in battles and fell apart, whereas the armor that's in good condition today is the armor of younger men, not full-grown, who outgrew their first suits, couldn't use them any more, and hung then on the wall as mementoes. (Or tossed them in the cellar.)
I asked my dad about this, and he wanted to know how that theory applied to the low doorways and small furniture. Heh.
I think Herbert Illig's theory is probably in this category, Herbert Illig, in case you missed it, believes that this is actually the year 1712, because the years 614–911 never actually occurred. Rather, they were created by an early 7th-century political conspiracy to rewrite history and tamper with the calendar. Unfortunately, most of the source material is in German, which I cannot read. But it would seem that cross-comparisons of astronomical and historical records should squash this theory pretty flat.
 In high school I tried to promulgate the rumor that John Entwistle and
Keith Moon were so disgusted by the poor quality of the album
Odds & Sods that they refused to pose for the cover
photograph. The rest of the band responded by finding
two approximate lookalikes to stand in for Moon and Enwistle, and by
adopting a cover design calculated to obscure the impostors' faces as
much as possible.
In high school I tried to promulgate the rumor that John Entwistle and
Keith Moon were so disgusted by the poor quality of the album
Odds & Sods that they refused to pose for the cover
photograph. The rest of the band responded by finding
two approximate lookalikes to stand in for Moon and Enwistle, and by
adopting a cover design calculated to obscure the impostors' faces as
much as possible.
This sort of thing was in some ways much harder to pull off successfully in 1985 than it is today. But if you have heard this story before, please forget it, because I made it up.
Addendum 20150513: I have several times heard an argument against hate speech laws on the grounds that no other law punishes a person not for what they did but for what was in their mind. There may be good arguments against hate speech laws, this is not one. If you are the lookout for a failed bank robbery, you will be charged with bank robbery, despite having done nothing but stand on a public streetcorner; if you were the getaway driver you will be charged with bank robbery even if you paid the parking meter. Honest mistakes are distinguished from from fraud based on state of mind: fraud requires an intent to deceive. Assault, battery, and even homicide can be defensible if you are acting in self-defense, which requires a belief that one is in imminent danger. Identical behavior can result in a charge of criminal negligence, manslaughter, second-degree murder, or first-degree murder depending only on the perpetrator's state of mind. Criminal conspiracy is just two people talking in a room, nothing illegal about that, they might have been discussing a mystery novel, except they weren't, they were planning a crime. And so on.
I would like to acknowledge the generous gift of Jack Kennedy. Thank you very much!
This acknowledgement is not intended to be apropos of this blog post. I just decided I should start acknowledging gifts, and this happened to be the first post since I made the decision.
[ See also: radioactive potassium and "Crappiest literary theory this month". ]
[ Addendum 20090214: A similar equivocation of "your" is mentioned by Plato. ]
[Other articles in category /misc] permanent link
Thu, 12 Feb 2009
More Uzi-clubbing: a counterexample
Last year I wrote an
article about iterating over a hash, searching for a certain key.
Larry Wall called said this was like "clubbing someone to death with a
loaded Uzi", because the whole point of a hash is that you don't have
to scan all the keys to find the one you want.
I ended the article by saying:
I had already realized that you could, in principle, commit this error with a regular array instead of with a hash, but I had never seen an example until...Just recently I saw another example, which I think is interesting because it seems to be a counterexample. It's part of a somewhat longer Java program. The crucial section is:
...
LINE: while ( ( line = in.readLine()) != null ) {
String[] fields = line.split("\t");
...
for ( int i = 0; i < fields.length; i++ ) {
if ( ! isEmpty(fields[i]) ) {
switch(i) {
case 0: citation.setCitationType(fields[i]); break;
case 1: setAuthors(citation,fields[i],personHome,false); break;
case 2: citation.setPublishYear(Integer.parseInt(fields[i])); break;
case 3: citation.setTitle(fields[i]); break;
...
case 19: citation.setURL(fields[i]); break;
case 20: citation.setDoi(fields[i]); break;
default: warn("Empty field expected, found: " + fields[i] + " for line: " + line); break;
}
}
}
}
...
The Perlishness of this Java code might lead you to think that I wrote
it, but I did not.My temptation here was to replace the loop and the switch with code like this:
citation.setCitationType(fields[0]);
setAuthors(citation,fields[1],personHome,false);
citation.setPublishYear(Integer.parseInt(fields[2]));
citation.setTitle(fields[3]);
...
citation.setURL(fields[19]);
citation.setDoi(fields[20]);
We lost the warnings, but there were only 4 of those, so we can add
them back explicitly:
if (! isEmpty(fields[13])) warn("Empty field expected...");
This might have been an improvement, except that we also lost the
isEmpty tests on the nonempty fields. To get them back we
must spend at least all our gains, possibly more:
if (! isEmpty(fields[0])) citation.setCitationType(fields[0]);
if (! isEmpty(fields[1])) setAuthors(citation,fields[1],personHome,false);
if (! isEmpty(fields[2])) citation.setPublishYear(Integer.parseInt(fields[2]));
if (! isEmpty(fields[3])) citation.setTitle(fields[3]);
...
if (! isEmpty(fields[13])) warn("Empty field expected...");
...
if (! isEmpty(fields[19])) citation.setURL(fields[19]);
if (! isEmpty(fields[20])) citation.setDoi(fields[20]);
So at least in this case, my instinct to eliminate the loop-switch was
not helpful. There are plenty of Java-esque techniques for cutting up
the complexity and sweeping each little piece underneath its own
little carpet ("Replace fields with an object! Or with a
series of 20 objects!") but nothing that actually reduces the entia
multiplicantis. There may be ways to easily improve this code, but
I have not been able to think of any.
[Other articles in category /prog] permanent link
Fri, 06 Feb 2009
Maybe energy is really real
About a year ago I dared to write down my crackpottish musings about
whether energy is a real thing, or whether it is just a mistaken
reification. I made what I thought was a good analogy with the center
of gravity, a useful mathematical abstraction that nobody claims is
actually real.
I call it crackpottish, but I do think I made a reasonable case, and of the many replies I got to that article, I don't think anyone said conclusively that I was a complete jackass. (Of course, it might be that none of the people who really know wanted to argue with a crackpot.) I have thought about it a lot before and since; it continues to bother me.
But I few months ago I did remember an argument that energy is a real thing. Specifically, I remembered Noether's theorem. Noether's theorem, if I understand correctly, claims that for every symmetry in the physical universe, there is a corresponding conservation law, and vice versa.
For example, let's suppose that space itself is uniform. That is, let's suppose that the laws of physics are invariant under a change of position that is a translation. In this special case, Noether's theorem says that the laws must include conservation of momentum: conservation of momentum is mathematically equivalent to the claim that physics is invariant unter a translation transformation.
Perhaps this is a good time to add that I do not (yet) understand Noether's theorem, that I am only parroting stuff that I have read elsewhere, and that my usual physics-related disclaimer applies: I understand just barely enough physics to spin a plausible-sounding line of bullshit.
Anyway, going on with my plausible-sounding bullshit about Noether's theorem, invariance of the laws under a spatial rotation is equivalent to the law of conservation of angular momentum. Actually I think I might have remembered that one wrong. But the crucial one for me I am sure I am not remembering wrong: invariance of physical law under a translation in time rather than in space is equivalent to conservation of energy. Aha.
If this is right, then perhaps there is a good basis for the concept of energy after all, because any physics that is time-invariant must have an equivalent concept of energy. Time-invariance might not be true, but I have no philosophical objection to it, nor do I claim that the notion is incoherent.
So it seems that if I am to understand this properly, I need to understand Noether's theorem. Maybe I'll make that a resolution for 2009. First stop, Wikipedia, to find out what the prerequisites are.
[Other articles in category /physics] permanent link
Thu, 29 Jan 2009
A simple trigonometric identity
A few nights ago I was writing up notes for my
category theory reading group, and I wanted to include a commutative
diagram on three objects. I was using Paul Taylor's stupendously good
diagrams.sty
package, which lets you put the vertices of the diagram in the cells
of a LaTeX table, and then draw arrows between them. I had drawn the
following diagram:
So that night as I was waiting to fall asleep, I thought about the problem of finding lattice points that are at the vertices of an equilateral triangle. This is a sort of two-dimensional variation on the problem of finding rational approximations to surds, which is a topic that has turned up here many times over the years.
Or rather, I wanted to find lattice points that are almost at the vertices of an equilateral triangle, because I was pretty sure that there were no equilateral lattice triangles. But at the time I could not remember a proof. I started doing some calculations based on the law of cosines, which was a mistake, because nobody but John Von Neumann can do calculations like that in their head as they wait to fall asleep, and I am not John Von Neumann, in case you hadn't noticed.
A simple proof that there are no equilateral lattice triangles has just now occurred to me, though, and I am really pleased with it, so we are about to have a digression.
The area A of an equilateral triangle is s√3/2, where s is the length of the side. And s has the form √t because of the Pythagorean theorem, so A = √(3t)/2, where t is a sum of two squares, because the endpoints of the side are lattice points.
By Pick's theorem, the area of any lattice triangle is a half-integer. So 3t is a perfect square, and thus there are an odd number of threes in t's prime factorization.
But t is a sum of two squares, and by the sum of two squares theorem, its prime factorization must have an even number of threes. We now have a contradiction, so there was no such triangle.
Wasn't that excellent? That is just the sort of thing that I could have thought up while waiting to fall asleep, so it proves even more conclusively that starting with the law of cosines was a mistake.
Okay, end of digression. Back to the law of cosines. We have a triangle with sides a, b, and c, and opposite angles A, B, and C, and you no doubt recall from high school that c2 = a2 + b2 - 2ab cos C. We'll call this "law C".
Before I fell alseep, it occurred to me that you could take the analogous law B, which is b2 = a2 + c2 - 2ac cos B, and substitute the right-hand side for the b2 term in law C. Then a bunch of stuff will cancel out and you should either get something interesting or something tautological. Von Neumann would have known right away which it was, but I needed paper.
So today I got out the paper and did the thing, and came up with the very simple relation that:
c = a cos B + b cos AWhich holds in any triangle. But somehow I had never seen this before, or, if I had, I had completely forgotten it.
The thing is so simple that I thought that it must be wrong, or I would have known it already. But no, it checked out for the easy cases (right triangles, equilateral triangles, trivial triangles) and the geometric proof is easy: Just drop a perpendicular from C. The foot of the perpendicular divides the base c into two segments, which, by the simplest possible trigonometry, have lengths a cos B and b cos A, respectively. QED.
Perhaps that was anticlimactic. Have I mentioned that I have a sign on the door of my office that says "Penn Institute of Lower Mathematics"? This is the kind of thing I'm talking about.
I will let you all know if I come up with anything about the almost-equilateral lattice triangles. Clearly, you can approximate the equilateral triangle as closely as you like by making the lattice coordinates sufficiently large, just as you can approximate √3 as closely as you like with rationals by making the numerator and denominator sufficiently large. Proof: Your computer draws equilateral-seeming triangles on the screen all the time.
I note also that it is important that the lattice is two-dimensional. In three or more dimensions the triangle (1,0,0,0...), (0,1,0,0...), (0,0,1,0...) is a perfectly equilateral lattice triangle with side √2.
[ Addendum 20090130: Vilhelm Sjöberg points out that the area of an equilateral triangle is s2√3/4, not s√3/2. Whoops. This spoils my lovely proof, because the theorem now follows immediately from Pick's: s2 is an integer by Pythagoras, so the area is irrational rather than a half-integer as Pick's theorem requires. ]
[ Addendum 20140403: As a practical matter, one can draw a good lattice approximation to an equilateral triangle by choosing a good rational approximation to !!\sqrt3!!, say !!\frac ab!!, and then drawing the points !!(0,0), (b,a),!! and !!(2b, 0)!!. The rational approximations to !!\sqrt3!! quickly produce triangles that are indistinguishable from equilateral. For example, the rational approximation !!\frac74!! gives the isosceles triangle with vertices !!(0,0), (4,7), (8,0)!! which has one side of length 8 and two sides of length !!\sqrt{65}\approx 8.06!!, an error of less than one percent. The next such approximation, !!\frac{26}{15}!!, gives a triangle that is correct to about 1 part in 1800. (For more about rational approximations to !!\sqrt3!!, see my article on Archimedes and the square root of 3.) ]
[ Addendum 20181126: Even better ways to make 60-degree triangles on lattice points. ]
[Other articles in category /math] permanent link
Tue, 27 Jan 2009
Amusements in Hyperspace
[ Michael
Lugo's post on n-spheres today reminded me that I've been
wanting for some time to repost this item that I wrote back in
1999. ]
This evening I tried to imagine life in a 1000-dimensional universe. I didn't get too far, but what I did get seemed pretty interesting.
What's it like? Well, it's very dark. Lamps wouldn't work very well, because if the illumination one foot from the source is I, then the illumination two feet from the source is I · 9.3·10-302.
Actually it's even worse than that; there's a double whammy. Suppose you had a cubical room ten feet across. If you thought it was hard to light up the dark corners of a big room in Boston in February, imagine how much worse it is in hyperspace where the corners are 158 feet away.
There are some upsides, however. Rooms won't have to be ten feet on a side because everything will be smaller. You take up about 70,000 cubic centimeters of space; in hyperspace that is just not a lot of room, because a box barely more than a centimeter on a side takes up 70,000 hypercentimeters. In fact, a box barely more than a centimeter on a side can hold as much as you want; an 11 millimeter box already contains 2.5·1041 hypercentimeters.
It's hard to put people in prison in hyperspace, because there are so many directions that you can go to get out. Flatland prison cells have four walls; ours have six, if you count the ceiling and the floor. Hyperspace prison cells have 2000 walls, and each one is very expensive to build.
So that's hyperspace: Big, dark, and easy to get around.
Addenda
20120510
An anonymous commenter on Colm Mulcahy's blog observed that "high dimension cubes are qualitatively more like hedgehogs than building blocks". And recently someone asked on stackexchange.math for "What are some examples of a mathematical result being counterintuitive?"; the top-scoring reply concerned the bizarre behavior of high-dimension cubes. ]
20200325
More about this on the Matrix67 blog. (In Chinese.)
20240808
Reddit user `ink_atom` has drawn a cartoon on this topic.
[Other articles in category /math] permanent link
Sat, 24 Jan 2009
Higher-Order Perl: nonmemoizing streams
The first version of tail() in the streams chapter looks like this:
sub tail {
my $s = shift;
if (is_promise($s->[1])) {
return $s->[1]->(); # Force promise
} else {
return $s->[1];
}
}
But this is soon replaced with a version that caches the value
returned by the promise:
sub tail {
my $s = shift;
if (is_promise($s->[1])) {
$s->[1] = $s->[1]->(); # Force and save promise
}
return $s->[1];
}
The reason that I give for this in the book is a performance reason.
It's accompanied by an extremely bad explanation. But I couldn't do
any better at the time.There are much stronger reasons for the memoizing version, also much easier to explain.
Why use streams at all instead of the iterators of chapter 4? The most important reason, which I omitted from the book, is that the streams are rewindable. With the chapter 4 iterators, once the data comes out, there is no easy way to get it back in. For example, suppose we want to process the next bit of data from the stream if there is a carrot coming up soon, and a different way if not. Consider:
# Chapter 4 iterators
my $data = $iterator->();
if (carrot_coming_soon($iterator)) {
# X
} else {
# Y
}
sub carrot_coming_soon {
my $it = shift;
my $soon = shift || 3;
while ($soon-- > 0) {
my $next = $it->();
return 1 if is_carrot($next);
}
return; # No carrot
}
Well, this probably doesn't work, because the carrot_coming_soon()
function extracts and discards the upcoming data from the iterator,
including the carrot itself, and now that data is lost.One can build a rewindable iterator:
sub make_rewindable {
my $it = shift;
my @saved; # upcoming values in LIFO order
return sub {
my $action = shift || "next";
if ($action eq "put back") {
push @saved, @_;
} elsif ($action eq "next") {
if (@saved) { return pop @saved; }
else { return $it->(); }
}
};
}
But it's kind of a pain in the butt to use:
sub carrot_coming_soon {
my $it = shift;
my $soon = shift || 3;
my @saved;
my $saw_carrot;
while ($soon-- > 0) {
push @saved, $it->();
$saw_carrot = 1, last if is_carrot($saved[-1]);
}
$it->("put back", @saved);
return $saw_carrot;
}
Because you have to explicitly restore the data you extracted.With the streams, it's all much easier:
sub carrot_coming_soon {
my $s = shift;
my $soon = shift || 3;
while ($seen-- > 0) {
return 1 if is_carrot($s->head);
drop($s);
}
return;
}
The working version of carrot_coming_soon() for streams looks just like
the non-working version for iterators.But this version of carrot_coming_soon() only works for memoizing streams, or for streams whose promise functions are pure. Let's consider a counterexample:
my $bad = filehandle_stream(\*DATA);
sub filehandle_stream {
my $fh = shift;
return node(scalar <$fh>,
promise { filehandle_stream($fh) });
}
__DATA__
fish
dog
carrot
goat rectum
Now consider what happens if I do this:
$carrot_soon = carrot_coming_soon($bad);
print "A carrot appears soon after item ", head($bad), "\n"
if $carrot_soon;
It says "A carrot appears soon after item fish". Fine.
That's because $bad is a node whose head contains
"fish". Now let's see what's after the fish:
print "After ", head($bad), " is ", head(tail($bad)), "\n";
This should print After fish is dog, and for the memoizing
streams I used in the book, it does. But a non-memoizing stream will
print "After fish is goat rectum". Because
tail($bad) invokes the promise function, which, since the
next() was not saved after carrot_coming_soon()
examined it, builds a new node, which reads the next item from the
filehandle, which is "goat rectum".I wish I had explained the rewinding property of the streams in the book. It's one of the most significant omissions I know about. And I wish I'd appreciated sooner that the rewinding property only works if the tail() function autosaves the tail node returned from the promise.
[Other articles in category /prog/perl] permanent link
Thu, 22 Jan 2009
Archimedes and the square root of 3, revisited
Back in 2006 I discussed
Archimedes' calculation of the approximate value of π. In the
calculation, he needed rational approximations to several irrational
quantities, such as √3, and pulled approximations like 265/153
apparently out of thin air.
I pointed out that although the approximations seem to come out of thin air, a little thought reveals where they probably did come from; it's not very hard. Briefly, you tabulate a2 and 3b2, and look for numbers from one column that are close to numbers from the other; see the previous article for details. But Dr. Chuck Lindsey, the author of a superb explanation of Archimedes' methods, and a professor at Florida Gulf Coast University, seemed mystified by the appearance of the fraction 265/153:
Throughout this proof, Archimedes uses several rational approximations to various square roots. Nowhere does he say how he got those approximations—they are simply stated without any explanation—so how he came up with some of these is anybody's guess.I left it there for a few years, but just recently I got puzzled email from a gentleman named Peter Nockolds. M. Nockolds was not puzzled by the 265/153. Rather, he wanted to know why so many noted historians of mathematics should be so puzzled by the 265/153.
This was news to me. I did not know anyone else had been puzzled by the 265/153. I had assumed that nearly everyone else saw it the same way that M. Nockolds and I did. But M. Nockolds provided me with a link to an extensive discussion of the matter, which included quotations from several noted mathematicians and historians of mathematics:
It would seem...that [Archimedes] had some (at present unknown) method of extracting the square root of numbers approximately.
—W.W Rouse Ball, Short Account of The History of Mathematics, 1908
...the calculation [of π] starts from a greater and lesser limit to the value of √3, which Archimedes assumes without remark as known, namely 265/153 < √3 < 1351/780. How did Archimedes arrive at this particular approximation? No puzzle has exercised more fascination upon writers interested in the history of mathematics... The simplest supposition is certainly [the "Babylonian method"; see Kline below]. Another suggestion...is that the successive solutions in integers of the equations x2-3y2=1 and x2-3y2=-2 may have been found...in a similar way to...the Pythagoreans. The rest of the suggestions amount for the most part to the use of the method of continued fractions more or less disguised.Heath said "The simplest supposition is certainly ..." and then followed with the "Babylonian method", which is considerably more complicated than the extremely simple method I suggested in my earlier article. Morris Kline explains the Babylonian method:
—T. Heath, A History of Greek Mathematics, 1921
He also obtained an excellent approximation to √3, namely 1351/780 > √3 > 265/153, but does not explain how he got this result. Among the many conjectures in the historical literature concerning its derivation the following is very plausible. Given a number A, if one writes it as a2 ± b where a2 is the rational square nearest to A, larger or smaller, and b is the remainder, then a ± b/2a > √A > a ± b/(2a±1). Several applications of this procedure do produce Archimedes' result.And finally:
—M. Kline, Mathematical Thought From Ancient To Modern Times, 1972
Archimedes approximated √3 by the slightly smaller value 265/153... How he managed to extract his square roots with such accuracy...is one of the puzzles that this extraordinary man has bequeathed to us.Nockolds asked me "Have you had any feedback from historians of maths who explain why it wasn't so easy to arrive at 265/153 or even 1351/780? Have you any idea why they make such a big deal out of this?"
—P. Beckmann, A History of π, 1977
No, I'm mystified. Even working with craptastic Greek numerals, it would not take Archimedes very long to tabulate kn2 far enough to discover that 3·7802 = 13512 - 1. Or, if you don't like that theory, try this one: He tabulated n2 and 3n2 far enough to discover the following approximations:
| 2 | / | 1 |
| 5 | / | 3 |
| 7 | / | 4 |
| 19 | / | 11 |
| 26 | / | 15 |
| 71 | / | 41 |
| 97 | / | 56 |
I know someone wants to claim that this is nothing more than the Babylonian method. But this is missing an important point. Although this sort of numeric tinkering might well lead you to discover the Babylonian method, especially if you were Archimedes, it is not the Babylonian method, and it can be done in complete ignorance of the Babylonian method. But it yields the required approximations anyway.
So I will echo Nockolds' puzzlement here. There are a lot of things that Archimedes did that were complex and puzzling, but this is not one of them. You do not need sophisticated algebraic technique to find approximations to surds. You only need to do (at most) a few hours of integer calculation. The puzzle is why people like Rouse Ball and Heath think it is puzzling.
There's an explanation I'm groping for but can't quite articulate, but which goes something like this: Perhaps mathematicians of the late Victorian age lent too much weight to theory and analysis, and not enough to heuristic and simple technique. As a lifelong computer programmer, I have a great appreciation for what can be accomplished by just grinding out the numbers. See my anecdote about the square root algorithm used by the ENIAC, for example. I guessed then that perhaps computer science professors know more about mathematics than I expect, but less about computation. I can imagine the same thing of Victorian mathematicians—but not of Archimedes.
One thing you often hear about pre-19th-century mathematicians is that they were great calculators. I wonder if appreciation of simple arithmetic technique might not have been sometimes lost to the mathematicans from the very end of the pre-computation age, say 1880–1940.
Then again, perhaps I'm not giving them enough credit. Maybe there's something going on that I missed. I haven't checked the original sources to see what they actually say, so who knows? Perhaps Heath discusses the technique I suggested, and then rejects it for some fascinating reason that I, not being an expert in Greek mathematics, can't imagine. If I find out anything else, I will report further.
[Other articles in category /math] permanent link
Wed, 21 Jan 2009
The loophole in the U.S. Constitution: recent developments
Some time ago I wrote a couple of articles [1]
[2]
on the famous story that
Kurt Gödel claimed to have found a loophole in the United States
Constitution through which the U.S. could have become a dictatorship. I
proposed a couple of speculations about what Gödel's loophole
might have been, and reported on another one by
Peter Suber.
Recently Jeffrey Kegler wrote to inform me of some startling new developments on this matter. Although it previously appeared that the story was probably true, there was no firsthand evidence that it had actually occurred. The three witnesses would have been Philip Forman (the examining judge), Oskar Morgenstern and Albert Einstein. But, although Morgenstern apparently wrote up an account of the epsiode, it was lost.
Until now, that is. The Institute for Advanced Study (where Gödel, Einstein, and Morgenstern were all employed) posted an account on its web site, and M. Kegler was perceptive enough to realize that this account was probably written by someone who had access to the lost Morgenstern document but did not realize its significance. M. Kegler followed up the lead, and it turned out to be correct.
Kegler's Morgenstern website has a lot of additional detail, including the original document itself.
Now came an exciting development. [Gödel] rather excitedly told me that in looking at the Constitution, to his distress, he had found some inner contradictions, and he could show how in a perfectly legal manner it would be possible for somebody to become a dictator and set up a Fascist regime, never intended by those who drew up the Constitution.But before I let you get too excited about this, a warning: Morgenstern doesn't tell us what Gödel's loophole was! (Kegler's reading is that Morgenstern didn't care.) So although the truth of story has finally been proved beyond doubt, the central mystery remains.
The document is worth reading anyway. It's only three pages long, and it paints a fascinating picture of both Gödel, who is exactly the sort of obsessive geek that you always imagined he was, and of Einstein, who had a cruel streak that he was careful not to show to the public. Kegler's website is also worth reading for its insightful analysis of the lost document and its story.
[Other articles in category /law] permanent link
Tue, 20 Jan 2009
Triples and Closure
Lately I've been reading Lambek and Scott's Introduction to
Higher-Order Categorical Logic, which is too advanced for me.
(Yoneda Lemma on page 10. Whew!) But you can get some value out of
books that are too hard if you pay attention. Last night I learned
that monads are analogous to closure operators.
In topology, we have the idea of a "closure" of a set, which is essentially the union of the set with its boundary. For example, consider an open disk D, say the set of all points less than one mile from my house. The boundary of this set is a circle with radius one mile, centered at my house. The closure of D is the union of D with its boundary, and so is closed disk consisting of all points less than or equal to one mile from my house.
Representing the closure of a set S as C(S), we have the obvious theorem that S ⊂ C(S), because the closure includes everything in S, plus the boundary.
Another easy, but not quite obvious theorem is that C(C(S)) ⊂ C(S). This says that once you take the closure, you have included the boundary, and you do not get any more boundary by taking the closure again. The closure of a set is "closed"; the closure of a "closed" set C is just C.
A third fundamental theorem about closures is that A⊂ B → C(A) ⊂ C(B).
Now we turn to monads. A monad is first of all a functor, which, if you restrict your attention to programming languages, means that a monad is a type constructor M with an associated function fmap such that for any function f of type α → β, fmap f has type M α → M β.
But a monad is also equipped with two other functions. There is a return function, which has type α → M α, and a join function, which has type M M α → M α.
Haskell provides monads with a "bind" function, written >>=, which is interdefinable with join:
join x = x >>= id
a >>= b = join (fmap b a)
but we are going to forget about >>= for now.So the monad is equipped with three fundamental operations:
fmap :: (a → b) → (M a → M b)
join :: M M a → M a
return :: a → M a
The three basic theorems about topological closures are:
(A ⊂ B) → (C(A) ⊂ C(B)If we imagine that ⊂ is a special kind of implication, the similarity with the monad laws is clear. And ⊂ is a special kind of implication, since (A ⊂ B) is just an abbreviation for (x ∈ A → x ∈ B).
C(C(A)) ⊂ C(A)
A ⊂ C(A)
If we name the three closure theorems "fmap", "join", and "return", we might guess that "bind" also turns out to be a theorem. And it is, because >>= has the type M a → (a → M b) → M b. The corresponding theorem is:
x ∈ C(A) → (A ⊂ C(B)) → x ∈ C(B)If the truth of this is hard to see, it is partly because the implications are in an unnatural order. The theorem is stated in the form P → Q → R, but it would be easier to understand as the equivalent Q → P → R:
A ⊂ C(B) → x ∈ C(A) → x ∈ C(B)Or more briefly:
A ⊂ C(B) → C(A) ⊂ C(B)This is quite true. We can prove it from the other three theorems as follows. Suppose A ⊂ C(B). Then by "fmap", C(A) ⊂ C(C(B)). By "join", C(C(B)) ⊂ C(B). By transitivity of ⊂, C(A) ⊂ C(B). This is what we wanted.
Haskell defines a =<< operator which is the same as >>= except with the arguments forwards instead of backwards:
=<< :: (a → M b) → M a → M b
a =<< b = b >>= a
The type of this function is analogous to the bind theorem, and I have
seen claims in the literature that the argument order is in some ways
more natural. Where the >>= function takes a value first, and then
feeds it to a given function, the =<< function makes more sense as a
curried function, taking a function of type a → M
b and yielding the corresponding function of type
M a → M
b.I think it's also worth noticing that the structure of the proof of the bind theorem (invoke "fmap" and then "join") is exactly the same as the structure of the code that defines "bind".
We can go the other way also, and prove the "join" theorem from the "bind" theorem. The definition of join in terms of >>= is:
join a = a >>= id
Following the program again, id in the
program code corresponds to the theorem that B ⊂ B
for any B. A special case of this theorem is that
C(B) ⊂ C(B) for any B. Then in
the "bind" theorem:
A ⊂ C(B) → C(A) ⊂ C(B)take A = C(B):
C(B) ⊂ C(B) → C(C(B)) ⊂ C(B)The left side of the implication is satisfied, so we conclude the consequent, C(C(B)) ⊂ C(B), which is what we wanted.
But wait, monad operations are also required to satisfy some monad laws. For example, join (return x) = x. How does this work out in topological closure world?
In programming language world, x here is required to have monad type. Monad types correspond to closed sets, so this is a theorem about closed sets. The theorem says that if X is a closed set, then the closure of X is the same as x. This is true.
The identity between these two things can be found in (surprise) category theory. In category theory, a monad is a (categorial) functor equipped with two natural transformations, the "return" and "join" operations. The categorial version of a closure operator is essentially the same.
Closure operations have a natural opposite. In topology, it is the "interior of" operation. The interior of a set is what you get if you discard the boundary of the set. The interior of a closed disc is an open disc; the interior of an open disc is the same open disc. Interior operations satisfy laws analogous but opposite to those enjoyed by closures:
Notice that the third theorem does not get turned around. I think this is because it comes from the functor itself, which goes the same way, not from the natural transformations, which go the other way. But I have not finished thinking abhout it carefully yet.
S ⊂ C(S) I(T) ⊂ T C(C(S)) ⊂ C(S) I(T) ⊂ I(I(T)) A⊂ B → C(A) ⊂ C(B) A⊂ B → I(A) ⊂ I(B)
Sooner or later I am going to program in Haskell with comonads, and it gives me a comfortable feeling to know that I am pre-equipped with a way to understand them as interior operations.
I have an idea that the power of mathematics comes principally from the places where it succeeds in understanding two different things as aspects of the same thing. For example, why is group theory so useful? Because it understands transformations of objects (say, rotations of a polyhedron) and algebraic operations as essentially the same thing. If you have a hard problem about one, you can often make it into an easier problem about the other one. Similarly analytic geometry transforms numerical problems into geometric problems and back again. Most often the geometry is harder than the numerical problem, and you use it in that direction, but often you go in the other direction instead.
It is quite possible that this notion is too vague to qualify as an actual theory. But category theory fits the description. Category theory lets you say that types are objects, type constructors are functors, and polymorphic functions are natural transformations. Then you can understand natural transformations as structure-preserving maps of something or other and get some insight into polymorphic functions, or vice-versa.
Category theory is a large agglomeration of such identities. Lambek and Scott's book starts with several slogans about category theory. One of these is that many objects of interest to mathematicians form categories, such as the category of sets. Another is that many objects of interest to mathematicians are categories. (For example, each set is a discrete category.) So one of the reasons category theory is so extremely useful is that it sets up these multiple entities as different aspects of the same thing.
I went to lunch and found more to say on the subject, but it will have to wait until another time.
[Other articles in category /math] permanent link
Wed, 07 Jan 2009
Addenda to recent articles 200811
- Earlier I discussed an interesting technique for flag variables in
Bourne shell programs. I did a little followup research.
I looked into several books on Unix shell programs, including:
- Linux Shell Scripting with Bash (Burtch)
- Unix Shell Programming 3ed. (Kochan and Wood)
- Mastering UNIX Shell Scripting (Michael)
But two readers sent me puzzled emails, to tell me that they had been using the true/false technique for years are were surprised that I found it surprising. Brooks Moses says that at his company they have a huge build system in Bourne shell, and they are trying to revise the boolean tests to the style I proposed. And Tom Limoncelli reports that code by Bill Cheswick and Hal Burch (Bell Labs guys) often use this technique. Tom speculates that it's common among the old farts from Bell Labs. Also, Adrián Pérez writes that he has known about this for years.
It's tempting to write to Kernighan to ask about it, but so far I have been able to resist.
- My first meta-addendum: In October's
addenda I summarized the results of a paper of Coquand,
Hancock, and Setzer about the inductive strength of various theories.
This summary was utterly wrong. Thanks to Charles Stewart and to
Peter Hancock for correcting me.
The topic was one I had hoped to get into anyway, so I may discuss it at more length later on.
[Other articles in category /addenda] permanent link







