Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| A draft of a short introduction to topology |
| git-reset |
| Linus Torvalds' Greatest Invention |
| Revert-all-buffers |
| Semi-boneless ham |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 24 Nov 2010
git-reset
The Git subcommand git-reset is very frequently used, and is one of very few
commonly-used Git commands that can permanently destroy real work.
Once work is in the repository, it is almost completely safe from any
catastrophe. But git-reset also affects the working tree, and it is quite
possible to utterly destroy a day's work by doing git-reset --hard at the wrong
time. Unfortunately, the manual is unusually bad, with a huge pile of
this stuff:
working index HEAD target working index HEAD
----------------------------------------------------
A B C D --soft A B D
--mixed A D D
--hard D D D
--merge (disallowed)
working index HEAD target working index HEAD
----------------------------------------------------
A B C C --soft A B C
--mixed A C C
--hard C C C
--merge (disallowed)
Six more of these tables follow, giving the impression that git-reset is quite complicated. Sure, I'm gonna memorize 256 table entries. Or look up the results on the table before every git-reset. Not.
The thing to notice about the two tables I quoted above is that they are redundant, because the second one is simply a special case of the first, with D replaced by C. So if you were really in love with the tables, you might abbreviate the 64 table entries to 28:
working index target working index HEAD
----------------------------------------------------
A B C --soft A B C
--mixed A C C
--hard C C C
--merge (disallowed)
But even this is much more complicated than it should be. git-reset does up
to three things:
- It points the HEAD ref at a new 'target' commit, if you specified one.
- Then it copies the tree of the HEAD commit to the index, unless you said --soft.
- Finally, it copies the contents of the index to the working tree, if you said --hard.
Tables are good for computers to understand, because they have a uniform format and computers are unfazed by giant masses of redundant data. The computer will not understand the data regardless of how well-structured they are, so there is no reason to adopt a representation that showcases the structure.
For humans, however, tables are most useful when there is no deeper understanding of the structure to be had, because the structure tends to get lost in the profusion of data, as it did here.
[ Thanks to Aristotle Pagaltzis for pointing out that git checkout can also destroy the working tree, and for other corrections. ]
[Other articles in category /prog] permanent link
Mon, 15 Nov 2010
A draft of a short introduction to topology
One of my ongoing projects is to figure out how to explain topology
briefly. For example, What is
Topology?, putatively part 1 of a three-part series that I have
not yet written parts 2 or 3 of yet.
CS grad students often have to take classes in category theory. These classes always want to use groups and topological spaces as examples, and my experience is that at this point many of the students shift uncomfortably in their seats since they have not had undergraduate classes in group theory, topology, analysis, or anything else relevant. But you do not have to know much topology to be able to appreciate the example, so I tried to write up the minimal amount necessary. Similarly, if you already understand intuitionistic logic, you do not need to know much topology to understand the way in which topological spaces are natural models for intuitionistic logic—but you do need to know more than zero.
So a couple of years ago I wrote up a short introduction to topology for first-year computer science grad students and other people who similarly might like to know the absolute minimum, and only the absolute minimum, about topology. It came out somewhat longer than I expected, 11 pages, of which 6 are the introduction, and 5 are about typical applications to computer science. But it is a very light, fluffy 11 pages, and I am generally happy with it.
I started writing this shortly after my second daughter was born, and I have not yet had a chance to finish it. It contains many errors. Many, many errors. For example, there is a section at the end about the compactness principle, which can only be taken as a sort of pseudomathematical lorem ipsum. This really is a draft; it is only three-quarters finished.
But I do think it will serve a useful function once it is finished, and that finishing it will not take too long. If you have any interest in this project, I invite you to help.
The current draft is version 0.6 of 2010-11-14. I do not want old erroneous versions wandering around confusing people in my name, so please do not distribute this draft after 2010-12-15. I hope to have an improved draft available here before that.
Please do send me corrections, suggestions, questions, advice, patches, pull requests, or anything else.
- PDF
- LaTeX source
- Github git repository (git://github.com/mjdominus/topology-doc.git)
[Other articles in category /math] permanent link
Wed, 10 Nov 2010
Revert-all-buffers
This is another article about a trivial tool that is worth more to me
than it cost to make. It's my new revert-all-buffers
function for Emacs.
Here's the use case: I'm editing 17 files, and I've saved a bunch of changes to them. Then I commit the changes with git, and then I change the working copy of the files out from under Emacs by doing some other git operation—I merge in another branch, or do a rebase, or something like that.
Now when I go back to edit the files, the Emacs buffers are out of date. Emacs notices that, and for each file, it will at some point ask me "Contents of ... have changed on disk; do you really want to edit the buffer?", interrupting my train of thought. I can answer the question by typing r, which will refresh the buffer from the disk version, but having to do that for every buffer is a pain, because I know all those files have changed, and I don't want to be asked each time.
Here's the solution:
(defun revert-all-buffers ()
"Refreshes all open buffers from their respective files"
(interactive)
(let* ((list (buffer-list))
(buffer (car list)))
(while buffer
(when (and (buffer-file-name buffer)
(not (buffer-modified-p buffer)))
(set-buffer buffer)
(revert-buffer t t t))
(setq list (cdr list))
(setq buffer (car list))))
(message "Refreshed open files"))
I have this function bound to some otherwise useless key: it runs
through all the buffers, and for each one that has an associated file,
and has no unsaved changes, it reverts the contents from the
version on the disk.This occasionally fails, most often because I have removed or renamed a file from the disk that I still have open in Emacs. Usually the response is to close the buffer, or reopen it from the new name. I could probably handle that properly in 99% of cases just by having Emacs close the buffer, but the other cases could be catastrophic, so I'm leaving it the way it is for a while.
I swiped the code, with small changes, from EmacsWiki.
[Other articles in category /prog] permanent link
Mon, 08 Nov 2010
Semi-boneless ham
The Math Project on Wikipedia is having a discussion about whether or
not to have an article about the jargon term "semi-infinite", which I
have long considered one of my favorite jargon terms, because it
sounds so strange, but makes so much sense. A structure is
semi-infinite when it is infinite in one direction but not in the
other. For example, the set of positive integers is semi-infinite,
since it possesses a least element (1) but no greatest element.
Similarly rays in geometry are semi-infinite.
The term is informal, however, and it's not clear just what it should mean in all cases. For example, consider the set S of 1/n for every positive integer n. Is this set semi-infinite? It is bounded in both directions, since it is contained in [0, 1]. But as you move left through the set, you ancounter an infinite number of elements, so it ought to be semi-infinite in the same sense that S ∪ { 1-x : x ∈ S } is fully-infinite. Whatever sense that is.
Informal and ill-defined it may be, but the term is widely used; one can easily find mentions in the literature of semi-infinite paths, semi-infinite strips, semi-infinite intervals, semi-infinite cylinders, and even semi-infinite reservoirs and conductors.
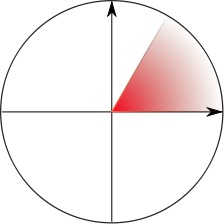
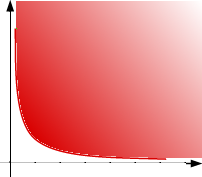 The term has spawned an
offshoot, the even stranger-sounding "quarter-infinite". This seems
to refer to a geometric object that is unbounded in the same way that
a quarter-plane is unbounded, where "in the same way" is left rather
vague. Consider the set (depicted at left) of all points of the plane
for which 0 ≤ |y/x| ≤ √3, for example; is
this set quarter-infinite, or only 1/6-infinite? Is the set of points
(depicted at right) with xy > 1 and x, y >
0 quarter-infinite? I wouldn't want to say. But the canonical
example is simple: the product of two semi-infinite intervals is a
quarter-infinite set.
The term has spawned an
offshoot, the even stranger-sounding "quarter-infinite". This seems
to refer to a geometric object that is unbounded in the same way that
a quarter-plane is unbounded, where "in the same way" is left rather
vague. Consider the set (depicted at left) of all points of the plane
for which 0 ≤ |y/x| ≤ √3, for example; is
this set quarter-infinite, or only 1/6-infinite? Is the set of points
(depicted at right) with xy > 1 and x, y >
0 quarter-infinite? I wouldn't want to say. But the canonical
example is simple: the product of two semi-infinite intervals is a
quarter-infinite set.
I was going to say that I had never seen an instance of the obvious next step, the eighth-infinite solid, but in researching this article I did run into a few. I can't say it trips off the tongue, however. And if we admit that a half of a quarter-infinite plane segment is also eighth-infinite, we could be getting ourselves into trouble.
(This all reminds me of the complaint of J.H. Conway of the increasing use of the term "biunique". Conway sarcastically asked if he should expect to see "triunique" and soforth, culminating in the idiotic "polyunique".)
Sometimes "semi" really does mean exactly one-half, as in "semimajor axis" (the longest segment from the center of an ellipse to its boundary), "semicubic parabola" (determined by an equation with a term kx3/2), or "semiperimeter" (half the perimeter of a triangle). But just as often, "semi" is one of the dazzling supply of mathematical pejoratives. ("Abnormal, irregular, improper, degenerate, inadmissible, and otherwise undesirable", says Kelley's General Topology.) A semigroup, for example, is not half of a group, but rather an algebraic structure that possesses less structure than a group. Similarly, one has semiregular polyhedra and semidirect products.
I was planning to end with a note that mathematics has so far avoided the "demisemi-" prefix. But alas! Google found this 1971 paper on Demi-semi-primal algebras and Mal'cev-type conditions.
[Other articles in category /math] permanent link
Fri, 05 Nov 2010
Linus Torvalds' Greatest Invention
Happy Guy Fawkes' Day!
On Wednesday night I gave a talk for the Philadelphia Linux Users' Group on "Linus Torvalds' Greatest Invention". I was hoping that some people would show up expecting it to be Linux, but someone spilled the beans ahead of time and everyone knew it was going to be about Git. But maybe that wasn't so bad because a bunch of people showed up to hear about Git.
But then they were probably disappointed because I didn't talk at all about how to use Git. I talked a little about what it would do, and some about implementation. I used to give a lot of talks of the type "a bunch of interesting crap I threw together about X", but in recent years I've felt that a talk needs to have a theme. So for quite a while I knew I wanted to talk about Git internals, but I didn't know what the theme was.
Then I realized that the theme could be that Git proves that Linus was really clever. With Linux, the OS was already designed for him, and he didn't have to make a lot of the important decisions, like what it means to be a file. But Git is full of really clever ideas that other people might not have thought of.
Anyway, the slides are online if you are interested in looking.
[Other articles in category /misc] permanent link


