Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 29 Oct 2021
The nonassociativity of the cartesian product
!!\def\pr#1#2{\langle{#1},{#2}\rangle}!!
Set theory doesn't include the ordered pair as a primitive type; ordered pairs have to be represented as sets somehow. This caused technical problems in Principia Mathematica, as I explained a couple of years ago:
In 1910 … a crucial piece of machinery was missing: the ordered pair.
This technical problem was solved the following year, by Norbert Wiener. We usually use the simpler definition invented later by Kazimierz Kuratowski:
!!\def\kp#1#2{\{\{{#1}\}, \{{#1},{#2}\}\}}!!
$$\pr ab = \kp ab$$
This works well enough (and it has worked well enough that we have used it for a hundred years) but it has some warts. We define the cartesian product of two sets like this: $$A\times B = \{\pr ab \mid a\in A\text{ and }b\in B\}$$
With Kuratwoski pairs, and this definition of product, it is not the case that $$A\times(B\times C) = (A\times B)\times C\qquad\color{darkred}{Not!}$$ because on the left side the elements look like $$\pr a{\pr bc} = \kp a{\kp bc}$$ and on the right side the corresponding element looks like $$\pr{\pr ab}c = \kp{\kp ab}c.$$
This doesn't present any serious technical problems; see Henning Makholm's discussion here. He says:
The nitty-gritty of getting such details to work completely formally is not generally worth the trouble.
Even with highly fussy technical details like this, you can almost always find some mathematician who said “Ah, but you have to be a little bit careful, because…”. As far as I know, this matter is an exception. If anyone thinks there is something interesting going on here that deserves further examination, I have not heard of it. Everyone ignores the matter.
Category theory takes the high road away from the issue, breezily dismissing it with a remark about how !!A\times(B\times C)!! and !!(A\times B)\times C!! are isomorphic, and equal up to unique isomorphism. This is the right answer, because as Wiener said in 1911, the structure of the pairs as actual sets is “largely a matter of choice”, and the whole point of category theory is to ignore this sort of irrelevant distraction, focusing on the API rather than on the internal implementation.
But last week I wondered: what if you do actually want !!A\times(B\times C)!! be the exact same set as !!(A\times B)\times C!!, and not just naturally isomorphic? Is there some clever way to define ordered pairs so that this happens?
I got the question all written up for Math Stack Exchange, when I realized the answer: No.
Consider the special case where !!A = \{a\}, B=\{b\},!! and !!C = \{c\}!!. Then !!A\times(B\times C) = (A\times B)\times C!! implies $$\pr a{\pr bc} = \pr{\pr ab}c.$$
But this violates the one property that we absolutely require of ordered pairs, which is that !!\pr pq = \pr rs!! if and only if !!p=r!! and !!q=s!!. To have !!\pr a{\pr bc} = \pr{\pr ab}c!! would imply !!a=\pr ab!!, which would imply !!\pr a{b'} = a = \pr ab!! even when !!b'\ne b!!.
Oh well, it would have been fun.
[Other articles in category /math] permanent link
Thu, 28 Oct 2021
Kuratowski pairs and Wiener pairs
I mentioned a couple of years back that Principia Mathematica was bloated with repetitive material because they hadn't been able to unify the idea of a relation and a set, because the ordered pair hadn't been invented yet. There's a section that defines set union, !!\cup!!, and then proves that it is commutative and associative and so on, and later there is a separate section that defines relation union, !!\dot\cup!!, and proves the exact same theorems in the same way. In 2021 (or even in 1921) we would say that a relation is a set of ordered pairs, and that relation union is just a special case of set union.
To do this we have to interpret ordered pairs set-theoretically. The method we usually use for this was invented by Kazimierz Kuratowski:
$$\langle a, b\rangle = \{\{a\}, \{a,b\}\}$$
But there were earlier developments that also sufficed. Hausdorff suggested the more intuitive, but technically more complex:
$$\langle a, b\rangle = \{\{a, 1\}, \{b, 2\}\}$$
where !!1!! and !!2!! are any two objects that are not among the things we want to include in our ordered pairs. And even earlier, the first interpretation of pairs as sets was in 1911 by Norbert Wiener. In modern notation, Wiener's definition is:
$$\langle a, b\rangle = \{\{\{a\}, \emptyset\}, \{\{b\}\}\}.$$
Wiener actually used the notation of Principia Mathematica, which I reproduce for your amusement:
$$\def\i{\iota`} \i(\i\i a\cup \i\Lambda)\cup\i\i\i b $$
The !!\i x!! notation means essentially the same as !!\{x\}!!. I thought Principia Mathematica had a better way to write !!\{x, y\}!! than as !!\i x\cup\i y!!, but if so I can't remember what it is.
Someone once told me that Wiener's definition is more complicated than Kuratowski's because it had to function in the context of Whitehead and Russell's type theory. Kuratowski was working later, in set theory, so could use a simpler definition that wouldn't function in type theory because the types didn't match up. I had never thought carefully about this until now but it seems to be wrong. The Kuratowski pair requires !!a!! and !!b!! to be the same type, or else you can't put them both into the class !!\{a, b\}!!. But the Wiener pair requires this also. Say !!a!! and !!b!! have type !!n!!. Then !!\{a\}!! and !!\{b\}!! have type !!n+1!!, and !!\{\{a\}, \emptyset\}!! and !!\{\{b\}\}!! have type !!n+2!!. And because they have the same type we can put them both into the class !!\{\{\{a\}, \emptyset\}, \{\{b\}\}\}!!. But for this to work, !!a!! and !!b!! have to have the same type to begin with.
I wanted to find out what Wiener said about this, and Wikipedia referred me to his paper A Simplification of the logic of relations, and helpfully pointed out that it was reprinted in van Heijenoort's Source Book in Mathematical Logic, which I have on the shelf. (I love when this happens. It makes me feel like a scholar.) Wiener agrees: !!a!! and !!b!! must have the same type. But, he points out, if !!a!! and !!b!! have different types you can still make it work by adjusting the nesting level of !!a!! or !!b!! accordingly. For example, if !!b!! had a type one higher than !!a!!, you could use !!\{\{\{a\}, \emptyset\}, \{b\}\}!! instead.
In any case the Kuratowski thing is still simpler. I wonder why Wiener didn't think of it first. But he does say “the particular method selected of doing this is largely a matter of choice”, so perhaps he didn't consider the details important. As in fact they aren't. The important point, and the real point of Wiener's paper, is that you can now construe a two-place relation as a class of ordered pairs.
The paper ends by observing that this fixes the !!\cup!!-versus-!!\dot\cup!! extravagance of Principia Mathematica, since now !!R\cup S = R\,\dot\cup\, S!!. Similarly the class of relations is now a subclass of the class of classes, and so forth.
[ Addendum 20211030: This construction makes the cartesian product nonassociative, but nobody cares. ]
[ Addendum 20211101: One way in which Wiener pairs are simpler than Kuratowski pairs. ]
[Other articles in category /math] permanent link
Wed, 27 Oct 2021Is the idea here that If you're watching the pot, it'll seem like it takes longer than it should?
Or is the idea that if you keep taking the lid off to check if it's boiling yet, the heat will escape and it will actually take longer than it should?
[Other articles in category /misc] permanent link
Tue, 26 Oct 2021[ Content warning: pointless. ]
A colleague of mine recently remarked:
lose rhymes with choose; loose rhymes with goose
The parallel construction suggests that the two cases are similar. They're not. The words lose and choose are unique exceptions, and loose and goose aren't. All the -oose words other than choose rhyme with loose goose moose, and all the -ose words other than lose (and sometimes close) rhyme with rose nose pose.
English spelling is full of awful quagmires, but I don't remember noticing this one before. “-ough” gets talked up a lot, it's overplayed. This Goose thing is at least as bad.
For example, consider these rhyming words:
| booze ooze | choose | coos moos shoos woos zoos | chews crews jews news slews yews | dues clues rues sprues sues | lose | shoes | twos | cruise |
What a mess.
Shoes and woes don't rhyme.
Shoes rhymes with lose, but lose does not rhyme with close.
Close does rhyme with woes, and it also rhymes with gross, but they don't rhyme with each other. I suppose it is excusable that gross doesn't rhyme with woes, but it also doesn't rhyme with boss. And gross rhymes with dose for some reason. You'd think dose would rhyme with hose but if you want it to do that you have to spell it doze. Which at least makes sense: dose, unvoiced, doze, voiced. There are seven ways to write that -oze sound in doze, and the only words that I can find that actually spell it -oze are doze and froze:
| chose close hose nose pose rose | bows crows grows mows rows shows slows snows sows tows | does roes toes goes hoes joes sloes woes | doze froze | nos | owes | sews |
The most common ending here is -ows and looking at a word that has it you can't tell if it's crows shows slows or brows cows vows. Sometimes it's both, like with sows sows bows bows rows rows.
Oh, and does, which you see there in column 3 with toes and goes, but which is also an extremely common word that is usually pronounced “duz”, completely unlike any other word spelled that way. When it obviously should have been pronounced the way dues is.
Going the other way we have goose and loose which seems okay at first but turns into its own little quagmire:
| goose loose moose noose | deuce | juice sluice | spruce | use | Zeus |
At least you can't get these words mixed up with other words spelled the same way. Except for use and use. The consonant is voiced when it's a verb, unvoiced when it's a noun. Because reasons.
Well, for completeness I suppose I should do use:
| fuse | mews pews spews | hues | views | use |
Brits might want me to put news here and maybe some of its siblings.
Ugh, this could go on forever. Half the -ouse words rhyme with mouse and the other half rhyme with rouse. And the most important one rhymes with both: house.
Hmm, there's that verb-voiced, noun-unvoiced thing again. I should look into that. The close thing is similar: voiced is a verb, unvoiced is an adjective.
My respect for people who learn English as a second language was already high, but it has just gone up several notches.
[Other articles in category /lang] permanent link
Sat, 16 Oct 2021
Who is the namesake of the old Hungarian name for the month of June?
[ Previously ]
One oddity about the old-style Hungarian month names that I do not have time to investigate is that the old name of June was Szent Iván hava, Saint Ivan's month, or possibly Saint John's month. “John” in Hungarian is not Iván, it is Ján or János, at least at present. Would a Hungarian understand Szent Iván as a recognizably foreign name? I wonder which saint this is actually?
There is a Saint Ivan of Rila, but he is Bulgarian, so that could be a coincidence. Hungarian Wikipedia strangely does not seem to have an article about the most likely candidate, St. John the Evangelist, so I could not check if that John is known there as Ján or Iván or something else.
It does have an article about John the Baptist, who in Hungarian called Keresztelő János, not Iván. But that article links to the page about St. John the Baptist's Eve, which is titled Szent Iván éjszakája.
Further complicating the whole matter of Szent Iván hava is the issue that there have always been many Slavs in Hungary. The original birth record page is marked “KULA, HUNGARY”, which if correct puts it in what is now called Kula, Serbia — Hungary used to be bigger than it is now. Still why would the name of the month be in Slavic and not Magyar?
Do any of my Gentle Readers understand what is going on here?
[ Addendum: The English Wikipedia page for the Bulgarian Saint Ivan of Rila gives the Bulgarian-language version of his name. It's not written as Иван (“Ivan”) but as Йоан (“John”). The Bulgarian Wikipedia article about him is titled Иван Рилски (“Ivan Rilski”) but in the first line and the header of the infobox, his name is given instead as Йоан. I do not understand the degree to which John and Ivan are or are not interchangeable in this context. ]
[ Addendum 20211018: Michael Lugo points out that it is unlikely to be Ivan of Rila, whose feast day is in October. M. Lugo is right. This also argues strongly against the namesake of Szent Iván hava being John the Evangelist, as his feast is in December. The feast of John the Baptist is in June, so the Szent Iván of Szent Iván hava is probably John the Baptist, same as in Szent Iván éjszakája. I would still like to know why it is Szent Iván and not Szent János though. ]
[Other articles in category /calendar] permanent link
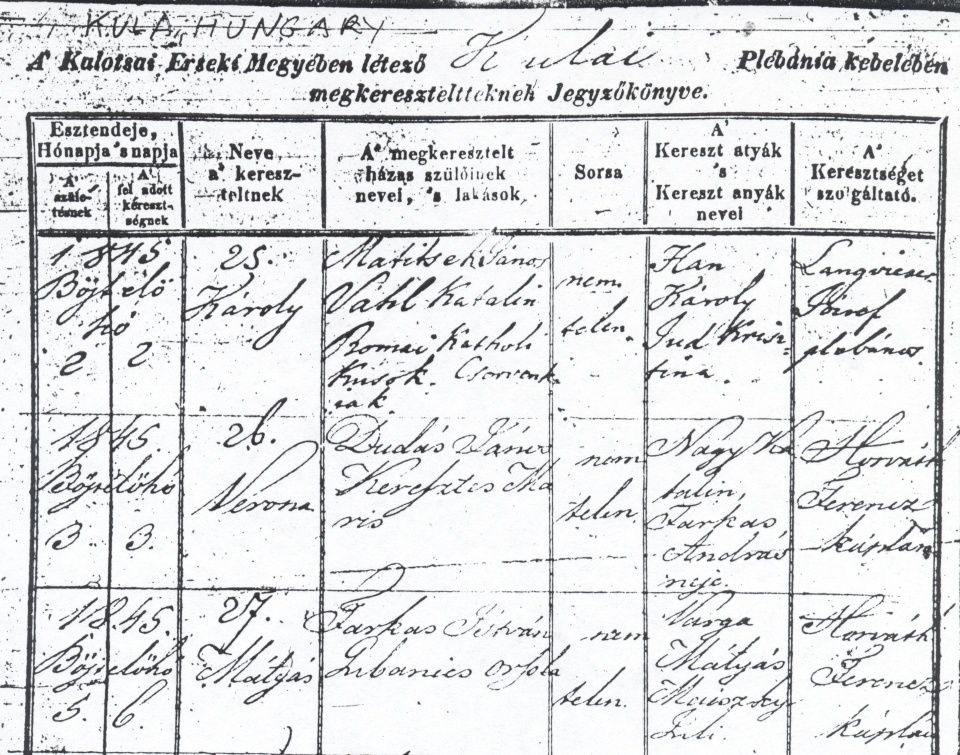
Fri, 15 Oct 2021I had a conversation with a co-worker about the origin of his name, in which he showed me the original Hungarian birth record of one of his ancestors. (The sample below does not include the line with that record.)
I had a fun time digging through this to figure out what it said. As you see, the scan quality is not good. The person writing the records has good handwriting, but not perfect, and not all the letters are easy to make out. (The penmanship of the second and third lines is noticeably better than the first.) Hungarian has letters ö and ő, which are different, but hard to distinguish when written longhand. The printed text is in a small font and is somewhat smudged. For example, what does this say?

Is the first letter in the second line an ‘f’ or a long ‘s’? Is “A’” an abbreviation, and if so what for? Is that a diacritical mark over the ‘e’ in the third line, or just a smudge? Except for the last, I don't know, but kereztségnek is something about baptism, maybe a dative form or something, so that column is baptism dates. This resolves one of the puzzles, which is why there are two numbers in the two leftmost columns: one is the birth date and one is the baptism date, and sometimes the baptism was done on a different day. For example, in the third line the child Mátyás (“Matthew”) was born on the 5th, and baptized on the 6th.
But the 6th of what? The box says “1845 / something” and presumably the something is the name of the month.
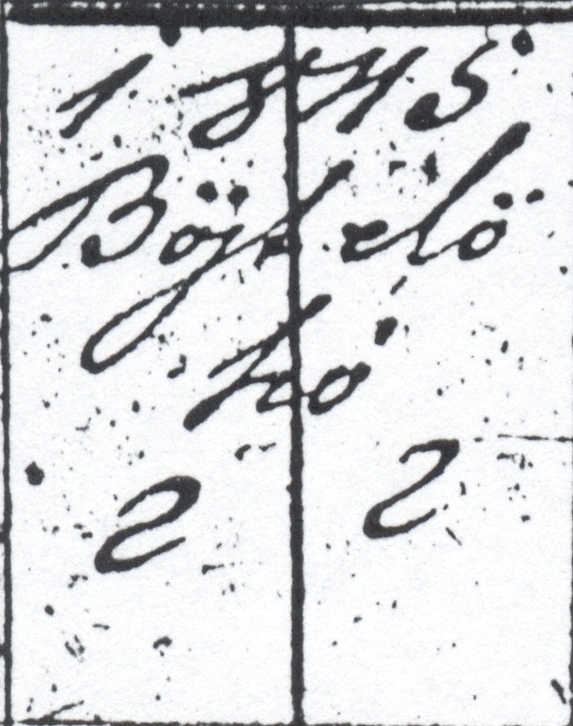
But I couldn't quite make it out (Bójkeló kó maybe?) and Google did not find anything to match my several tries. No problem, I can go the other direction: just pull up a list of the names of the months in Hungarian and see which one matches.
That didn't work. The names of the months in Hungarian are pretty much the same as in English (január, február, etc.) and there is nothing like Bójkeló kó. I was stuck.
But then I had a brainwave and asked Google for “old hungarian month names”. Paydirt! In former times, the month of February was called böjt elő hava, (“the month before fast”; hava is “month”) which here is abbreviated to Böjt elő ha’.
So that's what I learned: sometime between 1845 and now, the Hungarians changed the names of the months.
This page at fromhungarywithlove says that these month names were used from the 16th century until “the first third of the 20th century”.
[ Addendum 20211016: A further puzzle: The old name for June was “St. Iván's month”. Who was St. Iván? ]
[Other articles in category /calendar] permanent link
Sun, 10 Oct 2021“Salient” seems to have lost its original meaning, and people mostly use it as if it were synonymous with “relevant” or “pertinent”. This is unfortunate. It's from Latin salīre, which is to jump, and it originally meant something that jumps out at you. In a document, the salient point isn't necessarily the one that is most important, most crucial, or most worth consideration; it's the one that jumps out.
It is useful to have a word specifically for something that jumps out, but people no longer understand it that way.
Cognates of salīre include “assail" and “assault”, “salmon” (the jumping fish), and the mysterious “somersault”.
[Other articles in category /lang] permanent link
This Imgur gallery has a long text post, about a kid who saw the movie Labyrinth in London and met David Bowie after. The salient part was:
He seemed surprised I would want to know, and he told me the whole thing, all out of order, and I eked the details out of him.
This is a use of “eke” that I haven't seen before. Originally “eke” meant an increase, or a small addition, and it was also used in the sense of “also”. For example, from the prologue to the Wife of Bath's tale:
I hadde the bettre leyser for to pleye, And for to se, and eek for to be seye
(“I had more opportunity to play, and to see, and also to be seen.”)
Or also, “a nickname” started out as “an ekename”, an also-name.
From this we get the phrase “to eke out a living”, which means that you don't have quite enough resources, but by some sort of side hustle you are able to increase them to enough to live on.
But it seems to me that from there the meaning changed a little, so that while “eke out a living” continued to mean to increase one's income to make up a full living, it also began to connote increasing one's income bit by bit, in many small increments. This is the sense in which it appears to be used in the original quotation:
He seemed surprised I would want to know, and he told me the whole thing, all out of order, and I eked the details out of him.
Addenda
Searching for something in a corpus of Middle English can be very frustrating. I searched and searched the University of Michigan Corpus of Middle English Prose and Verse looking for the Chaucer quotation, and couldn't find it, because it has “to se” and “to be seye”, but I searched for “to see” and “to seye”; it has “eek” and I had been searching for “eke”. Ouch.
In the Chaucer, “leyser” is “leisure”, but a nearly-dead sense that we now see only in “complete the task at your leisure”.
[Other articles in category /lang] permanent link
Fri, 08 Oct 2021
Diminishing resources in the Korean Language
Hangul, the Korean alphabet, was originally introduced in the year 1443. At that time it had 28 letters, four of which have since fallen out of use. If the trend continues, the Korean alphabet will be completely used up by the year 7889, preceded by an awful period in which all the words will look like
앙 앙앙앙 앙앙 앙 앙앙앙앙 앙
and eventually
ㅏㅏㅏㅏㅏㅏㅏㅏㅏㅏ!
[Other articles in category /lang] permanent link
Tue, 05 Oct 2021Some traditional miracles ascribed to saints and other holy people are better than others. Jesus walking on water and quieting the storm are impressive and showy, but essentially unhelpful. Contrasting this kind of show-magic with the miracles of the Buddha, Jorge Luis Borges describes “a miracle of courtesy”:
The Buddha has to cross a desert at noon. The gods, from their thirty-three heavens, each send him down a parasol. The Buddha does not want to slight any of the gods, so he turns himself into thirty-three Buddhas. Each god sees a Buddha protected by the parasol he sent.
(It's Borges, so it's also possible he just made it up.)
My favorites of the Christian miracles are the miracles of the loaves and fishes, which are miracles of generosity and compassion. A multitude of people have come to see Jesus heal the sick:
As evening approached, the disciples came to him and said, “This is a remote place, and it’s already getting late. Send the crowds away, so they can go to the villages and buy themselves some food.”
Jesus replied, “They do not need to go away. You give them something to eat.”
“We have here only five loaves of bread and two fish,” they answered.
“Bring them here to me,” he said. And he directed the people to sit down on the grass. Taking the five loaves and the two fish and looking up to heaven, he gave thanks and broke the loaves. Then he gave them to the disciples, and the disciples gave them to the people. They all ate and were satisfied and the disciples picked up twelve basketfuls of broken pieces that were left over.
Much better than walking on water.
Anyway, that is peripheral to what I wanted to write about. Lately I learned that there is a painting by Il Sodoma (1477–1549, original name Giovanni Antonio Bazzi) titled St Benedict repairs a Broken Colander through Prayer.
A broken what now? Colander? Like, the thing I use to drain my tortellini?

I looked in the Big Dictionary to find out if maybe “colander” might sometimes mean something more impressive than the kitchen utensil, maybe some expensive and specialized piece of church equipment. Nope:
A vessel, usually of metal, closely perforated at the bottom with small holes, and used as a sieve or strainer in cookery.
There doesn't appear to be any such thing in the painting:
St. Benedict is kneeling in prayer, second from left, wearing a halo. The colander, it turns out, is the two rectangular brown things by his knees. As you see, one piece is visibly cracked. I don't know what is the red schmutz on the other piece.
(The long-haired guy in the middle, with the expensive gloves, is Il Sodoma himself. He is known to have kept pet badgers, which also make an appearance here.)
Google searches for "st. benedict" "colander" were no help. They
mostly produced references to this painting again.
I then wondered if maybe “colander” was a mistranslation. The Italian title for this painting is Come Benedetto risalda lo capistero che si era rotto. The Goog translates this as “How Benedict heals the broken master”, which was quite confusing. Google further confused me by glossing risalda as “rises”, which made me wonder if the repair of the broken colander (risalda lo capistero) was somehow a metaphor for the rising of Jesus. The idea seems rather silly, but Renaissance thinking does not always make sense to me, so I did not rule it out immediately. But no, risalda is repair, and capistero is a colander, or more precisely a sieve. The Goog's translation was simply wrong. (Fair enough, Google Translate is not intended to translate early-renaissance Italian.)
Book 2 of the Dialogues of Pope Gregory is about St. Benedict, and chapter 1 is titled “How he made a broken sieve whole and sound”:
It fell so out that his nurse borrowed of the neighbors a sieve to make clean wheat, which being left negligently on the table, by chance it was broken in two pieces, Whereupon she fell pitifully weeping, because she had borrowed it. The devout and religious youth Benedict, seeing his nurse so lamenting, moved with compassion, took away with him both the pieces of the sieve, and with tears fell to his prayers; and after he had done, rising up he found it so whole, that the place could not be seen where before it was broken.
So “colander” isn't quite right, but it's not too far off. The implement is probably made of wood, not metal. But it is indeed a perforated kitchen utensil. The suntanned lady on the left of the painting is the nurse, gazing ruefully at the table.
The colander is a tray for sifting wheat. The upper part (at left, with the big crack in it) has some sort of perforations or screen, which don't show up well in the painting. The lower part (at right) is a tray in which the sifted material is caught.
The right side of the painting depicts a later time after the colander has been repaired. The miraculous sieve has been hung up on a column (top center) for the wonderment of a crowd of admiring visitors.
Saint Anthony could command animals and was such an arresting speaker that even fish came to hear him preach. Some saints invoke the power of God to heal the blind and paralyzed, the drowned, the leprous, and the epileptic. St. Benedict healed a broken colander.
[Other articles in category /religion] permanent link
Sun, 03 Oct 2021
Simpson's paradox and Maxine Hong Kingston's mom
Yesterday's Simpson's paradox example reminds me of Maxine Hong Kingston's mother in The Woman Warrior:
When a sick person was about to die, my mother could read the fact of it a year ahead of time on the daughters-in-law’s faces. … My mother would take one look at the daughter-in-law who answered the door at the sick house and she’d say, “Find another doctor.” She would not touch death; therefore, untainted, she brought only health from house to house. “She must be a Jesus convert,” the people from the far villages said. “All her patients get well.”
[Other articles in category /math] permanent link
Sat, 02 Oct 2021
Simplest example of Simpson's paradox
I had read many times about Simpson's paradox but it never quite clicked for me. I saw many examples, but I couldn't quite get what was really going on. And I could never remember the numbers in the examples, so I couldn't ponder it while waiting for the bus or whatever.
Last month I sat down and thought about it, with the idea of coming up with the simplest and most memorable possible example. Here it is.
Imagine there is a disease that kills 50% of the people who get it.
There is a pill you can take if you get the disease. Of the people who take the pills, 80% die.
It looks like the pills are killing people. But they aren't, they are helpful.
This is Simpson's paradox.
What is really happening is that half the people with the disease have mild cases and half have severe cases. A patient with a mild case will get better on their own. But everyone with a severe case dies unless they receive treatment.
People with mild cases don't bother to take the pills, because they are going to get better anyway.
Only people with severe cases take the pills. 80% of them die, but without the pills they all would have died.
Now I understand Simpson's paradox.
[Other articles in category /math] permanent link
Fri, 01 Oct 2021Imagine an alien force, vastly more powerful than us, landing on Earth and demanding the value of !!R(5, 5)!! or they will destroy our planet. In that case, we should marshal all our computers and all our mathematicians and attempt to find the value. But suppose, instead, that they ask for yo mama's weight in pounds. In that case, we should attempt to destroy the aliens.
(With posthumous apologies to Paul Erdős)
[Other articles in category /math] permanent link
Ida-related flooding in Philadelphia
On September 1, Hurricane Ida hit Pennsylvania. Several tornadoes touched down near where I live in Philadelphia, and five people were killed. Fortunately Philadelphia itself was spared, and from where I live it only appeared to be an unusually-heavy rainstorm.
But Philadelphia is on the Schuylkill River, and all the water that Ida dumped northwest of Philadelphia ended up in the Schuylkill, which flooded epically and historically.
I-95 and I-76 also run through Philadelphia, and connecting them, in a deep trench along the northern boundary of the business district, is the Vine Street Expressway. Normally it looks like this:
(Google Street View, July 2019)
But on September 1 it looked like this:
Holy cow. I'd never seen anything like this before. How long would the expressway be shut down? I had no idea.
Toph and I went up there on September 4 to see the damage, but by then there wasn't much to see. It looked like this:
Traffic was flowing normally in the eastbound lane (far side). The westbound lane (near side, with the cone) was still closed but it was obvious that they were finishing the cleanup. That's some amazing work. I have no idea how you even begin to get something like that cleaned up, and no idea how to get it done in three days.
The streets were a little dirtier than usual, but if I hadn't known to look I probably wouldn't have noticed. (Philadelphia.) We did pass houses that had piles of ruined books outside, and we encountered two gentlemen who were glumly carrying out loads of soggy carpet from their flooded basement.
We walked on the path that runs by the river, which is normally about two or three meters above the level of the river itself. The river didn't look higher than usual, but we did see signs of the flood. The path is between the river and the train tracks, and there is a fence to keep you from crossing the tracks.
Here's picture I took on September 4:
The river has piled driftwood and other trash at the base of the fence. The fence itself is clogged with leaves and paper, left there when the river poured through it as through a sieve. The river not only overtopped its banks and flooded the footpath, it must have reached at least to the top of the fence.
Here's another shot of the fence. Over here the sieve became too clogged to let the water through and the entire fence collapsed. The on-ramp for the expressway is visible in the background.
Here's Google's Street View picture of what the fence was like in July 2016:
I have no special point to make, and leave you with this, which I think should be part of the Philadelphia historical archives. Content warning: unsanitary behavior.
[Other articles in category /misc] permanent link