Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sat, 27 Jan 2007
Software archaeology
For appropriate values of "everyone", everyone knows that Unix files
do not record any sort of "creation time". A fairly frequently asked
question in Unix programming forums, and other related forums, such as
Perl programming forums, is how to get the creation date of a file;
the answer is that you cannot do that because it is not there.
This lack is exacerbated by several unfortunate facts: creation times are available on Windows systems; the Unix inode contains three timestamps, one of which is called the "ctime", and the "c" is suggestive of the wrong thing; Perl's built-in stat function overloads the return value to return the Windows creation time in the same position (on Windows) as it returns the ctime (on Unix).
So we see questions like this one, which appeared this week on the Philadelphia Linux Users' Group mailing list:
How does one check and change ctime?And when questioned as to why he or she wanted to do this, this person replied:
We are looking to change the creation time. From what I understand, ctime is the closest thing to creation time.There is something about this reply that irritates me, but I'm not quite sure what it is. Several responses come to mind: "Close" is not sufficient in system programming; the ctime is not "close" to a creation time, in any sense; before you go trying to change the thing, you ought to do a minimal amount of research to find out what it is. It is a perfect example of the Wrong Question, on the same order as that poor slob all those years ago who wanted to know how to tell if a file was a hard link or a soft link.
But anyway, that got me thinking about ctimes in general, and I did some research into the history and semantics of the thing, and made some rather surprising discoveries.
One good reference for the broad outlines of early Unix is the paper that Dennis Ritchie and Ken Thompson published in Communications of the ACM in 1974. This was updated in 1978, but the part I'm quoting wasn't revised and is current to 1974. Here is what it has to say about the relevant parts of the inode structure:
An error? I don't think so. Here is corroborating evidence, the stat man page from the first edition of Unix, from 1971:IV. IMPLEMENTATION OF THE FILE SYSTEM
... The entry found thereby (the file's i-node) contains the description of the file:... time of creation, last use, and last modification
NAME stat -- get file status
SYNOPSIS sys stat; name; buf / stat = 18.
DESCRIPTION name points to a null-terminated string naming a file; buf is the
address of a 34(10) byte buffer into which information is placed
concerning the file. It is unnecessary to have any permissions at all
with respect to the file, but all directories leading to the file
must be readable.
After stat, buf has the following format:
buf, +1 i-number
+2, +3 flags (see below)
+4 number of links
+5 user ID of owner size in bytes
+6,+7 size in bytes
+8,+9 first indirect block or contents block
...
+22,+23 eighth indirect block or contents block
+24,+25,+26,+27 creation time
+28,+29, +30,+31 modification time
+32,+33 unused
(Dennis Ritchie provides the Unix
first edition manual; the stat page is in section
2.1.) Now how about that?
When did the ctime change from being called a "creation time" to a "change time"? Did the semantics change too, or was the "creation time" description a misnomer? If I can't find out, I might write to Ritchie to ask. But this is, of course, a last resort.
In the meantime, I do have the source code for the fifth edition kernel, but it appears that, around that time (1975 or so), there was no creation time. At least, I can't find one.
The inode operations inside the kernel are defined to operate on struct inodes:
struct inode {
char i_flag;
char i_count;
int i_dev;
int i_number;
int i_mode;
char i_nlink;
char i_uid;
char i_gid;
char i_size0;
char *i_size1;
int i_addr[8];
int i_lastr;
} inode[NINODE];
The i_lastr field is what we would now call the atime. (I
suppose it stands for "last read".) The mtime and ctime are not
there, because they are not stored in the in-memory copy of the inode.
They are fetched directly from the disk when needed.We can see an example of this in the stat1 function, which is the backend for the stat and fstat system calls:
1 stat1(ip, ub)
2 int *ip;
3 {
4 register i, *bp, *cp;
5
6 iupdat(ip, time);
7 bp = bread(ip->i_dev, ldiv(ip->i_number+31, 16));
8 cp = bp->b_addr + 32*lrem(ip->i_number+31, 16) + 24;
9 ip = &(ip->i_dev);
10 for(i=0; i<14; i++) {
11 suword(ub, *ip++);
12 ub =+ 2;
13 }
14 for(i=0; i<4; i++) {
15 suword(ub, *cp++);
16 ub =+ 2;
17 }
18 brelse(bp);
19 }
ub is the user buffer into which the stat data will be
deposited. ip is the inode structure from which most of
this data will be copied. The
suword utility copies a two-byte unsigned integer ("short
unsigned word") from source to destination. This is done starting at
the i_dev field (line 9), which effectively skips the two
earlier fields, i_flag and i_count, which are
internal kernel matters that are none of the user's business. 14 words are copied from the inode structure starting from this position, including the device and i-number fields, the mode, the link count, and so on, up through the addresses of the data or indirect blocks. (In modern Unixes, the stat call omits these addresses.) Then four words are copied out of the cp buffer, which has been read from the inode actually on the disk; these eight bytes are at position 24 in the inode, and ought to contain the mtime and the ctime. The question is, which is which? This simple question turns out to have a surprisingly complicated answer.
When an inode is modified, the IUPD flag is set in the i_flag member. For example, here is chmod, which modifies the inode but not the underlying data. On a modern unix system, we would expect this to update the ctime, but not the mtime. Let's see what it does in version 5:
1 chmod()
2 {
3 register *ip;
4
5 if ((ip = owner()) == NULL)
6 return;
7 ip->i_mode =& ~07777;
8 if (u.u_uid)
9 u.u_arg[1] =& ~ISVTX;
10 ip->i_mode =| u.u_arg[1]&07777;
11 ip->i_flag =| IUPD;
12 iput(ip);
13 }
Line 10 is the important one; it sets the mode on the in-memory copy
of the inode to the argument supplied by the user. Then line 11 sets
the IUPD flag to indicate that the inode has been modified.
Line 12 calls iput, whose principal job is to maintain the
kernel's internal reference count of the number of file descriptors
that are attached to this inode. When this number reaches zero, the
inode is written back to disk, and discarded from the kernel's open
file table. The iupdat function, called from iput,
is the one that actually writes the modified inode back to the
disk:
1 iupdat(p, tm)
2 int *p;
3 int *tm;
4 {
5 register *ip1, *ip2, *rp;
6 int *bp, i;
7
8 rp = p;
9 if((rp->i_flag&(IUPD|IACC)) != 0) {
10 if(getfs(rp->i_dev)->s_ronly)
11 return;
12 i = rp->i_number+31;
13 bp = bread(rp->i_dev, ldiv(i,16));
14 ip1 = bp->b_addr + 32*lrem(i, 16);
15 ip2 = &rp->i_mode;
16 while(ip2 < &rp->i_addr[8])
17 *ip1++ = *ip2++;
18 if(rp->i_flag&IACC) {
19 *ip1++ = time[0];
20 *ip1++ = time[1];
21 } else
22 ip1 =+ 2;
23 if(rp->i_flag&IUPD) {
24 *ip1++ = *tm++;
25 *ip1++ = *tm;
26 }
27 bwrite(bp);
28 }
29 }
What is going on here? p is the in-memory copy of the inode
we want to update. It is immediately copied into a register, and
called by the alias rp thereafter. tm is the time
that the kernel should write into the mtime field of the inode.
Usually this is the current time, but the smdate system call
("set modified date") supplies it from the user instead. Lines 16–17 copy the mode, link count, uid, gid, "size", and "addr" fields from the in-memory copy of the inode into the block buffer that will be written back to the disk. Lines 18–22 update the atime if the IACC flag is set, or skip it if not. Then, if the IUPD flag is set, lines 24–25 write the tm value into the next slot in the buffer, where the mtime is stored. The bwrite call on line 27 commits the data to the disk; this results in a call into the appropriate device driver code.
There is no sign of updating the ctime field, but recall that we started this search by looking at what the chmod call does; it sets IUPD, which eventually results in the updating of the mtime field. So the mtime field is not really an mtime field as we now know it; it is doing the job that is now done by the ctime field. And in fact, the dump command predicates its decision about whether to dump a file on the contents of the mtime field. Which is really the ctime field. So functionally, dump is doing the same thing it does now.
It's possible that I missed it, but I cannot find the advertised creation time anywhere. The logical place to look is in the maknode function, which allocates new inodes. The maknode function calls ialloc to get an unused inode from the device, and this initializes its mode (as specified by the user), its link count (to 1), and its uid and gid (to the current process's uid and gid). It does not set a creation time. The ialloc function is fairly complicated, but as far as I can tell it is not setting any creation time either.
Working it from the other end, asking who might look at the ctime field, we have the find command, which has a -mtime option, but no -ctime option. The dump command, as noted before, uses the mtime. Several commands perform stat calls and declare structs to hold the result. For example, pr, which prints files with nice pagination, declares a struct inode, which is the inode as returned by stat, as opposed to the inode as used internally by the kernel—what we would call a struct stat now. There was no /usr/include in the fifth edition, so the pr command contains its own declaration of the struct inode. It looks like this:
struct inode {
int dev;
...
int atime[2];
int mtime[2];
};
No sign of the ctime, which would have been after the mtime
field. (Of course, it could be there anyway, unmentioned in the
declaration, since it is last.) And similarly, the ls command
has:
struct ibuf {
int idev;
int inum;
...
char *iatime[2];
char *imtime[2];
};
A couple of commands have extremely misleading declarations. Here's
the struct inode from the prof command, which prints
profiling reports:
struct inode {
int idev;
...
int ctime[2];
int mtime[2];
int fill;
};
The atime field has erroneously been called ctime here, but
it seems that since prof does not use the atime, nobody
noticed the bug. And there's a mystery fill field at the
end, as if prof is expecting one more field, but doesn't know
what it will be for. The declaration of ibuf in the
ln command has similar oddities.So the creation time advertised by the CACM paper (1974) and the version 1 manual (1971) seems to have disappeared by the time of version 5 (1975), if indeed it ever existed.
But there was some schizophrenia in the version 5 system about whether there was a third date in addition to the atime and the mtime. The stat call copied it into the stat buffer, and some commands assumed that it would be there, although they weren't sure what it would be for, and none of them seem look at it. It's quite possible that there was at one time a creation date, which had been eliminated by the time of the fifth edition, leaving behind the vestigial remains we saw in commands like ln and prof and in the code of the stat1 function.
Functionally, the version 5 mtime is actually what we would now call the ctime: it is updated by operations like chmod that in modern Unix will update the ctime but not the mtime. A quick scan of the Lions Book suggests that it was the same way in version 6 as well. I imagine that the ctime-mtime distinction arose in version 7, because that was the last version before the BSD/AT&T fork, and nearly everything common to those two great branches of the Unix tree was in version 7.
Oh, what the hell; I have the version 7 source code; I may as well look at it. Yes, by this time the /usr/include/sys/stat.h file had been invented, and does indeed include all three times in the struct stat. So the mtime (as we now know it) appears to have been introduced in v7.
One sometimes hears that early Unix had atime and mtime, and that ctime was introduced later. But actually, it appears that early Unix had atime and ctime, and it was the mtime that was introduced later. The confusion arises because in those days the ctime was called "mtime".
Addendum: It occurs to me now that the version 5 mtime is not precisely like the modern ctime, because it can be set via the smdate call, which is analogous to the modern utime call. The modern ctime cannot be set at all.
(Totally peripheral addendum: Google search for dmr puts Dennis M. Ritchie in fourth position, not the first. Is this grave insult to our community to be tolerated? I think not! It must be avenged! With fire and steel!)
[ Addendum 20070127: Unix source code prior to the fifth edition is lost. The manuals for the third and fourth editions are available from the Unix Heritage Society. The manual for the third edition (February 1973) mentions the creation time, but by the fourth edition (November 1973) the stat(2) man page no longer mentions a creation time. In v4, the two dates in the stat structure are called actime (modern atime) and modtime (modern mtime/ctime). ]
[Other articles in category /Unix] permanent link
Fri, 26 Jan 2007
Environmental manipulations
Unix is full of little utility programs that run some other program in
a slightly modified environment. For example, the nohup
command:
SYNOPSIS
nohup COMMAND [ARG]...DESCRIPTION
Run COMMAND, ignoring hangup signals.
The nohup basically does signal(NOHUP, SIG_IGN) before calling execvp(COMMAND, ARGV) to execute the command.
Similarly, there is a chroot command, run as chroot new-root-directory command args..., which runs the specified command with its default root inode set to somewhere else. And there is a nice command, run as nice nice-value-adjustment command args..., which runs the specified command with its "nice" value changed. And there is an env environment-settings command args... which runs the specified command with new variables installed into the environment. The standard sudo command could also be considered to be of this type.
I have also found it useful to write trivial commands called indir, which runs a command after chdir-ing to a new directory, and stopafter, which runs a command after setting the alarm timer to a specified amount, and, just today, with-umask, which runs a command after setting the umask to a particular value.
I could probably have avoided indir and with-umask. Instead of indir DIR COMMAND, I could use sh -c 'cd DIR; exec COMMAND', for example. But indir avoids an extra layer of horrible shell quotes, which can be convenient.
Today it occurred to me to wonder if this proliferation of commands was really the best way to solve the problem. The sh -c '...' method solves it partly, for those parts of the process user area to which correspond shell builtin commands. This includes the working directory, umask, and environment variables, but not the signal table, the alarm timer, or the root directory.
There is no standardized interface to all of these things at any level. At the system call level, the working directory is changed by the chdir system call, the root directory by chroot, the alarm timer by alarm, the signal table by a bunch of OS-dependent nonsense like signal or sigaction, the nice value by setpriority, environment variables by a potentially complex bunch of memory manipulation and pointer banging, and so on.
Since there's no single interface for controlling all these things, we might get a win by making an abstraction layer for dealing with them. One place to put this abstraction layer is at the system level, and might look something like this:
/* declares USERAREA_* constants,
int userarea_set(int, ...)
and void *userarea_get(int)
*/
#include <sys/userarea.h>
userarea_set(USERAREA_NICE, 12);
userarea_set(USERAREA_CWD, "/tmp");
userarea_set(USERAREA_SIGNAL, SIGHUP, SIG_IGN);
userarea_set(USERAREA_UMASK, 0022);
...
This has several drawbacks. One is that it requires kernel hacking.
A subitem of this is that it will never become widespread, and that if
you can't (or don't want to) replace your kernel, it cannot be made to
work for you. Another is that it does not work for the environment
variables, which are not really administered by the kernel. Another
is that it does not fully solve the original problem, which is to
obviate the plethora of nice, nohup, sudo,
and env commands. You would still have to write a command
to replace them. I had thought of another drawback, but forgot it while I
was writing the last two sentences.You can also put the abstraction layer at the C library level. This has fewer drawbacks. It no longer requires kernel hacking, and can provide a method for modifying the environment. But you still need to write the command that uses the library.
We may as well put the abstraction layer at the Unix command level. This means writing a command in some language, like Perl or C, which offers a shell-level interface to manipulating the process environment, perhaps something like this:
newenv nice=12 cwd=/tmp signal=HUP:IGNORE umask=0022 -- command args...Then newenv has a giant dispatch table inside it to process the settings accordingly:
...
nice => sub { setpriority(PRIO_PROCESS, $$, $_) },
cwd => sub { chdir($_) },
signal => sub {
my ($name, $result) = split /:/;
$SIG{$name} = $result;
},
umask => sub { umask(oct($_)) },
...
One question to ask is whether something like this already exists.
Another is, if not, whether it's because there's some reason why it's
a bad idea, or because there's a simpler solution, or just because
nobody has done it yet.
[Other articles in category /Unix] permanent link
Wed, 24 Jan 2007
Length of baseball games
In an earlier
article, I asserted that the average length of a baseball game was
very close to 9 innings. This is a good rule of thumb, but it is also
something of a coincidence, and might not be true in every year.
The canonical game, of course, lasts 9 innings. However, if the score is tied at the end of 9 innings, the game can, and often does, run longer, because the game is extended to the end of the first complete inning in which one team is ahead. So some games run longer than 9 innings: games of 10 and 11 innings are quite common, and the major-league record is 25.
Counterbalancing this effect, however, are two factors. Most important is that when the home team is ahead after the first half of the ninth inning, the second half is not played, since it would be a waste of time. So nearly half of all games are only 8 1/2 innings long. This depresses the average considerably. Together with the games that are stopped early on account of rain or other environmental conditions, the contribution from the extra-inning tie games is almost exactly cancelled out, and the average ends up close to 9.
[Other articles in category /games] permanent link
Tue, 23 Jan 2007 In need of some bathroom reading last week, I grabbed my paperback copy of Thomas Hobbes' Leviathan, which is always a fun read. The thing that always strikes me about Leviathan is that almost every sentence makes me nod my head and mutter "that is so true," and then want to get in an argument with someone in which I have the opportunity to quote that sentence to refute them. That may sound like a lot to do on every sentence, but the sentences in Leviathan are really long.Here's a random example:
And as in arithmetic unpractised men must, and professors themselves may often, err, and cast up false; so also in any other subject of reasoning, the ablest, most attentive, and most practised men may deceive themselves, and infer false conclusions; not but that reason itself is always right reason, as well as arithmetic is a certain and infallible art: but no one man's reason, nor the reason of any one number of men, makes the certainty; no more than an account is therefore well cast up because a great many men have unanimously approved it. And therefore, as when there is a controversy in an account, the parties must by their own accord set up for right reason the reason of some arbitrator, or judge, to whose sentence they will both stand, or their controversy must either come to blows, or be undecided, for want of a right reason constituted by Nature; so is it also in all debates of what kind soever: and when men that think themselves wiser than all others clamour and demand right reason for judge, yet seek no more but that things should be determined by no other men's reason but their own, it is as intolerable in the society of men, as it is in play after trump is turned to use for trump on every occasion that suit whereof they have most in their hand. For they do nothing else, that will have every of their passions, as it comes to bear sway in them, to be taken for right reason, and that in their own controversies: bewraying their want of right reason by the claim they lay to it.Gosh, that is so true. Leviathan is of course available online at many locations; here is one such.
Anyway, somewhere in the process of all this I learned that Hobbes had some mathematical works, and spent a little time hunting them down. The Penn library has links to online versions of some, so I got to read a little with hardly any investment of effort. One that particularly grabbed my attention was "Three papers presented to the Royal Society against Dr. Wallis".
Wallis was a noted mathematician of the 17th century, a contemporary of Isaac Newton, and a contributor to the early development of the calculus. These days he is probably best known for the remarkable formula:
$${\pi\over2} = {2\over1}{2\over3}{4\over3}{4\over5}{6\over5}{6\over7}{8\over7}\cdots$$
So I was reading this Hobbes argument against Wallis, and I hardly got through the first page, because it was so astounding. I will let Hobbes speak for himself:
Hobbes says, in short, that the square root of 100 squares is not 10 unit lengths, but 10 squares. That is his whole argument.The Theoreme.
The four sides of a Square, being divided into any number of equal parts, for example into 10; and straight lines being drawn through opposite points, which will divide the Square into 100 lesser Squares; The received Opinion, and which Dr. Wallis commonly useth, is, that the root of those 100, namely 10, is the side of the whole Square.
The Confutation.
The Root 10 is a number of those Squares, whereof the whole containeth 100, whereof one Square is an Unitie; therefore, the Root 10, is 10 Squares: Therefore the root of 100 Squares is 10 Squares, and not the side of any Square; because the side of a Square is not a Superfices, but a Line.
Hobbes, of course, is totally wrong here. He's so totally wrong that it might seem hard to believe that he even put such a totally wrong notion into print. One wants to imagine that maybe we have misunderstood Hobbes here, that he meant something other than what he said. But no, he is perfectly lucid as always. That is a drawback of being such an extremely clear writer: when you screw up, you cannot hide in obscurity.
Here is the original document, in case you cannot believe it.
I picture the members of the Royal Society squirming in their seats as Hobbes presents this "confutation" of Wallis. There is a reason why John Wallis is a noted mathematician of the 17th century, and Hobbes is not a noted mathematician at all. Oh well!
Wallis presented a rebuttal sometime later, which I was not going to mention, since I think everyone will agree that Hobbes is totally wrong. But it was such a cogent rebuttal that I wanted to quote a bit from it:
Like as 10 dozen is the root, not of 100 dozen, but of 100 dozen dozen. ... But, says he, the root of 100 soldiers, is 10 soldiers. Answer: No such matter, for 100 soldiers is not the product of 10 soldiers into 10 soldiers, but of 10 soldiers into the number 10: And therefore neither 10, nor 10 soldiers, is the root of it.Post scriptum: The remarkable blog Giornale Nuovo recently had an article about engraved title pages of English books, and mentioned Leviathan's famous illustration specifically. Check it out.
[Other articles in category /math] permanent link
Mon, 22 Jan 2007
Linogram circular problems
The problems are not related to geometric circles; the are logically
circular.
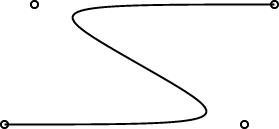 In the course of preparing my sample curve diagrams, one of which is
shown at right, I ran into several related bugs in the way that arrays
were being handled. What I really wanted to do was to define a
labeled_curve object, something like this:
In the course of preparing my sample curve diagrams, one of which is
shown at right, I ran into several related bugs in the way that arrays
were being handled. What I really wanted to do was to define a
labeled_curve object, something like this:
define labeled_curve extends curve {
spot s[N];
constraints { s[i] = control[i]; }
}
That is, it is just like an ordinary curve, except that it also has a
"spot" at each control point. A "spot" is a graphic element that
marks the control point, probably with a small circle or something of
the sort:
define spot extends point {
circle circ(r=0.05);
constraints {
circ.c.x = x; circ.c.y = y;
}
}
A spot is like a point, and so it has an x
and a y coordinate. But it also has a circle, circ,
which is centered at this location. (circ.c is the center of
the circle.)When I first tried this, it didn't work because linogram didn't understand that a labeled_curve with N = 4 control points would also have four instances of circ, four of circ.c, four of circ.c.x, and so on. It did understand that the labeled curve would have four instances of s, but the multiplicity wasn't being propagated to the subobjects of s.
I fixed this up in pretty short order.
But the same bug persisted for circ.r, and this is not so easy to fix. The difference is that while circ.c is a full subobject, subject to equation solving, and expected to be unknown, circ.r is a parameter, which much be specified in advance.
N, the number of spots and control points, is another such parameter. So there's a first pass through the object hierarchy to collect the parameters, and then a later pass figures out the subobjects. You can't figure out the subobjects without the parameters, because until you know the value of parameters like N, you don't know how many subobjects there are in arrays like s[N].
For subobjects like S[N].circ.c.x, there is no issue. The program gathers up the parameters, including N, and then figures out the subobjects, including S[0].circ.c.x and so on. But S[0].circ.r, is a parameter, and I can't say that its value will be postponed until after the values of the parameters are collected. I need to know the values of the parameters before I can figure out what the parameters are.
This is not a show-stopper. I can think of at least three ways forward. For example, the program could do a separate pass for param index parameters, resolving those first. Or I could do a more sophisticated dependency analysis on the parameter values; a lot of the code for this is already around, to handle things like param number a = b*2, b=4, c=a+b+3, d=c*5+b. But I need to mull over the right way to proceed.
Consider this oddity in the meantime:
define snark {
param number p = 3;
}
define boojum {
param number N = s[2].p;
snark s[N];
}
Here the program needs to know the value of N in order to
decide how many snarks are in a boojum. But the number N itself is
determined by examining the p parameter in snark 2, which
itself will not exist if N is less than 3. Should this sort of
nonsense be allowed? I'm not sure yet.When you invent a new kind of program, there is an interesting tradeoff between what you want to allow, what you actually do allow, and what you know how to implement. I definitely want to allow the labeled_curve thing. But I'm quite willing to let the snark-boojum example turn into some sort of run-time failure.
[Other articles in category /linogram] permanent link
Sun, 21 Jan 2007
Recent Linogram development update
Lately most of my spare time (and some not-spare time) has been going
to linogram. I've been posting updates pretty regularly at
the main linogram page. But I don't know if
anyone ever looks at that page. That got me thinking that it was not
convenient to use, even for people who are interested in
linogram, and that maybe I should have an RSS/Atom feed for
that page so that people who are interested do not have to keep
checking back.
Then I said "duh", because I already have a syndication feed for this page, so why not just post the stuff here?
So that is what I will do. I am about to copy a bunch of stuff from that page to this one, backdating it to match when I posted it.
The new items are: [1] [2] [3] [4] [5].
People who only want to hear about linogram, and not about
anything else, can subscribe to
 this RSS feed
or
this RSS feed
or
 this Atom feed.
this Atom feed.
[Other articles in category /linogram] permanent link
Sat, 20 Jan 2007
Another Linogram success story
I've been saying for a while that a well-designed system surprises
even the designer with its power and expressiveness. Every time
linogram surprises me, I feel a flush of satisfaction because
this is evidence that I designed it well. I'm beginning to think that
linogram may be the best single piece of design I've
ever done.
Here was today's surprise. For a long time, my demo diagram has been a rough rendering of one of the figures from Higher-Order Perl:
(It's big, so this is a reduced version; click to expand it.)
I wanted component k in the middle of the diagram to be a curved line, but since I didn't have curved lines yet, I used two straight lines instead, as shown below:
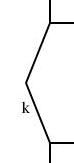
define bentline {
line upper, lower;
param number depth = 0.2;
point start, end, center;
constraints {
center = upper.end = lower.start;
start = upper.start; end = lower.end;
start.x = end.x = center.x + depth;
center.y = (start.y + end.y)/2;
}
}
...
bentline k;
label klbl(text="k") = k.upper.center - (0.1, 0);
...
constraints {
...
k.start = plus.sw; k.end = times.nw;
...
}
So I had defined a thing called a bentline, which is a line
with a slight angle in it. Or more precisely, it's two
approximately-vertical lines joined end-to-end. It has three
important reference points: start, which is the top point,
end, the bottom point, which is directly under the top
point, and center, halfway in between, but displaced
leftward by depth. I now needed to replace this with a curved line. This meant removing all the references to start, end, upper and so forth, since curves don't have any of those things. A significant rewrite, in other words.
But then I had a happy thought. I added the following definition to the file:
require "curve";
define bentline_curved extends bentline {
curve c(N=3);
constraints {
c.control[0] = start;
c.control[1] = center;
c.control[2] = end;
}
draw { c; }
}
A bentline_curved is now the same as a bentline, but
with an extra curved line, called c, which has three control
points, defined to be identical with start, center,
and end. These three points inherit all the same constraints
as before, and so are constrained in the same way and positioned in
the same way. But instead of drawing the two lines, the
bentline_curved draws only the curve. I then replaced:
bentline k;
with:
bentline_curved k;
and recompiled the diagram. The result is below:This diagram is identical, except that arc k has changed from a bent line to a curve. Compare:
 | 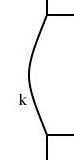
|
I didn't foresee this when I designed the linogram language. Sometimes when you try a new kind of program for the first time, you keep getting unpleasant surprises. You find things you realize you didn't think through, or that have unexpected consequences, or features that turn out not to be as powerful as you need, or that mesh badly with other features. Then you have to go back and revisit your design, fix problems, try to patch up mismatches, and so forth. In contrast, the appearance of the sort of pleasant surprise like the one in this article is exactly the opposite sort of situation, and makes me really happy.
[Other articles in category /linogram] permanent link
Linogram development: 20070120 Update
The array feature is working, pending some bug fixes. I have not yet
found all the bugs, I think. But the feature has definitely moved
from the does-not-work-at-all phase into the mostly-works phase. That
is, I am spending most of my time tracking down bugs, rather than
writing large amount of code. The test suite is expanding rapidly.
The regular polygons are working pretty well, and the curves are working pretty well. Here are some simple examples:
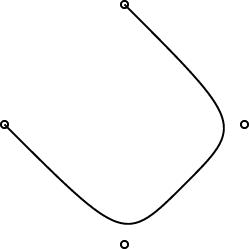
| 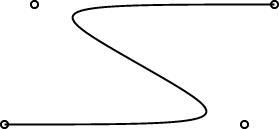
|
One interesting design problem turned up that I had not foreseen. I had planned for the curve object to be specified by 2 or more control points. (The control points are marked by little circles in the demo pictures above.) The first and last controlpoints would be endpoints, and the curve would start at point 0, then head toward point 1, veer off toward point 2, then veer off toward point 3, etc., until it finally ended at point N. You can see this in the pictures.
This is like the behavior of pic, which has good-looking curves. You don't want to require that the curve pass through all the control points, because that does not give it enough freedom to be curvy. And this behavior is easy to get just by using a degree-N Bézier curve, which was what I planned to do.
However, PostScript surprised me. I had thought that it had degree-N Bézier curves, but it does not. It has only degree-3 ("cubic") Bézier curves. So then I was left with the puzzle of how to use PostScript's Bézier curves to get what I wanted. Or should I just change the definition of curve in linogram to be more like what PostScript wanted? Well, I didn't want to do that, because linogram is supposed to be generic, not a front-end to PostScript. Or, at least, not a front-end only to PostScript.
I did figure out a compromise. The curves generated by the PostScript drawer are made of PostScript's piecewise-cubic curves, but, as you can see from the demo pictures, they still have the behavior I want. The four control points in the small demos above actually turn into two PostScript cubic Bézier curves, with a total of seven control points. If you give linogram the points A, B, C, and D, the PostScript engine draws two cubic Bézier curves, with control points {A, B, B, (B + C)/2} and {(B + C)/2, C, C, D}, respectively. Maybe I'll write a blog article about why I chose to do it this way.
One drawback of this approach is that the curves turn rather sharply near the control points. I may tinker with the formula later to smooth out the curves a bit, but I think for now this part is good enough for beta testing.
[Other articles in category /linogram] permanent link
Wed, 17 Jan 2007
Linogram development: 20070117 Update
The array feature is almost complete, perhaps entirely complete.
Fully nontrivial tests are passing. For example, here is test
polygon002 from the distribution:
require "polygon";
polygon t1(N=3), t2(N=3);
constraints {
t1.v[0] = (0, 0);
t1.v[1] = (1, 1);
t1.v[2] = (2, 3);
t2.v[i] = t1.v[i-1];
}
This defines two polygons, t1 and
t2, each with three sides. The three vertices of
t1 are specified explicitly. Triangle
t2 is the same, but with the vertices numbered
differently: t2.v0 =
t1.v2,
t2.v1 =
t1.v0, and
t2.v2 =
t1.v1. Each of the triangles also
has three edges, defined implicitly by the definition in
polygon.lino:
require "point";
require "line";
define polygon {
param index N;
point v[N];
line e[N];
constraints {
e[i].start = v[i];
e[i].end = v[i+1];
}
}
All together, there are 38 values here: 2 coordinates for each of
three vertices of each of the two triangles makes 12; 2 coordinates
for each of two endpoints of each of three edges of each of the two
triangles is another 24, and the two N values themselves
makes a total of 12 + 24 + 2 = 38.All of the equations are rather trivial. All the difficulty is in generating the equations in the first place. The program must recognize that the variable i in the polygon definition is a dummy iterator variable, and that it is associatated with the parameter N in the polygon definition. It must propagate the specification of N to the right place, and then iterate the equations appropriately, producing something like:
e0.end = v0+1Then it must fold the constants in the subscripts and apply the appropriate overflow semantics—in this case, 2+1=0.
e1.end = v1+1
e2.end = v2+1
Open figures still don't work properly. I don't think this will take too long to fix.
The code is very messy. For example, all the Type classes are in a file whose name is not Type.pm but Chunk.pm. I plan to have a round of cleanup and consolidation after the 2.0 release, which I hope will be soon.
[Other articles in category /linogram] permanent link
Tue, 09 Jan 2007
R3 is not a square
I haven't done a math article for a while. The most recent math
things I read were some papers on the following theorem: Obviously,
there is a topological space X such that X3 =
R3, namely, X = R. But is there a space
X such that X2 = R3? ("=" here denotes
topological homeomorphism.)
It would be rather surprising if there were, since you could then describe any point in space unambiguously by giving its two coordinates from X. This would mean that in some sense, R3 could be thought of as two-dimensional. You would expect that any such X, if it existed at all, would have to be extremely peculiar.
I had been wondering about this rather idly for many years, but last week a gentleman on IRC mentioned to me that there had been a proof in the American Mathematical Monthly a couple of years back that there was in fact no such X. So I went and looked it up.
The paper was "Another Proof That R3 Has No Square Root", Sam B. Nadler, Jr., American Mathematical Monthly vol 111 June–July 2004, pp. 527–528. The proof there is straightforward enough, analyzing the topological dimension of X and arriving at a contradiction.
But the Nadler paper referenced an earlier paper which has a much better proof. The proof in "R3 Has No Root", Robbert Fokkink, American Mathematical Monthly vol 109 March 2002, p. 285, is shorter, simpler, and more general. Here it is.
A linear map Rn → Rn can be understood to preserve or reverse orientation, depending on whether its determinant is +1 or -1. This notion of orientation can be generalized to arbitrary homeomorphisms, giving a "degree" deg(m) for every homeomorphism which is +1 if it is orientation-preserving and -1 if it is orientation-reversing. The generalization has all the properties that one would hope for. In particular, it coincides with the corresponding notions for linear maps and differentiable maps, and it is multiplicative: deg(f o g) = deg(f)·deg(g) for all homeomorphisms f and g. In particular ("fact 1"), if h is any homeomorphism whatever, then h o h is an orientation-preserving map.
Now, suppose that h : X2 → R3 is a homeomorphism. Then X4 is homeomorphic to R6, and we can view quadruples (a,b,c,d) of elements of X as equivalent to sextuples (p,q,r,s,t,u) of elements of R.
Consider the map s on X4 which takes (a,b,c,d) → (d,a,b,c). Then s o s is the map (a,b,c,d) → (c,d,a,b). By fact 1 above, s o s must be an orientation-preserving map.
But translated to the putatively homeomorphic space R6, the map (a,b,c,d) → (c,d,a,b) is just the linear map on R6 that takes (p,q,r,s,t,u) → (s,t,u,p,q,r). This map is orientation-reversing, because its determinant is -1. This is a contradiction. So X4 must not be homeomorphic to R6, and X2 therefore not homeomorphic to R3.
The same proof goes through just fine to show that R2n+1 = X2 is false for all n, and similarly for open subsets of R2n+1.
The paper also refers to an earlier paper ("The cartesian product of a certain nonmanifold and a line is E4", R.H. Bing, Annals of Mathematics series 2 vol 70 1959 pp. 399–412) which constructs an extremely pathological space B, called the "dogbone space", not even a manifold, which nevertheless has B × R3 = R4. This is on my desk, but I have not read this yet, and I may never.
[Other articles in category /math] permanent link
Mon, 08 Jan 2007
State of the Blog 2006
This is the end of the first year of my blog. The dates on the early
articles say that I posted a few in 2005, but they are deceptive. I
didn't want a blog with only one post in it, so I posted a bunch of
stuff that I had already written, and backdated it to the dates on
which I had written it. The blog first appeared on 8 January, 2006,
and this was the date on which I wrote its first articles.
Output
Not counting this article, I posted 161 articles this year, totalling about 172,000 words, which I think is not a bad output. About 1/4 of this output was about mathematics.The longest article was the one about finite extension fields of Z2; the shortest was the MadHatterDay commemorative. Other long articles included some math ones (metric spaces, the Pólya-Burnside theorem) and some non-math ones (how Forbes magazine made a list of the top 20 tools and omitted the hammer, do aliens feel disgust?).
I drew, generated, or appropriated about 300 pictures, diagrams, and other illustrations, plus 66 mathematical formulas. This does not count the 50 pictures of books that I included, but it does include 108 little colored squares for the article on the Pólya-Burnside counting lemma.
Financial
I incurred the costs of Dreamhosting (see below). But these costs are offset because I am also using the DreamHost as a remote backup for files. So it has some non-blog value, and will also result in a tax deduction.None of the book links earned me any money from kickbacks. However, the blog did generate some income. When Aaron Swartz struck oil, he offered to give away money to web sites that needed it. Mine didn't need it, but a little later he published a list of web sites he'd given money to, and I decided that I was at least as deserving as some of them. So I stuck a "donate" button on my blog and invited Aaron to use it. He did. Thanks, Aaron!
I now invite you to use that button yourself. Here are two versions that both do the same thing:
My MacArthur Fellowship check has apparently been held up in the mail.
Popularity
The most popular article was certainly the one on Design Patterns of 1972. I had been thinking this one over for years, and I was glad it attracted as much attention as it did. Ralph Johnson (author of the Design Patterns book) responded to it, and I learned that Design Patterns is not the book that Johnson thought it was. Gosh, I'm glad I didn't write that book.The followup to the Design Patterns article was very popular also. Other popular articles were on risk, the envelope paradox, the invention of the = sign, and ten science questions every high school graduate should be able to answer.
My own personal favorites are the articles about alien disgust, the manufacture of round objects, and what makes π so peculiar. In that last one, I think I was skating on the thin edge of crackpotism.
The article about Forbes' tool list was mentioned in The New York Times.
The blog attracted around five hundred email messages, most of which were intelligent and thoughtful, and most of which I answered. But my favorite email message was from the guy who tried to convince me that rock salt melts snow because it contains radioactive potassium.
System administration
I moved the blog twice. It originally resided on www.plover.com, which is in my house. I had serious network problems in July and August, Verizon's little annual gift to me. When I realized that the blog was be much more popular than I expected, and that I wanted it to be reliably available, I moved it to newbabe.pobox.com, which I'd had an account on for years but had never really used. This account was withdrawn a few months later, so I rented space at Dreamhost, called blog.plover.com, and moved it there. I expect it will stay at Dreamhost for quite a while.Moving the blog has probably cost me a lot of readers. I know from the logs that many of them have not moved from newbabe to Dreamhost. Traffic on the new site just after the move was about 25% lower than on the old site just before the move. Oh well.
If the blog hadn't moved so many times, it would be listed by Technorati as one of the top ten blogs on math and science, and one of the top few thousand overall. As it is, the incoming links (which are what Technorati uses to judge blog importance) are scattered across three different sites, so it appears to be three semi-popular blogs rather than one very popular blog. This would bother me, if Technorati rankings weren't so utterly meaningless.
Policy
I made a couple of vows when I started the blog. A number of years ago on my use.perl.org journal I complained extensively about some people I worked with. They deserved everything I said, but the remarks caused me a lot of trouble and soured me on blogs for many years. When I started this blog, I vowed that I wouldn't insult anyone personally, unless perhaps they were already dead and couldn't object. Some people have no trouble with this, but for someone like me, who is a seething cauldron of bile, it required a conscious effort.I think I've upheld this vow pretty well, and although there have been occasions on which I've called people knuckleheaded assholes, it has always been either a large group (like Biblical literalists) or people who were dead (like this pinhead) or both.
Another vow I made was that I wasn't going to include any tedious personal crap, like what music I was listening to, or whether the grocery store was out of Count Chocula this week. I think I did okay on that score. There are plenty of bloggers who will tell you about the fight they had with their girlfriend last night, but very few that will analyze abbreviations in Medieval Latin. So I have the Medieval Latin abbreviations audience pretty much to myself. I am a bit surprised at how thoroughly I seem to have communicated my inner life, in spite of having left out any mention of Count Chocula. This is a blog of what I've thought, not what I've done.
What I didn't post this year
My blog directory contains 55 unpublished articles, totalling 39,500 words, in various states of incompleteness; compare this with the 161 articles I did complete.The longest of these unpublished articles was written some time after my article on the envelope paradox hit the front page of Reddit. Most of the Reddit comments were astoundingly obtuse. There were about nine responses of the type "That's cute, but the fallacy is...", each one proposing a different fallacy. All of the proposed fallacies were completely wrong; most of them were obviously wrong. (There is no fallacy; the argument is correct.) I decided against posting this rebuttal article for several reasons:
- It wouldn't have convinced anyone who wasn't already convinced,
and might have unconvinced someone who was. I can't lay out the
envelope paradox argument any more briefly or clearly than I did; all
I can do is make the explanation longer.
- It came perilously close to violating the rule about insulting
people who are still alive. I'm not sure how the rule applies to
anonymous losers on Reddit, but it's probably better to err on the
side of caution. And I wasn't going to be able to write the article
without insulting them, because some of them were phenomenally
stupid.
- I wasn't sure anyone but me would be interested in the details of
what a bunch of knuckleheaded lowlifes infest the Reddit comment
board. Many of you, for example, read Slashdot regularly, and see
dozens of much more ignorant and ill-considered comments every
day.
- How much of a cretin would I have to be to get in an argument with
a bunch of anonymous knuckleheads on a computer bulletin board? It's
like trying to teach a pig to sing. Well, okay, I did get in an
argument with them over on Reddit; that was pretty stupid. And then I
did write the rebuttal article, which was at least as stupid, but which I
can at least ascribe to my seething cauldron of bile. But it's never
too late to stop acting stupid, and at least I stopped before I
cluttered up my beautiful blog with a four-thousand-word rebuttal.
The article about metric spaces was supposed to be one of a three-part series, which I still hope to finish eventually. I made several attempts to write another part in this series, about the real numbers and why we have them at all. This requires explanation, because the reals are mathematically and philosophically quite artificial and problematic. (It took me a lot of thought to convince myself that they were mathematically inevitable, and that the aliens would have them too, but that is another article.) The three or four drafts I wrote on this topic total about 2,100 words, but I still haven't quite got it where I want it, so it will have to wait.
I wrote 2,000 words about oddities in my brain, what it's good at and what not, and put it on the shelf because I decided it was too self-absorbed. I wrote a complete "frequently-asked questions" post which answered the (single) question "Why don't you allow comments?" and then suppressed it because I was afraid it was too self-absorbed. Then I reread it a few months later and thought it was really funny, and almost relented. Then I read it again the next month and decided it was better to keep it suppressed. I'm not indecisive; I'm just very deliberate.
I finished a 2,000-word article about how to derive the formulas for least-squares linear regression and put it on the shelf because I decided that it was boring. I finished a 1,300-word article about quasiquotation in Lisp and put it on the shelf because I decided it was boring. (Here's the payoff from the quasiquotation article: John McCarthy, the inventor of Lisp, took both the concept and the name directly from W.V.O. Quine, who invented it in 1940.)
Had I been writing this blog in 2005, there would have been a bunch of articles about Sir Thomas Browne, but I was pretty much done with him by the time I started the blog. (I'm sure I will return someday.) There would have been a bunch of articles about John Wilkins's book on the Philosophical Language, and some on his book about cryptography. (The Philosophical Language crept in a bit anyway.) There would have been an article about Charles Dickens's book Great Expectations, which I finished reading about a year and a half ago.
An article about A Christmas Carol is in the works, but I seem to have missed the seasonal window on that one, so perhaps I'll save it for next December. I wrote an article about how to calculate the length of the day, and writing a computer progam to tell time by the old Greek system, which divides the daytime into twelve equal hours and the nighttime into twelve equal hours, so that the night hours are longer than the day ones in the winter, and shorter in the summer. But I missed the target date (the solstice) for that one, so it'll have to wait until at least the next solstice. I wrote part of an article about Hangeul (the Korean alphabet), planning to publish it on Hangeul Day (the Koreans have a national holiday celebrating Hangeul) but I couldn't find the quotations I wanted from 1445, so I put it on the shelf. This week I'm reading Gari Ledyard's doctoral thesis, The Korean Language Reform of 1446, so I may acquire more information about that and be able to finish the article. (I highly recommend the Ledyard thing; it's really well-written.) I recently wrote about 1,000 words about Vernor Vinge's new novel Rainbows End, but that's not finished yet.
A followup to the article about why you don't have one ear in the middle of your face is in progress. It's delayed by two things: first, I made a giant mistake in the original article, and I need to correct it, but that means I have to figure out what the mistake is and how to correct it. And second, I have to follow up on a number of fascinating references about directional olfaction.
Sometimes these followups eventually arrive,as the one about ssh-agent did, and sometimes they stall. A followup to my early article about the nature of transparency, about the behavior of light, and the misconception of "the speed of light in glass", ran out of steam after a page when I realized that my understanding of light was so poor that I would inevitably make several gross errors of fact if I finished it.
I spent a lot of the summer reading books about inconsistent mathematics, including Graham Priest's book In Contradiction, but for some reason no blog articles came of it. Well, not exactly. What has come out is an unfinished 1,230-word article against the idea that mathematics is properly understood as being about formal systems, an unfinished 1,320-word article about the ubiquity of the Grelling-Nelson paradox, an unfinished 1,110-word article about the "recursion theorem" of computer science, and an unfinished 1,460-word article about paraconsistent logic and the liar paradox.
I have an idea that I might inaugurate a new section of the blog, called "junkheap", where unfinished articles would appear after aging in the cellar for three years, regardless what sort of crappy condition they are in. Now that the blog is a year old, planning something two years out doesn't seem too weird.
I also have an ideas file with a couple hundred notes for future articles, in case I find myself with time to write but can't think of a topic. Har.
Surprises
I got a number of unpredictable surprises when I started the blog.
One was that I wasn't really aware of LiveJournal, and its "friends"
pages. I found it really weird to see my equation-filled articles on
subvocal reading and Baroque scientific literature appearing on these
pages, sandwiched between posts about Count Chocula from people named
"Taldin the Blue Unicorn". Okay, whatever.
I was not expecting that so many of my articles would take the form "ABCDEFG. But none of this is really germane to the real point of this article, which is ... HIJKLMN." But the more articles I write in this style, the more comfortable I am with it. Perhaps in a hundred years graduate students will refer to an essay of this type, with two loosely-coupled sections of approximately the same length, linked by an apologetic phrase, as "Dominus-style".
Wrong wrong wrong!
I do not have a count of the number of mistakes and errors I made that I corrected in later articles, although I wish I did. Nor do I have a count of the number of mistakes that I did not correct.However, I do know that the phrase "I don't know" (and variations, like "did not know") appears 67 times, in 44 of the 161 articles. I would like to think that this is one of the things that will set my blog apart from others, and I hope to improve these numbers in the coming years.
Thanks
Thanks to all my readers for their interest and close attention, and for making my blog a speedy success.
[Other articles in category /meta] permanent link
Fri, 05 Jan 2007
ssh-agent, revisited
My recent article about reusing
ssh-agent processes attracted a lot of mail, most of it very
interesting.
- A number of people missed an important piece of context: since the
article was filed in 'oops' section of my
blog, it was intended as a description of a mistake I had made.
The mistake in this case being to work really hard on the first
solution I thought of, rather than to back up at early signs of
trouble, and scout around for a better and simpler solution. I need
to find a way to point out the "oops" label more clearly, and at the
top of the article instead of at the bottom.
- Several people pointed out other good solutions to my problem. For
example, Adam Sampson and Robert Loomans pointed out that versions of
ssh-agent support a -a option, which orders the process to
use a particular path for its Unix domain socket, rather than making
up a path, as it does by default. You can then use something like
ssh-agent -a $HOME/.ssh/agent when you first start the agent,
and then you always know where to find the socket.
- An even simpler solution is as follows: My principal difficulty was in
determining the correct value for the SSH_AGENT_PID variable.
But it turns out that I don't need this; it is only used for
ssh-agent -k, which kills the existing ssh-agent process.
For authentication, it is only necessary to have
SSH_AUTH_SOCK set. The appropriate value for this variable
is readily determined by scanning /tmp, as I noted in the
original article. Thanks to Aristotle Pagaltzis and Adam Turoff for
pointing this out.
- Several people pointed me to the keychain
project. This program is a front-end to ssh-agent. It contains
functions to check for a running agent, and to start one if there is
none yet, and to save the environment settings to a file, as I did
manually in my article.
- A number of people suggested that I should just run ssh-agent from my
X session manager. This suggests that they did not read the article
carefully; I already do this. Processes running on my home machine,
B, all inherit the ssh-agent settings from the session manager
process. The question is what to do when I remote login from a
different machine, say A, and want the login shell, which was
not started under X, to acquire the same settings.
Other machines trust B, but not A, so credential forwarding is not the solution here either.
- After extracting the ssh-agent process's file descriptor
table with ls -l /proc/pid/fd, and getting:
lrwx------ 1 mjd users 64 Dec 12 23:34 3 -> socket:[711505562]I concluded that the identifying information, 711505562, was useless. Aaron Crane corrected me on this; you can find it listed in /proc/net/unix, which gives the pathname in the filesystem:
% grep 711505562 /proc/net/unix ce030540: 00000002 00000000 00010000 0001 01 711505562 /tmp/ssh-tNT31655/agent.31655I had suggested that the kernel probably maintained no direct mapping from the socket i-number to the filesystem path, and that obtaining this information would require difficult grovelling of the kernel data structures. But apparently to whatever extent that is true, it is irrelevant, since the /proc/net/unix driver has already been written to do it.
- Saving the socket information in a file solves another problem I
had. Suppose I want some automated process, say the cron job that
makes my offsite network backups, to get access to SSH credentials. I
can store the credentials in an ssh-agent process, and save the
variable settings to a file. The backup process can then reinstate
the settings from the file, and will thenceforward have the
credentials for the remote login.
- Finally, I should add that since implementing this scheme for the first time on 21 November, I have started exactly zero new ssh-agent processes, so I consider it a rousing success.
[Other articles in category /Unix] permanent link
Messages from the future
I read a pretty dumb article today about passwords that your future
self could use when communicating with you backwards in time, to
authenticate his identity to you. The idea was that you should make
up a password now and commit it to memory so that you can use it later
in case you need to communicate backwards in time.
This is completely unnecessary. You can wait until you have evidence of messages from the future before you do this.
Here's what you should do. If someone contacts you, claiming to be your future self, have them send you a copy of some document—the Declaration of Independence, for example, or just a letter of introduction from themselves to you, but really it doesn't need to be more than about a hundred characters long—encrypted with a one-time pad. The message, being encrypted, will appear to be complete gibberish.
Then pull a coin out of your pocket and start flipping it. Use the coin flips as the one-time pad to decrypt the message; record the pad as you obtain it from the coin.
Don't do the decryption all at once. Use several coins, in several different places, over a period of several weeks.
Don't even use coins. Say to yourself one day, on a whim, "I think I'll decrypt the next bit of the message by looking out the window and counting red cars that go by. If an odd number of red cars go by in the next minute, I'll take that as a head, and if an even number of red cars go by, I'll take that as a tail." Go to the museum and use their Geiger counter for the next few bits. Use the stock market listings for a few of the bits, and the results of the World Series for a couple.
If the message is not actually from your future self, the coin flips and other random bits you generate will not decrypt it, and you will get complete gibberish.
But if the coin flips and other random bits miraculously turn out to decrypt the message perfectly, you can be quite sure that you are dealing with a person from the future, because nobody else could possibly have predicted the random bits.
Now you need to make sure the person from the future is really you. Make up a secret password. Encrypt the one-time pad with a conventional secret-key method, using your secret password as the key. Save the encrypted pad in several safe places, so that you can get it later when you need it, and commit the password to memory. Destroy the unencrypted version of the pad. (Or just memorize the pad. It's not as hard as you think.)
Later, when the time comes to send a message into the past, go get the pad from wherever you stashed it and decrypt it with the secret key you committed to memory. This gives you a complete record of the results of the coin flips and other events that the past-you used to decrypt your message. You can then prepare your encrypted message accordingly.
[Other articles in category /CS] permanent link