Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 29 Aug 2018
On long road trips I spend a lot of time listening to music and even more time talking to myself. My recent road trip was longer than usual and I eventually grew tired of these amusements. I got the happy idea that I might listen to an audiobook, something I've never done before. Usually the thought of sitting and listening to someone droning out a book for 14 hours makes me want to dig my heart out with a spoon (“You say a word. Then I think for a long time. Then you say another word.”) but I had a long drive and I was not going anywhere anyway, so thought it might be a good way to pass the time.
The first thing I thought to try was Ann Leckie's Ancillary Justice, which everyone says is excellent, and which I had wanted to read. I was delighted to learn that I could listen to the first hour or so before paying anything, so I downloaded the sample.
It was intolerable. The voice actor they chose (Celeste Ciulla) was hilariously inappropriate, so much so that, had I not gotten the book from the most unimpeachable source, I would have suspected I was being pranked. Ancillary Justice is a hard-boiled military story in which the protagonist is some sort of world-weary slave or robot, or at least so I gather from the first half of the first chapter. Everything that appears in the first chapter is terrible: the people, the situation, the weather. It opens with these words:
The body lay naked and facedown, a deathly gray, spatters of blood staining the snow around it. It was minus fifteen degrees Celsius and a storm had passed just hours before.
But Ms. Ciulla's voice… there's nothing wrong with it, maybe — but for some other book. I can imagine listening to her reading What Katy Did or Eight Cousins or some other 19th-century girl story.
I found myself mockingly repeating Ciulla's pronunciation. And about twelve minutes in I gave up and turned it off. Here's a sample of that point. It ends with:
Is Ciulla even capable of growling? Unclear.
I figured that the book was probably good, and I was afraid Ciulla would ruin it for me permanently.
Spotify had a recording of Sir Christopher Lee reading Dr. Jekyll and Mr. Hyde, so I listened to that instead.
I think I could do a better job reading than most of the audiobook actors I sampled, and I might give it a try later. I think I might start with The 13 Clocks. Or maybe something by C.A. Stephens, which is in the public domain.
[Other articles in category /book] permanent link
Tue, 28 Aug 2018Yogi, accompanied by his constant companion Boo-Boo Bear, would often try to steal picnic baskets from campers in the park, much to the displeasure of Park Ranger Smith.

[Other articles in category /misc] permanent link
How quickly did dentists start trying to use X-rays?
I had dental x-rays today and I wondered how much time elapsed between the discovery of x-rays and their use by dentists.
About two weeks, it turns out. Roentgen's original publication was in late 1895. Dr. Otto Walkhoff made the first x-ray picture of teeth 14 days later. The exposure took 25 minutes.
Despite the long exposure time, dentists had already begun using x-rays in their practices in the next two years. Dr. William J. Morton presented the new technology to the New York Odontological Society in April 1896, and his dental radiography, depicting a molar with an artificial crown clearly visible, was published in a dental journal later that year.
Morton's subject had been a dried skull. The first dental x-ray of a living human in the United States was made by Charles Edmund Kells in April or May of 1896. In July at the annual meeting of the Southern Dental Association he presented a dental clinic in which he demonstrated the use of his x-ray equipment on live patients. The practice seems to have rapidly become routine.
The following story about Morton is not dental-related but I didn't want to leave it out:
In March 1896, strongman Eugene Sandow, considered the father of modern bodybuilding, turned to Morton in an effort to locate the source of a frustrating pain he was experiencing in his foot. Apparently Sandow had stepped on some broken glass, but even his personal physician could not specify the location of the glass in his foot. The potential for the x-ray must have seemed obvious, and Sandow reached out specifically to Morton to see if he could be of help. Morton was eager to oblige. He turned the x-rays on Sandow’s foot and located the shard of glass disturbing Sandow’s equanimity. A surgeon subsequently operated and removed the glass, and the story made national news.
(Daniel S. Goldberg, “The Early Days of the X-Ray”)
The first dental x-ray machine was manufactured in 1923 by Victor X-ray Company, which later became part of General Electric.
In preparing this article I was fortunate to have access to B. Martinez, In a New Light: Early X-Ray Technology in Dentistry, 1890–1955, Arizona State University, 2013.
[Other articles in category /tech] permanent link
Mon, 27 Aug 2018
Linear mappings of projective space
[ Epistemic status: uninformed musings; anything and everything in here might be wrong or ill-conceived. ]
Suppose !!V!! is some vector space, and let !!V_n!! be the family of all !!n!!-dimensional subspaces of !!V!!. In particular !!V_1!! is the family of all one-dimensional subspaces of !!V!!. When !!V!! is euclidean space, !!V_1!! is the corresponding projective space.
if !!L!! is a nonsingular linear mapping !!V\to V!!, then !!L!! induces a mapping !!L_n!! from !!V_n\to V_n!!. (It does not make sense to ask at this point if the induced mapping is linear because we do not have any obvious linear structure on the projective space. Or maybe there is but I have not heard of it.)
The eigenspaces of !!V!! are precisely the fixed points of !!L_n!!.
(Wrong! Any subspace generated by an !!n!!-set of eigenvectors is a fixed point of !!L_n!!. But such a subspace is not in general an eigenspace. (Note this includes the entire space as a special case.) The converse, however, does hold, since any eigenspace is generated by a subset of eigenvectors.)
Now it is an interesting and useful fact that for typical mappings, say from !!\Bbb R\to\Bbb R!!, fixed points tend to be attractors or repellers. (For example, see this earlier article.) This is true of !!L_1!! also. One-dimensional eigenspaces whose eigenvalues are larger than !!1!! are attractors of !!L_1!!, and those whose eigenvalues are smaller than !!1!! are repellers, and this is one reason why the eigenspaces are important: if !!L!! represents the evolution of state space, then vectors in !!V!! will tend to evolve toward being eigenvectors.
So consider, say, the projective plane !!\Bbb P^2!!, under the induced mapping of some linear operator on !!\Bbb R^3!!. There will be (typically) three special points in !!\Bbb P^2!! and other points will typically tend to gravitate towards one or more of these. Isn't this interesting? Is the three-dimensional situation more interesting than the two-dimensional one? What if a point attracts in one dimension and repels in the other? What can the orbits look like?
Or consider the Grassmanian space !!Gr(2, \Bbb R^3)!! of all planes in !!\Bbb R^3!!. Does a linear operator on !!\Bbb R^3!! tend to drive points in !!Gr(2, \Bbb R^3)!! toward three fixed points? (In general, I suppose !!Gr(k, \Bbb R^n)!! will have !!n\choose k!! fixed points, some of which might attract and some repel.) Is there any geometric intuition for this?
I have been wanting to think about Grassmanian spaces more for a long time now.
[Other articles in category /math] permanent link
Sat, 25 Aug 2018
A software archaeology screwup
This week I switched from using the konsole terminal program to using gnome-terminal,
because the former gets all sorts of font widths and heights wrong for
high-bit characters like ⇒ and ③, making it very difficult to edit
such text, and the latter, I discovered doesn't. Here's how konsole
displays the text ☆☆★★★ “Good” as I move the cursor rightwards
through it:


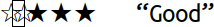
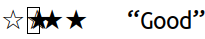
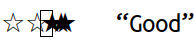




Uggggggh. Why did I put up with this bullshit for so long?
(I know, someone is going to write in and say the problem isn't in konsole,
it's in the settings for the KooKooFont 3.7.1 package, and I can
easily fix this by adding, removing, or adjusting the appropriate
directives in
/usr/share/config/fontk/config/fontulator-compat.d/04-spatulation,
and… I don't care, gnome-terminal works and konsole doesn't.)
So I switched terminals, but this introduced a new problem: konsole would
detect when a shell command had been run, and automatically retitle
the tab it was run in, until the command exited. I didn't realize until this
feature went away how much I had been depending on it to tell the tabs
apart. Under gnome-terminal all the tabs just said Terminal.
Reaching back into my memory, to a time even before there were tabs, I
recalled that there used to be a simple utility I could run on the
command line to set a terminal title. I did remember xsetname,
which sets the X window title, but I didn't want that in this
case. I looked around through the manual and my bin directory and
didn't find it, so I decided to write it fresh.
It's not hard. There's an escape sequence which, if received by the terminal, should cause it to retitle itself. If the terminal receives
ESC ] 0 ; pyrzqxgl \cG
it will change its title to pyrzqxgl. (Spaces in the display above
are for clarity only and should be ignored.)
It didn't take long to write the program:
#!/usr/bin/python3
from sys import argv, stderr
if len(argv) != 2:
print("Usage: title 'new title'", file=stderr)
exit(-2)
print("\033]0;{}\a".format(argv[1]), end="")
The only important part here is the last line. I named the program
title, installed it in ~/bin, and began using it
immediately.
A few minutes later I was looking for the tab that had an SSH session
to the machine plover.com, and since the title was still Terminal,
once I found it, I ran title plover, which worked. Then I stopped
and frowned. I had not yet copied the program to Plover. What just
happened?
Plover already had a ~/bin/title that I wrote no less than
14½ years ago:
-rwxr-xr-x 1 mjd mjd 138 Feb 11 2004 /home/mjd/bin/title
Here it is:
#!/usr/bin/perl
my $title = join " ", @ARGV;
$title = qx{hostname -s || hostname} if $title eq "";
chomp $title;
print "\e]0;$title\cG";
Why didn't I find that before I wrote the other one?
The old program is better-written too. Instead of wasting code to print a usage message if I didn't use it right, I had spent that code in having it do something useful instead.
This is not the first time I have done something like this.
Oh well, at least I can reacquire the better UI now that I know about it.
[ Addendum 20220127: I did it again ]
[Other articles in category /oops] permanent link
Thu, 23 Aug 2018
Frank Baum's uncomfortable relationship with Oz
L. Frank Baum's The Wonderful Wizard of Oz was a runaway success, and he wrote thirteen sequels. It's clear that he didn't want to write 13 more Oz books. He wanted to write fantasy adventure generally. And he did pretty well at this. His non-Oz books like Zixi of Ix and John Dough and the Cherub are considerably above average, but were not as commercially successful.
In the sequel to The Wonderful Wizard, titled The Marvelous Land of Oz, he brought back the Scarecrow, the Tin Woodman, and Glinda, with the other characters being new. But the fans demanded Dorothy (who returned in every book thereafter) and the Wizard (from book 4 onward).
Book 3, Ozma of Oz, is excellent, definitely my favorite. It introduces the malevolent Nome King, whom Baum seems to have loved, as he returned over and over. Ozma of Oz has a superb plot with building dramatic tension involving a frightening magical competition. But by the fourth book, Dorothy and the Wizard in Oz, Baum had gone too many times to the well. The new characters (a workhorse, a farmhand, and a pink kitten) are forgettable and forgotten. There is no plot, just visits to a series of peculiar locations, terminating in the characters’ arrival in Oz. Steve Parker, whose summary review of the Oz books has stuck with me for many years, said:
The Oz books fall into two categories: Icky-cute twee travelogues (characters go from icky-cute place to icky-cute place. Nothing happens) and darned good stories (key feature: they have conflict).
Signs of this are already in The Wonderful Wizard itself. The original book is roughly in three phases: Dorothy and her associates journey to the Emerald City, where they confront the Wizard. The Wizard demands that they destroy the Wicked Witch of the West, which they do, but then abandons Dorothy. And then there is a third part in which they travel south to ask Glinda to help send Dorothy home.
In the 1939 MGM movie, which otherwise sticks closely to the plot of the book, the third part was omitted entirely. Glinda arrives immediately after the Wizard absconds and wraps up the story. As a small child I was incensed by this omission. But if I were making a movie of The Wizard of Oz I would do exactly the same. The third part of the book is superfluous. The four companions visit a country where everyone is a decorative china figure (nothing happens), a forest where the trees refuse to admit them (the Woodman chops them), another forest where the denizens are being terrorized by a monster (the Lion kills the monster), and a hill guarded by surly armless men whose heads fly off like corks from popguns (they fly over). Having bypassed these obstacles, they arrive at Glinda's palace and the story can get moving again.
But it isn't until Dorothy and the Wizard in Oz that the “twee travelogue” mode really gets going, and it continues in the fifth book, The Road to Oz.
By the sixth book, The Emerald City of Oz, it was clear that Baum was sick of the whole thing. The story is in two parts that alternate chapters. In one set of chapters, Dorothy and her uncle and aunt go on a pointless carriage tour of twee locations in Oz, completely unaware that in the intervening chapters, the wicked General Guph is gathering armies of malevolent beings to tunnel under the desert, destroy Oz, and enslave the Oz people. These chapters with Guph are really good, some of the best writing Baum ever did. Guph is easily the most interesting person in the book and Baum is certainly more interested in him than in Dorothy's visit to the town where everything is made of biscuits, the town where everything is made of paper, the town where everyone is made of jigsaw puzzles, and the town where everyone is a rabbit. But Baum couldn't really go through with his plan to destroy Oz. At the end of the book Guph's plan is foiled.
Baum nevertheless tried to throw Holmes down Reichenbach Falls. Glinda casts a powerful magic spell to seal off Oz from the rest of the world entirely:
The writer of these Oz stories has received a little note from Princess Dorothy of Oz which, for a time, has made him feel rather discontented. The note was written on a broad white feather from a stork's wing, and it said:
You will never hear anything more about Oz, because we are now cut off forever from all the rest of the world. But Toto and I will always love you and all the other children who love us.
DOROTHY GALE.
But as for Conan Doyle, it didn't work. The public demanded more, and just as Holmes came back from the grave, so did Oz. After a delay of three years, the seventh book, The Patchwork Girl of Oz, appeared. By this time Baum had had an inspiration. This book is the sort of magical fantasy he wanted to write. People only wanted to read about Oz, so Baum has set it in the Oz continuity. Ojo and his uncle supposedly live in the Munchkin country, but must flee their home in search of food, despite the fact that nobody in Oz ever has to do that. They visit the magician Dr. Pipt. He is is stated to be the same as the anonymous one mentioned in passing in The Marvelous Land of Oz, but this is not a plot point. Until the second half there is no significant connection to the rest of the series. The characters are all new (the Patchwork Girl, the Glass Cat, and the Woozy) and go on a quest to restore Ojo's uncle, who has been accidentally turned to stone. (Dorothy and other familiar characters do eventually join the proceedings.)
Baum apparently felt this was an acceptable compromise, because he repeatedly used this tactic of grafting Oz bits onto an otherwise unrelated fantasy adventure. The following book, Tik-Tok of Oz, takes the pattern quite far. Its main characters are Queen Ann and her subjects. Ann is Queen of Oogaboo, which is part of Oz, except, ha ha, fooled you, it isn't:
Away up in the mountains, in a far corner of the beautiful fairyland of Oz, lies a small valley which is named Oogaboo … the simple folk of Oogaboo never visited Ozma.
Oogaboo is separated from the rest of Oz by a mountain pass, and when Ann and her army try to reach Oz through this pass, it is magically twisted around by Glinda (who does not otherwise appear in the book) and they come out somewhere else entirely. A variety of other characters join them, including Polychrome and the Shaggy Man (from the awful Road to Oz), and Tik-Tok (from Ozma) and they struggle with the perennially villainous Nome King, of whom Baum seemingly never tired. But there is no other connection to Oz until the plot has been completely wrapped up, around the end of chapter 23. Then Ozma and Dorothy appear from nowhere and bring everyone to Oz for two unbearably sentimental final chapters.
The ninth book, The Scarecrow of Oz, often cited as the best of the series, follows exactly the same pattern. The main characters of this one are Trot, Cap'n Bill, and the Ork, who had appeared before in two of Baum's non-Oz novels, which did not sell well. No problem, Baum can bring them to Oz, where they may find more popularity among readers. So he has them find their way to Oogaboo. Excuse me, to Jinxland.
“I'm sorry to say that Jinxland is separated from the rest of the Quadling Country by that row of high mountains you see yonder, which have such steep sides that no one can cross them. So we live here all by ourselves, and are ruled by our own King, instead of by Ozma of Oz.”
The main plot takes place entirely in Jinxland, and concerns the struggles of Pon, the gardener's boy, to marry the Princess Gloria against the wishes of King Krewl. The Scarecrow is dispatched to Jinxland to assist, but none of the other Oz people plays an important part, and once the plot is wrapped up in chapter 20 Ozma and Dorothy arrange to bring everyone back to the Emerald City for a party at which Baum drops the names of all the characters who did not otherwise appear in the book.
The excellent tenth book, Rinkitink in Oz, repeats the pattern. In fact, Rinkitink was written much earlier, around 1907, but Baum couldn't get it published. So in 1916 he appended a couple of chapters in which Dorothy and the Wizard appear from nowhere to resolve the plot, and then in chapter 22 Ozma brings everyone back to the Emerald City for a party at which Baum drops the names of all the characters who did not otherwise appear in the book.
Well, you get the idea. The last few books are pretty good when they are in the "not really Oz but let's say it is" mode of The Scarecrow or Rinkitink, and pretty awful when they are in "twee travelogue" mode of The Road to Oz:
The Lost Princess of Oz has a good plot with a new set of characters from Oogaboo (excuse me — I mean from the Yip Country) searching for a stolen magical dishpan, and a travelogue plot with Dorothy etc. searching for Ozma. The characters meet up at the end and defeat the evil shoemaker who has stolen both, and Baum recycles his “the enchanted person was in the little boy's pocket the whole time” trope from Ozma of Oz. Probably they all go back to the Emerald City for a name-dropping party, but I forget.
The Tin Woodman of Oz, generally considered one of the worst of the books, is almost entirely travelogue. There are no new characters of note.
The Magic of Oz sees the return (again!) of the Nome King and a new scheme to destroy Oz. Again, it takes place in Oogaboo. Excuse me, in Gugu Forest:
In the central western part of the Gillikin Country is a great tangle of trees called Gugu Forest … home of most of the wild beasts that inhabit Oz. These are seldom disturbed in their leafy haunts because there is no reason why Oz people should go there, except on rare occasions, and most parts of the forest have never been seen by any eyes but the eyes of the beasts who make their home there.
Dorothy and the Wizard do play an important part. The plot is wrapped up with the same device as in The Emerald City.
Oh, and the book ends with a literal birthday party at which the omitted characters are mentioned by name.
Glinda of Oz, like the several that precede it, takes place in Oogaboo, this time called the Skeezer country. Ozma says:
The Skeezer Country is 'way at the upper edge of the Gillikin Country, with the sandy, impassable desert on one side and the mountains of Oogaboo on another side. That is a part of the Land of Oz of which I know very little.
Glinda, Dorothy, Ozma, and the Wizard do appear, but spend much of the book trapped in the underwater city of the Skeezers. Meanwhile the interesting part of the story concerns Ervic, a Skeezer who schemes and dissembles in order to persuade a recalcitrant witch to disenchant three Adepts of Magic who have been transformed into fish. For variety, the scene with every previous character sitting around a table is at the beginning instead of at the end.
Glinda was published posthumously, and Baum, who had died in 1919, was free of Oz at last.
[Other articles in category /book] permanent link
Mon, 20 Aug 2018
Miscellaneous addenda about Catholic priest sex abuse
I hope and expect this will be my last post on this loathsome subject.
Diocesan vs. religious priests
In the previous article, I said:
let us say that there are currently around 1620 priests total in the other six dioceses. (This seems on the high side, since my hand-count of Pittsburgh priests contains only about 200. I don't know what to make of this.)
Later I added a guess about why:
I wonder if it is because my hand counts, taken from diocesan directory pages, include only diocesan priests, where the total of 2500 also includes the religious priests. I should look into this.
I think this is probably correct. The list of Pittsburgh priests has a section at the bottom headed “Religious Priests Serving in the Diocese”, but it is empty.
Kennedy's Catholic Directory
While attempting to get better estimates for the total number of active priests, I located part of The Official Catholic Directory of P.J. Kennedy & Sons for the year 1980, available on the Internet Archive. It appears that this is only one volume of many, and unfortunately IA does not seem to have the others. Luckily, though, this happens to be the volume that includes information for Philadelphia, Pittsburgh, and Scranton. It reports:
| Philadelphia | Pittsburgh | Scranton | |
|---|---|---|---|
| (p. 695) | (p. 715) | (p. 892) | |
| Priests: diocesian active in diocese | 831 | 547 | 374 |
| Priests: active outside diocese | 33 | 29 | 13 |
| Priests: retired, sick or absent: | 121 | 60 | 52 |
| Diocesan Priests in foreign missions | 2 | 2 | 26 |
| Religious Priests resident in diocese | 553 | 243 | 107 |
| Religious Priests from diocese in foreign missions: | 93 | 78 | 26 |
| Total Priests in Diocese | 1631 | 957 | 572 |
I have no idea how authoritative this is, or what is the precise meaning of “official” in the title. The front matter would probably explain, but it does not appear in the one volume I have. The cover also advises “Important: see explanatory notes, pp. vi–viii”, which I have not seen.
The Directory also includes information for the Ukrainian Catholic Archepathy of Philadelphia, which, being part of a separate (but still Catholic) church is separate from the Philadelphia Roman Catholic dioceses. (It reports 127 total priests.) It's not clear whether to absorb this into my estimate because I'm not sure if it was part of the total number I got from the Pennsylvania Catholic Conference.
But I am not going back to check because I feel there is no point in trying to push on in this way. An authoritative and accurate answer is available from the official census, and my next step, should I care to take one, should be to go to the library and look at it, rather than continuing to pile up inaccurate guesses based on incomplete information.
Sipe's earlier estimate
Jonathan Segal points out that A.W. Richard Sipe, a famous expert on clergy sexual abuse, had estimated in 1990 that about 6% of U.S. priests has sexually abused children. This is close to my own estimate of 6.1% for the six Pennsylvania dioceses. Most of this agreement should be ascribed to luck.
Final remark
In 1992, Sinéad O'Connor became infamous for protesting systematic Catholic sex abuse by tearing up a photograph of John Paul II on live American television. She was almost universally condemned. (The Wikipedia article has a few of the details.)
This week, America: The Jesuit Review, which claims to be “the leading Catholic journal of opinion in the United States”, reported:
Pope Francis issued a letter to Catholics around the world Monday condemning the "crime" of priestly sexual abuse and its cover-up and demanding accountability…
The Vatican issued the three-page letter ahead of Francis' trip this weekend to Ireland, a once staunchly Roman Catholic country where the church's credibility has been damaged by years of revelations that priests raped and molested children with impunity and their superiors covered up for them.
(“Pope Francis issues new letter on sex abuse: ‘We showed no care for the little ones’”.)
A lot of people owe Sinéad O'Connor a humble apology.
[ Update 20230726: Sinéad O'Connor has died, probably without having received an apology from most of those people. ]
[Other articles in category /religion] permanent link
Fri, 17 Aug 2018
What fraction of Pennsylvania Catholic priests were child molesters?
The grand jury report on Catholic clergy sexual abuse has been released and I have been poring over it. The great majority of it is details about the church's handling of the 301 “predator priests” that the grand jury identified.
I have seen several places the suggestion that this is one-third of a total of 900. This is certainly not the case. There may be 900 priests there now, but the report covers all the abuse that the grand jury found in examining official records from the past seventy years or so. Taking a random example, pages 367–368 of the report concern the Reverend J. Pascal Sabas, who abused a 14-year-old boy starting in 1964. Sabas was ordained in 1954 and died in 1996.
I tried to get a good estimate of the total number of priests over the period covered by the report. Information was rather sketchy. The Vatican does do an annual census of priests, the Annuarium Statisticum Ecclesiae, but I could not find it online and hardcopies sell for around €48. Summary information by continent is reported elsewhere [2], but the census unfortunately aggregates North and South America as a single continent. I did not think it reasonable to try to extrapolate from the aggregate to the number of priests in the U.S. alone, much less to Pennsylvania.
Still we might get a very rough estimate as follows. The Pennsylvania Catholic Conference says that there were a total of just about 2500 priests in Pennsylvania in 2017 or 2016. The Philadelphia Archdiocese and the Altoona-Johnstown Diocese are not discussed in the grand jury report, having been the subject of previous investigations. The official websites of these two dioceses contain lists of priests and I counted 792 in the Philadelphia directory and 80 in the Altoona-Johnstown directory, so let us say that there are currently around 1620 priests total in the other six dioceses. (This seems on the high side, since my hand-count of Pittsburgh priests contains only about 200. I don't know what to make of this.)
[ Addendum 20180820: I wonder if it is because my hand counts, taken from diocesan directory pages, include only diocesan priests, where the total of 2500 also includes the religious priests. I should look into this. ]
Suppose that in 1950 there were somewhat more, say 2160. The average age of ordination is around 35 years; say that a typical priestly career lasts around 40 years further. So say that each decade, around one-quarter of the priesthood retires. If around 84% of the retirees are replaced, the replacement brings the total number back up to 96% of its previous level, so that after 70 years about 75% remain. Then the annual populations might be approximately:
$$\begin{array}{rrrrr} \text{year} & \text{total population} & \text{retirements} & \text{new arrivals} & \\ 1950 & 2160 & 540 & 453 \\ 1960 & 2073 & 518 & 434 \\ 1970 & 1989 & 497 & 417 \\ 1980 & 1909 & 477 & 400 \\ 1990 & 1832 & 458 & 384 \\ 2000 & 1758 & 439 & 368 \\ 2010 & 1687 & 421 & 354 \\ \hline \text{(total)} & & 3350 & 2810 \\ \end{array}$$
From the guesses above we might estimate a total number of individual priests serving between 1950 and 2018 as !!2160 + 2810 - 70 = 4900!!. (That's 2160 priests who were active in 1950, plus 2810 new arrivals since then, except minus !!354\cdot20\% \approx 70!! because it's only 2018 and 20% of the new arrivals for 2010–2020 haven't happened yet.)
So the 301 predator priests don't represent one-third of the population, they probably represent “only” around !!\frac{301}{4900} \approx 6.1\%!!.
The church's offical response is availble.
[ Addenda: An earlier version of this article estimated around 900 current priests instead of 1620; I believe that this was substantially too low. Also, that earlier version incorrectly assumed that ordinations equalled new priests, which is certainly untrue, since ordained priests can and do arrive in Pennsylvania from elsewhere. ]
[ Addendum 20180820: Some followup notes. ]
[Other articles in category /religion] permanent link
Tue, 14 Aug 2018A few years ago Katara was very puzzled by traffic jams and any time we were in a traffic slowdown she would ask questions about it. For example, why is traffic still moving, and why does your car eventually get through even though the traffic jam is still there? Why do they persist even after the original cause is repaired? But she seemed unsatisfied with my answers. Eventually in a flash of inspiration I improvised the following example, which seemed to satisfy her, and I still think it's a good explanation.
Suppose you have a four-lane highway where each lane can carry up to 25 cars per minute. Right now only 80 cars per minute are going by so the road is well under capacity.
But then there is a collision or some other problem that blocks one of the lanes. Now only three lanes are open and they have a capacity of 75 cars per minute. 80 cars per minute are arriving, but only 75 per minute can get past the blockage. What happens now? Five cars more are arriving every minute than can leave, and they will accumulate at the blocked point. After two hours, 600 cars have piled up.
But it's not always the same 600 cars! 75 cars per minute are still leaving from the front of the traffic jam. But as they do, 80 cars have arrived at the back to replace them. If you are at the back, there are 600 cars in front of you waiting to leave. After a minute, the 75 at the front have left and there are only 525 cars in front of you; meanwhile 80 more cars have joined the line. After 8 minutes all the cars in front of you have left and you are at the front and can move on. Meanwhile, the traffic jam has gotten bigger.
Suppose that after two hours the blockage is cleared. The road again has a capacity of 100 cars per minute. But cars are still arriving at 80 per minute, so each minute 20 more cars can leave than arrived. There are 600 waiting, so it takes another 30 minutes for the entire traffic jam to disperse.
This leaves out some important second-order (and third-order) effects. For example, traffic travels more slowly on congested roads; maximum safe speed decreases with following distance. But as a first explanation I think it really nails the phenomenon.
[Other articles in category /tech] permanent link
Wed, 08 Aug 2018In my original article, I said:
I was fairly confident I had seen something like this somewhere before, and that it was not original to me.
Jeremy Yallop brought up an example that I had definitely seen before.
In 2008 Conor McBride and Ross Paterson wrote an influential paper, “Idioms: applicative programming with effects” that introduced the idea of an applicative functor, a sort of intermediate point between functors and monads. It has since made its way into standard Haskell and was deemed sufficiently important to be worth breaking backward compatibility.
McBride and Paterson used several notations for operations in an
applicative functor. Their primary notation was !!\iota!! for what is
now known as pure and !!\circledast!! for what has since come to be written
as <*>. But the construction
$$\iota f \circledast is_1 \circledast \ldots \circledast is_n$$
came up so often they wanted a less cluttered notation for it:
We therefore find it convenient, at least within this paper, to write this form using a special notation
$$ [\![ f is_1 \ldots is_n ]\!] $$
The brackets indicate a shift into an idiom where a pure function is applied to a sequence of computations. Our intention is to provide a sufficient indication that effects are present without compromising the readability of the code.
On page 5, they suggested an exercise:
… show how to replace !![\![!! and !!]\!]!! by identifiers
iIandIiwhose computational behaviour delivers the above expansion.
They give a hint, intended to lead the reader to the solution, which
involves a function named iI that does some legerdemain on the front
end and then a singleton type data Ii = Ii that terminates the legerdemain on
the back end. The upshot is that one can write
iI f x y Ii
and have it mean
(pure f) <*> x <*> y
The haskell wiki has details, written by Don Stewart when the McBride-Paterson paper was still in preprint. The wiki goes somewhat further, also defining
data J = J
so that
iI f x y J z Ii
now does a join on the result of f x y before applying the result
to z.
I have certainly read this paper more than once, and I was groping for this example while I was writing the original article, but I couldn't quite put my finger on it. Thank you, M. Yallop!
[ By the way, I am a little bit disappointed that the haskell wiki is not called “Hicki”. ]
[Other articles in category /prog/haskell] permanent link
In the previous article I described a rather odd abuse of the Haskell type system to use a singleton type as a sort of pseudo-keyword, and asked if anyone had seen this done elsewhere.
Joachim Breitner reported having seen this before. Most recently in
LiquidHaskell, which defines a QED singleton
type:
data QED = QED
infixl 2 ***
(***) :: a -> QED -> Proof
_ *** _ = ()
so that they can end every proof with *** QED:
singletonP x
= reverse [x]
==. reverse [] ++ [x]
==. [] ++ [x]
==. [x]
*** QED
This example is from Vazou et al., Functional Pearl: Theorem Proving
for All, p. 3. The authors
explain: “The QED argument serves a purely aesthetic purpose,
allowing us to conclude proofs with *** QED.”.
Or see the examples from the bottom of the LH splash
page, proving the
associative law for ++.
I looked in the rest of the LiquidHaskell distribution but did not find any other uses of the singleton-type trick. I would still be interested to see more examples.
[ Addendum: Another example. ]
[Other articles in category /prog/haskell] permanent link
Is this weird Haskell technique something I made up?
A friend asked me the other day about techniques in Haskell to pretend
to make up keywords. For example, suppose we want something like a
(monadic) while loop, say like this:
while cond act =
cond >>= \b -> if b then act >> while cond act
else return ()
This uses a condition cond (which might be stateful or
exception-throwing or whatever, but which must yield a boolean value)
and an action act (likewise, but its value is ignored) and it
repeates the action over and over until the condition is false.
Now suppose for whatever reason we don't like writing it as while
condition action and we want instead to write while condition do
action or something of that sort. (This is a maximally simple
example, but the point should be clear even though it is silly.) My
first suggestion was somewhat gross:
while c _ a = ...
Now we can write
while condition "do" action
and the "do" will be ignored. Unfortunately we can also write
while condition "wombat" action and you know how programmers are
when you give them enough rope.
But then I had a surprising idea. We can define it this way:
data Do = Do
while c Do a = ...
Now we write
while condition
Do action
and if we omit or misspell the Do we get a compile-time type error
that is not even too obscure.
For a less trivial (but perhaps sillier) example, consider:
data Exception a = OK a | Exception String
instance Monad Exception where ...
data Catch = Catch
data OnSuccess = OnSuccess
data AndThen = AndThen
try computation Catch handler OnSuccess success AndThen continuation =
case computation of OK a -> success >> (OK a) >>= continuation
Exception e -> (handler e) >>= continuation
The idea here is that we want to try a computation, and do one thing
if it succeeds and another if it throws an exception. The point is
not the usefulness of this particular and somewhat contrived exception
handling construct, it's the syntactic sugar of the Catch,
OnSuccess, and AndThen:
try (evaluate some_expression)
Catch (\error -> case error of "Divison by zero" -> ...
... )
OnSuccess ...
AndThen ...
I was fairly confident I had seen something like this somewhere before, and that it was not original to me. But I've asked several Haskell experts and nobody has said it was familar. I thought perhaps I had seen it somewhere in Brent Yorgey's code, but he vehemently denied it.
So my question is, did I make up this technique of using a one-element type as a pretend keyword?
[ Addendum: At least one example of this trick appears in LiquidHaskell. I would be interested to hear about other places it has been used. ]
[ Addendum: Jeremy Yallop points out that a similar trick was hinted at in McBride and Paterson “Idioms: applicative programming with effects” (2008), with which I am familiar, although their trick is both more useful and more complex. So this might have been what I was thinking of. ]
[Other articles in category /prog/haskell] permanent link
Thu, 02 Aug 2018
How to explain infinity to kids
A professor of mine once said to me that all teaching was a process of lying, and then of replacing the lies with successively better approximations of the truth. “I say it's like this,” he said, “and then later I say, well, it's not actually like that, it's more like this, because the real story is too complicated to explain all at once.” I wouldn't have phrased it like this, but I agree with him in principle. One of the most important issues in pedagogical practice is deciding what to leave out, and for how long.
Kids inevitably want to ask about numerical infinity, and many adults will fumble the question, mumbling out some vague or mystical blather. Mathematics is prepared to offer a coherent and carefully-considered answer. Unfortunately, many mathematically-trained people also fumble the question, because mathematics is prepared to offer too many answers. So the mathematical adult will often say something like “well, it's a lot of things…” which for this purpose is exactly not what is wanted. When explaining the concept for the very first time, it is better to give a clear and accurate partial explanation than a vague and imprecise overview. This article suggests an answer that is short, to the point, and also technically correct.
In mathematics “infinity” names a whole collection of not always closely related concepts from analysis, geometry, and set theory. Some of the concepts that come under this heading are:
The !!+\infty!! and !!-\infty!! one meets in real analysis, which can be seen either as a convenient fiction (with “as !!x!! goes to infinity” being only a conventional rephrasing of “as !!x!! increases without bound”) or as the endpoints in the two-point compactification of !!\Bbb R!!.
The !!\infty!! one meets in complex analysis, which is a single point one adds to compactify the complex plane into the Riemann sphere.
The real version of the preceding, the “point at infinity” on the real projective line.
The entire “line at infinity” that bounds the real projective plane.
The vast family of set-theoretic infinite cardinals !!\aleph_0, \aleph_1, \ldots!!.
The vast family of set-theoretic infinite ordinals, !!\omega, \omega+1, \ldots, \epsilon_0, \ldots, \Omega, \ldots!!.
I made a decision ahead of time that when my kids first asked what infinity was, I would at first adopt the stance that “infinity” referred specifically to the set-theoretic ordinal !!\omega!!, and that the two terms were interchangeable. I could provide more details later on. But my first answer to “what is infinity” was:
It's the smallest number you can't count to.
As an explanation of !!\omega!! for kids, I think this is flawless. It's brief and it's understandable. It phrases the idea in familiar terms: counting. And it is technically unimpeachable. !!\omega!! is, in fact, precisely the unique smallest number you can't count to.
How can there be a number that you can't count to? Kids who ask about infinity are already quite familiar with the idea that the sequence of natural numbers is unending, and that they can count on and on without bound. “Imagine taking all the numbers that you could reach by counting,” I said. “Then add one more, after all of them. That is infinity.” This is a bit mind-boggling, but again it is technically unimpeachable, and the mind-bogglyness of it is nothing more than the intrinsic mind-bogglyness of the concept of infinity itself. None has been added by vagueness or imprecise metaphor. When you grapple with this notion, you are grappling with the essence of the problem of the completed infinity.

In my experience all kids make the same move at this point, which is to ask “what comes after infinity?” By taking “infinity” to mean !!\omega!!, we set ourselves up for an answer that is much better than the perplexing usual one “nothing comes after infinity”, which, if infinity is to be considered a number, is simply false. Instead we can decisively say that there is another number after infinity, which is called “infinity plus one”. This suggests further questions. “What comes after infinity plus one?” is obvious, but a bright kid will infer the existence of !!\omega\cdot 2!!. A different bright kid might ask about !!\omega-1!!, which opens a different but fruitful line of discussion: !!\omega!! is not a successor ordinal, it is a limit ordinal.
Or the kid might ask if infinity plus one isn't equal to infinity, in which case you can discuss the non-commutativity of ordinal addition: if you add the “plus one” at the beginning, it is the same (except for !!\omega!! itself, the picture has just been shifted over on the page):

But if you add the new item at the other end, it is a different picture:

Before there was only one extra item on the right, and now there are two. The first picture exemplifies the Dedekind property, which is an essential feature of infinity. But the existence of an injection from !!\omega+1!! to !!\omega!! does not mean that every such map is injective.
Just use !!\omega!!. Later on the kid may ask questions that will need to be answered with “Earlier, I did not tell you the whole story.” That is all right. At that point you can reveal the next thing.
[ Addendum 20220226: Joel D. Hamkins wrote a Math Stack Exchange post in which he made the same suggestion: “In my experience with children, one of the easiest-to-grasp concepts of infinity is provided by the transfinite ordinals…”. ]
[Other articles in category /math] permanent link



