Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 23 Jul 2014
When do n and 2n have the same digits?
[This article was published last month on the math.stackexchange blog, which seems to have died young, despite many earnest-sounding promises beforehand from people who claimed they would contribute material. I am repatriating it here.]
A recent question on math.stackexchange asks for the smallest positive integer !!A!! for which the number !!2A!! has the same decimal digits in some other order.
Math geeks may immediately realize that !!142857!! has this property, because it is the first 6 digits of the decimal expansion of !!\frac 17!!, and the cyclic behavior of the decimal expansion of !!\frac n7!! is well-known. But is this the minimal solution? It is not. Brute-force enumeration of the solutions quickly reveals that there are 12 solutions of 6 digits each, all permutations of !!142857!!, and that larger solutions, such as 1025874 and 1257489 seem to follow a similar pattern. What is happening here?
Stuck in Dallas-Fort Worth airport one weekend, I did some work on the problem, and although I wasn't able to solve it completely, I made significant progress. I found a method that allows one to hand-calculate that there is no solution with fewer than six digits, and to enumerate all the solutions with 6 digits, including the minimal one. I found an explanation for the surprising behavior that solutions tend to be permutations of one another. The short form of the explanation is that there are fairly strict conditions on which sets of digits can appear in a solution of the problem. But once the set of digits is chosen, the conditions on that order of the digits in the solution are fairly lax.
So one typically sees, not only in base 10 but in other bases, that the solutions to this problem fall into a few classes that are all permutations of one another; this is exactly what happens in base 10 where all the 6-digit solutions are permutations of !!124578!!. As the number of digits is allowed to increase, the strict first set of conditions relaxes a little, and other digit groups appear as solutions.
Notation
The property of interest, !!P_R(A)!!, is that the numbers !!A!! and !!B=2A!! have exactly the same base-!!R!! digits. We would like to find numbers !!A!! having property !!P_R!! for various !!R!!, and we are most interested in !!R=10!!. Suppose !!A!! is an !!n!!-digit numeral having property !!P_R!!; let the (base-!!R!!) digits of !!A!! be !!a_{n-1}\ldots a_1a_0!! and similarly the digits of !!B = 2A!! are !!b_{n-1}\ldots b_1b_0!!. The reader is encouraged to keep in mind the simple example of !!R=8, n=4, A=\mathtt{1042}, B=\mathtt{2104}!! which we will bring up from time to time.
Since the digits of !!B!! and !!A!! are the same, in a different order, we may say that !!b_i = a_{P(i)}!! for some permutation !!P!!. In general !!P!! might have more than one cycle, but we will suppose that !!P!! is a single cycle. All the following discussion of !!P!! will apply to the individual cycles of !!P!! in the case that !!P!! is a product of two or more cycles. For our example of !!a=\mathtt{1042}, b=\mathtt{2104}!!, we have !!P = (0\,1\,2\,3)!! in cycle notation. We won't need to worry about the details of !!P!!, except to note that !!i, P(i), P(P(i)), \ldots, P^{n-1}(i)!! completely exhaust the indices !!0. \ldots n-1!!, and that !!P^n(i) = i!! because !!P!! is an !!n!!-cycle.
Conditions on the set of digits in a solution
For each !!i!! we have $$a_{P(i)} = b_{i} \equiv 2a_{i} + c_i\pmod R $$ where the ‘carry bit’ !!c_i!! is either 0 or 1 and depends on whether there was a carry when doubling !!a_{i-1}!!. (When !!i=0!! we are in the rightmost position and there is never a carry, so !!c_0= 0!!.) We can then write:
$$\begin{align} a_{P(P(i))} &= 2a_{P(i)} + c_{P(i)} \\ &= 2(2a_{i} + c_i) + c_{P(i)} &&= 4a_i + 2c_i + c_{P(i)}\\ a_{P(P(P(i)))} &= 2(4a_i + 2c_i + c_{P(P(i)})) + c_{P(i)} &&= 8a_i + 4c_i + 2c_{P(i)} + c_{P(P(i))}\\ &&&\vdots\\ a_{P^n(i)} &&&= 2^na_i + v \end{align} $$
all equations taken !!\bmod R!!. But since !!P!! is an !!n!!-cycle, !!P^n(i) = i!!, so we have $$a_i \equiv 2^na_i + v\pmod R$$ or equivalently $$\big(2^n-1\big)a_i + v \equiv 0\pmod R\tag{$\star$}$$ where !!v\in\{0,\ldots 2^n-1\}!! depends only on the values of the carry bits !!c_i!!—the !!c_i!! are precisely the binary digits of !!v!!.
Specifying a particular value of !!a_0!! and !!v!! that satisfy this equation completely determines all the !!a_i!!. For example, !!a_0 = 2, v = \color{darkblue}{0010}_2 = 2!! is a solution when !!R=8, n=4!! because !!\bigl(2^4-1\bigr)\cdot2 + 2\equiv 0\pmod 8!!, and this solution allows us to compute
$$\def\db#1{\color{darkblue}{#1}}\begin{align} a_0&&&=2\\ a_{P(0)} &= 2a_0 &+ \db0 &= 4\\ a_{P^2(0)} &= 2a_{P(0)} &+ \db0 &= 0 \\ a_{P^3(0)} &= 2a_{P^2(0)} &+ \db1 &= 1\\ \hline a_{P^4(0)} &= 2a_{P^3(0)} &+ \db0 &= 2\\ \end{align}$$
where the carry bits !!c_i = \langle 0,0,1,0\rangle!! are visible in the third column, and all the sums are taken !!\pmod 8!!. Note that !!a_{P^n(0)} = a_0!! as promised. This derivation of the entire set of !!a_i!! from a single one plus a choice of !!v!! is crucial, so let's see one more example. Let's consider !!R=10, n=3!!. Then we want to choose !!a_0!! and !!v!! so that !!\left(2^3-1\right)a_0 + v \equiv 0\pmod{10}!! where !!v\in\{0\ldots 7\}!!. One possible solution is !!a_0 = 5, v=\color{darkblue}{101}_2 = 5!!. Then we can derive the other !!a_i!! as follows:
$$\begin{align} a_0&&&=5\\ a_{P(0)} &= 2a_0 &+ \db1 &= 1\\ a_{P^2(0)} &= 2a_{P(0)} &+ \db0 &= 2 \\\hline a_{P^3(0)} &= 2a_{P^2(0)} &+ \db1 &= 5\\ \end{align}$$
And again we have !!a_{P^n(0)}= a_0!! as required.
Since the bits of !!v!! are used cyclically, not every pair of !!\langle a_0, v\rangle!! will yield a different solution. Rotating the bits of !!v!! and pairing them with different choices of !!a_0!! will yield the same cycle of digits starting from a different place. In the first example above, we had !!a_0 = 2, v = 0010_2 = 2!!. If we were to take !!a_0 = 4, v = 0100_2 = 4!! (which also solves !!(\star)!!) we would get the same cycle of values of the !! a\_i !! but starting from !!4!! instead of from !!2!!, and similarly if we take !!a_0=0, v = 1000_2 = 8!! or !!a_0 = 1, v = 0001_2!!. So we can narrow down the solution set of !!(\star)!! by considering only the so-called necklaces of !!v!! rather than all !!2^n!! possible values. Two values of !!v!! are considered equivalent as necklaces if one is a rotation of the other. When a set of !!v!!-values are equivalent as necklaces, we need only consider one of them; the others will give the same cyclic sequence of digits, but starting in a different place. For !!n=4!!, for example, the necklaces are !!0000, 0001, 0011, 0101, 0111, !! and !!1111!!; the sequences !!0110, 1100,!! and !!1001!! being equivalent to !!0011!!, and so on.
Example
Let us take !!R=9, n=3!!, so we want to find 3-digit numerals with property !!P_9!!. According to !!(\star)!! we need !!7a_i + v \equiv 0\pmod{9}!! where !!v\in\{0\ldots 7\}!!. There are 9 possible values for !!a_i!!; for each one there is at most one possible value of !!v!! that makes the sum zero:
$$\begin{array}{rrr} a_i & 7a_i & v \\ \hline 0 & 0 & 0 \\ 1 & 7 & 2 \\ 2 & 14 & 4 \\ 3 & 21 & 6 \\ 4 & 28 & \\ 5 & 35 & 1 \\ 6 & 42 & 3 \\ 7 & 49 & 5 \\ 8 & 56 & 7 \\ \end{array} $$
(For !!a_i=4!! there is no solution.) We may disregard the non-necklace values of !!v!!, as these will give us solutions that are the same as those given by necklace values of !!v!!. The necklaces are:
$$\begin{array}{rl} 000 & 0 \\ 001 & 1 \\ 011 & 3 \\ 111 & 7 \end{array}$$
so we may disregard the solutions exacpt when !!v=0,1,3,7!!. Calculating the digit sequences from these four values of !!v!! and the corresponding !!a_i!! we find:
$$\begin{array}{ccl} a_0 & v & \text{digits} \\ \hline 0 & 0 & 000 \\ 5 & 1 & 512 \\ 6 & 3 & 637 \\ 8 & 7 & 888 \ \end{array} $$
(In the second line, for example, we have !!v=1 = 001_2!!, so !!1 = 2\cdot 5 + 0; 2 = 1\cdot 2 + 0;!! and !!5 = 2\cdot 2 + 1!!.)
Any number !!A!! of three digits, for which !!2A!! contains exactly the same three digits, in base 9, must therefore consist of exactly the digits !!000, 125, 367,!! or !!888!!.
A warning
All the foregoing assumes that the permutation !!P!! is a single cycle. In general, it may not be. Suppose we did an analysis like that above for !!R=10, n=5!! and found that there was no possible digit set, other than the trivial set 00000, that satisfied the governing equation !!(2^5-1)a_0 + v\equiv 0\pmod{10}!!. This would not completely rule out a base-10 solution with 5 digits, because the analysis only rules out a cyclic set of digits. There could still be a solution where !!P!! was a product of a !!2!! and a !!3!!-cycle, or a product of still smaller cycles.
Something like this occurs, for example, in the !!n=4, R=8!! case. Solving the governing equation !!(2^5-1)a_0 + v \equiv 0\pmod 8!! yields only four possible digit cycles, namely !!\{0,1,2,4\}, \{1,3,6,4\}, \{2,5,2,5\}!!, and !!\{3,7,6,5\}!!. But there are several additional solutions: !!2500_8\cdot 2 = 5200_8, 2750_8\cdot 2 = 5720_8, !! and !!2775_8\cdot 2 = 5772_8!!. These correspond to permutations !!P!! with more than one cycle. In the case of !!2750_8!!, for example, !!P!! exchanges the !!5!! and the !!2!!, and leaves the !!0!! and the !!7!! fixed.
For this reason we cannot rule out the possibility of an !!n!!-digit solution without first considering all smaller !!n!!.
The Large Equals Odd rule
When !!R!! is even there is a simple condition we can use to rule out certain sets of digits from being single-cycle solutions. Recall that !!A=a_{n-1}\ldots a_0!! and !!B=b_{n-1}\ldots b_0!!. Let us agree that a digit !!d!! is large if !!d\ge \frac R2!! and small otherwise. That is, !!d!! is large if, upon doubling, it causes a carry into the next column to the left.
Since !!b_i =(2a_i + c_i)\bmod R!!, where the !!c_i!! are carry bits, we see that, except for !!b_0!!, the digit !!b_i!! is odd precisely when there is a carry from the next column to the right, which occurs precisely when !!a_{i-1}!! is large. Thus the number of odd digits among !!b_1,\ldots b_{n-1}!! is equal to the number of large digits among !!a_1,\ldots a_{n-2}!!. This leaves the digits !!b_0!! and !!a_{n-1}!! uncounted. But !!b_0!! is never odd, since there is never a carry in the rightmost position, and !!a_{n-1}!! is always small (since otherwise !!B!! would have !!n+1!! digits, which is not allowed). So the number of large digits in !!A!! is exactly equal to the number of odd digits in !!B!!. And since !!A!! and !!B!! have exactly the same digits, the number of large digits in !!A!! is equal to the number of odd digits in !!A!!. Observe that this is the case for our running example !!1042_8!!: there is one odd digit and one large digit (the 4).
When !!R!! is odd the analogous condition is somewhat more complicated, but since the main case of interest is !!R=10!!, we have the useful rule that:
For !!R!! even, the number of odd digits in any solution !!A!! is equal to the number of large digits in !!A!!.
Conditions on the order of digits in a solution
We have determined, using the above method, that the digits !!\{5,1,2\}!! might form a base-9 numeral with property !!P_9!!. Now we would like to arrange them into a base-9 numeral that actually does have that property. Again let us write !!A = a_2a_1a_0!! and !!B=b_2b_1b_0!!, with !!B=2A!!. Note that if !!a_i = 1!!, then !!b_i = 3!! (if there was a carry from the next column to the right) or !!b_i=2!! (if there was no carry), but since !!b_i\in{5,1,2}!!, we must have !!b_i = 2!! and therefore !!a_{i-1}!! must be small, since there is no carry into position !!i!!. But since !!a_{i-1}!! is also one of !!\{5,1,2\}!!, and it cannot also be !!1!!, it must be !!2!!. This shows that the 1, unless it appears in the rightmost position, must be to the left of the !!2!!; it cannot be to the left of the !!5!!. Similarly, if !!a_i = 2!! then !!b_i = 5!!, because !!4!! is impossible, so the !!2!! must be to the left of a large digit, which must be the !!5!!. Similar reasoning produces no constraint on the position of the !!5!!; it could be to the left of a small digit (in which case it doubles to !!1!!) or a large digit (in which case it doubles to !!2!!). We can summarize these findings as follows:
$$\begin{array}{cl} \text{digit} & \text{to the left of} \\ \hline 1 & 1, 2, \text{end} \\ 2 & 5 \\ 5 & 1,2,5,\text{end} \end{array}$$
Here “end” means that the indicated digit could be the rightmost.
Furthermore, the left digit of !!A!! must be small (or else there would be a carry in the leftmost place and !!2A!! would have 4 digits instead of 3) so it must be either 1 or 2. It is not hard to see from this table that the digits must be in the order !!125!! or !!251!!, and indeed, both of those numbers have the required property: !!125_9\cdot 2 = 251_9!!, and !!251_9\cdot 2 = 512_9!!.
This was a simple example, but in more complicated cases it is helpful to draw the order constraints as a graph. Suppose we draw a graph with one vertex for each digit, and one additional vertex to represent the end of the numeral. The graph has an edge from vertex !!v!! to !!v'!! whenever !!v!! can appear to the left of !!v'!!. Then the graph drawn for the table above looks like this:
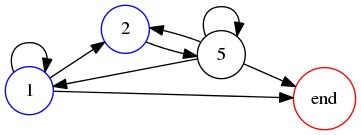
A 3-digit numeral with property !!P_9!! corresponds to a path in this graph that starts at one of the nonzero small digits (marked in blue), ends at the red node marked ‘end’, and visits each node exactly once. Such a path is called hamiltonian. Obviously, self-loops never occur in a hamiltonian path, so we will omit them from future diagrams.
Now we will consider the digit set !!637!!, again base 9. An analysis similar to the foregoing allows us to construct the following graph:
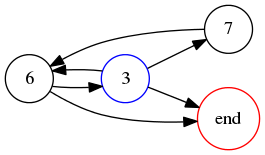
Here it is immediately clear that the only hamiltonian path is !!3-7-6-\text{end}!!, and indeed, !!376_9\cdot 2 = 763_9!!.
In general there might be multiple instances of a digit, and so multiple nodes labeled with that digit. Analysis of the !!0,0,0!! case produces a graph with no legal start nodes and so no solutions, unless leading zeroes are allowed, in which case !!000!! is a perfectly valid solution. Analysis of the !!8,8,8!! case produces a graph with no path to the end node and so no solutions. These two trivial patterns appear for all !!R!! and all !!n!!, and we will ignore them from now on.
Returning to our ongoing example, !!1042!! in base 8, we see that !!1!! and !!2!! must double to !!2!! and !!4!!, so must be to the left of small digits, but !!4!! and !!0!! can double to either !!0!! or !!1!! and so could be to the left of anything. Here the constraints are so lax that the graph doesn't help us narrow them down much:
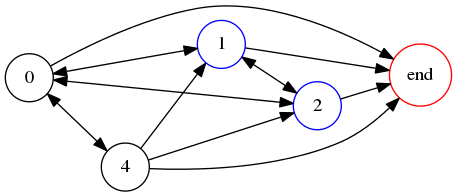
Observing that the only arrow into the 4 is from 0, so that the 4 must follow the 0, and that the entire number must begin with 1 or 2, we can enumerate the solutions:
1042
1204
2041
2104
If leading zeroes are allowed we have also:
0412
0421
All of these are solutions in base 8.
The case of !!R=10!!
Now we turn to our main problem, solutions in base 10.
To find all the solutions of length 6 requires an enumeration of smaller solutions, which, if they existed, might be concatenated into a solution of length 6. This is because our analysis of the digit sets that can appear in a solution assumes that the digits are permuted cyclically; that is, the permutations !!P!! that we considered had only one cycle each.
There are no smaller solutions, but to prove that the length 6 solutions are minimal, we must analyze the cases for smaller !!n!! and rule them out. We now produce a complete analysis of the base 10 case with !!R=10!! and !!n\le 6!!. For !!n=1!! there is only the trivial solution of !!0!!, which we disregard. (The question asked for a positive number anyway.)
!!n=2!!
For !!n=2!!, we want to find solutions of !!3a_i + v \equiv 0\pmod{10}!! where !!v!! is a two-bit necklace number, one of !!00_2, 01_2, !! or !!11_2!!. Tabulating the values of !!a_i!! and !!v\in\{0,1,3\}!! that solve this equation we get:
$$\begin{array}{ccc} v& a_i \\ \hline 0 & 0 \\ 1& 3 \\ 3& 9 \\ \end{array}$$
We can disregard the !!v=0!! and !!v=3!! solutions because the former yields the trivial solution !!00!! and the latter yields the nonsolution !!99!!. So the only possibility we need to investigate further is !!a_i = 3, v = 1!!, which corresponds to the digit sequence !!36!!: Doubling !!3!! gives us !!6!! and doubling !!6!!, plus a carry, gives us !!3!! again.
But when we tabulate of which digits must be left of which informs us that there is no solution with just !!3!! and !!6!!, because the graph we get, once self-loops are eliminated, looks like this:
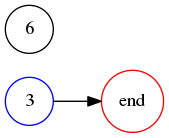
which obviously has no hamiltonian path. Thus there is no solution for !!R=10, n=2!!.
!!n=3!!
For !!n=3!! we need to solve the equation !!7a_i + v \equiv 0\pmod{10}!! where !!v!! is a necklace number in !!\{0,\ldots 7\}!!, specifically one of !!0,1,3,!! or !!7!!. Since !!7!! and !!10!! are relatively prime, for each !!v!! there is a single !!a_i!! that solves the equation. Tabulating the possible values of !!a_i!! as before, and this time omitting rows with no solution, we have:
$$\begin{array}{rrl} v & a_i & \text{digits}\\ \hline 0& 0 & 000\\ 1& 7 & 748 \\ 3& 1 & 125\\ 7&9 & 999\\ \end{array}$$
The digit sequences !!0,0,0!! and !!9,9,9!! yield trivial solutions or nonsolutions as usual, and we will omit them in the future. The other two lines suggest the digit sets !!1,2,5!! and !!4,7,8!!, both of which fail the “odd equals large” rule.
This analysis rules out the possibility of a digit set with !!a_0 \to a_1 \to a_2 \to a_1!!, but it does not completely rule out a 3-digit solution, since one could be obtained by concatenating a one-digit and a two-digit solution, or three one-digit solutions. However, we know by now that no one- or two-digit solutions exist. Therefore there are no 3-digit solutions in base 10.
!!n=4!!
For !!n=4!! the governing equation is !!15a_i + v \equiv 0\pmod{10}!! where !!v!! is a 4-bit necklace number, one of !!\{0,1,3,5,7,15\}!!. This is a little more complicated because !!\gcd(15,10)\ne 1!!. Tabulating the possible digit sets, we get:
$$\begin{array}{crrl} a_i & 15a_i& v & \text{digits}\\ \hline 0 & 0 & 0 & 0000\\ 1 & 5 & 5 & 1250\\ 1 & 5 & 15 & 1375\\ 2 & 0 & 0 & 2486\\ 3 & 5 & 5 & 3749\\ 3 & 5 & 15 & 3751\\ 4 & 0 & 0 & 4862\\ 5 & 5 & 5 & 5012\\ 5 & 5 & 5 & 5137\\ 6 & 0 & 0 & 6248\\ 7 & 5 & 5 & 7493\\ 7 & 5 & 5 & 7513\\ 8 & 0 & 0 & 8624 \\ 9 & 5 & 5 & 9874\\ 9 & 5 & 15 & 9999 \\ \end{array}$$
where the second column has been reduced mod !!10!!. Note that even restricting !!v!! to necklace numbers the table still contains duplicate digit sequences; the 15 entries on the right contain only the six basic sequences !!0000, 0125, 1375, 2486, 3749, 4987!!, and !!9999!!. Of these, only !!0000, 9999,!! and !!3749!! obey the odd equals large criterion, and we will disregard !!0000!! and !!9999!! as usual, leaving only !!3749!!. We construct the corresponding graph for this digit set as follows: !!3!! must double to !!7!!, not !!6!!, so must be left of a large number !!7!! or !!9!!. Similarly !!4!! must be left of !!7!! or !!9!!. !!9!! must also double to !!9!!, so must be left of !!7!!. Finally, !!7!! must double to !!4!!, so must be left of !!3,4!! or the end of the numeral. The corresponding graph is:
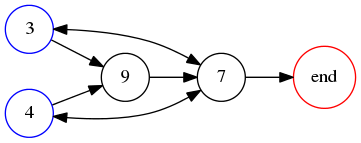
which evidently has no hamiltonian path: whichever of 3 or 4 we start at, we cannot visit the other without passing through 7, and then we cannot reach the end node without passing through 7 a second time. So there is no solution with !!R=10!! and !!n=4!!.
!!n=5!!
We leave this case as an exercise. There are 8 solutions to the governing equation, all of which are ruled out by the odd equals large rule.
!!n=6!!
For !!n=6!! the possible solutions are given by the governing equation !!63a_i + v \equiv 0\pmod{10}!! where !!v!! is a 6-bit necklace number, one of !!\{0,1,3,5,7,9,11,13,15,21,23,27,31,63\}!!. Tabulating the possible digit sets, we get:
$$\begin{array}{crrl} v & a_i & \text{digits}\\ \hline 0 & 0 & 000000\\ 1 & 3 & 362486 \\ 3 & 9 & 986249 \\ 5 & 5 & 500012 \\ 7 & 1 & 124875 \\ 9 & 7 & 748748 \\ 11 & 3 & 362501 \\ 13 & 9 & 986374 \\ 15 & 5 & 500137 \\ 21 & 3 & 363636 \\ 23 & 9 & 989899 \\ 27 & 1 & 125125 \\ 31 & 3 & 363751 \\ 63 & 9 & 999999 \\ \end{array}$$
After ignoring !!000000!! and !!999999!! as usual, the large equals odd rule allows us to ignore all the other sequences except !!124875!! and !!363636!!. The latter fails for the same reason that !!36!! did when !!n=2!!. But !!142857!! , the lone survivor, gives us a complicated derived graph containing many hamiltonian paths, every one of which is a solution to the problem:
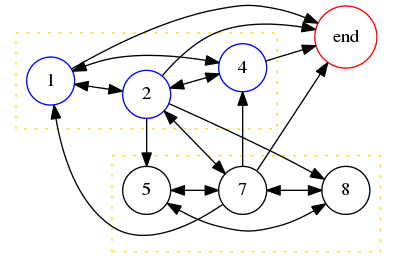
It is not hard to pick out from this graph the minimal solution !!125874!!, for which !!125874\cdot 2 = 251748!!, and also our old friend !!142857!! for which !!142857\cdot 2 = 285714!!.
We see here the reason why all the small numbers with property !!P_{10}!! contain the digits !!124578!!. The constraints on which digits can appear in a solution are quite strict, and rule out all other sequences of six digits and all shorter sequences. But once a set of digits passes these stringent conditions, the constraints on it are much looser, because !!B!! is only required to have the digits of !!A!! in some order, and there are many possible orders, many of which will satisfy the rather loose conditions involving the distribution of the carry bits. This graph is typical: it has a set of small nodes and a set of large nodes, and each node is connected to either all the small nodes or all the large nodes, so that the graph has many edges, and, as in this case, a largish clique of small nodes and a largish clique of large nodes, and as a result many hamiltonian paths.
Onward
This analysis is tedious but is simple enough to perform by hand in under an hour. As !!n!! increases further, enumerating the solutions of the governing equation becomes very time-consuming. I wrote a simple computer program to perform the analysis for given !!R!! and !!n!!, and to emit the possible digit sets that satisfied the large equals odd criterion. I had wondered if every base-10 solution contained equal numbers of the digits !!1,2,4,8,5,!! and !!7!!. This is the case for !!n=7!! (where the only admissible digit set is !!\{1,2,4,5,7,8\}\cup\{9\}!!), for !!n=8!! (where the only admissible sets are !!\{1,2,4,5,7,8\}\cup \{3,6\}!! and !!\{1,2,4,5,7,8\}\cup\{9,9\}!!), and for !!n=9!! (where the only admissible sets are !!\{1,2,4,5,7,8\}\cup\{3,6,9\}!! and !!\{1,2,4,5,7,8\}\cup\{9,9,9\}!!). But when we reach !!n=10!! the increasing number of necklaces has loosened up the requirements a little and there are 5 admissible digit sets. I picked two of the promising-seeming ones and quickly found by hand the solutions !!4225561128!! and !!1577438874!!, both of which wreck any theory that the digits !!1,2,4,5,8,7!! must all appear the same number of times.
Acknowledgments
Thanks to Karl Kronenfeld for corrections and many helpful suggestions.
[Other articles in category /math] permanent link
Sat, 19 Jul 2014
Similarity analysis of quilt blocks
As I've discussed elsewhere, I once wrote a program to enumerate all
the possible quilt blocks of a certain type. The quilt blocks in
question are, in quilt jargon, sixteen-patch half-square triangles. A
half-square triangle, also called a “patch”, is two triangles of fabric sewn together, like
this: 
Then you sew four of these patches into a four-patch, say like this:

Then to make a sixteen-patch block of the type I was considering, you take four identical four-patch blocks, and sew them together with rotational symmetry, like this:

It turns out that there are exactly 72 different ways to do this. (Blocks equivalent under a reflection are considered the same, as are blocks obtained by exchanging the roles of black and white, which are merely stand-ins for arbitrary colors to be chosen later.) Here is the complete set of 72:








































































It's immediately clear that some of these resemble one another, sometimes so strongly that it can be hard to tell how they differ, while others are very distinctive and unique-seeming. I wanted to make the computer classify the blocks on the basis of similarity.
My idea was to try to find a way to get the computer to notice which
blocks have distinctive components of one color. For example, many
blocks have a distinctive diamond shape  in the center.
in the center.
Some have a pinwheel like this:

which also has the diamond in the middle, while others have a different kind of pinwheel with no diamond:

I wanted to enumerate such components and ask the computer to list which blocks contained which shapes; then group them by similarity, the idea being that that blocks with the same distinctive components are similar.
The program suite uses a compact notation of blocks and of shapes that makes it easy to figure out which blocks contain which distinctive components.
Since each block is made of four identical four-patches, it's enough just to examine the four-patches. Each of the half-square triangle patches can be oriented in two ways:

Here are two of the 12 ways to orient the patches in a four-patch:
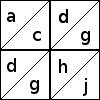
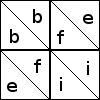
Each 16-patch is made of four four-patches, and you must imagine that the
four-patches shown above are in the upper-left position in the
16-patch. Then symmetry of the 16-patch block means that triangles with the
same label are in positions that are symmetric with respect to the
entire block. For example, the two triangles labeled b are on
opposite sides of the block's northwest-southeast diagonal. But there
is no symmetry of the full 16-patch block that carries triangle d to
triangle g, because d is on the edge of the block, while g is in the interior.
Triangles must be colored opposite colors if they are part of the same patch, but other than that there are no constraints on the coloring.
A block might, of course, have patches in both orientations:
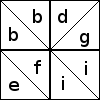
All the blocks with diagonals oriented this way are assigned
descriptors made from the letters bbdefgii.
Once you have chosen one of the 12 ways to orient the diagonals in the
four-patch, you still have to color the patches. A descriptor like
bbeeffii describes the orientation of the diagonal lines in the
squares, but it does not describe the way the four patches are
colored; there are between 4 and 8 ways to color each sort of
four-patch. For example, the bbeeffii four-patch shown earlier can be colored in six different ways:







In each case, all four diagonals run from northwest to southeast. (All other ways of coloring this four-patch are equivalent to one of these under one or more of rotation, reflection, and exchange of black and white.)
We can describe a patch by listing the descriptors of the eight triangles, grouped by which triangles form connected regions. For example, the first block above is:


b/bf/ee/fi/i
because there's an isolated white b triangle, then a black parallelogram
made of a b and an f patch, then a white triangle made from the
two white e triangles, then another parallelogram made from the black f
and i, and finally in the middle, the white i. (The two white e
triangles appear to be separated, but when four of these four-patches are
joined into a 16-patch block, the two white e patches will be
adjacent and will form a single large triangle:  )
)
The other five bbeeffii four-patches are, in the same order they are shown above:
b/b/e/e/f/f/i/i
b/b/e/e/fi/fi
b/bfi/ee/f/i
bfi/bfi/e/e
bf/bf/e/e/i/i
All six have bbeeffii, but grouped differently depending on the
colorings. The second one (
b/b/e/e/f/f/i/i) has no regions with
more than one triangle; the fifth (
bfi/bfi/e/e) has two large regions of three triangles each, and two
isolated triangles. In the latter four-patch, the bfi in the
descriptor has three letters because the patch has a corresponding
distinctive component made of three triangles.
I made up a list of the descriptors for all 72 blocks; I think I did
this by hand. (The work directory contains a blocks
file that maps
blocks to their descriptors, but the
Makefile does
not say how to build it, suggesting that it was not automatically
built.) From this list one can automatically
extract a
list of descriptors of interesting
shapes: an
interesting shape is two or more letters that appear together in some
descriptor. (Or it can be the single letter j, which is
exceptional; see below.) For example, bffh represents a distinctive
component. It can only occur in a patch that has a b, two fs, and
an h, like this one:
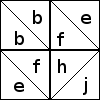
and it will only be significant if the b, the two fs, and the h are
the same color:

in which case you get this distinctive and interesting-looking hook component.
There is only one block that includes this distinctive hook component;
it has descriptor b/bffh/ee/j, and looks like this:  . But some of the distinctive
components are more common. The
. But some of the distinctive
components are more common. The ee component represents the large white half-diamonds on the four sides.
A block with "ee" in its descriptor always looks like this:

and the blocks formed from such patches always have a distinctive half-diamond component on each edge, like this:

(The stippled areas vary from block to block, but the blocks with ee
in their descriptors always have the half-diamonds as shown.)
The blocks listed at http://hop.perl.plover.com/quilt/analysis/images/ee.html
all have the ee component. There are many differences between them, but
they all have the half-diamonds in common.
Other distinctive components have similar short descriptors. The two pinwheels I
mentioned above are

gh and

fi, respectively; if you look at
the list of gh blocks
and
the list of fi blocks
you'll see all the blocks with each kind of pinwheel.
Descriptor j is an exception. It makes an interesting shape all by itself,
because any block whose patches have j in their descriptor will have
a distinctive-looking diamond component in the center. The four-patch looks like
this:

so the full sixteen-patch looks like this:

where the stippled parts can vary. A look at the list of blocks with
component
j will
confirm that they all have this basic similarity.
I had made a list of the descriptors for each of the 72 blocks, and from this I extracted a list of the descriptors for interesting component shapes. Then it was only a matter of finding the component descriptors in the block descriptors to know which blocks contained which components; if the two blocks share two different distinctive components, they probably look somewhat similar.
Then I sorted the blocks into groups, where two blocks were in the same group if they shared two distinctive components. The resulting grouping lists, for each block, which other blocks have at least two shapes in common with it. Such blocks do indeed tend to look quite similar.
This strategy was actually the second thing I tried; the first thing didn't work out well. (I forget just what it was, but I think it involved finding polygons in each block that had white inside and black outside, or vice versa.) I was satisfied enough with this second attempt that I considered the project a success and stopped work on it.
The complete final results were:
- This tabulation of blocks that are somewhat similar
- This tabulation of blocks that are distinctly similar (This is the final product; I consider this a sufficiently definitive listing of “similar blocks”.)
- This tabulation of blocks that are extremely similar
And these tabulations of all the blocks with various distinctive components: bd bf bfh bfi cd cdd cdf cf cfi ee eg egh egi fgh fh fi gg ggh ggi gh gi j
It may also be interesting to browse the work directory.
[Other articles in category /misc] permanent link
Fri, 18 Jul 2014
On uninhabited types and inconsistent logics
Earlier this week I gave a talk about the Curry-Howard isomorphism. Talks never go quite the way you expect. The biggest sticking point was my assertion that there is no function with the type a → b. I mentioned this as a throwaway remark on slide 7, assuming that everyone would agree instantly, and then we got totally hung up on it for about twenty minutes.
Part of this was my surprise at discovering that most of the audience (members of the Philly Lambda functional programming group) was not familiar with the Haskell type system. I had assumed that most of the members of a functional programming interest group would be familiar with one of Haskell, ML, or Scala, all of which have the same basic type system. But this was not the case. (Many people are primarily interested in Scheme, for example.)
I think the main problem was that I did not make clear to the audience what Haskell means when it says that a function has type a → b. At the talk, and then later on Reddit people asked
what about a function that takes an integer and returns a string: doesn't it have type a → b?
If you know one of the HM languages, you know that of course it
doesn't; it has type Int → String, which is not the same at all. But I
wasn't prepared for this confusion and it took me a while to formulate
the answer. I think I underestimated the degree to which I have
internalized the behavior of Hindley-Milner type systems after twenty
years. Next time, I will be better prepared, and will say something
like the following:
A function which takes an integer and returns a string does not have
the type a → b; it has the type Int → String. You must pass it an
integer, and you may only use its return value in a place that makes
sense for a string. If f has this type, then 3 +
f 4 is a compile-time type error because Haskell knows that f
returns a string, and strings do not work with +.
But if f had
the type a → b, then 3 + f 4 would be legal, because context requires that
f return a number, and the type a → b says that it can return a
number, because a number is an instance of the completely general type
b. The type a → b, in contrast to Int → String, means that b
and a are completely unconstrained.
Say function f had type a → b. Then you would be able to use the
expression f x in any context that was expecting any sort of return
value; you could write any or all of:
3 + f x
head(f x)
"foo" ++ f x
True && f x
and they would all type check correctly, regardless of the type of x. In the first line, f x would return a number; in the second line f would return a list; in the third line it would return a string, and in the fourth line it would return a boolean. And in each case f could be able to do what was required regardless of the type of x, so without even looking at x. But how could you possibly write such a function f? You can't; it's impossible.
Contrast this with the identity function id, which has type a → a. This says that id always returns a value whose type is the same as
that if its argument. So you can write
3 + id x
as long as x has the right type for +, and you can write
head(id x)
as long as x has the
right type for head, and so on. But for f to have the type a → b, all those
would have to work regardless of the type of the argument to f. And
there is no way to write such an f.
Actually I wonder now if part of the problem is that we like to write a → b when what we really mean is the type ∀a.∀b.a → b. Perhaps making the quantifiers explicit would clear things up? I suppose it probably wouldn't have, at least in this case.
The issue is a bit complicated by the fact that the function
loop :: a -> b
loop x = loop x
does have the type a → b, and, in a language with exceptions, throw
has that type also; or consider Haskell
foo :: a -> b
foo x = undefined
Unfortunately, just as I thought I was getting across the explanation of why there can be no function with type a → b, someone brought up exceptions and I had to mutter and look at my shoes. (You can also take the view that these functions have type a → ⊥, but the logical principle ⊥ → b is unexceptionable.)
In fact, experienced practitioners will realize, the instant the type
a → b appears, that they have written a function that never returns.
Such an example was directly responsible for my own initial interest
in functional programming and type systems; I read a 1992 paper (“An
anecdote about ML type
inference”)
by Andrew R. Koenig in which he described writing a merge sort
function, whose type was reported (by the SML type inferencer) as [a]
-> [b], and the reason was that it had a bug that would cause it to
loop forever on any nonempty list. I came back from that conference
convinced that I must learn ML, and Higher-Order Perl was a direct
(although distant) outcome of that conviction.
Any discussion of the Curry-Howard isomorphism, using Haskell as an example, is somewhat fraught with trouble, because Haskell's type logic is utterly inconsistent. In addition to the examples above, in Haskell one can write
fix :: (a -> a) -> a
fix f = let x = fix f
in f x
and as a statement of logic, !!(a\to a)\to a!! is patently false. This might be an argument in favor of the Total Functional Programming suggested by D.A. Turner and others.
[Other articles in category /CS] permanent link
Wed, 16 Jul 2014
Guess what this does (solution)
A few weeks ago I asked people to predict, without trying it first, what this would print:
perl -le 'print(two + two == five ? "true" : "false")'
(If you haven't seen this yet, I recommend that you guess, and then test your guess, before reading the rest of this article.)
People familiar with Perl guess that it will print true; that is
what I guessed. The reasoning is as follows: Perl is willing to treat
the unquoted strings two and five as strings, as if they had been
quoted, and is also happy to use the + and == operators on them,
converting the strings to numbers in its usual way. If the strings
had looked like "2" and "5" Perl would have treated them as 2 and
5, but as they don't look like decimal numerals, Perl interprets them
as zeroes. (Perl wants to issue a warning about this, but the warning is not enabled by default.
Since the two and five are treated as
zeroes, the result of the == comparison are true, and the string
"true" should be selected and printed.
So far this is a little bit odd, but not excessively odd; it's the
sort of thing you expect from programming languages, all of which more
or less suck. For example, Python's behavior, although different, is
about equally peculiar. Although Python does require that the strings
two and five be quoted, it is happy to do its own peculiar thing
with "two" + "two" == "five", which happens to be false: in Python
the + operator is overloaded and has completely different behaviors
on strings and numbers, so that while in Perl "2" + "2" is the
number 4, in Python is it is the string 22, and "two" + "two"
yields the string "twotwo". Had the program above actually printed
true, as I expected it would, or even false, I would not have
found it remarkable.
However, this is not what the program does do. The explanation of two paragraphs earlier is totally wrong. Instead, the program prints nothing, and the reason is incredibly convoluted and bizarre.
First, you must know that print has an optional first argument. (I
have plans for an article about how optional first arguments are almost
always a bad move, but contrary to my usual practice I will not insert
it here.) In Perl, the print function can be invoked in two ways:
print HANDLE $a, $b, $c, …;
print $a, $b, $c, …;
The former prints out the list $a, $b, $c, … to the filehandle
HANDLE; the latter uses the default handle, which typically points
at the terminal. How does Perl decide which of these forms is being
used? Specifically, in the second form, how does it know that $a is
one of the items to be printed, rather than a variable containing the filehandle
to print to?
The answer to this question is further complicated by the fact that
the HANDLE in the first form could be either an unquoted string,
which is the name of the handle to print to, or it could be a variable
containing a filehandle value. Both of these prints should do the
same thing:
my $handle = \*STDERR;
print STDERR $a, $b, $c;
print $handle $a, $b, $c;
Perl's method to decide whether a particular print uses an explicit
or the default handle is a somewhat complicated heuristic. The basic
rule is that the filehandle, if present, can be distinguished because
its trailing comma is omitted. But if the filehandle were allowed to
be the result of an arbitrary expression, it might be difficult for
the parser to decide where there was a a comma; consider the
hypothetical expression:
print $a += EXPRESSION, $b $c, $d, $e;
Here the intention is that the $a += EXPRESSION, $b expression
calculates the filehandle value (which is actually retrieved from $b, the
$a += … part being executed only for its side effect) and the
remaining $c, $d, $e are the values to be printed. To allow this
sort of thing would be way too confusing to both Perl and to the
programmer. So there is the further rule that the filehandle
expression, if present, must be short, either a simple scalar
variable such as $fh, or a bare unquoted string that is in the right
format for a filehandle name, such as HANDLE. Then the parser need
only peek ahead a token or two to see if there is an upcoming comma.
So for example, in
print STDERR $a, $b, $c;
the print is immediately followed by STDERR, which could be a
filehandle name, and STDERR is not followed by a comma, so STDERR
is taken to be the name of the output handle. And in
print $x, $a, $b, $c;
the print is immediately followed by the simple scalar value $x,
but this $x is followed by a comma, so is considered one of the
things to be printed, and the target of the print is the default
output handle.
In
print STDERR, $a, $b, $c;
Perl has a puzzle: STDERR looks like a filehandle, but it is
followed by a comma. This is a compile-time error; Perl complains “No
comma allowed after filehandle” and aborts. If you want to print the
literal string STDERR, you must quote it, and if you want to print A, B,
and C to the standard error handle, you must omit the first comma.
Now we return to the original example.
perl -le 'print(two + two == five ? "true" : "false")'
Here Perl sees the unquoted string two which could be a filehandle
name, and which is not followed by a comma. So it takes the first
two to be the output handle name. Then it evaluates the expression
+ two == five ? "true" : "false"
and obtains the value true. (The leading + is a unary plus
operator, which is a no-op. The bare two and five are taken to be
string constants, which, compared with the numeric == operator, are
considered to be numerically zero, eliciting the same warning that I
mentioned earlier that I had not enabled. Thus the comparison Perl
actually does is is 0 == 0, which is true, and the resulting string is
true.)
This value, the string true, is then printed to the filehandle named
two. Had we previously opened such a filehandle, say with
open two, ">", "output-file";
then the output would have been sent to the filehandle as usual.
Printing to a non-open filehandle elicits an optional warning from
Perl, but as I mentioned, I have not enabled warnings, so the print
silently fails, yielding a false value.
Had I enabled those optional warnings, we would have seen a plethora of them:
Unquoted string "two" may clash with future reserved word at -e line 1.
Unquoted string "two" may clash with future reserved word at -e line 1.
Unquoted string "five" may clash with future reserved word at -e line 1.
Name "main::two" used only once: possible typo at -e line 1.
Argument "five" isn't numeric in numeric eq (==) at -e line 1.
Argument "two" isn't numeric in numeric eq (==) at -e line 1.
print() on unopened filehandle two at -e line 1.
(The first four are compile-time warnings; the last three are issued
at execution time.) The crucial warning is the one at the end,
advising us that the output of print was directed to the filehandle
two which was never opened for output.
[ Addendum 20140718: I keep thinking of the following remark of Edsger W. Dijkstra:
[This phenomenon] takes one of two different forms: one programmer places a one-line program on the desk of another and … says, "Guess what it does!" From this observation we must conclude that this language as a tool is an open invitation for clever tricks; and while exactly this may be the explanation for some of its appeal, viz., to those who like to show how clever they are, I am sorry, but I must regard this as one of the most damning things that can be said about a programming language.
But my intent is different than what Dijkstra describes. His programmer is proud, but I am disgusted. Incidentally, I believe that Dijkstra was discussing APL here. ]
[ Addendum 20150508: I never have much sympathy for the school of thought that says that you should always always enable warnings in every Perl program; I think Perl produces too many spurious warnings for that. But I also think this example is part of a cogent argument in the other direction. ]
[Other articles in category /prog/perl] permanent link
Here's a Perl quiz that I confidently predict nobody will get right. Without trying it first, what does the following program print?
perl -le 'print(two + two == five ? "true" : "false")'
(I will discuss the surprising answer tomorrow.)
[Other articles in category /prog/perl] permanent link
Mon, 14 Jul 2014
Types are theorems; programs are proofs
[ Summary: I gave a talk Monday night on the Curry-Howard isomorphism; my talk slides are online. ]
I sent several proposals to !!con, a conference of ten-minute talks. One of my proposals was to explain the Curry-Howard isomorphism in ten minutes, but the conference people didn't accept it. They said that they had had four or five proposals for talks about the Curry-Howard isomorphism, and didn't want to accept more than one of them.
The CHI talk they did accept turned out to be very different from the one I had wanted to give; it discussed the Coq theorem-proving system. I had wanted to talk about the basic correspondence between pair types, union types, and function types on the one hand, and reasoning about logical conjunctions, disjunctions, and implications on the other hand, and the !!con speaker didn't touch on this at all.
But mathematical logic and programming language types turn out to be the same! A type in a language like Haskell can be understood as a statement of logic, and the statement will be true if and only if there is actually a value with the corresponding type. Moreover, if you have a proof of the statement, you can convert the proof into a value of the corresponding type, or conversely if you have a value with a certain type you can convert it into a proof of the corresponding statement. The programming language features for constructing or using values with function types correspond exactly to the logical methods for proving or using statements with implications; similarly pair types correspond to logical conjunction, and union tpyes to logical disjunction, and exceptions to logical negation. I think this is incredible. I was amazed the first time I heard of it (Chuck Liang told me sometime around 1993) and I'm still amazed.
Happily Philly Lambda, a Philadelphia-area functional programming group, had recently come back to life, so I suggested that I give them a longer talk about about the Curry-Howard isomorphism, and they agreed.
I gave the talk yesterday, and the materials are online. I'm not sure how easy they will be to understand without my commentary, but it might be worth a try.
If you're interested and want to look into it in more detail, I suggest you check out Sørensen and Urzyczyn's Lectures on the Curry-Howard Isomorphism. It was published as an expensive yellow-cover book by Springer, but free copies of the draft are still available.
[Other articles in category /CS] permanent link


