Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 22 Dec 2017
A couple of years ago I wrote here about some interesting projects I had not finished. One of these was to enumerate and draw orthogonal polygons.
An orthogonal polygon is simply one whose angles are all right angles. All rectangles are orthogonal polygons, but there are many other types. For example, here are examples of orthogonal decagons:
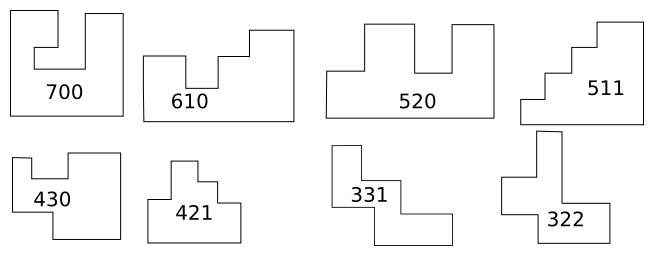
If you ignore the lengths of the edges, and pay attention only to the direction that the corners turn, the orthogonal polygons fall into types. The rectangle is the only type with four sides. There is also only one type with six sides; it is an L-shaped hexagon. There are four types with eight sides, and the illustration shows the eight types with ten sides.
Contributing to OEIS was a life goal of mine and I was thrilled when I was able to contribute the sequence of the number of types of orthogonal !!2n!!-gons.
Enumerating the types is not hard. For !!2n!!-gons, there is one type for each “bracelet” of !!n-2!! numbers whose sum is !!n+2!!.[1]
In the illustration above, !!n=5!! and each type is annotated with its !!5-2=3!! numbers whose sum is !!n+2=7!!. But the number of types increases rapidly with the number of sides, and it soons becomes infeasible to draw them by hand as I did above. I had wanted to write a computer program that would take a description of a type (the sequence) and render a drawing of one of the polygons of that type.
The tricky part is how to keep the edges from crossing, which is not allowed. I had ideas for how to do this, but it seemed troublesome, and also it seemed likely to produce ugly, lopsided examples, so I did not implement it. And eventually I forgot about the problem.
But Brent Yorgey did not forget, and he had a completely different idea. He wrote a program to convert a type description to a set of constraints on the !!x!! and !!y!! coordinates of the vertices, and fed the constraints to an SMT solver, which is a system for finding solutions to general sets of constraints. The outcome is as handsome as I could have hoped. Here is M. Yorgey's program's version of the hand-drawn diagram above:
M. Yorgey rendered beautiful pictures of all types of orthogonal polygons up to 12 sides. Check it out on his blog.
[1]
“Bracelet”
is combinatorist jargon for a sequence of things where the ends are
joined together: you can start in the middle, run off one end and come
back to the other end, and that is considered the same bracelet. So
for example ABCD and BCDA and CDAB are all the same
bracelet. And also, it doesn't matter which direction you go, so
that DCBA, ADCB, and BADC are also the same bracelet again.
Every bracelet made from from A, B, C, and D is equivalent to
exactly one of ABCD, ACDB, or ADBC.
[ Addendum 20180202: M. Yorgey has more to say about it on his blog. ]
[Other articles in category /math] permanent link
Thu, 21 Dec 2017
Philadelphians, move to the back of the bus!
I have lived in Philadelphia almost 28 years, and I like it very much. I grew up in New York, and I have some of the typical New Yorker snobbery about the rest of the world, a sort of patronizing “oh, isn't that cute, at least you tried” attitude. This is not a good thing, and I have tried to get rid of it, with only partial success. Philadelphia is not New York and it is never going to be New York, and I am okay with that. When I first got here I was more doubtful, but I made an effort to find and appreciate things about Philadelphia that were better than in New York. There are many, but it took me a while to start noticing them.
In 1992 I wrote an article that began:
Someone asked me once what Philadelphia has that New York doesn't. I couldn't come up with anything good.
But the article explained explained that since then, I had found an excellent answer. I wrote about how I loved the Schuylkill river and how New York had nothing like the it. In Philadelphia you are always going back and forth across the Schuylkill river, sometimes in cars or buses or trains, sometimes on a bike, sometimes on foot. It is not a mighty river like the Hudson. (The Delaware fills that role for us.) The Schuylkill is smaller, but still important. The 1992 article said:
It makes what might otherwise be a static and monolithic entity into a dynamic and variable one. Manhattan is monolithic, like a giant baked potato. Philadelphia is complex inside, with structure and sub-organs, like your heart.
New York has rivers you can cross, but, like much of New York, they are not to human scale. Crossing the Brooklyn Bridge or the George Washington Bridge on foot are fun things to do, once in a while. But they are big productions, a thing you might want to plan ahead, as a special event. Crossing the Schuylkill on foot is something you do all the time. In 1993 I commuted across the Schuylkill on foot twice a day and it was lovely. I took a photograph of it each time, and enjoyed comparing the many looks of the Schuylkill.
Once I found that point of attachment, I started to find many more things about Philadelphia that are better than in New York. Just a few that come to mind:
In New York, if you run into someone you know but had not planned to see, or meet a stranger with whom you have a common acquaintance, you are stunned. It is an epic coincidence, not quite a once-in-a-lifetime kind of thing, but maybe not a once-a-year thing either. In Philadelphia it is still unusual enough to be an interesting and happy surprise but not so rare as to make you wonder if you are being pranked.
In Philadelphia, if you are walking down the street, and say hello to a stranger sitting on their stoop, they will say hello back to you. In New York they will stare at you as though you had just come from the moon, perhaps wondering what your angle is.
If you live in New York, it is preferable to spend all of August in your vacation home, even if it is located on the shore of the lake of boiling pitch in the eighth circle of Hell. The weather is more pleasant in the eighth circle than it is in New York in August, and the air is cleaner. Never in 28 years in Philadelphia have I endured weather that is as bad as New York in August.
This is only a partial list. Philadelphia is superior to New York in many ways, and I left out the most important ones. I am very fond of Philadelphia, which is why I have lived here for 28 years. I can appreciate its good points, and when I encounter its bad points I no longer snarl and say “In New York we knew how to do this right.” Usually.
Usually.
One thing about Philadelphia is seriously broken. Philadelphians do not know how to get on a bus.
Every culture has its own customs. Growing up as a New Yorker, I learned early and deeply a cardinal part of New York's protocol: Get out of the way. Seriously, if you visit New York and you can't get anything else right, at least get out of the way. Here is advice from Nathan Pyle's etiquette guide for newcomers to New York:

Insofar as I still have any authority to speak for New Yorkers, I endorse the advice in this book on their behalf. Quite a lot of it consists of special cases of “get out of the way”. Tip #41 says so in so many words: “Basically anything goes as long as you stay out of the way.” Tip #31 says to take your luggage off the subway seat next to you, and put it on your lap. Tip #65 depicts the correct way of stopping on the sidewalk to enjoy a slice of pizza: immediately adjacent to a piece of street furniture that the foot traffic would have had to have gone around anyway.
Suppose you get on the bus in New York. You will find that the back of the bus is full, and the front is much less so. You are at the front. What do you do now? You move as far back as is reasonably possible — up to the beginning of the full section — so that the next person to get in can do the same. This is (obviously, if you are a New Yorker) the only way to make efficient use of the space and fill up the bus.
In Philadelphia, people do not do this. People get on the bus, move as far back as is easy and convenient, perhaps halfway, or perhaps only a few feet, and then stop, as the mood takes them. And so it often happens that when the bus arrives the new passengers will have to stand in the stepwell, or can't get on at all — even though the bus is only half full. Not only is there standing room in the back, but there are usually seats in the back. The bus abandons people at the stop, because there is no room for them to get on, because there is someone standing halfway down blocking the aisle, and the person just in front of them doesn't want to push past them, and those two people block everyone else.
In New York, the passengers in front would brusquely push their way past these people and perhaps rebuke them. New Yorkers are great snarlers, but Philadelphians seem to be too polite to snarl at strangers. Nobody in Philadelphia says anything, and the space is wasted. People with kids and packages are standing up because people behind them can't be bothered to sit down.
I don't know what the problem is with these people. Wouldn't it easier to move to the back of the bus and to sit down in the empty seats than it is to stand up and block the aisle? I have tried for a quarter of a century to let go of the idea that people in New York are smarter and better and people elsewhere are slow-witted rubes, and I have mostly succeeded. But where Philadelphians are concerned, this bus behavior is a major sticking point.
In New York we knew how to do this right.
[Other articles in category /misc] permanent link
Mon, 18 Dec 2017A few weeks ago I was writing something about Turkey, and I needed a generic Turkish name, analogous to “John Doe”. I was going to use “Osman Yılmaz”, which I think would have been a decent choice, but I decided it would be more fun to ask a Turkish co-worker what the correct choice would be. I asked Kıvanç Yazan, who kindly allowed himself to be nerdsniped and gave me a great deal of information. In the rest of this article, anything about Turkish that is correct should be credited to him, while any mistakes are surely my own.
M. Yazan informs me that one common choice is “Ali Veli”. Here's a link he gave me to Ekşisözlük, which is the Turkish analog of Urban Dictionary, explaining (in Turkish) the connotations of “John Doe”. The page also mentions “John Smith”, which in turn links to a page about a footballer named Ali Öztürk—in fact two footballers. ([1] [2]) which is along the same lines as my “Osman Yılmaz” suggestion.
But M. Yazan told me about a much closer match for “John Doe”. It is:
sarı çizmeli Mehmet Ağa
which translates as “Mehmet Agha with yellow boots”. (‘Sarı’ = ‘yellow’; ‘çizmeli’ = ‘booted’.)
This oddly specific phrase really seems to be what I was looking for. M. Yazan provided several links:
- Ekşisözlük again
The official dictionary of the Turkish government
Unfortunately I can't find any way to link to the specific entry, but the definition it provides is “kim olduğu, nerede oturduğu bilinmeyen kimse” which means approximately “someone whose identity/place is unknown”.
A paper on “Personal Names in Sayings and Idioms”.
This is in Turkish, but M. Yazan has translated the relevant part as follows:
At the time when yellow boots were in fashion, a guy from İzmir put "Mehmet Aga" in his account book. When time came to pay the debt , he sent his servant and asked him to find "Mehmet Aga with yellow boots". The helper did find a Mehmet Aga, but it was not the one they were looking for. Then guy gets angry at his servant, to which his helper responded, “Sir, this is a big city, there are lots of people with yellow boots, and lots of people named Mehmet! You should write it in your book one more time!”
Another source I found was this online Turkish-English dictionary which glosses it as “Joe Schmoe”.
Finding online mentions of sarı çizmeli Mehmet Ağa is a little bit tricky, because he is also the title of a song by the very famous Turkish musician Barış Manço, and the references to this song swamp all the other results. This video features Manço's boots and although we cannot see for sure (the recording is in grayscale) I presume that the boots are yellow.
Thanks again, Kıvanç!
[ Addendum: The Turkish word for “in style” is “moda”. I guessed it was a French loanword. Kıvanç tells me I was close: it is from Italian. ]
[ Addendum 20171219: Wikipedia has an impressive list of placeholder names by language that includes Mehmet Ağa. ]
[ Addendum 20180105: The Hebrew version of Mehmet Ağa is at least 2600 years old! ]
[Other articles in category /lang] permanent link
Fri, 15 Dec 2017
Wasteful and frugal proofs in Ramsey theory
This math.se question asks how to show that, among any 11 integers, one can find a subset of exactly six that add up to a multiple of 6. Let's call this “Ebrahimi’s theorem”.
This was the last thing I read before I put away my phone and closed my eyes for the night, and it was a race to see if I would find an answer before I fell asleep. Sleep won the race this time. But the answer is not too hard.
First, observe that among any five numbers there are three that sum to a multiple of 3: Consider the remainders of the five numbers upon division by 3. There are three possible remainders. If all three remainders are represented, then the remainders are !!\{0,1,2\}!! and the sum of their representatives is a multiple of 3. Otherwise there is some remainder with three representatives, and the sum of these three is a multiple of 3.
Now take the 11 given numbers. Find a group of three whose sum is a multiple of 3 and set them aside. From the remaining 8 numbers, do this a second time. From the remaining 5 numbers, do it a third time.
We now have three groups of three numbers that each sum to a multiple of 3. Two of these sums must have the same parity. The six numbers in those two groups have an even sum that is a multiple of 3, and we win.
Here is a randomly-generated example:
$$3\quad 17\quad 35\quad 42\quad 44\quad 58\quad 60\quad 69\quad 92\quad 97\quad 97$$
Looking at the first 5 numbers !!3\ 17\ 35\ 42\ 44!! we see that on division by 3 these have remainders !!0\ 2\ 2\ 0\ 2!!. The remainder !!2!! is there three times, so we choose those three numbers !!\langle17\ 35\ 44\rangle!!, whose sum is a multiple of 3, and set them aside.
Now we take the leftover !!3!! and !!42!! and supplement them with three more unused numbers !!58\ 60\ 69!!. The remainders are !!0\ 0\ 1\ 0\ 0!! so we take !!\langle3\ 42\ 60\rangle!! and set them aside as a second group.
Then we take the five remaining unused numbers !!58\ 69\ 92\ 97\ 97!!. The remainders are !!1\ 0\ 2\ 1\ 1!!. The first three !!\langle 58\ 69\ 92\rangle!!have all different remainders, so let's use those as our third group.
The three groups are now !! \langle17\ 35\ 44\rangle, \langle3\ 42\ 60\rangle, \langle58\ 69\ 92\rangle!!. The first one has an even sum and the second has an odd sum. The third group has an odd sum, which matches the second group, so we choose the second and third groups, and that is our answer:
$$3\qquad 42\qquad 60\qquad 58 \qquad 69 \qquad 92$$
The sum of these is !!324 = 6\cdot 54!!.
This proves that 11 input numbers are sufficient to produce one output set of 6 whose sum is a multiple of 6. Let's write !!E(n, k)!! to mean that !!n!! inputs are enough to produce !!k!! outputs. That is, !!E(n, k)!! means “any set of !!n!! numbers contains !!k!! distinct 6-element subsets whose sum is a multiple of 6.” Ebrahimi’s theorem, which we have just proved, states that !!E(11, 1)!! is true, and obviously it also proves !!E(n, 1)!! for all larger !!n!!.
I would like to consider the following questions:
- Does this proof suffice to show that !!E(10, 1)!! is false?
- Does this proof suffice to show that !!E(11, 2)!! is false?
I am specifically not asking whether !!E(10, 1)!! or !!E(11, 2)!! are actually false. There are easy counterexamples that can be found without reference to the proof above. What I want to know is if the proof, as given, contains nontrivial information about these questions.
The reason I think this is interesting is that I think, upon more careful examination, that I will find that the proof above does prove at least one of these, perhaps with a very small bit of additional reasoning. But there are many similar proofs that do not work this way. Here is a famous example. Let !!W(n, k)!! be shorthand for the following claim:
Let the integers from 1 to !!n!! be partitioned into two sets. Then one of the two sets contains !!k!! distinct subsets of three elements of the form !!\{a, a+d, a+2d\}!! for integers !!a, d!!.
Then:
Van der Waerden's theorem: !!W(325, 1)!! is true.
!!W()!!, like !!E()!!, is monotonic: van der Waerden's theorem trivially implies !!W(n, 1)!! for all !!n!! larger than 325. Does it also imply that !!W(n, 1)!! is false for smaller !!n!!? No, not at all; this is actually untrue. Does it also imply that !!W(325, k)!! is false for !!k>1!!? No, this is false also.
Van der Waerden's theorem takes 325 inputs (the integers) and among them finds one output (the desired set of three). But this is extravagantly wasteful. A better argument shows that only 9 inputs were required for the same output, and once we know this it is trivial that 325 inputs will always produce at least 36 outputs, and probably a great many more.
Proofs of theorems in Ramsey theory are noted for being extravagant in exactly this way. But the proof of Ebrahimi's theorem is different. It is not only frugal, it is optimally so. It uses no more inputs than are absolutely necessary.
What is different about these cases? What is the source the frugality of the proof of Ebrahimi’s theorem? Is there a way that we can see from examination of the proof that it will be optimally frugal?
Ebrahimi’s theorem shows !!E(11, 1)!!. Suppose instead we want to show !!E(n, 2)!! for some !!n!!. From Ebrahimi’s theorem itself we immediately get !!E(22, 2)!! and indeed !!E(17, 2)!!. Is this the best we can do? (That is, is !!E(16, 2)!! false?) I bet it isn't. If it isn't, what went wrong? Or rather, what went right in the !!k=1!! case that stopped working when !!k>1!!?
I don't know.
[Other articles in category /math] permanent link
Sat, 09 Dec 2017The Volokh Conspiracy is a frequently-updated blog about legal issues. It reports on interesting upcoming court cases and recent court decisions and sometimes carries thoughtful and complex essays on legal theory. It is hosted by, but not otherwise affiliated with, the Washington Post.
Volokh periodically carries a “roundup of recent federal court decisions”, each with an intriguing one-paragraph summary and a link to the relevant documents, usually to the opinion itself. I love reading federal circuit court opinions. They are almost always carefully thought out and clearly-written. Even when I disagree with the decision, I almost always concede that the judges have a point. It often happens that I read the decision and say “of course that is how it must be decided, nobody could disagree with that”, and then I read the dissenting opinion and I say exactly the same thing. Then I rub my forehead and feel relieved that I'm not a federal circuit court judge.
This is true of U.S. Supreme Court decisions also. Back when I had more free time I would sometimes visit the listing of all recent decisions and pick out some at random to read. They were almost always really interesting. When you read the newspaper about these decisions, the newspaper always wants to make the issue simple and usually tribal. (“Our readers are on the (Red / Blue) Team, and the (Red / Blue) Team loves mangel-wurzels. Justice Furter voted against mangel-wurzels, that is because he is a very bad man who hates liberty! Rah rah team!”) The actual Supreme Court is almost always better than this.
For example we have Clarence Thomas's wonderful dissent in the case of Gonzales v. Raich. Raich was using marijuana for his personal medical use in California, where medical marijuana had been legal for years. The DEA confiscated and destroyed his supplier's plants. But the Constitution only gives Congress the right to regulate interstate commerce. This marijuana had been grown in California by a Californian, for use in California by a Californian, in accordance with California law, and had never crossed any state line. In a 6–3 decision, the court found that the relevant laws were nevertheless a permitted exercise of Congress's power to regulate commerce. You might have expected Justice Thomas to vote against marijuana. But he did not:
If the majority is to be taken seriously, the Federal Government may now regulate quilting bees, clothes drives, and potluck suppers throughout the 50 States. This makes a mockery of Madison’s assurance to the people of New York that the “powers delegated” to the Federal Government are “few and defined,” while those of the States are “numerous and indefinite.”
Thomas may not be a fan of marijuana, but he is even less a fan of federal overreach and abuse of the Commerce Clause. These nine people are much more complex than the newspapers would have you believe.
But I am digressing. Back to Volokh's federal court roundups. I have to be careful not to look at these roundups when I have anything else that must be done, because I inevitably get nerdsniped and read several of them. If you enjoy this kind of thing, this is the kind of thing you will enjoy.
I want to give some examples, but can't decide which sound most interesting, so here are three chosen at random from the most recent issue:
Warden at Brooklyn, N.Y., prison declines prisoner’s request to keep stuffed animals. A substantial burden on the prisoner’s sincere religious beliefs?
Online reviewer pillories Newport Beach accountant. Must Yelp reveal the reviewer’s identity?
With no crosswalks nearby, man jaywalks across five-lane avenue, is struck by vehicle. Is the church he was trying to reach negligent for putting its auxiliary parking lot there?
[ Addendum 20171213: Volokh has just left the Washington Post, and moved to Reason, citing changes in the Post's paywall policies. ]
[ Addendum 20210628: Much has changed since Gonzales v. Raich, and today Justice Thomas observed that even if the majority's argument stood up in 2004, justified by the Necessary and Proper clause, it no longer does, as the federal government no longer appears consider the prohibition of marijuana necessary or proper. ]
[ Addendum 20231218: This article lacks a clear, current link to the Short Circuit summaries that it discusses. Here's an index of John Ross' recent Short Circuit posts. ]
[Other articles in category /law] permanent link
Fri, 08 Dec 2017I drink a lot of coffee at work. Folks there often make a pot of coffee and leave it on the counter to share, but they never make decaf and I drink a lot of decaf, so I make a lot of single cups of decaf, which is time-consuming. More and more people swear by the AeroPress, which they say makes single cups of excellent coffee very quickly. It costs about $30. I got one and tried it out.
The AeroPress works like this: There is a cylinder, open at the top, closed but perforated at the bottom. You put a precut circle of filter paper into the bottom and add ground coffee on top of it. You put the cylinder onto your cup, then pour hot water into the cylinder.
So far this is just a regular single-cup drip process. But after a minute, you insert a plunger into the cylinder and push it down gently but firmly. The water is forced through the grounds and the filter into the cup.
In theory the press process makes better coffee than drip, because there is less opportunity to over-extract. The AeroPress coffee is good, but I did not think it tasted better than drip. Maybe someone else, fussier about coffee than I am, would be more impressed.
Another the selling points is that the process fully extracts the grounds, but much more quickly than a regular pourover cone, because you don't have to wait for all the dripping. One web site boasts:
Aeropress method shortens brew time to 20 seconds or less.
It does shorten the brew time. But you lose all the time again washing out the equipment. The pourover cone is easier to clean and dry. I would rather stand around watching the coffee drip through the cone than spend the same amount of time washing the coffee press.
The same web site says:
Lightweight, compact design saves on storage space.
This didn't work for me. I can't put it in my desk because it is still wet and it is difficult to dry. So it sits on a paper towel on top of my desk, taking up space and getting in the way. The cone dries faster.
The picture above makes it look very complicated, but the only interesting part itself is the press itself, shown at upper left. All the other stuff is unimportant. The intriguing hexagon thing is a a funnel you can stick in the top of the cylinder if you're not sure you can aim the water properly. The scoop is a scoop. The flat thing is for stirring the coffee in the cylinder, in case you don't know how to use a spoon. I threw mine away. The thing on the right is a holder for the unused paper filters. I suspect they were afraid people wouldn't want to pay $30 for just the press, so they bundled in all this extra stuff to make it look like you are getting more than you actually are. In the computer biz we call this “shovelware”.
My review: The AeroPress gets a solid “meh”. You can get a drip cone for five bucks. The advantages of the $30 AeroPress did not materialize for me, and are certainly not worth paying six times as much.
[Other articles in category /tech] permanent link
Wed, 06 Dec 2017As I mentioned before, I have started another
blog, called Content-type:
text/shitpost. While I don't recommend that you read it regularly,
you might want to scan over this list of the articles from November
2017 to see if anything catches your eye.
- FIRST POST!!1!
- The Vampire Flying Frog
- “As the crow flies”
- The ephod
- The uselessness of consistency proofs
- Bertrand Russell's Slack channel
- The Zimbabwean coup
- Non-star multiplication operators
- Canaan Banana
- Shitposting on Math StackExchange
- Colored beans
- How I rate restaurants
- A problem that looks harder than it is
- Dirty jokes that are orientation and gender nonspecific
- My secret identity
- My cute fantasy
- The Wise Men of Princeton
- The Hot Potato
- The fiber guys are here!
- The Hot Potato (addendum)
- Stealing Club
- The kids disappear and then come back
- Head Over Feet
- Intriguing trending hashtags
- Character-building exercises
- What’s the most annoying question to ask a nun in 1967?
- The Garden Court Eatery
- Mixing up left and right
- Mmmm fries
- A vector space over a field of scalars
- People are more than one person
- The most annoying question to ask a nun, explained
- Coma collective
- Computers suck: episode 17771 of 31279
- Abutment for multiplication and other things
- Today's 419 scam is…
- Abutments
- More multiplication by abutment
- Who is a convicted rapist?
- Code reviews
- Bjarne Stroustrup's many crimes against programming
- Colorado Appeals Court goes to Middle School
- Do NOT Resuscitate
I plan to continue to post monthly summaries here.
[Other articles in category /meta/shitpost] permanent link
Fri, 01 Dec 2017
Slaughter electric needle injector

[ This article appeared yesterday on Content-type:
text/shitpost but I decided later
there was nothing wrong with it, so I have moved it here. Apologies
if you are reading it twice. ]
At the end of the game Portal, one of the AI cores you must destroy starts reciting GLaDOS's cake recipe. Like GLaDOS herself, it starts reasonably enough, and then goes wildly off the rails. One of the more memorable ingredients from the end of the list is “slaughter electric needle injector”.
I looked into this a bit and I learned that there really is a slaughter electric needle injector. It is not nearly as ominous as it sounds. The needles themselves are not electric, and it has nothing to do with slaughter. Rather, it is a handheld electric-powered needle injector tool that happens to be manufactured by the Slaughter Instrument Company, Inc, founded more than a hundred years ago by Mr. George Slaughter.
Slaughter Co. manufactures tools for morticians and enbalmers
preparing bodies for burial. The electric needle
injector
is one such tool; they also manufacture a cordless electric needle
injector,
mentioned later as part of the same cake recipe.

The needles themselves are quite benign. They are small, with delicate six-inch brass wires attached, and cost about twenty-five cents each. The needles and the injector are used for securing a corpse's mouth so that it doesn't yawn open during the funeral. One needle is injected into the upper jaw and one into the lower, and then the wires are twisted together, holding the mouth shut. The mortician clips off the excess wire and tucks the ends into the mouth. Only two needles are needed per mouth.
There are a number of explanatory videos on YouTube, but I was not able to find any actual demonstrations.
[Other articles in category /tech] permanent link






