Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| More about ZF's asymmetry between union and intersection |
| On the consistency of PA |
| Rewriting published history in Git |
| The non-duality of open and closed sets |
| The weird ethics of life insurance |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 26 Aug 2012
Rewriting published history in Git
My earlier article about my
habits using Git attracted some comment, most of which was
favorable. But one recurring comment was puzzlement about my seeming
willingness to rewrite published history. In practice, this was not
at all a problem, I think for three reasons:
- Rewriting published history is not nearly as confusing as people seem to think it will be.
- I worked in a very small shop with very talented developers, so the necessary communication was easy.
- Our repository setup and workflow were very well-designed and unusually effective, and made a lot of things easier, including this one.
If there are N developers, there are N+1 repositories.
There is a master repository to which only a few very responsible persons can push. It is understood that history in this repository should almost never be rewritten, only in the most exceptional circumstances. We usually call this master repository gitbox. It has only a couple of branches, typically master and deployed. You had better not push incomplete work to master, because if you do someone is likely to deploy it. When you deploy a new version from master, you advance deployed up to master to match.
In addition, each developer has their own semi-public repository, named after them, which everyone can read, but which nobody but them can write. Mine is mjd, and that's what we call it when discussing it, but my personal git configuration calls it origin. When I git push origin master I am pushing to this semi-public repo.
It is understood that this semi-public repository is my sandbox and I am free to rewrite whatever history I want in it. People building atop my branches in this repo, therefore, know that they should be prepared for me to rewrite the history they see there, or to contact me if they want me to desist for some reason.
When I get the changes in my own semi-public repository the way I want them, then I push the changes up to gitbox. Nothing is considered truly "published" until it is on the master repo.
When a junior programmer is ready to deploy to the master repository, they can't do it themselves, because they only have read access on the master. Instead, they publish to their own semi-private repository, and then notify a senior programmer to review the changes. The senior programmer will then push those changes to the master repository and deploy them.
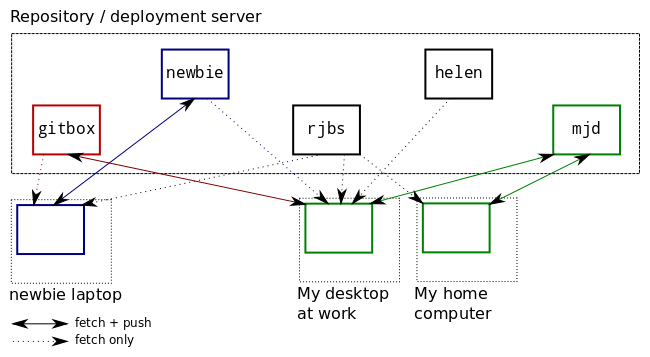
If I do work from three or four different machines, I can use the mjd repo to exchange commits between them. At the end of the day I will push my work-in-progress up to the mjd repo, and then if I want to look at it later that evening, I can fetch the work-in-progress to my laptop or another home computer.
I can create and abandon many topic branches without cluttering up the master repository's history. If I want to send a change or a new test file to a co-worker, I can push it to mjd and then point them at the branch there.
A related note: There is a lot of FUD around the rewriting of published history. For example, the "gitinfo" robot on the #git IRC channel has a canned message:
Rewriting public history is a very bad idea. Anyone else who may have pulled the old history will have to git pull --rebase and even worse things if they have tagged or branched, so you must publish your humiliation so they know what to do. You will need to git push -f to force the push. The server may not allow this. See receive.denyNonFastForwards (git-config)I think this grossly exaggerates the problems. Very bad! Humiliation! The server may deny you! But dealing with a rebased upstream branch is not very hard. It is at worst annoying: you have to rebase your subsequent work onto the rewritten branch and move any refs that pointed to that branch. If you don't have any subsequent work, you might still have to move refs, if you have any that point to it, but you might not have any.
[ Thanks to Rik Signes for helping me put this together. ]
[Other articles in category /prog] permanent link
Sat, 25 Aug 2012
On the consistency of PA
A monk asked Li Fu, "Master, how do we know that the Peano axioms are
consistent?"
Li Fu said, "The axioms are consistent because they have a model."
[Other articles in category /math] permanent link
Fri, 24 Aug 2012
More about ZF's asymmetry between union and intersection
In an article earlier this
week, I explored some oddities of defining a toplogy in terms of
closed sets rather than open sets, mostly as a result of analogous
asymmetry in the ZF
set theory axioms.
Let's review those briefly. The relevant axioms concern the operations by which sets can be constructed. There are two that are important. First is the axiom of union, which says that if !!{\mathcal F}!! is a family of sets, then we can form !!\bigcup {\mathcal F}!!, which is the union of all the sets in the family.
The other is actually a family of axioms, the specification axiom schema. It says that for any one-place predicate !!\phi(x)!! and any set !!X!! we can construct the subset of !!X!! for which !!\phi!! holds:
$$\{ x\in X \;|\; \phi(x) \}$$
Both of these are required. The axiom of union is for making bigger sets out of smaller ones, and the specification schema is for extracting smaller sets from bigger ones. (Also important is the axiom of pairing, which says that if !!x!! and !!y!! are sets, then so is the two-element set !!\{x, y\}!!; with pairing and union we can construct all the finite sets. But we won't need it in this article.)
Conspicuously absent is an axiom of intersection. If you have a family !!{\mathcal F}!! of sets, and you want a set of every element that is in some member of !!{\mathcal F}!!, that is easy; it is what the axiom of union gets you. But if you want a set of every element that is in every member of !!{\mathcal F}!!, you have to use specification.
Let's begin by defining this compact notation: $$\bigcap_{(X)} {\mathcal F}$$
for this longer formula: $$\{ x\in X \;|\; \forall f\in {\mathcal F} . x\in f \}$$
This is our intersection of the members of !!{\mathcal F}!!, taken "relative to !!X!!", as we say in the biz. It gives us all the elements of !!X!! that are in every member of !!{\mathcal F}!!. The !!X!! is mandatory in !!\bigcap_{(X)}!!, because ZF makes it mandatory when you construct a set by specification. If you leave it out, you get the Russell paradox.
Most of the time, though, the !!X!! is not very important. When !!{\mathcal F}!! is nonempty, we can choose some element !!f\in {\mathcal F}!!, and consider !!\bigcap_{(f)} {\mathcal F}!!, which is the "normal" intersection of !!{\mathcal F}!!. We can easily show that $$\bigcap_{(X)} {\mathcal F}\subseteq \bigcap_{(f)} {\mathcal F}$$ for any !!X!! whatever, and this immediately implies that $$\bigcap_{(f)} {\mathcal F} = \bigcap_{(f')}{\mathcal F}$$ for any two elements of !!{\mathcal F}!!, so when !!{\mathcal F}!! contains an element !!f!!, we can omit the subscript and just write $$\bigcap {\mathcal F}$$ for the usual intersection of members of !!{\mathcal F}!!.
Even the usually troublesome case of an empty family !!{\mathcal F}!! is no problem. In this case we have no !!f!! to use for !!\bigcap_{(f)} {\mathcal F}!!, but we can still take some other set !!X!! and talk about !!\bigcap_{(X)} \emptyset!!, which is just !!X!!.
Now, let's return to topology. I suggested that we should consider the following definition of a topology, in terms of closed sets, but without an a priori notion of the underlying space:
A co-topology is a family !!{\mathcal F}!! of sets, called "closed" sets, such that:
- The union of any two elements of !!{\mathcal F}!! is again in !!{\mathcal F}!!, and
- The intersection of any subfamily of !!{\mathcal F}!! is again in !!{\mathcal F}!!.
It now immediately follows that !!U!! itself is a closed set, since it is the intersection !!\bigcap_{(U)} \emptyset!! of the empty subfamily of !!{\mathcal F}!!.
If !!{\mathcal F}!! itself is empty, then so is !!U!!, and !!\bigcap_{(U)} {\mathcal F} = \emptyset!!, so that is all right. From here on we will assume that !!{\mathcal F}!! is nonempty, and therefore that !!\bigcap {\mathcal F}!!, with no relativization, is well-defined.
We still cannot prove that the empty set is closed; indeed, it might not be, because even !!M = \bigcap {\mathcal F}!! might not be empty. But as David Turner pointed out to me in email, the elements of !!M!! play a role dual to the extratoplogical points of a topological space that has been defined in terms of open sets. There might be points that are not in any open set anywhere, but we may as well ignore them, because they are topologically featureless, and just consider the space to be the union of the open sets. Analogously and dually, we can ignore the points of !!M!!, which are topologically featureless in the same way. Rather than considering !!{\mathcal F}!!, we should consider !!{\widehat{\mathcal F}}!!, whose members are the members of !!{\mathcal F}!!, but with !!M!! subtracted from each one:
$${\widehat{\mathcal F}} = \{\hat{f}\in 2^U \;|\; \exists f\in {\mathcal F} . \hat{f} = f\setminus M \}$$
So we may as well assume that this has been done behind the scenes and so that !!\bigcap {\mathcal F}!! is empty. If we have done this, then the empty set is closed.
Now we move on to open sets. An open set is defined to be the complement of a closed set, but we have to be a bit careful, because ZF does not have a global notion of the complement !!S^C!! of a set. Instead, it has only relative complements, or differences. !!X\setminus Y!! is defined as: $$X\setminus Y = \{ x\in X \;|\; x\notin Y\} $$
Here we say that the complement of !!Y!! is taken relative to !!X!!.
For the definition of open sets, we will say that the complement is taken relative to the universe of discourse !!U!!, and a set !!G!! is open if it has the form !!U\setminus f!! for some closed set !!f!!.
Anatoly Karp pointed out on Twitter that we know that the empty set is open, because it is the relative complement of !!U!!, which we already know is closed. And if we ensure that !!\bigcap {\mathcal F}!! is empty, as in the previous paragraph, then since the empty set is closed, !!U!! is open, and we have recovered all the original properties of a topology.
But gosh, what a pain it was; in contrast recovering the missing axioms from the corresponding open-set definition of a topology was painless. (John Armstrong said it was bizarre, and probably several other people were thinking that too. But I did not invent this bizarre idea; I got it from the opening paragraph of John L. Kelley's famous book General Topology, which has been in print since 1955.
Here Kelley deals with the empty set and the universe in two sentences, and never worries about them again. In contrast, doing the same thing for closed sets was fraught with technical difficulties, mostly arising from ZF. (The exception was the need to repair the nonemptiness of the minimal closed set !!M!!, which was not ZF's fault.)
On the other hand, perhaps this conclusion is knocking down a straw man. I think working mathematicians probably don't concern themselves much with whether their stuff works in ZF, much less with what silly contortions are required to make it work in ZF. I think day-to-day mathematical work, to the extent that it needs to deal with set theory at all, handles it in a fairly naïve way, depending on a sort of folk theory in which there is some reasonably but not absurdly big universe of discourse in which one can take complements and intersections, and without worrying about this sort of technical detail.
[ MathJax doesn't work in Atom or RSS syndication feeds, and can't be made to work, so if you are reading a syndicated version of this article, such as you would in Google Reader, or on Planet Haskell or PhillyLinux, you are seeing inlined images provided by the Google Charts API. The MathJax looks much better, and if you would like to compare, please visit my blog's home site. ]
[Other articles in category /math] permanent link
Tue, 21 Aug 2012
The non-duality of open and closed sets
I had long thought that it doesn't matter if we define a topology in
terms of open sets or in terms of closed sets, because the two
definitions are in every way dual and equivalent. This seems not to
be the case: the definition in terms of closed sets seems to be
slightly weaker than the definition in terms of open sets.
We can define a topology without reference to the underlying space as follows: A family !!{\mathfrak I}!! of sets is a topology if it is closed under pairwise intersections and arbitrary unions, and we call a set "open" if it is an element of !!{\mathfrak I}!!. From this we can recover the omitted axiom that says that !!\emptyset!! is open: it must be in !!{\mathfrak I}!! because it is the empty union !!\bigcup_{g\in\emptyset} g!!. We can also recover the underlying space of the topology, or at least some such space, because it is the unique maximal open set !!X=\bigcup_{g\in{\mathfrak I}} g!!. The space !!X!! might be embedded in some larger space, but we won't ever have to care, because that larger space is topologically featureless. From a topological point of view, !!X!! is our universe of discourse. We can then say that a set !!C!! is "closed" whenever !!X\setminus C!! is open, and prove all the usual theorems.
If we choose to work with closed sets instead, we run into problems. We can try starting out the same way: A family !!{\mathfrak I}!! of sets is a co-topology if it is closed under pairwise unions and arbitrary intersections, and we call a set "closed" if it is an element of !!{\mathfrak I}!!. But we can no longer prove that !!\emptyset\in{\mathfrak I}!!. We can still recover an underlying space !!X = \bigcup_{c\in{\mathfrak I}} c!!, but we cannot prove that !!X!! is closed, or identify any maximal closed set analogous to the maximal open set of the definition of the previous paragraph. We can construct a minimal closed set !!\bigcap_{c\in{\mathfrak I}} c!!, but we don't know anything useful about it, and in particular we don't know whether it is empty, whereas with the open-sets definition of a topology we can be sure that the empty set is the unique minimal open set.
We can repair part of this asymmetry by changing the "pairwise unions" axiom to "finite unions"; then the empty set is closed because it is a finite union of closed sets. But we still can't recover any maximal closed set. Given a topology, it is easy to identify the unique maximal closed set, but given a co-topology, one can't, and indeed there may not be one. The same thing goes wrong if one tries to define a topology in terms of a Kuratowski closure operator.
We might like to go on and say that complements of closed sets are open, but we can't, because we don't have a universe of discourse in which we can take complements.
None of this may make very much difference in practice, since we usually do have an a priori idea of the universe of discourse, and so we do not care much whether we can define a topology without reference to any underlying space. But it is at least conceivable that we might want to abstract away the underlying space, and if we do, it appears that open and closed sets are not as exactly symmetric as I thought they were.
Having thought about this some more, it seems to me that the ultimate source of the asymmetry here is in our model of set theory. The role of union and intersection in ZF is not as symmetric as one might like. There is an axiom of union, which asserts that the union of the members of some family of sets is again a set, but there is no corresponding axiom of intersection. To get the intersection of a family of sets !!\mathcal S!!, you use a specification axiom. Because of the way specification works, you cannot take an empty intersection, and there is no universal set. If topology were formulated in a set theory with a universal set, such as NF, I imagine the asymmetry would go away.
[ This is my first blog post using MathJax, which I hope will completely replace the ad-hoc patchwork of systems I had been using to insert mathematics. Please email me if you encounter any bugs. ]
[ Addendum 20120823: MathJax depends on executing Javascript, and so it won't render in an RSS or Atom feed or on any page where the blog content is syndicated. So my syndication feed is using the Google Charts service to render formulas for you. If the formulas look funny, try looking at http://blog.plover.com/ directly. ]
[ Addendum 20120824: There is a followup to this article. ]
[Other articles in category /math] permanent link
Wed, 15 Aug 2012
The weird ethics of life insurance
Many life insurance policies, including my own, include a clause that
says that they will not pay out in case of suicide. This not only
reduces the risk to the insurance company, it also removes an
important conflict of interest from the client. I own a life
insurance policy, and I am glad that I do not have this conflict of
interest, which, as I suffer from chronic depression, would only add
to my difficulties.
Without this clause, the insurance company might find itself in the business of enabling suicide, or even of encouraging people to commit suicide. Completely aside from any legal or financial problems this would cause for them, it is a totally immoral position to be in, and it is entirely creditable that they should try to avoid it.
But enforcement of suicide clauses raises some problems. The insurance company must investigate possible suicides, and enforce the suicide clauses, or else they have no value. So the company pays investigators to look into claims that might be suicides, and if their investigators determine that a death was due to suicide, the company must refuse to pay out. I will repeat that: the insurance company has a moral obligation to refuse to pay out if, in their best judgment, the death was due to suicide. Otherwise they are neglecting their duty and enabling suicide.
But the company's investigators will not always be correct. Even if their judgments are made entirely in good faith, they will still sometimes judge a death to be suicide when it wasn't. Then the decedent's grieving family will be denied the life insurance benefits to which they are actually entitled.
So here we have a situation in which even if everyone does exactly what they should be doing, and behaves in the most above-board and ethical manner possible, someone will inevitably end up getting horribly screwed.
[ Addendum 20120816: It has been brought to my attention that this post constains significant omissions and major factual errors. I will investigate further and try to post a correction. ]
Addendum 20220422: I never got around to the research, but the short summary is, the suicide determination is not made by the insurance company, but by the county coroner, who is independent of the insurer. This does point the way to a possible exploit, that the insurer could bribe or otherwise suborn the coroner. But this sort of exploit is present in all systems. My original point, that the hypothetical insurance company investigators would have a conflict of interest, has been completely addressed. ]
[Other articles in category /law] permanent link




