Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMAMJ |
| J | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 240 |
| Programming | 99 |
| Language | 93 |
| Miscellaneous | 69 |
| Book | 50 |
| Tech | 49 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 24 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Fri, 31 Dec 2021
Horrible insurance kerfuffle gone good
I doubt this story will be of interest to anyone but me, but it's the best thing that happened to me this month.
Back in October I bought a new house and arranged a homeowners’ insurance policy for it. The main purpose of such a policy is that if your house is destroyed by fire or some other calamity, the homeowners’ insurance people will arrange to build you a new house in the same place. If you have a mortgage, the lienholder will require a policy as a condition of the mortgage, but it's a good idea to have one even if you aren't required to. Usually the rebuild-the-house coverage is bundled with theft insurance, in case your house is robbed, and personal injury insurance, in case someone slips on your sidewalk.
I called the company that had brokered the policy for my previous house, and they assigned me to Brenda Wyman. Brenda presented me with one option: Company S. I said I was surprised at how high Company S's premium was. Brenda told me that Company S had by far the lowest premium. I asked if she had called the company that provided the insurance for my previous house. She said she had. I asked how much their quote was for. She told me, and the number was indeed larger than the quote from Company S. At this point I was tired of trying to extract information from Brenda and let it drop.
The insurance coverage is contingent on the insurer doing an inspection of the house to make sure it is not a hazard and is not about to fall down. Company S did their inspection in mid-November, but didn't notify me of the results until December. On December 6, they sent Brenda a letter: they had found seven things wrong with the house. I had until January 7 to fix them or they would cancel my insurance.
I was upset by this. Some of the seven things were minor, but two were not. The company wanted major roof work done. I was already in negotiations with roofers, but it might take me more than 31 days to select the roofer, sign the contract, and schedule and complete the work. There were major holidays coming up: roofers wouldn't work on Christmas. Roofing work is contingent on dry weather and I don't control the weather. Company S also demanded that I tear up and repour the cement in the alley that adjoins the house.
I could think of three ways to proceed:
- Attempt to schedule the work and get it all done by January 7
- Attempt to negotiate with Company S to get an extension, should it be impossible to complete all the work by January 7
- Arrange a new insurance policy with a different company
I started work on (1) and (2) and made a to-do item to proceed with (3) in a week depending on how things looked.
For (2) I immediately wrote back to Brenda to point out that the demands were unreasonable and might be impossible to satisfy. Was there any flexibility in the date? I also asked if there was a way to contact Company S directly.
Brenda's reply was reassuring. She claimed that Company S wouldn't require that all work be completed by January 7. It was enough for them, she said, that forward progress was being made, and if I had signed contracts by January 7 that would satisfy them.
Nevertheless I contacted Company S's customer service number, hoping to get something in writing. The customer service guy was brief and to the point: they didn't care that the holidays were coming up. They didn't care that I had only been given a few weeks to fix major items. They wouldn't give me an extension. But I could write to the inspections department and see if they said anything different.
I emailed the inspections department to see what they said, laying out the situation in detail: I had already addressed two of the seven items; I had verbal agreements to get three more finished by January 7, and I was working on the two major items. But I couldn't be certain the work would be complete by January 7 and if they insisted, I would have to obtain coverage elsewhere. The inspections department had promised to reply in 24 to 48 business hours.
Meanwhile I continued to talk to contractors about the major plumbing, cement, and roofing work that Company S had demanded.
I had emailed the inspections department midday Wednesday December 8 and been expecting a reply later that week. I didn't hear back from them until late Tuesday the 14th. At first I was only somewhat irritated, but then I realized: they had only promised a response in 24 to 48 business hours. There are only 40 business hours in a week, and they had replied 36 business hours after receiving my message, well before their promised deadline. That was even more irritating than when I thought they had replied late.
But at least their reply was brief, clear and direct:
We are unable to offer an extension. Please place the insured home with another carrier by 1/07/22.
I reported to Brenda:
I talked to Company S about this, to see if there was any leeway on the deadline. They told me there wasn't and suggested I should get different insurance.
Please hook me up with someone else.
Brenda continued to insist that Company S would give me an extension:
When I discussed with Company S, they advised me that as long as you are making progress with this and show contracts they could extend it. I would need this information to contact them with it.
I was not going to trust Brenda's say-so when I had it from the horse's mouth that the situation was the exact opposite. What if I proceeded with Brenda's plan, provided the documentation she suggested, and then on January 7, Company S refused to give me the hoped-for extension that they had already told me they would refuse to give me? Even Brenda had only said “they could extend it”, not “they would extend it”.
I said:
That's the opposite of what they told me. I got email yesterday from Company S that says:
We are unable to offer an extension. Please place the insured home with another carrier by 1/07/22.If it's sufficient for me to be making progress and show contracts, I want it in writing from them this week.
Brenda did not seem to appreciate the situation, that on one hand I had a vague, secondhand suggestion that I could maybe get an extension, and on the other hand I had a clear commitment directly from Company S to cancel my policy on January 7.
Brenda talked to Company S again but did not get any actual commitments. Her contact said:
Hello Brenda, you can have the insured call customer service to discuss the issues.The best way to resolve this is to email photos of any corrections made to the inspections inbox for review…
I reminded Brenda that I had already spoken to customer service and they had told me they would not negotiate, and that I similarly had a written reply from their inspections group saying the same thing. I also pointed out:
I emailed them at 1PM on Wednesday Dec 8th and didn't hear back until the following Monday. That is not an effective way to communicate when the situation is changing day-to-day as it is here.
Brenda and I were also having some difficulty communicating, it seemed:
You can send me the things you have right now and I can contact them and see what can be done.I understand your frustration with this, but when it comes to what they are wanting I am also stuck trying to resolve it for you but I do have to present the proof of repairs for them to even consider.
I made one more attempt to communicate with Brenda. I summarized the progress I had made and when work was scheduled.
I told them all this in the email I sent their inspections department last week, and their reply was “we are unable to offer an extension. Please place the insured home with another carrier by 1/07/22.”
So that is what I am asking you to do.
To me that seems clear, direct, and unambiguous. But not to Brenda, who said:
If you can change those verbal agreements to actually written up agreement on their letterhead that would show you are doing it but can’t be done til after 1/7. Especially since you put a deposit down with the cement person.Definitely send me the pictures of the trees trimmed and vines removed.
Brenda wanted me to contact the barely-literate cement guy and have him write up the agreement on “letterhead” (that he surely didn't have), and for what? To send to Company S, which had already told me twice that they didn't want it.
That seemed to be the end of that road. I hate repeating myself and I wasn't going to ask Brenda a third time. If Brenda wouldn't find me another insurer, I would find one without her. My first couple of tries didn't bear fruit but the third one did. The new agent (not Brenda or anyone who works for Brenda's company) told me:
Brenda had arranged too much insurance for me; I was paying to have the Company S agree to spend up to $X to rebuild my house, but rebuilding the house couldn't possibly cost more than $⅔X.
Most homeowners’ insurance companies would have given me a six-month grace period to make the necessary repairs. Company S was notoriously inflexible.
The new guy was able to arrange new coverage for me with an insurance premium 15% lower than the one Brenda had gotten me. I notified Company S the next day that I was ending my coverage and wanted a refund. (To their credit, this was completely painless, and the refund check arrived timely.)
I didn't bother to inform Brenda. Maybe I'll hear from her again, maybe I won't. She has all the information she needs to figure out what happened, if she cares to.
Okay, why have I written down this long story? Because it made me really happy. It is a distillation of my growth as an adult.
Faced with a difficult and complicated situation, I was able to deal with it constructively and timely. I didn't crawl under the covers. I didn't procrastinate. I didn't take the superficially easy way out, of crossing my fingers, hoping that Brenda was right and that I wouldn't get screwed on January 7.
I pursued a three-prong approach. I'm bad at long-term planning, good at short-term improvising, and the key to being a successful improviser is to leave as many options open for as long as you can. I did that this time. When Brenda wouldn't help me find new insurance, I found it myself. But if I hadn't found new insurance, maybe it would have turned out Brenda was right and I could get an extension. Or even if Brenda had been wrong, maybe I could have completed the repairs by January 7. There were a lot of ways this could have gone, a lot of ways it could have turned out okay, and I pushed everything forward in parallel until I found a way through.
I executed my plans timely. The whole business was over in less than two weeks: I got the inspection warning from Company S on December 6, and canceled their policy effective the 17th. There's a decent chance that, even had I not been able to get a new insurance policy, I would have been able to complete the repairs before the deadline; two of the seven items had been taken care of and four more scheduled on or before January 7. The cement guy demolished the old alley on December 21 and poured the new one on the 23rd. (The roof stuff is going to be more complicated and once I got my new insurance with the six-month grace period I stopped worrying about it.)
And I didn't lose my temper. I didn't insult Brenda or the innocent Company S customer service rep. I wasn't sarcastic. I didn't whine.
I solved an adult problem like an adult! I was grinning about this for several days around December 17–20. This is the sort of thing that only a middle-aged person can get excited about, but I like middle age, which has been really good for me in so many ways. I wonder, what would my 22-year old self have thought about this story? Would he have been surprised? Amazed? Astounded? (Horrified?) I don't think he would have forseen this degree of competence.
Happy new year, readers. May the coming twelve months be better for you than the previous.
[ Addendum: The insurance agent's name is not actually ‘Brenda Wyman’. Absolutely nothing in this post has any connection with any real person with that name. ]
[Other articles in category /brain] permanent link
Thu, 30 Dec 2021
A little more about the pedagogy of what it means to be transcendental
[ This is a followup to In simple English, what does it mean to be transcendental? ]
A while back a Math SE user posted a comment on my simple explanation of transcendental and algebraic numbers that asked why my explanation had contained some redundancies:
Are there any numbers for which division is necessary? I can't think of any. Likewise, subtracting integers is redundant; I believe all you need is "you can add any integer; you can multiply by any non-zero integer; you can multiply by x."
This is true! I had said:
We will play a game. Suppose you have some number !!x!!. You start with !!x!! and then you can add, subtract, multiply, or divide by any integer, except zero. You can also multiply by !!x!!. You can do these things as many times as you want. If the total becomes zero, you win.
and you don't need subtraction or division. (The underlying mathematical fact that motivated this answer is that integer polynomials are the free ring over the integers. For a ring you only need addition and multiplication.) So why did I mention subtraction and division? They're not mathematically necessary, doesn't it make the answer more complicated to put them in?
I had considered this carefully, and had decided it was simpler this way. The target audience is a person with no significant mathematical training. To a mathematician, it's obvious that inclusion of integers includes subtraction as a special case because you can simply add a negative integer. But non-mathematicians are not used to thinking this way. They have been taught that there are four arithmetic operations. If I mention all four, they will understand that all the operations of basic arithmetic are allowed. But if I had said only "addition and multiplication" many people would have been distracted and wondered "why just those two? Why not some other two?". Including all four avoids this distraction.
I could have said only “addition and multiplication” and later on explained that allowing subtraction and division doesn't change anything. I think this would have been an inferior choice. It's best to get to the point as quickly as possible. In this case the point is that all the operations of basic arithmetic are allowed. The fact that you can omit two is not relevant. My version is shorter and clearer, and avoids the whole issue.
If my version were less technically correct, that would be a major drawback. Sacrificing correctness for clarity is a seductive but usually harmful choice. The result may appear more clear, when it actually isn't, because of the subtle errors that have been papered over. In this case, though, nothing was sacrificed. It's 100% correct both ways. Mathematicians might prefer the minimal statement, but whole point of this answer is that it is correct even though it is not written in the way that a mathematician would prefer.
I'd like to boil this down to a pithy maxim, but I'm not sure I can do it without being inane. There's something in it about how, when you write something for non mathematicians, you should try to write every part of it for non-mathematicians, not just at the surface presentation but in the deeper layers too.
There's also something about how you should be very careful to distinguish the underlying mathematical truth on the one hand, from the practices that mathematicians have developed to help them in their day-to-day business, or to help them communicate with other mathematicians, or that are merely historical accidents, on the other. The underlying truth is the important part. The rest can be jettisoned.
[Other articles in category /math/se] permanent link
Mon, 22 Nov 2021On Saturday I was thinking about how each of !!48, 49, 50!! is a multiple of a square number, and similarly !!98, 99, 100!!. No such sequence of four numbers came immediately to mind. The smallest example turns out to be !!242, 243, 244, 245!!.
Let's say a number is “squareful” if it has the form $$a\cdot b^2$$ for !!b>1!!. The opposite, “squarefree”, is a standard term, but “non-squarefree” sounds even worse than “squareful”. Do ten consecutive squareful numbers exist, and if so, how can we find them?
I did a little algebraic tinkering but didn't come up with anything. If !!n,n+1, n+2!! are consecutive squareful numbers, then so are !!2n, 2n+2, 2n+4!!, except they aren't consecutive, but maybe we could find the right !!n!! so that !!2n+1!! and !!2n+3!! are also squareful. I couldn't make this work though, so I wrote some brute-force search programs to get the lay of the land.
The computer quickly produced sequences of length 7:
$$\begin{array}{rcrr} 217070 & = & 4430 \ · & 7^2 \\ 217071 & = & 24119 \ · & 3^2 \\ 217072 & = & 54268 \ · & 2^2 \\ 217073 & = & 17 \ · & 113^2 \\ 217074 & = & 1794 \ · & 11^2 \\ 217075 & = & 8683 \ · & 5^2 \\ 217076 & = & 54269 \ · & 2^2 \end{array} $$
and length 8:
$$\begin{array}{rcrr} 1092747 & = & 3027 \ · & 19^2 \\ 1092748 & = & 273187 \ · & 2^2 \\ 1092749 & = & 22301 \ · & 7^2 \\ 1092750 & = & 43710 \ · & 5^2 \\ 1092751 & = & 9031 \ · & 11^2 \\ 1092752 & = & 273188 \ · & 2^2 \\ 1092753 & = & 121417 \ · & 3^2 \\ 1092754 & = & 6466 \ · & 13^2 \\ \end{array} $$
Neither of these suggested anything to me, and nor did any of the other outputs, so I stuck !!1092747!! into OEIS. With numbers like that you don't even have to ask for the whole sequence, you only need to ask for the one number. Six sequences came up but the first five are all the same and were what I was looking for: A045882: Smallest term of first run of (at least) n consecutive integers which are not squarefree.
This led me to Louis Marmet's paper First occurrences of square-free gaps and an algorithm for their computation. The paper provides the earliest sequences of !!k!! consecutive squareful numbers, for !!k≤ 18!!, and bounds for how far out these sequences must be when !!k≤24!!. This is enough to answer the questions I originally asked:
Are there ten consecutive squareful numbers? Yes, the smallest example starts at !!262\,315\,467!!, found in 1999 by D. Bernier.
How can we find them? Marmet gives a sieve method that starts simple and becomes increasingly elaborate.
The paper is from 2007, so it seems plausible that the same algorithms on 2021 computers could produce some previously unknown results.
[ Addendum 20211124: The original version of this article ended “The general problem, of whether there are arbitrarily long sequences of squareful numbers, seems to be open.” This is completely wrong. Daniel Wagner and Shreevatsa R. pointed out that the existence of arbitrarily long sequences is quite elementary. Pick any squares you like that do not share a common factor, say for example !!49, 9, 4,!! and !!25!!. Now (because Chinese remainder theorem) you can find consecutive numbers that are multiples of those specific squares; in this case !!28322, 28323, 28324, 28325!!. ]
[ In only vaguely related news, I was driving Toph to school this morning, and a car in front of mine had license plate number !!5625 = 75^2!!. ]
[Other articles in category /math] permanent link
Thu, 18 Nov 2021
In simple English, what does it mean to be transcendental?
I've been meaning to write this up for a while, but somehow never got around to it. In my opinion, it's the best Math Stack Exchange post I've ever written. And also remarkable: its excellence was widely recognized. Often I work hard and write posts that I think are really good, and they get one or two upvotes; that's okay, because the work is its own reward. And sometimes I write posts that are nothing at all that get a lot of votes anyway, and that is okay because the Math SE gods are fickle. But this one was great and it got what it deserved.
I am really proud of it, and in this post I am going to boast as shamelessly as I can.
The question was:
There were several answers posted immediately that essentially recited the definition, some better than others. At the time I arrived, the most successful of these was by Akiva Weinberger, which already had around fifty upvotes.
… Numbers like this, that satisfy polynomial equations, are called algebraic numbers. … A real (or complex) number that's not algebraic is called transcendental.
If you're going to essentially quote the definition, I don't think you can do better than to explain it the way Akiva Weinberger did. It was a good answer!
Once one answer gets several upvotes, it moves to the top of the list, right under the question itself. People see it first, and they give it more votes. A new answer has zero votes, and is near the bottom of the page, so people tend it ignore it. It's really hard for new answers to surpass a highly-upvoted previous answer. And while fifty upvotes on some stack exchanges is not a large number, on Math SE fifty is a lot; less than 0.2% of answers score so high.
I was unhappy with the several quoting-the-definition answers. Because honestly "numbers… that satisfy polynomial equations" is not “simple English” or “layman's terms” as the OP requested. Okay, transcendental numbers have something to do with polynomial equations, but why do we care about polynomial equations? It's just explaining one obscure mathematical abstraction in terms of second one.
I tried to think a little deeper. Why do we care about polynomials? And I decided: it's because the integer polynomials are the free ring over the integers. That's not simple English either, but the idea is simple and I thought I could explain it simply. Here's what I wrote:
We will play a game. Suppose you have some number !!x!!. You start with !!x!! and then you can add, subtract, multiply, or divide by any integer, except zero. You can also multiply by !!x!!. You can do these things as many times as you want. If the total becomes zero, you win.
For example, suppose !!x!! is !!\frac23!!. Multiply by !!3!!, then subtract !!2!!. The result is zero. You win!
Suppose !!x!! is !!\sqrt[3] 7!!. Multiply by !!x!!, then by !!x!! again, then subtract !!7!!. You win!
Suppose !!x!! is !!\sqrt2 +\sqrt3!!. Here it's not easy to see how to win. But it turns out that if you multiply by !!x!!, subtract 10, multiply by !!x!! twice, and add !!1!!, then you win. (This is not supposed to be obvious; you can try it with your calculator.)
But if you start with !!x=\pi!!, you cannot win. There is no way to get from !!\pi!! to !!0!! if you add, subtract, multiply, or divide by integers, or multiply by !!\pi!!, no matter how many steps you take. (This is also not supposed to be obvious. It is a very tricky thing!)
Numbers like !!\sqrt 2+ \sqrt 3!! from which you can win are called algebraic. Numbers like !!\pi!! with which you can't win are called transcendental.
Why is this interesting? Each algebraic number is related arithmetically to the integers, and the winning moves in the game show you how so. The path to zero might be long and complicated, but each step is simple and there is a path. But transcendental numbers are fundamentally different: they are not arithmetically related to the integers via simple steps.
This answer was an immediate hit. It rocketed past the previous top answer into the stratosphere. Of 190,000 Math SE, answers, there are twenty with scores over 500; mine is 13th.
The original version left off the final paragraph (“Why is this interesting?”). Fortunately, someone posted a comment pointing out the lack. They were absolutely right, and I hastened to fix it.
I love this answer for several reasons:
It's not as short as possible, but it's short enough.
It's almost completely jargonless. It doesn't use the word “coefficient”. You don't have to know what a polynomial is. You only have to understand grade-school arithmetic. You don't even need to know what a square root is; you can still try the example if you have a calculator with a square root button.
Sometimes to translate a technical concept into plain language, one must sacrifice perfect accuracy, or omit important details. This explanation is technically flawless.
One often sees explanations of “irrational number” that refer to the fact such a number has a nonrepeating decimal expansion. While this is true, it's a not what irrationality is really about, but a secondary property. The true core of the matter is that an irrational number is not the ratio of any two integers.
My post didn't use the word “polynomial” and took a somewhat different path than the typical explanation, but it nevertheless hit directly at the core of the topic, not at a side issue. The “path to zero” thing isn't some property that algebraic numbers happen to have, it's the crucial issue, only phrased a little differently.
Also I had some unusually satisfying exchanges with critical commenters. There are a few I want to call out for triumphant mockery, but I have a policy of not mocking private persons on this blog, and this is just the kind of situation I intended to apply it to.
This is some good work. When I stand in judgment and God asks me if I did my work as well as I could, this is going to be one of the things I bring up.
[ Addendum 20211230: More about one of the finer points of this answer's pedagogical approach. ]
[Other articles in category /math/se] permanent link
Tue, 16 Nov 2021I had a small dispute this week about whether the Osborne 1 computer from 1981 could be considered a “laptop”. It certainly can't:
 Bilby, CC BY 3.0 via Wikimedia
Commons
Bilby, CC BY 3.0 via Wikimedia
Commons
The Osborne was advertised as a “portable” computer. Wikipedia describes it, more accurately, as “luggable”. I had a friend who owned one, and at the time I remarked “those people would call the Rock of Gibraltar ‘portable’, if it had a handle.”.
Looking into it a little more this week, I learned that the Osborne weighed 24½ pounds. Or, in British terms, 1¾ stone. If your computer has a weight measurable in “stone”, it ain't portable.
[Other articles in category /tech] permanent link
Sat, 13 Nov 2021
I said it was obvious but it was false
In a recent article about Norbert Wiener's construction of ordered pairs, I wrote:
The first thing I thought of was $$\pi_2(p) = \bigcup \{x\in p: |x| = 1\}$$ (“give me the contents of the singleton elements of !!p!!”) but one could also do $$\pi_2(p) = \{x: \{\{x\}\} \in p\},$$ and it's obvious that both of these are correct.
I said “it's obvious that both are correct”, but actually no! The first one certainly seems correct, but when I thought about it more carefully, I realized that the first formula is extremely complex, vastly moreso than the second. That !!|x|!! notation, so intuitive and simple-seeming, is hiding a huge amount of machinery. It denotes the cardinality of the set !!x!!, and cardinality is not part of the base language of set theory. Normally we don't worry about this much, but in this context, where we are trying to operate at the very bottom bare-metal level of set theory, it is important.
To define !!|x|!! requires a lot of theoretical apparatus. First we have to define the class of ordinals. Then we can show that every well-ordered set is order-isomorphic to some ordinal. Zermelo's theorem says that !!x!! has a well-ordering !!W!!, and then !!\langle x, W\rangle!! is order-isomorphic to some ordinal. There might be multiple such ordinals, but Zermelo's theorem guarantees there is at least one, and we can define !!|x|!! to be the smallest such ordinal. Whew! Are we done yet?
We are not. There is still more apparatus hiding in the phrases “well-ordering” and “order-isomorphic”: a well-ordering is certain kind of relation, and an order isomorphism is a certain kind of function. But we haven't defined relations and functions yet, and we can't, because we still don't have ordered pairs! And what is that !!\langle x, W\rangle!! notation supposed to mean anyway? Oh, it's just the… um… whoops.
So the !!|x|=1!! idea is not just inconveniently complex, but circular.
We can get rid of some of the complexity if we restrict the notion to finite sets (that eliminates the need for the full class of ordinals, for the axiom of choice and the full generality of Zermelo's theorem, and we can simplify it even more if we strip down our definition to the minimum requirements, which is that we only need to recognize cardinalities as large as 2.
But if we go that way we may as well dispense with a general notion of cardinality entirely, which is what the second definition does. Even without cardinality, we can still define a predicate which is true if and only if !!x!! is a singleton. That's simply: $$\operatorname{singleton}(x) \equiv_{def} \exists y. x = \{y\}.$$
One might want to restrict the domain of !!y!! here, depending on context.¹
To say that !!x!! has exactly two elements² we proceed analogously: $$\exists y. \exists z. z\ne y \land x = \{y, z\}.$$ And similarly we can define a predicate “has exactly !!n!! elements” for any fixed number !!n!!, even for infinite !!n!!. But a general definition of cardinality at this very early stage is far out of reach.
[ Addendum 20220414: I have no idea what I was thinking of when I said “… even for infinite !!n!!” in the previous paragraph, and I suspect that it is false. ]
¹ This issue is not as complex as it might appear. Although it appears that !!y!! must range over all possible sets, we can sidestep this by restricting our investigation to some particular universe of discourse, which can be any set of sets that we like. The restricted version of !!x\mapsto |x|!! is a true function, an actual set in the universe, rather than a class function.
² There does not seem to be any standard jargon for a set with exactly two elements . As far as I can tell, “doubleton” is not used. “Unordered pair” is not quite right, because the unordered pair !!\{a, a\}!! has only one element, not two.
[Other articles in category /oops] permanent link
Fri, 12 Nov 2021
Stack Exchange is a good place to explain initial and terminal objects in the category of sets
The fact that singleton sets are terminal in the category of sets, and the empty set is initial, is completely elementary, so it's often passed over without discussion. But understanding it requires understanding the behavior of empty functions, and while there is nothing complex about that, novices often haven't thought it through, because empty functions are useless except for the important role they play in Set. So it's not unusual to see questions like this one:
I have trouble understanding the difference between initial and terminal objects in category theory. … Why there can be morphism from empty set to any other set? And why there is not morphism to empty set as well?
I'm happy with the following answer, which is of the “you already knew this, you only thought you didn't” type. It doesn't reveal any new information, it doesn't present any insights. All it does is connect together some things that the querent hasn't connected before.
This kind of connecting is an important part of pedagogy, one that Math Stack Exchange is uniquely well-suited to deal with. It is not well-handled by the textbook (which should not be spending time or space on such an elementary issue) or in lectures (likewise). In practice it's often handled by the TA (or the professor), during office hours, which isn't a good way to do it: the TA will get bored after the second time, and most students never show up to office hours anyway. It can be well-handled if the class has a recitation section where a subset of the students show up at a set time for a session with the TA, but upper-level classes like category theory don't usually have enough students to warrant this kind of organization. When I taught at math camp, we would recognize this kind of thing on the fly and convene a tiny recitation section just to deal with the one issue, but again, very few category theory classes take place at math camp.
Stack Exchange, on the other hand, is a great place to do this. There are no time or space limitations. One person can write up the answer, and then later querents can be redirected to the pre-written answer.
Your confusion seems to be not so much about initial and terminal objects, but about what those look like in the category of sets. Looking at the formal definition of “function” will help make clear some of the unusual cases such as functions with empty domains.
A function from !!A!! to !!B!! can be understood as a set of pairs $$\langle a,b\rangle$$ where !!a\in A!! and !!b\in B!!. And:
There must be exactly one pair !!\langle a,b\rangle!! for each element !!a!! of !!A!!.
Exactly one, no more and no less, or the set of pairs is not a function.
For example, the function that takes an integer !!n!! and yields its square !!n^2!! can be understood as the (infinite) set of ordered pairs:
$$\{ \ldots ,\langle -2, 4\rangle, \langle -1, 1\rangle, \langle 0, 0\rangle ,\langle 1, 1\rangle, \langle 2, 4\rangle\ldots\}$$
And for each integer !!n!! there is exactly one pair !!\langle n, n^2\rangle!!. Some numbers can be missing on the right side (for example, there is no pair !!\langle n, 3\rangle!!) and some numbers can be repeated on the right (for example the function contains both !!\langle -2, 4\rangle!! and !!\langle 2, 4\rangle!!) but on the left each number appears exactly once.
Now suppose !!A!! is some set !!\{a_1, a_2, \ldots\}!! and !!B!! is a set with only one element !!\{b\}!!. What does a function from !!A!! to !!B!! look like? There is only one possible function: it must be: $$\{ \langle a_1, b\rangle, \langle a_2, b\rangle, \ldots\}.$$ There is no choice about the left-side elements of the pairs, because there must be exactly one pair for each element of !!A!!. There is also no choice about the right-side element of each pair. !!B!! has only one element, !!b!!, so the right-side element of each pair must be !!b!!.
So, if !!B!! is a one-element set, there is exactly one function from !!A!! to !!B!!. This is the definition of “terminal”, and one-element sets are terminal.
Now what if it's !!A!! that has only one element? We have !!A=\{a\}!! and !!B=\{b_1, b_2, \ldots\}!!. How many functions are there now? Only one?
One function is $$\{\langle a, b_1\rangle\}$$ another is $$\{\langle a, b_2\rangle\}$$ and another is $$\{\langle a, b_3\rangle\}$$ and so on. Each function is a set of pairs where the left-side elements come from !!A!!, and each element of !!A!! is in exactly one pair. !!A!! has only one element, so there can only be one pair in each function. Still, the functions are all different.
You said:
I would find it more intuitive if one-element set would be initial object too.
But for a one-element set !!A!! to be initial, there must be exactly one function !!A\to B!! for each !!B!!. And we see above that usually there are many functions !!A\to B!!.
Now we do functions on the empty set. Suppose !!A!! is !!\{a_1, a_2, \ldots\}!! and !!B!! is empty. What does a function from !!A\to B!! look like? It must be a set of pairs, it must have exactly one pair for each element of !!a!!, and the right-side of each pair must be an element of !!B!!. But !!B!! has no elements, so this is impossible: $$\{\langle a_1, ?\rangle, \langle a_2, ?\rangle, \ldots\}.$$
There is nothing to put on the right side of the pairs. So there are no functions !!A\to\varnothing!!. (There is one exception to this claim, which we will see in a minute.)
What if !!A!! is empty and !!B!! is not, say !!\{b_1, b_2, \ldots\}!!? A function !!A\to B!! is a set of pairs that has exactly one pair for each element of !!A!!. But !!A!! has no elements. No problem, the function has no pairs! $$\{\}$$
A function is a set of pairs, and the set can be empty. This is called the “empty function”. When !!A!! is the empty set, there is exactly one function from !!A\to B!!, the empty function, no matter what !!B!! is. This is the definition of “initial”, so the empty set is initial.
Does the empty set have an identity morphism? It does; the empty function !!\{ \}!! is its identity morphism. This is the one exception to the claim that there are no functions from !!A\to\varnothing!!: if !!A!! is also empty, the empty function is such a function, the only one.
The issue for topological spaces is exactly the same:
- When !!B!! has only one element, there is exactly one continuous map !!A\to B!! for every !!A!!.
- When !!A!! is empty, there is exactly one continuous map !!A\to B!! for every !!B!!: the empty function is the homeomorphism.
- When !!A!! has only one element, there are usually many continuous maps !!A\to B!!, one different one for each element of !!B!!.
There are categories in which the initial and terminal objects are the same:
In the category of groups, the trivial group (with one element) is both initial and terminal.
A less important but simpler example is Set*, the category of pointed sets, whose objects are nonempty sets in which one element has been painted red. The morphisms of Set* are ordinary functions that map the red element in the domain to the red element of the codomain.
I hope this was some help.
[ Thanks to Rupert Swarbrick for pointing out that I wrote “homeomorphism” instead of “continuous map” ]
[Other articles in category /math/se] permanent link
Wed, 10 Nov 2021
Annoying Kuratowski pair projection formula
In a recent article I complained that it was too difficult to extract the second component from a Kuratowski pair. The formula given by Wikipedia is not simple:
$$\pi_2(p) = \bigcup\left\{\left. x \in \bigcup p\,\right|\,\bigcup p \neq \bigcap p \implies x \notin \bigcap p \right\}$$
I said “It's so non-obvious that I suspect that it's wrong”. Matthijs Blom then contacted me with this formal correctness proof using the Lean theorem prover. (Raw source code.)
I have also convinced myself that it is correct, using old-fashioned methods.
!!\def\pr#1#2{\langle{#1},{#2}\rangle}!! !!\def\kp#1#2{\{\{{#1}\}, \{{#1},{#2}\}\}}!!
Let's recall !!p = \pr ab = \kp ab!! and observe that then $$ \bigcup p = \{a, b\}\\ \bigcap p = \{a\} $$
where possibly !!a=b!!. Then the Wikipedia formula can be written as:
$$\pi_2(\pr ab) = \bigcup\left\{\left. x \in \{a, b\} \,\right| \,\{a, b\} \neq \{a\} \implies x \notin \{a\} \right\}.$$
!!\{a, b\} \ne \{a\}!! can be rewritten as !!b\ne a!!. The !!x\notin\{a\}!! can be rewritten as !!x\ne a!!. We can rewrite the whole !!S\implies T!! thing as !!\lnot S\lor T!!:
$$\pi_2(\pr ab) = \bigcup\left\{\left. x \in \{a, b\} \,\right| \,a = b \lor x \ne a \right\}.$$
When !!a≠b!! the !!a=b!! clause in the guard condition vanishes, leaving
$$\begin{align} \pi_2(\pr ab) & = \bigcup\left\{\left. x \in \{a, b\} \,\right| \,x \ne a \right\} \\ % & = \bigcup\{ x \in \{ b\} \} \\ & = \bigcup\{b\} \\ & = b. \end{align} $$
When !!a=b!!, the !!\{a,b\}!! expression reduces to !!\{b\}!! and the guard condition !!a = b \lor x \ne a!! is always true, so we get:
$$\begin{align} \pi_2(\pr ab) & = \bigcup\{ x \in \{b\}\} \\ & = \bigcup\{b\} \\ & = b. \end{align} $$
[Other articles in category /math] permanent link
Tue, 09 Nov 2021
Not the expected examples of nonbinary characters in fiction
A member of the Recurse Center community recently asked for recommendations of fiction that set in a place where gender is not generally undersood as binary. It's easy to come up with recent examples, especially in SF, but a surprising older example occurred to me. Isaac Asimov, not usually remembered for his nuanced treatment of gender, wrote a novel whose three-sexed alien society is not merely set dressing, but a major plot and character point.
The Gods Themselves is closely concerned with the three-sexed aliens in a parallel universe. Each of three sexes has a very strictly prescribed gender role. It's important to the outcome of the story that the three main characters each have difficulty conforming to their prescribed role, precisely because they're exceptionally gifted individuals. Their difficulty in performing the roles is presented as growing out of their extraordinary personalities and also as a source of those exceptional abilities.
I think there are parts of the book the deal with humans also, perhaps exclusively male humans. (I read it only once, decades ago.) I don't remember those parts as clearly.
Anyway, three-sexed gender-nonconformant aliens. By Isaac Asimov, of all people. 1972.
It won the Hugo, Locus, and Nebula awards. Check it out.
[ Addendum 20211110: A reader informs me that there is a significant female human character that I had forgotten. Sorry, Ike! ]
[Other articles in category /book] permanent link
Sat, 06 Nov 2021
History of Science Shitcommenting
A recent post on History of Science and Mathematics stack exchange asks:
What makes the right angle special enough to be distinguished in the French metric system?
…
Why was the right angle chosen? A somewhat equivalent question: Out of all possible angles, why is the right angle particularly special?
This kind of question astounds me. It reminds me of this episode from Understood Betsy:
She weighed out the salt needed on the scales, and was very much surprised to find that there really is such a thing as an ounce. She had never met it before outside the pages of her arithmetic book, and she didn't know it lived anywhere else.
Does this person seriously not know what a right angle is, apart from some formal definition involving ninety degrees or whatever? Do they know that a right angle lives outside the pages of a mathematics text? Maybe not!
Anyway, I was shocked, and left this comment:
RIGHT ANGLE SPECIAL. IF WALL NOT BUILT AT RIGHT ANGLE TO GROUND, FALL DOWN.
I expected this would be quickly deleted, and might even earn me a reprimand from the moderators. It didn't, and now has seven upvotes.
[Other articles in category /misc] permanent link
Tue, 02 Nov 2021
One way in which Wiener pairs are simpler than Kuratowski pairs
!!\def\kp#1#2{\{\{{#1}\}, \{{#1},{#2}\}\}}!!
!!\def\nwp#1#2{\{\{\{{#1}\}, \emptyset\}, \{\{{#2}\}\}\}}!!
In a recent article about Wiener's definition of ordered pairs, I said:
In any case the Kuratowski thing is still simpler. I wonder why Wiener didn't think of it first. … Perhaps he didn't consider the details important.
But today I thought of a specific technical advantage that Wiener's definition has over Kuratowski's. The Kuratowski definition is
$$\langle a, b\rangle = \kp ab$$
and in the special case where !!a=b!!, this reduces to:
$$\kp aa = \{\{a\}, \{a\}\} = \{\{a\}\}$$
This can complicate the proofs. For example suppose you want to prove that if !!\langle p,q\rangle = \langle r,s\rangle!! then !!p=r!! and !!q=s!!. You might like to start by saying that each side represents a set of two elements, and then compare the elements. But you can't, because either might be a set with one element, so there's a special case. Or maybe you have to worry about what happens if !!b=\{a\}!!, is it still all right?
With the Wiener pair, it easy to see that nothing like this can happen:
$$\langle a, b\rangle = \nwp ab$$
Here, no matter what !!a!! and !!b!! might be, !!\langle a, b\rangle!! is a set with two elements. The set !!\{\{a\}, \emptyset\}!! must have exactly two elements; it's impossible that !!\{a\} = \emptyset!!. And since !!\{\{a\}, \emptyset\}!! has two elements, it's impossible for it to equal !!\{\{b\}\}!!, which has one element. So !!\langle a, b\rangle!! is always a two-element set !!\{P_a, P_b\}!!. When !!a=b!! there's no special case. You just get $$\nwp aa$$ which doesn't look any different.
This analysis explains another possibly puzzling feature of Wiener's definition: Why !!\nwp ab!! and not the apparently simpler !!{\{\{a, \emptyset\}, \{b\}\}}!!? But that proposal, like Kuratowski's, has annoying special cases. For example, the proposal collases to !!\{\{\emptyset\}\}!! when !!a=b=\emptyset!!.
The components of a Wiener pair are easy to extract again: the !!P_b!! component is a singleton, satisfying !!\bigcup P_b = b!!, and the !!P_a!! component is a two-element set satisfying !!\bigcup P_a = a!!. This is all considerably simpler than with the Kuratowski pair, where you can't get !!b!! alone, you can only get !!\{a, b\}!! and then you have to take the !!a!! back out, except that if !!a=b!! you musn't. To extract the second component from a Wiener pair is easy. The first thing I thought of was $$\pi_2(p) = \bigcup \{x\in p: |x| = 1\}$$ (“give me the contents of the singleton elements of !!p!!”) but one could also do $$\pi_2(p) = \{x: \{\{x\}\} \in p\},$$ and it's obvious that both of these are correct. [ Addendum 20211112: Obvious perhaps, but wrong; the first one is not correct! ]
The analogous formula given by Wikipedia for the Kuratowski pair is not at all obvious:
$$\pi_2(p) = \bigcup\left\{\left. x \in \bigcup p\,\right|\,\bigcup p \neq \bigcap p \implies x \notin \bigcap p \right\}$$
It's so non-obvious that I suspect that it's wrong. (Wikipedia.) But I don't want to put in the effort it would take to check it.
[ Addendum 20211110: Matthijs Blom and I have confirmed that the formula is correct. ]
[ Addendum 20211112: my suggested definition of !!\pi_2(p) = \bigcup \{x\in p: |x| = 1\}!! does not work, because at this point we have not yet defined what !!|x|!! means. And we can't, because it requires functions and relations, which we can't define without an adequate model for orderded pairs. ]
[Other articles in category /math] permanent link
Mon, 01 Nov 2021!!\def\zpr#1#2{\langle{#1},{#2}\rangle}\def\zkp#1#2{\{\{{#1}\}, \{{#1},{#2}\}\}}!!In Friday's article about the cartesian product I needed to show what the Kuratowski ordered-pair construction looks like when you nest the pairs. I originally wrote out the TeX for these by hand, but later decided I ought to use TeX macros to generate the formulas. First I did
\def\pr#1#2{\langle{#1},{#2}\rangle}
so that \pr ab would turn into !!\zpr ab!! and \pr a{\pr bc} would
turn into !!\zpr a{\zpr bc}!!.
Then I defined a macro for Kuratowski pairs. The Kuratowski pair for !!\zpr ab!! is the set !!\zkp ab!!, which is kind of a mess:
\def\kp#1#2{\{\{{#1}\}, \{{#1},{#2}\}\}}
Then the nested Kuratowski pairs turn into:
$$\begin{array}{cc} \verb+\kp a{\kp bc}+ & \zkp a{\zkp bc} \\ \verb+\kp{\kp ab}c+ & \zkp{\zkp ab}c \\ \end{array} $$
When I got this far I realized that my hand-expansion of
\kp{\kp ab}c had actually been wrong! I had originally written: $$
\{\{\{a\}, \{a, b\}\}, \{\{\{a\}, \{a, b\}\}, c\}\}.\qquad\color{\maroon}{Wrong!}$$
(There's a pair of braces missing around the first of the two !!\zkp ab!!.)
I used to give classes on programming style and technique, and one of the maxims I taught was “let the computer do the work”: use the computer to automate repetitive or error-prone tasks.
I was going to say I wish I'd taken my own advice here but hey — I did take my own advice, and it worked!
[Other articles in category /prog] permanent link
Fri, 29 Oct 2021
The nonassociativity of the cartesian product
!!\def\pr#1#2{\langle{#1},{#2}\rangle}!!
Set theory doesn't include the ordered pair as a primitive type; ordered pairs have to be represented as sets somehow. This caused technical problems in Principia Mathematica, as I explained a couple of years ago:
In 1910 … a crucial piece of machinery was missing: the ordered pair.
This technical problem was solved the following year, by Norbert Wiener. We usually use the simpler definition invented later by Kazimierz Kuratowski:
!!\def\kp#1#2{\{\{{#1}\}, \{{#1},{#2}\}\}}!!
$$\pr ab = \kp ab$$
This works well enough (and it has worked well enough that we have used it for a hundred years) but it has some warts. We define the cartesian product of two sets like this: $$A\times B = \{\pr ab \mid a\in A\text{ and }b\in B\}$$
With Kuratwoski pairs, and this definition of product, it is not the case that $$A\times(B\times C) = (A\times B)\times C\qquad\color{darkred}{Not!}$$ because on the left side the elements look like $$\pr a{\pr bc} = \kp a{\kp bc}$$ and on the right side the corresponding element looks like $$\pr{\pr ab}c = \kp{\kp ab}c.$$
This doesn't present any serious technical problems; see Henning Makholm's discussion here. He says:
The nitty-gritty of getting such details to work completely formally is not generally worth the trouble.
Even with highly fussy technical details like this, you can almost always find some mathematician who said “Ah, but you have to be a little bit careful, because…”. As far as I know, this matter is an exception. If anyone thinks there is something interesting going on here that deserves further examination, I have not heard of it. Everyone ignores the matter.
Category theory takes the high road away from the issue, breezily dismissing it with a remark about how !!A\times(B\times C)!! and !!(A\times B)\times C!! are isomorphic, and equal up to unique isomorphism. This is the right answer, because as Wiener said in 1911, the structure of the pairs as actual sets is “largely a matter of choice”, and the whole point of category theory is to ignore this sort of irrelevant distraction, focusing on the API rather than on the internal implementation.
But last week I wondered: what if you do actually want !!A\times(B\times C)!! be the exact same set as !!(A\times B)\times C!!, and not just naturally isomorphic? Is there some clever way to define ordered pairs so that this happens?
I got the question all written up for Math Stack Exchange, when I realized the answer: No.
Consider the special case where !!A = \{a\}, B=\{b\},!! and !!C = \{c\}!!. Then !!A\times(B\times C) = (A\times B)\times C!! implies $$\pr a{\pr bc} = \pr{\pr ab}c.$$
But this violates the one property that we absolutely require of ordered pairs, which is that !!\pr pq = \pr rs!! if and only if !!p=r!! and !!q=s!!. To have !!\pr a{\pr bc} = \pr{\pr ab}c!! would imply !!a=\pr ab!!, which would imply !!\pr a{b'} = a = \pr ab!! even when !!b'\ne b!!.
Oh well, it would have been fun.
[Other articles in category /math] permanent link
Thu, 28 Oct 2021
Kuratowski pairs and Wiener pairs
I mentioned a couple of years back that Principia Mathematica was bloated with repetitive material because they hadn't been able to unify the idea of a relation and a set, because the ordered pair hadn't been invented yet. There's a section that defines set union, !!\cup!!, and then proves that it is commutative and associative and so on, and later there is a separate section that defines relation union, !!\dot\cup!!, and proves the exact same theorems in the same way. In 2021 (or even in 1921) we would say that a relation is a set of ordered pairs, and that relation union is just a special case of set union.
To do this we have to interpret ordered pairs set-theoretically. The method we usually use for this was invented by Kazimierz Kuratowski:
$$\langle a, b\rangle = \{\{a\}, \{a,b\}\}$$
But there were earlier developments that also sufficed. Hausdorff suggested the more intuitive, but technically more complex:
$$\langle a, b\rangle = \{\{a, 1\}, \{b, 2\}\}$$
where !!1!! and !!2!! are any two objects that are not among the things we want to include in our ordered pairs. And even earlier, the first interpretation of pairs as sets was in 1911 by Norbert Wiener. In modern notation, Wiener's definition is:
$$\langle a, b\rangle = \{\{\{a\}, \emptyset\}, \{\{b\}\}\}.$$
Wiener actually used the notation of Principia Mathematica, which I reproduce for your amusement:
$$\def\i{\iota`} \i(\i\i a\cup \i\Lambda)\cup\i\i\i b $$
The !!\i x!! notation means essentially the same as !!\{x\}!!. I thought Principia Mathematica had a better way to write !!\{x, y\}!! than as !!\i x\cup\i y!!, but if so I can't remember what it is.
Someone once told me that Wiener's definition is more complicated than Kuratowski's because it had to function in the context of Whitehead and Russell's type theory. Kuratowski was working later, in set theory, so could use a simpler definition that wouldn't function in type theory because the types didn't match up. I had never thought carefully about this until now but it seems to be wrong. The Kuratowski pair requires !!a!! and !!b!! to be the same type, or else you can't put them both into the class !!\{a, b\}!!. But the Wiener pair requires this also. Say !!a!! and !!b!! have type !!n!!. Then !!\{a\}!! and !!\{b\}!! have type !!n+1!!, and !!\{\{a\}, \emptyset\}!! and !!\{\{b\}\}!! have type !!n+2!!. And because they have the same type we can put them both into the class !!\{\{\{a\}, \emptyset\}, \{\{b\}\}\}!!. But for this to work, !!a!! and !!b!! have to have the same type to begin with.
I wanted to find out what Wiener said about this, and Wikipedia referred me to his paper A Simplification of the logic of relations, and helpfully pointed out that it was reprinted in van Heijenoort's Source Book in Mathematical Logic, which I have on the shelf. (I love when this happens. It makes me feel like a scholar.) Wiener agrees: !!a!! and !!b!! must have the same type. But, he points out, if !!a!! and !!b!! have different types you can still make it work by adjusting the nesting level of !!a!! or !!b!! accordingly. For example, if !!b!! had a type one higher than !!a!!, you could use !!\{\{\{a\}, \emptyset\}, \{b\}\}!! instead.
In any case the Kuratowski thing is still simpler. I wonder why Wiener didn't think of it first. But he does say “the particular method selected of doing this is largely a matter of choice”, so perhaps he didn't consider the details important. As in fact they aren't. The important point, and the real point of Wiener's paper, is that you can now construe a two-place relation as a class of ordered pairs.
The paper ends by observing that this fixes the !!\cup!!-versus-!!\dot\cup!! extravagance of Principia Mathematica, since now !!R\cup S = R\,\dot\cup\, S!!. Similarly the class of relations is now a subclass of the class of classes, and so forth.
[ Addendum 20211030: This construction makes the cartesian product nonassociative, but nobody cares. ]
[ Addendum 20211101: One way in which Wiener pairs are simpler than Kuratowski pairs. ]
[Other articles in category /math] permanent link
Wed, 27 Oct 2021Is the idea here that If you're watching the pot, it'll seem like it takes longer than it should?
Or is the idea that if you keep taking the lid off to check if it's boiling yet, the heat will escape and it will actually take longer than it should?
[Other articles in category /misc] permanent link
Tue, 26 Oct 2021[ Content warning: pointless. ]
A colleague of mine recently remarked:
lose rhymes with choose; loose rhymes with goose
The parallel construction suggests that the two cases are similar. They're not. The words lose and choose are unique exceptions, and loose and goose aren't. All the -oose words other than choose rhyme with loose goose moose, and all the -ose words other than lose (and sometimes close) rhyme with rose nose pose.
English spelling is full of awful quagmires, but I don't remember noticing this one before. “-ough” gets talked up a lot, it's overplayed. This Goose thing is at least as bad.
For example, consider these rhyming words:
| booze ooze | choose | coos moos shoos woos zoos | chews crews jews news slews yews | dues clues rues sprues sues | lose | shoes | twos | cruise |
What a mess.
Shoes and woes don't rhyme.
Shoes rhymes with lose, but lose does not rhyme with close.
Close does rhyme with woes, and it also rhymes with gross, but they don't rhyme with each other. I suppose it is excusable that gross doesn't rhyme with woes, but it also doesn't rhyme with boss. And gross rhymes with dose for some reason. You'd think dose would rhyme with hose but if you want it to do that you have to spell it doze. Which at least makes sense: dose, unvoiced, doze, voiced. There are seven ways to write that -oze sound in doze, and the only words that I can find that actually spell it -oze are doze and froze:
| chose close hose nose pose rose | bows crows grows mows rows shows slows snows sows tows | does roes toes goes hoes joes sloes woes | doze froze | nos | owes | sews |
The most common ending here is -ows and looking at a word that has it you can't tell if it's crows shows slows or brows cows vows. Sometimes it's both, like with sows sows bows bows rows rows.
Oh, and does, which you see there in column 3 with toes and goes, but which is also an extremely common word that is usually pronounced “duz”, completely unlike any other word spelled that way. When it obviously should have been pronounced the way dues is.
Going the other way we have goose and loose which seems okay at first but turns into its own little quagmire:
| goose loose moose noose | deuce | juice sluice | spruce | use | Zeus |
At least you can't get these words mixed up with other words spelled the same way. Except for use and use. The consonant is voiced when it's a verb, unvoiced when it's a noun. Because reasons.
Well, for completeness I suppose I should do use:
| fuse | mews pews spews | hues | views | use |
Brits might want me to put news here and maybe some of its siblings.
Ugh, this could go on forever. Half the -ouse words rhyme with mouse and the other half rhyme with rouse. And the most important one rhymes with both: house.
Hmm, there's that verb-voiced, noun-unvoiced thing again. I should look into that. The close thing is similar: voiced is a verb, unvoiced is an adjective.
My respect for people who learn English as a second language was already high, but it has just gone up several notches.
[Other articles in category /lang] permanent link
Sat, 16 Oct 2021
Who is the namesake of the old Hungarian name for the month of June?
[ Previously ]
One oddity about the old-style Hungarian month names that I do not have time to investigate is that the old name of June was Szent Iván hava, Saint Ivan's month, or possibly Saint John's month. “John” in Hungarian is not Iván, it is Ján or János, at least at present. Would a Hungarian understand Szent Iván as a recognizably foreign name? I wonder which saint this is actually?
There is a Saint Ivan of Rila, but he is Bulgarian, so that could be a coincidence. Hungarian Wikipedia strangely does not seem to have an article about the most likely candidate, St. John the Evangelist, so I could not check if that John is known there as Ján or Iván or something else.
It does have an article about John the Baptist, who in Hungarian called Keresztelő János, not Iván. But that article links to the page about St. John the Baptist's Eve, which is titled Szent Iván éjszakája.
Further complicating the whole matter of Szent Iván hava is the issue that there have always been many Slavs in Hungary. The original birth record page is marked “KULA, HUNGARY”, which if correct puts it in what is now called Kula, Serbia — Hungary used to be bigger than it is now. Still why would the name of the month be in Slavic and not Magyar?
Do any of my Gentle Readers understand what is going on here?
[ Addendum: The English Wikipedia page for the Bulgarian Saint Ivan of Rila gives the Bulgarian-language version of his name. It's not written as Иван (“Ivan”) but as Йоан (“John”). The Bulgarian Wikipedia article about him is titled Иван Рилски (“Ivan Rilski”) but in the first line and the header of the infobox, his name is given instead as Йоан. I do not understand the degree to which John and Ivan are or are not interchangeable in this context. ]
[ Addendum 20211018: Michael Lugo points out that it is unlikely to be Ivan of Rila, whose feast day is in October. M. Lugo is right. This also argues strongly against the namesake of Szent Iván hava being John the Evangelist, as his feast is in December. The feast of John the Baptist is in June, so the Szent Iván of Szent Iván hava is probably John the Baptist, same as in Szent Iván éjszakája. I would still like to know why it is Szent Iván and not Szent János though. ]
[Other articles in category /calendar] permanent link
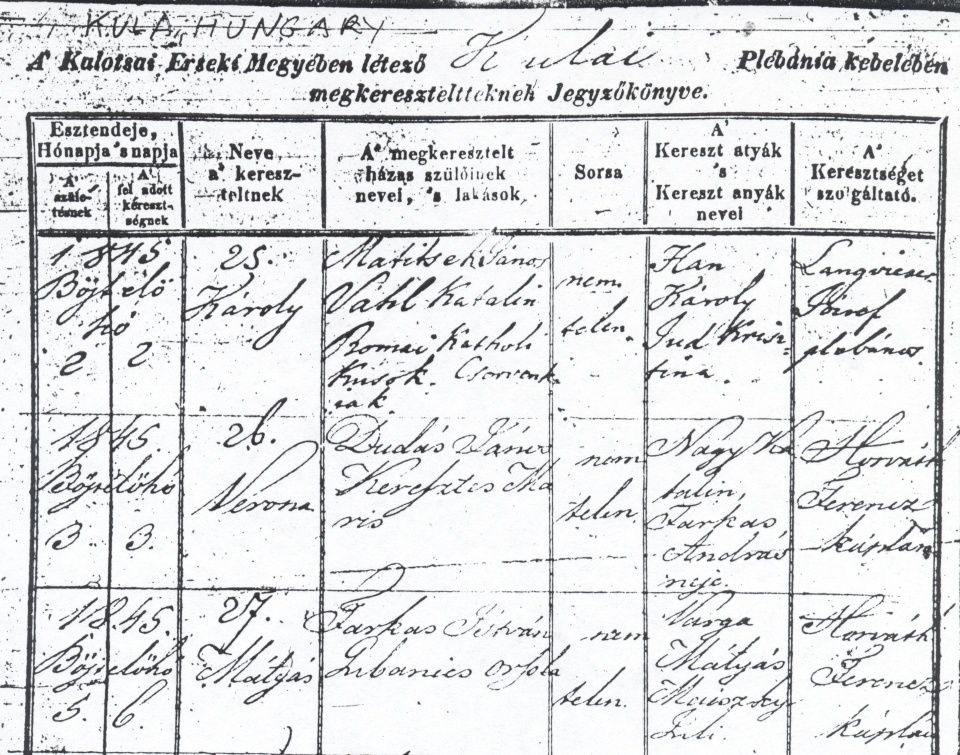
Fri, 15 Oct 2021I had a conversation with a co-worker about the origin of his name, in which he showed me the original Hungarian birth record of one of his ancestors. (The sample below does not include the line with that record.)
I had a fun time digging through this to figure out what it said. As you see, the scan quality is not good. The person writing the records has good handwriting, but not perfect, and not all the letters are easy to make out. (The penmanship of the second and third lines is noticeably better than the first.) Hungarian has letters ö and ő, which are different, but hard to distinguish when written longhand. The printed text is in a small font and is somewhat smudged. For example, what does this say?

Is the first letter in the second line an ‘f’ or a long ‘s’? Is “A’” an abbreviation, and if so what for? Is that a diacritical mark over the ‘e’ in the third line, or just a smudge? Except for the last, I don't know, but kereztségnek is something about baptism, maybe a dative form or something, so that column is baptism dates. This resolves one of the puzzles, which is why there are two numbers in the two leftmost columns: one is the birth date and one is the baptism date, and sometimes the baptism was done on a different day. For example, in the third line the child Mátyás (“Matthew”) was born on the 5th, and baptized on the 6th.
But the 6th of what? The box says “1845 / something” and presumably the something is the name of the month.
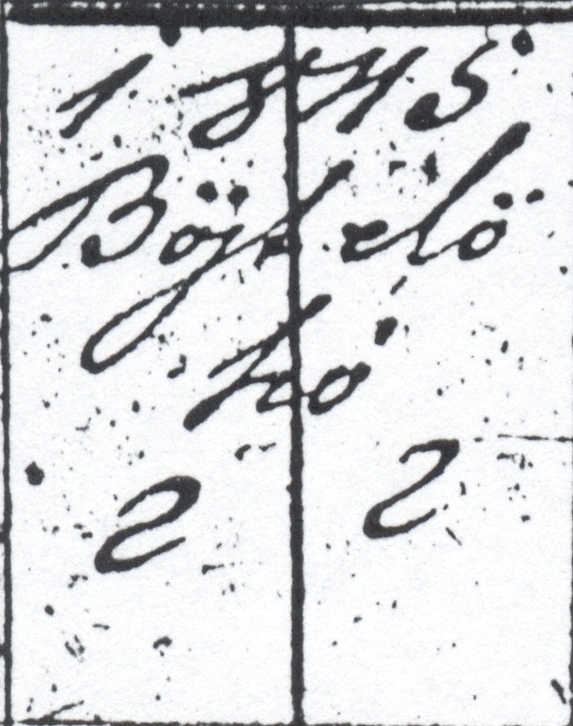
But I couldn't quite make it out (Bójkeló kó maybe?) and Google did not find anything to match my several tries. No problem, I can go the other direction: just pull up a list of the names of the months in Hungarian and see which one matches.
That didn't work. The names of the months in Hungarian are pretty much the same as in English (január, február, etc.) and there is nothing like Bójkeló kó. I was stuck.
But then I had a brainwave and asked Google for “old hungarian month names”. Paydirt! In former times, the month of February was called böjt elő hava, (“the month before fast”; hava is “month”) which here is abbreviated to Böjt elő ha’.
So that's what I learned: sometime between 1845 and now, the Hungarians changed the names of the months.
This page at fromhungarywithlove says that these month names were used from the 16th century until “the first third of the 20th century”.
[ Addendum 20211016: A further puzzle: The old name for June was “St. Iván's month”. Who was St. Iván? ]
[Other articles in category /calendar] permanent link
Sun, 10 Oct 2021“Salient” seems to have lost its original meaning, and people mostly use it as if it were synonymous with “relevant” or “pertinent”. This is unfortunate. It's from Latin salīre, which is to jump, and it originally meant something that jumps out at you. In a document, the salient point isn't necessarily the one that is most important, most crucial, or most worth consideration; it's the one that jumps out.
It is useful to have a word specifically for something that jumps out, but people no longer understand it that way.
Cognates of salīre include “assail" and “assault”, “salmon” (the jumping fish), and the mysterious “somersault”.
[Other articles in category /lang] permanent link
This Imgur gallery has a long text post, about a kid who saw the movie Labyrinth in London and met David Bowie after. The salient part was:
He seemed surprised I would want to know, and he told me the whole thing, all out of order, and I eked the details out of him.
This is a use of “eke” that I haven't seen before. Originally “eke” meant an increase, or a small addition, and it was also used in the sense of “also”. For example, from the prologue to the Wife of Bath's tale:
I hadde the bettre leyser for to pleye, And for to se, and eek for to be seye
(“I had more opportunity to play, and to see, and also to be seen.”)
Or also, “a nickname” started out as “an ekename”, an also-name.
From this we get the phrase “to eke out a living”, which means that you don't have quite enough resources, but by some sort of side hustle you are able to increase them to enough to live on.
But it seems to me that from there the meaning changed a little, so that while “eke out a living” continued to mean to increase one's income to make up a full living, it also began to connote increasing one's income bit by bit, in many small increments. This is the sense in which it appears to be used in the original quotation:
He seemed surprised I would want to know, and he told me the whole thing, all out of order, and I eked the details out of him.
Addenda
Searching for something in a corpus of Middle English can be very frustrating. I searched and searched the University of Michigan Corpus of Middle English Prose and Verse looking for the Chaucer quotation, and couldn't find it, because it has “to se” and “to be seye”, but I searched for “to see” and “to seye”; it has “eek” and I had been searching for “eke”. Ouch.
In the Chaucer, “leyser” is “leisure”, but a nearly-dead sense that we now see only in “complete the task at your leisure”.
[Other articles in category /lang] permanent link
Fri, 08 Oct 2021
Diminishing resources in the Korean Language
Hangul, the Korean alphabet, was originally introduced in the year 1443. At that time it had 28 letters, four of which have since fallen out of use. If the trend continues, the Korean alphabet will be completely used up by the year 7889, preceded by an awful period in which all the words will look like
앙 앙앙앙 앙앙 앙 앙앙앙앙 앙
and eventually
ㅏㅏㅏㅏㅏㅏㅏㅏㅏㅏ!
[Other articles in category /lang] permanent link
Tue, 05 Oct 2021Some traditional miracles ascribed to saints and other holy people are better than others. Jesus walking on water and quieting the storm are impressive and showy, but essentially unhelpful. Contrasting this kind of show-magic with the miracles of the Buddha, Jorge Luis Borges describes “a miracle of courtesy”:
The Buddha has to cross a desert at noon. The gods, from their thirty-three heavens, each send him down a parasol. The Buddha does not want to slight any of the gods, so he turns himself into thirty-three Buddhas. Each god sees a Buddha protected by the parasol he sent.
(It's Borges, so it's also possible he just made it up.)
My favorites of the Christian miracles are the miracles of the loaves and fishes, which are miracles of generosity and compassion. A multitude of people have come to see Jesus heal the sick:
As evening approached, the disciples came to him and said, “This is a remote place, and it’s already getting late. Send the crowds away, so they can go to the villages and buy themselves some food.”
Jesus replied, “They do not need to go away. You give them something to eat.”
“We have here only five loaves of bread and two fish,” they answered.
“Bring them here to me,” he said. And he directed the people to sit down on the grass. Taking the five loaves and the two fish and looking up to heaven, he gave thanks and broke the loaves. Then he gave them to the disciples, and the disciples gave them to the people. They all ate and were satisfied and the disciples picked up twelve basketfuls of broken pieces that were left over.
Much better than walking on water.
Anyway, that is peripheral to what I wanted to write about. Lately I learned that there is a painting by Il Sodoma (1477–1549, original name Giovanni Antonio Bazzi) titled St Benedict repairs a Broken Colander through Prayer.
A broken what now? Colander? Like, the thing I use to drain my tortellini?

I looked in the Big Dictionary to find out if maybe “colander” might sometimes mean something more impressive than the kitchen utensil, maybe some expensive and specialized piece of church equipment. Nope:
A vessel, usually of metal, closely perforated at the bottom with small holes, and used as a sieve or strainer in cookery.
There doesn't appear to be any such thing in the painting:
St. Benedict is kneeling in prayer, second from left, wearing a halo. The colander, it turns out, is the two rectangular brown things by his knees. As you see, one piece is visibly cracked. I don't know what is the red schmutz on the other piece.
(The long-haired guy in the middle, with the expensive gloves, is Il Sodoma himself. He is known to have kept pet badgers, which also make an appearance here.)
Google searches for "st. benedict" "colander" were no help. They
mostly produced references to this painting again.
I then wondered if maybe “colander” was a mistranslation. The Italian title for this painting is Come Benedetto risalda lo capistero che si era rotto. The Goog translates this as “How Benedict heals the broken master”, which was quite confusing. Google further confused me by glossing risalda as “rises”, which made me wonder if the repair of the broken colander (risalda lo capistero) was somehow a metaphor for the rising of Jesus. The idea seems rather silly, but Renaissance thinking does not always make sense to me, so I did not rule it out immediately. But no, risalda is repair, and capistero is a colander, or more precisely a sieve. The Goog's translation was simply wrong. (Fair enough, Google Translate is not intended to translate early-renaissance Italian.)
Book 2 of the Dialogues of Pope Gregory is about St. Benedict, and chapter 1 is titled “How he made a broken sieve whole and sound”:
It fell so out that his nurse borrowed of the neighbors a sieve to make clean wheat, which being left negligently on the table, by chance it was broken in two pieces, Whereupon she fell pitifully weeping, because she had borrowed it. The devout and religious youth Benedict, seeing his nurse so lamenting, moved with compassion, took away with him both the pieces of the sieve, and with tears fell to his prayers; and after he had done, rising up he found it so whole, that the place could not be seen where before it was broken.
So “colander” isn't quite right, but it's not too far off. The implement is probably made of wood, not metal. But it is indeed a perforated kitchen utensil. The suntanned lady on the left of the painting is the nurse, gazing ruefully at the table.
The colander is a tray for sifting wheat. The upper part (at left, with the big crack in it) has some sort of perforations or screen, which don't show up well in the painting. The lower part (at right) is a tray in which the sifted material is caught.
The right side of the painting depicts a later time after the colander has been repaired. The miraculous sieve has been hung up on a column (top center) for the wonderment of a crowd of admiring visitors.
Saint Anthony could command animals and was such an arresting speaker that even fish came to hear him preach. Some saints invoke the power of God to heal the blind and paralyzed, the drowned, the leprous, and the epileptic. St. Benedict healed a broken colander.
[Other articles in category /religion] permanent link
Sun, 03 Oct 2021
Simpson's paradox and Maxine Hong Kingston's mom
Yesterday's Simpson's paradox example reminds me of Maxine Hong Kingston's mother in The Woman Warrior:
When a sick person was about to die, my mother could read the fact of it a year ahead of time on the daughters-in-law’s faces. … My mother would take one look at the daughter-in-law who answered the door at the sick house and she’d say, “Find another doctor.” She would not touch death; therefore, untainted, she brought only health from house to house. “She must be a Jesus convert,” the people from the far villages said. “All her patients get well.”
[Other articles in category /math] permanent link
Sat, 02 Oct 2021
Simplest example of Simpson's paradox
I had read many times about Simpson's paradox but it never quite clicked for me. I saw many examples, but I couldn't quite get what was really going on. And I could never remember the numbers in the examples, so I couldn't ponder it while waiting for the bus or whatever.
Last month I sat down and thought about it, with the idea of coming up with the simplest and most memorable possible example. Here it is.
Imagine there is a disease that kills 50% of the people who get it.
There is a pill you can take if you get the disease. Of the people who take the pills, 80% die.
It looks like the pills are killing people. But they aren't, they are helpful.
This is Simpson's paradox.
What is really happening is that half the people with the disease have mild cases and half have severe cases. A patient with a mild case will get better on their own. But everyone with a severe case dies unless they receive treatment.
People with mild cases don't bother to take the pills, because they are going to get better anyway.
Only people with severe cases take the pills. 80% of them die, but without the pills they all would have died.
Now I understand Simpson's paradox.
[Other articles in category /math] permanent link
Fri, 01 Oct 2021Imagine an alien force, vastly more powerful than us, landing on Earth and demanding the value of !!R(5, 5)!! or they will destroy our planet. In that case, we should marshal all our computers and all our mathematicians and attempt to find the value. But suppose, instead, that they ask for yo mama's weight in pounds. In that case, we should attempt to destroy the aliens.
(With posthumous apologies to Paul Erdős)
[Other articles in category /math] permanent link
Ida-related flooding in Philadelphia
On September 1, Hurricane Ida hit Pennsylvania. Several tornadoes touched down near where I live in Philadelphia, and five people were killed. Fortunately Philadelphia itself was spared, and from where I live it only appeared to be an unusually-heavy rainstorm.
But Philadelphia is on the Schuylkill River, and all the water that Ida dumped northwest of Philadelphia ended up in the Schuylkill, which flooded epically and historically.
I-95 and I-76 also run through Philadelphia, and connecting them, in a deep trench along the northern boundary of the business district, is the Vine Street Expressway. Normally it looks like this:
(Google Street View, July 2019)
But on September 1 it looked like this:
Holy cow. I'd never seen anything like this before. How long would the expressway be shut down? I had no idea.
Toph and I went up there on September 4 to see the damage, but by then there wasn't much to see. It looked like this:
Traffic was flowing normally in the eastbound lane (far side). The westbound lane (near side, with the cone) was still closed but it was obvious that they were finishing the cleanup. That's some amazing work. I have no idea how you even begin to get something like that cleaned up, and no idea how to get it done in three days.
The streets were a little dirtier than usual, but if I hadn't known to look I probably wouldn't have noticed. (Philadelphia.) We did pass houses that had piles of ruined books outside, and we encountered two gentlemen who were glumly carrying out loads of soggy carpet from their flooded basement.
We walked on the path that runs by the river, which is normally about two or three meters above the level of the river itself. The river didn't look higher than usual, but we did see signs of the flood. The path is between the river and the train tracks, and there is a fence to keep you from crossing the tracks.
Here's picture I took on September 4:
The river has piled driftwood and other trash at the base of the fence. The fence itself is clogged with leaves and paper, left there when the river poured through it as through a sieve. The river not only overtopped its banks and flooded the footpath, it must have reached at least to the top of the fence.
Here's another shot of the fence. Over here the sieve became too clogged to let the water through and the entire fence collapsed. The on-ramp for the expressway is visible in the background.
Here's Google's Street View picture of what the fence was like in July 2016:
I have no special point to make, and leave you with this, which I think should be part of the Philadelphia historical archives. Content warning: unsanitary behavior.
[Other articles in category /misc] permanent link
Wed, 01 Sep 2021A recent Math StackExchange question asks “Prove every permutation of the alphabet contains a subset of six letters in order”. That is, you take a string of length 26 that contains each letter once; you can find a subsequence of six letters that is either increasing or decreasing.
Choosing a permutation at random, suppose we have:
q y x u l i n g w o c k j d r p f v t s h e a z b m
Then the sequence x w v t s e b has length 7 and is in descending
order. Or:
t h e q u i c k b r o w n f x j m p s v r l z y d g
This contains the ascending sequence h q r s v y. Also the
descending sequence t q o n m l d.
I thought about this for a while but couldn't make any progress. But OP had said “I know I have to construct a partially ordered set and possibly use Dilworth's Theorem…” so I looked up Dilworth's theorem.
It turns out I did actually know Dilworth's theorem. It is about partially-ordered sets. Dilworth's theorem says that if you partition a partially-ordered set into totally-ordered subsets, called ‘chains’, then the number of such chains is at least as big as the size of the largest “antichain”. An antichain is a subset in which no two elements are comparable.
This was enough of a hint, and I found the solution pretty quickly after that. Say that !!S[i]!! is the position of letter !!i!! in the string !!S!!. Define the partial order !!\prec!!: $$ i\prec j \qquad \equiv \qquad i < j \text{ and } S[i] < S[j] $$
That is, !!i\prec j!! means that !!i!! is alphabetically earlier than !!j!! and its position in !!S!! is to the left of !!j!!. This is obviously a partial ordering of the letters of the alphabet. Chains under !!\prec!! are, by definition, ascending sequences of letters from !!S!!. It's easy to show that antichains are descending sequences.
Partition !!S!! into chains. If any chain has length !!6!! or more, that is an ascending sequence of letters and we win.
If not, then no chain has more than 5 letters, and so there must be at least !!6!! chains, because !!5·5=25!! and there are !!26!! letters. Since there are at least !!6!! chains, Dilworth's theorem tells us there is an antichain of at least !!6!! letters, and hence a descending sequence of that length, and we win.
Once you have the idea to use Dilworth's theorem, the problem collapses. (You also have to invent the right !!\prec!! relation, but there's really only one possible choice.)
Maybe I'll write a followup article about how just having a theorem doesn't necessarily mean you have an algorithm. Mathematicians will say “partition !!S!! into chains,” but actually programming something like that might be nontrivial. Then finding the antichain among the chains might also be nontrivial.
[Other articles in category /math] permanent link
Sat, 28 Aug 2021In a transparent attempt to capitalize on the runaway success of The Wonderful Wizard of Oz, the publishers of L. Frank Baum's earlier book A New Wonderland re-released it under the title The Magical Monarch of Mo. What if this ploy had actually worked? Would the book have inspired a movie?
We're off to see the Monarch,
The Marvelous Monarch of Mo…
Naah, it kinda falls apart after that.
[Other articles in category /book] permanent link
On Twitter, Mike Coutermarsh suggested:
Job interview: “algorithms”
Reality: “Turn a 127 message deep slack thread between 5 engineers into a decision”
I suppose this was meant facetiously but I think it might contain the germ of a good idea.
Applicants are usually given timed a programming quiz. What if instead, the candidate was supplied with the 127-message Slack thread and given 24 hours to write up a proposal document? I honestly think this might produce good results.
Such a submission would be extremely probative of the candidate's talents and abilities, including:
- reading and understanding technical arguments
- balancing engineering tradeoffs
- foreseeing potential issues
- writing clear English
- planning
- seriousness
- writing coherent, well-organized, and persuasive documents
It is much more difficult to cheat on this task than on a typical programming exercise. The candidate certainly can't submit a prewritten essay that they found somewhere; that would be easy to detect. A candidate who can take someone else's prewritten essay and quickly rewrite it to plausibly appear original is probably quite well-qualified on many of the important metrics! (Plus an additional important one: the ability to do research. They had to locate, recognize, and read the essay they rewrote.)
It shouldn't be hard to change up the essay topic periodically, since the engineers will be producing several of those 127-message Slack threads every month. This also tends to impede cheating.
When a good candidate comes for an in-person interview, you have a ready-made topic of conversation. Instead of coding at the whiteboard, you can ask them to discuss their proposal.
Complaints that this would discriminate against candidates with poor command of English do not hold water. Good command of English is one of the job requirements, and the whole point of a job interview is to discriminate against unqualified candidates. Besides, if the hiring process encourages candidates to improve their English writing abilities, rather than cramming a bunch of red-black-tree algorithms, language trivia, or irrelevant brainteasters, so much the better for everyone.
[Other articles in category /misc] permanent link
The most important combinator in combinatory logic is the !!S!! combinator, defined simply:
$$ S x y z ⇒ (x z)(y z) $$
or in !!\lambda!!-calculus terms:
$$ S = \lambda x y z. (x z)(y z). $$
A wonderful theorem states that any !!\lambda!!-expression with no free variables can be converted into a combinator expression that contains only the combinators !!S, K,!! and !!I!!, where !!S!! is really the only interesting one of the three, !!I!! being merely the identity function, and !!K!! a constructor of constant functions:
$$ \begin{align} I x & = x \\ K x y & = x \\ \end{align} $$
In fact one can get along without !!I!! since !!S K K = I!!.
A not-too-infrequently-asked question is why the three combinators are named as they are. The !!I!! is an identity function and pretty obvious stands for “identity”.
Similarly the !!K!! constructs constant functions: !!K x!! is the combinator which ignores its argument and yields !!x!!. So it's not hard to imagine that !!K!! is short for Konstant, which is German for “constant”; no mystery there.
But why !!S!!? People typically guess that it stands for “substitution”, the idea being that if you have some application $$A\,B$$ then !!S!! allows one to substitute some term !!T!! for a free variable !!v!! in both !!A!! and !!B!! prior to the application:
$$ S\, A\, B\, T = A[v/T]\, B[v/T]. $$
Although this seems plausible, it's not correct.
Combinatory logic was introduced in a 1924 paper of Moses Schönfinkel. In it, he defines a family of combinators including the standard !!S!!, !!K!!, and !!I!!; he shows that only !!S!! and !!K!! are required. His initial set of combinators comprises the following:
$$ \begin{array}{cllrl} I & \textit{Identitätsfunktion} & \text{“identity function”}& I\,x =& x \\ C & \textit{Konstanzfunktion} & \text{“constancy function”} & C\,x\,y =& x \\ T & \textit{Vertauschungsfunktion} & \text{“swap function”} & T\,x\,y\,z=& x\,z\,y \\ Z & \textit{Zusammensetzungsfunktion} & \text{“composition function”} & Z\,x\,y\,z=& x\,(y\,z) \\ S & \textit{Verschmelzungsfunktion} & \text{“fusion function”} & S\,x\,y\,z=& x\,z\,(y\,z) \end{array} $$
(Schönfinkel also had combinators representing logical operations (one corresponding to the Sheffer stroke, which had been discovered in 1913), and to quantification, but those don't concern us right now.)
!!T!! and !!Z!! are now usually called !!C!! and !!B!!. These names probably originated in Curry's Grundlagen der kombinatorischen Logik (1930). Curry 1930 is probably also the origin of the change from !!C!! to !!K!!. I have no idea why Schönfinkel chose to abbreviate Konstanzfunktion as !!C!! instead of !!K!!. Curry notes that for !!I, K, B, C, S!! Schönfinkel has !!I, C, Z, T, S!!, but does not explain his changes. In Curry and Feys’ influential 1958 book on combinatory logic, the !!B!! and !!C!! combinators given names that are are literal translations of Schönfinkel's: “elementary permutator” and “elementary compositor”.
Returning to the !!S!! combinator, one sees that its German name in Schönfinkel's paper, Verschmelzungsfunktion, begins with the letter V, but so does Vertauschungsfunktion, so abbreviating either with V would have been ambiguous. Schönfinkel instead chose to abbreviate Verschmelzungsfunktion with S for its root schmelzen, “fusion”, and Vertauschungsfunktion with T for its root tauschen, “swap”. The word schmelzen is akin to English words “melt” and “smelt”.
The “swap” is straightforward: the !!T!! combinator swaps the order of the arguments to !!x!! in !!x\,y\,z!!: $$T\,x\,y\,z = x\,z\,y$$ but does not otherwise alter the structure of the expression.
But why is !!S!! the “melting” or “fusion” combinator? It's because Schönfinkel was interested in reducing abitrary mathematical expressions to combinators. He will sometimes have an application !!(f\, x)(g\, x)!! and he wants to ‘fuse’ the two occurrences of !!x!!. He can do this by rewriting the expression as !!S\, f\, g\, x!!. Schönfinkel says:
Der praktische Nutzen der Function !!S!! besteht ersichtlich darin, daß sie es ermöglicht, mehrmals auftresnde Veränderliche — und bis zu einem gewissen Grade auch individuelle Functionen — nur einmal auftreten zu lassen.
Clearly, the practical use of the function !!S!! will be to enable us to reduce the number of occurrences of a variable — and to some extent also of a particular function — from several to a single one.
(Translation from van Heijenoort, p. 362.)
So there you have it: the !!S!! combinator is so-named not for substitution, but because S is the first letter of schmelzen, ‘to fuse’.
References
Schönfinkel, M. “Über die Bausteine der mathematischen Logik” (“On the building-blocks of mathematical logic”), Mathematische Annalen (1969), p. 305–316; Berlin, Göttingen, Heidelberg.
English translation in Van Heijenoort, Jean (ed.) From Frege to Gödel: a Source Book in Mathematical Logic, 1879–1931 (1967) pp. 355–366 Harvard University Press; Cambridge and London.
Curry, H.B. “Grundlagen der kombinatorischen Logik” (“Fundamentals of combinatory logic”), American Journal of Mathematics Vol. 52, No. 3 (Jul., 1930), pp. 509-536.
Curry, H.B. and Robert Feys Combinatory Logic (1958) p. 152 North-Holland Publishing Company, Amsterdam.
[Other articles in category /math] permanent link
Thu, 22 Jul 2021Take some real number !!\alpha!! and let its convergents be !!c_0, c_1, c_2, \ldots!!. Now consider the convergents of !!2\alpha!!. Sometimes they will include !!2c_0, 2c_1, 2c_2, \ldots!!, sometimes only some of these.
For example, the convergents of !!\pi!! and !!2\pi!! are
$$ \begin{array}{rlc}
\pi & \approx &
\color{darkblue}{3},&&& \color{darkblue}{\frac{22}{7}}, &
\color{darkblue}{\frac{333}{106}}, && \color{darkblue}{\frac{355}{113}}, &
\color{darkblue}{\frac{103993}{33102}}, &&
\frac{104348}{33215}, &
\color{darkblue}{\frac{208341}{66317}}, &
\ldots \\
2\pi & \approx &
\color{darkblue}{6}, & \frac{19}{3}, & \frac{25}{4}, & \color{darkblue}{\frac{44}{7}}, &
\color{darkblue}{\frac{333}{53}}, &
\frac{377}{60}, &
\color{darkblue}{\frac{710}{113}}, &
\color{darkblue}{\frac{103393}{16551}}, &
\frac{312689}{49766}, &&
\color{darkblue}{\frac{416682}{66317}}, &
\ldots
\end{array}
$$
Here are the analogous lists for !!\frac{1+\sqrt{5}}2!! and !!1+\sqrt5!!:
$$ \begin{array}{rlc} \frac12\left({1+\sqrt{5}}\right)& \approx & 1, & 2, & \color{darkblue}{\frac32}, & \frac53, & \frac85, & \color{darkblue}{\frac{13}8}, & \frac{21}{13}, & \frac{34}{21}, & \color{darkblue}{\frac{55}{34}}, & \frac{89}{55}, & \frac{144}{89}, & \color{darkblue}{\frac{233}{144}}, & \frac{377}{233}, &\frac{610}{377} , & \color{darkblue}{\frac{987}{610} }, & \ldots \\ 1+\sqrt{5} & \approx & & & \color{darkblue}{3}, &&& \color{darkblue}{\frac{13}4}, &&& \color{darkblue}{\frac{55}{17}}, &&& \color{darkblue}{\frac{233}{72}}, &&& \color{darkblue}{\frac{987}{305}}, & \ldots \end{array} $$
This time all the convergents in the second list are matched by convergents in the first list. The number !!\frac{1+\sqrt5}{2}!! is notorious because it's the real number whose convergents converge the most slowly. I'm surprised that !!1+\sqrt5!! converges so much more quickly; I would not have expected the factor of 2 to change the situation so drastically.
I haven't thought about this at all yet, but it seems to me that a promising avenue would be to look at what Gosper's algorithm would do for the case !!x\mapsto 2x!! and see what simplifications can be done. This would probably produce some insight, and maybe a method for constructing a number !!\alpha!! so that all the convergents of !!2\alpha!! are twice those of !!\alpha!!.
[Other articles in category /math] permanent link
Fri, 09 Jul 2021
“Forensic” doesn't mean what I thought it did
Last week at work we released bad code, which had somehow survived multiple reviews. I was very interested in finding out how this happened, dug into the Git history to find out, and wrote a report. Originally I titled the report something like “Forensic analysis of Git history” (and one of my co-workers independently referred to the investigation as forensic) but then I realized I wasn't sure what “forensic” meant. I looked it up, and learned it was the wrong word.
A forensic analysis is one performed in the service of a court or court case. “Forensic” itself is from Latin forum, which is a public assembly place where markets were held and court cases were heard.
Forensic medicine is medicine in service of a court case, for example to determine a cause of death. For this reason it often refers to a postmortem examination, and I thought that “forensic” meant a postmortem or other retrospective analysis. That was the sense I intended it. But no. I had written a postmortem analysis, but not a forensic one.
[Other articles in category /lang/etym] permanent link
Thu, 08 Jul 2021
A simple dice-throwing game that seems hard to play
I ran into a fun math problem yesterday, easy to ask, easy to understand, but somewhat open-ended and seems to produce fairly complex behavior. It might be a good problem for a bright high school student to tinker with.
Consider the following one-player game. You start with a total of n points. On each turn, you choose to throw either a four-, six-, or eight-sided die, and then subtract the number thrown from your point total. The game continues until your total reaches zero (and you win) or goes below zero (and you lose).
This game seems surprisingly difficult to analyze. The computer analysis is quite easy, but what I mean is, if someone comes to you offering to pay you a dollar if you can win starting with !!n=9!! points, and it would be spoilsportish to say “just wait here for half an hour while I write this computer program”, what's your good move?
Is there even a way to make an educated guess, short of doing a full analysis? The !!n≤4!! strategy is obvious, but even for !!n=5!! you need to start calculating: rolling the d4 is safe. Rolling the d6 gives you a chance of wiping out, but also a chance of winning instantly; is that an improvement? (Spoiler: it is, quite substantially so! Your chance of winning increases from !!36\%!! to !!40.7\%!!.)
With the game as described, and optimal play, the probability of winning approaches !!45.66\%!! as the number of points increases, and the strategy is not simple: the best strategy for !!n≤20!! uses the d4 in 13 cases, the d6 in 4 cases, and the d8 in 3 cases:
$$\begin{array}{rcl} n & \text{Best play} & \text{Win %} \\ \hline 1 & 4\quad & 25.00\% \\ 2 & 4\quad & 31.25 \\ 3 & 4\quad & 39.06 \\ 4 & 4\quad & 48.83 \\ \hline 5 & 6 & 40.69\% \\ 6 & 6 & 47.47 \\ 7 & 4\quad & 44.01 \\ 8 & \quad8 & 47.04 \\ \hline 9 & 4\quad & 44.80\% \\ 10 & 4\quad & 45.83 \\ 11 & 4\quad & 45.42 \\ 12 & 4\quad & 45.77 \\ \hline 13 & 6 & 45.48 \% \\ 14 & \quad8 & 45.73 \\ 15 & 4\quad & 45.60 \\ 16 & \quad8 & 45.71 \\ \hline 17 & 4\quad & 45.63 \% \\ 18 & 4\quad & 45.67 \\ 19 & 4\quad & 45.65 \\ 20 & 6 & 45.67 \end{array} $$
It seems fairly clear (and not hard to prove) that when the die with fewest sides has !!d!! sides, the good numbers of points are multiples of !!d!!, with !!kd+1!! somewhat worse, and then !!kd+2, kd+3, \ldots!! generally better and better to the next peak at !!kd+d!!. But there are exceptions: even if !!d!! is not the smallest die, if you have a !!d!!-sided die, it is good to have !!d!! points, and when you do you should roll the !!d!!-sided die.
I did get a little more insight after making the chart above and seeing the 4-periodicity. In a comment on my Math SE post I observed:
There is a way to see quickly that the d4 is better for !!n=7!!. !!n=1!! is the worst possible position. !!n=2,3,!! and !!4!! are increasingly good; !!4!! is best because you can't lose and you might win outright. After that !!5!! is bad again, but not as bad as !!1!!, with !!6,7,8!! increasingly good. The pattern continues this way, with !!4k−3,4k−2,4k−1,4k!! being increasingly good, and then !!4k+1!! being worse again but better than !!4k−3!!. For !!n=7!!, the d6 allows one to land on !!\{1,2,3,4,5,6\}!!, and the d4 on !!\{3,4,5,6\}!!. But !!1!! is worse than !!5!! and !!2!! is worse than !!6!!, so prefer the d4.
The d4-d6-d8 case is unusually confusing, because for example it's not clear whether from 12 points you should throw d4, hoping to land on 8, or d6, hoping to land on 6. (I haven't checked but I imagine the two strategies perform almost equally well; similarly it probably doesn't matter much if you throw the d4 or the d6 first from !!n=10!!.)
That the d6 is best for !!n=13!! is very surprising to me.
Why !!45.66\%!!? I don't know. With only one die, the winning probability for large !!n!! converges to !!\frac2{n+1}!! which I imagine is a fairly straightforward calculation (but I have not done it). For more than one die, it seems much harder.
Is there a way to estimate the winning probability for large !!n!!, given the list of dice? Actually yes, a little bit: the probability of winning with just a d4 is !!\frac 25!!, and the d6 and d8 can't hurt, so we know the chance of winning with all three dice available will be somewhat more than !!40\%!!, as it is. The value of larger dice falls off rapidly with the number of sides, so for example with d4+d6 the chance of winning increases from !!40\%!! to almost !!45\%!!, and adding the d8 only nudges this up to !!45.66\%!!.
The probability of winning with a d2 is !!\frac 23!!, and if you have a d3 also the probability goes up to !!\frac 34!!, which seems simple enough, but if you add a d4 instead of the d3 instead it goes to !!68.965\%!!, whatever that is. And Dfan Schmidt tells me that d3 + d4 converges to !!\frac{512}{891}!!.
I wrote it up for Math StackExchange but nobody has replied yet.
Here's Python code to calculate the values. Enjoy.
[ Addendum: Michael Lugo points out that the d2+d4 probability (“!!68.965\%!!, whatever that is”) is simply !!\frac{20}{29}!!, and gives some other similar results. One is that d3+d4+d5 has a winning probability of !!\frac{16}{27}!!; the small denominator is surprising. ]
[Other articles in category /math] permanent link
Wed, 07 Jul 2021Katara is interested in linguistics. When school was over for the year and she had time to think about things, I gave her all my old linguistics books. The other day for some reason I mentioned to her that I had known people who were engaged in formal research on the problem of how to get a computer to know what a pronoun referred to, and that this is very difficult.
(I once had a co-worker who claimed that it was simple: the pronoun always refers back to the nearest noun. It wasn't hard to go back in his Slack history and find a counterexample he had uttered a few minutes before.)
Today I wanted to tell Katara about dummy pronouns, which refer to nothing at all. I intended to send her the example from Wiktionary:
it is good to know that you are okay
I started my message:
Here's an interesting example of how hard it can be to find what a pronoun refers to
Then I realized I no longer needed the example.
[Other articles in category /lang] permanent link
Mon, 05 Jul 2021In English, this is called duckface:

In German, I've learned, it's Schlauchbootlippen.
Schlauch is “tube”. A Schlauchboot is a tube-boat — an inflatable rubber dingy. Schlauchbootlippen means dinghy-lips.
[Other articles in category /lang/etym] permanent link
Sun, 27 Jun 2021
Dogs that look like board games
In Korean, “바둑이” (/badugi/) is a common name for a spotted dog, especially a black-spotted dog. This is because “바둑” (/baduk/) is the native Korean name for the game of go, in which round black and white stones are placed on a board.
In English, black-and-white spotted dogs are sometimes named “Checkers” for essentially the same reason.
[Other articles in category /lang/etym] permanent link
Mon, 19 Apr 2021Recently I've been complaining about unforced translation errors. ([1] [2]) Here's one I saw today:

The translation was given as:
“honk honk, your Uber has arrived”
“Oleg, what the fuck”
Now, the Russian text clearly says “beep-beep” (“бип-бип”), not “honk honk”. I could understand translating this as "honk honk" if "beep beep" were not a standard car sound in English. But English-speaking cars do say “beep beep”, so why change the original?
(Also, a much smaller point: I have no objection to translating “Что за херня” as “what the fuck”. But why translate “Что за херня, Олег?” as “Oleg, what the fuck” instead of “What the fuck, Oleg”?)
[ Addendum 20210420: Katara suggested that perhaps the original translator was simply unaware that Anglophone cars also “beep beep”. ]
[Other articles in category /lang] permanent link
Wed, 14 Apr 2021A couple of days ago I discussed the epithet “soup-guzzling pie-muncher”, which in the original Medieval Italian was brodaiuolo manicator di torte. I had compained that where most translations rendered the delightful word brodaiuolo as something like “soup-guzzler” or “broth-swiller”, Richard Aldington used the much less vivid “glutton”.
A form of the word brodaiuolo appears in one other place in the Decameron, in the sixth story on the first day, also told by Emilia, who as you remember has nothing good to say about the clergy:
… lo 'nquisitore sentendo trafiggere la lor brodaiuola ipocrisia tutto si turbò…
J. M. Rigg (1903), who had elsewhere translated brodaiuolo as “broth-guzzling”, this time went with “gluttony”:
…the inquisitor, feeling that their gluttony and hypocrisy had received a home-thrust…
G. H. McWilliam (1972) does at least imply the broth:
…the inquisitor himself, on hearing their guzzling hypocrisy exposed…
John Payne (1886):
the latter, feeling the hit at the broth-swilling hypocrisy of himself and his brethren…
Cormac Ó Cuilleanáin's revision of Payne (2004):
…the inquisitor himself, feeling that the broth-swilling hypocrisy of himself and his brethren had been punctured…
And what about Aldington (1930), who dropped the ball the other time and rendered brodaiuolo merely as “glutton”? Here he says:
… he felt it was a stab at their thick-soup hypocrisy…
Oh, Richard.
I think you should have tried harder.
[Other articles in category /lang] permanent link
Mon, 12 Apr 2021A few months ago I was pondering what it might be like to be Donald Trump. Pretty fucking terrible, I imagine. What's it like, I wondered, to wake up every morning and know that every person in your life is only interested in what they can get from you, that your kids are eagerly waiting for you to die and get out of their way, and that there is nobody in the world who loves you? How do you get out of bed and face that bitter world? I don't know if I could do it. It doesn't get him off the hook for his terrible behavior, of course, but I do feel real pity for the man.
It got me to thinking about another pitiable rich guy, Ebeneezer Scrooge. Scrooge in the end is redeemed when he is brought face to face with the fact that his situation is similar to Trump's. Who cares that Scrooge has died? Certainly not his former business associates, who discuss whether they will attend his funeral:
“It's likely to be a very cheap funeral,” said the same speaker; “for, upon my life, I don't know of anybody to go to it. Suppose we make up a party, and volunteer.”
“I don't mind going if a lunch is provided," observed the gentleman with the excresence on his nose.
Later, the Spirit shows Scrooge the people who are selling the curtains stolen from his bed and the shirt stolen from his corpse, and Scrooge begs:
“If there is any person in the town who feels emotion caused by this man's death," said Scrooge, quite agonized, “show that person to me, Spirit, I beseech you!”
The Spirit complies, by finding a couple who had owed Scrooge money, and who will now, because he has died, have time to pay.
I can easily replace Scrooge with Trump in any of these scenes, right up to the end of chapter 4. But Scrooge in the end is redeemed. He did once love a woman, although she left him. Scrooge did have friends, long ago. He did have a sister who loved him, and though she is gone her son Fred still wants to welcome him back into the family. Did Donald Trump ever have any of those things?
[Other articles in category /book] permanent link
The ten storytellers in The Decameron aren't all well-drawn or easy to tell apart. In the introduction of my favorite edition, the editor, Cormac Ó Cuilleanáin, says:
Early in the book we are given hints that we are going to get to know these ten frame characters…. Among the Decameron storytellers, for instance, Pampinea emerges as being bossy, while Dioneo has a filthy mind. But little further character development takes place.
I agree, mostly. I can see Dioneo more clearly than Ó Cuilleanáin suggests. Dioneo reminds me of Roberto Benigni's filthy-minded Roman taxi driver in Night on Earth. I also get a picture of Bocaccio's character Filostrato, who is a whiny emo poet boy who complains that he woman he was simping for got tired of him and dumped him for someone else:
To be humble and obedient to her and to follow all her whims as closely as I could, was all of no avail to me, and I was soon abandoned for another. Thus I go from bad to worse, and believe I shall until I die.… The person who gave me the nickname of Filostrato [ “victim of love” ] knew what she was doing.
When it's Filostrato's turn to choose the theme for the day's stories, he makes the others tell stories of ill-starred love with unhappy endings. They comply, but are relieved when it is over. (Dioneo, who is excused from the required themes, tells instead a farcical story of a woman who hides her secret lover in a chest after he unwittingly drinks a powerful sedative.)
Ah, but Emilia. None of the characters in the Decameron is impressed with the manners or morals of priests. But Emilia positively despises them. Her story on the third day is a good example. The protagonist, Tedaldo, is meeting his long-lost mistress Ermellina; she broke off the affair with him seven years ago on the advice of a friar who advised that she ought to remain faithful to her husband. Tedaldo is disguised as a friar himself, and argues that she should resume the affair. He begins by observing that modern friars can not always be trusted:
Time was when the friars were most holy and worthy men, but those who today take the name and claim the reputation of friars have nothing of the friar but the costume. No, not even that,…
Modern friars, narrates Emilia, "strut about like peacocks" showing off their fine clothes. She goes on from there, complaining about friars' vanity, and greed, and lust, and hypocrisy, getting more and more worked up until you can imagine her frothing at the mouth. This goes on for about fifteen hundred words before she gets back to Tedaldo and Ermellina, just at the same time that I get around to what I actually meant to write about in this article: Emilia has Tedaldo belittle the specific friar who was the original cause of his troubles,
who must without a doubt have been some soup-guzzling pie-muncher…
This was so delightful that I had to write a whole blog post just to show it to you. I look forward to calling other people soup-guzzling pie-munchers in the coming months.
But, as with the earlier article about the two-bit huckster I had to look up the original Italian to see what it really said. And, as with the huckster, the answer was, this was pretty much what Bocaccio had originally written, which was:
il qual per certo doveva esser alcun brodaiuolo manicator di torte…
Brodaiuolo is akin to “broth”, and it has that disparaging diminutive “-uolo” suffix that we saw before in mercantuolo.
A manicator is a gobbler; it's akin to “munch”, “manger”, and “mandible”, to modern Italian mangia and related French manger. A manicator di torte is literally a gobbler of pies.
Delightful! I love Bocaccio.
While I was researching this article I ran into some other English translations of the phrase. The translation at Brown University's Decameron Web is by J.M. Rigg:
some broth-guzzling, pastry-gorging knave without a doubt
which I award full marks. The translation of John Payne has
must for certain have been some broth-swilling, pastry-gorger
and two revised versions of Payne, by Singleton and Ó Cuilleanáin, translate it similarly.
But the translation of Richard Aldington only says:
who must certainly have been some fat-witted glutton.
which I find disappointing.
I often wonder why translators opt to water down their translations like this. Why discard the vivid and specific soup and pie in favor of the abstract "fat-witted glutton"? What could possibly be the justification?
Translators have a tough job. A mediocre translator will capture only the surface meaning and miss the subtle allusions, the wordplay, the connotations. But here, Aldington hasn't even captured the surface meaning! How hard is it to see torte and include pie in your translation somewhere? I can't believe that his omitting it was pure carelessness, only that Aldington thought that he was somehow improving on the original. But how, I can't imagine.
Well, I can imagine a little. Translations can also be too literal. Let's consider the offensive Spanish epithet pendejo. Literally, this is a pubic hair. But to translate it in English as "pubic hair" would be a mistake, since English doesn't use that term in the same way. A better English translation is "asshole". This is anatomically illogical, but linguistically correct, because the metaphor in both languages has worn thin. When an anglophone hears someone called an “asshole” they don't normally imagine a literal anus, and I think similarly Spanish-speakers don't picture a literal pubic hair for pendejo. Brodaiuolo could be similar. Would a 14th-century Florentine, hearing brodaiuolo, picture a generic glutton, or would they imagine someone literally holding a soup bowl up to their face? We probably don't know. But I'm inclined to think that “soup-guzzler” is not too rich, because by this point in Emilia's rant we can almost see the little flecks of spittle flying out of here mouth.
I'm offended by Aldington's omission of pie-munching.
[ Addendum 20210414: More translations of brodaiuolo. ]
[Other articles in category /book] permanent link
Mon, 29 Mar 2021The King James Version of Job 19:26 says:
And though after my skin worms destroy this body, yet in my flesh shall I see God:
I find this mysterious for two reasons. First, I cannot understand the grammar. How is this supposed to be parsed? I can't come up with any plausible way to parse this so that it is grammatically correct.
Second, how did the worms get in there? No other English translation mentions worms and they appear to be absent from the original Hebrew. Did the KJV writers mistranslate something? (Probably not, there is nothing in the original to mistranslate.) Or is it just an interpolation?
Pretty ballsy, to decide that God left something out the first time around, but that you can correct His omission.
[Other articles in category /book] permanent link
Fri, 26 Mar 2021
Something I didn't know and I bet you didn't either
The Panama Canal has a loyalty program.
If you're planning to ship at least 450,000 TEU per year, you can register in advance and get a discount on your tolls.
[Other articles in category /misc] permanent link
Sun, 21 Mar 2021
Two sentences that made me stop to think
In The ancient fabric that no one knows how to make:
Islam was born in Bangladesh and moved to London about 20 years ago.
Whaaaat? Then I realized: It's someone named “Islam”. Okay.
In Wikipedia's article on some comic book person called “Steppenwolf”:
His decapitated head is crushed by the foot of Darkseid, enraged by his lieutenant's failure.
For this to be correct, Steppenwolf would have to have a second head growing out of his main head. Then if someone cut off the second head, the main head would be a decapitated head.
Not out of the question for a comic book person, but in this case not correct. I changed it to “disembodied head”.
[ Addendum 20210322: Shortly afterward, another editor changed it to “severed head”, which I agree is better. ]
[Other articles in category /misc] permanent link
Sun, 14 Mar 2021Many years ago I bought tickets to see Depeche Mode live, and I wondered if I wasn't making a mistake. Would they appear on stage, press “play” on the sequencers, and then stand around doing nothing while Dave Gahan sang?
And yes, it was pretty much like that. They were definitely overstaffed. I think there were four people on stage and at any particular time one or two of them were standing around looking bored.
I hadn't thought of this in a long time, but I was reading a Washington Times article about the German synth-pop band Alphaville, contemporaries of Depeche Mode. The article is from 2017, and includes this exchange:
Question: How is it possible that you’ve never played live in America before?
Answer: In the ‘80s we didn’t play live at all because we couldn’t play.
Meaning, they couldn't play any actual instruments. Marian Gold sang, but the rest of the music was preprogrammed on sequencers or assembled in an editing studio. The group composed and produced the music, but there simply was no "performance" in real time. I have to credit Alphaville for refusing to pretend to be performers and instrumentalists.
(For an contrasting approach, consider The Residents, who face the same issue and have dealt with it in a completely different way. The Residents’ stage show is elaborate and spectacular. You hear the music, but there's no way to know who's playing it. There are people on the stage, but are they the composers? Are they instrumentalists? Are they even in the band? Who knows? And does it matter? No, not really. The Residents have never had names or separate identities anyway. I imagine that Daft Punk took a similar approach.)
[Other articles in category /music] permanent link
Fri, 12 Mar 2021For no particular reason, I looked up the Trans-Siberian Railway today and learned that its name in Russian is
Транссибирская магистраль
pronounced roughly “trans-siberskaya magistral”. The Транссибирская is clear, but what is магистраль?
Wiktionary says it means "main line" or "trunkline". But it doesn't give an etymology. Still, it's not hard to guess: it's akin to the French (and also English) word “magistral” which means something that relates to a master.
So it's the Trans-Siberian master train line. But "train line” is implicit, the way English-speaking recording engineers use "master" to refer to a master tape, or Americans will call a trunk road an "arterial". English loves to turn adjectives into nouns in that way, but I didn't know that Russian did it also.
[Other articles in category /lang] permanent link
Thu, 11 Mar 2021I recently read Finkel and Taylor's excellent little book Cuneiform. On page 27 they discuss the kinds of texts that young boys studied in school:
Alongside ‘citizenship training’ through hymns, myths and law codes, schoolboys learnt how to debate. They trained on texts arguing the benefits to mankind of antagonistic pairs: winter and summer, sheep and grain or bird and fish.
“Hey,” I said. “I've read that!” I love when this happens, something pops up that I would have wanted to know a little more about, but it's already something I do know a little more about. I feel like I'm getting somewhere in my project of reading every book ever written. Progress!
From The Debate Between Bird and Fish, Sumerian, around 4000 years ago:
“You cause damage in the vegetable plots; you are a nuisance. In the damp parts of fields, there are your unpleasing footprints. Bird, you are shameless: you fill the courtyard with your droppings.”
Bird retorts:
You are bereft of hips!
It's not so much a debate as a diss battle.
- Debate between Bird and Fish, complete translation
- Wikipedia article
[ Addendum 20210312: Now I would like to see an cartoon version of the debate, animated by Chuck Jones. ]
[Other articles in category /lang] permanent link
Mon, 08 Mar 2021
Canon in Euopean languages and Arabic
Today I was reading about Avicenna's work The Canon of Medicine and learned that the original Arabic title
القانون في الطب
is rendered in Latin script as al-Qānūn fī al-Ṭibb with al-Qānun (“the law”) being translated into English as “Canon” (“rule” or “law”). The English word comes via French and Latin, ultimately from Greek κανών, “rule”.
Is the resemblance between Qānūn and κανών a coincidence, or is the Arabic word originally borrowed from Greek?
I was about to write the next sentence “and where could I have looked this up?” but then I remembered that this kind of thing can be looked up in English Wiktionary. English Wiktionary is not a dictionary of English, but a universal dictionary in English. It not only defines English words, but also words in many other languages, with the descriptions and etmologies written in English.
So I looked it up, and it is a Greek loanword!
The Internet is amazing and wonderful. Truly, we live in an age of marvels.
[Other articles in category /lang/etym] permanent link
Sun, 07 Mar 2021(Summary: Henry Baker's web site has disappeared after 30 years. I kept an archive.)
Henry G. Baker is a computer programmer and computer scientist, one of the founders of the Symbolics company that made Lisp Machines.
I discovered Baker's writing probably in the early 1990s and immediately put him on my “read everything this person writes” list. I found everything he wrote clear and well-reasoned. I always learned something from reading it. He wrote on many topics, and when he wrote about a topic I hadn't been interested in, I became interested in it because he made it interesting.
Sometimes I thought Baker was mistaken about something. But usually it was I who was mistaken.
Baker had a web site with an archive of his articles and papers. It disappeared last year sometime. But I have a copy that I made around 1998, Just In Case.
Baker's web site is a good example of mid-1990s web design. Here's his “Gratuitous Waste of Bandwidth” page. It features a link to a 320×240 pixel color photo of Baker, and an inlined monochrome GIF version of it.

| 
|
Browsers at the time could inline GIF files but not JPEGs, and it would have been rude to inline a color JPEG because that would have forced the user to wait while the browser downloaded the entire 39kb color image. It was a rather different time.
Some of my favorite articles of his were:
CONS Should not CONS its Arguments, or, a Lazy Alloc is a Smart Alloc
(The Internet Archive also has a more recent copy of the site.)
Addendum 20220108
I just rediscovered this note I wrote in 2006 but never published:
The bozo bit isn't really a bit; it works in the other direction too. Some people are so consistently thoughtful and insightful that I go looking for stuff they have said, and pay extra-close attention to it, particularly if I disagree with it, because that indicates a greater-than-average chance that I am mistaken about something.
Henry Baker is one of these people. I try to read everything Henry Baker writes, extra carefully, because in the past I've determined that he seems to be correct about almost everything. If M. Baker says something I think is probably wrong, that's a good sign that I should reconsider, because there's a decent chance that I'm the one that's wrong.
[Other articles in category /prog] permanent link
Sat, 06 Mar 2021Last week I thought “there must be a restaurant in California somewhere called ‘Pasta la Vista, Baby’”, so I asked the Goog. The Goog says it does not know of one!
It says there is a ‘Pasta La Vista’ in Winnipeg, which I was not expecting, and also one called ‘Pasta A La Vista‘ which has an acceptable excuse, since it is in Bella Vista, AR.
There are quite a few Pasta La Vistas in Europe. And there is one called ‘Pasta la Vista Baby’. It is near the University in Örebro, sixth-largest city in Sweden. This isn't the last place I would have expected to find ‘Pasta la Vista Baby’, but I don't think it's in the top thousand either.
[Other articles in category /food] permanent link
Tue, 02 Mar 2021Often when I'm reading something that was translated from another language, I get to wondering what the original was. Often this appears in connection with some sort of wordplay. For example, the first chapter of Stanisław Lem's novel The Cyberiad begins:
One day Trurl the constructor put together a machine that could create anything starting with n. When it was ready, he tried it out, ordering it to make needles, then nankeens and negligees, which it did, then nail the lot to narghiles filled with nepenthe and numerous other narcotics. The machine carried out his instructions to the letter. Still not completely sure of its ability, he had it produce, one after the other, nimbuses, noodles, nuclei, neutrons, naphtha, noses, nymphs, naiads, and natrium. This last it could not do, and Trurl, considerably irritated, demanded an explanation.
"Never heard of it," said the machine.
"What? But it's only sodium. You know, the metal, the element..."
"Sodium starts with an s, and I work only in n."
In the end Trurl asks the machine to make “nothing”, which is an important plot point.
Okay, but The Cyberiad was written in Polish. I wondered for years: was it “N” in Polish also? If the Polish word for “nothing” happened to begin with a “W”, then the Polish text would have had to have had a machine that could create anything starting with “W”. Then the translator couldn't keep the “W” the way it was, because the whole point of the story leads up to “nothing”; they have to rewrite the whole thing with “N”.
One day I met the translator, Michael Kandel, and was able to ask. And yes, it was originally “N”; the polish word for “nothing” is nic.
(Here's a related question on SF Stack Exchange. It discusses how the original “N” items turn into their somewhat-similar “N” counterparts in English.)
But anyway, I meant to talk about Pippi Longstocking, which was originally written in Swedish.
Pippi and the Ibex
In one episode, Pippi goes to school, where the teacher tries to teach her the alphabet. She shows her a card with a letter ‘i' and a picture of an ibex. Pippi says:
“I think it looks exactly like a straight line with a little fly speck over it. But what I'd really like to know is, what has the ibex to do with the fly speck?”
Clearly Pippi is describing a lowercase letter ‘i’. “Ibex” is a pretty strange choice of animal, in English or in Swedish, so I wondered: was the picture an ibex in the original Swedish? It turns out it was not! “Ibex” in Swedish is stenbock. In the original Swedish, the picture is an igelkott, a hedgehog.
Well, in the translation I had as a kid, by Florence Lamborn, it was an ibex. But a different English translation (by Tiina Nunnaly) makes it an iguana, and another that I found, by Edna Hurup, contains the following elaborate invention:
[The teacher] therefore brought out a picture of a pretty little green island surrounded by blue water.
My philosophy of translation is opposed to this sort of thing. I will take all sorts of liberties, and I might make up an island if I have to, but having done so I would not describe it in detail as Ms. Hurup did so shamelessly. In the original the hedgehog is not described:
Därför tog hon fram en liten vacker plansch föreställande en igelkott.
(“Therefore, she took out a small, beautiful poster depicting a hedgehog.”)
Pluttification
Today I was thinking about Pippi, and I recalled that one of her goals in attending school was to learn “pluttification”:
“Hey, everybody,” hollered Pippi, swinging her big hat. "Am I in time for pluttification?”
In English “pluttification” is obviously Pippi's misunderstanding of “multiplication”:
“All kinds of things,” said the officer. “Lots of useful things, like the multiplication tables, for instance.”
“I've been fine for nine years without any pluttification tables,” said Pippi…
What was pluttification in Swedish?
It turns out, it wasn't any different. The Swedish for “multiplication tables” is multiplikationstabellen.
”Hejsvejs”, hojtade Pippi och svängde sin stora hatt. ”Kommer jag lagom till pluttifikationen?”
Pippi's Name
Long ago I wondered about Pippi's full name, which in the Lamborn version I read was:
Pippilotta Delicatessa Windowshade Mackrelmint Ephraim's Daughter Longstocking
The original Swedish was:
Pippilotta Viktualia Rullgardina Krusmynta Efraimsdotter Långstrump
and the English was a fairly close translation. Viktualier is “victuals”, and I think turning it into “Delicatessa” is clever. (Viktualia is actually a real Swedish name, although quite rare.) Rullgardina is exactly “windowshade”. (Literally “roll-curtain”.) Krusmynta is a nonsense compound of krus (see below) and mynta (mint). I thought that krus was “mackerel” but I can't find anyone to agree with me; everyone says that the Swedish for “mackerel” is makrill, as in most European languages.
The Nunnaly translation has:
Pippilotta Comestibles Windowshade Curlymint Ephraimsdaughter Longstocking
“Commestibles” is terrible, but “Curlymint” is just fine, because krusig is indeed “curly”.
The Hurup translation says:
Pippilotta Provisionia Gaberdina Dandeliona Ephraimsdaughter Longstocking
I don't like “Provisionia”, but it can be defended as a more literal translation than “Delicatessa”. I can't imagine why Hurup decided to replace “Windowshade Curlymint” with “Gaberdina Dandeliona”.
English Wikipedia has a whole section about this if you are not tired of it yet.
Negerkung
I recall that in the version I read, Captain Ephraim was "formerly the Terror of the Seas, and now a cannibal king", and that the original Swedish version of “cannibal king” was negerkung, “king of the negroes”. Mathilda Haraldsson's undergraduate thesis describes this as a “quite strong expression”, but adds that in the 1940s neger was considered inoffensive. (Recall that in the United States at the time, “negro” was the polite term.) It does appear that some people today consider negerkung offensive. And in any case it was never accurate; the people in question are not Africans, but Polynesians. In the Swedish version I looked at just now, the word has been changed to söderhavskung, “King of the South Seas”.
To me the most offensive part of all this is Lamborn's description of Ephraim's subjects as “cannibals” . As far as I can tell, the original Swedish says nothing about cannibalism, and this is a disgusting and completely unnecessary invention. Nunnaly makes it just “king of the natives” but Hurup inexplicably retains “Cannibal King”.
Norwegian Wikipedia has an article about Lindgren's use of negerkung, but Swedish Wikipedia does not!
[ Addendum: I just noticed that my discussion of the cannibal thing omits the word “racist”. This was an oversight. The cannibal thing is racist. ]
[ Addendum 20210303: Justin Pearson, Anders Nielsen, and Adam Sjøgren have each informed me that krusmynta
is not a nonsense compound as I said. It is a standard term for
spearmint. Also,
se.wikipedia.org is not Swedish Wikipedia. The language code for Swedish is sv. Wikipedia SE is Northern Sami
Wikipedia. ]
[ Addendum 20230507: The official Astrid Lindgren web site says “Did you know? Pippi's full name is: Pippilotta Victoriaria Tea-cosy Appleminta Ephraim’s-daughter Longstocking”. I have nothing good to say about any of this. ]
[ Addendum 20230509: Wikipedia informs me that, in English, spearmint is sometimes called “mackerel mint", so it is clear now that Lamborn's translation of krusmynta is quite literal. I applaud her choice of the alliterative and rhythmic “mackerelmint” instead of the mundane “spearmint”. ]
[Other articles in category /lang] permanent link
Mon, 01 Mar 2021
More fuckin' user interface design
Yesterday I complained that Google couldn't find a UI designer who wouldn't do this:

Today I'm going to complain about the gmail button icons. Maybe they were designed by the same person?
Check out the two buttons I have circled.
One of these "archives" the messages, which means that it moves the messages out of the Inbox.
The other button moves the messages into the Inbox.
I don't know the right way to express this, but I know the wrong way
when I see it, and the wrong way is  and
and  .
.
How about, ummm, maybe make the arrows go in opposite directions? How about, put the two buttons next to one another so that the user at least is likely to notice that both of them exist? Maybe come up with some sort of symbol for an archive, like a safe or a cellar or something, and use the same symbol in both icons, once with an arrow going in and once with an arrow coming out? Or did Google test this and they found that the best user experience was when one button was black and one was white? (“Oh, shit!" says the confused Google engineer, “I was holding the survey results upside-down.”)
I explained in the last article that I consider myself an incompetent
designer. But I don't think I'm incompetent enough to have let  and
and  into production.
into production.
Hey, Google, would you like to hire me? Someone once said that genius is the ability to do effortlessly what most people can't do at all, and it appears that compared with Google UI engineers, I'm a design genius. For an adequately generous salary, I will be happy to whack your other designers on their heads with a rolled-up newspaper until they learn to stop this bullshit.
[Other articles in category /tech] permanent link
Sat, 27 Feb 2021
Fuckin' user interface design, I swear
I'm so old I can remember when forms were introducted to the web; as you can imagine it was a big advance. The initial spec included the usual text boxes, radio buttons, and so forth, two types of “submit” buttons, and a “reset” button. Clicking “reset” would reset the form contents to a defined initial state, normally empty.
So you'd have a bunch of form widgets, and then, at the bottom, a Submit button, and next to it, a Reset button.
Even as an innocent youth, I realized this was a bad design. It is just setting people up for failure. They might get the form all filled out, be about to submit it, but click a few pixels off, hit the Reset button by mistake, and have to start all over again.
Obviously, the Submit button should be over on the left, just under the main form, where the user will visit it in due course after dealing with the other widgets, and the Reset button should be way over on the right, where it is less likely to be hit by accident.
(Or, more likely, it shouldn't be anywhere; in most cases it is nothing but an attractive nuisance. How often does someone need to reset the form anyway? How badly would they have to screw it up to decide that it would be quicker to start over than to simply correct their errors?)
Does my “obviously” come across as superior and condescending? Honestly, it comes from a place of humility. My thinking is like this:
- The field of user inteface design is skilled work
- I have no training or experience in this field
- Also, I have no talent in design generally (Just look at this page!)
- Experience has proved that I am very stupid about this whole area
- But this particular problem is apparent even to a blockhead like me
- So it must be extremely obvious
But maybe I'm not giving myself enough credit. I said “obviously” but it sure wasn't obvious to many people at the time. I remember 90% of the forms I encountered having that Reset button at the bottom, at least into the late 1990s.
And it's on my mind because my co-workers had a discussion about it at work last week: don't put the Cancel button right next to the Submit button. If this was obvious to dumbass me in 1994, why isn't it common knowledge by now?
Don't put the Yes button right next to the No button. That encourages mistakes. Obviously.
Don't put the commonly-used "close this window" keyboard shortcut right next to the infrequently-used and irreversible "quit this application" shortcut. In particular, don't put "close this window" on control-W and "quit this application" on control-Q. I'm looking at you, Firefox.
And that brings me to my real point. Can we talk about Google Meet?
These three buttons are at the bottom of the Google Meet videoconferencing app. The left one temporarily mutes and unmutes the microphone. The right one controls the camera similarly.

And if you click the button in between, you immediately leave the meeting and quit the app.
Now, as I said I'm pretty damn stupid when it comes to design, but geez, louise. Couldn't Google find someone less stupid than me?
[ Addendum 20210228: Google fucks up again. ]
[Other articles in category /tech] permanent link
Tue, 16 Feb 2021Katara is toiling through A.P. Chemistry this year. I never took A.P. Chemistry but I did take regular high school chemistry and two semesters of university chemistry so it falls to me to help her out when things get too confusing. Lately she has been studying gas equilibria and thermodynamics, in which the so-called ideal gas law plays a central role: $$ PV=nRT$$
This is when you have a gas confined in a container of volume !!V!!. !!P!! is the pressure exerted by the gas on the walls of the container, the !!n!! is the number of gas particles, and the !!T!! is the absolute temperature. !!R!! is a constant, called the “ideal gas constant”. Most real gases do obey this law pretty closely, at least at reasonably low pressures.
The law implies all sorts of interesting things. For example, if you have gas in a container and heat it up so as to double the (absolute) temperature, the gas would like to expand into twice the original volume. If the container is rigid the pressure will double, but if the gas is in a balloon, the balloon will double in size instead. Then if you take the balloon up in an airplane so that the ambient pressure is half as much, the balloon will double in size again.
I had seen this many times and while it all seems reasonable and makes sense, I had never really thought about what it means. Sometimes stuff in physics doesn't mean anything, but sometimes you can relate it to a more fundamental law. For example, in The Character of Physical Law, Feynman points out that the Archimedean lever law is just an expression of the law of conservation of energy, as applied to the potential energy of the weights on the arms of the lever. Thinking about the ideal gas law carefully, for the first time in my life, I realized that it is also a special case of the law of conservation of energy!
The gas molecules are zipping around with various energies, and this kinetic energy manifests on the macro scale as as pressure (when they bump into the walls of the container) and as volume (when they bump into other molecules, forcing the other particles away.)
The pressure is measured in units of dimension !!\frac{\rm force}{\rm area}!!, say newtons per square meter. The product !!PV!! of pressure and volume is $$ \frac{\rm force}{\rm area}\cdot{\rm volume} = \frac{\rm force}{{\rm distance}^2}\cdot{\rm distance}^3 = {\rm force}\cdot{\rm distance} = {\rm energy}. $$ So the equation is equating two ways to measure the same total energy of the gas.
Over on the right-hand side, we also have energy. The absolute temperature !!T!! is the average energy per molecule and the !!n!! counts the number of molecules; multiply them and you get the total energy in a different way.
The !!R!! is nothing mysterious; it's just a proportionality constant required to get the units to match up when we measure temperature in kelvins and count molecules in moles. It's analogous to the mysterious Cookie Constant that relates energy you have to expend on the treadmill with energy you gain from eating cookies. The Cookie Constant is !!1043 \frac{\rm sec}{\rm cookie}!!. !!R!! happens to be around 8.3 joules per mole per kelvin.
(Actually I think there might be a bit more to !!R!! than I said, something about the Boltzmann distribution in there.)
Somehow this got me and Katara thinking about what a mole of chocolate chips would look like. “Better use those mini chips,” said Katara.
[Other articles in category /physics] permanent link
Mon, 15 Feb 2021Today someone tweeted about an earlier blog article of mine, saying
10° bir kvadratda ən böyük şəhərləri görə biləcəyiniz bir xəritə olan bir sayt.
I looked at that and frowned, and said “What language is that? … is it Azerbaijani?” And it is Azerbaijani! Last time I encountered Azerbaijani I did not recognize it. So I not only learned something last April, I remembered it the following February when it came up again. Yay me!
[Other articles in category /lang] permanent link
Sat, 13 Feb 2021Yesterday I wondered who Robert Altman had cast as Bluto in his 1980 live-action film Popeye. The answer turned out to be Paul L. Smith, who seemingly was born to play the part:
I have thought for years about how Shelley Duval was seemingly born to play the part of Olive Oyl. (I remember the Mad magazine parody making this observation at the time, and it wasn't funny because it was so obvious.) I have somtimes wondered if Altman got the idea to make a Popeye movie specifically so that he could cast Duval as Olive Oyl.
Anyway, Paul L. Smith, who already looked like Bluto. He was in a fair number of TV productions in the 70s and 80s, and I think it's possible that I saw him in one or another one. But the only other role of his that I remember clearly is from David Lynch's 1984 Dune. He plays Glossu “the Beast” Rabban. Who in many ways is not that different from Bluto: Large, violent, dangerous for his brutality but not his cunning.
Obviously the Baron wanted to cast Feyd-Rautha as Popeye, but events got away from him and Paul became Popeye instead. In a Dune-Popeye crossover I can see Alia as Swee'Pea. That means that Chani has to be Olive, which I can live with.
The correspondence isn't perfect, of course. There is nobody in Popeye like Lady Jessica or Stilgar. (Leto is obviously Poopdeck Pappy.) On the other side, where is J. Wellington Wimpy? It's been a while since I read the book, but I don't remember him appearing. Reverend Mother Gaius Helen Mohiam is clearly the Sea Hag.
Me spinach musk flow! If ya controlsk the spinach, ya controlsk the uni-voice! Ag-ag-ag-ag-ag!
[Other articles in category /misc] permanent link
Mon, 08 Feb 2021I was reading The Life and Prankes of Long Meg of Westminster (1655), which opens with the story of how Long Meg first came to London with a posse of three or four girlfriends. After long travel they came within sight of London, “which joyed their hearts greatly.” But as they got closer, Meg's friends became less cheerful, and she said to them:
What Lasses in a dumpe, and we so nigh London?
If someone had asked me to guess when “in a dump” or “in the dumps” had been coined, I think I would have guessed sometime in the early 20th century. Nope! The Big Dictionary has cites back to 1535, which is when Long Meg takes place. It also cites a 1785 dictionary for “down in the dumps” specifically. The phrase is not connected with the dump where you dump a load of trash, which is of much later coinage.
It transpires that the lasses are in a dumpe because they realize that time has come to pay the carrier who has helped transport them to London, and believe he is likely to try to cheat them and take everything they have. Meg says she will reason sweetly with the carrier, and if that doesn't work, she will beat the crap out of him.
The carrier does try to take everything they have, but becomes much more helpful after Meg has beaten him with a cudgel.
Here it is if you would like to read it yourself.
[Other articles in category /lang] permanent link
Sun, 07 Feb 2021
More things that changed in later editions of Snow White
As you know, I've recently been looking into the original version of Snow White from 1812. ([1] [2]) I knew that the 1812 version of the Grimm stories was a lot rougher and more gruesome than the later editions, but I missed many of the details. For example, in the later versions, the evil queen orders her hunter to bring back Snow White's liver and lungs as proof that he has murdered her. In the first edition, she wants the liver and lungs so that she can eat them.
After Snow White is poisoned with the apple, the dwarfs put her in a glass coffin. A prince happens by and begs them to give it to him, which they do. In the later versions, the servants carrying away the coffin stumble, the apple is dislodged from Snow White's throat, and she returns to life.
In the original version, they get the coffin back to the prince's palace without mishap. There the prince has the servants carry it from room to room so that he can gaze at it always. (Ugh.)
Finally, the servants are so fed up with this that one of them takes Snow White out of the coffin, stands her up, and, saying
We are plagued the whole day long, just because of such a dead girl
he clouts her in the back from pure spite.
The apple is dislodged, and Snow White marries the prince.
[Other articles in category /book] permanent link
Sat, 06 Feb 2021Git comes with
a very complicated shell function,, called
__git_ps1,
for interpolating Git information into your shell prompt. A typical
use would be:
PS1='>>> $(__git_ps1) :) '
PS1 is the variable that contains the shell's main prompt. Before
printing the prompt, the shell does variable and command interpolation
on this string. This means that if PS1 contains something like $(command
args...), the shell replaces that string with the output from running
command args…. Here, it runs __git_ps1 and inserts the output into the
prompt. In the simplest case, __git_ps1 emits the name of the
currently-checked-out branch, so that the shell will actually print
this prompt:
>>> the-branch :)
But __git_ps1 has many other features besides. If you are in the middle
of a rebase or cherry-pick operation, it will emit something
like
the-branch|REBASE-i 1/5
or
the-branch|CHERRY-PICKING
instead. If HEAD is detached, it can still display the head
location in several formats. There are options to have the emitted string
indicate when the working tree is dirty and other things. My own
PS1 looks like this:
PS1='[$(_path) $(__git_ps1 "(%s)" )]> '
The _path command is something I
wrote to emit the path of the current working directory, abbreviated
in a contextually dependent way. It makes my prompt look like this:
[lib/app (the-branch)]>
Here lib/app is the path relative to the root of the repository.
The %s thing is an additional formatting instruction to __git_ps1.
After it computes the description string, __git_ps1 inserts it into
"(%s)" in place of the %s, and emits the result of that
replacement. If you don't give __git_ps1 an argument, it uses "(%s) "
as a default, which has an extra space compared with what I have.
Lately I have been experimenting with appending .mjd.yyyymmdd to my
public branch names, to help me remember to delete my old dead
branches from the shared repository. This makes the branch names
annoyingly long:
gh1067-sort-dates-chronologically.mjd.20210103
gh1067-sort-dates-no-test.mjd.20210112
gh1088-cache-analysis-list.mjd.20210105
and these annoyingly long names appear in the output of __git_ps1 that is
inserted into my shell prompts.
One way to deal with this is to have the local branch names be
abbreviated and configure their upstream names to the long versions.
And that does work: I now have a little program called new-branch
that creates a new branch with the local short name, pushes it to the
long remote name, and sets the upstream. But I also wanted a generic
mechanism for abbreviating or transforming the branch name in the
prompt.
The supplied __git_ps1 function didn't seem to have an option
for that, or a callback for modifying the branch name before inserting
it into the prompt. I could have copied the function, modified the
parts I wanted, and used the modified version in place of the supplied
version, but it is 243 lines long, so I preferred not to do that.
But __git_ps1 does have one hook. Under the right circumstances,
it will attempt to colorize the prompt by inserting terminal
escape codes. To do this it invokes __git_ps_colorize_gitstring to
insert the escape codes into the various prompt components before it
assembles them. I can work with that!
The goal is now:
- Figure out how to tell
__git_ps1to call__git_ps_colorize_gitstring - Figure out how
__git_ps1and__git_ps_colorize_gitstringcommunicate prompt components - Write my own
__git_ps_colorize_gitstringto do something else
How to tell __git_ps1 to call __git_ps_colorize_gitstring
You have to do two things to get __git_ps1 to call the hook:
Set
GIT_PS1_SHOWCOLORHINTSto some nonempty string. I set it totrue, which is a little deceptive, becausefalsewould have worked as well.Invoke
__git_ps1with two or more arguments.
Unfortunately, invoking the __git_ps1 with two or more arguments changes
its behavior in another way. It still computes a string, but it no
longer prints the string. Instead, it computes the string and
assigns it to PS1. This means that
PS1="$(__git_ps arg arg….)"
won't work properly: the next time the shell wants to prompt, it will
evaluate PS1, which will call __git_ps arg arg…, which will set
PS1 to some string like (the-branch). Then the next time the
shell wants to print the prompt, it will evaluate PS1, which will be
just some dead string like (the-branch), with nothing in it to call
__git_ps1 again.
So we need to use a different shell feature. Instead of setting PS1
directly, we set PROMPT_COMMAND. This command is run before the
prompt is printed. Although this doesn't have anything to do directly
with the prompt, the command can change the prompt. If we set
PROMPT_COMMAND to invoke __git_ps1, and if __git_ps1 modifies PS1, the
prompt will change.
Formerly I had had this:
PS1='[$(_path) $(__git_ps1 "(%s)")]> '
but instead I needed to use:
GIT_PS1_SHOWCOLORHINTS=true
PROMPT_COMMAND='__git_ps1 "[$(_path) " " ] "' "(%s)"
Here __git_ps1 is getting three arguments:
"[$(_path) "" ] ""(%s)"
__git_ps1 computes its description of the Git state and inserts it into
the third argument in place of the %s. Then it takes the result of
this replacement, appends the first argument on the front and the
second on the back, and sets the prompt to the result. The shell will
still invoke _path in the course of evaluating the first string,
before passing it to __git_ps1 as an argument. Whew.
How __git_ps1 communicates prompt components to __git_ps_colorize_gitstring
The end result of all this rigamarole is that __git_ps1 is now being
called before every prompt, as before, but now it will also invoke
__git_ps_colorize_gitstring along the way. What does that actually get us?
The internals of __git_ps_colorize_gitstring aren't documented because I don't think this
is a planned use case, and __git_ps_colorize_gitstring isn't an advertised part of the
interface. __git_ps1 does something to construct the prompt, possibly
colorizing it in the process, but how it does the colorizing is
forbidden knowledge. From looking at the code I can see that the
colorizing is done by __git_ps_colorize_gitstring, and I needed to know what was going in
inside.
The (current) interface is that __git_ps1 puts the various components of
the prompts into a family of single-letter variables, which __git_ps_colorize_gitstring
modifies. Here's what these variables do, as best as I have been able
to ascertain:
bcontains a description of the current HEAD, either the current branch name or some other description
cindicates if you are in a bare repository
iindicates if changes have been recorded to the index
pcontains information about whether the current head is behind or ahead of its upstream branch
rdescribes the rebase / merge / cherry-pick state
sindicates if there is something in the stash
uindicates whether there are untracked files
windicates whether the working tree is dirty
zis the separator between the branch name and the other indicators
Oddly, the one thing I wanted to change is the only one that __git_ps_colorize_gitstring
doesn't modify: the b variable that contains the name or
description of the current branch. Fortunately, it does exist and
there's nothing stopping me from writing a replacement __git_ps_colorize_gitstring that
does modify it.
Write a replacement for __git_ps_colorize_gitstring to do something else
So in the end all I needed was:
GIT_PS1_SHOWCOLORHINTS=true
PROMPT_COMMAND='__git_ps1 "[$(_path) " " ] "' "(%s)"
__git_ps1_colorize_gitstring () {
b=${b%%.[0-9][0-9][0-9][0-9][0-9][0-9][0-9][0-9]}
b=${b%%.mjd}
}
The ${b%%PAT} thing produces the value of the variable b, except
that if the value ends with something matching the pattern PAT, that
part is removed. So the first assignment trims a trailing
.20210206 from the branch name, if there is one, and the second
trims off a trailing .mjd. If I wanted to trim off the leading gh
also I could use b=${b##gh}.
There's probably some way to use this in addition to the standard
__git_ps_colorize_gitstring, rather than in place of it. But I don't know how.
In conclusion
This was way harder to figure out than it should have been.
[Other articles in category /prog] permanent link
Wed, 03 Feb 2021Katara and I went to visit the town of Gap, PA. In Gap there are so many eagles that they have these special bins for getting rid of the extras.
[Other articles in category /misc] permanent link
Tue, 02 Feb 2021This is the famous self-portrait of Hildebert, a 12th century scribe in what is now the Czech Republic. In this picture, Hildebert is shaking his fist at a mouse, which is eating his lunch.
There is quite a lot going on here! First off, Hildebert is carrying one of his quill pens behind his ear. This seems to me like a good way to get ink in your hair, and I wonder if medieval scribes often had smudges on their forheads.
I think the thing in his hand is a piece of bread. But what is on the table? I think the mouse is eating Hildebert's cheese (we can see the already-cut piece under the mouse's butt) and there seems to have been a small roast bird of some type, which the mouse has upset but which has not yet hit the floor. The table with the mouse is labeled Mensa hildeberti, “Hildebert's table”, in case it was unclear just whose lunch was being stolen.
Hildebert seems to be wearing a long garment with fancy matching sleeves and collar, and over that what looks like a chiton. I wonder if Hildebert really wore a chiton?
On the left of the picture is a really interesting piece of equipment. Until I saw this picture, it had never occurred to me that the lap desk had been invented before I was born. But here it is, almost nine hundred years ago. And it certainly is a lap desk, having no legs. In this picture the lap desk is supported by a backward-headed lion, but in actual practice such luxuries are probably hard to come by, so Hildebert would have put the desk on his lap.
The two long curvy things on the left edge of the lap desk are not legs. They are inkhorns: sawn-off animal horns, filled with ink. When you need to get more ink on your quill, you dip the end in the inkhorn. I had heard of inkhorns but until I saw this picture I had never understood how you used them: they won't stand up, and if you lay them down the ink will spill. But Hildebert's picture makes it perfectly clear: the lap desk has a couple of round holes in it, and you slide the inkhorns into the holes until they stop. Very nice! Next to the inkhorns are two extra quills, and along the bottom edge of the lap desk there is a ridge to keep the paper or parchment from sliding into your lap. I am pretty sure that the lion is holding the desk by the bottom edge, so that it is presented to Hildebert sideways. Hildebert is too enraged by the mouse to care about this.
Also on the desk is a booklet, in which (according to Wikipedia) Hildebert has written:
Pessime mus, saepius me provocas ad iram. Ut te deus perdat
I think I can make this out. (Medieval scribes used a great many abbreviations. For example, iram is written as “irã”. Similarly, the hildeberti above the table is abbreviated to “hildebti”. If you are interested, I discussed scribal abbreviations a couple of years ago.)
Wikipedia's translation of this is:
Most wicked mouse, you incite me to anger once too often. May God destroy you.
I think the phrasing and the fist-shaking, directed at a mouse, are meant by Hildebert to be a humorous overreaction.
Underneath Hildebert is a drawing of his colleague Everwin (EVERWINVS). Everwin seems to be painting some sort of decoration with a brush. Check out his fancy sleeves and matching socks!
I am not sure what Hildebert is holding in his left hand or whether it intersects the lion's arm. My best guess is that it is Hildebert's table knife, and that the picture means to show it passing in front of the lion, not intersecting the lion.
Many thanks to Marnanel Thurman for bringing this to my attention.
[Other articles in category /art] permanent link
Mon, 01 Feb 2021
The magic mirror in Snow White
A few weeks ago I was thinking about Snow White and in the course of doing that I looked up the original German version of 1812. (Snow White herself is story #53, on page 238.)
The magic mirror is introduced this way:
Die Königin … hatte auch einen Spiegel, vor trat sie alle Morgen und fragte: …
(“The queen… also had a mirror, before which she stood every morning and asked…”)
The mirror is simply einen Spiegel, a mirror, not a specifically magic mirror. That seems to have been a later interpolation. In the 1857 edition, it says Sie hatte einen wunderbaren Spiegel…. There is no wunderbaren in the original.
I prefer the original. The mirror recites poetry; to say it is a magic mirror is superfluous.
But on second thought, is it? There is another explanation: in the original version, perhaps the mirror is an ordinary one, and the queen is psychotic.
Certainly nobody else hears the mirror speaking. And the queen tells the hunter not only to kill Snow White in the forest, but to bring back Snow White's lungs and liver, so that the she may eat them. With salt! (die will ich mit Salz kochen und essen.) Now I prefer the original even more. The later version, which unequivocally states that the mirror is magic, is much less terrifying.
I suppose the argument against this reading is that the mirror also provides the queen with real information: Snow White is still alive, and living with the seven dwarfs. I think the original text does imply that the queen was aware of the seven dwarfs, but how might she have known that Snow White was still alive? Well, she did eat the lungs and liver, which had actually come from a young wild boar (junger Frischling). Perhaps she was satisfied at first, but then there was something about the taste, or the texture, not quite what she expected… it gnawed at her for hours, and then in a flash of rage she realized what she had actually eaten…
[ Addendum 20210202: In case you wanted to see it,

Note, by the way, that in 1812 the umlaut marks in Königin etc. still looked like small letter ‘e’; they had not yet been reduced to diareses. ]
[ Addendum 20210207: another startling detail that was revised in the later editions. ]
[ Addendum 20210321: The more I think about the queen's psychosis, the more obvious it seems that this is the correct explanation. ]
[Other articles in category /book] permanent link
Sun, 31 Jan 2021
Early warning signs of shitty software
Here's a screenshot of menu on the documentation page of a package I'm using. You can see right away that the software is going to be crappy:
Major warning sign: The items are not in alphabetical order. (They are in numeric order, but the numbers are not displayed.)
- Was alphabetization too hard for these people?
Or did they simply not think for one second about who would want to use this menu and how?
If you are looking up a particular function to find out what it does, you have to do linear search on the list to find the one you want.
Yes, you could do full-text search on the whole page, but then what is the menu for?
Minor warning sign: But at least they included an API function to
generate the frequently-used HTTP 418 I'm a teapot status.
<sarcasm>Clearly a lot of thought here about what really matters.</sarcasm>
[Other articles in category /prog] permanent link
Sun, 03 Jan 2021Tonight I was thinking of
Mirror, mirror, on the wall
Who is the fairest of them all?
I remembered that the original was in German and wondered whether it had always rhymed. It turns out that it had:
Spieglein, Spieglein an der Wand,
Wer ist die Schönste im ganzen Land?
The English is a pretty literal translation.
When the wunderbare Spiegel gives the Queen the bad news, it says:
Frau Königin, Ihr seid die Schönste hier,
Aber Schneewittchen ist tausendmal schöner als Ihr.
(“Queen, you are the fairest one here, but Little Snow White is a thousand times as fair as you.”)
When the dwarfs see Snow White in one of their beds, they cry
Ei, du mein Gott!
which is German for “zOMG”.
Later the Queen returns to the mirror, expecting a better answer, but she gets this:
Frau Königin, Ihr seid die Schönste hier,
Aber Schneewittchen über den Bergen
Bei den sieben Zwergen
Ist noch tausendmal schöner als Ihr.
(“Queen, you are the fairest here, but Little Snow White up on the mountain with the seven dwarfs is still a thousand times as fair as you.”)
I like the way this poem here interpolates the earlier version, turning the A-A rhyme into A-B-B-A. The English version I have has “in the glen / little men” in place of “über den Bergen / sieben Zwergen”. The original is much better, but I am not sure English has any good rhymes for “dwarfs”. Except “wharfs”, but putting the dwarfs by the wharfs is much worse than putting them in the glen.
[ Thanks to Gaal Yahas for correcting my translation of noch and to Mario Lang for correcting my German grammar. ]
[ Addendum 20200115: Was the mirror magical? ]
[Other articles in category /lang] permanent link
Fri, 01 Jan 2021
My big mistake about dense sets
I made a big mistake in a Math Stack Exchange answer this week. It turned out that I believed something that was completely wrong.
Here's the question, are terminating decimals dense in the reals?. It asks if the terminating decimals (that is, the rational numbers of the form !!\frac m{10^n}!!) are dense in the reals. “Dense in the reals” means that if an adversary names a real number !!r!! and a small distance !!d!!, and challenges us to find a terminating decimal !!t!! that is closer than !!d!! to point !!r!!, we can always do it. For example, is there a terminating decimal !!t!! that is within !!0.0000001!! of !!\sqrt 2!!? There is: !!\frac{14142135}{10^7} = 1.4142135!! is closer than that; the difference is less than !!0.00000007!!.
The answer to the question is ‘yes’ and the example shows why: every real number has a decimal expansion, and if you truncate that expansion far enough out, you get a terminating decimal that is as close as you like to the original number. This is the obvious and straightforward way to prove it, and it's just what the top-scoring answer did.
I thought I'd go another way, though. I said that it's enough to show that for any two terminating decimals, !!a!! and !!b!!, there is another one that lies between them. I remember my grandfather telling me long ago that this was a sufficient condition for a set to be dense in the reals, and I believed him. But it isn't sufficient, as Noah Schweber kindly pointed out.
(It is, of course, necessary, since if !!S!! is a subset of !!\Bbb R!!, and !!a,b\in S!! but no element of !!S!! between these, then there is no element of !!S!! that is less than distance !!\frac{b-a}2!! of !!\frac{a+b}2!!. Both !!a!! and !!b!! are at that distance, and no other point of !!S!! is closer.)
The counterexample that M. Schweber pointed out can be explained quickly if you know what the Cantor middle-thirds set is: construct the Cantor set, and consider the set of midpoints of the deleted intervals; this set of midpoints has the property that between any two there is another, but it is not dense in the reals. I was going to do a whole thing with diagrams for people who don't know the Cantor set, but I think what follows will be simpler.
Consider the set of real numbers between 0 and 1. These can of course be represented as decimals, some terminating and some not. Our counterexample will consist of all the terminating decimals that end with !!5!!, and before that final !!5!! have nothing but zeroes and nines. So, for example, !!0.5!!. To the left and right of !!0.5!!, respectively, are !!0.05!! and !!0.95!!.
In between (and around) these three are: $$\begin{array}{l} \color{darkblue}{ 0.005 }\\ 0.05 \\ \color{darkblue}{ 0.095 }\\ 0.5 \\ \color{darkblue}{ 0.905 }\\ 0.95 \\ \color{darkblue}{ 0.995 }\\ \end{array}$$
(Dark blue are the new ones we added.)
And in between and around these are:
$$\begin{array}{l} \color{darkblue}{ 0.0005 }\\ 0.005 \\ \color{darkblue}{ 0.0095 }\\ 0.05 \\ \color{darkblue}{ 0.0905 }\\ 0.095 \\ \color{darkblue}{ 0.0995 }\\ 0.5 \\ \color{darkblue}{ 0.9005 }\\ 0.905 \\ \color{darkblue}{ 0.9095 }\\ 0.95 \\ \color{darkblue}{ 0.9905 }\\ 0.995 \\ \color{darkblue}{ 0.9995 }\\ \end{array}$$
Clearly, between any two of these there is another one, because around !!0.????5!! we've added !!0.????05!! before and !!0.????95!! after, which will lie between !!0.????5!! and any decimal with fewer !!?!! digits before it terminates. So this set does have the between-each-two-is-another property that I was depending on.
But it should also be clear that this set is not dense in the reals, because, for example, there is obviously no number of this type that is near !!0.7!!.
(This isn't the midpoints of the middle-thirds set, it's the midpoints of the middle-four-fifths set, but the idea is exactly the same.)
Happy New Year, everyone!
[Other articles in category /math] permanent link