Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Addenda to recent articles 200805 |
| Defunctionalization and Java |
| Freshman electromagnetism questions: answer 3 |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 29 Jun 2008
Freshman electromagnetism questions: answer 3
Last year I asked a bunch
of basic questions about electromagnetism. Many readers wrote in with
answers and explanations, which I still hope to write up in detail.
In the meantime, however, I figured out the answer to one of the
questions by myself.
I had asked:
And one day a couple of months ago it occurred to me that yes, of course the electron vibrates up and down, because that is how radio antennas work. The EM wave comes travelling by, and the electrons bound in the metal antenna vibrate up and down. When electrons vibrate up and down in a metal wire, it is called an alternating current. Some gizmo at the bottom end of the antenna detects the alternating current and turns it back into the voice of Don Imus.
- Any beam of light has a time-varying electric field, perpendicular to the direction that the light is travelling. If I shine a light on an electron, why doesn't the electron vibrate up and down in the varying electric field? Or does it?
I thought about it a little more, and I realized that this vibration effect is also how microwave ovens work. The electromagnetic microwave comes travelling by, and it makes the electrons in the burrito vibrate up and down. But these electrons are bound into water molecules, and cannot vibrate freely. Instead, the vibrational energy is dissipated as heat, so the burrito gets warm.
So that's one question out of the way. Probably I have at least three reader responses telling me this exact same thing. And perhaps someday we will all find out together...
[Other articles in category /physics] permanent link
Tue, 17 Jun 2008
Defunctionalization and Java
A couple of weeks ago I was introduced to the notion of defunctionalization by this
article on Ken
Knowles' blog. Defunctionalization is a program transformation that removes the
higher-order functions from a program. The idea is that you replace
something like λx.x+y with a data structure that
encapsulates a value of y somewhere, say (HOLD y). And
instead of using the language's built-in function application to
apply this object directly to an argument x, you write a
synthetic applicator that takes (HOLD y) and x and
returns x + y. And anyone who wanted to apply
λx.x+y to some argument x in some context
in which y was bound should first construct (HOLD y),
then use the synthetic applicator on (HOLD y) and x.
Consider, for example, the following Haskell program:
-- Haskell
aux f = f 1 + f 10
res x = aux (λz -> z + x)
The defunctionalization of this example is:
-- Haskell
data Hold = HOLD Int
fake_apply (HOLD a) b = a + b
aux held = fake_apply held 1 + fake_apply held 10
res x = aux (HOLD x)
I hope this will make the idea clear.M. Knowles cites the paper Defunctionalization at work by Olivier Danvy and Lasse R. Nielsen, which was lots of fun. (My Haskell example above is a simplification of the example from page 5 of Danvy and Nielsen.) Among other things, Danvy and Nielsen point out that this defunctionalization transformation is in a certain sense dual to the transformation that turns ordinary data structures into λ-terms in Church encoding. Church encloding turns data items like pairs or booleans into higher-order functions; defunctionalization turns them back again.
Section 1.4 of the Danvy and Nielsen paper lists a whole bunch of contexts in which this technique has been studied and used, but one thing I didn't think I saw there is that this is essentially the transformation that Java programmers use when they want to use closures.
For example, suppose a Java programmer wants to write something like aux in:
-- Haskell
aux f = f 1 + f 10
res x = aux (λz -> z + x)
But they can't, because Java doesn't have closures.So instead, they do this:
/* Java */
class Hold {
private int a;
public Hold(int a) {
this.a = a;
}
public int fake_apply(int b) {
return this.a + b;
}
}
private static int aux(Hold h) {
return h.fake_apply(1) + h.fake_apply(10);
}
static int res(int x) {
Hold h = new Hold(x);
return aux(h);
}
Where the class Hold corresponds directly to the
data type Hold in the defunctionalized Haskell code.Here is a real example. Consider GNU Emacs. When I enter text-mode in Emacs, I want a bunch of subsystems to be notified. Emacs has a text-mode-hook variable, which is basically a list of functions, and when an Emacs buffer is put into text-mode, Emacs invokes the hooks. Any subsystem that wants to be notified puts its own hook function into that variable. If I wanted to accomplish something similar in Haskell or SML, I would similarly use a list of functions.
In Java, the corresponding facility is called java.util.Observable. Were one implementing Emacs in Java (perish the thought!) the mode object would inherit from Observable, and so would provide an addObserver method for adding a hook to a list somewhere. When the mode was switched to text-mode, the mode object would call notifyObservers, which would loop over the hook list, calling the hooks. So far this is just like Emacs Lisp.
But in Java the hooks are not functions, as they are in Emacs, because in Java functions are not first-class entities. Instead, the hooks are objects which conform to the Observer interface specification, and instead of invoking functions directly, the notifyObservers method calls the update method on each hook object.
Here's another example. I wrote a recursive descent parser in Java a while back. An ActionParser is just like a Parser, except that if its parse succeeds, it invokes a callback. If I were programming in SML or Haskell or Perl, an ActionParser would be nothing but a Parser with an associated closure, something like this:
# Perl
package ActionParser;
sub new {
my ($class, $parser, $action) = @_;
bless { Parser => $parser,
Action => $action } => $class;
}
# Just like the embedded parser, but invoke the action on success
sub parse {
my $self = shift;
my $input = shift;
my $result = $self->{Parser}->parse($input);
if ($result->success)
$self->{Action}->($result); # Invoke action
}
return $result;
}
Here the Action member is expected to be a closure, which is
automatically invoked if the parse succeeds. To use this, I would
write something like this:
# Perl
my $missiles;
...
my $parser = ActionParser->new($otherParser,
sub { $missiles->launch() }
);
$parser->parse($input);
And then if the input parses correctly, the parser launches the
missiles from the anonymous closure, which has captured the local
$missiles object.But in Java, you have no closures. Instead, you defunctionalize, and represent closures with objects:
/* Java */
abstract class Action {
void invoke(ParseResults results) {}
}
class ActionParser extends Parser {
Action action;
Parser parser;
ActionParser(Parser p, Action a) {
action = a;
parser = p;
}
ParseResults Parse(Input input) {
ParseResults res = this.parser.Parse(input);
if (res.isSuccess) {
this.action.invoke(res);
}
return res;
}
}
To use this, one writes something like this:
/* Java */
class LaunchMissilesAction extends Action {
Missiles m;
LaunchMissilesAction(Missiles m) { this.m = m; }
void invoke(ParseResults results) {
m.launch();
}
}
...
Action a = new LaunchMissilesAction(missiles);
Parser p = new ActionParser(otherParser, a);
p.parse(input);
The constructor argument missiles takes the place of a free
variable in a closure. The closure itself has been replaced with
an object from an ad hoc class, just as in Danvy and Nielsen's
formulation, the closure is replaced with a synthetic data object that
holds the values of the free variables. The invoke method
plays the role of fake_apply.Now, it's not a particularly interesting observation that this can be done. The interesting part, I think, is that this is what Java programmers actually do. And also, perhaps, that Danvy and Nielsen didn't mention it in their paper, because I think the technique is pretty widespread.
[Other articles in category /prog] permanent link
Sun, 01 Jun 2008
Addenda to recent articles 200805
- Regarding the bicameral mind
theory put forth in Julian Jaynes' book The Origin of
Consciousness in the breakdown of the Bicameral Mind, Carl
Witty informs me that the story "Sour Note on Palayata", by James
Schmitz, features a race of bicameral aliens whose mentality is
astonishingly similar to the bicameral mentality postulated by Julian
Jaynes. M. Witty describes it as follows:
The story features a race of humanoid aliens with a "public" and a "private" mind. The "public" mind is fairly stupid, and handles all interactions with the real world; and the "private" mind is intelligent and psychic. The private mind communicates psychically with the private minds of other members of the race, but has only limited influence over the public mind; this influence manifests as visions and messages from God.
This would not be so remarkable, since Jaynes' theories have been widely taken up by some science fiction authors. For example, they appear in Neal Stephenson's novel Snow Crash, and even more prominently in his earlier novel The Big U, so much so that I wondered when reading it how anyone could understand it without having read Jaynes first. But Schmitz's story was published in 1956, twenty years before the publication of The Origin of Consciousness. - Also in connection with Jaynes: I characterized his theory as
"either a work of profound genius, or of profound crackpottery". I
should have mentioned that this
characterization was not lost on Jaynes himself. In his book, he
referred to his own theory as "preposterous".
- Many people wrote in with more commentary about my articles on
artificial Finnish
[1]
[2]:
- I had said that "[The one-letter word 'i'] appears in my sample
in connection with Sukselaisen
I hallitus, whatever that is". Several people
explained that this "I" is actually a Roman numeral 1, denoting the ordinal number
"first", and that Sukselaisen
I hallitus is the first government headed by V. J. Sukselaisen.
I had almost guessed this—I saw "Sukselaisen I" in the source material and guessed that the "I" was an ordinal, and supposed that "Sukselaisen I" was analogous to "Henry VIII" in English. But when my attempts to look up the putative King Sukselaisen I met with failure, and I discovered that "Sukselaisen I" never appeared without the trailing "hallitus", I decided that there must be more going on than I had supposed, as indeed there was. Thanks to everyone who explained this.
- Marko Heiskanen says that the (fictitious) word
yhdysvalmistämistammonit is "almost correct", at least up to the
nonsensical plural component "tammonit". The vowel harmony failure
can be explained away because compound words in Finnish do not respect the
vowel harmony rules anyway.
- Several people objected to my program's generation of the word
"klee": Jussi Heinonen said "Finnish has quite few words that begin with
two consonants", and Jarkko Hietaniemi said "No word-initial "kl":s
possible in native Finnish words". I checked, and my sample Finnish
input contains "klassisesta", which Jarkko explained was a loanword,
I suppose from Russian.
Had I used a larger input sample, oddities like "klassisesta" would have had less influence on the output.
- I acquired my input sample by selecting random articles from
Finnish Wikipedia, but my random sampling was rather unlucky, since it
included articles about Mikhail Baryshnikov (not Finnish), Dmitry Medvevev
(not Finnish), and Los Angeles (also not Finnish). As a result, the
input contained too many strange un-Finnish letters, like B, D, š, and
G, and so therefore did the output. I could have been more careful in
selecting the input data, but I didn't want to take the time.
Medvedev was also the cause of that contentious "klassisesta", since, according to Wikipedia, "Medvedev pitää klassisesta rock-musiikista". The Medvedev presidency is not even a month old and already he has this international incident to answer for. What catastrophes could be in the future?
- Another serious problem with my artificial Finnish is that the
words were too long; several people complained about this, and the
graph below shows the problem fairly clearly:
The x-axis is word length, and the y-axis is frequency, on a logarithmic scale, so that if 1/100 of the words have 17 letters, the graph will include the point (17, -2). The red line, "in.dat", traces the frequencies for my 6 kilobyte input sample, and the blue line, "pseudo.dat", the data for the 1000-character sample I published in the article. ("Ävivät mena osakeyhti...") The green line, "out.dat", is a similar trace for a 6 kb N=3 text I generated later. The long right tail is clearly visible. My sincere apologies to color-blind (and blind) readers.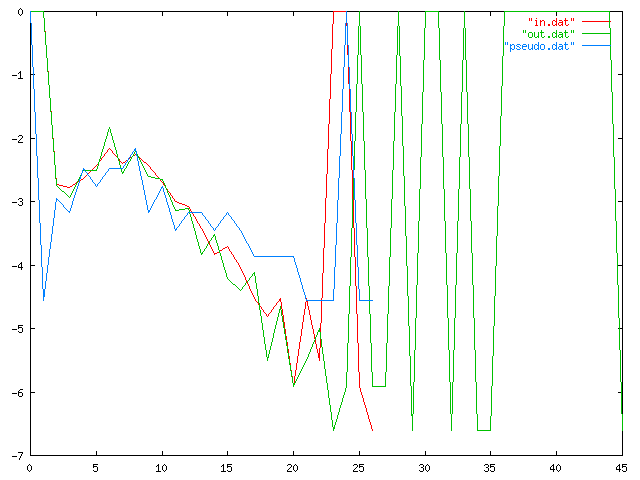
I am not sure exactly what happened here, but I can guess. The Markov process has a limited memory, 3 characters in this case, so in particular is has essentially no idea how long the words are that it is generating. This means that the word lengths that it generates should appear in roughly an exponential distribution, with the probability of a word of length N approximately equal to !!\lambda e^{-\lambda N} !!, where 1/λ is the mean word length.
But there is no particular reason why word lengths in Finnish (or any other language) should be exponentially distributed. Indeed, one would expect that the actual distribution would differ from exponential in several ways. For example, extremely short words are relatively uncommon compared with what the exponential distribution predicts. (In the King James Bible, the most common word length is 3, then 4, with 1 and 8 tied for a distant seventh place.) This will tend to push the mean rightwards, and so it will skew the Markov process' exponential distribution rightwards as well.
I can investigate the degree to which both real text and Markov process output approximate a theoretical exponential distribution, but not today. Perhaps later this month.
My thanks again to the many helpful Finnish speakers who wrote in on these and other matters, including Marko Heiskanen, Shae Erisson, Antti-Juhani Kaijanaho, Ari Loytynoja, Ilmari Vacklin, Jarkko Hietaniemi, Jussi Heinonen, Nuutti-Iivari Meriläinen, and any others I forgot to mention.
- I had said that "[The one-letter word 'i'] appears in my sample
in connection with Sukselaisen
I hallitus, whatever that is". Several people
explained that this "I" is actually a Roman numeral 1, denoting the ordinal number
"first", and that Sukselaisen
I hallitus is the first government headed by V. J. Sukselaisen.
- My explanation of Korean
vowel harmony rules in that article is substantively correct, but
my description of the three vowel groups was badly wrong. I have
apparently forgotten most of the tiny bit I once knew about Middle
Korean. For a correct description, see
the Wikipedia article
or
this
blog post. My thanks to the anonymous author of the blog post for
his correction.
- Regarding the
transitivity of related-by-blood-ness, Toth András told me about a
(true!) story from the life of Hungarian writer Karinthy
Frigyes:
Karinthy Frigyes got married two times, the Spanish flu epidemic took his first wife away. A son of his was born from his first marriage, then his second wife brought a boy from his previous husband, and a common child was born to them. The memory of this the reputed remark: "Aranka, your child and my child beats our child."
(The original Hungarian appears on this page, and the surprisingly intelligible translation was provided by M. Toth and the online translation service at webforditas.hu. Thank you, M. Toth.
- Chung-chieh Shan tells me that the missing
document-viewer feature that I described is available in recent
versions of xdvi. Tanaeem M. Moosa says
that it is also available in Adobe Reader
8.1.2.
[Other articles in category /addenda] permanent link


