Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 01 Dec 2014
Why my book can be downloaded for free
People are frequently surprised that my book, Higher-Order Perl, is available as a free download from my web site. They ask if it spoiled my sales, or if it was hard to convince the publisher. No and no.
I sent the HOP proposal to five publishers, expecting that two or three would turn it down, and that I would pick from the remaining two or three, but somewhat to my dismay, all five offered to publish it, and I had to decide who.
One of the five publishers was Morgan Kaufmann. I had never heard of Morgan Kaufmann, but one day around 2002 I was reading the web site of Philip Greenspun. Greenspun was incredibly grouchy. He found fault with everything. But he had nothing but praise for Morgan Kaufmann. I thought that if Morgan Kaufmann had pleased Greenspun, who was nearly impossible to please, then they must be really good, so I sent them the proposal. (They eventually published the book, and did a superb job; I have never regretted choosing them.)
But not only Morgan Kaufmann but four other publishers had offered to publish the book. So I asked a number of people for advice. I happened to be in London one week and Greenspun was giving a talk there, which I went to see. After the talk I introduced myself and asked for his advice about picking the publisher.
Greenspun reiterated his support for Morgan Kaufmann, but added that the publisher was not important. Instead, he said, I should make sure to negotiate permission to make the book available for free on my web site. He told me that compared with the effort that you put into the book, the money you get back is insignificant. So if you write a book it should not be because you want to make a lot of money from it but because you have an idea that you want to present to the world. And as an author, you owe it to yourself to get your idea in front of as many people as possible. By putting the book in your web site, you make it available to many people who would not otherwise have access to it: poor people, high school students, people in developing countries, and so on.
I thought that Greenspun's idea made sense; I wanted my ideas about programming to get to as many people as possible. Also, demanding that I make the book available on my web site for free seemed like a good way to narrow down the five publishers to two or three.
The first part of that plan worked out well. The second part not so well: all five publishers agreed. Some agreed reluctantly and some agreed willingly, but they all agreed. Eventually I had the book published by Morgan Kaufmann, and after a delay that seemed long at the time but in retrospect seems not so long, I put the book on my web site. It has been downloaded many times. (It's hard to say how many, since browsers often download just the portion of the PDF file that they need to display.)
Would the book have made more money if it were not available as a free download? We can't know for sure, but I don't think so. The book has always sold well, and has made a significant amount of money for me and for Morgan Kaufmann. The amount I made is small compared to the amount of work I had to put in, just as Greenspun said, but it was nothing to sneeze at either. Even now, ten years later, it is still selling and I still get a royalty check every six months. For my book to have lasted ten years is extremely rare. Most computer books disappear without a trace after six months.
Part of this is that it's an unusually good book. But I think the longevity is partly because it is available as a free download. Imagine that person A asks a question on an Internet forum, and person B says that HOP has a section that could help with the question. If A wants to follow up, they now must find a copy of HOP. If the book is out of print, this can be difficult. It may not be in the library; it almost certainly isn't in the bookstore. Used copies may be available, but you have to order them and have them shipped, and if you don't like it once it arrives, you are stuck with it. The barrier is just too high to be convenient. But since HOP is available on my web site, B can include a link, or A can find it with an easy web search. The barrier is gone! And now I have another reader who might mention it to someone else, and they might even buy a copy. Instead of drifting away into obscurity, HOP is a book that people can recommend over and over.
So my conclusion is, Greenspun's advice was exactly correct. As an author, you owe it to yourself to make your book available to as many people as possible. And the publisher may agree, so be sure to ask.
[ Addendum: Some people are just getting the news, but the book was published in 2005, and has been available as a free download since 2008. ]
[Other articles in category /book] permanent link
Sat, 29 Nov 2014I don't have impostor syndrome about programming, advanced mathematics, or public speaking. I cheerfully stand up in rooms full of professional programmers and authoritatively tell them what I think they should do.
However, when I put up shelves in the bathroom back in May, I was a psychological mess. For every little thing that went wrong—and there were quite a lot—I got all stressed out and wondered why I dared to perform this task. The outcome was good, but I had a lot of stress getting there.
I put in one plexiglass shelf, for which I had bought heavy-duty wall anchors in case the kids leaned on it, and two metal shelves higher up, which came with their own screws and anchors.
Here's a partial list of things that worried me:
- The two upper shelves came with a paper template that I held up to the wall to mark where the holes should be drilled. What if the two shelves were slightly different and their templates were different and I needed to use both templates on the wall instead of using the same template twice?
- When I putting the heavy-duty wall anchors into the drywall, big divots of plaster fell out of the wall around the anchors.
- Then I filled in the holes with filler, and got filler in the screw holes in the wall anchors, and stressed about this. What if the filler in the sockets somehow prevented the screws from going into the anchors or caused some other unforeseeable problem?
- The filler looked sloppy and I worried that it would look absurdly ugly to everyone who came into the bathroom. (The shelf would have hidden the ugly screw job from a normal view, except that it was made of plexiglass, so the filled holes were visible through it.)
- I didn't know how big to drill the holes for the smaller wall anchors and stressed about it, examining the wall anchor packaging for some hint. There was none.
- I wanted to insert the wall anchors into the holes with my rubber mallet. Where the hell is it? Then I stressed about using a claw hammer instead and maybe squishing the anchors, and spent a while looking for a piece of wood or something to soften the hammer blows. Eventually I gave up looking, wondering if I was dooming the project.
- I guessed how big to make the hole for the anchor, and was wrong; my hole was too small. I didn't realize this until I had the first anchor halfway in. Then I stressed that I might ruin it when I pulled it back out of the wall.
- Then I stressed about the size of the holes again when I drilled larger holes. What if I make the hole too big, and then have to fill all the holes and re-measure and re-drill the whole thing?
- The anchors didn't go into two of the holes. I needed to yank them back out, then redrill the holes, with the outer end a little messy, or the anchors wouldn't go all the way into the holes. Again I worried about spoiling the anchors.
- When I drilled the holes, sometimes the drill suddenly went all the way into the wall and the rotating chuck left a circular scar on the paint.
- Also, two of the holes didn't drill easily; I had to lean on the drill really hard to get it to go through. For a while I was concerned that there was some undrillable metal thing in the wall just where I wanted my hole, and I would have to fill in all the holes and remeasure and redrill the whole thing.
- Even though I had marked the wall for the lower shelf by holding the shelf against the wall and then poking a pencil through the actual holes, when time came to put the bolts in place, I found that the two holes were slightly too far apart. Somehow this worked itself out.
On review, I see that several of these worries could have been completely avoided if I had had a supply of extra wall anchors.
Stuff that could have worried me but (rightly or wrongly) didn't:
I knew enough to go to the store to buy wall anchors and screws for the bottom shelf, which did not come with its own hardware. There are a lot of different kinds of anchors, and I did not worry too much that I was getting the wrong thing.
I was concerned (although not worried) that the screws holding the bottom shelf to the wall might stress the plastic too much and cause it to crack, either immediately or over time. Obvious solution: insert washers between the screw heads and the shelf. I went to the hardware store to get nylon washers; they didn't have any. So I got thin metal washers instead. I did not worry about this; I was sure (perhaps wrongly) that metal washers would do the job.
When I asked the hardware people for plastic washers, they looked totally blank. “Plastic... washers?” they asked, as if this were a heretofore unimaginable combination. I could have felt like an idiot, but instead I felt, correctly I think, that they were idiots.
For some reason, I was not even slightly worried about properly leveling the marks for the holes. I used a spirit level, which I consider pretty fancy.
I was careful not to over-tighten the screws holding the plexiglass shelf in place, so as to avoid cracking them, but I was at no time afraid that I would somehow crack them anyway.
[Added in July: I have reread this article for the first time. I can report that all the worries I had about whether the shelves would look good have come to nothing; they all look just fine and I had forgotten all the things I was afraid would look bad. But I really do need to buy a couple of boxes of plastic wall anchors so I can stop worrying about spoiling the four I have.]
[The shelves look crooked in the picture, but that is because I am holding the camera crooked; in real life they look great.]
[ A later visit to a better hardware store confirmed that plastic washers do exist, and I did not hallucinate them. The rubber mallet still has not come to light.]
[Other articles in category /brain] permanent link
Sat, 22 Nov 2014
Within this instrument, resides the Universe
When opportunity permits, I have been trying to teach my ten-year-old daughter Katara rudiments of algebra and group theory. Last night I posed this problem:
Mary and Sue are sisters. Today, Mary is three times as old as Sue; in two years, she will be twice as old as Sue. How old are they now?
I have tried to teach Katara that these problems have several phases. In the first phase you translate the problem into algebra, and then in the second phase you manipulate the symbols, almost mechanically, until the answer pops out as if by magic.
There is a third phase, which is pedagogically and practically essential. This is to check that the solution is correct by translating the results back to the context of the original problem. It's surprising how often teachers neglect this step; it is as if a magician who had made a rabbit vanish from behind a screen then forgot to take away the screen to show the audience that the rabbit had vanished.
Katara set up the equations, not as I would have done, but using four unknowns, to represent the two ages today and the two ages in the future:
$$\begin{align} MT & = 3ST \\ MY & = 2SY \\ \end{align} $$
(!!MT!! here is the name of a single variable, not a product of !!M!! and !!T!!; the others should be understood similarly.)
“Good so far,” I said, “but you have four unknowns and only two equations. You need to find two more relationships between the unknowns.” She thought a bit and then wrote down the other two relations:
$$\begin{align} MY & = MT + 2 \\ SY & = ST + 2 \end{align} $$
I would have written two equations in two unknowns:
$$\begin{align} M_T & = 3S_T\\ M_T+2 & = 2(S_T + 2) \end{align} $$
but one of the best things about mathematics is that there are many ways to solve each problem, and no method is privileged above any other except perhaps for reasons of practicality. Katara's translation is different from what I would have done, and it requires more work in phase 2, but it is correct, and I am not going to tell her to do it my way. The method works both ways; this is one of its best features. If the problem can be solved by thinking of it as a problem in two unknowns, then it can also be solved by thinking of it as a problem in four or in eleven unknowns. You need to find more relationships, but they must exist and they can be found.
Katara may eventually want to learn a technically easier way to do it, but to teach that right now would be what programmers call a premature optimization. If her formulation of the problem requires more symbol manipulation than what I would have done, that is all right; she needs practice manipulating the symbols anyway.
She went ahead with the manipulations, reducing the system of four equations to three, then two and then one, solving the one equation to find the value of the single remaining unknown, and then substituting that value back to find the other unknowns. One nice thing about these simple problems is that when the solution is correct you can see it at a glance: Mary is six years old and Sue is two, and in two years they will be eight and four. Katara loves picking values for the unknowns ahead of time, writing down a random set of relations among those values, and then working the method and seeing the correct answer pop out. I remember being endlessly delighted by almost the same thing when I was a little older than her. In The Dying Earth Jack Vance writes of a wizard who travels to an alternate universe to learn from the master “the secret of renewed youth, many spells of the ancients, and a strange abstract lore that Pandelume termed ‘Mathematics.’”
“I find herein a wonderful beauty,” he told Pandelume. “This is no science, this is art, where equations fall away to elements like resolving chords, and where always prevails a symmetry either explicit or multiplex, but always of a crystalline serenity.”
After Katara had solved this problem, I asked if she was game for something a little weird, and she said she was, so I asked her:
Mary and Sue are sisters. Today, Mary is three times as old as Sue; in two years, they will be the same age. How old are they now?
“WHAAAAAT?” she said. She has a good number sense, and immediately saw that this was a strange set of conditions. (If they aren't the same age now, how can they be the same age in two years?) She asked me what would happen. I said (truthfully) that I wasn't sure, and suggested she work through it to find out. So she set up the equations as before and worked out the solution, which is obvious once you see it: Both girls are zero years old today, and zero is three times as old as zero. Katara was thrilled and delighted, and shared her discovery with her mother and her aunt.
There are some powerful lessons here. One is that the method works even when the conditions seem to make no sense; often the results pop out just the same, and can sometimes make sense of problems that seem ill-posed or impossible. Once you have set up the equations, you can just push the symbols around and the answer will emerge, like a familiar building approached through a fog.
But another lesson, only hinted at so far, is that mathematics has its own way of understanding things, and this is not always the way that humans understand them. Goethe famously said that whatever you say to mathematicians, they immediately translate it into their own language and then it is something different; I think this is exactly what he meant.
In this case it is not too much of a stretch to agree that Mary is three times as old as Sue when they are both zero years old. But in the future I plan to give Katara a problem that requires Mary and Sue to have negative ages—say that Mary is twice as old as Sue today, but in three years Sue will be twice as old—to demonstrate that the answer that pops out may not be a reasonable one, or that the original translation into mathematics can lose essential features of the original problem. The solution that says that !!M_T=-2, S_T=-1 !! is mathematically irreproachable, and if the original problem had been posed as “Find two numbers such that…” it would be perfectly correct. But translated back to the original context of a problem that asks about the ages of two sisters, the solution is unacceptable. This is the point of the joke about the spherical cow.
[Other articles in category /math] permanent link
Wed, 23 Jul 2014
When do n and 2n have the same digits?
[This article was published last month on the math.stackexchange blog, which seems to have died young, despite many earnest-sounding promises beforehand from people who claimed they would contribute material. I am repatriating it here.]
A recent question on math.stackexchange asks for the smallest positive integer !!A!! for which the number !!2A!! has the same decimal digits in some other order.
Math geeks may immediately realize that !!142857!! has this property, because it is the first 6 digits of the decimal expansion of !!\frac 17!!, and the cyclic behavior of the decimal expansion of !!\frac n7!! is well-known. But is this the minimal solution? It is not. Brute-force enumeration of the solutions quickly reveals that there are 12 solutions of 6 digits each, all permutations of !!142857!!, and that larger solutions, such as 1025874 and 1257489 seem to follow a similar pattern. What is happening here?
Stuck in Dallas-Fort Worth airport one weekend, I did some work on the problem, and although I wasn't able to solve it completely, I made significant progress. I found a method that allows one to hand-calculate that there is no solution with fewer than six digits, and to enumerate all the solutions with 6 digits, including the minimal one. I found an explanation for the surprising behavior that solutions tend to be permutations of one another. The short form of the explanation is that there are fairly strict conditions on which sets of digits can appear in a solution of the problem. But once the set of digits is chosen, the conditions on that order of the digits in the solution are fairly lax.
So one typically sees, not only in base 10 but in other bases, that the solutions to this problem fall into a few classes that are all permutations of one another; this is exactly what happens in base 10 where all the 6-digit solutions are permutations of !!124578!!. As the number of digits is allowed to increase, the strict first set of conditions relaxes a little, and other digit groups appear as solutions.
Notation
The property of interest, !!P_R(A)!!, is that the numbers !!A!! and !!B=2A!! have exactly the same base-!!R!! digits. We would like to find numbers !!A!! having property !!P_R!! for various !!R!!, and we are most interested in !!R=10!!. Suppose !!A!! is an !!n!!-digit numeral having property !!P_R!!; let the (base-!!R!!) digits of !!A!! be !!a_{n-1}\ldots a_1a_0!! and similarly the digits of !!B = 2A!! are !!b_{n-1}\ldots b_1b_0!!. The reader is encouraged to keep in mind the simple example of !!R=8, n=4, A=\mathtt{1042}, B=\mathtt{2104}!! which we will bring up from time to time.
Since the digits of !!B!! and !!A!! are the same, in a different order, we may say that !!b_i = a_{P(i)}!! for some permutation !!P!!. In general !!P!! might have more than one cycle, but we will suppose that !!P!! is a single cycle. All the following discussion of !!P!! will apply to the individual cycles of !!P!! in the case that !!P!! is a product of two or more cycles. For our example of !!a=\mathtt{1042}, b=\mathtt{2104}!!, we have !!P = (0\,1\,2\,3)!! in cycle notation. We won't need to worry about the details of !!P!!, except to note that !!i, P(i), P(P(i)), \ldots, P^{n-1}(i)!! completely exhaust the indices !!0. \ldots n-1!!, and that !!P^n(i) = i!! because !!P!! is an !!n!!-cycle.
Conditions on the set of digits in a solution
For each !!i!! we have $$a_{P(i)} = b_{i} \equiv 2a_{i} + c_i\pmod R $$ where the ‘carry bit’ !!c_i!! is either 0 or 1 and depends on whether there was a carry when doubling !!a_{i-1}!!. (When !!i=0!! we are in the rightmost position and there is never a carry, so !!c_0= 0!!.) We can then write:
$$\begin{align} a_{P(P(i))} &= 2a_{P(i)} + c_{P(i)} \\ &= 2(2a_{i} + c_i) + c_{P(i)} &&= 4a_i + 2c_i + c_{P(i)}\\ a_{P(P(P(i)))} &= 2(4a_i + 2c_i + c_{P(P(i)})) + c_{P(i)} &&= 8a_i + 4c_i + 2c_{P(i)} + c_{P(P(i))}\\ &&&\vdots\\ a_{P^n(i)} &&&= 2^na_i + v \end{align} $$
all equations taken !!\bmod R!!. But since !!P!! is an !!n!!-cycle, !!P^n(i) = i!!, so we have $$a_i \equiv 2^na_i + v\pmod R$$ or equivalently $$\big(2^n-1\big)a_i + v \equiv 0\pmod R\tag{$\star$}$$ where !!v\in\{0,\ldots 2^n-1\}!! depends only on the values of the carry bits !!c_i!!—the !!c_i!! are precisely the binary digits of !!v!!.
Specifying a particular value of !!a_0!! and !!v!! that satisfy this equation completely determines all the !!a_i!!. For example, !!a_0 = 2, v = \color{darkblue}{0010}_2 = 2!! is a solution when !!R=8, n=4!! because !!\bigl(2^4-1\bigr)\cdot2 + 2\equiv 0\pmod 8!!, and this solution allows us to compute
$$\def\db#1{\color{darkblue}{#1}}\begin{align} a_0&&&=2\\ a_{P(0)} &= 2a_0 &+ \db0 &= 4\\ a_{P^2(0)} &= 2a_{P(0)} &+ \db0 &= 0 \\ a_{P^3(0)} &= 2a_{P^2(0)} &+ \db1 &= 1\\ \hline a_{P^4(0)} &= 2a_{P^3(0)} &+ \db0 &= 2\\ \end{align}$$
where the carry bits !!c_i = \langle 0,0,1,0\rangle!! are visible in the third column, and all the sums are taken !!\pmod 8!!. Note that !!a_{P^n(0)} = a_0!! as promised. This derivation of the entire set of !!a_i!! from a single one plus a choice of !!v!! is crucial, so let's see one more example. Let's consider !!R=10, n=3!!. Then we want to choose !!a_0!! and !!v!! so that !!\left(2^3-1\right)a_0 + v \equiv 0\pmod{10}!! where !!v\in\{0\ldots 7\}!!. One possible solution is !!a_0 = 5, v=\color{darkblue}{101}_2 = 5!!. Then we can derive the other !!a_i!! as follows:
$$\begin{align} a_0&&&=5\\ a_{P(0)} &= 2a_0 &+ \db1 &= 1\\ a_{P^2(0)} &= 2a_{P(0)} &+ \db0 &= 2 \\\hline a_{P^3(0)} &= 2a_{P^2(0)} &+ \db1 &= 5\\ \end{align}$$
And again we have !!a_{P^n(0)}= a_0!! as required.
Since the bits of !!v!! are used cyclically, not every pair of !!\langle a_0, v\rangle!! will yield a different solution. Rotating the bits of !!v!! and pairing them with different choices of !!a_0!! will yield the same cycle of digits starting from a different place. In the first example above, we had !!a_0 = 2, v = 0010_2 = 2!!. If we were to take !!a_0 = 4, v = 0100_2 = 4!! (which also solves !!(\star)!!) we would get the same cycle of values of the !! a\_i !! but starting from !!4!! instead of from !!2!!, and similarly if we take !!a_0=0, v = 1000_2 = 8!! or !!a_0 = 1, v = 0001_2!!. So we can narrow down the solution set of !!(\star)!! by considering only the so-called necklaces of !!v!! rather than all !!2^n!! possible values. Two values of !!v!! are considered equivalent as necklaces if one is a rotation of the other. When a set of !!v!!-values are equivalent as necklaces, we need only consider one of them; the others will give the same cyclic sequence of digits, but starting in a different place. For !!n=4!!, for example, the necklaces are !!0000, 0001, 0011, 0101, 0111, !! and !!1111!!; the sequences !!0110, 1100,!! and !!1001!! being equivalent to !!0011!!, and so on.
Example
Let us take !!R=9, n=3!!, so we want to find 3-digit numerals with property !!P_9!!. According to !!(\star)!! we need !!7a_i + v \equiv 0\pmod{9}!! where !!v\in\{0\ldots 7\}!!. There are 9 possible values for !!a_i!!; for each one there is at most one possible value of !!v!! that makes the sum zero:
$$\begin{array}{rrr} a_i & 7a_i & v \\ \hline 0 & 0 & 0 \\ 1 & 7 & 2 \\ 2 & 14 & 4 \\ 3 & 21 & 6 \\ 4 & 28 & \\ 5 & 35 & 1 \\ 6 & 42 & 3 \\ 7 & 49 & 5 \\ 8 & 56 & 7 \\ \end{array} $$
(For !!a_i=4!! there is no solution.) We may disregard the non-necklace values of !!v!!, as these will give us solutions that are the same as those given by necklace values of !!v!!. The necklaces are:
$$\begin{array}{rl} 000 & 0 \\ 001 & 1 \\ 011 & 3 \\ 111 & 7 \end{array}$$
so we may disregard the solutions exacpt when !!v=0,1,3,7!!. Calculating the digit sequences from these four values of !!v!! and the corresponding !!a_i!! we find:
$$\begin{array}{ccl} a_0 & v & \text{digits} \\ \hline 0 & 0 & 000 \\ 5 & 1 & 512 \\ 6 & 3 & 637 \\ 8 & 7 & 888 \ \end{array} $$
(In the second line, for example, we have !!v=1 = 001_2!!, so !!1 = 2\cdot 5 + 0; 2 = 1\cdot 2 + 0;!! and !!5 = 2\cdot 2 + 1!!.)
Any number !!A!! of three digits, for which !!2A!! contains exactly the same three digits, in base 9, must therefore consist of exactly the digits !!000, 125, 367,!! or !!888!!.
A warning
All the foregoing assumes that the permutation !!P!! is a single cycle. In general, it may not be. Suppose we did an analysis like that above for !!R=10, n=5!! and found that there was no possible digit set, other than the trivial set 00000, that satisfied the governing equation !!(2^5-1)a_0 + v\equiv 0\pmod{10}!!. This would not completely rule out a base-10 solution with 5 digits, because the analysis only rules out a cyclic set of digits. There could still be a solution where !!P!! was a product of a !!2!! and a !!3!!-cycle, or a product of still smaller cycles.
Something like this occurs, for example, in the !!n=4, R=8!! case. Solving the governing equation !!(2^5-1)a_0 + v \equiv 0\pmod 8!! yields only four possible digit cycles, namely !!\{0,1,2,4\}, \{1,3,6,4\}, \{2,5,2,5\}!!, and !!\{3,7,6,5\}!!. But there are several additional solutions: !!2500_8\cdot 2 = 5200_8, 2750_8\cdot 2 = 5720_8, !! and !!2775_8\cdot 2 = 5772_8!!. These correspond to permutations !!P!! with more than one cycle. In the case of !!2750_8!!, for example, !!P!! exchanges the !!5!! and the !!2!!, and leaves the !!0!! and the !!7!! fixed.
For this reason we cannot rule out the possibility of an !!n!!-digit solution without first considering all smaller !!n!!.
The Large Equals Odd rule
When !!R!! is even there is a simple condition we can use to rule out certain sets of digits from being single-cycle solutions. Recall that !!A=a_{n-1}\ldots a_0!! and !!B=b_{n-1}\ldots b_0!!. Let us agree that a digit !!d!! is large if !!d\ge \frac R2!! and small otherwise. That is, !!d!! is large if, upon doubling, it causes a carry into the next column to the left.
Since !!b_i =(2a_i + c_i)\bmod R!!, where the !!c_i!! are carry bits, we see that, except for !!b_0!!, the digit !!b_i!! is odd precisely when there is a carry from the next column to the right, which occurs precisely when !!a_{i-1}!! is large. Thus the number of odd digits among !!b_1,\ldots b_{n-1}!! is equal to the number of large digits among !!a_1,\ldots a_{n-2}!!. This leaves the digits !!b_0!! and !!a_{n-1}!! uncounted. But !!b_0!! is never odd, since there is never a carry in the rightmost position, and !!a_{n-1}!! is always small (since otherwise !!B!! would have !!n+1!! digits, which is not allowed). So the number of large digits in !!A!! is exactly equal to the number of odd digits in !!B!!. And since !!A!! and !!B!! have exactly the same digits, the number of large digits in !!A!! is equal to the number of odd digits in !!A!!. Observe that this is the case for our running example !!1042_8!!: there is one odd digit and one large digit (the 4).
When !!R!! is odd the analogous condition is somewhat more complicated, but since the main case of interest is !!R=10!!, we have the useful rule that:
For !!R!! even, the number of odd digits in any solution !!A!! is equal to the number of large digits in !!A!!.
Conditions on the order of digits in a solution
We have determined, using the above method, that the digits !!\{5,1,2\}!! might form a base-9 numeral with property !!P_9!!. Now we would like to arrange them into a base-9 numeral that actually does have that property. Again let us write !!A = a_2a_1a_0!! and !!B=b_2b_1b_0!!, with !!B=2A!!. Note that if !!a_i = 1!!, then !!b_i = 3!! (if there was a carry from the next column to the right) or !!b_i=2!! (if there was no carry), but since !!b_i\in{5,1,2}!!, we must have !!b_i = 2!! and therefore !!a_{i-1}!! must be small, since there is no carry into position !!i!!. But since !!a_{i-1}!! is also one of !!\{5,1,2\}!!, and it cannot also be !!1!!, it must be !!2!!. This shows that the 1, unless it appears in the rightmost position, must be to the left of the !!2!!; it cannot be to the left of the !!5!!. Similarly, if !!a_i = 2!! then !!b_i = 5!!, because !!4!! is impossible, so the !!2!! must be to the left of a large digit, which must be the !!5!!. Similar reasoning produces no constraint on the position of the !!5!!; it could be to the left of a small digit (in which case it doubles to !!1!!) or a large digit (in which case it doubles to !!2!!). We can summarize these findings as follows:
$$\begin{array}{cl} \text{digit} & \text{to the left of} \\ \hline 1 & 1, 2, \text{end} \\ 2 & 5 \\ 5 & 1,2,5,\text{end} \end{array}$$
Here “end” means that the indicated digit could be the rightmost.
Furthermore, the left digit of !!A!! must be small (or else there would be a carry in the leftmost place and !!2A!! would have 4 digits instead of 3) so it must be either 1 or 2. It is not hard to see from this table that the digits must be in the order !!125!! or !!251!!, and indeed, both of those numbers have the required property: !!125_9\cdot 2 = 251_9!!, and !!251_9\cdot 2 = 512_9!!.
This was a simple example, but in more complicated cases it is helpful to draw the order constraints as a graph. Suppose we draw a graph with one vertex for each digit, and one additional vertex to represent the end of the numeral. The graph has an edge from vertex !!v!! to !!v'!! whenever !!v!! can appear to the left of !!v'!!. Then the graph drawn for the table above looks like this:
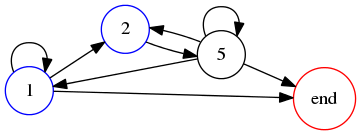
A 3-digit numeral with property !!P_9!! corresponds to a path in this graph that starts at one of the nonzero small digits (marked in blue), ends at the red node marked ‘end’, and visits each node exactly once. Such a path is called hamiltonian. Obviously, self-loops never occur in a hamiltonian path, so we will omit them from future diagrams.
Now we will consider the digit set !!637!!, again base 9. An analysis similar to the foregoing allows us to construct the following graph:
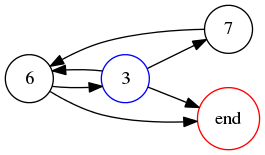
Here it is immediately clear that the only hamiltonian path is !!3-7-6-\text{end}!!, and indeed, !!376_9\cdot 2 = 763_9!!.
In general there might be multiple instances of a digit, and so multiple nodes labeled with that digit. Analysis of the !!0,0,0!! case produces a graph with no legal start nodes and so no solutions, unless leading zeroes are allowed, in which case !!000!! is a perfectly valid solution. Analysis of the !!8,8,8!! case produces a graph with no path to the end node and so no solutions. These two trivial patterns appear for all !!R!! and all !!n!!, and we will ignore them from now on.
Returning to our ongoing example, !!1042!! in base 8, we see that !!1!! and !!2!! must double to !!2!! and !!4!!, so must be to the left of small digits, but !!4!! and !!0!! can double to either !!0!! or !!1!! and so could be to the left of anything. Here the constraints are so lax that the graph doesn't help us narrow them down much:
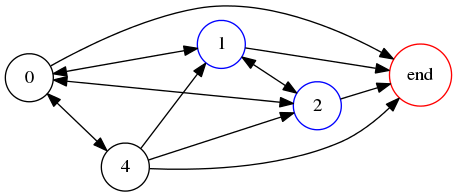
Observing that the only arrow into the 4 is from 0, so that the 4 must follow the 0, and that the entire number must begin with 1 or 2, we can enumerate the solutions:
1042
1204
2041
2104
If leading zeroes are allowed we have also:
0412
0421
All of these are solutions in base 8.
The case of !!R=10!!
Now we turn to our main problem, solutions in base 10.
To find all the solutions of length 6 requires an enumeration of smaller solutions, which, if they existed, might be concatenated into a solution of length 6. This is because our analysis of the digit sets that can appear in a solution assumes that the digits are permuted cyclically; that is, the permutations !!P!! that we considered had only one cycle each.
There are no smaller solutions, but to prove that the length 6 solutions are minimal, we must analyze the cases for smaller !!n!! and rule them out. We now produce a complete analysis of the base 10 case with !!R=10!! and !!n\le 6!!. For !!n=1!! there is only the trivial solution of !!0!!, which we disregard. (The question asked for a positive number anyway.)
!!n=2!!
For !!n=2!!, we want to find solutions of !!3a_i + v \equiv 0\pmod{10}!! where !!v!! is a two-bit necklace number, one of !!00_2, 01_2, !! or !!11_2!!. Tabulating the values of !!a_i!! and !!v\in\{0,1,3\}!! that solve this equation we get:
$$\begin{array}{ccc} v& a_i \\ \hline 0 & 0 \\ 1& 3 \\ 3& 9 \\ \end{array}$$
We can disregard the !!v=0!! and !!v=3!! solutions because the former yields the trivial solution !!00!! and the latter yields the nonsolution !!99!!. So the only possibility we need to investigate further is !!a_i = 3, v = 1!!, which corresponds to the digit sequence !!36!!: Doubling !!3!! gives us !!6!! and doubling !!6!!, plus a carry, gives us !!3!! again.
But when we tabulate of which digits must be left of which informs us that there is no solution with just !!3!! and !!6!!, because the graph we get, once self-loops are eliminated, looks like this:
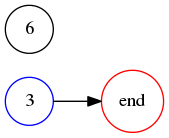
which obviously has no hamiltonian path. Thus there is no solution for !!R=10, n=2!!.
!!n=3!!
For !!n=3!! we need to solve the equation !!7a_i + v \equiv 0\pmod{10}!! where !!v!! is a necklace number in !!\{0,\ldots 7\}!!, specifically one of !!0,1,3,!! or !!7!!. Since !!7!! and !!10!! are relatively prime, for each !!v!! there is a single !!a_i!! that solves the equation. Tabulating the possible values of !!a_i!! as before, and this time omitting rows with no solution, we have:
$$\begin{array}{rrl} v & a_i & \text{digits}\\ \hline 0& 0 & 000\\ 1& 7 & 748 \\ 3& 1 & 125\\ 7&9 & 999\\ \end{array}$$
The digit sequences !!0,0,0!! and !!9,9,9!! yield trivial solutions or nonsolutions as usual, and we will omit them in the future. The other two lines suggest the digit sets !!1,2,5!! and !!4,7,8!!, both of which fail the “odd equals large” rule.
This analysis rules out the possibility of a digit set with !!a_0 \to a_1 \to a_2 \to a_1!!, but it does not completely rule out a 3-digit solution, since one could be obtained by concatenating a one-digit and a two-digit solution, or three one-digit solutions. However, we know by now that no one- or two-digit solutions exist. Therefore there are no 3-digit solutions in base 10.
!!n=4!!
For !!n=4!! the governing equation is !!15a_i + v \equiv 0\pmod{10}!! where !!v!! is a 4-bit necklace number, one of !!\{0,1,3,5,7,15\}!!. This is a little more complicated because !!\gcd(15,10)\ne 1!!. Tabulating the possible digit sets, we get:
$$\begin{array}{crrl} a_i & 15a_i& v & \text{digits}\\ \hline 0 & 0 & 0 & 0000\\ 1 & 5 & 5 & 1250\\ 1 & 5 & 15 & 1375\\ 2 & 0 & 0 & 2486\\ 3 & 5 & 5 & 3749\\ 3 & 5 & 15 & 3751\\ 4 & 0 & 0 & 4862\\ 5 & 5 & 5 & 5012\\ 5 & 5 & 5 & 5137\\ 6 & 0 & 0 & 6248\\ 7 & 5 & 5 & 7493\\ 7 & 5 & 5 & 7513\\ 8 & 0 & 0 & 8624 \\ 9 & 5 & 5 & 9874\\ 9 & 5 & 15 & 9999 \\ \end{array}$$
where the second column has been reduced mod !!10!!. Note that even restricting !!v!! to necklace numbers the table still contains duplicate digit sequences; the 15 entries on the right contain only the six basic sequences !!0000, 0125, 1375, 2486, 3749, 4987!!, and !!9999!!. Of these, only !!0000, 9999,!! and !!3749!! obey the odd equals large criterion, and we will disregard !!0000!! and !!9999!! as usual, leaving only !!3749!!. We construct the corresponding graph for this digit set as follows: !!3!! must double to !!7!!, not !!6!!, so must be left of a large number !!7!! or !!9!!. Similarly !!4!! must be left of !!7!! or !!9!!. !!9!! must also double to !!9!!, so must be left of !!7!!. Finally, !!7!! must double to !!4!!, so must be left of !!3,4!! or the end of the numeral. The corresponding graph is:
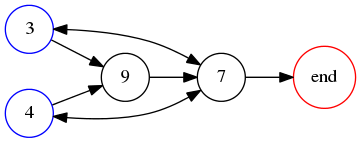
which evidently has no hamiltonian path: whichever of 3 or 4 we start at, we cannot visit the other without passing through 7, and then we cannot reach the end node without passing through 7 a second time. So there is no solution with !!R=10!! and !!n=4!!.
!!n=5!!
We leave this case as an exercise. There are 8 solutions to the governing equation, all of which are ruled out by the odd equals large rule.
!!n=6!!
For !!n=6!! the possible solutions are given by the governing equation !!63a_i + v \equiv 0\pmod{10}!! where !!v!! is a 6-bit necklace number, one of !!\{0,1,3,5,7,9,11,13,15,21,23,27,31,63\}!!. Tabulating the possible digit sets, we get:
$$\begin{array}{crrl} v & a_i & \text{digits}\\ \hline 0 & 0 & 000000\\ 1 & 3 & 362486 \\ 3 & 9 & 986249 \\ 5 & 5 & 500012 \\ 7 & 1 & 124875 \\ 9 & 7 & 748748 \\ 11 & 3 & 362501 \\ 13 & 9 & 986374 \\ 15 & 5 & 500137 \\ 21 & 3 & 363636 \\ 23 & 9 & 989899 \\ 27 & 1 & 125125 \\ 31 & 3 & 363751 \\ 63 & 9 & 999999 \\ \end{array}$$
After ignoring !!000000!! and !!999999!! as usual, the large equals odd rule allows us to ignore all the other sequences except !!124875!! and !!363636!!. The latter fails for the same reason that !!36!! did when !!n=2!!. But !!142857!! , the lone survivor, gives us a complicated derived graph containing many hamiltonian paths, every one of which is a solution to the problem:
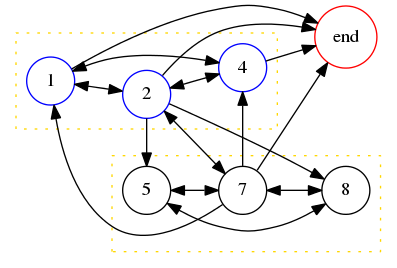
It is not hard to pick out from this graph the minimal solution !!125874!!, for which !!125874\cdot 2 = 251748!!, and also our old friend !!142857!! for which !!142857\cdot 2 = 285714!!.
We see here the reason why all the small numbers with property !!P_{10}!! contain the digits !!124578!!. The constraints on which digits can appear in a solution are quite strict, and rule out all other sequences of six digits and all shorter sequences. But once a set of digits passes these stringent conditions, the constraints on it are much looser, because !!B!! is only required to have the digits of !!A!! in some order, and there are many possible orders, many of which will satisfy the rather loose conditions involving the distribution of the carry bits. This graph is typical: it has a set of small nodes and a set of large nodes, and each node is connected to either all the small nodes or all the large nodes, so that the graph has many edges, and, as in this case, a largish clique of small nodes and a largish clique of large nodes, and as a result many hamiltonian paths.
Onward
This analysis is tedious but is simple enough to perform by hand in under an hour. As !!n!! increases further, enumerating the solutions of the governing equation becomes very time-consuming. I wrote a simple computer program to perform the analysis for given !!R!! and !!n!!, and to emit the possible digit sets that satisfied the large equals odd criterion. I had wondered if every base-10 solution contained equal numbers of the digits !!1,2,4,8,5,!! and !!7!!. This is the case for !!n=7!! (where the only admissible digit set is !!\{1,2,4,5,7,8\}\cup\{9\}!!), for !!n=8!! (where the only admissible sets are !!\{1,2,4,5,7,8\}\cup \{3,6\}!! and !!\{1,2,4,5,7,8\}\cup\{9,9\}!!), and for !!n=9!! (where the only admissible sets are !!\{1,2,4,5,7,8\}\cup\{3,6,9\}!! and !!\{1,2,4,5,7,8\}\cup\{9,9,9\}!!). But when we reach !!n=10!! the increasing number of necklaces has loosened up the requirements a little and there are 5 admissible digit sets. I picked two of the promising-seeming ones and quickly found by hand the solutions !!4225561128!! and !!1577438874!!, both of which wreck any theory that the digits !!1,2,4,5,8,7!! must all appear the same number of times.
Acknowledgments
Thanks to Karl Kronenfeld for corrections and many helpful suggestions.
[Other articles in category /math] permanent link
Sat, 19 Jul 2014
Similarity analysis of quilt blocks
As I've discussed elsewhere, I once wrote a program to enumerate all
the possible quilt blocks of a certain type. The quilt blocks in
question are, in quilt jargon, sixteen-patch half-square triangles. A
half-square triangle, also called a “patch”, is two triangles of fabric sewn together, like
this: 
Then you sew four of these patches into a four-patch, say like this:

Then to make a sixteen-patch block of the type I was considering, you take four identical four-patch blocks, and sew them together with rotational symmetry, like this:

It turns out that there are exactly 72 different ways to do this. (Blocks equivalent under a reflection are considered the same, as are blocks obtained by exchanging the roles of black and white, which are merely stand-ins for arbitrary colors to be chosen later.) Here is the complete set of 72:








































































It's immediately clear that some of these resemble one another, sometimes so strongly that it can be hard to tell how they differ, while others are very distinctive and unique-seeming. I wanted to make the computer classify the blocks on the basis of similarity.
My idea was to try to find a way to get the computer to notice which
blocks have distinctive components of one color. For example, many
blocks have a distinctive diamond shape  in the center.
in the center.
Some have a pinwheel like this:

which also has the diamond in the middle, while others have a different kind of pinwheel with no diamond:

I wanted to enumerate such components and ask the computer to list which blocks contained which shapes; then group them by similarity, the idea being that that blocks with the same distinctive components are similar.
The program suite uses a compact notation of blocks and of shapes that makes it easy to figure out which blocks contain which distinctive components.
Since each block is made of four identical four-patches, it's enough just to examine the four-patches. Each of the half-square triangle patches can be oriented in two ways:

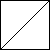
Here are two of the 12 ways to orient the patches in a four-patch:
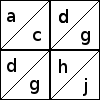
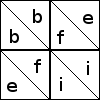
Each 16-patch is made of four four-patches, and you must imagine that the
four-patches shown above are in the upper-left position in the
16-patch. Then symmetry of the 16-patch block means that triangles with the
same label are in positions that are symmetric with respect to the
entire block. For example, the two triangles labeled b are on
opposite sides of the block's northwest-southeast diagonal. But there
is no symmetry of the full 16-patch block that carries triangle d to
triangle g, because d is on the edge of the block, while g is in the interior.
Triangles must be colored opposite colors if they are part of the same patch, but other than that there are no constraints on the coloring.
A block might, of course, have patches in both orientations:
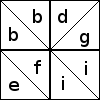
All the blocks with diagonals oriented this way are assigned
descriptors made from the letters bbdefgii.
Once you have chosen one of the 12 ways to orient the diagonals in the
four-patch, you still have to color the patches. A descriptor like
bbeeffii describes the orientation of the diagonal lines in the
squares, but it does not describe the way the four patches are
colored; there are between 4 and 8 ways to color each sort of
four-patch. For example, the bbeeffii four-patch shown earlier can be colored in six different ways:







In each case, all four diagonals run from northwest to southeast. (All other ways of coloring this four-patch are equivalent to one of these under one or more of rotation, reflection, and exchange of black and white.)
We can describe a patch by listing the descriptors of the eight triangles, grouped by which triangles form connected regions. For example, the first block above is:


b/bf/ee/fi/i
because there's an isolated white b triangle, then a black parallelogram
made of a b and an f patch, then a white triangle made from the
two white e triangles, then another parallelogram made from the black f
and i, and finally in the middle, the white i. (The two white e
triangles appear to be separated, but when four of these four-patches are
joined into a 16-patch block, the two white e patches will be
adjacent and will form a single large triangle:  )
)
The other five bbeeffii four-patches are, in the same order they are shown above:
b/b/e/e/f/f/i/i
b/b/e/e/fi/fi
b/bfi/ee/f/i
bfi/bfi/e/e
bf/bf/e/e/i/i
All six have bbeeffii, but grouped differently depending on the
colorings. The second one (
b/b/e/e/f/f/i/i) has no regions with
more than one triangle; the fifth (
bfi/bfi/e/e) has two large regions of three triangles each, and two
isolated triangles. In the latter four-patch, the bfi in the
descriptor has three letters because the patch has a corresponding
distinctive component made of three triangles.
I made up a list of the descriptors for all 72 blocks; I think I did
this by hand. (The work directory contains a blocks
file that maps
blocks to their descriptors, but the
Makefile does
not say how to build it, suggesting that it was not automatically
built.) From this list one can automatically
extract a
list of descriptors of interesting
shapes: an
interesting shape is two or more letters that appear together in some
descriptor. (Or it can be the single letter j, which is
exceptional; see below.) For example, bffh represents a distinctive
component. It can only occur in a patch that has a b, two fs, and
an h, like this one:
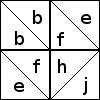
and it will only be significant if the b, the two fs, and the h are
the same color:

in which case you get this distinctive and interesting-looking hook component.
There is only one block that includes this distinctive hook component;
it has descriptor b/bffh/ee/j, and looks like this:  . But some of the distinctive
components are more common. The
. But some of the distinctive
components are more common. The ee component represents the large white half-diamonds on the four sides.
A block with "ee" in its descriptor always looks like this:

and the blocks formed from such patches always have a distinctive half-diamond component on each edge, like this:

(The stippled areas vary from block to block, but the blocks with ee
in their descriptors always have the half-diamonds as shown.)
The blocks listed at http://hop.perl.plover.com/quilt/analysis/images/ee.html
all have the ee component. There are many differences between them, but
they all have the half-diamonds in common.
Other distinctive components have similar short descriptors. The two pinwheels I
mentioned above are

gh and

fi, respectively; if you look at
the list of gh blocks
and
the list of fi blocks
you'll see all the blocks with each kind of pinwheel.
Descriptor j is an exception. It makes an interesting shape all by itself,
because any block whose patches have j in their descriptor will have
a distinctive-looking diamond component in the center. The four-patch looks like
this:

so the full sixteen-patch looks like this:

where the stippled parts can vary. A look at the list of blocks with
component
j will
confirm that they all have this basic similarity.
I had made a list of the descriptors for each of the 72 blocks, and from this I extracted a list of the descriptors for interesting component shapes. Then it was only a matter of finding the component descriptors in the block descriptors to know which blocks contained which components; if the two blocks share two different distinctive components, they probably look somewhat similar.
Then I sorted the blocks into groups, where two blocks were in the same group if they shared two distinctive components. The resulting grouping lists, for each block, which other blocks have at least two shapes in common with it. Such blocks do indeed tend to look quite similar.
This strategy was actually the second thing I tried; the first thing didn't work out well. (I forget just what it was, but I think it involved finding polygons in each block that had white inside and black outside, or vice versa.) I was satisfied enough with this second attempt that I considered the project a success and stopped work on it.
The complete final results were:
- This tabulation of blocks that are somewhat similar
- This tabulation of blocks that are distinctly similar (This is the final product; I consider this a sufficiently definitive listing of “similar blocks”.)
- This tabulation of blocks that are extremely similar
And these tabulations of all the blocks with various distinctive components: bd bf bfh bfi cd cdd cdf cf cfi ee eg egh egi fgh fh fi gg ggh ggi gh gi j
It may also be interesting to browse the work directory.
[Other articles in category /misc] permanent link
Fri, 18 Jul 2014
On uninhabited types and inconsistent logics
Earlier this week I gave a talk about the Curry-Howard isomorphism. Talks never go quite the way you expect. The biggest sticking point was my assertion that there is no function with the type a → b. I mentioned this as a throwaway remark on slide 7, assuming that everyone would agree instantly, and then we got totally hung up on it for about twenty minutes.
Part of this was my surprise at discovering that most of the audience (members of the Philly Lambda functional programming group) was not familiar with the Haskell type system. I had assumed that most of the members of a functional programming interest group would be familiar with one of Haskell, ML, or Scala, all of which have the same basic type system. But this was not the case. (Many people are primarily interested in Scheme, for example.)
I think the main problem was that I did not make clear to the audience what Haskell means when it says that a function has type a → b. At the talk, and then later on Reddit people asked
what about a function that takes an integer and returns a string: doesn't it have type a → b?
If you know one of the HM languages, you know that of course it
doesn't; it has type Int → String, which is not the same at all. But I
wasn't prepared for this confusion and it took me a while to formulate
the answer. I think I underestimated the degree to which I have
internalized the behavior of Hindley-Milner type systems after twenty
years. Next time, I will be better prepared, and will say something
like the following:
A function which takes an integer and returns a string does not have
the type a → b; it has the type Int → String. You must pass it an
integer, and you may only use its return value in a place that makes
sense for a string. If f has this type, then 3 +
f 4 is a compile-time type error because Haskell knows that f
returns a string, and strings do not work with +.
But if f had
the type a → b, then 3 + f 4 would be legal, because context requires that
f return a number, and the type a → b says that it can return a
number, because a number is an instance of the completely general type
b. The type a → b, in contrast to Int → String, means that b
and a are completely unconstrained.
Say function f had type a → b. Then you would be able to use the
expression f x in any context that was expecting any sort of return
value; you could write any or all of:
3 + f x
head(f x)
"foo" ++ f x
True && f x
and they would all type check correctly, regardless of the type of x. In the first line, f x would return a number; in the second line f would return a list; in the third line it would return a string, and in the fourth line it would return a boolean. And in each case f could be able to do what was required regardless of the type of x, so without even looking at x. But how could you possibly write such a function f? You can't; it's impossible.
Contrast this with the identity function id, which has type a → a. This says that id always returns a value whose type is the same as
that if its argument. So you can write
3 + id x
as long as x has the right type for +, and you can write
head(id x)
as long as x has the
right type for head, and so on. But for f to have the type a → b, all those
would have to work regardless of the type of the argument to f. And
there is no way to write such an f.
Actually I wonder now if part of the problem is that we like to write a → b when what we really mean is the type ∀a.∀b.a → b. Perhaps making the quantifiers explicit would clear things up? I suppose it probably wouldn't have, at least in this case.
The issue is a bit complicated by the fact that the function
loop :: a -> b
loop x = loop x
does have the type a → b, and, in a language with exceptions, throw
has that type also; or consider Haskell
foo :: a -> b
foo x = undefined
Unfortunately, just as I thought I was getting across the explanation of why there can be no function with type a → b, someone brought up exceptions and I had to mutter and look at my shoes. (You can also take the view that these functions have type a → ⊥, but the logical principle ⊥ → b is unexceptionable.)
In fact, experienced practitioners will realize, the instant the type
a → b appears, that they have written a function that never returns.
Such an example was directly responsible for my own initial interest
in functional programming and type systems; I read a 1992 paper (“An
anecdote about ML type
inference”)
by Andrew R. Koenig in which he described writing a merge sort
function, whose type was reported (by the SML type inferencer) as [a]
-> [b], and the reason was that it had a bug that would cause it to
loop forever on any nonempty list. I came back from that conference
convinced that I must learn ML, and Higher-Order Perl was a direct
(although distant) outcome of that conviction.
Any discussion of the Curry-Howard isomorphism, using Haskell as an example, is somewhat fraught with trouble, because Haskell's type logic is utterly inconsistent. In addition to the examples above, in Haskell one can write
fix :: (a -> a) -> a
fix f = let x = fix f
in f x
and as a statement of logic, !!(a\to a)\to a!! is patently false. This might be an argument in favor of the Total Functional Programming suggested by D.A. Turner and others.
[Other articles in category /CS] permanent link
Wed, 16 Jul 2014
Guess what this does (solution)
A few weeks ago I asked people to predict, without trying it first, what this would print:
perl -le 'print(two + two == five ? "true" : "false")'
(If you haven't seen this yet, I recommend that you guess, and then test your guess, before reading the rest of this article.)
People familiar with Perl guess that it will print true; that is
what I guessed. The reasoning is as follows: Perl is willing to treat
the unquoted strings two and five as strings, as if they had been
quoted, and is also happy to use the + and == operators on them,
converting the strings to numbers in its usual way. If the strings
had looked like "2" and "5" Perl would have treated them as 2 and
5, but as they don't look like decimal numerals, Perl interprets them
as zeroes. (Perl wants to issue a warning about this, but the warning is not enabled by default.
Since the two and five are treated as
zeroes, the result of the == comparison are true, and the string
"true" should be selected and printed.
So far this is a little bit odd, but not excessively odd; it's the
sort of thing you expect from programming languages, all of which more
or less suck. For example, Python's behavior, although different, is
about equally peculiar. Although Python does require that the strings
two and five be quoted, it is happy to do its own peculiar thing
with "two" + "two" == "five", which happens to be false: in Python
the + operator is overloaded and has completely different behaviors
on strings and numbers, so that while in Perl "2" + "2" is the
number 4, in Python is it is the string 22, and "two" + "two"
yields the string "twotwo". Had the program above actually printed
true, as I expected it would, or even false, I would not have
found it remarkable.
However, this is not what the program does do. The explanation of two paragraphs earlier is totally wrong. Instead, the program prints nothing, and the reason is incredibly convoluted and bizarre.
First, you must know that print has an optional first argument. (I
have plans for an article about how optional first arguments are almost
always a bad move, but contrary to my usual practice I will not insert
it here.) In Perl, the print function can be invoked in two ways:
print HANDLE $a, $b, $c, …;
print $a, $b, $c, …;
The former prints out the list $a, $b, $c, … to the filehandle
HANDLE; the latter uses the default handle, which typically points
at the terminal. How does Perl decide which of these forms is being
used? Specifically, in the second form, how does it know that $a is
one of the items to be printed, rather than a variable containing the filehandle
to print to?
The answer to this question is further complicated by the fact that
the HANDLE in the first form could be either an unquoted string,
which is the name of the handle to print to, or it could be a variable
containing a filehandle value. Both of these prints should do the
same thing:
my $handle = \*STDERR;
print STDERR $a, $b, $c;
print $handle $a, $b, $c;
Perl's method to decide whether a particular print uses an explicit
or the default handle is a somewhat complicated heuristic. The basic
rule is that the filehandle, if present, can be distinguished because
its trailing comma is omitted. But if the filehandle were allowed to
be the result of an arbitrary expression, it might be difficult for
the parser to decide where there was a a comma; consider the
hypothetical expression:
print $a += EXPRESSION, $b $c, $d, $e;
Here the intention is that the $a += EXPRESSION, $b expression
calculates the filehandle value (which is actually retrieved from $b, the
$a += … part being executed only for its side effect) and the
remaining $c, $d, $e are the values to be printed. To allow this
sort of thing would be way too confusing to both Perl and to the
programmer. So there is the further rule that the filehandle
expression, if present, must be short, either a simple scalar
variable such as $fh, or a bare unquoted string that is in the right
format for a filehandle name, such as HANDLE. Then the parser need
only peek ahead a token or two to see if there is an upcoming comma.
So for example, in
print STDERR $a, $b, $c;
the print is immediately followed by STDERR, which could be a
filehandle name, and STDERR is not followed by a comma, so STDERR
is taken to be the name of the output handle. And in
print $x, $a, $b, $c;
the print is immediately followed by the simple scalar value $x,
but this $x is followed by a comma, so is considered one of the
things to be printed, and the target of the print is the default
output handle.
In
print STDERR, $a, $b, $c;
Perl has a puzzle: STDERR looks like a filehandle, but it is
followed by a comma. This is a compile-time error; Perl complains “No
comma allowed after filehandle” and aborts. If you want to print the
literal string STDERR, you must quote it, and if you want to print A, B,
and C to the standard error handle, you must omit the first comma.
Now we return to the original example.
perl -le 'print(two + two == five ? "true" : "false")'
Here Perl sees the unquoted string two which could be a filehandle
name, and which is not followed by a comma. So it takes the first
two to be the output handle name. Then it evaluates the expression
+ two == five ? "true" : "false"
and obtains the value true. (The leading + is a unary plus
operator, which is a no-op. The bare two and five are taken to be
string constants, which, compared with the numeric == operator, are
considered to be numerically zero, eliciting the same warning that I
mentioned earlier that I had not enabled. Thus the comparison Perl
actually does is is 0 == 0, which is true, and the resulting string is
true.)
This value, the string true, is then printed to the filehandle named
two. Had we previously opened such a filehandle, say with
open two, ">", "output-file";
then the output would have been sent to the filehandle as usual.
Printing to a non-open filehandle elicits an optional warning from
Perl, but as I mentioned, I have not enabled warnings, so the print
silently fails, yielding a false value.
Had I enabled those optional warnings, we would have seen a plethora of them:
Unquoted string "two" may clash with future reserved word at -e line 1.
Unquoted string "two" may clash with future reserved word at -e line 1.
Unquoted string "five" may clash with future reserved word at -e line 1.
Name "main::two" used only once: possible typo at -e line 1.
Argument "five" isn't numeric in numeric eq (==) at -e line 1.
Argument "two" isn't numeric in numeric eq (==) at -e line 1.
print() on unopened filehandle two at -e line 1.
(The first four are compile-time warnings; the last three are issued
at execution time.) The crucial warning is the one at the end,
advising us that the output of print was directed to the filehandle
two which was never opened for output.
[ Addendum 20140718: I keep thinking of the following remark of Edsger W. Dijkstra:
[This phenomenon] takes one of two different forms: one programmer places a one-line program on the desk of another and … says, "Guess what it does!" From this observation we must conclude that this language as a tool is an open invitation for clever tricks; and while exactly this may be the explanation for some of its appeal, viz., to those who like to show how clever they are, I am sorry, but I must regard this as one of the most damning things that can be said about a programming language.
But my intent is different than what Dijkstra describes. His programmer is proud, but I am disgusted. Incidentally, I believe that Dijkstra was discussing APL here. ]
[ Addendum 20150508: I never have much sympathy for the school of thought that says that you should always always enable warnings in every Perl program; I think Perl produces too many spurious warnings for that. But I also think this example is part of a cogent argument in the other direction. ]
[Other articles in category /prog/perl] permanent link
Here's a Perl quiz that I confidently predict nobody will get right. Without trying it first, what does the following program print?
perl -le 'print(two + two == five ? "true" : "false")'
(I will discuss the surprising answer tomorrow.)
[Other articles in category /prog/perl] permanent link
Mon, 14 Jul 2014
Types are theorems; programs are proofs
[ Summary: I gave a talk Monday night on the Curry-Howard isomorphism; my talk slides are online. ]
I sent several proposals to !!con, a conference of ten-minute talks. One of my proposals was to explain the Curry-Howard isomorphism in ten minutes, but the conference people didn't accept it. They said that they had had four or five proposals for talks about the Curry-Howard isomorphism, and didn't want to accept more than one of them.
The CHI talk they did accept turned out to be very different from the one I had wanted to give; it discussed the Coq theorem-proving system. I had wanted to talk about the basic correspondence between pair types, union types, and function types on the one hand, and reasoning about logical conjunctions, disjunctions, and implications on the other hand, and the !!con speaker didn't touch on this at all.
But mathematical logic and programming language types turn out to be the same! A type in a language like Haskell can be understood as a statement of logic, and the statement will be true if and only if there is actually a value with the corresponding type. Moreover, if you have a proof of the statement, you can convert the proof into a value of the corresponding type, or conversely if you have a value with a certain type you can convert it into a proof of the corresponding statement. The programming language features for constructing or using values with function types correspond exactly to the logical methods for proving or using statements with implications; similarly pair types correspond to logical conjunction, and union tpyes to logical disjunction, and exceptions to logical negation. I think this is incredible. I was amazed the first time I heard of it (Chuck Liang told me sometime around 1993) and I'm still amazed.
Happily Philly Lambda, a Philadelphia-area functional programming group, had recently come back to life, so I suggested that I give them a longer talk about about the Curry-Howard isomorphism, and they agreed.
I gave the talk yesterday, and the materials are online. I'm not sure how easy they will be to understand without my commentary, but it might be worth a try.
If you're interested and want to look into it in more detail, I suggest you check out Sørensen and Urzyczyn's Lectures on the Curry-Howard Isomorphism. It was published as an expensive yellow-cover book by Springer, but free copies of the draft are still available.
[Other articles in category /CS] permanent link
Fri, 25 Apr 2014Last night I gave a talk for the New York Perl Mongers, and got to see a number of people that I like but don't often see. Among these was Michael Fischer, who told me of a story about myself that I had completely forgotten, but I think will be of general interest.
The front end of the story is this: Michael first met me at some conference, shortly after the publication of Higher-Order Perl, and people were coming up to me and presenting me with copies of the book to sign. In many cases these were people who had helped me edit the book, or who had reported printing errors; for some of those people I would find the error in the text that they had reported, circle it, and write a thank-you note on the same page. Michael did not have a copy of my book, but for some reason he had with him a copy of Oulipo Compendium, and he presented this to me to sign instead.
Oulipo is a society of writers, founded in 1960, who pursue “constrained writing”. Perhaps the best-known example is the lipogrammatic novel La Disparition, written in 1969 by Oulipo member Georges Perec, entirely without the use of the letter e. Another possibly well-known example is the Exercises in Style of Raymond Queneau, which retells the same vapid anecdote in 99 different styles. The book that Michael put in front of me to sign is a compendium of anecdotes, examples of Oulipan work, and other Oulipalia.
What Michael did not realize, however, was that the gods of fate were handing me an opportunity. He says that I glared at him for a moment, then flipped through the pages, found the place in the book where I was mentioned, circled it, and signed that.
The other half of that story is how I happened to be mentioned in Oulipo Compendium.
Back in the early 1990s I did a few text processing projects which would be trivial now, but which were unusual at the time, in a small way. For example, I constructed a concordance of the King James Bible, listing, for each word, the number of every verse in which it appeared. This was a significant effort at the time; the Bible was sufficiently large (around five megabytes) that I normally kept the files compressed to save space. This project was surprisingly popular, and I received frequent email from strangers asking for copies of the concordance.
Another project, less popular but still interesting, was an anagram
dictionary. The word list from Webster's Second International
dictionary was available, and it was an easy matter to locate all the
anagrams in it, and compile a file. Unlike the Bible concordance,
which I considered inferior to simply running grep, I still have the
anagram dictionary. It begins:
aal ala
aam ama
Aarhus (See `arusha')
Aaronic (See `Nicarao')
Aaronite aeration
Aaru aura
And ends:
zoosporic sporozoic
zootype ozotype
zyga gazy
zygal glazy
The cross-references are to save space. When two words are anagrams of one another, both are listed in both places. But when three or more words are anagrams, the words are listed in one place, with cross-references in the other places, so for example:
Ateles teasel stelae saltee sealet
saltee (See `Ateles')
sealet (See `Ateles')
stelae (See `Ateles')
teasel (See `Ateles')
saves 52 characters over the unabbreviated version. Even with this optimization, the complete anagram dictionary was around 750 kilobytes, a significant amount of space in 1991. A few years later I generated an improved version, which dispensed with the abbreviation, by that time unnecessary, and which attempted, sucessfully I thought, to score the anagrams according to interestingness. But I digress.
One day in August of 1994, I received a query about the anagram dictionary, including a question about whether it could be used in a certain way. I replied in detail, explaining what I had done, how it could be used, and what could be done instead, and the result was a reply from Harry Mathews, another well-known member of the Oulipo, of which I had not heard before. Mr. Mathews, correctly recognizing that I would be interested, explained what he was really after:
A poetic procedure created by the late Georges Perec falls into the latter category. According to this procedure, only the 11 commonest letters in the language can be used, and all have to be used before any of them can be used again. A poem therefore consists of a series of 11 multi-word anagrams of, in French, the letters e s a r t i n u l o c (a c e i l n o r s t). Perec discovered only one one-word anagram for the letter-group, "ulcerations", which was adopted as a generic name for the procedure.
Mathews wanted, not exactly an anagram dictionary, but a list of words acceptable for the English version of "ulcerations". They should contain only the letters a d e h i l n o r s t, at most once each. In particular, he wanted a word containing precisely these eleven letters, to use as the translation of "ulcerations".
Producing the requisite list was much easier then producing the anagram dictionary iself, so I quickly did it and sent it back; it looked like this:
a A a
d D d
e E e
h H h
i I i
l L l
n N n
o O o
r R r
s S s
t T t
ad ad da
ae ae ea
ah Ah ah ha
...
lost lost lots slot
nors sorn
nort torn tron
nost snot
orst sort
adehl heald
adehn henad
adehr derah
adehs Hades deash sadhe shade
...
deilnorst nostriled
ehilnorst nosethirl
adehilnort threnodial
adehilnrst disenthral
aehilnorst hortensial
The leftmost column is the alphabetical list of letters. This is so that if you find yourself needing to use the letters 'a d e h s' at some point in your poem, you can jump to that part of the list and immediately locate the words containing exactly those letters. (It provides somewhat less help for discovering the shorter words that contain only some of those letters, but there is a limit to how much can be done with static files.)
As can be seen at the end of the list, there were three words that each used ten of the eleven required letters: “hortensial”, “threnodial”, “disenthral”, but none with all eleven. However, Mathews replied:
You have found the solution to my immediate problem: "threnodial" may only have 10 letters, but the 11th letter is "s". So, as an adjectival noun, "threnodials" becomes the one and only generic name for English "Ulcerations". It is not only less harsh a word than the French one but a sorrowfully appropriate one, since the form is naturally associated with Georges Perec, who died 12 years ago at 46 to the lasting consternation of us all.
(A threnody is a hymn of mourning.)
A few years later, the Oulipo Compendium appeared, edited by Mathews, and the article on Threnodials mentions my assistance. And so it was that when Michael Fischer handed me a copy, I was able to open it up to the place where I was mentioned.
[ Addendum 20140428: Thanks to Philippe Bruhat for some corrections: neither Perec nor Mathews was a founding member of Oulipo. ]
[ Addendum 20170205: To my consternation, Harry Mathews died on Janury 25. There was nobody like him, and the world is a smaller and poorer place. ]
[ Addendum 20170909: I should have mentioned that my appearance in Oulipo Compendium was brought to my attention by Robin Houston. Thank you M. Houston! ]
[Other articles in category /lang] permanent link
Sat, 01 Mar 2014This week there has been an article floating around about “What happens when placeholder text doesn't get replaced. This reminds me of the time I made this mistake myself.
In 1996 I was programming a web site for a large company which sold cosmetics and skin care products in hundreds of department stores and malls around the country. The technology to actually buy the stuff online wasn't really mature yet, and the web was new enough that the company was worried that selling online would anger the retail channels. They wanted a web page where you would put in your location and it would tell you where the nearby stores were.
The application was simple; it accepted a city and state, looked them
up in an on-disk hash table, and then returned a status code to the
page generator. The status code was for internal use only. For
example, if you didn't fill in the form completely, the program would
return the status code MISSING, which would trigger the templating
engine to build a page with a suitable complaint message.
If the form was filled out correctly, but there was no match in the
database, the program would return a status code that the front end
translated to a suitably apologetic message. The status code I
selected for this was BACKWATER.
Which was all very jolly, until one day there was a program bug and
some user in Podunk, Iowa submitted the form and got back a page with
BACKWATER in giant letters.
Anyone could have seen that coming; I have no excuse.
[Other articles in category /oops] permanent link
Fri, 28 Feb 2014Intuitionistic logic is deeply misunderstood by people who have not studied it closely; such people often seem to think that the intuitionists were just a bunch of lunatics who rejected the law of the excluded middle for no reason. One often hears that intuitionistic logic rejects proof by contradiction. This is only half true. It arises from a typically classical misunderstanding of intuitionistic logic.
Intuitionists are perfectly happy to accept a reductio ad absurdum proof of the following form:
$$(P\to \bot)\to \lnot P$$
Here !!\bot!! means an absurdity or a contradiction; !!P\to \bot!! means that assuming !!P!! leads to absurdity, and !!(P\to \bot)\to \lnot P!! means that if assuming !!P!! leads to absurdity, then you can conclude that !!P!! is false. This is a classic proof by contradiction, and it is intuitionistically valid. In fact, in many formulations of intuitionistic logic, !!\lnot P!! is defined to mean !!P\to \bot!!.
What is rejected by intuitionistic logic is the similar-seeming claim that:
$$(\lnot P\to \bot)\to P$$
This says that if assuming !!\lnot P!! leads to absurdity, you can conclude that !!P!! is true. This is not intuitionistically valid.
This is where people become puzzled if they only know classical logic. “But those are the same thing!” they cry. “You just have to replace !!P!! with !!\lnot P!! in the first one, and you get the second.”
Not quite. If you replace !!P!! with !!\lnot P!! in the first one, you do not get the second one; you get:
$$(\lnot P\to \bot)\to \lnot \lnot P$$
People familiar with classical logic are so used to shuffling the !!\lnot !! signs around and treating !!\lnot \lnot P!! the same as !!P!! that they often don't notice when they are doing it. But in intuitionistic logic, !!P!! and !!\lnot \lnot P!! are not the same. !!\lnot \lnot P!! is weaker than !!P!!, in the sense that from !!P!! one can always conclude !!\lnot \lnot P!!, but not always vice versa. Intuitionistic logic is happy to agree that if !!\lnot P!! leads to absurdity, then !!\lnot \lnot P!!. But it does not agree that this is sufficient to conclude !!P!!.
As is often the case, it may be helpful to try to understand intuitionistic logic as talking about provability instead of truth. In classical logic, !!P!! means that !!P!! is true and !!\lnot P!! means that !!P!! is false. If !!P!! is not false it is true, so !!\lnot \lnot P!! and !!P!! mean the same thing. But in intuitionistic logic !!P!! means that !!P!! is provable, and !!\lnot P!! means that !!P!! is not provable. !!\lnot \lnot P!! means that it is impossible to prove that !!P!! is not provable.
If !!P!! is provable, it is certainly impossible to prove that !!P!! is not provable. So !!P!! implies !!\lnot \lnot P!!. But just because it is impossible to prove that there is no proof of !!P!! does not mean that !!P!! itself is provable, so !!\lnot \lnot P!! does not imply !!P!!.
Similarly,
$$(P\to \bot)\to \lnot P $$
means that if a proof of !!P!! would lead to absurdity, then we may conclude that there cannot be a proof of !!P!!. This is quite valid. But
$$(\lnot P\to \bot)\to P$$
means that if assuming that a proof of !!P!! is impossible leads to absurdity, there must be a proof of !!P!!. But this itself isn't a proof of !!P!!, nor is it enough to prove !!P!!; it only shows that there is no proof that proofs of !!P!! are impossible.
[ Addendum 20141124: This article by Andrej Bauer says much the same thing. ]
[ Addendum 20170508: This article by Robert Harper is another in the same family. ]
[Other articles in category /math] permanent link
Wed, 26 Feb 2014
2banner, which tells you when someone else is looking at the same web page
I was able to release a pretty nice piece of software today, courtesy
of my employer, ZipRecruiter. If you have a family of web pages, and
whenever you are looking at one you want to know when someone else is
looking at the same page, you can use my package. The package is
called 2banner, because it pops up a banner on a page whenever two
people are looking at it. With permission from ZipRecruiter, I have
put it on github, and you can download
and use it for free.
A typical use case would be a customer service organization. Say your
users create requests for help, and that the customer service reps have
to answer the requests. There is a web page with a list of all the
unserviced requests, and each one has a link to a page with details
about what is requested and how to contact the person who made the
request. But it might sometimes happes that Fred and Mary
independently decide to service the same request, which is at best a
waste of effort, and at worst confusing for the customer who gets
email from both Fred and Mary and doesn't know how to respond. With
2banner, when Mary arrives at the customer's page, she sees a banner
in the corner that says Fred is already looking at this page!, and
at the same time a banner pops up in Fred's browser that says Mary
has started looking at this page! Then Mary knows that Fred is
already on the case, and she can take over a different one, or Fred
and Mary can communicate and decide which of them will deal with this
particular request.
You can similarly trick out the menu page itself, to hide the menu items that someone is already looking out.
I wanted to use someone else's package for this, but I was not able to find one, so I wrote one myself. It was not as hard as I had expected. The system comprises three components:
The back-end database for recording who started looking at which pages and when. I assumed a SQL database and wrote a component that uses Perl's
DBIx::Classmodule to access it, but it would be pretty easy throw this away and use something else instead.An API server that can propagate notifications like “user X is now looking at page Y” and “user X is no longer looking at page Y” into the database, and which can answer the question “who else is looking at page Y right now?”. I used Perl's Catalyst framework for this, because our web app already runs under it. It would not be too hard to throw this away and use something else instead. You could even write a standalone server using
HTTP::Server, and borrow most of the existing code, and probably have it working in under an hour.A JavaScript thingy that lives in the web page, sends the appropriate notifications to the API server, and pops up the banner when necessary. I used jQuery for this. Probably there is something else you could use instead, but I have no idea what it is, because I know next to nothing about front-end web programming. I was happy to have the chance to learn a little about jQuery for this project.
Often a project seems easy but the more I think about it the harder it seems. This project was the opposite. I thought it sounded hard, and I didn't want to do it. It had been an outstanding request of the CS people for some time, but I guess everyone else thought it sounded hard too, because nobody did anything about it. But the longer I let it percolate around in my head, the simpler it seemed. As I considered it, one difficulty after another evaporated.
Other than the jQuery stuff, which I had never touched before, the hardest part was deciding what to do about the API server. I could easily have written a standalone, special-purpose API server, but I felt like it was the wrong thing, and anyway, I didn't want to administer one. But eventually I remembered that our main web site is driven by Catalyst, which is itself a system for replying to HTTP requests, which already has access to our database, and which already knows which user is making each request.
So it was natural to say that the API was to send HTTP requests to certain URLs on our web site, and easy-peasy to add a couple of handlers to the existing Catalyst application to handle the API requests, query the database, and send the right replies.
I don't know why it took me so long to think of doing the API server with Catalyst. If it had been someone else's suggestion I would probably feel dumb for not having thought of it myself, because in hindsight it is so obvious. Happily, I did think of it, because it is clearly the right solution for us.
It was not too hard to debug. The three components are largely independent of one another. The draft version of the API server responded to GET requests, which are easier to generate from the browser than the POST requests that it should be getting. Since the responses are in JSON, it was easy to see if the API server was replying correctly.
I had to invent techniques for debugging the jQuery stuff. I didn't know the right way to get diagnostic messages out of jQuery, so I put a big text area on the web page, and had the jQuery routines write diagnostic messages into it. I don't know if that's what other people do, but I thought it worked pretty well. JavaScript is not my ideal language, but I program in Perl all day, so I am not about to complain. Programming the front end in JavaScript and watching stuff happen on the page is fun! I like writing programs that make things happen.
The package is in ZipRecruiter's GitHub repository, and is available under a very lenient free license. Check it out.
(By the way, I really like working for ZipRecruiter, and we are hiring Perl and Python developers. Please send me email if you want to ask what it is like to work for them.)
[Other articles in category /tech] permanent link
Sun, 09 Feb 2014You sometimes hear people claim that there is no perfectly efficient machine, that every machine wastes some of its input energy in noise or friction.
However, there is a counterexample. An electric space heater is perfectly efficient. Its purpose is to heat the space around it, and 100% of the input energy is applied to this purpose. Even the electrical energy lost to resistance in the cord you use to plug it into the wall is converted to heat.
Wait, you say, the space heater does waste some of its energy. The coils heat up, and they emit not only heat, but also light, which is useless, being a dull orange color. Ah! But what happens when that light hits the wall? Most of it is absorbed, and heats up the wall. Some is reflected, and heats up a different wall instead.
Similarly, a small fraction of the energy is wasted in making a quiet humming noise—until the sound waves are absorbed by the objects in the room, heating them slightly.
Now it's true that some heat is lost when it's radiated from the outside of the walls and ceiling. But some is also lost whenever you open a window or a door, and you can't blame the space heater for your lousy insulation. It heated the room as much as possible under the circumstances.
So remember this when you hear someone complain that incandescent light bulbs are wasteful of energy. They're only wasteful in warm weather. In cold weather, they're free.
[Other articles in category /physics] permanent link
Sat, 08 Feb 2014I wrote some time ago about Moonpig's use of GUIDs: every significant object was given a unique ID. I said that this was a useful strategy I had only learned from Rik, and I was surprised to see how many previously tricky programming problems became simpler once the GUIDs were available. Some of these tricky problems are artifacts of Perl's somewhat limited implementation of hashes; hash keys must be strings, and the GUID gives you an instantaneous answer to any question about what the keys should be.
But it reminds me of a similar maxim which I was thinking about just yesterday: Every table in a relational database should have a record ID field. It often happens that I am designing some table and there is no obvious need for such a field. I now always put one in anyway, having long ago learned that I will inevitably want it for something.
Most recently I was building a table to record which web pages were being currently visited by which users. A record in the table is naturally identified by the pair of user ID and page URL; it is not clear that it needs any further keys.
But I put in a record ID anyway, because my practice is to always put in a record ID, and sure enough, within a few hours I was glad it was there. The program I was writing has not yet needed to use the record IDs. But to test the program I needed to insert and manipulate some test records, and it was much easier to write this:
update table set ... where record_id = 113;
than this:
update table set ... where user_id = 97531 and url = 'http://hostname:port/long/path/that/is/hard/to/type';
If you ever end up with two objects in the program that represesent record sets and you need to merge or intersect them synthetically, having the record ID numbers automatically attached to the records makes this quite trivial, whereas if you don't have them it is a pain in the butt. You should never be in such a situation, perhaps, but stranger things have happened. Just yesterday I found myself writing
function relativize (pathPat) {
var dummyA = document.createElement('a');
dummyA.href = document.URL;
return "http://" + dummyA.host + pathPat;
}
which nobody should have to do either, and yet there I was. Sometimes programming can be a dirty business.
During the bootstrapping of the user-url table project some records
with bad URLs were inserted by buggy code, and I needed to remove
them. The URLs all ended in % signs, and there's probably some easy
way to delete all the records where the URL ends in a % sign. But I
couldn't remember the syntax offhand, and looking up the escape
sequence for LIKE clauses would have taken a lot longer than what I
did do, which was:
delete from table where record_id in (43, 47, 49)
So the rule is: giving things ID numbers should be the default, because they are generally useful, like handles you can use to pick things up with. You need a good reason to omit them.
[Other articles in category /IT] permanent link
Sat, 01 Feb 2014My current employer uses an online quiz to pre-screen applicants for open positions. The first question on the quiz is a triviality, just to let the candidate get familiar with the submission and testing system. The question is to write a program that copies standard input to standard output. Candidates are allowed to answer the questions using whatever language they prefer.
Sometimes we get candidates who get a zero score on the test. When I see the report that they failed to answer even the trivial question, my first thought is that this should not reflect badly on the candidate. Clearly, the testing system itself is so hard to use that the candidate was unable to submit even a trivial program, and this is a failure of the testing system and not the candidate.
But it has happened more than once that when I look at the candidate's incomplete submissions I see that the problem, at least this time, is not necessarily in the testing system. There is another possible problem that had not even occurred to me. The candidate failed the trivial question because they tried to write the answer in Java.
I am reminded of Dijkstra's remark that the teaching of BASIC should be rated as a criminal offense. Seeing the hapless candidate get bowled over by a question that should be a mere formality makes me wonder if the same might be said of Java.
I'm not sure. It's possible that this is still a failure of the quiz. It's possible that the Java programmers have valuable skills that we could use, despite their inability to produce even a trivial working program in a short amount of time. I could be persuaded, but right now I have a doubtful feeling.
When you learn Perl, Python, Ruby, or Javascript, one of the things you learn is a body of technique for solving problems using hashes, which are an integral part of the language. When you learn Haskell, you similarly learn a body of technique for solving problems with lazy lists and monads. These kinds of powerful general-purpose tools are at the forefront of the language.
But when you learn Java, there aren't any powerful language features
you can use to solve many problems. Instead, you spend your time
learning a body of technique for solving problems in the language.
Java has hashes, but if you are aware of them at all, they are just
another piece of the immense Collections library, lost among the
many other sorts of collections, and you have no particular reason to
know about them or think about them. A good course of Java instruction
might emphasize the more useful parts of the Collections, but since
they're just another part of the library it may not be obvious that
hashes are any more or less useful than, say, AbstractAction or
zipOutputStream.
I was a professional Java programmer for three years (in a different organization), and I have meant for some time to write up my thoughts about it. I am often very bitter and sarcastic, and I willingly admit that I am relentlessly negative and disagreeable, so it can be hard to tell when I am in earnest about liking something. I once tried to write a complimentary article about Blosxom, which has generated my blog since 2006, and I completely failed; people thought I was being critical, and I had to write a followup article to clarify, and people still thought I was dissing Blosxom. Because this article about Java might be confused with sarcastic criticism, I must state clearly that everything in this article about Java is in earnest, and should be taken at face value. Including:
I really like Java
I am glad to have had the experience of programming in Java. I liked
programming in Java mainly because I found it very relaxing. With a
bad language, like say Fortran or csh, you struggle to do anything
at all, and the language fights with you every step of the way
forward. With a good language there is a different kind of struggle,
to take advantage of the language's strengths, to get the maximum
amount of functionality, and to achieve the clearest possible
expression.
Java is neither a good nor a bad language. It is a mediocre language, and there is no struggle. In Haskell or even in Perl you are always worrying about whether you are doing something in the cleanest and the best way. In Java, you can forget about doing it in the cleanest or the best way, because that is impossible. Whatever you do, however hard you try, the code will come out mediocre, verbose, redundant, and bloated, and the only thing you can do is relax and keep turning the crank until the necessary amount of code has come out of the spout. If it takes ten times as much code as it would to program in Haskell, that is all right, because the IDE will generate half of it for you, and you are still being paid to write the other half.
So you turn the crank, draw your paycheck, and you don't have to worry about the fact that it takes at least twice as long and the design is awful. You can't solve any really hard design problems, but there is a book you can use to solve some of the medium-hard ones, and solving those involves cranking out a lot more Java code, for which you will also be paid. You are a coder, your job is to write code, and you write a lot of code, so you are doing your job and everyone is happy.
You will not produce anything really brilliant, but you will probably not produce anything too terrible either. The project might fail, but if it does you can probably put the blame somewhere else. After all, you produced 576 classes that contain 10,000 lines of Java code, all of it seemingly essential, so you were doing your job. And nobody can glare at you and demand to know why you used 576 classes when you should have used 50, because in Java doing it with only 50 classes is probably impossible.
(Different languages have different failure modes. With Perl, the project might fail because you designed and implemented a pile of shit, but there is a clever workaround for any problem, so you might be able to keep it going long enough to hand it off to someone else, and then when it fails it will be their fault, not yours. With Haskell someone probably should have been fired in the first month for choosing to do it in Haskell.)
So yes, I enjoyed programming in Java, and being relieved of the responsibility for producing a quality product. It was pleasant to not have to worry about whether I was doing a good job, or whether I might be writing something hard to understand or to maintain. The code was ridiculously verbose, of course, but that was not my fault. It was all out of my hands.
So I like Java. But it is not a language I would choose for answering test questions, unless maybe the grade was proportional to the number of lines of code written. On the test, you need to finish quickly, so you need to optimize for brevity and expressiveness. Java is many things, but it is neither brief nor expressive.
When I see that some hapless job candidate struggled for 15 minutes and 14 seconds to write a Java program for copying standard input to standard output, and finally gave up, without even getting to the real questions, it makes me sad that their education, which was probably expensive, has not equipped them with with better tools or to do something other than grind out Java code.
[Other articles in category /prog] permanent link
Thu, 30 Jan 2014
Twingler, a generic data structure munger
(Like everything else in this section, these are notes for a project that was never completed.)
Introduction
These incomplete notes from 1997-2001 are grappling with the problem of transforming data structures in a language like Perl, Python, Java, Javascript, or even Haskell. A typical problem is to take an input of this type:
[
[Chi, Ill],
[NY, NY],
[Alb, NY],
[Spr, Ill],
[Tr, NJ],
[Ev, Ill],
]
and to transform it to an output of this type:
{ Ill => [Chi, Ev, Spr],
NY => [Alb, NY],
NJ => [Tr],
}
One frequently writes code of this sort, and it should be possible to specify the transformation with some sort of high-level declarative syntax that is easier to read and write than the following gibberish:
my $out;
for my $pair (@$in) {
push @{$out->{$pair->[0]}}, $pair->[1];
}
for my $k (keys %$out) {
@{$out->{$k}} = sort @{$out->{$k}};
}
This is especially horrible in Perl, but it is bad in any language. Here it is in a hypothetical language with a much less crusty syntax:
for pair (in.items) :
out[pair[0]].append(pair[1])
for list (out.values) :
list.sort
You still can't see what it really going on without executing the code in your head. It is hard for a beginner to write, and hard to anyone to understand.
Original undated notes from around 1997–1998
Consider this data structure DS1:
[
[Chi, Ill],
[NY, NY],
[Alb, NY],
[Spr, Ill], DS1
[Tr, NJ],
[Ev, Ill],
]
This could be transformed several ways:
{
Chi => Ill,
NY => NY,
Alb => NY,
Spr => Ill, DS2
Tr => NJ,
Ev => Ill,
}
{ Ill => [Chi, Spr, Ev],
NY => [NY, Alb], DS3
NJ => Tr,
}
{ Ill => 3,
NY => 2,
NJ => 1,
}
[ Chi, Ill, NY, NY, Alb, NY, Spr, Ill, Tr, NJ, Ev, Ill] DS4
Basic idea: Transform original structure of nesting depth N into an N-dimensional table. If Nth nest is a hash, index table ranks by hash keys; if an array, index by numbers. So for example, DS1 becomes
1 2
1 Chi Ill
2 NY NY
3 Alb NY
4 Spr Ill
5 Tr NJ
6 Ev Ill
Or maybe hashes should be handled a little differently? The original basic idea was more about DS2 and transformed it into
Ill NY NJ
Chi X
NY X
Alb X
Spr X
Tr X
Ev X
Maybe the rule is: For hashes, use a boolean table indexed by keys and values; for arrays, use a string table index by integers.
Notation idea: Assign names to the dimensions of the table, say X and Y. Then denote transformations by:
[([X, Y])] (DS1)
{(X => Y)} (DS2)
{X => [Y]} (DS3)
[(X, Y)] (DS4)
The (...) are supposed to incdicate a chaining of elements within the larger structure. But maybe this isn't right.
At the bottom: How do we say whether
X=>Y, X=>Z
turns into
[ X => Y, X => Z ] (chaining)
or [ X => [Y, Z] ] (accumulation)
Consider
A B C
D . . .
E . .
F . .
<...> means ITERATE over the thing inside and make a list of the
results. It's basically `map'.
Note that:
<X,Y> |= (D,A,D,B,D,C,E,A,E,B,F,A,F,C)
<X,[<Y>]> |= (D,[A,B,C],E,[A,B],F,[A,C])
Brackets and braces just mean brackets and braces. Variables at the same level of nesting imply a loop over the cartesian join. Variables subnested imply a nested loop. So:
<X,Y> means
for x in X
for y in Y
push @result, (x,y) if present(x,y);
But
<X,<Y>> means
for x in X
for y in Y
push @yresult, (y) if present(x,y);
push @result, @yresult
Hmmm. Maybe there's a better syntax for this.
Well, with this plan:
DS1: [ <[X,Y]> ]
DS2: { <X=>Y> }
DS3: { <X => [<Y>]> }
DS4: [ <X, Y> ]
It seems pretty flexible. You could just as easily write
{ <X => max(<Y>) }
and you'd get
{ D => C, E => B, F => C }
If there's a `count' function, you can get
{ D => 3, E => 2, F => 2 }
or maybe we'll just overload scalar' to meancount'.
Question: How to invert this process? That's important so that you can ask it to convert one data structure to another. Also, then you could write something like
[ <city, state> ] |= { <state => [<city>] > }
and omit the X's and Y's.
Real example: From proddir. Given
ID / NAME / SHADE / PALETTE / DESC
For example:
A / AAA / red / pink / Aaa
B / BBB / yellow / tawny / Bbb
A / AAA / green / nude / Aaa
B / BBB / blue / violet / Bbb
C / CCC / black / nude / Ccc
Turn this into
{ A => [ AAA, [ [red, pink], [green, nude] ], Aaa],
B => [ BBB, [ [yellow, tawny], [blue, violet] ], Bbb],
C => [ CCC, [ [black, nude] ], CCC]
}
{ < ID => [
name,
[ <[shade, palette]> ]
desc
]>
}
Something interesting happened here. Suppose we have
[ [A, B]
[A, B]
]
And we ask for <A, B>. Do we get (A, B, A, B), or just (A, B)? Does
it remove duplicate items for us or not? We might want either.
In the example above, why didn't we get
{ A => [ AAA, [ [red, pink], [green, nude] ], Aaa],
A => [ AAA, [ [red, pink], [green, nude] ], Aaa],
B => [ BBB, [ [yellow, tawny], [blue, violet] ], Bbb],
B => [ BBB, [ [yellow, tawny], [blue, violet] ], Bbb],
C => [ CCC, [ [black, nude] ], CCC]
}
If the outer iteration was supposed to be over all id-name-desc triples? Maybe we need
<...> all triples
<!...!> unique triples only
Then you could say
<X> |= <!X!>
to indicate that you want to uniq a list.
But maybe the old notation already allowed this:
<X> |= keys %{< X => 1 >}
It's still unclear how to write the example above, which has unique key-triples. But it's in a hash, so it gets uniqed on ID anyway; maybe that's all we need.
1999-10-23
Rather than defining some bizarre metalanguage to describe the transformation, it might be easier all around if the user just enters a sample input, a sample desired output, and lets the twingler figure out what to do. Certainly the parser and internal representation will be simpler.
For example:
[ [ A, B ],
[ C, B ],
[ D, E ] ]
--------------
{ B => [A, C],
E => [D],
}
should be enough for it to figure out that the code is:
for my $a1 (@$input) {
my ($e1, $e2) = @$a1;
push @{$output{$e2}}, $e1;
}
Advantage: After generating the code, it can run it on the sample input to make sure that the output is correct; otherwise it has a bug.
Input grammar:
%token ELEMENT
expr: array | hash ;
array: '[' csl ']' ;
csl: ELEMENT | ELEMENT ',' csl | /* empty */ ;
hash: '{' cspl '}' ;
cspl: pair | pair ',' cspl | /* empty */ ;
pair: ELEMENT '=>' ELEMENT;
Simple enough. Note that (...) lines are not allowed. They are only useful at the top level. A later version can allow them. It can replace the outer (...) with [...] or {...] as appropirate when it sees the first top-level separator. (If there is a => at the top level, it is a hash, otherwise an array.)
Idea for code generation: Generate pseudocode first. Then translate to Perl. Then you can insert a peephole optimizer later. For example
foreachkey k (somehash) {
push somearray, $somehash{k}
}
could be optimized to
somearray = values somehash;
add into hash: as key, add into value, replace value add into array: at end only
How do we analyze something like:
[ [ A, B ],
[ C, B ],
[ D, E ] ]
--------------
{ B => [A, C],
E => [D],
}
Idea: Analyze structure of input. Analyze structure of output and figure out an expression to deposit each kind of output item. Iterate over input items. Collect all input items into variables. Deposit items into output in appropriate places.
For an input array, tag the items with index numbers. See where the indices go in the output. Try to discern a pattern. The above example:
Try #1:
A: 1
B: 2
C: 1
B: 2 -- consistent with B above
D: 1
E: 2
Output: 2 => [1, 1]
2 => [1]
OK—2s are keys, 1s are array elements.
A different try fails:
A: 1
B: 1
C: 2
B: 2 -- inconsistent, give up on this.
Now consider:
[ [ A, B ],
[ C, B ],
[ D, E ] ]
--------------
{ A => B,
C => B,
D => E,
}
A,C,D get 1; B,E get 2. this works again. 1s are keys, 2s are values.
I need a way of describing an element of a nested data structure as a simple descriptor so that I can figure out the mappings between descriptors. For arrays and nested arrays, it's pretty easy: Use the sequence of numeric indices. What about hashes? Just K/V? Or does V need to be qualified with the key perhaps?
Example above:
IN: A:11 B:12 22 C:21 D:31 E:32
OUT: A:K B:V C:K D:K E:V
Now try to find a mapping from the top set of labels to the bottom.
x1 => K, x2 => V works.
Problem with this:
[ [ A, B ],
[ B, C ],
]
------------
{ A => B,
B => C,
}
is unresolvable. Still, maybe this works well enough in most common cases.
Let's consider:
[[ A , AAA , red , pink , Aaa],
[ B , BBB , yellow , tawny , Bbb],
[ A , AAA , green , nude , Aaa],
[ B , BBB , blue , violet , Bbb],
[ C , CCC , black , nude , Ccc],
]
-------------------------------------------------------------
{ A => [ AAA, [ [red, pink], [green, nude] ], Aaa],
B => [ BBB, [ [yellow, tawny], [blue, violet] ], Bbb],
C => [ CCC, [ [black, nude] ], CCC]
}
A: 00,20 => K
AAA: 01,21 => V0
red: 02 => V100
pink: 03 => V101
Aaa: 04 => V2
B: 10,30 => K
C: 40 => K
etc.
Conclusion: x0 => K; x1 => V0; x2 => V100; x3 => V101; x4 => V2
How to reverse?
Simpler reverse example:
{ A => [ B, C ],
E => [ D ],
}
---------------------
[ [ A, B ],
[ A, C ],
[ E, D ],
]
A: K => 00, 10
B: V0 => 01
C: V1 => 11
D: V0 => 21
E: K => 20
Conclusion: K => x0; V => x1
This isn't enough information. Really, V => k1, where k is whatever
the key was!
What if V items have the associated key too?
A: K => 00, 10
B: V{A}0=> 01
C: V{A}1=> 11
D: V{E}0=> 21
E: K => 20
Now there's enough information to realize that B and C stay with the A, if we're smart enough to figure out how to use it.
2001-07-28
Sent to Nyk Cowham
2001-08-24
Sent to Timur Shtatland
2001-10-28
Here's a great example. The output from HTML::LinkExtor is a list
like
([img, src, URL1, losrc, URL2],
[a, href, URL3],
...
)
we want to transform this into
(URL1 => undef,
URL2 => undef,
URL3 => undef,
...
)
[Other articles in category /notes] permanent link
Sun, 19 Jan 2014
Notes on a system for abbreviating SQL queries
(This post inaugurates a new section on my blog, for incomplete notes. It often happens that I have some idea, usually for software, and I write up a bunch of miscellaneous notes about it, and then never work on it. I'll use this section to post some of those notes, mainly just because I think they might be interesting, but also in the faint hope that someone might get interested and do something with it.)
Why are simple SQL queries so verbose?
For example:
UPDATE batches b
join products p using (product_id)
join clients c using (client_id)
SET b.scheduled_date = NOW()
WHERE b.scheduled_date > NOW()
and b.batch_processor = 'batchco'
and c.login_name = 'mjd' ;
(This is 208 characters.)
I guess about two-thirds of this is unavoidable, but those join-using clauses ought to be omittable, or inferrable, or abbreviatable, or something.
b.batch_processor should be abbreviated to at least
batch_processsor, since that's the only field in those three tables
with that name. In fact it could probably be inferred from
b_p. Similarly c.login_name -> login_name -> log or l_n.
update batches set sch_d = NOW()
where sch_d > NOW()
and bp = 'batchco'
and cl.ln = 'mjd'
(Only 94 characters.)
cl.ln is inferrable: Only two tables begin with cl. None of the
field names in the client_transaction_view table look like
ln. So cl.ln unambiguously means client.login_name.
Then the question arises of how to join the batches to the clients. This is the only really interesting part of this project, and the basic rule is that it shouldn't do anything really clever. There is a graph, which the program can figure out from looking at the foreign key constraints. And the graph should clearly have a short path from batches through products to clients.
bp might be globally ambiguous, but it can be disambiguated by
assuming it's in one of the three tables involved.
If something is truly ambiguous, we can issue an intelligent request for clarification:
"bp" is ambiguous. Did you mean:
1. batches.batch_processor
2. batches.bun_predictor
0. None of the above
which? _
Overview
- Debreviate table names
- Figure out required joins and join fields
- Debreviate field names
Can 1 and 2 really be separated? They can in the example above, but maybe not in general.
I think separating 3 and putting it at the end is a good idea: don't
try to use field name abbreviations to disambiguate and debreviate
table names. Only go the other way. But this means that we can't
debreviate cl, since it might be client_transaction_view.
What if something like cl were left as ambiguous after stage 1, and
disambiguated only in stage 3? Then information would be unavailable
to the join resolution, which is the part that I really want to work.
About abbreviations
Abbreviations for batch_processor:
bp
b_p
ba_pr
batch_p
There is a tradeoff here: the more different kinds of abbreviations you accept, the more likely there are to be ambiguities.
About table inference
There could also be a preferences file that lists precedences for
tables and fields: if it lists clients, then anything that could
debreviate to clients or to client_transaction_view
automatically debreviates to clients. The first iteration could just
be a list of table names.
About join inference
Short join paths are preferred to long join paths.
If it takes a long time to generate the join graph, cache it. Build it automatically on the first run, and then rebuild it on request later on.
More examples
(this section blank)
Implementation notes
Maybe convert the input to a SQL::Abstract first, then walk the
resulting structure, first debreviating names, then inserting joins,
then debreviating the rest of the names. Then you can output the text
version of the result if you want to.
Note that this requires that the input be valid SQL. Your original idea for the abbreviated SQL began with
update set batches.sch_d = NOW()
rather than
update batches set sch_d = NOW()
but the original version would probably be ruled out by this implementation. In this case that is not a big deal, but this choice of implementation might rule out more desirable abbreviations in the future.
Correcting dumb mistakes in the SQL language design might be in Quirky's purview. For example, suppose you do
select * from table where (something)
Application notes
RJBS said he would be reluctant to use the abbreviated version of a query in a program. I agree: it would be very foolish to do so, because adding a table or a field might change the meaning of an abbreviated SQL query that was written into a program ten years ago and has worked ever since. This project was never intended to abbreviate queries in program source code.
Quirky is mainly intended for one-off queries. I picture it going into an improved replacement for the MySQL command-line client. It might also find use in throwaway programs. I also picture a command-line utility that reads your abbreviated query and prints the debreviated version for inserting into your program.
Miscellaneous notes
(In the original document this section was blank. I have added here some notes I made in pen on a printout of the foregoing, on an unknown date.)
Maybe also abbreviate update => u, where => w, and => &. This cuts
the abbreviated query from 94 to 75 characters.
Since debreviation is easier [than join inference] do it first!
Another idea: "id" always means the main table's primary key field.
[Other articles in category /notes] permanent link
Fri, 10 Jan 2014
DateTime::Moonpig, a saner interface to DateTime
(This article was previously published at the Perl Advent Calendar on 2013-12-23.)
The DateTime suite is an impressive tour de force, but I hate its interface. The methods it provides are usually not the ones you want, and the things it makes easy are often things that are not useful.
Mutators
The most obvious example is that it has too many mutators. I believe
that date-time values are a kind of number, and should be treated like
numbers. In particular they should be immutable. Rik Signes has
a hair-raising story
about an accidental mutation that caused a hard to diagnose bug,
because the add_duration method modifies the object on which it is
called, instead of returning a new object.
DateTime::Duration
But the most severe example, the one that drives me into a rage, is
that the subtract_datetime method returns a DateTime::Duration object,
and this object is never what you want, because it is impossible to
use it usefully.
For example, suppose you would like to know how much time elapses between 1969-04-02 02:38:17 EST and 2013-12-25 21:00:00 EST. You can set up the two DateTime objects for the time, and subtract them using the overloaded minus operator:
#!perl
my ($a) = DateTime->new( year => 1969, month => 04, day => 02,
hour => 2, minute => 38, second => 17,
time_zone => "America/New_York" ) ;
my ($b) = DateTime->new( year => 2013, month => 12, day => 25,
hour => 21, minute => 0, second => 0,
time_zone => "America/New_York" ) ;
my $diff = $b - $a;
Internally this invokes subtract_datetime to yield a
DateTime::Duration object for the difference. The
DateTime::Duration object $diff will contain the information
that this is a difference of 536 months, 23 days, 1101 minutes, and 43
seconds, a fact which seems to me to be of very limited usefulness.
You might want to know how long this interval is, so you can compare
it to similar intervals. So you might want to know how many seconds
this is. It happens that the two times are exactly 1,411,669,328
seconds apart, but there's no way to get the $diff object to
tell you this.
It seems like there are methods that will get you the actual
elapsed time in seconds, but none of them will do it. For example,
$diff->in_units('seconds') looks promising, but will
return 43, which is the 43 seconds left over after you've thrown away
the 536 months, 23 days, and 1101 minutes. I don't know what the use
case for this is supposed to be.
And indeed, no method can tell you how long the duration really is, because the subtraction has thrown away all the information about how long the days and months and years were—days, months and years vary in length—so it simply doesn't know how much time this object actually represents.
Similarly if you want to know how many days there are between the two dates, the DateTime::Duration object won't tell you because it can't tell you. If you had the elapsed seconds difference, you could convert it to the correct number of days simply by dividing by 86400 and rounding off. This works because, even though days vary in length, they don't vary by much, and the variations cancel out over the course of a year. If you do this you find that the elapsed number of days is approximately 16338.7653, which rounds off to 16338 or 16339 depending on how you want to treat the 18-hour time-of-day difference. This result is not quite exact, but the error is on the order of 0.000002%. So the elapsed seconds are useful, and you can compute other useful values with them, and get useful answers. In contrast, DateTime::Duration's answer of "536 months and 23 days" is completely useless because months vary in length by nearly 10% and DateTime has thrown away the information about how long the months were. The best you can do to guess the number of days from this is to multiply the 536 months by 30.4375, which is the average number of days in a month, and add 23. This is clumsy, and gets you 16337.5 days—which is close, but wrong.
To get what I consider a useful answer out of the DateTime objects you must not use the overloaded subtraction operator; instead you must do this:
#!perl
$b->subtract_datetime_absolute($a)->in_units('seconds')
What's DateTime::Moonpig for?
DateTime::Moonpig
attempts to get rid of the part of DateTime I don't like and keep the
part I do like, by changing the interface and leaving the internals
alone. I developed it for the Moonpig billing system that Rik
Signes and I did; hence the
name.
DateTime::Moonpig introduces five main changes to the interface of DateTime:
Most of the mutators are gone. They throw fatal exceptions if you try to call them.
The overridden addition and subtraction operators have been changed to eliminate DateTime::Duration entirely. Subtracting two DateTime::Moonpig objects yields the difference in seconds, as an ordinary Perl number. This means that instead of
#!perl $x = $b->subtract_datetime_absolute($a)->in_units('seconds')one can write
#!perl $x = $b - $aFrom here it's easy to get the approximate number of days difference: just divide by 86400. Similarly, dividing this by 3600 gets the number of hours difference.
An integer number of seconds can be added to or subtracted from a DateTime::Moonpig object; this yields a new object representing a time that is that many seconds later or earlier. Writing
$date + 2is much more convenient than writing$date->clone->add( seconds => 2 ).If you are not concerned with perfect exactness, you can write
#!perl sub days { $_[0] * 86400 } my $tomorrow = $now + days(1);This might be off by an hour if there is an intervening DST change, or by a second if there is an intervening leap second, but in many cases one simply doesn't care.
There is nothing wrong with the way DateTime overloads
<and>, so DateTime::Moonpig leaves those alone.The constructor is extended to accept an epoch time such as is returned by Perl's built-in
time()orstat()functions. This means that one can abbreviate this:#!perl DateTime->from_epoch( epoch => $epoch )to this:
#!perl DateTime::Moonpig->new( $epoch )The default time zone has been changed from DateTime's "floating" time zone to UTC. I think the "floating" time zone is a mistake, and best avoided. It has bad interactions with
set_time_zone, whichDateTime::Moonpigdoes not disable, because it is not actually a mutator—unless you use the "floating" time zone. An earlier blog article discusses this.I added a few additional methods I found convenient. For example there is a
$date->stthat returns the date and time in the formatYYYY-MM-DD HH:MM::SS, which is sometimes handy for quick debugging. (Thestis for "string".)
Under the covers, it is all just DateTime objects, which seem to do
what one needs. Other than the mutators, all the many DateTime
methods work just the same; you are even free to use
->subtract_datetime to obtain a DateTime::Duration object if you
enjoy being trapped in an absurdist theatre production.
When I first started this module, I thought it was likely to be a failed experiment. I expected that the Moonpig::DateTime objects would break once in a while, or that some operation on them would return a DateTime instead of a Moonpig::DateTime, which would cause some later method call to fail. But to my surprise, it worked well. It has been in regular use in Moonpig for several years.
I recently split it out of Moonpig, and released it to CPAN. I will be interested to find out if it works well in other contexts. I am worried that disabling the mutators has left a gap in functionality that needs to be filled by something else. I will be interested to hear reports from people who try.
[Other articles in category /prog/perl] permanent link
Sat, 04 Jan 2014There is a famous mistake of Augustin-Louis Cauchy, in which he is supposed to have "proved" a theorem that is false. I have seen this cited many times, often in very serious scholarly literature, and as often as not Cauchy's purported error is completely misunderstood, and replaced with a different and completely dumbass mistake that nobody could have made.
The claim is often made that Cauchy's Course d'analyse of 1821 contains a "proof" of the following statement: a convergent sequence of continuous functions has a continuous limit. For example, the Wikipedia article on "uniform convergence" claims:
Some historians claim that Augustin Louis Cauchy in 1821 published a false statement, but with a purported proof, that the pointwise limit of a sequence of continuous functions is always continuous…
The nLab article on "Cauchy sum theorem" states:
Non-theorem (attributed to Cauchy, 1821). Let !!f=(f_1,f_2,\ldots)!! be an infinite sequence of continuous functions from the real line to itself. Suppose that, for every real number !!x!!, the sequence !!(f_1(x), f_2(x), \ldots)!! converges to some (necessarily unique) real number !!f_\infty(x)!!, defining a function !!f_\infty!!; in other words, the sequence !!f!! converges pointwise? to !!f_\infty!!. Then !!f_\infty!! is also continuous.
Cauchy never claimed to have proved any such thing, and it beggars belief that Cauchy could have made such a claim, because the counterexamples are so many and so easily located. For example, the sequence !! f_n(x) = x^n!! on the interval !![-1,1]!! is a sequence of continuous functions that converges everywhere on !![0,1]!! to a discontinuous limit. You would have to be a mathematical ignoramus to miss this, and Cauchy wasn't.
Another simple example, one that converges everywhere in !!\mathbb R!!, is any sequence of functions !!f_n!! that are everywhere zero, except that each has a (continuous) bump of height 1 between !!-\frac1n!! and !!\frac1n!!. As !!n\to\infty!!, the width of the bump narrows to zero, and the limit function !!f_\infty!! is everywhere zero except that !!f_\infty(0)=1!!. Anyone can think of this, and certainly Cauchy could have. A concrete example of this type is $$f_n(x) = e^{-x^{2}/n}$$ which converges to 0 everywhere except at !! x=0 !!, where it converges to 1.
Cauchy's controversial theorem is not what Wikipedia or nLab claim. It is that that the pointwise limit of a convergent series of continuous functions is always continuous. Cauchy is not claiming that $$f_\infty(x) = \lim_{i\to\infty} f_i(x)$$ must be continuous if the limit exists and the !!f_i!! are continuous. Rather, he claims that $$S(x) = \sum_{i=1}^\infty f_i(x)$$ must be continuous if the sum converges and the !!f_i!! are continuous. This is a completely different claim. It premise, that the sum converges, is much stronger, and so the claim itself is much weaker, and so much more plausible.
Here the counterexamples are not completely trivial. Probably the best-known counterexample is that a square wave (which has a jump discontinuity where the square part begins and ends) can be represented as a Fourier series.
(Cauchy was aware of this too, but it was new mathematics in 1821. Lakatos and others have argued that the theorem, understood in the way that continuity was understood in 1821, is not actually erroneous, but that the idea of continuity has changed since then. One piece of evidence strongly pointing to this conclusion is that nobody complained about Cauchy's controversial theorem until 1847. But had Cauchy somehow, against all probability, mistakenly claimed that a sequence of continuous functions converges to a continuous limit, you can be sure that it would not have taken the rest of the mathematical world 26 years to think of the counterexample of !!x^n!!.)
The confusion about Cauchy's controversial theorem arises from a perennially confusing piece of mathematical terminology: a convergent sequence is not at all the same as a convergent series. Cauchy claimed that a convergent series of continuous functions has a continuous limit. He did not ever claim that a convergent sequence of continuous functions had a continuous limit. But I have often encountered claims that he did that, even though such such claims are extremely implausible.
The claim that Cauchy thought a sequence of continuous functions converges to a continuous limit is not only false but is manifestly so. Anyone making it has at best made a silly and careless error, and perhaps doesn't really understand what they are talking about, or hasn't thought about it.
[ I had originally planned to write about this controversial theorem in my series of articles about major screwups in mathematics, but the longer and more closely I looked at it the less clear it was that Cauchy had actually made a mistake. ]
[Other articles in category /math] permanent link



