Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 22 Dec 2017
A couple of years ago I wrote here about some interesting projects I had not finished. One of these was to enumerate and draw orthogonal polygons.
An orthogonal polygon is simply one whose angles are all right angles. All rectangles are orthogonal polygons, but there are many other types. For example, here are examples of orthogonal decagons:
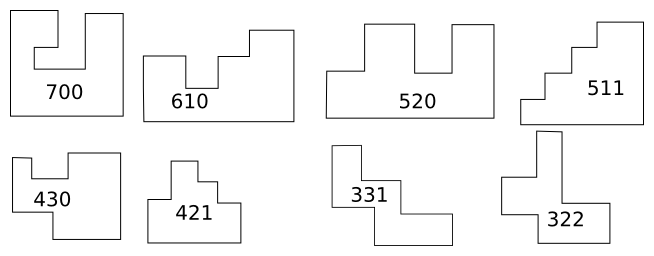
If you ignore the lengths of the edges, and pay attention only to the direction that the corners turn, the orthogonal polygons fall into types. The rectangle is the only type with four sides. There is also only one type with six sides; it is an L-shaped hexagon. There are four types with eight sides, and the illustration shows the eight types with ten sides.
Contributing to OEIS was a life goal of mine and I was thrilled when I was able to contribute the sequence of the number of types of orthogonal !!2n!!-gons.
Enumerating the types is not hard. For !!2n!!-gons, there is one type for each “bracelet” of !!n-2!! numbers whose sum is !!n+2!!.[1]
In the illustration above, !!n=5!! and each type is annotated with its !!5-2=3!! numbers whose sum is !!n+2=7!!. But the number of types increases rapidly with the number of sides, and it soons becomes infeasible to draw them by hand as I did above. I had wanted to write a computer program that would take a description of a type (the sequence) and render a drawing of one of the polygons of that type.
The tricky part is how to keep the edges from crossing, which is not allowed. I had ideas for how to do this, but it seemed troublesome, and also it seemed likely to produce ugly, lopsided examples, so I did not implement it. And eventually I forgot about the problem.
But Brent Yorgey did not forget, and he had a completely different idea. He wrote a program to convert a type description to a set of constraints on the !!x!! and !!y!! coordinates of the vertices, and fed the constraints to an SMT solver, which is a system for finding solutions to general sets of constraints. The outcome is as handsome as I could have hoped. Here is M. Yorgey's program's version of the hand-drawn diagram above:
M. Yorgey rendered beautiful pictures of all types of orthogonal polygons up to 12 sides. Check it out on his blog.
[1]
“Bracelet”
is combinatorist jargon for a sequence of things where the ends are
joined together: you can start in the middle, run off one end and come
back to the other end, and that is considered the same bracelet. So
for example ABCD and BCDA and CDAB are all the same
bracelet. And also, it doesn't matter which direction you go, so
that DCBA, ADCB, and BADC are also the same bracelet again.
Every bracelet made from from A, B, C, and D is equivalent to
exactly one of ABCD, ACDB, or ADBC.
[ Addendum 20180202: M. Yorgey has more to say about it on his blog. ]
[Other articles in category /math] permanent link
Thu, 21 Dec 2017
Philadelphians, move to the back of the bus!
I have lived in Philadelphia almost 28 years, and I like it very much. I grew up in New York, and I have some of the typical New Yorker snobbery about the rest of the world, a sort of patronizing “oh, isn't that cute, at least you tried” attitude. This is not a good thing, and I have tried to get rid of it, with only partial success. Philadelphia is not New York and it is never going to be New York, and I am okay with that. When I first got here I was more doubtful, but I made an effort to find and appreciate things about Philadelphia that were better than in New York. There are many, but it took me a while to start noticing them.
In 1992 I wrote an article that began:
Someone asked me once what Philadelphia has that New York doesn't. I couldn't come up with anything good.
But the article explained explained that since then, I had found an excellent answer. I wrote about how I loved the Schuylkill river and how New York had nothing like the it. In Philadelphia you are always going back and forth across the Schuylkill river, sometimes in cars or buses or trains, sometimes on a bike, sometimes on foot. It is not a mighty river like the Hudson. (The Delaware fills that role for us.) The Schuylkill is smaller, but still important. The 1992 article said:
It makes what might otherwise be a static and monolithic entity into a dynamic and variable one. Manhattan is monolithic, like a giant baked potato. Philadelphia is complex inside, with structure and sub-organs, like your heart.
New York has rivers you can cross, but, like much of New York, they are not to human scale. Crossing the Brooklyn Bridge or the George Washington Bridge on foot are fun things to do, once in a while. But they are big productions, a thing you might want to plan ahead, as a special event. Crossing the Schuylkill on foot is something you do all the time. In 1993 I commuted across the Schuylkill on foot twice a day and it was lovely. I took a photograph of it each time, and enjoyed comparing the many looks of the Schuylkill.
Once I found that point of attachment, I started to find many more things about Philadelphia that are better than in New York. Just a few that come to mind:
In New York, if you run into someone you know but had not planned to see, or meet a stranger with whom you have a common acquaintance, you are stunned. It is an epic coincidence, not quite a once-in-a-lifetime kind of thing, but maybe not a once-a-year thing either. In Philadelphia it is still unusual enough to be an interesting and happy surprise but not so rare as to make you wonder if you are being pranked.
In Philadelphia, if you are walking down the street, and say hello to a stranger sitting on their stoop, they will say hello back to you. In New York they will stare at you as though you had just come from the moon, perhaps wondering what your angle is.
If you live in New York, it is preferable to spend all of August in your vacation home, even if it is located on the shore of the lake of boiling pitch in the eighth circle of Hell. The weather is more pleasant in the eighth circle than it is in New York in August, and the air is cleaner. Never in 28 years in Philadelphia have I endured weather that is as bad as New York in August.
This is only a partial list. Philadelphia is superior to New York in many ways, and I left out the most important ones. I am very fond of Philadelphia, which is why I have lived here for 28 years. I can appreciate its good points, and when I encounter its bad points I no longer snarl and say “In New York we knew how to do this right.” Usually.
Usually.
One thing about Philadelphia is seriously broken. Philadelphians do not know how to get on a bus.
Every culture has its own customs. Growing up as a New Yorker, I learned early and deeply a cardinal part of New York's protocol: Get out of the way. Seriously, if you visit New York and you can't get anything else right, at least get out of the way. Here is advice from Nathan Pyle's etiquette guide for newcomers to New York:

Insofar as I still have any authority to speak for New Yorkers, I endorse the advice in this book on their behalf. Quite a lot of it consists of special cases of “get out of the way”. Tip #41 says so in so many words: “Basically anything goes as long as you stay out of the way.” Tip #31 says to take your luggage off the subway seat next to you, and put it on your lap. Tip #65 depicts the correct way of stopping on the sidewalk to enjoy a slice of pizza: immediately adjacent to a piece of street furniture that the foot traffic would have had to have gone around anyway.
Suppose you get on the bus in New York. You will find that the back of the bus is full, and the front is much less so. You are at the front. What do you do now? You move as far back as is reasonably possible — up to the beginning of the full section — so that the next person to get in can do the same. This is (obviously, if you are a New Yorker) the only way to make efficient use of the space and fill up the bus.
In Philadelphia, people do not do this. People get on the bus, move as far back as is easy and convenient, perhaps halfway, or perhaps only a few feet, and then stop, as the mood takes them. And so it often happens that when the bus arrives the new passengers will have to stand in the stepwell, or can't get on at all — even though the bus is only half full. Not only is there standing room in the back, but there are usually seats in the back. The bus abandons people at the stop, because there is no room for them to get on, because there is someone standing halfway down blocking the aisle, and the person just in front of them doesn't want to push past them, and those two people block everyone else.
In New York, the passengers in front would brusquely push their way past these people and perhaps rebuke them. New Yorkers are great snarlers, but Philadelphians seem to be too polite to snarl at strangers. Nobody in Philadelphia says anything, and the space is wasted. People with kids and packages are standing up because people behind them can't be bothered to sit down.
I don't know what the problem is with these people. Wouldn't it easier to move to the back of the bus and to sit down in the empty seats than it is to stand up and block the aisle? I have tried for a quarter of a century to let go of the idea that people in New York are smarter and better and people elsewhere are slow-witted rubes, and I have mostly succeeded. But where Philadelphians are concerned, this bus behavior is a major sticking point.
In New York we knew how to do this right.
[Other articles in category /misc] permanent link
Mon, 18 Dec 2017A few weeks ago I was writing something about Turkey, and I needed a generic Turkish name, analogous to “John Doe”. I was going to use “Osman Yılmaz”, which I think would have been a decent choice, but I decided it would be more fun to ask a Turkish co-worker what the correct choice would be. I asked Kıvanç Yazan, who kindly allowed himself to be nerdsniped and gave me a great deal of information. In the rest of this article, anything about Turkish that is correct should be credited to him, while any mistakes are surely my own.
M. Yazan informs me that one common choice is “Ali Veli”. Here's a link he gave me to Ekşisözlük, which is the Turkish analog of Urban Dictionary, explaining (in Turkish) the connotations of “John Doe”. The page also mentions “John Smith”, which in turn links to a page about a footballer named Ali Öztürk—in fact two footballers. ([1] [2]) which is along the same lines as my “Osman Yılmaz” suggestion.
But M. Yazan told me about a much closer match for “John Doe”. It is:
sarı çizmeli Mehmet Ağa
which translates as “Mehmet Agha with yellow boots”. (‘Sarı’ = ‘yellow’; ‘çizmeli’ = ‘booted’.)
This oddly specific phrase really seems to be what I was looking for. M. Yazan provided several links:
- Ekşisözlük again
The official dictionary of the Turkish government
Unfortunately I can't find any way to link to the specific entry, but the definition it provides is “kim olduğu, nerede oturduğu bilinmeyen kimse” which means approximately “someone whose identity/place is unknown”.
A paper on “Personal Names in Sayings and Idioms”.
This is in Turkish, but M. Yazan has translated the relevant part as follows:
At the time when yellow boots were in fashion, a guy from İzmir put "Mehmet Aga" in his account book. When time came to pay the debt , he sent his servant and asked him to find "Mehmet Aga with yellow boots". The helper did find a Mehmet Aga, but it was not the one they were looking for. Then guy gets angry at his servant, to which his helper responded, “Sir, this is a big city, there are lots of people with yellow boots, and lots of people named Mehmet! You should write it in your book one more time!”
Another source I found was this online Turkish-English dictionary which glosses it as “Joe Schmoe”.
Finding online mentions of sarı çizmeli Mehmet Ağa is a little bit tricky, because he is also the title of a song by the very famous Turkish musician Barış Manço, and the references to this song swamp all the other results. This video features Manço's boots and although we cannot see for sure (the recording is in grayscale) I presume that the boots are yellow.
Thanks again, Kıvanç!
[ Addendum: The Turkish word for “in style” is “moda”. I guessed it was a French loanword. Kıvanç tells me I was close: it is from Italian. ]
[ Addendum 20171219: Wikipedia has an impressive list of placeholder names by language that includes Mehmet Ağa. ]
[ Addendum 20180105: The Hebrew version of Mehmet Ağa is at least 2600 years old! ]
[Other articles in category /lang] permanent link
Fri, 15 Dec 2017
Wasteful and frugal proofs in Ramsey theory
This math.se question asks how to show that, among any 11 integers, one can find a subset of exactly six that add up to a multiple of 6. Let's call this “Ebrahimi’s theorem”.
This was the last thing I read before I put away my phone and closed my eyes for the night, and it was a race to see if I would find an answer before I fell asleep. Sleep won the race this time. But the answer is not too hard.
First, observe that among any five numbers there are three that sum to a multiple of 3: Consider the remainders of the five numbers upon division by 3. There are three possible remainders. If all three remainders are represented, then the remainders are !!\{0,1,2\}!! and the sum of their representatives is a multiple of 3. Otherwise there is some remainder with three representatives, and the sum of these three is a multiple of 3.
Now take the 11 given numbers. Find a group of three whose sum is a multiple of 3 and set them aside. From the remaining 8 numbers, do this a second time. From the remaining 5 numbers, do it a third time.
We now have three groups of three numbers that each sum to a multiple of 3. Two of these sums must have the same parity. The six numbers in those two groups have an even sum that is a multiple of 3, and we win.
Here is a randomly-generated example:
$$3\quad 17\quad 35\quad 42\quad 44\quad 58\quad 60\quad 69\quad 92\quad 97\quad 97$$
Looking at the first 5 numbers !!3\ 17\ 35\ 42\ 44!! we see that on division by 3 these have remainders !!0\ 2\ 2\ 0\ 2!!. The remainder !!2!! is there three times, so we choose those three numbers !!\langle17\ 35\ 44\rangle!!, whose sum is a multiple of 3, and set them aside.
Now we take the leftover !!3!! and !!42!! and supplement them with three more unused numbers !!58\ 60\ 69!!. The remainders are !!0\ 0\ 1\ 0\ 0!! so we take !!\langle3\ 42\ 60\rangle!! and set them aside as a second group.
Then we take the five remaining unused numbers !!58\ 69\ 92\ 97\ 97!!. The remainders are !!1\ 0\ 2\ 1\ 1!!. The first three !!\langle 58\ 69\ 92\rangle!!have all different remainders, so let's use those as our third group.
The three groups are now !! \langle17\ 35\ 44\rangle, \langle3\ 42\ 60\rangle, \langle58\ 69\ 92\rangle!!. The first one has an even sum and the second has an odd sum. The third group has an odd sum, which matches the second group, so we choose the second and third groups, and that is our answer:
$$3\qquad 42\qquad 60\qquad 58 \qquad 69 \qquad 92$$
The sum of these is !!324 = 6\cdot 54!!.
This proves that 11 input numbers are sufficient to produce one output set of 6 whose sum is a multiple of 6. Let's write !!E(n, k)!! to mean that !!n!! inputs are enough to produce !!k!! outputs. That is, !!E(n, k)!! means “any set of !!n!! numbers contains !!k!! distinct 6-element subsets whose sum is a multiple of 6.” Ebrahimi’s theorem, which we have just proved, states that !!E(11, 1)!! is true, and obviously it also proves !!E(n, 1)!! for all larger !!n!!.
I would like to consider the following questions:
- Does this proof suffice to show that !!E(10, 1)!! is false?
- Does this proof suffice to show that !!E(11, 2)!! is false?
I am specifically not asking whether !!E(10, 1)!! or !!E(11, 2)!! are actually false. There are easy counterexamples that can be found without reference to the proof above. What I want to know is if the proof, as given, contains nontrivial information about these questions.
The reason I think this is interesting is that I think, upon more careful examination, that I will find that the proof above does prove at least one of these, perhaps with a very small bit of additional reasoning. But there are many similar proofs that do not work this way. Here is a famous example. Let !!W(n, k)!! be shorthand for the following claim:
Let the integers from 1 to !!n!! be partitioned into two sets. Then one of the two sets contains !!k!! distinct subsets of three elements of the form !!\{a, a+d, a+2d\}!! for integers !!a, d!!.
Then:
Van der Waerden's theorem: !!W(325, 1)!! is true.
!!W()!!, like !!E()!!, is monotonic: van der Waerden's theorem trivially implies !!W(n, 1)!! for all !!n!! larger than 325. Does it also imply that !!W(n, 1)!! is false for smaller !!n!!? No, not at all; this is actually untrue. Does it also imply that !!W(325, k)!! is false for !!k>1!!? No, this is false also.
Van der Waerden's theorem takes 325 inputs (the integers) and among them finds one output (the desired set of three). But this is extravagantly wasteful. A better argument shows that only 9 inputs were required for the same output, and once we know this it is trivial that 325 inputs will always produce at least 36 outputs, and probably a great many more.
Proofs of theorems in Ramsey theory are noted for being extravagant in exactly this way. But the proof of Ebrahimi's theorem is different. It is not only frugal, it is optimally so. It uses no more inputs than are absolutely necessary.
What is different about these cases? What is the source the frugality of the proof of Ebrahimi’s theorem? Is there a way that we can see from examination of the proof that it will be optimally frugal?
Ebrahimi’s theorem shows !!E(11, 1)!!. Suppose instead we want to show !!E(n, 2)!! for some !!n!!. From Ebrahimi’s theorem itself we immediately get !!E(22, 2)!! and indeed !!E(17, 2)!!. Is this the best we can do? (That is, is !!E(16, 2)!! false?) I bet it isn't. If it isn't, what went wrong? Or rather, what went right in the !!k=1!! case that stopped working when !!k>1!!?
I don't know.
[Other articles in category /math] permanent link
Sat, 09 Dec 2017The Volokh Conspiracy is a frequently-updated blog about legal issues. It reports on interesting upcoming court cases and recent court decisions and sometimes carries thoughtful and complex essays on legal theory. It is hosted by, but not otherwise affiliated with, the Washington Post.
Volokh periodically carries a “roundup of recent federal court decisions”, each with an intriguing one-paragraph summary and a link to the relevant documents, usually to the opinion itself. I love reading federal circuit court opinions. They are almost always carefully thought out and clearly-written. Even when I disagree with the decision, I almost always concede that the judges have a point. It often happens that I read the decision and say “of course that is how it must be decided, nobody could disagree with that”, and then I read the dissenting opinion and I say exactly the same thing. Then I rub my forehead and feel relieved that I'm not a federal circuit court judge.
This is true of U.S. Supreme Court decisions also. Back when I had more free time I would sometimes visit the listing of all recent decisions and pick out some at random to read. They were almost always really interesting. When you read the newspaper about these decisions, the newspaper always wants to make the issue simple and usually tribal. (“Our readers are on the (Red / Blue) Team, and the (Red / Blue) Team loves mangel-wurzels. Justice Furter voted against mangel-wurzels, that is because he is a very bad man who hates liberty! Rah rah team!”) The actual Supreme Court is almost always better than this.
For example we have Clarence Thomas's wonderful dissent in the case of Gonzales v. Raich. Raich was using marijuana for his personal medical use in California, where medical marijuana had been legal for years. The DEA confiscated and destroyed his supplier's plants. But the Constitution only gives Congress the right to regulate interstate commerce. This marijuana had been grown in California by a Californian, for use in California by a Californian, in accordance with California law, and had never crossed any state line. In a 6–3 decision, the court found that the relevant laws were nevertheless a permitted exercise of Congress's power to regulate commerce. You might have expected Justice Thomas to vote against marijuana. But he did not:
If the majority is to be taken seriously, the Federal Government may now regulate quilting bees, clothes drives, and potluck suppers throughout the 50 States. This makes a mockery of Madison’s assurance to the people of New York that the “powers delegated” to the Federal Government are “few and defined,” while those of the States are “numerous and indefinite.”
Thomas may not be a fan of marijuana, but he is even less a fan of federal overreach and abuse of the Commerce Clause. These nine people are much more complex than the newspapers would have you believe.
But I am digressing. Back to Volokh's federal court roundups. I have to be careful not to look at these roundups when I have anything else that must be done, because I inevitably get nerdsniped and read several of them. If you enjoy this kind of thing, this is the kind of thing you will enjoy.
I want to give some examples, but can't decide which sound most interesting, so here are three chosen at random from the most recent issue:
Warden at Brooklyn, N.Y., prison declines prisoner’s request to keep stuffed animals. A substantial burden on the prisoner’s sincere religious beliefs?
Online reviewer pillories Newport Beach accountant. Must Yelp reveal the reviewer’s identity?
With no crosswalks nearby, man jaywalks across five-lane avenue, is struck by vehicle. Is the church he was trying to reach negligent for putting its auxiliary parking lot there?
[ Addendum 20171213: Volokh has just left the Washington Post, and moved to Reason, citing changes in the Post's paywall policies. ]
[ Addendum 20210628: Much has changed since Gonzales v. Raich, and today Justice Thomas observed that even if the majority's argument stood up in 2004, justified by the Necessary and Proper clause, it no longer does, as the federal government no longer appears consider the prohibition of marijuana necessary or proper. ]
[ Addendum 20231218: This article lacks a clear, current link to the Short Circuit summaries that it discusses. Here's an index of John Ross' recent Short Circuit posts. ]
[Other articles in category /law] permanent link
Fri, 08 Dec 2017I drink a lot of coffee at work. Folks there often make a pot of coffee and leave it on the counter to share, but they never make decaf and I drink a lot of decaf, so I make a lot of single cups of decaf, which is time-consuming. More and more people swear by the AeroPress, which they say makes single cups of excellent coffee very quickly. It costs about $30. I got one and tried it out.
The AeroPress works like this: There is a cylinder, open at the top, closed but perforated at the bottom. You put a precut circle of filter paper into the bottom and add ground coffee on top of it. You put the cylinder onto your cup, then pour hot water into the cylinder.
So far this is just a regular single-cup drip process. But after a minute, you insert a plunger into the cylinder and push it down gently but firmly. The water is forced through the grounds and the filter into the cup.
In theory the press process makes better coffee than drip, because there is less opportunity to over-extract. The AeroPress coffee is good, but I did not think it tasted better than drip. Maybe someone else, fussier about coffee than I am, would be more impressed.
Another the selling points is that the process fully extracts the grounds, but much more quickly than a regular pourover cone, because you don't have to wait for all the dripping. One web site boasts:
Aeropress method shortens brew time to 20 seconds or less.
It does shorten the brew time. But you lose all the time again washing out the equipment. The pourover cone is easier to clean and dry. I would rather stand around watching the coffee drip through the cone than spend the same amount of time washing the coffee press.
The same web site says:
Lightweight, compact design saves on storage space.
This didn't work for me. I can't put it in my desk because it is still wet and it is difficult to dry. So it sits on a paper towel on top of my desk, taking up space and getting in the way. The cone dries faster.
The picture above makes it look very complicated, but the only interesting part itself is the press itself, shown at upper left. All the other stuff is unimportant. The intriguing hexagon thing is a a funnel you can stick in the top of the cylinder if you're not sure you can aim the water properly. The scoop is a scoop. The flat thing is for stirring the coffee in the cylinder, in case you don't know how to use a spoon. I threw mine away. The thing on the right is a holder for the unused paper filters. I suspect they were afraid people wouldn't want to pay $30 for just the press, so they bundled in all this extra stuff to make it look like you are getting more than you actually are. In the computer biz we call this “shovelware”.
My review: The AeroPress gets a solid “meh”. You can get a drip cone for five bucks. The advantages of the $30 AeroPress did not materialize for me, and are certainly not worth paying six times as much.
[Other articles in category /tech] permanent link
Wed, 06 Dec 2017As I mentioned before, I have started another
blog, called Content-type:
text/shitpost. While I don't recommend that you read it regularly,
you might want to scan over this list of the articles from November
2017 to see if anything catches your eye.
- FIRST POST!!1!
- The Vampire Flying Frog
- “As the crow flies”
- The ephod
- The uselessness of consistency proofs
- Bertrand Russell's Slack channel
- The Zimbabwean coup
- Non-star multiplication operators
- Canaan Banana
- Shitposting on Math StackExchange
- Colored beans
- How I rate restaurants
- A problem that looks harder than it is
- Dirty jokes that are orientation and gender nonspecific
- My secret identity
- My cute fantasy
- The Wise Men of Princeton
- The Hot Potato
- The fiber guys are here!
- The Hot Potato (addendum)
- Stealing Club
- The kids disappear and then come back
- Head Over Feet
- Intriguing trending hashtags
- Character-building exercises
- What’s the most annoying question to ask a nun in 1967?
- The Garden Court Eatery
- Mixing up left and right
- Mmmm fries
- A vector space over a field of scalars
- People are more than one person
- The most annoying question to ask a nun, explained
- Coma collective
- Computers suck: episode 17771 of 31279
- Abutment for multiplication and other things
- Today's 419 scam is…
- Abutments
- More multiplication by abutment
- Who is a convicted rapist?
- Code reviews
- Bjarne Stroustrup's many crimes against programming
- Colorado Appeals Court goes to Middle School
- Do NOT Resuscitate
I plan to continue to post monthly summaries here.
[Other articles in category /meta/shitpost] permanent link
Fri, 01 Dec 2017
Slaughter electric needle injector

[ This article appeared yesterday on Content-type:
text/shitpost but I decided later
there was nothing wrong with it, so I have moved it here. Apologies
if you are reading it twice. ]
At the end of the game Portal, one of the AI cores you must destroy starts reciting GLaDOS's cake recipe. Like GLaDOS herself, it starts reasonably enough, and then goes wildly off the rails. One of the more memorable ingredients from the end of the list is “slaughter electric needle injector”.
I looked into this a bit and I learned that there really is a slaughter electric needle injector. It is not nearly as ominous as it sounds. The needles themselves are not electric, and it has nothing to do with slaughter. Rather, it is a handheld electric-powered needle injector tool that happens to be manufactured by the Slaughter Instrument Company, Inc, founded more than a hundred years ago by Mr. George Slaughter.
Slaughter Co. manufactures tools for morticians and enbalmers
preparing bodies for burial. The electric needle
injector
is one such tool; they also manufacture a cordless electric needle
injector,
mentioned later as part of the same cake recipe.

The needles themselves are quite benign. They are small, with delicate six-inch brass wires attached, and cost about twenty-five cents each. The needles and the injector are used for securing a corpse's mouth so that it doesn't yawn open during the funeral. One needle is injected into the upper jaw and one into the lower, and then the wires are twisted together, holding the mouth shut. The mortician clips off the excess wire and tucks the ends into the mouth. Only two needles are needed per mouth.
There are a number of explanatory videos on YouTube, but I was not able to find any actual demonstrations.
[Other articles in category /tech] permanent link
Thu, 30 Nov 2017Another public service announcement about Git.
There are a number of commands everyone learns when they first start out using Git. And there are some that almost nobody learns right away, but that should be the first thing you learn once you get comfortable using Git day to day.
One of these has the uninteresting-sounding name git-rev-parse. Git
has a bewildering variety of notations for referring to commits and
other objects. If you type something like origin/master~3, which
commit is that? git-rev-parse is your window into Git's
understanding of names:
% git rev-parse origin/master~3
37f2bc78b3041541bb4021d2326c5fe35cbb5fbb
A pretty frequent question is: How do I find out the commit ID of the current HEAD? And the answer is:
% git rev-parse HEAD
2536fdd82332846953128e6e785fbe7f717e117a
or if you want it abbreviated:
% git rev-parse --short HEAD
2536fdd
But more important than the command itself is the manual for the command. Whether you expect to use this command, you should read its manual. Because every command uses Git's bewildering variety of notations, and that manual is where the notations are completely documented.
When you use a ref name like master, Git finds it in
.git/refs/heads/master, but when you use origin/master, Git finds
it in .git/refs/remotes/origin/master, and when you use HEAD Git
finds it in .git/HEAD. Why the difference? The git-rev-parse
manual explains what Git is doing here.
Did you know that if you have an annoying long branch name like
origin/martin/f42876-change-tracking you can create a short alias
for it by sticking
ref: origin/martin/f42876-change-tracking
into .git/CT, and from then on you can do git log CT or git
rebase --onto CT or whatever?
Did you know that you can write topic@{yesterday} to mean “whatever
commit topic was pointing to yesterday”?
Did you know that you can write ':/penguin system' to refer to the most
recent commit whose commit message mentions the penguin system, and
that 'HEAD:/penguin system' means the most recent such commit on the
HEAD branch?
Did you know that there's a powerful sublanguage for ranges that you can
give to git-log to specify all sorts of useful things about which
commits you want to look at?
Once I got comfortable with Git I got in the habit of rereading the
git-rev-parse manual every few months, because each time I would
notice some new useful tool.
Check it out. It's an important next step.
[ Previous PSAs:
- Two things (beginners ought to know) about Git
- Git remote branches and Git's missing terminology
- Git's rejected push error
]
[Other articles in category /prog] permanent link
Mon, 27 Nov 2017National Coming Out Day began in the U.S. in 1988, and within couple of years I had started to observe it. A queer person, to observe the event, should make an effort, each October 11, to take the next step of coming out of the closet and being more visible, whatever that “next step” happens to be for them.
For some time I had been wearing a little pin that said BISEXUAL QUEER. It may be a bit hard for younger readers of my blog to understand that in 1990 this was unusual, eccentric, and outré, even in the extremely permissive and liberal environment of the University of Pennsylvania. People took notice of it and asked about it; many people said nothing but were visibly startled.
On October 11 of 1991, in one of the few overtly political acts of my life, I posted a carefully-composed manifesto to the department-wide electronic bulletin board, explaining that I was queer, what that meant for me, and why I thought Coming Out Day was important. Some people told me they thought this was brave and admirable, and others told me they thought it was inappropriate.
As I explained in my essay:
It seemed to me that if lots of queer people came out, that would show everyone that there is no reason to fear queers, and that it is not hard at all to live in a world full of queer people — you have been doing it all your life, and it was so easy you didn't even notice! As more and more queers come out of the closet, queerness will become more and more ordinary and commonplace, and people do not have irrational fear of the ordinary and commonplace.
I'm not sure what I would have said if you has asked me in 1991 whether I thought this extravagant fantasy would actually happen. I was much younger and more naïve than I am now and it's possible that I believed that it was certain to happen. Or perhaps I would have been less optimistic and replied with some variant on “maybe, I hope so”, or “probably not but there are other reasons to do it”. But I am sure that if you had asked me when I thought it would happen I would have guessed it would be a very long time, and that I might not live to see it.
Here we are twenty-five years later and to my amazement, this worked.
Holy cow, it worked just like we hoped! Whether I believed it or not at the time, it happened just as I said! This wild fantasy, this cotton-candy dream, had the result we intended. We did it! And it did not take fifty or one hundred years, I did live to see it. I have kids and that is the world they are growing up in. Many things have gotten worse, but not this thing.
It has not yet worked everywhere. But it will. We will keep chipping away at the resistance, one person at a time. It worked before and it will continue to work. There will be setbacks, but we are an unstoppable tide.
In 1991, posting a public essay was considered peculiar or inappropriate. In 2017, it would be eccentric because it would be unnecessary. It would be like posting a long manifesto about how you were going to stop wearing white shirts and start wearing blue ones. Why would anyone make a big deal of something so ordinary?
In 1991 I had queer co-workers whose queerness was an open secret, not generally known. Those people did not talk about their partners in front of strangers, and I was careful to keep them anonymous when I mentioned them. I had written:
This note is also to try to make other queers more comfortable here: Hi! You are not alone! I am here with you!
This had the effect I hoped, at least in some cases; some of those people came to me privately to thank me for my announcement.
At a different job in 1995 my boss had a same-sex partner that he did not mention. I had guessed that this was the case because all the people with opposite-sex partners did mention them. You could figure out who was queer by keeping a checklist in your mind of who had mentioned their opposite-sex partners, dates, or attractions, and then anyone you had not checked off after six months was very likely queer. (Yes, as a bisexual I am keenly aware that this does not always work.) This man and I both lived in Philadelphia, and one time we happened to get off the train together and his spouse was there to meet him. For a moment I saw a terrible apprehension in the face of this confident and self-possessed man, as he realized he would have to introduce me to his husband: How would I respond? What would I say?
In 2017, these people keep pictures on their desks and bring their partners to company picnics. If I met my boss’ husband he would introduce me without apprehension because if I had a problem with it, it would be my problem. In 2017, my doctor has pictures of her wedding and her wife posted on the Internet for anyone in the world to see, not just her friends or co-workers. Around here, at least, Coming Out Day has turned into an obsolete relic because being queer has turned into a big fat nothing.
And it will happen elsewhere also, it will continue to spread. Because if there was reason for optimism in 1991, how much more so now that visible queer people are not a rare minority but a ubiquitous plurality, now that every person encounters some of us every day, we know that this unlikely and even childish plan not only works, but can succeed faster and better than we even hoped?
HA HA HA TAKE THAT, LOSERS.
[Other articles in category /politics] permanent link
Fri, 24 Nov 2017Over the years many people have written to me to tell me they liked my blog but that I should update it more often. Now those people can see if they were correct. I suspect they will agree that they weren't.
I find that, especially since I quit posting to Twitter, there is a
lot of random crap that I share with my co-workers, friends, family,
and random strangers that they might rather do without. I needed a
central dumping ground for this stuff. I am not going to pollute
The Universe of Discourse with this material so I started
a new blog, called
Content-Type: text/shitpost. The
title was inspired by
a tweet of Reid McKenzie
that suggested that there should be a text/shitpost content type. I
instantly wanted to do more with the idea.
WARNING: Shitposts may be pointless, incomplete, poorly considered, poorly researched, offensive, vague, irritating, or otherwise shitty. The label is on the box. If you find yourself wanting to complain about the poor quality of a page you found on a site called shitpost.plover.com, maybe pause for a moment and consider what your life has come to.
I do not recommend that you check it out.
[Other articles in category /meta] permanent link
Wed, 22 Nov 2017
Mathematical pettifoggery and pathological examples
Mathematicians do tend to be the kind of people who quibble and pettifog over the tiniest details. This is because in mathematics, quibbling and pettifogging does work.
This example is technical, but I think I can explain it in a way that will make sense even for people who have no idea what the question is about. Don't worry if you don't understand the next paragraph.
In this math SE question: a user asks for an example of a connected topological space !!\langle X, \tau\rangle!! where there is a strictly finer topology !!\tau'!! for which !!\langle X, \tau'\rangle!! is disconnected. This is a very easy problem if you go about it the right way, and the right way follows a very typical pattern which is useful in many situations.
The pattern is “TURN IT UP TO 11!!” In this case:
- Being disconnected means you can find some things with a certain property.
- If !!\tau'!! is finer than !!\tau!!, that means it has all the same things, plus even more things of the same type.
- If you could find those things in !!\tau!!, you can still find them in !!\tau'!! because !!\tau'!! has everything that !!\tau!! does.
- So although perhaps making !!\tau!! finer could turn a connected space into a disconnected one, by adding the things you needed, it definitely can't turn a disconnected space into a connected one, because the things will still be there.
So a way to look for a connected space that becomes disconnected when !!\tau!! becomes finer is:
Start with some connected space. Then make !!\tau!! fine as you possibly can and see if that is enough.
If that works, you win. If not, you can look at the reason it didn't work, and maybe either fix up the space you started with, or else use that as the starting point in a proof that the thing you're looking for doesn't exist.
I emphasized the important point here. It is: Moving toward finer !!\tau!! can't hurt the situation and might help, so the first thing to try is to turn the fineness knob all the way up and see if that is enough to get what you want. Many situations in mathematics call for subtlety and delicate reasoning, but this is not one of those.
The technique here works perfectly. There is a topology !!\tau_d!! of maximum possible fineness, called the “discrete” topology, so that is the thing to try first. And indeed it answers the question as well as it can be answered: If !!\langle X, \tau\rangle!! is a connected space, and if there is any refinement !!\tau'!! for which !!\langle X, \tau'\rangle!! is disconnected, then !!\langle X, \tau_d\rangle!! will be disconnected. It doesn't even matter what connected space you start with, because !!\tau_d!! is always a refinement of !!\tau!!, and because !!\langle X, \tau_d\rangle!! is always disconnected, except in trivial cases. (When !!X!! has fewer than two points.)
Right after you learn the definition of what a topology is, you are presented with a bunch of examples. Some are typical examples, which showcase what the idea is really about: the “open sets” of the real line topologize the line, so that topology can be used as a tool for studying real analysis. But some are atypical examples, which showcase the extreme limits of the concept that are as different as possible from the typical examples. The discrete space is one of these. What's it for? It doesn't help with understanding the real numbers, that's for sure. It's a tool, it's the knob on the topology machine that turns the fineness all the way up.[1] If you want to prove that the machine does something or other for the real numbers, one way is to show that it always does that thing. And sometimes part of showing that it always does that thing is to show that it does that even if you turn the knob all the way to the right.
So often the first thing a mathematician will try is:
What happens if I turn the knob all the way to the right? If that doesn't blow up the machine, nothing will!
And that's why, when you ask a mathematician a question, often the first thing they will say is “ťhat fails when !!x=0!!” or “that fails when all the numbers are equal” or “ťhat fails when one number is very much bigger than the other” or “that fails when the space is discrete” or “that fails when the space has fewer than two points.” [2]
After the last article, Kyle Littler reminded me that I should not forget the important word “pathological”. One of the important parts of mathematical science is figuring out what the knobs are, how far they can go, what happens if you turn them all the way up, and what are the limits on how they can be set if we want the machine to behave more or less like the thing we are trying to study.
We have this certain knob for how many dents and bumps and spikes we can put on a sphere and have it still be a sphere, as long as we do not actually puncture or tear the surface. And we expected that no matter how far we turned this knob, the sphere would still divide space into two parts, a bounded inside and an unbounded outside, and that these regions should behave basically the same as they do when the sphere is smooth.[3]
But no, we are wrong, the knob goes farther than we thought. If we turn it to the “Alexander horned sphere” setting, smoke starts to come out of the machine and the red lights begin to blink.[4] Useful! Now if someone has some theory about how the machine will behave nicely if this and that knob are set properly, we might be able to add the useful observation “actually you also have to be careful not to turn that “dents bumps and spikes” knob too far.”
The word for these bizarre settings where some of the knobs are in the extreme positions is “pathological”. The Alexander sphere is a pathological embedding of !!S^2!! into !!\Bbb R^3!!.
[1] The leftmost setting on that knob, with the fineness turned all the way down, is called the “indiscrete topology” or the “trivial topology”.
[2] If you claim that any connected space can be disconnected by turning the “fineness” knob all the way to the right, a mathematican will immediately turn the “number of points” knob all the way to the left, and say “see, that only works for spaces with at least two points”. In a space with fewer than two points, even the discrete topology is connected.
[3]For example, if you tie your dog to a post outside the sphere, and let it wander around, its leash cannot get so tangled up with the sphere that you need to walk the dog backwards to untangle it. You can just slip the leash off the sphere.
[4] The dog can get its leash so tangled around the Alexander sphere that the only way to fix it is to untie the dog and start over. But if the “number of dimensions” knob is set to 2 instead of to 3, you can turn the “dents bumps and spikes” knob as far as you want and the leash can always be untangled without untying or moving the dog. Isn't that interesting? That is called the Jordan curve theorem.
[Other articles in category /math] permanent link
An instructive example of expected value
I think this example is very illuminating of something, although I'm not sure yet what.
Suppose you are making a short journey somewhere. You leave two minutes later than planned. How does this affect your expected arrival time? All other things being equal, you should expect to arrive two minutes later than planned. If you're walking or driving, it will probably be pretty close to two minutes no matter what happens.
Now suppose the major part of your journey involves a train that runs every hour, and you don't know just what the schedule is. Now how does your two minutes late departure affect your expected arrival time?
The expected arrival time is still two minutes later than planned. But it is not uniformly distributed. With probability !!\frac{58}{60}!!, you catch the train you planned to take. You are unaffected by your late departure, and arrive at the same time. But with probability !!\frac{2}{60}!! you miss that train and have to take the next one, arriving an hour later than you planned. The expected amount of lateness is
$$0 \text{ minutes}·\frac{58}{60} + 60 \text{ minutes}·\frac{2}{60} = 2 \text{ minutes}$$
the same as before.
[ Addendum: Richard Soderberg points out that one thing illuminated by this example is that the mathematics fails to capture the emotional pain of missing the train. Going in a slightly different direction, I would add that the expected value reduces a complex situation to a single number, and so must necessarily throw out a lot of important information. I discussed this here a while back in connection with lottery tickets.
But also I think this failure of the expected value is also a benefit: it does capture something interesting about the situation that might not have been apparent before: Considering the two minutes as a time investment, there is a sense in which the cost is knowable; it costs exactly two minutes. Yes, there is a chance that you will be hit by a truck that you would not have encountered had you left on time. But this is exactly offset by the hypothetical truck that passed by harmlessly two minutes before you arrived on the scene but which would have hit you had you left on time. ]
[Other articles in category /math] permanent link
Mon, 20 Nov 2017
Mathematical jargon for quibbling
Mathematicians tend not to be the kind of people who shout and pound their fists on the table. This is because in mathematics, shouting and pounding your fist does not work. If you do this, other mathematicians will just laugh at you. Contrast this with law or politics, which do attract the kind of people who shout and pound their fists on the table.
However, mathematicians do tend to be the kind of people who quibble and pettifog over the tiniest details. This is because in mathematics, quibbling and pettifogging does work.
Mathematics has a whole subjargon for quibbling and pettifogging, and also for excluding certain kinds of quibbles. The word “nontrivial” is preeminent here. To a first approximation, it means “shut up and stop quibbling”. For example, you will often hear mathematicians having conversations like this one:
A: Mihăilescu proved that the only solution of Catalan's equation !!a^x - b^y = 1!! is !!3^2 - 2^3!!.
B: What about when !!a!! and !!b!! are consecutive and !!x=y=1!!?
A: The only nontrivial solution.
B: Okay.
Notice that A does not explain what “nontrivial” is supposed to mean here, and B does not ask. And if you were to ask either of them, they might not be able to tell you right away what they meant. For example, if you were to inquire specifically about !!2^1 - 1^y!!, they would both agree that that is also excluded, whether or not that solution had occurred to either of them before. In this example, “nontrivial” really does mean “stop quibbling”. Or perhaps more precisely “there is actually something here of interest, and if you stop quibbling you will learn what it is”.
In some contexts, “nontrivial” does have a precise and technical meaning, and needs to be supplemented with other terms to cover other types of quibbles. For example, when talking about subgroups, “nontrivial” is supplemented with “proper”:
If a nontrivial group has no proper nontrivial subgroup, then it is a cyclic group of prime order.
Here the “proper nontrivial” part is not merely to head off quibbling; it's the crux of the theorem. But the first “nontrivial” is there to shut off a certain type of quibble arising from the fact that 1 is not considered a prime number. By this I mean if you omit “proper”, or the second “nontrivial”, the statement is still true, but inane:
If a nontrivial group has no subgroup, then it is a cyclic group of prime order.
(It is true, but vacuously so.) In contrast, if you omit the first “nontrivial”, the theorem is substantively unchanged:
If a group has no proper nontrivial subgroup, then it is a cyclic group of prime order.
This is still true, except in the case of the trivial group that is no longer excluded from the premise. But if 1 were considered prime, it would be true either way.
Looking at this issue more thoroughly would be interesting and might lead to some interesting conclusions about mathematical methodology.
- Can these terms be taxonomized?
- How do mathematical pejoratives relate? (“Abnormal, irregular, improper, degenerate, inadmissible, and otherwise undesirable”) Kelley says we use these terms to refer to “a problem we cannot handle”; that seems to be a different aspect of the whole story.
- Where do they fit in Lakatos’ Proofs and Refutations theory? Sometimes inserting “improper” just heads off a quibble. In other cases, it points the way toward an expansion of understanding, as with the “improper” polyhedra that violate Euler's theorem and motivate the introduction of the Euler characteristic.
- Compare with the large and finely-wrought jargon that distinguishes between proofs that are “elementary”, “easy”, “trivial”, “straightforward”, or “obvious”.
- Is there a category-theoretic formulation of what it means when we say “without loss of generality, take !!x\lt y!!”?
[ Addendum: Kyle Littler reminds me that I should not forget “pathological”. ]
[ Addendum 20240706: I forgot to mention that I wrote a followup article that discusses why this sort of quibbling is actually useful. ]
[Other articles in category /math] permanent link
Thu, 16 Nov 2017[ Warning: This article is meandering and does not end anywhere in particular ]
My recent article about system software errors kinda blew up the Reddit / Hacker News space, and even got listed on Voat, which I understand is the Group W Bench where they send you if you aren't moral enough to be in Reddit. Many people on these fora were eager to tell war stories of times that they had found errors in the compiler or other infrastructural software.
This morning I remembered another example that had happened to me. In the middle 1990s, I was just testing some network program on one of the Sun Solaris machines that belonged to the Computational Linguistics program, when the entire machine locked up. I had to go into the machine room and power-cycle it to get it to come back up.
I returned to my desk to pick up where I had left off, and the machine locked up, again just as I ran my program. I rebooted the machine again, and putting two and two together I tried the next run on a different, less heavily-used machine, maybe my desk workstation or something.
The problem turned out to be a bug in that version of Solaris: if you bound a network socket to some address, and then tried to connect it to the same address, everything got stuck. I wrote a five-line demonstration program and we reported the bug to Sun. I don't know if it was fixed.
My boss had an odd immediate response to this, something along the lines that connecting a socket to itself is not a sanctioned use case, so the failure is excusable. Channeling Richard Stallman, I argued that no user-space system call should ever be able to crash the system, no matter what stupid thing it does. He at once agreed.
I felt I was on safe ground, because I had in mind the GNU GCC bug reporting instructions of the time, which contained the following unequivocal statement:
If the compiler gets a fatal signal, for any input whatever, that is a compiler bug. Reliable compilers never crash.
I love this paragraph. So clear, so pithy! And the second sentence! It could have been left off, but it is there to articulate the writer's moral stance. It is a rock-firm committment in a wavering and uncertain world.
Stallman was a major influence on my writing for a long time. I first encountered his work in 1985, when I was browsing in a bookstore and happened to pick up a copy of Dr. Dobb's Journal. That issue contained the very first publication of the GNU Manifesto. I had never heard of Unix before, but I was bowled over by Stallman's vision, and I read the whole thing then and there, standing up.
(It hit the same spot in my heart as Albert Szent-Györgyi's The Crazy Ape, which made a similarly big impression on me at about the same time. I think programmers don't take moral concerns seriously enough, and this is one reason why so many of them find Stallman annoying. But this is what I think makes Stallman so important. Perhaps Dan Bernstein is a similar case.)
I have very vague memories of perhaps finding a bug in gcc, which is
perhaps why I was familiar with that particular section of the gcc
documentation. But more likely I just read it because I read
a lot of stuff. Also Stallman was probably on my “read everything he
writes” list.
Why was I trying to connect a socket to itself, anyway? Oh, it was a bug. I meant to connect it somewhere else and used the wrong variable or something. If the operating system crashes when you try, that is a bug. Reliable operating systems never crash.
[ Final note: I looked for my five-line program that connected a
socket to itself, but I could not find it. But I found something
better instead: an email I sent in April 1993 reporting a program that
caused g++ version 2.3.3 to crash with an internal compiler error.
And yes, my report does quote the same passage I quoted above. ]
[Other articles in category /prog] permanent link
Wed, 15 Nov 2017[ Credit where it is due: This was entirely Darius Bacon's idea. ]
In connection with “Recognizing when two arithmetic expressions are essentially the same”, I had several conversations with people about ways to normalize numeric expressions. In that article I observed that while everyone knows the usual associative law for addition $$ (a + b) + c = a + (b + c)$$ nobody ever seems to mention the corresponding law for subtraction: $$ (a+b)-c = a + (b-c).$$
And while everyone “knows” that subtraction is not associative because $$(a - b) - c ≠ a - (b-c)$$ nobody ever seems to observe that there is an associative law for subtraction: $$\begin{align} (a - b) + c & = a - (b - c) \\ (a -b) -c & = a-(b+c).\end{align}$$
This asymmetry is kind of a nuisance, and suggests that a more symmetric notation might be better. Darius Bacon suggested a simple change that I think is an improvement:
Write the negation of !!a!! as $$a\star$$ so that one has, for all !!a!!, $$a+a\star = a\star + a = 0.$$
The !!\star!! operation obeys the following elegant and simple laws: $$\begin{align} a\star\star & = a \\ (a+b)\star & = a\star + b\star \end{align} $$
Once we adopt !!\star!!, we get a huge payoff: We can eliminate subtraction:
Instead of !!a-b!! we now write !!a+b\star!!.
The negation of !!a+b\star!! is $$(a+b\star)\star = a\star + b{\star\star} = a\star +b.$$
We no longer have the annoying notational asymmetry between !!a-b!! and !!-b + a!! where the plus sign appears from nowhere. Instead, one is !!a+b\star!! and the other is !!b\star+a!!, which is obviously just the usual commutativity of addition.
The !!\star!! is of course nothing but a synonym for multiplication by !!-1!!. But it is a much less clumsy synonym. !!a\star!! means !!a\cdot(-1)!!, but with less inkjunk.
In conventional notation the parentheses in !!a(-b)!! are essential and if you lose them the whole thing is ruined. But because !!\star!! is just a special case of multiplication, it associates with multiplication and division, so we don't have to worry about parentheses in !!(a\star)b = a(b\star) = (ab)\star!!. They are all equal to just !!ab\star!!. and you can drop the parentheses or include them or write the terms in any order, just as you like, just as you would with !!abc!!.
The surprising associativity of subtraction is no longer surprising, because $$(a + b) - c = a + (b - c)$$ is now written as $$(a + b) + c\star = a + (b + c\star)$$ so it's just the usual associative law for addition; it is not even disguised. The same happens for the reverse associative laws for subtraction that nobody mentions; they become variations on $$ \begin{align} (a + b\star) + c\star & = a + (b\star + c\star) \\ & = a + (b+c)\star \end{align} $$ and such like.
The !!\star!! is faster to read and faster to say. Instead of “minus one” or “negative one” or “times negative one”, you just say “star”.
The !!\star!! is just a number, and it behaves like a number. Its role in an expression is the same as any other number's. It is just a special, one-off notation for a single, particularly important number.
Open questions:
Do we now need to replace the !!\pm!! sign? If so, what should we replace it with?
Maybe the idea is sound, but the !!\star!! itself is a bad choice. It is slow to write. It will inevitably be confused with the * that almost every programming language uses to denote multiplication.
The real problem here is that the !!-!! symbol is overloaded. Instead of changing the negation symbol to !!\star!! and eliminating the subtraction symbol, what if we just eliminated subtraction? None of the new notation would be incompatible with the old notation: !!-(a+-b) = b+-a!! still means exactly what it used to. But you are no longer allowed to abbreviate it to !!-(a-b) = b-a!!.
This would fix the problem of the !!\star!! taking too long to write: we would just use !!-!! in its place. It would also fix the concern of point 2: !!a\pm b!! now means !!a+b!! or !!a+-b!! which is not hard to remember or to understand. Another happy result: notations like !!-1!! and !!-2!! do not change at all.
Curious footnote: While I was writing up the draft of this article, it had a reminder in it: “How did you and Darius come up with this?” I went back to our email to look, and I discovered the answer was:
- Darius suggested the idea to me.
- I said, “Hey, that's a great idea!”
I wish I could take more credit, but there it is. Hmm, maybe I will take credit for inspiring Darius! That should be worth at least fifty percent, perhaps more.
[ This article had some perinatal problems. It escaped early from the laboratory, in a not-quite-finished state, so I apologize if you are seeing it twice. ]
[Other articles in category /math] permanent link
Sun, 12 Nov 2017
No, it is not a compiler error. It is never a compiler error.
When I used to hang out in the comp.lang.c Usenet group, back when
there was a comp.lang.c Usenet group, people would show up fairly
often with some program they had written that didn't work, and ask if
their compiler had a bug. The compiler did not have a bug. The
compiler never had a bug. The bug was always in the programmer's code
and usually in their understanding of the language.
When I worked at the University of Pennsylvania, a grad student posted to one of the internal bulletin boards looking for help with a program that didn't work. Another graduate student, a super-annoying know-it-all, said confidently that it was certainly a compiler bug. It was not a compiler bug. It was caused by a misunderstanding of the way arguments to unprototyped functions were automatically promoted.
This is actually a subtle point, obscure and easily misunderstood.
Most examples I have seen of people blaming the compiler are much
sillier. I used to be on the mailing list for discussing the
development of Perl 5, and people would show up from time to time to
ask if Perl's if statement was broken. This is a little
mind-boggling, that someone could think this. Perl was first released
in 1987. (How time flies!) The if statement is not exactly an
obscure or little-used feature. If there had been a bug in if it
would have been discovered and fixed by 1988. Again, the bug was
always in the programmer's code and usually in their understanding of
the language.
Here's something I wrote in October 2000,
which I think makes the case very clearly, this time concerning a
claimed bug in the stat() function, another feature that first
appeared in Perl 1.000:
On the one hand, there's a chance that the compiler has a broken
statand is subtracting 6 or something. Maybe that sounds likely to you but it sounds really weird to me. I cannot imagine how such a thing could possibly occur. Why 6? It all seems very unlikely.Well, in the absence of an alternative hypothesis, we have to take what we can get. But in this case, there is an alternative hypothesis! The alternative hypothesis is that [this person's] program has a bug.
Now, which seems more likely to you?
- Weird, inexplicable compiler bug that nobody has ever seen before
or
- Programmer fucked up
Hmmm. Let me think.
I'll take Door #2, Monty.
Presumably I had to learn this myself at some point. A programmer can waste a lot of time looking for the bug in the compiler instead of looking for the bug in their program. I have a file of (obnoxious) Good Advice for Programmers that I wrote about twenty years ago, and one of these items is:
Looking for a compiler bug is the strategy of LAST resort. LAST resort.
Anyway, I will get to the point. As I mentioned a few months ago, I built a simple phone app that Toph and I can use to find solutions to “twenty-four puzzles”. In these puzzles, you are given four single-digit numbers and you have to combine them arithmetically to total 24. Pennsylvania license plates have four digits, so as we drive around we play the game with the license plate numbers we see. Sometimes we can't solve a puzzle, and then we wonder: is it because there is no solution, or because we just couldn't find one? Then we ask the phone app.
The other day we saw the puzzle «5 4 5 1», which is very easy, but I asked the phone app, to find out if there were any other solutions that we missed. And it announced “No solutions.” Which is wrong. So my program had a bug, as my programs often do.
The app has a pre-populated dictionary containing all possible
solutions to all the puzzles that have solutions, which I generated
ahead of time and embedded into the app. My first guess was that bug
had been in the process that generated this dictionary, and that it
had somehow missed the solutions of «5 4 5 1». These would be indexed
under the key 1455, which is the same puzzle, because each list of
solutions is associated with the four input numbers in ascending
order. Happily I still had the original file containing the
dictionary data, but when I looked in it under 1455 I saw exactly
the two solutions that I expected to see.
So then I looked into the app itself to see where the bug was. Code Studio's underlying language is Javascript, and Code Studio has a nice debugger. I ran the app under the debugger, and stopped in the relevant code, which was:
var x = [getNumber("a"), getNumber("b"), getNumber("c"), getNumber("d")].sort().join("");
This constructs a hash key (x) that is used to index into the canned
dictionary of solutions. The getNumber() calls were retrieving the
four numbers from the app's menus, and I verified that the four
numbers were «5 4 5 1» as they ought to be. But what I saw next
astounded me: x was not being set to 1455 as it should have been.
It was set to 4155, which was not in the dictionary. And it was set
to 4155 because
the built-in sort() function
was sorting the numbers
into
the
wrong
order.

For a while I could not believe my eyes. But after another fifteen or thirty minutes of tinkering, I sent off a bug report… no, I did not. I still didn't believe it. I asked the front-end programmers at my company what my mistake had been. Nobody had any suggestions.
Then I sent off a bug report that began:
I think that Array.prototype.sort() returned a wrongly-sorted result when passed a list of four numbers. This seems impossible, but …
I was about 70% expecting to get a reply back explaining what I had
misunderstood about the behavior of Javascript's sort().
But to my astonishment, the reply came back only an hour later:
Wow! You're absolutely right. We'll investigate this right away.
In case you're curious, the bug was as follows: The sort() function
was using a bubble sort. (This is of course a bad choice, and I think
the maintainers plan to replace it.) The bubble sort makes several
passes through the input, swapping items that are out of order. It
keeps a count of the number of swaps in each pass, and if the number
of swaps is zero, the array is already ordered and the sort can stop
early and skip the remaining passes. The test for this was:
if (changes <= 1) break;
but it should have been:
if (changes == 0) break;
Ouch.
The Code Studio folks handled this very creditably, and did indeed fix it the same day. (The support system ticket is available for your perusal, as is the Github pull request with the fix, in case you are interested.)
I still can't quite believe it. I feel as though I have accidentally spotted the Loch Ness Monster, or Bigfoot, or something like that, a strange and legendary monster that until now I thought most likely didn't exist.
A bug in the sort() function. O day and night, but this is wondrous
strange!
[ Addendum 20171113: Thanks to Reddit user spotter for pointing me to a related 2008 blog post of Jeff Atwood's, “The First Rule of Programming: It's Always Your Fault”. ]
[ Addendum 20171113: Yes, yes, I know sort() is in the library, not in the compiler. I am using “compiler error” as a synecdoche
for “system software error”. ]
[ Addendum 20171116: I remembered examples of two other fundamental system software errors I have discovered, including one honest-to-goodness compiler bug. ]
[ Addendum 20200929: Russell O'Connor on a horrifying GCC bug ]
[Other articles in category /prog] permanent link
Sat, 11 Nov 2017
Randomized algorithms go fishing
A little while back I thought of a perfect metaphor for explaining what a randomized algorithm is. It's so perfect I'm sure it must have thought of many times before, but it's new to me.
Suppose you have a lake, and you want to know if there are fish in the lake. You dig some worms, pick a spot, bait the hook, and wait. At the end of the day, if you have caught a fish, you have your answer: there are fish in the lake.[1]
But what if you don't catch a fish? Then you still don't know. Perhaps you used the wrong bait, or fished in the wrong spot. Perhaps you did everything right and the fish happened not to be biting that day. Or perhaps you did everything right except there are no fish in the lake.
But you can try again. Pick a different spot, try a different bait, and fish for another day. And if you catch a fish, you know the answer: the lake does contain fish. But if not, you can go fishing again tomorrow.
Suppose you go fishing every day for a month and you catch nothing. You still don't know why. But you have a pretty good idea: most likely, it is because there are no fish to catch. It could be that you have just been very unlucky, but that much bad luck is unlikely.
But perhaps you're not sure enough. You can keep fishing. If, after a year, you have not caught any fish, you can be almost certain that there were no fish in the lake at all. Because a year-long run of bad luck is extremely unlikely. But if you are still not convinced, you can keep on fishing. You will never be 100% certain, but if you keep at it long enough you can become 99.99999% certain with as many nines as you like.
That is a randomized algorithm, for finding out of there are fish in a lake! It might tell you definitively that there are, by producing a fish. Or it might fail, and then you still don't know. But as long as it keeps failing, the chance that there are any fish rapidly becomes very small, exponentially so, and can be made as small as you like.
For not-metaphorical examples, see:
The Miller-Rabin primality test: Given an odd number K, is K composite? If it is, the Miller-Rabin test will tell you so 75% of the time. If not, you can go fishing again the next day. After n trials, you are either !!100\%!! certain that K is composite, or !!100\%-\frac1{2^{2n}}!! certain that it is prime.
Frievalds’ algorithm: given three square matrices !!A, B, !! and !!C!!, is !!C!! the product !!A×B!!? Actually multiplying !!A×B!! could be slow. But if !!A×B!! is not equal to !!C!!, Frievald's algorithm will quickly tell you that it isn't—half the time. If not, you can go fishing again. After n trials, you are either !!100\%!! certain that !!C!! is not the correct product, or !!100\%-\frac1{2^n}!! certain that it is.
[1] Let us ignore mathematicians’ pettifoggery about lakes that contain exactly one fish. This is just a metaphor. If you are really concerned, you can catch-and-release.
[Other articles in category /CS] permanent link
Tue, 07 Nov 2017
A modern translation of the 1+1=2 lemma

W. Ethan Duckworth of the Department of Mathematics and Statistics at Loyola University translated this into modern notation and has kindly given me permission to publish it here:

I think it is interesting and instructive to compare the two versions. One thing to notice is that there is no perfect translation. As when translating between two natural languages (German and English, say), the meaning cannot be preserved exactly. Whitehead and Russell's language is different from the modern language not only because the notation is different but because the underlying concepts are different. To really get what Principia Mathematica is saying you have to immerse yourself in the Principia Mathematica model of the world.
The best example of this here is the symbol “1”. In the modern translation, this means the number 1. But at this point in Principia Mathematica, the number 1 has not yet been defined, and to use it here would be circular, because proposition ∗54.43 is an important step on the way to defining it. In Principia Mathematica, the symbol “1” represents the class of all sets that contain exactly one element.[1] Following the definition of ∗52.01, in modern notation we would write something like:
$$1 \equiv_{\text{def}} \{x \mid \exists y . x = \{ y \} \}$$
But in many modern universes, that of ZF set theory in particular, there is no such object.[2] The situation in ZF is even worse: the purported definition is meaningless, because the comprehension is unrestricted.
The Principia Mathematica notation for !!|A|!!, the cardinality of set !!A!!, is !!Nc\,‘A!!, but again this is only an approximate translation. The meaning of !!Nc\,‘A!! is something close to
the unique class !!C!! such that !!x\in C!! if and only if there exists a one-to-one relation between !!A!! and !!x!!.
(So for example one might assert that !!Nc\,‘\Lambda = 0!!, and in fact this is precisely what proposition ∗101.1 does assert.) Even this doesn't quite capture the Principia Mathematica meaning, since the modern conception of a relation is that it is a special kind of set, but in Principia Mathematica relations and sets are different sorts of things. (We would also use a one-to-one function, but here there is no additional mismatch between the modern concept and the Principia Mathematica one.)
It is important, when reading old mathematics, to try to understand in modern terms what is being talked about. But it is also dangerous to forget that the ideas themselves are different, not just the language.[3] I extract a lot of value from switching back and forth between different historical views, and comparing them. Some of this value is purely historiological. But some is directly mathematical: looking at the same concepts from a different viewpoint sometimes illuminates aspects I didn't fully appreciate. And the different viewpoint I acquire is one that most other people won't have.
One of my current low-priority projects is reading W. Burnside's important 1897 book Theory of Groups of Finite Order. The value of this, for me, is not so much the group-theoretic content, but in seeing how ideas about groups have evolved. I hope to write more about this topic at some point.
[1] Actually the situation in Principia Mathematica is more complicated. There is a different class 1 defined at each type. But the point still stands.
[2] In ZF, if !!1!! were to exist as defined above, the set !!\{1\}!! would exist also, and we would have !!\{1\} \in 1!! which would contradict the axiom of foundation.
[3] This was a recurring topic of study for Imre Lakatos, most famously in his little book Proofs and Refutations. Also important is his article “Cauchy and the continuum: the significance of nonstandard analysis for the history and philosophy of mathematics.” Math. Intelligencer 1 (1978), #3, p.151–161, which I discussed here earlier, and which you can read in its entireity by paying the excellent people at Elsevier the nominal and reasonable—nay, trivial—sum of only US$39.95.
[Other articles in category /math] permanent link
Thu, 02 Nov 2017
I missed an easy solution to a silly problem
A few years back I wrote a couple of articles about the extremely poor macro plugin I wrote for Blosxom. ([1] [2]). The feature-poorness of the macro system is itself the system's principal feature, since it gives the system simple behavior and simple implementation. Sometimes this poverty means I have to use odd workarounds to get it to do what I want, but they are always simple workarounds and it is never hard to figure out why it didn't do what I wanted.
Yesterday, though, I got stuck. I had defined a macro, ->, which
the macro system would replace with →. Fine. But later in the
file I had an HTML comment:
<!-- blah blah -->
and the macro plugin duly transformed this to
<!-- blah blah -→
creating an unterminated comment.
Normally the way I would deal with this would be to change the name of
the macro from -> to something else that did not conflict with HTML
syntax, but I was curiously resistant to this. I could not think of
anything I wanted to use instead. (After a full night's sleep, it
seems to me that => would have been just fine.)
I then tried replacing --> with -->. I didn't expect
this to work, and indeed it didn't. Those &# escapes only work for
text parts of an HTML document, and cannot be used for HTML syntax.
They remove the special meaning of character sequences, which is the opposite
of what I need here.
Eventually, I just deleted the comment and moved on. That worked, although it was obviously suboptimal. I was too tired to think, and I just wanted the problem out of the way. I wish I had been a little less impulsive, because there are at least two other solutions I overlooked:
I could have defined an
END-HTML-COMMENTmacro that expanded to-->and then used it at the end of the comment. The results of macro expansion are never re-expanded, so the resulting-->would not have been subject to further replacement. This is ugly, but would have done the job, and I have used this sort of technique before.Despite its smallness, the macro plugin has had feature creep over the years, and some of these features I put in and then forgot about. (Bad programmer! No cookie!) One of these lost features is the directive
#undefall, which instructs the plugin to forget all the macro definitions. I could have solved the problem by sticking this in just before the broken comment.(The plugin does not (yet) have a selective
#undef. It would be easy to add, but the module has too many features already.)
Yesterday morning I asked my co-workers if there was an alternative HTML comment syntax, or some way to modify the comment ending sequence so that the macro plugin wouldn't spoil it. (I think there isn't, and a short look at the HTML 5.0 standard didn't suggest any workaround.)
One of the co-workers was Tye McQueen. He said that as far as he knew
there was no fix to the HTML comments that was like what I had asked
for. He asked whether I could define a second macro, -->, which
would expand to -->.
I carefully explained why this wouldn't work: when two macro definitions share a prefix, and they both match, the macro system does not make any guarantee about which substitution it will perform. If there are two overlapping macros, say:
#define pert curt
#define per bloods
then the string pertains might turn into curtains (if the first
substitution is performed) or into bloodstains (if the second is).
But you don't know which it will be, and it might be different each
time. I could fix this, but at present I prefer the answer to be
“don't define a macro that is a prefix of another macro.”
Then M. McQueen gently pointed out that -> is not a prefix of -->.
It is a suffix. My objection does not apply, and his suggestion
solves the problem.
When I write an Oops post I try to think about what lesson I can learn from the mistake. This time there isn't too much, but I do have a couple of ideas:
Before giving up on some piece of software I've written, look to see if I foresaw the problem and put in a feature to deal with it. I have a notion that this would work surprisingly often.
There are two ways to deal with the problem of writing software with too many features, and I have worked on this problem for many years from only one direction: try to write fewer features. But I could also come at it from the opposite direction: try to make better use of the features that I do write.
It feels odd that this should seem to me like a novel idea, but there it is.
Try to get more sleep.
(I haven't published an oops article in far too long, and it certainly isn't because I haven't been making mistakes. I will try to keep it in mind.)
[Other articles in category /oops] permanent link
Tue, 31 Oct 2017
The Blind Spot and the cut rule
[ The Atom and RSS feeds have done an unusually poor job of preserving the mathematical symbols in this article. It will be much more legible if you read it on my blog. ]
Lately I've been enjoying The Blind Spot by Jean-Yves Girard, a very famous logician. (It is translated from French; the original title is Le Point Aveugle.) This is an unusual book. It is solidly full of deep thought and technical detail about logic, but it is also opinionated, idiosyncratic and polemical. Chapter 2 (“Incompleteness”) begins:
It is out of question to enter into the technical arcana of Gödel’s theorem, this for several reasons:
(i) This result, indeed very easy, can be perceived, like the late paintings of Claude Monet, but from a certain distance. A close look only reveals fastidious details that one perhaps does not want to know.
(ii) There is no need either, since this theorem is a scientific cul-de-sac : in fact it exposes a way without exit. Since it is without exit, nothing to seek there, and it is of no use to be expert in Gödel’s theorem.
(The Blind Spot, p. 29)
He continues a little later:
Rather than insisting on those tedious details which «hide the forest», we shall spend time on objections, from the most ridiculous to the less stupid (none of them being eventually respectable).
As you can see, it is not written in the usual dry mathematical-text style, presenting the material as a perfect and aseptic distillation of absolute truth. Instead, one sees the history of logic, the rise and fall of different theories over time, the interaction and relation of many mathematical and philosophical ideas, and Girard's reflections about it all. It is a transcription of a lecture series, and reads like one, including all of the speaker's incidental remarks and offhand musings, but written down so that each can be weighed and pondered at length. Instead of wondering in the moment what he meant by some intriguing remark, then having to abandon the thought to keep up with the lecture, I can pause and ponder the significance. Girard is really, really smart, and knows way more about logic than I ever will, and his offhand remarks reward this pondering. The book is profound in a way that mathematics books often aren't. I wanted to provide an illustrative quotation, but to briefly excerpt a profound thought is to destroy its profundity, so I will have to refrain.[1])
The book really gets going with its discussion of Gentzen's sequent calculus in chapter 3.
Between around 1890 (when Peano and Frege began to liberate logic from its medieval encrustations) and 1935 when the sequent calculus was invented, logical proofs were mainly in the “Hilbert style”. Typically there were some axioms, and some rules of deduction by which the axioms could be transformed into other formulas. A typical example consists of the axioms $$A\to(B\to A)\\ (A \to (B \to C)) \to ((A \to B) \to (A \to C)) $$ (where !!A, B, C!! are understood to be placeholders that can be replaced by any well-formed formulas) and the deduction rule modus ponens: having proved !!A\to B!! and !!A!!, we can deduce !!B!!.
In contrast, sequent calculus has few axioms and many deduction rules. It deals with sequents which are claims of implication. For example: $$p, q \vdash r, s$$ means that if we can prove all of the formulas on the left of the ⊢ sign, then we can conclude some of the formulas on the right. (Perhaps only one, but at least one.)
A typical deductive rule in sequent calculus is:
$$ \begin{array}{c} Γ ⊢ A, Δ \qquad Γ ⊢ B, Δ \\ \hline Γ ⊢ A ∧ B, Δ \end{array} $$
Here !!Γ!! and !!Δ!! represent any lists of formulas, possibly empty. The premises of the rule are:
!!Γ ⊢ A, Δ!!: If we can prove all of the formulas in !!Γ!!, then we can conclude either the formula !!A!! or some of the formulas in !!Δ!!.
!!Γ ⊢ B, Δ!!: If we can prove all of the formulas in !!Γ!!, then we can conclude either the formula !!B!! or some of the formulas in !!Δ!!.
From these premises, the rule allows us to deduce:
!!Γ ⊢ A ∧ B, Δ!!: If we can prove all of the formulas in !!Γ!!, then we can conclude either the formula !!A \land B!! or some of the formulas in !!Δ!!.
The only axioms of sequent calculus are utterly trivial:
$$ \begin{array}{c} \phantom{A} \\ \hline A ⊢ A \end{array} $$
There are no premises; we get this deduction for free: If can prove !!A!!, we can prove !!A!!. (!!A!! here is a metavariable that can be replaced with any well-formed formula.)
One important point that Girard brings up, which I had never realized despite long familiarity with sequent calculus, is the symmetry between the left and right sides of the turnstile ⊢. As I mentioned, the interpretation of !!Γ ⊢ Δ!! I had been taught was that it means that if every formula in !!Γ!! is provable, then some formula in !!Δ!! is provable. But instead let's focus on just one of the formulas !!A!! on the right-hand side, hiding in the list !!Δ!!. The sequent !!Γ ⊢ Δ, A!! can be understood to mean that to prove !!A!!, it suffices to prove all of the formulas in !!Γ!!, and to disprove all the formulas in !!Δ!!. And now let's focus on just one of the formulas on the left side: !!Γ, A ⊢ Δ!! says that to disprove !!A!!, it suffices to prove all the formulas in !!Γ!! and disprove all the formulas in !!Δ!!.
The all-some correspondence, which had previously caused me to wonder why it was that way and not something else, perhaps the other way around, has turned into a simple relationship about logical negation: the formulas on the left are positive, and the ones on the right are negative.[2]) With this insight, the sequent calculus negation laws become not merely simple but trivial:
$$ \begin{array}{cc} \begin{array}{c} Γ, A ⊢ Δ \\ \hline Γ ⊢ \lnot A, Δ \end{array} & \qquad \begin{array}{c} Γ ⊢ A, Δ \\ \hline Γ, \lnot A ⊢ Δ \end{array} \end{array} $$
For example, in the right-hand deduction: what is sufficient to prove !!A!! is also sufficient to disprove !!¬A!!.
(Compare also the rule I showed above for ∧: It now says that if proving everything in !!Γ!! and disproving everything in !!Δ!! is sufficient for proving !!A!!, and likewise sufficient for proving !!B!!, then it is also sufficient for proving !!A\land B!!.)
But none of that was what I planned to discuss; this article is (intended to be) about sequent calculus's “cut rule”.
I never really appreciated the cut rule before. Most of the deductive rules in the sequent calculus are intuitively plausible and so simple and obvious that it is easy to imagine coming up with them oneself.
But the cut rule is more complicated than the rules I have already shown. I don't think I would have thought of it easily:
$$ \begin{array}{c} Γ ⊢ A, Δ \qquad Λ, A ⊢ Π \\ \hline Γ, Λ ⊢ Δ, Π \end{array} $$
(Here !!A!! is a formula and !!Γ, Δ, Λ, Π!! are lists of formulas, possibly empty lists.)
Girard points out that the cut rule is a generalization of modus ponens: taking !!Γ, Δ, Λ!! to be empty and !!Π = \{B\}!! we obtain:
$$ \begin{array}{c} ⊢ A \qquad A ⊢ B \\ \hline ⊢ B \end{array} $$
The cut rule is also a generalization of the transitivity of implication:
$$ \begin{array}{c} X ⊢ A \qquad A ⊢ Y \\ \hline X ⊢ Y \end{array} $$
Here we took !!Γ = \{X\}, Π = \{Y\}!!, and !!Δ!! and !!Λ!! empty.
This all has given me a much better idea of where the cut rule came from and why we have it.
In sequent calculus, the deduction rules all come in pairs. There is a rule about introducing ∧, which I showed before. It allows us to construct a sequent involving a formula with an ∧, where perhaps we had no ∧ before. (In fact, it is the only way to do this.) There is a corresponding rule (actually two rules) for getting rid of ∧ when we have it and we don't want it:
$$ \begin{array}{cc} \begin{array}{c} Γ ⊢ A\land B, Δ \\ \hline Γ ⊢ A, Δ \end{array} & \qquad \begin{array}{c} Γ ⊢ A\land B, Δ \\ \hline Γ ⊢ B, Δ \end{array} \end{array} $$
Similarly there is a rule (actually two rules) about introducing !!\lor!! and a corresponding rule about eliminating it.
The cut rule seems to lie outside this classification. It is not paired.
But Girard showed me that it is part of a pair. The axiom
$$ \begin{array}{c} \phantom{A} \\ \hline A ⊢ A \end{array} $$
can be seen as an introduction rule for a pair of !!A!!s, one on each side of the turnstile. The cut rule is the corresponding rule for eliminating !!A!! from both sides.
Sequent calculus proofs are much easier to construct than Hilbert-style proofs. Suppose one wants to prove !!B!!. In a Hilbert system the only deduction rule is modus ponens, which requires that we first prove !!A\to B!! and !!A!! for some !!A!!. But what !!A!! should we choose? It could be anything, and we have no idea where to start or how big it could be. (If you enjoy suffering, try to prove the simple theorem !!A\to A!! in the Hilbert system I described at the beginning of the article. (Solution)
In sequent calculus, there is only one way to prove each kind of thing, and the premises in each rule are simply related to the consequent we want. Constructing the proof is mostly a matter of pushing the symbols around by following the rules to their conclusions. (Or, if this is impossible, one can conclude that there is no proof, and why.[3]) Construction of proofs can now be done entirely mechanically!
Except! The cut rule does require one to guess a formula: If one wants to prove !!Γ, Λ ⊢ Δ, Π!!, one must guess what !!A!! should appear in the premises !!Γ, A ⊢ Δ!! and !!Λ ⊢ A, Π!!. And there is no constraint at all on !!A!!; it could be anything, and we have no idea where to start or how big it could be.
The good news is that Gentzen, the inventor of sequent calculus, showed that one can dispense with the cut rule: it is unnecessary:
In Hilbert-style systems, based on common sense, the only rule is (more or less) the Modus Ponens : one reasons by linking together lemmas and consequences. We just say that one can get rid of that : it is like crossing the English Channel with fists and feet bound !
(The Blind Spot, p. 61)
Gentzen's demonstration of this shows how one can take any proof that involves the cut rule, and algorithmically eliminate the cut rule from it to obtain a proof of the same result that does not use cut. Gentzen called this the “Hauptsatz” (“principal theorem”) and rightly so, because it reduces construction of logical proofs to an algorithm and is therefore the ultimate basis for algorithmic proof theory.
The bad news is that the cut-elimination process can super-exponentially increase the size of the proof, so it does not lead to a practical algorithm for deciding provability. Girard analyzed why, and what he discovered amazed me. The only problem is in the contraction rules, which had seemed so trivial and innocuous—uninteresting, even—that I had never given them any thought:
$$ \begin{array}{cc} \begin{array}{c} Γ, A, A ⊢ Δ \\ \hline Γ, A ⊢ Δ \end{array} & \qquad \begin{array}{c} Γ ⊢ A, A, Δ \\ \hline Γ ⊢ A, Δ \end{array} \end{array} $$
And suddenly Girard's invention of linear logic made sense to me. In linear logic, contraction is forbidden; one must use each formula in one and only one deduction.
Previously it had seemed to me that this was a pointless restriction. Now I realized that it was no more of a useless hair shirt than the intuitionistic rejection of the law of the proof by contradiction: not a stubborn refusal to use an obvious tool of reasoning, but a restriction of proofs to produce better reasoning. With the rejection of contraction, cut-elimination no longer explodes proof size, and automated theorem proving becomes practical:
This is why its study is, implicitly, at the very heart of these lectures.
(The Blind Spot, p. 63)
The book is going to get into linear logic later in the next chapter. I have read descriptions of linear logic before, but never understood what it was up to. (It has two logical and operators, and two logical or operators; why?) But I am sure Girard will explain it marvelously.
- In place of a profound excerpt, I will present the following, which isn't especially profound but struck a chord for me: “By the way, nothing is more arbitrary than a modal logic « I am done with this logic, may I have another one ? » seems to be the motto of these guys.” (p. 24)
- Compare my alternative representation of arithmetic expressions that collapses addition and subtraction, and multiplication and division.
- A typically Girardian remark is that analytic tableaux are “the poor man's sequents”.
A brief but interesting discussion of The Blind Spot on Hacker News.
[Other articles in category /math/logic] permanent link
Sun, 15 Oct 2017
Counting increasing sequences with Burnside's lemma
[ I started this article in March and then forgot about it. Ooops! ]
Back in February I posted an article about how there are exactly 715 nondecreasing sequences of 4 digits. I said that !!S(10, 4)!! was the set of such sequences and !!C(10, 4)!! was the number of such sequences, and in general $$C(d,n) = \binom{n+d-1}{d-1} = \binom{n+d-1}{n}$$ so in particular $$C(10,4) = \binom{13}{4} = 715.$$
I described more than one method of seeing this, but I didn't mention the method I had found first, which was to use the Cauchy-Frobenius-Redfeld-Pólya-Burnside counting lemma. I explained the lemma in detail some time ago, with beautiful illustrated examples, so I won't repeat the explanation here. The Burnside lemma is a kind of big hammer to use here, but I like big hammers. And the results of this application of the big hammer are pretty good, and justify it in the end.
To count the number of distinct sequences of 4 digits, where some sequences are considered “the same” we first identify a symmetry group whose orbits are the equivalence classes of sequences. Here the symmetry group is !!S_4!!, the group that permutes the elements of the sequence, because two sequences are considered “the same” if they have exactly the same digits but possibly in a different order, and the elements of !!S_4!! acting on the sequences are exactly what you want to permute the elements into some different order.
Then you tabulate how many of the 10,000 original sequences are left fixed by each element !!p!! of !!S_4!!, which is exactly the number of cycles of !!p!!. (I have also discussed cycle classes of permutations before.) If !!p!! contains !!n!! cycles, then !!p!! leaves exactly !!10^n!! of the !!10^4!! sequences fixed.
| Cycle class | Number of cycles | How many permutations? | Sequences left fixed |
 | 4 | 1 | 10,000 |
 | 3 | 6 | 1,000 |
 
| 2 | 3 + 8 = 11 | 100 |

| 1 | 6 | 10 |
| 24 | 17,160 |
(Skip this paragraph if you already understand the table. The four rows above are an abbreviation of the full table, which has 24 rows, one for each of the 24 permutations of order 4. The “How many permutations?” column says how many times each row should be repeated. So for example the second row abbreviates 6 rows, one for each of the 6 permutations with three cycles, which each leave 1,000 sequences fixed, for a total of 6,000 in the second row, and the total for all 24 rows is 17,160. There are two different types of permutations that have two cycles, with 3 and 8 permutations respectively, and I have collapsed these into a single row.)
Then the magic happens: We average the number left fixed by each permutation and get !!\frac{17160}{24} = 715!! which we already know is the right answer.
Now suppose we knew how many permutations there were with each number of cycles. Let's write !!\def\st#1#2{\left[{#1\atop #2}\right]}\st nk!! for the number of permutations of !!n!! things that have exactly !!k!! cycles. For example, from the table above we see that $$\st 4 4 = 1,\quad \st 4 3 = 6,\quad \st 4 2 = 11,\quad \st 4 1 = 6.$$
Then applying Burnside's lemma we can conclude that $$C(d, n) = \frac1{n!}\sum_i \st ni d^i .\tag{$\spadesuit$}$$ So for example the table above computes !!C(10,4) = \frac1{24}\sum_i \st 4i 10^i = 715!!.
At some point in looking into this I noticed that $$\def\rp#1#2{#1^{\overline{#2}}}% \def\fp#1#2{#1^{\underline{#2}}}% C(d,n) = \frac1{n!}\rp dn$$ where !!\rp dn!! is the so-called “rising power” of !!d!!: $$\rp dn = d\cdot(d+1)(d+2)\cdots(d+n-1).$$ I don't think I had a proof of this; I just noticed that !!C(d, 1) = d!! and !!C(d, 2) = \frac12(d^2+d)!! (both obvious), and the Burnside's lemma analysis of the !!n=4!! case had just given me !!C(d, 4) = \frac1{24}(d^4 +6d^3 + 11d^2 + 6d)!!. Even if one doesn't immediately recognize this latter polynomial it looks like it ought to factor and then on factoring it one gets !!d(d+1)(d+2)(d+3)!!. So it's easy to conjecture !!C(d, n) = \frac1{n!}\rp dn!! and indeed, this is easy to prove from !!(\spadesuit)!!: The !!\st n k!! obey the recurrence $$\st{n+1}k = n \st nk + \st n{k-1}\tag{$\color{green}{\star}$}$$ (by an easy combinatorial argument1) and it's also easy to show that the coefficients of !!\rp nk!! obey the same recurrence.2
In general !!\rp nk = \fp{(n+k-1)}k!! so we have !!C(d, n) = \rp dn = \fp{(n+d-1)}n = \binom{n+d-1}d = \binom{n+d-1}{n-1}!! which ties the knot with the formula from the previous article. In particular, !!C(10,4) = \binom{13}9!!.
I have a bunch more to say about this but this article has already been in the oven long enough, so I'll cut the scroll here.
[1] The combinatorial argument that justifies !!(\color{green}{\star})!! is as follows: The Stirling number !!\st nk!! counts the number of permutations of order !!n!! with exactly !!k!! cycles. To get a permutation of order !!n+1!! with exactly !!k!! cycles, we can take one of the !!\st nk!! permutations of order !!n!! with !!k!! cycles and insert the new element into one of the existing cycles after any of the !!n!! elements. Or we can take one of the !!\st n{k-1}!! permutations with only !!k-1!! cycles and add the new element in its own cycle.)
[2] We want to show that the coefficients of !!\rp nk!! obey the same recurrence as !!(\color{green}{\star})!!. Let's say that the coefficient of the !!n^i!! term in !!\rp nk!! is !!c_i!!. We have $$\rp n{k+1} = \rp nk\cdot (n+k) = \rp nk \cdot n + \rp nk \cdot k $$ so the coefficient of the the !!n^i!! term on the left is !!c_{i-1} + kc_i!!.
[Other articles in category /math] permanent link
Wed, 20 Sep 2017
Gompertz' law for wooden utility poles
Gompertz' law says that the human death rate increases exponentially with age. That is, if your chance of dying during this year is !!x!!, then your chance of dying during next year is !!cx!! for some constant !!c>1!!. The death rate doubles every 8 years, so the constant !!c!! is empirically around !!2^{1/8} \approx 1.09!!. This is of course mathematically incoherent, since it predicts that sufficiently old people will have a mortality rate greater than 100%. But a number of things are both true and mathematically incoherent, and this is one of them. (Zipf's law is another.)
The Gravity and Levity blog has a superb article about this from 2009 that reasons backwards from Gompertz' law to rule out certain theories of mortality, such as the theory that death is due to the random whims of a fickle god. (If death were entirely random, and if you had a 50% chance of making it to age 70, then you would have a 25% chance of living to 140, and a 12.5% chance of living to 210, which we know is not the case.)
Gravity and Levity says:
Surprisingly enough, the Gompertz law holds across a large number of countries, time periods, and even different species.
To this list I will add wooden utility poles.
A couple of weeks ago Toph asked me why there were so many old rusty staples embedded in the utility poles near our house, and this is easy to explain: people staple up their yard sale posters and lost-cat flyers, and then the posters and flyers go away and leave behind the staples. (I once went out with a pliers and extracted a few dozen staples from one pole; it was very satisfying but ultimately ineffective.) If new flyer is stapled up each week, that is 52 staples per year, and 1040 in twenty years. If we agree that 20 years is the absolute minimum plausible lifetime of a pole, we should not be surprised if typical poles have hundreds or thousands of staples each.
But this morning I got to wondering what is the expected lifetime of a wooden utility pole? I guessed it was probably in the range of 40 to 70 years. And happily, because of the Wonders of the Internet, I could look it up right then and there, on the way to the trolley stop, and spend my commute time reading about it.
It was not hard to find an authoritative sounding and widely-cited 2012 study by electric utility consultants Quanta Technology.
Summary: Most poles die because of fungal rot, so pole lifetime varies widely depending on the local climate. An unmaintained pole will last 50–60 years in a cold or dry climate and 30-40 years in a hot wet climate. Well-maintained poles will last around twice as long.
Anyway, Gompertz' law holds for wooden utility poles also. According to the study:
Failure and breakdown rates for wood poles are thought to increase exponentially with deterioration and advancing time in service.
The Quanta study presents this chart, taken from the (then forthcoming) 2012 book Aging Power Delivery Infrastructures:
The solid line is the pole failure rate for a particular unnamed utility company in a median climate. The failure rate with increasing age clearly increases exponentially, as Gompertz' law dictates, doubling every 12½ years or so: Around 1 in 200 poles fails at age 50, around 1 in 100 of the remaining poles fails at age 62.5, and around 1 in 50 of the remaining poles fails at age 75.
(The dashed and dotted lines represent poles that are removed from service for other reasons.)
From Gompertz' law itself and a minimum of data, we can extrapolate the maximum human lifespan. The death rate for 65-year-old women is around 1%, and since it doubles every 8 years or so, we find that 50% of women are dead by age 88, and all but the most outlying outliers are dead by age 120. And indeed, the human longevity record is currently attributed to Jeanne Calment, who died in 1997 at the age of 122½.
Similarly we can extrapolate the maximum service time for a wooden utility pole. Half of them make it to 90 years, but if you have a large installed base of 110-year-old poles you will be replacing about one-seventh of them every year and it might make more sense to rip them all out at once and start over. At a rate of one yard sale per week, a 110-year-old pole will have accumulated 5,720 staples.
The Quanta study does not address deterioration of utility poles due to the accumulation of rusty staples.
[ Addendum 20220521: More about utility poles and their maintenance ]
[Other articles in category /tech] permanent link
Sun, 27 Aug 2017This is a collection of leftover miscellanea about twenty-four puzzles. In case you forgot what that is:
The puzzle «4 6 7 9 ⇒ 24» means that one should take the numbers 4, 6, 7, and 9, and combine them with the usual arithmetic operations of addition, subtraction, multiplication, and division, to make the number 24. In this case the unique solution is $$6\times\frac{7 + 9}{4}.$$ When the target number is 24, as it often is, we omit it and just write «4 6 7 9».
Prior articles on this topic:
- A simple but difficult arithmetic puzzle (July 2016)
- Solving twenty-four puzzles (March 2017)
- Recognizing when two arithmetic expressions are essentially the same (August 2017)
How many puzzles have solutions?
For each value of !!T!!, there are 715 puzzles «a b c d ⇒ T». (I discussed this digression in two more earlier articles: [1] [2].) When the target !!T = 24!!, 466 of the 715 puzzles have solutions. Is this typical? Many solutions of «a b c d» puzzles end with a multiplication of 6 and 4, or of 8 and 3, or sometimes of 12 and 2—so many that one quickly learns to look for these types of solutions right away. When !!T=23!!, there won't be any solutions of this type, and we might expect that relatively few puzzles with prime targets have solutions.
This turns out to be the case:
The x-axis is the target number !!T!!, with 0 at the left, 300 at right, and vertical guide lines every 25. The y axis is the number of solvable puzzles out of the maximum possible of 715, with 0 at the bottom, 715 at the top, and horizontal guide lines every 100.
Dots representing prime number targets are colored black. Dots for numbers with two prime factors (4, 6, 9, 10, 14, 15, 21, 22, etc.) are red; dots with three, four, five, six, and seven prime factors are orange, yellow, green, blue, and purple respectively.
Two countervailing trends are obvious: Puzzles with smaller targets have more solutions, and puzzles with highly-composite targets have more solutions. No target number larger than 24 has as many as 466 solvable puzzles.
These are only trends, not hard rules. For example, there are 156 solvable puzzles with the target 126 (4 prime factors) but only 93 with target 128 (7 prime factors). Why? (I don't know. Maybe because there is some correlation with the number of different prime factors? But 72, 144, and 216 have many solutions, and only two different prime factors.)
The smallest target you can't hit is 417. The following numbers 418 and 419 are also impossible. But there are 8 sets of four digits that can be used to make 416 and 23 sets that can be used to make 420. The largest target that can be hit is obviously !!6561 = 9⁴!!; the largest target with two solutions is !!2916 = 4·9·9·9 = 6·6·9·9!!.
(The raw data are available here).
There is a lot more to discover here. For example, from looking at the chart, it seems that the locally-best target numbers often have the form !!2^n3^m!!. What would we see if we colored the dots according to their largest prime factor instead of according to their number of prime factors? (I tried doing this, and it didn't look like much, but maybe it could have been done better.)
Making zero
As the chart shows, 705 of the 715 puzzles of the type «a b c d ⇒ 0», are solvable. This suggests an interesting inverse puzzle that Toph and I enjoyed: find four digits !!a,b,c, d!! that cannot be used to make zero. (The answers).
Identifying interesting or difficult problems
(Caution: this section contains spoilers for many of the most interesting puzzles.)
I spent quite a while trying to get the computer to rank puzzles by difficulty, with indifferent success.
Fractions
Seven puzzles require the use of fractions. One of these is the notorious «3 3 8 8» that I mentioned before. This is probably the single hardest of this type. The other six are:
«1 3 4 6»
«1 4 5 6»
«1 5 5 5»
«1 6 6 8»
«3 3 7 7»
«4 4 7 7»
(Solutions to these (formatted image); solutions to these (plain text))
«1 5 5 5» is somewhat easier than the others, but they all follow pretty much the same pattern. The last two are pleasantly symmetrical.
Negative numbers
No puzzles require the use of negative intermediate values. This surprised me at first, but it is not hard to see why. Subexpressions with negative intermediate values can always be rewritten to have positive intermediate values instead.
For instance, !!3 × (9 + (3 - 4))!! can be rewritten as !!3 × (9 - (4 - 3))!! and !!(5 - 8)×(1 -9)!! can be rewritten as !!(8 - 5)×(9 -1)!!.
A digression about tree shapes
In one of the earlier articles I asserted that there are only two possible shapes for the expression trees of a puzzle solution:
| 
|
| Form A | Form B |
(Pink square nodes contain operators and green round nodes contain numbers.)
Lindsey Kuper pointed out that there are five possible shapes, not two. Of course, I was aware of this (it is a Catalan number), so what did I mean when I said there were only two? It's because I had the idea that any tree that wasn't already in one of those two forms could be put into form A by using transformations like the ones in the previous section.
For example, the expression !!(4×((1+2)÷3))!! isn't in either form, but we can commute the × to get the equivalent !!((1+2)÷3)×4!!, which has form A. Sometimes one uses the associative laws, for example to turn !!a ÷ (b × c)!! into !!(a ÷ b) ÷ c!!.
But I was mistaken; not every expression can be put into either of these forms. The expression !!(8×(9-(2·3))!! is an example.
Unusual intermediate values
The most interesting thing I tried was to look for puzzles whose solutions require unusual intermediate numbers.
For example, the puzzle «3 4 4 4» looks easy (the other puzzles with just 3s and 4s are all pretty easy) but it is rather tricky because its only solution goes through the unusual intermediate number 28: !!4 × (3 + 4) - 4!!.
I ranked puzzles as follows: each possible intermediate number appears in a certain number of puzzle solutions; this is the score for that intermediate number. (Lower scores are better, because they represent rarer intermediate numbers.) The score for a single expression is the score of its rarest intermediate value. So for example !!4 × (3 + 4) - 4!! has the intermediate values 7 and 28. 7 is extremely common, and 28 is quite unusual, appearing in only 151 solution expressions, so !!4 × (3 + 4) - 4!! receives a fairly low score of 151 because of the intermediate 28.
Then each puzzle received a difficulty score which was the score of its easiest solution expression. For example, «2 2 3 8» has two solutions, one (!!(8+3)×2+2!!) involving the quite unusual intermediate value 22, which has a very good score of only 79. But this puzzle doesn't count as difficult because it also admits the obvious solution !!8·3·\frac22!! and this is the solution that gives it its extremely bad score of 1768.
Under this ranking, the best-scoring twenty-four puzzles, and their scores, were:
«1 2 7 7» 3
* «4 4 7 7» 12
* «1 4 5 6» 13
* «3 3 7 7» 14
* «1 5 5 5» 15
«5 6 6 9» 23
«2 5 7 9» 24
«2 2 5 8» 25
«2 5 8 8» 45
«5 8 8 8» 45
«2 2 2 9» 47
* «1 3 4 6» 59
* «1 6 6 8» 59
«2 4 4 9» 151
«3 4 4 4» 151
* «3 3 8 8» 152
«6 8 8 9» 152
«2 2 2 7» 155
«2 2 5 7» 155
«2 3 7 7» 155
«2 4 7 7» 155
«2 5 5 7» 155
«2 5 7 7» 156
«4 4 8 9» 162
(Something is not quite right here. I think «2 5 7 7» and «2 5 5 7» should have the same score, and I don't know why they don't. But I don't care enough to do it over.)
Most of these are at least a little bit interesting. The seven puzzles that require the use of fractions appear; I have marked them with stars. The top item is «1 2 7 7», whose only solution goes through the extremely rare intermediate number 49. The next items require fractions, and the one after that is «5 6 6 9», which I found difficult. So I think there's some value in this procedure.
But is there enough value? I'm not sure. The last item on the list, «4 4 8 9», goes through the unusual number 36. Nevertheless I don't think it is a hard puzzle.
(I can also imagine that someone might see the answer to «5 6 6 9» right off, but find «4 4 8 9» difficult. The whole exercise is subjective.)
Solutions with unusual tree shapes
I thought about looking for solutions that involved unusual sequences of operations. Division is much less common than the other three operations.
To get it right, one needs to normalize the form of expressions, so that the shapes !!(a + b) + (c + d)!! and !!a + (b + (c + d))!! aren't counted separately. The Ezpr library can help here. But I didn't go that far because the preliminary results weren't encouraging.
There are very few expressions totaling 24 that have the form !!(a÷b)÷(c÷d)!!. But if someone gives you a puzzle with a solution in that form, then !!(a×d)÷(b×c)!! and !!(a×d) ÷ (b÷c)!! are also solutions, and one or another is usually very easy to see. For example, the puzzle «1 3 8 9» has the solution !!(8÷1)÷(3÷9)!!, which has an unusual form. But this is an easy puzzle; someone with even a little experience will find the solution !!8 × \frac93 × 1!! immediately.
Similarly there are relatively few solutions of the form !!a÷((b-c)÷d)!!, but they can all be transformed into !!a×d÷(b-c)!! which is not usually hard to find. Consider $$\frac 8{\left(\frac{6 - 4}6\right)}.$$ This is pretty weird-looking, but when you're trying to solve it one of the first things you might notice is the 8, and then you would try to turn the rest of the digits into a 3 by solving «4 6 6 ⇒ 3», at which point it wouldn't take long to think of !!\frac6{6-4}!!. Or, coming at it from the other direction, you might see the sixes and start looking for a way to make «4 6 8 ⇒ 4», and it wouldn't take long to think of !!\frac8{6-4}!!.
Ezpr shape
Ezprs (see previous article) correspond more closely than abstract syntax trees do with our intuitive notion of how expressions ought to work, so looking at the shape of the Ezpr version of a solution might give better results than looking at the shape of the expression tree. For example, one might look at the number of nodes in the Ezpr or the depth of the Ezpr.
Ad-hockery
When trying to solve one of these puzzles, there are a few things I always try first. After adding up the four numbers, I then look for ways to make !!8·3, 6·4,!! or !!12·2!!; if that doesn't work I start branching out looking for something of the type !!ab\pm c!!.
Suppose we take a list of all solvable puzzles, and remove all the very easy ones: the puzzles where one of the inputs is zero, or where one of the inputs is 1 and there is a solution of the form !!E×1!!.
Then take the remainder and mark them as “easy” if they have solutions of the form !!a+b+c+d, 8·3, 6·4,!! or !!12·2!!. Also eliminate puzzles with solutions of the type !!E + (c - c)!! or !!E×\left(\frac cc\right)!!.
How many are eliminated in this way? Perhaps most? The remaining puzzles ought to have at least intermediate difficulty, and perhaps examining just those will suggest a way to separate them further into two or three ranks of difficulty.
I give up
But by this time I have solved so many twenty-four puzzles that I am no longer sure which ones are hard and which ones are easy. I suspect that I have seen and tried to solve most of the 466 solvable puzzles; certainly more than half. So my brain is no longer a reliable gauge of which puzzles are hard and which are easy.
Perhaps looking at puzzles with five inputs would work better for me now. These tend to be easy, because you have more to work with. But there are 2002 puzzles and probably some of them are hard.
Close, but no cigar
What's the closest you can get to 24 without hitting it exactly? The best I could do was !!5·5 - \frac89!!. Then I asked the computer, which confirmed that this is optimal, although I felt foolish when I saw the simpler solutions that are equally good: !!6·4 \pm\frac 19!!.
The paired solutions $$5 × \left(4 + \frac79\right) < 24 < 7 × \left(4 - \frac59\right)$$ are very handsome.
Phone app
The search program that tells us when a puzzle has solutions is only useful if we can take it with us in the car and ask it about license plates. A phone app is wanted. I built one with Code Studio.
Code Studio is great. It has a nice web interface, and beginners can write programs by dragging blocks around. It looks very much like MIT's scratch project, which is much better-known. But Code Studio is a much better tool than Scratch. In Scratch, once you reach the limits of what it can do, you are stuck, and there is no escape. In Code Studio when you drag around those blocks you are actually writing JavaScript underneath, and you can click a button and see and edit the underlying JavaScript code you have written.
Suppose you need to convert A to 1 and B to 2 and so on. Scratch
does not provide an ord function, so with Scratch you are pretty
much out of luck; your only choice is to write a 26-way if-else tree,
which means dragging around something like 104 stupid blocks. In Code
Studio, you can drop down to the JavaScript level and type in ord
to use the standard ord function. Then if you go back to blocks,
the ord will look like any other built-in function block.
In Scratch, if you want to use a data structure other than an array, you are out of luck, because that is all there is. In Code Studio, you can drop down to the JavaScript level and use or build any data structure available in JavaScript.
In Scratch, if you want to initialize the program with bulk data, say a precomputed table of the solutions of the 466 twenty-four puzzles, you are out of luck. In Code Studio, you can upload a CSV file with up to 1,000 records, which then becomes available to your program as a data structure.
In summary, you spend a lot of your time in Scratch working around the limitations of Scratch, and what you learn doing that is of very limited applicability. Code Studio is real programming and if it doesn't do exactly what you want out of the box, you can get what you want by learning a little more JavaScript, which is likely to be useful in other contexts for a long time to come.
Once you finish your Code Studio app, you can click a button to send the URL to someone via SMS. They can follow the link in their phone's web browser and then use the app.
Code Studio is what Scratch should have been. Check it out.
Thanks
Thanks to everyone who contributed to this article, including:
- my daughters Toph and Katara
- Shreevatsa R.
- Dr. Lindsey Kuper
- Darius Bacon
- everyone else who emailed me
[Other articles in category /math] permanent link
Sun, 20 Aug 2017
Recognizing when two arithmetic expressions are essentially the same
[ Warning: The math formatting in the RSS / Atom feed for this article is badly mutilated. I suggest you read the article on my blog. ]
In this article, I discuss “twenty-four puzzles”. The puzzle «4 6 7 9 ⇒ 24» means that one should take the numbers 4, 6, 7, and 9, and combine them with the usual arithmetic operations of addition, subtraction, multiplication, and division, to make the number 24. In this case the unique solution is !!6·\frac{7 + 9}{4}!!.
When the target number after the
⇒is 24, as it often is, we omit it and just write «4 6 7 9». Every example in this article has target number 24.This is a continuation of my previous articles on this topic:
- A simple but difficult arithmetic puzzle (July 2016)
- Solving twenty-four puzzles (March 2017)
My first cut at writing a solver for twenty-four puzzles was a straightforward search program. It had a couple of hacks in it to cut down the search space by recognizing that !!a+E!! and !!E+a!! are the same, but other than that there was nothing special about it and I've discussed it before.
It would quickly and accurately report whether any particular twenty-four
puzzle was solvable, but as it turned out that wasn't quite good
enough. The original motivation for the program was this: Toph and I
play this game in the car. Pennsylvania license plates have three
letters and four digits, and if we see a license plate FBV 2259 we
try to solve «2 2 5 9». Sometimes we can't find a solution and
then we wonder: it is because there isn't one, or is it because we
just didn't get it yet? So the searcher turned into a phone app,
which would tell us whether there was solution, so we'd know whether
to give up or keep searching.
But this wasn't quite good enough either, because after we would find that first solution, say !!2·(5 + 9 - 2)!!, we would wonder: are there any more? And here the program was useless: it would cheerfully report that there were three, so we would rack our brains to find another, fail, ask the program to tell us the answer, and discover to our disgust that the three solutions it had in mind were:
$$ 2 \cdot (5 + (9 - 2)) \\ 2 \cdot (9 + (5 - 2)) \\ 2 \cdot ((5 + 9) - 2) $$
The computer thinks these are different, because it uses different data structures to represent them. It represents them with an abstract syntax tree, which means that each expression is either a single constant, or is a structure comprising an operator and its two operand expressions—always exactly two. The computer understands the three expressions above as having these structures:

| 
| 
|
It's not hard to imagine that the computer could be taught to understand that the first two trees are equivalent. Getting it to recognize that the third one is also equivalent seems somewhat more difficult.
Commutativity and associativity
I would like the computer to understand that these three expressions should be considered “the same”. But what does “the same” mean? This problem is of a kind I particularly like: we want the computer to do something, but we're not exactly sure what that something is. Some questions are easy to ask but hard to answer, but this is the opposite: the real problem is to decide what question we want to ask. Fun!
Certainly some of the question should involve commutativity and associativity of addition and multiplication. If the only difference between two expressions is that one has !!a + b!! where the other has !!b + a!!, they should be considered the same; similarly !!a + (b + c)!! is the same expression as !!(a + b) + c!! and as !!(b + a) + c!! and !!b + (a + c)!! and so forth.
The «2 2 5 9» example above shows that commutativity and associativity are not limited to addition and multiplication. There are commutative and associative properties of subtraction also! For example, $$a+(b-c) = (a+b)-c$$ and $$(a+b)-c = (a-c)+b.$$ There ought to be names for these laws but as far as I know there aren't. (Sure, it's just commutativity and associativity of addition in disguise, but nobody explaining these laws to school kids ever seems to point out that subtraction can enter into it. They just observe that !!(a-b)-c ≠ a-(b-c)!!, say “subtraction isn't associative”, and leave it at that.)
Closely related to these identities are operator inversion identities like !!a-(b+c) = (a-b)-c!!, !!a-(b-c) = (a-b)+c!!, and their multiplicative analogues. I don't know names for these algebraic laws either.
One way to deal with all of this would to build a complicated comparison function for abstract syntax trees that tried to transform one tree into another by applying these identities. A better approach is to recognize that the data structure is over-specified. If we want the computer to understand that !!(a + b) + c!! and !!a + (b + c)!! are the same expression, we are swimming upstream by using a data structure that was specifically designed to capture the difference between these expressions.
Instead, I invented a data structure, called an Ezpr (“Ez-pur”), that can represent expressions, but in a somewhat more natural way than abstract syntax trees do, and in a way that makes commutativity and associativity transparent.
An Ezpr has a simplest form, called its “canonical” or “normal” form. Two Ezprs represent essentially the same mathematical expression if they have the same canonical form. To decide if two abstract syntax trees are the same, the computer converts them to Ezprs, simplifies them, and checks to see if resulting canonical forms are identical.
The Ezpr
Since associativity doesn't matter, we don't want to represent it. When we (humans) think about adding up a long column of numbers, we don't think about associativity because we don't add them pairwise. Instead we use an addition algorithm that adds them all at once in a big pile. We don't treat addition as a binary operation; we normally treat it as an operator that adds up the numbers in a list. The Ezpr makes this explicit: its addition operator is applied to a list of subexpressions, not to a pair. Both !!a + (b + c)!! and !!(a + b) + c!! are represented as the Ezpr
SUM [ a b c - ]
which just says that we are adding up !!a!!, !!b!!, and !!c!!. (The
- sign is just punctuation; ignore it for now.)
Similarly the Ezpr MUL [ a b c ÷ ] represents the product of !!a!!,
!!b!!, and !!c!!. (Please ignore the ÷ sign for the time being.)
To handle commutativity, we want those [ a b c ] lists to be bags.
Perl doesn't have a built-in bag object, so instead I used arrays and
required that the array elements be in sorted order. (Exactly which
sorted order doesn't really matter.)
Subtraction and division
This doesn't yet handle subtraction and division, and the way I chose
to handle them is the only part of this that I think is at all
clever. A SUM object has not one but two bags, one for the positive
and one for the negative part of the expression. An expression like
!!a - b + c - d!! is represented by the Ezpr:
SUM [ a c - b d ]
and this is also the representation of !!a + c - b - d!!, of !!c + a
- d - b!!, of !!c - d+ a-b!!, and of any other expression of the
idea that we are adding up !!a!! and !!c!! and then deducting !!b!!
and !!d!!. The - sign separates the terms that are added from those
that are subtracted.
Either of the two bags may be empty, so for example !!a + b!! is just
SUM [ a b - ].
Division is handled similarly. Here conventional mathematical
notation does a little bit better than in the sum case: MUL [ a c ÷ b
d ] is usually written as !!\frac{ac}{bd}!!.
Ezprs handle the associativity and commutativity of subtraction and division quite well. I pointed out earlier that subtraction has an associative law !!(a + b) - c = a + (b - c)!! even though it's not usually called that. No code is required to understand that those two expressions are equal if they are represented as Ezprs, because they are represented by completely identical structures:
SUM [ a b - c ]
Similarly there is a commutative law for subtraction: !!a + b - c = a - c + b!! and once again that same Ezpr does for both.
Ezpr laws
Ezprs are more flexible than binary trees. A binary tree can represent the expressions !!(a+b)+c!! and !!a+(b+c)!! but not the expression !!a+b+c!!. Ezprs can represent all three and it's easy to transform between them. Just as there are rules for building expressions out of simpler expressions, there are a few rules for combining and manipulating Ezprs.
Lifting and flattening
The most important transformation is lifting, which is the Ezpr
version of the associative law. In the canonical form of an Ezpr, a
SUM node may not have subexpressions that are also SUM nodes. If
you have
SUM [ a SUM [ b c - ] - … ]
you should lift the terms from the inner sum into the outer one:
SUM [ a b c - … ]
effectively transforming !!a+(b+c)!! into !!a+b+c!!. More generally, in
SUM [ a SUM [ b - c ]
- d SUM [ e - f ] ]
we lift the terms from the inner Ezprs into the outer one:
SUM [ a b f - c d e ]
This effectively transforms !!a + (b - c) - d - (e - f))!! to !!a + b + f - c - d - e!!.
Similarly, when a MUL node contains another MUL, we can flatten
the structure.
Say we are converting the expression !!7 ÷ (3 ÷ (6 × 4))!! to an Ezpr. The conversion function is recursive and the naïve version computes this Ezpr:
MUL [ 7 ÷ MUL [ 3 ÷ MUL [ 6 4 ÷ ] ] ]
But then at the bottom level we have a MUL inside a MUL, so the
4 and 6 in the innermost MUL are lifted upward:
MUL [ 7 ÷ MUL [ 3 ÷ 6 4 ] ]
which represents !!\frac7{\frac{3}{6\cdot 4}}!!.
Then again we have a MUL inside a MUL, and again the
subexpressions of the innermost MUL can be lifted:
MUL [ 7 6 4 ÷ 3 ]
which we can imagine as !!\frac{7·6·4}3!!.
The lifting only occurs when the sub-node has the same type as its
parent; we may not lift terms out of a MUL into a SUM or vice
versa.
Trivial nodes
The Ezpr SUM [ a - ] says we are adding up just one thing, !!a!!,
and so it can be eliminated and replaced with just !!a!!. Similarly
SUM [ - a ] can be replaced with the constant !!-a!!, if !!a!! is a
constant. MUL can be handled similarly.
An even simpler case is SUM [ - ] which can be replaced by the
constant 0; MUL [ ÷ ] can be replaced with 1. These sometimes arise
as a result of cancellation.
Cancellation
Consider the puzzle «3 3 4 6». My first solver found 49 solutions to this puzzle. One is !!(3 - 3) + (4 × 6)!!. Another is !!(4 + (3 - 3)) × 6!!. A third is !!4 × (6 + (3 - 3))!!.
I think these are all the same: the solution is to multiply the 4 by the 6, and to get rid of the threes by subtracting them to make a zero term. The zero term can be added onto the rest of expression or to any of its subexpressions—there are ten ways to do this—and it doesn't really matter where.
This is easily explained in terms of Ezprs: If the same subexpression appears in both of a node's bags, we can drop it. For example, the expression !!(4 + (3 -3)) × 6!! starts out as
MUL [ 6 SUM [ 3 4 - 3 ] ÷ ]
but the duplicate threes in SUM [ 3 4 - 3 ] can be canceled, to
leave
MUL [ 6 SUM [ 4 - ] ÷ ]
The sum is now trivial, as described in the previous section, so can be eliminated and replaced with just 4:
MUL [ 6 4 ÷ ]
This Ezpr records the essential feature of each of the three solutions to «3 3 4 6» that I mentioned: they all are multiplying the 6 by the 4, and then doing something else unimportant to get rid of the threes.
Another solution to the same puzzle is !!(6 ÷ 3) × (4 × 3)!!. Mathematically we would write this as !!\frac63·4·3!! and we can see this is just !!6×4!! again, with the threes gotten rid of by multiplication and division, instead of by addition and subtraction. When converted to an Ezpr, this expression becomes:
MUL [ 6 4 3 ÷ 3 ]
and the matching threes in the two bags are cancelled, again leaving
MUL [ 6 4 ÷ ]
In fact there aren't 49 solutions to this puzzle. There is only one, with 49 trivial variations.
Identity elements
In the preceding example, many of the trivial variations on the !!4×6!! solution involved multiplying some subexpression by !!\frac 33!!. When one of the input numbers in the puzzle is a 1, one can similarly obtain a lot of useless variations by choosing where to multiply the 1.
Consider «1 3 3 5»: We can make 24 from !!3 × (3 + 5)!!. We then have to get rid of the 1, but we can do that by multiplying it onto any of the five subexpressions of !!3 × (3 + 5)!!:
$$ 1 × (3 × (3 + 5)) \\ (1 × 3) × (3 + 5) \\ 3 × (1 × (3 + 5)) \\ 3 × ((1 × 3) + 5) \\ 3 × (3 + (1×5)) $$
These should not be considered different solutions.
Whenever we see any 1's in either of the bags of a MUL node,
we should eliminate them.
The first expression above, !!1 × (3 × (3 + 5))!!, is converted to the Ezpr
MUL [ 1 3 SUM [ 3 5 - ] ÷ ]
but then the 1 is eliminated from the MUL node leaving
MUL [ 3 SUM [ 3 5 - ] ÷ ]
The fourth expression, !!3 × ((1 × 3) + 5)!!, is initially converted to the Ezpr
MUL [ 3 SUM [ 5 MUL [ 1 3 ÷ ] - ] ÷ ]
When the 1 is eliminated from the inner MUL, this leaves a trivial
MUL [ 3 ÷ ] which is then replaced with just 3, leaving:
MUL [ 3 SUM [ 5 3 - ] ÷ ]
which is the same Ezpr as before.
Zero terms in the bags of a SUM node can similarly be dropped.
Multiplication by zero
One final case is that MUL [ 0 … ÷ … ] can just be simplified to 0.
The question about what to do when there is a zero in the denominator
is a bit of a puzzle.
In the presence of division by zero, some of our simplification rules
are questionable. For example, when we have MUL [ a ÷ MUL [ b ÷ c ]
], the lifting rule says we can simplify this to MUL [ a c ÷ b
]—that is, that !!\frac a{\frac bc} = \frac{ac}b!!. This is correct,
except that when !!b=0!! or !!c=0!! it may be nonsense, depending on what else is
going on. But since zero denominators never arise in the solution of
these puzzles, there is no issue in this application.
Results
The Ezpr module is around 200 lines of Perl code, including
everything: the function that converts abstract syntax trees to Ezprs,
functions to convert Ezprs to various notations (both MUL [ 4 ÷ SUM [
3 - 2 ] ] and 4 ÷ (3 - 2)), and the two versions of the
normalization process described in the previous section. The
normalizer itself is about 35 lines.
Associativity is taken care of by the Ezpr structure itself, and
commutativity is not too difficult; as I mentioned, it would have been
trivial if Perl had a built-in bag structure. I find it much easier
to reason about transformations of Ezprs than abstract syntax trees.
Many operations are much simpler; for example the negation of
SUM [ A - B ] is simply SUM [ B - A ]. Pretty-printing is also easier
because the Ezpr better captures the way we write and think about
expressions.
It took me a while to get the normalization tuned properly, but the results have been quite successful, at least for this problem domain. The current puzzle-solving program reports the number of distinct solutions to each puzzle. When it reports two different solutions, they are really different; when it fails to support the exact solution that Toph or I found, it reports one essentially the same. (There are some small exceptions, which I will discuss below.)
Since there is no specification for “essentially the same” there is no hope of automated testing. But we have been using the app for several months looking for mistakes, and we have not found any. If the normalizer failed to recognize that two expressions were essentially similar, we would be very likely to notice: we would be solving some puzzle, be unable to find the last of the solutions that the program claimed to exist, and then when we gave up and saw what it was we would realize that it was essentially the same as one of the solutions we had found. I am pretty confident that there are no errors of this type, but see “Arguable points” below.
A harder error to detect is whether the computer has erroneously conflated two essentially dissimilar expressions. To detect this we would have to notice that an expression was missing from the computer's solution list. I am less confident that nothing like this has occurred, but as the months have gone by I feel better and better about it.
I consider the problem of “how many solutions does this puzzle really have to have?” been satisfactorily solved. There are some edge cases, but I think we have identified them.
Code for my solver is on
Github. The Ezpr code
is in the Ezpr package in the Expr.pm
file.
This code is all in the public domain.
Some examples
The original program claims to find 35 different solutions to «4 6 6 6». The revised program recognizes that these are of only two types:
| !!4 × 6 × 6 ÷ 6!! | MUL [ 4 6 - ] |
| !!(6 - 4) × (6 + 6)!! | MUL [ SUM [ 6 - 4 ] SUM [ 6 6 - ] ÷ ] |
Some of the variant forms of the first of those include:
$$
6 × (4 + (6 - 6)) \\
6 + ((4 × 6) - 6) \\
(6 - 6) + (4 × 6) \\
(6 ÷ 6) × (4 × 6) \\
6 ÷ ((6 ÷ 4) ÷ 6) \\
6 ÷ (6 ÷ (4 × 6)) \\
6 × (6 × (4 ÷ 6)) \\
(6 × 6) ÷ (6 ÷ 4) \\
6 ÷ ((6 ÷ 6) ÷ 4) \\
6 × (6 - (6 - 4)) \\
6 × (6 ÷ (6 ÷ 4)) \\
\ldots
$$
In an even more extreme case, the original program finds 80 distinct expressions that solve «1 1 4 6», all of which are trivial variations on !!4·6!!.
Of the 715 puzzles, 466 (65%) have solutions; for 175 of these the solution is unique. There are 3 puzzles with 8 solutions each («2 2 4 8», «2 3 6 9», and «2 4 6 8»), one with 9 solutions («2 3 4 6»), and one with 10 solutions («2 4 4 8»).
The 10 solutions for «2 4 4 8» are as follows:
| !!4 × 8 - 2 × 4 !! | SUM [ MUL [ 4 8 ÷ ] - MUL [ 2 4 ÷ ] ] |
| !!4 × (2 + 8 - 4) !! | MUL [ 4 SUM [ 2 8 - 4 ] ÷ ] |
| !!(8 - 4) × (2 + 4) !! | MUL [ SUM [ 8 - 4 ] SUM [ 2 4 - ] ÷ ] |
| !!4 × (4 + 8) ÷ 2 !! | MUL [ 4 SUM [ 4 8 - ] ÷ 2 ] |
| !!(4 - 2) × (4 + 8) !! | MUL [ SUM [ 4 - 2 ] SUM [ 4 8 - ] ÷ ] |
| !!8 × (2 + 4/4) !! | MUL [ 8 SUM [ 1 2 - ] ÷ ] |
| !!2 × 4 × 4 - 8 !! | SUM [ MUL [ 2 4 4 ÷ ] - 8 ] |
| !!8 + 2 × (4 + 4) !! | SUM [ 8 MUL [ 2 SUM [ 4 4 - ] ÷ ] - ] |
| !!4 + 4 + 2 × 8 !! | SUM [ 4 4 MUL [ 2 8 ÷ ] - ] |
| !!4 × (8 - 4/2) !! | MUL [ 4 SUM [ 8 - MUL [ 4 ÷ 2 ] ] ÷ ] |
A complete listing of every essentially different solution to every «a b c d» puzzle is available here. There are 1,063 solutions in all.
Arguable points
There are a few places where we have not completely pinned down what it means for two solutions to be essentially the same; I think there is room for genuine disagreement.
Any solution involving !!2×2!! can be changed into a slightly different solution involving !!2+2!! instead. These expressions are arithmetically different but numerically equal. For example, I mentioned earlier that «2 2 4 8» has 8 solutions. But two of these are !! 8 + 4 × (2 + 2)!! and !! 8 + 4 × 2 × 2!!. I am willing to accept these as essentially different. Toph, however, disagrees.
A similar but more complex situation arises in connection with «1 2 3 7». Consider !!3×7+3!!, which equals 24. To get a solution to «1 2 3 7», we can replace either of the threes in !!3×7+3!! with !!(1+2)!!, obtaining !!((1 + 2) × 7) + 3!! or !! (3×7)+(1 +2)!!. My program considers these to be different solutions. Toph is unsure.
It would be pretty easy to adjust the normalization process to handle these the other way if the user wanted that.
Some interesting puzzles
«1 2 7 7» has only one solution, quite unusual. (Spoiler) «2 2 6 7» has two solutions, both somewhat unusual. (Spoiler)
Somewhat similar to «1 2 7 7» is «3 9 9 9» which also has an unusual solution. But it has two other solutions that are less surprising. (Spoiler)
«1 3 8 9» has an easy solution but also a quite tricky solution. (Spoiler)
One of my neighbors has the license plate JJZ 4631.
«4 6 3 1» is one of the more difficult puzzles.
What took so long?
I have enough material for at least three or four more articles about this that I hope to publish here in the coming weeks.
But the previous article on this subject ended similarly, saying
I hope to write a longer article about solvers in the next week or so.
and that was in July 2016, so don't hold your breath.
And here we are, five months later!
This article was a huge pain to write. Sometimes I sit down to write something and all that comes out is dreck. I sat down to write this one at least three or four times and it never worked. The tortured Git history bears witness. In the end I had to abandon all my earlier drafts and start over from scratch, writing a fresh outline in an empty file.
But perseverance paid off! WOOOOO.
[ Addendum 20170825: I completely forgot that Shreevatsa R. wrote a very interesting article on the same topic as this one, in July of last year soon after I published my first article in this series. ]
[ Addendum 20170829: A previous version of this article used the notations SUM [ … # … ]
and MUL [ … # … ], which I said I didn't like. Zellyn Hunter has
persuaded me to replace these with SUM [ … - … ] and MUL
[ … ÷ … ]. Thank you M. Hunter! ]
[Other articles in category /math] permanent link
Tue, 08 Aug 2017I should have written about this sooner, by now it has been so long that I have forgotten most of the details.
I first encountered Paul Erdős in the middle 1980s at a talk by János Pach about almost-universal graphs. Consider graphs with a countably infinite set of vertices. Is there a "universal" graph !!G!! such that, for any finite or countable graph !!H!!, there is a copy of !!H!! inside of !!G!!? (Formally, this means that there is an injection from the vertices of !!H!! to the vertices of !!G!! that preserves adjacency.) The answer is yes; it is quite easy to construct such a !!G!! and in fact nearly all random graphs have this property.
But then the questions become more interesting. Let !!K_\omega!! be the complete graph on a countably infinite set of vertices. Say that !!G!! is “almost universal” if it includes a copy of !!H!! for every finite or countable graph !!H!! except those that contain a copy of !!K_\omega!!. Is there an almost universal graph? Perhaps surprisingly, no! (Sketch of proof.)
I enjoyed the talk, and afterward in the lobby I got to meet Ron Graham and Joel Spencer and talk to them about their Ramsey theory book, which I had been reading, and about a problem I was working on. Graham encouraged me to write up my results on the problem and submit them to Mathematics Magazine, but I unfortunately never got around to this. Graham was there babysitting Erdős, who was one of Pach's collaborators, but I did not actually talk to Erdős at that time. I think I didn't recognize him. I don't know why I was able to recognize Graham.
I find the almost-universal graph thing very interesting. It is still an open research area. But none of this was what I was planning to talk about. I will return to the point. A couple of years later Erdős was to speak at the University of Pennsylvania. He had a stock speech for general audiences that I saw him give more than once. Most of the talk would be a description of a lot of interesting problems, the bounties he offered for their solutions, and the progress that had been made on them so far. He would intersperse the discussions with the sort of Erdősism that he was noted for: referring to the U.S. and the U.S.S.R. as “Sam” and “Joe” respectively; his ever-growing series of styles (Paul Erdős, P.G.O.M., A.D., etc.) and so on.
One remark I remember in particular concerned the $3000 bounty he offered for proving what is sometimes known as the Erdős-Túran conjecture: if !!S!! is a subset of the natural numbers, and if !!\sum_{n\in S}\frac 1n!! diverges, then !!S!! contains arbitrarily long arithmetic progressions. (A special case of this is that the primes contain arbitrarily long arithmetic progressions, which was proved in 2004 by Green and Tao, but which at the time was a long-standing conjecture.) Although the $3000 was at the time the largest bounty ever offered by Erdős, he said it was really a bad joke, because to solve the problem would require so much effort that the per-hour payment would be minuscule.
I made a special trip down to Philadelphia to attend the talk, with the intention of visiting my girlfriend at Bryn Mawr afterward. I arrived at the Penn math building early and wandered around the halls to kill time before the talk. And as I passed by an office with an open door, I saw Erdős sitting in the antechamber on a small sofa. So I sat down beside him and started telling him about my favorite graph theory problem.
Many people, preparing to give a talk to a large roomful of strangers, would have found this annoying and intrusive. Some people might not want to talk about graph theory with a passing stranger. But most people are not Paul Erdős, and I think what I did was probably just the right thing; what you don't do is sit next to Erdős and then ask how his flight was and what he thinks of recent politics. We talked about my problem, and to my great regret I don't remember any of the mathematical details of what he said. But he did not know the answer offhand, he was not able solve it instantly, and he did say it was interesting. So! I had a conversation with Erdős about graph theory that was not a waste of his time, and I think I can count that as one of my lifetime accomplishments.
After a little while it was time to go down to the auditorium for the the talk, and afterward one of the organizers saw me, perhaps recognized me from the sofa, and invited me to the guest dinner, which I eagerly accepted. At the dinner, I was thrilled because I secured a seat next to Erdős! But this was a beginner mistake: he fell asleep almost immediately and slept through dinner, which, I learned later, was completely typical.
[Other articles in category /math] permanent link
Sun, 06 Aug 2017Yesterday I discussed an interesting failure on the part of Shazam, a phone app that can recognize music by listening to it. I said I had no idea how it worked, but I did not let that stop me from pulling the following vague speculation out of my butt:
I imagine that it does some signal processing to remove background noise, accumulates digests of short sections of the audio data, and then matches these digests against a database of similar digests, compiled in advance from a corpus of recordings.
Julia Evans provided me with the following reference: “An Industrial-Strength Audio Search Algorithm” by Avery Li-Chun Wang of Shazam Entertainment, Ltd. Unfortunately the paper has no date, but on internal evidence it seems to be from around 2002–2006.
M. Evans summarizes the algorithm as follows:
- find the strongest frequencies in the music and times at which those frequencies happen
- look at pairs !!(freq_1, time_1, freq_2, time_2)!! and turn those into pairs into hashes (by subtracting !!time_1!! from !!time_2!!)
- look up those hashes in your database
She continues:
so basically Shazam will only recognize identical recordings of the same piece of music—if it's a different performance the timestamps the frequencies happen at will likely be different and so the hashes won't match
Thanks Julia!
Moving upwards from the link Julia gave me, I found a folder of papers maintained by Dan Ellis, formerly of the Columbia University Electrical Engineering department, founder of Columbia's LabROSA, the Laboratory for the Recognition and Organization of Speech and Audio, and now a Google research scientist.
In the previous article, I asked about research on machine identification of composers or musical genre. Some of M. Ellis’s LabROSA research is closely related to this. See for example:
There is a lot of interesting-looking material available there for free. Check it out.
(Is there a word for when someone gives you a URL like
http://host/a/b/c/d.html and you start prying into
http://host/a/b/c/ and http://host/a/b/ hoping for more goodies?
If not, does anyone have a suggestion?)
[Other articles in category /tech] permanent link
Sat, 05 Aug 2017
Another example of a machine perception failure
IEEE Spectrum has yet another article about fooling computer vision algorithms with subtle changes that humans don't even notice. For more details and references to the literature, see this excellent article by Andrej Karpathy. Here is a frequently-reprinted example:

The classifier is 57.7% confident that the left-hand image is a panda. When the image is perturbed—by less than one part in 140—with the seemingly-random pattern of colored dots to produce the seemingly identical image on the right, the classifier identifies it as a gibbon with 99.3% confidence.
(Illustration from Goodfellow, Shlens, and Szegedy, “Explaining and Harnessing Adversarial Examples”, International Conference on Learning Representations 2015.)
Here's an interesting complementary example that surprised me recently. I have the Shazam app on my phone. When activated, the app tries to listen for music, and then it tries to tell you what the music was. If I'm in the pharmacy and the background music is something I like but don't recognize, I can ask Shazam what it is, and it will tell me. Magic!
Earlier this year I was in the car listening to the radio and I tried this, and it failed. I ran it again, and it failed again. I pulled over to the side of the road, activated the app, and held the phone's microphone up to the car's speaker so that Shazam could hear clearly. Shazam was totally stumped.
So I resumed driving and paid careful attention when the piece ended so that I wouldn't miss when the announcer said what it was. It had been Mendelssohn's fourth symphony.
Shazam can easily identify Mendelssohn's fourth symphony, as I confirmed later. In fact, it can identify it much better than a human can—in some ways. When I tested it, it immediately recognized not only the piece, but the exact recording I used for the test: it was the 1985 recording by the London Symphony Orchestra, conducted by Claudio Abbado.
Why had Shazam failed to recognize the piece on the radio? Too much background noise? Poor Internet connectivity? Nope. It was because the piece was being performed live by the Detroit Symphony Orchestra and as far as Shazam was concerned, it had never heard it before. For a human familiar with Mendelssohn's fourth symphony, this would be of no import. This person would recognize Mendelssohn's fourth symphony whenever it was played by any halfway-competent orchestra.
But Shazam doesn't hear the way people do. I don't know what it does (really I have no idea), but I imagine that it does some signal processing to remove background noise, accumulates digests of short sections of the audio data, and then matches these digests against a database of similar digests, compiled in advance from a corpus of recordings. The Detroit Orchestra's live performance hadn't been in the corpus, so there was no match in the database.
Shazam's corpus has probably a couple of dozen recordings of Mendelssohn's fourth symphony, but it has no idea that all these recordings are of the same piece, or that they sound very similar, because to Shazam they don't sound similar at all. I imagine it doesn't even have a notion of whether two pieces in the corpus sound similar, because it knows them only as distillations of short snatches, and it never compares corpus recordings with one another. Whatever Shazam is doing is completely different from what people do. One might say it hears the sound but not the music, just as the classifier from the Goodfellow paper sees the image but not the panda.
I wonder about a different example. When I hear an unfamiliar piece on the radio, I can often guess who wrote it. “Aha,” I say. “This is obviously Dvořák.” And then more often than not I am right, and even when I am not right, I am usually very close. (For some reasonable meaning of “close” that might be impossible to explain to Shazam.) In one particularly surprising case, I did this with Daft Punk, at that time having heard exactly two Daft Punk songs in my life. Upon hearing this third one, I said to myself “Huh, this sounds just like those Daft Punk songs.” I not claiming a lot of credit for this; Daft Punk has a very distinctive sound. I bring it up just to suggest that whatever magic Shazam is using probably can't do this even a little bit.
Do any of my Gentle Readers know anything about research on the problem of getting a machine to identify the author or genre of music from listening to it?
[ Addendum 20170806: Julia Evans has provided a technical reference and a high-level summary of Shazam's algorithm. This also led me to a trove of related research. ]
[Other articles in category /tech] permanent link
Mon, 31 Jul 2017
Sabotaged by Polish orthography
This weekend my family was doing a bookstore event related to Fantastic Beasts and Where to Find Them. One of the movie's characters, Jacob Kowalski, dreams of becoming a baker, and arrives to a bank appointment with a suitcase full of Polish confections, including pączki, a sort of Polish jelly donut. My wife wanted to serve these at the event.
The little tail on the ą in pączki is a diacritical mark called an ogonek, which is Polish for “little tail”. If I understand correctly, this nasalizes the sound of the a so that it is more like /an/, and furthermore in modern Polish the value of this particular letter has changed so that pączki is pronounced something like “pawnch-kee”. (Polish “cz” is approximately like English “ch”.)
I was delegated to travel to Philadelphia's Polish neighborhood to obtain the pączki. This turned out to be more difficult than I expected. The first address I visited was simply wrong. When I did find the bakery I was looking for, it was sold out of pączki. The bakery across the street was closed, so I started walking down Allegheny Avenue looking for the next bakery.
Before I got there, though, I passed a storefront with a sign listing its goods and services in blue capital letters. One of the items was PACZKI. Properly, of course, this should be PĄCZKI but Poles often omit the ogonek, especially when buying blue letter decals in Philadelphia, where large blue ogoneks are often unavailable. But when I went in to ask I immediately realized that I had probably made a mistake. The store seemed to sell toiletries, paper goods, and souvenirs, with no baked goods in sight.
I asked anyway: “Your sign outside says you sell PĄCZKI?”
“No,” replied the storekeeper. “Pach-kee.”
I thought she was correcting my pronunciation. “But I thought the ogonek made it ‘pawnch-kee’?”
“No, not pawnch-kee. Pach-kee. For sending, to Poland.” She pointed at a box.
I had misunderstood the sign. It did not say PĄCZKI, but PACZKI, which I have since learned means “boxes”.
The storekeeper directed me to the deli across the street, where I was able to buy the pączki. I also bought some interesting-looking cold roast pork loin and asked what it was called. A customer told me it was “po-lend-witsa”, and from this I was able to pick out the price label on the deli case, which said “POLEDWICA”.
After my embarrassment about the boxes I was concerned that I didn't understand ogoneks as well as I thought I did. I pointed to the ‘E’. “Shouldn't there be an ogonek on the ‘E’ here?”
“Yes,” he said, and shrugged. They had left it off, just as I had (incorrectly) thought had happened on the PACZKI sign.
I think the only way to win this one would have been to understand enough of the items in blue capital letters to guess from context that it really was PACZKI and not PĄCZKI.
Addenda
2017080
A thirty-year-old mystery has been cleared up! When I was a teenager the news was full of the struggles of the Polish workers’ union Solidarity and its charismatic leader, Lech Walesa, later president of Poland. But his name was always pronounced ‘walensa’. Why? Last night I suddenly understood the mysterious ‘n’: the name was actually ‘Walęsa’! ]
[ (Well, not quite. That does explain the mystery ‘n’. But on looking it up, I find that the name is actually ‘Wałęsa’. The ‘W’ is more like English ‘v’ than like English ‘w’, and the ‘ł’ is apparently very much like English ‘w’. So the correct pronunciation of ‘Wałęsa’ is more like ‘va-wen-sa’ than ‘wa-len-sa’. Perhaps the people who pronounced the ę but not the W or the ł were just being pretentious.) ]
20170803
Maciej Cegłowski says that “paczki” is more like “packages” than like “boxes”; Google translate suggests “parcels”. He would also like me to remind you that “paczki” and “pączki” are plural, the singulars being “paczka” and “pączek”, respectively.
Alicja Raszkowska she loves my use of “ogoneks” (the English plural) in place of the Polish “ogonki”. ]
Maciej also says “For Polish speakers, your post is like watching someone dive from a high platform onto a cactus.”
20210710
Today I was looking at a list of common Polish surnames, and one was Dąbrowski. Trying to pronounce this out loud, I suddenly understood where the American name “Dombrowski” comes from. As with pączki (pronounced like “pawnch-kee”), Dąbrowski is pronounced something like “dawm-brovski”, with the nasalization of the /a/ sounding to an Anglophone more like an /m/ than an /n/ because of the following labial consonant. So “Dombrowski” is a pretty good representation English represenation of this name. ]
20240717
Juliusz Chroboczek is the author of a software package that tweaks Postscript files to add correct diacritic marks when printing documents written in ISO 8859-2, such as is used by Polish. It is called Ogonkify.
[Other articles in category /lang] permanent link
Fri, 28 Jul 2017Neal Stephenson's Seveneves is very fat, so I bought it to read on a long trip this summer. I have mixed feelings about Stephenson, but there are a lot of things I like about his writing. A few years ago I wrote a long review of his “Baroque Cycle” in which I said:
People have been complaining for years that Stephenson's books are "too long". But it seems to me now that the real problem with his earlier books is that they were not long enough.
I am a fan of short books. Usually, I agree with the opinion of Jorge Luis Borges, who said “Writing long books is a laborious and impoverishing act of foolishness: expanding in five hundred pages an idea that could be perfectly explained in a few minutes.”
But Stephenson, I think, is one of very few exceptions who does better writing longer books than shorter ones. I said:
Stephenson at 600 pages is a semi-coherent rambler; to really get what he is saying, you have to turn him up to 2,700 pages.
I was interested to see how that bore out in Seveneves. The good news: Stephenson has learned how to write a good 600-page book. The bad news: Seveneves is 900 pages long.
Seveneves is in three parts of roughly equal size. The first two parts deal with an astronomical catastrophe (never explained) that destroys the moon and renders the earth uninhabitable, and with the efforts of humans to establish a space habitat that will outlive the catastrophe. These first two parts told a story with a beginning and an end. They contain a lot of geeky details about the technical aspects of setting up a space habitat, which I enjoyed. I would gladly read any number of 600-page Stephenson books about space technology, an area in which he is an expert. I said ten years ago that his article Mother Earth, Mother Board about undersea telecommunications cables was brilliant. Ten years on, I'm giving it a promotion: it's one of the best nonfiction essays I've ever read on any topic. If you are one of the people who consider the mass of technical detail in Stephenson's novels to be tedious bloat, I think you probably don't want to read Seveneves. But then, if that's you, you probably gave up on Stephenson a long time ago.
Anyway, the first two parts begin with the destruction of the moon, and end with the establishment of the human space colony. Along the way there are many challenges faced by some fairly interesting characters. Had Stephenson stopped there, I think nobody would have complained.
I realized partway through that he was not going to stop there and I was excited. “Aha!” I said. “The book is in four parts! The first two will deal with the establishment of the colony, and then the last two will take place thousands of years in the future, and deal with the resettlement of Earth.” I was pleased with Stephenson's daring: So many writers would have written just the first two parts, and would not been confident enough to go on. Stephenson has many flaws, but an excess of caution is not one of them, and I was looking forward to parts 3 and 4.
Then something went terribly wrong: He wrote part 3, but not part 4.
At the end of part 2, Seveneves takes all the characters and the world of the first two parts, wipes the blackboard clean and starts over. Which would be fine, if what followed was complete and well-developed. But it is only 300 pages long and Stephenson has never been able to write a 300-page story; Stephenson at 300 pages is a blatherer. The 300 pages contains a lot of implausible-seeming stuff about future technology. In 2006 I said that while I loved his long descriptions of real technologies, I found his descriptions of fanciful technology vacuous:
When they're fictitious technologies and imaginary processes, it's just wankery, a powerful exercise of imagination for no real purpose. Well, maybe the idea will work, and maybe it won't, and it is necessarily too vague to really give you a clear idea of what is going on.
Much of the appeal was gone for me. I can enjoy 600 pages of talk about how people in the 21st century would construct the cheapest possible space habitat. I cannot tolerate that much material about how Stephenson imagines people in the 71st century might organize their flying cities.
And the plot is just awful. The new characters are one-dimensional, and they spend most of the third part literally doing nothing. They are assembled into a team of seven by a nebulous authority for some secret purpose; neither they nor we are told what it is. They go from place to place to investigate something or other, making several pointless stops and excursions and wondering, as I did, what was going on and when something was actually going to happen. Nothing happens for 250 pages, and then when finally something does happen there is not enough space left in the book to finish it up, and the novel ends in the air, as so many of Stephenson's novels do.
There were several ways this could have been fixed. The whole third part could have gotten the axe. Considered as a 600-page novel, I think the first two parts of Seveneves are excellent. I said before that “Stephenson at 600 pages is a semi-coherent rambler”. That is clearly no longer true.
Or the third part could have been delayed for a year or two, after Stephenson had first expanded it from 300 to 900 pages and then trimmed it back down to 600 pages. The resulting novel of the 71st century could have been published separately, or the first two parts of Seveneves could have been held back until it was ready; it doesn't matter. In some alternate universe he wrote that second novel and it could be have been really good, even great. The character development might have been better. The mysterious project organizers might have been revealed. We might have gotten some wonderful fish-out-of-water moments with Sonar Taxlaw. (Sonar Taxlaw fanfic, please!) The book could have ended with the characters finding out what actually happened to the moon back on page 1.
So that's my review: once again, people will say this book's great defect was that it was too long, but actually, the real problem is that it was too short.
I used to hope that Stephenson's editors would take him more firmly in hand and make him write books that started in one place and ended in another, but by now I have given up. It is too late. The books keep selling and at this point nobody is going to mess with success.
Having bought Seveneves because of its fatness, I then decided it was too fat to actually carry around on my trip. Instead I took Yoon-Ha Lee's Ninefox Gambit, which is not fat. But it didn't need to be fat, because instead it was so brilliant that when I finished reading the last page I turned back to the first page and started over, something I don't think I have done in the last thirty years.
I may have something more to say about Ninefox Gambit another time; it fits right into an unfinished article I was writing in 2012 about Stephenson's Anathem and Burgess’ A Clockwork Orange.
[ Addendum: It occurred to me on the bus that that putative four-part novel makes sense in another way. The Seven Eves themselves lie at the exact center of the four-part novel, bridging the transition between the first half and the second half, a structure that perfectly justifies the title's palindromic styling as “Seveneves”. Except no, part 4 is missing and the promised symmetry is spoiled. ]
[ Addendum 20191216: I revived an article I wrote in 2002 about Stephenson's first novel The Big U. ]
[Other articles in category /book] permanent link
Mon, 19 Jun 2017On Saturday I posted an article explaining how remote branches and remote-tracking branches work in Git. That article is a prerequisite for this one. But here's the quick summary:
When dealing with a branch (say, master) copied from a remote repository (say, origin), there are three branches one must consider:
The copy of master in the local repository The copy of master in the remote repository The local branch origin/master that records the last known position of the remote branch
Branch 3 is known as a “remote-tracking branch”. This is because it tracks the remote branch, not because it is itself a remote branch. Actually it is a local copy of the remote branch. From now on I will just call it a “tracking branch”.The git-fetch command (green) copies branch (2) to (3).
The git-push command (red) copies branch (1) to (2), and incidentally updates (3) to match the new (2).
The diagram at right summarizes this.
We will consider the following typical workflow:
- Fetch the remote
masterbranch and check it out. - Do some work and commit it on the local
master. - Push the new work back to the remote.
But step 3 fails, saying something like:
! [rejected] master -> master (fetch first)
error: failed to push some refs to '../remote/'
hint: Updates were rejected because the remote contains work that you do
hint: not have locally. This is usually caused by another repository pushing
hint: to the same ref. You may want to first integrate the remote changes
hint: (e.g., 'git pull ...') before pushing again.
hint: See the 'Note about fast-forwards' in 'git push --help' for details.
In older versions of Git the hint was a little shorter:
hint: Updates were rejected because the tip of your current branch is behind
hint: its remote counterpart. Merge the remote changes (e.g. 'git pull')
hint: before pushing again.
hint: See the 'Note about fast-forwards' in 'git push --help' for details.
Everyone at some point gets one of these messages, and in my experience it is one of the most confusing and distressing things for beginners. It cannot be avoided, worked around, or postponed; it must be understood and dealt with.
Not everyone gets a clear explanation. (Reading it over, the actual message seems reasonably clear, but I know many people find it long and frighting and ignore it. It is tough in cases like this to decide how to trade off making the message shorter (and perhaps thereby harder to understand) or longer (and frightening people away). There may be no good solution. But here we are, and I am going to try to explain it myself, with pictures.)
In a large project, the remote branch is always moving, as other
people add to it, and they do this without your knowing about it.
Immediately after you do the fetch in step 1 above, the
tracking branch origin/master reflects the state of the
remote branch. Ten seconds later, it may not; someone else may have
come along and put some more commits on the remote branch in the
interval. This is a fundamental reality that new Git users must
internalize.
Typical workflow
We were trying to do this:
- Fetch the remote
masterbranch and check it out. - Do some work and commit it on the local
master. - Push the new work back to the remote.
and the failure occurred in step 3. Let's look at what each of these operations actually does.
1. Fetch the remote master branch and check it out.
git checkout master
The black circles at the top represent some commits that we want to
fetch from the remote repository. The fetch copies them to the local
repository, and the tracking branch origin/master points to
the local copy. Then we check out master and the local branch
master also points to the local copy.
Branch names like master or origin/master are called “refs”. At
this moment all three refs refer to the same commit (although there are
separate copies in the two repositories) and the three branches have
identical contents.
2. Do some work and commit it on the local master.
git add …
git commit …
…
The blue dots on the local master branch are your new commits. This
happens entirely inside your local repository and doesn't involve the
remote one at all.
But unbeknownst to you, something else is happening where you can't see it. Your collaborators or co-workers are doing their own work in their own repositories, and some of them have published this work to the remote repository. These commits are represented by the red dots in the remote repository. They are there, but you don't know it yet because you haven't looked at the remote repository since they appeared.
3. Push the new work back to the remote.
Here we are trying to push our local master, which means that we are
asking the remote repo to overwrite its master with our local
one. If the remote repo agreed to this, the red commits would be lost
(possibly forever!) and would be completely replaced by the blue
commits. The error message that is the subject of this article is Git
quite properly refusing to fulfill your request:
! [rejected] master -> master (fetch first)
error: failed to push some refs to '../remote/'
hint: Updates were rejected because the remote contains work that you do
hint: not have locally. This is usually caused by another repository pushing
hint: to the same ref. You may want to first integrate the remote changes
hint: (e.g., 'git pull ...') before pushing again.
hint: See the 'Note about fast-forwards' in 'git push --help' for details.
Let's read through that slowly:
Updates were rejected because the remote contains work that you do not have locally.
This refers specifically to the red commits.
This is usually caused by another repository pushing to the same ref.
In this case, the other repository is your co-worker's repo, not shown
in the diagram. They pushed to the same ref (master) before you did.
You may want to first integrate the remote changes (e.g., 'git pull ...') before pushing again.
This is a little vague. There are many ways one could conceivably “integrate the remote changes” and not all of them will solve the problem.
One alternative (which does not integrate the changes) is to use
git push -f. The -f is for “force”, and instructs the remote
repository that you really do want to discard the red commits in favor
of the blue ones. Depending on who owns it and how it is configured,
the remote repository may agree to this and discard the red commits,
or it may refuse. (And if it does agree, the coworker whose commits
you just destroyed may try to feed you poisoned lemonade, so
use -f with caution.)
See the 'Note about fast-forwards' in 'git push --help' for details.
To “fast-forward” the remote ref means that your local branch is a direct forward extension of the remote branch, containing everything that the remote branch does, in exactly the same order. If this is the case, overwriting the remote branch with the local branch is perfectly safe. Nothing will be lost or changed, because the local branch contains everything the remote branch already had. The only change will be the addition of new commits at the end.
There are several ways to construct such a local branch, and choosing between them depends on many factors including personal preference, your familiarity with the Git tool set, and the repository owner's policies. Discussing all of this is outside the scope of the article, so I'll just use one as an example: We are going to rebase the blue commits onto the red ones.
4. Refresh the tracking branch.
The first thing to do is to copy the red commits into the local repo;
we haven't even seen them yet. We do that as before, with
git-fetch. This updates the
tracking branch with a copy of the remote branch
just as it did in step 1.
If instead of git fetch origin master we did git pull --rebase
origin master, Git would do exactly the same fetch, and then
automatically do a rebase as described in the next section. If we did
git pull origin master without --rebase, it would do exactly the
same fetch, and then instead of a rebase it would do a merge, which I
am not planning to describe. The point to remember is that git pull
is just a convenient way to combine the commands of this section and
the next one, nothing more.
5. Rewrite the local changes.
Now is the moment when we “integrate the remote changes” with our own
changes. One way to do this is git rebase origin/master. This tells
Git to try to construct new commits that are just like the blue ones,
but instead of starting from the last black commit, they will start from the
last red one. (For more details about how this works,
see my talk slides about it.)
There are many alternatives here to rebase, some quite elaborate,
but that is a subject for another article, or several other articles.
If none of the files modified in the blue commits have also been modified in any of the red commits, there is no issue and everything proceeds automatically. And if some of the same files are modified, but only in non-overlapping portions, Git can automatically combine them. But if some of the files are modified in incompatible ways, the rebase process will stop in the middle and ask how to proceed, which is another subject for another article. This article will suppose that the rebase completed automatically. In this case the blue commits have been “rebased onto” the red commits, as in the diagram at right.
The diagram is a bit misleading here: it looks as though those black
and red commits appear in two places in the local repository, once on
the local master branch and once on the tracking branch. They don't.
The two branches share those commits, which are stored only once.
Notice that the command is git rebase origin/master. This is
different in form from git fetch origin master or git push origin
master. Why a slash instead of a space? Because with git-fetch or
git-push, we tell it the name of the remote repo, origin, and the
name of the remote branch we want to fetch or push, master. But
git-rebase operates locally and has no use for the name of a remote
repo. Instead, we give it the name of the branch onto which we want to
rebase the new commits. In this case, the target branch is the
tracking branch origin/master.
6. Try the push again.
We try the exact same git push origin master that failed in step 3,
and this time it succeeds, because this time the operation is a
“fast-forward”. Before, our blue commits would have replaced the red
commits. But our rewritten local branch does not have that problem: it
includes the red commits in exactly the same places as they are
already on the remote branch. When the remote repository replaces its
master with the one we are pushing, it loses nothing, because the
red commits are identical. All it needs to do is to add the
blue commits onto the end and then move its master ref forward to
point to the last blue commit instead of to the last red commit. This
is a “fast-forward”.
At this point, the push is successful, and the git-push command also
updates the tracking branch to reflect that the remote branch
has moved forward. I did not show this in the illustration.
But wait, what if someone else had added yet more commits to the
remote master while we were executing steps 4 and 5? Wouldn't our
new push attempt fail just like the first one did? Yes, absolutely!
We would have to repeat steps 4 and 5 and try a third time. It is
possible, in principle, to be completely prevented from pushing
commits to a remote repo because it is always changing so quickly that
you never get caught up on its current state. Repeated push failures
of this type are sign that the project is large enough that
repository's owner needs to set up a more structured code release
mechanism than “everyone lands stuff on master whenever they feel
like it”.
An earlier draft of this article ended at this point with “That is all I have to say about this.” Ha!
Unavoidable problems
Everyone suffers through this issue at some point or another. It is tempting to wonder if Git couldn't somehow make it easier for people to deal with. I think the answer is no. Git has multiple, distributed repositories. To abandon that feature would be to go back to the dark ages of galley slaves, smallpox, and SVN. But if you have multiple distributed anythings, you must face the issue of how to synchronize them. This is intrinsic to distributed systems: two components receive different updates at the same time, and how do you reconcile them?
For reasons I have discussed before, it does not appear possible to automate the reconciliation in every case in a source code control system, because sometimes the reconciliation may require going over to a co-worker's desk and arguing for two hours, then calling in three managers and the CTO and making a strategic decision which then has to be approved by a representative of the legal department. The VCS is not going to do this for you.
I'm going to digress a bit and then come back to the main point.
Twenty-five years ago I taught an introductory programming class in C.
The previous curriculum had tried hard to defer pointers to the middle
of the semester, as K&R does (chapter 7, I think). I decided this was
a mistake. Pointers are everywhere in C and without them you can't
call scanf or pass an array to a function (or access the command-line
arguments or operate on strings or use most of the standard library
or return anything that isn't a
number…). Looking back a few years later I wrote:
Pointers are an essential part of [C's] solution to the data hiding problem, which is an essential issue. Therefore, they cannot be avoided, and in fact should be addressed as soon as possible. … They presented themselves in the earliest parts of the material not out of perversity, but because they were central to the topic.
I developed a new curriculum that began treating pointers early on, as early as possible, and which then came back to them repeatedly, each time elaborating on the idea. This was a big success. I am certain that it is the right way to do it.
(And I've been intending since 2006 to write an article about K&R's crappy discussion of pointers and how its deficiencies and omissions have been replicated down the years by generation after generation of C programmers.)
I think there's an important pedagogical principle here. A good teacher makes the subject as simple as possible, but no simpler. Many difficult issues, perhaps most, can be ignored, postponed, hidden, prevaricated, fudged, glossed over, or even solved. But some must be met head-on and dealt with, and for these I think the sooner they are met and dealt with, the better.
Push conflicts in Git, like pointers in C, are not minor or peripheral; they are an intrinsic and central issue. Almost everyone is going to run into push conflicts, not eventually, but right away. They are going to be completely stuck until they have dealt with it, so they had better be prepared to deal with it right away.
If I were to write a book about Git, this discussion would be in chapter 2. Dealing with merge conflicts would be in chapter 3. All the other stuff could wait.
That is all I have to say about this. Thank you for your kind attention, and thanks to Sumana Harihareswara and AJ Jordan for inspiration.
[Other articles in category /prog] permanent link
Sat, 17 Jun 2017
Git remote branches and Git's missing terminology
Beginning and even intermediate Git users have several common problem areas, and one of these is the relationship between remote and local branches. I think the basic confusion is that it seems like there ought to be two things, the remote branch and the local one, and you copy back and forth between them. But there are not two but three, and the Git documentation does not clearly point this out or adopt clear terminology to distinguish between the three.
Let's suppose we have a remote repository, which could be called
anything, but is typically named origin. And we have a local
repository which has no name; it's just the local repo.
And let's suppose we're working on a branch named master, as one
often does.
There are not two but three branches of interest, and they might all be pointing to different commits:
The branch named
masterin the local repo. This is where we do our work and make our commits. This is the local branch. It is at the lower left in the diagram.The branch named
masterin the remote repo. This is the remote branch, at the top of the diagram. We cannot normally see this at all because it is (typically) on another computer and (typically) requires a network operation to interact with it. So instead, we mainly deal with…The branch named
origin/masterin the local repo. This is the tracking branch, at the lower right in the diagram.We never modify the tracking branch ourselves. It is automatically maintained for us by Git. Whenever Git communicates with the remote repo and learns something about the disposition of the remote
masterbranch, it updates the local branchorigin/masterto reflect what it has learned.
I think this triangle diagram is the first thing one ought to see when
starting to deal with remote repositories and with git-fetch and
git-push.
The Git documentation often calls the tracking branch the “remote-tracking branch”. It is important to understand that the remote-tracking branch is a local branch in the local repository. It is called the “remote-tracking” branch because it tracks the state of the remote branch, not because it is itself remote. From now on I will just call it the “tracking branch”.
Now let's consider a typical workflow:
We use
git fetch origin master. This copies the remote branchmasterfrom the remote repo to the tracking branchorigin/masterin the local repo. This is the green arrow in the diagram.If other people have added commits to the remote
masterbranch since our last fetch, now is when we find out what they are. We can compare the local branchmasterwith the tracking branchorigin/masterto see what is new. We might usegit log origin/masterto see the new commits, orgit diff origin/masterto compare the new versions of the files with the ones we had before. These commands do not look at the remote branch! They look at the copy of the remote branch that Git retrieved for us. If a long time elapses between the fetch and the compare, the actual remote branch might be in a completely different place than when we fetched at it.(Maybe you use
pullinstead offetch. Butpullis exactly likefetchexcept that it doesmergeorrebaseafter the fetch completes. So the process is the same; it merely combines this step and the next step into one command. )We decide how to combine our local master with
origin/master. We might usegit merge origin/masterto merge the two branches, or we might usegit rebase origin/masterto copy our new local commits onto the commits we just fetched. Or we could usegit reset --hard origin/masterto throw away our local commits (if any) and just take the ones on the tracking branch. There are a lot of things that could happen here, but the blue arrow in the diagram shows the general idea: we see new stuff inorigin/masterand update the localmasterto include that new stuff in some way.After doing some more work on the local
master, we want to publish the new work. We usegit push origin master. This is the red arrow in the diagram. It copies the localmasterto the remotemaster, updating the remotemasterin the process. If it is successful, it also updates the tracking branchorigin/masterto reflect the new position of the remotemaster.
In the last step, why is there no slash in git push origin master?
Because origin/master is the name of the tracking branch, and
the tracking branch is not involved. The push command gets
two arguments: the name of the remote (origin) and the branch to
push (master) and then it copies the local branch to the remote one
of the same name.
Deleting a branch
How do we delete branches? For the local branch, it's easy: git
branch -d master does it instantly.
For the tracking branch, we include the -r flag: git branch
-d -r origin/master. This deletes the tracking branch, and
has no effect whatever on the remote repo. This is a very unusual
thing to do.
To delete the remote branch, we have to use git-push because that
is the only way to affect the remote repo. We use git push origin
:master. As is usual with a push, if this is successful Git also
deletes the tracking branch origin/master.
This section has glossed over an important point: git branch -d
master does not delete the master branch, It only deletes the
ref, which is the name for the branch. The branch itself remains.
If there are other refs that refer to it, it will remain as long as
they do. If there are no other refs that point to it, it will be
deleted in due course, but not immediately. Until the branch is
actually deleted, its contents can be recovered.
Hackery
Another way to delete a local ref (whether tracking or not) is just to
go into the repository and remove it. The repository is usually in a
subdirectory .git of your working tree, and if you cd .git/refs
you can see where Git records the branch names and what they refer to.
The master branch is nothing more nor less than a file heads/master
in this directory, and its contents are the commit ID of the commit to
which it refers. If you edit this commit ID, you have pointed the
ref at a different commit. If you remove the file, the ref is
gone. It is that simple.
Tracking branches are similar. The origin/master ref is
in .git/refs/remotes/origin/master.
The remote master branch, of course, is not in your repository at
all; it's in the remote repository.
Poking around in Git's repository is fun and rewarding. (If it
worries you, make another clone of the repo, poke around in the clone,
and throw it away when you are finished poking.) Tinkering with the
refs is a good place to start Git repo hacking: create a couple of
branches, move them around, examine them, delete them again, all
without using git-branch. Git won't know the difference. Bonus fun
activity: HEAD is defined by the file .git/HEAD. When you make a
new commit, HEAD moves forward. How does that
work?
There is a
gitrepository-layout manual
that says what else you can find in the repository.
Failed pushes
We're now in a good position to understand one of the most common problems that Git beginners face: they have committed some work, and they want to push it to the remote repository, but Git says
! [rejected] master -> master (fetch first)
error: failed to push some refs to 'remote'
something something fast-forward, whatever that is
My article explaining this will appear here on Monday. (No, I really mean it.)
Terminology problems
I think one of the reasons this part of Git is so poorly understood is
that there's a lack of good terminology in this area. There needs to
be a way to say "the local branch named master” and “the branch
named master in the remote named origin” without writing a five-
or nine-word phrase every time. The name origin/master looks like
it might be the second of these, but it isn't. The documentation uses
the descriptive but somewhat confusing term “remote-tracking branch”
to refer to it. I think abbreviating this to “tracking branch” would
tend to clear things up more than otherwise.
I haven't though of a good solution to the rest of it yet. It's
tempting to suggest that we should abbreviate “the branch named
master in the remote named origin” to something like
“origin:master” but I think that would be a disaster. It would be
too easy to confuse with origin/master and also with the use of the
colon in the refspec arguments to git-push. Maybe something like
origin -> master that can't possibly be mistaken for part of a shell
command and that looks different enough from origin/master to make
clear that it's related but not the same thing.
Git piles yet another confusion on this:
$ git checkout master
Branch master set up to track remote branch master from origin.
This sounds like it has something to with the remote-tracking branch,
but it does not! It means that the local branch master has been
associated with the remote origin so that fetches and pushes that
pertain to it will default to using that remote.
I will think this over and try to come up with something that sucks a little less. Suggestions are welcome.
[Other articles in category /prog] permanent link
Thu, 15 Jun 2017Rik Signes brought to my attention that since version 5.1 Unicode has contained the following excitingly-named characters:
0C78 ౸ TELUGU FRACTION DIGIT ZERO FOR ODD POWERS OF FOUR
0C79 ౹ TELUGU FRACTION DIGIT ONE FOR ODD POWERS OF FOUR
0C7A ౺ TELUGU FRACTION DIGIT TWO FOR ODD POWERS OF FOUR
0C7B ౻ TELUGU FRACTION DIGIT THREE FOR ODD POWERS OF FOUR
0C7C ౼ TELUGU FRACTION DIGIT ONE FOR EVEN POWERS OF FOUR
0C7D ౽ TELUGU FRACTION DIGIT TWO FOR EVEN POWERS OF FOUR
0C7E ౾ TELUGU FRACTION DIGIT THREE FOR EVEN POWERS OF FOUR
I looked into this a little and found out what they are for. It makes a lot of sense! The details were provided by “Telugu Measures and Arithmetic Marks” by Nāgārjuna Venna.
Telugu is the third-most widely spoken language in India, spoken mostly in the southeast part of the country. Traditional Telugu units of measurement are often divided into four or eight subunits. For example, the tūmu is divided into four kuṁcamulu, the kuṁcamulu, into four mānikalu, and the mānikalu into four sōlalu.
These days they mainly use liters like everyone else. But the traditional measurements are mostly divided into fours, so amounts are written with a base-10 integer part and a base-4 fractional part. The characters above are the base-4 fractional digits.
To make the point clearer, I hope, let's imagine that we are using the Telugu system, but with the familar western-style symbols 0123456789 instead of the Telugu digits ౦౧౨౩౪౫౬౭౮౯. (The Telugu had theirs first of course.) And let's use 0-=Z as our base-four fractional digits, analogous to Telugu ౦౼౽౾. (As in Telugu, we'll use the same zero symbol for both the integer and the fractional parts.) Then to write the number of gallons (7.4805195) in a cubic foot, we say
7.-Z=Z0
which is 7 gallons plus one (-) quart plus three (Z) cups plus two (=) quarter-cups plus three (Z) tablespoons plus zero (0) drams, a total of 7660 drams almost exactly. Or we could just round off to 7.=, seven and a half gallons.
(For the benefit of readers who might be a bit rusty on the details of these traditional European measurements, I should mention that there are four drams in a tablespoon, four tablespoons in a quarter cup, four quarter cups in a cup, four cups in a quart, and four quarts in a gallon, so 4⁵ = 1024 drams in a gallon and 7.4805195·4⁵ = 7660.052 drams in a cubic foot. Note also that these are volume (fluid) drams, not mass drams, which are different.)
We can omit the decimal point (as the Telegu did) and write
7-Z=Z0
and it is still clear where the integer part leaves off and the fraction begins, because we are using special symbols for the fractional part. But no, this isn't quite enough, because if we wrote 20ZZ= it might not be clear whether we meant 20.ZZ= or 2.0ZZ=.
So the system has an elaboration. In the odd positions, we don't use the 0-=Z symbols; we use Q|HN instead. And we don't write 7-Z=Z0, we write
7|ZHZQ
This is always unambiguous: 20.ZZ= is actually written 20NZH and 2.0ZZ= is written 2QZN=, quite different.
This is all fanciful in English, but Telugu actually did this. Instead of 0-=Z they had ౦౼౽౾ as I mentioned before. And instead of Q|HN they had ౸౹౺౻. So if the Telugu were trying to write 7.4805195, where we had 7|ZHZQ they might have written ౭౹౾౺౾౸. Like us, they then appended an abbreviation for the unit of measurement. Instead of “gal.” for gallon they might have put ఘ (letter “gha”), so ౭౹౾౺౾౸ఘ. It's all reasonably straightforward, and also quite sensible. If you have ౭౹౾౺ tūmu, you can read off instantly that there are ౺ (two) sōlalu left over, just as you can see that $7.43 has three pennies left over.
Notice that both sets of Telugu fraction digits are easy to remember: the digits for 3 have either three horizonal strokes ౾ or three vertical strokes ౻, and the others similarly.
I have an idea that the alternating vertical-horizontal system might have served as an error-detection mechanism: if a digit is omitted, you notice right away because the next symbol is wrong.
I find this delightful. A few years back I read all of The Number Concept: Its Origin and Development (1931) by Levi Leonard Conant, hoping to learn something really weird, and I was somewhat disappointed. Conant spends most of his book describing the number words and number systems used by dozens of cultures and almost all of them are based on ten, and a few on five or twenty. (“Any number system which passes the limit 10 is reasonably sure to have either a quinary, a decimal, or a vigesimal structure.”) But he does not mention Telugu!
[ Addendum 20200821: Bengali currency amounts do something similar, but the sections alternate between base-10 and base-4 numerals! ]
[Other articles in category /math] permanent link
Wed, 07 Jun 2017
Annual self-evaluation time, woo-hoo!
It's annual performance evaluation time at my employer, ZipRecruiter, and as part of that I have to write a self-evaluation. I know many people dread these, and I used to dread them, but these days I like doing it. Instead of being a torture or even a chore, for the last couple of years I have come out of it feeling much better about my job and my performance than I went in.
I think that is about 20% because my company does it in a good way, 30% because it suits my personality, and 50% because I have learned how to handle it well. The first half of that might not help you much, but if you're an evaluation loather, you might be able to transfer some of the second half and make it a little less horrible for yourself.
How ZipRecruiter does self-evaluations
I will get this out of the way because it's quick. ZipRecruiter does these evaluations in a way that works well for me. They do not pester me with a million questions. They ask only four, which are roughly:
- What were your main accomplishments this year?
- Describe areas you feel require improvement.
- What do you hope to accomplish in the coming year?
- How can your manager help you?
I very much appreciate this minimalist approach. It gets right to the point, covers all the important issues and nothing more. None of these questions feels to me like a meaningless bureaucratism or a waste of time.
Answering the questions thoroughly takes (only) two or three hours, but would take less if I didn't write such detailed answers; I'm sure I could write an acceptable report in an hour. I can see going in that it will be a finite process.
Why this suits my personality well
If you have followed this blog for a while, you may have noticed that I like writing essays, particularly essays about things I have been working on or thinking about. ZipRecruiter's self-evaluation process invites me to write a blog post about my year's work. This is not everyone's cup of tea, but it is right up my alley. Tea alley. Hee hee.
My brain has problems
My big problems with writing a self-evaluation are first, that I have a very poor memory, and second, that I think of myself as a lazy slacker who spends a lot of time goofing off and who accomplishes very little. These combine badly at evaluation time.
In the past, I would try to remember what work I did in the previous year so I could write it up. My memory is poor, so I wouldn't remember most of what I had done, and then it was easy to come to the conclusion that I had not done very much, probably because I was a lazy slacker whose spent a lot of time goofing off. I would go through several iterations of this, until, tormented by guilt and self-hatred, I would write that into the self-evaluation. This is not a practice I would recommend.
If there were two projects, A and B, and I promptly finished A but B dragged on and was running late, which one would I be more likely to remember when the time came to write the self-evaluation report? B, of course. It was still on my mind because I spent so long thinking about it and because it was still in progress. But I had forgotten about A immediately after putting it to rest. Since I could remember only the unfinished projects, I would conclude that I was a lazy slacker who never finished anything, and write that into the self-evaluation. This is also a a practice I recommend you avoid.
The ticketing system is my bionic brain
The way I have been able to escape this horrible trap is by tracking every piece of work I do, every piece, as a ticket in our ticketing system. People often come to me and ask me to do stuff for them, and I either write up a ticket or I say “sure, write me a ticket”. If they ask why I insist on the ticket (they usually don't), I say it's because when self-evaluation time comes around I want to be able to take credit for working on their problem. Everyone seems to find this reasonable.
Then, when it's time to write the self-evaluation, the first thing I do is visit the ticket website, select all my tickets from the past year, and sort them into chronological order. I look over the list of ticket titles and make a list of stuff that might be worth mentioning on the evaluation. I will have forgotten about three-fourths of it. If I didn't have the list in the ticketing system, I would only remember the most recent one-fourth and conclude that I spent three-fourths of my time goofing off because I am a lazy slacker. Instead, there is this long list of the year's accomplishments, too many to actually include in the report.
Well, this is not rocket science. One is called upon to describe the year's accomplishments. Even people with better memory than me surely cannot remember all this without keeping records, can they? Anyway I surely cannot, so I must keep records and then consult them when the time comes. Put that way, it seems obvious. Why did it take so long to figure out? But there are a lot of happy little details that were not so obvious.
Instead of thinking “Why didn't I finish big project X? I must have been goofing off. What a lazy slacker I am” I think “holy cow, I resolved 67 tickets related to big project X! That is great progress! No wonder I got hardly anything else done last fall” and also “holy cow, X has 78 resolved tickets and 23 still open. It is huge! No wonder it is not finished yet.”
Writing “I completed 67 tickets related to X” is a lot more concrete than “I worked hard on X”. If you are neurotic in the way I am, and concerned that you might be a lazy slacker, it feels much more persuasive. I have an idea that it sounds better to my boss also, particularly if he were to be called upon to discuss it with his manager. (“Under my leadership, Mark completed 67 tickets related to X!”) Andy Lester says that your job is to make your boss happy, and that means making it easy for him to do his job, which is to make his boss happy. So this is no small thing.
Instead of thinking “Gee, the CTO declared top priority initiative Y, and while everyone else was working hard on it I mostly ignored it because I am a lazy slacker” I might see that I have tagged 9 tickets “top priority initiative Y”. Then on the report, I proudly boast “I completed 9 tickets in support of the CTO's mandate, including (most important one) and (most impressive one).” This also comes under the heading of “make it easy for your boss to do his job”.
Instead of completely forgetting that I did project Z, I see the tickets and can put it in my report.
Instead of remembering awful project W, which dragged on for months, and thinking what a lazy slacker I was because I couldn't get it done, I have a progress record in the ticket and the details might suggest a different interpretation: Project W sucked, but I nevertheless pursued it doggedly to completion, even though it took months.
I might remember that I once helped Jones, but what did I help him with? Did I really spend much time on him? Without looking at the ticket list, I might not realize that I helped Jones every few weeks all year long. This sort of pattern is often apparent only in the retrospective summary. With the ticket system, instead of “oh, Jones sometimes asks me questions, I guess” I can see that supporting Jones was an ongoing thing and he kept coming back. This goes into the report: “I provided ongoing support to Jones, including (some cherry-picked example that makes me look especially good).”
One question (#2) on the report form is “Describe areas you feel require improvement”. If I wrote in last year's report that I would like to improve at doing X, I can look in the ticket system for specific evidence that I might have improved, even if I wasn't consciously trying to improve X at the time. Probably there is something somewhere that can at least be spun as an attempt to improve at X. And if it didn't actually improve X, I can still ask myself why it didn't and what might work instead, and put that in the report as something to try next time, which is question #3.
Hey, look at that, I am evaluating my prior performance and making informed corrections. That might be a useful practice. Wouldn't it be great if I took time every so often to do that? Some sort of periodic self-evaluation perhaps?
Another question (#3) is “What would you like to do in the coming year?” If I wrote in last year's report said “I would like to do more of X” I can look for evidence that I did do that, and then write it into this year's report: “Last year I said I would try to do more of X, and I did.”
Even if I were having a bad year and got very little done—and this has happened—having a list of the stuff I did get done leaves me in a much better position to write the report than not having such a list.
None of this good stuff would be possible without an actual record of what I did. If there weren't a ticketing system, I would have to invent one or maybe tattoo it on my chest like the guy in Memento. Even aside from its use in writing annual self-evaluations, keeping a work diary is crucial for me, because without it I can't remember day-to-day what I am working on and what needs to happen next. And even for people with better memory than me, are they really going to remember all 317 things they did for work this year, or that 67 of them pertained to big project X? If they can that's great but I doubt it.
Keeping a work record is part of my job
I think it is important to maintain the correct attitude to this. It would be easy to imagine ticket management as unproductive time that I wasted instead of accomplishing something useful. This is wrong. The correct attitude is to consider ticket updates to be part of my work product: I produce code. I produce bug fixes. I produce documentation, reports, and support interactions. And I also produce ticket updates. This is part of my job and while I am doing it I am not goofing off, I am not procrastinating, I am doing my job and earning my salary. If I spent the whole day doing nothing but updating tickets, that would be a day well-spent.
Compare “I produce ticket updates” with “I produce unit tests”. The attitude for ticket updates is the same as for testing. When something happens in a project, I update the ticket, because keeping the tickets updated is part of the project, just like writing tests is. An organization that fails to support ticket updates is broken in the same way as one that fails to support test development.
My boss gets email every time I update a ticket. I don't know if he reads these, but he has the option to, and I don't need to worry as much that maybe he thinks I am a lazy slacker who is goofing off, because he is getting a stream of automatic notifications about what I am up to. I'm not my boss but if I were I would appreciate this very much.
Maybe some of this can help you?
There might be some use in this even for people who aren't already in the habit of writing self-absorbed blog posts.
If doing the annual self-evaluation makes you suffer, maybe it would help to practice writing some blog posts. You don't have to publish them or show anyone. Next time you finish a project, set aside thirty or sixty minutes to try to write up a little project report: What worked, what didn't, what are you pleased about, what was surprising, what was fun, what was annoying? I'm not certain this will help but it seems like this is a skill that might get easier with practice, and then when you have to write your annual self-evaluation it might be easier because you have more practice doing it. Also, you would have a little file of material to draw on and would not have to start from zero.
If your employer's process requires you to fill in some giant questionnaire, it might be easier to do if you go into it with answers to the four basic questions prepared ahead of time. (I imagine that it's even possible that if you address the four big questions and ignore everything on the giant questionnaire that doesn't pertain to them, everyone will be perfectly satisfied and nobody will notice the omissions.)
And keep a work diary! Tattoo it on your chest if you have to. If it seems daunting, realize that you don't have to do it all at once. Keeping a work diary of some sort is forgiving in the same way as writing unit tests:
It's not all-or-nothing, you don't have to test every piece of code to get any benefit from testing. If you write tests for 1% of the code, you get about 1% of the benefit, and you can ramp up.
If you break your test-writing streak you don't have to start over from zero. If you didn't write any tests for the code you wrote last week, that's a shame, but it doesn't affect the benefit you can get from writing a unit test for whatever you're working on today.
The work diary is similar. When time comes to write your evaluation, a small and incomplete record is better than no record at all. If you forget to write in the diary for a month, that's a shame, but it doesn't affect the benefit you can get from writing down today what you did today.
Our ticketing system
This isn't important, but I expect someone will want to know: At work we use FogBugz. Some of my co-workers dislike it but I have no major complaints. If you want to try it on your own, they have a seven-day free trial offer, after which you can sign up for a permanent free account that supports up to two users. I am experimenting with using a free tier account to manage my personal to-do list.
Coming soon
I wrote another 2,000 words about my specific practices for managing tickets. I hope it'll be along in a few days.
[ Addendum 20190701: Julia Evans has written an article on the same topic, but with more details, useful suggestions I hadn't thought of, and also without all the neurosis.
I don't know why I haven't published my promised article on ticket management. (“Coming soon”, ha ha.) It looks pretty good. Later this week, maybe? ]
[Other articles in category /misc] permanent link
Thu, 11 May 2017I'm almost done with anagrams. For now, anyway. I think. This article is to mop up the last few leftover anagram-related matters so that I can put the subject to rest.
(Earlier articles: [1] [2] [3] [•] )
Code is available
Almost all the code I wrote for this project is available on Github.
The documentation is not too terrible, I think.
Anagram lists are available
I have also placed my scored anagram lists on my web site. Currently available are:
Original file from the 1990s. This contains 23,521 anagram pairs, the results of my original scoring algorithm on a hand-built dictionary that includes the Unix spellcheck dictionary (
/usr/dict/words), the Webster's Second International Dictionary word list, and some lexicons copied from a contemporaneous release of WordNet. This file has been in the same place on my web site since 1997 and is certainly older than that.New file from February. Unfortunately I forget what went into this file. Certainly everything in the previous file, and whatever else I had lying around, probably including the Moby Word Lists. It contains 38,333 anagram pairs.
Very big listing of Wikipedia article titles. (11 MB compressed) I acquired the current list of article titles from the English Wikipedia; there are around 13,000,000 of these. I scored these along with the other lexicons I had on hand. The results include 1,657,150 anagram pairs. See below for more discussion of this.
!!Con talk
On Saturday I gave a talk about the anagram-scoring work at !!Con in New York. The talk was not my best work, since I really needed 15 minutes to do a good job and I was unwilling to cut it short enough. (I did go overtime, which I deeply regret.) At least nobody came up to me afterward and complained.
Talk materials are on my web site and I will link other talk-related stuff from there when it becomes available. The video will be available around the end of May, and the text transcript probably before that.
[ Addendum 20170518: The video is available thanks to Confreaks. ]
Both algorithms are exponential
The day after the talk an attendee asked me a very good question: why did I say that one algorithm for scoring algorithms was better than the other, when they are both exponential? (Sorry, I don't remember who you were—if you would like credit please drop me a note.)
The two algorithms are:
A brute-force search to construct all possible mappings from word A to word B, and then calculate the minimum score over all mappings (more details)
The two words are converted into a graph; we find the maximum independent set in the graph, and the size of the MIS gives the score (more details)
The answer to this excellent question begins with: just because two problems are both hard doesn't mean they are equally hard. In this case, the MIS algorithm is better for several reasons:
The number of possible mappings from A to B depends on the number of repeated letters in each word. For words of length n, in the worst case this is something like !! n! !!. This quantity is superexponential; it eventually exceeds !! c^n !! for all constants !!c!!. The naïve algorithm for MIS is only exponential, having !!c=2!!.
The problem size for the mapping algorithm depends on the number of repeated letters in the words. The problem size for the MIS algorithm depends on the number of shared adjacent letter pairs in the two words. This is almost always much smaller.
There appears to be no way to score all the mappings without constructing the mappings and scoring them. In contrast, MIS is well-studied and if you don't like the obvious !!2^n!! algorithm you can do something cleverer that takes only !!1.22^n!!.
Branch-and-bound techniques are much more effective for the MIS problem, and in this particular case we know something about the graph structure, which can be exploited to make them even more effective. For example, when calculating the score for
chromophotolithograph photochromolithographmy MIS implementation notices the matching trailing
olithographparts right away, and can then prune out any part of the MIS search that cannot produce a mapping with fewer than 11 chunks. Doing this in the mapping-generating algorithm is much more troublesome.
Stuff that didn't go into the talk
On Wednesday I tried out the talk on Katara and learned that it was around 75% too long. I had violated my own #1 content rule: “Do not begin with a long introduction”. My draft talk started with a tour of all my favorite anagrams, with illustrations. Included were:
“Please”
 and “asleep” and “elapse”.
and “asleep” and “elapse”.“Spectrum”
 and “crumpets”
and “crumpets”
 ; my wife noticed this while
we were at a figure-skating event at the Philadelphia
Spectrum, depicted
above.
; my wife noticed this while
we were at a figure-skating event at the Philadelphia
Spectrum, depicted
above.“English”
 and “shingle”
and “shingle”  ; I came up with this looking at a
teabag while at breakfast with my wife's parents. This prompted my
mother-in-law to remark that it must be hard to always be thinking
about such things—but then she admitted that when she sees long
numerals she always checks them for divisibility by 9.
; I came up with this looking at a
teabag while at breakfast with my wife's parents. This prompted my
mother-in-law to remark that it must be hard to always be thinking
about such things—but then she admitted that when she sees long
numerals she always checks them for divisibility by 9.“Soupmaster”
 and
and
 “mousetraps”. The
picture here is not perfect. I wanted a picture of the Soupmaster
restaurant that was at the Liberty Place food court in Philadelphia,
but I couldn't find one.
“mousetraps”. The
picture here is not perfect. I wanted a picture of the Soupmaster
restaurant that was at the Liberty Place food court in Philadelphia,
but I couldn't find one.I also wanted to show the back end of a Honda Integra and a picture of granite, but I couldn't find a good picture of either one before I deleted them from the talk. (My wife also gets credit for noticing this one.) [ Addendum 20170515: On the road yesterday I was reminded of another one my wife noticed: “Pontiac” / “caption”. ]
Slide #1 defines what anagrams actually are, with an example of “soapstone” / “teaspoons”. I had originally thought I might pander to the left-wing sensibilities of the !!Con crowd by using the example “Donald Trump” / “Lord Dampnut” and even made the illustration. I eventually rejected this for a couple of reasons. First, it was misleading because I only intended to discuss single-word anagrams. Second, !!Con is supposed to be fun and who wants to hear about Donald Trump?
But the illustration might be useful for someone else, so here it is. Share and enjoy.
After I rejected this I spent some time putting together an alternative, depicting “I am Lord Voldemort” / “Tom Marvolo Riddle”. I am glad I went with the soapstone teaspoons instead.
People Magazine
Clearly one important ingredient in finding good anagrams is that they should have good semantics. I did not make much of an effort in this direction. But it did occur to me that if I found a list of names of well-known people I might get something amusing out of it. For example, it is well known that “Britney Spears” is an anagram of “Presbyterians” which may not be meaningful but at least provides something to mull over.
I had some trouble finding a list of names of well-known people, probably because I do not know where to look, but I did eventually find a list of a few hundred on the People Magazine web site so I threw it into the mix and was amply rewarded:
| Cheryl Burke | Huckleberry |

| 
|
I thought Cheryl Burke was sufficiently famous, sufficiently recently, that most people might have heard of her. (Even I know who she is!) But I gave a version of the !!Con talk to the Philadelphia Perl Mongers the following Monday and I was the only one in the room who knew. (That version of the talk took around 75 minutes, but we took a lot of time to stroll around and look at the scenery, much of which is in this article.)
I had a struggle finding the right Cheryl Burke picture for the !!Con talk. The usual image searches turned up lots of glamour and fashion pictures and swimsuit pictures. I wanted a picture of her actually dancing and for some reason this was not easy to find. The few I found showed her from the back, or were motion blurred. I was glad when I found the one above.
Wikipedia
A few days before the !!Con talk my original anagram-scoring article hit #1 on Hacker News. Hacker News user Pxtl suggested using the Wikipedia article title list as an input lexicon. The article title list is available for download from the Wikimedia Foundation so you don't have to scrape the pages as Pxtl suggested. There are around 13 million titles and I found all the anagrams and scored them; this took around 25 minutes with my current code.
The results were not exactly disappointing, but neither did they deliver anything as awesomely successful as “cinematographer” / “megachiropteran”. The top scorer by far was “ACEEEFFGHHIILLMMNNOORRSSSTUV”, which is the pseudonym of 17th-century German writer Hans Jakob Christoffel von Grimmelshausen. Obviously, Grimmelshausen constructed his pseudonym by sorting the letters of his name into alphabetical order.
(Robert Hooke famously used the same scheme to claim priority for discovery of his spring law without actually revealing it. He published the statement as “ceiiinosssttuv” and then was able to claim, two years later, that this was an anagram of the actual law, which was “ut tensio, sic vis”. (“As the extension, so the force.”) An attendee of my Monday talk wondered if there is some other Latin phrase that Hooke could have claimed to have intended. Perhaps someone else can take the baton from me on this project.)
Anyway, the next few top scorers demonstrate several different problems:
21 Abcdefghijklmnopqrstuvwxyz / Qwertyuiopasdfghjklzxcvbnm
21 Abcdefghijklmnopqrstuvwxyz / Qwertzuiopasdfghjklyxcvbnm
21 Ashland County Courthouse / Odontorhynchus aculeatus
21 Daniel Francois Malherbe / Mindenhall Air Force Base
20 Christine Amongin Aporu / Ethnic groups in Romania
20 Message force multiplier / Petroleum fiscal regimes
19 Cholesterol lowering agent / North West Regional College
19 Louise de Maisonblanche / Schoenobius damienella
19 Scorpaenodes littoralis / Steroidal spirolactones
The “Qwerty” ones are intrinsically uninteresting and anyway we could have predicted ahead of time that they would be there. And the others are just sort of flat. “Odontorhynchus aculeatus” has the usual problems. One can imagine that there could be some delicious irony in “Daniel Francois Malherbe” / “Mindenhall Air Force Base” but as far as I can tell there isn't any and neither was Louise de Maisonblanche killed by an S. damienella. (It's a moth. Mme de Maisonblanche was actually killed by Variola which is not an anagram of anything interesting.)
Wikipedia article titles include many trivial variations. For example, many people will misspell “Winona Ryder” as “Wynona Rider”, so Wikipedia has pages for both, with the real article at the correct spelling and the incorrect one redirecting to it. The anagram detector cheerfully picks these up although they do not get high scores. Similarly:
- there are a lot of articles about weasels that have alternate titles about “weasles”
- there are a lot of articles about the United States or the United Kingdom that have alternate titles about the “Untied States” or the “Untied Kingdom”
- Articles about the “Center for” something or other with redirects to (or from) the “Centre for” the same thing.
- There is an article about “Major professional sports leagues in Canada and the United States” with a redirect from “Major professional sports leagues in the United States and Canada”.
- You get the idea.
The anagram scorer often had quite a bit of trouble with items like these because they are long and full of repeated letter pairs. The older algorithm would have done even worse. If you're still wondering about the difference between two exponential algorithms, some of these would make good example cases to consider.
As I mentioned above you can download the Wikipedia anagrams from my web site and check for yourself. My favorite item so far is:
18 Atlantis Casino Resort Spa / Carter assassination plot
Romania
Some words appear with surprising frequency and I don't know why. As I mentioned above one of the top scorers was “Ethnic groups in Romania” and for some reason Romania appears in the anagram list over and over again:
20 Christine Amongin Aporu / Ethnic groups in Romania
17 List of Romanian actors / Social transformation
15 Imperial Coronation / Romanian riot police
14 Rakhine Mountains / Romanians in the UK
14 Mindanao rasbora / Romanians abroad
13 Romanian poets / ramosopinnate
13 Aleuron carinatum / Aromanian culture
11 Resita Montana / Romanian state
11 Monte Schiara / The Romaniacs
11 Monetarianism / Romanian Times
11 Marion Barnes / Romanian Serb
11 Maarsen railway station / Romanian State Railways
11 Eilema androconia / Nicolae de Romania
11 Ana Maria Norbis / Arabs in Romania
( 170 more )
Also I had never thought of this before, but Romania appears in this unexpected context:
09 Alicia Morton / Clitoromania
09 Carinito Malo / Clitoromania
(Alicia Morton played Annie in the 1999 film. Carinito Malo is actually Cariñito Malo. I've already discussed the nonequivalence of “n” and “ñ” so I won't beat that horse again.)
Well, this is something I can investigate. For each string of letters, we have here the number of Wikipedia article titles in which the string appears (middle column), the number of anagram pairs in which the string appears (left column; anagrams with score less than 6 are not counted) and the quotient of the two (right column).
romania 110 4106 2.7%
serbia 109 4400 2.5%
croatia 68 3882 1.8%
belarus 24 1810 1.3%
ireland 140 11426 1.2%
andorra 7 607 1.2%
austria 60 5427 1.1%
russia 137 15944 0.9%
macedonia 28 3167 0.9%
france 111 14785 0.8%
spain 64 8880 0.7%
slovenia 18 2833 0.6%
wales 47 9438 0.5%
portugal 17 3737 0.5%
italy 21 4353 0.5%
denmark 19 3698 0.5%
ukraine 12 2793 0.4%
england 37 8719 0.4%
sweden 11 4233 0.3%
scotland 16 4945 0.3%
poland 22 6400 0.3%
montenegro 4 1446 0.3%
germany 16 5733 0.3%
finland 6 2234 0.3%
albania 10 3268 0.3%
slovakia 3 1549 0.2%
norway 9 3619 0.2%
greece 10 8307 0.1%
belgium 3 2414 0.1%
switzerland 0 5439 0.0%
netherlands 1 3522 0.0%
czechia 0 75 0.0%
As we see, Romania and Serbia are substantially ahead of the others.
I suspect that it is a combination of some lexical property (the
interesting part) and the relatively low coverage of those countries
in English Wikipedia. That is, I think if we were to identify the
lexical component, we might well find that russia has more of it,
but scores lower than romania because Russia is much more important.
My apologies if I
accidentally omitted your favorite European country.
[ Oh, crap, I just realized I left out Bosnia. ]
Lesbians
Another one of the better high scorers turns out to be the delightful:
16 Lesbian intercourse / Sunrise Celebration
“Lesbian”, like “Romania”, seems to turn up over and over; the next few are:
11 Lesbian erotica / Oreste Bilancia
11 Pitane albicollis / Political lesbian
12 Balearic islands / Radical lesbians
12 Blaise reaction / Lesbian erotica
(43 more)
Wikipedia says:
The Blaise reaction is an organic reaction that forms a β-ketoester from the reaction of zinc metal with a α-bromoester and a nitrile.
A hundred points to anyone who can make a genuinely funny joke out of this.
Oreste Bilancia is an Italian silent-film star, and Pitane albicollis is another moth. I did not know there were so many anagrammatic moths. Christian Bale is an anagram of Birthana cleis, yet another moth.
[ Addendum 20220227: Sean Carney has applied my method to the headwords from Urban Dictionary and says “even though it doesn’t score quite as well, in my mind, the clear winner is genitals be achin / cheating lesbian”. ]
I ran the same sort of analysis on lesbian as on romania, except
that since it wasn't clear what to compare it to, I picked a bunch of
random words.
nosehair 3 3 100.0%
margarine 4 16 25.0%
penis 95 573 16.6%
weasel 11 271 4.1%
phallus 5 128 3.9%
lesbian 26 863 3.0%
center 340 23969 1.4%
flowers 14 1038 1.3%
trumpet 6 487 1.2%
potato 10 941 1.1%
octopus 4 445 0.9%
coffee 12 1531 0.8%
It seems that lesbian appears with unusually high but not remarkably
high frequency. The unusual part is its participation in so many
anagrams with very high scores. The outstanding item here is
penis. (The top two being rare outliers.) But penis still wins
even if I throw away anagrams with scores less than 10 (instead of
less than 6):
margarine 1 16 6.2%
penis 13 573 2.3%
lesbian 8 863 0.9%
trumpet 2 487 0.4%
flowers 4 1038 0.4%
center 69 23969 0.3%
potato 2 941 0.2%
octopus 1 445 0.2%
coffee 1 1531 0.1%
weasel 0 271 0.0%
phallus 0 128 0.0%
nosehair 0 3 0.0%
Since I'm sure you are wondering, here are the anagrams of margarine
and nosehair:
07 Nosehair / Rehsonia
08 Aso Shrine / Nosehairs
09 Nosehairs / hoariness
04 Margaret Hines / The Margarines
07 Magerrain / margarine
07 Ramiengar / margarine
08 Rae Ingram / margarine
11 Erika Armstrong / Stork margarine
I think “Margaret Hines” / “The Margarines” should score more than 4, and that this exposes a defect in my method.
Acrididae graphs
Here is the graph constructed by the MIS algorithm for the pair “acrididae” / “cidaridae”, which I discussed in an earlier article and also mentioned in my talk.
Each maximum independent set in this graph corresponds to a minimum-chunk mapping between “acrididae” and “cidaridae”. In the earlier article, I claimed:
This one has two maximum independent sets
which is wrong; it has three, yielding three different mappings with five chunks:

| 
| 
|

| 
| 
|
My daughter Katara points out that the graphs above resemble grasshoppers. My Gentle Readers will no doubt recall that acrididae is the family of grasshoppers, comprising around 10,000 species. I wanted to find an anagram “grasshopper” / “?????? graph”. There are many anagrams of “eoprs” and “eoprss” but I was not able to find anything good. The best I could do was “spore graphs”.
Thank you, Gentle Readers, for taking this journey with me. I hope nobody walks up to me in the next year to complain that my blog does not feature enough anagram-related material.
[ Addendum 20230423: A discussion on LanguageHat of the original article includes the interesting Russian pair австралопитек / ватерполистка. австралопитек is an Australopithecus. ватерполистка is a female water polo player. ]
[Other articles in category /lang] permanent link
Mon, 08 May 2017
An anagrammatic cautionary tale

I previously claimed that “cinematographer” / “megachiropteran” was the best anagram in English. Scoring all the anagrams in the list of 13 million Wikipedia article titles did not refute this, but it did reveal that “cinematographer” is also an anagram of “Taichang Emperor”.
The Taichang Emperor (泰昌) lived from 1582 to 1620 and was the 14th emperor of the Ming Dynasty. His reign as emperor lasted only 29 days, after which he died of severe diarrhea. Wikipedia says:
According to non-official primary sources, the Taichang Emperor's illness was brought about by excessive sexual indulgence after he was presented with eight maidens by Lady Zheng.
To counteract the diarrhea, the emperor took a “red pill” offered to him by a court official:
It was recorded in official Ming histories that the Taichang Emperor felt much better after taking the red pill, regained his appetite and repeatedly praised Li Kezhuo as a "loyal subject". That same afternoon, the emperor took a second pill and was found dead the next morning.
Surely this tale of Ming China has something to teach us even today.
[Other articles in category /misc] permanent link
Sun, 02 Apr 2017A Unix system administrator of my acquaintance once got curious about
what people were putting into /dev/null. I think he also may have
had some notion that it would contain secrets or other interesting
material that people wanted thrown away. Both of these ideas are
stupid, but what he did next was even more stupid: he decided to
replace /dev/null with a plain file so that he could examine its
contents.
The root filesystem quickly filled up and the admin had to be called
back from dinner to fix it. But he found that he couldn't fix it: to
create a Unix device file you use the mknod command, and its
arguments are the major and minor device numbers of the device to
create. Our friend didn't remember the correct minor device
number. The ls -l command will tell you the numbers of a device file
but he had removed /dev/null so he couldn't use that.
Having no other system of the same type with an intact device file to
check, he was forced to restore /dev/null from the tape backups.
[Other articles in category /Unix] permanent link
Sun, 05 Mar 2017Lately my kids have been interested in puzzles of this type: You are given a sequence of four digits, say 1,2,3,4, and your job is to combine them with ordinary arithmetic operations (+, -, ×, and ÷) in any order to make a target number, typically 24. For example, with 1,2,3,4, you can go with $$((1+2)+3)×4 = 24$$ or with $$4×((2×3)×1) = 24.$$
I said I had found an unusually difficult puzzle of this type, which is to make 2,5,6,6 total to 17. This is rather difficult. (I will reveal the solution later in this article.) Several people independently wrote to advise me that it is even more difficult to make 3,3,8,8 total to 24. They were right; it is amazingly difficult. After a couple of weeks I finally gave up and asked the computer, and when I saw the answer I didn't feel bad that I hadn't gotten it myself. (The solution is here if you want to give up without writing a program.)
From now on I will abbreviate the two puzzles of the previous paragraph as «2 5 6 6 ⇒ 17» and «3 3 8 8 ⇒ 24», and others similarly.
The article also inspired a number of people to write their own solvers and send them to me, and comparing them was interesting. My solver followed the tree search technique that I described in chapter 5 of Higher-Order Perl, and which has become so familiar to me that by now I can implement it without thinking about it very hard:
Invent a data structure that represents the state of a possibly-incomplete search. This is just a list of the stuff one needs to keep track of while searching. (Let's call this a node.)
Build a function which recognizes when a node represents a successful search.
Build a function which takes a node, computes all the ways the search could proceed from that point, and returns a list of nodes for those slightly-more-advanced searches.
Initialize a queue with a node representing a search that has just begun.
Do this:
until ( queue.is_empty() ) { current_node = queue.get_next() if ( is_successful( current_node ) ) { print the solution } queue.push( slightly_more_complete_searches( current_node ) ) }
This is precisely a breadth-first search. To make it into depth-first
search, replace the queue with a stack. To make a heuristically
directed search, replace get_next with a function that looks at the
queue and chooses the best-looking node from which to proceed. Many
other variations are possible, which is the advantage of this
synthetic approach over letting the search arise organically from a
recursive searcher. (Higher-Order Perl says “Recursive functions
naturally perform depth-first
searches.” (page
203)) In Python or Ruby one would be able to use yield and would
not have to manage the queue explicitly, but in this case the queue
management is trivial.
In my solver, each node contains a list of available expressions, annotated with its numerical value. Initially, the expressions are single numbers and the values are the same, say
[ [ "2" => 2 ], [ "3" => 3 ], [ "4" => 4 ], [ "6" => 6 ] ]
Whether you represent expressions as strings or as something more structured depends on what you need to do with them at the end. If you just need to print them out, strings are good enough and are easy to handle.
A node represents a successful search if it contains only a single expression and if the expression's value is the target sum, say 24:
[ [ "(((6÷2)+3)×4)" => 24 ] ]
From a node, the search should proceed by selecting two of the expressions, removing them from the node, selecting a legal operation, combining the two expressions into a single expression, and inserting the result back into the node. For example, from the initial node shown above, the search might continue by subtracting the fourth expression from the second:
[ [ "2" => 2 ], [ "4" => 4 ], [ "(3-6)" => -3 ] ]
or by multiplying the second and the third:
[ [ "2" => 2 ], [ "(3×4)" => 12 ], [ "6" => 6 ] ]
When the program encounters that first node it will construct both of these, and many others, and put them all into the queue to be investigated later.
From
[ [ "2" => 2 ], [ "(3×4)" => 12 ], [ "6" => 6 ] ]
the search might proceed by dividing the first expression by the third:
[ [ "(3×4)" => 12 ], [ "(2÷6)" => 1/3 ] ]
Then perhaps by subtracting the first from the second:
[ [ "((2÷6)-(3×4))" => -35/3 ] ]
From here there is no way to proceed, so when this node is removed from the queue, nothing is added to replace it. Had it been a winner, it would have been printed out, but since !!-\frac{35}3!! is not the target value of 24, it is silently discarded.
To solve a puzzle of the «a b c d ⇒ t» sort requires examining a few thousand nodes. On modern hardware this takes approximately zero seconds.
The actual code for my solver is a lot of Perl gobbledygook that may not be of general interest so I will provide a link for people who are interested in deciphering it. It also represents my second attempt: I lost the code that I described in the earlier article and had to rewrite it. It is rather bigger than I would have liked.
Stuff goes wrong
People showed me a lot of programs to solve this, and many didn't work. There are a few hard cases that several of them get wrong.
Fractions
Some puzzles require that some subexpressions have fractional values. Many of the programs people showed me used integer arithmetic (sometimes implicitly and unintentionally) and failed to solve those puzzles. We can detect this by asking for a solution to «2 5 6 6 ⇒ 17», which requires a fraction. The solution is !!6×(2+(5÷6))!!. A program using integer arithmetic will calculate !!5÷6 = 0!! and fail to recognize the solution.
Several people on Twitter made this mistake and then mistakenly claimed that there was no solution at all. Usually it was possible to correct their programs by changing
inputs = [ 2, 2, 5, 6 ]
to
inputs = [ 2.0, 2.0, 5.0, 6.0 ]
or something like that.
Some people also surprised me by claiming that I had lied when I stated that the puzzle could be solved without any “underhanded tricks”, and that the use of intermediate fractions was itself an underhanded trick. Your Honor, I plead not guilty. I originally described the puzzle this way:
You are given a sequence of four digits, say 1,2,3,4, and your job is to combine them with ordinary arithmetic operations (+, -, ×, and ÷) in any order to make a target number, typically 24.
The objectors are implicitly claiming that when you combine 5 and 6 with the “ordinary arithmetic operation” of division, you get something other than !!\frac56!!. This is an indefensible claim.
I wasn't even trying to be tricky! It never occurred to me that fractions were something that some people would consider underhanded, and now that it has been suggested, I reject the suggestion. Folks, the result of division can be a fraction. Fractions are not some sort of obscure mathematical pettifoggery. They have been with us for at least 3,500 years now, so it is time everyone got used to them.
Floating-point error
Some programs used floating-point arithmetic to deal with the fractions and then fell foul of floating-point error. I will defer discussion of this to a future article.
I've complained about floating-point numbers on this blog before. ( 1 2 3 4 5 ) God, how I loathe them.
[ Addendum 20170825: Looking back on our old discussion from July 2016, I see that Lindsey Kuper said to me:
One nice thing about using Racket or Scheme is that it handles the numeric stuff so nicely. If you weren't careful, I could imagine in Python a solution failing because it evaluated to 16.99999999999999997 or something.
Good call, Dr. Kuper! ]
Expression construction
A more subtle error that several programs made was to assume that all expressions can be constructed by combining a previous expression with a single input number. For example, to solve «2 3 5 7 ⇒ 24», you multiply 3 by 7 to get 21, then add 5 to get 26, then subtract 2 to get 24.
But not every puzzle can be solved this way. Consider «2 3 5 7 ⇒ 41». You start by multiplying 2 by 3 to get 6, but if you try to combine the 6 with either 5 or 7 at this point you will lose. The only solution is to put the 6 aside and multiply 5 by 7 to get 35. Then add the 6 and the 35 to get 41.
Another way to put this is that an unordered binary tree with 4 leaves can take two different shapes. (Imagine filling the green circles with numbers and the pink squares with operators.)
| 
|
The right-hand type of structure is sometimes necessary, as with «2 3 5 7 ⇒ 41». But several of the proposed solutions produced only expressions with structures like that on the left.
Here's Sebastian Fischer's otherwise very elegant Haskell solution, in its entirety:
import Data.List ( permutations )
solution = head
[ (a,x,(b,y,(c,z,d)))
| [a,b,c,d] <- permutations [2,5,6,6],
ops <- permutations [((+),'+'),((-),'-'),((*),'*'),((/),'/')],
let [u,v,w] = map fst $ take 3 ops,
let [x,y,z] = map snd $ take 3 ops,
(a `u` (b `v` (c `w` d))) == 17
]
You can see the problem in the last line. a, b, c, and d are
numbers, and u, v, and w are operators. The program evaluates
an expression to see if it has the value 17, but the expression always
has the left-hand shape. (The program has another limitation: it
never uses the same operator twice in the expression. That second
permutations should be (sequence . take 3 . repeat) or
something. It can still solve «2 5 6 6 ⇒ 17», however.)
Often the way these programs worked was to generate every possible permutation of the inputs and then apply the operators to the input lists stackwise: pop the first two values, combine them, push the result, and repeat. Here's a relevant excerpt from a program by Tim Dierks, this time in Python:
for ordered_values in permutations(values):
for operations in product(ops, repeat=len(values)-1):
result, formula = calc_result(ordered_values, operations)
Here the expression structure is implicit, but the current result is always made by combining one of the input numbers with the old result.
I have seen many people get caught by this and similar traps in the
past. I once posed the problem of enumerating all the strings of
balanced parentheses of a given length,
and several people assumed that all such strings have the form ()S,
S(), or (S), where S is a shorter string of the same type. This
seems plausible, and it works up to length 6, but (())(()) does not
have that form.
Division by zero
A less common error exhibited by some programs was a failure to properly deal with division by zero. «2 5 6 6 ⇒ 17» has a solution, and if a program dies while checking !!2+(5÷(6-6))!! and doesn't find the solution, that's a bug.
Programs that worked
Ingo Blechschmidt (Haskell)
Ingo Blechschmidt showed me a solution in
Haskell. The code is quite short.
M. Blechschmidt's program defines a synthetic expression type and an
evaluator for it. It defines a function arb which transforms an
ordered list of numbers into a list of all possible expressions over
those numbers. Reordering the list is taken care of earlier, by
Data.List.permutations.
By “synthetic expression type” I mean this:
data Exp a
= Lit a
| Sum (Exp a) (Exp a)
| Diff (Exp a) (Exp a)
| Prod (Exp a) (Exp a)
| Quot (Exp a) (Exp a)
deriving (Eq, Show)
Probably 80% of the Haskell programs ever written have something like this in them somewhere. This approach has a lot of boilerplate. For example, M. Blechschmidt's program then continues:
eval :: (Fractional a) => Exp a -> a
eval (Lit x) = x
eval (Sum a b) = eval a + eval b
eval (Diff a b) = eval a - eval b
eval (Prod a b) = eval a * eval b
eval (Quot a b) = eval a / eval b
Having made up our own synonyms for the arithmetic operators (Sum for
!!+!!, etc.) we now have to explain to Haskell what they mean. (“Not
expressions, but an incredible simulation!”)
I spent a while trying to shorten the code by using a less artificial expression type:
data Exp a
= Lit a
| Op ((a -> a -> a), String) (Exp a) (Exp a)
but I was disappointed; I was only able to cut it down by 18%, from 34 lines to 28. I hope to discuss this in a future article. By the way, “Blechschmidt” is German for “tinsmith”.
Shreevatsa R. (Python)
Shreevatsa R. showed me a solution in Python. It generates every possible expression and prints it out with its value. If you want to filter the voluminous output for a particular target value, you do that later. Shreevatsa wrote up an extensive blog article about this which also includes a discussion about eliminating duplicate expressions from the output. This is a very interesting topic, and I have a lot to say about it, so I will discuss it in a future article.
Jeff Fowler (Ruby)
Jeff Fowler of the Recurse Center wrote a compact solution in Ruby that he described as “hot garbage”. Did I say something earlier about Perl gobbledygook? It's nice that Ruby is able to match Perl's level of gobbledygookitude. This one seems to get everything right, but it fails mysteriously if I replace the floating-point constants with integer constants. He did provide a version that was not “egregiously minified” but I don't have it handy.
Lindsey Kuper (Scheme)
Lindsey Kuper wrote a series of solutions in the Racket dialect of Scheme, and discussed them on her blog along with some other people’s work.
M. Kuper's first draft was 92 lines long (counting whitespace) and when I saw it I said “Gosh, that is way too much code” and tried writing my own in Scheme. It was about the same size. (My Perl solution is also not significantly smaller.)
Martin Janecke (PHP)
I saved the best for last. Martin Janecke showed me an almost flawless solution in PHP that uses a completely different approach than anyone else's program. Instead of writing a lot of code for generating permutations of the input, M. Janecke just hardcoded them:
$zahlen = [
[2, 5, 6, 6],
[2, 6, 5, 6],
[2, 6, 6, 5],
[5, 2, 6, 6],
[5, 6, 2, 6],
[5, 6, 6, 2],
[6, 2, 5, 6],
[6, 2, 6, 5],
[6, 5, 2, 6],
[6, 5, 6, 2],
[6, 6, 2, 5],
[6, 6, 5, 2]
]
Then three nested loops generate the selections of operators:
$operatoren = [];
foreach (['+', '-', '*', '/'] as $x) {
foreach (['+', '-', '*', '/'] as $y) {
foreach (['+', '-', '*', '/'] as $z) {
$operatoren[] = [$x, $y, $z];
}
}
}
Expressions are constructed from templates:
$klammern = [
'%d %s %d %s %d %s %d',
'(%d %s %d) %s %d %s %d',
'%d %s (%d %s %d) %s %d',
'%d %s %d %s (%d %s %d)',
'(%d %s %d) %s (%d %s %d)',
'(%d %s %d %s %d) %s %d',
'%d %s (%d %s %d %s %d)',
'((%d %s %d) %s %d) %s %d',
'(%d %s (%d %s %d)) %s %d',
'%d %s ((%d %s %d) %s %d)',
'%d %s (%d %s (%d %s %d))'
];
(I don't think those templates are all necessary, but hey, whatever.)
Finally, another set of nested loops matches each ordering of the
input numbers with each selection of operators, uses sprintf to plug
the numbers and operators into each possible expression template, and
uses @eval to evaluate the resulting expression to see if it has the
right value:
foreach ($zahlen as list ($a, $b, $c, $d)) {
foreach ($operatoren as list ($x, $y, $z)) {
foreach ($klammern as $vorlage) {
$term = sprintf ($vorlage, $a, $x, $b, $y, $c, $z, $d);
if (17 == @eval ("return $term;")) {
print ("$term = 17\n");
}
}
}
}
If loving this is wrong, I don't want to be right. It certainly satisfies Larry Wall's criterion of solving the problem before your boss fires you. The same approach is possible in most reasonable languages, and some unreasonable ones, but not in Haskell, which was specifically constructed to make this approach as difficult as possible.
M. Janecke wrote up a blog article about this, in
German. He says “It's not an elegant
program and PHP is probably not an obvious choice for arithmetic
puzzles, but I think it works.” Indeed it does. Note that the use of
@eval traps the division-by-zero exceptions, but unfortunately falls
foul of floating-point roundoff errors.
Thanks
Thanks to everyone who discussed this with me. In addition to the people above, thanks to Stephen Tu, Smylers, Michael Malis, Kyle Littler, Jesse Chen, Darius Bacon, Michael Robert Arntzenius, and anyone else I forgot. (If I forgot you and you want me to add you to this list, please drop me a note.)
Coming up
I have enough material for at least three or four more articles about this that I hope to publish here in the coming weeks.
But the previous article on this subject ended similarly, saying
I hope to write a longer article about solvers in the next week or so.
and that was in July 2016, so don't hold your breath.
[ Addendum 20170820: the next article is ready. I hope you weren't holding your breath! ]
[ Addendum 20170828: yet more about this ]
[Other articles in category /math] permanent link
Thu, 23 Feb 2017
Miscellaneous notes on anagram scoring
My article on finding the best anagram in English was well-received, and I got a number of interesting comments about it.
A couple of people pointed out that this does nothing to address the issue of multiple-word anagrams. For example it will not discover “I, rearrangement servant / Internet anagram server” True, that is a different problem entirely.
Markian Gooley informed me that “megachiropteran / cinematographer” has been long known to Scrabble players, and Ben Zimmer pointed out that A. Ross Eckler, unimpressed by “cholecystoduodenostomy / duodenocholecystostomy”, proposed a method almost identical to mine for scoring anagrams in an article in Word Ways in 1976. M. Eckler also mentioned that the “remarkable” “megachiropteran / cinematographer” had been published in 1927 and that “enumeration / mountaineer” (which I also selected as a good example) appeared in the Saturday Evening Post in 1879!
The Hacker News comments were unusually pleasant and interesting. Several people asked “why didn't you just use the Levenshtein distance”? I don't remember that it ever occured to me, but if it had I would have rejected it right away as being obviously the wrong thing. Remember that my original chunking idea was motivated by the observation that “cholecystoduodenostomy / duodenocholecystostomy” was long but of low quality. Levenshtein distance measures how far every letter has to travel to get to its new place and it seems clear that this would give “cholecystoduodenostomy / duodenocholecystostomy” a high score because most of the letters move a long way.
Hacker News user
tyingqtried it anyway, and reported that it produced a poor outcome. The top-scoring pair by Levenshtein distance is “anatomicophysiologic physiologicoanatomic”, which under the chunking method gets a score of 3. Repeat offender “cholecystoduodenostomy / duodenocholecystostomy” only drops to fourth place.A better idea seems to be Levenshtein score per unit of length, suggested by lobste.rs user
cooler_ranch.A couple of people complained about my “notaries / senorita” example, rightly observing that “senorita” is properly spelled “señorita”. This bothered me also while I was writing the article. I eventually decided although “notaries” and “señorita” are certainly not anagrams in Spanish (even supposing that “notaries” was a Spanish word, which it isn't) that the spelling of “senorita” without the tilde is a correct alternative in English. (Although I found out later that both the Big Dictionary and American Heritage seem to require the tilde.)
Hacker News user
ggambettaobserved that while ‘é’ and ‘e’, and ‘ó’ and ‘o’ feel interchangeable in Spanish, ‘ñ’ and ‘n’ do not. I think this is right. The ‘é’ is an ‘e’, but with a mark on it to show you where the stress is in the word. An ‘ñ’ is not like this. It was originally an abbreviation for ‘nn’, introduced in the 18th century. So I thought it might make sense to allow ‘ñ’ to be exchanged for ‘nn’, at least in some cases.(An analogous situation in German, which may be more familiar, is that it might be reasonable to treat ‘ö’ and ‘ü’ as if they were ‘oe’ and ‘ue’. Also note that in former times, “w” and “uu” were considered interchangeable in English anagrams.)
Unfortunately my Spanish dictionary is small (7,000 words) and of poor quality and I did not find any anagrams of “señorita”. I wish I had something better for you. Also, “señorita” is not one of the cases where it is appropriate to replace “ñ” with “nn”, since it was never spelled “sennorita”.
I wonder why sometimes this sort of complaint seems to me like useless nitpicking, and other times it seems like a serious problem worthy of serious consideration. I will try to think about this.
Mike Morton, who goes by the anagrammatic nickname of “Mr. Machine Tool”, referred me to his Higgledy-piggledy about megachiropteran / cinematographer, which is worth reading.
Regarding the maximum independent set algorithm I described yesterday, Shreevatsa R. suggested that it might be conceptually simpler to find the maximum clique in the complement graph. I'm not sure this helps, because the complement graph has a lot more edges than the original. Below right is the complement graph for “acrididae / cidaridae”. I don't think I can pick out the 4-cliques in that graph any more than the independent sets in the graph on the lower-left, and this is an unusually favorable example case for the clique version, because the original graph has an unusually large number of edges.
But perhaps the cliques might be easier to see if you know what to look for: in the right-hand diagram the four nodes on the left are one clique, and the four on the right are the other, whereas in the left-hand diagram the two independent sets are all mixed together.
An earlier version of the original article mentioned the putative 11-pointer “endometritria / intermediator”. The word “endometritria” seemed pretty strange, and I did look into it before I published the article, but not carefully enough. When Philip Cohen wrote to me to question it, I investigated more carefully, and discovered that it had been an error in an early WordNet release, corrected (to “endometria”) in version 1.6. I didn't remember that I had used WordNet's word lists, but I am not surprised to discover that I did.
A rare printing of Webster's 2¾th American International Lexican includes the word “endometritriostomoscopiotomous” but I suspect that it may be a misprint.
Philippe Bruhat wrote to inform me of Alain Chevrier’s book notes / sténo, a collection of thematically related anagrams in French. The full text is available online.
Alexandre Muñiz, who has a really delightful blog, and who makes and sells attractive and clever puzzles of his own invention. pointed out that soapstone teaspoons are available. The perfect gift for the anagram-lover in your life! They are not even expensive.
Thanks also to Clinton Weir, Simon Tatham, Jon Reeves, Wei-Hwa Huang, and Philip Cohen for their emails about this.
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link
Tue, 21 Feb 2017
Moore's law beats a better algorithm
Yesterday I wrote about the project I did in the early 1990s to find the best anagrams. The idea is to give pair of anagram words a score, which is the number of chunks into which you have to divide one word in order to rearrange the chunks to form the other word. This was motivated by the observation that while “cholecysto-duodeno-stomy” and “duodeno-cholecysto-stomy” are very long words that are anagrams of one another, they are not interesting because they require so few chunks that the anagram is obvious. A shorter but much more interesting example is “aspired / diapers”, where the letters get all mixed up.
I wrote:
One could do this with a clever algorithm, if one were available. There is a clever algorithm, based on finding maximum independent sets in a certain graph. I did not find this algorithm at the time; nor did I try. Instead, I used a brute-force search.
I wrote about the brute-force search yesterday. Today I am going to discuss the clever algorithm. (The paper is Avraham Goldstein, Petr Kolman, Jie Zheng “Minimum Common String Partition Problem: Hardness and Approximations”, The Electronic Journal of Combinatorics, 12 (2005).)
The plan is to convert a pair of anagrams into a graph that expresses
the constraints on how the letters can move around when one turns into
the other. Shown below is the graph for comparing
acrididae (grasshoppers)
with cidaridae (sea
urchins):
The “2,4” node at the top means that the letters ri at position
2 in acrididae match the letters ri at position 4 in cidaridae;
the “3,1” node is for the match between the first id and the first
id. The two nodes are connected by an edge to show that the two
matchings are incompatible: if you map the ri to the ri, you
cannot also map the first id to the first id; instead you have to
map the first id to the second one, represented by the node “3,5”,
which is not connected to “2,4”. A maximum independent set in this
graph is a maximum selection of compatible matchings in the words,
which corresponds to a division into the minimum number of chunks.
Usually the graph is much less complicated than this. For simple cases it is empty and the maximum independent set is trivial. This one has two maximum independent sets, one (3,1; 5,5; 6,6; 7,7) corresponding to the obvious minimum splitting:

and the other (2,4; 3,5; 5,1; 6,2) to this other equally-good splitting:
[ Addendum 20170511: It actually has three maximum independent sets. ]
In an earlier draft of yesterday's post, I wrote:
I should probably do this over again, because my listing seems to be incomplete. For example, it omits “spectrum / crumpets” which would have scored 5, because the Webster's Second list contains crumpet but not crumpets.
I was going to leave it at that, but then I did do it over again, and this time around I implemented the “good” algorithm. It was not that hard. The code is on GitHub if you would like to see it.
To solve the maximum independent set instances, I used a guided brute-force search. Maximum independent set is NP-complete, and so the best known algorithm for it runs in exponential time. But the instances in which we are interested here are small enough that this doesn't matter. The example graph above has 8 nodes, so one needs to check at most 256 possible sets to see which is the maximum independent set.
I collated together all the dictionaries I had handy. (I didn't know yet about SCOWL.) These totaled 275,954 words, which is somewhat more than Webster's Second by itself. One of the new dictionaries did contain crumpets so the result does include “spectrum / crumpets”.
The old scored anagram list that I made in the 1990s contained 23,521 pairs. The new one contains 38,333. Unfortunately most of the new stuff is of poor quality, as one would expect. Most of the new words that were missing from my dictionary the first time around are obscure. Perhaps some people would enjoy discovering that that “basiparachromatin” and “Marsipobranchiata” are anagrams, but I find it of very limited appeal.
But the new stuff is not all junk. It includes:
10 antiparticles paternalistic
10 nectarines transience
10 obscurantist subtractions11 colonialists oscillations
11 derailments streamlined
which I think are pretty good.
I wasn't sure how long the old program had taken to run back in the early nineties, but I was sure it had been at least a couple of hours. The new program processes the 275,954 inputs in about 3.5 seconds. I wished I knew how much of this was due to Moore's law and how much to the improved algorithm, but as I said, the old code was long lost.
But then just as I was finishing up the article, I found the old brute-force code that I thought I had lost! I ran it on the same input, and instead of 3.5 seconds it took just over 4 seconds. So almost all of the gain since the 1990s was from Moore's law, and hardly any was from the “improved” algorithm.
I had written in the earlier article:
In 2016 [ the brute force algorithm ] would probably still [ run ] quicker than implementing the maximum independent set algorithm.
which turned out to be completely true, since implementing the maximum independent set algorithm took me a couple of hours. (Although most of that was building out a graph library because I didn't want to look for one on CPAN.)
But hey, at least the new program is only twice as much code!
[ Addendum: The program had a minor bug: it would disregard
capitalization when deciding if two words were anagrams, but then
compute the scores with capitals and lowercase letters distinct. So
for example Chaenolobus was considered an anagram of unchoosable,
but then the Ch in Chaenolobus would not be matched to the ch in
unchoosable, resulting in a score of 11 instead of 10. I have
corrected the program and the output. Thanks to Philip Cohen for
pointing this out. ]
[ Addendum 20170223: More about this ]
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link
I found the best anagram in English
I planned to publish this last week sometime but then I wrote a line of code with three errors and that took over the blog.
A few years ago I mentioned in passing that in the 1990s I had constructed a listing of all the anagrams in Webster's Second International dictionary. (The Webster's headword list was available online.)
This was easy to do, even at the time, when the word list itself, at 2.5 megabytes, was a file of significant size. Perl and its cousins were not yet common; in those days I used Awk. But the task is not very different in any reasonable language:
# Process word list
while (my $word = <>) {
chomp $word;
my $sorted = join "", sort split //, $word; # normal form
push @{$anagrams{$sorted}}, $word;
}
for my $words (values %anagrams) {
print "@$words\n" if @$words > 1;
}
The key technique is to reduce each word to a normal form so that
two words have the same normal form if and only if they are anagrams
of one another. In this case we do this by sorting the letters into
alphabetical order, so that both megalodon and moonglade become
adeglmnoo.
Then we insert the words into a (hash | associative array | dictionary), keyed by their normal forms, and two or more words are anagrams if they fall into the same hash bucket. (There is some discussion of this technique in Higher-Order Perl pages 218–219 and elsewhere.)
(The thing you do not want to do is to compute every permutation of the letters of each word, looking for permutations that appear in the word list. That is akin to sorting a list by computing every permutation of the list and looking for the one that is sorted. I wouldn't have mentioned this, but someone on StackExchange actually asked this question.)
Anyway, I digress. This article is about how I was unhappy with the results of the simple procedure above. From the Webster's Second list, which contains about 234,000 words, it finds about 14,000 anagram sets (some with more than two words), consisting of 46,351 pairs of anagrams. The list starts with
aal ala
and ends with
zolotink zolotnik
which exemplify the problems with this simple approach: many of the 46,351 anagrams are obvious, uninteresting or even trivial. There must be good ones in the list, but how to find them?
I looked in the list to find the longest anagrams, but they were also disappointing:
cholecystoduodenostomy duodenocholecystostomy
(Webster's Second contains a large amount of scientific and medical jargon. A cholecystoduodenostomy is a surgical operation to create a channel between the gall bladder (cholecysto-) and the duodenum (duodeno-). A duodenocholecystostomy is the same thing.)
This example made clear at least one of the problems with boring anagrams: it's not that they are too short, it's that they are too simple. Cholecystoduodenostomy and duodenocholecystostomy are 22 letters long, but the anagrammatic relation between them is obvious: chop cholecystoduodenostomy into three parts:
cholecysto duodeno stomy
and rearrange the first two:
duodeno cholecysto stomy
and there you have it.
This gave me the idea to score a pair of anagrams according to how many chunks one had to be cut into in order to rearrange it to make the other one. On this plan, the “cholecystoduodenostomy / duodenocholecystostomy” pair would score 3, just barely above the minimum possible score of 2. Something even a tiny bit more interesting, say “abler / blare” would score higher, in this case 4. Even if this strategy didn't lead me directly to the most interesting anagrams, it would be a big step in the right direction, allowing me to eliminate the least interesting.
This rule would judge both “aal / ala” and “zolotink / zolotnik” as being uninteresting (scores 2 and 4 respectively), which is a good outcome. Note that some other boring-anagram problems can be seen as special cases of this one. For example, short anagrams never need to be cut into many parts: no four-letter anagrams can score higher than 4. The trivial anagramming of a word to itself always scores 1, and nontrivial anagrams always score more than this.
So what we need to do is: for each anagram pair, say
acrididae (grasshoppers)
and cidaridae (sea
urchins), find the smallest number of chunks into which we can chop
acrididae so that the chunks can be rearranged into cidaridae.
One could do this with a clever algorithm, if one were available. There is a clever algorithm, based on finding maximum independent sets in a certain graph. (More about this tomorrow.) I did not find this algorithm at the time; nor did I try. Instead, I used a brute-force search. Or rather, I used a very small amount of cleverness to reduce the search space, and then used brute-force search to search the reduced space.
Let's consider a example, scoring the anagram “abscise / scabies”.
You do not have to consider every possible permutation of
abscise. Rather, there are only two possible mappings from the
letters of abscise to the letters of scabies. You know that the
C must map to the C, the A must map to the A, and so
forth. The only question is whether the first S of abscise maps to
the first or to the second S of scabies. The first mapping gives
us:
and the second gives us

because the S and the C no longer go to adjoining positions. So
the minimum number of chunks is 5, and this anagram pair gets a score
of 5.
To fully analyze cholecystoduodenostomy by this method required considering 7680
mappings. (120 ways to map the five O's × 2 ways to map the two
C's × 2 ways to map the two D's, etc.) In the 1990s this took a
while, but not prohibitively long, and it worked well enough that I
did not bother to try to find a better algorithm. In 2016 it would
probably still run quicker than implementing the maximum independent
set algorithm. Unfortunately I have lost the code that I wrote then
so I can't compare.
Assigning scores in this way produced a scored anagram list which began
2 aal ala
and ended
4 zolotink zolotnik
and somewhere in the middle was
3 cholecystoduodenostomy duodenocholecystostomy
all poor scores. But sorted by score, there were treasures at the end, and the clear winner was
I declare this the single best anagram in English. It is 15 letters
long, and the only letters that stay together are the E and the R.
“Cinematographer” is as familiar as a 15-letter word can be, and
“megachiropteran” means a giant bat. GIANT BAT! DEATH FROM
ABOVE!!!
And there is no serious competition. There was another 14-pointer, but both its words are Webster's Second jargon that nobody knows:
14 rotundifoliate titanofluoride
There are no score 13 pairs, and the score 12 pairs are all obscure. So this is the winner, and a deserving winner it is.
I think there is something in the list to make everyone happy. If you are the type of person who enjoys anagrams, the list rewards casual browsing. A few examples:
7 admirer married
7 admires sidearm8 negativism timesaving
8 peripatetic precipitate
8 scepters respects
8 shortened threnodes
8 soapstone teaspoons9 earringed grenadier
9 excitation intoxicate
9 integrals triangles
9 ivoriness revisions
9 masculine calumnies10 coprophagist topographics
10 chuprassie haruspices
10 citronella interlocal11 clitoridean directional
11 dispensable piebaldness
“Clitoridean / directional” has been one of my favorites for years. But my favorite of all, although it scores only 6, is
6 yttrious touristy
I think I might love it just because the word yttrious is so delightful. (What a debt we owe to Ytterby, Sweden!)
I also rather like
5 notaries senorita
which shows that even some of the low-scorers can be worth looking at. Clearly my chunk score is not the end of the story, because “notaries / senorita” should score better than “abets / baste” (which is boring) or “Acephali / Phacelia” (whatever those are), also 5-pointers. The length of the words should be worth something, and the familiarity of the words should be worth even more.
Here are the results:
In former times there was a restaurant in Philadelphia named “Soupmaster”. My best unassisted anagram discovery was noticing that this is an anagram of “mousetraps”.
[ Addendum 20170222: There is a followup article comparing the two algorithms I wrote for computing scores. ]
[ Addendum 20170222: An earlier version of this article mentioned the putative 11-pointer “endometritria / intermediator”. The word “endometritria” seemed pretty strange, and I did look into it before I published the article, but not carefully enough. When Philip Cohen wrote to me to question it, I investigated more carefully, and discovered that it had been an error in an early WordNet release, corrected (to “endometria”) in version 1.6. I didn't remember that I had used WordNet's word lists, but I am not surprised to discover that I did. ]
[ Addendum 20170223: More about this ]
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link
Thu, 16 Feb 2017
Automatically checking for syntax errors with Git's pre-commit hook
Previous related article
Earlier related article
Over the past couple of days I've written about how I committed a syntax error on a cron script, and a co-worker had to fix it on Saturday morning. I observed that I should have remembered to check the script for syntax errors before committing it, and several people wrote to point out to me that this is the sort of thing one should automate.
(By the way, please don't try to contact me on Twitter. It won't work. I have been on Twitter Vacation for months and have no current plans to return.)
Git has a “pre-commit hook” feature, which means that you can set up a program that will be run every time you attempt a commit, and which can abort the commit if it doesn't like what it sees. This is the natural place to put an automatic syntax check. Some people suggested that it should be part of the CI system, or even the deployment system, but I don't control those, and anyway it is much better to catch this sort of thing as early as possible. I decided to try to implement a pre-commit hook to check syntax.
Unlike some of the git hooks, the pre-commit hook is very simple to use. It gets run when you try to make a commit, and the commit is aborted if the hook exits with a nonzero status.
I made one mistake right off the bat: I wrote the hook in Bourne shell, even though I swore years ago to stop writing shell scripts. Everything that I want to write in shell should be written in Perl instead or in some equivalently good language like Python. But the sample pre-commit hook was written in shell and when I saw it I went into automatic shell scripting mode and now I have yet another shell script that will have to be replaced with Perl when it gets bigger. I wish I would stop doing this.
Here is the hook, which, I should say up front, I have not yet tried in day-to-day use. The complete and current version is on github.
#!/bin/bash
function typeof () {
filename=$1
case $filename in
*.pl | *.pm) echo perl; exit ;;
esac
line1=$(head -1 $1)
case $line1 in '#!'*perl )
echo perl; exit ;;
esac
}
Some of the sample programs people showed me decided which files
needed to be checked based only on the filename. This is not good
enough. My most important Perl programs have filenames with no
extension. This typeof function decides which set of checks to
apply to each file, and the minimal demonstration version here can do
that based on filename or by looking for the #!...perl line in the
first line of the file contents. I expect that this function will
expand to include other file types; for example
*.py ) echo python; exit ;;
is an obvious next step.
if [ ! -z $COMMIT_OK ]; then
exit 0;
fi
This block is an escape hatch. One day I will want to bypass the hook
and make a commit without performing the checks, and then I can
COMMIT_OK=1 git commit …. There is actually a --no-verify flag to
git-commit that will skip the hook entirely, but I am unlikely to
remember it.
(I am also unlikely to remember COMMIT_OK=1. But I know from
experience that I will guess that I might have put an escape hatch
into the hook. I will also guess that there might be a flag to
git-commit that does what I want, but that will seem less likely to
be true, so I will look in the hook program first. This will be a
good move because my hook is much shorter than the git-commit man
page. So I will want the escape hatch, I will look for it in the best place,
and I will find it. That is worth two lines of code. Sometimes I feel
like the guy in Memento. I have not yet resorted to tattooing
COMMIT_OK=1 on my chest.)
exec 1>&2
This redirects the standard output of all subsequent commands to go to
standard error instead. It makes it more convenient to issue error
messages with echo and such like. All the output this hook produces
is diagnostic, so it is appropriate for it to go to standard error.
allOK=true
badFiles=
for file in $(git diff --cached --name-only | sort) ; do
allOK is true if every file so far has passed its checks.
badFiles is a list of files that failed their checks. the
git diff --cached --name-only function interrogates the Git index
for a list of the files that have been staged for commit.
type=$(typeof "$file")
This invokes the typeof function from above to decide the type of
the current file.
BAD=false
When a check discovers that the current file is bad, it will signal
this by setting BAD to true.
echo
echo "## Checking file $file (type $type)"
case $type in
perl )
perl -cw $file || BAD=true
[ -x $file ] || { echo "File is not executable"; BAD=true; }
;;
* )
echo "Unknown file type: $file; no checks"
;;
esac
This is the actual checking. To check Python files, we would add a
python) … ;; block here. The * ) case is a catchall. The perl
checks run perl -cw, which does syntax checking without executing
the program. It then checks to make sure the file is executable, which
I am sure is a mistake, because these checks are run for .pm files,
which are not normally supposed to be executable. But I wanted to
test it with more than one kind of check.
if $BAD; then
allOK=false;
badFiles="$badFiles;$file"
fi
done
If the current file was bad, the allOK flag is set false, and the
commit will be aborted. The current filename is appended to badFiles
for a later report. Bash has array variables but I don't remember how
they work and the manual made it sound gross. Already I regret not
writing this in a real language.
After the modified files have been checked, the hook exits successfully if they were all okay, and prints a summary if not:
if $allOK; then
exit 0;
else
echo ''
echo '## Aborting commit. Failed checks:'
for file in $(echo $badFiles | tr ';' ' '); do
echo " $file"
done
exit 1;
fi
This hook might be useful, but I don't know yet; as I said, I haven't
really tried it. But I can see ahead of time that it has a couple of
drawbacks. Of course it needs to be built out with more checks. A
minor bug is that I'd like to apply that is-executable check to Perl
files that do not end in .pm, but that will be an easy fix.
But it does have one serious problem I don't know how to fix yet. The hook checks the versions of the files that are in the working tree, but not the versions that are actually staged for the commit!
The most obvious problem this might cause is that I might try to commit some files, and then the hook properly fails because the files are broken. Then I fix the files, but forget to add the fixes to the index. But because the hook is looking at the fixed versions in the working tree, the checks pass, and the broken files are committed!
A similar sort of problem, but going the other way, is that I might
make several changes to some file, use git add -p to add the part I
am ready to commit, but then the commit hook fails, even though the
commit would be correct, because the incomplete changes are still in
the working tree.
I did a little tinkering with git stash save -k to try to stash the
unstaged changes before running the checks, something like this:
git stash save -k "pre-commit stash" || exit 2
trap "git stash pop" EXIT
but I wasn't able to get anything to work reliably. Stashing a modified index has never worked properly for me, perhaps because there is something I don't understand. Maybe I will get it to work in the future. Or maybe I will try a different method; I can think of several offhand:
The hook could copy each file to a temporary file and then run the check on the temporary file. But then the diagnostics emitted by the checks would contain the wrong filenames.
It could move each file out of the way, check out the currently-staged version of the file, check that, and then restore the working tree version. (It can skip this process for files where the staged and working versions are identical.) This is not too complicated, but if it messes up it could catastrophically destroy the unstaged changes in the working tree.
Check out the entire repository and modified index into a fresh working tree and check that, then discard the temporary working tree. This is probably too expensive.
This one is kind of weird. It could temporarily commit the current index (using
--no-verify), stash the working tree changes, and check the files. When the checks are finished, it would unstash the working tree changes, usegit-reset --softto undo the temporary commit, and proceed with the real commit if appropriate.Come to think of it, this last one suggests a much better version of the same thing: instead of a pre-commit hook, use a post-commit hook. The post-commit hook will stash any leftover working tree changes, check the committed versions of the files, unstash the changes, and, if the checks failed, undo the commit with
git-reset --soft.
Right now the last one looks much the best but perhaps there's something straightforward that I didn't think of yet.
[ Thanks to Adam Sjøgren, Jeffrey McClelland, and Jack Vickeridge for discussing this with me. Jeffrey McClelland also suggested that syntax checks could be profitably incorporated as a post-receive hook, which is run on the remote side when new commits are pushed to a remote. I said above that running the checks in the CI process seems too late, but the post-receive hook is earlier and might be just the thing. ]
[ Addendum: Daniel Holz wrote to tell me that the Yelp pre-commit frameworkhandles the worrisome case of unstaged working tree changes. The strategy is different from the ones I suggested above. If I'm reading this correctly, it records the unstaged changes in a patch file, which it sticks somewhere, and then checks out the index. If all the checks succeed, it completes the commit and then tries to apply the patch to restore the working tree changes. The checks in Yelp's framework might modify the staged files, and if they do, the patch might not apply; in this case it rolls back the whole commit. Thank you M. Holtz! ]
[Other articles in category /prog] permanent link
Tue, 14 Feb 2017
More thoughts on a line of code with three errors
Yesterday I wrote, in great irritation, about a line of code I had written that contained three errors.
I said:
What can I learn from this? Most obviously, that I should have tested my code before I checked it in.
Afterward, I felt that this was inane, and that the matter required a little more reflection. We do not test every single line of every program we write; in most applications that would be prohibitively expensive, and in this case it would have been excessive.
The change I was making was in the format of the diagnostic that the program emitted as it finished to report how long it had taken to run. This is not an essential feature. If the program does its job properly, it is of no real concern if it incorrectly reports how long it took to run. Two of my errors were in the construction of the message. The third, however, was a syntax error that prevented the program from running at all.
Having reflected on it a little more, I have decided that I am only really upset about the last one, which necessitated an emergency Saturday-morning repair by a co-worker. It was quite acceptable not to notice ahead of time that the report would be wrong, to notice it the following day, and to fix it then. I would have said “oops” and quietly corrected the code without feeling like an ass.
The third problem, however, was serious. And I could have prevented it with a truly minimal amount of effort, just by running:
perl -cw the-script
This would have diagnosed the syntax error, and avoided the main problem at hardly any cost. I think I usually remember to do something like this. Had I done it this time, the modified script would have gone into production, would have run correctly, and then I could have fixed the broken timing calculation on Monday.
In the previous article I showed the test program that I wrote to test the time calculation after the program produced the wrong output. I think it was reasonable to postpone writing this until after program ran and produced the wrong output. (The program's behavior in all other respects was correct and unmodified; it was only its report about its running time that was incorrect.) To have written the test ahead of time might be an excess of caution.
There has to be a tradeoff between cautious preparation and risk. Here I put everything on the side of risk, even though a tiny amount of caution would have eliminated most of the risk. In my haste, I made a bad trade.
[ Addendum 20170216: I am looking into automating the perl -cw check. ]
[Other articles in category /prog] permanent link
Mon, 13 Feb 2017
How I got three errors into one line of code
At work we had this script that was trying to report how long it had
taken to run, and it was using DateTime::Duration:
my $duration = $end_time->subtract_datetime($start_time);
my ( $hours, $minutes, $seconds ) =
$duration->in_units( 'hours', 'minutes', 'seconds' );
log_info "it took $hours hours $minutes minutes and $seconds seconds to run"
This looks plausible, but because
DateTime::Duration is shit,
it didn't work. Typical output:
it took 0 hours 263 minutes and 19 seconds to run
I could explain to you why it does this, but it's not worth your time.
I got tired of seeing 0 hours 263 minutes show up in my cron email
every morning, so I went to fix it. Here's what I changed it to:
my $duration = $end_time->subtract_datetime_absolute($start_time)->seconds;
my ( $hours, $minutes, $minutes ) = (int(duration/3600), int($duration/60)%60, $duration%3600);
I was at some pains to get that first line right, because getting
DateTime to produce a useful time interval value is a tricky
proposition. I did get the first line right. But the second line is
just simple arithmetic, I have written it several times before, so I
dashed it off, and it contains a syntax error, that duration/3600 is
missing its dollar sign, which caused the cron job to crash the next
day.
A co-worker got there before I did and fixed it for me. While he was
there he also fixed the $hours, $minutes, $minutes that should have
been $hours, $minutes, $seconds.
I came in this morning and looked at the cron mail and it said
it took 4 hours 23 minutes and 1399 seconds to run
so I went back to fix the third error, which is that $duration%3600
should have been $duration%60. The thrice-corrected line has
my ( $hours, $minutes, $seconds ) = (int($duration/3600), int($duration/60)%60, $duration%60);
What can I learn from this? Most obviously, that I should have tested my code before I checked it in. Back in 2013 I wrote:
Usually I like to draw some larger lesson from this sort of thing. … “Just write the tests, fool!”
This was a “just write the tests, fool!” moment if ever there was one. Madame Experience runs an expensive school, but fools will learn in no other.
I am not completely incorrigible. I did at least test the fixed code before I checked that in. The test program looks like this:
sub dur {
my $duration = shift;
my ($hours, $minutes, $seconds ) = (int($duration/3600), int($duration/60)%60, $duration%60);
sprintf "%d:%02d:%02d", $hours, $minutes, $seconds;
}
use Test::More;
is(dur(0), "0:00:00");
is(dur(1), "0:00:01");
is(dur(59), "0:00:59");
is(dur(60), "0:01:00");
is(dur(62), "0:01:02");
is(dur(122), "0:02:02");
is(dur(3599), "0:59:59");
is(dur(3600), "1:00:00");
is(dur(10000), "2:46:40");
done_testing();
It was not necessary to commit the test program, but it was necessary to write it and to run it. By the way, the test program failed the first two times I ran it.
Three errors in one line isn't even a personal worst. In 2012 I posted here about getting four errors into a one-line program.
[ Addendum 20170215: I have some further thoughts on this. ]
[Other articles in category /oops] permanent link
Tue, 07 Feb 2017
How many 24 puzzles are there?
[ Note: The tables in this article are important, and look unusually crappy if you read this blog through an aggregator. The properly-formatted version on my blog may be easier to follow. ]
A few months ago I wrote about puzzles of the following type: take four digits, say 1, 2, 7, 7, and, using only +, -, ×, and ÷, combine them to make the number 24. Since then I have been accumulating more and more material about these puzzles, which will eventually appear here. But meantime here is a delightful tangent.
In the course of investigating this I wrote programs to enumerate the solutions of all possible puzzles, and these programs were always much faster than I expected at first. It appears as if there are 10,000 possible puzzles, from «0,0,0,0» through «9,9,9,9». But a moment's thought shows that there are considerably fewer, because, for example, the puzzles «7,2,7,1», «1,2,7,7», «7,7,2,1», and «2,7,7,1» are all the same puzzle. How many puzzles are there really?
A back-of-the-envelope estimate is that only about 1 in 24 puzzles is really distinct (because there are typically 24 ways to rearrange the elements of a puzzle) and so there ought to be around !!\frac{10000}{24} \approx 417!! puzzles. This is an undercount, because there are fewer duplicates of many puzzles; for example there are not 24 variations of «1,2,7,7», but only 12. The actual number of puzzles turns out to be 715, which I think is not an obvious thing to guess.
Let's write !!S(d,n)!! for the set of sequences of length !!n!! containing up to !!d!! different symbols, with the duplicates removed: when two sequences are the same except for the order of their symbols, we will consider them the same sequence.
Or more concretely, we may imagine that the symbols are sorted into nondecreasing order, so that !!S(d,n)!! is the set of nondecreasing sequences of length !!n!! of !!d!! different symbols.
Let's also write !!C(d,n)!! for the number of elements of !!S(d,n)!!.
Then !!S(10, 4)!! is the set of puzzles where input is four digits. The claim that there are !!715!! such puzzles is just that !!C(10,4) = 715!!. A tabulation of !!C(\cdot,\cdot)!! reveals that it is closely related to binomial coefficients, and indeed that $$C(d,n)=\binom{n+d-1}{d-1}.\tag{$\heartsuit$}$$
so that the surprising !!715!! is actually !!\binom{13}{9}!!. This is not hard to prove by induction, because !!C(\cdot,\cdot)!! is easily shown to obey the same recurrence as !!\binom\cdot\cdot!!: $$C(d,n) = C(d-1,n) + C(d,n-1).\tag{$\spadesuit$}$$
To see this, observe that an element of !!C(d,n)!! either begins with a zero or with some other symbol. If it begins with a zero, there are !!C(d,n-1)!! ways to choose the remaining !!n-1!! symbols in the sequence. But if it begins with one of the other !!d-1!! symbols it cannot contain any zeroes, and what we really have is a length-!!n!! sequence of the symbols !!1\ldots (d-1)!!, of which there are !!C(d-1, n)!!.
| 0 0 0 0 | 1 1 1 |
| 0 0 0 1 | 1 1 2 |
| 0 0 0 2 | 1 1 3 |
| 0 0 0 3 | 1 1 4 |
| 0 0 1 1 | 1 2 2 |
| 0 0 1 2 | 1 2 3 |
| 0 0 1 3 | 1 2 4 |
| 0 0 2 2 | 1 3 3 |
| 0 0 2 3 | 1 3 4 |
| 0 0 3 3 | 1 4 4 |
| 0 1 1 1 | 2 2 2 |
| 0 1 1 2 | 2 2 3 |
| 0 1 1 3 | 2 2 4 |
| 0 1 2 2 | 2 3 3 |
| 0 1 2 3 | 2 3 4 |
| 0 1 3 3 | 2 4 4 |
| 0 2 2 2 | 3 3 3 |
| 0 2 2 3 | 3 3 4 |
| 0 2 3 3 | 3 4 4 |
| 0 3 3 3 | 4 4 4 |
Now we can observe that !!\binom74=\binom73!! (they are both 35) so that !!C(5,3) = C(4,4)!!. We might ask if there is a combinatorial proof of this fact, consisting of a natural bijection between !!S(5,3)!! and !!S(4,4)!!. Using the relation !!(\spadesuit)!! we have:
$$ \begin{eqnarray} C(4,4) & = & C(3, 4) + & C(4,3) \\ C(5,3) & = & & C(4,3) + C(5,2) \\ \end{eqnarray}$$
so part of the bijection, at least, is clear: There are !!C(4,3)!! elements of !!S(4,4)!! that begin with a zero, and also !!C(4,3)!! elements of !!S(5, 3)!! that do not begin with a zero, so whatever the bijection is, it ought to match up these two subsets of size 20. This is perfectly straightforward; simply match up !!«0, a, b, c»!! (blue) with !!«a+1, b+1, c+1»!! (pink), as shown at right.
But finding the other half of the bijection, between !!S(3,4)!! and !!S(5,2)!!, is not so straightforward. (Both have 15 elements, but we are looking for not just any bijection but for one that respects the structure of the elements.) We could apply the recurrence again, to obtain:
$$ \begin{eqnarray} C(3,4) & = \color{darkred}{C(2, 4)} + \color{darkblue}{C(3,3)} \\ C(5,2) & = \color{darkblue}{C(4,2)} + \color{darkred}{C(5,1)} \end{eqnarray}$$
and since $$ \begin{eqnarray} \color{darkred}{C(2, 4)} & = \color{darkred}{C(5,1)} \\ \color{darkblue}{C(3,3)} & = \color{darkblue}{C(4,2)} \end{eqnarray}$$
we might expect the bijection to continue in that way, mapping !!\color{darkred}{S(2,4) \leftrightarrow S(5,1)}!! and !!\color{darkblue}{S(3,3) \leftrightarrow S(4,2)}!!. Indeed there is such a bijection, and it is very nice.
To find the bijection we will take a detour through bitstrings. There is a natural bijection between !!S(d, n)!! and the bit strings that contain !!d-1!! zeroes and !!n!! ones. Rather than explain it with pseudocode, I will give some examples, which I think will make the point clear. Consider the sequence !!«1, 1, 3, 4»!!. Suppose you are trying to communicate this sequence to a computer. It will ask you the following questions, and you should give the corresponding answers:
- “Is the first symbol 0?” (“No”)
- “Is the first symbol 1?” (“Yes”)
- “Is the second symbol 1?” (“Yes”)
- “Is the third symbol 1?” (“No”)
- “Is the third symbol 2?” (“No”)
- “Is the third symbol 3?” (“Yes”)
- “Is the fourth symbol 3?” (“No”)
- “Is the fourth symbol 4?” (“Yes”)
At each stage the
computer asks about the identity of the next symbol. If the answer is
“yes” the computer has learned another symbol and moves on to the next
element of the sequence. If it is “no” the computer tries guessing a
different symbol. The “yes” answers become ones and “no”
answers become zeroes, so that the resulting bit string is 0 1 1 0 0 1 0 1.
It sometimes happens that the computer figures out all the elements of the sequence before using up its !!n+d-1!! questions; in this case we pad out the bit string with zeroes, or we can imagine that the computer asks some pointless questions to which the answer is “no”. For example, suppose the sequence is !!«0, 1, 1, 1»!!:
- “Is the first symbol 0?” (“Yes”)
- “Is the second symbol 0?” (“No”)
- “Is the second symbol 1?” (“Yes”)
- “Is the third symbol 1?” (“Yes”)
- “Is the fourth symbol 1?” (“Yes”)
The bit string is 1 0 1 1 1 0 0 0, where the final three 0 bits are
the padding.
We can reverse the process, simply taking over the role of the
computer. To find the sequence that corresponds to the bit string
0 1 1 0 1 0 0 1, we ask the questions ourselves and use the bits as the
answers:
- “Is the first symbol 0?” (“No”)
- “Is the first symbol 1?” (“Yes”)
- “Is the second symbol 1?” (“Yes”)
- “Is the third symbol 1?” (“No”)
- “Is the third symbol 2?” (“Yes”)
- “Is the fourth symbol 2?” (“No”)
- “Is the fourth symbol 3?” (“No”)
- “Is the fourth symbol 4?” (“Yes”)
We have recovered the sequence !!«1, 1, 2, 4»!! from the
bit string 0 1 1 0 1 0 0 1.
This correspondence establishes relation !!(\heartsuit)!! in a different way from before: since there is a natural bijection between !!S(d, n)!! and the bit strings with !!d-1!! zeroes and !!n!! ones, there are certainly !!\binom{n+d-1}{d-1}!! of them as !!(\heartsuit)!! says because there are !!n+d-1!! bits and we may choose any !!d-1!! to be the zeroes.
We wanted to see why !!C(5,3) = C(4,4)!!. The detour above shows that there is a simple bijection between
!!S(5,3)!! and the bit strings with 4 zeroes and 3 ones
on one hand, and between
!!S(4,4)!! and the bit strings with 3 zeroes and 4 ones
on the other hand. And of course the bijection between the two sets of bit strings is completely obvious: just exchange the zeroes and the ones.
The table below shows the complete bijection between !!S(4,4)!! and its descriptive bit strings (on the left in blue) and between !!S(5, 3)!! and its descriptive bit strings (on the right in pink) and that the two sets of bit strings are complementary. Furthermore the top portion of the table shows that the !!S(4,3)!! subsets of the two families correspond, as they should—although the correct correspondence is the reverse of the one that was displayed earlier in the article, not the suggested !!«0, a, b, c» \leftrightarrow «a+1, b+1, c+1»!! at all. Instead, in the correct table, the initial digit of the !!S(4,4)!! entry says how many zeroes appear in the !!S(5,3)!! entry, and vice versa; then the increment to the next digit says how many ones, and so forth.
| !!S(4,4)!! | (bits) | (complement bits) | !!S(5,3)!! |
|---|---|---|---|
| 0 0 0 0 | 1 1 1 1 0 0 0 | 0 0 0 0 1 1 1 | 4 4 4 |
| 0 0 0 1 | 1 1 1 0 1 0 0 | 0 0 0 1 0 1 1 | 3 4 4 |
| 0 0 0 2 | 1 1 1 0 0 1 0 | 0 0 0 1 1 0 1 | 3 3 4 |
| 0 0 0 3 | 1 1 1 0 0 0 1 | 0 0 0 1 1 1 0 | 3 3 3 |
| 0 0 1 1 | 1 1 0 1 1 0 0 | 0 0 1 0 0 1 1 | 2 4 4 |
| 0 0 1 2 | 1 1 0 1 0 1 0 | 0 0 1 0 1 0 1 | 2 3 4 |
| 0 0 1 3 | 1 1 0 1 0 0 1 | 0 0 1 0 1 1 0 | 2 3 3 |
| 0 0 2 2 | 1 1 0 0 1 1 0 | 0 0 1 1 0 0 1 | 2 2 4 |
| 0 0 2 3 | 1 1 0 0 1 0 1 | 0 0 1 1 0 1 0 | 2 2 3 |
| 0 0 3 3 | 1 1 0 0 0 1 1 | 0 0 1 1 1 0 0 | 2 2 2 |
| 0 1 1 1 | 1 0 1 1 1 0 0 | 0 1 0 0 0 1 1 | 1 4 4 |
| 0 1 1 2 | 1 0 1 1 0 1 0 | 0 1 0 0 1 0 1 | 1 3 4 |
| 0 1 1 3 | 1 0 1 1 0 0 1 | 0 1 0 0 1 1 0 | 1 3 3 |
| 0 1 2 2 | 1 0 1 0 1 1 0 | 0 1 0 1 0 0 1 | 1 2 4 |
| 0 1 2 3 | 1 0 1 0 1 0 1 | 0 1 0 1 0 1 0 | 1 2 3 |
| 0 1 3 3 | 1 0 1 0 0 1 1 | 0 1 0 1 1 0 0 | 1 2 2 |
| 0 2 2 2 | 1 0 0 1 1 1 0 | 0 1 1 0 0 0 1 | 1 1 4 |
| 0 2 2 3 | 1 0 0 1 1 0 1 | 0 1 1 0 0 1 0 | 1 1 3 |
| 0 2 3 3 | 1 0 0 1 0 1 1 | 0 1 1 0 1 0 0 | 1 1 2 |
| 0 3 3 3 | 1 0 0 0 1 1 1 | 0 1 1 1 0 0 0 | 1 1 1 |
| 1 1 1 1 | 0 1 1 1 1 0 0 | 1 0 0 0 0 1 1 | 0 4 4 |
| 1 1 1 2 | 0 1 1 1 0 1 0 | 1 0 0 0 1 0 1 | 0 3 4 |
| 1 1 1 3 | 0 1 1 1 0 0 1 | 1 0 0 0 1 1 0 | 0 3 3 |
| 1 1 2 2 | 0 1 1 0 1 1 0 | 1 0 0 1 0 0 1 | 0 2 4 |
| 1 1 2 3 | 0 1 1 0 1 0 1 | 1 0 0 1 0 1 0 | 0 2 3 |
| 1 1 3 3 | 0 1 1 0 0 1 1 | 1 0 0 1 1 0 0 | 0 2 2 |
| 1 2 2 2 | 0 1 0 1 1 1 0 | 1 0 1 0 0 0 1 | 0 1 4 |
| 1 2 2 3 | 0 1 0 1 1 0 1 | 1 0 1 0 0 1 0 | 0 1 3 |
| 1 2 3 3 | 0 1 0 1 0 1 1 | 1 0 1 0 1 0 0 | 0 1 2 |
| 1 3 3 3 | 0 1 0 0 1 1 1 | 1 0 1 1 0 0 0 | 0 1 1 |
| 2 2 2 2 | 0 0 1 1 1 1 0 | 1 1 0 0 0 0 1 | 0 0 4 |
| 2 2 2 3 | 0 0 1 1 1 0 1 | 1 1 0 0 0 1 0 | 0 0 3 |
| 2 2 3 3 | 0 0 1 1 0 1 1 | 1 1 0 0 1 0 0 | 0 0 2 |
| 2 3 3 3 | 0 0 1 0 1 1 1 | 1 1 0 1 0 0 0 | 0 0 1 |
| 3 3 3 3 | 0 0 0 1 1 1 1 | 1 1 1 0 0 0 0 | 0 0 0 |
Observe that since !!C(d,n) = \binom{n+d-1}{d-1} = \binom{n+d-1}{n} = C(n+1, d-1)!! we have in general that !!C(d,n) = C(n+1, d-1)!!, which may be surprising. One might have guessed that since !!C(5,3) = C(4,4)!!, the relation was !!C(d,n) = C(d+1, n-1)!! and that !!S(d,n)!! would have the same structure as !!S(d+1, n-1)!!, but it isn't so. The two arguments exchange roles. Following the same path, we can identify many similar ‘coincidences’. For example, there is a simple bijection between the original set of 715 puzzles, which was !!S(10,4)!!, and !!S(5,9)!!, the set of nondecreasing sequences of !!0\ldots 4!! of length !!9!!.
[ Thanks to Bence Kodaj for a correction. ]
[ Addendum 20170829: Conway and Guy, in The Book of Numbers, describe the same bijection, but a little differently; see their discussion of the Sweet Seventeen deck on pages 70–71. ]
[ Addendum 20171015: More about this, using Burnside's lemma. ]
[Other articles in category /math] permanent link
Tue, 31 Jan 2017Below, One Liberty Place, the second-tallest building in my home city of Philadelphia. (Completed 1987, height 288 meters.)
Below, Zhongtian International Mansion at Fortune Plaza, the tallest building in Ürümqi, capital city of Xinjiang in northwest China.
(Completed 2007, height 230 meters.)
[ Addendum: Perhaps I should mention that One Liberty Place is itself widely seen as a knockoff of the much more graceful and elegant Chrysler Building in New York City. (Completed 1930, height 319 meters.) ]
[ Addendum: I brought this to the attention of GroJLart, the foulmouthed architecture blogger who knows everything, absolutely everything, about Philadelphia buildings, and he said “Thanks. I wrote an article on the same subject in 2011”. Of course. ]
[Other articles in category /misc] permanent link
Mon, 30 Jan 2017
Digit symbols in the Parshvanatha magic square
In last month's article about the magic square at the Parshvanatha temple, shown at right, I said:
It has come to my attention that the digit symbols in the magic square are not too different from the current forms of the digit symbols in the Gujarati script. The temple is not very close to Gujarat or to the area in which Gujarati is common, so I guess that the digit symbols in Indian languages have evolved in the past thousand years, with the Gujarati versions remaining closest to the ancient forms, or else perhaps Gujarati was spoken more widely a thousand years ago. I would be interested to hear about this from someone who knows.
Shreevatsa R. replied in detail, and his reply was so excellent that, finding no way to improve it by adding or taking away, I begged his permission to republish it without change, which he generously granted.
Am sending this email to say:
- Why it shouldn't be surprising if the temple had Gujarati numerals
- Why the numerals aren't Gujarati numerals :-)
The Parshvanatha temple is located in the current state of Madhya Pradesh. Here is the location of the temple within a map of the state:
And here you can see that the above state of Madhya Pradesh (14 in the image below) is adjacent to the state of Gujarat (7):
The states of India are (sort of) organized along linguistic lines, and neighbouring states often have overlap or similarities in their languages. So a priori it shouldn't be too surprising if the language is that of a neighbouring state.
But, as you rightly say, the location of the Parshvanatha temple is actually quite far from the state (7) where Gujarat is spoken; it's closer to 27 in the above map (state named Uttar Pradesh).
Well, the Parshvanatha temple is believed to have been built "during the reign of the Chandela king Dhanga", and the Chandela kings were feudatories (though just beginning to assert sovereignty at the time) of the Gurjara-Pratihara kings, and "Gurjara" is where the name of the language of "Gujarati" comes from. So it's possible that they used the "official" language of the reigning kings, as with colonies. In fact the green area of the Gurjara-Pratihara kings in this map covers the location of the Parshvanatha temple:

But actually this is not a very convincing argument, because the link between Gurjara-Pratiharas and modern Gujarati is not too strong (at least I couldn't find it in a few minutes on Wikipedia :P)
So moving on...
Are the numerals really similar to Gujarati numerals? These are the numbers 1 to 16 from your blog post, ordered according to the usual order:








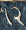


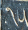

These are the numerals in a few current Indic scripts (as linked from your blog post):
Look at the first two rows above. Perhaps because of my familiarity with Devanagari, I cannot really see any big difference between the Devanagari and Gujarati symbols except for the 9: the differences are as minor as variation between fonts. (To see how much the symbols can change because of font variation, one can go to Google Fonts' Devanagari page and Google Fonts' Gujarati page and click on one of the sample texts and enter "० १ २ ३ ४ ५ ६ ७ ८ ९" and "૦ ૧ ૨ ૩ ૪ ૫ ૬ ૭ ૮ ૯" respectively, then "Apply to all fonts". Some fonts are bad, though.)
(In fact, even the Gurmukhi and Tibetan are somewhat recognizable, for someone who can read Devanagari.)
So if we decide that the Parshvanatha temple's symbols are actually closer not to modern Gujarati but to modern Devanagari (e.g. the "3" has a tail in the temple symbols which is present in Devanagari but missing in Gujarati), then the mystery disappears: Devanagari is still the script used in the state of Madhya Pradesh (and Uttar Pradesh, etc: it's the script used for Hindi, Marathi, Nepali, Sanskrit, and many other languages).
Finally, for the complete answer, we can turn to history.
The Parshvanatha temple was built during 950 to 970 CE. Languages: Modern Gujarati dates from 1800, Middle Gujarati from ~1500 to 1800, Old Gujarati from ~1100 to 1500. So the temple is older than the earliest language called "Gujarati". (Similarly, modern Hindi is even more recent.) Turning to scripts instead: see under Brahmic scripts.
- Nagari, 8th century
- Devanagari, 13th century
- Gujarati 16th century
So at the time the temple was built, neither Gujarati script nor Devanagari proper existed. The article on the Gujarati script traces its origin to the Devanagari script, which itself is a descendant of Nagari script.
At right are the symbols from the Nagari script, which I think are closer in many respects to the temple symbols.
So overall, if we trace the numerals in (a subset of) the family tree of scripts:
Brahmi > Gupta > Nagari > Devanagari > Gujarati
we'll find that the symbols of the temple are somewhere between the "Nagari" and "Devanagari" forms. (Most of the temple digits are the same as in the "Nagari" example above, except for the 5 which is closer to the Devanagari form.)
BTW, your post was about the numerals, but from being able to read modern Devanagari, I can also read some of the words above the square: the first line ends with ".. putra śrī devasarmma" (...पुत्र श्री देवसर्म्म) (Devasharma, son of...), and these words have the top bar which is missing in Gujarati script.
[Other articles in category /lang] permanent link





























