Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 29 Oct 2018
Warning: Long and possibly dull.
I spent a big chunk of today fixing a bug that should have been easy but that just went deeper and deeper. If you look over in the left sidebar there you'll se a sub-menu titled “subtopics” with a per-category count of the number of articles in each section of this blog. (Unless you're using a small display, where the whole sidebar is suppressed.) That menu was at least a year out of date. I wanted to fix it.
The blog software I use is the wonderfully terrible
Blosxom. It has a plugin system,
and the topic menu was generated by a plugin that I wrote some time
ago. When the topic plugin starts up it opens two Berkeley
DB files. Each is a simple
key-value mapping. One maps topic names to article counts. The other
is just a set of article IDs for the articles that have already been
counted. These key-value mappings are exposed in Perl as hash
variables.
When I regenerate the static site, the topic plugin has a
subroutine, story, that is called for each article in each generated
page. The business end of the subroutine looks something like this:
sub story {
# ... acquire arguments ..
if ( $Seen{ $article_id } ) {
return;
} else {
$topic_count{ $article_topic }++;
$Seen{ $article_id } = 1;
}
}
The reason the menu wasn't being updated is that at some point in the
past, I changed the way story plugins were called. Out of the box,
Blosxom passes story a list of five arguments, like this:
my ($pkg, $path, $filename, $story_ref, $title_ref) = @_;
Over the years I had extended this to eight or nine, and I felt it was getting unwieldy, so at some point I changed it to pass a hash, like this:
my %args = (
category => $path, # directory of this story
filename => $fn, # filename of story, without suffix
...
)
$entries = $plugin->story(\%args);
When I made this conversion, I had to convert all the plugins. I
missed converting topic. So instead of getting the eight or nine
arguments it expected, it got two: the plugin itself, and the hash.
Then it used the hash as the key into the databases, which by now
were full of thousands of entries for things like HASH(0x436c1d)
because that is what Perl silently and uselessly does if you try to
use a hash as if it were a string.
Anyway, this was easily fixed, or should have been easily fixed. All I needed to do was convert the plugin to use the new calling convention. Ha!
One thing all my plugins do when they start up is write a diagnostic log, something like this:
sub start {
open F, ">", "/tmp/topic.$>";
print F "Writing to $blosxom::plugin_state_dir/topics\n";
}
Then whenever the plugin has something to announce it just does
print F. For example, when the plugin increments the count for a
topic, it inserts a message like this:
print F "'$article_id' is item $topic_count{$article_topic} in topic $article_topic.\n";
If the article has already been seen, it remains silent.
Later I can look in /tmp/topic.119 or whatever to see what it said.
When I'm debugging a plugin, I can open an Emacs buffer on this file
and put it in auto-revert mode so that Emacs always displays the
current contents of the file.
Blosxom has an option to generate pages on demand for a web browser,
and I use this for testing. https://blog.plover.com/PATH is the
static version of the article, served from a pre-generated static
file. But https://blog.plover.com/test/PATH calls Blosxom as a CGI
script to generate the article on the fly and send it to the browser.
So I visited https://blog.plover.com/test/2018/, which should
generate a page with all the articles from 2018, to see what the
plugin put in the file. I should have seen it inserting a lot of
HASH(0x436c1d) garbage:
'lang/etym/Arabic-2' is article 1 in topic HASH(0x22c501b)
'addenda/200801' is article 1 in topic HASH(0x5300aa2)
'games/poker-24' is article 1 in topic HASH(0x4634a79)
'brain/pills' is article 1 in topic HASH(0x1a9f6ab)
'lang/long-s' is article 1 in topic HASH(0x29489be)
'google-roundup/200602' is article 1 in topic HASH(0x360e6f5)
'prog/van-der-waerden-1' is article 1 in topic HASH(0x3f2a6dd)
'math/math-se-gods' is article 1 in topic HASH(0x412b105)
'math/pow-sqrt-2' is article 1 in topic HASH(0x23ebfe4)
'aliens/dd/p22' is article 1 in topic HASH(0x878748)
I didn't see this. I saw the startup message and nothing else. I did
a bunch of very typical debugging, such as having the plugin print a
message every time story was called:
sub story {
print F "Calling 'story' (@_)\n";
...
}
Nothing. But I knew that story was being called. Was I maybe
editing the wrong file on disk? No, because I could introduce a
syntax error and the browser would happily report the resulting 500
Server Error. Fortunately, somewhere along the way I changed
open F, ">", "/tmp/topic.$>";
to
open F, ">>", "/tmp/topic.$>";
and discovered that each time I loaded the page, the plugin was run
exactly twice. When I had had >, the second run would immediately
overwrite the diagnostics from the first run.
But why was the plugin being run twice? This took quite a while to track down. At first I suspected that Blosxom was doing it, either on purpose or by accident. My instance of Blosxom is a hideous Frankenstein monster that has been cut up and reassembled and hacked and patched dozens of times since 2006 and it is full of unpleasant surprises. But the problem turned out to be quite different. Looking at the Apache server logs I saw that the browser was actually making two requests, not one:
100.14.199.174 - mjd [28/Oct/2018:18:00:49 +0000] "GET /test/2018/ HTTP/1.1" 200 213417 "-" ...
100.14.199.174 - mjd [28/Oct/2018:18:00:57 +0000] "GET /test/2018/BLOGIMGREF/horseshoe-curve-small.mp4 HTTP/1.1" 200 623 ...
Since the second request was for a nonexistent article, the story
callback wasn't invoked in the second run. So I would see the startup
message, but I didn't see any messages from the story callback.
They had been there in the first run for the first request, but that
output was immediately overwritten on the second request.
BLOGIMGREF is a tag that I include in image URLs, that expands to
whatever is the appropriate URL for the images for the particular
article it's in. This expansion is done by a different plugin, called
path2, and apparently in this case it wasn't being expanded. The
place it was being used was easy enough to find; it looked like this:
<video width="480" height="270" controls>
<source src="BLOGIMGREF/horseshoe-curve-small.mp4" type="video/mp4">
</video>
So I dug down into the path2 plugin to find out why BLOGIMGREF
wasn't being replaced by the correct URL prefix, which should have
been in a different domain entirely.
This took a very long time to track down, and I think it was totally
not my fault. When I first wrote path2 I just had it do a straight
text substitution. But at some point I had improved this to use a real
HTML parser, supplied by the Perl HTML::TreeBuilder module. This
would parse the article body and return a tree of HTML::Element
objects, which the plugin would then filter, looking for img and a
elements. The plugin would look for the magic tags and replace them
with the right URLs.
This magic tag was not in an img or an a element, so the plugin
wasn't finding it. I needed to tell the plugin to look in source
elements also. Easy fix! Except it didn't work.
Then began a tedious ten-year odyssey through the HTML::TreeBuilder
and HTML::Element modules to find out why it hadn't worked. It took
a long time because I'm good at debugging. When you lose your wallet,
you look in the most likely places first, and I know from many years
of experience what the most likely places are — usually in my
misunderstanding of the calling convention of some library I didn't
write, or my misunderstanding of what it was supposed to do; sometimes
in my own code. The downside of this is that when the wallet is in
an unlikely place it takes a really long time to find it.
The end result this time was that it wasn't in any of the usual
places. It was 100% not my fault: HTML::TreeBuilder has a bug in
its parser. For
some reason it completely ignores source elements:
perl -MHTML::TreeBuilder -e '$z = q{<source src="/media/horseshoe-curve-small.mp4" type="video/mp4"/>}; HTML::TreeBuilder->new->parse($z)->eof->elementify()->dump(\*STDERR)'
The output is:
<html> @0 (IMPLICIT)
<head> @0.0 (IMPLICIT)
<body> @0.1 (IMPLICIT)
No trace of the source element. I reported the bug, commented out
the source element in the article, and moved on. (The article was
unpublished, in part because I could never get the video to play
properly in the browser. I had been tearing my hair about over it,
but now I knew why! The BLOGIMGREF in the URL was not being
replaced! Because of a bug in the HTML parser!)
With that fixed I went back to finish the work on the topic plugin.
Now that the diagnostics were no longer being overwritten by the bogus
request for /test/2018/BLOGIMGREF/horseshoe-curve-small.mp4, I
expected to see the HASH(0x436c1d) garbage. I did, and I fixed
that. Then I expected the 'article' is article 17 in topic prog
lines to go away. They were only printed for new articles that hadn't
been seen before, and by this time every article should have been in
the %Seen database.
But no, every article on the page, every article from 2018, was being processed every time I rebuilt the page. And the topic counts were going up, up, up.
This also took a long time to track down, because again the cause was so unlikely. I must have been desperate because I finally found it by doing something like this:
if ( $Seen{ $article_id } ) {
return;
} else {
$topic_count{ $article_topic }++;
$Seen{ $article_id } = 1;
die "WTF!!" unless $Seen{ $article_id };
}
Yep, it died. Either Berkeley DB, or Perl's BerkeleyDB module, was
just flat-out not working. Both of them are ancient, and this kind of
shocking bug should have been shaken out 20 years go. WTF, indeed,
I fixed this by discarding the entire database and rebuilding it. I
needed to clean out the HASH(0x436c1d) crap anyway.
I am sick of DB files. I am never using them again. I have been bitten too many times. From now on I am doing the smart thing, by which I mean the dumb thing, the worse-is-better thing: I will read a plain text file into memory, modify it, and write out the modified version whem I am done. It will be simple to debug the code and simple to modify the database.
Well, that sucked. Usually this sort of thing is all my fault, but this time I was only maybe 10% responsible.
At least it's working again.
[ Addendum: I learned that discarding the source element is a
⸢feature⸣ of HTML::Parser. It has a list of valid HTML4 tags and by
default it ignores any element that isn't one. The maintainer won't
change the default to HTML5 because that might break backward
compatibility for people who are depending on this behavior. ]
[Other articles in category /prog/bug] permanent link
Sun, 28 Oct 2018
More about auto-generated switch-cases
Yesterday I described what I thought was a cool hack I had seen in
rsync, to try several
possible methods and then remember which one worked so as to skip the
others on future attempts. This was abetted by a different hack, for
automatically generating the case labels for the switch, which I
thought was less cool.
Simon Tatham wrote to me with a technique for compile-time generation
of case labels that I liked better. Recall that the context is:
int set_the_mtime(...) {
static int switch_step = 0;
switch (switch_step) {
#ifdef METHOD_1_MIGHT_WORK
case ???:
if (method_1_works(...))
break;
switch_step++;
/* FALLTHROUGH */
#endif
#ifdef METHOD_2_MIGHT_WORK
case ???:
if (method_2_works(...))
break;
switch_step++;
/* FALLTHROUGH */
#endif
... etc. ...
}
return 1;
}
M. Tatham suggested this:
#define NEXT_CASE switch_step = __LINE__; case __LINE__
You use it like this:
int set_the_mtime(...) {
static int switch_step = 0;
switch (switch_step) {
default:
#ifdef METHOD_1_MIGHT_WORK
NEXT_CASE:
if (method_1_works(...))
break;
/* FALLTHROUGH */
#endif
#ifdef METHOD_2_MIGHT_WORK
NEXT_CASE:
if (method_2_works(...))
break;
/* FALLTHROUGH */
#endif
... etc. ...
}
return 1;
}
The case labels are no longer consecutive, but that doesn't matter;
all that is needed is for them to be distinct. Nobody is ever going
to see them except the compiler. M. Tatham called this
“the case __LINE__ trick”, which suggested to me that it was
generally known. But it was new to me.
One possible drawback of this method is that if the file contains more
than 255 lines, the case labels will not fit in a single byte. The
ultimate effect of this depends on how the compiler handles switch.
It might be compiled into a jump table with !!2^{16}!! entries, which
would only be a problem if you had to run your program in 1986. Or it
might be compiled to an if-else tree, or something else we don't want.
Still, it seems like a reasonable bet.
You could use case 0: at the beginning instead of default:, but
that's not as much fun. M. Tatham observes that it's one of very few
situations in which it makes sense not to put default: last. He
says this is the only other one he knows:
switch (month) {
case SEPTEMBER:
case APRIL:
case JUNE:
case NOVEMBER:
days = 30;
break;
default:
days = 31;
break;
case FEBRUARY:
days = 28;
if (leap_year)
days = 29;
break;
}
Addendum 20181029: Several people have asked for an explanation of why
the default is in the middle of the last switch. It follows the
pattern of a very well-known mnemonic
poem that goes
Thirty days has September,
April, June and November.
All the rest have thirty-one
Except February, it's a different one:
It has 28 days clear,
and 29 each leap year.
Wikipedia says:
[The poem has] been called “one of the most popular and oft-repeated verses in the English language” and “probably the only sixteenth-century poem most ordinary citizens know by heart”.
[Other articles in category /prog] permanent link
Sat, 27 Oct 2018
A fun optimization trick from rsync
I was looking at the rsync source code today and I saw a neat trick
I'd never seen before. It wants to try to set the mtime on a file,
and there are several methods that might work, but it doesn't know
which. So it tries them in sequence, and then it remembers which one
worked and uses that method on subsequent calls:
int set_the_mtime(...) {
static int switch_step = 0;
switch (switch_step) {
case 0:
if (method_0_works(...))
break;
switch_step++;
/* FALLTHROUGH */
case 1:
if (method_1_works(...))
break;
switch_step++;
/* FALLTHROUGH */
case 2:
...
case 17:
if (method_17_works(...))
break;
return -1; /* ultimate failure */
}
return 0; /* success */
}
The key item here is the static switch_step variable. The first
time the function is called, its value is 0 and the switch starts at
case 0. If methods 0 through 7 all fail and method 8 succeeds,
switch_step will have been set to 8, and on subsequent calls to the
function the switch will jump immediately to case 8.
The actual code is a little more sophisticated than this. The list of
cases is built depending on the setting of several compile-time config
flags, so that the code that is compiled only includes the methods
that are actually callable. Calling one of the methods can produce
three distinguishable results: success, real failure (because of
permission problems or some such), or a sort of fake failure
(ENOSYS) that only means that the underlying syscall is
unimplemented. This third type of result is the one where it makes
sense to try another method. So the cases actually look like this:
case 7:
if (method_7_works(...))
break;
if (errno != ENOSYS)
return -1; /* real failure */
switch_step++;
/* FALLTHROUGH */
On top of this there's another trick: since the various cases are
conditionally compiled depending on the config flags, we don't know
ahead of time which ones will be included. So the case labels
themselves are generated at compile time this way:
#include "case_N.h"
if (method_7_works(...))
break;
...
#include "case_N.h"
if (method_8_works(...))
break;
...
The first time we #include "case_N.h", it turns into case 0:; the
second time, it turns into case 1:, and so on:
#if !defined CASE_N_STATE_0
#define CASE_N_STATE_0
case 0:
#elif !defined CASE_N_STATE_1
#define CASE_N_STATE_1
case 1:
...
#else
#error Need to add more case statements!
#endif
Unfortunately you can only use this trick one switch per file.
Although I suppose if you really wanted to reuse it you could make a
reset_case_N.h file which would contain
#undef CASE_N_STATE_0
#undef CASE_N_STATE_1
...
[ Addendum 20181028: Simon Tatham brought up a technique for
generating the case labels that we agree is
better than what rsync did. ]
[Other articles in category /prog] permanent link
Fri, 26 Oct 2018
A snide addendum about implicit typeclass instances
In an earlier article I demanded:
Maybe someone can explain to me why this is a useful behavior, and then explain why it is so useful that it should happen automatically …
“This” being that instead of raising a type error, Haskell quietly accepts this nonsense:
fmap ("super"++) (++"weasel")
but it clutches its pearls and faints in horror when confronted with this expression:
fmap ("super"++) "weasel"
Nobody did explain this.
But I imagined
someone earnestly explaining: “Okay, but in the first case, the
(++"weasel") is interpreted as a value in the environment functor,
so fmap is resolved to its the environment instance, which is (.).
That doesn't happen in the second example.”
Yeah, yeah, I know that. Hey, you know what else is a functor? The
identity functor. If fmap can be quietly demoted to its (->) e
instance, why can't it also be quietly demoted to its Id instance,
which is ($), so that fmap ("super"++) "weasel" can quietly
produce "superweasel"?
I understand this is a terrible idea. To be clear, what I want is for it to collapse on the divan for both expressions. Pearl-clutching is Haskell's finest feature and greatest strength, and it should do it whenever possible.
[Other articles in category /prog/haskell] permanent link
Tue, 23 Oct 2018A few years back I asked on history stackexchange:
Wikipedia's article on the Halifax Gibbet says, with several citations:
…ancient custom and law gave the Lord of the Manor the authority to execute summarily by decapitation any thief caught with stolen goods to the value of 13½d or more…
My question being: why 13½ pence?
This immediately attracted an answer that was no good at all. The author began by giving up:
This question is historically unanswerable.
I've met this guy and probably you have too: he knows everything worth knowing, and therefore what he doesn't know must be completely beyond the reach of mortal ken. But that doesn't mean he will shrug and leave it at that, oh no. Having said nobody could possibly know, he will nevertheless ramble for six or seven decreasingly relevant paragraphs, as he did here.
45 months later, however, a concise and pertinent answer was given by Aaron Brick:
13½d is a historical value called a loonslate. According to William Hone, it has a Scottish origin, being two-thirds of the Scottish pound, as the mark was two-thirds of the English pound. The same value was proposed as coinage for South Carolina in 1700.
This answer makes me happy in several ways, most of them positive. I'm glad to have a lead for where the 13½ pence comes from. I'm glad to learn the odd word “loonslate”. And I'm glad to be introduced to the bizarre world of pre-union Scottish currency, which, in addition to the loonslate, includes the bawbee, the unicorn, the hardhead, the bodle, and the plack.
My pleasure has a bit of evil spice in it too. That fatuous claim that the question was “historically unanswerable” had been bothering me for years, and M. Brick's slam-dunk put it right where it deserved.
I'm still not completely satisfied. The Scottish mark was worth ⅔ of a pound Scots, and the pound Scots, like the English one, was divided not into 12 pence but into 20 shillings of 12 pence each, so that a Scottish mark was worth 160d, not 13½d. Brick cites William Hone, who claims that the pound Scots was divided into twelve pence, rather than twenty shillings, so that a mark was worth 13⅔ pence, but I can't find any other source that agrees with him. Confusing the issue is that starting under the reign of James VI and I in 1606, the Scottish pound was converted to the English at a rate of twelve-to-one, so that a Scottish mark would indeed have been convertible to 13⅔ English pence, except that the English didn't denominate pence in thirds, so perhaps it was legally rounded down to 13½ pence. But this would all have been long after the establishment of the 13½d in the Halifax gibbet law and so unrelated to it.
Or would it? Maybe the 13½d entered popular consciousness in the 17th century, acquired the evocative slang name “hangman’s wages”, and then an urban legend arose about it being the cutoff amount for the Halifax gibbet, long after the gibbet itself was dismantled arond 1650. I haven't found any really convincing connection between the 13½d and the gibbet that dates earlier than 1712. The appearance of the 13½d in the gibbet law could be entirely the invention of Samuel Midgley.
I may dig into this some more. The 1771 Encyclopædia Britannica has a 16-page article on “Money” that I can look at. I may not find out what I want to know, but I will probably find out something.
[Other articles in category /history] permanent link
Getting Applicatives from Monads and “>>=” from “join”
I complained recently about GHC not being able to infer an
Applicative instance from a type that already has a Monad
instance, and there is a related complaint that the Monad instance
must define >>=. In some type classes, you get a choice about
what to define, and then the rest of the functions are built from the
ones you provided. To take a particular simple example, with Eq
you have the choice of defining == or /=, and if you omit one
Haskell will construct the other for you. It could do this with >>=
and join, but it doesn't, for technical reasons I don't
understand
[1]
[2]
[3].
But both of these problems can be worked around. If I have a Monad instance, it seems to work just fine if I say:
instance Applicative Tree where
pure = return
fs <*> xs = do
f <- fs
x <- xs
return (f x)
Where this code is completely canned, the same for every Monad.
And if I know join but not >>=, it seems to work just fine if I say:
instance Monad Tree where
return = ...
x >>= f = join (fmap f x) where
join tt = ...
I suppose these might faul foul of whatever problem is being described in the documents I linked above. But I'll either find out, or I won't, and either way is a good outcome.
[ Addendum: Vaibhav Sagar points out that my definition of <*> above
is identical to that of Control.Monad.ap, so that instead of
defining <*> from scratch, I could have imported ap and then
written <*> = ap. ]
[ Addendum 20221021: There are actually two definitions of <*> that will work. [1] [2] ]
[Other articles in category /prog/haskell] permanent link
Mon, 22 Oct 2018While I was writing up last week's long article about Traversable, I wrote this stuff about Applicative also. It's part of the story but I wasn't sure how to work it into the other narrative, so I took it out and left a remark that “maybe I'll publish a writeup of that later”. This is a disorganized collection of loosely-related paragraphs on that topic.
It concerns my attempts to create various class instance definitions for the following type:
data Tree a = Con a | Add (Tree a) (Tree a)
deriving (Eq, Show)
which notionally represents a type of very simple expression tree over values of type a.
I need some function for making Trees that isn't too
simple or too complicated, and I went with:
h n | n < 2 = Con n
h n = if even n then Add (h (n `div` 2)) (h (n `div` 2))
else Add (Con 1) (h (n - 1))
which builds trees like these:
2 = 1 + 1
3 = 1 + (1 + 1)
4 = (1 + 1) + (1 + 1)
5 = 1 + ((1 + 1) + (1 + 1))
6 = (1 + (1 + 1)) + (1 + (1 + 1))
7 = 1 + (1 + (1 + 1)) + (1 + (1 + 1))
8 = ((1 + 1) + (1 + 1)) + ((1 + 1) + (1 + 1))
Now I wanted to traverse h [1,2,3] but I couldn't do that because I
didn't have an Applicative instance for Tree. I had been putting off
dealing with this, but since Traversable doesn't really make sense without
Applicative I thought the day of reckoning would come. Here it was. Now is
when I learn how to fix all my broken monads.
To define an Applicative instance for Tree I needed to define pure, which
is obvious (it's just Con) and <*> which would apply a tree of
functions to a tree of inputs to get a tree of results. What the hell
does that mean?
Well, I can kinda make sense of it. If I apply one function to a
tree of inputs, that's straightforward, it's just fmap, and I get a
tree of results. Suppose I have a tree of functions, and I replace
the function at each leaf with the tree of its function's results.
Then I have a tree of trees. But a tree that has trees at its leaves
is just a tree. So I could write some tree-flattening function that
builds the tree of trees, then flattens out the type. In fact this is just
join that I already know from Monad world.
The corresponding operation for lists takes a list of lists
and flattens them into a single list.) Flattening a tree is quite easy to do:
join (Con ta) = ta
join (Add ttx tty) = Add (join ttx) (join tty)
and since this is enough to define a Monad instance for Tree I
suppose it is enough to get an Applicative instance also, since every Monad
is an Applicative. Haskell makes this a pain. It should be able to infer
the Applicative from this, and I wasn't clever enough to do it myself. And
there ought to be some formulaic way to get <*> from >>= and
join and fmap, the way you can get join from >>=:
join = (>>= id)
but I couldn't find out what it was. This gets back to my original
complaint: Haskell now wants every Monad instance to be an instance
of Applicative, but if I give it the fmap and the join and the return
it ought to be able to figure out the Applicative instance itself instead of
refusing to compile my program. Okay, fine, whatever. Haskell's
gonna Hask.
(I later realized that building <*> when you have a Monad instance
is easy once you know the recipe; it's just:
fs <*> xs = do
f <- fs
x <- xs
return (f x)
So again, why can't GHC infer <*> from my Monad instance, maybe
with a nonfatal warning?
Warning: No Applicative instance provided for Tree; deriving one from Monad
This is not a rhetorical question.)
(Side note: it seems like there ought to be a nice short abbreviation
of the (<*>) function above, the way one can write join = (>>=
id). I sought one but did not find any. One can eliminate the do
notation to obtain the expression:
fs <*> xs = fs >>= \f -> xs >>= \x -> return (f x)
but that is not any help unless we can simplify the expression with
the usual tricks, such as combinatory logic and η-conversion. I was
not able to do this, and the automatic pointfree
converter produced
(. ((. (return .)) . (>>=))) . (>>=) ARGH MY EYES.)
Anyway I did eventually figure out my <*> function for trees by
breaking the left side into cases. When the tree of functions is Con
f it's a single function and we can just use fmap to map it over
the input tree:
(Con f) <*> tv = fmap f tv
And when it's bigger than that we can break it up recursively:
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
Once this is written it seemed a little embarrassing that it took me so long to figure out what it meant but this kind of thing always seems easier from the far side of the fence. It's hard to understand until you understand it.
Actually that wasn't quite the <*> I wanted. Say we have a tree of
functions and a tree of arguments.

Add (Con (* 10))
(Con (* 100))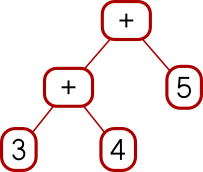
Add (Add (Con 3) (Con 4)) (Con 5)I can map the whole tree of functions over each single leaf on the right, like this:
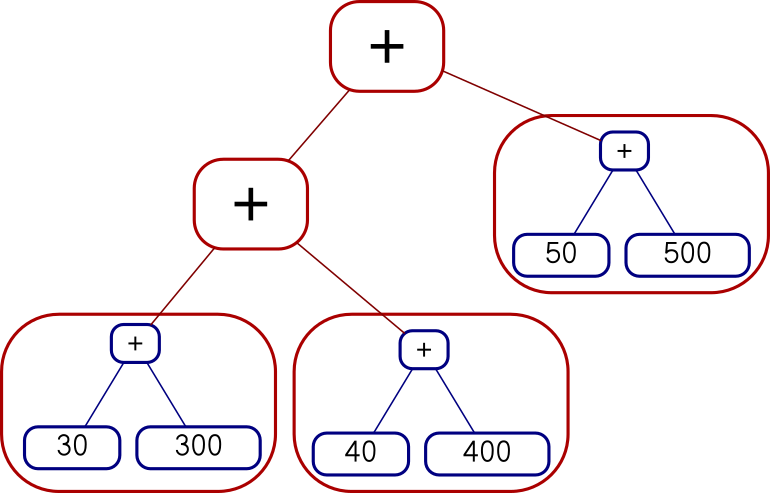
Add (Add (Add (Con 30) (Con 300))
(Add (Con 40) (Con 400)))
(Add (Con 50) (Con 500))
or I can map each function over the whole tree on the right, like this:
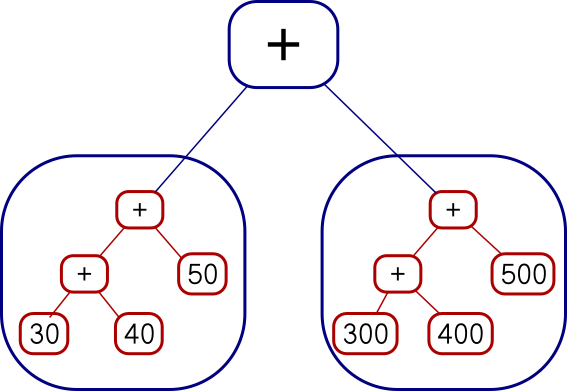
Add
(Add (Add (Con 30) (Con 40)) (Con 50))
(Add (Add (Con 300) (Con 400)) (Con 500))The code I showed earlier does the second of those. You can see it from
the fmap f tv expression, which takes a single function and maps it over a whole
tree of values. I had actually wanted the other one, but there isn't
anything quite like fmap for that. I was busy trying to
understand Applicative and I was afraid if I got distracted trying to invent
a reverse fmap I might lose the thread. This happens to me a lot
with Haskell. I did eventually go back and figure it out. The
reverse fmap is
pamf fs v = fmap ($ v) fs -- good
or
pamf = flip (fmap . flip id) -- yuck
Now there's a simple answer to this which occurs to me now that I
didn't think of before, but I'm going to proceed with how I planned to
do it before, with pamf. The <*> that I didn't want looked like this:
(Con f) <*> tv = fmap f tv
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
I need to do the main recursion on the values argument instead of on the functions argument:
tf <*> (Con v) = pamf tf v
where pamf fs v = fmap ($ v) fs
tf <*> (Add lv rv) = Add (tf <*> lv) (tf <*> rv)
(This is an interesting example: usually the base case is trivial and the recursive clause is harder to write, but this time it's the base case that's not perfectly straightforward.)
Anyway, this worked, but there was an easier solution at hand. The difference between the first version and the second is exactly the same as the difference between
fs <*> xs = do
f <- fs
x <- xs
return (f x)
and
fs <*> xs = do
x <- xs
f <- fs
return (f x)
Digging deeper into why this worked this way was interesting, but it's bed time, so I'm going to cut the scroll here.
[ Addendum 20221021: More about the two versions of <*> and a third version that doesn't work. ]
[Other articles in category /prog/haskell] permanent link
Sat, 20 Oct 2018
I struggle to understand Traversable
Haskell evolved a lot since the last time I seriously wrote any
Haskell code, so much so that all my old programs broke. My Monad
instances don't compile any more because I'm no longer allowed to
have a monad which isn't also an instance of Applicative. Last time I used
Haskell, Applicative wasn't even a thing. I had read the McBride and
Paterson paper that introduced applicative functors, but that was
years ago, and I didn't remember any of the details. (In fact, while
writing this article, I realized that the paper I read was a preprint,
and I probably read it before it was published, in 2008.) So to
resuscitate my old code I had to implement a bunch of <*> functions
and since I didn't really understand what it was supposed to be doing
I couldn't do that. It was a very annoying experience.
Anyway I got that more or less under control (maybe I'll publish a
writeup of that later) and moved on to Traversable which, I hadn't realized
before, was also introduced in that same paper. (In the
prepublication version, Traversable had been given the unmemorable name
IFunctor.) I had casually looked into this several times in the
last few years but I never found anything enlightening. A Traversable is a
functor (which must also implement Foldable, but let's pass over that
for now, no pun intended) that implements a traverse method with the
following signature:
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
The traversable functor itself here is t. The f thing is an
appurtenance. Often one looks at the type of some function and says “Oh, that's what
that does”, but I did not get any understanding from this signature.
The first thing to try here is to make it less abstract. I was thinking about Traversable this time because I thought I might want it for a certain type of tree structure I was working with. So I defined an even simpler tree structure:
data Tree a = Con a | Add (Tree a) (Tree a)
deriving (Eq, Show)
Defining a bunch of other cases wouldn't add anything to my understanding, and it would make it take longer to try stuff, so I really want to use the simplest possible example here. And this is it: one base case, one recursive case.
Then I tried to make this type it into a Traversable instance. First we need it to be a Functor, which is totally straightforward:
instance Functor Tree where
fmap f (Con a) = Con (f a)
fmap f (Add x y) = Add (fmap f x) (fmap f y)
Then we need it to be a Foldable, which means it needs to provide a
version of foldr. The old-fashioned foldr was
foldr :: (a -> b -> b) -> b -> [a] -> b
but these days the list functor in the third place has been generalized:
foldr :: Foldable f => (a -> b -> b) -> b -> f a -> b
The idea is that foldr fn collapses a list of as into a single b
value by feeding in the as one at a time. Each time, foldr takes
the previous b and the current a and constructs a new b. The
second argument is the initial value of b.
Another way to think about it is that every list has the form
e1 : e2 : .... : []
and foldr fn b applied to this list replaces the (:) calls with fn
and the trailing [] with b, giving me
e1 `f` e2 `f` .... `f` b
The canonical examples for lists are:
sum = foldr (+) 0
(add up the elements, starting with zero) and
length = foldr (\_ -> (+ 1)) 0
(ignore the elements, adding 1 to the total each time, starting with
zero). Also foldr (:) [] is the identity function for lists because
it replaces the (:) calls with (:) and the trailing [] with [].
Anyway for Tree it looks like this:
instance Foldable Tree where
foldr f b (Con a) = f a b
foldr f b (Add x y) = (foldr f) (foldr f b x) y
The Con clause says to take the constant value and combine it with
the default total. The Add clause says to first fold up the
left-side subtree x to a single value, then use that as the initial
value for folding up the right-side subtree y, so everything gets
all folded up together. (We could of course do the right subtree
before the left; the results would be different but just as good.)
I didn't write this off the top of my head, I got it by following the types, like this:
In the first clause
foldr f b (Con a) = ???we have a function
fthat wants anavalue and abvalue, and we have both anaand ab, so put the tabs in the slots.In the second clause
foldr f b (Add x y) = ???fneeds anavalue and none is available, so we can't usefby itself. We can only use it recursively viafoldr. So forgetf, we will only be dealing only withfoldr f, which has typeb -> Tree a -> b. We need to apply this to abvalue and the only one we have isb, and then we need to apply that to one of the subtrees, sayx, and thus we have synthesized thefoldr f b xsubexpression. Then pretty much the same process gets us the rest of it: we need aband the only one we have now isfoldr f b x, and then we need another tree and the only one we haven't used isy.
It turns out it is easier and more straightforward to write foldMap
instead, but I didn't know that at the time. I won't go into it
further because I have already digressed enough. The preliminaries
are done, we can finally get on to the thing I wanted, the Traversable:
instance Traversable Tree where
traverse = ....
and here I was stumped. What is this supposed to actually do?
For our Tree functor it has this signature:
traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
Okay, a function a -> f b I understand, it turns each tree leaf
value into a list or something, so at each point of the tree it gets
out a list of bs, and it potentially has one of those for each item
in the input tree. But how the hell do I turn a tree of lists into
a single list of Tree b? (The answer is that the secret sauce is
in the Applicative, but I didn't understand that yet.)
I scratched my head and read a bunch of different explanations and none of them helped. All the descriptions I found were in either prose or mathematics and I still couldn't figure out what it was for. Finally I just wrote a bunch of examples and at last the light came on. I'm going to show you the examples and maybe the light will come on for you too.
We need two Traversable functors to use as examples. We don't have a Traversable
implementation for Tree yet so we can't use that. When I think of
functors, the first two I always think of are List and Maybe, so
we'll use those.
> traverse (\n -> [1..n]) Nothing
[Nothing]
> traverse (\n -> [1..n]) (Just 3)
[Just 1,Just 2,Just 3]
Okay, I think I could have guessed that just from the types. And
going the other way is not very interesting because the output, being
a Maybe, does not have that much information in it.
> let f x = if even x then Just (x `div` 2) else Nothing
If the !!x!! is even then the result is just half of !!x!!, and otherwise the division by 2 “fails” and the result is nothing. Now:
> traverse f [ 1, 2, 3, 4 ]
Nothing
> traverse f [ 10, 4, 18 ]
Just [5,2,9]
It took me a few examples to figure out what was going on here: When
all the list elements are even, the result is Just a list of half of
each. But if any of the elements is odd, that spoils the whole result
and we get Nothing. (traverse f [] is Just [] as one would
expect.)
That pretty much exhausts what can be done with lists and maybes. Now
I have two choices about where to go next: I could try making both
functors List, or I could use a different functor entirely. (Making
both Maybe seemed like a nonstarter.) Using List twice seemed
confusing, and when I tried it I could kinda see what it was doing but
I didn't understand why. So I took a third choice: I worked up a Traversable
instance for Tree just by following the types even though I didn't
understand what it ought to be doing. I thought I'd at least see if I
could get the easy clause:
traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
instance Traversable Tree where
traverse fn (Con a) = ...
In the ... I have fn :: a -> f b and I have at hand a single a. I need to
construct a Tree b. The only way to get a b is to apply fn to
it, but this gets me an f b and I need f (Tree b). How do I get the
Tree in there? Well, that's what Con is for, getting Tree in
there, it turns a t into Tree t. But how do I do that inside of
f? I tinkered around a little bit and eventually found
traverse fn (Con a) = Con <$> (fn a)
which not only type checks but looks like it could even be correct.
So now I have a motto for what <$> is about: if I have some
function, but I want to use it inside of some applicative functor
f, I can apply it with <$> instead of with $.
Which, now that I have said it myself, I realize it is exactly what
everyone else was trying to tell me all along: normal function
application takes an a -> b and applies to to an a giving a b.
Applicative application takes an f (a -> b) and applies it to an f a
giving an f b. That's what applicative functors are all about,
doing stuff inside of f.
Okay, I can listen all day to an explanation of what an electric drill does, but until I hold it in my hand and drill some holes I don't really understand.
Encouraged, I tried the hard clause:
traverse fn (Add x y) = ...
and this time I had a roadmap to follow:
traverse fn (Add x y) = Add <$> ...
The Con clause had fn a at that point to produce an f b but that won't
work here because we don't have an a, we have a whole Tree a, and we
don't need an f b, we need an f (Tree b). Oh, no problem,
traverse fn supposedly turns a Tree a into an f (Tree b), which
is just what we want.
And it makes sense to have a recursive call to traverse because this is the
recursive part of the recursive data structure:
traverse fn (Add x y) = Add <$> (traverse fn x) ...
Clearly traverse fn y is going to have to get in there somehow, and
since the pattern for all the applicative functor stuff is
f <$> ... <*> ... <*> ...
let's try that:
traverse fn (Add x y) = Add <$> (traverse fn x) <*> (traverse fn y)
This looks plausible. It compiles, so it must be doing something.
Partial victory! But what is it doing? We can run it and see, which
was the whole point of an exercise: work up a Traversable instance for Tree
so that I can figure out what Traversable is about.
Here are some example trees:
t1 = Con 3 -- 3
t2 = Add (Con 3) (Con 4) -- 3 + 4
t3 = Add (Add (Con 3) (Con 4)) (Con 2) -- (3 + 4) + 2
(I also tried Add (Con 3) (Add (Con 4) (Con 2)) but it did not
contribute any new insights so I will leave it out of this article.)
First we'll try Maybe. We still have that f function from before:
f x = if even x then Just (x `div` 2) else Nothing
but traverse f t1, traverse f t2, and traverse f t3 only produce
Nothing, presumably because of the odd numbers in the trees. One
odd number spoils the whole thing, just like in a list.
So try:
traverse f (Add (Add (Con 10) (Con 4)) (Con 18))
which yields:
Just (Add (Add (Con 5) (Con 2)) (Con 9))
It keeps the existing structure, and applies f at each value
point, just like fmap, except that if f ever returns Nothing
the whole computation is spoiled and we get Nothing. This is
just like what traverse f was doing on lists.
But where does that spoilage behavior come from exactly? It comes
from the overloaded behavior of <*> in the Applicative instance of Maybe:
(Just f) <*> (Just x) = Just (f x)
Nothing <*> _ = Nothing
_ <*> Nothing = Nothing
Once we get a Nothing in there at any point, the Nothing takes
over and we can't get rid of it again.
I think that's one way to think of traverse: it transforms each
value in some container, just like fmap, except that where fmap
makes all its transformations independently, and reassembles the exact
same structure, with traverse the reassembly is done with the
special Applicative semantics. For Maybe that means “oh, and if at any
point you get Nothing, just give up”.
Now let's try the next-simplest Applicative, which is List. Say,
g n = [ 1 .. n ]
Now traverse g (Con 3) is [Con 1,Con 2,Con 3] which is not exactly
a surprise but traverse g (Add (Con 3) (Con 4)) is something that
required thinking about:
[Add (Con 1) (Con 1),
Add (Con 1) (Con 2),
Add (Con 1) (Con 3),
Add (Con 1) (Con 4),
Add (Con 2) (Con 1),
Add (Con 2) (Con 2),
Add (Con 2) (Con 3),
Add (Con 2) (Con 4),
Add (Con 3) (Con 1),
Add (Con 3) (Con 2),
Add (Con 3) (Con 3),
Add (Con 3) (Con 4)]
This is where the light finally went on for me. Instead of thinking
of lists as lists, I should be thinking of them as choices. A list
like [ "soup", "salad" ] means that I can choose soup or salad, but
not both. A function g :: a -> [b] says, in restaurant a, what
bs are on the menu.
The g function says what is on the menu at each node. If a node has
the number 4, I am allowed to choose any of [1,2,3,4], but if it has
the number 3 then the choice 4 is off the menu and I can choose only
from [1,2,3].
Traversing g over a Tree means, at each leaf, I am handed a menu,
and I make a choice for what goes at that leaf. Then the result of
traverse g is a complete menu of all the possible complete trees I
could construct.
Now I finally understand how the t and the f switch places in
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
I asked “how the hell do I turn a tree of lists into a single list
of Tree b”? And that's the answer: each list is a local menu of
dishes available at one leaf, and the result list is the global menu
of the complete dinners available over the entire tree.
Okay! And indeed traverse g (Add (Add (Con 3) (Con 4)) (Con 2)) has
24 items, starting
Add (Add (Con 1) (Con 1)) (Con 1)
Add (Add (Con 1) (Con 1)) (Con 2)
Add (Add (Con 1) (Con 2)) (Con 1)
...
and ending
Add (Add (Con 3) (Con 4)) (Con 1)
Add (Add (Con 3) (Con 4)) (Con 2)
That was traversing a list function over a Tree. What if I go the
other way? I would need an Applicative instance for Tree and I didn't
really understand Applicative yet so that wasn't going to happen for a
while. I know I can't really understand Traversable without understanding
Applicative first but I wanted to postpone the day of reckoning as long as
possible.
What other functors do I know? One easy one is the functor that takes
type a and turns it into type (String, a). Haskell even has a
built-in Applicative instance for this, so I tried it:
> traverse (\x -> ("foo", x)) [1..3]
("foofoofoo",[1,2,3])
> traverse (\x -> ("foo", x*x)) [1,5,2,3]
("foofoofoofoo",[1,25,4,9])
Huh, I don't know what I was expecting but I think that wouldn't have
been it. But I figured out what was going on: the built-in Applicative
instance for the a -> (String, a) functor just concatenates the
strings. In general it is defined on a -> (m, b) whenever m is a
monoid, and it does fmap on the right component and uses monoid
concatenation on the left component. So I can use integers instead of
strings, and it will add the integers instead of concatenating the
strings. Except no, it won't, because there are several ways to make
integers into a monoid, but each type can only have one kind of
Monoid operations, and if one was wired in it might not be the one I
want. So instead they define a bunch of types that are all integers
in obvious disguises, just labels stuck on them that say “I am not an
integer, I am a duck”; “I am not an integer, I am a potato”. Then
they define different overloadings for “ducks” and “potatoes”. Then
if I want the integers to get added up I can put duck labels on my
integers and if I want them to be multiplied I can stick potato labels
on instead. It looks like this:
import Data.Monoid
h n = (Sum 1, n*10)
Sum is the duck label. When it needs to combine two
ducks, it will add the integers:
> traverse h [5,29,83]
(Sum {getSum = 3},[50,290,830])
But if we wanted it to multiply instead we could use the potato label,
which is called Data.Monoid.Product:
> traverse (\n -> (Data.Monoid.Product 7, 10*n)) [5,29,83]
(Product {getProduct = 343}, [50,290,830])
There are three leaves, so we multiply three sevens and get 343.
Or we could do the same sort of thing on a Tree:
> traverse (\n -> (Data.Monoid.Product n, 10*n)) (Add (Con 2) (Add (Con 3) (Con 4)))
(Product {getProduct = 24}, Add (Con 20) (Add (Con 30) (Con 40)))
Here instead of multiplying together a bunch of sevens we multiply together the leaf values themselves.
The McBride and Paterson paper spends a couple of pages talking about
traversals over monoids, and when I saw the example above it started
to make more sense to me. And their ZipList example became clearer
too. Remember when we had a function that gave us a menu at every
leaf of a tree, and traverse-ing that function over a tree gave us a
menu of possible trees?
> traverse (\n -> [1,n,n*n]) (Add (Con 2) (Con 3))
[Add (Con 1) (Con 1),
Add (Con 1) (Con 3),
Add (Con 1) (Con 9),
Add (Con 2) (Con 1),
Add (Con 2) (Con 3),
Add (Con 2) (Con 9),
Add (Con 4) (Con 1),
Add (Con 4) (Con 3),
Add (Con 4) (Con 9)]
There's another useful way to traverse a list function. Instead of taking each choice at each leaf we make a single choice ahead of time about whether we'll take the first, second, or third menu item, and then we take that item every time:
> traverse (\n -> Control.Applicative.ZipList [1,n,n*n]) (Add (Con 2) (Con 3))
ZipList {getZipList = [Add (Con 1) (Con 1),
Add (Con 2) (Con 3),
Add (Con 4) (Con 9)]}
There's a built-in instance for Either a b also. It's a lot like
Maybe. Right is like Just and Left is like Nothing. If all
the sub-results are Right y then it rebuilds the structure with all
the ys and gives back Right (structure). But if any of the
sub-results is Left x then the computation is spoiled and it gives
back the first Left x. For example:
> traverse (\x -> if even x then Left (x `div` 2) else Right (x * 10)) [3,17,23,9]
Right [30,170,230,90]
> traverse (\x -> if even x then Left (x `div` 2) else Right (x * 10)) [3,17,22,9]
Left 11
Okay, I think I got it.
Now I just have to drill some more holes.
[Other articles in category /prog/haskell] permanent link
Tue, 16 Oct 2018
I redesign the LA Times’ Hurricane Maria chart
This could have been a great chart, but I think it has a big problem:
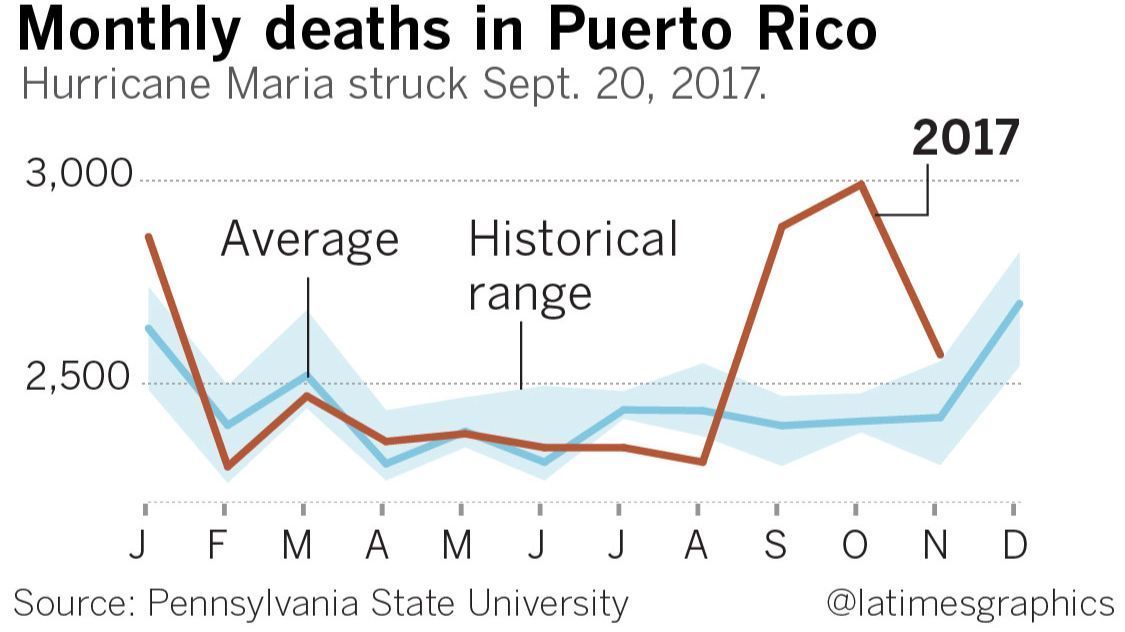
It appears that the death toll started increasing in early August, even though the hurricane didn't hit until 20 September. According to this chart, the hurricane was shortly followed by a drastic decrease in the death rate.
What's actually going on is that the August value is a total for all of August and is typically low, the September value is a total for all of September and is atypically high, and the chart designer has drawn a straight line between the August and September values, implying a linear increase over the course of August. The data for August is at the mark “A” on the chart, which seems reasonable, except that one has to understand that “A” as marking the end of August instead of the beginning, which is the opposite of the usual convention.
I think a bar chart would have been a better choice here. The lines imply continuous streams of data, but the reality is that each line represents only twelve data points. Maybe something like this instead?
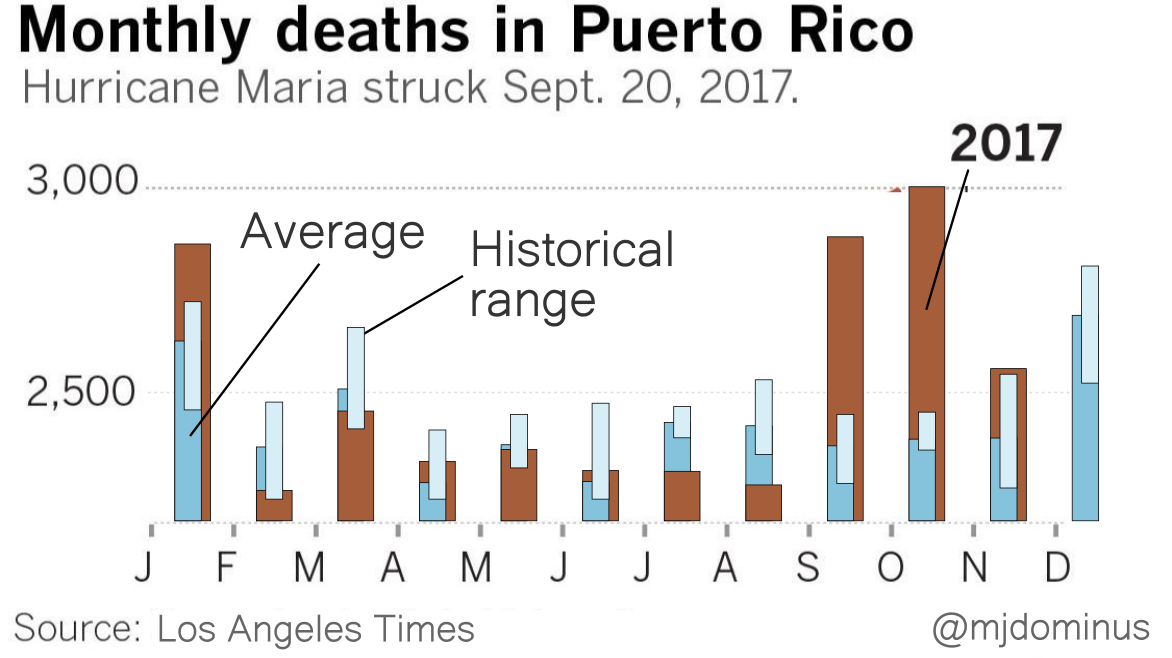
I'm not sure the historical range bars are really adding much.
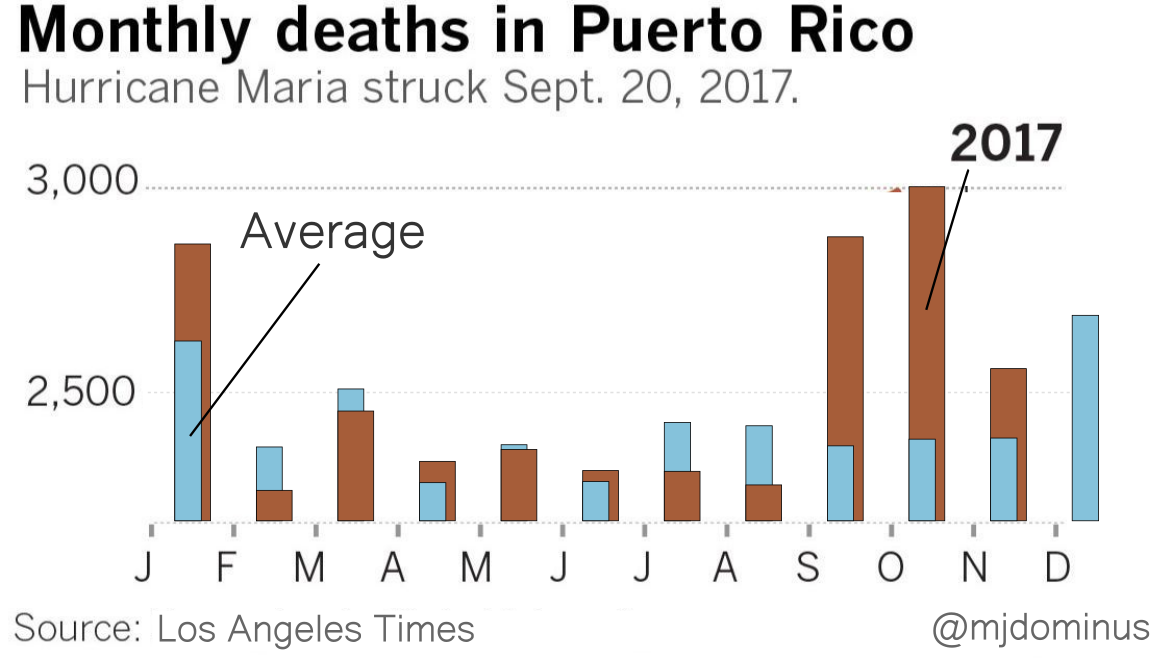
If I were designing this from scratch I think I might replace the blue bars with brackets (although maybe the LA Times knows that their readership finds those confusing?). Or maybe plot the difference between the 2017 data and ths historical average. But I think you get the point.
[Other articles in category /IT] permanent link
Mon, 15 Oct 2018
'The' reader monad does not exist
Reading over my recent article complaining about the environment functor I realized there's yet another terminology problem that makes the discussion unnecessarily confusing. “The” environment functor isn't unique. There is a family of environment functors, one for each possible environment type e. If g is the environment functor at type e, a value of type g t is a function e → t. But e could be anything and if g and h are environment functors at two different types e and e’ they are of course different functors.
This is even obvious from the definition:
data Environ e t = Env (e -> t)
instance Functor (Environ e) where
fmap f (Env x) = Env $ \e -> f (x e)
The functor isn't Environ, it's Environ e, and the functor
instance declaration, as it says on line 2. (It seems to me that the
notation is missing a universal quantifier somewhere, but I'm not
going to open that issue.)
We should speak of Environ e as an environment functor, not
the environment functor. So for example instead of:
When operating in the environment functor,
fmaphas the type(a -> b) -> g a -> g b
I should have said:
When operating in an environment functor,
fmaphas the type(a -> b) -> g a -> g b
And instead of:
A function
p -> qis aqparcel in the environment functor
I should have said:
A function
p -> qis aqparcel in an environment functor
or
A function
p -> qis aqparcel in the environment functor atp
although I'm not sure I like the way the prepositions are proliferating there.
The same issue affects ⸢the⸣ reader monad, ⸢the⸣ state monad, and many others.
I'm beginning to find remarkable how much basic terminology Haskell is missing or gets wrong. Mathematicians have a very keen appreciation of the importance of specific and precise terminology, and you'd think this would have filtered into the Haskell world. People are forever complaining that Haskell uses unfamiliar terms like “functor”, and the community's response is (properly, I think) that these terms are pre-existing and there is no point to inventing a new term that will be just as unfamiliar, or, worse, lure people into thinking that the know what it means when they don't. You don't want to call a functor a “container”, says the argument, because many functors (environment functors for example) are nothing at all like containers. I think this is wise.
But having planted their flag on that hill, the Haskell folks don't
then use their own terminology correctly. I complained years
ago that the term
“monad” was used interchangeably for four subtly different concepts,
and here we actually have a fifth. I pointed out that in the case of
Environment e t, common usage refers to both Environment e and
Environment e t as monads, and only the first is correct. But when
people say “the environment monad” they mean that Environment itself
is a monad, which it is not.
[Other articles in category /prog/haskell] permanent link
Thu, 11 Oct 2018Is there any good terminology for a value of type
f awhenfis an arbitrary functor? I will try calling anf tvalue a “tparcel” and see how that works.
The more I think about “parcel” the happier I am with it. It strongly
suggests container types, of course, so that a t parcel might be a
boxful of ts. But it also hints at some other possible situations:
- You might open the parcel and find it empty. (
Maybe t) - You might open the parcel and find, instead of the
tyou expected, a surprising prank snake. (Either ErrorMessage t) - You might open the parcel and find that your
thas been shipped with assembly required. (env -> t) - The parcel might explode when you open it. (
IO t) - And, of course, a burrito is a sort of parcel of meat and beans.
I coined “parcel” thinking that one would want different terminology
for values of type f t depending on whether f was a functor
(“parcel”) or also a monad (“mote”). Of course every mote is a
parcel, but not always vice versa. Now I'm not sure that both terms
are needed. Non-monadic functors are unusual, and non-applicative
functors rare, so perhaps one term will do for all three.
[Other articles in category /prog/haskell] permanent link
I hate the environment functor
Here we have the well-known fmap function:
fmap :: Functor f => (a -> b) -> f a -> f b
It takes a single function and a (collection of input values / decorated input value / something something input value) and produces a (collection of output values / decorated output value / something something output value).
Yow, that's not going to work. Is there any good terminology for a
value of type f a when f is an arbitrary functor? A while back I
discussed a similar
problem and suggested
the term “mote” for a value in a monadic type. I will try calling an
f t value a “t parcel and see how that works. So
[t], Maybe t, and IO t are all examples of t parcels, in
various functors.
Starting over then. Here we have the well-known fmap function:
fmap :: Functor f => (a -> b) -> f a -> f b
It takes a single function, and an a parcel, and produces a b
parcel, by applying the function independently to the a values in
the parcel.
Here is a sort of reversed version of fmap that I call pamf:
pamf :: Functor f => f (a -> b) -> a -> f b
It takes a parcel of functions, and a single input and produces a
parcel of outputs, by applying each function in the parcel
independently to the single a value. It can be defined in terms of
fmap:
pamf fs a = fmap ($ a) fs
So far so good. Now I ask you to predict the type of
pamf fmap
Certainly it should start out with
pamf fmap :: (Functor f, Functor g) => ...
because the pamf and the fmap might be operating in two different
functors, right? Indeed, if I compose the functions the other way
around, fmap pamf, the type does begin this way; it is:
(Functor f, Functor g) => f (g (a -> b)) -> f (a -> g b)
The f here is the functor in which fmap operates, and the g is
the functor in which pamf is operating. In general fmap takes an
arbitrary function
a -> b
and lifts it to a new function that operates in the f functor:
f a -> f b
Here it has taken pamf, which is a function
g (a -> b) -> (a -> g b)
and lifted it to a new function that operates in the f functor:
f (g (a -> b)) -> f (a -> g b)
This is complicated but straightforward. Okay, that was fmap pamf.
What about pamf fmap though? The computed type is
pamf fmap :: Functor f => f a -> (a -> b) -> f b
and when I saw this I said “What. Where did g go? What happened to
g?”
Then I paused and for a while and said “… I bet it's that goddamn environment thing again.” Yep, that's what it was. It's the environment functor, always turning up where I don't want it and least expect it, like that one guy we all went to college with. The environment functor, by the way, is yet another one of those things that Haskell ought to have a standard name for, but doesn't. The phrase “the reader monad” is fairly common, but here I only want the functor part of the monad. And people variously say “reader monad”, “environment monad”, and “evaluation monad” to mean the same thing. In this article, it will be the environment functor.
Here's what happened. Here are fmap and pamf again:
fmap :: Functor f => (p -> q) -> f p -> f q
pamf :: Functor g => g (a -> b) -> a -> g b
The first argument to pamf should be a parcel in the g functor.
But fmap is not a parcel, so pamf fmap will be a type error,
right? Wrong! If you are committed enough, there is a way to
construe any function as a parcel. A function p -> q is a q
parcel in the environment functor. Say that g denotes an
environment functor. In this functor, a parcel of type g t is a
function which consults an “environment” of type e and yields a
result of type t. That is, $$g\ t \equiv e \to t.$$
When operating in the environment functor, fmap has the type (a ->
b) -> g a -> g b, which is shorthand for (a -> b) -> (e -> a) -> (e
-> b). This instance of fmap is defined this way:
fmap f x = \e -> f (x e)
or shorter and more mysteriously
fmap = (.)
which follows by η-reduction, something Haskell enthusiasts never seem to get enough of.
In fmap f x, the x isn't the actual value to give to f; instead
it's a parcel, as it always is with fmap. In the context of the
environment functor, x is a function that consults the environment
e and returns an a. The result of fmap f x is a new parcel: it
uses x to consult the supplied environment for a value of type a,
which it then feeds to f to get the required value of type b.
In the application pamf fmap, the left side pamf wants fmap to
be a parcel. But it's not a parcel, it's a function. So, type error,
right? No! Any function is a parcel if you want it to be, it's a
parcel in the environment functor! And fmap is a function:
fmap :: Functor f => (p -> q) -> f p -> f q
so it can be understood as a parcel in the environment functor, where
the environment e has type p -> q. Then pamf is operating in
this environment functor, so $$g\ t = (p \to q) \to t.$$ A g t parcel
is a function that consults an “environment” of type p -> q and
somehow produces a t value. (Haskell folks, who are obsessed with
currying all the things, will write this as the
nearly unreadable g = ((->) (p -> q)).)
We wanted pamf to have this type:
pamf :: Functor g => g (a -> b) -> a -> g b
and since Haskell has decided that g must be the environment functor
with !!g\ x \equiv (p \to q) \to x!!,
this is an abbreviation for:
pamf :: ((p -> q) -> (a -> b)) -> a -> ((p -> q) -> b)
To apply this to fmap, we have to unify the type of pamf's
argument, which is (p -> q) -> (a -> b), and the type of fmap,
which is (p -> q) -> (f p -> f q). Then !!a\equiv f\ p!! and !!b
\equiv f\ q!!, so the result of pamf fmap is
pamf fmap :: Functor f => f p -> ((p -> q) -> f q)
Where did g go? It was specialized to mean the environment functor
((->) (p -> q)), so it's gone.
The funny thing about the type of pamf fmap is that it is exactly
the type of flip fmap, which is fmap with the order of its two
arguments reversed:
(flip fmap) x f ≡ fmap f x
and indeed, by some theorem or other, because the types are identical,
the functions themselves must be identical also! (There are some side
conditions, all of which hold here.) The two functions pamf fmap and
flip fmap are identical. Analogous to the way fmap, restricted
to the environment functor, is identical to (.), pamf, when
similarly restricted, is exactly
flip. You can even see this from its type:
pamf :: ((p -> q) -> (a -> b)) -> a -> ((p -> q) -> b)
Or, cleaning up some superfluous parentheses and inserting some new ones:
pamf :: ((p -> q) -> a -> b) -> (a -> (p -> q) -> b)
And putting !!c = p\to q!!:
pamf :: (c -> a -> b) -> (a -> c -> b)
flip :: ( the same )
Honestly, I would have preferred a type error: “Hey, dummy, fmap has
the wrong type to be an argument to pamf, which wants a functorial
value.” Instead I got “Okay, if you want functions to be a kind of
functor I can do that, also wouldn't it be simpler if the universe was
two-dimensional and there were only three kinds of quarks? Here you
go, no need to thank me!” Maybe someone can explain to me why this is
a useful behavior, and then explain why it is so useful that it should
happen automatically and implicitly instead of being triggered
by some lexical marker like:
newtype Environment e a = Environment (e -> a)
instance Functor (Environment e) where
fmap f (Environment x) = Environment $ \e -> f (x e)
I mean, seriously, suppose you wrote a + b where b was
accidentally a function instead of a number. What if when you did
that, instead of a type error, Haskell would silently shift into some
restricted domain in which it could implicitly interpret b as a
number in some weird way and give you something totally bizarre?
Isn't the whole point of Haskell supposed to be that it doesn't
implicitly convert things that way?
[ Addendum 20181111: Apparently, everyone else hates it too. ]
[Other articles in category /prog/haskell] permanent link
Wed, 10 Oct 2018Minecraft makes maps in-game, and until now I would hold up the map in the game, take a screenshot, print it out, and annotate the printout.
Now I can do better. I have a utility that takes multiple the map files direcly from the Minecraft data directory and joins them together into a single PNG image that I can then do whatever with. Here's a sample, made by automatically processing the 124(!) maps that exist in my current Minecraft world.

Notice how different part of the result are at different resolutions. That is because Minecraft maps are in five different resolutions, from !!2^{14}!! to !!2^{22}!! square meters in area, and these have been stitched together properly. My current base of operations is a little comma-shaped thingy about halfway down in the middle of the ocean, and on my largest ocean map it is completely invisible. But here it has been interpolated into the correct tiny scrap of that big blue map.
Bonus: If your in-game map is lost or destroyed, the data file still hangs around, and you can recover the map from it.
Source code is on Github. It needs some work:
- You have to manually decompress the map files
- It doesn't show banners or other markers
- I got bored typing in the color table and didn't finish
- Invoking it is kind of heinous
./dumpmap $(./sortbyscale map_*) | pnmtopng > result.png
Patches welcome!
[Other articles in category /games] permanent link
Mon, 08 Oct 2018
Notes on using git-replace to get rid of giant objects
A couple of years ago someone accidentally committed a 350 megabyte
file to our Git repository. Now it's baked in. I wanted to get rid
of it. I thought that I might be able to work out a partial but
lightweight solution using git-replace.
Summary: It didn't work.
Details
In 2016 a programmer commited a 350 megabyte file to my employer's repo, then in the following commit they removed it again. Of course it's still in there, because someone might check out the one commit where it existed. Everyone who clones the repo gets a copy of the big file. Every copy of the repo takes up an extra 350 megabytes on disk.
The usual way to fix this is onerous:
Use
git-filter-branchto rebuild all the repository history after the bad commit.Update all the existing refs to point to the analogous rebuilt objects.
Get everyone in the company to update all the refs in their local copies of the repo.
I thought I'd tinker around with git-replace to see if there was
some way around this, maybe something that someone could do locally on
their own repo without requiring everyone else to go along with it.
The git-replace command annotates the Git repository to say that
whenever object A is wanted, object B should be used instead. Say
that the 350 MB file has an ID of
ffff9999ffff9999ffff9999ffff9999ffff9999. I can create a small file
that says
This is a replacement object. It replaces a very large file
that was committed by mistake. To see the commit as it really
was, use
git --no-replace-objects show 183a5c7e90b2d4f6183a5c7e90b2d4f6183a5c7e
git --no-replace-objects checkout 183a5c7e90b2d4f6183a5c7e90b2d4f6183a5c7e
or similarly. To see the file itself, use
git --no-replace-objects show ffff9999ffff9999ffff9999ffff9999ffff9999
I can turn this small file into an object with git-add; say the new
small object has ID 1111333311113333111133331111333311113333. I
then run:
git replace ffff9999ffff9999ffff9999ffff9999ffff9999 1111333311113333111133331111333311113333
This creates
.git/refs/replace/ffff9999ffff9999ffff9999ffff9999ffff9999, which
contains the text 1111333311113333111133331111333311113333.
thenceforward, any Git command that tries to access the original
object ffff9999 will silently behave as if it were 11113333
instead. For example, git show 183a5c7e will show the diff between
that commit and the previous, as if the user had committed my small
file back in 2016 instead of their large one. And checking out that
commit will check out the small file instead of the large one.
So far this doesn't help much. The checkout is smaller, but nobody was likely to have that commit checked out anyway. The large file is still in the repository, and clones and transfers still clone and transfer it.
The first thing I tried was a wan hope: will git gc discard the
replaced object? No, of course not. The ref in refs/replace/
counts as a reference to it, and it will never be garbage-collected.
If it had been, you would no longer be able to examine it with the
--no-replace-objects commands. So much for following the rules!
Now comes the hacking part: I am going to destroy the actual object. Say for example, what if:
cp /dev/null .git/objects/ff/ff9999ffff9999ffff9999ffff9999ffff9999
Now the repository is smaller! And maybe Git won't notice, as long as
I do not use --no-replace-objects?
Indeed, much normal Git usage doesn't notice. For example, I can make
new commits with no trouble, and of course any other operation that
doesn't go back as far as 2016 doesn't notice the change. And
git-log works just fine even past the bad commit; it only looks at
the replacement object and never notices that the bad object is
missing.
But some things become wonky. You get an error message when you clone
the repo because an object is missing. The replacement refs are local
to the repo, and don't get cloned, so clone doesn't know to use the
replacement object anyway. In the clone, you can use git replace -f
.... to reinstate the replacement, and then all is well unless
something tries to look at the missing object. So maybe a user could
apply this hack on their own local copy if they are willing to
tolerate a little wonkiness…?
No. Unfortunately, there is a show-stopper: git-gc no longer
works in either the parent repo or in the clone:
fatal: unable to read ffff9999ffff9999ffff9999ffff9999ffff9999
error: failed to run repack
and it doesn't create the pack files. It dies, and leaves behind a
.git/objects/pack/tmp_pack_XxXxXx that has to be cleaned up by hand.
I think I've reached the end of this road. Oh well, it was worth a look.
[ Addendum 20181009: A lot of people have unfortunately missed the point of this article, and have suggested that I use BFG or reposurgeon. I have a small problem and a large problem. The small problem is how to remove some files from the repository. This is straightforward, and the tools mentioned will help with it. But because of the way Git works, the result is effectively a new repository. The tools will not help with the much larger problem I would have then: How to get 350 developers to migrate to the new repository at the same time. The approach I investigated in this article was an attempt to work around this second, much larger problem. ]
[Other articles in category /prog] permanent link
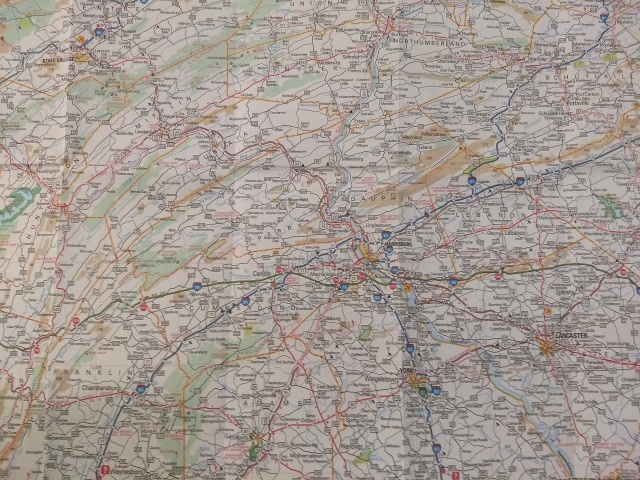
Sat, 06 Oct 2018Last week we visited Toph's school and I saw a big map of Pennsylvania. I was struck by something I had never noticed before. Here's a detail of central Pennsylvania, an area roughly 100 miles (160 km) square:
As you can see, a great many lines on this map start in the lower left, proceed in roughly parallel tracks north-by-northeast, then bend to the right, ending in the upper right corner. Many of the lines represent roads, but some represent county borders, and some represent natural features such as forests and rivers.
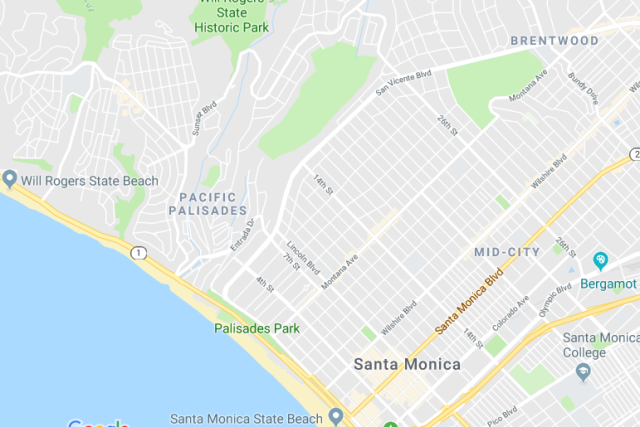
When something like this happens, it is almost always for some topographic reason. For example, here's a map of two adjacent communities in Los Angeles:
You can see just from the pattern of the streets that these two places must have different topography. The streets in Santa Monica are a nice rectangular grid. The streets in Pacific Palisades are in groups of concentric squiggles. This is because Pacific Palisades is hilly, and the roads go in level curves around the hills, whereas Santa Monica is as flat as a squid.
I had never noticed before that all the lines in central Pennsylvania go in the same direction. From looking at the map, one might guess that central Pennsylvania was folded into many long parallel wrinkles, and that the roads, forests, and rivers mostly lay in the valleys between the wrinkles. This is indeed the case. This part of Pennsylvania is part of the Ridge-and-Valley Appalachians, and the pattern of ridges and valleys extends far beyond Pennsylvania.
The wrinkling occurred over a long period, ending around 260 million years ago, in an event called the Alleghanian orogeny. North America and Africa (then part of the supercontinents Euramerica and Gondwana, respectively) collided with one another, and that whole part of North America crumpled up like a sheet of aluminum foil. People in Harrisburg and State College are living in the crumples.
[Other articles in category /misc] permanent link