Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Thu, 13 Feb 2020
Gentzen's rules for natural deduction
Here is Gerhard Gentzen's original statement of the rules of Natural Deduction (“ein Kalkül für ‘natürliche’, intuitionistische Herleitungen”):
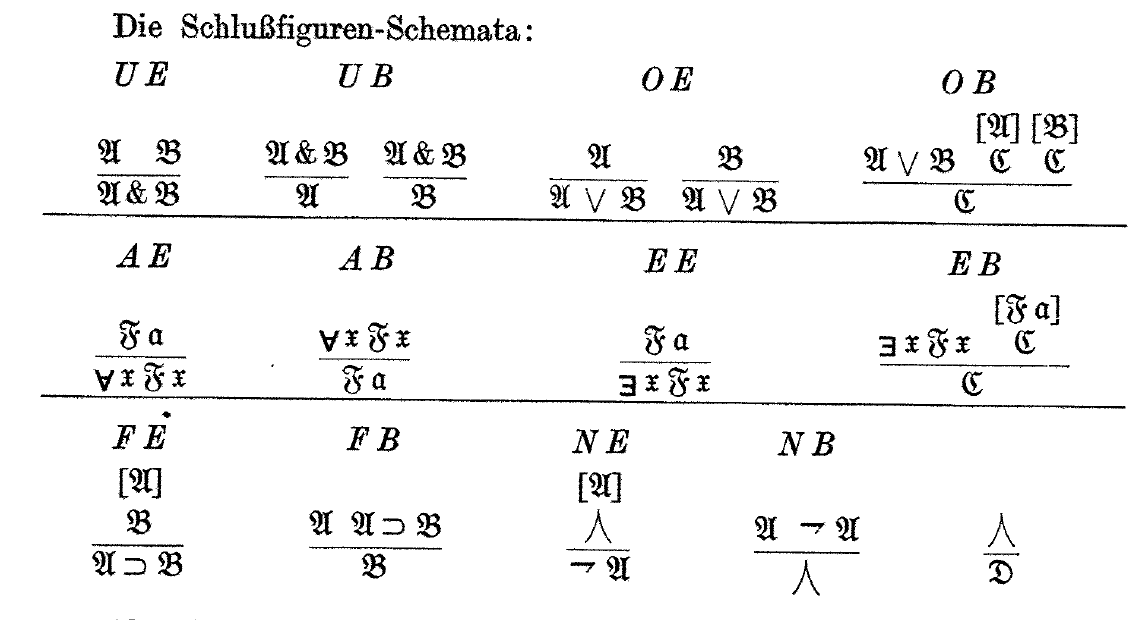
Natural deduction looks pretty much exactly the same as it does today, although the symbols are a little different. But only a little! Gentzen has not yet invented !!\land!! for logical and, and is still using !!\&!!. But he has invented !!\forall!!. The style of the !!\lnot!! symbol is a little different from what we use now, and he has that tent thingy !!⋏!! where we would now use !!\bot!!. I suppose !!⋏!! didn't catch on because it looks too much like !!\land!!. (He similarly used !!⋎!! to mean !!\top!!, but as usual, that doesn't appear in the deduction rules.)
We still use Gentzen's system for naming the rules. The notations “UE” and “OB” for example, stand for “und-Einführung” and “oder-Beseitigung”, which mean “and-introduction” and “or-elimination”.
Gentzen says (footnote 4, page 178) that he got the !!\lor, \supset, \exists!! signs from Russell, but he didn't want to use Russell's signs !!\cdot, \equiv, \sim, ()!! because they already had other meanings in mathematics. He took the !!\&!! from Hilbert, but Gentzen disliked his other symbols. Gentzen objected especially to the “uncomfortable” overbar that Hilbert used to indicate negation (“[Es] stellt eine Abweichung von der linearen Anordnung der Zeichen dar”). He attributes his symbols for logical equivalence (!!\supset\subset!!) and negation to Heyting, and explains that his new !!\forall!! symbol is analogous to !!\exists!!. I find it remarkable how quickly this caught on. Gentzen also later replaced !!\&!! with !!\land!!. Of the rest, the only one that didn't stick was !!\supset\subset!! in place of !!\equiv!!. But !!\equiv!! is much less important than the others, being merely an abbreviation.
Gentzen died at age 35, a casualty of the World War.
Source: Gerhard Gentzen, “Untersuchungen über das logische Schließen I”, pp. 176–210 Mathematische Zeitschrift v. 39, Springer, 1935. The display above appears on page 186.
[ Addendum 20200214: Thanks to Andreas Fuchs for correcting my German grammar. ]
[Other articles in category /math/logic] permanent link


