Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 08 Jul 2020
Ron Graham has died. He had a good run. When I check out I will probably not be as accomplished or as missed as Graham, even if I make it to 84.
I met Graham once and he was very nice to me, as he apparently was to everyone. I was planning to write up a reminiscence of the time, but I find I've already done it so you can read that if you care.
Graham's little book Rudiments of Ramsey Theory made a big impression on me when I was an undergraduate. Chapter 1, if I remember correctly, is a large collection of examples, which suited me fine. Chapter 2 begins by introducing a certain notation of Erdős and Rado: !!\left[{\Bbb N\atop k}\right]!! is the family of subsets of !!\Bbb N!! of size !!k!!, and
$$\left[{\Bbb N\atop k}\right] \to \left[{\Bbb N\atop k}\right]_r$$
is an abbreviation of the statement that for any !!r!!-coloring of members of !!\left[{\Bbb N\atop k}\right]!! there is always an infinite subset !!S\subset \Bbb N!! for which every member of !!\left[{S\atop k}\right]!! is the same color. I still do not find this notation perspicuous, and at the time, with much less experience, I was boggled. In the midst of my bogglement I was hit with the next sentence, which completely derailed me:
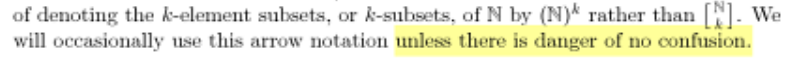
After this I could no longer think about the mathematics, but only about the sentence.
Outside the mathematical community Graham is probably best-known for juggling, or for Graham's number, which Wikipedia describes:
At the time of its introduction, it was the largest specific positive integer ever to have been used in a published mathematical proof.
One of my better Math Stack Exchange posts was in answer to the question Graham's Number : Why so big?. I love the phrasing of this question! And that, even with the strange phrasing, there is an answer! This type of huge number is quite typical in proofs of Ramsey theory, and I answered in detail.
The sense of humor that led Graham to write “danger of no confusion” is very much on display in the paper that gave us Graham's number. If you are wondering about Graham's number, check out my post.
[Other articles in category /math] permanent link


