Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Calculating π with atan2() |
| Obtuse axiomatization of category theory |
| Philadelphia Slaughterhouse Hotel |
| Philadelphia Slaughterhouse Hotel |
| The New York City passport office |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 23 Jul 2019
Obtuse axiomatization of category theory
About ten years ago I started an article, addressed to my younger self, reviewing various books in category theory. I doubt I will ever publish this. But it contained a long, plaintive digression about Categories, Allegories by Peter Freyd and Andre Scedrov:
I keep this one around on the shelf just so that I can pick it up ever few months and marvel at its opacity.
It is a superb example of the definition-theorem-remark style of mathematics textbooks. I have heard that this was a style pioneered by a book you are already familiar with, John Kelley's General Topology of 1955. If so, all I can say is, sometimes it works, and sometimes it doesn't. It worked for Kelley in 1955 writing about topology.
Here is an example of what is wrong with this book.
Everyone who knows anything about category theory knows that a category is a sort of abstraction of a domain of mathematical objects, like sets, groups, or topological spaces. A category has a bunch of "objects", which are the sets, the groups, or the topological spaces, and it has a bunch of "morphisms", which are maps between the objects that preserve the objects' special structure, be it algebraic, topological, or whatever. If the objects are sets, the morphisms are simply functions. If the objects are groups, the morphisms are group homomorphisms; if the objects are topological spaces, the morphisms are continuous maps. The basic point of category theory is to study the relationships between these structure-preserving maps, independent of the underlying structure of the objects themselves. We ignore the elements of the sets or groups, and the points in the topological spaces, and instead concentrate on the relationships between whole sets, groups, and spaces, by way of these "morphisms".
Here is the opening section of Categories, Allegories:
1.1 BASIC DEFINITIONS
The theory of CATEGORIES is given by two unary operations and a binary partial operation. In most contexts lower-case variables are used for the 'individuals' which are called morphisms or maps. The values of the operations are denoted and pronounced as:The axioms:
!!□x!! the source of !!x!!, !!x□!! the target of !!x!!, !!xy!! the composition of !!x!! and !!y!!,
!!xy!! is defined iff !!x□ = □y!!, !!(□x)□ = □x!! and !!□(x□) = x□!!, !!(□x)x = x!! and !!x(x□) = x!!, !!□(xy) = □(x(□y))!! and !!(xy)□ = ((x□)y)□!!, !!x(yz) = (xy)z!!.
In light of my capsule summary of category theory, can you figure out what is going on here? Even if you already know what is supposed to be going on you may not be able to make much sense of this. What to make of the axiom that !!□(xy) = □(x(□y))!!, for example?
The explanation is that Freyd has presented a version of category theory in which the objects are missing. Since every object !!X!! in a category is associated with a unique identity morphism !!{\text{id}}_X!! from !!X!! to itself, Freyd has identified each object with its identity morphism. If !!x:C\to D!!, then !!□x!! is !!{\text{id}}_C!! and !!x□!! is !!{\text{id}}_D!!. The axiom !!(□x)□ = □x!! is true because both sides are equal to !!{\text{id}}_C!!.
Still, why phrase it this way? And what about that !!□(x(□y))!! thing? I guessed it was a mere technical device, similar to the one that we can use to reduce five axioms of group theory to three. Normally, one defines a group to have an identity element !!e!! such that !!ex=xe=x!! for all !!x!!, and each element !!x!! has an inverse !!x^{-1}!! such that !!xx^{-1} = x^{-1}x = e!!. But if you are trying to be clever, you can observe that it is sufficient for there to be a left identity and a left inverse:
There must be an identity !!e!! such that !!ex=x!! for all !!x!!, and for each !!x!! there must be an !!x^{-1}!! such that !!x^{-1}x=e!!.
We no longer require !!xe=x!! or !!xx^{-1}=e!!, but it turns out that you can prove these anyway, from what is left. The fact that you can discard two of the axioms is mildly interesting, but of very little practical value in group theory.
I thought that probably the !!□(x(□y))!! thing was some similar bit of “cleverness”, and that perhaps by adopting this one axiom Freyd was able to reduce his list of axioms. For example, from that mysterious fourth axiom !!□(xy) = □(x(□y))!! you can conclude that !!xy!! is defined if and only if !!x(□y)!! is, and therefore, by the first axiom, that !!x□ = □y!! if and only if !!x□ = □(□y)!!, so that !!□y = □(□y)!!. So perhaps the phrasing of the axiom was chosen to allow Freyd to dispense with an additional axiom stating that !!□y = □(□y)!!.
Today I tinkered with it a little bit and decided I think not.
Freyd has:
$$\begin{align} xy \text{ is defined if and only if } x□ & = □y \tag{1} \\ (□x)□ & = □x \tag{2} \\ (□x)x & = x \tag{3} \\ □(xy) & = □(x(□y)) \tag{4} \end{align} $$
and their duals. Also composition is associative, which I will elide.
In place of 4, let's try this much more straightforward axiom:
$$ □(xy) = □x\tag{$4\star$} $$
I can now show that !!1, 2, 3, 4\star!! together imply !!4!!.
First, a lemma: !!□(□x) = □x!!. Axiom !!3!! says !!(□x)x = x!!, so therefore !!□((□x)x) = □x!!. By !!4\star!!, the left-hand side reduces to !!□(□x)!!, and we are done.
Now I want to show !!4!!, that !!□(xy) = □(x(□y))!!. Before I can even discuss the question I first need to show that !!x(□y)!! is defined whenever !!xy!! is; that is, whenever !!x□ = □y!!. But by the lemma, !!□y=□(□y)!!, so !!x□ = □(□y)!!, which is just what we needed.
At this point, !!4\star!! implies !!4!! directly: both sides of !!4!! have the form !!□(xz)!!, and !!4\star!! tells us that both are equal to !!□x!!.
Conversely, !!4!! implies !!4\star!!. So why didn't Freyd use !!4\star!! instead of !!4!!? I emailed him to ask, but he's 83 so I may not get an answer. Also, knowing Freyd, there's a decent chance I won't understand the answer if I do get one.
My plaintive review of this book continued:
Another, briefer complaint about this book: Early on, no later than page 13, Freyd begins to allude to "Lazard sheaves". These are apparently an important example. Freyd does not define or explain what "Lazard sheaves" are. Okay, you are expected to do some background reading, perhaps. Fair enough. But you are doomed, because "Lazard sheaves" is Freyd's own private coinage, and you will not be able to look it up under that name.
Apparently some people like this book. I don't know why, and perhaps I never will.
[Other articles in category /math] permanent link
Thu, 11 Jul 2019
The New York City passport office
Earlier this week I reported on a good visit I had had to the Philadelphia offices of the Social Security Administration.
Philadelphia government offices, in my experience, are generally better than those I have visited elsewhere. I've never been to the New York DMV office (do they even have one?) but the Philadelphia ones are way better than the New Jersey ones I used to use. Instead of standing in line for forty-five minutes, you get a number and sit down until your number is called.
The passport office was the biggest surprise. I first went in to deal with some passport thing shortly after I arrived in Philadelphia, maybe 1990 or so. The office was clean and quiet, the line was short, I got my business done quickly. None of those is the case in the New York passport office.
The New York passport office. Wow. Where to begin? I want to say that it defies description. But, I learned later, it has been described by no less a person than Samuel Beckett:
The abode is a flattened cylinder with rubber walls fifty meters in circumference and eighteen meters high. It is constantly illuminated by a dim, yellow light, and the temperature fluctuates between 5°C to 25°C, sometimes in as small an interval as four seconds. This leads to extremely parched skin, and the bodies brush against each other like dry leaves. Kisses make an "indescribable sound" and the rubber makes the footsteps mostly silent. There are 200 inhabitants, or one per square meter. Some are related to each other. Some are even married to each other, but the conditions make recognition difficult.
Here's a story of the New York passport office told to me by a friend many years ago. He stood in the line for forty-five minutes, and when he reached the window, he handed over his forms. The clerk glared at him for a few seconds, then, without a word, pushed them back.
“Is something wrong?” asked my friend.
There was a long pause. The clerk, too disgusted or enraged to reply immediately, finally said “They're not stapled.”
“Oh,” said my friend. “I see you have a stapler on your desk there.”
“You're supposed to staple them.”
“May I use your stapler?”
“No, your stapler is on the table at the back of the room.”
At this point my friend realized he was dealing with a monster. “Okay, but I can come right back to the window afterward, right?”
“No, you have to wait, like everyone else.”
At that moment my friend felt a tap on his shoulder. A man a few places behind him in line reached into his suit pocket and handed him a stapler. My friend says that as he stapled his papers and turned them in, the look on the clerk's face was of someone whose whole day had just been ruined.
“Thanks so much,” said my friend to Stapler Man. “Why did you happen to have a stapler in your pocket?”
“Oh,” said Stapler Man. “I do a lot of business at the passport office.”
[Other articles in category /misc] permanent link
Sun, 07 Jul 2019[ I wrote this in 2007 and forgot to publish it. Or maybe I was planning to finish it first. But if so I have no idea what I was originally planning to say, so here we are. ]
In computer programs, it's quite common to need a numerical value for π. Often you see something like:
#define PI 3.141592654
This has the drawback of not representing π as exactly as possible. But to do that in C probably requires putting in 16 digits after the decimal point, and most people don't have so much memorized. And anyway, you don't really know at compile time what the floating-point precision will be; some platforms support quad-width floats. So you can do better, maybe, by using the math library to calculate π. And people do:
static double pi = 4*atan2(1,1);
The atan2(y, x) function produces the (almost-)unique value θ from the range !![-\pi, \pi]!! such that a ray from the origin, passing through point (x, y), makes angle θ with the x-axis.
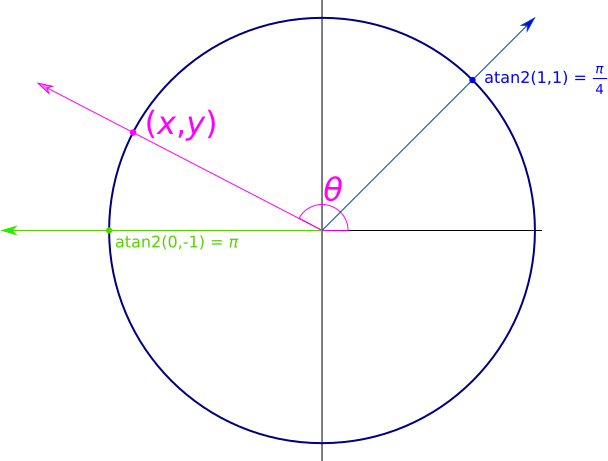
Note that the arguments have y first and x second.
For example, atan2(17, 0) returns !!\frac\pi
2!!, because a line at angle !!\frac\pi 2!! passes through the point
(0, 17). Similarly, atan2(-17, 0) returns -!!\frac\pi 2!!.
You can use atan2 to calculate π, by using
!!4·{\operatorname{atan}}2(1,1)!!, as I mentioned above. Many people
do; Google searching finds hundreds of examples. The manual for the
standard Perl module constant.pm mentions this example.
But this is a bit strange. Why is this so well-known? Why calculate 4*atan2(1,1) when $$\pi = {\operatorname{atan}}2(0,-1)$$ produces the same result and is simpler?
(Obligatory IEEE 754 complaining: atan2 should return an always-unique value from
!!(-\pi, \pi]!!, but I have to say “almost-unique” because as usual IEEE
754 fucks everything up, this time with its stupid distinction between
0 and -0.)
[ Addendum: Leah Neukirchen suggests that the atan2(1,1) is a
translation from earlier systems that provide a single-argument atan
function but no atan2. In those systems, there is no
workable analogue of atan2(0, -1) because the transformation
!!{\operatorname{atan}}2(y, x)\Rightarrow
{\operatorname{atan}}\left(\frac yx\right)!! gives !!{\operatorname{atan}}(0)!!, which doesn't work for this
application as it yields !!0!! instead of the desired !!\pi!!. And
similarly in languages with atan but not atan2 there is no analogue of !!\pi =
2·{\operatorname{atan}}2(1, 0)!!. So the simplest thing you can do is pi = 4 * atan(1),
and after the transformation above one gets !!\pi = 4·{\operatorname{atan}}2(1,1)!!. ]
[Other articles in category /prog] permanent link
Tue, 02 Jul 2019
Philadelphia Slaughterhouse Hotel
More information about the mysterious slaughterhouse hotel has come to light, thanks to Chas. Owens, Pete Krawczyk, and this useful blog post by D.S. Rosenstein.
Most important, the perplexing “hotel” is not intended for humans. “Hotel” is apparently stockyard jargon for a place where livestock are quartered temporarily just prior to slaughter. I am so glad to have this cleared up.
Also, M. Rosenstein has a photograph of the fancy abattoir with the spires:
They don't make industrial buildings like they used to. Check out the ornamental pattern in the bricks on the lower floor and the baluster along the riverside façade.
[ Addendum: Josh Bevan of Hidden City Philadelphia on When Cattle Men Reigned In The West (of Philadelphia). ]
[Other articles in category /history] permanent link
Mon, 01 Jul 2019
Philadelphia Slaughterhouse Hotel
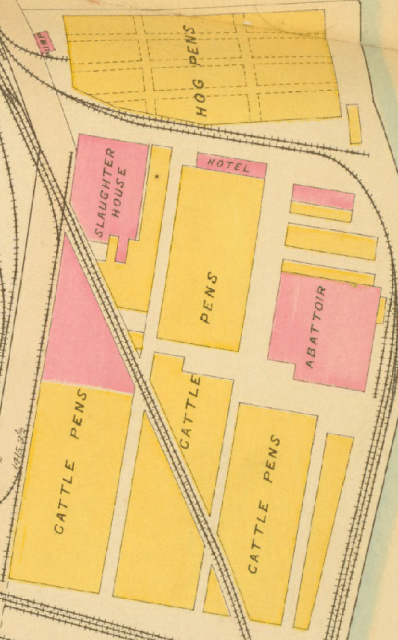
Yesterday on my other blog I posted about the most hilariously mislocated hotel I've ever heard of. It's the hotel that in 1910 was located in the Philadelphia stockyards, just the other side of the railroad tracks from the hog pens, between the slaughter house and the abbatoir:
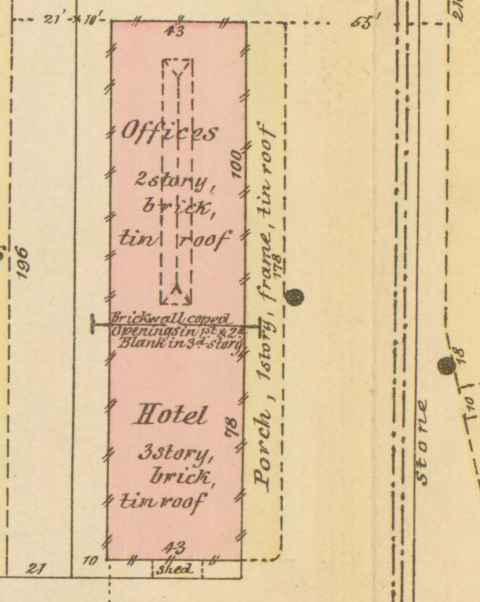
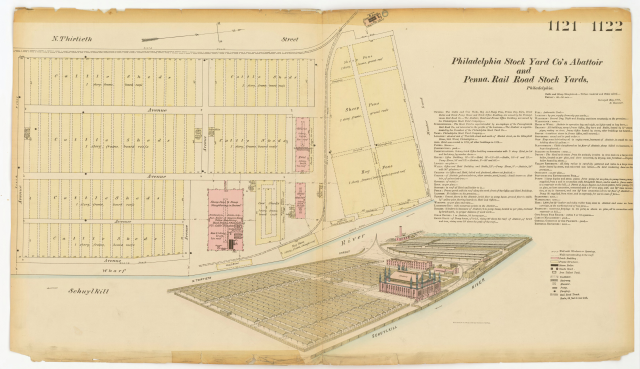
I thought that would be the end of it, but Chas. Owens did a little digging around and found a picture of the hotel, provided by the Greater Philadelphia GeoHistory Network. It's from R. Hexamer's insurance survey of 1877. At that time, the building was partly a hotel and partly the offices of the Philadelphia Stock Yard Company.
The survey includes a map of the site and a description of the facilities. Here's the detailed plan of the hotel:
The full image is 105 MB:
None of these buildings is still standing. (As I mentioned yesterday, the site is now occupied by the Cira Centre.) But the neighborhood's history as the center of Philadelphia's meatpacking district is not completely lost. According to this marvelous article from Hidden City Philadelphia, in 1906 the D.B. Martin company built a new combination office building and slaughterhouse only two blocks away at 3000 Market Street. Here's my favorite detail from the article:
Five hundred head of cattle at a time would be held on the rooftop cow pens, right above the heads of the company’s executives,
That building still stands, although I believe it's no longer used as a slaughterhouse.
[ Addendum 20190702: The “hotel” is explained: it is a temporary residence for livestock, not for humans. ]
[Other articles in category /history] permanent link