Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 17 Jun 2018
Bounded does not imply totally bounded
I somehow managed to miss the notion of totally bounded when I was learning topology, and it popped up on stack exchange recently. It is a stronger version of boundedness for metric spaces: a space !!M!! is totally bounded if, for any chosen !!\epsilon!!, !!M!! can be covered by a finite family of balls of radius !!\epsilon!!.
This is a strictly stronger property than ordinary boundedness, so the question immediately comes up: what is an example of a space that is bounded but not totally bounded. Many examples are well-known. For example, the infinite-dimensional unit ball is bounded but not totally bounded. But I didn't think of this right away.
Instead I thought of the following rather odd example: Let !!S!! be the closed unit disc and assign each point a polar coordinate !!\langle r,\theta\rangle!! as usual. Now consider the following metric:
$$ d(\langle r_1, \theta_1\rangle, \langle r_2, \theta_2\rangle) = \begin{cases} r_1, & \qquad \text{ if $r_2 = 0$} \\ \lvert r_1 - r_2 \rvert, & \qquad\text{ if $\theta_1 = \theta_2$} \\ r_1 + r_2 & \qquad\text{ otherwise} \\ \end{cases} $$
The idea is this: you can travel between points only along the radii of the disc. To get from !!p_1!! to !!p_2!! that are on different radii, you must go through the origin:
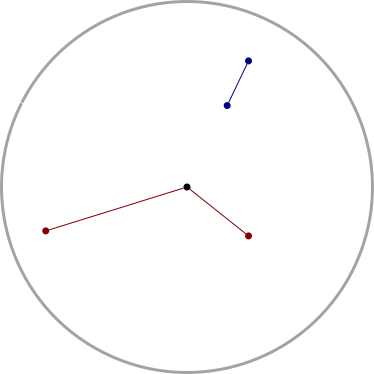
Now clearly when !!\epsilon < \frac12!!, the !!\epsilon!!-ball that covers each point point !!\left\langle 1, \theta\right\rangle!! lies entirely within one of the radii, and so an uncountable number of such balls are required to cover the disc.
It seems like this example could be useful in other circumstances too. Does it have a name?
[ Addendum 2018-07-18: Several Gentle Readers have informed me that this metric has not just one name, but several. ]
[Other articles in category /math] permanent link


