Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 31 Jul 2020
What does it mean to expand a function “in powers of x-1”?
A recent Math Stack Excahnge post was asked to expand the function !!e^{2x}!! in powers of !!(x-1)!! and was confused about what that meant, and what the point of it was. I wrote an answer I liked, which I am reproducing here.
You asked:
I don't understand what are we doing in this whole process
which is a fair question. I didn't understand this either when I first learned it. But it's important for practical engineering reasons as well as for theoretical mathematical ones.
Before we go on, let's see that your proposal is the wrong answer to this question, because it is the correct answer, but to a different question. You suggested: $$e^{2x}\approx1+2\left(x-1\right)+2\left(x-1\right)^2+\frac{4}{3}\left(x-1\right)^3$$
Taking !!x=1!! we get !!e^2 \approx 1!!, which is just wrong, since actually !!e^2\approx 7.39!!. As a comment pointed out, the series you have above is for !!e^{2(x-1)}!!. But we wanted a series that adds up to !!e^{2x}!!.
As you know, the Maclaurin series works here:
$$e^{2x} \approx 1+2x+2x^2+\frac{4}{3}x^3$$
so why don't we just use it? Let's try !!x=1!!. We get $$e^2\approx 1 + 2 + 2 + \frac43$$
This adds to !!6+\frac13!!, but the correct answer is actually around !!7.39!! as we saw before. That is not a very accurate approximation. Maybe we need more terms? Let's try ten:
$$e^{2x} \approx 1+2x+2x^2+\frac{4}{3}x^3 + \ldots + \frac{8}{2835}x^9$$
If we do this we get !!7.3887!!, which isn't too far off. But it was a lot of work! And we find that as !!x!! gets farther away from zero, the series above gets less and less accurate. For example, take !!x=3.1!!, the formula with four terms gives us !!66.14!!, which is dead wrong. Even if we use ten terms, we get !!444.3!!, which is still way off. The right answer is actually !!492.7!!.
What do we do about this? Just add more terms? That could be a lot of work and it might not get us where we need to go. (Some Maclaurin series just stop working at all too far from zero, and no amount of terms will make them work.) Instead we use a different technique.
Expanding the Taylor series “around !!x=a!!” gets us a different series, one that works best when !!x!! is close to !!a!! instead of when !!x!! is close to zero. Your homework is to expand it around !!x=1!!, and I don't want to give away the answer, so I'll do a different example. We'll expand !!e^{2x}!! around !!x=3!!. The general formula is $$e^{2x} \approx \sum \frac{f^{(i)}(3)}{i!} (x-3)^i\tag{$\star$}\ \qquad \text{(when $x$ is close to $3$)}$$
The !!f^{(i)}(x)!! is the !!i!!'th derivative of !! e^{2x}!! , which is !!2^ie^{2x}!!, so the first few terms of the series above are:
$$\begin{eqnarray} e^{2x} & \approx& e^6 + \frac{2e^6}1 (x-3) + \frac{4e^6}{2}(x-3)^2 + \frac{8e^6}{6}(x-3)^3\\ & = & e^6\left(1+ 2(x-3) + 2(x-3)^2 + \frac34(x-3)^3\right)\\ & & \qquad \text{(when $x$ is close to $3$)} \end{eqnarray} $$
The first thing to notice here is that when !!x!! is exactly !!3!!, this series is perfectly correct; we get !!e^6 = e^6!! exactly, even when we add up only the first term, and ignore the rest. That's a kind of useless answer because we already knew that !!e^6 = e^6!!. But that's not what this series is for. The whole point of this series is to tell us how different !!e^{2x}!! is from !!e^6!! when !!x!! is close to, but not equal to !!3!!.
Let's see what it does at !!x=3.1!!. With only four terms we get $$\begin{eqnarray} e^{6.2} & \approx& e^6(1 + 2(0.1) + 2(0.1)^2 + \frac34(0.1)^3)\\ & = & e^6 \cdot 1.22075 \\ & \approx & 492.486 \end{eqnarray}$$
which is very close to the correct answer, which is !!492.7!!. And that's with only four terms. Even if we didn't know an exact value for !!e^6!!, we could find out that !!e^{6.2}!! is about !!22.075\%!! larger, with hardly any calculation.
Why did this work so well? If you look at the expression !!(\star)!! you can see: The terms of the series all have factors of the form !!(x-3)^i!!. When !!x=3.1!!, these are !!(0.1)^i!!, which becomes very small very quickly as !!i!! increases. Because the later terms of the series are very small, they don't affect the final sum, and if we leave them out, we won't mess up the answer too much. So the series works well, producing accurate results from only a few terms, when !!x!! is close to !!3!!.
But in the Maclaurin series, which is around !!x=0!!, those !!(x-3)^i!! terms are !!x^i!! terms intead, and when !!x=3.1!!, they are not small, they're very large! They get bigger as !!i!! increases, and very quickly. (The !! i! !! in the denominator wins, eventually, but that doesn't happen for many terms.) If we leave out these many large terms, we get the wrong results.
The short answer to your question is:
Maclaurin series are only good for calculating functions when !!x!! is close to !!0!!, and become inaccurate as !!x!! moves away from zero. But a Taylor series around !!a!! has its “center” near !!a!! and is most accurate when !!x!! is close to !!a!!.
[Other articles in category /math/se] permanent link
Wed, 29 Jul 2020Toph left the cap off one of her fancy art markers and it dried out, so I went to get her a replacement. The marker costs $5.85, plus tax, and the web site wanted a $5.95 shipping fee. Disgusted, I resolved to take my business elsewhere.
On Wednesday I drove over to a local art-supply store to get the marker. After taxes the marker was somehow around $8.50, but I also had to pay $1.90 for parking. So if there was a win there, it was a very small one.
But also, I messed up the parking payment app, which has maybe the worst UI of any phone app I've ever used. The result was a $36 parking ticket.
Lesson learned. I hope.
[Other articles in category /oops] permanent link
Today I learned:
There is a genus of ankylosaurs named Zuul after “demon and demi-god Zuul, the Gatekeeper of Gozer, featured in the 1984 film Ghostbusters”.
The type species of Zuul is Zuul crurivastator, which means “Zuul, destroyer of shins”. Wikipedia says:
The epithet … refers to a presumed defensive tactic of ankylosaurids, smashing the lower legs of attacking predatory theropods with their tail clubs.
My eight-year-old self is gratified that the ankylosaurids are believed to attack their enemies’ ankles.
The original specimen of Z. crurivastator, unusually-well preserved, was nicknamed “Sherman”.
Here is a video of Dan Aykroyd discussing the name, with Sherman.
[Other articles in category /bio] permanent link
Wed, 15 Jul 2020
More trivia about megafauna and poisonous plants
A couple of people expressed disappointment with yesterday's article, which asked were giant ground sloths immune to poison ivy?, but then failed to deliver on the implied promise. I hope today's article will make up for that.
Elephants
I said:
Mangoes are tropical fruit and I haven't been able to find any examples of Pleistocene megafauna that lived in the tropics…
David Formosa points out what should have been obvious: elephants are megafauna, elephants live where mangoes grow (both in Africa and in India), elephants love eating mangoes [1] [2] [3], and, not obvious at all…
Elephants are immune to poison ivy!
Captive elephants have been known to eat poison ivy, not just a little bite, but devouring entire vines, leaves and even digging up the roots. To most people this would have cause a horrific rash … To the elephants, there was no rash and no ill effect at all…
It's sad that we no longer have megatherium. But we do have elephants, which is pretty awesome.
Idiot fruit
The idiot fruit is just another one of those legendarily awful creatures that seem to infest every corner of Australia (see also: box jellyfish, stonefish, gympie gympie, etc.); Wikipedia says:
The seeds are so toxic that most animals cannot eat them without being severely poisoned.
At present the seeds are mostly dispersed by gravity. The plant is believed to be an evolutionary anachronism. What Pleistocene megafauna formerly dispersed the poisonous seeds of the idiot fruit?
A wombat. A six-foot-tall wombat.
I am speechless with delight.
[Other articles in category /bio] permanent link
Tue, 14 Jul 2020
Were giant ground sloths immune to poison ivy?
The skin of the mango fruit contains urushiol, the same irritating chemical that is found in poison ivy. But why? From the mango's point of view, the whole point of the mango fruit is to get someone to come along and eat it, so that they will leave the seed somewhere else. Posioning the skin seems counterproductive.
An analogous case is the chili pepper, which contains an irritating chemical, capsaicin. I think the answer here is believed to be that while capsaicin irritates mammals, birds are unaffected. The chili's intended target is birds; you can tell from the small seeds, which are the right size to be pooped out by birds. So chilis have a chemical that encourages mammals to leave the fruit in place for birds.
What's the intended target for the mango fruit? Who's going to poop out a seed the size of a mango pit? You'd need a very large animal, large enough to swallow a whole mango. There aren't many of these now, but that's because they became extinct at the end of the Pleistocene epoch: woolly mammoths and rhinoceroses, huge crocodiles, giant ground sloths, and so on. We may have eaten the animals themselves, but we seem to have quite a lot of fruits around that evolved to have their seeds dispersed by Pleistocene megafauna that are now extinct. So my first thought was, maybe the mango is expecting to be gobbled up by a giant gound sloth, and have its giant seed pooped out elsewhere. And perhaps its urushiol-laden skin makes it unpalatable to smaller animals that might not disperse the seeds as widely, but the giant ground sloth is immune. (Similarly, I'm told that goats are immune to urushiol, and devour poison ivy as they do everything else.)
Well, maybe this theory is partly correct, but even if so, the animal definitely wasn't a giant ground sloth, because those lived only in South America, whereas the mango is native to South Asia. Ground slots and avocados, yes; mangos no.
Still the theory seems reasonable, except that mangoes are tropical fruit and I haven't been able to find any examples of Pleistocene megafauna that lived in the tropics. Still I didn't look very hard.
Wikipedia has an article on evolutionary anachronisms that lists a great many plants, but not the mango.
[ Addendum: I've eaten many mangoes but never noticed any irritation from the peel. I speculate that cultivated mangoes are varieties that have been bred to contain little or no urushiol, or that there is a post-harvest process that removes or inactivates the urushiol, or both. ]
[ Addendum 20200715: I know this article was a little disappointing and that it does not resolve the question in the title. Sorry. But I wrote a followup that you might enjoy anyway. ]
[Other articles in category /bio] permanent link
Wed, 08 Jul 2020Ron Graham has died. He had a good run. When I check out I will probably not be as accomplished or as missed as Graham, even if I make it to 84.
I met Graham once and he was very nice to me, as he apparently was to everyone. I was planning to write up a reminiscence of the time, but I find I've already done it so you can read that if you care.
Graham's little book Rudiments of Ramsey Theory made a big impression on me when I was an undergraduate. Chapter 1, if I remember correctly, is a large collection of examples, which suited me fine. Chapter 2 begins by introducing a certain notation of Erdős and Rado: !!\left[{\Bbb N\atop k}\right]!! is the family of subsets of !!\Bbb N!! of size !!k!!, and
$$\left[{\Bbb N\atop k}\right] \to \left[{\Bbb N\atop k}\right]_r$$
is an abbreviation of the statement that for any !!r!!-coloring of members of !!\left[{\Bbb N\atop k}\right]!! there is always an infinite subset !!S\subset \Bbb N!! for which every member of !!\left[{S\atop k}\right]!! is the same color. I still do not find this notation perspicuous, and at the time, with much less experience, I was boggled. In the midst of my bogglement I was hit with the next sentence, which completely derailed me:
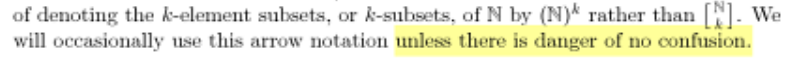
After this I could no longer think about the mathematics, but only about the sentence.
Outside the mathematical community Graham is probably best-known for juggling, or for Graham's number, which Wikipedia describes:
At the time of its introduction, it was the largest specific positive integer ever to have been used in a published mathematical proof.
One of my better Math Stack Exchange posts was in answer to the question Graham's Number : Why so big?. I love the phrasing of this question! And that, even with the strange phrasing, there is an answer! This type of huge number is quite typical in proofs of Ramsey theory, and I answered in detail.
The sense of humor that led Graham to write “danger of no confusion” is very much on display in the paper that gave us Graham's number. If you are wondering about Graham's number, check out my post.
[Other articles in category /math] permanent link
Addendum to “Weirdos during the Depression”
[ Previously ]
Ran Prieur had a take on this that I thought was insightful:
I would frame it like this: If you break rules that other people are following, you have to pretend to be unhappy, or they'll get really mad, because they don't want to face the grief that they could have been breaking the rules themselves all this time.
[Other articles in category /addenda] permanent link
Mon, 06 Jul 2020
Weird constants in math problems
Michael Lugo recently considered a problem involving the allocation of swimmers to swim lanes at random, ending with:
If we compute this for large !!n!! we get !!f(n) \sim 0.4323n!!, which agrees with the Monte Carlo simulations… The constant !!0.4323!! is $$\frac{(1-e^{-2})}2.$$
I love when stuff like this happens. The computer is great at doing a quick random simulation and getting you some weird number, and you have no idea what it really means. But mathematical technique can unmask the weird number and learn its true identity. (“It was Old Man Haskins all along!”)
A couple of years back Math Stack Exchange had Expected Number and Size of Contiguously Filled Bins, and although it wasn't exactly what was asked, I ended up looking into this question: We take !!n!! balls and throw them at random into !!n!! bins that are lined up in a row. A maximal contiguous sequence of all-empty or all-nonempty bins is called a “cluster”. For example, here we have 13 balls that I placed randomly into 13 bins:
In this example, there are 8 clusters, of sizes 1, 1, 1, 1, 4, 1, 3, 1. Is this typical? What's the expected cluster size?
It's easy to use Monte Carlo methods and find that when !!n!! is large, the average cluster size is approximately !!2.15013!!. Do you recognize this number? I didn't.
But it's not hard to do the calculation analytically and discover that that the reason it's approximately !!2.15013!! is that the actual answer is $$\frac1{2(e^{-1} - e^{-2})}$$ which is approximately !!2.15013!!.
Math is awesome and wonderful.
(Incidentally, I tried the Inverse Symbolic Calculator just now, but it was no help. It's also not in Plouffe's Miscellaneous Mathematical Constants)
[ Addendum 20200707: WolframAlpha does correctly identify the !!2.15013!! constant. ]
[Other articles in category /math] permanent link
Useful and informative article about privately funded border wall
The Philadelphia Inquirer's daily email newsletter referred me to this excellent article, by Jeremy Schwartz and Perla Trevizo.
Wow!” I said. “This is way better than the Inquirer's usual reporting. I wonder what that means?” Turns out it meant that the Inquirer was not responsible for the article. But thanks for the pointer, Inquirer folks!
The article is full of legal, political, and engineering details about why it's harder to build a border wall than I would have expected. I learned a lot! I had known about the issue that most of the land is privately owned. But I hadn't considered that there are international water-use treaties that come into play if the wall is built too close to the Rio Grande, or that the wall would be on the river's floodplain. (Or that the Rio Grande even had a floodplain.)
He built a privately funded border wall. It's already at risk of falling down if not fixed, courtesy of The Texas Tribune and ProPublica.
[Other articles in category /tech] permanent link



