Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Thu, 30 Mar 2006
Blog Posts Escape from Lab
Yesterday I decided to put my blog posts into CVS. As part of doing
that, I copied the blog articles tree. I must have made a mistake,
because not all the files were copied in the way I wanted.
To prevent unfinished articles from getting out before they are ready, I have a Blosxom plugin that suppresses any article whose name is title.blog if it is accompanied by a title.notyet file. I can put the draft of an article in the .notyet file and then move it to .blog when it's ready to appear, or I can put the draft in .blog with an empty or symbolic-link .notyet alongside it, and then remove the .notyet file when the article is ready.
I also use this for articles that will never be ready. For example, a while back I got the idea that it might be funny if I were to poſt ſome articles with long medial letter 'ſ' as one ſees in Baroque printing and writing. To try out what this would look like I copied one of my articles---the one on Baroque writing ſtyle ſeemed appropriate---and changed the filename from baroque-style.blog to baroque-ftyle.blog. Then I created baroque-ftyle.notyet ſo that nobody would ever ſee my ſtrange experiment.
But somehow in the big shakeup last night, some of the notyet files got lost, and so this post and one other escaped from my laboratory into the outside world. As I explained in an earlier post, I can remove these from my web site, but aggregators like Bloglines.com will continue to display my error. it's tempting to blame this on Blosxom, or on CVS, or on the sysadmin, or something like that, but I think the most likely explanation for this one is that I screwed up all by myself.
The other escapee was an article about the optional second argument in Perl's built-in bless function, which in practice is never omitted. This article was so dull that I abandoned it in the middle, and instead addressed the issue in passing in an article on a different subject.
So if your aggregator is displaying an unfinished and boring article about one-argument bless, or a puzzling article that seems like a repeat of an earlier one, but with all the s's replaced with ſ's, that is why.
These errors might be interesting as meta-information about how I work. I had hoped not to discuss any such meta-issues here, but circumstances seem to have forced me to do it at least a little. One thing I think might be interesting is what my draft articles look like. Some people rough out an article first, then go back and fix it it. I don't do that. I write one paragraph, and then when it's ready, I write another paragraph. My rough drafts look almost the same as my finished product, right up to the point at which they stop abruptly, sometimes in the middle of a sentence.
Another thing you might infer from these errors is that I have a lot of junk sitting around that is probably never going to be used for anything. Since I started the blog, I've written about 85,000 words of articles that were released, and about 20,000 words of .notyet. Some of the .notyet stuff will eventually see the light of day, of course. For example, I have about 2500 words of addenda to this month's posts that are scheduled for release tomorrow, 1000 words about this month's Google queries and the nature of "authority" on the Web, 1000 words about the structure of the real numbers, 1300 words about the Grelling-Nelson paradox, and so on.
But I alſo have that 1100-word experiment about what happens to an article when you use long medial s's everywhere. (Can you believe I actually conſidered doing this in every one of my poſts? It's tempting, but just a little too idioſyncratic, even for me.) I have 500 words about why to attend a colloquium, how to convince everyone there that you're a genius, and what's wrong with education in general. I have 350 words that were at the front of my article about the 20 most important tools that explained in detail why most criticism of Forbes' list would be unfair; it wasted a whole page at the beginning of that article, so I chopped it out, but I couldn't bear to throw it away. I have two thirds of a 3000-word article written about why my brain is so unusual and how I've coped with its peculiar limitations. That one won't come out unless I can convince myself that anyone else will find it more than about ten percent as interesting as I find it.
[Other articles in category /oops] permanent link
Tue, 28 Mar 2006
The speed of electricity
For some reason I have needed to know this several times in the past
few years: what is the speed of electricity? And for some reason,
good answers are hard to come by.
(Warning: as with all my articles on physics, readers are cautioned that I do not know what I am talking about, but that I can talk a good game and make up plenty of plausible-sounding bullshit that sounds so convincing that I believe it myself. Beware of bullshit.)
If you do a Google search for "speed of electricity", the top hit is Bill Beaty's long discourse on the subject. In this brilliantly obtuse article, Beaty manages to answer just about every question you might have about everything except the speed of electricity, and does so in a way that piles confusion on confusion.
Here's the funny thing about electricity. To have electricity, you need moving electrons in the wire, but the electrons are not themselves the electricity. It's the motion, not the electrons. It's like that joke about the two rabbinical students who are arguing about what makes tea sweet. "It's the sugar," says the first one. "No," disagrees the other, "it's the stirring." With electricity, it really is the stirring.
We can understand this a little better with an analogy. Actually, several analogies, each of which, I think, illuminates the others. They will get progressively closer to the real truth of the matter, but readers are cautioned that these are just analogies, and so may be misleading, particularly if overextended. Also, even the best one is not really very good. I am introducing them primarily to explain why I think M. Beaty's answer is obtuse.
- Consider a
garden hose a hundred feet long. Suppose the hose is already full of
water. You turn on the hose at one end, and water starts coming out
the other end. Then you turn off the hose, and the water stops coming
out. How long does it take for the water to stop coming out? It
probably happens pretty darn fast, almost instantaneously.
This shows that the "signal" travels from one end of the hose to the other at a high speed—and here's the key idea—at a much higher speed than the speed of the water itself. If the hose is one square inch in cross-section, its total volume is about 5.2 gallons. So if you're getting two gallons per minute out of it, that means that water that enters the hose at the faucet end doesn't come out the nozzle end until 156 seconds later, which is pretty darn slow. But it certainly isn't the case that you have to wait 156 seconds for the water to stop coming out after you turn off the faucet. That's just how long it would take to empty the hose. And similarly, you don't have to wait that long for water to start coming out when you turn the faucet on, unless the hose was empty to begin with.
The water is like the electrons in the wire, and electricity is like that signal that travels from the faucet to the nozzle when you turn off the water. The electrons might be travelling pretty slowly, but the signal travels a lot faster.
- You're waiting in the check-in line at the airport. One of the
clerks calls "Can I help who's next?" and the lady at the front of the
line steps up to the counter. Then the next guy in line steps up to
the front of the line. Then the next person steps up. Eventually,
the last person in line steps up. You can imagine that there's a
"hole" that opens up at the front of the line, and the hole travels
backwards through the line to the back end.
How fast does the hole travel? Well, it depends. But one thing is sure: the speed at which the hole moves backward is not the same as the speed at which the people move forward. It might take the clerks another hour to process the sixty people in line. That does not mean that when they call "next", it will take an hour for the hole to move all the way to the back. In fact, the rate at which the hole moves is to a large extent independent of how fast the people in the line are moving forward.
The people in the line are like electrons. The place at which the people are actually moving—the hole—is the electricity itself.
- In the ocean, the waves start far out from shore, and then roll in
toward the shore. But if you look at a cork bobbing on the waves, you
see right away that even though the waves move toward the shore, the
water is staying in pretty much the same place. The cork is
not moving toward the shore; it's bobbing up and down, and it might
well stay in the same place all day, bobbing up and down. It should
be pretty clear that the speed with which the water and the cork are
moving up and down is only distantly related to the speed with which
the waves are coming in to shore. The water is like the electrons,
and the wave is like the electricity.
- A bomb explodes on a hill, and sometime later Ike on the next hill
over hears the bang. This is because the exploding bomb compresses
the air nearby, and then the compressed air expands, compressing the
air a little way away again, and the compressed air expands and
compresses the air a little way farther still, and so there's a wave
of compression that spreads out from the bomb until eventually the air
on the next hill is compressed and presses on Ike's eardrums. It's
important to realize that no individual air molecule has traveled from
hill A to hill B. Each air molecule stays in pretty much the same
place, moving back and forth a bit, like the water in the water waves
or the people in the airport queue. Each person in the airport line
stays in pretty much the same place, even though the "hole" moves all
the way from the front of the line to the back. Similarly, the air
molecules all stay in pretty much the same place even as the
compression wave goes from hill A to hill B. When you speak to
someone across the room, the sound travels to them at a speed of 680
miles per hour, but they are not bowled over by hurricane-force winds.
(Thanks to Aristotle Pagaltzis for suggesting that I point this out.)
Here the air molecules are like the electrons in the wire, and the
sound is like the electricity.
I believe that when someone asks for the speed of electricity, what they are typically after is something like: When I flip the switch on the wall, how long before the light goes on? Or: the ALU in my computer emits some bits. How long before those bits get to the output bus? Or again: I send a telegraph message from Nova Scotia to Ireland on an undersea cable. How long before the message arrives in Ireland? Or again: computers A and B are on the same branch of an ethernet, 10 meters apart. How long before a packet emitted by A's ethernet hardware gets to B's ethernet hardware?
M. Beaty's answer about the speed of the electrons is totally useless as an answer to this kind of question. It's a really detailed, interesting answer to a question to which hardly anyone was interested in the answer.
Here the analogy with the speed of sound really makes clear what is wrong with M. Beaty's answer. I set off a bomb on one hill. How long before Ike on the other hill a mile away hears the bang? Or, in short, "what is the speed of sound?" M. Beaty doesn't know what the speed of sound is, but he is glad to tell you about the speed at which the individual air molecules are moving back and forth, although this actually has very little to do with the speed of sound. He isn't going to tell you how long before the tsunami comes and sweeps away your village, but he has plenty to say about how fast the cork is bobbing up and down on the water.
That's all fine, but I don't think it's what people are looking for when they want the speed of electricity. So the individual charges in the wire are moving at 2.3 mm/s; who cares? As M. Beaty was at some pains to point out, the moving charges are not themselves the electricity, so why bring it up?
I wanted to end this article with a correct and pertinent answer to the question. For a while, I was afraid I was going to have to give up. At first, I just tried looking it up on the web. Many people said that the electricity travels at the speed of light, c. This seemed rather implausible to me, for various reasons. (That's another essay for another day.) And there was widespread disagreement about how fast it really was. For example:
But then I found this page on the characteristic impedance of coaxial cables and other wires, which seems rather more to the point than most of the pages I have found that purport to discuss the "speed of electricity" directly.
From this page, we learn that the thing I have been referring to as the "speed of electricity" is called, in electrical engineering jargon, the "velocity factor" of the wire. And it is a simple function of the "dielectric constant" not of the wire material itself, but of the insulation between the two current-carrying parts of the wire! (In typical physics fashion, the dielectric "constant" is anything but; it depends on the material of which the insulation is made, the temperature, and who knows what other stuff they aren't telling me. Dielectric constants in the rest of the article are for substances at room temperature.) The function is simply:
$$V = {c\over\sqrt{\varepsilon_r}}$$
where V is the velocity of electricity in the wire, and εr is the dielectric constant of the insulating material, relative to that of vacuum. Amazingly, the shape, material, and configuration of the wire doesn't come into it; for example it doesn't matter if the wire is coaxial or twin parallel wires. (Remember the warning from the top of the page: I don't know what I am talking about.) Dielectric constants range from 1 up to infinity, so velocity ranges from c down to zero, as one would expect. This explains why we find so many inconsistent answers about the speed of electricity: it depends on a specific physical property of the wire. But we can consider some common examples.Wikipedia says that the dielectric constant of rubber is about 7 (and this website specifies 6.7 for neoprene) so we would expect the speed of electricity in rubber-insulated wire to be about 0.38c. This is not quite accurate, because the wires are also insulated by air and by the rest of the universe. But it might be close to that. (Remember that warning!)
The dielectric constant of air is very small—Wikipedia says 1.0005, and the other site gives 1.0548 for air at 100 atmospheres pressure—so if the wires are insulated only by air, the speed of electricity in the wires should be very close to the speed of light.
We can also work the calculation the other way: this web page says that signal propagation in an ethernet cable is about 0.66c, so we infer that the dielectric constant for the insulator is around 1/0.662 = 2.3. We look up this number in a a table of dielectric constants and guess from that that the insulator might be polyethylene or something like it. (This inference would be correct.)
What's the lower limit on signal propagation in wires? I found a reference to a material with a dielectric constant of 2880. Such a material, used as an insulator between two wires, would result in a velocity of about 2% of c, which is still 5600 km/s. this page mentions cement pastes with "effective dielectric constants" up around 90,000, yielding an effective velocity of 1/300 c, or 1000 km/s.
Finally, I should add that the formula above only applies for direct currents. For varying currents, such as are typical in AC power lines, the dielectric constant apparently varies with time (some constant!) and the analysis is more complicated.
[ Addendum 20180904: Paul Martin suggests that I link to this useful page about dielectric constants. It includes an extensive table of the εr for various polymers. Mostly they are between 2 and 3. ]
[Other articles in category /physics] permanent link
Sun, 26 Mar 2006
Approximations and the big hammer
In today's
article about rational approximations to √3, I said that "basic
algebra tells us that √(1-ε) ≈ 1 - ε/2 when
ε is small".
A lot of people I know would be tempted to invoke calculus for this, or might even think that calculus was required. They see the phrase "when ε is small" or that the statement is one about limits, and that immediately says calculus.
Calculus is a powerful tool for producing all sorts of results like that one, but for that one in particular, it is a much bigger, heavier hammer than one needs. I think it's important to remember how much can be accomplished with more elementary methods.
The thing about √(1-ε) is simple. First-year algebra tells us that (1 - ε/2)2 = 1 - ε + ε2/4. If ε is small, then ε2/4 is really small, so we won't lose much accuracy by disregarding it.
This gives us (1 - ε/2)2 ≈ 1 - ε, or, equivalently, 1 - ε/2 ≈ √(1 - ε). Wasn't that simple?
[Other articles in category /math] permanent link
Sat, 25 Mar 2006
Achimedes and the square root of 3
In my recent
discussion of why π might be about 3, I mentioned in passing
that Archimedes, calculating the approximate value of π used 265/153
as a rational approximation to √3. The sudden appearance of the
fraction 265/153 is likely to make almost anyone say "huh"? Certainly
it made me say that. And even Dr. Chuck Lindsey, who wrote up the
detailed explanation of Archimedes' work from which I learned
about the 265/153 in the first place, says:
Throughout this proof, Archimedes uses several rational approximations to various square roots. Nowhere does he say how he got those approximations—they are simply stated without any explanation—so how he came up with some of these is anybody's guess.It's a bit strange that Dr. Lindsey seems to find this mysterious, because I think there's only one way to do it, and it's really easy to find, so long as you ask the question "how would Archimedes go about calculating rational approximations to √3", rather than "where the heck did 265/153 come from?" It's like one of those pencil mazes they print in the Sunday kids' section of the newspaper: it looks complicated, but if you work it in the right direction, it's trivial.
Suppose you are a mathematician and you do not have a pocket calculator. You are sure to need some rational approximations to √3 somewhere along the line. So you should invest some time and effort into calculating some that you can store in the cupboard for when you need them. How can you do that?
You want to find pairs of integers a and b with a/b ≈ √3. Or, equivalently, you want a and b with a2 ≈ 3b2. But such pairs are easy to find: Simply make a list of perfect squares 1 4 9 16 25 36 49..., and their triples 3 12 27 48 75 108 147..., and look for numbers in one list that are close to numbers in the other list. 22 is close to 3·12, so √3 ≈ 2/1. 72 is close to 3·42, so √3 ≈ 7/4. 192 is close to 3·112, so √3 ≈ 19/11. 972 is close to 3·562, so √3 ≈ 97/56.
Even without the benefits of Hindu-Arabic numerals, this is not a very difficult or time-consuming calculation. You can carry out the tabulation to a couple of hundred entries in a few hours, and if you do you will find that 2652 = 70225, and 3·1532 is 70227, so that √3 ≈ 265/153.
Once you understand this, it's clear why Archimedes did not explain himself. By saying that √3 was approximately 265/153, had had exhausted the topic. By saying so, you are asserting no more and no less than that 3·1532 ≈ 2652; if the reader is puzzled, all they have to do is spend a minute carrying out the multiplication to see that you are right. The only interesting point that remains is how you found those two integers in the first place, but that's not part of Archimedes' topic, and it's pretty obvious anyway.
[ Addendum 20090122: Dr. Lindsey was far from the only person to have been puzzled by this. More here. ]
In my article about the peculiarity of π, I briefly mentioned continued fractions, saying that if you truncate the continued fraction representation of a number, you get a rational number that is, in a certain sense, one of the best possible rational approximations to the original number. I'll eventually explain this in detail; in the meantime, I just want to point out that 265/153 is one of these best-possible approximations; the mathematics jargon is that 265/153 is one of the "convergents" of √3.
The approximation of √n by rationals leads one naturally to the so-called "Pell's equation", which asks for integer solutions to ax2 - by2 = ±1; these turn out to be closely related to the convergents of √(a/b). So even if you know nothing about continued fractions or convergents, you can find good approximations to surds.
Here's a method that I learned long ago from Patrick X. Gallagher of Columbia University. For concreteness, let's suppose we want an approximation to √3. We start by finding a solution of Pell's equation. As noted above, we can do this just by tabulating the squares. Deeper theory (involving the continued fractions again) guarantees that there is a solution. Pick one; let's say we have settled on 7 and 4, for which 72 ≈ 3·42.
Then write √3 = √(48/16) = √(49/16·48/49) = 7/4·√(48/49). 48/49 is close to 1, and basic algebra tells us that √(1-ε) ≈ 1 - ε/2 when ε is small. So √3 ≈ 7/4 · (1 - 1/98). 7/4 is 1.75, but since we are multiplying by (1 - 1/98), the true approximation is about 1% less than this, or 1.7325. Which is very close—off by only about one part in 4000. Considering the very small amount of work we put in, this is pretty darn good. For a better approximation, choose a larger solution to Pell's equation.
More generally, Gallagher's method for approximating √n is: Find integers a and b for which a2 ±1 = nb2; such integers are guaranteed to exist unless n is a perfect square. Then write √n = √(nb2 / b2) = √((a2 ± 1) / b2) = √(a2/b2 · (a2 ± 1)/a2) = a / b · √((a2 ± 1) / a2) = a/b · √(1 ± 1/a2) ≈ a/b · (1 ± 1 / 2a2).
Who was Pell? Pell was nobody in particular, and "Pell's equation" is a complete misnomer. The problem was (in Europe) first studied and solved by Lord William Brouncker, who, among other things, was the founder and the first president of the Royal Society. The name "Pell's equation" was attached to the problem by Leonhard Euler, who got Pell and Brouncker confused—Pell wrote up and published an account of the work of Brouncker and John Wallis on the problem.
G.H. Hardy says that even in mathematics, fame and history are sometimes capricious, and gives the example of Rolle, who "figures in the textbooks of elementary calculus as if he had been a mathematician like Newton." Other examples abound: Kuratowski published the theorem that is now known as Zorn's Lemma in 1923, Zorn published different (although related) theorem in 1935. Abel's theorem was published by Ruffini in 1799, by Abel in 1824. Pell's equation itself was first solved by the Indian mathematician Brahmagupta around 628. But Zorn did discover, prove and publish Zorn's lemma, Abel did discover, prove and publish Abel's theorem, and Brouncker did discover, prove and publish his solution to Pell's equation. Their only failings are to have been independently anticipated in their work. Pell, in contrast, discovered nothing about the equation that carries his name. Hardy might have mentioned Brouncker, whose significant contribution to number theory was attributed to someone else, entirely in error. I know of no more striking mathematical example of the capriciousness of fame and history.
[Other articles in category /math] permanent link
Mon, 20 Mar 2006
The 20 most important tools
Forbes magazine recently ran an article on The
20 Most Important Tools. I always groan when I hear that some big
magazine has done something like that, because I know what kind of
dumbass mistake they are going to make: they are going to put Post-It
notes at #14. The Forbes folks did not make this
mistake. None of their 20 items were complete losers.
In fact, I think they did a pretty good job. They assembled a panel of experts, including Don Norman and Henry Petroski; they also polled their readers and their senior editors. The final list isn't the one I would have written, but I don't claim that it's worse than one I would have written.
Criticizing such a list is easy—too easy. To make the rules fair, it's not enough to identify items that I think should have been included. I must identify items that I think nearly everyone would agree should have been included.
Unfortunately, I think there are several of these.
First, to the good points of the list. It doesn't contain any major clinkers. And it does cover many vitally important tools. It provokes thought, which is never a bad thing. It was assembled thoughtfully, so one is not tempted to dismiss any item without first carefully considering why it is in there.
Here's the Forbes list:
- The Knife
- The Abacus
- The Compass
- The Pencil
- The Harness
- The Scythe
- The Rifle
- The Sword
- Eyeglasses
- The Saw
- The Watch
- The Lathe
- The Needle
- The Candle
- The Scale
- The Pot
- The Telescope
- The Level
- The Fish Hook
- The Chisel
Categories
The Forbes items are also allowed to stand for categories. For example, "the Rifle" really stands for portable firearms, including muskets and such. "The pencil" includes pens and writing brushes. (Why put "the pencil" and not "the pen"? I imagine Henry Petroski arguing about it until everyone else got tired and gave up.) The spoon, had they included it, would have stood for eating utensils in general.But here is my first quibble: it's not really clear why some items stood for whole groups, and others didn't. The explanatory material points out that five other items on the list are special cases of the knife: the scythe, lathe, saw, chisel, and sword. The inclusion of the knife as #1 on the list is, I think, completely inarguable. The power and the antiquity of the knife would put it in the top twenty already.
Consider its unmatched versatility as well and you just push it up into first place, and beyond. Make a big knife, and you have a machete; bigger still, and you have a sword. Put a knife on the end of a stick and you have an axe; put it on a longer stick and you have a spear. Bend a knife into a circle and you have a sickle; make a bigger sickle and you have a scythe. Put two knives on a hinge or a spring and you have shears. Any of these could be argued to be in the top twenty. When you consider that all these tools are minor variations on the same device, you inevitably come to the conclusion that the knife is a tool that, like Babe Ruth among baseball players, is ridiculously overqualified even for inclusion with the greatest.
But Forbes people gave the sword a separate listing (#8), and a sword is just a big knife. It serves the same function as a knife and it serves it in the same mechanical way. So it's hard to understand why the Forbes people listed them separately. If you're going to list the sword separately, how can you omit the axe or the spear? Grouping the items is a good idea, because otherwise the list starts to look like the twenty most important ways to use a knife. But I would have argued for listing the sword, axe, chisel, and scythe under the heading of "knife".
I find the other knifelike devices less objectionable. The saw is fundamentally different from a knife, because it is made and used differently, and operates in a different way: it is many tiny knives all working in the same direction. And the lathe is not a special case of the knife, because the essential feature of the lathe is not the sharp part but the spinning part. (I wouldn't consider the lathe a small, portable implement, but more about that below.)
Pounding
I said that I was required to identify items that everyone would agree are major omissions. I have two such criticisms. One is that the list has room for six cutting tools, but no pounding tools. Where is the club? Where is the hammer? I could write a whole article about the absurdity of omitting the hammer. It's like leaving Abraham Lincoln off of a list of the twenty greatest U.S. presidents. It's like leaving Albert Einstein off of a list of the twenty greatest scientists. It's like leaving Honus Wagner off of a list of the twenty greatest baseball players.No, I take it back. It's not like any of those things. Those things should all be described as analogous to leaving the hammer of the list of the twenty most important tools, not the other way around.
Was the hammer omitted because it's not a simple, portable physical implement? Clearly not.
Was the hammer omitted because it's an abstract fundamental machine, like the lever? Is a hammer really just a lever? Not unless a knife is just a wedge.
Is the hammer subsumed in one of the other items? I can't see any candidates. None of the other items is for pounding.
Did the Forbes panel just forget about it? That would have been weird enough. Two thousand Forbes readers, ten editors, and Henry Petroski all forgot about the hammer? Impossible. If you stop someone on the street and ask them to name a tool, odds are that they will say "hammer". And how can you make a list of the twenty most important tools, include the chisel as #20, and omit the hammer, without which the chisel is completely useless?
The article says:
We eventually came up with a list of more than 100 candidate tools. There was a great deal of overlap, so we collapsed similar items into a single category, and chose one tool to represent them. That left us with a final list of 33 items, each one a part of a particular class or style of tool; for instance, the spoon is representative of all eating utensils.Perhaps the hammer was one of the 13 classes of tools that didn't make the cut? The writer of the article, David M. Ewalt, kindly provided me with a complete list of the 33 classes, including the also-rans. The hammer was not with the also-rans; I'm not sure if I find that more or less disturbing.
Also-rans
Well, enough about hammers. The 13 classes that did not make the cut were:
- spoon
- longbow
- broom
- paper clip
- computer mouse
- floppy disk
- syringe
- toothbrush
- barometer
- corkscrew
- gas chromatograph
- condom
- remote control
"Gas chromatograph" seems to be someone's attempt to steer the list away from ancient inventions and to include some modern tools on the list. This is a worthy purpose. But I wish that they had thought of a better representative than the gas chromatograph. It seems to me that most tools of modern invention serve only very specialized purposes. The gas chromatograph is not an exception. I've never used a gas chromatograph. I don't think I know anyone who has. I've never seen a gas chromatograph. I might well go to the grave without using one. How is it possible that the gas chromatograph is one of the 33 most important tools of all time, beating out the hammer?
With "syringe", I imagine the authors were thinking of the hypodermic needle, but maybe they really were thinking of the syringe in general, which would include the meat syringe, the vacuum pipette, and other similar devices. If the latter, I have no serious complaint; I just wanted to point out the possible misunderstanding.
"Paper clip" is just the kind of thing I was afraid would appear. The paper clip isn't one of the top hundred most important tools, perhaps not even one of the top thousand. If the hammer were annihilated, civilization would collapse within twenty-four hours. If the paper clip were annihilated, we would shrug, we would go back to using pins, staples, and ribbons to bind our papers, and life would go on. If the pin isn't qualified for the list, the paper clip isn't even close.
I was speechless at the inclusion of the corkscrew in a list of essential tools that omits both bottles and corks, reduced to incoherent spluttering. The best I could do was mutter "insane".
I don't know exactly what was intended by "remote control", but it doesn't satisfy the criteria. The idea of remote control is certainly important, but this is not a list of important ideas or important functions but important tools. If there were a truly universal remote control that I could carry around with me everywhere and use to open doors, extinguish lights, summon vehicles, and so on, I might agree. But each particular remote control is too specialized to be of any major value.
Putting the computer mouse on the list of the twenty (or even 33) most important tools is like putting the pastrami on rye on the list of the twenty most important foods. Tasty, yes. Important? Surely not. In the same class as the soybean? Absurd.
The floppy disk is already obsolete.
Other comparisons
The telescope
Returning to the main list, eyeglasses and telescopes are both special cases of the lens, but their fundamentally different uses seem to me to clearly qualify them for separate listing; fair enough. I'm not sure I would have included the telescope, though. Is the telescope the most useful and important object of its type? Maybe I'm missing something, but it seems to me that most of the uses of the telescope are either scientific or military. The military value of the telescope is not in the same class as the value of the sword or the rifle. The scientific value of the telescope, however, is enormous. So it's on it scientific credentials that the telescope goes into the list, if at all.But the telescope has a cousin, the microscope. Is the telescope's scientific value comparable to that of the microscope? I would argue that it is not. Certainly the microscope is much more widely used, in almost any branch of science you could name except astronomy. The telescope enabled the discovery that the earth is not the center of the universe, a discovery of vast philosophical importance. Did the microscope lead to fundamental discoveries of equal importance? I would argue that the discovery of microorganisms was at least as important in every way.
Arguing that "X is in the list, so Y should be too" is a slippery slope that leads to a really fat list in which each mistaken inclusion justifies a dozen more. I won't make that argument in this article. But the reverse argument, that "Y isn't in the list so X shouldn't be either", is much safer. If the microscope isn't important enough to make the list, then neither is the telescope.
The level
This is the only tool on the list that I thought was a serious mistake, not quite on the order of the Post-It note, but silly in the same way, if to a much lesser degree. It is another item of the type exemplified by the telescope, an item that is on the list, but whose more useful and important cousin is omitted. Why the level and not the plumb line? The plumb line does everything a level does, and more. The level tells you when things are horizontal; the plumb line tells you when they are horizontal or vertical, depending on what you need. The plumb line is simpler and older. The plumb line finds the point or surface B that is directly below point A; the level does nothing of the kind.I'm boggled; I don't know what the level is doing there. But the fact that my most serious complaint about any particular item is with item #18 shows how well-done I think the list is overall.
Sewing
The needle made the list at #13, but thread did not. A lot of sewing things missed out. Most of these, I think, are not serious omissions. The spinning wheel, for example: hand-spinning works adequately, although more slowly. The thimble? Definitely not in the top twenty. The button, with frogs and other clasps included? Maybe, maybe not. But one omission is serious, and must be considered seriously: the loom. I suppose it was eliminated for being too big; there can be no other excuse. But the lathe is #12, and the lathe is not normally small or portable.There are small, portable lathes. But there are also small, portable looms, hand looms, and so on. I think the loom has a better claim to being a tool in this sense than a lathe does. Cloth is surely one of the ten most important technological inventions of all time, up there with the knife, the gun, and the pot. Cloth does not belong on the Forbes list, because it is not a tool. But omission of the loom surprises me.
Grinding
 Similarly, the omission of the windmill is quite
understandable. But what about the quern? Flour is surely a
technology of the first importance., Grain can be ground into flour
without a windmill, and in many places was or still is. This morning
I planned to write that it must have been omitted because it is
hardly used any more, but then I thought a little harder and realized
that I own not one but two devices that are essentially querns. (One
for grinding coffee beans, the other for peppercorns.) I wouldn't want to argue that the quern is on the top twenty, but I think
it's worth considering.
Similarly, the omission of the windmill is quite
understandable. But what about the quern? Flour is surely a
technology of the first importance., Grain can be ground into flour
without a windmill, and in many places was or still is. This morning
I planned to write that it must have been omitted because it is
hardly used any more, but then I thought a little harder and realized
that I own not one but two devices that are essentially querns. (One
for grinding coffee beans, the other for peppercorns.) I wouldn't want to argue that the quern is on the top twenty, but I think
it's worth considering.
Male bias?
In fact, the list seems to omit a lot of important handicraft and home items that have fallen into disfavor. Male bias, perhaps? I briefly considered writing this article with the male-bias angle as the main point, but it's not my style. The authors might learn something from consideration of this question anyway.The pot made the list, but not the potter's wheel. An important omission, perhaps? I think not, that a good argument could be made that the potter's wheel was only an incremental improvement, not suitable for the top twenty.
I do wonder what happened to rope; here I could only imagine that they decided it wasn't a "tool". (M. Ewalt says that he is at a loss to explain the omission of rope.) And where's the basket? Here I can't imagine what the argument was.
Carrying
With the mention of baskets, I can't put off any longer my biggest grievance about the list: Where is the bag?The bag! Where is the bag?
I will say it again: Where is the bag?
Is the bag a small, portable implement? Yes, almost by definition. "Stop for a minute and think about what you've done today--every job you've accomplished, every task you've completed." begins the Forbes article. Did I have my bag with me? I did indeed. I started the day by opening up a bag of grapes to eat for breakfast. Then I made my lunch and put it in a bag, which I put into another, larger bag with my pens and work papers. Then I carried it all to work on my bicycle. Without the bag, I couldn't have carried these things to work. Could I have gotten that stuff to work without a bag? No, I would not have had my hands free to steer the bicycle. What if I had walked, instead of riding? Still probably not; I would have dropped all the stuff.
The bag, guys!. Which of you comes to work in the morning without a bag? I just polled the folks in my office; thirteen of fourteen brought bags to work today. Which of you carries your groceries home from the store without a bag? Paleolithic people carried their food in bags too. Did you use a lathe today? No? A telescope? No? A level? A fish hook? A candle? Did you use a bag today? I bet you did. Where is the bag?
The only container on the Forbes list is the pot. Could the bag be considered to be included under the pot? M. Ewalt says that it was, and it was omitted for that reason. I believe this is a serious error. The bag is fundamentally different from the pot. I can sum up the difference in one sentence: the pot is for storage; the bag is for transportation.
Each one has several advantages not possessed by the other. Unlike the pot, the bag is lightweight and easy to carry; pots are bulky. You can sling the bag over your shoulder. The bag is much more accommodating of funny-shaped objects: It's much easier to put a hacked-up animal or a heterogeneous bunch of random stuff into a bag than into a pot. My bag today contains some pads of paper, a package of crackers, another bag of pens, a toy octopus, and a bag of potato chips. None of this stuff would fit well into a pot. The bag collapses when it's empty; the pot doesn't.
The pot has several big advantages over the bag:
- The pot is rigid. It tends
to protect its contents more than a bag would, both from thumping and
banging, and from rodents, which can gnaw through bags but not through
pots.
- The pot is impermeable. This means that it is easy to clean,
which is an
important health and safety issue. Solids, such as grain or beans,
are protected from damp when stored in pots, but not in bags. And the
pot, being impermeable, can be used to store liquids such as food
and lighting oils; making a bag for
storing liquids is possible but nontrivial. (Sometimes permeability
is an advantage; we store dirty laundry in bags and baskets, never pots.)
- The pot is
fireproof, and so can be used for cooking. Being both fireproof
and impermeable, the pot enables the preparation of soup, which
increases the supply of available food and the energy that can be
extracted from the food.
I have no objection to Forbes' inclusion of the pot on their list, none at all. In fact, I think that it should be put higher than #16. But the bag needs to be listed too.
Other possible omissions
After the hammer, the bag, and rope, I have no more items that I think are so inarguable that they are sure substitutes for items in Forbes' list. There are items I think are probably better choices, but I think it is arguable, and, as I explained at the beginning of the article, I don't want to take cheap shots. Any list of the 20 most important tools will leave out a lot of important tools; switching around which tools are omitted is no guarantee of an objectively better list. For discussion purposes only, I'll mention tongs (including pliers), baskets, and shovels. Of the items on Forbes' near-miss list that I would want to consider are the bow, the broom and the spoon.
Revised list
Here, then, is my revised list. It's still not the list I would have made up from scratch, but I wanted to try to retain as much of the Forbes list as I could, because I think the items at the bottom are judgement calls, and there is plenty of room for reasonable disagreement about any of them.Linguists found a while ago that if you ask subjects to judge whether certain utterances are grammatically correct or not, they have some difficulty doing it, and their answers do not show a lot of agreement with other subjects'. But if you allow them an "I'm not sure" category, they have a lot less difficulty, and you do see a lot of agreement about which utterances people are unsure about. I think a similar method may be warranted here. Instead of the tools that are in or out of the list, I'm going to make two lists: tools that I'm sure are in the list, and tools that I'm not sure are out of the list.
The Big Eight, tools that I think you'd have to be crazy to omit, are:
- Knife (includes sword, axe, scythe, chisel, spear, shears, scissors)
- Hammer (includes club, mace, sledgehammer, mallet)
- Bag (includes wineskin, water skin, leather bottle, purse)
- Pot (includes plate, bowl, pitcher, rigid bottle, mortar)
- Rope (includes string and thread)
- Harness (includes collar and yoke)
- Pen (includes pencil, writing brush, etc.)
- Gun (includes rifle and musket, but not cannon)
- Compass
- Plumb line (includes level)
- Sewing needle
- Candle (includes lamp, lantern, torch)
- Ladder
- Eyeglasses (includes contact lenses)
- Saw
- Balance
- Fishhook
- Lathe
- Abacus (includes counting board)
- Microscope
The other adjustments are minor: The pot got a big promotion, from #16 to #4. The pencil is represented by the pen, instead of the other way around. The rifle is teamed with the musket as "the gun". The telescope is replaced with the microscope. The level is replaced with the plumb line. The scale is replaced by the balance, which is more a terminological difference than anything else.
The omission of mine that worries me the most is the basket. I left it out because although it didn't seem very much like either the pot or the bag, it did seem too much like both of them. I worry about omitting the pin, but I'm not sure it qualifies as a "tool".
If I were to get another 13 slots, I might include:
- Basket
- Broom
- Horn
- Pry bar
- Quern
- Radio (Walkie-talkies)
- Scraper
- Shovel
- Spoon
- Tape
- Tongs
- Touchstone
- Welding torch
[ Addendum 20190610: Miles Gould points out that the bag may in fact have been essential to the evolution of human culture. This blog post by Scott Alexander, reviewing The Secret Of Our Success (Joseph Henrich, Princeton University Press, 2015) says, in part:
Humans are persistence hunters: they cannot run as fast as gazelles, but they can keep running for longer than gazelles (or almost anything else). Why did we evolve into that niche? The secret is our ability to carry water. Every hunter-gatherer culture has invented its own water-carrying techniques, usually some kind of waterskin. This allowed humans to switch to perspiration-based cooling systems, which allowed them to run as long as they want.]
[Other articles in category /tech] permanent link
Blosxom sucks
Several people were upset at my recent
discussion of Blosxom. Specifically, I said that it sucked.
Strange to say, I meant this primarily as a compliment. I am going to
explain myself here.
Before I start, I want to set your expectations appropriately. Bill James tells a story about how he answered the question "What is Sparky Anderson's strongest point as a [baseball team] manager?" with "His won-lost record". James was surprised to discover that when people read this with the preconceived idea that he disliked Anderson's management, they took "his record" as a disparagement, when he meant it as a compliment.
I hope that doesn't happen here. This article is a long compliment to Blosxom. It contains no disparagement of Blosxom whatsoever. I have technical criticisms of Blosxom; I left them out of this article to avoid confusion. So if I seem at any point to be saying something negative about Blosxom, please read it again, because that's not the way I meant it.
As I said in the original article, I made some effort to seek out the smallest, simplest, lightest-weight blogging software I could. I found Blosxom. It far surpassed my expectations. The manual is about three pages long. It was completely trivial to set up. Before I started looking, I hypothesized that someone must have written blog software where all you do is drop a text file in a directory somewhere and it magically shows up on the blog. That was exactly what Blosxom turned out to be. When I said it was a smashing success, I was not being sarcastic. It was a smashing success.
The success doesn't end there. As I anticipated, I wasn't satisfied for long with Blosxom's basic feature set. Its plugin interface let me add several features without tinkering with the base code. Most of these have to do with generating a staging area where I could view posts before they were generally available to the rest of the world. The first of these simply suppressed all articles whose filenames contained test. This required about six lines of code, and took about fifteen minutes to implement, most of which was time spent reading the plugin manual. My instance of Blosxom is now running nine plugins, of which I wrote eight; the ninth generates the atom-format syndication file.
The success of Blosxom continued. As I anticipated, I eventually reached a point at which the plugin interface was insufficient for what I wanted, and I had to start hacking on the base code. The base code is under 300 lines. Hacking on something that small is easy and rewarding.
I fully expect that the success of Blosxom will continue. Back in January, when I set it up, I foresaw that I would start with the basic features, that later I would need to write some plugins, and still later I would need to start hacking on the core. I also foresaw that the next stage would be that I would need to throw the whole thing away and rewrite it from scratch to work the way I wanted to. I'm almost at that final stage. And when I get there, I won't have to throw away my plugins. Blosxom is so small and simple that I'll be able to write a Blosxom-compatible replacement for Blosxom. Even in death, the glory of Blosxom will live on.
So what did I mean by saying that Blosxom sucks? I will explain.
Following Richard Gabriel, I think there are essentially two ways to do a software design:
- You can try to do the Right Thing, where the Right Thing is very complex, subtle, and feature-complete.
- You can take the "Worse-is-Better" approach, and try to cover most of the main features, more or less, while keeping the implementation as simple as possible.
Worse, because the Right Thing is very difficult to achieve, and very complex and subtle, it is rarely achieved. Instead, you get a complex and subtle system that is complexly and subtly screwed up. Often, the designer shoots for something complex, subtle, and correct, and instead ends up with a big pile of crap. I could cite examples here, but I think I've offended enough people for one day.
In contrast, with the "Worse-is-Better" approach, you do not try to do the Right Thing. You try to do the Good Enough Thing. You bang out something short and simple that seems like it might do the job, run it up the flagpole, and see if it flies. If not, you bang on it some more.
Whereas the Right Thing approach is hard to get correct, the Worse-is-Better approach is impossible to get correct. But it is very often a win, because it is much easier to achieve "good enough" than it is to achieve the Right Thing. You expend less effort in doing so, and the resulting system is often simple and easy to manage.
If you screw up with the Worse-is-Better approach, the end user might be able to fix the problem, because the system you have built is small and simple. It is hard to screw it up so badly that you end with nothing but a pile of crap. But even if you do, it will be a much smaller pile of crap than if you had tried to construct the Right Thing. I would very much prefer to clean up a small pile of crap than a big one.
Richard Gabriel isn't sure whether Worse-is-Better is better or worse than The Right Thing. As a philosophical question, I'm not sure either. But when I write software, I nearly always go for Worse is Better, for the usual reasons, which you might infer from the preceding discussion. And when I go looking for other people's software, I look for Worse is Better, because so very few people can carry out the Right Thing, and when they try, they usually end up with a big pile of crap.
When I went looking for blog software back in January, I was conscious that I was looking for the Worse-is-Better software to an even greater degree than usual. In addition to all the reasons I have given above, I was acutely conscious of the fact that I didn't really know what I wanted the software to do. And if you don't know what you want, the Right Thing is the Wrong Thing, because you are not going to understand why it is the Right Thing. You need some experience to see the point of all the complexity and subtlety of the Right Thing, and that was experience I knew I did not have. If you are as ignorant as I was, your best bet is to get some experience with the simplest possible thing, and re-evaluate your requirements later on.
When I found Blosxom, I was delighted, because it seemed clear to me that it was Worse-is-Better through and through. And my experience has confirmed that. Blosxom is a triumph of Worse-is-Better. I think it could serve as a textbook example.
Here is an example of a way in which Blosxom subscribes to the Worse-is-Better philosophy. A program that handles plugins seems to need some way to let the plugins negotiate amongst themselves about which ones will run and in what order. Consider Blosxom's filter callback. What if one plugin wants to force Blosxom to run its filter callback before the other plugins'? What if one plugin wants to stop all the subsequent plugins from applying their filters? What if one plugin filters out an article, but a later plugin wants to rescue it from the trash heap? All these are interesting and complex questions. The Apache module interface is an interesting and complex answer to some of these questions, an attempt to do The Right Thing. (A largely successful attempt, I should add.)
Faced with these interesting and complex questions, Blosxom sticks its head in the sand, and I say that without any intent to disparage Blosxom. The Blosxom answer is:
- Plugins run in alphabetic order.
- Each one gets its crack at a data structure that contains the articles.
- When all the plugins have run, Blosxom displays whatever's left in the data structure.
So Blosxom is a masterpiece of Worse-is-Better. I am a Worse-is-Better kind of guy anyway, and Worse-is-Better was exactly what I was looking for in this case, so I was very pleased with Blosxom, and I still am. I got more and better Worse-is-Better for my software dollar than usual.
When I stuck a "BLOSXOM SUX" icon on my blog pages, I was trying to express (in 80×15 pixels) my evaluation of Blosxom as a tremendously successful Worse-is-Better design. Because it might be the Wrong Thing instead of the Right Thing, but it was the Right Wrong Thing, and I'd sure rather have the Right Wrong Thing than the Wrong Right Thing.
And when I said that "Blosxom really sucks... in the best possible way", that's what I meant. In a world full of bloated, grossly over-featurized software that still doesn't do quite what you want, Blosxom is a spectacular counterexample. It's a slim, compact piece of software that doesn't do quite what you want---but because it is slim and compact, you can scratch your head over it for couple of minutes, take out the hammer and tongs, and get it adjusted the way you want.
Thanks, Rael. I think you did a hell of a job. I am truly sorry that was not clear from my earlier article.
[Other articles in category /oops] permanent link
Sat, 18 Mar 2006
Mysteries of color perception
Color perception is incredibly complicated, and almost the only
generalization of it that can be made is "everything you think you
know is probably wrong." The color wheel, for example, is totally
going to flummox the aliens, when they arrive. "What the heck do you
mean, 'violet is a mixture of red and blue'? Violet is nothing
like red. Violet is less like red than any other color except
ultraviolet! Red is even less like violet than it is like blue, for
heaven's sake. What is wrong with you people?"
Well, what is wrong with us is that, because of an engineering oddity in our color sensation system, we think red and violet look somewhat similar, and more alike than red and green.
But anyway, my real point was to note that the colors in  look a lot different against
a gray background than they do against the blue background in the bar
on the left. People who read this blog through an aggregator are just
going to have to click through the link for once.
look a lot different against
a gray background than they do against the blue background in the bar
on the left. People who read this blog through an aggregator are just
going to have to click through the link for once.
[Other articles in category /aliens] permanent link
Who farted?
The software that generates these web pages from my blog entries is Blosxom. When I decided I wanted
to try blogging, I did a web search for something like "simplest
possible blogging software", and found a page that discussed Bryar.
So I located the Bryar manual. The first sentence in the Bryar manual
says "Bryar is a piece of blog production software, similar in style
to (but considerably more complex than) Rael Dornfest's
blosxom." So I dropped Bryar and got Blosxom. This was a
smashing success: It was running within ten minutes. Now, two months
later, I'm thinking about moving everything to Bryar, because Blosxom
really sucks.  .
But for me it was a huge success, and I probably wouldn't have started
a blog if I hadn't found it. It sucks in the best possible way:
because it's drastically under-designed and excessively lightweight.
That is much better than sucking because it is drastically
over-designed and excessively heavyweight. It also sucks in some
less ambivalent ways, but I'm not here (today) to criticize Blosxom,
so let's move on.
.
But for me it was a huge success, and I probably wouldn't have started
a blog if I hadn't found it. It sucks in the best possible way:
because it's drastically under-designed and excessively lightweight.
That is much better than sucking because it is drastically
over-designed and excessively heavyweight. It also sucks in some
less ambivalent ways, but I'm not here (today) to criticize Blosxom,
so let's move on.
Until the big move to Bryar, I've been writing plugins for Blosxom. When I was shopping for blog software, one of my requirements that that the thing be small and simple enough to be hackable, since I was sure I would inevitably want to do something that couldn't be accomplished any other way. With Blosxom, that happened a lot sooner than it should have (the plugin interface is inadequate), but the fallback position of hacking the base code worked quite well, because it is fairly small and fairly simple.
Most recently, I had to hack the Blosxom core to get the menu you can see on the left side of the page, with the titles of the recent posts. This should have been possible with a plugin. You need a callback (story) in the plugin that is invoked once per article, to accumulate a list of title-URL pairs, and then you need another callback (stories_done) that is invoked once after all the articles have been scanned, to generate the menu and set up a template variable for insertion into the template. Then, when Blosxom fills the template, it can insert the menu that was set up by the plugin.
With stock Blosxom, however, this is impossible. The first problem you encounter is that there is no stories_done callback. This is only a minor problem, because you can just have a global variable that holds the complete menu so far at all times; each time story is invoked, it can throw away the incomplete menu that it generated last time and replace it with a revised version. After the final call to story, the complete menu really is complete:
sub story {
my ($pkg, $path, $filename, $story_ref, $title_ref, $body_ref,
$dir, $date) = @_;
return unless $dir eq "" && $date eq "";
return unless $blosxom::flavour eq "html";
my $link = qq{<a href="$blosxom::url$path/$filename.$blosxom::flavour">} .
qq{<span class=menuitem>$$title_ref</span></a>};
push @menu, $link;
$menu = join " / ", @menu;
}
That strategy is wasteful of CPU time, but not enough to notice. You
could also fix it by hacking the base code to add a
stories_done callback, but that strategy is wasteful of
programmer time.But it turns out that this doesn't work, and I don't think there is a reasonable way to get what I wanted without hacking the base code. (Blosxom being what it is, hacking the base code is a reasonable solution.) This is because of a really bad architecture decision inside of Blosxom. The page is made up of three independent components, called the "head", the "body", and the "foot". There are separate templates of each of these. And when Blosxom generates a page, it does so in this sequence:
- Fill "head" template and append result to output
- Process articles
- Fill "body" template and append result to output
- Fill "foot" template and append result to output
So I had to go in and hack the Blosxom core to make it fractionally less spiky:
- Process articles
- Fill "head" template and append result to output
- Fill "body" template and append result to output
- Fill "foot" template and append result to output
- Process articles
- Fill and output templates:
- Fill "head" template and append result to output
- Fill "body" template and append result to output
- Fill "foot" template and append result to output
#include head
#include body
#include foot
But if I were to finish the article with that discussion, then
the first half of the article would have been relevant and to the
point, and as regular readers know, We Don't Do That Here. No, there
must come a point about a third of the way through each article at
which I say "But anyway, the real point of this note is...".Anyway, the real point of this note is to discuss was the debugging technique I used to fix Blosxom after I made this core change, which broke the output. The menu was showing up where I wanted, but now all the date headers (like the "Sat, 18 Mar 2006" one just above) appeared at the very top of the page body, before all the articles.
The way Blosxom generates output is by appending it to a variable $output, which eventually accumulates all the output, and is printed once, right at the very end. I had found the code that generated the "head" part of the output; this code ended with $output .= $head to append the head part to the complete output. I moved this section down, past the (much more complicated) section that scanned the articles themselves, so that the "head" template, when filled, would have access to information (such as menus) accumulated while scanning the articles.
But apparently some other part of the program was inserting the date headers into the output while scanning the articles. I had to find this. The right thing to do would have been just to search the code for $output. This was not sure to work: there might have been dozens of appearances of $output, making it a difficult task to determine which one was the responsible appearance. Also, any of the plugins, not all of which were written by me, could have been modifying $output, so it would not have been enough just to search the base code.
Still, I should have started by searching for $output, under the look-under-the-lamppost principle. (If you lose your wallet in a dark street start by looking under the lamppost. The wallet might not be there, but you will not waste much time on the search.) If I had looked under the lamppost, I would have found the lost wallet:
$curdate ne $date and $curdate = $date and $output .= $date;
That's not what I did. Daunted by the theoretical difficulties, I
got out a big hammer. The hammer is of some technical interest, and
for many problems it is not too big, so there is some value in
presenting it.Perl has a feature called tie that allows a variable to be enchanted so that accesses to it are handled by programmer-defined methods instead of by Perl's usual internal processes. When a tied variable $foo is stored into, a STORE method is called, and passed the value to be stored; it is the responsibility of STORE to put this value somewhere that it can be accessed again later by its counterpart, the FETCH method.
There are a lot of problems with this feature. It has an unusually strong risk of creating incomprehensible code by being misused, since when you see something like $this = $that you have no way to know whether $this and $that are tied, and that what you think is an assignment expression is actually STORE($this, FETCH($that)), and so is invoking two hook functions that could have completely arbitrary effects. Another, related problem is that the compiler can't know that either, which tends to disable the possibility of performing just about any compile-time optimization you could possibly think of. Perhaps you would like to turn this:
for (1 .. 1000000) { $this = $that }
into just this:
$this = $that;
Too bad; they are not the same, because $that might be tied
to a FETCH function that will open the pod bay doors the
142,857th time it is called. The unoptimized code opens the pod bay
doors; the "optimized" code does not.But tie is really useful for certain kinds of debugging. In this case the question is "who was responsible for inserting those date headers into $output?" We can answer the question by tieing $output and supplying a STORE callback that issues a report whenever $output is modified. The code looks like this:
package who_farted;
sub TIESCALAR {
my ($package, $fh) = @_;
my $value = "";
bless { value => \$value, fh => $fh } ;
}
This is the constructor; it manufactures an object to which the
FETCH and STORE methods can be directed. It is the
responsibility of this object to track the value of $output,
because Perl won't be tracking the value in the usual way. So the
object contains a "value" member, holding the value that is stored in
$object. It also contains a filehandle for printing
diagnostics. The FETCH method simply returns the current
stored value:
sub FETCH {
my $self = shift;
${$self->{value}};
}
The basic STORE method is simple:
sub STORE {
my ($self, $val) = @_;
my $fh = $self->{fh};
print $fh "Someone stored '$val' into \$output\n";
${$self->{value}} = $val;
}
It issues a diagnostic message about the new value, and stores the new
value into the object so that FETCH can get it later. But
the diagnostic here is not useful; all it says is that "someone"
stored the value; we need to know who, and where their code is. The
function st() generates a stack trace:
sub st {
my @stack;
my $spack = __PACKAGE__;
my $N = 1;
while (my @c = caller($N)) {
my (undef, $file, $line, $sub) = @c;
next if $sub =~ /^\Q$spack\E::/o;
push @stack, "$sub ($file:$line)";
} continue { $N++ }
@stack;
}
Perl's built-in caller() function returns information about
the stack frame N levels up. For clarity, st() omits
information about frames in the who_farted class itself.
(That's the next if... line.)The real STORE dumps the stack trace, and takes some pains to announce whether the value of $output was entirely overwritten or appended to:
sub STORE {
my ($self, $val) = @_;
my $old = $ {$self->{value}};
my $olen = length($old);
my ($act, $what) = ("set to", $val);
if (substr($val, 0, $olen) eq $old) {
($act, $what) = ("appended", substr($val, $olen));
}
$what =~ tr/\n/ /;
$what =~ s/\s+$//;
my $fh = $self->{fh};
print $fh "var $act '$what'\n";
print $fh " $_\n" for st();
print $fh "\n";
${$self->{value}} = $val;
}
To use this, you just tie $output at the top of the base
code:
open my($DIAGNOSTIC), ">", "/tmp/who-farted" or die $!;
tie $output, 'who_farted', $DIAGNOSTIC;
This worked well enough. The stack trace informed me that the
modification of interest was occurring in the
blosxom::generate function at line 290 of
blosxom.cgi. That was the precise location of the lost
wallet. It was, as I said, a big hammer to use to squash a mosquito of
a problem---but the mosquito is dead.A somewhat more useful version of this technique comes in handy in situations where you have some program, say a CGI program, that is generating the wrong output; maybe there is a "1" somewhere in the middle of the output and you don't know what part of the program printed "1" to STDOUT. You can adapt the technique to watch STDOUT instead of a variable. It's simpler in some ways, because STDOUT is written to but never read from, so you can eliminate the FETCH method and the data store:
package who_farted;
sub rig_fh {
my ($handle, $diagnostic) = shift;
my $mode = shift || "<";
open my($aux_handle), "$mode&=", $handle or die $!;
tie *$handle, __PACKAGE__, $aux_handle, $diagnostic;
}
sub TIEHANDLE {
my ($package, $aux_handle, $diagnostic) = @_;
bless [$aux_handle, $diagnostic] => $package;
}
sub PRINT {
my ($aux_handle, $diagnostic) = @$self;
print $aux_handle @_;
my $str = join("", @_);
print $diagnostic "$str:\n";
print $diagnostic " $_\n" for st();
print $diagnostic "\n";
}
To use this, you put something like rig_fh(\*STDOUT,
$DIAGNOSTIC, ">") in the main code. The only tricky part is that some
part of the code (rig_fh here) must manufacture a new, untied
handle that points to the same place that STDOUT did before
it was tied, so that the output can actually be printed.Something it might be worth pointing out about the code I showed here is that it uses the very rare one-argument form of bless:
package who_farted;
sub TIESCALAR {
my ($package, $fh) = @_;
my $value = "";
bless { value => \$value, fh => $fh } ;
}
Normally the second argument should be $package, so that the
object is created in the appropriate package; the default is to create
it in package who_farted. Aren't these the same? Yes,
unless someone has tried to subclass who_farted and inherit
the TIESCALAR method. So the only thing I have really gained
here is to render the TIESCALAR method uninheritable.
<sarcasm>Gosh, what a tremendous
benefit</sarcasm>. Why did I do it this way? In
regular OO-style code, writing a method that cannot be inherited is
completely idiotic. You very rarely have a chance to write a
constructor method in a class that you are sure will never be
inherited. This seemed like such a case. I decided to take advantage
of this non-feature of Perl since I didn't know when the opportunity would come by again."Take advantage of" is the wrong phrase here, because, as I said, there is not actually any advantage to doing it this way. And although I was sure that who_farted would never be inherited, I might have been wrong; I have been wrong about such things before. A smart programmer requires only ten years to learn that you should not do things the wrong way, even if you are sure it will not matter. So I violated this rule and potentially sabotaged my future maintenance efforts (on the day when the class is subclassed) and I got nothing, absolutely nothing in return.
Yes. It is completely pointless. A little Dada to brighten your day. Anyone who cannot imagine a lobster-handed train conductor sleeping in a pile of celestial globes is an idiot.
[Other articles in category /oops] permanent link
Fri, 17 Mar 2006
More on Emotions
In yesterday's
long article about emotions, I described the difficulty like
this:
There's another kind of embarrassment that occurs when you see something you shouldn't. For example, you walk into a room and see your mother-in-law putting on her bra. You are likely to feel embarrassed. What's the connection with the embarrassment you feel when you fall off a ledge? I don't know; I'm not even sure they are the same. Perhaps we need a new word.This morning I mentioned to Lorrie that the idea of "embarrassment" seemed to cover two essentially different situations. She told me that our old friend Robin Bernstein had noticed this also, and had suggested that the words "enza" and "zenza" be used respectively for the two feelings of embarrassment for one's self and for embarrassment for other people.
I also thought of another emotion that was not on my list of basic emotions, but seems different from the others. This emotion does not, so far as I know, have a word in English. It is the emotion felt (by most people) when regarding a happy baby, the one that evokes the "Awwww!" response.
 This is a very powerful response in most people, for
evolutionarily obvious reasons. It is so powerful that it is even
activated by baby animals, dolls, koala bears, toy ducks, and, in
general, anything small and round. Even, to a slight extent, ball
bearings. (Don't you find ball bearings at least a little bit cute?
I certainly do.)
This is a very powerful response in most people, for
evolutionarily obvious reasons. It is so powerful that it is even
activated by baby animals, dolls, koala bears, toy ducks, and, in
general, anything small and round. Even, to a slight extent, ball
bearings. (Don't you find ball bearings at least a little bit cute?
I certainly do.)
The aliens might or might not have this emotion. If they are aliens who habitually protect and raise their young, I think it is inevitable. The aliens might be the type to eat their young, in which case they probably will not feel this way, although they might still have that response to their eggs, in which case expect them to feel warmly about ball bearings.
I also gave some more thought to Ashley, the Pacemate who claimed that her most embarrassing moment was crashing into the back of a trash truck and totaling her car. I tried to understand why I found this such a strange response. The conclusion I finally came to was that I had found it inappropriate because I would have expected fear, anger, or guilt to predominate. If Ashley is in a vehicle colision severe enough to ruin her car, I felt, she should experience fear for her own safety or that of others, anger at having wrecked her car, guilt at having carelessly damaged someone else's property or health. But embarrassment suggested to me that her primary concern was for her reputation: now the whole world thinks that Ashley is a bad driver.
 If you don't see what I'm getting at here, the following situational
change might make it clearer:
If you don't see what I'm getting at here, the following situational
change might make it clearer:
Most Embarrassing momentYou almost crippled seventy schoolkids? Gosh, that must have been embarrassing!Ashley (alternate universe version): Crashing into the back of a school bus full of kids and totaling my car!
Having made the analysis explicit for myself, and pinned down what seemed strange to me about Ashley's embarrassment, it no longer seems so strange to me. Here's why: It wasn't a school bus, but a garbage truck. Garbage trucks are big and heavy. The occupants were much less likely to have been injured than was Ashley herself, partly because they were in a truck and also because Ashley struck the back of the truck and not the front. The truck was almost certainly less severely damaged than Ashley's car was, perhaps nearly unscathed. And of course it was impossible that the truck's cargo was damaged. So a large part of the motivation for fear and guilt is erased, simply because the other vehicle in the collision was a garbage truck. I would have been angry that my car was wrecked, but if Ashley isn't, who am I to judge? Probably she's just a better person than I am.
But I still find the reaction odd. I wonder if some of what Ashley takes to be embarrassment isn't actually disgust. But at least I no longer find it completely bizarre.
Finally, thinking about this led me to identify another emotion that I think might belong on the master list: relief.
[Other articles in category /aliens] permanent link
Thu, 16 Mar 2006
Emotions
I was planning to write another article about π, and its appearance
in Coulomb's law, or perhaps an article about how to calculate the volume
of a higher-dimensional analogue of a sphere.
But John Speno says he always skips the math stuff on my blog, and the last couple of days have been unrelievedly mathematical. So instead, John, I have written an article about the comparison of emotions, whether the 18-toed Sirian ghost worms will understand why you are holding your nose, Homer Simpson, the evolutionary justification for disgust, the Indiana Pacers cheerleading squad, Paris Hilton, and maggots. Skip this, I dare you.
My shrink had a little trope that she'd trot out when she asked me how I had felt about something and I wasn't sure. "Mad, sad, glad, scared," she'd say, and that was helpful, because those four do cover an awful lot of situations. And learning to recognize those four is very important.
But one day she pushed the idea too far and asserted that those were the only emotions there are.
That's clearly wrong. Even discounting emotions that might be considered variations on the big four, such as: (anger) rage, annoyance, resentment, frustration, (sadness) grief, disappointment, remorse, loneliness, (happiness) delight, joy, pride, (fear) nervousness, dread, terror, panic, and so on, we still have:
- Boredom
- Disgust
- Envy
- Guilt
- Jealousy
- Lust
- Shame
- Surprise
Some of these may require explanation. People sometimes use the word "disgust" metaphorically to refer to a feeling that is really nine parts anger to one part boredom, as when they say they are disgusted with the state of American politics. But that's not what I mean by it here. The disgust I'm referring to is the feeling you have when you have been on vacation and come back to discover that the power went out while you were away and the meat in the refrigerator has spoiled and slid out onto the kitchen floor where it is now festering with thousands of squirming, white, eyeless maggots, and the instant you see it, your reaction is to (a) turn away, (b) hold your nose, and (c) vomit. I suppose it's possible that some people would have that very reaction to American politics; it's certainly understandable. But I don't think that's what people usually mean when they say that politics disgusts them. Or if they do mean it, they mean it only in a hyperbolic sense.
People often confuse guilt and shame, but they are really orthogonal. You feel guilt when you have done something you believe is ethically or morally wrong. You feel shame when other people observe you doing something that they shouldn't see, whether or not that thing is ethically or morally wrong. The problem is with the observing, not with the thing that is being observed. I think the following example will help clear up the confusion: One might or might not feel guilty about picking one's nose, although I think most people don't feel guilty when they do it. But even someone who picks their nose entirely without guilt, probably feels ashamed if someone else catches them in the act.
The other two that are often confused are envy and jealousy. Here I think the confusion is caused simply because people don't know what the words mean. Envy is what you feel when you want what someone else has; you can envy someone else's car or their lunch or their special relationship with their lover. Jealousy is much more specific. You are jealous when you have a special relationship with a person, and you are afraid that you are going to lose them to a third person. You can envy someone else's possession of a ham sandwich, but jealousy of a ham sandwich is impossible.
I might be willing to believe the proposition these eight, plus the original four (anger, sadness, happiness, and fear) constitute a complete set of "primary colors" for human emotion, and that you can consider the others as being mixtures of various amounts of these twelve. For example, you go up on stage to accept an award, and your trousers fall off, and you feel embarrassed. What is embarrassment? It's maybe five parts shame, two parts fear, and one part surprise. Take away any of these three things, and you no longer have embarrassment, but something else. Add in anger and you have humiliation.
If someone wants to argue that jealousy is compounded from fear, anger, and envy, and should be removed from the list in favor of affection or confusion, I won't complain. The list is necessarily dependent on culture, and even more so on the individual making it. Not every culture will have anything like jealousy; perhaps most won't. Romantic love seems to be a uniquely European invention, dating from around the 13th century.
Another problem with the list is that even within one culture, there may not be agreement on which kinds of feelings qualify as emotions. Does hunger qualify? Or fatigue? It seems to me that some emotions are more rooted in the physical processes of the body, and others less so. Guilt is at the "high" end of that scale: it refers to a feeling you have in your mind when you have done something that you feel you shouldn't have. It is hardly associated with the body at all. A brain in a vat could feel guilt, and probably does. At the "low" end of the scale is disgust, the experience of which is much less about an the social constructions in your mind than it is about your stomach trying to turn itself inside out. I think hunger and fatigue are even farther down the scale of body-vs-mind than disgust; below even those is pain, and at the very bottom are feelings like the one you have in your arm when you open a door, which is purely physical and has no emotional content whatsoever. The counterparts at the top end of the scale are plans, analyses, and the like, which are purely mental and have no emotional content. Emotion is somewhere in between, and I can imagine that someone else could want to exclude disgust or guilt from a list of emotions because they were too far down from the middle of the scale.
An exercise I love to do is to try to consider what we will have in common with the space aliens. For example, do the space aliens consider the P=NP problem interesting? Do the space aliens consider the set of real numbers as a fundamental object, or as an obscure construction only of interest to set theorists? I will probably address these topics in future articles. Meanwhile, this article, believe it or not, started out as a discussion of whether the space aliens, when they arrive, will already know how to play chess. (Well, obviously not. But it is less obvious that they will not already know how to play go. I will write that article sooner or later.)
But now we might ask what kinds of emotions the aliens will have. The question seems at first glance to be completely impossible. But I believe that partial answers are possible.
As emotions get higher up on the body-to-mind scale, it becomes less likely that they will be shared by the aliens; such emotions are not even cross-cultural among humans. Our experience of guilt is very much dependent on our culture, and in particular on our relationship to law and authority, much of which is the result of two thousand years of Christian philosophizing. The converse is that emotions that are low on the body-to-mind scale are much more universal among people. Perhaps not everyone feels guilt. But everyone feels disgust.
Disgust is particularly easy to analyze from the point of view of natural selection. It is to a large extent an aversion to dangerous biohazards: rotten food and carcasses; decay, including mold, and things that look like mold; excrement, vomit, and other body substances that should be inside but that have come out; disembowelment and bodily mutilation; deformity and disease. Rotting meat is extremely poisonous, so an automatic aversion reaction makes evolutionary sense: the people who turned away in disgust lived longer than the people who saw an opportunity for a free lunch. Excrement, and particularly human excrement, harbors bacteria dangerous to humans, so an automatic aversion reaction makes evolutionary sense. Deformity is similar. Perhaps whatever caused it is not contagious—but perhaps it is, and evolution wants to stay on the safe side.
I think it is inevitable that the aliens will have these same kinds of reactions, for the same reasons. Aliens will have a strong aversion reaction if you put them in front of a chunk of rotting alien flesh, or show them an alien with its internal organs on the outside. Why? Because those things are dangerous to aliens, and so all the aliens who didn't have that reaction have died long ago of horrible diseases. I don't think it's a big step to identify this reaction with disgust.
Similarly, aliens might not have eyes, if they come from a place with no ambient short-wavelength electromagnetic radiation; say, the surface of Jupiter. But the aliens will have chemical senses, analogous to smell and taste, because there are chemicals everywhere. Every life form on earth has chemical senses, even down to bacteria. This is because you cannot use the Homer Simpson strategy of ingesting everything you encounter; you would quickly die. (Homer is fictitious, or he would be dead long ago.) You need some way of distinguishing which items are food, so that you can eat the things that are food and ignore the other things. So you need to have a sense of smell and taste.
What happens when you smell or taste something that is really harmful? You had better have some kind of aversion reaction, and you do, because all the 18-toed Sirian ghost worms without those reactions ate stuff that disagreed with them, and died young; you are the product of a long line of ghost worms that do have a sense of smell and feel disgust when they wander into a biohazard zone.
We can push this even further. I conjecture that we can even predict some of the aliens' body language. When presented with something that smells bad—say rotten food—an alien's response will be to hold its nose, if it has an olfactory sense that can be disabled by closing the organ off from the outside world. If the alien asks me what I think of Paris Hilton, and I hold my nose, the alien will understand that Paris Hilton is being insulted, and will understand something of the way in which Paris Hilton is being insulted. Chemical senses, I think, must be so universal that even noseless aliens will understand the gesture, once the structure and function of the human nose is explained to them. "Oh, I see," says the alien. "You have closed off your chemical sense organ so that Ms. Hilton's noxious effluvia cannot penetrate. Yes, I quite understand! Unfortunately, for us it is not possible since our olfactory bulbs are distributed throughout our skins. But I am sure we have all wanted to do something like that at one time or another."
Disgust, being one of the lowest emotions on the mind-body scale, is one of the easiest to attribute to the aliens. Even going a little higher is risky. Will the aliens feel lust? Quite possibly. Even a giant amoeba that reproduces by fission might feel something akin to lust when the time comes, a powerful urge to divide in two. Will the aliens feel anger? Perhaps, but here we're on shaky ground.
Long ago, I had a conversation with Matthew Stone, in which he told me how different cultures have different notions of even apparently simple emotions such as rage. Rage, he said, is characterized by the following situation: you want something, but there is some insurmountable obstacle to your getting it, and so you are frustrated. When you become enraged, your response is to attack the obstacle and try to destroy it.
But, said M. Stone, in Polish, when you want something, and there is an insurmountable obstacle, and you are frustrated, you do not have a fit of rage in which you go nuts and attack the obstacle. Instead, you have a fit of złość, in which you go nuts and attack everything around you at random.
Or, in some other culture that I forget, if you want something to which there is an insurmountable obstacle, and you are frustrated, then you have a fit of some emotion I don't remember the name of, in which you go nuts and kill yourself.
These seem to me to be distinctly different from rage, if not fundamentally so. Variations on jealousy are even easier to invent.
I don't know how much of all this is true, how much was wrong before M. Stone heard it, how much he said that was right but I misunderstood, and how much I understood correctly but got wrong between then and now. It might all be nonsense. But one can still get some mileage out of attributing złost, rather than rage, to the aliens.
 Embarrassment is another one of the more universal emotions. I've
seen my cat act embarrassed, typically when he falls off of a ledge,
or tries to jump from A to B but only makes it partway,
and goes splat.
Embarrassment is another one of the more universal emotions. I've
seen my cat act embarrassed, typically when he falls off of a ledge,
or tries to jump from A to B but only makes it partway,
and goes splat.
There's another kind of embarrassment that occurs when you see something you shouldn't. For example, you walk into a room and see your mother-in-law putting on her bra. You are likely to feel embarrassed. What's the connection with the embarrassment you feel when you fall off a ledge? I don't know; I'm not even sure they are the same. Perhaps we need a new word.
The Indiana Pacers basketball team had a web site on which they listed the "most embarrassing moments" of each of their cheerleaders, the Pacemates. (I keep wanting to call them the "Pacemakers", but even I know that is wrong.)
When I first planned to discuss this, it was because my random sample of responses picked up mostly strange ones, and I was ready to conclude that the Pacemates and I were not of the same species. I planned to complain that none of the Pacemates had apparently ever farted in public. But a more thorough survey revealed that the Pacemates were much less surprising in their embarrassment than I had originally thought. As embarrassing moments go, you would be hard-pressed to find a more typical example than that of falling down in the middle of a carefully-choreographed public dance exhibition, and that is mostly what they said. Both I and my cat can understand the embarrassment of these mishaps:
Lindsay: I usually don't get embarrassed, but one time, I did fall off stage at a national dance competition.I don't know what the trumpet has to do with it, but my cat and I can sympathize with the part about slipping on the ice while trying to board the school bus.Darcy: Last year during Pacers player introductions when the lights were out, Boomer ran into me and knocked me down to the floor!
Amanda: When I was cheering at an IU game, I went back for a back handspring and in the middle of Assembly Hall court, I landed flat on my head.
Kim: When I was in sixth grade, I slipped and fell on the ice trying to get on the school bus. I had on a skirt and dress shoes and was carrying my trumpet!
I find it rather comforting that the Pacemates are embarrassed by the same things that embarrass me or my cat or both. I had been worried that all the embarrassing moments would be strange and puzzling, like this one:
Ashley: Crashing into the back of a trash truck and totaling my car!Items like this had made me wonder if the author and I were using the word in the same way. But for the most part I felt that I could understand and empathize, and when I looked at the complete list, I was delighted to discover just what I had asked for:
Nikki: During speech class of my freshman year of college, I was giving a speech on the health care industry and I...well, let's just say for the rest of the semester, my classmates nicknamed me "Toot-Toot!"There is a crucial scene in Larry Niven's novel World of Ptavvs about embarrassment among aliens. Kzanol is an alien invader. In order to escape from Kzanol's telepathic control, the protagonist, Larry Greenberg, must understand how the aliens shield themselves from each others' commands. He has access to Kzanol's memories, and finds the memory he wants in an episode from Kzanol's childhood in which Kzanol involuntarily defecated in front of his father's houseguests. I'm sure that Pacemate Nikki would sympathize.
[Other articles in category /aliens] permanent link
Wed, 15 Mar 2006
Why pi is 3
At the end of my post about why π is so peculiar, I said:
Simon [Cozens] also asked me why the number came out to be around 3, rather than around 5 or 57, and there I was on much shakier ground. I did not have any clever insights, and all I could do was itemize a bunch of stuff that seemed to bear on the issue. It will probably appear here in a future article.
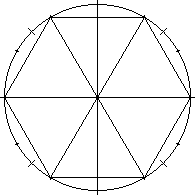 1.
The most obviously germane fact I came up with was this:
Inscribe a regular hexagon in the unit circle. Such a hexagon
obviously has a perimeter of 6. The circle goes through the same six
points, but instead of taking direct paths between them, it takes a
circuitous route, so its perimeter is a bit more than 6.
Therefore pi is a bit more than 3.
1.
The most obviously germane fact I came up with was this:
Inscribe a regular hexagon in the unit circle. Such a hexagon
obviously has a perimeter of 6. The circle goes through the same six
points, but instead of taking direct paths between them, it takes a
circuitous route, so its perimeter is a bit more than 6.
Therefore pi is a bit more than 3.Several people have written to me to point this out, and nobody has pointed out anything different, which I think supports my contention that this is the most obviously germane fact available.
Also, as I replied to M. Cozens:
I do not know any way to calculate the perimeter of a circle without considering it as a limiting case of a polygon with a lot of very short sides, so I think any investigation of why pi is 3.14 and not something else will have to start here.If you circumscribe a hexagon around the circle, a little basic geometry reveals an upper bound: π < 2√3. By using polygons with more sides, you get better bounds. With a square, you get only that 2√2 < π < 4, for example; the hexagon improves this to 3 < π < 2√3. About 2200 years ago Archimedes did the calculation for 96-gons and got the value correct to two decimal places: 3 + 10/71 < π < 3 + 1/7.
(This raises an interesting question: with a 96-gon, you would expect the bounds to involve things like √3, like the hexagon does. Where do the weird fractions 10/71 and 1/7 come from? Answer: A bound of the type 2√3 was of limited use to the Greeks, because it replaces the poorly-understood number π with another poorly-understood number √3. So Archimedes replaced surds with rational approximations; for example, early on he replaces √3 with the rational approximation 265/153. (See Dr. Chuck Lindsey's detailed explanation of Archimedes' calculation, and my explanation of where 265/153 comes from.) I'd like to work through this and see what he would have come up with if he had done the exact calculation, but it'll take me some time.)
Anyway, the other items I sent to M. Cozens were:
2. The shortest curve that can enclose a unit area has length 2π. (Or conversely, the largest area that can be enclosed by a unit path is 1/4π.)This is going to depend strongly on the Euclidean metric again. I don't know how to extend a general metric to give an area measure; indeed, I'm not sure yet of a sensible way to ask the question. I have to think about it. (Yes, I'm sure someone has already studied this, and I could simply look it up, but I will get a lot more out of the answer if I think about the question myself for a while before peeking in the back of the book. There is, as they say, no royal road to geometry.)
The "wordless" proof of the Pythagorean theorem shows that I'll have to be very careful in making the extension from length to area in Manhattan:
Independent of the metric, this proof demonstrates that the two small white thingies on the left have the same area as the large white thingy on the right. In Euclidean space, this equality establishes the Pythagorean theorem. It had better not do so in Manhattan, because the Pythagorean theorem is false in Manhattan; in the diagram, c is not equal to √(a2 + b2) but to a + b.
I think I've convinced myself that a square with side s in Manhattan still has area s2. And I'm pretty sure that those two white thingies on the left are squares, and so have areas a2 and b2, respectively.
But this implies that the large white thing on the right has area a2 + b2, and therefore that it is not a square, and does not have area c2 as labeled, because c = a + b, and c2 is not equal to a2 + b2.
Squares in Manhattan are required to have edges that are parallel to the coordinate axes. I think. I don't know where to go next; maybe I'll figure it out on the way home from work today.
 The next item is my second favorite, after the
observation about the inscribed hexagon:
The next item is my second favorite, after the
observation about the inscribed hexagon:
3. If you put a penny on the table, then you can get at most six other pennies to touch it at the same time. This is closely related to the fact that 6 is the largest integer less than 2π. Analogous results hold in higher dimensions. The area of a sphere is 4π, or about 12.5; you can get 12 spheres to touch another sphere at the same time, but not 13.This business of the spheres touching a central sphere is known as the "kissing number problem"; we say that the "kissing number in two dimensions" is 6, and the "kissing number in three dimensions" is 12.
After this item, I was pretty much out of circle-related facts. So I switched tactics and tried to look at things that seemed completely unrelated to circles:
4. &pi satisfies the equation:M. Cozens had observed that you can get π by using integral calculus to calculate the area of a unit circle:x - x3/6 + x5/120 - x7/5040 + ... = 0This was the only thing I could come up with that seemed both fairly elementary, and at the same time a good way to get π out without putting it in to begin with.
So I started trying to come up with ways to get π that seem to have nothing to do with circles. The infinite polynomial was the first thing I came up with.
It can be related to the circles, but not easily, which I think is an advantage. You need to be able to relate it to circles, or else it doesn't tell you anything about why the perimeter of the circle is pi. But it mustn't be too closely related, because I think that items 1-3 probably exhaust what can be gotten directly from the circles.I just know that some smart person out there is itching to point out that the polynomial is just the Maclaurin expansion for sin(π), and of course that is how I came up with it. (What, did you think it was just a lucky guess?) But if you did not know about the Maclaurin series, you might be quite shocked to discover that π was a zero of this expression. The terms are already starting to get small by the time you get to π9/362880, so in spite of the transcendentality of π we have a 9th-degree polynomial of which it is almost a zero, a polynomial that is based on elementary notions, in which there is no obvious circle.
Item 5 was the Buffon's needle problem, but I said that the appearance of π there appeared to be an obvious consequence of its appearing as the perimeter of a unit circle, so let's pass on to the next thing.
6. The probability that two randomly-selected integers are relatively prime is 6/π2. I said:
This gets π out, without putting it in anywhere obvious, but does not seem to me to be elementary. And how you could relate it to the circle, I have no idea.But now, the relationship with circles seems somewhat clearer to me. You can turn this into a geometry problem like this: You are standing at the origin, looking out on an infinite orchard of apple trees. There is a tree at (a, b) for every pair of integers. The trees have zero width, but when one tree is directly behind another tree, it is blocked and you cannot see it. What fraction of the trees are visible?
There is one visible tree for each (rational) direction you can look in. So there's a relationship between the points on a circle and the visible trees.
(Digression: if the trees have positive diameter, only a finite number are visible from the origin. If the diameter is d, let the number of visible trees be v(d). Estimate v. I believe this problem is still open.)
7. The next item I mentioned was that 1 + 1/4 + 1/9 + ... = π2/6. This is probably related to the orchard thing somehow.
It might be that a good understanding of this identity will lead one to a good understanding of why π is a bit more than 3. It might also be that it has some relationship with the circle. But I told M. Cozens that if he wanted someone to make sense out of this, "you really need to be talking to someone with expertise in analytic number theory, instead of to me." I'll stand by that.
8. Finally, I pointed out that π does not appear only in circles; it also appears in spheres. For example, the volume of a unit sphere is 4π/3. By this time I was scraping the barrel. It is pretty obvious that π is going to get into spheres because spheres are just stacks of circles, and π is already in the circles. Adding together a bunch of line segments that have no relation more complicated than a square root is one thing; it is surprising to see π come out of that. But adding together a bunch of circles that all involve π and getting out something that involves π again is no surprise.
As I said, the inscribed hexagon thing sweems the most germane, followed closely by the kissing number.
A couple of people have written to me to point out that π also appears in a number of constants and laws from physics, such as Coulomb's law. I believe that these appearances are invariably derived from the appearance of π as the circumference, and, in many cases, that this is quite obvious. I'll address this in detail in a future article. The inclusion of π in these formulas signals their dependence on Euclidean space, which has some interesting implications, since general relativity claims that real space is non-Euclidean: we shouldn't expect Coulomb's law to hold over large distances, for example. I imagine that this is old news to the astrophysicists, but it might be a surprise to the physics graduate students.
[Other articles in category /math] permanent link
Mon, 13 Mar 2006
Why pi?
Simon Cozens wrote to me yesterday to ask what the heck was up with
π:
what property of a circle makes it . . . an irrational number. . . perhaps about as arbitrary a number as you can get.I thought about this pretty hard, and, to my amazement, I came up with a plausible answer. So here we are.
The one-paragraph summary: My theory is that the association of the very weird and complex number π with a geometric object as simple as a circle is a reflection of the underlying fundamental complexity of Euclidean geometry: specifically, that its metric is a nonlinear function.
First I'm going to spend some time arguing that π does require explanation. I expect that almost everyone will agree that π is weird; if you do agree, feel free to skip this section. Then I'll discuss Euclidean and non-Euclidean geometries. This is important, because the relation between π and circles appears to be a special property of Euclidean geometry, one which does not occur, for example, in spherical geometry. Finally, I'll look at the essential properties of Euclidean geometry, and why I think it is more complex than people usually realize.
π is complex and bizarre
In this section, I'm going to argue that the question is indeed worth asking. π is an extremely peculiar number, even by mathematical standards. You often hear π mentioned in the same breath with e, another constant of fundamental mathematical importance. But e is much more tractable than π is, and much better understood.In fact, the degree to which π is not understood is rather shocking when you consider its ubiquity.
If you don't need to be persuaded that π is unusually weird, even as transcendental numbers go, you may want to skip to the next section. Really, this section is here to address people who think they know more mathematics than they do, who want to argue that π is no more or less complicated than any other number. But I think it is.
It should be fairly clear that, as a representation of real numbers, decimal fractions are not very satisfactory. For example, you might like simple numbers to have simple representations. But the representation of 1/3 is 0.33333...., which isn't even finite. The fact that a complicated number like like 3674/31250 ("0.117568") has a simpler representation than a simple number like 1/3 just demonstrates that the system is defective. 3674/31250 gets a simple representation not because it is a simple number, but because 31250 happens to divide 106.
This being the case, it is perhaps not too surprising that nobody can make head or tail of the representation of π, which is 3.14159265358979... . As far as I know, the state of our current understanding of this representation of π can be summed up as:
None
But that might just be the fault of the representation. The representation is based on the number 10, and it is not clear that π has anything to do with 10, so our failure to find an answer here may just indicate that the question was not worth asking.There are better representations of real numbers; one such is the so-called "continued fraction representation". I don't want to explain this in detail in this article, but I can refer you to a talk I gave on the subject. But an itemization of this representation's desirable properties may be persuasive even if you don't know how it works:
- In
continued fraction notation, a number has a finite representation when,
and only when, it is rational.
- The representation is not inappropriately snuggly with the number
10, or with any other number.
- Simple rationals have simple
representations and more complicated rationals have more complicated
representations. For example, 1/3 is represented as [0; 3] and
3674/31250 is represented as [0; 8, 1, 1, 43, 4, 5].
- Some irrational numbers have simple (although infinite)
representations. For example, in the customary system, √2 is an
incomprehensible soup of digits starting 1.414213562... . In the continued
fraction system, it is [1; 2, 2, 2, 2, ...].
- If you turn an irrational number into a rational one by chopping
off the infinite tail of the continued fraction representation, you
get a very closely-related rational result, one that is numerically as
close as possible to the original number. This is not true of the
decimal fraction. If you chop off √2 after a couple of terms of
decimal fraction, you get 1.41, which is 141/100. If you chop off
√ after a couple of terms of continued fraction, you get [1; 2,
2], which is 7/5. This is slightly less accurate than 141/100, but
the denominator is twenty times smaller. If you chop a little later,
you get [1; 2, 2, 2], which is 17/12, which is a lot more accurate
than 141/100, even though the denominator is only 12.
But it doesn't work for π. The continued fraction representation of π is [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, ...], and as far as I know, the state of our current understanding of this representation of π can be summed up as:
None
So much for continued fractions.We might hope for some understanding about why π is irrational. The proof that √2 is irrational is elementary, and dates back to the Greeks; you can understand it as being related to the fact that 2 is not a perfect square. π was not shown to be irrational until 1761, and the proof is not simple, which means that nobody knows a simple argument about why it should be the complicated thing it is, rather than a simple fraction.
So π is complex and poorly-understood, even compared with other important transcendental numbers like e.
Euclidean geometry
M. Cozens asked:Is pi inherent in our definition of a circle, or our particular geometry, or our planet, or could the ratio be different in different worlds?I think this question is very insightful. π, at least as it relates to circles, is inherent in a particular geometry, namely, Euclidean geometry.
Euclidean geometry takes its name from Euclid, who wrote Elements, an extremely influential treatise on geometry, about 2300 years ago. Most of the Elements is concerned with plane geometry, which takes place in an infinite, flat two-dimensional space. π arises naturally in this kind of space as the perimeter of a circle.
Non-Euclidean geometry
In non-Euclidean spaces, π is geometrically much less important. For example, consider geometry done on a sphere. If we keep the definition of "line" as the path of shortest distance between two points, then our "lines" turn out to be great circles on the sphere—that is, circles whose centers are at the center of the sphere; the equator is an example. The 49th parallel is not a "line" because it's not a path of shortest distance; for any two points on the 49th parallel, there's a path between them over the surface of the sphere that is shorter than the one along the parallel. (This may seem strange, but it's true, and it's why direct flights from New York to Taipei often stop off in Anchorage, Alaska.) In addition to being a line, the equator is also an example of a circle. What's a circle? Circles look pretty much the way you expect them to. A circle is the set of all points that are some fixed distance from a center point. The equator is all the points that are a certain fixed distance from the north pole. The 49th parallel is also a circle; its center is also the north pole.
 The "diameter" of a circle is the longest possible "line" you can draw
from one point on the circle to another. A diameter of a circle has
the property that it always goes through the center of the circle, as
you would hope and expect. For the equator, a diameter goes through
the north pole. The picture to the right shows the equator in red,
its center, the north pole, in yellow, and a diameter of the equator
in blue. The 49th parallel is in green.
The "diameter" of a circle is the longest possible "line" you can draw
from one point on the circle to another. A diameter of a circle has
the property that it always goes through the center of the circle, as
you would hope and expect. For the equator, a diameter goes through
the north pole. The picture to the right shows the equator in red,
its center, the north pole, in yellow, and a diameter of the equator
in blue. The 49th parallel is in green.
Let's say that the circumference of the equator, the red line, is 1. Then the length of the equator's diameter, the blue line, is 1/2. If we were expecting to divide the circumference by the diameter and get π, we are in for a surprise, because we just got 2 instead.
For the 49th parallel, the ratio of circumference to diameter is larger: I calculate about 2.88. For smaller circles, the ratio is larger still. For very small circles, the ratio is very close to π, because a small circle can't tell whether it's on a sphere or in a plane; up close the two things look the same.
So the relation between π and circles is actually a special property of Euclidean geometry. Circles in non-Euclidean spaces have a perimeter-to-diameter ratio that is different from π.
Euclidean metric
The single fundamental property of Euclidean geometry is that the distance between two points, say (x1, y1) and (x2, y2), is ((x2-x1)2 + (y2-y1)2)1/2. (Or, in higher-dimensional spaces, the obvious extension of this formula.) If you change the way you measure distance, you get a different kind of geometry with different kinds of circles that have different perimeter-to-diameter ratios. In an earlier article, I discussed an alternative distance function, called the Manhattan distance, which gives diamond-shaped circles whose perimeter-to-diameter ratio is always 4.The Euclidean distance function is nothing more than the familiar Pythagorean theorem. It is very difficult for me to imagine any reasonable way to do plane geometry without the Pythagorean theorem. It is just too simple. Even the proof is simple:
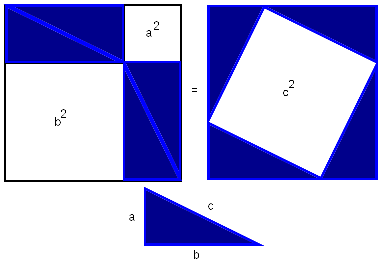
So the relationship of π (which is complicated) to circles (which appear to be simple) is grounded in the Euclidean distance formula. If you change the distance formula, π is no longer related to circles. So the weirdness must be due, at least in part, to some complexity in the Euclidean distance formula.
But what's complex about the Euclidean distance formula? How could it be simpler?
Actually, I think it only seems simple because it is so familiar. The Euclidean distance formula is, in some ways, deeply weird. I realized this a few months ago, but everyone I mentioned it to acted like I was insane. But now I'm pretty sure. I think the essence of the problem with π is that the Euclidean distance function is nonlinear in the two spatial coordinates x and y.
Nonlinearity of the Euclidean metric
Linear functions are very well-behaved. If F is a linear function, then F(a+b) = F(a) + F(b), which means that you can calculate the contributions of a and b independently of each other. To calculate F of some very complicated argument, you can break the argument into simple components and deal with them all separately. With quadratic functions like the Euclidean distance function, you cannot do this; complex problems are not easily decomposable into simple ones.For the Euclidean metric, it means that the horizontalness and verticalosity are not independent, but are tangled together and cannot be separated.
What do we really mean by the perimeter of a circle? The circle is the set of points (x, y) which are at distance 1 from the point (0,0). The only meaningful way I know to talk about the length of this set is to calculate it as a limit of an approximate polygonal path as the path gets more and more segments. So you are necessarily dragging in an infinite limiting process, and such processes are always complicated.
If the distance function were linear, it wouldn't matter, because then you could treat the horizontal and vertical components separately, and when you did that, you would be dealing with paths in one dimension, which, being straight lines, would be simple. You can see this if you consider the Manhattan distance function: It doesn't matter how you get from (x1, y1) to (x2, y2); whatever path you take, whether you take a lot of steps or only one, the distance is always |x2-x1| + |y2-y1|, because the distance function is linear, and thus there is no interaction between the x parts and the y parts. But with a nonlinear distance function like the Euclidean metric, it does matter what path you take.
I was thinking a few months ago about how peculiar this is. I cannot think of anything else that behaves this way. Suppose you have two jugs and you start filling them with milk. You find that to fill each jug separately requires one quart, but to fill both at once requires only 1.4142 quarts. Wouldn't that freak you out? But space does behave like that. To drive ten miles north takes a gallon of gas. To drive ten miles east takes a gallon of gas. North and east are perpendicular and should be completely independent of each other. To drive ten miles north and ten miles east should require two gallons of gas. But it requires only 1.4142 gallons. How the heck did that happen?
I believe that this strange entanglement between north and east, two things one might have supposed were independent, is the ultimate root of what makes the circumference of a circle such a peculiar number. I was very pleased to have this confirmation that the entanglement between horizontal and vertical is strange and complex, because, as I mentioned before, when I tried to explain to people what I found strange about it, they thought I was nuts.
One-dimensional circles
My theory is that the peculiar length of a circle's perimeter is a result of the peculiar interaction between the otherwise apparently independent spatial dimensions in Euclidean space. If this theory is correct, we should expect that the corresponding perimeter in a one-dimensional space will not be peculiar. A one-dimensional Euclidean space, having only one dimension, has no strange interactions between independent directions. And indeed, this is the case! The perimeter of a one-dimensional circle does not involve π. It's simply 2; the "area" (which is really length) is 2r. You only get difficult numbers in spaces of at least 2 dimensions.
Why 3?
M. Cozens also asked me why the number came out to be around 3, rather than around 5 or 57, and there I was on much shakier ground. I did not have any clever insights, and all I could do was itemize a bunch of stuff that seemed to bear on the issue. It will probably appear here in a future article.[ Addendum: Here it is. ]
[Other articles in category /math] permanent link
Sun, 12 Mar 2006
Naomi Wolf and Big Ethel
Aaron Swartz has done a text search of The Beauty Myth
and concluded that Wolf never intended Big Ethel to serve as an
example of intelligence, contrary to what I asserted in my previous
article. M. Swartz says:
Judging from a search on Amazon, the only time Ethel is mentioned is in the context of noting that an attractive woman is often paired with an unattractive one: "... Veronica and Ethel in Riverdale; ... and so forth. Male culture seems happiest to imagine two women together when they are defined as being one winner and one loser in the beauty myth." (59f)I still question the aptness of the example, since, again, the principal case in which two women are imagined together in Archie comics is not Veronica and Ethel, but Veronica and Betty, both of whom are portrayed as "winners". Betty and Veronica are major characters; Ethel is not. But the error isn't nearly as serious as the one I said Wolf had made.
The most serious error here is mine: I should have considered and discussed the possibility that my friend was misquoting Wolf. That I didn't do this was unfair to Wolf and entirely my fault. Since I haven't read the book myself, I should have realized what shaky ground I was on, and taken pains to point this out. And yet other possibilities are:
- That my friend didn't misquote Wolf at all, and I misunderstood her at the time, or
- that my friend correctly quoted Wolf and I understood her at the time, but my memory of the episode (which occurred around 1993) is faulty.
[Other articles in category /lang/etym] permanent link
On saying too much, or, bad things come in threes
Long ago, I had a conversation with a woman who had recently read
Naomi Wolf's book The Beauty Myth. She was extolling the
book, which I had not read, and mentioned that Wolf had an extensive
discussion of the popular dichotomy between beauty and intelligence.
She told me that Wolf had cited Archie comics as
containing an example of this dichotomy, in the characters of Veronica
and Big Ethel.
I had been nodding and agreeing up to that point. But at the mention of Big Ethel I was quite startled, and said that that spoiled the argument for me, and made me doubt the conclusion. I now had doubts about what had seemed so plausible a moment before.
Veronica is indeed one half of a contrasting pair in Archie comics. But Veronica and Big Ethel? No. Veronica is not complementary to Big Ethel. The counterpart of Veronica is Betty. The contrast is not between beauty and brains but between rich and poor, and between their derived properties, spoiled and sweet. A good point could be made about Veronica and Betty, but it was not the point that Wolf wanted to make; her citation of Veronica and Big Ethel as exemplifying the opposition of beauty and intelligence was just bizarre. Big Ethel, to my knowledge, has never been portrayed as unusually intelligent. She is characterized by homeliness and by her embarrassing and unrequited attraction to Jughead, not by intelligence.
Why would this make me doubt the conclusion of Wolf's argument? Because I had been fully ready to believe the conclusion, that our culture manufactures a division between attractiveness and intelligence for women, and makes them choose one or the other. I had imagined that it would be easy to produce examples demonstrating the point. But the example Wolf chose was completely inept. And, as I said at the time, "Naomi Wolf is very smart, and has studied this closely and thought about it for a long time. If that is the best example that she can come up with, then perhaps I'm wrong, and there really aren't as many examples as I thought there would be." Without the example, I would have agreed with the conclusion. With the example, intended to support the conclusion, I wasn't so sure.
Now, I come to the real point of this note. Paul Vallely has written an article for The Independent on "How Islamic inventors changed the world". He lists twenty of the most influential contributions of the Muslim world, including the discovery of coffee, inoculation, and the fountain pen. I am not so clear on the history of the technology here. Some of it I know is correct; some is plausible; some is extremely dubious. (The crank, not invented before 1206? Please.) But the whole article is spoiled for me, except as a topic of derision, because of three errors.
Item #1 concerns the discovery of the coffee bean. One might expect this to have been discovered in prehistoric times by local Ethiopians, long before the founding of Islam. But I'm in no position to argue with it, and I was ready to give Vallely the benefit of the doubt.
Item #2 on Vallely's list was more worrying. It says "Ibn al-Haitham....set up the first Camera Obscura (from the Arab word qamara for a dark or private room)." It may or may not be true that "qamara" is an "Arab word" (by which I suppose Vallely means an "Arabic word") for "chamber", but it is certainly true that this word, if it exists, is not the source of the English word "camera". I don't know from "qamara", but "camera obscura" is Latin for "dark chamber". "Camera" means "chamber" in Latin and has for thousands of years. The two words, in fact, are etymologically the same, which is why they have almost the same spelling. It is for this reason that the part of a legal hearing held in the judge's private chambers is said to be "in camera".
There might be an Arabic word "qamara", for all I know. If there is, it might be derived from the Latin. (The Latin word is not derived from Arabic, either; it is from Greek καμαρα, which refers to anything with an arched cover.) Two things are sure: The English word "camera" is not derived from Arabic, and Vallely did not bother to pick up a dictionary before he said that it was.
Anyone can make a mistake. But I started to get excited when I read item 3, which is about the game of chess. Vallely says "The word rook comes from the Persian rukh, which means chariot." This is true, sort of, but it is off in a subtle way. The rooks or castles of modern chess did start out as chariots. (Moving castles around never did make much sense.) And "rook" is indeed from Persian rukh. But rukh doesn't exactly mean a chariot. It means a chariot in the game of chess. The Persian word for a chariot outside of chess was different. (I don't remember what it was.) Saying that rukh is the Persian word for chariot is like saying that "rook" is the English word for castle.
I was only on item 3 and had already encountered one serious error of etymology and one other item which although it wasn't exactly an error, was peculiar. I considered that I wouldn't really have enough material for a blog post, unless Vallely made at least one more serious mistake. But there were still 17 of 20 items left. So I read on. Would Vallely escape?
No, or I would not have written this article. Item 17 says "The modern cheque comes from the Arabic saqq, a written vow to pay for goods when they were delivered...". But no. The correct etymology is fascinating and bizarre. "Cheque" is derived from Norman French "exchequer", which was roughly the equivalent of the treasury and internal revenue department in England starting around 1300. Why was the internal revenue department called the exchequer? Because it was named after the chessboard, which was also called "exchequer".
What do chessboards have to do with internal revenue? Ah, I am glad you wondered. Hindu-Arabic numerals had not yet become popular in Europe; numbers were still recorded using Roman numerals. It is extremely difficult to calculate efficiently with Roman numerals. How, then did the internal revenue department calculate taxes owed and amounts payable?
They used an abacus. But it wasn't an abacus like modern Chinese or Japanese abacuses, with beads strung on wires. A medieval European abacus was a table with a raised edge and a grid of squares ruled on it. The columns of squares represented ones, tens, hundreds, and so on. You would put metal counters, called jettons, on the squares to represent numbers. Three jettons on a "hundred" square represented three hundred; four jettons on the square to its right represented forty. Each row of squares recorded a separate numeral. To add two numerals together, just take the jettons from one row, move them to the other row, and then resolve the carrying appropriately: Ten jettons on a square can be removed and replaced with a single jetton on the square to the left.
The internal revenue department, the "exchequer", got its name from these counting-boards covered with ruled squares like chessboards.
(The word "exchequer" meaning a chessboard was derived directly from the name of the game: Old French eschecs, Medieval Latin scacci, and so on, all from shah, which means "king" in Persian. The word "checkered" is also closely related.)
So, in summary: the game is "chess", or eschek in French; the board is therefore exchequer, and since the counting-tables of the treasury department look like chessboards, the treasury department itself becomes known as the exchequer. The treasury department, like all treasury departments, issues notes promising to pay certain sums at certain times, and these notes are called "exchequer notes" or just "exchequers", later shortened (by the English) to "cheques" or (by Americans) to "checks". Arabic saqq, if there is such a word, does not come into it. Once again, it is clear that Vallely's research was shoddy.
While I was writing up this article, yet another serious error came to light. Item 11 says "The windmill was invented in 634 for a Persian caliph...". Now, I am not very knowledgeable about history, and my historical education is very poor. But that was so peculiar that it startled even me. 634 seemed to me much too early for any clever inventions to be attributed to Muslims. Then I looked it up, and so it was. Muhammad himself had only died in 632.
As for the Persian caliph Vallely mentions, he did not exist. The caliphs are the successors of Muhammad, so of course there was one in 634---the first one, in fact. Abu Bakr reigned from the death of the Prophet in 632 until his own death in 634; he was succeeded by `Umar. Neither was Persian. They were both Arabs, as you would expect of Muslim leaders in 634. There were no Persian caliphs in 634.
My own ignorance of Islam and its history is vast and deep, but at least I had a vague idea that 634 was extremely early. Vallely could have looked up the date of the founding of the caliphate as easily as I did. Why didn't he? Well, perhaps it was just a typo, and should have said 834 or 934. In that case it's just poor editing and inattention. But perhaps it was a genuine factual error, in which case Vallely was not only not paying attention, but is apparently even less familiar with Islamic history than I am, difficult as that is to achieve. In which case we have this article about the twenty greatest contributions of Islam written by a guy who literally does not know the first thing about Islam.
And so this article, which I hoped to enjoy, was spoiled by a series of errors. I am very sympathetic to the idea that the brilliant history of Islamic science and engineering has been neglected by European scholarship. One of my very first blog posts was about the Islamic use of algebra to solve complex probate problems. Just last week I was reading about al-Biruni's invention, around 1000 years ago, of an improved method for measuring the size of the earth, a topic that Vallely treats as item 18. But after reading Vallely's article, I worried a bit that the case might have been overstated. Perhaps the contributions of Muslims are not as large as I had thought?
Fortunately, there was an alternative: the conclusion is correct, and the inept support from the author speaks only to the author's ineptness, not to the validity of the conclusion. I did not have that alternative with Naomi Wolf, who is not inept. (Also, see this addendum.)
With only cursory attention, I found three major errors of fact in this one short article. How many more did I miss, I wonder? Did Abbas ibn Firnas really invent a working parachute, as Vallely says? Maybe it was someone else. Maybe there was no parachute. Maybe there was, but it didn't work. Maybe the whole thing is a propaganda invention by someone who wants to promote Islam, and has suckered Vallely into repeating fiction. Maybe all of these. Someone knows the truth, but it isn't me, and I can't trust Vallely.
Were the Turks vaccinating people eighty years before the Europeans, or did Vallely swallow a tall tale? I don't know, and I can't trust Vallely.
People sometimes joke "I am stupider for having read this," but I really believe this was the case here. The article is worse than useless, because it has polluted my brain with a lot of unreliable non-information. I will have to be careful not to think that quilted fabrics were first brought to Europe by the crusaders, who got them from the Muslims. My real fear is that the "fact" will remain in my brain for years, long after I have forgotten how unreliable Vallely is, and that I will bring it out again as real information, which it is not. True or not, it is too unreliable to be information.
The best I can hope for now is that I will forget everything Vallely says, and meet the true parts again somewhere else in the future. In the meantime, I am worse off for having read it.
[ Addendum 20200204: Thirteen years later, it occurred to me to wonder: Why does Arabic chess have chariots anyway? ]
[Other articles in category /lang/etym] permanent link
Sat, 11 Mar 2006
On the manufacture of spherical objects
In an
earlier post, I mentioned shot towers, which were used up into
the 19th century for the manufacture of lead shot. The shot must be
made spherical, or else it won't work properly when it's fired from a
musket barrel; it will get stuck, or the expanding gases will blow
past it and leave it in the barrel, or something of the sort. (Rifle
bullets, in contrast, are very much not spherical. I would
like to write an article about this someday, but at present that one
statement has nearly exhausted my store of information on this
fascinating subject.)
The manufacture of spherical objects is a nontrivial matter; hence the invention of shot towers. Molten lead is poured through a copper sieve at the top of the tower, and the resulting droplets are allowed to plummet to the bottom of the tower. (Incidentally, "plummet" is the most correct possible word here. It is derived from the Latin plumbum = "lead", and means "to fall like lead".) At the bottom, the droplets land in a tub of water. The congealed droplets are recovered from the tub and sorted for size; they are also sorted for roundness by being rolled down a large table. Insufficiently round shot are melted and dropped again.
 This method is obviously only suited to the mass production of
bullets; it makes lots of bullets of different sizes at the same time,
and requires a giant tower. In one of the Laura Ingalls Wilder books,
the author describes her father, Charles Ingalls, making bullets one
at a time by the hearth. He would melt pieces of lead broken off a
big chunk, and pour the melted lead into a spherical bullet mold.
When the lead had cooled the bullet was turned out of the mold, and
the sprue and flash trimmed off with a knife. I don't know for sure,
but I imagine from the description that the mold looked something like
the picture at the right. (All pictures in this article get bigger if
you click them.)
This method is obviously only suited to the mass production of
bullets; it makes lots of bullets of different sizes at the same time,
and requires a giant tower. In one of the Laura Ingalls Wilder books,
the author describes her father, Charles Ingalls, making bullets one
at a time by the hearth. He would melt pieces of lead broken off a
big chunk, and pour the melted lead into a spherical bullet mold.
When the lead had cooled the bullet was turned out of the mold, and
the sprue and flash trimmed off with a knife. I don't know for sure,
but I imagine from the description that the mold looked something like
the picture at the right. (All pictures in this article get bigger if
you click them.)
 Round bullets could also be manufactured by stamping. The picture to
the left shows a Civil-war era bullet mold, shaped like a
scissors. A cold lead wire was put into the end
of the mold and the handles were closed. This cut the end off the
wire and pressed it into a spherical shape.
Round bullets could also be manufactured by stamping. The picture to
the left shows a Civil-war era bullet mold, shaped like a
scissors. A cold lead wire was put into the end
of the mold and the handles were closed. This cut the end off the
wire and pressed it into a spherical shape.
[ Addendum 20070307: the bullet mold at right is probably used for casting bullets, not for stamping them. See this addendum for more details. ]
Simon Cozens inspired this article by writing to inform me that shot towers were also used to manufacture ball bearings. (But what were the bearings made of? I don't know. I imagine that lead ball bearings would deform too easily to be useful. ) Modern ball bearings are manufactured by a casting process, followed by machine polishing to remove the flash and any imperfections.
 When I was in college, my professor brought to my attention the famous stone
spheres of Costa Rica. These spheres range in size up to seven
feet in diameter. He asked me to think about how the spheres might
have been made. It is not clear, by the way, how close to spherical
they actually are. Supposing that they really are nearly spherical, I
have an educated guess, but I'm going to work around to it. In the
meantime, you might like to puzzle about this yourself. The spheres
were probably made sometime between 800 and 2200 years ago, so you are
not allowed to use a CAD system.
When I was in college, my professor brought to my attention the famous stone
spheres of Costa Rica. These spheres range in size up to seven
feet in diameter. He asked me to think about how the spheres might
have been made. It is not clear, by the way, how close to spherical
they actually are. Supposing that they really are nearly spherical, I
have an educated guess, but I'm going to work around to it. In the
meantime, you might like to puzzle about this yourself. The spheres
were probably made sometime between 800 and 2200 years ago, so you are
not allowed to use a CAD system.
 When you make a submarine, it's
very important that the hull be as exactly circular (in cross-section)
as possible, so as to distribute the water pressure evenly. How do
you make sure that your submarine hull is not deviating from the ideal
of circularity? The first thing that was tried was to measure the
distance across the hull in all directions, to make sure that
all the diameters had the same length. Shapes with this property
are said to have constant width. The first submarines the
Germans made using this technique buckled and collapsed when they were
subjected to high pressures. Why? Because they weren't circular!
Circles do have constant width, but there are many other shapes that
also have constant width; the shape to the left, known as a
Reuleaux triangle, is an example. Constant width is no
guarantee of circularity.
When you make a submarine, it's
very important that the hull be as exactly circular (in cross-section)
as possible, so as to distribute the water pressure evenly. How do
you make sure that your submarine hull is not deviating from the ideal
of circularity? The first thing that was tried was to measure the
distance across the hull in all directions, to make sure that
all the diameters had the same length. Shapes with this property
are said to have constant width. The first submarines the
Germans made using this technique buckled and collapsed when they were
subjected to high pressures. Why? Because they weren't circular!
Circles do have constant width, but there are many other shapes that
also have constant width; the shape to the left, known as a
Reuleaux triangle, is an example. Constant width is no
guarantee of circularity.
The Germans eventually solved the problem by making giant wooden forms and comparing the submarine's hull to the wooden form as construction progressed. It's easy to make a two-dimensional wooden form: take a big piece of wood, drive in a nail, tie a string to the nail, and draw a circle around the nail. Then cut out the circle and throw it away, and cut the remaining piece in half; you now have two semicircular forms, as large as you want. If you try to fit the form around the outside of the submarine, you will immediately see whether the hull deviates from circularity. I believe this technique is still used for submarine hulls.
I suspect that the Costa Rica spheres were made similarly. You start with a big lump of rock, a chisel, and a semicircular form of the appropriate size. Then you start chiseling at the rock, checking it for circularity by fitting the form to it, and cutting away the parts that don't match. The only difference from the submarine is that you need to check for circularity in multiple planes. You can do this by rotating the form around the point you are working on. The Costa Ricans can't make their forms out of sheets of plywood, of course, but they should be able to make them out of something.
Baseballs are made spherical by a completely different process. The outside of a baseball is a leather cover, most of a baseball is made of yarn, which is wound around a cork until the baseball is the correct size. The tension in the yarn makes the yarn want to move inward, toward the center of the ball. If part of the ball of yarn is too narrow, then that part is closer to the center and the subsequent yarn will tend to to move there, evening it out. Rubber-band-balls are spherical for similar reasons.
Billiard balls were originally made either from wood or were cut whole from elephants' tusks. I don't know how they were made spherical, although the wooden-form technique seems likely to work. Modern billiard balls are cast in molds and then polished.
[ I discussed some other round objects, including gumballs, marbles, and pellets of taconite ore, in a followup article. ]
[Other articles in category ] permanent link
Fri, 10 Mar 2006
The Wrong Alcott
I went to the library yesterday, and as usual I was wandering in the
stacks hoping for a lucky find. This time I got "The Young Husband"
(subtitle: "Duties of Man in the Marriage Relation") by "Alcott".
This book was written in 1846 by William Andrus Alcott, as a sequel to his 1844 (presumably successful) book "The Young Wife". It is a book of domestic advice for recently-married men. Like many advice books, it is a curious mix of good advice, bad advice, and totally bizarre advice that apparently came from the planet Zorkulon. For example, Alcott advises the young husband to forbid his family all fictional literature. He thinks it's all trash, and time spent reading it is time wasted that could have been spent reading something moral and improving, such as (presumably) Alcott's own series of moral and improving advice books. He says that arguments in favor of any particular novel are akin to arguments in favor of champagne: this particular liquor may seem tasty and harmless, but it's still the demon alcohol in a pretty disguise, sure to lead the imbiber to ruin and despair.
I took the book off the shelf not because I have a specific interest in moral advice for Victorian-age Americans, but because I knew a bit about Louisa May Alcott's family life. Louisa May Alcott, as I am sure you recall, was the author several extremely popular books for children, including, most notably, Little Women, which has been continuously in print since its publication in 1868. I settled down to read her father's advice book intending to savor the delicious irony, because Alcott's father was an amazingly bad husband, and this is visible throughout all of her fiction.
Little Women, for example, concerns the life of the four March sisters and their mother. Where is Mr. March? He's off fighting in the Civil War, not because he was drafted, and not because his family doesn't need him, but as a matter of principle. He barely appears, while the female Marches struggle along without him.
I'm more familiar with Eight Cousins, which is even weirder. The story concerns Rose and her extended family, twenty-one people in all, and among those twenty-one people there is no example of a wholly and happily married couple. Rose, the protagonist, has been orphaned shortly before the story opens. She is sent away into the care of her aunts. The aunts include Aunt Plenty, who is a widow; Aunts Clara and Jessie, whose husbands are away on a trading voyages for the entire book; Aunt Myra, also a widow, and Aunt Peace, whose fiancé died the day of their wedding.
Aunt Jane does have a husband, who is a busy, industrious merchant—except when Jane is around; then he is always asleep. Rose's guardian is Uncle Alex, who is a bachelor.
This theme of the absent or ineffective husband and father runs all through Louisa May Alcott's fiction, and it's easy to guess why: her own father was often absent, and when he was around he was still useless. He made little money, and spent what money he did make on utopian schemes. Lorrie told me a story about how he got the idea that they should eat nothing but apples, and so they did. The only thing that stood between the Alcotts and starvation was the income from Louisa May's writing.
So I was really interested to see what advice Alcott's dad would have to offer on the subject of being a good husband and father, and chuckled whenever he talked insistently about the duties that the husband owes to his family. I quite enjoyed it.
Unfortunately, it was all in vain, because the author, William Andrus Alcott, was not the father of Louisa May Alcott. He was a cousin. Louisa May's father was Amos Bronson Alcott. Whoops.
All of which is presented as a partial explanation of why I have not posted any blog items this week. Sometimes the stuff I'm reading and thinking about is suitable for the blog, sometimes not. I was all excited at the prospect of writing about William Andrus Alcott's advice book, but the humor and irony vanished in a case of mistaken identity.
I could post about what I had for breakfast, but I foreswore such stuff when I decided to start the blog in the first place. If you want that kind of blog, you can't do better than to visit the always engaging blog of Eric Brill.
[Other articles in category /book] permanent link
Sun, 05 Mar 2006
My favorite NP-complete problem
At last
year's open source conference, I gave a talk about fundamental
problems of computer science. I talked about undecidable problems
and NP-complete problems, and some other stuff. It was only a
45-minute talk, but I worked hard to make it as accessible as I
could.
For the NP-completeness section, I discussed the knapsack problem. In this problem, you have a bunch of items you can take on a trip, each of which has a value and a size. Your luggage is of limited size, so the total size of the items you take on the trip must not exceed this limit. Subject to this constraint, you want to take the items whose total value is as large as possible. (Actually, in the talk, I used the decision problem version of this, rather than the optimization problem version, to avoid sticky questions from the know-it-alls in the audience.)
Knapsack is a pretty good example problem. It's simple, easy to understand, and reasonably easy to see why it might be interesting. But after I gave the talk, I thought of a much better example. I deeply regret that I didn't come up with it in time to put it in the talk. Fortunately, I now have a blog. Read on; here's the coolest NP-complete problem ever.
Each episode of Sesame Street now ends with a fifteen-minute segment called Elmo's World, featuring Elmo, a small red monster. Elmo is extremely popular, and the segments have been released on videotape and DVD. Each of these segments has a topic of interest to toddlers, such as:
| Babies | Dancing | Food |
| Bananas | Dogs | Games |
| Baths | Drawing | Hair |
| Bicycles | Ears | Hands |
| Birds | Exercise | |
| Birthdays | Families | Music |
| Books | Farms | Plants |
| Bugs | Feet | Singing |
| Cats | Firefighters | Water |

 When the segments are released
on video, they are bundled in groups of three. Usually, the three
segments will have a common theme. For example, the video Wake
Up With Elmo! (left) gathers together the three segments about
"sleep", "getting dressed", and "tooth brushing". Another video
(right) collects the segments about "food", "water", and
"exercise".
When the segments are released
on video, they are bundled in groups of three. Usually, the three
segments will have a common theme. For example, the video Wake
Up With Elmo! (left) gathers together the three segments about
"sleep", "getting dressed", and "tooth brushing". Another video
(right) collects the segments about "food", "water", and
"exercise".
Your job is to plan the video releases. Sesame Workshop gives you a list of which sets of three segments are considered to be thematically related. Your job is to select items from this list that exhaust the available segments, without using any segment more than once.
Each segment might be part of several different thematically-related groups. For example, the "dancing" segment could be released on a physical-activity-themed video, along with the "bicycle" and "exercise" segments, or it could be released on a party-themed video, along with the "birthday" and "games" segments. If you choose to release the physical activity collection, you foreclose the possibility of releasing the party collection, and you will have to find something else to do with the "birthday" and "games" segments.
This problem is NP-complete. The official computer science jargon name for it is exact cover by 3-sets, or just X3C.
 The Sesame Workshop people were not able to solve the
problem. One of the videos in the series is about flowers, bananas,
and hair.
The Sesame Workshop people were not able to solve the
problem. One of the videos in the series is about flowers, bananas,
and hair.
[ Addendum 20160515: I turned this into a talk for !!Con 2016. Talk materials are on my web site. ]
[Other articles in category /CS] permanent link
Sat, 04 Mar 2006
Structured BASIC
Aristotle Pagaltzis
reminisces about programming microcomputers in BASIC in the
1980s:
That's what I started with, on the Acorn Electron. And I remember being excited about finding and understanding DEF FN. I also remember my disappointment about how limited it was. I remember my frustration whenever BASIC forced me into writing messy code.I remember my frustration with this too. I realized fairly early on that it was important to organize one's code in a modular fashion. My clearest memory of this was in developing an Adventure-style program. Each of the locations in the world was assigned a sequence number. Location #23 was handled by lines 2300--2399 of the program. Lines 2300--2319 would print the description of the location. Line 2320 would set the variables that recorded the player's location, and called the subroutine to print the descriptions of the other objects at that location. Line 2380 would call the subroutine that prompted the user for their next command. Other lines in between would provide the implementation of whatever special effects were required for that location.
All the important utility subroutines were at mnemonic line numbers; the main loop was at line 50000, and the command processing was at 51000. Special handling for objects was in the 40000 range, with one hundred statement numbers reserved for each object.
After each user command was processed, control was dispatched back to the appropriate part of the program, depending on where the player was now. Microsoft BASIC didn't have a computed GOTO, so the dispatch was performed by a jump table. I was unhappy with the jump table, recognizing that it didn't scale well.
Object sizes and descriptions were stored in a table. I don't know why I didn't store the location descriptions in the table in the same way, but I suspect that I tried and found that my microcomputer didn't have enough string memory. I also discovered that the algorithm that mapped statement numbers to code did not scale well to programs with a lot of numbered statements; editing the program grew intolerably slow once the world contained more than about fifty locations.
Still, I was pleased with the outcome. My goal (at the tender age of sixteen, or whatever) had been to adopt conventions that made it easy to extend or modify the world and to add new locations or objects, and I felt at the time that I had achieved that.
M. Pagaltzis says:
I guess I have a natural penchant for structured code. Penchant? Instinct.I think anyone who is really interested in writing programs in BASIC and who reflects on the results of his projects is going to come to the conclusion that BASIC is a very poor tool for the job. These problems force themselves on everyone, and if you are thoughtful you will see the problems and try to come up with some techniques to solve them.
I really wish I could see those old programs again. I'm sure I would learn a lot from them.
I do have some code I wrote in C as long ago as 1987. I remember that shortly after that I got sick of programming and took a vacation from it for a year.
One day the following year I was reading netnews, and I overheard a colleague complaining about his CS homework. He had to write a program in C to count the number of occurrences of each word in its input, using a binary tree to store the words. I said he was complaining about nothing and that I, a math major, could turn out such a program in two hours. I don't know why I said this, since I hadn't done any C programming in a year, and I didn't have any significant experience with C, but I was inspired, and I did finish it quickly, and it worked. I have been programming regularly ever since. I still have the source code for that program.
Here's the funny thing about the programs from that time: when I look at the pre-vacation programs, they look to me as though they were written by someone else. When I look at the tree-sort program or any other program I have written since then, I recognize it as my own code.
I don't know what happened in my brain during my one-year vacation, but my current programming style first emerged in that tree-sort program, and the code from after the break has all been a lot better than the code I wrote before.
I'd like to take another vacation, but I can't now, because I have to earn a living.
[Other articles in category /prog] permanent link
On risk
Consider the following game: You bet one dollar on the throw of a die.
If the die comes up 6, you get your dollar back plus 25 more dollars.
Otherwise, you lose your dollar. You can play as much as you want to.
This is a great moneymaking proposition, because your expected winnings
are four dollars on each game. Play a hundred times, you can expect to
be about four hundred dollars ahead. Even if you're only allowed to
play once, you would probably choose to play this game.
I pulled some sleight-of-hand in the previous paragraph. I said the game was a good deal "because" the expected winnings were positive. But that's not sufficient. If it were, the following game would also be a good deal: You bet one million dollars on the throw of a die. If the die comes up 6, you get your million back plus 25 million more. Otherwise, you lose your million.
For some people, the second game is a good deal. For most people, including me, it's obviously a very bad idea. To get a million dollars, I'd at least have to mortgage everything I owned. Then I'd be under a crushing debt for the rest of my life, with 83% likelihood. But the expected return of the two games is the same; this shows that a good expected return is not a sufficient condition for a good investment.
The difference, of course, is that the second game is much riskier than the first.
I think most people understand this, but nevertheless you still hear them say a lot of dumb stuff about risk. For example, many people like to say that the lottery is a stupidity tax on people who don't understand basic arithmetic, and that nobody would play the lottery unless they were very stupid, because it's trivial to see that the expected return is very poor.
I used to meet people at parties who said this. I would point out that by this reasoning, fire insurance is also a stupidity tax on people who don't understand basic arithmetic, because it's clear that the expected return on fire insurance is negative. I did get argument from folks from time to time, but it's really not arguable. If fire insurance didn't have an expected negative return for the customer, the insurance company would go out of business. In fact, the insurance company employs a whole department full of mathematicians whose job it is to make sure that the value of the premium you pay exceeds the expected cost of the benefits that the company will pay. So there are only three choices here:
- You're better at simple arithmetic than the insurance company's actuarial department, or
- You should avoid buying insurance, since it's just a sucker bet, or
- The issue of insurance and lotteries is a little more complex than that.
Once again the issue is not so much the expected return as it is risk. You pay the insurance premiums in order to mitigate the risk of a fire. One big fire could wipe you out completely. So you insure your house against fire so that you can't be completely wiped out. In return, you pay small, predictable sums of money regularly.
Another way to look at this is to consider the idea of a utility function. This is just a fancy term for the observation that the usefulness of money is not a linear function of the face value of the money. Once you have a million dollars, the utility of another hundred is much lower than it is to someone who only has ten thousand.
When you calculate expected returns, you need to calculate the expected increase of the utility, not the expected return of the nominal face value of the money. Consider this thought experiment: you may bet one cent on a game that will pay you ten thousand dollars if you win, which it will do one time in two million. Do you play? Well, maybe you do, because if you lose, so what? It's only one cent, and you will never miss it. The utility of one cent is essentially zero. The utility of ten thousand dollars, on the other hand, is very high, much higher than two million times zero. But if you like this game, you're open to the same charge of not understanding simple arithmetic as the lottery people are, because the expected return is very low, about the same as the lottery. The game is the same as the lottery, only the cost and the payoff are each a hundred times smaller.
In the fire insurance scenario, I am betting a small amount of money, with comparatively low utility, against a very large amount with much higher utility. One can view the lottery as analogous. If I buy a lottery ticket for $1, it's not because I misunderstand arithmetic. It's because the utility of $1 is low for me. I could blow $.85 on a candy bar tomorrow at lunch without thinking about it much. But the utility of winning millions is very high. With ten million dollars, I could pay off my mortgage, quit my job, and spend the rest of my life travelling around and writing articles. The value of even a hundred-millionth chance of this happening might well be higher than the value of gobbling one more candy bar that my body didn't need anyway.
Here's an exercise I've been doing lately, trying to estimate the value I ascribe to my own life. I am afraid that this is a trite subject, If so, I apologize. But if not, try it yourself, and you might discover something interesting. Suppose you have the option to play Russian Roulette, in return for which you will receive a fee of x. The gun has one million chambers, one of which holds a bullet. If you get the bullet, you die. Otherwise you collect the fee. What is the minimum value for x that will induce you to play? Would you play if x were one million dollars? I would. It's an almost sure million, and a million is a huge amount of money to me. And I probably take bigger than million-to-one risks every time I cross the street, so why not? So one might say that this demonstrates that my own estimate of the value of my own life is less than 1012 dollars.
Would I play for a thousand dollars? No, probably not. But where's the cutoff? Ten thousand is a maybe, a hundred thousand is a probably. (I rather suspect that the cutoff is on the same order of magnitude as the mortgage on my house. This thought threatens to open a whole can of disturbing philosophical worms.)
Now let's up the risk. I've already agreed to bet my life on a million-to-one chance in return for a million dollars. The expected-value theory says that I should also be willing to bet it on a thousand-to-one chance for a billion dollars. Am I? No way. The utility of a billion dollars is much less than a thousand times the utility of a million, for me. For Donald Trump, it might be different.
As a final exercise in thinking about risk, consider this: Folks at NASA estimate that your chance of being killed by a meteorite are on the order of 1 in 25,000. It's not because you're likely to be hit in the head. Nobody in recorded history has been killed by a meteor. It's because really big meteors do come by every so often, and when (not if, but when) one hits the earth, it'll kill just about everyone.
[ Addendum 20060425: There is a followup article to this one. ]
[ Addendum 20160208: There reports today that a man in Tamil Nadu has been killed by a meteor. ]
[Other articles in category ] permanent link
Fri, 03 Mar 2006
John Wilkins invents the meter
| Buy An Essay Towards a Real Character and a Philosophical Language from Bookshop.org (with kickback) (without kickback) |
In skimming over it, I noticed that Wilkins' language contained words for units of measure: "line", "inch", "foot", "standard", "pearch", "furlong", "mile", "league", and "degree". I thought oh, this was another example of a foolish Englishman mistaking his own provincial notions for universals. Wilkins' language has words for Judaism, Christianity, Islam; everything else is under the category of paganism and false gods, and I thought that the introduction of words for inches and feet was another case like that one. But when I read the details, I realized that Wilkins had been smarter than that.
Wilkins recognizes that what is needed is a truly universal measurement standard. He discusses a number of ways of doing this and rejects them. One of these is the idea of basing the standard on the circumference of the earth, but he thinks this is too difficult and inconvenient to be practical.
But he settles on a method that he says was suggested by Christopher Wren, which is to base the length standard on the time standard (as is done today) and let the standard length be the length of a pendulum with a known period. Pendulums are extremely reliable time standards, and their period depends only their length and on the local effect of gravity. Gravity varies only a very little bit over the surface of the earth. So it was a reasonable thing to try.
Wilkins directed that a pendulum be set up with the heaviest, densest possible spherical bob at the end of lightest, most flexible possible cord, and that the length of the cord be adjusted until the period of the pendulum was as close to one second as possible. So far so good. But here is where I am stumped. Wilkins did not simply take the standard length as the length from the fulcrum to the center of the bob. Instead:
...which being done, there are given these two Lengths, viz. of the String, and of the Radius of the Ball, to which a third Proportional must be found out; which must be as the length of the String from the point of Suspension to the Centre of the Ball is to the Radius of the Ball, so must the said Radius be to this third which being so found, let two fifths of this third Proportional be set off from the Centre downwards, and that will give the Measure desired.Wilkins is saying, effectively: let d be the distance from the point of suspension to the center of the bob, and r be the radius of the bob, and let x be such that d/r = r/x. Then d+(0.4)x is the standard unit of measurement.
Huh? Why 0.4? Why does r come into it? Why not just use d? Huh?
These guys weren't stupid, and there must be something going on here that I don't understand. Can any of the physics experts out there help me figure out what is going on here?
Anyway, the main point of this note is to point out an extraordinary coincidence. Wilkins says that if you follow his instructions above, the standard unit of measurement "will prove to be . . . 39 Inches and a quarter". In other words, almost exactly one meter.
I bet someone out there is thinking that this explains the oddity of the 0.4 and the other stuff I don't understand: Wilkins was adjusting his definition to make his standard unit come out to exactly one meter, just as we do today. (The modern meter is defined as the distance traveled by light in 1/299,792,458 of a second. Why 299,792,458? Because that's how long it happens to take light to travel one meter.) But no, that isn't it. Remember, Wilkins is writing this in 1668. The meter wasn't invented for another 110 years.
[ Addendum 20070915: There is a followup article, which explains the mysterious (0.4)x in the formula for the standard length. ]
Having defined the meter, which he called the "Standard", Wilkins then went on to define smaller and larger units, each differing from the standard by a factor that was a power of 10. So when Wilkins puts words for "inch" and "foot" into his universal language, he isn't putting in words for the common inch and foot, but rather the units that are respectively 1/100 and 1/10 the size of the Standard. His "inch" is actually a centimeter, and his "mile" is a kilometer, to within a fraction of a percent.
Wilkins also defined units of volume and weight measure. A cubic Standard was called a "bushel", and he had a "quart" (1/100 bushel, approximately 10 liters) and a "pint" (approximately one liter). For weight he defined the "hundred" as the weight of a bushel of distilled rainwater; this almost precisely the same as the original definition of the gram. A "pound" is then 1/100 hundred, or about ten kilograms. I don't understand why Wilkins' names are all off by a factor of ten; you'd think he would have wanted to make the quart be a millibushel, which would have been very close to a common quart, and the pound be the weight of a cubic foot of water (about a kilogram) instead of ten cubic feet of water (ten kilograms). But I've read this section over several times, and I'm pretty sure I didn't misunderstand.
Wilkins also based a decimal currency on his units of volume: a "talent" of gold or silver was a cubic standard. Talents were then divided by tens into hundreds, pounds, angels, shillings, pennies, and farthings. A silver penny was therefore 10-5 cubic Standard of silver. Once again, his scale seems off. A cubic Standard of silver weighs about 10.4 metric tonnes. Wilkins' silver penny is about is nearly ten cubic centimeters of metal, weighing 104 grams (about 3.5 troy ounces), and his farthing is 10.4 grams. A gold penny is about 191 grams, or more than six ounces of gold. For all its flaws, however, this is the earliest proposal I am aware of for a fully decimal system of weights and measures, predating the metric system, as I said, by about 110 years.
[Other articles in category /physics] permanent link
Wed, 01 Mar 2006
Google query roundup
My blog continues to attract interesting Google queries. I had fun
looking over the queries and writing about them last month, so I
thought I'd try it again.
Sometimes the queries are for very specific information that I can't provide:
1 the four type of flowers by aristotle 1 c-source code for earth revolving sun 1 colleges christian goldbach went to 1 moon sky rhode island position feb 01-feb 14 1 what is robert hooke' s middle name? 1 scientific definition on why fingers get pruney 1 source code of unrestricted simplex protocol in cI thought the reason that the fingers get pruney is that the skin has absorbed water, which makes it get bigger, and since it has nowhere to go, it bunches up. I haven't a clue where Christian Goldbach went to college, and I don't even have a clue why anyone would care, since Goldbach is a nobody. I don't know Robert Hooke's middle name, although there I can see why you might want to know, since Hooke was one of the foremost scientists of the 17th century. Did he even have a middle name?
| Buy An Essay Towards a Real Character and a Philosophical Language from Bookshop.org (with kickback) (without kickback) |
In the "you're asking the wrong question, so all you'll get is the wrong answer" department:
1 books typical copies soldThe only remotely reasonable answer I can imagine here is "zero". There were some related questions that were more sensical:
1 "typical royalties" 1 total o'reilly books sold 1 typical royaltiesI don't know how many O'Reilly books have sold, but I bet if you wrote to ask them, they would tell you.
In the "damn, I wish I had the foggiest idea" department:
1 what happens inside the chrysalisDamn, I wish I had the foggiest idea.
Sometimes, the page to which the user is referred is just perfect for their query:
1 every natural number is either a fibonacci number or it can be written as a sum of nonconsecutive fibonacci numbersThis is my favorite of that type:
6 how many people can use an armonica properlyThis query came up last month; apparently the author is trying it over and over. (The 6 indicates that the query was placed six times.) Last month when I saw it, it inspired me to discuss the armonica in some detail; I can only assume that the original author came back and saw my discussion, in which I answered the question.
Contrary to this, however, is this recurring query:
1 linear math system eliminate debtI didn't know what the author was after last month, and I still don't.
Some of the queries are even more depressing. For example:
1 which expression represents the number 96 written as a
product of primes?
This is depressing because, first, it's obviously a case of some kid
typing in his homework questions verbatim, and second, because the
problem is so very easy. It's not as though he was asked for
the expression that represents the number 6,951,541,603 as a product
of primes. Here's another one like that:
1 greatest common factor of 36 and 63The depressing thing here is that the author hasn't figured out that the way to answer this question is to search for greatest common factor and then read and understand the documents you find. Searching for this one specific arithmetic fact is just silly. It's like trying to multiply 17 and 7 by searching for product of 17 and 7, which also doesn't work.
But sometimes searching for the exact question you want answered does work:
1 a rope lying over the top of a fence is the same length on each side. it weighs one third of a pound per foot. on one end hangs a monkey holding a banana, and on the other end a weight equal to the weight of the monkey. the banana weighs two ounces per inch. the rope is as long (in feet) as the age of the monkey (in years), and the weight of the monkey (in ounces) is the same as the age of the monkey's mother. the combined age of the monkey and its mother is thirty years. one half of the weight of the monkey, plus the weight of the banana, is one forth as much as the weight of the weight and the weight of the rope. the monkey's mother is half as old as the monkey will be when it is three times as old as its mother was when she she was half as old as the monkey will be when when it is as old as its mother will be when she is four times as old as the monkey was when it was twice as its mother was when she was one third as old as the monkey was when it was old as is mother was when she was three times as old as the monkey was when it was one fourth as old as it is now. how long is the banana?And behold, the answer is here. The question comes from Games for the Superintelligent, by Jim Fixx, although it isn't all that difficult. When it was first posed to me, probably around 1980, I was stumped by the long final statement about the monkey's mother's age. I could turn the rest of the information into algebra, but I couldn't understand that final statement. It didn't occur to me at the time to try looking at simpler versions of the same thing, such as "the monkey's mother is half as old as the monkey is now" or "the monkey's mother is half as old as the monkey will be when it is three times as old as its mother is now". These are pretty clear, and demonstrate the pattern for the rest of the sentence, which is a lot simpler than it first appears.
Speaking of problems that are simpler than they first appear, Jeff Abrahamson told me a good one a few months ago: One-tenth of a sphere is painted red, the rest blue. Show that there must exist eight blue points that lie at the vertices of a cube.
1 how did they invent the chinese symbolsNow this is an interesting question. My recollection from my 1991 visit to the National Palace Museum in Taipei is that the earliest known Chinese writing appears on the so-called "oracle bones". The ancient Chinese would foretell the future by heating the shoulder blades of oxen until the bones cracked. (The oxen were dead and the bones cleaned before this process was employed.) The cracks were then annotated with marks indicating their interpretations.
As for the symbols themselves, there are a number of explanations. Some, such as the symbols for "sun"
 , "moon"
, "moon"
 , and "tree"
, and "tree"  are clearly pictographic. That is, they are stylized pictures of the
sun, the moon, and a tree. Others are compounds; for example, the
character for "man"
are clearly pictographic. That is, they are stylized pictures of the
sun, the moon, and a tree. Others are compounds; for example, the
character for "man"  is a compound of the
characters for "power"
is a compound of the
characters for "power"  and "field"
and "field"  ; the character for "east"
; the character for "east"  , the direction of the rising sun, depicts the
sun rising behind a tree; the character for "grove"
, the direction of the rising sun, depicts the
sun rising behind a tree; the character for "grove" 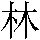 is two trees, and "forest"
is two trees, and "forest" 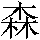 is three trees.
is three trees.
Others are phonetically motivated. For example, the word for
"ridgepole"  is a compound of
"wood"
is a compound of
"wood"  and "east"
and "east"  . The tree makes sense, because ridgepoles are
made of wood, but why "east"? It's because the word for
"ridgepole" is pronounced dòng, exactly the same as the word for
"east". Lots of words are dòng, but this is the
wooden dòng. The "east" component tells you how to
pronounce it, and the "wood" component hints at the meaning.
. The tree makes sense, because ridgepoles are
made of wood, but why "east"? It's because the word for
"ridgepole" is pronounced dòng, exactly the same as the word for
"east". Lots of words are dòng, but this is the
wooden dòng. The "east" component tells you how to
pronounce it, and the "wood" component hints at the meaning.
Writing Systems, by Geoffrey Sampson, has a chapter about this; I recommend both the chapter and the rest of the book.
1 fundamental theorem of phyllotaxisPhyllotaxis is the tendency of plants to put out leaves in certain directions; I probably mentioned them in connection with Fibonacci numbers. I had no idea there was a fundamental theorem of phyllotaxis. But, amazingly, there is. I think it relates the angle at which successive leaves appear on the stem with the resulting periodic pattern of leaves overall. I may do some further research on this later this month.
Other fundamental theorems include: the fundamental theorem of arithmetic, which says that every positive integer has a unique factorization into primes; the fundamental theorem of algebra, which says that every nth degree polynomial has n roots over the complex numbers; and the fundamental theorem of calculus, which relates the integral and differential calculus by saying that if f' is the derivative function of f, then:
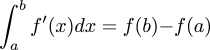
1 doctor dolittle racism 1 dr dolittle prince bumpo racism 1 dr doolittle racismWhen I posted my Doctor Dolittle article, I was hoping that it would become The Place to Go for information on that particular topic, since I seem to have done a lot more analysis than anyone else I could find. Now it's Google listing #6.
I think a lot could be said about the presence or absence of racism in the Dolittle books, although I wouldn't expect much agreement on such a hot-button topic. But I imagine there would be more agreement that the changes that were made to the book in the name of greater racial sensitivity are rather weird.
[Other articles in category /google-roundup] permanent link
What is topology?
Popular descriptions of topology tell you that it's like geometry, but
bending and stretching are allowed, so that a sphere is considered the
same as a cube, or a doughnut is the same as a coffee cup. There's
some truth in that, but it really doesn't get across the idea of what
topology is really like or really about.
Over the years I've spent a lot of time thinking about how to briefly explain topology to someone with only an ordinary math background, say one year of college calculus. Usually when I try hard to find good short explanations of things like this, I'm successful. So far, I haven't found any such explanation of topology. I haven't given up, though.
The difficulty is that topology was invented to give mathematicians a better understanding of analysis and the structure of the real numbers. Analysis was invented to give mathematicians a better understanding of calculus and limit processes. Calculus was invented to solve physics problems. So topology is three degrees removed from anything real. Contrast this with, say, graph theory, where the central object of study, the graph, is only one degree removed from something real. If you understand the vertices of a graph as computers and the edges as network connections, you can immediately see the point of graph theory. To understand the point of topology, you need to understand the point of analysis, and to understand the point of analysis, you need to understand the point of calculus. That's a lot of stuff to pack into a short explanation.
On top of that, you have the difficulty that topology has become a field of study in itself, with sub-branches that have nothing to do with the original goal of better understanding of the reals. The structure of the Tychonoff corkscrew (a particularly bizarre and counterintuitive topological object) may illuminate certain facts in set theory, but it has nothing to do with better understanding of the real numbers.
I think I can explain topology clearly, just not briefly. This is the first in what I hope will be a series of articles in which I'll try to do that.
The first thing to know is that mathematicians think of the real numbers as being points in an infinite line, with zero in the middle, and the positive numbers stretching away to the right and negative numbers to the left. Real numbers are points on this line, with a number n to the right of m if n > m . So mathematicians have a visual and spatial conception of numbers as well as a quantitative conception.

One consequence of this view is that a set of numbers is not merely an arithmetic object. It also has geometric properties, such as a length (find the smallest and largest numbers in the set, and subtract the smaller from the larger) and whether the set is a single connected piece or the union of smaller, disconnected components. Another consequence of this view of numbers as points on a line is that mathematicians refer to the numbers as "points" and to the set of numbers as a "space".
One idea that appears over and over again in analysis, and which is the source of the single driving idea of topology, is the notion of an open interval.
An open interval is very simple: it's just the set of all numbers in between two points. The notation (a, b) represents the set of all numbers greater than a and less than b. In the mathematician's mental picture of the real numbers, the interval (1, 5/2) looks like this:
There is a different notation for an interval that does include the endpoints, a so-called closed interval; [a, b] represents the set of all points greater than or equal to a and less than or equal to b. So [a, b] includes all the points of (a, b), and, additionally, a and b themselves:
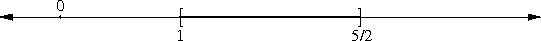
This matter of the endpoints is crucial. Open and closed intervals have very different behaviors, stemming from the fact that a closed interval contains its boundary points and an open interval does not. A point inside an open interval can be close to the edge, but not at the edge, because the open interval omits the edge. But a closed interval does include the edge.
In a closed interval, the points a and b are clearly special, and quite different from the other points in the interval, in a way that I will make more precise in a moment. But in an open interval, there is a certain sense in which all the points behave the same.
Here's the essential property of an open interval, as identified by topologists. If you choose any point p in the open interval, you can draw a little circle around p so that all the points inside the circle are also in the interval. For example, consider the open interval (1, 5/2) and the point 2, which is inside the interval:

We can do this for any point at all that is in the interval, as long as we make the circle sufficiently small:
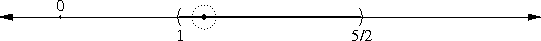
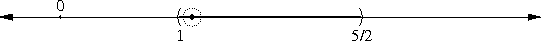
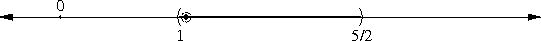
This is not true of closed intervals. A circle around the point 1 will include some points outside of the closed interval [1, 5/2], no matter how small we make the circle:
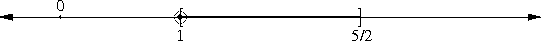
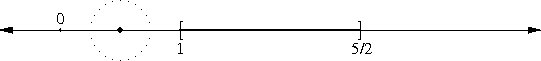
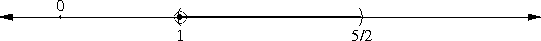
Mathematicians sum up all these properties by saying that a closed interval contains all the points of its boundary, whereas an open interval contains none of them.
This business of the small circle drawn around a particular point p is clearly important, so it's good to have a name for it. The idea is that we're trying to look at what happens "close to" p. But to pin that down, we need a notion of what "close to" means, so we need a way of measuring distances.
In the real numbers, measuring distances is easy. The distance between a and b is just |a - b|. |x| denotes the absolute value of x, which means that if x is negative, you make it positive instead. For |a - b|, it simply means that you should subtract the smaller one from the larger, and not the other way around. This is because you don't want to have negative distances, and you want the distance between 4 and 3 to be the same as the distance between 3 and 4.
Then mathematicians formalize those little circles this way: they say that the "ball" of radius ε around some point p, symbolized as Bε(p), is just the set of all points whose distance from p is less than ε. The use of the odd word "ball" here should tip you off that we're soon going to generalize this from one to three dimensions. In one dimension, balls are actually open intervals, and Bε(p) is precisely the interval (p - ε, p + ε). In two dimensions, the balls are discs, and in three dimensions they are actually ball-shaped.
The balls capture a flexible notion of "closeness": two points are "close" if they are inside the same ball. By making the balls small enough, we can make the notion of "close" as restrictive as we want. In this sense, we can see that no matter how restrictive we make the notion of closeness, there are always some points in an open interval that are close to the end of the interval—but no point is "close" for all possible notions of closeness; there is always some sufficiently restrictive definition under which a particular point is far from the end. Closed sets are different, and contain points that are close to the end for any definition of "close".
Similarly, the sets (1, 2) and (2, 3) are close together, for any definition of "close", although they don't actually intersect, or even touch, since you can't get from one to the other without leaving the sets entirely.
The essential property of open intervals that I mentioned before can be phrased in terms of the balls in this way: a set G is said to be open if, for any point p of G, there is some positive number ε such that Bε(p) is entirely contained in G.
Open intervals are open, but they are are not the only open sets. Let S be set of all points in either (1, 2) or (3, 4). S is open, but it's not an interval. But open sets all look pretty much the same; all open sets are unions of non-overlapping intervals, for example. There are some unbounded open sets, such as the set of all positive numbers, but we can think of that as the interval (0, ∞). Similarly (-∞, 3), the set of all numbers less than 3, is open. And the set of all real numbers is open, since it contains every ball whatsoever, but we can think of that set as (-∞, ∞).
Other concepts can be defined in terms of the balls. For example, a "limit point" of a set S is a point p for which any ball around p must contain some point of S other than p. 5/2 is a limit point of both the open interval (1, 5/2) and the closed interval [1, 5/2] because every ball Bε(5/2) contains points of both intervals other than 5/2 itself. The open interval omits 5/2, but the closed set includes it. One can define a closed set as a set that includes all of its limit points.
With these definitions, plenty of useful stuff follows, such as: Every open set is a union of non-overlapping open intervals. For every closed set C, there is some open set G such that every real number is in either C or in G but not both. The union or intersection of any two open sets is another open set. The union or intersection of any two closed sets is another closed set. Every ball is an open set. Every finite set is closed.
Other geometric notions come out of this too. For example, an "interior point" of a set S is a point p for which there's some Bε(p) is completely contained in S. Then an open set is precisely a set whose points are all interior points. Every point in [1, 5/2] is an interior point except the boundary points 1 and 5/2. We can define the "interior" of a set as the set of all its interior points, a "boundary point" as a point in a set that isn't an interior point, and the "boundary" of a set as the set of all its boundary points.
To generalize these notions to more complex spaces, we can generalize the idea of distance. Consider points in the plane, for example. These points have a well-known distance function, the so-called Pythagorean distance, which says that the distance between (a, b) and (c, d) is, as usual, √((c-a)2 + (d-b)2). If we use this as our definition of distance, and defined balls as before, we find that Bε(p) is just a disc of radius ε centered at p.
The definitions still make sense. Consider the set of points in the plane that are on or inside the circle of radius 1 centered at a particular point p. The boundary of this set, even under the very abstract definitions above, is just what you would expect: the boundary is the circle itself. The interior is the disc that lies inside the circle, including the center but not the edge. Once again, open sets are sets in the plane that omit their boundaries, and closed sets are those sets that include their boundaries. Most theorems still work; for example, the intersection of two open sets is still an open set, and balls are still examples of open sets.
We've started with a very thin, weak-looking base, which was simply the idea of measuring distances. From the simple idea of measurement, we get the balls, and from the balls we get ways to understand geometric notions like boundaries and interiors, and analytic notions like limits.
A metric space is a generalization of the idea of measuring distance. The "space" is now a set of things, which could be anything at all: points, or numbers, or train stations, or whatever. The things are customarily called "points". The "metric" describes how you are planning to measure the distance between two points.
To be a sensible distance function, the metric needs to have a few simple properties. It must never be negative, must be zero when measuring the distance from a point to itself, and must be positive when measuring the distance between two different points. It must be symmetric, which means that the distance from a to b must be the same as the distance from b to a in all cases. And the metric must satisfy the triangle inequality, which just means that the length of a route from a to b that stops off at c in between must be at least as long as the one that goes directly from a to b.
In mathematical notation, we write d(a, b) to represent the distance from a to b. We then want d to have the following properties:
- d(a, b) ≥ 0
- d(a, b) = 0 if and only if a = b
- d(a, b) = d(b, a)
- d(a, b) ≤ d(a, c) + d(c, b)
Once you have the metric, you can define the balls: the ball Bε(p) is still the set of all points q for which d(p, q) < ε. (This ball is sometimes written as Bd,ε(p), because it depends on the metric.) And once you have defined the balls, you can define the open and closed sets.
One thing this gets you is that you can talk about notions of closeness and nearness and limits in spaces that are much less tractable than lines and planes. For example, if you want to do analysis on the surface of a torus (a doughnut shape) this gives you a theoretical basis for treating it as a subset of ordinary three-dimensional space, and helps you understand which theorems of analysis will work on the torus and which ones won't.
Another thing it gets you is the opportunity to consider analogous notions in spaces that are nothing at all like lines or planes. Sometimes this might lead to insights that are useful in analysis. Sometimes it might not. But it does keep mathematicians employed.
Here's one example—I'm not sure whether it's genuinely useful or whether it serves primarily to keep mathematicians employed. Let's consider a plane, but instead of using the usual Pythagorean distance formula, let's say that the distance between (a, b) and (c, d) is |a-c| + |b-d|. This corresponds to a world in which you can only travel due north, south, east, and west; for this reason it is sometimes called the "Manhattan distance". In Manhattan, when you want to go from (a, b) to (c, d), you first walk east or west on b street, for a distance of |a-c|, until you get to c avenue. You then turn ninety degrees and walk north (or south) on c avenue, for a distance of |b-d|, until you reach the intersection with d street. The path is shown below:
But one interesting thing about the Manhattan metric is that it doesn't affect which sets are open or closed. So in a certain way, it doesn't matter whether you measure distance according to the usual function or according to the Manhattan metric.
A metric that is different is the "discrete" metric. In this metric, the distance between points p and q is 1, unless they are the same point, in which case it is 0. You may want to check to make sure that this metric has the requisite properties.
Balls in the discrete metric are even weirder than the diamond-shaped balls of the Manhattan metric. A ball around p either includes p and nothing else (if its radius is less than or equal to 1) or else it includes the entire universe (if its radius is bigger than 1). In a space measured with the discrete metric, nothing is close to anything else. Our typical example of closeness was the interval (1, 5/2) and the point 1, which was not inside the interval, but was close to it, because any Bε(1) overlapped the interval, no matter how small ε was. But in the discrete metric, the point is not close to the interval, because the ball B1/2(1) does not overlap the interval—it contains only the point 1, and nothing else!
In this article, I've tried to give a motivated and historical account of some of the basic notions of topology, and how they are generalizations of ideas of analysis, for the purpose of better understanding analysis. But I should break the news now that topology, when studied on its own, starts from a somewhat more abstract place. Instead of starting with a metric, and getting the balls from the metric, and the open sets from the balls, it starts with the open sets, and formulates the properties directly in terms of the open sets. This allows you to clean away a lot of unnecessary complication involving arithmetic and questions about Pythagorean vs. Manhattan distances and so on. The usual properties, like "interior" and "boundary" and "connected" can be formulated entirely in terms of the open sets.
Now suppose you have two sets, A and B, with two different definitions of open sets. And suppose you know some way to transform A into B and back again, say by rotating it or something, so that open sets in A are transformed into open sets in B, and vice versa on the way back. Then in a certain sense the open sets of A and B are the same, and anything that will be true of A's open sets will be true of B's as well. Since all the properties of interest are defined solely in terms of the open sets, any of these properties possessed by A will also be possessed by B and vice versa, so in terms of topological properties, A and B are the same.
The transformations that preserve the open sets are easy to understand intuitively: You can bend, stretch, or twist the sets any way you want. But you can't add or subtract material, or poke holes in them, or close up holes that were there before, and you can't tear the sets apart unless you glue them back together afterwards. You can crumple the sets, but you can't crush or explode them; points that were different before the transformation must remain different, and vice versa. A circle can be transformed into a square, by straightening out the sides; I hinted at this before when I mentioned that the Pythagorean and the Manhattan metrics yield the same open sets. But the circle can't be transformed into a line (you'd have to rip it apart) or a figure-eight (two formerly different points would have to fuse together at the waist of the 8). Spheres and cubes are topologically the same, but spheres are not the same as discs, or planes, or balls, or coffee cups.
I hope to develop this explanation further in future articles. My plans are to go backwards a little, and write an article about the structure of the real numbers, explaining why the open intervals are so important for calculus and analysis. And I hope to go forward and write an article about point-set topology, which abandons the metrics entirely in favor of dealing directly with the open sets.
[Other articles in category /math] permanent link
Addenda to recent articles 200602
Here are some notes on posts from the last month that I couldn't find
better places for.
- Regarding my
bad solution to the problem of preventing multiple simultaneous SMTP
connections from the same place, Chris Siebenmann suggests that a
better strategy is to centralize all SMTP access through a single
server that can manage the connections in any convenient way, without
IPC, and fork child processes to perform the actual SMTP transactions.
I had ended my post with "duh", but this suggestion requires an even
bigger "duh", because I am already running such a server and
modifying it appropriately would have been even easier than the
modification I did make to the SMTP program. Thank you,
M. Siebenmann. Duh!
- Regarding the 3n+1
domain, I should mention first that my use of the word "domain" is
incorrect here. A domain, properly speaking, is required to have both
addition and multiplication; the 3n+1 system supports only
multiplication. Addition doesn't work because (for example) 1+1 is
undefined in this system, 2 having been omitted.
I may discuss this in more detail in a future post.
- Regarding Perl's
accidental s/.../.../ee feature, John Macdonald remarks that
he thinks it was first discovered by Randal Schwartz, not Tom
Christiansen, as I said. M. Macdonald suggests that
M. Schwartz first used it in the form
s/.../.../eieio in a "Just Another Perl Hacker" signature,
and that M. Christiansen then invented the
s/(\$\w+)/$1/ee form as a way to make real use of it.
-
Regarding Robert Hooke's
mismeasurement of the frequency of G above middle C, I referred to
Benjamin Wardhaugh's suggestion that the error was in the length of
the pendulum he used to mention the time. Carl Witty points out that
this is unlikely, for two reasons. First, Hooke would have been quite
familiar with how to make a pendulum of the correct length to time a
one-second interval; indeed, he probably would have had such pendulums
sitting around, ready to be used. And second, the period of a
pendulum is proportional to the square root of its length, so to get
the error of a factor of √2 in the measurement of the frequency
of the brass wire, Hooke's pendulum would have had to be twice
as long as it should have been.
In reply, I suggested several possible causes of error:
- Perhaps the initial wire was not vibrating at precisely 1 Hz.
Synchronization with the 1 Hz pendulum might have been done by eye.
Any error in the original frequency would have been multiplied by 136
in the final result.
- The halving of the wire might not have been exact.
- If the tension in the wire changed during the halving process, the shortened wire would have a frequency different from twice that of the unshortened wire.
- The note produced by the one-foot wire might not have been
exactly G. it could have varied somewhat from true G without being
detected by the musical observers.
- G in 1664 wasn't 384 Hz anyway. In fact, I haven't finished
finding out just what Hooke meant by it, since pitches weren't fully
standardized; I don't know what Hooke intended for the reader to
understand from his assertion that it was 272 Hz. See Wikipedia's
discussion, for example.
- I don't yet know that the second was accurately measured. You
need a pendulum that strokes exactly 86,400 times per day. They would
have had to calibrate it against sandglasses and such things. How
accurate was that calibration?
- Even if the second was accurately measured, was it the same second
that we use today? I'm not sure. I should be able to find this out
by reading Hooke's lectures on gravitation (which I have handy) and
seeing what he gives as the acceleration due to the earth's gravity.
M. Witty also wondered if the fact that apparent error in the measurement was almost exactly √2 was a coincidence. I imagine so, but I could easily be wrong.
- Perhaps the initial wire was not vibrating at precisely 1 Hz.
Synchronization with the 1 Hz pendulum might have been done by eye.
Any error in the original frequency would have been multiplied by 136
in the final result.
-
Regarding non-oral reading,
I said:
Someone once told me that some famous scholar, I think perhaps Thomas Aquinas, was the only one of his contemporaries to read non-orally, that they were astonished at how the information would just fly from the book into his mind without his having to read it.
Ricardo J. B. Signes has confirmed this, except that it wasn't Aquinas. He says that Augustine wrote of Ambrose that "When he read, his eyes travelled over the page and his heart sought the sense, but voice and tongue were silent." Thanks, Ricardo. -
Regarding John Wilkins' artificial
language,
I said:
. . . a certain bishop John Wilkins had invented a language in which the meaning of each word would be immediately apparent from its spelling.
I have now obtained a copy of this book, and it uses "salmon" as an example. Wilkins' word for "salmon" is "zana". The first two letters always identify one of forty primary classifications for things; animal words begin with "z", and fish with "za". Each major group is divided into nine subgroups; the third letter identifies which of the nine subgroups the thing is in, with "n" denoting the ninth. The ninth subgroup of fish are "squamous river fish". Each subgroup is then divided into (usually) nine species, and the fourth letter identifies which of the nine species the thing is in with "a" denoting the second. The "squamous river fish" are divided as follows:(I don't have an example handy, so I will make one up. All words that begin with "p" are animals. Words beginning with "pa" are birds, those with "pe" are fish, and so forth. Words beginning with "pel" are fish with fins and scales. Words for fin-fish that live in rivers and streams all begin with "pela". "pelam" is a salmon.)
Bigger fish Voracious fish With loose scales With one fin, near the tail; wide mouths, and sharp teeth (1) With two fins Common to both fresh and salt water (2) Common to fresh water only Spotted (3) Not spotted More round (4) More broad or compressed (5) With close, compact scales (6) Not voracious Bigger Those that live in standing waters (7) Those that live in running waters Those that are thick and round (8) Those that are broad and deep (9) Lesser (10) Smallest river fish In the lower parts of the water With one fin on the back (11) With two fins and a broad head (12) In the upper parts of the water (13) - Regarding British
assertions that Americans speak of nothing but dollars, John
Bodoni writes in with the following quotation from Ayn Rand's book
Atlas Shrugged:
"If you ask me to name the proudest distinction of Americans, I would choose--because it contains all the others--the fact that they were the people who created the phrase 'to make money.' No other language or nation had ever used these words before; men had always thought of wealth as a static quantity--to be seized, begged, inherited, shared, looted or obtained as a favor. Americans were the first to understand that wealth has to be created."
I looked this up, and I found that it is not true. The OED has citations back to 1472:- 1472 R. CALLE in Paston Lett. (1976) II. 356, I truste be Ester to make of money..at the leeste l marke.
- 1546 O. JOHNSON in H. Ellis Orig. Lett. Eng. Hist. 2nd Ser. II. 175 Besides the monney that I shal make of the said wares.
- 1583 T. STOCKER tr. Tragicall Hist. Ciuile Warres Lowe Countries II. 64 [They] furnished him with all the money they were able to make.
- 1588 R. PARKE tr. J. G. de Mendoza Hist. China 45 Then may the
husband afterwardes sell his wife for a slave, and make money
of her for the dowrie he gaue her.
[Other articles in category /addenda] permanent link

