Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 18 Dec 2022
Recently I encountered the Dutch phrase den goede of den kwade, which means something like "the good [things] or the bad [ones]”, something like the English phrase “for better or for worse”.
Goede is obviously akin to “good”, but what is kwade? It turns out it is the plural of kwaad, which does mean “bad”. But are there any English cognates? I couldn't think of any, which is surprising, because Dutch words usually have one. (English is closely related to Frisian, which is still spoken in the northern Netherlands.)
I rummaged the dictionary and learned that it kwaad is akin to “cud”, the yucky stuff that cows regurgitate. And “cud” is also akin to “quid”, which is a chunk of chewing tobacco that people chew on like a cow's cud. (It is not related to the other quids.)
I was not expecting any of that.
[ Addendum: this article, which I wrote at 3:00 in the morning, is filled with many errors, including some that I would not have made if it had been daytime. Please disbelieve what you have read, and await a correction. ]
[ Addendum 20221229: Although I wrote that attendum the same day, I forgot to publish it. I am now so annoyed that I can't bring myself to write the corrections. I will do it next year. Thanks to all the very patient Dutch people who wrote to correct my many errors. ]
[Other articles in category /lang/etym] permanent link
A few days ago I was thinking about Rosneft (Росне́фть), the Russian national oil company. The “Ros” is obviously short for Rossiya, the Russian word for Russia, but what is neft?
“Hmm,” I wondered. “Maybe it is akin to naphtha?”
Yes! Ultimately both words are from Persian naft, which is the Old Persian word for petroleum. Then the Greeks borrowed it as νάφθα (naphtha) and the Russians, via Turkish. Petroleum is neft in many other languages, not just the ones you would expect like Azeri, Dari, and Turkmen, but also Finnish, French, Hebrew, and Japanese.
Sometimes I guess this stuff and it's just wrong, but it's fun when I get it right. I love puzzles!
[ Addendum 20230208: Tod McQuillin informs me that the Japanese word for petroleum is not related to naphtha; he says it is 石油 /sekiyu/ (literally "rock oil") or オイル /oiru/. The word I was thinking of was ナフサ /nafusa/ which M. McQuillin says means naphtha, not petroleum. (M. McQuillin also supposed that the word is borrowed from English, which I agree seems likely.)
I think my source for the original claim was this list of translations on Wiktionary. It is labeled as a list of words meaning “naturally occurring liquid petroleum”, and includes ナフサ and also entries purporting to be Finish, French, and Hebrew. I did not verify any of the the claims in Wiktionary, which could be many varieties of incorrect. ]
[Other articles in category /lang/etym] permanent link
Tue, 13 Dec 2022A while back I wrote about how Katara disgustedly reported that some of her second-grade classmates had formed a stealing club and named it “Stealing Club”.
Anyway,
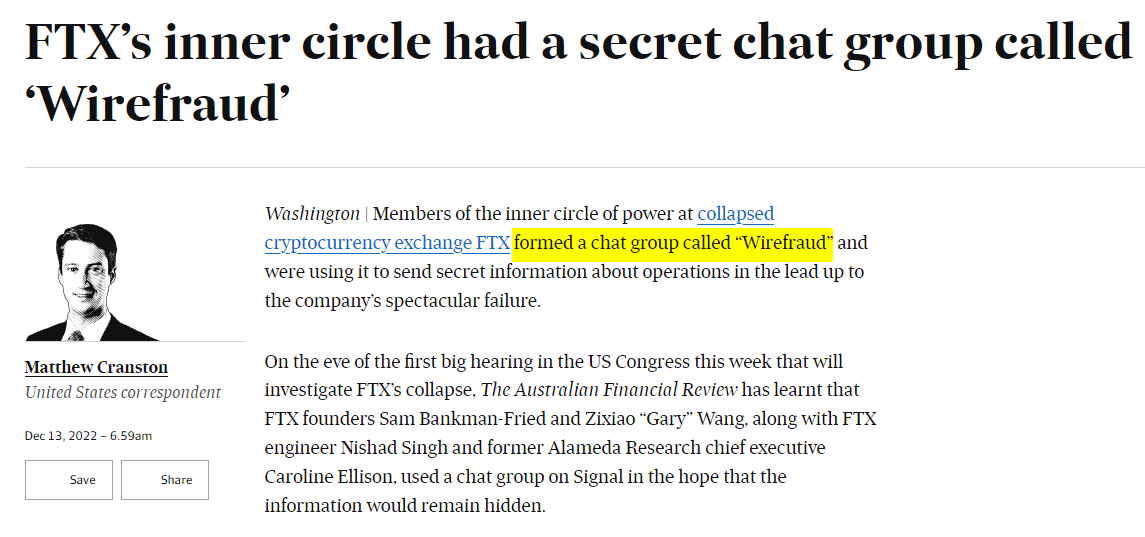
(Original source: Australian Financial Review)
[Other articles in category /law] permanent link
Sun, 04 Dec 2022
Addenda to recent articles 202211
I revised my chart of Haskell's numbers to include a few missing things, uncrossed some of the arrows, and added an explicit public domain notice,
The article contained a typo, a section titled “Shuff that don't work so good”. I decided this was a surprise gift from the Gods of Dada, and left it uncorrected.
My very old article about nonstandard adjectives now points out that the standard term for “nonstandard adjective” is “privative adjective”.
Similar to my suggested emoji for U.S. presidents, a Twitter user suggested emoji for UK prime ministers, some of which I even understand.
I added some discussion of why I did not use a cat emoji for President Garfield. A reader called January First-of-May suggested a tulip for Dutch-American Martin Van Buren, which I gratefully added.
In my article on adaptive group testing, Sam Dorfman and I wondered if there wasn't earlier prior art in the form of coin-weighing puzzles. M. January brought to my attention that none is known! The earliest known coin-weighing puzzles date back only to 1945. See the article for more details.
Some time ago I wrote an article on “What was wrong with SML?”. I said “My sense is that SML is moribund” but added a note back in April when a reader (predictably) wrote in to correct me.
However, evidence in favor of my view appeared last month when the Haskell Weekly News ran their annual survey, which included the question “Which programming languages other than Haskell are you fluent in?”, and SML was not among the possible choices. An oversight, perhaps, but a rather probative one.
I wondered if my earlier article was the only one on the Web to include the phrase “wombat coprolites”. It wasn't.
[Other articles in category /addenda] permanent link
Software horror show: SAP Concur
This complaint is a little stale, but maybe it will still be interesting. A while back I was traveling to California on business several times a year, and the company I worked for required that I use SAP Concur expense management software to submit receipts for reimbursement.
At one time I would have had many, many complaints about Concur. But today I will make only one. Here I am trying to explain to the Concur phone app where my expense occurred, maybe it was a cab ride from the airport or something.
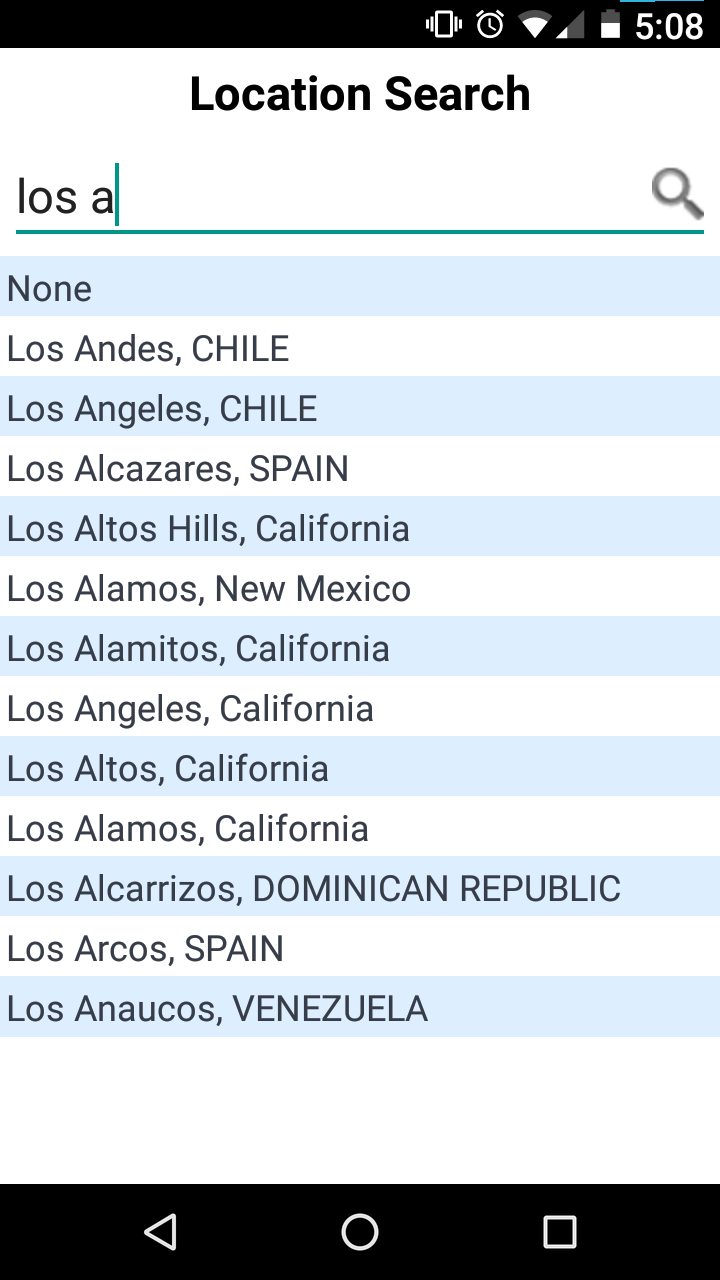
I had to interact with this control every time there was another expense to report, so this is part of the app's core functionality.
There are a lot of good choices about how to order this list. The best ones require some work. The app might use the phone's location feature to figure out where it is and make an educated guess about how to order the place names. (“I'm in California, so I'll put those first.”) It could keep a count of how often this user has chosen each location before, and put most commonly chosen ones first. It could store a list of the locations the user has selected before and put the previously-selected ones before the ones that had never been selected. It could have asked, when the expense report was first created, if there was an associated location, say “California”, and then used that to put California places first, then United States places, then the rest. It could have a hardwired list of the importance of each place (or some proxy for that, like population) and put the most important places at the top.
The actual authors of SAP Concur's phone app did none of these things. I understand. Budgets are small, deadlines are tight, product managers can be pigheaded. Sometimes the programmer doesn't have the resources to do the best solution.
But this list isn't even alphabetized.
There are two places named Los Alamos; they are not adjacent. There are two places in Spain; they are also not adjacent. This is inexcusable. There is no resource constraint that is so stringent that it would prevent the programmers from replacing
displaySelectionList(matches)
with
displaySelectionList(matches.sorted())
They just didn't.
And then whoever reviewed the code, if there was a code review, didn't
say “hey, why didn't you use displaySortedSelectionList here?”
And then the product manager didn't point at the screen and say “wouldn't it be better to alphabetize these?”
And the UX person, if there was one, didn't raise any red flag, or if they did nothing was done.
I don't know what Concur's software development and release process is like, but somehow it had a complete top-to-bottom failure of quality control and let this shit out the door.
I would love to know how this happened. I said a while back:
Assume that bad technical decisions are made rationally, for reasons that are not apparent.
I think this might be a useful counterexample. And if it isn't, if the individual decision-makers all made choices that were locally rational, it might be an instructive example on how an organization can be so dysfunctional and so filled with perverse incentives that it produces a stack of separately rational decisions that somehow add up to a failure to alphabetize a pick list.
Addendum : A possible explanation
Dennis Felsing, a former employee of SAP working on their HANA database, has suggested how this might have come about. Suppose that the app originally used a database that produced the results already sorted, so that no sorting in the client was necessary, or at least any omitted sorting wouldn't have been noticed. Then later, the backend database was changed or upgraded to one that didn't have the autosorting feature. (This might have happened when Concur was acquired by SAP, if SAP insisted on converting the app to use HANA instead of whatever it had been using.)
This change could have broken many similar picklists in the same way. Perhaps there was large and complex project to replace the database backend, and the unsorted picklist were discovered relatively late and were among the less severe problems that had to be overcome. I said “there is no resource constraint that is so stringent that it would prevent the programmers from (sorting the list)”. But if fifty picklists broke all at the same time for the same reason? And you weren't sure where they all were in the code? At the tail end of a large, difficult project? It might have made good sense to put off the minor problems like unsorted picklists for a future development cycle. This seems quite plausible, and if it's true, then this is not a counterexample of “bad technical decisions are made rationally for reasons that are not apparent”. (I should add, though, that the sorting issue was not fixed in the next few years.)
In the earlier article I said “until I got the correct explanation, the only explanation I could think of was unlimited incompetence.” That happened this time also! I could not imagine a plausible explanation, but M. Felsing provided one that was so plausible I could imagine making the decision the same way myself. I wish I were better at thinking of this kind of explanation.
[Other articles in category /prog] permanent link
Sun, 27 Nov 2022
Whatever became of the Peanuts kids?
One day I asked Lorrie if she thought that Schroeder actually grew up to be a famous concert pianist. We agreed that he probably did. Or at least Schroeder has as good a chance as anyone does. To become a famous concert pianist, you need to have talent and drive. Schroeder clearly has talent (he can play all that Beethoven and Mozart on a toy piano whose black keys are only painted on) and he clearly has drive. Not everyone with talent and drive does succeed, of course, but he might make it, whereas some rando like me has no chance at all.
That led to a longer discussion about what became of the other kids. Some are easier than others. Who knows what happens to Violet, Sally, (non-Peppermint) Patty, and Shermy? I imagine Violet going into realty for some reason.
As a small child I did not understand that Lucy's “psychiatric help 5¢” lemonade stand was hilarious, or that she would have been the literally worst psychiatrist in the world. (Schulz must have known many psychiatrists; was Lucy inspired by any in particular?) Surely Lucy does not become an actual psychiatrist. The world is cruel and random, but I refuse to believe it is that cruel. My first thought for Lucy was that she was a lawyer, perhaps a litigator. Now I like to picture her as a union negotiator, and the continual despair of the management lawyers who have to deal with her.
Her brother Linus clearly becomes a university professor of philosophy, comparative religion, Middle-Eastern medieval literature, or something like that. Or does he drop out and work in a bookstore? No, I think he's the kind of person who can tolerate the grind of getting a graduate degree and working his way into a tenured professorship, with a tan corduroy jacket with patches on the elbows, and maybe a pipe.
Peppermint Patty I can imagine as a high school gym teacher, or maybe a yoga instructor or massage therapist. I bet she'd be good at any of those. Or if we want to imagine her at the pinnacle of achievement, coach of the U.S. Olympic softball team. Marcie is calm and level-headed, but a follower. I imagine her as a highly competent project manager.
In the conversation with Lorrie, I said “But what happens to Charlie Brown?”
“You're kidding, right?” she asked.
“No, why?”
“To everyone's great surprise, Charlie Brown grows up to be a syndicated cartoonist and a millionaire philanthropist.”
Of course she was right. Charlie Brown is good ol' Charlie Schulz, whose immense success surprised everyone, and nobody more than himself.
Charles M. Schulz was born 100 years ago last Saturday.
[ Addendum 20221204: I forgot Charlie Brown's sister Sally. Unfortunately, the vibe I get from Sally is someone who will be sucked into one of those self-actualization cults like Lifespring or est. ]
[Other articles in category /humor] permanent link
Sat, 26 Nov 2022I was delighted to learn some time ago that there used to be giant wombats, six feet high at the shoulders, unfortunately long extinct.
It's also well known (and a minor mystery of Nature) that wombats have cubical poop.
Today I wondered, did the megafauna wombat produce cubical megaturds? And if so, would they fossilize (as turds often do) and leave ten-thousand-year-old mineral cubescat littering Australia? And if so, how big are these and where can I see them?
A look at Intestines of non-uniform stiffness mold the corners of wombat feces (Yang et al, Soft Matter, 2021, 17, 475–488) reveals a nice scatter plot of the dimensions of typical wombat scat, informing us that for (I think) the smooth-nosed (common) wombat:
- Length: 4.0 ± 0.6 cm
- Height: 2.3 ± 0.3 cm
- Width: 2.5 ± 0.3 cm
Notice though, not cubical! Clearly longer than they are thick. And I wonder how one distinguishes the width from the height of a wombat turd. Probably the paper explains, but the shitheads at Soft Matter want £42.50 plus tax to look at the paper. (I checked, and Alexandra was not able to give me a copy.)
Anyway the common wombat is about 40 cm long and 20 cm high, while the extinct giant wombats were nine or ten times as big: 400 cm long and 180 cm high, let's call it ten times. Then a propportional giant wombat scat would be a cuboid approximately 24 cm (9 in) wide and tall, and 40 cm (16 in) long. A giant wombat poop would be as long as… a wombat!
But not the imposing monoliths I had been hoping for.
Yang also wrote an article Duration of urination does not change with body size, something I have wondered about for a long time. I expected bladder size (and so urine quantity) to scale with the body volume, the cube of the body length. But the rate of urine flow should be proportional to the cross-sectional area of the urethra, only the square of the body length. So urination time should be roughly proportional to body size. Yang and her coauthors are decisive that this is not correct:
we discover that all mammals above 3 kg in weight empty their bladders over nearly constant duration of 21 ± 13 s.
What is wrong with my analysis above? It's complex and interesting:
This feat is possible, because larger animals have longer urethras and thus, higher gravitational force and higher flow speed. Smaller mammals are challenged during urination by high viscous and capillary forces that limit their urine to single drops. Our findings reveal that the urethra is a flow-enhancing device, enabling the urinary system to be scaled up by a factor of 3,600 in volume without compromising its function.
Wow. As Leslie Orgel said, evolution is cleverer than you are.
However, I disagree with the conclusion: 21±13 is not “nearly constant duration”. This is a range of 8–34s, with some mammals taking four times as long as others.
The appearance of the fibonacci numbers here is surely coincidental, but wouldn't it be awesome if it wasn't?
[ Addendum: I wondered if this was the only page on the web to contain the bigram “wombat coprolites”, but Google search produced this example from 2018:
Have wombats been around for enough eons that there might be wombat coprolites to make into jewelry? I have a small dinosaur coprolite that is kind of neat but I wouldn't make that turd into a necklace, it looks just like a piece of poop.
]
[ Addendum 20230209: I read the paper, but it does not explain what the difference is between the width of a wombat scat and the height. I wrote to Dr. Yang asking for an explantion, but she did not reply. ]
[Other articles in category /bio] permanent link
Tue, 08 Nov 2022
Addenda to recent articles 202210
I haven't done one of these in a while. And there have been addenda. I thought hey, what if I ask Git to give me a list of commits from October that contain the word ‘Addendum’. And what do you know, that worked pretty well. So maybe addenda summaries will become a regular thing again, if I don't forget by next month.
Most of the addenda resulted in separate followup articles, which I assume you will already have seen. ([1] [2] [3]) I will not mention this sort of addendum in future summaries.
In my discussion of lazy search in Haskell I had a few versions that used
do-notation in the list monad, but eventually abandoned it n favor of explicitconcatMap. For example:s nodes = nodes ++ (s $ concatMap childrenOf nodes)I went back to see what this would look like with
donotation:s nodes = (nodes ++) . s $ do n <- nodes childrenOf nMeh.
Regarding the origin of the family name ‘Hooker’, I rejected Wiktionary's suggestion that it was an occupational name for a maker of hooks, and speculated that it might be a fisherman. I am still trying to figure this out. I asked about it on English Language Stack Exchange but I have not seen anything really persuasive yet. One of the answers suggests that it is a maker of hooks, spelled hocere in earlier times.
(I had been picturing wrought-iron hooks for hanging things, and wondered why the occupational term for a maker of these wasn't “Smith”. But the hooks are supposedly clothes-fastening hooks, made of bone or some similar finely-workable material. )
The OED has no record of hocere, so I've asked for access to the Dictionary of Old English Corpus of the Bodleian library. This is supposedly available to anyone for noncommercial use, but it has been eight days and they have not yet answered my request.
I will post an update, if I have anything to update.
[Other articles in category /addenda] permanent link
Fri, 04 Nov 2022
A map of Haskell's numeric types
I keep getting lost in the maze of Haskell's numeric types. Here's the map I drew to help myself out. (I think there might have been something like this in the original Haskell 1998 report.)
Ovals are typeclasses. Rectangles are types. Black mostly-straight arrows show instance relationships. Most of the defined functions have straightforward types like !!\alpha\to\alpha!! or !!\alpha\to\alpha\to\alpha!! or !!\alpha\to\alpha\to\text{Bool}!!. The few exceptions are shown by wiggly colored arrows.
Basic plan
After I had meditated for a while on this picture I began to understand the underlying organization. All numbers support !!=!! and !!\neq!!. And there are three important properties numbers might additionally have:
Ord: ordered; supports !!\lt\leqslant\geqslant\gt!! etc.Fractional: supports divisionEnum: supports ‘pred’ and ‘succ’
Integral types are both Ord and Enum, but they are not
Fractional because integers aren't closed under division.
Floating-point and rational types are Ord and Fractional but not
Enum because there's no notion of the ‘next’ or ‘previous’ rational
number.
Complex numbers are numbers but not Ord because they don't admit a
total ordering. That's why Num plus Ord is called Real: it's
‘real’ as constrasted with ‘complex’.
More stuff
That's the basic scheme. There are some less-important elaborations:
Real plus Fractional is called RealFrac.
Fractional numbers can be represented as exact rationals or as
floating point. In the latter case they are instances of
Floating. The Floating types are required to support a large
family of functions like !!\log, \sin,!! and π.
You can construct a Ratio a type for any a; that's a fraction
whose numerators and denominators are values of type a. If you do this, the
Ratio a that you get is a Fractional, even if a wasn't one. In particular,
Ratio Integer is called Rational and is (of course) Fractional.
Shuff that don't work so good
Complex Int and Complex Rational look like they should exist, but
they don't really. Complex a is only an instance of Num when a
is floating-point. This means you can't even do 3 :: Complex
Int — there's no definition of fromInteger.
You can construct values of type Complex Int, but you can't do
anything with them, not even addition and subtraction. I think the
root of the problem is that Num requires an abs
function, and for complex numbers you need the sqrt function to be
able to compute abs.
Complex Int could in principle support most of the functions
required by Integral (such as div and mod) but Haskell
forecloses this too because its definition of Integral requires
Real as a prerequisite.
You are only allowed to construct Ratio a if a is integral.
Mathematically this is a bit odd. There is a generic construction,
called the field of quotients, which takes
a ring and turns it into a field, essentially by considering all the
formal fractions !!\frac ab!! (where !!b\ne 0!!), and with !!\frac ab!!
considered equivalent to !!\frac{a'}{b'}!! exactly when !!ab' = a'b!!.
If you do this with the integers, you get the rational numbers; if you
do it with a ring of polynomials, you get a field of rational functions, and
so on. If you do it to a ring that's already a field, it still
works, and the field you get is trivially isomorphic to the original
one. But Haskell doesn't allow it.
I had another couple of pages written about yet more ways in which the numeric class hierarchy is a mess (the draft title of this article was "Haskell's numbers are a hot mess") but I'm going to cut the scroll here and leave the hot mess for another time.
[ Addendum: Updated SVG and PNG to version 1.1. ]
[Other articles in category /prog/haskell] permanent link
Mon, 31 Oct 2022Content warning: something here to offend almost everyone
A while back I complained that there were no emoji portraits of U.S. presidents. Not that there a Chester A. Arthur portrait would see a lot of use. But some of the others might come in handy.
I couldn't figure them all out. I have no idea what a Chester Arthur emoji would look like. And I assigned 🧔🏻 to all three of Garfield, Harrison, and Hayes, which I guess is ambiguous but do you really need to be able to tell the difference between Garfield, Harrison, and Hayes? I don't think you do. But I'm pretty happy with most of the rest.
| George Washington | 💵 |
| John Adams | |
| Thomas Jefferson | 📜 |
| James Madison | |
| James Monroe | |
| John Quincy Adams | 🍐 |
| Andrew Jackson | |
| Martin Van Buren | 🌷 |
| William Henry Harrison | 🪦 |
| John Tyler | |
| James K. Polk | |
| Zachary Taylor | |
| Millard Fillmore | ⛽ |
| Franklin Pierce | |
| James Buchanan | |
| Abraham Lincoln | 🎭 |
| Andrew Johnson | 💩 |
| Ulysses S. Grant | 🍸 |
| Rutherford B. Hayes | 🧔🏻 |
| James Garfield | 🧔🏻 |
| Chester A. Arthur | |
| Grover Cleveland | 🔂 |
| Benjamin Harrison | 🧔🏻 |
| Grover Cleveland | 🔂 |
| William McKinley | |
| Theodore Roosevelt | 🧸 |
| William Howard Taft | 🛁 |
| Woodrow Wilson | 🎓 |
| Warren G. Harding | 🫖 |
| Calvin Coolidge | 🙊 |
| Herbert Hoover | ⛺ |
| Franklin D. Roosevelt | 👨🦽 |
| Harry S. Truman | 🍄 |
| Dwight D. Eisenhower | 🪖 |
| John F. Kennedy | 🍆 |
| Lyndon B. Johnson | 🗳️ |
| Richard M. Nixon | 🐛 |
| Gerald R. Ford | 🏈 |
| Jimmy Carter | 🥜 |
| Ronald Reagan | 💸 |
| George H. W. Bush | 👻 |
| William J. Clinton | 🎷 |
| George W. Bush | 👞 |
| Barack Obama | 🇰🇪 |
| Donald J. Trump | 🍊 |
| Joseph R. Biden | 🕶️ |
Honorable mention: Benjamin Franklin 🪁
Dishonorable mention: J. Edgar Hoover 👚
If anyone has better suggestions I'm glad to hear them. Note that I considered, and rejected 🎩 for Lincoln because it doesn't look like his actual hat. And I thought maybe McKinley should be 🏔️ but since they changed the name of the mountain back I decided to save it in case we ever elect a President Denali.
(Thanks to Liam Damewood for suggesting Harding, and to Colton Jang for Clinton's saxophone.)
Addenda
20221106
Twitter user Simon suggests emoji for UK prime ministers.
20221108
Rasmus Villemoes makes a good suggestion of 😼 for Garfield. I had considered this angle, but abandoned it because there was no way to be sure that the cat would be orange, overweight, or grouchy. Also the 🧔🏻 thing is funnier the more it is used. But I had been unaware that there is CAT FACE WITH WRY SMILE until M. Villemoes brought it to my attention, so maybe. (Had there been an emoji resembling a lasagna I would have chosen it instantly.)
20221108
January First-of-May has suggested 🌷 for Maarten van Buren, a Dutch-American whose first language was not English but Dutch. Let it be so!
20221218
Lorrie Kim reminded me that an old friend of ours, a former inhabitant of New Orleans, used to pass through Jackson Square, see the big statue of Andrew Jackson, and reflect gleefully on how he was covered in pigeon droppings. Lorrie suggested that I add a pigeon to the list above.
However, while there is a generic "bird" emoji, it is not specifically a pigeon. There are also three kinds of baby chicks; chickens both male and female; doves, ducks, eagles, flamingos, owls, parrots, peacocks, penguins, swans and turkeys; also single eggs and nests with multiple eggs. But no pigeons.
20250205
I got Anthropic's LLM, Claude, to help me with these, and it had some excellent suggestions.
[Other articles in category /history] permanent link
Sun, 30 Oct 2022A while back, discussing Vladimir Putin (not putain) I said
In English we don't seem to be so quivery. Plenty of people are named “Hoare”. If someone makes a joke about the homophone, people will just conclude that they're a boor.
Today I remembered Frances Trollope and her son Anthony Trollope. Where does the name come from? Surely it's not occupational?
Happily no, just another coincidence. According to Wikipedia it is a toponym, referring to a place called Troughburn in Northumberland, which was originally known as Trolhop, “troll valley”. Sir Andrew Trollope is known to have had the name as long ago as 1461.
According to the Times of London, Joanna Trollope, a 6th-generation descendant of Frances, once recalled
a night out with a “very prim and proper” friend who had the surname Hoare. The friend was dismayed by the amusement she caused in the taxi office when she phoned to book a car for Hoare and Trollope.
I guess the common name "Hooker" is occupational, perhaps originally referring to a fisherman.
[ Frances Trollope previously on this blog: [1] [2] ]
[ Addendum: (Wiktionary says that Hooker is occupational, a person who makes hooks. I find it surprising that this would be a separate occupattion. And what kind of hooks? I will try to look into this later. ]
[Other articles in category /lang] permanent link
Sun, 23 Oct 2022
This search algorithm is usually called "group testing"
Yesterday I described an algorithm that locates the ‘bad’ items among a set of items, and asked:
does this technique have a name? If I wanted to tell someone to use it, what would I say?
The answer is: this is group testing, or, more exactly, the “binary splitting” version of adaptive group testing, in which we are allowed to adjust the testing strategy as we go along. There is also non-adaptive group testing in which we come up with a plan ahead of time for which tests we will perform.
I felt kinda dumb when this was pointed out, because:
- A typical application (and indeed the historically first application) is for disease testing
- My previous job was working for a company doing high-throughput disease testing
- I found out about the job when one of the senior engineers there happened to overhear me musing about group testing
- Not only did I not remember any of this when I wrote the blog post, I even forgot about the disease testing application while I was writing the post!
Oh well. Thanks to everyone who wrote in to help me! Let's see, that's Drew Samnick, Shreevatsa R., Matt Post, Matt Heilige, Eric Harley, Renan Gross, and David Eppstein. (Apologies if I left out your name, it was entirely unintentional.)
I also asked:
Is the history of this algorithm lost in time, or do we know who first invented it, or at least wrote it down?
Wikipedia is quite confident about this:
The concept of group testing was first introduced by Robert Dorfman in 1943 in a short report published in the Notes section of Annals of Mathematical Statistics. Dorfman's report – as with all the early work on group testing – focused on the probabilistic problem, and aimed to use the novel idea of group testing to reduce the expected number of tests needed to weed out all syphilitic men in a given pool of soldiers.
Eric Harley said:
[It] doesn't date back as far as you might think, which then makes me wonder about the history of those coin weighing puzzles.
Yeah, now I wonder too. Surely there must be some coin-weighing puzzles in Sam Loyd or H.E. Dudeney that predate Dorfman?
Dorfman's original algorithm is not the one I described. He divides the items into fixed-size groups of n each, and if a group of n contains a bad item, he tests the n items individually. My proposal was to always split the group in half. Dorfman's two-pass approach is much more practical than mine for disease testing, where the test material is a body fluid sample that may involve a blood draw or sticking a swab in someone's nose, where the amount of material may be limited, and where each test offers a chance to contaminate the sample.
Wikipedia has an article about a more sophisticated of the binary-splitting algorithm I described. The theory is really interesting, and there are many ingenious methods.
Thanks to everyone who wrote in. Also to everyone who did not. You're all winners.
[ Addendum 20221108: January First-of-May has brought to my attention section 5c of David Singmaster's Sources in Recreational Mathematics, which has notes on the known history of coin-weighing puzzles. To my surprise, there is nothing there from Dudeney or Loyd; the earliest references are from the American Mathematical Monthly in 1945. I am sure that many people would be interested in further news about this. ]
[Other articles in category /prog] permanent link
Fri, 21 Oct 2022
More notes on deriving Applicative from Monad
A year or two ago I wrote about what you do if you already have a Monad and you need to define an Applicative instance for it. This comes up in converting old code that predates the incorporation of Applicative into the language: it has these monad instance declarations, and newer compilers will refuse to compile them because you are no longer allowed to define a Monad instance for something that is not an Applicative. I complained that the compiler should be able to infer this automatically, but it does not.
My current job involves Haskell programming and I ran into this issue again in August, because I understood monads but at that point I was still shaky about applicatives. This is a rough edit of the notes I made at the time about how to define the Applicative instance if you already understand the Monad instance.
pure is easy: it is identical to return.
Now suppose we
have >>=: how can we get <*>? As I eventually figured out last
time this came up, there is a simple solution:
fc <*> vc = do
f <- fc
v <- vc
return $ f v
or equivalently:
fc <*> vc = fc >>= \f -> vc >>= \v -> return $ f v
And in fact there is at least one other way to define it is just as good:
fc <*> vc = do
v <- vc
f <- fc
return $ f v
(Control.Applicative.Backwards
provides a Backwards constructor that reverses the order of the
effects in <*>.)
I had run into this previously
and written a blog post about it.
At that time I had wanted the second <*>, not the first.
The issue came up again in August because, as an exercise, I was trying to
implement the StateT state transformer monad constructor from scratch. (I found
this very educational. I had written State before, but StateT was
an order of magnitude harder.)
I had written this weird piece of code:
instance Applicative f => Applicative (StateT s f) where
pure a = StateT $ \s -> pure (s, a)
stf <*> stv = StateT $
\s -> let apf = run stf s
apv = run stv s
in liftA2 comb apf apv where
comb = \(s1, f) (s2, v) -> (s1, f v) -- s1? s2?
It may not be obvious why this is weird. Normally the definition of
<*> would look something like this:
stf <*> stv = StateT $
\s0 -> let (s1, f) = run stf s0
let (s2, v) = run stv s1
in (s2, f v)
This runs stf on the initial state, yielding f and a new state
s1, then runs stv on the new state, yielding v and a final state
s2. The end result is f v and the final state s2.
Or one could just as well run the two state-changing computations in the opposite order:
stf <*> stv = StateT $
\s0 -> let (s1, v) = run stv s0
let (s2, f) = run stf s1
in (s2, f v)
which lets stv mutate the state first and gives stf the result
from that.
I had been unsure of whether I wanted to run stf or stv first. I
was familiar with monads, in which the question does not come up. In
v >>= f you must run v first because you will pass its value
to the function f. In an Applicative there is no such dependency, so I
wasn't sure what I neeeded to do. I tried to avoid the question by
running the two computations ⸢simultaneously⸣ on the initial state
s0:
stf <*> stv = StateT $
\s0 -> let (sf, f) = run stf s0
let (sv, v) = run stv s0
in (sf, f v)
Trying to sneak around the problem, I was caught immediately, like a
small child hoping to exit a room unseen but only getting to the
doorway. I could run the computations ⸢simultaneously⸣ but on the
very next line I still had to say what the final state was in the end:
the one resulting from computation stf or the one resulting from
computation stv. And whichever I chose, I would be discarding the
effect of the other computation.
My co-worker Brandon Chinn
opined that this must
violate one of the
applicative functor laws.
I wasn't sure, but he was correct.
This implementation of <*> violates the applicative ”interchange”
law that requires:
f <*> pure x == pure ($ x) <*> f
Suppose f updates the state from !!s_0!! to !!s_f!!. pure x and
pure ($ x), being pure, leave it unchanged.
My proposed implementation of <*> above runs the two
computations and then updates the state to whatever was the result of
the left-hand operand, sf discarding any updates performed by the right-hand
one. In the case of f <*> pure x the update from f is accepted
and the final state is !!s_f!!.
But in the case of pure ($ x) <*> f the left-hand operand doesn't do
an update, and the update from f is discarded, so the final state is
!!s_0!!, not !!s_f!!. The interchange law is violated by this implementation.
(Of course we can't rescue this by yielding (sv, f v) in place of
(sf, f v); the problem is the same. The final state is now the
state resulting from the right-hand operand alone, !!s_0!! on the
left side of the law and !!s_f!! on the right-hand side.)
Stack Overflow discussion
I worked for a while to compose a question about this for Stack Overflow, but it has been discussed there at length, so I didn't need to post anything:
<**>is a variant of<*>with the arguments reversed. What does "reversed" mean?- How arbitrary is the "ap" implementation for monads?
- To what extent are Applicative/Monad instances uniquely determined?
That first thread contains this enlightening comment:
Functors are generalized loops
[ f x | x <- xs];Applicatives are generalized nested loops
[ (x,y) | x <- xs, y <- ys];Monads are generalized dynamically created nested loops
[ (x,y) | x <- xs, y <- k x].
That middle dictum provides another way to understand why my idea of running the effects ⸢simultaneously⸣ was doomed: one of the loops has to be innermost.
The second thread above (“How arbitrary is the ap implementation for
monads?”) is close to what I was aiming for in my question, and
includes a wonderful answer by Conor McBride (one of the inventors of
Applicative). Among other things, McBride points out that there are at least
four reasonable Applicative instances consistent with the monad
definition for nonempty lists.
(There is a hint in his answer here.)
Another answer there sketches a proof that if the applicative
”interchange” law holds for some applicative functor f, it holds for
the corresponding functor which is the same except that its <*>
sequences effects in the reverse order.
[Other articles in category /prog/haskell] permanent link
Thu, 20 Oct 2022Last week I was in the kitchen and Katara tried to tell Toph a secret she didn't want me to hear. I said this was bad opsec, told them that if they wanted to exchange secrets they should do it away from me, and without premeditating it, I uttered the following:
You shouldn't talk about things you shouldn't talk about while I'm in the room while I'm in the room.
I suppose this is tautological. But it's not any sillier than Tarski's observation that "snow is white" is true exactly if snow is white, and Tarski is famous.
I've been trying to think of more examples that really work. The best I've been able to come up with is:
You shouldn't eat things you shouldn't eat because they might make you sick, because they might make you sick.
I'm trying to decide if the nesting can be repeated. Is this grammatical?
You shouldn't talk about things you shouldn't talk about things you shouldn't talk about while I'm in the room while I'm in the room while I'm in the room.
I think it isn't. But if it is, what does it mean?
[ Previously, sort of. ]
[Other articles in category /lang] permanent link
Wed, 19 Oct 2022
What's this search algorithm usually called?
Consider this problem:
Input: A set !!S!! of items, of which an unknown subset, !!S_{\text{bad}}!!, are ‘bad’, and a function, !!\mathcal B!!, which takes a subset !!S'!! of the items and returns true if !!S'!! contains at least one bad item:
$$ \mathcal B(S') = \begin{cases} \mathbf{false}, & \text{if $S'\cap S_{\text{bad}} = \emptyset$} \\ \mathbf{true}, & \text{otherwise} \\ \end{cases} $$
Output: The set !!S_{\text{bad}}!! of all the bad items.
Think of a boxful of electronic components, some of which are defective. You can test any subset of components simultaneously, and if the test succeeds you know that each of those components is good. But if the test fails all you know is that at least one of the components was bad, not how many or which ones.
The obvious method is simply to test the components one at a time:
$$ S_{\text{bad}} = \{ x\in S \mid \mathcal B(\{x\}) \} $$
This requires exactly !!|S|!! calls to !!\mathcal B!!.
But if we expect there to be relatively few bad items, we may be able to do better:
- Call !!\mathcal B(S)!!. That is, test all the components at once. If none is bad, we are done.
- Otherwise, partition !!S!! into (roughly-equal) halves !!S_1!! and !!S_2!!, and recurse.
In the worst case this takes (nearly) twice as many calls as just calling !!\mathcal B!! on the singletons. But if !!k!! items are bad it requires only !!O(k\log |S|)!! calls to !!\mathcal B!!, a big win if !!k!! is small compared with !!|S|!!.
My question is: does this technique have a name? If I wanted to tell someone to use it, what would I say?
It's tempting to say "binary search" but it's not very much like binary search. Binary search finds a target value in a sorted array. If !!S!! were an array sorted by badness we could use something like binary search to locate the first bad item, which would solve this problem. But !!S!! is not a sorted array, and we are not really looking for a target value.
Is the history of this algorithm lost in time, or do we know who first invented it, or at least wrote it down? I think it sometimes pops up in connection with coin-weighing puzzles.
[ Addendum 20221023: this is the pure binary-splitting variation of adaptive group testing. I wrote a followup. ]
[Other articles in category /prog] permanent link
Tue, 18 Oct 2022In Perl I would often write a generic tree search function:
# Perl
sub search {
my ($is_good, $children_of, $root) = @_;
my @queue = ($root);
return sub {
while (1) {
return unless @queue;
my $node = shift @queue;
push @queue, $children_of->($node);
return $node if $is_good->($node);
}
}
}
For example, see Higher-Order Perl, section 5.3.
To use this, we provide two callback functions. $is_good checks
whether the current item has the properties we were searching for.
$children_of takes an item and returns its children in the tree.
The search function returns an iterator object, which, each time it is
called, returns a single item satisfying the $is_good predicate, or
undef if none remains. For example, this searches the space of all
strings over abc for palindromic strings:
# Perl
my $it = search(sub { $_[0] eq reverse $_[0] },
sub { return map "$_[0]$_" => ("a", "b", "c") },
"");
while (my $pal = $it->()) {
print $pal, "\n";
}
Many variations of this are possible. For example, replacing push
with unshift changes the search from breadth-first to depth-first.
Higher-Order Perl shows how to modify it to do heuristically-guided search.
I wanted to do this in Haskell, and my first try didn’t work at all:
-- Haskell
search1 :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search1 isGood childrenOf root =
s [root]
where
s nodes = do
n <- nodes
filter isGood (s $ childrenOf n)
There are two problems with this. First, the filter is in the wrong
place. It says that the search should proceed downward only from the
good nodes, and stop when it reaches a not-good node.
To see what's wrong with this, consider a search for palindromes. Th
string ab isn't a palindrome, so the search would be cut off
at ab, and never proceed downward to find aba or abccbccba.
It should be up to childrenOf to decide how to
continue the search. If the search should be pruned at a particular
node, childrenOf should return an empty list of children. The
$isGood callback has no role here.
But the larger problem is that in most cases this function will compute
forever without producing any output at all, because the call to s
recurses before it returns even one list element.
Here’s the palindrome example in Haskell:
palindromes = search isPalindrome extend ""
where
isPalindrome s = (s == reverse s)
extend s = map (s ++) ["a", "b", "c"]
This yields a big fat !!\huge \bot!!: it does nothing, until memory is exhausted, and then it crashes.
My next attempt looked something like this:
search2 :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search2 isGood childrenOf root = filter isGood $ s [root]
where
s nodes = do
n <- nodes
n : (s $ childrenOf n)
The filter has moved outward, into a single final pass over the
generated tree. And s now returns a list that at least has the node
n on the front, before it recurses. If one doesn’t look at the nodes
after n, the program doesn’t make the recursive call.
The palindromes program still isn’t right though. take 20
palindromes produces:
["","a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa",
"aaaaaaaaa", "aaaaaaaaaa","aaaaaaaaaaa","aaaaaaaaaaaa",
"aaaaaaaaaaaaa","aaaaaaaaaaaaaa", "aaaaaaaaaaaaaaa",
"aaaaaaaaaaaaaaaa","aaaaaaaaaaaaaaaaa", "aaaaaaaaaaaaaaaaaa",
"aaaaaaaaaaaaaaaaaaa"]
It’s doing a depth-first search, charging down the leftmost branch to
infinity. That’s because the list returned from s (a:b:rest) starts
with a, then has the descendants of a, before continuing with b
and b's descendants. So we get all the palindromes beginning with
“a” before any of the ones beginning with "b", and similarly all
the ones beginning with "aa" before any of the ones beginning with
"ab", and so on.
I needed to convert the search to breadth-first, which is memory-expensive but at least visits all the nodes, even when the tree is infinite:
search3 :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search3 isGood childrenOf root = filter isGood $ s [root]
where
s nodes = nodes ++ (s $ concat (map childrenOf nodes))
This worked. I got a little lucky here, in that I had already had the
idea to make s :: [n] -> [n] rather than the more obvious s :: n ->
[n]. I had done that because I wanted to do the n <- nodes thing,
which is no longer present in this version. But it’s just what we need, because we
want s to return a list that has all the nodes at the current
level (nodes) before it recurses to compute the nodes farther down.
Now take 20 palindromes produces the answer I wanted:
["","a","b","c","aa","bb","cc","aaa","aba","aca","bab","bbb","bcb",
"cac", "cbc","ccc","aaaa","abba","acca","baab"]
While I was writing this version I vaguely wondered if there was something that combines concat and map, but I didn’t follow up on it until just now. It turns out there is and it’s called concatMap. 😛
search3' :: (n -> Bool) -> (n -> [n]) -> n -> [n]
search3' isGood childrenOf root = filter isGood $ s [root]
where
s nodes = nodes ++ (s $ concatMap childrenOf nodes)
So this worked, and I was going to move on. But then a brainwave hit me: Haskell is a lazy language. I don’t have to generate and filter the tree at the same time. I can generate the entire (infinite) tree and filter it later:
-- breadth-first tree search
bfsTree :: (n -> [n]) -> [n] -> [n]
bfsTree childrenOf nodes =
nodes ++ bfsTree childrenOf (concatMap childrenOf nodes)
search4 isGood childrenOf root =
filter isGood $ bfsTree childrenOf [root]
This is much better because it breaks the generation and filtering into independent components, and also makes clear that searching is nothing more than filtering the list of nodes. The interesting part of this program is the breadth-first tree traversal, and the tree traversal part now has only two arguments instead of three; the filter operation afterwards is trivial. Tree search in Haskell is mostly tree, and hardly any search!
With this refactoring we might well decide to get rid of search entirely:
palindromes4 = filter isPalindrome allStrings
where
isPalindrome s = (s == reverse s)
allStrings = bfsTree (\s -> map (s ++) ["a", "b", "c"]) [""]
And then I remembered something I hadn’t thought about in a long, long time:
[Lazy evaluation] makes it practical to modularize a program as a generator that constructs a large number of possible answers, and a selector that chooses the appropriate one.
That's exactly what I was doing and what I should have been doing all along. And it ends:
Lazy evaluation is perhaps the most powerful tool for modularization … the most powerful glue functional programmers possess.
(”Why Functional Programming Matters”, John Hughes, 1990.)
I felt a little bit silly, because I wrote a book about lazy functional programming and yet somehow, it’s not the glue I reach for first when I need glue.
[ Addendum 20221023: somewhere along the way I dropped the idea of
using the list monad for the list construction, instead using explicit
map and concat. But it could be put back. For example:
s nodes = (nodes ++) . s $ do
n <- nodes
childrenOf n
I don't think this is an improvement on just using concatMap. ]
[Other articles in category /prog/haskell] permanent link
Thu, 13 Oct 2022
Today I realized I'm annoyed by the word "stethoscope". "Scope" is Greek for "look at". The telescope is for looking at far things (τῆλε). The microscope is for looking at small things (μικρός). The endoscope is for looking inside things (ἔνδον). The periscope is for looking around things (περί). The stethoscope is for looking at chests (στῆθος).
Excuse me? The hell it is! Have you ever tried looking through a stethoscope? You can't see for shit.
It should obviously have been called the stethophone.
(It turns out that “stethophone” was adopted as the name for a later elaboration of the stethoscope, shown at right, that can listen to two parts of the chest at the same time, and deliver the sounds to different ears.)
Stethophone illustration is in the public domain, via Wikipedia.
[Other articles in category /lang/etym] permanent link
Mon, 12 Sep 2022
Coat of arms of Zeppelin-Wappen
"Can we choose a new coat of arms?"
"What's wrong with the one we have?"
"What's wrong with it? It's nauseated goat!"
"I don't know what your problem is, it's been the family crest for generations."
"Please, I'm begging."
"Okay, how about a compromise: I'll get a new coat of arms, but it must include a reference to the old one."
"I guess I can live with that."

[ Source: Wikipedia ]
[Other articles in category /misc] permanent link
Thu, 08 Sep 2022When Albino Luciani was crowned Pope, he chose his papal name by concatenating the names of his two predecessors, John XXIII and Paul VI, to become John Paul. He died shortly after, and was succeeded by Karol Wojtyła who also took the name John Paul. Wojtyła missed a great opportunity to adopt Luciani's strategy. Had he concatenated the names of his predecessors, he would have been Paul John Paul. In this alternate universe his successor, Benedict XVI, would have been John Paul Paul John Paul, and the current pope, Francis, would have been Paul John Paul John Paul Paul John Paul. Each pope would have had a unique name, at the minor cost of having the names increase exponentially in length.
(Now I wonder if any dynasty has ever adopted the less impractical strategy of naming their rulers after binary numerals, say:
King Juan
King Juan Cyril
King Juan Juan
King Juan Cyril Cyril
King Juan Cyril Juan
King Juan Juan Cyril
(etc)
Or perhaps !!0, 1, 00, 01, 10, 11, 000, \ldots!!. There are many variations, some actually reasonable.)
I sometimes fantasize that Philadelphia-area Interstate highways are going to do this. The main east-west highway around here is I-76. (Not so-called, as many imagine, in honor of Philadelphia's role in the American revolution of 1776, but simply because it lies south of I-78 and north of I-74 and I-70.) A connecting segment that branches off of I-76 is known as I-676. Driving to one or the other I often see signs that offer both:
I often fantasize that this is a single sign for I-76676, and that this implies an infinite sequence of highways designated I-67676676, I-7667667676676, and so on.
Finally, I should mention the cleverly-named fibonacci salad, which you make by combining the leftovers from yesterday's salad and the previous day's.
[ Addendum: Do you know the name of the swagman in Waltzing Matilda? It's Juan. The song says so: “Juan's a jolly swagman…” ]
[Other articles in category /math] permanent link
Wed, 06 Jul 2022
Things I wish everyone knew about Git (Part II)
This is a writeup of a talk I gave in December for my previous employer. It's long so I'm publishing it in several parts:
- Part I:
- Part II (you are here):
- More coming later:
- Branches are fictitious
- Committing partial changes
- Push and fetch; tracking branches
- Aliases and custom commands
The most important material is in Part I.
It is really hard to lose stuff
A Git repository is an append-only filesystem. You can add snapshots
of files and directories, but you can't modify or delete anything.
Git commands sometimes purport to modify data. For
example git commit --amend suggests that it amends a commit.
It doesn't. There is no such thing as amending a commit; commits are
immutable.
Rather, it writes a completely new commit, and then kinda turns its back on the old one. But the old commit is still in there, pristine, forever.
In a Git repository you can lose things, in the sense of forgetting
where they are. But they can almost always be found again, one way or
another, and when you find them they will be exactly the same as they
were before. If you git commit --amend and change your mind later,
it's not hard to get the old ⸢unamended⸣ commit back if you want it
for some reason.
If you have the SHA for a file, it will always be the exact same version of the file with the exact same contents.
If you have the SHA for a directory (a “tree” in Git jargon) it will always contain the exact same versions of the exact same files with the exact same names.
If you have the SHA for a commit, it will always contain the exact same metainformation (description, when made, by whom, etc.) and the exact same snapshot of the entire file tree.
Objects can have other names and descriptions that come and go, but the SHA is forever.
(There's a small qualification to this: if the SHA is the only way to refer to a certain object, if it has no other names, and if you haven't used it for a few months, Git might discard it from the repository entirely.)
But what if you do lose something?
There are many good answers to this question but I think the one to
know first is git-reflog, because it covers the great majority of
cases.
The git-reflog command means:
“List the SHAs of commits I have visited recently”
When I run git reflog the top of the output says what commits I
had checked out at recently, with the top line being the commit I have checked
out right now:
523e9fa1 HEAD@{0}: checkout: moving from dev to pasha
5c31648d HEAD@{1}: pull: Fast-forward
07053923 HEAD@{2}: checkout: moving from pr2323 to dev
...
The last thing I did was check out the branch named pasha; its tip
commit is at 523e9f1a.
Before
that, I did git pull and Git updated my local dev branch from the
remote one, updating it to 5c31648d.
Before that, I had switched to dev from a different branch,
pr2323. At that time, before the pull, dev referred to commit
07053923.
Farther down in the output are some commits I visited last August:
...
58ec94f6 HEAD@{928}: pull --rebase origin dev: checkout 58ec94f6d6cb375e09e29a7a6f904e3b3c552772
e0cfbaee HEAD@{929}: commit: WIP: model classes for condensedPlate and condensedRNAPlate
f8d17671 HEAD@{930}: commit: Unskip tests that depend on standard seed data
31137c90 HEAD@{931}: commit (amend): migrate pedigree tests into test/pedigree
a4a2431a HEAD@{932}: commit: migrate pedigree tests into test/pedigree
1fe585cb HEAD@{933}: checkout: moving from LAB-808-dao-transaction-test-mode to LAB-815-pedigree-extensions
...

Suppose I'm caught in some horrible Git nightmare. Maybe I deleted the entire test suite or accidentally put my Small Wonder fanfic into a commit message or overwrote the report templates with 150 gigabytes of goat porn. I can go back to how things were before. I look in the reflog for the SHA of the commit just before I made my big blunder, and then:
git reset --hard 881f53fa
Phew, it was just a bad dream.
(Of course, if my colleagues actually saw the goat porn, it can't fix that.)
I would like to nominate Wile E. Coyote to be the mascot of Git. Because Wile E. is always getting himself into situations like this one:
But then, in the next scene, he is magically unharmed. That's Git.
Finding old stuff with git-reflog
git reflogby itself lists the places thatHEADhas beengit reflog some-branchlists the places thatsome-branchhas been- That
HEAD@{1}thing in thereflogoutput is another way to name that commit if you don't want to use the SHA. - You can abbreviate it to just
@{1}. The following locutions can be used with any git command that wants you to identify a commit:
@{17}(HEADas it was 17 actions ago)@{18:43}(HEADas it was at 18:43 today)@{yesterday}(HEADas it was 24 hours ago)dev@{'3 days ago'}(devas it was 3 days ago)some-branch@{'Aug 22'}(some-branchas it was last August 22)
(Use with
git-checkout,git-reset,git-show,git-diff, etc.)Also useful:
git show dev@{'Aug 22'}:path/to/some/file.txt“Print out that file, as it was on
dev, asdevwas on August 22”
It's all still in there.
What if you can't find it?
Don't panic! Someone with more experience can probably find it for you. If you have a local Git expert, ask them for help.
And if they are busy and can't help you immediately, the thing you're looking for won't disappear while you wait for them. The repository is append-only. Every version of everything is saved. If they could have found it today, they will still be able to find it tomorrow.
(Git will eventually throw away lost and unused snapshots, but typically not anything you have used in the last 90 days.)
What if you regret something you did?
Don't panic! It can probably put it back the way it was.
Git leaves a trail
When you make a commit, Git prints something like this:
your-topic-branch 4e86fa23 Rework foozle subsystem
If you need to find that commit again, the SHA 4e86fa23 is in your
terminal scrollback.
When you fetch a remote branch, Git prints:
6e8fab43..bea7535b dev -> origin/dev
What commit was origin/dev before the fetch? At 6e8fab43.
What commit is it now? bea7535b.
What if you want to look at how it was before? No problem, 6e8fab43
is still there. It's not called origin/dev any more, but the SHA is
forever. You can still check it out and look at it:
git checkout -b how-it-was-before 6e8fab43
What if you want to compare how it was with how it is now?
git log 6e8fab43..bea7535b
git show 6e8fab43..bea7535b
git diff 6e8fab43..bea7535b
Git tries to leave a trail of breadcrumbs in your terminal. It's constantly printing out SHAs that you might want again.
A few things can be lost forever!
After all that talk about how Git will not lose things, I should point
out the exceptions. The big exception is that if you have created
files or made changes in the working tree, Git is unaware of them
until you have added them with git-add. Until then, those changes
are in the working tree but not in the repository, and if you discard
them Git cannot help you get them back.
Good advice is Commit early and often. If you don't commit, at
least add changes with git-add. Files added but not committed are
saved in the repository,
although they can be hard to find
because they haven't been packaged into a commit with a single SHA id.
Some people automate this: they have a process that runs every few minutes and commits the current working tree to a special branch that they look at only in case of disaster.
The dangerous commands are
git-resetandgit-checkout
which modify the working tree, and so might wipe out changes that aren't in the repository. Git will try to warn you before doing something destructive to your working tree changes.
git-rev-parse
We saw a little while ago that Git's language for talking about commits and files is quite sophisticated:
my-topic-branch@{'Aug 22'}:path/to/some/file.txt
Where is this language documented? Maybe not where you would expect: it's in the
manual for git-rev-parse.
The git rev-parse command is less well-known than it should be. It takes a
description of some object and turns it into a SHA.
Why is that useful? Maybe not, but
The
git-rev-parseman page explains the syntax of the descriptions Git understands.
A good habit is to skim over the manual every few months. You'll pick up something new and useful every time.
My favorite is that if you use the syntax :/foozle you get the most
recent commit on the current branch whose message mentions
foozle. For example:
git show :/foozle
or
git log :/introduce..:/remove
Coming next week (probably), a few miscellaneous matters about using Git more effectively.
[Other articles in category /prog/git] permanent link
Wed, 29 Jun 2022
Things I wish everyone knew about Git (Part I)
This is a writeup of a talk I gave in December for my previous employer. It's long so I'm publishing it in several parts:
- Part I (you are here):
- Part II: (coming later)
- More coming later still:
- Branches are fictitious
- Committing partial changes
- Push and fetch; tracking branches
- Aliases and custom commands
How to approach Git; general strategy
Git has an elegant and powerful underlying model based on a few simple concepts:
- Commits are immutable snapshots of the repository
- Branches are named sequences of commits
- Every object has a unique ID, derived from its content
Built atop this elegant system is a flaming trash pile.
The command set wasn't always well thought out, and then over the years it grew by accretion, with new stuff piled on top of old stuff that couldn't be changed because Backward Compatibility. The commands are non-orthogonal and when two commands perform the same task they often have inconsistent options or are described with different terminology. Even when the individual commands don't conflict with one another, they are often badly-designed and confusing. The documentation is often very poorly written.
What this means
With a lot of software, you can opt to use it at a surface level without understanding it at a deeper level:
“I don't need to
know how it works.
I just want to know which commands to run.”
This is often an effective strategy, but
with Git, this does not work.
You can't “just know which commands to run” because the commands do not make sense!
To work effectively with Git, you must have a model of what the repository is like, so that you can formulate questions like “is the repo on this state or that state?” and “the repo is in this state, how do I get it into that state?”. At that point you look around for a command that answers your question, and there are probably several ways to do what you want.
But if you try to understand the commands without the model, you will suffer, because the commands do not make sense.
Just a few examples:
git-resetdoes up to three different things, depending on flagsgit-checkoutis worseThe opposite of
git-pushis notgit-pull, it'sgit-fetchetc.
If you try to understand the commands without a clear idea of the model, you'll be perpetually confused about what is happening and why, and you won't know what questions to ask to find out what is going on.
READ THIS
When I first used Git it drove me almost to tears of rage and frustration. But I did get it under control. I don't love Git, but I use it every day, by choice, and I use it effectively.
The magic key that rescued me was
John Wiegley's
Git From the
Bottom Up
Git From the Bottom Up explains the model. I read it. After that I wept no more. I understood what was going on. I knew how to try things out and how to interpret what I saw. Even when I got a surprise, I had a model to fit it into.
That's the best advice I have. Read Wiegley's explanation. Set aside time to go over it carefully and try out his examples. It fixed me.
If I were going to tell every programmer just one thing about Git, that would be it.
The rest of this series is all downhill from here.
But if I were going to tell everyone just one more thing, it would be:
It is very hard to
permanently lose work.
If something seems to have gone wrong, don't panic.
Remain calm and ask an expert.
Many more details about that are in the followup article.
[Other articles in category /prog/git] permanent link
Thu, 02 Jun 2022
Disabling the awful Macbook screen lock key
(The actual answer is at the very bottom of the article, if you want to skip my complaining.)
My new job wants me to do my work on a Macbook Pro, which in most ways is only a little more terrible than the Linux laptops I am used to. I don't love anything about it, and one of the things I love the least is the Mystery Key. It's the blank one above the delete key:
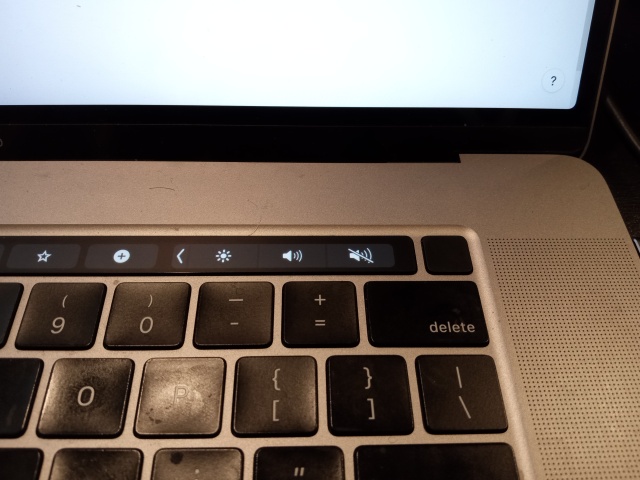
This is sometimes called the power button, and sometimes the TouchID. It is a sort of combined power-lock-unlock button. It has something to do with turning the laptop on and off, putting it to sleep and waking it up again, if you press it in the right way for the right amount of time. I understand that it can also be trained to recognize my fingerprints, which sounds like something I would want to do only a little more than stabbing myself in the eye with a fork.
If you tap the mystery button momentarily, the screen locks, which is very convenient, I guess, if you have to pee a lot. But they put the mystery button right above the delete key, and several times a day I fat-finger the delete key, tap the corner of the mystery button, and the screen locks. Then I have to stop what I am doing and type in my password to unlock the screen again.
No problem, I will just turn off that behavior in the System Preferences. Ha ha, wrong‑o. (Pretend I inserted a sub-article here about the shitty design of the System Preferences app, I'm not in the mood to actually do it.)
Fortunately there is a discussion of the issue on the Apple community support forum. It was posted nearly a year ago, and 316 people have pressed the button that says "I have this question too". But there is no answer. YAAAAAAY community support.
Here it is again. 292 more people have this question. This time there is an answer!
practice will teach your muscle memory from avoiding it.

This question was tough to search for. I found a lot of questions about disabling touch ID, about configuring the touch ID key to lock the screen, basically every possible incorrect permutation of what I actually wanted. I did eventually find what I wanted on Stack Exchange and on Quora — but no useful answers.
There was a discussion of the issue on Reddit:
How do you turn off the lock screen when you press the Touch ID button on MacBook Pro. Every time I press the Touch ID button it locks my screen and its super irritating. how do I disable this?
I think the answer might be my single favorite Reddit comment ever:
My suggestion would be not to press it unless you want to lock the screen. Why do you keep pressing it if that does something you don't want?

Victory!
I did find a solution! The key to the mystery was provided by Roslyn
Chu. She suggested
this page from 2014
which has an incantation that worked back in ancient times.
That incantation didn't work on my computer, but it put me on the
trail to the right one. I did need to use the defaults command and
operate on the com.apple.loginwindow thing, but the property name
had changed since 2014. There seems to be no way to interrogate the
meaningful property names; you can set anything you want, just like
Unix environment variables. But
The current developer documentation for the com.apple.loginwindow thing
has the current list of properties and one of them is the one I want.
To fix it, run the following command in a terminal:
defaults write com.apple.loginwindow DisableScreenLockImmediate -bool yes
They documenation claims will it will work on macOS 10.13 and later; it did work on my 12.4 system.
Something something famous Macintosh user experience.
[ The cartoon is from howfuckedismydatabase.com. ]
[ Update 20250130: While looking for the answer I found a year-old post on Reddit asking for the same thing, but with no answer. So when I learned the answer, I posted it there. Now, three years later still, I have a grateful reply from someone who needed the same formula! ]
[Other articles in category /tech] permanent link
Sat, 28 May 2022
“Llaves” and other vanishing consonants
Lately I asked:
Where did the ‘c’ go in llave (“key”)? It's from Latin clavīs…
Several readers wrote in with additional examples, and I spent a little while scouring Wiktionary for more. I don't claim that this list is at all complete; I got bored partway through the Wiktionary search results.
| Spanish | English | Latin antecedent |
|---|---|---|
| llagar | to wound | plāgāre |
| llama | flame | flamma |
| llamar | to summon, to call | clāmāre |
| llano | flat, level | plānus |
| llantén | plaintain | plantāgō |
| llave | key | clavis |
| llegar | to arrive, to get, to be sufficient | plicāre |
| lleno | full | plēnus |
| llevar | to take | levāre |
| llorar | to cry out, to weep | plōrāre |
| llover | to rain | pluere |
I had asked:
Is this the only Latin word that changed ‘cl’ → ‘ll’ as it turned into Spanish, or is there a whole family of them?
and the answer is no, not exactly. It appears that llave and llamar are the only two common examples. But there are many examples of the more general phenomenon that
(consonant) + ‘l’ → ‘ll’
including quite a few examples where the consonant is a ‘p’.
Spanish-related notes
Eric Roode directed me to this discussion of “Latin CL to Spanish LL” on the WordReference.com language forums. It also contains discussion of analogous transformations in Italian. For example, instead of plānus → llano, Italian has → piano.
Alex Corcoles advises me that Fundéu often discusses this sort of issue on the Fundéu web site, and also responds to this sort of question on their Twitter account. Fundéu is the Foundation of Emerging Spanish, a collaboration with the Royal Spanish Academy that controls the official Spanish language standard.
Several readers pointed out that although llave is the key that opens your door, the word for musical keys and for encryption keys is still clave. There is also a musical instrument called the claves, and an associated technical term for the rhythmic role they play. Clavícula (‘clavicle’) has also kept its ‘c’.
The connection between plicāre and llegar is not at all clear to me. Plicāre means “to fold”; English cognates include ‘complicated’, ‘complex’, ‘duplicate’, ‘two-ply’, and, farther back, ‘plait’. What this has to do with llegar (‘to arrive’) I do not understand. Wiktionary has a long explanation that I did not find convincing.
The levāre → llevar example is a little weird. Wiktionary says "The shift of an initial 'l' to 'll' is not normal".
Llaves also appears to be the Spanish name for the curly brace characters
{and}. (The square brackets are corchetes.)
Not related to Spanish
The llover example is a favorite of the Universe of Discourse, because Latin pluere is the source of the English word plover.
French parler (‘to talk’) and its English descendants ‘parley’ and ‘parlor’ are from Latin parabola.
Latin plōrāre (‘to cry out’) is obviously the source of English ‘implore’ and ‘deplore’. But less obviously, it is the source of ‘explore’. The original meaning of ‘explore’ was to walk around a hunting ground, yelling to flush out the hidden game.
English ‘autoclave’ is also derived from clavis, but I do not know why.
Wiktionary's advanced search has options to order results by “relevance” and last-edited date, but not alphabetically!
Thanks
- Thanks to readers Michael Lugo, Matt Hellige, Leonardo Herrera, Leah Neukirchen, Eric Roode, Brent Yorgey, and Alex Corcoles for hints clues, and references.
[ Addendum: Andrew Rodland informs me that an autoclave is so-called because the steam pressure inside it forces the door lock closed, so that you can't scald yourself when you open it. ]
[ Addendum 20230319: llevar, to rise, is akin to the English place name Levant which refers to the region around Syria, Israel, Lebanon, and Palestine: the “East”. (The Catalán word llevant simply means “east”.) The connection here is that the east is where the sun (and everything else in the sky) rises. We can see the same connection in the way the word “orient”, which also means an eastern region, is from Latin orior, “to rise”. ]
[Other articles in category /lang/etym] permanent link
Thu, 26 May 2022
Quick Spanish etymology question
Where did the ‘c’ go in llave (“key”)? It's from Latin clavīs, like in “clavicle”, “clavichord”, “clavier” and “clef”.
Is this the only Latin word that changed ‘cl’ → ‘ll’ as it turned into Spanish, or is there a whole family of them?
[ Addendum 20220528: There are more examples. ]
[Other articles in category /lang/etym] permanent link
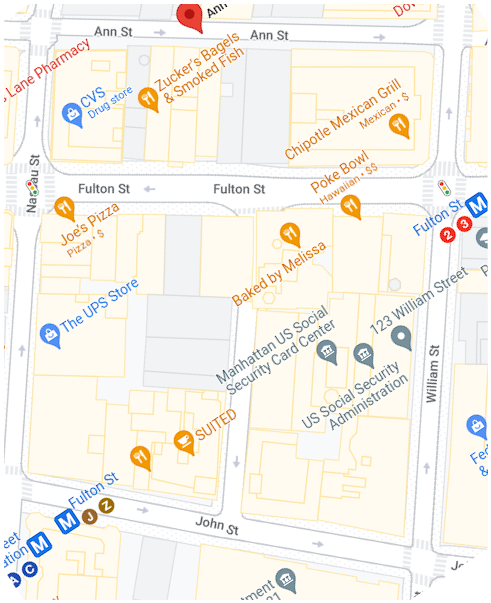
Sat, 21 May 2022Sometime in the previous millennium, my grandfather told me this joke:
Why is Fulton Street the hottest street in New York?
Because it lies between John and Ann.
I suppose this might have been considered racy back when he heard it from his own grandfather. If you didn't get it, don't worry, it wasn't actually funny.
Today I learned the Philadelphia version of the joke, which is a little better:
What's long and black and lies between two nuts?
Sansom Street.
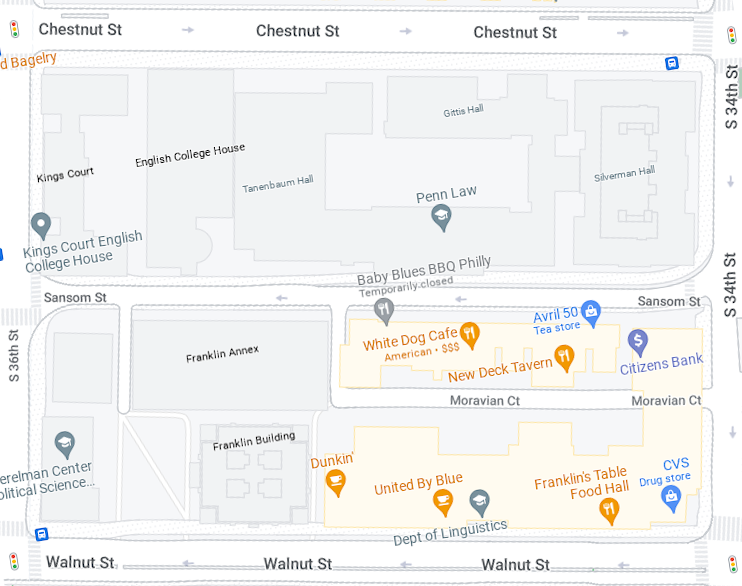
I think it that the bogus racial flavor improves it (it looks like it might turn out to be racist, and then doesn't). Some people may be more sensitive; to avoid making them uncomfortable, one can replace the non-racism with additional non-obscenity and ask instead “what's long and stiff and lies between two nuts?”.
There was a “what's long and stiff” joke I heard when I was a kid:
What's long and hard and full of semen?
A submarine.
Eh, okay. My opinion of puns is that they can be excellent, when they are served hot and fresh, but they rapidly become stale and heavy, they are rarely good the next day, and the prepackaged kind is never any good at all.
The antecedents of the “what's long and stiff” joke go back hundreds of years. The Exeter Book, dating to c. 950 CE, contains among other things ninety riddles, including this one I really like:
A curious thing hangs by a man's thigh,
under the lap of its lord. In its front it is pierced,
it is stiff and hard, it has a good position.
When the man lifts his own garment
above his knee, he intends to greet
with the head of his hanging object that familiar hole
which is the same length, and which he has often filled before.
(The implied question is “what is it?”.)
The answer is of course a key. Wikipedia has the original Old English if you want to compare.
Finally, it is off-topic but I do not want to leave the subject of the Exeter Book riddles without mentioning riddle #86. It goes like this:
Wiht cwom gongan
þær weras sæton
monige on mæðle,
mode snottre;
hæfde an eage
ond earan twa,
ond II fet,
XII hund heafda,
hrycg ond wombe
ond honda twa,
earmas ond eaxle,
anne sweoran
ond sidan twa.
Saga hwæt ic hatte.
I will adapt this very freely as:
What creature has two legs and two feet, two arms and two hands, a back and a belly, two ears and twelve hundred heads, but only one eye?
The answer is a one-eyed garlic vendor.
[Other articles in category /humor] permanent link
Sat, 14 May 2022A while back I wrote a shitpost about octahedral cathedrals and in reply Daniel Wagner sent me this shitpost of a cat-hedron:
But that got me thinking: the ‘hedr-’ in “octahedron” (and other -hedrons) is actually the Greek word ἕδρα (/hédra/) for “seat”, and an octahedron is a solid with eight “seats”. The ἕδρα (/hédra/) is akin to Latin sedēs (like in “sedentary”, or “sedate”) by the same process that turned Greek ἡμι- (/hémi/, like in “hemisphere”) into Latin semi- (like in “semicircle”) and Greek ἕξ (/héx/, like in “hexagon”) into Latin sex (like in “sextet”).
So a cat-hedron should be a seat for cats. Such seats do of course exist:

But I couldn't stop there because the ‘hedr-’ in “cathedral” is the same word as the one in “octahedron”. A “cathedral” is literally a bishop's throne, and cathedral churches are named metonymically for the literal throne they contain or the metaphorical one represent. A cathedral is where a bishop has his “seat” of power.
So a true cathedral should look like this:

[Other articles in category /lang/etym] permanent link
Tue, 03 May 2022The Wonderful Wizard of Oz
Certainly the best-known and most memorable of the disembodied heads of Oz is the one that the Wizard himself uses when he first appears to Dorothy:
In the center of the chair was an enormous Head, without a body to support it or any arms or legs whatever. There was no hair upon this head, but it had eyes and a nose and mouth, and was much bigger than the head of the biggest giant.
As Dorothy gazed upon this in wonder and fear, the eyes turned slowly and looked at her sharply and steadily. Then the mouth moved, and Dorothy heard a voice say:
“I am Oz, the Great and Terrible. Who are you, and why do you seek me?”
Those Denslow illustrations are weird. I wonder if the series would have lasted as long as it did, if Denslow hadn't been replaced by John R. Neill in the sequel.
This head, we learn later, is only a trick:
He pointed to one corner, in which lay the Great Head, made out of many thicknesses of paper, and with a carefully painted face.
"This I hung from the ceiling by a wire," said Oz; "I stood behind the screen and pulled a thread, to make the eyes move and the mouth open."
The Wonderful Wizard of Oz has not one but two earlier disembodied heads, not fakes but violent decaptitations. The first occurs offscreen, in the Tin Woodman's telling of how he came to be made of tin; I will discuss this later. The next to die is an unnamed wildcat that was chasing the queen of the field mice:
So the Woodman raised his axe, and as the Wildcat ran by he gave it a quick blow that cut the beast’s head clean off from its body, and it rolled over at his feet in two pieces.
Later, the Wicked Witch of the West sends a pack of forty wolves to kill the four travelers, but the Woodman kills them all, decapitating at least one:
As the leader of the wolves came on the Tin Woodman swung his arm and chopped the wolf's head from its body, so that it immediately died. As soon as he could raise his axe another wolf came up, and he also fell under the sharp edge of the Tin Woodman's weapon.
After the Witch is defeated, the travelers return to Oz, to demand their payment. The Scarecrow wants brains:
“Oh, yes; sit down in that chair, please,” replied Oz. “You must excuse me for taking your head off, but I shall have to do it in order to put your brains in their proper place.” … So the Wizard unfastened his head and emptied out the straw.
On the way to the palace of Glinda, the travelers pass through a forest whose inhabitants have been terrorized by a giant spider monster:
Its legs were quite as long as the tiger had said, and its body covered with coarse black hair. It had a great mouth, with a row of sharp teeth a foot long; but its head was joined to the pudgy body by a neck as slender as a wasp's waist. This gave the Lion a hint of the best way to attack the creature… with one blow of his heavy paw, all armed with sharp claws, he knocked the spider's head from its body.
That's the last decapitation in that book. Oh wait, not quite. They must first pass over the hill of the Hammer-Heads:
He was quite short and stout and had a big head, which was flat at the top and supported by a thick neck full of wrinkles. But he had no arms at all, and, seeing this, the Scarecrow did not fear that so helpless a creature could prevent them from climbing the hill.
It's not as easy as it looks:
As quick as lightning the man's head shot forward and his neck stretched out until the top of the head, where it was flat, struck the Scarecrow in the middle and sent him tumbling, over and over, down the hill. Almost as quickly as it came the head went back to the body, …
So not actually a disembodied head. The Hammer-Heads get only a Participation trophy.
Well! That gets us to the end of the first book. There are 13 more.
The Marvelous Land of Oz
One of the principal characters in this book is Jack Pumpkinhead, who is a magically animated wooden golem, with a carved pumpkin for a head.
The head is not attached too well. Even before Jack is brought to life, his maker observes that the head is not firmly attached:
Tip also noticed that Jack's pumpkin head had twisted around until it faced his back; but this was easily remedied.
This is a recurring problem. Later on, the Sawhorse complains:
"Even your head won't stay straight, and you never can tell whether you are looking backwards or forwards!"
The imperfect attachement is inconvenient when Jack needs to flee:
Jack had ridden at this mad rate once before, so he devoted every effort to holding, with both hands, his pumpkin head upon its stick…
Unfortunately, he is not successful. The Sawhorse charges into a river:
The wooden body, with its gorgeous clothing, still sat upright upon the horse's back; but the pumpkin head was gone, and only the sharpened stick that served for a neck was visible.… Far out upon the waters [Tip] sighted the golden hue of the pumpkin, which gently bobbed up and down with the motion of the waves. At that moment it was quite out of Tip's reach, but after a time it floated nearer and still nearer until the boy was able to reach it with his pole and draw it to the shore. Then he brought it to the top of the bank, carefully wiped the water from its pumpkin face with his handkerchief, and ran with it to Jack and replaced the head upon the man's neck.
There are four illustrations of Jack with his head detached.
The Sawhorse (who really is very disagreeable) has more complaints:
"I'll have nothing more to do with that Pumpkinhead," declared the Saw-Horse, viciously. "he loses his head too easily to suit me."
Jack is constantly worried about the perishability of his head:
“I am in constant terror of the day when I shall spoil."
"Nonsense!" said the Emperor — but in a kindly, sympathetic tone. "Do not, I beg of you, dampen today's sun with the showers of tomorrow. For before your head has time to spoil you can have it canned, and in that way it may be preserved indefinitely."
At one point he suggests using up a magical wish to prevent his head from spoiling.
The Woggle-Bug rather heartlessly observes that Jack's head is edible:
“I think that I could live for some time on Jack Pumpkinhead. Not that I prefer pumpkins for food; but I believe they are somewhat nutritious, and Jack's head is large and plump."
At one point, the Scarecrow is again disassembled:
Meanwhile the Scarecrow was taken apart and the painted sack that served him for a head was carefully laundered and restuffed with the brains originally given him by the great Wizard.
There is an illustration of this process, with the Scarecrow's trousers going through a large laundry-wringer; perhaps they sent his head through later.
The protagonists need to escape house arrest in a palace, and they assemble a flying creature, which they bring to life with the same magical charm that animated Jack and the Sawhorse. For the creature's head:
The Woggle-Bug had taken from its position over the mantle-piece in the great hallway the head of a Gump. … The two sofas were now bound firmly together with ropes and clothes-lines, and then Nick Chopper fastened the Gump's head to one end.
Once brought to life, the Gump is extremely puzzled:
“The last thing I remember distinctly is walking through the forest and hearing a loud noise. Something probably killed me then, and it certainly ought to have been the end of me. Yet here I am, alive again, with four monstrous wings and a body which I venture to say would make any respectable animal or fowl weep with shame to own.”
Flying in the Gump thing, the Woggle-Bug he cautions Jack:
"Not unless you carelessly drop your head over the side," answered the Woggle-Bug. "In that event your head would no longer be a pumpkin, for it would become a squash."
and indeed, when the Gump crash-lands, Jack's head is again in peril:
Jack found his precious head resting on the soft breast of the Scarecrow, which made an excellent cushion…
Whew. But the peril isn't over; it must be protected from a flock of jackdaws, in an unusual double-decaptitation:
[The Scarecrow] commanded Tip to take off Jack's head and lie down with it in the bottom of the nest… Nick Chopper then took the Scarecrow to pieces (all except his head) and scattered the straw… completely covering their bodies.
Shortly after, Jack's head must be extricated from underneath the Gump's body, where it has rolled. And the jackdaws have angrily scattered all the Scarecrow's straw, leaving him nothing but his head:
"I really think we have escaped very nicely," remarked the Tin Woodman, in a tone of pride.
"Not so!" exclaimed a hollow voice.
At this they all turned in surprise to look at the Scarecrow's head, which lay at the back of the nest.
"I am completely ruined!" declared the Scarecrow…
They re-stuff the Scarecrow with banknotes.
At the end of the book, the Gump is again disassembled:
“Once I was a monarch of the forest, as my antlers fully prove; but now, in my present upholstered condition of servitude, I am compelled to fly through the air—my legs being of no use to me whatever. Therefore I beg to be dispersed."
So Ozma ordered the Gump taken apart. The antlered head was again hung over the mantle-piece in the hall…
It reminds me a bit of Dixie Flatline. I wonder if Baum was famillar with that episode? But unlike Dixie, the head lives on, as heads in Oz are wont to do:
You might think that was the end of the Gump; and so it was, as a flying-machine. But the head over the mantle-piece continued to talk whenever it took a notion to do so, and it frequently startled, with its abrupt questions, the people who waited in the hall for an audience with the Queen.
The Gump's head makes a brief reappearance in the fourth book, startling Dorothy with an abrupt question.
Ozma of Oz
Oz fans will have been anticipating this section, which is a highlight on any tour of the Disembodied Heads of Oz. For it features the Princess Langwidere:
Now I must explain to you that the Princess Langwidere had thirty heads—as many as there are days in the month.
I hope you're buckled up.
But of course she could only wear one of them at a time, because she had but one neck. These heads were kept in what she called her "cabinet," which was a beautiful dressing-room that lay just between Langwidere's sleeping-chamber and the mirrored sitting-room. Each head was in a separate cupboard lined with velvet. The cupboards ran all around the sides of the dressing-room, and had elaborately carved doors with gold numbers on the outside and jewelled-framed mirrors on the inside of them.
When the Princess got out of her crystal bed in the morning she went to her cabinet, opened one of the velvet-lined cupboards, and took the head it contained from its golden shelf. Then, by the aid of the mirror inside the open door, she put on the head—as neat and straight as could be—and afterward called her maids to robe her for the day. She always wore a simple white costume, that suited all the heads. For, being able to change her face whenever she liked, the Princess had no interest in wearing a variety of gowns, as have other ladies who are compelled to wear the same face constantly.
Oh, but it gets worse. Foreshadowing:
After handing head No. 9, which she had been wearing, to the maid, she took No. 17 from its shelf and fitted it to her neck. It had black hair and dark eyes and a lovely pearl-and-white complexion, and when Langwidere wore it she knew she was remarkably beautiful in appearance.
There was only one trouble with No. 17; the temper that went with it (and which was hidden somewhere under the glossy black hair) was fiery, harsh and haughty in the extreme, and it often led the Princess to do unpleasant things which she regretted when she came to wear her other heads.
Langwidere and Dorothy do not immediately hit it off. And then the meeting goes completely off the rails:
"You are rather attractive," said the lady, presently. "Not at all beautiful, you understand, but you have a certain style of prettiness that is different from that of any of my thirty heads. So I believe I'll take your head and give you No. 26 for it."
Dorothy refuses, and after a quarrel, the Princess imprisons her in a tower.
Ozma of Oz contains only this one head-related episode, but I think it surpasses the other books in the quality of the writing and the interest of the situation.
Dorothy and the Wizard in Oz
This loser of a book has no disembodied heads, only barely a threat of one. Eureka the Pink Kitten has been accused of eating one of the Wizard's tiny trained piglets.
[Ozma] was just about to order Eureka's head chopped off with the Tin Woodman's axe…
The Wizard does shoot a Gargoyle in the eye with his revolver, though.
The Road to Oz
In this volume the protagonists fall into the hands of the Scoodlers:
It had the form of a man, middle-sized and rather slender and graceful; but as it sat silent and motionless upon the peak they could see that its face was black as ink, and it wore a black cloth costume made like a union suit and fitting tight to its skin. …
The thing gave a jump and turned half around, sitting in the same place but with the other side of its body facing them. Instead of being black, it was now pure white, with a face like that of a clown in a circus and hair of a brilliant purple. The creature could bend either way, and its white toes now curled the same way the black ones on the other side had done.
"It has a face both front and back," whispered Dorothy, wonderingly; "only there's no back at all, but two fronts."
Okay, but I promised disembodied heads. The Scoodlers want to make the protagonists into soup. When Dorothy and the others try to leave, the Scoodlers drive them back:
Two of them picked their heads from their shoulders and hurled them at the shaggy man with such force that he fell over in a heap, greatly astonished. The two now ran forward with swift leaps, caught up their heads, and put them on again, after which they sprang back to their positions on the rocks.
The problem with this should be apparent.
The characters escape from their prison and, now on guard for flying heads, they deal with them more effectively than before:
The shaggy man turned around and faced his enemies, standing just outside the opening, and as fast as they threw their heads at him he caught them and tossed them into the black gulf below. …
They should have taken a hint from the Hammer-Heads, who clearly have the better strategy. If you're going to fling your head at trespassers, you should try to keep it attached somehow.
Presently every Scoodler of the lot had thrown its head, and every head was down in the deep gulf, and now the helpless bodies of the creatures were mixed together in the cave and wriggling around in a vain attempt to discover what had become of their heads. The shaggy man laughed and walked across the bridge to rejoin his companions.
Brutal.
That is the only episode of head-detachment that we actually see. The shaggy man and Button Bright have their heads changed into a donkey's head and a fox's head, respectively, but manage to keep them attached. Jack Pumpkinhead makes a return, to explain that he need not have worried about his head spoiling:
I've a new head, and this is the fourth one I've owned since Ozma first made me and brought me to life by sprinkling me with the Magic Powder."
"What became of the other heads, Jack?"
"They spoiled and I buried them, for they were not even fit for pies. Each time Ozma has carved me a new head just like the old one, and as my body is by far the largest part of me I am still Jack Pumpkinhead, no matter how often I change my upper end.
He now lives in a pumpkin field, so as to be assured of a ready supply of new heads.
The Emerald City of Oz
By this time Baum was getting tired of Oz, and it shows in the lack of decapitations in this tired book.
In one of the two parallel plots, the ambitious General Guph promises the Nome King that he will conquer Oz. Realizing that the Nome armies will be insufficient, he hires three groups of mercenaries. The first of these aren't quite headless, but:
These Whimsies were curious people who lived in a retired country of their own. They had large, strong bodies, but heads so small that they were no bigger than door-knobs. Of course, such tiny heads could not contain any great amount of brains, and the Whimsies were so ashamed of their personal appearance and lack of commonsense that they wore big heads, made of pasteboard, which they fastened over their own little heads.
Don't we all know someone like that?
To induce the Whimsies to fight for him, Guph promises:
"When we get our Magic Belt," he made reply, "our King, Roquat the Red, will use its power to give every Whimsie a natural head as big and fine as the false head he now wears. Then you will no longer be ashamed because your big strong bodies have such teenty-weenty heads."
The Whimsies hold a meeting and agree to help, except for one doubter:
But they threw him into the river for asking foolish questions, and laughed when the water ruined his pasteboard head before he could swim out again.
While Guph is thus engaged, Dorothy and her aunt and uncle are back in Oz sightseeing. One place they visit is the town of Fuddlecumjig. They startle the inhabitants, who are “made in a good many small pieces… they have a habit of falling apart and scattering themselves around…”
The travelers try to avoid startling the Fuddles, but they are unsuccessful, and enter a house whose floor is covered with little pieces of the Fuddles who live there.
On one [piece] which Dorothy held was an eye, which looked at her pleasantly but with an interested expression, as if it wondered what she was going to do with it. Quite near by she discovered and picked up a nose, and by matching the two pieces together found that they were part of a face.
"If I could find the mouth," she said, "this Fuddle might be able to talk, and tell us what to do next."
They do succeed in assembling the rest of the head, which has red hair:
"Look for a white shirt and a white apron," said the head which had been put together, speaking in a rather faint voice. "I'm the cook."
This is fortunate, since it is time for lunch.
Jack Pumpkinhead makes an appearance later, but his head stays on his body.
The Patchwork Girl of Oz
As far as I can tell, there are no decapitations in this book. The closest we come is an explanation of Jack Pumpkinhead's head-replacement process:
“Just now, I regret to say, my seeds are rattling a bit, so I must soon get another head."
"Oh; do you change your head?" asked Ojo.
"To be sure. Pumpkins are not permanent, more's the pity, and in time they spoil. That is why I grow such a great field of pumpkins — that I may select a new head whenever necessary."
"Who carves the faces on them?" inquired the boy.
"I do that myself. I lift off my old head, place it on a table before me, and use the face for a pattern to go by. Sometimes the faces I carve are better than others--more expressive and cheerful, you know--but I think they average very well."
Some people the protagonists meet in their travels use the Scarecrow as sports equipment, but his head remains attached to the rest of him.
Tik-tok of Oz
This is a pretty good book, but there are no disembodied heads that I could find.
The Scarecrow of Oz
As you might guess from the title, the Scarecrow loses his head again. Twice.
Only a short time elapsed before a gray grasshopper with a wooden leg came hopping along and lit directly on the upturned face of the Scarecrow’s head.
The Scarecrow and the grasshopper (who is Cap'n Bill, under an enchantment) have a philosophical conversation about whether the Scarecrow can be said to be alive, and a little later Trot comes by and reassembles the Scarecrow. Later he nearly loses it again:
… the people thought they would like him for their King. But the Scarecrow shook his head so vigorously that it became loose, and Trot had to pin it firmly to his body again.
The Scarecrow is not yet out of danger. In chapter 22 he falls into a waterfall and his straw is ruined. Cap'n Bill says:
“… the best thing for us to do is to empty out all his body an’ carry his head an’ clothes along the road till we come to a field or a house where we can get some fresh straw.”
This they do, with the disembodied head of the Scarecrow telling stories and giving walking directions.
Rinkitink in Oz
No actual heads are lost in the telling of this story. Prince Inga kills a giant monster by bashing it with an iron post, but its head (if it even has one; it's not clear) remains attached. Rinkitink sings a comic song about a man named Ned:
A red-headed man named Ned was dead;
Sing fiddle-cum-faddle-cum-fi-do!
In battle he had lost his head;
Sing fiddle-cum-faddle-cum-fi-do!
'Alas, poor Ned,' to him I said,
'How did you lose your head so red?'
Sing fiddle-cum-faddle-cum-fi-do!
But Ned does not actually appear in the story, and we only get to hear the first two verses of the song because Bilbil the goat interrupts and begs Rinkitink to stop.
Elsewhere, Nikobob the woodcutter faces a monster named Choggenmugger, hacks off its tongue with his axe, splits its jaw in two, and then chops it into small segments, “a task that proved not only easy but very agreeable”. But there is no explicit removal of its head and indeed, the text and the pictures imply that Choggenmugger is some sort of giant sausage and has no head to speak of.
The Lost Princess of Oz
No disembodied heads either. The nearest we come is:
At once there rose above the great wall a row of immense heads, all of which looked down at them as if to see who was intruding.
These heads, however, are merely the heads of giants peering over the wall.
Two books in a row with no disembodied heads. I am becoming discouraged. Perhaps this project is not worth finishing. Let's see, what is coming next?
Oh.
Right then…
The Tin Woodman of Oz
This is the mother lode of decapitations in Oz. As you may recall, in The Wonderful Wizard of Oz the Tin Woodman relates how he came to be made of tin. He dismembered himself with a cursed axe, and after amputating all four of his limbs, he had them replaced with tin prostheses:
The Wicked Witch then made the axe slip and cut off my head, and at first I thought that was the end of me. But the tinsmith happened to come along, and he made me a new head out of tin.
One would expect that they threw the old head into a dumpster. But no! In The Tin Woodman of Oz we learn that it is still hanging around:
The Tin Woodman had just noticed the cupboards and was curious to know what they contained, so he went to one of them and opened the door. There were shelves inside, and upon one of the shelves which was about on a level with his tin chin the Emperor discovered a Head—it looked like a doll's head, only it was larger, and he soon saw it was the Head of some person. It was facing the Tin Woodman and as the cupboard door swung back, the eyes of the Head slowly opened and looked at him. The Tin Woodman was not at all surprised, for in the Land of Oz one runs into magic at every turn.
"Dear me!" said the Tin Woodman, staring hard. "It seems as if I had met you, somewhere, before. Good morning, sir!"
"You have the advantage of me," replied the Head. "I never saw you before in my life."
This creepy scene is more amusing than I remembered:
"Haven't you a name?"
"Oh, yes," said the Head; "I used to be called Nick Chopper, when I was a woodman and cut down trees for a living."
"Good gracious!" cried the Tin Woodman in astonishment. "If you are Nick Chopper's Head, then you are Me—or I'm You—or—or— What relation are we, anyhow?"
"Don't ask me," replied the Head. "For my part, I'm not anxious to claim relationship with any common, manufactured article, like you. You may be all right in your class, but your class isn't my class. You're tin."
Apparently Neill enjoyed this so much that he illustrated it twice, once as a full-page illustration and once as a spot illustration on the first page of the chapter:
The chapter, by the way, is titled “The Tin Woodman Talks to Himself”.
Later, we get the whole story from Ku-Klip, the tinsmith who originally assisted the amputated Tin Woodman. Ku-Klip explains how he used leftover pieces from the original bodies of both the Tin Woodman and the Tin Soldier (a completely superfluous character whose backstory is identical to the Woodman's) to make a single man, called Chopfyt:
"First, I pieced together a body, gluing it with the Witch's Magic Glue, which worked perfectly. That was the hardest part of my job, however, because the bodies didn't match up well and some parts were missing. But by using a piece of Captain Fyter here and a piece of Nick Chopper there, I finally got together a very decent body, with heart and all the trimmings complete."
The Tin Soldier is spared the shock of finding his own head in a closet, since Ku-Klip had used it in Chopfyt.
I'm sure you can guess where this is going.
Whew, that was quite a ride. Fortunately we are near the end and it is all downhill from here.
The Magic of Oz
This book centers around Kiki Aru, a grouchy Munchkin boy who discovers an extremely potent magical charm for transforming creatures. There are a great many transformations in the book, some quite peculiar and humiliating. The Wizard is turned into a fox and Dorothy into a lamb. Six monkeys are changed into giant soldiers. There is a long episode in which Trot and Cap'n Bill are trapped on an enchanted island, with roots growing out of their feets and into the ground. A giraffe has its tail bitten off, and there is the usual explanation about Jack Pumpkinhead's short shelf life. But I think everyone keeps their heads.
Glinda of Oz
There are no decapitations in this book, so we will have to settle for a consolation prize. The book's plot concerns the political economy of the Flatheads.
Dorothy knew at once why these mountain people were called Flatheads. Their heads were really flat on top, as if they had been cut off just above the eyes and ears.
The Flatheads carry their brains in cans. This is problematic: an ambitious flathead has made himself Supreme Dictator, and appropriated his enemies’ cans for himself.
The protagonists depose the Supreme Dictator, and Glinda arranges for each Flathead to keep their own brains in their own head where they can't be stolen, in a scene reminiscent of when the Scarecrow got his own brains, way back when.
That concludes our tour of the Disembodied Heads of Oz. Thanks for going on this journey with me.
[ Previously, Frank Baum's uncomfortable relationship with Oz. Coming up eventually, an article on domestic violence in Oz. Yes, really ]
[Other articles in category /book] permanent link
Sat, 30 Apr 2022
Mental illness, attention deficit disorder, and suffering
Freddie DeBoer has an article this week titled “Mental illness doesn't make you special”. Usually Freddie and I are in close agreement and this article is not an exception. I think many of M. DeBoer's points are accurate. But his subtitle is “Why do neurodiversity activists claim suffering is beautiful?” Although I am not a neurodiversity activist and I will not claim that suffering is beautiful, that subtitle stung, because I saw a little bit of myself in the question. I would like to cut off a small piece of that question and answer it.
This is from Pippi Longstocking, by Astrid Lindgren (1945):
'No, I don't suffer from freckles,' said Pippi.
Then the lady understood, but she took one look at Pippi and burst out, 'But, my dear child, your whole face is covered with freckles!'
'I know that,' said Pippi, 'but I don't suffer from them. I love them.'
I suffer from attention deficit disorder. Like Pippi Longstocking suffers from freckles.
M. DeBoer says:
There is, for example, a thriving ADHD community on TikTok and Tumblr: people who view their attentional difficulties not as an annoyance to be managed with medical treatment but as an adorable character trait that makes them sharper and more interesting than others around them.
For me the ADD really is a part of my identity — not my persona, which is what I present to the world, but my innermost self, the way I am actually am. I would be a different person without it. I might be a better person, or a happier or more successful one (I don't know) but I'd definitely be someone different.
And it's really not all bad. I understand that for many people ADD is a really major problem with no upsides. For me it's a major problem with upsides. And after living with it for fifty years, I've found ways to mitigate the problems and to accept the ones I haven't been able to mitigate.
I learned long ago never to buy nice gloves because I will inevitably leave them somewhere, perhaps on a store counter, or perhaps in the pocket of a different jacket. In the winter I only wear the cheapest and most disposable work gloves or garden gloves. They work better than nothing, and I can buy six pairs at a time, so that when I need gloves there's a chance I will find a pair in the pocket of the jacket I'm wearing, and if I lose a pair I can pick up another from the stack by the front door.
I used to constantly miss appointments. “Why don't you get a calendar?” people would say, but then I would have to remember the calendar, remember to check the calendar, and not lose the calendar, all seemingly impossible for me. The arrival of smartphones improved my life in so many ways. Now I do carry my calendar everywhere and I miss fewer appointments.
(Why could I learn to carry a smartphone and not a calendar? For one thing, the smartphone is smaller and fits in my pocket. For another, I really do carry it literally everywhere, which I wouldn't do with a calendar. I don't have to remember to check it because it makes a little noise when I have an appointment. It has my phone and my email and my messages in it. It has the books and magazines I'm reading. It has a calculator in it and a notepad. I used to try to carry all that crap separately and every day I would find that I wanted one that I had left at home that day. No longer.)
There are bigger downsides to ADD, like the weeks when I can't focus on work, or when I get distracted by some awesome new thing and don't do the things I should be doing, or how I lose interest in projects and don't always finish them, blah blah blah. I am not going to complain about any of that, it is just part of being me and I like who I am pretty well. Everyone has problems and mine are less severe than many.
And some of the upsides are just great. When it's working, the focus and intensity I get from the ADD are powerful. Not just useful, but fun. When I'm deep into a blog post or a math paper the intense focus brings me real joy. I love being smart and when the ADD is working well it makes me a lot smarter. I don't suffer from freckles, I love them.
When I was around seventeen I took a Real Analysis class at Columbia University. Toward the end of the year the final was coming up. One Saturday morning I sat down at the dining room table, with my class notes, proving every theorem that we had proved in class, starting from page 1. When I couldn't prove it on my own I would consult the notes or the textbook. By dinner time I had finished going through the semester and was ready to take the final. I got an A.
Until I got to college I didn't understand how people could spend hours a day “studying”. When I got there I found out. When my first-year hallmates were “studying” they were looking out the window, playing with their pencils, talking to their roommates, all sorts of stuff that wasn't studying. When I needed to study I would hide somewhere and study. I think the ability to focus on just one thing for a few hours at a time is a great gift that ADD has given me.
I sometimes imagine that the Devil offers me a deal: I will give up the ADD in return for a million dollars. I would have to think very, very carefully before taking that deal and I don't know whether I would say yes.
But if the Devil came and offered to cure my depression, and the price was my right arm? That question is easy. I would say “sounds great, but what's the catch?”
Depression is not something with upsides and downsides. It is a terrible illness, the blight of my life, the worst thing that has ever happened to me. It is neither an adorable character trait nor an annoyance to be managed with medical treatment. It is a severe chronic illness, one that is often fatal. In a good year it is kept in check by medical treatment but it is always lurking in the background and might reappear any morning. It is like the Joker: perhaps today he is locked away in Arkham, but I am not safe, I am never safe, I am always wondering if this is the day he will escape and show up at my door to maim or kill me.
I won't write in detail about how I've suffered from depression in my life. It's not something I want to revisit and it's not something my readers would find interesting. You wouldn't be inspired by my brave resolve in the face of adversity. It would be like watching a movie about someone with a chronic bowel disorder who shits his pants every day until he dies. There's no happy ending. It's not heroic. It's sad, humiliating, and boring.
DeBoer says:
This is what it’s actually like to have a mental illness: no desire to justify or celebrate or honor the disease, only the desire to be rid of it.
I agree 100%. This is what it is like to have a mental illness. In two words: it sucks.
And this is why I find it so very irritating that there is no term for my so-called ⸢attention deficit disorder⸣ that does not have the word “disorder” baked into it. I know what a disorder is, and my ADD isn't one. I want a word for this part of my brain chemistry that does not presume, axiomatically, that it is an illness. Why does any deviation from the standard have to be a disorder? Why do we medicalize human variation?
I understand that for some people it really is a disorder, that they have no desire to justify or celebrate or honor their attention deficit. For those people the term “attention deficit disorder” might be a good one. Not for me. I have a weird thing in my brain that makes it work differently from the way most other people's brains do. In many ways it works less well. I lose hats and miss doctor appointments. But that is not a mental illness. Most people aren't as good at math as I am; that's not a mental illness either. People have different brains.
Things can be problems in two different ways. Some variations from human standard are intrinsic problems. These might be illnesses. But many problems are extrinsic. Homosexual orientation used to be considered a mental illness. But you're queer your main problem is that other people treat you like crap. They hate you and they're allowed to tell you how much they hate you. They tell you you're not allowed to love or marry or have sex or bring up children. It sucks! But “I'm unhappy because people treat me like crap” is not a mental illness! The correct fix for this extrinsic problem isn't “stop being queer”, it's “stop treating queer people like crap!”
DeBoer says:
Today’s activists never seem to consider that there is something between terrible stigma and witless celebration, that we are not in fact bound to either ignore mental illness or treat it as an identity.
I agree somewhat, but that doesn't mean that the stigma isn't a real issue. With mental illnesses many of the problems are intrinsic, and are deep and hard to solve. But some of the problems of mental illness are extrinsic, caused by stigma and should be addressed. Mentally ill people will still be mentally ill, but at least they wouldn't be stigmatized. Mentally ill people are unhappy because they're mentally ill. But they are also unhappy because people treat them like crap.
Many of the downsides of ADD would be less troublesome for everyone, if our world was a little more accepting of difference, a little more willing to accommodate people who were stamped in a slightly different shape than the other cogs in the machine. In Pippi Longstocking world, why do people suffer from freckles? Not because of the freckles themselves, but only because other people tell them that their freckles are ugly and unlovable. Nobody has to suffer from freckles, if people would just stop being assholes about freckles.
ADD is a bigger problem than freckles. Some of its problems are intrinsic. It definitely contributes to making me unreliable. I don't think it is a delightful quirk that I am constantly losing gloves (and hats and jackets and bags and keys and wallets and everything else). People depending on me to do work timely are sometimes justifiably angry or disappointed when I don't. I'll accept responsibility for that. I've worked my whole life to try to do better.
But when the world has been willing to let me what I can do in the way that I can do it, the results have been pretty good. When the world has insisted that I do things the way ⸢everyone else⸣ does them, it hasn't always gone so well. And if you examine the “everyone else” there it starts to look threadbare because almost everyone is divergent in one way or another, and almost everyone needs some accommodation or other. There is no such thing as “the way everyone else does”. I can do some fine things that many other people can't.
I don't think “neurodivergent” is a very good term for how I'm different, not least because it's vague. But at least it doesn't frame my unusual and wonderful brain as a “disorder”.
Returning to Freddie DeBoer's article:
There is, for example, a thriving ADHD community on TikTok and Tumblr: people who view their attentional difficulties not as an annoyance to be managed with medical treatment but as an adorable character trait that makes them sharper and more interesting than others around them.
Some people do have it worse than others. I'm lucky. But that doesn't change the fact that some of those attentional difficulties are more like freckles: a character trait, perhaps even one that someone might find adorable, that other people are being assholes about. Isn't it fair to ask whether some of the extrinsic problems, the stigma, could be ameliorated if society were a little more flexible and a little more accommodating of individual differences, and would stop labeling every difference as a disorder?
[Other articles in category /brain] permanent link
Tue, 26 Apr 2022[ I hope this article won't be too controversial. My sense is that SML is moribund at this point and serious ML projects that still exist are carried on in OCaml. But I do observe that there was a new SML/NJ version released only six months ago, so perhaps I am mistaken. ]
It was apparent that SML had some major problems. When I encountered Haskell around 1998 it seemed that Haskell at least had a story for how these problems might be fixed.
A reader wrote to ask:
I was curious what the major problems you saw with SML were.
I actually have notes about this that I made while I was writing the first article, and was luckily able to restrain myself from writing up at the time, because it would have been a huge digression. But I think the criticism is technically interesting and may provide some interesting historical context about what things looked like in 1995.
I had three main items in mind. Every language has problems, but these three seemed to me be the deep ones where a drastically different direction was needed.
Notation for types and expressions in this article will be a mishmash of SML, Haskell, and pseudocode. I can only hope that the examples will all be simple enough that the meaning is clear.
Mutation
Reference type soundness
It seems easy to write down the rules for type inference in the presence of references. This turns out not to be the case.
The naïve idea was: for each type α there is a corresponding
type ref α, the type of memory cells containing a value of type
α. You can create a cell with an initialized value by using the
ref function: If v has type α, then ref v has type ref α
and its value is a cell that has been initialized to contain the value
v. (SML actually calls the type α ref, but the meaning is the same.)
The reverse of this is the operator ! which takes a reference of
type ref α and returns the referenced value of type α.
And finally,
if m is a reference, then you can overwrite the value stored in its
its memory cell by saying with m := v. For example:
m = ref 4 -- m is a cell containing 4
m := 1 + !m -- overwrite contents with 1+4
print (2 * !m) -- prints 10
The type rules seem very straightforward:
ref :: α → ref α
(!) :: ref α → α
(:=) :: ref α × α → unit
(Translated into Haskellese, that last one would look more like (ref α, α) → ()
or perhaps ref α → α → () because Haskell loves currying.)
This all seems clear, but it is not sound. The prototypical example is:
m = ref (fn x ⇒ x)
Here m is a reference to the identity function. The identity
function has type α → α, so variable m has type ref(α → α).
m := not
Now we assign the Boolean negation operator to m. not has type
bool → bool, so the types can be unified: m has type ref(α →
α). The type elaborator sees := here and says okay, the first
argument has type
ref(α → α), the second has type bool → bool, I can unify that, I
get α = bool, everything is fine.
Then we do
print ((!m) 23)
and again the type checker is happy. It says:
mhas typeref(α → α)!mhas typeα → α23has typeint
and that unifies, with α = int, so the result will have type
int. Then the runtime blithely invokes the boolean not
function on the argument 23. OOOOOPS.
SML's reference type variables
A little before the time I got into SML, this problem had been discovered and a patch
put in place to prevent it. Basically, some type variables were
ordinary variables, other types (distinguished by having names that began
with an underscore) were special “reference type variables”. The ref
function didn't have type α → ref α, it had type _α → ref _α.
The type elaboration algorithm was stricter when specializing
reference types than when specializing ordinary types. It was
complicated, clearly a hack, and I no longer remember the details.
At the time I got out of SML, this hack been replaced with a more complicated hack, in which the variables still had annotations to say how they related to references, but instead of a flag the annotation was now a number. I never understood it. For details, see this section of the SML '97 documentation, which begins “The interaction between polymorphism and side-effects has always been a troublesome problem for ML.”
After this article was published, Akiva Leffert reminded me that SML later settled on a third fix to this problem, the “value restriction”, which you can read about in the document linked previously. (I thought I remembered there being three different systems, but then decided that I was being silly, and I must have been remembering wrong. I wasn't.)
Haskell's primary solution to this is to burn it all to the ground. Mutation doesn't cause any type problems because there isn't any.
If you want something like ref which will break purity, you
encapsulate it inside the State monad or something like it, or else
you throw up your hands and do it in the IO monad, depending on what
you're trying to accomplish.
Scala has a very different solution to this problem, called covariant and contravariant traits.
Impure features more generally
More generally I found it hard to program in SML because I didn't understand the evaluation model. Consider a very simple example:
map print [1..1000]
Does it print the values in forward or reverse order? One could implement it either way. Or perhaps it prints them in random order, or concurrently. Issues of normal-order versus applicative-order evaluation become important. SML has exceptions, and I often found myself surprised by the timing of exceptions. It has mutation, and I often found that mutations didn't occur in the order I expected.
Haskell's solution to this again is monads. In general it promises
nothing at all about execution order, and if you want to force
something to happen in a particular sequence, you use the monadic bind
operator >>=. Peyton-Jones’ paper
“Tackling the Awkward Squad”
discusses the monadic approach to impure features.
Combining computations that require different effects (say, state
and IO and exceptions) is very badly handled by Haskell. The
standard answer is to use a stacked monadic type like IO ExceptionT a
(State b) with monad transformers. This requires explicit liftings
of computations into the appropriate monad. It's confusing and
nonorthogonal. Monad composition is non-commutative so that IO
(Error a) is subtly different from Error (IO a), and you may find
you have the one when you need the other, and you need to rewrite a
large chunks of your program when you realize that you stacked your
monads in the wrong order.
My favorite solution to this so far is algebraic effect systems. Pretnar's 2015 paper “An Introduction to Algebraic Effects and Handlers” is excellent. I see that Alexis King is working on an algebraic effect system for Haskell but I haven't tried it and don't know how well it works.
Overloading and ad-hoc polymorphism
Arithmetic types
Every language has to solve the problem of 3 + 0.5. The left
argument is an integer, the right argument is something else, let's
call it a float. This issue is baked into the hardware, which has two
representations for numbers and two sets of machine instructions for
adding them.
Dynamically-typed languages have an easy answer: at run time, discover that the left argument is an integer, convert it to a float, add the numbers as floats, and yield a float result. Languages such as C do something similar but at compile time.
Hindley-Milner type languages like ML have a deeper problem: What is the type of the addition function? Tough question.
I understand that OCaml punts on this. There are two addition
functions with different names. One, +, has type int × int → int. The other,
+., has type float × float → float. The expression 3 + 0.5 is
ill-typed because its right-hand argument is not an integer. You
should have written something like int_to_float 3 +. 0.5.
SML didn't do things this way. It was a little less inconvenient and a
little less conceptually simple. The + function claimed to
have type α × α → α, but this was actually a lie. At compile
time it would be resolved to either int × int → int
or to float × float → float. The problem expression above was still
illegal. You needed to write int_to_float 3 + 0.5, but at least
there was only one symbol for addition and you were still writing +
with no adornments. The explicit
calls to int_to_float and similar conversions still cluttered up the
code, sometimes severely
The overloading of + was a special case in the compiler.
Nothing like it was available to the programmer. If you wanted to
create your own numeric type, say a complex number, you could not overload
+ to operate on it. You would have to use |+| or some other
identifier. And you couldn't define anything like this:
def dot_product (a, b) (c, d) = a*c + b*d -- won't work
because SML wouldn't know which multiplication and addition to use;
you'd have to put in an explicit type annotation and have two versions
of dot_product:
def dot_product_int (a : int, b) (c, d) = a*c + b*d
def dot_product_float (a : float, b) (c, d) = a*c + b*d
Notice that the right-hand sides are identical. That's how you can tell that the language is doing something stupid.
That only gets you so far. If you might want to compute the dot product of an int vector and a float vector, you would need four functions:
def dot_product_ii (a : int, b) (c, d) = a*c + b*d
def dot_product_ff (a : float, b) (c, d) = a*c + b*d
def dot_product_if (a, b) (c, d) = (int_to_float a) * c + (int_to_float b)*d
def dot_product_fi (a, b) (c, d) = a * (int_to_float c) + b * (int_to_float d)
Oh, you wanted your vectors to maybe have components of different types? I guess you need to manually define 16 functions then…
Equality types
A similar problem comes up in connection with equality. You can write
3 = 4 and 3.0 = 4.0 but not 3 = 4.0; you need to say int_to_float 3
= 4.0. At least the type of = is clearer here; it really is
α × α → bool because you can compare not only numbers but also
strings, booleans, lists, and so forth. Anything, really, as
indicated by the free variable α.
Ha ha, I lied, you can't actually compare functions. (If you could, you could
solve the halting problem.) So the α in the type of = is not
completely free; it mustn't be replaced by a function type. (It is also
questionable whether it should work for real numbers, and I think SML
changed its mind about this at one point.)
Here, OCaml's +. trick was unworkable. You cannot have a different
identifier for equality comparisons at every different type. SML's
solution was a further epicycle on the type system. Some type
variables were designated “equality type variables”. The type of =
was not
α × α → bool
but
''α × ''α → bool
where ''α means that the α can be instantiated only for an
“equality type” that admits equality comparisons. Integers were an
equality type, but functions (and, in some versions, reals) were not.
Again, this
mechanism was not available to the programmer. If your type was a
structure, it would be an equality type if and only if all its members
were equality types. Otherwise you would have to write your own
synthetic equality function and name it === or something. If !!t!!
is an equality type, then so too is “list of !!t!!”, but this sort of
inheritance, beautifully handled in general by Haskell's type subclass
feature, was available in SML only as a couple of hardwired special cases.
Type classes
Haskell dealt with all these issues reasonably well with type classes,
proposed in Wadler and Blott's 1988 paper
“How to make ad-hoc polymorphism less ad hoc”.
In Haskell, the addition function now has type Num a ⇒ a → a → a
and the equality function has type Eq a ⇒ a → a → Bool. Anyone can
define their own instance of Num and define an addition function for
it. You need an explicit conversion if you want to add it to an
integer:
some_int + myNumericValue -- No
toMyNumericType some_int + myNumericValue -- Yes
but at least it can be done. And you can define a type class and overload toMyNumericType so that
one identifier serves for every type you can convert to your type. Also, a
special hack takes care of lexical constants with no explicit conversion:
23 + myNumericValue -- Yes
-- (actually uses overloaded fromInteger 23 instead)
As far as I know Haskell still doesn't have a complete solution to the
problem of how to make numeric types interoperate smoothly. Maybe
nobody does. Most dynamic languages with ad-hoc polymorphism will
treat a + b differently from b + a, and can give you spooky action
at a distance problems. If type B isn't overloaded, b + a will
invoke the overloaded addition for type A, but then if someone defines
an overloaded addition operator for B, in a different module, the
meaning of every b + a in the program changes completely because it
now calls the overloaded addition for B instead of the one for A.
In Structure and Interpretation of Computer Programs, Abelson and Sussman describe an arithmetic system in which the arithmetic types form an explicit lattice. Every type comes with a “promotion” function to promote it to a type higher up in the lattice. When values of different types are added, each value is promoted, perhaps repeatedly, until the two values are the same type, which is the lattice join of the two original types. I've never used anything like this and don't know how well it works in practice, but it seems like a plausible approach, one which works the way we usually think about numbers, and understands that it can add a float to a Gaussian integer by construing both of them as complex numbers.
[ Addendum 20220430: Phil Eaton informs me that my sense of SML's moribundity is exaggerated: “Standard ML variations are in fact quite alive and the number of variations is growing at the moment”, they said, and provided a link to their summary of the state of Standard ML in 2020, which ends with a recommendation of SML's “small but definitely, surprisingly, not dead community.” Thanks, M. Eaton! ]
[ Addendum 20221108: On the other hand, the Haskell Weekly News annual survey this year includes a question that asks “Which programming languages other than Haskell are you fluent in?” and the offered choices include C#, Ocaml, Scala, and even Perl, but not SML. ]
[Other articles in category /prog/haskell] permanent link
Mon, 25 Apr 2022
Unordered pairs and the axiom of binary choice
A few days ago I demanded a way to construct an unordered pair !![x, y]!! with the property that $$[x, y] = [y, x]$$ for all !!x!! and !!y!!, and also formulas !!P_1!! and !!P_2!! that would extract the components again, not necessarily in any particular order (since there isn't one) but so that $$[P_1([x, y]), P_2([x, y])] = [x, y]$$ for all !!x!! and !!y!!.
Several readers pointed out that such formulas surely do not exist, as their existence would prove the axiom of binary choice. This is a sort of baby brother of the infamous Axiom of Choice. The full Axiom of Choice (“AC”) can be stated this way:
Let !!\mathcal I!! be some index set.
Let !!\mathscr F!! be a family of nonempty sets indexed by !!\mathcal I!!; we can think of !!\mathscr F!! as a function that takes an element !!i \in \mathcal I !! and produces a nonempty set !!\mathscr F_i!!.
Then (Axiom of Choice) there is a function !!\mathcal C!! such that, for each !!i\in \mathcal I!!, $$\mathcal C(i) \in \mathscr F_i.$$
(From this it also follows that $$\{ \mathcal C(i) \mid i\in \mathcal I \},$$ the collection of elements selected by !!\mathcal C!!, is itself a set.)
This is all much more subtle than it may appear, and was the subject of a major investigation between 1914 and 1963. The standard axioms of set theory, called ZF, are consistent with the truth of Axiom of Choice, but also consistent with its falsity. Usually we work in models of set theory in which we assume not just ZF but also AC; then the system is called ZFC. Models of ZF where AC does not hold are very weird. (Models where AC does hold are weird also, but much less so.)
One can ask about all sorts of weaker versions of AC. For example, what if !!\mathcal I!! and !!\mathscr F!! are required to be countable? The resulting “axiom of countable choice”, is strictly weaker than AC: ZFC obviously includes countable choice as a restricted case, but there are models of ZF that satisfy countable choice but not AC in its fullest generality.
Rather than restricting the size of !!\mathscr F!! itself, we can consider what happens when we restrict the size of its elements. For example, what if !!\mathscr F!! is a collection of finite sets? Then we get the “axiom of finite choice”. This is also known to be independent of ZF.
What if we restrict the elements of !!\mathscr F!! yet further, so that !!\mathscr F!! is a family of sets, each of which has exactly two elements? Then we have the “axiom of binary choice”. Finite choice obviously implies binary choice. But the converse implication does not hold. This is not at all obvious. Binary choice is known to imply the corresponding version of binary choice in which each member of !!\mathscr F!! has exactly four elements, and is known not to imply the version in which each member has exactly three elements. (Further details in this Math SE post.)
But anyway, readers pointed out that, if there were a first-order formula !!P_1!! with the properties I requested, it would prove binary choice. We could understand each set !!\mathscr F_i!! as an unordered pair !![a_i, b_i]!! and then
$$ \{ \langle i, P_1([a_i, b_i])\rangle \mid i\in \mathcal I \},$$
which is the function !!i\mapsto P_1(\mathscr F_i)!!, would be a choice function for !!\mathscr F!!. But this would constitute a proof of binary choice in ZF, which we know is impossible.
Thanks to Carl Witty, Daniel Wagner, Simon Tatham, and Gareth McCaughan for pointing this out.
[Other articles in category /math] permanent link
Thu, 21 Apr 2022
Pushing back against contract demands is scary but please try anyway
A year or two ago I wrote a couple of articles about the importance of pushing back against unreasonable contract provisions before you sign the contract. [1: Strategies] [2: Examples]
My last two employers have unintentionally had deal-breaker clauses in contracts they wanted me to sign before starting employment. Both were examples I mentioned in the previous article about things you should never agree to. One employer asked me to yield ownership of my entire work product during the term of my employment, including things I wrote on my own time on my own equipment, such as these blog articles. I think the employer should own only the things they pay me to create, during my working hours.
When I pointed this out to them I got a very typical reply: “Oh, we don't actually mean that, we only want to own things you produced in the scope of your employment.” What they said they wanted was what I also wanted.
This typical sort of reply is almost always truthful. That is all they want. It's important to realize that your actual interests are aligned here! The counterparty honestly does agree with you.
But you mustn't fall into the trap of signing the contract anyway, with the idea that you both understand the real meaning and everything will be okay. You may agree today, but that can change. The company's management or ownership can change. Suppose you are an employee of the company for many years, it is very successful, it goes public, and the new Board of Directors decides to exert ownership of your blog posts? Then the oral agreement you had with the founder seven years before will be worth the paper it is not printed on. The whole point of a written contract is that it can survive changes of agency and incentive.
So in this circumstance, you should say “I'm glad we are in agreement on this. Since you only want ownership of work produced in the scope of my employment, let's make sure the contract says that.”
If they continue to push back, try saying innocently “I don't understand why you would want to have X in the written agreement if what you really want is Y.” (It could be that they really do want X despite their claims otherwise. Wouldn't it be good to find that out before it was too late to back out?)
Pushing back against incorrect contract clauses can be scary. You want the job. You are probably concerned that the whole deal will fall through because of some little contract detail. You may be concerned that you are going to get a reputation as a troublemaker before you even start the job. It's very uncomfortable, and it's hard to be brave. But this is a better-than-usual place to try to be brave, not just for yourself.
If the employer is a good one, they want the contract to be fair, and if the contract is unfair it's probably by accident. But they have a million other things to do other than getting the legal department to fix the contract, so it doesn't get fixed, simply because of inertia.
If, by pushing back, you can get the employer to fix their contract, chances are it will stay fixed for everyone in the future also, simply because of inertia. People who are less experienced, or otherwise in a poorer negotiating position than you were, will be able to enjoy the benefits that you negotiated. You're negotiating not just for yourself but for the others who will follow you.
And if you are like me and you have a little more power and privilege than some of the people who will come after, this is a great place to apply some of it. Power and privilege can be used for good or bad. If you have some, this is a situation where you can use some for good.
It still scary! In this world of giant corporations that control everything, each of us is a tiny insect, hoping not to be heedlessly trampled. I am afraid to bargain with such monsters. But I know that as a middle-aged white guy with experience and savings and a good reputation, I have the luxury of being able to threaten to walk away from a job offer over an unfair contract clause. This is an immense privilege and I don't want to let it go to waste.
We should push back against unfair conditions pressed on us by corporations. It can be frightening and risky to do this, because they do have more power than we do. But we all deserve fairness. If it seems too risky to demand fair treatment for yourself, perhaps draw courage from the thought that you're also helping to make things more fair for other people. We tiny insects must all support one another if we are to survive with dignity.
[ Addendum 20220424: A correspondent says: “I also have come to hate articles like yours because they proffer advice to people with the least power to do anything.” I agree, and I didn't intend to write another one of those. My idea was to address the article to middle-aged white guys like me, who do have a little less risk than many people, and exhort them to take the chance and try to do something that will help people. In the article I actually wrote, this point wasn't as prominent as I meant it to be. Writing is really hard. ]
[Other articles in category /law] permanent link
Sun, 17 Apr 2022I just went through an extensive job search, maybe the most strenuous of my life. I hadn't meant to! I wrote a blog post asking where I should apply for Haskell jobs, and I thought three or four people would send suggestions. Instead I was contacted by around fifty people, many of whom ran Haskell-related companies and invited me to apply, after it hit #1 on Hacker News. So I ran with it.
I had written:
At some point I'll need another job. I would really like it to be Haskell programming…
One question that came up in several interviews was “why do you want to learn Haskell?” I had a lot of trouble with this question, and often rambled about the answer to some other question instead. A couple of times I started by saying “well, I've been interested in Haskell for about twenty years…” (does not answer the question) and then I'd go on about how I got interested in Haskell in the first place (also does not answer the question).
Sometimes this did touch on some deeper reasons. By the time I learned Haskell I had been programming in SML for a while, and it was apparent that SML had some major problems. When I encountered Haskell around 1998 it seemed that Haskell at least had a story for how these problems might be fixed.
But why did I get interested in SML? I'm not sure how I encountered it but by that time I had been programming for ten or fifteen years and it appeared that strong type systems were eventually going to lead to big improvements. Programming is still pretty crappy, but it is way better than it was when I started.One reason is that languages are much better. I'm interested in programming and in how to make it less crappy.
But none of this really answers the question. Yes, I've wanted to know more for decades. But the question is why do I want to learn Haskell? Sometimes these kinds of questions do have a straightforward answer. For example, “I think it will be a good career move”. That was not the answer in this case. Nor “I think it will pay me a lot of money” or “I'm interested in smart contracts and a lot of smart contract work is done in Haskell”.
I'm remembering something written I think by Douglas Hofstadter (but possibly Daniel Dennett? John Haugeland?) where you have a person (or AI program) playing chess, and you ask them “Why did you move the knight to e4?” The chess player answers “To attack the bishop on g5.”
“Why did you want to attack the bishop on g5?”
“That bishop is impeding development of my kingside pieces, and if I could get rid of it I could develop a kingside attack.”
“Why do you want to develop a kingside attack?”
“Uhh… if it is effective enough it could force the other player to resign.”
“But why do you want to force the other player to resign?”
“Because that's how you win a game of chess, dummy.”
“Why do you want to win the game?”
“…”
You can imagine this continuing yet further, but eventually it will reach a terminal point at which the answer to “Why do you want to…” is the exasperated cry “I just do!” (Or the first person turns five years old and grows out of the why-why-why phase.)
I wonder if the computer also feels exasperation at this kind of questioning? But it has an out; it can terminate the questions by replying “Because that's what I was programmed to do”. Anyway when people asked why I wanted to learn Haskell, I felt that exasperation. Sometimes I tried using the phrase “it's a terminal goal”, but I was never sure that my meaning was clear. Even at the end of the interviewing process I didn't have a good answer ready, and was still stammering out answers like “I just wanna know!”
(I realize now that “because that's what I was programmed to do” sometimes works for non-artifical intelligences also. When Katara was small she asked me why I loved her, and I answered “because that's how I'm made.”)
Now that the job hunt is all over, I think I've thought of a better reply to “why do you want to learn Haskell, anyway?” that might be easier to understand and which I like because it seems like such a good way to explain myself to strangers. The new answer is:
I'm the kind of person who gets on a bus and takes it to the last stop, just to see where it goes.
This is excellent! It not only explains me to other people, it helps explain me to myself. Of course I knew this about myself before but putting it into a little motto like that makes it easier to understand, remember, and reason from. It's useful to understand why you do the things you do and why you want the things you want, and this motto helps me by compacting a lot of information about myself into a pithy summary.
One thing I like about the motto is that it is not just metaphorically true. It's a good metaphor for the Haskell thing. I am still riding the Haskell bus to see where it ends up. But also, I do literally get on buses just to find out where they go.
In Haifa about twenty years ago, I got on a bus to see where it would go. I rode for a while, looking out the window, seeing and thinking many things. When I saw something that looked like a big open-air market I got out to see what it was about. It was a big open-air market, not like anything I had seen before. It was just the kind of thing I wanted to see when I visited a foreign country, but wouldn't have known to ask. Sometimes “what can I see that we don't have where I come from” works, but often the things you don't have at home are so ordinary where you are that your host doesn't think to show them to you. At the Haifa market, I remember seeing fresh dates for the first time. (In the U.S. they are always dried.) I bought some; they were pretty good even though they looked like giant cockroaches.
Another wonderful example of something I wanted to see but didn't know about until I got to it was Reg Hartt's Cineforum. Reg Hartt is a movie enthusiast in Toronto who runs a private movie theatre in his living room. Walking around Toronto one day I saw a poster advertising one of his shows, featuring Disney and Warner Brothers cartoons that had been banned for being too racist, and the post was clearly the call of fate. Of course I'm going to attend a cartoon show in some stranger's living room in Toronto. Hartt handed me a beer on the way in and began a long, meandering rant about the history of these cartoons. One guy in the audience interrupted “just start the show” and Hartt shot back “This is the show!” Reg Hartt is my hero.
In Lisbon I was walking around at random and happened on the train station, so I went in and got on the first train I saw and took it to the end of the line, which turned out to be in Cascais. I looked around, had lunch, and spent time feeding a packet of sugar to some ants. It was a good day.
In Philadelphia I often take the #42 bus, which runs west on Walnut Street from downtown to where I live. The #9 bus runs along the same route part of the way, but before it gets to my neighborhood it turns right and goes somewhere else called Andorra. After a few years of wondering what Andorra was like I got on the #9 bus to find out. It's way out at the city limits, in far Roxborough. Similarly I once took the #34 trolley to the end of the line to see where it went. There was a restaurant there called Bubba's Bar-B-Que, which was pretty good. Since then it has become a Jamaican restaurant which is also pretty good. I have also taken the #42 itself to the end of the line to learn where it turns around.
I once drove the car to Stenton Avenue and drove the whole length of Stenton Avenue, because I kept hearing about Stenton Avenue but didn't know where it was or what was on it.
I used to take SEPTA, the Philadelphia commuter rail, to Trenton, because that was the cheapest way to get to New York. Along the way the train would pass through a station called Andalusia but it would never stop there. The conductor would come through the train asking if anyone wanted to debark at Andalusia but nobody ever did. And nobody was ever waiting on the Andalusia platform, so the train had no reason to stop. I wondered for years what was in Andalusia. Once I got a car, I drove there to see what there was. It was a neighborhood, and I climbed down to the (no longer used) SEPTA station to poke around. Going in the other direction on SEPTA I have visited Marcus Hook and Wilmington just to see what they were like.
One especially successful trip was a few years ago when I decided to drive to Indianapolis. When I told people I was taking a road trip to Indianapolis they would ask “why, what is in Indianapolis?” I answered that I didn't know, and I was going there to find out. And when I did get there I found out that Indianapolis is really cool! I enjoyed walking around their central square which has a very cool monument and also a bronze statue of America's greatest president, William Henry Harrison. I had planned to stay in Indianapolis longer, but while I was eating breakfast I learned that the Indiana state fair was taking place about fifteen minutes south, and I had never been to a state fair, so I went to see that. I saw many things, including an exhibition of antique tractors and a demonstration of veterinary surgery, and I ate chocolate-covered bacon on a stick. After I got back from Indianapolis I had an answer to the question “why, what is in Indianapolis?” The answer was: The Indiana State Fair. (I have a blog post I haven't finished about all the other stuff I saw on that trip, and maybe someday I will finish it.)
On another road trip I decided to drive in a loop around Chesapeake Bay, just to see what there was to see. I started in New Castle which is noteworthy for being the center of the only U.S. state border that is a circular arc. I ate Smith Island cake. I drove over the Chesapeake Bay Bridge-Tunnel-Bridge-Tunnel-Bridge which was awesome, totally awesome, and stopped in the middle for an hour to look around. I made stops in towns called Onancock and Bivalve just for the names. I blundered into the Blackwater National Wildlife Refuge, another place I would never have planned to visit but I'm glad I visited. I took the Oxford-Bellevue ferry which has been running between Oxford and Bellevue since 1683. I'm not much for souvenirs, but my Oxford-Bellvue Ferry t-shirt is a prized possession.
When I was a small child my parents had a British Monopoly board and I was fascinated by the place names. When I got my first toy octopus I named it Fenchurch after Fenchurch Street Station. And when I visited London I took the Underground to the Fenchurch Street stop one night to see what was there. It turned out that near Fenchurch Street is a building that is made inside-out. It has all the fire stairs and HVAC ducts on the outside so that the inside can be a huge and spacious atrium. I had had no idea this building even existed and I probably wouldn't have found out if I hadn't decided to visit Fenchurch Street for no particular reason other than to see what was there.
In Vienna I couldn't sleep, went out for a walk at midnight, and discovered the bicycle vending machines. So I rented a bicycle and biked around Vienna and ran across the wacky Hundertwasserhaus which I had not heard of before. Amazing! In Cleveland I went for a long walk by the river past a lot of cement factories and things like that, but eventually came out at the West Side Market. Then I went into a café and asked if there was a movie theatre around. They said there wasn't but they sometimes projected movies on the wall and would I like to see one? And that's how I saw Indiscreet with Gloria Swanson. I was in Cleveland again a few years ago and wandering around at night I happened across the Little Kings Lounge. The outside of the Little Kings Lounge frightened me but I eventually decided that spending the rest of my life wondering what it was like inside would be worse than anything that was likely to happen if I did go in. The inside was much less scary than the outside. There was a bar and a pool table. I drank apple-flavored Crown Royal. They had a sign announcing their proud compliance with the Cleveland indoor smoking ban, the most sarcastic sign I've ever seen.
In Taichung I spent a lot of time at the science museum, but I also spent a lot of time walking to and from the science museum through some very ordinary neighborhoods, and time walking around at random at night. The Taichung night market I had been to fifteen years before was kind of tired out, but going in a different direction I stumbled into a new, fresher night market. In Hong Kong I was leafing through my guidebook, saw a picture of the fish market on Cheung Chau, and decided I had to go see it. I took the ferry to Cheung Chau with no idea what I would find or where I would stay, and spent the weekend there, one of the greatest weekends of my life. I did find the fish market, and watched a woman cutting the heads off of live fish with a scissors. Spaulding Gray talks about searching for a “perfect moment” and how he couldn't leave Cambodia because he hadn't yet had his perfect moment. My first night on Cheung Chau I sat outside, eating Chinese fish dinner and drinking Negro Modelo, watching the fishing boats come into the harbor at sunset, and I had my perfect moment.
A few months back I wrote about going to the Pennsylvania-Delaware-Maryland border to see what it was like. You can read about that if you want. A few years back I biked out to Hog Island, supposedly the namesake of the hoagie, to find out what was there. It turned out there is a fort, and that people go there with folding chairs to fish in the Delaware River. On the way I got to bike over the George C. Platt Bridge, look out over South Phildelphia (looked good, smelled bad) and pick up a German army-style motorcycle helmet someone had abandoned in the roadway. Some years later I found out that George Platt was buried in a cemetery that was on the way to my piano lesson, so I stopped in to visit his grave. Most interesting result of that trip: Holy Cross cemetery numbers their zones and will tell you which zone someone is in, but it doesn't help much because the zones are not arranged in order.
I was on a cruise to Alaska and the boat stopped in Skagway for a few hours before turning around. I walked around Skagway for a while but there was not much to see; I thought it was a dumpy tourist trap and I walked back to the harbor. There was a “water taxi” to Haines so I went to Haines to see what was in Haines. The water taxi trip was lovely, I looked out at the fjords and the bald eagles. Haines was charming and pretty. In Haines I enjoyed the Alaska summer weather, saw the elementary school, bought an immersion heater at a hardware store, and ate spoon bread at The Bamboo Room restaurant. Then I took the water taxi back again. Years later when I returned to Skagway, this time with Lorrie, I already knew what to do. We went directly to the next dock over to get on the water taxi and get some spoon bread.
Sometimes I do have a destination in mind. When I was in Paris my hosts asked me if there was anything I wanted to see and I said I would like to visit the Promenade Plantée, which I had read about once in some magazine. My hosts had not heard of the Promenade Plantée but I did get myself there and walked the whole thing. (We have something like it in Philadelphia now but it's not as good, yet.) What did I see? A lot of plants, French people, and a view of Paris apartment buildings that is different from the one I would have gotten from street level. Sometimes I do tourist stuff: I spent hours at the Sagrada Família, the Giant's Causeway, and the Holy Sepulchre, all super-interesting. But when I go somewhere my main activity is: walk around at random and see what there is. In Barcelona I also happened across September 11th Street, in Belfast I accidentally attended the East Belfast Lantern Festival, and in Jerusalem I stopped in an internet café where each keyboard was labeled in four different scripts. (Hebrew, Latin, Cyrillic, and Arabic.)
Today a friend showed me this funny picture:
Maybe so! But as the kind of person who gets on a bus and takes it to the last stop, just to see where it goes, I'm fully prepared for the possibility that the last stop is a dead end. That's okay. As my twenty-year-old self was fond of saying “to travel is better than to arrive”. The point of the journey is the journey, not the destination.
[ Addendum 20220422: I think I heard about the Promenade Plantée from this Boston Globe article from 2002. ]
[ Addendum 20220422: Apparently I need to get back to Haines because there is a hammer museum I should visit. ]
[ Addendum 20220426: A reader asked for details of my claim that “SML had some major problems”, so I wrote it up: What was wrong with SML? ]
[Other articles in category /brain] permanent link
Sat, 16 Apr 2022
Notable items missing from English Wikipedia
Want to write a new Wikipedia article but can't think of a subject not already covered? Here are some items that are notable and should be easy to source:
Richard Dattner, U.S. proponent of the “Adventure Playground” movement and designer of playgrounds, including the famous one in New York's Central Park near 67th Street.
Publications International v. Meredith Corp, U.S. federal law case that held that while cookbooks are protected by copyright, the recipes themselves are not.
Dorrance H. Hamilton Charitable Trust. Hamilton was heir to the Campbell's Soup fortune and a noted philanthropist. Her name is on many buildings and other institutions around the Philadelphia area. Wikipedia does have an article about Hamilton, but it is sadly incomplete and does not mention the Trust.
Victor Dubourg, a journalist who angered Louis XV with his criticism, was induced to visit France under some pretext, and then was kidnapped and imprisoned in Mont-Saint-Michel for the rest of his life. Stories about the conditions of his confinement vary, ranging from the awful and terrifying to the terrifying and awful. (French Wikipedia)
Knox v. United States. Knox was convicted of possession of child pornography for owning videotapes of girls in leotards and swimsuits but not engaged in sexual acts or even simulated acts. The U.S. Solicitor General, in a confession of error, joined in Knox's plea to the Supreme Court to vacate the conviction. The Court agreed and remanded the case to the lower court — which convicted him again. Knox appealed the second conviction, but the Solicitor General again changed their view and this time supported the conviction!
Branly Cadet, U.S. sculptor, created the Octavius V. Catto memorial at Philadelphia City Hall, and the Jackie Robinson sculpture at Dodger Statdium.
The Rowland Company, founded 1732, oldest still-operating manufacturing company in the U.S.. There are older businesses, but they are mostly taverns and inns.
Beth Irene Stroud, ordained Methodist minister who came out as lesbian and was consequently defrocked in 2004. The United Methodist Church “affirms that all people are of sacred worth and are equally valuable in the sight of God” but apparently draws the line at lesbian ministers.
[Other articles in category /wikipedia] permanent link
Fri, 15 Apr 2022A great deal of attention has been given to the encoding of ordered pairs as sets. I lately discussed the usual Kuratowski definition:
$$\langle a, b \rangle = \{\{a\}, \{a, b\}\}$$
but also the advantages of the ealier Wiener definition:
$$\langle a, b \rangle = \{\{\{a\},\emptyset\}, \{ \{ b\}\}\}$$
One advantage of the Wiener construction is that the Kuratowski pair has an odd degenerate case: if !!a=b!! it is not really a pair at all, it's a singleton. The Wiener pair always has exactly two elements.
Unordered pairs don't get the same attention because the implementation is simple and obvious. The unordered pair !![a, b]!! can be defined to be !! \{a, b\}!! which has the desired property. The desired property is:
$$[a, b] = [c, d] \\ \text{if and only if} \\ a=c \land b=d\quad \text{or} \quad a=d\land b=c $$
But the implementation as !!\{a, b\}!! suffers from the same drawback as the Kuratowski pair: if !!a=b!!, it's not actually a pair!
So I wonder:
Is there a set !![a, b]!! with the following properties:
!![a, b] = [c, d]!! if and only if !!a=c \land b=d!! or !! a=d\land b=c!!
!![a, b]!! has exactly two elements for all !!a!! and !!b!!
Put that way, a solution is $$ [a, b] = \{ \{ a, b \}, \emptyset \}\tag{$\color{darkred}{\spadesuit}$}$$ but that is very unsatisfying. There must be some further property I want the solution to have, which is not possessed by !!(\color{darkred}{\spadesuit})!!, but I don't know yet what it is. Is it that I want it to be possible to extract the two elements again? I am not sure what that means, but whatever it means, if !!\{ a, b\}!! does it, then so does !!(\color{darkred}{\spadesuit})!!.
But that does also suggest another property that neither of those enjoys:
There should be formulas !!F_1!! and !!F_2!! such that for all !![a, b]!!:
- !!F_1([a, b]) = a!! or !!b!!
- !!F_2([a, b]) = a!! or !!b!!
- !!F_1([a, b]) = F_2([a, b])!! if and only if !!a=b!!
I think this can be abbreviated to simply:
!![F_1([a, b]), F_2([a, b])] = [a, b]!!
There may be some symmetry argument why there are no such formulas, but if so I can't think of it offhand. Perhaps further consideration of !![a, a]!! will show that what I want is incoherent.
Today is the birthday of Leonhard Euler. Happy 315th, Lenny!
[ Addendum 20220422: Several readers pointed out that the !!F_i!! formulas are effectively choice functions, so there can be no simple solution. Further details. ]
[Other articles in category /math] permanent link
Mon, 11 Apr 2022
At last, an internet commenter I can agree with
Browsing around Math StackExchange today, I encountered this question, ‘Unique’ doesn't have a unique meaning, which pointed out that the phrase “Every boy has a unique shirt” is at least confusing. (Do all the boys share a single shirt?)
“Aha,” I said. “I know what's wrong there: it should be ‘every boy has a distinct shirt’.” I scrolled down to see if I should write that as an answer. But I noticed that the question had been posted in 2012, and guessed that probably someone had already said what I was going to say. Indeed, when I looked at the comments, I saw that the third one said:
If I meant that no shirt belongs to two boys, I would say "every boy has a distinct shirt".
Okay, that saves me the trouble of replying at least. I went to click the upvote button on the comment, but there was no button,
because
the comment had been posted, in August of 2012, by me.
[Other articles in category /math/se] permanent link
Mon, 04 Apr 2022If you're losing the game, try instead playing the different game that is one level up.
I remembered a wonderful example of this: The Chen Sheng and Wu Guang Uprising of 209 BCE. As Wikipedia tells it:
[Chen Sheng] was a military captain along with Wu Guang when the two of them were ordered to lead 900 soldiers to Yuyang to help defend the northern border against Xiongnu. Due to storms, it became clear that they could not get to Yuyang by the deadline, and according to law, if soldiers could not get to their posts on time, they would be executed. Chen Sheng and Wu Guang, believing that they were doomed, led their soldiers to start a rebellion.
The uprising was ultimately unsuccessful, but it at least bought Chen Sheng and Wu Guang some time.
[Other articles in category /history] permanent link
Sun, 03 Apr 2022When I used to work for ZipRecruiter I would fly cross-country a few times a year to visit the offices. A couple of those times I spent the week hanging around with a business team to learn what what they did and if there was anything I could do to help. There were always inspiring problems to tackle. Some problems I could fix right away. Others turned into bigger projects. It was fun. I like learning about other people's jobs. I like picking low-hanging fruits. And I like fixing things for people I can see and talk to.
One important project that came out of one of those visits was: whenever we took on a new customer or partner, an account manager would have to fill out a giant form that included all the business information that our system would need to know to handle the account.
But often, the same customer would have multiple “accounts” to represent different segments of their business. The account manager would create an account that was almost exactly like the one that already existed. They'd carefully fill out the giant form, setting all the values for the new account to whatever they were for the account that already existed. It was time-consuming and tedious, and also error-prone.
The product managers hadn't wanted to solve this. In their minds, this giant form was going to go away, so time spent on it would be wasted. They had grand plans.
“Okay suppose,” I said, talking to the Account Management people who actually had to fill out this form, “on the page for an existing account, there was a button you could click that said “make another account just like this one”, and it wouldn't actually make the account, it would just take you to the same form as always, but the form would be already filled in with the current values for the account you just came from? Then you'd only need to change the few items that you wanted to change.”
The account managers were in favor of this idea. It would save time and prevent errors.
Doing this was straightforward and fairly quick. The form was generated by a method in the application. I gave the method an extra optional parameter, an account ID, that told the method to pre-fill the form with the data for the specified account. The method would do a single extra database lookup, and pass the resulting data to the page. I had to make a large number of changes to the giant form to default its fields to the existing-account data if that was provided, but they were completely routine. I added a link on the already-existing account information pages, to call up the form and supply the account ID for the correct pre-filling. I don't remember there being anything tricky. It took me a couple of days, and probably saved the AM team hundreds of hours of toil and error.
Product's prediction that the giant form would soon go away did not come to pass for any reasonable interpretation of “soon”. (What a surprise!)
This is the kind of magic that sometimes happens when an engineer gets to talk directly to the users to find out what they are doing. When it works, it works really well. ZipRecruiter was willing to let me do this kind of work and then would reward me for it.
But that wasn't my favorite project from that visit. My favorite was the new menu item I added for an account manager named Olaf.
Every month, Olaf had to produce a report that included how many “conversion transitions” had occurred in the previous month. I don't remember what the “conversion transitions” were or what they were actually called. It was probably some sort of business event, maybe something like a potential customer moving from one phase of the sales process to another. All I needed to know then, and all you need to know now is: they were some sort of events, each with an associated date, and a few hundred were added to a database each month.
There was a web app that provided Account Management with information about the conversion transitions. Olaf would navigate to the page about conversion transitions and there would be a form for filtering conversion transitions in various ways: by customer name, and also a menu with common date filtering choices: select all the conversion transitions from the current month, select the conversion transitions of the last thirty days, or whatever. Somewhere on the back end this would turn into a database query, and then the app would display “317 conversion transitions selected” and the first pageful of events.
Around the beginning of a new month, say August, Olaf would need to write his July report. He would visit the web app and it would immediately tell him that there had been 9 events so far in August. But Olaf needed the number for July. But there was no menu item for July. There was a menu item for “last 30 days”, but that wasn't what he wanted, since it omitted part of July and included part of August,
What Olaf would do, every month, was select “last 60 days”, page forward until he got to the page with the first conversion transition from July, and hand-count the events on that page. Then he would advance through the pages one by one, counting events, until he got to the last one from July. Then he would write the count into his report.
I felt a cold fury. The machine's job is to collate information for reports. It was not doing its job, and to pick up the slack, Olaf, a sentient being, was having to pretend to be a machine. Also, since my job is to make sure the machine is doing its job, this felt to me like an embarrassing professional failure.
“Olaf,” I said, “I am going to fix this for you.”
Fixing it was not as simple as I had expected. But it wasn't anything out of the ordinary and I did it. I added the new menu item, and then had to plumb the desired functionality through three or four levels of software, maybe through some ad-hoc network API, into whatever was actually querying the database, so that alongside the “last 30 days” and “current month” queries, the app also knew how to query for “previous month”.
Once this was done, Olaf would just select “previous month” from the menu, and the first page of July conversion transitions would appear, with a display “332 conversion transitions selected”. Then he could copy the number 332 into his report without having to look at anything else.
From a purely business perspective, this project probably cost the company money. The programming, which was in a part of the system I had never looked at before, took something like a full day of my time including the code changes, testing, and deployment. Olaf couldn't have been spending more than an hour a month on his hand count of conversion transitions. So the cost-benefit break-even point was at least several months out, possibly many years depending on how much Olaf's time was worth.
But the moral calculus was in everyone's favor. What is money, after all, compared with good and evil? If ZipRecruiter could stop trampling on Olaf's soul every month, and the only cost was a few hours of my time, that was time and money well-spent making the world a better place. And one reason I liked working for ZipRecruiter and stayed there so long was that I believed the founders would agree.
[Other articles in category /tech] permanent link
Sat, 26 Mar 2022While writing the recent article about Devika Icecreamwala (born Patel) I acquired the list of most common U.S. surnames. (“Patel” is 95th most common; there are about 230,000 of them.) Once I had the data I did many various queries on it, and one of the things I looked for was names with no vowels. Here are the results:
| name | rank | count |
|---|---|---|
| NG | 1125 | 31210 |
| VLK | 68547 | 287 |
| SMRZ | 91981 | 200 |
| SRP | 104156 | 172 |
| SRB | 129825 | 131 |
| KRC | 149395 | 110 |
| SMRT | 160975 | 100 |
It is no surprise that Ng is by far the most common. It's an English transcription of the Cantonese pronunciation of 吳, which is one of the most common names in the world. 吳 belongs to at least twenty-seven million people. Its Mandarin pronunciation is Wu, which itself is twice as common in the U.S. as Ng.
I suspect the others are all Czech. Vlk definitely is; it's Czech for “wolf”. (Check out the footer of the Vlk page for eighty other common names that all mean “wolf”, including Farkas, López, Lovato, Lowell, Ochoa, Phelan, and Vuković.)
Similarly Smrz is common enough that Wikipedia has a page about it. In Czech it was originally Smrž, and Wikipedia mentions Jakub Smrž, a Czech motorcycle racer. In the U.S. the confusing háček is dropped from the z and one is left with just Smrz.
The next two are Srp and Srb. Here it's a little harder to guess. Srb means a Serbian person in several Slavic languages, including Czech and it's not hard to imagine that it is a Czech toponym for a family from Serbia. (Srb is also the Serbian word for a Serbian person, but an immigrant to the U.S. named Srb, coming from Czechia, might fill out the immigration form with “Srb” and might end up with their name spelled that way, whereas a Serbian with that name would write the unintelligible Срб and would probably end up with something more like Serb.) There's also a town in Croatia with the name Srb and the surname could mean someone from that town.
I'm not sure whether Srp is similar. The Serbian-language word for the Serbian language itself is Srpski (српски), but srp is also Slavic for “sickle” and appears in quite a few Slavic agricultural-related names such as Sierpiński. (It's also the name for the harvest month of August.)
Next is Krc. I guessed maybe this was Czech for “church” but it seems that that is kostel. There is a town south of Prague named Krč and maybe Krc is the háčekless American spelling of the name of a person whose ancestors came from there.
Last is Smrt. Wikipedia has an article about Thomas J. Smrt but it doesn't say whether his ancestry was Czech. I had a brief fantasy that maybe some of the many people named Smart came from Czech families originally named Smrt, but I didn't find any evidence that this ever happened; all the Smarts seem to be British. Oh well.
[ Bonus trivia: smrt is the Czech word for “death”, which we also meet in the name of James Bond's antagonist SMERSH. SMERSH was a real organization, its name a combination of смерть (/smiert/, “death”) and шпио́нам (/shpiónam/, “to spies”). Шпио́нам, incidentally, is borrowed from the French espion, and ultimately akin to English spy itself. ]
[ Addenda 20220327: Thanks to several readers who wrote to mention that Smrž is a morel and Krč is (or was) a stump or a block of wood, I suppose analogous to the common German name Stock. Petr Mánek corrected my spelling of háček and also directed me to KdeJsme.cz, a web site providing information about Czech surnames. Finally, although Smrt is not actually a shortened form of Smart I leave you with this consolation prize. ]
[Other articles in category /lang/etym] permanent link
For a long while I've been planning an article about occupational surnames, but it's not ready and this is too delightful to wait.
There is, in California, a dermatologist named:
Awesome.
“Wala” is an Indian-language suffix that indicates a person who deals in, transports, or otherwise has something to do with the suffixed thing. You may have heard of the famous dabbawalas of Mumbai. A dabba is a lunchbox, and in Mumbai thousands of dabbawalas supply workers with the hot lunches that were cooked fresh in the workers’ own homes that morning.
Similarly, an icecreamwala is an ice cream vendor. Apparently there was some point during the British Raj that the Brits went around handing out occupational surnames, and at least one ice cream wala received the name Icecreamwala.
It is delightful enough that Dr. Icecreamwala exists, but the story gets better. Icecreamwala is her married name. She was born Devika Patel. Some people might have stuck with Patel, preferring the common and nondescript to the rare and wonderful. Not Dr. Icecreamwala! She not only changed her name, she embraced the new one. Her practice is called Icecreamwala Dermatology and their internet domain is icecreamderm.com.
Ozy Brennan recently considered the problem of which parent's surnames to give to the children. and suggested that they choose whichever is coolest. Dr. Icecreamwala appears to be in agreement.
[ Addendum 20220328: Vaibhav Sagar informs me that Icecreamwala is probably rendered in Hindi as आइसक्रीमवाला. ]
[Other articles in category /misc] permanent link
Fri, 25 Mar 2022I tried playing Red Dead Redemption 2 last week. I was a bit disappointed because I was hoping for Old West Skyrim but it's actually Old West GTA. I'm not sure how long I will continue.
Anyway, I acquired a new horse and was prompted to name it. My first try, “Pongo”, was rejected by the profanity filter. Puzzled, I supposed I had mistyped and included a ZWNJ or something. No, it was rejecting "Pongo”.
The only meaning I know for “Pongo” is that it is the name of the daddy dog in 101 Dalmatians. So I asked the Goog. The Goog shrugged and told me that was the only Pongo it knew also.
Steeling myself, I asked Urban Dictionary, preparing to learn that Pongo was obscene, racist, or probably both. Urban Dictionary told me that “Pongo” is 1900-era Brit slang for a soldier. (Which I suppose explains its appearance as the name of the dog.) Nothing obscene or racist.
I'm stumped. I forget what I ended up naming the horse.
[ Addendum 20220521: Apparently I'm not the first person to be puzzled by this. ]
[Other articles in category /lang] permanent link
Mon, 14 Mar 2022Yesterday I discussed /dev/full and asked why there wasn't a
generalization of it, and laid out out some very 1990s suggestions that I
have had in the back of my mind since the 1990s. I ended by
acknowledging that there was probably a more modern solution in user
space:
Eh, probably the right solution these days is to
LD_PRELOADa complete mock filesystem library that has any hooks you want in it.
Carl Witty suggested that there is a more modern solution in userspace, FUSE, and Leah Neukirchen filled in the details:
UnreliableFS is a FUSE-based fault injection filesystem that allows to change fault-injections in runtime using simple configuration file.
Also, Dave Vasilevsky suggested that something like this could be done with the device mapper.
I think the real takeaway from this is that I had not accepted the hard truth that all Unix is Linux now, and non-Linux Unix is dead.
Thanks everyone who sent suggestions.
[ Addendum: Leah Neukirchen informs me that FUSE also runs on FreeBSD, OpenBSD and macOS, and reminds me that there are a great many MacOS systems. I should face the hard truth that my knowledge of Unix systems capabilities is at least fifteen yers out of date. ]
[Other articles in category /Unix] permanent link
Sun, 13 Mar 2022Suppose you're writing some program that does file I/O. You'd like to include a unit test to make sure it properly handles the error when the disk fills up and the write can't complete. This is tough to simulate. The test itself obviously can't (or at least shouldn't) actually fill the disk.
A while back some Unix systems introduced a device called
/dev/full. Reading from /dev/full returns zero bytes, just like
/dev/zero. But all attempts to write to /dev/full fail with
ENOSPC, the system error that indices a full disk. You can set up
your tests to try to write to /dev/full and make sure they fail
gracefully.
That's fun, but why not generalize it? Suppose there was a
/dev/error device:
#include <sys/errdev.h>
error = open("/dev/error", O_RDWR);
ioctl(error, ERRDEV_SET, 23);
The device driver would remember the number 23 from this ioctl call,
and the next time the process tried to read or write the error
descriptor, the request would fail and set errno to 23, whatever
that is. Of course you wouldn't hardwire the 23, you'd actually do
#include <sys/errno.h>
ioctl(error, ERRDEV_SET, EBUSY);
and then the next I/O attempt would fail with EBUSY.
Well, that's the way I always imagined it, but now that I think about
it a little more, you don't need this to be a device driver. It
would be better if instead of an ioctl it was an fcntl that you
could do on any file descriptor at all.
Big drawback: the most common I/O errors are probably EACCESS and
ENOENT, failures in the open, not in the actual I/O. This idea
doesn't address that at all. But maybe some variation would work
there. Maybe for those we go back to the original idea, have a
/dev/openerror, and after you do ioctl(dev_openerror, ERRDEV_SET,
EACCESS), the next call to open fails with EACCESS. That might
be useful.
There are some security concerns with the fcntl version of the idea.
Suppose I write a malicious program that opens some file descriptor,
dups it to standard input, does fcntl(1, ERRDEV_SET,
ESOMEWEIRDERROR), then execs the target program t. Hapless t tries
to read standard input, gets ESOMEWEIRDERROR, and then does
something unexpected that it wasn't supposed to do. This particular attack is
easily foiled: exec should reset all the file descriptor saved-error
states. But there might be something more subtle that I haven't
thought of and in OS security there usually is.
Eh, probably the right solution these days is to LD_PRELOAD a
complete mock filesystem library that has any hooks you want in it. I
don't know what the security implications of LD_PRELOAD are but I
have to believe that someone figured them all out by now.
[ Addendum 20220314: Better solutions exist. ]
[Other articles in category /Unix] permanent link
Wed, 09 Mar 2022
Bad but interesting mathematical notation idea
Zaz Brown showed up on Math SE yesterday with a proposal to make mathematical notation more uniform. It's been pointed out several times that the expressions
$$y^n = x \qquad n = \log_y x \qquad y=\sqrt[n]x $$
all mean the same thing, and yet look completely different. This has led to proposals to try to unify the three notations, although none has gone anywhere. (For example, this Math SE thread .)
!!\def\o{\overline}\def\u{\underline}!!
In this new thread, M. Brown has an interesting observation: exponentiation also unifies addition and multiplication. So write !!\o x!! to mean !!e^x!!, and !!\u x!! to mean !!\ln x!!, and leave multiplication as it is. Now !!x^y!! can be written as !!\o{\u x y}!! and !!x+y!! can be written as !!\u{\bar x \! \bar y}!!.
Well, this is a terrible idea, and I'll explain why I think so in some detail. But I really hope nobody will think I mean this as any sort of criticism of its author. I have a lot of ideas too, and most of them are amazingly bad, way worse than this one. Having bad ideas doesn't make someone a bad person. And just because an idea is bad, doesn't mean it wasn't worth considering; thinking about ideas is how you decide which ones are bad and which aren't. M. Brown's idea was interesting enough for me to think about it and write an article. That's a compliment, not a criticism.
I'm deeply interested in notation. I think mathematicians don't yet understand the power of mathematical notation and what it does. We use it, but we don't understand it. I've observed before that you can solve algebraic equations or calculus problems just by “pushing around the symbols”. But why can you do that? Where is the meaning, and how do the symbols capture the meaning? How does that work? The fact that symbols in general can somehow convey meaning is a deep philosophical mystery, not just in mathematics but in all communication, and nobody understands how it works. Mathematical symbols can be even more amazing: they don't just tell you what other people were thinking, they tell you things themselves. You rearrange them in a certain way and they smile and whisper secrets: “now you can see this function is everywhere zero”, “this is evidently unbounded” or “the result is undefined when !!\lvert x_1\rvert > \frac 23!!”. It's almost as if the symbols are doing some of the thinking for you.
Anyway this particular idea is not good, but maybe we can learn something from its failure modes?
Here's how you would write !!x^2+x!!: $$\u{\o{\o{2\u x}}{\o x}}$$
Zaz Brown suggested that this expression might be better written as !!x{\u{\o x \o 1}}!!, which is analogous to !!x(x+1)!!, but I think that reply misses a very important point: you need to be able to write both expressions so that you can equate them, or transform one into the other. The expression !!x(x+1)!! is useful because you can see at a glance that it is composite for all integer !!x!! larger than 1, and actually twice a composite for sufficiently large !!x!!. (This is the kind of thing I had in mind when I said the symbols whisper secrets to you.) !!x^2+x!! is useful in different ways: you can see that it's !!\Theta(x^2)!! and it's !!(x+1)^2 - (x+1)!! and so on. Both are useful and you need to be able to turn one into the other easily. Good notation facilitates that sort of conversion.
M. Brown's proposal actually has at least two components. One component is its choice of multiplication, exponentials and logarithms as the only first-class citizens. The other is the specific way that was chosen to write these, with the over- and underbars. This second component is no good at all, for purely typographic reasons. These three expressions look almost identical but have completely different meanings: $$ \u{\o a\, \o c}\qquad \u{\o { ac}} \qquad \o{\u a\, \u c}.$$
In fact, the two on the right were almost indistinguishable until I told MathJax to put in some extra space. I'm sure you can imagine similar problems with !!\u{\o{\o{2\u x}}}{\o x}!! turning into !!\u{\o{\o{2\u x x}}}!! or !!\u{\o{\o{2\u x }x}}!! or whatever. Think of how easy it is to drop a minus sign; this is much worse.
[ Addendum 20220308: Earlier, I had said that !!x+y!! could be written as !!\u{\bar x\bar y}!!. A Gentle Reader pointed out that the bar on the bottom wasn't connected but should have been, as on the far right of this screenshot:

I meant it to be connected and what I wrote asked for it to be connected, but MathJax, which formats the math formulas on the blog, didn't connect it. To remove the gap, I had to explicitly subtract space between the !!x!! and the !!y!!. ]
But maybe the other component of the proposal has something to it and we will find out what it is if we fix the typographic problem with the bars. What's a good alternative?
Maybe !!\o x = x^\bullet!! and !!\u x = x_\bullet!! ? On the one hand we get the nice property that !!x^\bullet_\bullet = x!!. But I think the dots would make my head swim. Perhaps !!\o x = x\top!! and !!\u x = x\bot!!? Let's try.
Good notation facilitates transformation of expressions into equal expressions. The !!\top\bot!! notation allows us to easily express the simple identities $$a\top\bot \quad = \quad a\bot\top \quad = \quad a.$$ That kind of thing is good, although the dots did it better. But I couldn't find anything else like it.
Let's see what the distributive law looks like. In standard notation it is $$a(b+c) = ab + ac.$$ In the original bar notation it was $$a\u{\o b\o c} = \u{\o{ab}\, \o{ac}}.$$ This looks uncouth but perhaps would not be worse once one got used to it.
With the !!\top\bot!! idea we have
$$ a(b\top c\top)\bot = ((ab)\top(ac)\top)\bot. $$
I had been hoping that by making the !!\top!! and !!\bot!! symbols postfix we'd be able to avoid parentheses. That didn't happen: without the parentheses you can't distinguish between !!(ab)\top!! and !!a(b\top)!!. Postfix notation is famous for allowing you to omit parentheses, but that's only if your operators all have fixed arity. Here the invisible variadic multiplication ruins that. And making it visible dyadic multiplication is not really an improvement:
$$ ab\top c\top\cdot\cdot\bot = ab\cdot\top ac\cdot \top\cdot \bot. $$
You know what I think would happen if we actually tried to use this idea? Someone would very quickly invent an abbreviation for !!\u{\o {x_1}\, \o {x_2} \cdots \o{x_k}}!!, I don't know, something like “!!x_1 + x_2 + \ldots + x_k!!” maybe. (It looks crazy, I know, but it might just work.) Because people might like to discuss the fact that $$ \u{\o 2\, \o 3 } = 5$$ and without an addition sign there seems to be no way to explain why this should be.
Well, I have been turning away from the real issue for a while now, but !!a(b\top c\top)\bot = !! !!((ab)\top(ac)\top)\bot!! forces me to confront it. The standard expression of the distributive law equates a computation with two operations and another with three. The computations expressed by the new notation involve five and six operations respectively. Put this way, the distributive law is no longer simple!
This reminds me of the earlier suggestion that if !!x^2+x!! is too complicated, one can write !!x(x+1)!! instead. But expressions don't only express a result, they express a way of arriving at that result. The purpose of an equation is to state that two different computations arrive at the same result. Yes, it's true that $$a+b = \ln e^ae^b,$$ but the two computations are not the same! If they were, the statement would be vacuous. Instead, it says that the simple computation on the left arrives at the same result as the complicated one on the right, an interesting thing to know. “!!2+3=5!!” might imply that !!e^2\cdot e^3=e^5!! but it doesn't say the same thing.
Here's my takeaway from consideration of the Zaz Brown proposal:
It's not sufficient for a system of notation to have a way of expressing every result; it has to be able to express every possible computation.
Put that way, other instructive examples come to mind. Consider Egyptian fractions. It's known that every rational number between !!0!! and !!1!! can be written in the form $$\frac1{a_1} + \frac1{a_2} + \ldots + \frac1{a_n}$$ where !!\{ a_i\}!! is a strictly increasing sequence of positive integers. For example $$\frac 7{23} = \frac 14 + \frac1{19} + \frac1{583} + \frac1{1019084}$$ or with a bit more ingenuity, $$\frac7{23} = \frac16 + \frac1{12} + \frac1{23} + \frac1{138} + \frac1{276},$$ longer but less messy. The ancient Egyptians did in fact write numbers this way, and when they wanted to calculate !!2\cdot\frac17!!, they had to look it up in a table, because writing !!\frac27!! was not an expressible computation, it had to be expressed in terms of reciprocals and sums, so !!2\cdot\frac 17 = \frac14 + \frac1{28}!!. They could write all the numbers, but they couldn't write all the ways of making the numbers.
(Neither can we. We can write the real root of !!x^3-2!! as !!\sqrt[3]2!!, but there is no effective notation for the real root of !!x^5+x-1!!. The best we can do is something like “!!0.75488\ldots!!”, which is even less effective than how the Egyptians had to write !!\frac27!! as !!\frac14+\frac1{28}!!.)
Anyway I think my conclusion from all this is that a practical mathematical notation really must have a symbol for addition, which is not at all surprising. But it was fun and interesting to see what happened without it. It didn't work well, but maybe the next idea will be better.
Thanks again, Zaz Brown.
[ Addendum 20230422: I discussed the Egyptians’ table of !!\frac 2n!! a couple of years ago, and why a more general table wasn't needed. ]
[Other articles in category /math/se] permanent link
Mon, 28 Feb 2022
Quicker and easier ways to get more light
Hacker News today is discussing this article by Lincoln Quirk about ways to get more light in your home office.
Why?
You might do this because you have trouble seeing.
Or because you find you are more productive when the room is brighter.
Or perhaps you have seasonal affective disorder, for which more light is a recognized treatment. For SAD you can buy these cute little light therapy boxes that are supposed to help, but they don't, because they are not bright enough to make a difference. Waste of money.
Quirk's summary
Quirk says:
I want an all-in-one “light panel” that produces at least 20000 lumens and can be mounted to a wall or ceiling, with no noticeable flicker, good CRI, and adjustable (perhaps automatically adjusting) color temperature throughout the day.
and describes some possible approaches.
One is to buy 25 ordinary LED bulbs, and make some sort of contraption to mount them on the wall or ceiling. This is cheap, but you have to figure out how to mount the bulbs and then you have to do it. And you have to manage 25 bulbs, which might annoy you.
Quirk points out that 815-lumen LED bulbs can be had for $1.93, for a cost of $2.75 / kilolumen (klm).
Another suggestion of Quirk's is to use LED strips, but I think you'd have to figure out how to control them, and they are expensive: Quirk says $16 / klm.
Here's what I did that was easy and relatively inexpensive
This thing is a “corn bulb”, so-called because it is a long cylinder with many LEDs arranged on in like kernels on a corn cob. A single bulb fits into a standard light socket but delivers up to twelve times as much light as a standard bulb.
You can buy them from the DragonLight company.
| power | Cost | Luminance | |
|---|---|---|---|
| (W) | (lm) | (bulbs) | |
| 25 | $22 | 3000 | 1.9 |
| 35 | $26 | 4200 | 2.6 |
| 50 | $33 | 6000 | 3.8 |
| 54 | $35 | 6200 | 3.9 |
| 80 | $60 | 9600 | 6 |
The fourth column is the corn bulb's luminance compared with a standard 100W incandescent bulb, which I think emits around 1600 lm.
Cost varies from $7.33 / klm at the top of the table to $4.93 / klm at the bottom.
I got an 80-watt corn bulb ($60) for my office. It is really bright, startlingly bright, too bright to look at directly. It was about a month before I got used to it and stopped saying “woah” every time I flipped the switch. I liked it so much I bought a 120-watt bulb for the other receptacle. I'd like to post a photo, but all you would be able to see is a splotch.
The two bulbs cost around $140 total and jointly deliver 24,000 lumens, which is as much light as 15 or 16 bright incandescent bulbs, for $5.83 / klm. It's twice as expensive as the cheap solution but has the great benefit that I didn't have to think about it, it was as simple as putting new bulbs into the two sockets I already had. Also, as I said, I started with one $60 bulb to see whether I liked it. If you are interested in what it is like to have a much better-lit room, this is a low-risk and low-effort way to find out.
Corn bulbs are available in different color temperatures. In my view the biggest drawback is that each bulb carries a cooling fan built into its base. The fan runs at 40–50 dB, and many people would find it disturbing. [Addendum 20220403: Fanless bulbs are now available. See below.] Lincoln Quirk says he didn't like the light quality; I like it just fine. The color is not adjustable, but if you have two separately-controllable sockets you could put a bulb of one color in each socket and switch between them.
I found out about the corn bulbs from YOU NEED MORE LUMENS by David Chapman, and Your room can be as bright as the outdoors by Ben Kuhn. Thanks very much to Benjamin Esham for figuring this out for me; I had forgotten where I got the idea.
[ Addendum 20220403: Gábor Lehel points out that DragonLight now sells fanless bulbs in all wattages. Apparently because the bulb housing is all-aluminum, the bulb can dissipate enough heat even without the fan. Thanks! ]
[Other articles in category /tech] permanent link
Sat, 26 Feb 2022
I vent my rage at dumbass Math SE comments
[ Content warning: ranting ]
An article I've had in progress for a while is an essay about the dogmatic slogan that “infinity is not a number”. As research for that article I got Math Stack Exchange to disgorge all the comments that used that phrase. There were several dozen.
Most of them were just inane, or ill-considered; some contained genuine technical errors. But this one was so annoying that I have paused to complain about it individually:
One thing many laypeople do not understand or realize is that infinity is not a number, it's not equal to any number, and that two infinities can be different (or the same) in size from one another."
That is not “one thing”. It is three things.
A person who is unclear on the distinction between !!1!! and !!3!! should withhold their opinions about the nature of infinity.
[ Addendum 20220301: I did not clearly communicate which side of the “infinity is not a number” issue I am on. Here's my preliminary statement on the matter: The facile and prevalent claim that “infinity is not a number”, to the extent that it isn't inane, is false. I hope this is sufficiently clear. ]
[Other articles in category /math/se] permanent link
Thu, 24 Feb 2022
More about the axioms of infinity and the empty set
[ Content warning: inconclusive nattering ]
Yesterday I discussed how one can remove the symbol !!\varnothing!! from the statement of the axiom of infinity (“!!A_\infty!!”). Normally, !!A_\infty!! looks like this:
$$\exists S (\color{darkblue}{\varnothing \in S}\land (\forall x\in S) x\cup\{x\}\in S).$$
But the “!!\varnothing!!” is just an abbreviation for “some set !!Z!! with the property !!\forall y. y\notin Z!!”, so one should understand the statement above as shorthand for:
$$\exists S (\color{darkblue}{(\exists Z.(\forall y. y\notin Z)\land (Z \in S))} \\ \land (\forall x\in S) x\cup\{x\}\in S).\tag{$\heartsuit$}$$
(The !!\cup!! and !!\{x\}!! signs should be expanded analogously, as abbreviations for longer formulas, but we will ignore them today.)
Thinking on it a little more, I realized that you could conceivably get into big trouble by doing this, for a reason very much like the one that concerned me initially. Suppose that, in !!(\heartsuit)!!, in place of $$\exists Z.(\color{darkgreen}{\forall y. y\notin Z})\land (Z \in S),$$ we had $$\exists Z.(\color{darkred}{\forall y. y\in Z\iff y\notin y})\land (Z \in S).$$
Now instead of !!Z!! having the empty-set property, it is required to have the Russell set property, and we demand that the infinite set !!S!! include an element with that property. But there is provably no such !!Z!!, which makes the axioms inconsistent. My request that !!\varnothing!! be proved to exist before it be used in the construction of !!S!! was not entirely silly.
My original objection partook of a few things:
- You ought not to use the symbol “!!\varnothing!!” without defining it
I believe that expanding abbreviations as we did above addresses this issue adequately.
- But to be meaningful, any such definition requires an existence proof and perhaps even a uniqueness proof
“Meaningful” is the wrong word here. I'm willing to agree that the defined symbol necessarily has a sense. But without an existence proof the symbol may not refer to anything. This is still a live issue, because if the symbol doesn't denote anything, your axiom has a big problem and ruins the whole theory. The axiom has a sense, but if it asserts the existence of some derived object, as this one does, the theory is inconsistent, and if it asserts the universality of some derived property, the theory is vacuous.
I think embedding the existence claim inside another axiom, as is done in !!(\heartsuit)!!, makes it easier to overlook the existence issue. Why use complicated axioms when you could use simpler ones? But technically this is not a big deal: if !!Z!! doesn't exist, then neither does !!S!!, and the axioms are inconsistent, regardless of whether we chose to embed the definition of !!Z!! in !!A_\infty!! or leave it separate.
One reason to prefer simpler axioms is that we hope it will be easier to detect that something is wrong with them. But set theorists do spend a lot of time thinking about the consistency of their theories, and understand the consistency issues much better than I do. If they think it's not a problem to embed the axiom of the empty set into !!A_\infty!!, who am I to disagree?
[Other articles in category /math] permanent link
Wed, 23 Feb 2022
My mistake about errors in the presentation of axiomatic set theory
[ Content warning: highly technical mathematics ]
A couple of weeks ago I claimed:
Many presentations of axiomatic set theory contain an error
I realized recently that there's a small but significant error in many presentations of the Zermelo-Frankel set theory: Many authors omit the axiom of the empty set, claiming that it is omittable. But it is not.
Well, it sort of is and isn't at the same time. But the omission that bothered me is not really an error. The experts were right and I was mistaken.
(Maybe I should repeat my disclaimer that I never thought there was a substantive error, just an error of presentation. Only a crackpot would reject the substance of ZF set theory, and I am not prepared to do that this week.)
My argument was something like this:
You want to prevent the axioms from being vacuous, so you need to be able to prove that at least one set exists.
One way to do this is with an explicit “axiom of the empty set”: $$\exists Z. \forall y. y\notin Z$$
But many presentations omit this, remarking that the axiom of infinity (“!!A_\infty!!”) also asserts the existence of a set, and the empty set can be obtained from that one via specification.
The axiom of infinity is usually stated in this form: $$\exists S (\varnothing \in S\land (\forall x\in S) x\cup\{x\}\in S).$$ But, until you prove that the empty set actually exists, it is not meaningful to include the symbol !!\varnothing!! in your axiom, since it does not actually refer to anything, and the formula above is formally meaningless.
I ended by saying:
You really do need an explicit axiom [of the empty set]. As far as I can tell, you cannot get away without it.
Several people tried to explain my error, pointing out that !!\varnothing!! is not part of the language of set theory, so the actual formal statement of !!A_\infty!! doesn't include the !!\varnothing!! symbol anyway. But I didn't understand the point until I read Eike Schulte's explanation. M. Schulte delved into the syntactic details of what we really mean by abbreviations like !!\varnothing!!, and why they are meaningful even before we prove that the abbreviation refers to something. Instead of explicitly mentioning !!\varnothing!!, which had bothered me, M. Schulte suggested this version of !!A_\infty!!:
$$\exists S (\color{darkblue}{(\exists Z.(\forall y. y\notin Z)\land (Z \in S))} \\ \land (\forall x\in S) x\cup\{x\}\in S).$$
We don't have to say that !!S!! (the infinite set) includes !!\varnothing!!, which is subject to my quibble about !!\varnothing!! not being meaningful. Instead we can just say that !!S!! includes some element !!Z!! that has the property !!\forall y.y\notin Z!!; that is, it includes an element !!Z!! that happens to be empty.
A couple of people had suggested something like this before M. Schulte did, but I either didn't understand or I felt this didn't contradict my original point. I thought:
I claimed that you can't get rid of the empty set axiom. And it hasn't been gotten rid of; it is still there, entire, just embedded in the statement of !!A_\infty!!.
In a conversation elsewhere, I said:
You could embed the axiom of pairing inside the axiom of infinity using the same trick, but I doubt anyone would be happy with your claim that the axiom of pairing was thereby unnecessary.
I found Schulte's explanation convincing though. The !!A_\infty!! that Schulte suggested is not a mere conjunction of axioms. The usual form of !!A_\infty!! states that the infinite set !!S!! must include !!\varnothing!!, whatever that means. The rewritten form has the same content, but more explicit: !!S!! must include some element !!Z!! that has the emptiness property (!!\forall y. y\notin Z!!) that we want !!\varnothing!! to have.
I am satisfied. I hereby recant the mistaken conclusion of that article.
Thanks to everyone who helped me out with this: Ben Zinberg, Asaf Karagila, Nick Drozd, and especially to Eike Schulte. There are now only 14,823,901,417,522 things remaining that I don't know. Onward to zero!
[ Addendum 20220224: A bit more about this. ]
[Other articles in category /math] permanent link
Tue, 22 Feb 2022
“Shall” and “will” strike back from beyond the grave
In former times and other dialects of English, there was a distinction between ‘shall’ and ‘will’. To explain the distinction correctly would require research, and I have a busy day today. Instead I will approximate it by saying that up to the middle of the 19th century, ‘shall’ referred to events that would happen in due course, whereas ‘will' was for events brought about intentionally, by force of will. An English child of the 1830's, stamping its foot and shouting “I will have another cookie”, was expressing its firm intention to get the cookie against all opposition. The same child shouting “I shall have another cookie” was making a prediction about the future that might or might not have turned out to be correct.
In American English at least, this distinction is dead. In The American Language, H.L. Mencken wrote:
Today the distinction between will and shall has become so muddled in all save the most painstaking and artificial varieties of American that it may almost be said to have ceased to exist.
That was no later than 1937, and he had been observing the trend as early as the first edition (1919):
… the distinction between will and shall, preserved in correct English but already breaking down in the most correct American, has been lost entirely in the American common speech.
But yesterday, to my amazement, I found myself grappling with it! I had written:
The problem to solve here … [is] “how can OP deal with the inescapable fact that they can't and won't pass the exam”.
To me, the “won't” connoted a willful refusal on the part of OP, in the sense of “I won't do it!”, and not what I wanted to express, which was an inevitable outcome. I'm not sure whether anyone else would have read it the same way, but I was happier after I rewrote it:
The problem to solve here … [is] “how can OP deal with the inescapable fact that they cannot and will not pass the exam”.
I could also gotten the meaning I wanted by replacing “can't and won't” with “can't and shan't” — except that “shan't’ is dead, I never use it, and, had I thought of it, I would have made a rude and contemptuous nose noise.
Mencken says “the future in English is most commonly expressed by neither shall nor will, but by the must commoner contraction 'll’. In this case that wasn't true! I wonder if he missed the connotation of “won't” that I felt, or if the connotation arose after he wrote his book, or if it's just something idiosyncratic to me.
[Other articles in category /lang] permanent link
Mon, 21 Feb 2022
What to do if you're about to fail real analysis for the second time?
A few months ago a Reddit user came to r/math
with this tale of woe:
I failed real analysis horrifically the first time … and my resit takes place in a few days. I still feel completely and utterly unprepared. I can't do the homework questions and I can't do the practice papers. I'm really quite worried that I'll fail and have to resit the whole year (can't afford) or get kicked out of uni (fuck that).
Does anyone have tips or advice, or just any general words of comfort to help me through this mess? Cheers.
The first thing that came to mind for me was “wow, you're fucked”. There was a time in my life when I might have posted that reply but I'm a little more mature now and I know better.
I read some of the replies. The top answer was a link to a pirated copy of Aksoy and Khamsi's A Problem Book in Real Analysis. A little too late for that, I think. Hapless OP must re-sit the exam in a few days and can't do the homework questions or practice papers; the answer isn't simply “more practice”, because there isn't time.
The second-highest-voted reply was similar: “Pick up Stephen Abbott's Understanding Analysis”. Same. It's much too late for that.
The third reply was fatuous: “understand the proofs done in the
textbook/lecture completely, since a lot of the techniques used to
prove those statements you will probably need to use while doing
problems”. <sarcasm>Yes, great advice, to pass the exam just understand the
material completely, so simple, why doesn't everyone just do that?</sarcasm>
Here's one I especially despised:
Don't worry. Real analysis is a lot of work and you never have the time to understand everything there.
“Don't worry”! Don't worry about having to repeat the year? Don't worry about getting kicked out of university? I honestly think “wow, you're fucked” would be less damaging. In the book of notoriously ineffective problem-solving strategies, chapter 1 is titled “Pretend there is No Problem”.
This was amusing but unhelpful:
We are all going to die. Compared to death, real analysis is nothing to fear.
(However, another user disagreed: “Compared to real analysis, death is nothing to fear”.)
Some comments offered hints: focus on topology, try proof by contradiction. Too little, and much too late.
Most of the practical suggestions, in my opinion, were answering the wrong question. They all started from the premise that it would be possible for Hapless OP to pass the exam. I see no evidence that this was the case. If Hapless OP had showed up on Reddit having failed the midterm, or even a few weeks ahead of the final, that would be a very different situation. There would still have been time to turn things around. OP could get tutoring. They could go to office hours regularly. They could organize a study group. They could work hard with one of those books that the other replies mentioned. But with “a few days” left? Not a chance.
The problem to solve here isn't “how can OP pass the exam”. It's “how can OP deal with the inescapable fact that they cannot and will not pass the exam”.
Way downthread there was some advice (from user tipf) that was gloomy but which, unlike the rest of the comments, engaged the real issue, that Hapless OP wasn't going to pass the exam the following week:
I would seriously rethink getting a pure math major. It's not a very marketable major outside academia, and sinking a bunch of money into it (e.g. re-taking a whole year) is just not a good idea under almost any circumstance.
Pessimistic, yes, but unlike the other suggestions, it actually engages with Hapless OP's position as they described it (“have to resit the whole year (can't afford)”).
When we reframe the question as “how can OP deal the fact that they won't pass the exam”, some new paths become available for exploration. I suggested:
[OP] should go consult with the math department people immediately, today, explain that they are not prepared and ask what can be done. Perhaps there is no room for negotiation, but in that case OP would be no worse off than they are now. But there may be an administrative solution.
For example, just hypothetically, what if the math department administrative assistant said:
You can get special permission to re-sit the exam in three months time, if you can convince the Dean that you had special extenuating hardships.
This is not completely implausible, and if true might put Hapless OP in a much better position!
Now you might say “Dominus, you just made that up as an example, there is no reason to think it is actually true.” And you would be quite correct. But we could make up fifty of these, and the chances would pretty good that one of them was actually true. The key is to find out which one.
And OP can't find out what is available unless they go talk to someone in the math department. Certainly not by moping in their room reading Reddit. Every minute spent moping is time that could be better spent tracking down the Dean, or writing the letter, or filing the forms, or whatever might be required to improve the situation.
Along the same lines, I suggested:
perhaps the department already has a plan for what to do with people who can't pass real analysis. Maybe they will say something constructive like “many people in your situation change to a Statistics major” or something like that.
I don't know if Hapless OP would have been happy with a Statistics major; they didn't say. But again, the point is, there may be options that are more attractive than “get kicked out of uni”, and OP should go find out what they are.
The higher-level advice here, which I think is generally good, is that while asking on Reddit is quick and easy, it's not likely to produce anything of value. It's like looking for your lost wallet under the lamppost because the light is good. But it doesn't work; you need to go ask the question to the people who actually know what the solutions might be and who are in a position to actually do something about the problem.
[ Addendum 20220222: Still higher-level advice is: if you're losing the game, try instead playing the different game that is one level up. ]
[Other articles in category /math] permanent link
Fri, 11 Feb 2022
Geometric proof that the mediant lies between its arguments
The mediant of two fractions !!\frac ab!! and !!\frac cd!! is simply !!\frac{a+c}{b+d}!!. It appears often in connection with the theory of continued fractions, and a couple of months ago I put it to use in this post about Newton's method. There the crucial property was that if $$\frac ab < \frac cd$$ then $$\frac ab < \frac{a+c}{b+d} < \frac cd.$$
This can be proved with straightforward algebra:
$$\begin{align} \frac ab & < \frac cd \\ ad & < bc \\ ab + ad & < ab + bc \\ a(b+d) & < (a+c) b \\ \frac ab & < \frac{a+c}{b+d} \end{align}$$
and similarly for the !!\frac cd!! side.
But Reddit user asenseofbeauty recently suggested a lovely visual proof that makes the result intuitively clear:
!!\def\pt#1#2{\langle{#1},{#2}\rangle}!! The idea is simply this: !!\frac ab!! is the slope of the line from the origin !!O!! through the point !!P=\pt ba!! (blue) and !!\frac cd!! is the slope of the line through !!Q=\pt dc!! (red). The point !!\pt{b+d}{a+c}!! is the fourth vertex of the parallelogram with vertices at !!O, P, Q!!, and !!\frac{a+c}{b+d}!! is the slope of the parallelogram's diagonal. Since the diagonal lies between the two sides, the slope must also lie in the middle somewhere.
The embedded display above should be interactive. You can drag around the red and blue points and watch the diagonal with slope !!\frac{a+b}{c+d}!! slide around to match.
In case the demo doesn't work, here's a screenshot showing that !!\frac 25 < \frac{2+4}{5+3} < \frac 43!!:
[ Addendum 20220215: The source was this Reddit comment from asenseofbeauty. ]
[Other articles in category /math] permanent link
Wed, 09 Feb 2022
If I haven't replied to your email about Haskell…
Perhaps someone out there wants to take a chance on a senior programmer with thirty years of experience who wants to make a move into Haskell.
This worked better than I expected. Someone posted it to Hacker News, and it reached #1. I got 45 emails with suggestions about where to apply, and some suggestions through other channels also. Many thanks to everyone who contributed.
I'm answering the messages in the order I received them. Thoughtful replies take time. If I haven't answered yours yet, it's not that I am uninterested, or I am blowing you off. It's because I got 45 emails.
Thanks for your patience and understanding.
[Other articles in category /meta] permanent link
Mon, 07 Feb 2022
I would like a job writing Haskell
Perhaps someone out there wants to take a chance on a senior programmer with thirty years of experience who wants to make a move into Haskell.
I'm between jobs right now, having resigned my old one without having a new one lined up. It's been a pleasant vacation but it can't go on forever. At some point I'll need another job.
I would really like it to be Haskell programming but I don't know where to look. I hope maybe one of my Gentle Readers does.
I don't have any professional or substantial Haskell experience, but a Haskell shop might be happy to get me anyway. I think I'm well-prepared to rapidly get up to speed writing production Haskell programs:
Although I have never been paid to write Haskell, I'm not a newbie. I have been using Haskell on and off for twenty years. I have been immersed in the Haskell ecosystem since the 1998 language standard was fresh. I've read the important papers. I know how the language has evolved. I know how to read the error messages. Haskell has featured regularly on my blog since I started it.
I solidly understand the Hindley-Milner type elaboration algorithm and the typeclass stuff that Haskell puts on top of that. I have successfully written many thousands of lines of SML, which uses an earlier version of the same system. I'm 100% behind the strong-typing philosophy.
I have a mathematics background. I know the applicable category theory. I understand what it means when someone says that a monad is a monoid in the category of endofunctors. I won't be scared if someone talks about η-conversion, or confused if they talk about lifting a type.
I am quite comfortable with lazy data structures and with higher-order functional constructs such as parser combinators. In fact, I wrote a book about them.
I'm not sure I should admit this, but I'm the person who explained why monads are like burritos.
If you're interested, or if you know someone who might be,
here's my résumé.
please feel free to pass it around or to ask me questions at
mjd@pobox.com.
Thanks for your kind attention.
Big restriction: I live in Philadelphia and cannot relocate. I have no objection to occasional travel, and a long history of sucessful remote work.
[ Addendum 20220209: If you emailed me and haven't heard back, it's only because response was overwhelming and I haven't gotten to your message yet. Thank you! ]
[Other articles in category /meta] permanent link
Sun, 06 Feb 2022
A one-character omission caused my Python program to hang (not)
I just ran into a weird and annoying program behavior. I was
writing a Python program, and when I ran it, it seemed to hang.
Worried that it was stuck in some sort of resource-intensive loop I
interrupted it, and then I got what looked like an error message from
the interpreter. I tried this several more times, with the same
result; I tried putting exit(0) near the top of the program to
figure out where the slowdown was, but the behavior didn't change.
The real problem was that the first line which said:
#/usr/bin/env python3
when it should have been:
#!/usr/bin/env python3
Without that magic #! at the beginning, the file is processed not by
Python but by the shell, and the first thing the shell saw was
import re
which tells it to run the import command.
I didn't even know there was an import command. It runs an X client
that waits for the user to click on a window, and then writes a dump
of the window contents to a file. That's why my program seemed to
hang; it was waiting for the click.
I might have picked up on this sooner if I had actually looked at the error messages:
./license-plate-game.py: line 9: dictionary: command not found
./license-plate-game.py: line 10: syntax error near unexpected token `('
./license-plate-game.py: line 10: `words = read_dictionary(dictionary)'
In particular, dictionary: command not found is the shell giving
itself away. But I was so worried about the supposedly resource-bound
program crashing my session that I didn't look at the actual output,
and assumed it was Python-related syntax errors.
I don't remember making this mistake before but it seems like it would be an easy mistake to make. It might serve as a good example when explaining to nontechnical people how finicky and exacting programming can be. I think it wouldn't be hard to understand what happened.
This computer stuff is amazingly complicated. I don't know how anyone gets anything done.
[Other articles in category /Unix] permanent link
Sat, 05 Feb 2022
Factoring composite numbers into nearly equal factors
Pennsylvania license plate numbers have four digits and when I'm driving I habitually try to factor these. (This hasn't yet led to any serious injury or property damage…) In general factoring is a hardish problem but when !!n<10000!! the worst case is !!9991 = 97·103!! which is not out of reach. The toughest part is when you find a factor like !!661!! or !!667!! and have to decide if it is prime. For !!667!! you might notice right off that it is !!676-9 = (26+3)(26-3)!! but for !!661!! you have to wonder if maybe there is something like that and you just haven't thought of it yet. (There isn't.)
A related problem is the Nearly Equal Factors (NEF) problem: given
!!n!!, find !!a!! and !!b!!, as close as possible, with !!ab=n!!. If
!!n!! has one large prime factor, as it often does, this is quite
easy. For example suppose we are driving on the Interstate and are
behind a car with license plate GJA 6968. First we divide this by
!!8!!, so !!871!!, which is obviously not divisible by !!2, 3, 5, 7,!!
or !!11!!. So try !!13!!: !!871-780 = 91!! so !!871 = 13·67!!. If we
throw the !!67!! into the !!a!! pile and the other factors into the
!!b!! pile we get !!6968 = 67· 104!! and it's obvious we can't divide
up the factors more evenly: the !!67!! has to go somewhere and if we
put anything else with it, its pile is now at least !!2·67 = 134!!
which is already bigger than !!104!!. So !!67·104!! is the best we
can do.
When I first started thinking about this I thought maybe there could be a divide-and-conquer algorithm. For example, suppose !!n=4m!!. Then if we could find an optimal !!ab=m!!, we could conclude that the optimal factorization of !!n!! would simply be !!n = 2a· 2b!!. Except no, that is completely wrong; a counterexample is !!n=20!! where the optimal factorization is !!5·4!!, not !!(2·5)·(2·1)!!. So it's not that simple.
It's tempting to conclude that NEF is NP-hard, because it does look a lot like Partition. In Partition someone hands you a list of numbers and demands to know of they can be divided into two piles with equal sums. This is NP-hard, and so the optimization version of it, where you are asked to produce two piles as nearly equal as possible, is at least as hard. The NEF problem seems similar: if you know the prime factors !!n=p_1p_2…p_k!! then you can imagine that someone handed you the numbers !!\log p_1, … \log p_k!! and asked you to partition them into two nearly-equal piles. But this reduction is in the wrong direction; it only proves that Partition is at least as hard as NEF. Could there be a reduction in the other direction? I don't see anything obvious, but maybe there is something known about Partition or Knapsack that shows that even this restricted version is hard. [ Addendum: see below. ]
In practice, the first-fit-decreasing (FFD) algorithm usually performs well for this sort of problem. In FFD we go through the prime factors in decreasing order, and throw each one into the bin that is least full. This always works when there is one large prime factor. For example with !!6968!! we throw the !!67!! into the !!a!! bin, then the !!13!! and two of the !!2!!s into the !!b!! bin, at which point we have !!67·52!!, so the final !!2!! goes into the !!b!! bin also, and this is optimal. FFD does find the optimal solution much of the time, but not always. It works for !!20!! but fails for !!72 = 2^33^2!! because the first thing it does is to put the threes into separate bins. But the optimal solution !!72=9·8!! puts them in the same bin. Still it works for nearly all small numbers.
I would like to look into whether FFD it produces optimal results almost all of the time, and if so how almost? Wikipedia seems to say that the corresponding FFD algorithm for Partition, called LPT-first scheduling is guaranteed to produce a larger total which is no more than !!\frac76!! as big as the optimal, which would mean that for the NEF problem !!n=ab!! and !!a\ge b!! it will produce an !!a!! value no more than !!OPT^{7/6}!! where !!OPT!! is the minimum possible !!a!!.
Some small-number cases where FFD fails are:
$$ \begin{array}{rccc} n & \text{FFD} = ab & \text{Optimal} & \frac{\log(a)}{\log(OPT)} (≤ 1.167) \\ 72 & 12·6 & 9·8 & 1.131 \\ 180 & 18·10 & 15·12 & 1.067 \\ 240 & 20·12 & 16·15 & 1.080 \\ 288 & 24·12 & 18·16 & 1.100 \\ 336 & 28·12 & 21·16 & 1.094 \\ 540 & 30·18 & 27·20 & 1.032 \\ \end{array} $$
I wrote code to compute these and then I lost it.
I would also like to look at algorithms for NEF that don't begin by factoring !!n!!. We can guarantee to find optimal solutions with brute force, and in some cases this works very well. Consider !!240!! we begin by computing (in at most !!O(\log^2 n)!! time) the integer square root of !!240!!, which is !!15!!. Then since !!240!! is a multiple of !!15!! we have !!240=16·15!! and we win. In general of course it is not so easy, and it fails even in some cases where !!n!! is easy to factor. !!n=p^{2k+1}!! is especially unfortunate. Say !!n=243!! so the square root is !!15!!, which is not a factor of !!243!!. So we try !!14,!! then !!13,12,11,10!! and at last we find !!243=27·9!!.
[ Addendum 20220207: Dan Brumleve points out that it is NP-complete to decide whether, given numbers !!L, U, N!!, there is a number !!f!! in !! [L, U]!! that divides !!N!!. Using this, he shows that it is probably NP-complete to decide whether a given !!N!! is a product of two integers with !!\lvert a-b\rvert ≤ N^{1/4}!!. “Probably” here means that the reduction from Partition is polynomial time if Cramér's conjecture is correct. ]
[Other articles in category /math] permanent link
Today I learned that Julie Cypher, longtime partner of Melissa Etheridge, was actually born under the name Julie Cypher. Her dad's last name was Cypher, and it's apparently not even a very rare name.
It happens pretty often that I run into names and say to myself “wow, I'm glad that's not my name”. Or even “that's a cool name, but not as cool as ‘Dominus’.” But ‘Cypher’ is as cool as ‘Dominus’.
[ Addendum: I have mentioned before that Dominus is my birth name, not a recent invention. It came from Hungary, where it is in wider use than it is here. ]
[ Addendum 20220315: Today's “wow, I'm glad that's not my name” moment was in connection with Patience D. Roggensack. If you were writing a novel and gave a character that name, people would complain you were being precious. ]
[Other articles in category /misc/til] permanent link
Fri, 04 Feb 2022
An unexpected turn of phrase from Robertson Davies
Dave Turner has been tinkering with a game he calls Semantle and this reminded me of Robertson Davies' novel What's Bred in the Bone, which includes a minor character named Charlie Fremantle. This is how my brain works.
While I was looking up Charlie Fremantle I got sucked back into What's Bred in the Bone which is one of my favorite Davies novels. There is a long passage about Charlie and what he was like around 1933:
Charlie found Oxford painfully confining; he wanted to get out into the world and change it for the better, whether the world wanted it or not. He had advanced political ideas. He had read Marx — though not a great deal of him, for Charlie found thick, dense books a clog upon his soaring spirit. He had made a few Marxist speeches at the Union, and was admired by other untrammelled spirits like himself. His Marxism could be summed up as a conviction that whatever was, was wrong, and that the destruction of the existing order was the inevitable preamble to any beginning of the just society; the hope of the future lay with the workers, and all the workers needed was sympathetic leadership by people like himself, who had seen through the hypocrisy, stupidity, and bloody-mindedness of the upper class into which they themselves had been born.… Charlie was the upper class flinging itself into the struggle for justice on behalf of the oppressed; Charlie was Byron, determined to free the Greeks without having any clear notion of what or who the Greeks were; Charlie was a Grail knight of social justice.
A Grail knight of social justice! A social justice warrior! And one of a subtype we easily recognize among us even today. Davies wrote that sentence in 1985.
(But now that I look into it, I wonder what he meant to communicate by that phrase? In 1933, when that part of the book takes place, the phrase “social justice” was associated most closely with Father Charles Coughlin, founder of a political movement called the National Union for Social Justice, and publisher of the Social Justice periodical. Unlike Charlie, though, Coughlin was strongly anti-communist, which makes me wonder why Davies attached the phrase to him. Coincidence? I doubt that Davies was unaware of Coughlin in 1933, or had forgotten about him by 1985.)
[ A reader asks if Davies, as a Canadian, would have been aware of Father Coughlin. I think probably. Wikipedia says Coughlin's radio show reached millions of people, perhaps as many as 30 million a week. The show was based in Detroit, so many of these listeners must have been Canadian. At that time Davies was a university student in Kingston, Ontario. Coughlin, incidentally, was also Canadian. ]
[Other articles in category /book] permanent link
Thu, 03 Feb 2022Driving around today I passed by Mosaic Community Church. I first understood “mosaic” in the sense of colored tiles, but shortly after realized it is probably “Mosaic” (that is, pertaining to Moses) and not “mosaic”. But maybe not, perhaps it is an intentional double meaning, with “mosaic” meant to suggest a diverse congregation.
This got me thinking about words that completely change meaning when you capitalize them. The word “polish” came to mind.
I wondered if there were any other examples and realized there must be a great many boring ones of a certain type, which I confirmed when I got home: Pennsylvania has towns named Perry, Auburn, Potter, Bath, and so on. I think what makes “Polish” and “Mosaic” more interesting may be that their meanings are not proper nouns themselves but are derived adjectives.
[Other articles in category /lang] permanent link
Fri, 28 Jan 2022
Was the Lollipop Guild inspired by W.W. Denslow?
Yesterday I was thinking on these creepy Munchkins, and wondering what they were doing there:
It occurred to me that these guys are quite consistent with the look of the original illustrations, by W.W. Denslow. Here's Denslow's picture of three Munchkins greeting Dorothy:
(Click for complete illustration.)
Denslow and Frank Baum had a falling out after the publication of The Wonderful Wizard of Oz, and the illustrations for the thirteen sequels were done by John R. Neill, in a very different style. Dorothy aged up to eleven or twelve years old, and became a blonde with a fashionable bob.
[Other articles in category /art] permanent link
Thu, 27 Jan 2022
One song to the tune of another
I just randomly happened upon this recording of Pippa Evans singing “How Much is that Doggie in the Window” to the tune of “Cabaret”, and this reminded me of something I was surprised I hadn't mentioned before.
In the 1939 MGM production of The Wizard of Oz, there is a brief musical number, The Lollipop Guild, that has the same music as the refrain of Money, also from Cabaret. I am not aware of anyone else who has noticed this.
One has the lyrics “money makes the world go around” and the other has “We represent the lollipop guild”. And the two songs not only have the same rhythm, but the same melody and both are accompanied by the same twitchy, mechanical dance, performed by three creepy Munchkins in one case and by creepy Liza Minelli and Joel Grey in the other.
Surely the writers of Cabaret didn't do this on purpose? Did they? While it seems plausible that they might have forgotten the “Lollipop Guild” bit, I think it's impossible that they could both have missed it completely; they would have been 11 and 12 years old when The Wizard of Oz was first released.
(Now I want to recast The Wizard of Oz with Minelli as Dorothy and Grey as the Wizard. Bonus trivia, Liza Minelli is Judy Garland's daughter. Bonus bonus trivia, Joel Grey originated the role of the Wizard in the stage production of Wicked).
Addendum
Some time later I was wondering what the hell inspired the Lollipop Guild in the first place, and I had a brainwave.
[Other articles in category /music] permanent link
Yet another software archaeology failure
I have this nice little utility program called
menupick.
It's a filter that reads a list of items on standard input, prompts
the user to select one or more of them, then prints the selected items
on standard output. So for example:
emacs $(ls *.blog | menupick)
displays a list of those files and a prompt:
0. Rocketeer.blog
1. Watchmen.blog
2. death-of-stalin.blog
3. old-ladies.blog
4. self-esteem.blog
>
Then I can type 1 2 4 to select items 1, 2, and 4, or 1-4 !3 (“1
through 4, but not 3”) similarly. It has some other features I use
less commonly. It's a useful component in other commands, such as
this oneliner
git-addq
that I use every day:
git add $(git dirtyfiles "$@" | menupick -1)
(The -1 means that if the standard input contains only a single item,
just select it without issuing a prompt.)
The interactive prompting runs in a loop, so that if the menu is long
I can browse it a page at a time, adding items, or maybe removing
items that I have added before, adjusting the selection until I have
what I want. Then entering a blank line terminates the interaction.
This is useful when I want to ponder the choices, but for some of the
most common use cases I wanted a way to tell menupick “I am only
going to select a single item, so don't loop the interaction”. I have
wanted that for a long time but never got around to implementing it
until this week. I added a -s flag which tells it to terminate the
interaction instantly, once a single item has been selected.
I modified the copy in $HOME/bin/menupick, got it working the way I
wanted, then copied the modified code to my utils git repository to commit
and push the changes. And I got a very sad diff, shown here only in part:
diff --git a/bin/menupick b/bin/menupick
index bc3967b..b894652 100755
--- a/bin/menupick
+++ b/bin/menupick
@@ -129,7 +129,7 @@ sub usage {
-1: if there is only one item, select it without prompting
-n pagesize: maximum number of items on each page of the menu
(default 30)
- -q: quick mode: exit as soon as at least one item has been selected
+ -s: exit immediately once a single item has been selected
Commands:
Each line of input is a series of words of the form
I had already implemented almost the exact same feature, called it
-q, and completely forgotten to use it, completely failed to install
it, and then added the new -s feature to the old version of the
program 18 months later.
(Now I'm asking myself: how could I avoid this in the future? And the clear answer is: many people have a program that downloads and installs their utiities and configuration from a central repository, and why don't I have one of those myself? Double oops.)
[ Previously; previouslier ]
[Other articles in category /oops] permanent link
Mon, 24 Jan 2022
Excessive precision in crib slat spacing?
A couple of years back I wrote:
You sometimes read news articles that say that some object is 98.42 feet tall, and it is clear what happened was that the object was originally reported to be 30 meters tall …
As an expectant parent, I was warned that if crib slats are too far apart, the baby can get its head wedged in between them and die. How far is too far apart? According to everyone, 2⅜ inches is the maximum safe distance. Having been told this repeatedly, I asked in one training class if 2⅜ inches was really the maximum safe distance; had 2½ inches been determined to be unsafe? I was assured that 2⅜ inches was the maximum. And there's the opposite question: why not just say 2¼ inches, which is presumably safe and easier to measure accurately?
But sometime later I guessed what had happened: someone had determined that 6 cm was a safe separation, and 6cm is 2.362 inches. 2⅜ inches exceeds this by only !!\frac1{80}!! inch, about half a percent. 7cm would have been 2¾ in, and that probably is too big or they would have said so.
The 2⅜, I have learned, is actually codified in U.S. consumer product safety law. (Formerly it was at 16 CFR 1508; it has since moved and I don't know where it is now.) And looking at that document I see that it actually says:
The distance between components (such as slats, spindles, crib rods, and corner posts) shall not be greater than 6 centimeters (2⅜ inches) at any point.
Uh huh. Nailed it.
I still don't know where they got the 6cm from. I guess there is someone at the Commerce Department whose job is jamming babies’ heads between crib bars.
[Other articles in category /tech] permanent link
Sun, 23 Jan 2022
Annoying mathematical notation
Recently I've been thinking that maybe the thing I really dislike about set theory might the power set axiom. I need to do a lot more research about this, so any blog articles about it will be in the distant future. But while looking into it I ran across an example of a mathematical notation that annoyed me.
This paper of Gitman, Hamkins, and Johnstone considers a subtheory of ZFC, which they call “!!ZFC-!!”, obtained by omitting the power set axiom. Fine so far. But the main point of the paper:
Nevertheless, these deficits of !!ZFC-!! are completely repaired by strengthening it to the theory !!ZFC^−!!, obtained by using collection rather than replacement in the axiomatization above.
Got that? They are comparing two theories that they call “!!ZFC-!!” and “!!ZFC^-!!”.
(Blog post by Gitman (archived))
[ Previously ]
[Other articles in category /math] permanent link
Sat, 22 Jan 2022A couple of weeks ago I had this dumb game on my phone, there are these characters fighting monsters. Each character has a special power that charges up over time, and then when you push a button the character announces their catch phrase and the special power activates.
This one character with the biggest hat had the catch phrase
I follow my own destiny!
and I began to dread activating this character's power. Every time, I wanted to grab them by the shoulders and yell “That's what destiny is, you don't get a choice!” But they kept on saying it.
So I had to delete the whole thing.
[Other articles in category /misc] permanent link
Fri, 21 Jan 2022
A proposal for improved language around divisibility
Divisibility and modular residues are among the most important concepts in elementary number theory, but the terminology for them is clumsy and hard to pronounce.
- !!n!! is divisible by !!5!!
- !!n!! is a multiple of !!5!!
- !!5!! divides !!n!!
The first two are 8 syllables long. The last one is tolerably short but is backwards. Similarly:
- The mod-!!5!! residue of !!n!! is !!3!!
is awful. It can be abbreviated to
- !!n!! has the form !!5k+3!!
but that is also long, and introduces a dummy !!k!! that may be completely superfluous. You can say “!!n!! is !!3!! mod !!5!!” or “!!n!! mod !!5!! is !!3!!” but people find that confusing if there is a lot of it piled up.
Common terms should be short and clean. I wish there were a mathematical jargon term for “has the form !!5k+3!!” that was not so cumbersome. And I would like a term for “mod-5 residue” that is comparable in length and simplicity to “fifth root”.
For mod-!!2!! residues we have the special term “parity”. I wonder if something like “!!5!!-ity” could catch on? This doesn't seem too barbaric to me. It's quite similar to the terminology we already use for !!n!!-gons. What is the name for a polygon with !!33!! sides? Is it a triskadekawhatever? No, it's just a !!33!!-gon, simple.
Then one might say things like:
“Primes larger than !!3!! have !!6!!-ity of !!±1!!”
“The !!4!!-ity of a square is !!0!! or !!1!!” or “a perfect square always has !!4!!-ity of !!0!! or !!1!!”
“A number is a sum of two squares if and only its prime factorization includes every prime with !!4!!-ity !!3!! an even number of times.”
“For each !!n!!, the set of numbers of !!n!!-ity !!1!! is closed under multiplication”
For “multiple of !!n!!” I suggest that “even” and “odd” be extended so that "!!5!!-even" means a multiple of !!5!!, and "!!5!!-odd" means a nonmultiple of !!5!!. I think “!!n!! is 5-odd” is a clear improvement on “!!n!! is a nonmultiple of 5”:
“The sum or product of two !!n!!-even numbers is !!n!!-even; the product of two !!n!!-odd numbers is !!n!!-odd, if !!n!! is prime, but the sum may not be. (!!n=2!! is a special case)”
“If the sum of three squares is !!5!!-even, then at least one of the squares is !!5!!-even, because !!5!!-odd squares have !!5!!-ity !!±1!!, and you cannot add three !!±1's!! to get zero”
“A number is !!9!!-even if the sum of its digits is !!9!!-even”
It's conceivable that “5-ity” could be mistaken for “five-eighty” but I don't think it will be a big problem in practice. The stress is different, the vowel is different, and also, numbers like !!380!! and !!580!! just do not come up that often.
The next mouth-full-of-marbles term I'd want to take on would be “is relatively prime to”. I'd want it to be short, punchy, and symmetric-sounding. I wonder if it would be enough to abbreviate “least common multiple” and “greatest common divsor” to “join” and “meet” respectively? Then “!!m!! and !!n!! are relatively prime” becomes “!!m!! meet !!n!! is !!1!!” and we get short phrasings like “If !!m!! is !!n!!-even, then !!m!! join !!n!! is just !!m!!”. We might abbreviate a little further: “!!m!! meet !!n!! is 1” becomes just “!!m!! meets !!n!!”.
[ Addendum: Eirikr Åsheim reminds me that “!!m!! and !!n!! are coprime” is already standard and is shorter than “!!m!! is relatively prime to !!n!!”. True, I had forgotten. ]
[Other articles in category /math] permanent link
Thu, 20 Jan 2022Instead of multiplying the total by 3 at each step, you can multiply it by 2, which gives you a (correct but useless) test for divisibility by 8.
But one reader was surprised that I called it “useless”, saying:
I only know of one test for divisibility by 8: if the last three digits of a number are divisible by 8, so is the original number. Fine … until the last three digits are something like 696.
Most of these divisibility tricks are of limited usefulness, because they are not less effort than short division, which takes care of the general problem. I discussed short division in the first article in this series with this example:
Suppose you want to see if 1234 is divisible by 7. It's 1200-something, so take away 700, which leaves 500-something. 500-what? 530-something. So take away 490, leaving 40-something. 40-what? 44. Now take away 42, leaving 2. That's not 0, so 1234 is not divisible by 7.
For a number like 696, take away 640, leaving 56. 56 is divisible by 8, so 696 is also. Suppose we were doing 996 instead? From 996 take away 800 leaving 196, and then take away 160 leaving 36, which is not divisible by 8. For divisibility by 8 you can ignore all but the last 3 digits but it works quite well for other small divisors, even when the dividend is large.
This not not what I usually do myself, though. My own method is a bit hard to describe but I will try. The number has the form !!ABB!! where !!BB!! is a multiple of 4, or else we would not be checking it in the first place. The !!BB!! part has a ⸢parity⸣, it is either an even multiple of 4 (that is, a multiple of 8) or an odd multiple of 4 (otherwise). This ⸢parity⸣ must match the (ordinary) parity of !!A!!. !!ABB!! is divisible by 8 if and only if the parities match. For example, 104 is divisible by 8 because both parts are ⸢odd⸣. Similarly 696 where both parts are ⸢even⸣. But 852 is not divisible by 8, because the 8 is even but the 52 is ⸢odd⸣.
[Other articles in category /math] permanent link
Wed, 19 Jan 2022The news today contains the story “Italian Senate Accidentally Plays 30 Seconds Of NSFW Tifa Lockhart Video” although I have not been able to find any source I would consider reliable. TheGamer reports:
The conference was hosted Monday by Nobel Prize winner Giorgio Parisi and featured several Italian senators. At some point during the Zoom call, a user … broke into the call and started broadcasting hentai videos.
Assuming this is accurate, it is disappointing on so many levels. Most obviously because if this was going to happen at all one would hope that it was an embarrassing mistake on the part of someone who was invited to the call, perhaps even the Nobel laureate, and not just some juvenile vandal who ran into the room with a sock on his dick.
If someone was going to go to the trouble of pulling this prank at all, why some run-of-the mill computer-generated video? Why not something really offensive? Or thematically appropriate, such as a scene from one of Cicciolina's films?
I think the guy who did this should feel ashamed of his squandered opportunity, and try a little harder next time. The world is watching!
[Other articles in category /misc] permanent link
The squares are kinda Fibonacci-like
I got a cute little surprise today. I was thinking: suppose someone gives you a large square integer and asks you to find the next larger square. You can't really do any better than to extract the square root, add 1, and square the result. But if someone gives you two consecutive square numbers, you can find the next one with much less work. Say the two squares are !!b = n^2!! and !!a = n^2+2n+1!!, where !!n!! is unknown. Then you want to find !!n^2+4n+4!!, which is simply !!2a-b+2!!. No square rooting is required.
So the squares can be defined by the recurrence $$\begin{align} s_0 & = 0 \\ s_1 & = 1 \\ s_{n+1} & = 2s_n - s_{n-1} + 2\tag{$\ast$} \end{align} $$
This looks a great deal like the Fibonacci recurrence:
$$\begin{align} f_0 & = 0 \\ f_1 & = 1 \\ f_{n+1} & = f_n + f_{n-1} \end{align} $$
and I was a bit surprised because I thought all those Fibonacci-ish recurrences turned out to be approximately exponential. For example, !!f_n = O(\phi^n)!! where !!\phi=\frac12(1 + \sqrt 5)!!. And actually the !!f_0!! and !!f_1!! values don't matter, whatever you start with you get !!f_n = O(\phi^n)!!; the differences are small and are hidden in the Landau sign.
Similarly, if the recurrence is !!g_{n+1} = 2g_n + g_{n-1}!! you get !!g_n = O((1+\sqrt2)^n)!!, exponential again. So I was surprised that !!(\ast)!! produced squares instead of something exponential.
But as it turns out, it is producing something exponential. Sort of. Kind of. Not really.
!!\def\sm#1,#2,#3,#4{\left[\begin{smallmatrix}{#1}&{#2}\\{#3}&{#4}\end{smallmatrix}\right]}!!
There are a number of ways to explain the appearance of the !!\phi!! constant in the Fibonacci sequence. Feel free to replace this one with whatever you prefer: The Fibonacci recurrence can be written as $$\left[\matrix{1&1\\1&0}\right] \left[\matrix{f_n\\f_{n-1}}\right] = \left[\matrix{f_{n+1}\\f_n}\right] $$ so that $$\left[\matrix{1&1\\1&0}\right]^n \left[\matrix{1\\0}\right] = \left[\matrix{f_{n+1}\\f_n}\right] $$
and !!\phi!! appears because it is the positive eigenvalue of the square matrix !!\sm1,1,1,0!!. Similarly, !!1+\sqrt2!! is the positive eigenvalue of the matrix !!\sm 2,1,1,0!! that arises in connection with the !!g_n!! sequences that obey !!g_{n+1} = 2g_n + g_{n-1}!!.
For !!s_n!! the recurrence !!(\ast)!! is !!s_{n+1} = 2s_n - s_{n-1} + 2!!, Briefly disregarding the 2, we get the matrix form
$$\left[\matrix{2&-1\\1&0}\right]^n \left[\matrix{s_1\\s_0}\right] = \left[\matrix{s_{n+1}\\s_n}\right] $$
and the eigenvalues of !!\sm2,-1,1,0!! are exactly !!1!!. Where the Fibonacci sequence had !!f_n \approx k\cdot\phi^n!! we get instead !!s_n \approx k\cdot1^n!!, and instead of exploding, the exponential part remains well-behaved and the lower-order contributions remain significant.
If the two initial terms are !!t_0!! and !!t_1!!, then !!n!!th term of the sequence is simply !!t_0 + n(t_1-t_0)!!. That extra !!+2!! I temporarily disregarded in the previous paragraph is making all the interesting contributions: $$0, 0, 2, 6, 12, 20, \ldots, n(n-1) \ldots$$ and when you add the !!t_0 + n(t_1-t_0)!! and put !!t_0=0, t_1=1!! you get the squares.
So the squares can be considered a sort of Fibonacci-ish approximately exponential sequence, except that the exponential part doesn't matter because the base of the exponent is !!1!!.
How about that.
[Other articles in category /math] permanent link
Tue, 18 Jan 2022This morning Katara and I were taking our vitamins, and Katara asked why vitamin K was letter “K”.
I said "It stands for ‘koagulation’.”
“No,” replied Katara.
“Yes,” I said.
“No.”
“Yes.”
By this time she must have known something was up, because she knows that I will make up lots of silly nonsense, but if challenged I will always recant immediately.
“‘Coagulation’ doesn't start with a ‘K’.”
Lorrie says she discovered the secret to dealing with me, thirty years ago: always take everything I say at face value. The unlikely-seeming things are true more often than not, and the few that aren't I will quickly retract.
[Other articles in category /misc] permanent link
I started to write an addendum to last week's article about how Mike Wazowski is not scary:
I have to admit that if Mike Wazowski popped out of my closet one night, I would scream like a little boy.
And then I remembered something I haven't thought of for a long, long time.
My parents owned a copy of this poster, originally by an artist named Karl Smith:

When I was a small child, maybe three or four, I was terrified of the creature standing by the word “Night”:
One night after bedtime I was dangling my leg over the edge of the bed and something very much like this creature popped right up through the floor and growled at me to get back in bed. I didn't scream, but it scared the crap out of me.
I no longer remember why I was so frightened by this one creature in particular, rather than say the snail-bodied flamingo or the dimetrodon with the head of Shaggy Rogers. And while are obviously a lot of differences between this person and Mike Wazowski (most obviously, the wrong number of eyes) there are also some important similarities. If Mike himself had popped out of the floor I would probably have been similarly terrified.
So, Mike, if you're reading this, please know that I accept your non-scariness not as a truly held belief, but only as a conceit of the movie.
[ If any of my Gentle Readers knows anything more about Karl Smith or this poster in particular, I would be very interested to hear it. ]
[Other articles in category /brain] permanent link
Sun, 16 Jan 2022Yesterday I related Wikitionary's explanation of why Vladamir Putin's name is transliterated in French as Poutine:
in French, “Putin” would be pronounced /py.tɛ̃/, exactly like putain, which means “whore”.
In English we don't seem to be so quivery. Plenty of people are named “Hoare”. If someone makes a joke about the homophone, people will just conclude that they're a boor. “Hoare” or “hoar” is an old word for a gray-white color, one of a family of common hair-color names along with “Brown”, “White”, and “Grey”.
There is a legend at Harvard University that its twelve residential houses are named for the first twelve presidents of Harvard: Dunster House, Eliot House, Mather House, and so on. Except, says the legend, they were unwilling to name a house after the fourth president, Leonard Hoar, and called it North House instead. The only part of this that is true is that most of the houses were named for presidents of Harvard.
(The common name “Green” is not a hair-color name. It refers to someone who lives by the green.)
[ Addendum 20221030: Yet more on this ridiculous topic. ]
[Other articles in category /lang] permanent link
I don't even want to know what happened here.
All I can think of is this guy:
[ Addendum: Joe Ardent informs me that the suggestions are actually provided by Goofle. ]
[Other articles in category /misc] permanent link
Sat, 15 Jan 2022In French Canada, poutine is a dish of fried potatoes with cheese curds and brown gravy. But today I learned that in French, Vladimir Putin's name is Vladimir Poutine.

| = | 
|
| Poutine |
Wiktionary explains: in French, “Putin” would be pronounced /py.tɛ̃/, exactly like putain, which means “whore”. “Poutine” is silly, but at least comparatively inoffensive.
Mario Tremblay of Montréal gave in to temptation, and opened a poutine restaurant named “Vladimir Poutine". There was a poutine dish on the menu named “Vladimir Poutine”. In a sort of nod to borscht, it was topped with beet confit. The restaurant has since closed.
[ Other people who are accidentally foods ]
Left-hand poutine photograph by Joe Shlabotnik from Forest Hills, Queens, USA, CC BY 2.0 https://creativecommons.org/licenses/by/2.0, via Wikimedia Commons. Right-hand photograph also via Wikimedia Commons.
[ Addendum 20220116: Further musings on names with bad homophones ]
[ Addendum 20220307: a Paris restaurant, La Maison de la Poutine, defends itself against insults and threats from people confused about the meaning of poutine in the restaurant's name. Further reporting from Business Insider. ]
[ Addendum 20221030: Yet more names with bad homophones ]
[Other articles in category /lang] permanent link
Thu, 13 Jan 2022
Monsters University was a refreshing departure from the moral inanity of the typical kids’ movie
Back when it was fresh, I read this 2013 article by Luke Epplin, You Can Do Anything: Must Every Kids' Movie Reinforce the Cult of Self-Esteem?, and I've wanted to blog about it ever since. I agree with the author's thesis, which is:
No genre in recent years has been more thematically rigid than the computer-animated children's movie. … These movies revolve around anthropomorphized outcasts who must overcome the restrictions of their societies or even species to realize their impossible dreams.
Having had two kids grow up during that decade, I sympathize and agree. I have one serious complaint with the article, though. Epplin gives a list of examples:
- Kung Fu Panda (fat panda becomes kung fu master)
- Ratatouille (rat becomes French chef)
- Wreck-It Ralph (“8-bit villain yearns to be a video-game hero”)
- Monsters University (“unscary monster pursues a career as a top-notch scarer”)
- Turbo (“common garden snail … dreams of racing glory”)
- Planes (“unsatisfied crop-duster yearns to … compete in the famed Wings Around the Globe race”)
Yes, okay, I agree. I have only one complaint. This is terribly unjust to Monsters University.
I am not a fan of Monsters University. I don't regret seeing it once, but I will not be disappointed if I never see it again. But it does not belong in that list. I came out of the theatre saying “wow, at least it wasn't that same old Disney bullshit”. Monsters University is very consciously a negative reaction to the cult-of-self-esteem movies, a repudiation of them.
Monsters University sets up the same situation as the other self-esteem movies: the protagonist, Mike Wazowski, wants desperately to be a “scarer”, one of the monsters who pops out of a closet to scare a child after bedtime. He wants it so much! He works so hard! He may be competing against scarier monsters, but none of them has Mike's drive, they're all coasting on their actual talent. None has Mike's dreams or his commitment. None has learned as much about the theory and technique of scaring.
There's a problem, though: Mike, voiced by Billy Crystal, isn't scary.

Epplin complains:
The restless protagonists of these films never have to wake up to the reality that crop-dusters simply can't fly faster than sleek racing aircraft. Instead, it's the naysaying authority figures who need to be enlightened about the importance of never giving up on your dreams, no matter how irrational, improbable, or disruptive to the larger community.
Monsters University has that naysaying authority figure, a college dean (Helen Mirren) who tells Mike in three words why he will never be a scarer: “You're not scary.” Mike is determined to prove her wrong!
Mike fails.
Catastrophically, humiliatingly, disgracefully. The movie is merciless.
Any success Mike appeared to have was illusory, procured by cheating. (Mike was unaware of the cheating, but in the depths of his self-deception he doesn't question his improbable success.) In fact the dean was exactly right: Mike isn't scary. As anyone can see by looking at him.
After being exposed as a cheat, Mike is expelled from Monsters University.
An epilogue shows that Mike and his friend Sully have gotten jobs working in the mail room of the power plant where the real scarers work. They work their way up to the cafeteria, and beyond. It's a long, hard slog, and takes years, but the road ends in success: Sully (who is scary) is a top scarer, and (as we know from Monsters, Inc.) Mike is his coach and support, accomplished, respected, and admired as an indispensable part of Sully's top-performing team.
The naysaying dean is never refuted. She's right. Mike isn't scary. And even if he had been, he's more valuable as Sully's pit crew. He's found his real calling.
As I said, I didn't think much of the movie. But it absolutely did not follow the formula. And its moral lessons are ones I can really get behind. Not “never give up on your dreams, no matter how irrational”, which is stupid advice. But instead “life has ups and downs but goes on” and “success, when it comes, takes a lot of toil and hard work”. And one of my favorites: “play the hand you're dealt”.
(For some other articles appreciating Monsters University's unusual willingness to engage with failure and subsequent course correction, see “‘Monsters University’, Failure, and ‘Rudy’” and “Monsters University and the importance of failure in pop culture”.)
[ Addendum 20220118: It must be admitted that Mike Wazowski would be damn scary if run into unexpectedly. But movies are movies. ]
[Other articles in category /movie] permanent link
Sun, 09 Jan 2022
Many presentations of axiomatic set theory contain an error
[ Content warning: highly technical mathematics ]
[ Addendum 20220223: Also, I was mistaken. ]
I realized recently that there's a small but significant error in many presentations of the Zermelo-Frankel set theory: Many authors omit the axiom of the empty set, claiming that it is omittable. But it is not.
The overarching issue is as follows. Most of the ZF axioms are of this type:
If !!\mathcal A!! is some family of sets, then [something derived from !!\mathcal A!!] is also a set.
The axiom of union is a typical example. It states that if !!\mathcal A!! is some family of sets, then there is also a set !!\bigcup \mathcal A!!, which is the union of the members of !!\mathcal A!!. The other axioms of this type are the axioms of pairing, specification, power set, replacement, and choice.
There is a minor technical problem with this approach: where do you get the elements of !!\mathcal A!! to begin with? If the axioms only tell you how to make new sets out of old ones, how do you get started? The theory is a potentially vacuous one in which there aren't any sets! You can prove that if there were any sets they would have certain properties, but not that there actually are any such things.
This isn't an entirely silly quibble. Prior to the development of axiomatic set theory, mathematicians had been using a model called naïve set theory, and after about thirty years it transpired that the theory was inconsistent. Thirty years of work about a theory of sets, and then it turned out that there was no possible universe of sets that satisfied the requirements of the theory! This precipitated an upheaval in mathematics a bit similar to the quantum revolution in physics: the top-down view is okay, but the most basic underlying theory is just wrong.
If we can't prove that our new theory is consistent, we would at least like to be sure it isn't trivial, so we would like to be sure there are actually some sets. To ensure this, the very least we can get away with is this axiom:
!!A_S!!: There exists a set !!S!!.
This is enough! From !!A_S!! and specification, we can prove that there is an empty subset of !!S!!. Then from extension, we can prove that this empty subset is the unique empty set. This justifies assigning a symbol to it, usually !!\varnothing!! or just !!0!!. Once we have the empty set, pairing gives us !!\{0,0\} = \{0\} = 1!!, then !!\{0, 1\} = 2!! , and so on. Once we have these, the axioms of union and infinity show that !!\omega!! is a set, then from that the axiom of power sets gets us uncountable sets, and the sky is the limit. But we need something like !!A_S!! to get started.
In place of !!A_S!! one can have:
!!A_\varnothing!!: There exists a set !!\varnothing!! with the property that for all !!x!!, !!x\notin\varnothing!!.
Presentations of ZF sometimes include this version of the axiom. It is easily seen to be equivalent to !!A_S!!, in the sense that from either one you can prove the other.
I wanted to see how this was handled in Thomas Jech's Set Theory, which is a standard reference text for axiomatic set theory. Jech includes a different version of !!A_S!!, initially given (page 3) as:
!!A_∞!!: There exists an infinite set.
This is also equivalent to !!A_S!! and !!A_\varnothing!!, if you are willing to tolerate the use of the undefined term “infinite”. Jech of course is perfectly aware that while this is an acceptable intuitive introduction to the axiom of infinity, it's not formally meaningful without a definition of “infinite”. When he's ready to give the formal version of the axiom, he states it like this:
$$\exists S (\varnothing \in S\land (\forall x\in S) x\cup\{x\}\in S).$$
(“There is a set !!S!! that includes !!\varnothing!! and, whenever it includes some !!x!!, also includes !!x\cup\{x\}!!.” (3rd edition, p. 12))
Except, oh no, “!!\varnothing!!” has not yet been defined, and it can't be, because the thing we want it to refer to cannot, at this point, be proved to actually exist.
Maybe you want to ask why we can't use it without proving that it exists. That is exactly what went wrong with naïve set theory, and we don't want to repeat that mistake.
I brought this up on math Stack Exchange and Asaf Karagila, the resident axiomatic set theory expert, seemed to wonder why I complained about !!\varnothing!! but not about !!\{x\}!! and !!\cup!!. But the issue doesn't come up with !!\{x\}!! and !!\cup!!, which can be independently defined using the axioms of pairing and union, and then used to state the axiom of infinity. In contrast, if we're depending on the axiom of infinity to prove the existence of !!\varnothing!!, it's circular for us to assume it exists while writing the statement of the axiom. We can't depend on !!A_∞!! to define !!\varnothing!! if the very meaning of !!A_∞!! depends on !!\varnothing!! itself.
That's the error: the axioms, as stated by Jech, are ill-founded. This is a little hard to see because of the way he prevaricates the actual statement of the axiom of infinity. On page 8 he states !!A_\varnothing!!, which would work if it were included, but he says “we have not included [!!A_\varnothing!!] among the axioms, because it follows from the axiom of infinity.”
But this is wrong. You really do need an explicit axiom like !!A_\varnothing!! or !!A_S!!. As far as I can tell, you cannot get away without it.
This isn't specifically a criticism of Jech or the book; a great many presentations of axiomatic set theory make the same mistake. I used Jech as an example because his book is a well-known authority. (Otherwise people will say “well perhaps, but a more careful writer would have…”. Jech is a careful writer.)
This is also not a criticism of axiomatic set theory, which does not collapse just because we forgot to include the axiom of the empty set.
[ Addendum 20220223: As could perhaps have been predicted, I was mistaken. Details here. Thanks to Math SE user Eike Schulte for explaining my error in a way I could understand. ]
[ Addendum 20220224: A bit more about this. ]
[Other articles in category /math] permanent link
Thu, 06 Jan 2022
Another test for divisibility by 7
[ Previously ]
Recently I thought of another way to check for divisibility by !!7!!. Let's consider !!\color{darkblue}{3269}!!. The rule is: take the current total (initially 0), triple it, and add the next digit to the right. So here we do:
$$ \begin{align} \color{darkblue}{3}·3 & + \color{darkblue}{2} & = && \color{darkred}{11} \\ \color{darkred}{11}·3 & + \color{darkblue}{6} & = && \color{darkred}{39} \\ \color{darkred}{39}·3 & + \color{darkblue}{9} & = && \color{darkred}{126} \\ \end{align} $$
and the final number, !!\color{darkred}{126} !!, is a multiple of !!7!! if and only if the initial one was. If you're not sure about !!126!! you can check it the same way:
$$ \begin{align} \color{darkblue}{1} ·3 & + \color{darkblue}{2} & = && \color{darkred}{5} \\ \color{darkred}{5} ·3 & + \color{darkblue}{6} & = && \color{darkred}{21} \\ \end{align} $$
If you're not sure about !!\color{darkred}{21} !!, you calculate !!2·3+1=7!! and if you're not sure about !!7!!, I can't help.
You can simplify the arithmetic by reducing everything mod !!7!! whenever it gets inconvenient, so checking !!3269!! really looks like this:
$$ \begin{align} \color{darkblue}{3} ·3 & + \color{darkblue}{2} & = && 11 = \color{darkred}{4} \\ \color{darkred}{4} ·3 & + \color{darkblue}{6} & = && 18 = \color{darkred}{4} \\ \color{darkred}{4} ·3 & + \color{darkblue}{9} & = && 21 = \color{darkred}{0} \\ \end{align} $$
This is actually practical.
I'm so confident this is already in the Wikipedia article about divisibility testing that I didn't bother to actually check. But I did check the email that Eric Roode sent me in 2018 about divisibility testing, and confirmed that it was in there.
Instead of multiplying the total by 3 at each step, you can multiply it by 2, which gives you a (correct but useless) test for divisibility by 8. Or you can multiply it by 1, which gives you the usual (correct and useful) test for divisibility by 9. Or you can multiply it by 0, which gives you a slightly silly (but correct) version of the usual test for divisibility by 10. Or you can multiply it by -1, which which gives you exactly the usual test for divisibility by 11.
You can of course push it farther in either direction, but none of the results seems particularly interesting as a practical divisibility test.
I wish I had known about this as a kid, though, because I would probably have been interested to discover that the pattern continues to work: if at each step you multiply by !!k!!, you get a test for divisibility by !!10-k!!. Sure, you can take !!k=9!! or !!k=10!! if you like, go right ahead, it still works.
And if you do it for base-!!r!! numerals, you get a test for divisibility by !!r-k!!, so this is a sort of universal key to divisibility tests. In base 16, the triple-and-add method tests not for divisibility by 7 but for divisibilty by 13. If you want to test for divisibility by !!7!! you can use double-and-add instead, which is a nice wrinkle.
The tests you get aren't in general any easier than just doing short division, of course. At least they are easy to remember!
[Other articles in category /math] permanent link
Tue, 04 Jan 2022
All polynomials of degree 3 or greater factor over the reals
A couple of years ago I wrote:
One day when I was in high school, I bumped into the fact that !!\sqrt{7 + 4 \sqrt 3}!!, which looks just like a 4th-degree number, is actually a 2nd-degree number. It's numerically equal to !!2 + \sqrt 3!!. At the time, I was totally boggled.
I had a kind of similar surprise around the same time in connection with the polynomial !!x^4+1!!.
Everyone in high school algebra learns that !!x^2-1 = (x-1)(x+1)!! but that !!x^2+1!! does not similarly factor over the reals; in the jargon it is irreducible.
Every cubic polynomial does factor over the reals, though, because every cubic polynomial has a real root, and a polynomial with real root !!r!! has !!x-r!! as a factor; this is Descartes’ theorem. (It's easy to explain why all cubic polynomials have roots. Every cubic polynomial !!P(x)!! has the form !! ax^3!! plus some lower-order terms. As !!x!! goes to !!±∞!! the lower-order terms are insignificant and !!P(x)!! goes to !!a·±∞!!. Since the value of !!P(x)!! changes sign, !!P(x)!! must be zero at some point.)
For example, $$\begin{align} x^3+1 & = (x+1)(x^2- x+1) \\ x^3-1 & = (x-1)(x^2+ x+1) \\ \end{align}$$
So: polynomials with real roots always factor, cubics always have roots, so cubics factor. Also !!x^2+1!! has no real roots, and doesn't factor. And !!x^4+1!!, which looks pretty much the same as !!x^2+1!!, also has no real roots, and so behaves the same as !!x^2+1!! so doesn't factor…
Wrong! It has no real roots, true, but it still factors over the reals:
$$x^4+1 = (x^2 + \sqrt2· x + 1) (x^2 - \sqrt2· x + 1)$$
Neither of the two factors has a real root. I was kinda blown away by this, sometime back in the 1980s.
The fundamental theorem of algebra tells us that the only irreducible real polynomials have degree 1 or 2. Every polynomial of degree 3 or higher can be expressed as a product of polynomials of degrees 1 and 2. I knew this, but somehow didn't put the pieces together in my head.
Raymond Smullyan observes that almost everyone has logically inconsistent beliefs. His example is that while you individually believe a large number of separate claims, you probably also believe that at least one of those claims is false, so you don't believe their conjunction. This is an example of a completely different type: I simultaneously believed that every polynomial had roots over the complex numbers, and also that !!x^4+1!! was irreducible.
[ Addendum 20220221: I didn't remember when I wrote this that I had already written essentially the same article back in 2006. ]
[Other articles in category /math] permanent link