Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Thu, 20 Apr 2023
Math SE report 2023-04: Simplest-possible examples, pointy regions, and nearly-orthogonal vectors
Polyhedra has more corners than facets
This one was a bit puzzling because it asked:
Is it true that [a polyhedron] has always more/as many corners than facets? I haven't found a counterexample…
(By ‘facets’ I assume OP meant ‘faces’.)
This is puzzling because there are so many counterexamples. For example, every dipyramid has this property. A dipyramid is what you get if you take two pyramids and glue their bases together. Maybe you want to say this is obscure, but an octahedron is a dipyramid and one might expect anyone asking about polyhedra to know about octahedra. I wonder what examples this person did consider?
In fact, for any polyhedron with !!F!! faces and !!V!! vertices, there is a corresponding “dual” polyhedron with !!V!! faces and !!F!! vertices, so for almost any polyhedron you can think of, if that polyhedron is not already a counterexample, then its dual is. A cube is not, but its dual is — this is the octahedron again.
Finding sets !!A!!, !!B!!, and !!C!! such that !!A\in B!!, !!B \in C!!, but !!A \notin C!!
I thought this one was pedagogically interesting. OP made a mistake in their approach that is quite common:
The problem tells us !!B = \{A,b_1,b_2,\ldots\}!! and !!C = \{B,c_1,c_2\}!!.
The mistake OP made here was to start by trying to find the most general possible example. Yes, if !!A\in B!! then in general !!B = \{A,b_1,b_2,\ldots\}!!. This might be a more helpful observation if the question had asked for some universal property of all such !!A, B, C!!. Then you could add constraints to the general case and see if you had anything left at the end. But this problem only asked for one example. So instead of considering the most general case of !!A\in B!!, and therefore the most complex form of the idea, the first thing one should try is the simplest possible example of !!A\in B!!, which is just !!B = \{A\}.!!
Then similarly one should try !!C = \{B\}!!. Obviously the required properties !!A\in B!! and !!B\in C!! are satisfied. What about !!A\notin C!!?
Since the only element of !!C!! is !!B!!, the answer is easy: !!A\notin C!! unless !!A=B = \{A\}!!
So now we just have to avoid !!A=\{A\}!!. Again let's try the simplest thing that could possibly work: !!A=\emptyset!!. And then we win, because indeed !!\emptyset\ne \{\emptyset\}!!, since the left side is empty and the right side isn't.
Did we get lucky here? No! The axiom of foundation guarantees that literally any !!A!! will work. But you don't have to know that to find an example, because literally any !!A!! will work.
This is Lower Mathematics in action. The abstract approach is useful if you are trying to prove some theorem, but if all you want is to find an example, the abstract approach is overkill.
Volume obtained by rotating a region around two different lines
OP considered the region bounded by the curves !!y=x^2!! and !!y=\sqrt x!! for !!0\le x, y\le 1!!, and then the solids of revolution obtained by revolving this region around the lines !!y=0!! and !!y=1!!. They said:
I expected the volume obtained by rotating about !!y=1!! to be identical with the volume obtained by rotating about the !!x!!-axis. To my surprise, calculation shows different results.
Many people would have posted an answer to this that simply did the calculation, sometimes one with no words in it. But I think this misses the point of the question, which is about OP's intuition. Why were they wrong?
Something that has been on my mind lately is an elaboration of a certain principle of pedagogy. Everyone knows the principle:
It's not enough to show the student the answer; you should try to show them how to find the answer.
Not everyone follows this, but at least most people are aware of it.
But my decades of experience watching people teach math have led me to believe that this is insufficient. There's a higher-order version of this principle that is also important:
It's not enough to show the student how you can find the answer; you should try to show them how they could have found the answer.
And by ‘they’ I don't mean ‘a student’; I mean the student, the specific one sitting in front of you, who knows what they know and can do what they can do.
This is hard.
(I think the !!A\in B, B\in C, A\notin C!! thing above is another example of this. Three people answered that question by pulling solutions out of thin air, but how much does that help OP solve the next problem of this type?)
Anyway, I digress. The region in question looks like this:
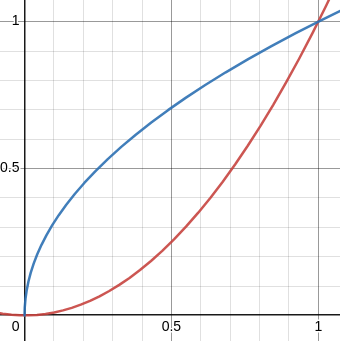
I observed that the upper end is much narrower than the lower end. You could count boxes to verify this, but I think it's obvious, and said:
Which end would you rather be poked with?
Then I pointed out that if you revolve the region around !!y=1!!, the thick end travels a long way and sweeps out a large volume, whereas if you revolve it around !!y=0!! the thick end is closer to the axis of revolution, so does not sweep out so much volume. So just from looking at the picture, one might guess that the volume will be larger when revolved around !!y=1!!, which is what OP originally reported.
I did not actually do the calculation, so it's conceivable that I was utterly wrong, but I suspect not.
Definition of Graph Isomorphism
This was not that interesting, but it is a demonstration of a couple of things:
Finding the simplest possible example
Because it's usually easier for someone to understand a simple example well enough to generalize it than it is for them to understand an abstract, general construction well enough to specialize it to an example.
Math SE will often ignore subtle answers to challenging questions, while giving many upvotes to trivialities
This post and the octahedron one were my most upvoted posts of the month and also the most trivial. This is why one should ignore upvotes: they are not correlated with anything of real importance.
Help understanding proof: classifying groups of order 21
I may have kinda blown this one. My answer was way too long. OP was asking about specific steps in some group theory proof, ultimately related to the formula $$(aba^{-1})^n = ab^na^{-1}.$$
Algebraically this is quite easy to show, and I did. But it also has deep and essential intuitive content, which I summarized like this:
It says that if you are going to repeat several times the operation of turning your head, then doing !!b!!, then turning your head back, you can skip some of the head-turning and just turn your head once, do operation !!b!! repeatedly, and turn your head back at the end.
This !!aba^{-1}!! thing, called “conjugation”, is incredibly important in group theory, and I have often felt that my group theory course did not make this clear. As I recall the course observed that the mapping !!\varphi_a : x\mapsto axa^{-1}!! is always a group automorphism, went on from there. Which indeed it is, but so what? Why do we care about that particular transformation, anyway?
But the intuitive content of the statement about the automophism is that the symmetries of an object don't change when you turn your head. That's why it's important!
When are two rotations of a sphere conjugate? Exactly when they rotate by the same amount around their respective axes. (“Turn your head!”)
Why are two permutations conjugate if and only if they have the same cycle structure? Because this exactly when they are equivalent under renaming of the objects being permuted; renaming the objects is analogous to "turning your head" for this kind of symmetry.
So whenever the topic of conjugation comes up, I am tempted to launch into a long explanation of the significance of conjugation and its intuitive understanding. Which might have been helpful in this case, but it might have been a completely unnecessary distraction, and I should probably have resisted.
What definition of "nearly orthogonal" would result in "In a 10,000-dimensional space there are millions of nearly orthogonal vectors"?
This was one of those cases where OP asked a very slightly under-baked question and several people jumped in to say it made no mathematical sense at all. (“It's a figure of speech” says one comment. No, it isn't. “I doubt that reference is to a precisely defined concept”, says another. There are more things in heaven and earth, Horatio… “I call bullshit, or imprecise speech,” says a third. Heavens, such foul language!)
I have complained about this at length in the past: I think Math SE persons are too quick to jump from “I have not heard of that” to “it does not exist” and then to “it cannot exist”, or from “I don't quite understand that” to “nobody can understand that” and then to “that is incomprehensible nonsense”.
Two vectors !!u!! and !!v!! are said to be orthogonal if their inner product !!\langle u,v\rangle!! is exactly zero. So if you don't know what “nearly orthogonal” means, you might guess that it means that the inner product is nearly zero: $$\left\lvert \langle u,v\rangle \right\rvert < \epsilon$$ for some small specified !!\epsilon!!. The angle between !!u!! and !!v!! would then be approximately between !!\frac\pi2 - \epsilon!! and !!\frac\pi2 + \epsilon!!, which is nearly a right angle; hence “nearly orthogonal”. This is not exactly subtle thinking.
Another user helpfully linked to a Math Overflow post that discussed essentially the same question, with the title “Almost orthogonal vectors”. So bullshit it isn't, and the question there was sufficiently clear that six people thought it was worth answering, including some guy named Tim Gowers.
I didn't know the answer (although I do now!), but if you don't know the answer, you can still sometimes be useful by writing up the answers of other people who are smarter than yourself, that is called “scholarship”.
In writing it up I almost made a horrible mistake. At one point my draft said something like:
The top answer there gives a bound and claims it is implied by the Johnson-Lindenstrauss lemma. I think the bound might not be quite correct, because the Johnson-Lindenstrauss lemma seems to apply to a somewhat different situation, and…
Fortunately, I realized before posting that that person who had written that answer that was in fact William B. Johnson after whom the Johnson-Lindenstrauss lemma was named, and there was quite a good chance that he did not misapply his own theorem. Heh. Yikes.
It's funny now, but if I had actually made that mistake I would have been mortified.
Also
I have an article with pretty diagrams about how to expand a Taylor series around !!x=\pi!!, with a nice Desmos demonstration that you might enjoy playing with. Press the little ▶️ button in the box that defines the parameter !!a!! and watch the cubic polynomials whip back and forth.
[ Addendum 20230421: Eric Roode says that the animation reminds him of “the robot from Lost in Space sliding back and forth, waving its arms wildly, and saying ‘Danger, Will Robinson! Danger!’”. Same. ]
I have already written a separate article about this post that asks how to compute the integral $$\int_0^{2000} e^{x/2-\lfloor x/2\rfloor}\; dx$$
which you might like to read if you didn't already.
[Other articles in category /math/se] permanent link


