Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 19 Mar 2018
I had a fun idea this morning. As a kid I was really interested in polar coordinates and kind of disappointed that there didn't seem to be any other coordinate systems to tinker with. But this morning I realized there were a lot.
Let !!F(c)!! be some parametrized family of curves that partition the plane, or almost all of the plane, say except for a finite number of exceptions. If you have two such families !!F_1(c)!! and !!F_2(c)!!, and if each curve in !!F_1!! intersects each curve in !!F_2!! in exactly one point (again with maybe a few exceptions) then you have a coordinate system: almost every point !!P!! lies on !!F_1(a)!! and !!F_2(b)!! for some unique choice of !!\langle a, b\rangle!!, and these are its coordinates in the !!F_1–F_2!! system.
For example, when !!F_1(c)!! is the family of lines !!x=c!! and !!F_2(c)!! is the family of lines !!y=c!! then you get ordinary Cartesian coordinates, and when !!F_1(c)!! is the family of circles !!x^2+y^2=c!! and !!F_2(c)!! is the family !!y=cx!! (plus also !!x=0!!) you get standard polar coordinates, which don't quite work because the origin is in every member of !!F_2!!, but it's the only weird exception.
But there are many other families that work. To take a particularly simple example you can pick some constant !!k!! and then take
$$\begin{align} F_1(c): && x & =c \\ F_2(c): && y & =kx+c. \end{align} $$
This is like Cartesian coordinates except the axes are skewed. I did know about this when I was a kid but I considered it not sufficiently interesting.
For a more interesting example, try
$$\begin{align} F_1(c): && x^2-y^2 & =c \\ F_2(c): && xy & =c \end{align} $$
which looks like this:
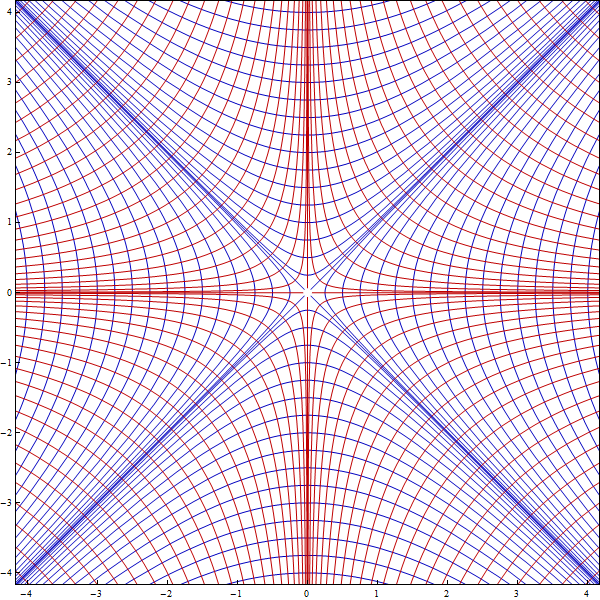 The hyperbolas
!!x^2-y^2 = c!! (in blue) and !!xy=c!! (in red)
The hyperbolas
!!x^2-y^2 = c!! (in blue) and !!xy=c!! (in red)
I've seen that illustration before but I don't think I thought of using it as a coordinate system. Well, okay, every pair of hyperbolas intersects in two points, not one. So it's a parametrization of the boundary of real projective space or something, fine. Still fun!
In the very nice cases (such as the hyperbolas) each pair of curves is orthogonal at their point of intersection, but that's not a requirement, as with the skew Cartesian system. I'm pretty sure that if you have one family !!F!! you can construct a dual family !!F'!! that is orthogonal to it everywhere by letting !!F'!! be the paths of gradient descent or something. I'm not sure what the orthogonality is going to be important for but I bet it's sometimes useful.
You can also mix and match families, so for example take:
$$\begin{align} F_1(c): && x & =c \\ F_2(c): && xy & =c \end{align} $$
Some examples work better than others. The !!xy=c!! hyperbolas are kind of a mess when !!c=0!!, and they don't go together with the !!x^2+y^2=c!! circles in the right way at all: each circle intersects each hyperbola in four points. But it occurs to me that as with the projective plane thingy, we don't have to let that be a problem. Take !!S!! to be the quotient space of the plane where two points are identified if their !!F_1–F_2!!-coordinates are the same and then investigate !!S!!. Or maybe go more directly and take !!S = F_1 \times F_2!! (literally the Cartesian product), and then topologize !!S!! in some reasonably natural way. Maybe just give it the product topology. I dunno, I have to think about it.
(I was a bit worried about how to draw the hyperbola picture, but I tried Google Image search for “families of orthogonal hyperbolas”, and got just what I needed. Truly, we live in an age of marvels!)
[Other articles in category /math] permanent link


