Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 22 Oct 2018
While I was writing up last week's long article about Traversable, I wrote this stuff about Applicative also. It's part of the story but I wasn't sure how to work it into the other narrative, so I took it out and left a remark that “maybe I'll publish a writeup of that later”. This is a disorganized collection of loosely-related paragraphs on that topic.
It concerns my attempts to create various class instance definitions for the following type:
data Tree a = Con a | Add (Tree a) (Tree a)
deriving (Eq, Show)
which notionally represents a type of very simple expression tree over values of type a.
I need some function for making Trees that isn't too
simple or too complicated, and I went with:
h n | n < 2 = Con n
h n = if even n then Add (h (n `div` 2)) (h (n `div` 2))
else Add (Con 1) (h (n - 1))
which builds trees like these:
2 = 1 + 1
3 = 1 + (1 + 1)
4 = (1 + 1) + (1 + 1)
5 = 1 + ((1 + 1) + (1 + 1))
6 = (1 + (1 + 1)) + (1 + (1 + 1))
7 = 1 + (1 + (1 + 1)) + (1 + (1 + 1))
8 = ((1 + 1) + (1 + 1)) + ((1 + 1) + (1 + 1))
Now I wanted to traverse h [1,2,3] but I couldn't do that because I
didn't have an Applicative instance for Tree. I had been putting off
dealing with this, but since Traversable doesn't really make sense without
Applicative I thought the day of reckoning would come. Here it was. Now is
when I learn how to fix all my broken monads.
To define an Applicative instance for Tree I needed to define pure, which
is obvious (it's just Con) and <*> which would apply a tree of
functions to a tree of inputs to get a tree of results. What the hell
does that mean?
Well, I can kinda make sense of it. If I apply one function to a
tree of inputs, that's straightforward, it's just fmap, and I get a
tree of results. Suppose I have a tree of functions, and I replace
the function at each leaf with the tree of its function's results.
Then I have a tree of trees. But a tree that has trees at its leaves
is just a tree. So I could write some tree-flattening function that
builds the tree of trees, then flattens out the type. In fact this is just
join that I already know from Monad world.
The corresponding operation for lists takes a list of lists
and flattens them into a single list.) Flattening a tree is quite easy to do:
join (Con ta) = ta
join (Add ttx tty) = Add (join ttx) (join tty)
and since this is enough to define a Monad instance for Tree I
suppose it is enough to get an Applicative instance also, since every Monad
is an Applicative. Haskell makes this a pain. It should be able to infer
the Applicative from this, and I wasn't clever enough to do it myself. And
there ought to be some formulaic way to get <*> from >>= and
join and fmap, the way you can get join from >>=:
join = (>>= id)
but I couldn't find out what it was. This gets back to my original
complaint: Haskell now wants every Monad instance to be an instance
of Applicative, but if I give it the fmap and the join and the return
it ought to be able to figure out the Applicative instance itself instead of
refusing to compile my program. Okay, fine, whatever. Haskell's
gonna Hask.
(I later realized that building <*> when you have a Monad instance
is easy once you know the recipe; it's just:
fs <*> xs = do
f <- fs
x <- xs
return (f x)
So again, why can't GHC infer <*> from my Monad instance, maybe
with a nonfatal warning?
Warning: No Applicative instance provided for Tree; deriving one from Monad
This is not a rhetorical question.)
(Side note: it seems like there ought to be a nice short abbreviation
of the (<*>) function above, the way one can write join = (>>=
id). I sought one but did not find any. One can eliminate the do
notation to obtain the expression:
fs <*> xs = fs >>= \f -> xs >>= \x -> return (f x)
but that is not any help unless we can simplify the expression with
the usual tricks, such as combinatory logic and η-conversion. I was
not able to do this, and the automatic pointfree
converter produced
(. ((. (return .)) . (>>=))) . (>>=) ARGH MY EYES.)
Anyway I did eventually figure out my <*> function for trees by
breaking the left side into cases. When the tree of functions is Con
f it's a single function and we can just use fmap to map it over
the input tree:
(Con f) <*> tv = fmap f tv
And when it's bigger than that we can break it up recursively:
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
Once this is written it seemed a little embarrassing that it took me so long to figure out what it meant but this kind of thing always seems easier from the far side of the fence. It's hard to understand until you understand it.
Actually that wasn't quite the <*> I wanted. Say we have a tree of
functions and a tree of arguments.

Add (Con (* 10))
(Con (* 100))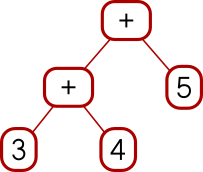
Add (Add (Con 3) (Con 4)) (Con 5)I can map the whole tree of functions over each single leaf on the right, like this:
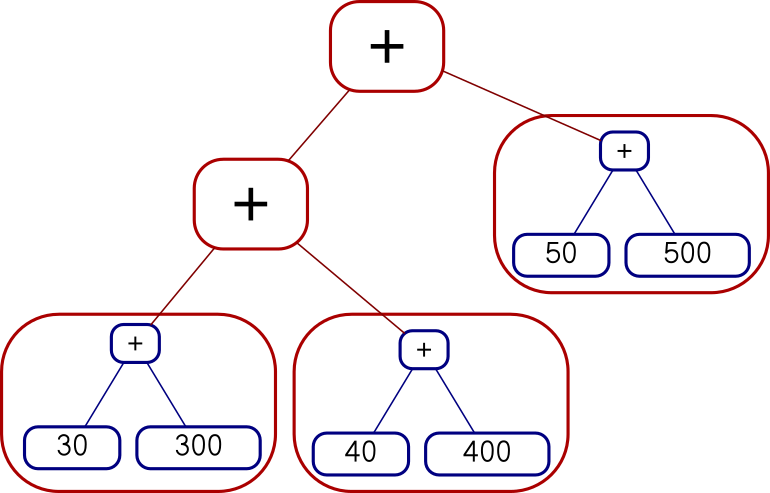
Add (Add (Add (Con 30) (Con 300))
(Add (Con 40) (Con 400)))
(Add (Con 50) (Con 500))
or I can map each function over the whole tree on the right, like this:
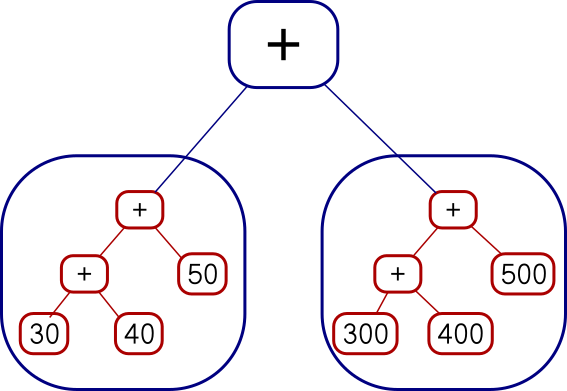
Add
(Add (Add (Con 30) (Con 40)) (Con 50))
(Add (Add (Con 300) (Con 400)) (Con 500))The code I showed earlier does the second of those. You can see it from
the fmap f tv expression, which takes a single function and maps it over a whole
tree of values. I had actually wanted the other one, but there isn't
anything quite like fmap for that. I was busy trying to
understand Applicative and I was afraid if I got distracted trying to invent
a reverse fmap I might lose the thread. This happens to me a lot
with Haskell. I did eventually go back and figure it out. The
reverse fmap is
pamf fs v = fmap ($ v) fs -- good
or
pamf = flip (fmap . flip id) -- yuck
Now there's a simple answer to this which occurs to me now that I
didn't think of before, but I'm going to proceed with how I planned to
do it before, with pamf. The <*> that I didn't want looked like this:
(Con f) <*> tv = fmap f tv
(Add lt rt) <*> tv = Add (lt <*> tv) (rt <*> tv)
I need to do the main recursion on the values argument instead of on the functions argument:
tf <*> (Con v) = pamf tf v
where pamf fs v = fmap ($ v) fs
tf <*> (Add lv rv) = Add (tf <*> lv) (tf <*> rv)
(This is an interesting example: usually the base case is trivial and the recursive clause is harder to write, but this time it's the base case that's not perfectly straightforward.)
Anyway, this worked, but there was an easier solution at hand. The difference between the first version and the second is exactly the same as the difference between
fs <*> xs = do
f <- fs
x <- xs
return (f x)
and
fs <*> xs = do
x <- xs
f <- fs
return (f x)
Digging deeper into why this worked this way was interesting, but it's bed time, so I'm going to cut the scroll here.
[ Addendum 20221021: More about the two versions of <*> and a third version that doesn't work. ]
[Other articles in category /prog/haskell] permanent link


