Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Thu, 29 Jan 2009
A simple trigonometric identity
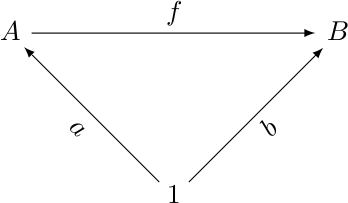
A few nights ago I was writing up notes for my
category theory reading group, and I wanted to include a commutative
diagram on three objects. I was using Paul Taylor's stupendously good
diagrams.sty
package, which lets you put the vertices of the diagram in the cells
of a LaTeX table, and then draw arrows between them. I had drawn the
following diagram:
So that night as I was waiting to fall asleep, I thought about the problem of finding lattice points that are at the vertices of an equilateral triangle. This is a sort of two-dimensional variation on the problem of finding rational approximations to surds, which is a topic that has turned up here many times over the years.
Or rather, I wanted to find lattice points that are almost at the vertices of an equilateral triangle, because I was pretty sure that there were no equilateral lattice triangles. But at the time I could not remember a proof. I started doing some calculations based on the law of cosines, which was a mistake, because nobody but John Von Neumann can do calculations like that in their head as they wait to fall asleep, and I am not John Von Neumann, in case you hadn't noticed.
A simple proof that there are no equilateral lattice triangles has just now occurred to me, though, and I am really pleased with it, so we are about to have a digression.
The area A of an equilateral triangle is s√3/2, where s is the length of the side. And s has the form √t because of the Pythagorean theorem, so A = √(3t)/2, where t is a sum of two squares, because the endpoints of the side are lattice points.
By Pick's theorem, the area of any lattice triangle is a half-integer. So 3t is a perfect square, and thus there are an odd number of threes in t's prime factorization.
But t is a sum of two squares, and by the sum of two squares theorem, its prime factorization must have an even number of threes. We now have a contradiction, so there was no such triangle.
Wasn't that excellent? That is just the sort of thing that I could have thought up while waiting to fall asleep, so it proves even more conclusively that starting with the law of cosines was a mistake.
Okay, end of digression. Back to the law of cosines. We have a triangle with sides a, b, and c, and opposite angles A, B, and C, and you no doubt recall from high school that c2 = a2 + b2 - 2ab cos C. We'll call this "law C".
Before I fell alseep, it occurred to me that you could take the analogous law B, which is b2 = a2 + c2 - 2ac cos B, and substitute the right-hand side for the b2 term in law C. Then a bunch of stuff will cancel out and you should either get something interesting or something tautological. Von Neumann would have known right away which it was, but I needed paper.
So today I got out the paper and did the thing, and came up with the very simple relation that:
c = a cos B + b cos AWhich holds in any triangle. But somehow I had never seen this before, or, if I had, I had completely forgotten it.
The thing is so simple that I thought that it must be wrong, or I would have known it already. But no, it checked out for the easy cases (right triangles, equilateral triangles, trivial triangles) and the geometric proof is easy: Just drop a perpendicular from C. The foot of the perpendicular divides the base c into two segments, which, by the simplest possible trigonometry, have lengths a cos B and b cos A, respectively. QED.
Perhaps that was anticlimactic. Have I mentioned that I have a sign on the door of my office that says "Penn Institute of Lower Mathematics"? This is the kind of thing I'm talking about.
I will let you all know if I come up with anything about the almost-equilateral lattice triangles. Clearly, you can approximate the equilateral triangle as closely as you like by making the lattice coordinates sufficiently large, just as you can approximate √3 as closely as you like with rationals by making the numerator and denominator sufficiently large. Proof: Your computer draws equilateral-seeming triangles on the screen all the time.
I note also that it is important that the lattice is two-dimensional. In three or more dimensions the triangle (1,0,0,0...), (0,1,0,0...), (0,0,1,0...) is a perfectly equilateral lattice triangle with side √2.
[ Addendum 20090130: Vilhelm Sjöberg points out that the area of an equilateral triangle is s2√3/4, not s√3/2. Whoops. This spoils my lovely proof, because the theorem now follows immediately from Pick's: s2 is an integer by Pythagoras, so the area is irrational rather than a half-integer as Pick's theorem requires. ]
[ Addendum 20140403: As a practical matter, one can draw a good lattice approximation to an equilateral triangle by choosing a good rational approximation to !!\sqrt3!!, say !!\frac ab!!, and then drawing the points !!(0,0), (b,a),!! and !!(2b, 0)!!. The rational approximations to !!\sqrt3!! quickly produce triangles that are indistinguishable from equilateral. For example, the rational approximation !!\frac74!! gives the isosceles triangle with vertices !!(0,0), (4,7), (8,0)!! which has one side of length 8 and two sides of length !!\sqrt{65}\approx 8.06!!, an error of less than one percent. The next such approximation, !!\frac{26}{15}!!, gives a triangle that is correct to about 1 part in 1800. (For more about rational approximations to !!\sqrt3!!, see my article on Archimedes and the square root of 3.) ]
[ Addendum 20181126: Even better ways to make 60-degree triangles on lattice points. ]
[Other articles in category /math] permanent link


