Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 16 Dec 2019
In 2006 I wrote an essay about Neal Stephenson's not-really-a-trilogy “Baroque Cycle” and then in 2017 another about his novel Seveneves. I was telling some folks about this, and regretting that I had never written about Anathem, which is my favorite of his books, when I remembered that long ago I wrote about his first novel The Big U.
I have mentioned The Big U before, in connection with Julian Jaynes’ bicameral mind theory, saying
I wondered when reading [The Big U] how anyone could understand it without having read Jaynes first
I still wonder this. I should write up a summary of the Jaynes someday.
I liked The Big U better than Stephenson did. Wikipedia says:
Stephenson has said he is not proud of this book. When Stephenson's Snow Crash was published in 1992 … The Big U was out of print and Stephenson was content to leave it that way. When original editions began selling on eBay for hundreds of dollars, he relented and allowed The Big U to be republished, saying that the only thing worse than people reading the book was paying that much to read it.
Here's my discussion of it, originally posted to
rec.arts.sf.written in early
2002.
It's a reply to a somewhat earlier post that reviewed all of
Stephenson's
novels.
Quotations are from the post to which I was replying.
The Big U (1984, reprinted in 2001)
This was Stephenson's first published novel. It is a satirical look at life at a huge university. It is absolutely dreadful,
It was the only one of Stephenson's books that I liked. (I have not yet read Cryptonomicon or Zodiac.)
In Snow Crash and The Diamond Age, I felt that Stephenson let the plot run away from him. He introduced characters and macguffins that were cool, but ultimately irrelevant. About halfway through Snow Crash, I said "Geez, if he doesn't stop bringing in new stuff, he's never going to finish dealing with the stuff he has." Three quarters of the way through, I said "Geez, he's never going to be able to tie up all these loose ends." And by the end of the book, that's what had happened. There's a famous saying about how you mustn't roll a cannon onto the stage in Act I unless you're planning to fire it in Act III. Snow Crash left more unfired cannons lying around the stage than any book I can remember reading. There was a lot to like in both books, but at the end I was left scratching my head, wondering what story had been told.
The Big U, in contrast, is a lot tighter. It is the story of one year at the U, from September to May, at the end of which SPOILER. Stephenson brought a whole bunch of stuff on stage and used every bit of it. The railgun was foreshadowed for the entire novel, and I said to myself "If he doesn't use the damn railgun, I'm never reading another one of his books." But he did get satisfactory use out of the railgun. There were no extraneous characters who were abandoned in the middle of the book with no explanation. The book had a beginning, a middle and an end. If Snow Crash had an end, I couldn't find it.
made worse by the fact almost everyone reading it will be familiar with his great later works and be expecting something that isn't painfully bad like this book is.
Well, if someone didn't find the book painfully bad, then they might not feel that it suffered by comparison with his 'great' later works. (Which in my opinion are overrated; that's another post for another day.) So this is a non sequitur.
I know there's no accounting for taste, but this is something I thought everyone could agree on.
There was no reason to have thought that, because almost all the criticisms you have of The Big U are quite personal.
Let's look at them:
Why is it bad? A story that is not funny
Just because you didn't think it was funny doesn't mean that other people will agree. Sometimes you can conclude that almost nobody could possibly find it funny (for example, because it was derivative or offensive) but I don't think any of those reasons apply it here. It appears that you made a personal judgment ("I don't think it's funny") and then extrapolated that to cover the entire universe. ("Therefore, it isn't funny, and nobody could possibly think it is funny.")
I thought it was funny. I almost never laugh when I read a book. I laughed when I read The Big U.
about unlikable characters
Same thing here. You didn't like the characters, but that doesn't mean that nobody will like them, and I don't know why you thought that nobody would like them. What didn't you like about them? Did they seem improbable? Did they behave irrationally? Could you give an example? I thought the jerky college students mostly behaved like jerky college students. When I was in college, several of the boys on my hall decided to take up chewing tobacco; they then spat their chaws into the hall water fountain and the floors of the showers, so that everyone else could enjoy it as much as they did. They would have fit right in at the Big U.
I liked the characters I was supposed to like and disliked the characters I was supposed to dislike.
which just gets worse and worse.
This doesn't even reach the level of criticism.
If you can reach the end of the book, you discover the whole thing seems to have been an excuse to have these various stereotyped groups engage in a firefight on the campus. Yes, a firefight, complete with machine guns, a jury-rigged tank, and so forth. Reads like some sort of adolescent day dream, for all the wrong reasons.
Finally a substantive criticism!
SPOILERS
I don't have a very clear recollection of the book (I read it only once, several years ago) but I seem to remember that some of the groups involved in the final showdown were
a gang of steam-tunnel-exploring geeks who have crossed over into an alternate universe in which their bizarre role-playing games are real,
a pack of giant mutant sewer rats,
the President of the University (who reminds me of a cross between Mr. White from You Bright and Risen Angels and Rambo. Well, no, that doesn't quite capture the essence of Septimus Severus Krupp. I don't know what to say except that he's an original.)
dorm inhabitants who have reverted to a Jaynesean bicameral mind mentality,
malevolent Slavic dwarves bent on constructing an atomic bomb, and
bats.
There are a lot of criticisms you could make of this book, but I don't think "stereotyped groups engage in firefight" is one of them. Firefight, yes. Stereotyped groups? How many novels have you read that involve a pack of bicameral college students whose god is an electric fan? Maybe the giant mutant sewer rats are old-hat. I saw them as more of an homage.
I don't think that the book was just an excuse for the firefight. The book builds towards the firefight in the same way that any book builds towards its climactic scene. But the firefight isn't the only reason for the book to exist. It has a theme, which is that the architecture of the Big U influences the behavior of its inhabitants, and because architecture is horrible, it makes the inhabitants horrible. The theme is developed, with many examples: The U is insular and inward-looking, so the inhabitants become selfish and arrogant. The U itself is made of identical parts in precisely artificial geometric arrangements, so the inhabitants lose their individuality and become mobs. The U is impersonal and inhuman, so the inhabitants become cruel and inhumane.
There's a lot of commentary on the relationship between the U and its inhabitants with the people who live in the surrounding neighborhood. Having grown up near Columbia University, I found this to be incisive.
There are many details of people being incidentally and unthinkingly screwed over by bureaucracy, very much in the style of the movie Brazil, or Douglas Adams' game Bureaucracy. (The Big U predates both.) I thought that the scene at the very beginning that introduced Sarah Johnson was an excellent satire of the casually destructive nature of bureaucratic screwups. I was strongly reminded of the conclusion I came to when I was trying to register for summer classes at Columbia: Absolutely everything is implicitly forbidden, and the only way to get anything is to make an appointment to get special permission from the Dean.
Another part of the book that stands out in my mind is the section dealing with the pettiness and stupidity of student (and all) government. I felt like I'd been waiting a long time to read that.
I don't know what to say about 'adolescent day dream', since I haven't read it recently enough to remember the tone. But I don't think that many adolescent daydreams are as bizarre and surprising as this one was.
In the future, I think your reviews might be more useful if you would avoid statements like "It was absolutely dreadful", which don't really tell anyone anything except that you thought it was dreadful.
[Other articles in category /book] permanent link
Fri, 13 Dec 2019
California corpse-tampering law
[ Content warning: dead bodies, sex crime, just plain nasty ]
A co-worker brought this sordid item to my attention: LAPD officer charged after allegedly fondling a dead woman's breast.
[A] Los Angeles Police Department officer … was charged Thursday with one felony count of having sexual contact with human remains without authority, officials said, after he allegedly fondled a dead woman's breast.
[The officer] was alone in a room with the deceased woman while his partner went to get paper work from a patrol car…. At that point, [he] turned off the body camera and inappropriately touched the woman. … A two-minute buffer on the camera captured the incident even though [he] had turned it off.
Yuck.
Chas. Owens then asked a very good question:
Okay, no one is commenting on “sexual contact with human remains without authority”
How does one go about getting authority to have sexual contact with human remains?
Is there a DMV for necrophiles?
I tried to resist this nerdsnipe, but I was unsuccessful. I learned that California does have a law on the books that makes it a felony to have unauthorized sex with human remains:
HEALTH AND SAFETY CODE - HSC
DIVISION 7. DEAD BODIES [7000 - 8030]
PART 1. GENERAL PROVISIONS [7000 - 7355]
CHAPTER 2. General Provisions [7050.5 - 7055]7052.
(a) Every person who willfully mutilates, disinters, removes from the place of interment, or commits an act of sexual penetration on, or has sexual contact with, any remains known to be human, without authority of law, is guilty of a felony. This section does not apply to any person who, under authority of law, removes the remains for reinterment, or performs a cremation.
…
(b)(2) “Sexual contact” means any willful touching by a person of an intimate part of a dead human body for the purpose of sexual arousal, gratification, or abuse.
(California HSC, section 7052)
I think this addresses Chas.’s question. Certainly there are other statutes that authorize certain persons to disinter or mutilate corpses for various reasons. (Inquests, for example.) A defendant wishing to take advantage of this exception would have to affirmatively claim that he was authorized to grope the corpse’s breast, and by whom. I suppose he could argue that the state had the burden of proof to show that he had not been authorized to fondle the corpse, but I doubt that many jurors would find this persuasive.
Previously on this blog: Legal status of corpses in 1911 England.
[Other articles in category /law] permanent link
Thu, 12 Dec 2019Many ‘bene-’ words do have ‘male-’ opposites. For example, the opposite of a benefactor is a malefactor, the opposite of a benediction is a malediction, and the opposite of benevolence is malevolence. But strangely there is no ‘malefit’ that is opposite to ‘benefit’.
Or so I wrote, and then I thought I had better look it up.
The Big Dictionary has six examples, one as recent as 1989 and one as early as 1755:
I took it into my head to try for a benefit, and to that end printed some bills… but… instead of five and twenty pounds, I had barely four…. The morning after my malefit, I was obliged to strip my friend of the ownly decent gown she had, and pledged it to pay the players.
(Charlotte Charke, A narrative of the life of Mrs. Charlotte Charke (youngest daughter of Colley Cibber, Esq.), 1755.)
(I think the “benefit” here is short for “benefit performance”, an abbreviation we still use today.)
Mrs. Charke seems to be engaging in intentional wordplay. All but one of the other citations similarly suggest intentional wordplay; for example:
Malefactors used to commit malefactions. Why could they not still be said to do so, rather than disbenefits, or, perhaps, stretching a point, commit malefits?
(P. Howard, Word in Your Ear, 1983.)
The one exception is from no less a person than J.R.R. Tolkien:
Some very potent fiction is specially composed to be inspected by others and to deceive, to pass as record; but it is made for the malefit of Men.
(Around 1973, Quoted in C. Tolkien, History of Middle-earth: Sauron Defeated, 1992.)
Incidentally, J.R.R. is quoted 362 times in the Big Dictionary.
[Other articles in category /lang/etym] permanent link
Tue, 26 Nov 2019A chalupa is a fried tortilla that has been filled with meat, shredded cheese, or whatever. But it is also the name of the mayor of Prague from 2002–2011.

| = | 
|
| Tortilla |
The boat-shaped food item is named after a kind of boat called a chalupa; I think the name is akin to English sloop. But in Czech a chalupa is neither a boat nor a comestible, but a cottage.
[ Other people whose names are accidentally boats ]
[ Addendum 20191201: I should probably mention that the two words are not pronounced the same; in Spanish, the “ch” is like in English “church”, and in Czech it is pronounced like in English “challah” or “loch”. To get the Spanish pronunciation in Czech you need to write “čalupa”, and this is indeed the way they spell the name of the fried-tortilla dish in Czech. ]
Addenda
20220115
Other people whose names are accidentally foods
20250616
Today I find myself working with a Czech person with the surname Cvítek. This, I have learned, is the Czech word for “pancake”.
[Other articles in category /lang/etym] permanent link
Sun, 24 Nov 2019
The least common divisor and the greatest common multiple
One day Katara reported that her middle school math teacher had gone into a rage (whether real or facetious I don't know) about some kids’ use of the phrase “greatest common multiple”. “There is no greatest common multiple!” he shouted.
But that got me thinking. There isn't a greatest common multiple, but there certainly is a least common divisor; the least common divisor of !!a!! and !!b!! is !!1!!, for any !!a!! and !!b!!.
The least common multiple and greatest common divisor are beautifully dual, via the identity $$\operatorname{lcm}(a,b)\cdot\gcd(a,b) = ab,$$ so if there's a simple least common divisor I'd expect there would be a greatest common multiple also. I puzzled over this for a minute and realized what is going on. Contrary to Katara's math teacher, there is a greatest common multiple if you understand things properly.
There are two important orderings on the positive integers. One is the familiar total ordering by magnitude: $$0 ≤ 1≤ 2≤ 3≤ 4≤ \ldots.$$ (The closely related !!\lt!! is nearly the same: !!a\lt b!! just means that !!a\le b!! and !!a\ne b!!.)
But there is another important ordering, more relevant here, in which the numbers are ordered not by magnitude but by divisibility. We say that !!a\preceq b!! only when !!b!! is a multiple of !!a!!. This has many of the same familiar and comforting properties that !!\le!! enjoys. Like !!\le!!, it is reflexive. That is, !!a\preceq a!! for all !!a!!, because !!a!! is a multiple of itself; it's !!a\cdot 1!!.
!!\preceq!! is also transitive: Whenever !!a\preceq b!! and !!b\preceq c!!, then also !!a\preceq c!!, because if !!b!! is a multiple of !!a!!, and !!c!! is a multiple of !!b!!, then !!c!! is a multiple of !!a!!.
Like !!\le!!, the !!\preceq!! relation is also antisymmetric. We can have both !!a≤b!! and !!b≤a!!, but only if !!a=b!!. Similarly, we can have both !!a\preceq b!! and !!b\preceq a!! but only if !!a=b!!.
But unlike the familiar ordering, !!\preceq!! is only a partial ordering. For any given !!a!! and !!b!! it must be the case that either !!a\le b!! or !!b \le a!!, with both occurring only in the case where !!a=b!!. !!\preceq!! does not enjoy this property. For any given !!a!! or !!b!!, it might be the case that !!a\preceq b!! or !!b\preceq a!!, or both (if !!a=b!!) or neither. For example, neither of !!15\preceq 10!! and !!10 \preceq 15!! holds, because neither of !!10!! and !!15!! is a multiple of the other.
The total ordering !!≤!! lines up the numbers in an infinite queue, first !!0!!, then !!1!!, and so on to infinity, each one followed directly by its successor.

The partial ordering !!\preceq!! is less rigid and more complex. It is not anything like an infinite queue, and it is much harder to draw. A fragment is shown below:
The nodes here have been arranged so that each number is to the left of all the numbers it divides. The number !!1!!, which divides every other number, is leftmost. The next layer has all the prime numbers, each one with a single arrow pointing to its single divisor !!1!!, although I've omitted most of them from the picture. The second layer has all the numbers of the form !!p^2!! and !!pq!! where !!p!! and !!q!! are primes: !!4, 6, 9, 10, 14, \ldots!!, each one pointing to its prime divisors in the first layer. The third layer should have all the numbers of the form !!p^3, p^2q, !! and !!pqr!!, but I have shown only !!8, 12, 18, !! and !!20!!. The complete diagram would extend forever to the right.
In this graph, “least” and “greatest” have a sort-of-geometric interpretation, “least” roughly corresponding to “leftmost”. But you have to understand “leftmost” in the correct way: it really means “leftmost along the arrows”. In the picture !!11!! is left of !!4!!, but that doesn't count because it's not left of 4 along an arrow path. In the !!\preceq!! ordering, !!11\not \preceq 4!! and !!4\not \preceq 11!!. Similarly “greatest” means “rightmost, but only along the arrows”.
A divisor of a number !!n!! is exactly a node that can be reached from !!n!! by following the arrows leftward. A common divisor of !!n!! and !!m!! is a node that can be reached from both !!n!! and !!m!!. And the greatest common divisor is the rightmost such node.
For example, the greatest common divisor of !!12!! and !!16!! is the rightmost node that can be reached by following arrows from both !!12!! and from !!16!!; that's !!4!!. The number !!8!! is right of !!4!! but can't be reached from !!12!!. The number !!12!! is right of !!4!! but can't be reached from !!16!!. The number !!2!! can be reached from both, but !!4!! is right of !!2!!. So the greatest common divisor is !!4!!.
Is there a least common divisor of !!n!! and !!m!!? Sure there is, it's the leftmost node that can be reached from both !!n!! and !!m!!. Clearly, it's always !!1!!, regardless of what !!n!! and !!m!! are.
Going in the other direction, a multiple of !!n!! is a node from which you can reach !!n!! by following the arrows. A common multiple of !!n!! and !!m!! is one from which you can reach both !!n!! and !!m!!, and the least common multiple of !!n!! and !!m!! is the leftmost such node.
But what about the greatest common multiple, angrily denied by Katara's math teacher? It should be the rightmost node from which you can reach both !!n!! and !!m!!. The diagram extends infinitely far to the right, so surely there isn't a rightmost such node?
Not so! There is a rightmost node! !!0!! is a multiple of !!n!! for every !!n!!, we have !!n \preceq 0!! for every !!n!!, and so zero is to the right of every other node. The diagram actually looks like this:
where I left out an infinite number of nodes in between !!0!! and the rest of the diagram.
It's a bit odd to think of !!0!! by itself there, all the way on the right, because in every other case, we have !!m \preceq n!! only when !!m≤ n!!. !!n=0!! is the only exception to that. But when you're thinking about divisibility, that's how you have to think about it: !!1!! is least, as you expect, not because it's smallest but because it's a divisor of every number. And dually, !!0!! is greatest, because it's a multiple of every number.
So that's the answer. Consideration of the seemingly silly question of the greatest common multiple has led us to a better understanding of the multiplicative structure of the integers, and we see that there is a greatest common multiple, which is exactly dual to the least common divisor, just as the least common multiple is dual to the greatest common divisor.
[Other articles in category /math] permanent link
Thu, 14 Nov 2019Katara and I are in a virtuous cycle where she thinks of some food she wants to eat and then asks me to cook it, I scratch my head and say "Well, I never did, but I could try", and then I do, and she tells me it was really good. This time she suggested I should make soondubu jjigae (순두부찌개), which is a Korean stew that features very soft tofu. (“Dubu” (두부) is tofu, and “soon dubu” is soft tofu.)
I did it and it came out good, everyone was happy and told me how great I am. Cooking for my family makes me feel like a good dad and husband. Hey, look, I am doing my job! I love when I do my job.
I thought maybe soondubu would be one of those things where you can make it at home with endless toil but in the end you have a product that is almost as good as the $6.95 version you could get from the place downstairs. But it was actually pretty easy. Korean cuisine is often very straightforward and this was one of those times. I approximately followed this recipe but with several changes. (One of these days I'll write a blog article about how so many people stress out about the details of recipes.) The overall method is:
Dice up some onion and garlic finely and put them in the pot with sesame oil and kochujang. Then you add the meat if you are doing that, and then about a half a cup of chopped up kimchi. Then you put in broth and you add the soondubu. Easy-peasy.
The recipe on that page called for beef but I used chicken meat in cubes because that was what Katara asked for. All the soondubu recipes I found call for kochugaru (red pepper flakes) instead of kochujang (red pepper soybean paste) but I didn't have any handy and so what?
Somewhere in the world there is some food snob who will sneer and say that Real Soondubu is always made with kochugaru, and using kochujang is totally inauthentic. But somewhere else there is someone who will say “well, my grandmother always liked to use kojujang instead”, and Grandma outranks the food snob. Also I decided this year that the whole idea of “authentic” recipes is bullshit and I am going to forget about it.
I used chicken broth out of a box. The recipe called for scallions but I think I didn't have any handy that time. The recipe called for anchovy paste but I left them out because Lorrie doesn't like the way they taste. But I put did in some thin slices of zucchini. We do have a nice Korean-style glazed earthenware pot which I cooked in and then transported directly to the table.
Everyone in my family likes soondubu and it made me really happy that they considered my first one successful.
[Other articles in category /food] permanent link
Mon, 11 Nov 2019All programming languages are equally crappy, but some are more equally crappy than others.
[Other articles in category /prog] permanent link
Wed, 06 Nov 2019
Help me ask why you didn't just…
Regarding the phrase “why didn't you just…”, Mike Hoye has something to say that I've heard expressed similarly by several other people:
Whenever you look at a problem somebody’s been working on for a week or a month or maybe years and propose a simple, obvious solution that just happens to be the first thing that comes into your head, then you’re also making it crystal clear to people what you think of them and their work.
(Specifically, that you think they must be a blockhead for not thinking of this solution immediately.)
I think this was first pointed out to me by Andy Lester.
I think the problem here may be different than it seems. When someone says “Why don't you just (whatever)” there are at least two things they might intend:
Why didn't you just use
sshd? I suppose it's because you're an incompetent nitwit.Why didn't you just use
sshd? I suppose it's because there's some good reason I'm not seeing. Can you please point it out?
Certainly the tech world is full of response 1. But I wonder how many people were trying to communicate response 2 and had it received as response 1 anyway? And I wonder how many times I was trying to communicate response 2 and had it received as response 1?
Mike Hoye doesn't provide any alternative phrasings, which suggests to me that he assumes that all uses of “why didn't you just” are response 1, and are meant to imply contempt. I assure you, Gentle Reader, that that is not the case.
Pondering this over the years, I have realized I honestly don't know how to express my question to make clear that I mean #2, without including a ridiculously long and pleading disclaimer before what should be a short question. Someone insecure enough to read contempt into my question will have no trouble reading it into a great many different phrasings of the question, or perhaps into any question at all. (Or so I imagine; maybe this is my own insecurities speaking.)
Can we agree that the problem is not simply with the word “just”, and that merely leaving it out does not solve the basic problem? I am not asking a rhetorical question here; can we agree? To me,
Why didn't you use
sshd?
seems to suffer from all the same objections as the “just”ful version and to be subject to all the same angry responses. Is it possible the whole issue is only over a difference in the connotations of “just” in different regional variations of English? I don't think it is and I'll continue with the article assuming that it isn't and that the solution isn't as simple as removing “just”.
Let me try to ask the question in a better better way:
There must be a good reason why you didn't use
sshdI don't see why you didn't use
sshdI don't understand why you didn't use
sshdI'd like to know why you didn't use
sshdI'm not clever enough to understand why you didn't use
sshd
I think the sort of person who is going to be insulted by the original version of my question will have no trouble being insulted by any of those versions, maybe interpreting them as:
There must be a good reason why you didn't use
sshd. Surely it's because you're an incompetent nitwit.I don't see why you didn't use
sshd. Maybe the team you're working with is incompetent?I don't understand why you didn't use
sshd. Probably it's because you're not that smart.I'd like to know why you didn't use
sshd. Is it because there's something wrong with your brain?I'm not clever enough to understand why you didn't use
sshd. It would take a fucking genius to figure that out.
The more self-effacing I make it, the more I try to put in that I think the trouble is only in my own understanding, the more mocking and sarcastic it seems to me and the more likely I think it is to be misinterpreted. Our inner voices can be cruel. Mockery and contempt we receive once can echo again and again in our minds. It is very sad.
So folks, please help me out here. This is a real problem in my life. Every week it happens that someone is telling me what they are working on. I think of what seems like a straightforward way to proceed. I assume there must be some aspect I do not appreciate, because the person I am talking to has thought about it a lot more than I have. Aha, I have an opportunity! Sometimes it's hard to identify what it is that I don't understand, but here the gap in my understanding is clear and glaring, ready to be filled.
I want to ask them about it and gain the benefit of their expertise,
just because I am interested and curious, and perhaps even because the
knowledge might come in useful. But then I run into trouble. I want
to ask “Why didn't you just use sshd?” with the understanding that
we both agree that that would be an obvious thing to try, and that I
am looking forward to hearing their well-considered reason why not.
I want to ask the question in a way that will make them smile, hold up
their index finger, and say “Aha! You might think that sshd would be
a good choice, but…”. And I want them to understand that I will not
infer from that reply that they think I am an incompetent nitwit.
What if I were to say
I suppose
sshdwasn't going to work?
Would that be safer? How about:
Naïvely, I would think that
sshdwould work for that
but again I think that suggests sarcasm. A colleague suggests:
So, I probably would've tried using
sshdhere. Would that not work out?
What to do? I'm in despair. Andy, any thoughts?
[Other articles in category /tech] permanent link
Tue, 05 Nov 2019A while back a YouTube video was going around titled Octopus Intelligence Experiment Takes an Unexpected Turn. Someone put food in a baby bottle with a screw cap and a rubber nipple. There was a hole drilled in the bottle so that the octopus could reach in to taste the food, but it was not large enough for the food to come out or for the octopus to go in. The idea, I suppose, was that the octopus would figure out how to unscrew the cap.
The “unpexected turn” was that instead of unscrewing the cap, the octopus just ripped the entire nipple out of the bottle.

I have mentioned this before but it bears repeating: this outcome should not have been an unexpected turn:
Crabs can be wrested from containers (Pieron, 1911; Schiller, 1948; Cousteau and Diole, 1973) but the results appear to be achieved by chance and there is little indication that the octopus can learn to deal with the situation more efficiently with practice. The animal approaches and struggles with the apparatus until something happens; if it learns anything as a result of its experience it is only to be more persistent and vigorous.
(Martin Wells, Octopus: Physiology and Behaviour of an Advanced Invertebrate (Springer, 1978), page 241.)
[Other articles in category /bio/octopus] permanent link
Mon, 04 Nov 2019We have had two of these plastic thingies cluttering up our dish drainer for years. We didn't know what they were but we didn't want to throw them away because what if they are important?
I got tired of them this weekend, and examined one more closely.
There wasn't any indication of what it had been part of, or what it
was for, but it did have the marking PART 2198768 on the back, so I
handed that to The Goog.
And the result was instantaneous and unequivocal: it belongs to my refrigerator. Specifically, it goes in the back of the freezer compartment to keep food from falling down into the back and blocking the drainage path.
Truly, we live in an age of marvels.
[Other articles in category /misc] permanent link
Sun, 03 Nov 2019I suddenly wondered: was Andy Warhol ever a TV show guest star? So I asked the Goog, and the answer was better than I could have imagined: in October 1985, Andy Warhol was a guest star on The Love Boat.
According to Wikipedia, one of the subpots of the episode was “a woman avoids Warhol, wanting to forget the time she was in one of his movies.” That is a lot more plausible than many Love Boat plots!
Also starring in that episode were Milton Berle, Tom Bosley and Marion Ross, Andy Griffith, and Cloris Leachman. TV Guide named it one of the hundred greatest episodes of any TV show ever.
Wow.
[Other articles in category /misc] permanent link
Wed, 30 Oct 2019
Russian names in English and English names in Russian
One day I was surprised to find that Michael Jordan's name in Russian is “Майкл” (‘mai-kl’), and not “Михаи́л” (‘Mikhail’, the Russian translation of Michael.) Which is just what I should have expected; we don't refer to Mikhail Gorbachev or Baryshnikov as “Michael”, and it would be just as odd, in the other direction, if the Russians referred to the famous basketball player “Mikhail” Jordan.
When I was taking high school Russian we were assigned Russian versions of our names and I was disappointed to receive “Марк” (“Mark”) rather than anything more interesting. My friend Jeremy was stiffed in a different way. Apparently there is no direct Russian analog of “Jeremy” so the teacher opted for “Юрий” (Yuri). Yuri is not in any way a correct translation of Jeremy; it is the Russian version of “George”. Looking into it now, I wish she had thought to use “Иереми́я” (Jeremiah), or perhaps “Иерони́м” (Jerome).

It's funny how sometimes these names can be so easy to translate and sometimes so difficult. Mark is Mark, Aleksandr is Alexander, Viktor is Victor, Ivan is John, Yuri is George, Yakov is Jacob (or maybe James), Fyedor is Theodore, nothing is William, and Igor is nothing.
Italian Maria is obviously English “Mary” but how do you translate Mario? English has no male version of “Mary”.
(Side note: it is so bizarre that James and Jacob are somehow the same name, that when you turn Iacobus / Jacques / Iago (Latin / French / Spanish) into English it somehow turns into James. Another: What knucklehead decided to translate Frère Jacques as Brother John?)
[ Addendum: My previous article discussed the Korean translation of 邓小平, the name of Chinese leader Deng Xiaoping. Brian Lee points out that the usual Korean translation of Chinese小 (“small”) is 소 (pronounced, roughly, as /shoo/), but, just as in my Michael-Jordan examples above, the Koreans have chosen to translate the name so as to preserve the foreign pronunciation, 샤오 (/shya-oh/). Thanks! ]
[ Addendum: Dmitry Ivanov points out that there is a second Russian version of George, less common but closer to the English version: Георгий (“Georgy”). He also drew my attention to another Russian version of Jeremy, Ерёма (“Yerema”). This led me to discover that Russian Wikipedia has an entire page about Jeremy-related names, and mentions at least the following:
- Еремей
- Ереми́й
- Ерене́й
- Ерёма
- Иереме́й
- Иереми́й
- Иереми́я
- Ириме́й
- Ярёма
Clearly, my high school Russian teacher blew it. ]
[Other articles in category /lang] permanent link
Tue, 29 Oct 2019Something I've been wondering about for a while: there's this vowel in Mandarin which is usually written as ‘e’, for example in Deng (Xiaoping, 邓小平) or in feng shui (風水). But it's not pronounced like the ‘e’ in English “bed” or “pen”. It seems to my untrained ear to be more like the Korean vowel ‘ㅓ’, which is sort of between English “bought” and “but”. So I had wanted for a while to look up how Deng's name was spelled in Korean to see if they used ‘ㅓ’ or some other vowel. Partial success. Sure enough, Deng is spelled with ‘ㅓ’ in Korean: 덩(샤오핑).
“Feng shui” is spelled differently in Korean, with a different vowel: 풍수. But that's not too surprising, since the term “feng shui” presumably entered the Korean language centuries ago, and not only was the Chinese pronunciation probably different then, the Korean pronunciation would have changed over time after the adoption. In contrast, Deng's name presumably wasn't translated into Korean until sometime in the 20th century.
I was surprised that “Xiaoping” turns into three syllables in Korean. But Korean doesn't have that /aʊ/ dipthong, so that's the best it can do. This reminds me now of how amused I was by Corn Flakes boxes in Korea: in Korean, “Flake” is a four-syllable word. (플레이크).
[Other articles in category /lang] permanent link
Mon, 28 Oct 2019
A solution in search of a problem
I don't remember right now what inspired this, but I got to thinking last week, what if I were to start writing the English letter ‘C’ in two forms, to distinguish its two pronunçiations? Speçifically, when ‘C’ gets the soft /s/ sound, we'll write it with a çedilla, and when it gets the hard /k/ sound we'll write it as usual.
Many improvements have been proposed to English spelling, and why not? Almost any change would be an improvement. But most orthographic innovations produçe barbaric or bizarre spellings. For example, “enuff” is still just wrong and may remain so for a long time. “Thru” and “donut” have been in common use long enough that not everyone thinks they look entirely bizarre, and I think only the Brits still object to “catalog” in plaçe of “catalogue”. But my ‘ç’ suggestion seems to me to be less violent. All the words are still spelled the same way. Nobody would have to deal with the shock of new spellings like “sirkular” or “klearanse”. I think the difficulty of adjusting to “çircular” and “clearançe” seems quite low.
On the other hand, the benefit also seems quite low. There aren't that many C’s to begin with. And who does this help, exactly? Foreigners who might otherwise have trouble deçiding how to pronounçe a particular ‘C’? Are there any people who actually have trouble reading “circle” and would be helped if it were spelled çircle”? And if there are, isn't c-vs-ç the least of their problems?
(Also, as Katara points out, ‘C’ is nearly superfluous in English as it is. You can almost always replaçe it with ‘S’ or ‘K’, accordingly. Although she did point out a counterexample: spelling “mace” as “mase” could be misleading. My proposal of “maçe”, though, is quite clear.)
I wonder, though, if this doesn't point the way toward a more general intervention that might be more generally helpful. The “ough” cluster gets a bad rap, but the real problems in English orthography are mostly in the totally inconsistent vowel spellings. Some diacritical marks might be a big help. For example, consider “bread” and “bead”. What if the close vowel in “bead” were indicated by spelling it “bēad”? Then it becomes easy to distinguish between “rēad” (/ɹid/, present tense) and “read” (/ɹɛd/, past tense), similarly “lēad” and “lead”. Native Anglophones will quickly learn to ignore the diacritical marks. A similar tactic might even help with the notorious “ough”. I don't really know what to do about words like “precious” or “ocean”, though. We can't leave them as they were, because that would unambiguously indicate the wrong pronunçiation “prekious”, “okean”. But to spell them “preçious” or “oçean” would be misleading. “Prećious”, maybe?
(I suppose someone wants to suggest “preşious” and “oşean”, but this is exactly what I'm trying to avoid. If you're going to do that you might as well go whole hog and use “preshus” and “oshun”.)
If you follow this path too far (and in the wrong direction) you end up with Unifon. I think this is a better direction and could end in a better plaçe. Maybe not better enough to be worth doing, though.
Peaçe out.
[Other articles in category /lang] permanent link
Fri, 25 Oct 2019Wikipedia's article on the etymology of gringo is quite good, well-cited, and I did not detect any fishy smells. I had previously tried to look up gringo in the Big Dictionary, but it only informed me that it was from Mexican Spanish, which is not really helpful. (I know that's because their jurisdiction stops at the English border, and they aren't responsible for anything outside, but really, OED folks? Nothing else?)
Anyway Wikipedia helped me out. I had gotten onto this gringos thing because yesterday I learned about gringas, which are white flour tortillas. I immediately wondered: are they called gringas because (like gringos) they're made of white paste? Or is it because they're eaten by gringos, who don't care for corn tortillas? The answer seems to be: both explanations are current, but nobody knows if either is correct.
On the way to gringo I spent a while reading about yanqui, which Latin Americans use to refer to northerners.
So do people in the USA for that matter. Southerners will angrily deny being “yanqui”. They reserve that term to mean anyone from the north, such as myself. But folks like me from the Mid-Atlantic states also deny being Yankees and will tell you that it only means people from New England. Many New Englanders will disclaim being truly Yankee and say that to meet true Yankees you need to go to Maine or maybe New Hampshire. And I suppose people in Maine use it to mean one particular old Yankee farmer who lives up near the Canadian border.
Anyway, I wonder: in Latin America, does “yanqui” always mean specifically USA-ians, or would it also include Canadians? Would a typical Mexican or Guatemalan person refer casually to Canadians as yanquis? Or, if they were drinking beer with a Canadian, and the Canadian refered to themselves as yanqui, would they correct them? (“You're not a yanqui, you're Canadian! Not the same thing at all!”)
If Mexicans do consider Canadians to be a species of yanqui, what do they make of the Québécois? Also yanqui? Or do Francophones get a pass? (What about the Cajuns for that matter?)
[ Addendum 20250202: Teri Kanefield writes about how “there are no Yankees here”, using it as a metaphor for authoritarianism: “There are no authoritarians here. The authoritarians are on the other side.”
[Other articles in category /lang/etym] permanent link
Fri, 11 Oct 2019In a recent article about fair cake division, I said:
Grandma can use the same method … to divide a regular 17-gonal cake into 23 equally-iced equal pieces.
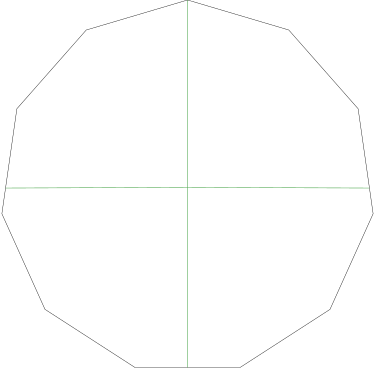
I got to wondering what that would look like, and the answer is, not very interesting. A regular 17-gon is pretty close to a circle, and the 23 pieces, which are quite narrow, look very much like equal wedges of a circle:
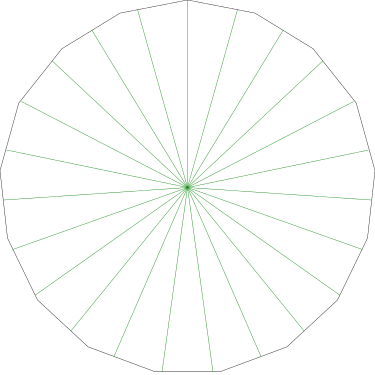
This is generally true, and it becomes more nearly so both as the number of sides of the polygon increases (it becomes more nearly circular) and as the number of pieces increases (the very small amount of perimeter included in each piece is not very different from a short circular arc).
Recall my observation
from last time that even in the nearly extreme case of 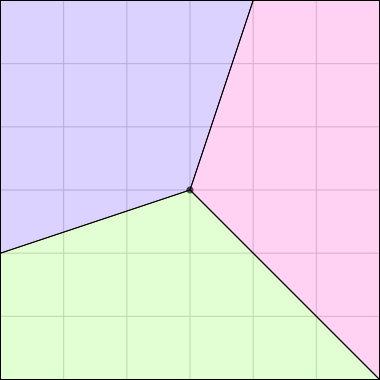 , the central angles deviate from equality by
only a few percent.
, the central angles deviate from equality by
only a few percent.
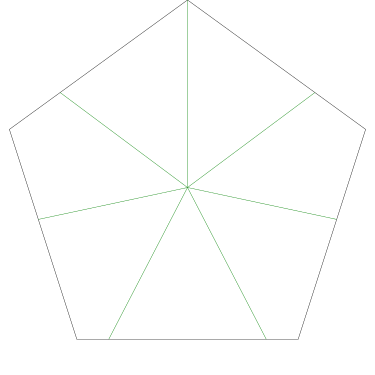
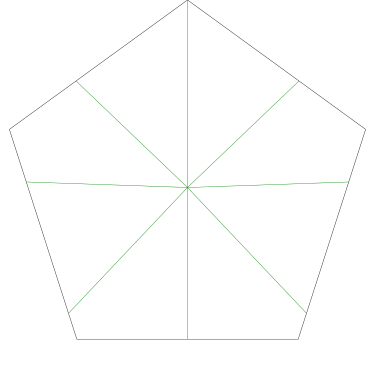
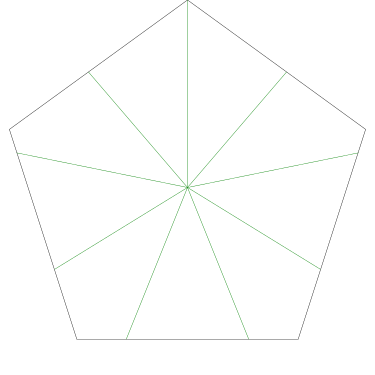
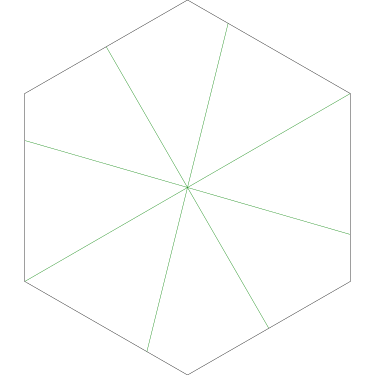
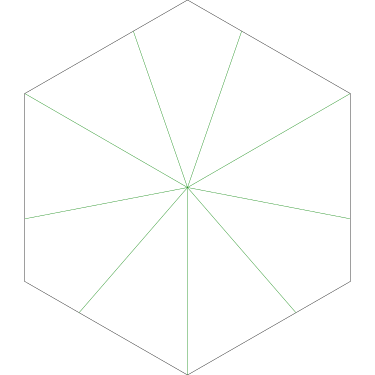
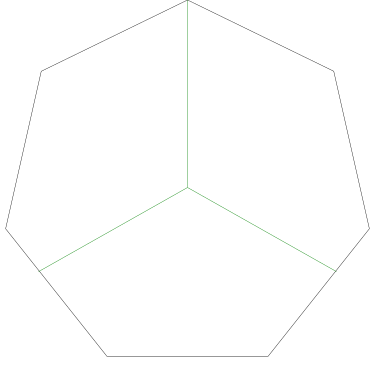
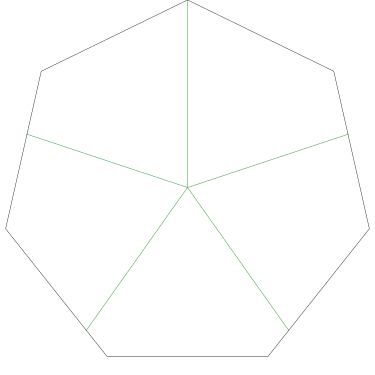
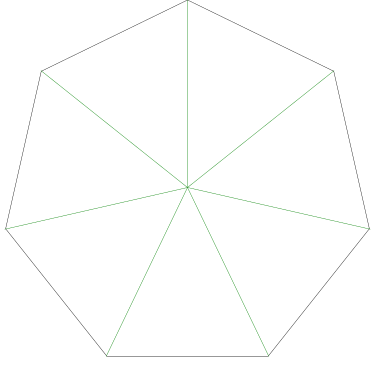
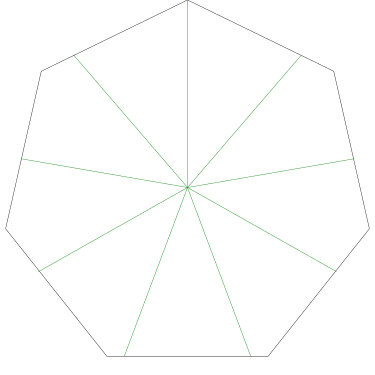
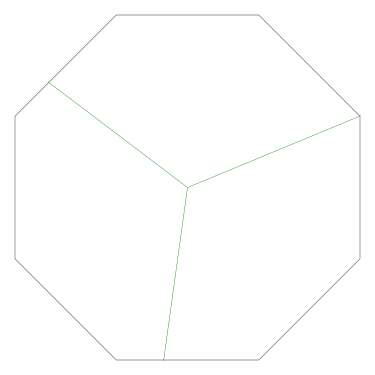
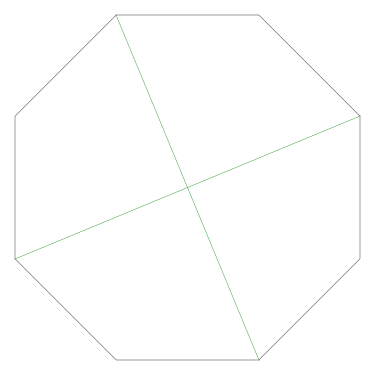
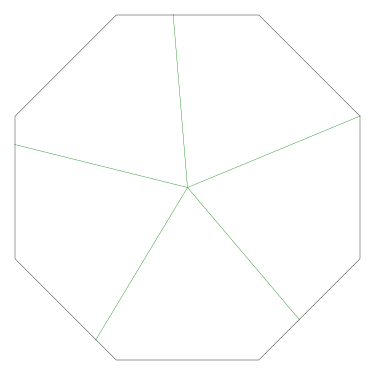
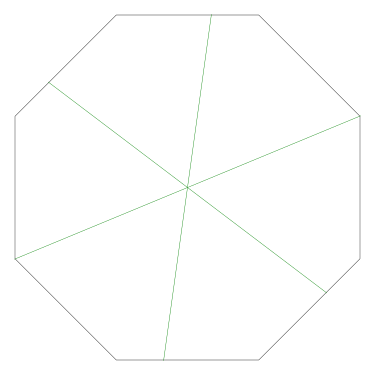
Of particular interest to me is this series of demonstrations of how to cut four pieces from a cake with an odd number of sides:
| 
| 
| 
|
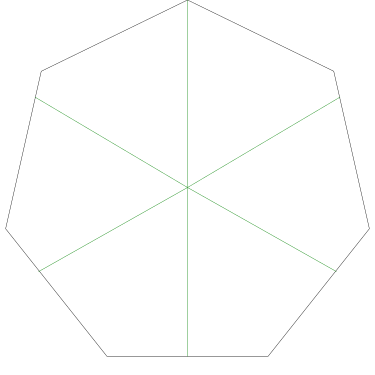
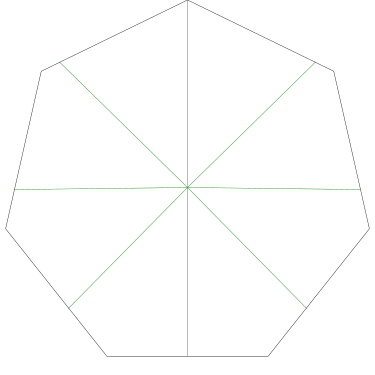
I think this shows that the whole question is a little bit silly: if you just cut the cake into equiangular wedges, the resulting slices are very close in volume and in frosting. If the nearly-horizontal cuts in the pentagon above had been perfectly straight and along the !!y!!-axis, they would have intersected the pentagon only 3% of a radius-length lower than they should have.
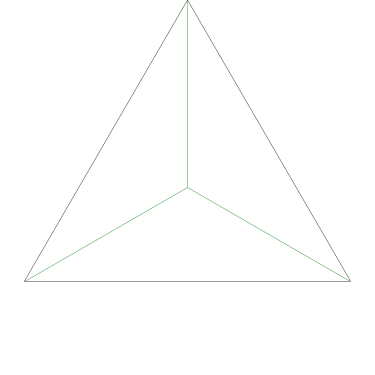
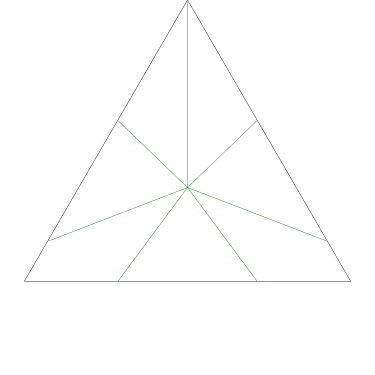
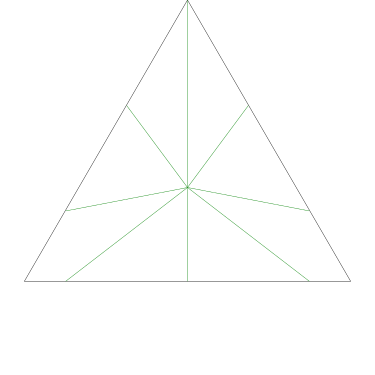
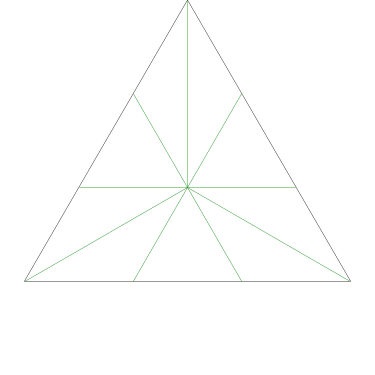
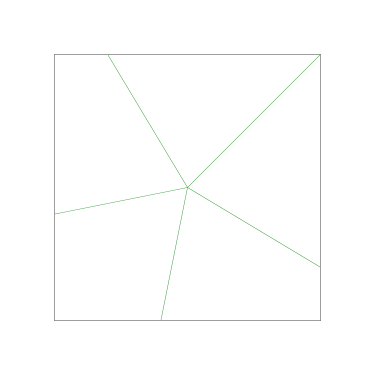
Some of the simpler divisions of simpler cakes are interesting. A solution to the original problem (of dividing a square cake into nine pieces) is highlighted.
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
The method as given works regardless of where you make the first cut. But the results do not look very different in any case:
| 
| 
| 
|
The original SVG files are also available, as is the program that wrote them.
[Other articles in category /math] permanent link
Thu, 10 Oct 2019
Incenters of chocolate-iced cakes
A MathOverflow post asks:
Puzzle 1: Grandma made a cake whose base was a square of size 30 by 30 cm and the height was 10 cm. She wanted to divide the cake fairly among her 9 grandchildren. How should she cut the cake?
Okay, this is obvious.
Puzzle 2: Grandma made a cake whose base was a square of size 30 by 30 cm and the height was 10 cm. She put chocolate icing on top of the cake and on the sides, but not on the bottom. She wanted to divide the cake fairly among her 9 grandchildren so that each child would get an equal amount of the cake and the icing. How should she cut the cake?
This one stumped me; the best I could do was to cut the cake into 27 slabs, each !!\frac{10}3×10×10!! cm, and each with between 1 and 5 units of icing. Then we can give three slabs to each grandkid, taking care that each kid's slabs have a total of 7 units of icing. This seems like it might work for an actual cake, but I suspected that it wasn't the solution that was wanted, because the problem seems like a geometry problem and my solution is essentially combinatorial.
Indeed, there is a geometric solution, which is more interesting, and which cuts the cake into only 9 pieces.
I eventually gave up and looked at the answer, which I will discuss below. Sometimes when I give up I feel that if I had had thought a little harder or given up a little later, I would have gotten the answer, but not this time. It depends on an elementary property of squares that I had been completely unaware of.
This is your last chance to avoid spoilers.
The solution given is this: Divide the perimeter of the square cake into 9 equal-length segments, each of length !!\frac{120}{9}!! cm. Some of these will be straight and others may have right angles; it does not matter. Cut from the center of the cake to the endpoints of these segments; the resulting pieces will satisfy the requirements.
“Wat.” I said. “If the perimeter lengths are equal, then the areas are equal? How can that be?”
This is obviously true for two pieces; if you cut the square from the center into two pieces into two parts that divide the perimeter equally, then of course they are the same size and shape. But surely that is not the case for three pieces?
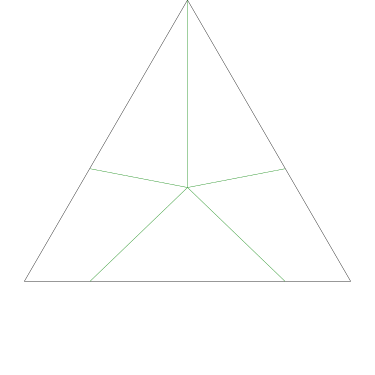
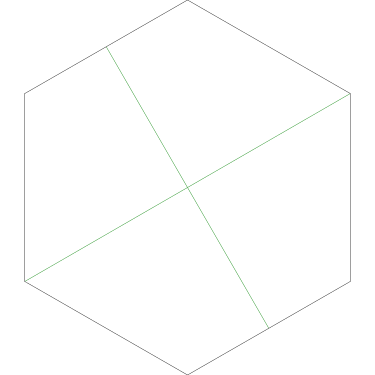
I could not believe it until I got home and drew some pictures on graph paper. Here Grandma has cut her cake into three pieces in the prescribed way:

The three pieces are not the same shape! But each one contains one-third of the square's outer perimeter, and each has an area of 12 square units. (Note, by the way, that although the central angles may appear equal, they are not; the blue one is around 126.9° and the pink and green ones are only 116.6°.)
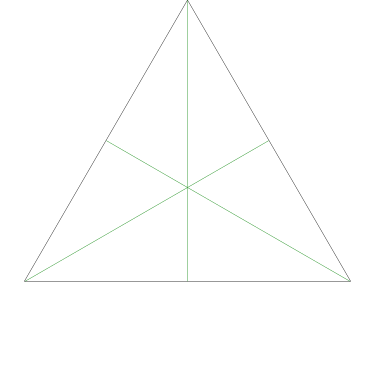
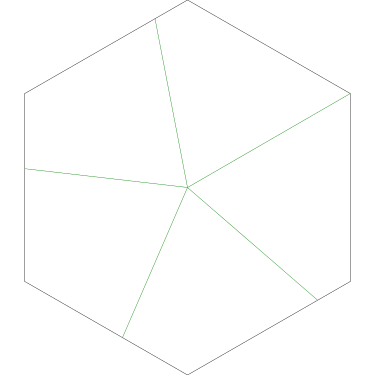
And indeed, any piece cut by Grandma from the center that includes one-third of the square's perimeter will have an area of one-third of the whole square:


The proof that this works is actually quite easy. Consider a triangle !!OAB!! where !!O!! is the center of the square and !!A!! and !!B!! are points on one of the square's edges.
The triangle's area is half its height times its base. The base is of course the length of the segment !!AB!!, and the height is the length of the perpendicular from !!O!! to the edge of the square. So for any such triangle, its area is proportional to the length of !!AB!!.
No two of the five triangles below are congruent, but each has the same base and height, and so each has the same area.
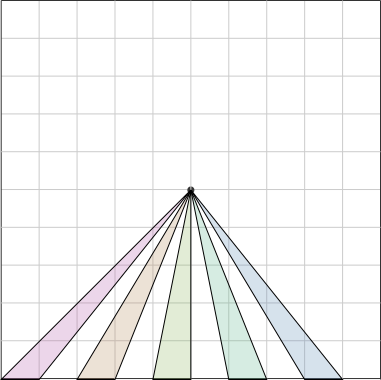
Since the center of the square is the same distance from each of the four edges, the same is true for any two triangles, regardless of which edge they arise from: the area of each triangle is proportional to the length of the square's perimeter at its base. Any piece Grandma cuts in this way, from the center of the cake to the edge, is a disjoint union of triangular pieces of this type, so the total area of any such piece is also proportional to the length of the square's perimeter that it includes.
That's the crucial property of the square that I had not known before: if you make cuts from the center of a square, the area of the piece you get is proportional to the length of the perimeter that it contains. Awesome!
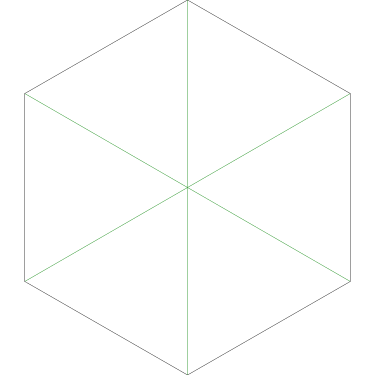
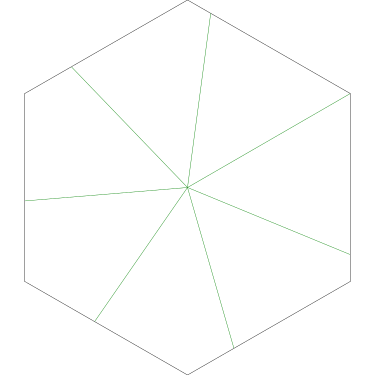
Here Grandma has used the same method to cut a pair of square cakes into ten equal-sized pieces that all the have same amount of icing.
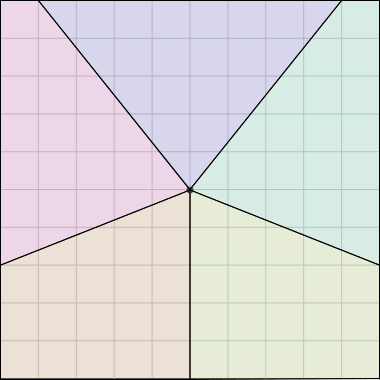
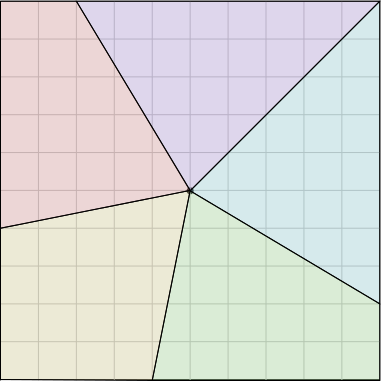
The crucial property here was that the square’s center is the same distance from each of its four edges. This is really obvious, but not every polygon has an analogous point. The center of a regular polygon always has this property, and every triangle has a unique point, called its incenter, which enjoys this property. So Grandma can use the same method to divide a triangular cake into 7 equally-iced equal pieces, if she can find its incenter, or to divide a regular 17-gonal cake into 23 equally-iced equal pieces.
Not every polygon does have an incenter, though. Rhombuses and kites always do, but rectangles do not, except when they are square. If Grandma tries this method with a rectangular sheet cake, someone will get shortchanged. I learned today that polygons that have incenters are known as tangential polygons. They are the only polygons in which can one inscribe a single circle that is tangent to every side of the polygon. This property is easy to detect: these are exactly the polygons in which all the angle bisectors meet at a single point. Grandma should be able to fairly divide the cake and icing for any tangential polygon.
I have probably thought about this before, perhaps in high-school geometry but perhaps not since. Suppose you have two lines, !!m!! and !!n!!, that cross at an acute angle at !!P!!, and you consider the set of points that are equidistant from both !!m!! and !!n!!. Let !!\ell!! be a line through !!P!! which bisects the angle between !!m!! and !!n!!; clearly any point on !!\ell!! will be equidistant from !!m!! and !!n!! by a straightforward argument involving congruent triangles.
Now consider a triangle !!△ABC!!. Let !!P!! be the intersection of the angle bisectors of angles !!∠ A!! and !!∠ B!!.
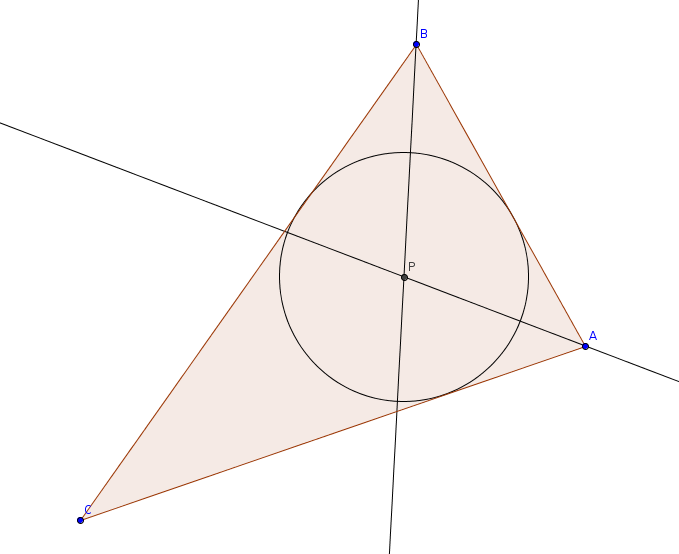
!!P!! is the same distance from both !!AB!! and !!AC!! because it is on the angle bisector of !!∠ A!!, and similarly it is the same distance from both !!AB!! and !!BC!! because it is on the angle bisector of !!∠ B!!.
So therefore !!P!! is the same distance from both !!AC!! and !!BC!! and it must be on the angle bisector of angle !!∠ C!! also. We have just shown that a triangle's three angle bisectors are concurrent! I knew this before, but I don't think I knew a proof.
[ Addendum 20191011: Many illustrated examples. ]
[Other articles in category /math] permanent link
Fri, 04 Oct 2019
Addenda to recent articles 201910
Several people have written in with helpful remarks about recent posts:
Regarding online tracking of legislation:
- Ed Davies directed my attention to www.legislation.gov.uk, an official organ of the British government, which says:
The aim is to publish legislation on this site simultaneously, or at least within 24 hours, of its publication in printed form.
M. Davies is impressed. So am I. Here is the European Union (Withdrawal) Act 2018.
Nik Clayton showed me the @unitedstates project, whcih among other things has a program that attempts to parse the United States Code and produce a tree-structured output.
Twitter user
@sunk818pointed out How I changed the law with a GitHub pull request. The title oversells what actually happened: the codified law contained a minor technical error, which could be corrected without requiring any actual legislation. But the takeaway is that the District of Columbia officially publishes its law to a Github repo.
This then led me to Standardizing the World’s Legislative Information — One hackathon at a time on the LII's VOXPOPULII blog.
(Reminder to readers: I do not normally read Twitter, and it is not a reliable way to contact me.)
Regarding the mysteriously wide letter ‘O’ on the Yeadon firehouse. I had I had guessed that it was not in the same family as the others, perhaps because the original one had been damaged. I asked Jonathan Hoefler, a noted font expert; he agreed.
But one reader, Steve Nicholson, pointed out that it is quite common, in Art Deco fonts, for the ‘O’ to be circular even when that makes it much wider than the other letters. He provided ten examples, such as Haute Corniche.
I suggested this to M. Hoefler, but he rejected the theory decisively:
True; it's a Deco mannerism to have 'modulated capitals'… . But this isn't a deco font, or a deco building, and in any case it would have been HIGHLY unlikely for a municipal sign shop to spec something like this for any purpose, let alone a firehouse. It's a wrong sort O, probably installed from the outset.
(The letter spacing suggests that this is the original ‘O’.)
Several people wrote to me about the problem of taking half a pill every day, in which I overlooked that the solution was simply the harmonic numbers.
Robin Houston linked to this YouTube video, “the frog problem”, which has the same solution, and observed that the two problems are isomorphic, proceeding essentially as Jonathan Dushoff does below.
Shreevatsa R. wrote a long blog article detailing their thoughts about the solution. I have not yet read the whole thing carefully but knowing M. Shreevatsa, it is well worth reading. M. Shreevatsa concludes, as I did, that a Markov chain approach is unlikely to be fruitful, but then finds an interesting approach to the problem using probability generating functions, and then another reformulating it as a balls-in-bins problem.
Jonathan Dushoff sent me a very clear and elegant solution and kindly gave me permission to publish it here:
The first key to my solution is the fact that you can add expectations even when variables are not independent.
In this case, that means that each time we break a pill we can calculate the probability that the half pill we produce will "survive" to be counted at the endpoint. That's the same as the expectation of the number of half-pills that pill will contribute to the final total. We can then just add these expectations to get the answer! A little counter-intuitive, but absolutely solid.
The next key is symmetry. If I break a half pill and there are !!j!! whole pills left, the only question for that half pill is the relative order in which I pick those !!j+1!! objects. In particular, any other half pills that exist or might be generated can be ignored for the purpose of this part of the question. By symmetry, any of these !!j+1!! objects is equally likely to be last, so the survival probability is !!\frac1{j+1}!!.
If I start with !!n!! pills and break one, I have !!n-1!! whole pills left, so the probability of that pill surviving is !!\frac1n!!. Going through to the end we get the answer:
$$\frac1n + \frac1{n-1} + \ldots + 1.$$
I have gotten feedback from several people about my Haskell type constructor clutter, which I will write up separately, probably, once I digest it.
Thanks to everyone who wrote in, even people I forgot to mention above, and even to the Twitter person who didn't actually write in.
[Other articles in category /addenda] permanent link
Thu, 03 Oct 2019I recently mentioned a citation listing on one of the pages of the United States Code at LII. It said:
(Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904; Pub. L. 86–342, title I, § 106, Sept. 21, 1959, 73 Stat. 612; Pub. L. 87–61, title I, § 106, June 29, 1961, 75 Stat. 123; Pub. L. 88–157, § 5, Oct. 24, 1963, 77 Stat. 277; Pub. L. 89–285, title I, § 101, Oct. 22, 1965, 79 Stat. 1028; Pub. L. 89–574, § 8(a), Sept. 13, 1966, 80 Stat. 768; Pub. L. 90–495, § 6(a)–(d), Aug. 23, 1968, 82 Stat. 817; Pub. L. 91–605, title I, § 122(a), Dec. 31, 1970, 84 Stat. 1726; Pub. L. 93–643, § 109, Jan. 4, 1975, 88 Stat. 2284; Pub. L. 94–280, title I, § 122, May 5, 1976, 90 Stat. 438; Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701; Pub. L. 96–106, § 6, Nov. 9, 1979, 93 Stat. 797; Pub. L. 102–240, title I, § 1046(a)–(c), Dec. 18, 1991, 105 Stat. 1995, 1996; Pub. L. 102–302, § 104, June 22, 1992, 106 Stat. 253; Pub. L. 104–59, title III, § 314, Nov. 28, 1995, 109 Stat. 586; Pub. L. 105–178, title I, § 1212(a)(2)(A), June 9, 1998, 112 Stat. 193; Pub. L. 112–141, div. A, title I, §§ 1519(c)(6), formerly 1519(c)(7), 1539(b), July 6, 2012, 126 Stat. 576, 587, renumbered § 1519(c)(6), Pub. L. 114–94, div. A, title I, § 1446(d)(5)(B), Dec. 4, 2015, 129 Stat. 1438.)
My comment was “Whew”.
But this wouldn't have been so awful if LII had made even a minimal effort to clean it up:
- Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904
- Pub. L. 86–342, title I, § 106, Sept. 21, 1959, 73 Stat. 612
- Pub. L. 87–61, title I, § 106, June 29, 1961, 75 Stat. 123
- Pub. L. 88–157, § 5, Oct. 24, 1963, 77 Stat. 277
- Pub. L. 89–285, title I, § 101, Oct. 22, 1965, 79 Stat. 1028
- Pub. L. 89–574, § 8(a), Sept. 13, 1966, 80 Stat. 768
- Pub. L. 90–495, § 6(a)–(d), Aug. 23, 1968, 82 Stat. 817
- Pub. L. 91–605, title I, § 122(a), Dec. 31, 1970, 84 Stat. 1726
- Pub. L. 93–643, § 109, Jan. 4, 1975, 88 Stat. 2284
- Pub. L. 94–280, title I, § 122, May 5, 1976, 90 Stat. 438
- Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701
- Pub. L. 96–106, § 6, Nov. 9, 1979, 93 Stat. 797
- Pub. L. 102–240, title I, § 1046(a)–(c), Dec. 18, 1991, 105 Stat. 1995, 1996
- Pub. L. 102–302, § 104, June 22, 1992, 106 Stat. 253
- Pub. L. 104–59, title III, § 314, Nov. 28, 1995, 109 Stat. 586
- Pub. L. 105–178, title I, § 1212(a)(2)(A), June 9, 1998, 112 Stat. 193
- Pub. L. 112–141, div. A, title I, §§ 1519(c)(6), formerly 1519(c)(7), 1539(b), July 6, 2012, 126 Stat. 576, 587, renumbered § 1519(c)(6), Pub. L. 114–94, div. A, title I, § 1446(d)(5)(B), Dec. 4, 2015, 129 Stat. 1438.
That's the result of s/; /<li>/g, nothing more.
(I wonder if that long citation at the end is actually two citations.)
[Other articles in category /IT] permanent link
The pain of tracking down changes in U.S. law
Last month when I was researching my article about the free coffee provision in U.S. federal highway law, I spent a great deal of time writing this fragment:
I knew that the provision was in 23 USC §131, but I should explain what this means.
The body of U.S. statutory law can be considered a single giant document, which is "codified" as the United States Code, or USC for short. USC is divided into fifty or sixty “titles” or subject areas, of which the relevant one here, title 23, concerns “Highways”. The titles are then divided into sections (the free coffee is in section 131), paragraphs, sub-paragraphs, and so on, each with an identifying letter. The free coffee is 23 USC §131 (c)(5).
But this didn't tell me when the coffee exception was introduced or in what legislation. Most of Title 23 dates from 1958, but the coffee sign exception was added later. When Congress amends a law, they do it by specifying a patch to the existing code. My use of the programmer jargon term “patch” here is not an analogy. The portion of the Federal-Aid Highway Act of 1978 that enacted the “free coffee” exception reads as follows:
ADVERTISING BY NONPROFIT ORGANIZATIONS
Sec. 121. Section 131(c) of title 23, United States Code, is amended—
(1) by striking out “and (4)” and inserting in lieu thereof “(4)”; and
(2) by striking out the period at the end thereof and inserting in lieu thereof a comma and the following: “and (5) signs, displays, and devices advertising the distribution of nonprofit organizations of free coffee […]”.
(The “[…]” is my elision. The Act includes the complete text that was to be inserted.)
The act is not phrased as a high-level functional description, such as “extend the list of exceptions to include: ... ”. It says to replace the text ‘and (4)’ with the text ‘(4)’; then replace the period with a comma; then …”, just as if Congress were preparing a patch in a version control system.
Unfortunately, the lack of an actual version control system makes it quite hard to find out when any particular change was introduced. The code page I read is provided by the Legal Information Institute at Cornell University. At the bottom of the page, there is a listing of the changes that went into this particular section:
(Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904; Pub. L. 86–342, title I, § 106, Sept. 21, 1959, 73 Stat. 612; Pub. L. 87–61, title I, § 106, June 29, 1961, 75 Stat. 123; Pub. L. 88–157, § 5, Oct. 24, 1963, 77 Stat. 277; Pub. L. 89–285, title I, § 101, Oct. 22, 1965, 79 Stat. 1028; Pub. L. 89–574, § 8(a), Sept. 13, 1966, 80 Stat. 768; Pub. L. 90–495, § 6(a)–(d), Aug. 23, 1968, 82 Stat. 817; Pub. L. 91–605, title I, § 122(a), Dec. 31, 1970, 84 Stat. 1726; Pub. L. 93–643, § 109, Jan. 4, 1975, 88 Stat. 2284; Pub. L. 94–280, title I, § 122, May 5, 1976, 90 Stat. 438; Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701; Pub. L. 96–106, § 6, Nov. 9, 1979, 93 Stat. 797; Pub. L. 102–240, title I, § 1046(a)–(c), Dec. 18, 1991, 105 Stat. 1995, 1996; Pub. L. 102–302, § 104, June 22, 1992, 106 Stat. 253; Pub. L. 104–59, title III, § 314, Nov. 28, 1995, 109 Stat. 586; Pub. L. 105–178, title I, § 1212(a)(2)(A), June 9, 1998, 112 Stat. 193; Pub. L. 112–141, div. A, title I, §§ 1519(c)(6), formerly 1519(c)(7), 1539(b), July 6, 2012, 126 Stat. 576, 587, renumbered § 1519(c)(6), Pub. L. 114–94, div. A, title I, § 1446(d)(5)(B), Dec. 4, 2015, 129 Stat. 1438.)
Whew.
Each of these is a citation of a particular Act of Congress. For example, the first one
Pub. L. 85–767, Aug. 27, 1958, 72 Stat. 904
refers to “Public law 85–767”, the 767th law enacted by the 85th Congress, which met during the Eisenhower administration, from 1957–1959. The U.S. Congress has a useful web site that contains a list of all the public laws, with links — but it only goes back to the 93rd Congress of 1973–1974.
And anyway, just knowing that it is Public law 85–767 is not (or was not formerly) enough to tell you how to look up its text. The laws must be published somewhere before they are codified, and scans of these publications, the United States Statutes at Large, are online back to the 82nd Congress. That is what the “72 Stat. 904” means: the publication was in volume 72 of the Statutes at Large, page 904. This citation style was obviously designed at a time when the best (or only) way to find the statute was to go down to the library and pull volume 72 off the shelf. It is well-designed for that purpose. Now, not so much.
Here's a screengrab of the relevant portion of the relevant part of the 1978 act:

The citation for this was:
Pub. L. 95–599, title I, §§ 121, 122, Nov. 6, 1978, 92 Stat. 2700, 2701
(Note that “title I, §§ 121, 122” here refers to the sections of the act itself, not the section of the US Code that was being amended; that was title 23, §131, remember.)
To track this down, I had no choice but to grovel over each of the links to the Statutes at Large, download each scan, and search over each one looking for the coffee provision. I kept written notes so that I wouldn't mix up the congressional term numbers with the Statutes volume numbers.
It ought to be possible, at least in principle, to put the entire U.S. Code into a version control system, with each Act of Congress represented as one or more commits, maybe as a merged topic branch. The commit message could contain the citation, something like this:
commit a4e2b2a1ca2d5245c275ddef55bf8169d72580df
Merge: 6829b2dd986 836108c2ba0
Author: ... <...>
Date: Mon Nov 6 00:00:00 1978 -0400
Surface Transportation Assistance Act of 1978
P.L. 95–599
92 Stat. 2689–2762
H.R. 11733
Merge branch `pl-95-599` to `master`
commit 836108c2ba0d5245c275ddef55bf8169d72580df
Author: ... <...>
Date: Mon Nov 6 00:00:00 1978 -0400
Federal-Aid Highway Act of 1978 (section 121)
(Surface Transportation Assistance Act of 1978, title I)
P.L. 95–599
92 Stat. 2689–2762
H.R. 11733
Signs advertising free coffee are no longer prohibited
within 660 feet of a federal highway.
diff --git a/USC/title23.md b/USC/title23.md
index 084bfc2..caa5a53 100644
--- a/USC/title23.md
+++ b/USC/title23.md
@@ -20565,11 +20565,16 @@ 23 U.S. Code § 131. Control of outdoor advertising
be changed at reasonable intervals by electronic process or by remote
control, advertising activities conducted on the property on which
-they are located, and (4) signs lawfully in existence on October 22,
+they are located, (4) signs lawfully in existence on October 22,
1965, determined by the State, subject to the approval of the
Secretary, to be landmark signs, including signs on farm structures or
natural surfaces, or historic or artistic significance the
preservation of which would be consistent with the purposes of this
-section.
+section, and (5) signs, displays, and devices advertising the
+distribution by nonprofit organizations of free coffee to individuals
+traveling on the Interstate System or the primary system. For the
+purposes of this subsection, the term “free coffee” shall include
+coffee for which a donation may be made, but is not required.
+
*(d)* In order to promote the reasonable, orderly and effective
Or maybe the titles would be directories and the sections would be numbered files in those directories. Whatever. If this existed, I would be able to do something like:
git log -Scoffee -p -- USC/title23.md
and the Act that I wanted would pop right out.
Preparing a version history of the United States Code would be a dauntingly large undertaking, but gosh, so useful. A good VCS enables you to answer questions that you previously wouldn't have even thought of asking.

This article started as a lament about how hard it was for me to track down the provenance of the coffee exception. But it occurs to me that this is the response of someone who has been spoiled by plenty. A generation ago it would have been unthinkable for me even to try to track this down. I would have had to start by reading a book about legal citations and learning what “79 Stat. 1028” meant, instead of just picking it up on the fly. Then I would have had to locate a library with a set of the Statutes at Large and travel to it. And here I am complaining about how I had to click 18 links and do an (automated!) text search on 18 short, relevant excerpts of the Statutes at Large, all while sitting in my chair.
My kids can't quite process the fact that in my childhood, you simply didn't know what the law was and you had no good way to find out. You could go down to the library, take the pertinent volumes of the USC off the shelf, and hope you had looked in all the appropriate places for the relevant statutes, but you could never be sure you hadn't overlooked something. OK, well, you still can't be sure, but now you can do keyword search, and you can at least read what it does say without having to get on a train.
Truly, we live in an age of marvels.
[ Addendum 20191004: More about this ]
[Other articles in category /law] permanent link
Wed, 02 Oct 2019Last month I mentioned that, while federal law generally prohibits signs and billboards about signs within ⅛ mile of a federal highway, signs offering free coffee are allowed.
Vilhelm Sjöberg brought to my attention the 2015 U.S. Supreme Court decision in Reed v. Town of Gilbert. Under the Reed logic, the exemption for free coffee may actually be unconsitutional. The majority's opinion states, in part:
The Sign Code is content based on its face. It defines the categories of temporary, political, and ideological signs on the basis of their messages and then subjects each category to different restrictions. The restrictions applied thus depend entirely on the sign’s communicative content.
The court concluded that the Sign Code (of the town of Gilbert, AZ) was therefore subject to the very restrictive standard of strict scrutiny, which required that it be struck down unless the government could demonstrate both that it was necessary to a “compelling state interest” and that it be “narrowly tailored” to achieving that interest. The Gilbert Sign Code did not survive this analysis.
Although the court unanimously struck down the Sign Code, a concurrence, written by Justice Kagan and joined by Ginsburg and Breyer, faulted the majority's reasoning:
On the majority’s view, courts would have to determine that a town has a compelling interest in informing passersby where George Washington slept. And likewise, courts would have to find that a town has no other way to prevent hidden-driveway mishaps than by specially treating hidden-driveway signs. (Well-placed speed bumps? Lower speed limits? Or how about just a ban on hidden driveways?)
Kagan specifically mentioned the “free coffee” exception as being one of many that would be imperiled by the court's reasoning in this case.
Thanks very much to M. Sjöberg for pointing this out.
[Other articles in category /law] permanent link
Tue, 01 Oct 2019
How do I keep type constructors from overrunning my Haskell program?
Here's a little function I wrote over the weekend as part of a suite for investigating Yahtzee:
type DiceChoice = [ Bool ]
type DiceVals = [ Integer ]
type DiceState = (DiceVals, Integer)
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls [] ([], n) = [ ([], n-1) ]
allRolls [] _ = undefined
allRolls (chosen:choices) (v:vs, n) =
allRolls choices (vs,n-1) >>=
\(roll,_) -> [ (d:roll, n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
I don't claim this code is any good; I was just hacking around exploring the problem space. But it does do what I wanted.
The allRolls function takes a current game state, something like
( [ 6, 4, 4, 3, 1 ], 2 )
which means that we have two rolls remaining in the round, and the most recent roll of the five dice showed 6, 4, 4, 3, and 1, respectively. It also takes a choice of which dice to keep: The list
[ False, True, True, False, False ]
means to keep the 4's and reroll the 6, the 3, and the 1.
The allRolls function then produces a list of the possible resulting
dice states, in this case 216 items:
[ ( [ 1, 4, 4, 1, 1 ], 1 ) ,
( [ 1, 4, 4, 1, 2 ], 1 ) ,
( [ 1, 4, 4, 1, 3 ], 1 ) ,
…
( [ 6, 4, 4, 6, 6 ], 1 ) ]
This function was not hard to write and it did work adequately.
But I wasn't satisfied. What if I have some unrelated integer list
and I pass it to a function that is expecting a DiceVals, or vice
versa? Haskell type checking is supposed to prevent this from
happening, and by using type aliases I am forgoing this advantage.
No problem, I can easily make DiceVals and the others into datatypes:
data DiceChoice = DiceChoice [ Bool ]
data DiceVals = DiceVals [ Integer ]
data DiceState = DiceState (DiceVals, Integer)
The declared type of allRolls is the same:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
But now I need to rewrite allRolls, and a straightforward
translation is unreadable:
allRolls (DiceChoice []) (DiceState (DiceVals [], n)) = [ DiceState(DiceVals [], n-1) ]
allRolls (DiceChoice []) _ = undefined
allRolls (DiceChoice (chosen:choices)) (DiceState (DiceVals (v:vs), n)) =
allRolls (DiceChoice choices) (DiceState (DiceVals vs,n-1)) >>=
\(DiceState(DiceVals roll, _)) -> [ DiceState (DiceVals (d:roll), n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
This still compiles and it still produces the results I want. And it
has the type checking I want. I can no longer pass a raw integer
list, or any other isomorphic type, to allRolls. But it's
unmaintainable.
I could rename allRolls to something similar, say allRolls__, and
then have allRolls itself be just a type-checking front end to
allRolls__, say like this:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls (DiceChoice dc) (DiceState ((DiceVals dv), n)) =
allRolls__ dc dv n
allRolls__ [] [] n = [ DiceState (DiceVals [], n-1) ]
allRolls__ [] _ _ = undefined
allRolls__ (chosen:choices) (v:vs) n =
allRolls__ choices vs n >>=
\(DiceState(DiceVals roll,_)) -> [ DiceState (DiceVals (d:roll), n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
And I can do something similar on the output side also:
allRolls :: DiceChoice -> DiceState -> [ DiceState ]
allRolls (DiceChoice dc) (DiceState ((DiceVals dv), n)) =
map wrap $ allRolls__ dc dv n
where wrap (dv, n) = DiceState (DiceVals dv, n)
allRolls__ [] [] n = [ ([], n-1) ]
allRolls__ [] _ _ = undefined
allRolls__ (chosen:choices) (v:vs) n =
allRolls__ choices vs n >>=
\(roll,_) -> [ (d:roll, n-1) | d <- rollList ]
where rollList = if chosen then [v] else [ 1..6 ]
This is not unreasonably longer or more cluttered than the original
code. It does forgo type checking inside of allRolls__,
unfortunately. (Suppose that the choices and vs arguments had the
same type, and imagine that in the recursive call I put them in the
wrong order.)
Is this considered The Thing To Do? And if so, where could I have learned this, so that I wouldn't have had to invent it? (Or, if not, where could I have learned whatever is The Thing To Do?)
I find most Haskell instruction on the Internet to be either too elementary
pet the nice monad, don't be scared, just approach it very slowly and it won't bite
or too advanced
here we've enabled the
{-# SemispatulatedTypes #-}pragma so we can introduce an overloaded contravariant quasimorphism in the slice category
with very little practical advice about how to write, you know, an actual program. Where can I find some?
[Other articles in category /prog/haskell] permanent link
Fri, 27 Sep 2019
Typographical mysteries of Yeadon
Here are some pictures I took of the firehouse in Yeadon, PA.
Every time I drive past this, I wonder: is that the original letter “O”? Or was there originally a narrow “O” that was lost or damaged, and which couldn't be replaced with a matching letter?
Here's the Google Street View version, from November 2016. The letters are painted green, but the “O” is still the circular one.
[ Addendum 20191004: More about this ]
[Other articles in category /IT/typo] permanent link
Wed, 25 Sep 2019A couple of months ago I asked why the disco ball had to wait until the 20th century:
The 17th century could produce mirrors by gluing metal foil to the back of a piece of glass, so I wonder why they didn't. They wouldn't have been able to spotlight it, but they certainly could have hung it under an orbiculum. Was there a technological limitation, or did nobody happen to think of it?
I think the lighting issue is the show-stopper. To make good use of a disco ball you really do need a dark room and a spotlight. You can get reflections by hanging the ball under an orbiculum, but then the room will be lit by the orbiculum, and the reflections will be pale and washed out, at best.
Long ago I attended a series of lectures by Atsushi Akera on the hidden prerequisites for technological adoption. For example, you can't have practical skyscrapers without also inventing elevators, and you can't have practical automobiles without also inventing windshield wipers. (And windshields. And tires. And … )
This is an amusing example of the same sort. You can't have practical disco balls without also inventing spotlights.
But now I kinda wonder about the possibility of wowing theatre-goers in 1850 with a disco ball, lit by a sort of large hooded lantern containing a limelight and a (lighthouse-style) Fresnel lens.
[ Addendum: Apparently, nobody but me has ever used the word “orbiculum”. I don't know how I started using it, but it seems that the correct word for what I meant is oculus. ]
[ Addendum 20241218: I wondered what had become of Akera, and thanks to the Wonders of the Internet I was able to find out the delightful answer. She had had a career at Rensselaer in Troy, New York. Then she opened a café nearby, owned and run cooperatively by several transgender and non-gender-conforming people, presumably including herself. (She was male-preesnting when I knew her in the 1990s.) It gives me a warm feeling, seeing that the world is finding more ways to let people be themselves, and that because of the Internet I can sometimes share their joyful stories. ]
[Other articles in category /tech] permanent link
Yesterday Katara asked me about impeachment, and in mentioning the impeachment of Andrew Johnson, I realized that I didn't know who would have assumed the presidency, had Johnson been convicted. Who was Johnson's vice president?
Well, I couldn't remember because he didn't have one. Until the ratification of the 25th Amendment in 1967, there was no provision for the replacement of a vice-president except through a normal election.
Under the Presidential Succession Act of 1792, next in line was the President Pro Tempore of the Senate. This is a largely ceremonial position, filled by a senator, and elected by the Senate. The President Pro Tempore in 1868 was Benjamin Wade, senator from Ohio. Wade, as a senator, would be voting on Johnson's conviction and therefore had an enormous conflict of interest: if Johnson was removed, Wade would assume the presidency.
There were calls for Wade to abstain from voting. Which he did. Not! Ha ha, of course he didn't. He voted to convict.
The conviction, famously, fell short by one vote: it went 35–19 in favor of conviction, but they needed 36 votes to convict. Suppose it had gone 36-18, with Wade's vote being the 36th, and Wade taking over the presidency as a result? Wikipedia claims (with plausible citation) that at Wade told at least one other senator what cabinet position he could expect to receive in exchange for his vote to convict.
How could those 1792 folks not have foreseen this? Sheesh.
Government is hard. Really, really hard.
Thinking about the Civil War era of U.S. history, I always have ambivalent feelings. First, hope and relief: “Our current situation could be much worse than it is”, followed by dread: “Our current situation might get much worse than it is”.
[ Maybe I should also mention that many sources suggest that Johnson would have been removed had his successor been someone less divisive than Wade. ]
[Other articles in category /politics] permanent link
Tue, 17 Sep 2019Suppose you have a bottle that contains !!N!! whole pills. Each day you select a pill at random from the bottle. If it is a whole pill you eat half and put the other half back in the bottle. If it is a half pill, you eat it. How many half-pills can you expect to have in the bottle the day after you break the last whole pill?
Let's write !!H(N)!! for the expected number of half-pills left, if you start with !!N!!. It's easily seen that !!H(N) = 0, 1, \frac32!! for !!N=0,1,2!!, and it's not hard to calculate that !!H(3) = \frac{11}{6}!!.
For larger !!N!! it's easy to use Monte Carlo simulation, and find that !!H(30)!! is almost exactly !!4!!. But it's also easy to use dynamic programming and compute that $$H(30) = \frac{9304682830147}{2329089562800}$$ exactly, which is a bit less than 4, only !!3.994987!!. Similarly, the dynamic programming approach tells us that $$H(100) = \frac{14466636279520351160221518043104131447711}{2788815009188499086581352357412492142272}$$ which is about !!5.187!!.
(I hate the term “dynamic programming”. It sounds so cool, but then you find out that all it means is “I memoized the results in a table”. Ho hum.)
As you'd expect for a distribution with a small mean, you're much more likely to end with a small number of half-pills than a large number. In this graph, the red line shows the probability of ending with various numbers of half-pills for an initial bottle of 100 whole pills; the blue line for an initial bottle of 30 whole pills, and the orange line for an initial bottle of 5 whole pills. The data were generated by this program.
The !!E!! function appears to increase approximately logarithmically. It first exceeds !!2!! at !!N=4!!, !!3!! at !!N=11!!, !!4!! at !!N=31!!, and !!5!! at !!N=83!!. The successive ratios of these !!N!!-values are !!2.75, 2.81,!! and !!2.68!!. So we might guess that !!H(N)!! first exceeds 6 around !!N=228!! or so, and indeed !!H(226) < 6 < H(227)!!. So based on purely empirical considerations, we might guess that $$H(N) \approx \frac{\log{\frac{15}{22}N}}{\log 2.75}.$$
(The !!\frac{15}{22}!! is a fudge factor to get the curves to line up properly.)
I don't have any theoretical justification for this, but I think it might be possible to get a bound.
I don't think modeling this as a Markov process would work well. There are too many states, and it is not ergodic.
[ Addendum 20190919: Ben Handley informs me that !!H(n)!! is simply the harmonic numbers, !!H(n) = \sum_1^n \frac1n!!. I feel a little foolish that I did not notice that the first four terms matched. The appearance of !!H(3)=\frac{11}6!! should have tipped me off. Thank you, M. Handley. ]
[ Addendum 20190920: I was so fried when I wrote this that I also didn't notice that the denominator I guessed, !!2.75!!, is almost exactly !!e!!. (The correct value is !!e!!.) I also suspect that the !!\frac{15}{22}!! is just plain wrong, and ought to be !!e^\gamma!! or something like that, but I need to take a closer look. ]
[ Addendum 20191004: More about this ]
[Other articles in category /math] permanent link
Today it occurred to me that in the many comedy duos that feature a “straight man” and a “comedian”, the straight man is invariably named first. The central example, of course, is Abbott and Costello. But we also have:
- Laurel and Hardy
- Burns and Allen
- Rowan and Martin
- Martin and Lewis
- Bert and Ernie
and this even extends to entirely fictitious pairs such as Jeeves and Wooster, Harold and Kumar, or Sam and Max, Freelance Police. Also, if you are a mathematician, Smothers and Smothers. This is why people hate mathematicians.
I did Google search for "Kermit and Fozzie" (hits outnumber "Fozzie and Kermit" by around three-to-one) and "Kermit and Miss Piggy" (hits outnumber "Miss Piggy and Kermit", although only by about 60%.)
Wikipedia says this is no accident!
In vaudeville, effective straight men were much less common than comedians. The straight man's name usually appeared first and he usually received 60% of the take.
But my co-worker Jeff Culverhouse found a counterexample: Silent Bob is certainly the straight man of Jay and Silent Bob.
Wikipedia also has a list of American Comedy Duos. Not all of them follow the straight man / comedian pattern, and I don't recognize many of those that do. More research is needed.
Addenda
I wanted to find a gender-neutral term for "straight man", but failed.
20220623
I thought of another counterexample: Wallace and Gromit.
20230221
Google search hits for “Tom and Dick Smothers” outnumber those for “Dick and Tom Smothers” to more than 7 to 1. (20600 to 2670.) Dick was the straight man.
20250508
Michel Dingler points out that R2-D2 and C-3PO are another counterexample:
Popular consensus in my Mastodon timeline seems to agree.
I haven't seen it, but I suppose that in the action comedy series B.J. and the Bear, B.J. (played by Greg Evigan) is the straight man to the Bear (played by some monkey).
[Other articles in category /misc] permanent link
According to the New York Times of 10 March 1982:
In 1970, for example, President Nixon and Vice President Agnew did a piano duet built around their so-called ''Southern Strategy.'' No matter what song Mr. Nixon played, Mr. Agnew cut in with ''Dixie.'' The audience found it uproariously funny, as they did the spectacle of the Vice President clicking his heels, saluting and telling Mr. Nixon, ''Yes suh, Mr. President, ah agree with you completely on yoah Southern strategy.''
And yet the cruel earth refused to open and swallow everyone involved.
[Other articles in category /politics] permanent link
Mon, 16 Sep 201923 USC §131 controls the display of billboards and other signs within 660 feet of a federal interstate highway. As originally enacted in 1965, there were a few exceptions, such as directional signs, and signs advertising events taking place on the property on which they stood, or the sale or lease of that property.
Today I learned that under the Federal-Aid Highway Act of 1978, the list of exceptions was extended to include:
signs, displays, and devices advertising the distribution by nonprofit organizations of free coffee to individuals traveling on the Interstate System or the primary system.
There is no exception for free tea.
[ Addendum 20191002: A 2015 Supreme Court decision imperils the free coffee exception, according to three of the justices. I've written a detailed followup. ]
[Other articles in category /law] permanent link
Sat, 14 Sep 2019[ (Previously) ]
Wikipedia has an animation that shows the convergence of the Maclaurin series for the exponential function:
This makes it look a lot better-behaved than it is. First, because it only shows a narrow region around the center of convergence. But also, it emphasizes the right-hand quadrant, where the convergence is monotone.
If you focus on the left-hand side instead, you see the appoximations thrashing back and forth like a screen door in a hurricane:
This is the same as Wikipedia's animation, just focused on a slightly different region of the plane. But how different it looks!
(Individual frames are available)
[Other articles in category /math] permanent link
Fare-dodging insurance businesses
A recent article described a business that insured transit riders against being fined for fare-dodging, and asked:
Does anyone remember this? Can someone point me to a reference?
Florian Ilgenfritz wrote to tell me that they had heard of such a system in Berlin, and this let them to the German Wikipedia article on Schwarzfahrerversicherung, which is precisely what I was looking for. (“Schwarzfahrer“ is fare-dodging, literally “blackriding”, and “versicherung” is insurance.) The article mentions similar systems in Paris and Stockholm, and also one run by the student union of the University of Hanover, which had to shut down because increased fare enforcement on the Hanover metro depleted the benefits pool.
One Paris version, as described at this archived page, was amusingly called le Réseau pour l’Abolition des Transports Payants. (Its initials, RATP, are the same as those of the state-owned public transportation operator). Each RATP group was an insurance cooperative. Would-be fare-dodgers would meet at the beginning of the month and contribute to a pool, from which fines would be reimbursed.
The page says:
- a group will have 10–30 members
- each member will put 6–7 Euros into the kitty
- “even a very unlucky person cannot be fined more than 4 or 5 times a year”
Each member is putting in €72–84 per year. Even if every member is maximally unlucky, this is enough to cover a fine of €16–17, and two or three times that much of not everyone is caught so frequently.
NPR reported on the Stockholm version as recently as 2015, and the Paris version in 2010. There is a German-language article from Der Spiegel from around the same time. This article claims that in one Berlin association, only 50% of the members’ €11 monthly premium had to be paid out in benefits, leaving a €33,000 profit. No word on what happened to the profit. Perhaps it was reinvested for the benefit pool, or perhaps the least scrupulous of the fund organizers embezzled it.
Most Philadelphia public transit is guarded by turnstiles, making fare-dodging more troublesome. The exception is on the regional rail system, where the passenger can board, with or without a ticket, and the conductor comes around to punch tickets, or sell higher-priced on-train tickets to people without any. This is well enough enforced that a fare dodger would be caught almost every time and have to pay the higher price, so the insurance scheme would not be practical. But I remember back in the 1990s it would sometimes be worth while to ride regional rail for a couple of stops in Center City, rather than the subway. The on-board regional rail fare was substantially higher than the subway fare, but the chance of getting off the crowded train without having to buy a ticket was good.
A recent article in the Philadelphia Inquirer describes a different fare-dodging scheme. SEPTA will sell a weekly pass, good for up to 56 rides, for $25.50, or 45.5¢ per ride. The cash fare is $2.50. The fare-dodgers will buy a weekly pass, and then stand at the turnstile offering to let cash-fare riders use it for $2 cash. The cash-fare rider is ahead by $0.50 and the entrepreneur can earn a return of up to 449% on their $22.50 investment.
Exercise for the reader: where is the extra value here and why doesn't SEPTA capture it? Are the entrepreneurs increasing or depleting the public good?
Thanks to M. Ilgenfritz for the initial references, which provided enough for me to get started following up the details on my own.
[Other articles in category /misc] permanent link
Tue, 10 Sep 2019
Chicken-fondling discouraged by the CDC
This week, according to the Washington Post, Kissing chickens is bad for your health, CDC warns. (The story was also reported by Newsweek last week. )
Specifically, the CDC Investigation Notice advises:
Don’t kiss backyard poultry or snuggle them and then touch your face or mouth.
This isn't quite clear. Is it:
Don’t ((kiss backyard poultry)
or
((snuggle them) and (then touch your (face or mouth))))
or is it rather
Don’t (((kiss backyard poultry) or (snuggle them))
and (then touch your (face or mouth)))
I think they mean the former? But if it's the latter, then the Post has it wrong, and it's okay to kiss backyard poultry, as long as you don't then touch your face or mouth.
But is this really a pressing issue? Apparently so! Kissing chickens, according to the CDC research, is disturbingly common:
Among respondents with baby poultry exposure … 13% (53/400) reported kissing baby birds.
No word on how many of the 53 chicken-kissers tried to use their tongues.

[ Addendum 20210520: This has come around again:
The CDC reports that 163 people have contracted salmonella from backyard poultry, and again implores people not to kiss or snuggle them. ]
[ Addendum 20210523: The blonde lady, I have learned, is Tiara Soleim, who, when she was a contestant on The Bachelor, was also identified as a “chicken enthusiast”. The Tucker Carlson segment contains footage of her demonstrating how to snuggle and kiss chickens. ]
[Other articles in category /misc] permanent link
Sun, 08 Sep 2019
The exponential function is a miracle
The Maclaurin series for the exponential function converges for every complex number !!x!!: $$1 - x + \frac{x^2}{2} - \frac{x^3}{6} + \frac{x^4}{24} - \ldots = e^{-x} $$
Say that !!x!! is any reasonably large number, such as 5. Then !!e^{-x}!! is close to zero, But the terms of the series are not close to zero. For !!x=5!! we have: $$ 1 - 5 + 12.5 - 20.83 + 26.04 - 26.04 + 21.7 - 15.5 + 9.69 - 5.38 + \ldots \approx {\Large 0}$$
Somehow all these largish random numbers manage to cancel out almost completely. And the larger we make !!x!!, the more of these largish random numbers there are, the larger they are, and yet the more exactly they cancel out. For even as small an argument as !!x=20!!, the series begins with 52 terms that vary between 1 and forty-three million, and these somehow cancel out almost entirely. The sum of these 52 numbers is !!-0.4!!.
In this graph, the red lines are the various partial sums (!!1-x, 1-x+\frac{x^2}2, !! etc.) and the blue line is the total sum !!e^{-x}!!.
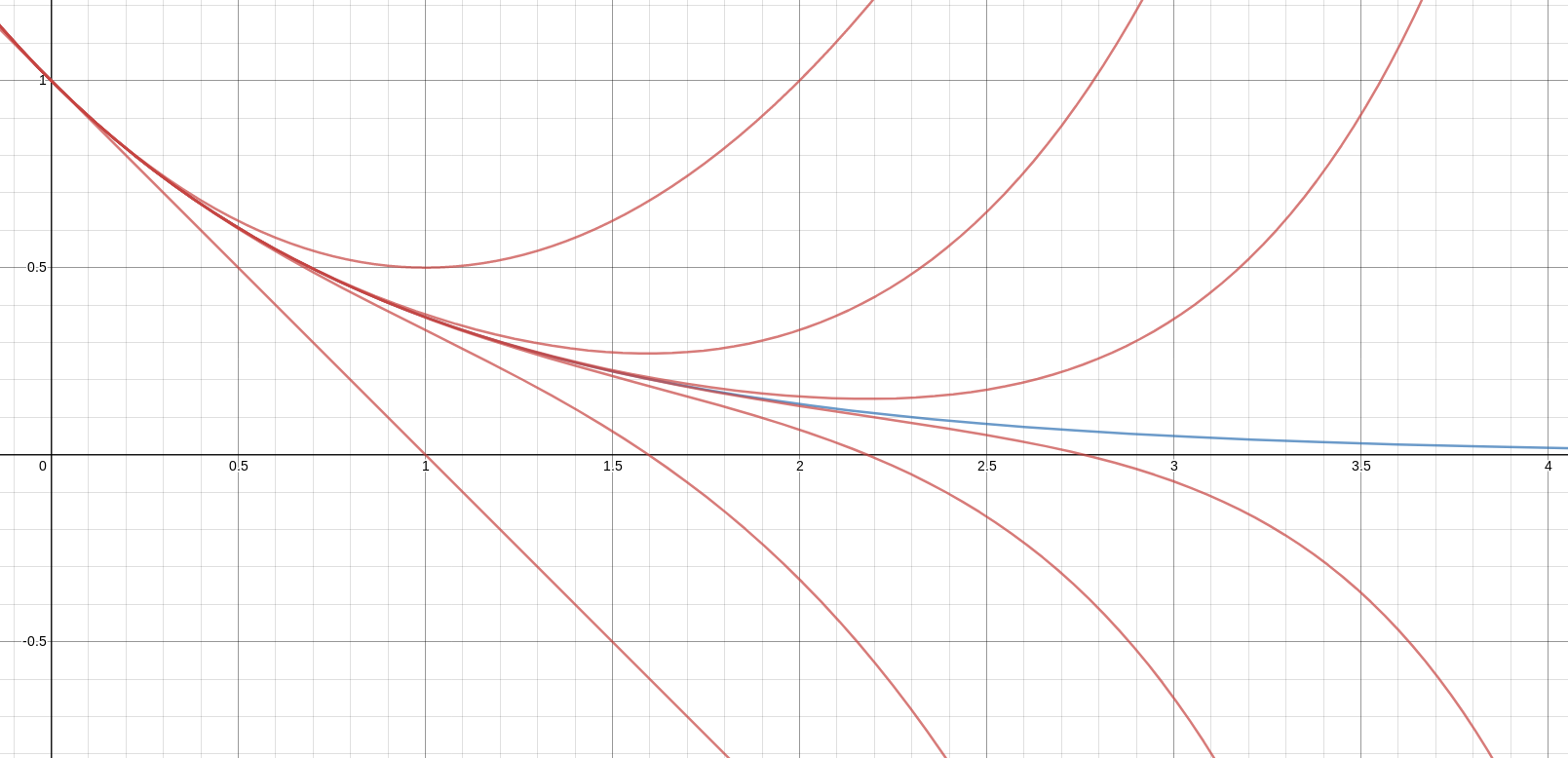
As you can see, each red line is a very bad approximation to the blue one, except within a rather narrow region. And yet somehow, it all works out in the end.
[ (Addendum) ]
[Other articles in category /math] permanent link
Mon, 02 Sep 2019I think a disco ball would not be out of place at Versailles.
This got me thinking about what if all of Versailles had been tricked out in awesome 1970's disco style? I could easily picture Louis XIV in a white leisure suit, open to the navel, with gold chains and bell-bottom trousers, his platform shoes glittering with real diamonds. (Surely you didn't think le Roi Soleil would wear rhinestones?)
I have been enjoying this mental picture for some time now, but part of it is wrong: the bell-bottoms. Louis didn't have a pretty face. But he had great legs, he knew it, and he never missed an opportunity to show them off:
Notice the recurring theme: skin-tight trousers or tights. Fancy garters. When he's wearing heavy state robes, they're cut away or swept back to expose his legs, and he always stands sideways or sticks them out so that you can see them.
(In that last picture, the diamond studded platform shoes, just as I said. Nailed it!)
Here Louis is fancifully depicted as Alexander the Great. He surely did not dress up in costume for the portrait. But the unknown painter knew what Louis liked and made him bare-legged, with a diaphanous blue tunic:
This is not a man who is going to wear bell-bottoms.
[ Addendum 20190903: “Louis loved ballet and frequently danced in court ballets during the early half of his reign. In general, Louis was an eager dancer who performed 80 roles in 40 major ballets.” Thanks to Akiva Leffert from bringing this to my attention. ]
[Other articles in category /misc] permanent link
Thu, 29 Aug 2019
More workarounds for semantic problems
Philippe Bruhat, a devious master of sending a single message that will be read in two different ways by two different recipients, suggested an alternative wording for magic phrase messages:
"I request that this commit be exempt from review for the following reasons: "
(followed by an actual explanation)
The Git hook will pattern-match the message and find the magic phrase,
which is I request that this commit be exempt from review for the
following reasons:. Humans, however, will read and understand the
actual explanation. I think M. Bruhat has put the first line in
quotes so that humans will not attempt to interpret it. In this case
it might not be a big problem if they did interpret it; at worst
they might be puzzled about why the request was being sent to them
rather than to the Git hook. But it also protects against the
situation where the secret phrase is “Craig said I could do this” or
“Chinga tu madre!”.
My only concern is that, depending on how the explanation was phrased, it might be ungrammatical. I think these quoted phrases should behave like nouns, as in
"Tinkle in the toidy" is a highly offensive phrase.
As written, M. Bruhat's suggestion has a dangling noun without even a punctuation mark. I suggested something like this:
This message includes the phrase "The fat man screams at midnight"
for the following reasons:
(followed by an actual explanation)
Or we could take a hint from the bronze age Assyrians, who began letters with formulas like:
To my lord Tukulti-Ninurta, say thus: …
Note that this is addressed not to Tukulti-Ninurta himself, but to the messenger who is to read the message to Tukulti-Ninurta. Following this pattern we might write our commit message in this form:
To the Git pre-receive hook, I say thus:
"Craig said I could do this"
because (actual explanation)
(I originally wrote “we could take a page from the Assyrians”, which is obviously ridiculous.)
Many thanks to M. Bruhat for discussing this with me, and to Rafaël Garcia-Suarez for bringing it to his attention.
[Other articles in category /tech] permanent link
Wed, 28 Aug 2019In a (still unpublished) discussion a while back, of the complexities of the idea of “opposites”, I said:
"Opposite" extends to all sorts of situations in which logic doesn't apply. Red is the opposite of green, but I'm not sure that it makes sense to ask for the logical negation of green. I suppose you can go with "not green", which is certainly quite different from "red".
A related example: Red is the opposite of green.
What's the opposite of “not green”? Is it “not red”? I think it isn't. The opposite of “not green” is “green”.
[Other articles in category /lang] permanent link
DLR is the Docklands Light Railway, a light rail system that operates in East London. The fare collection system is interesting. You buy a ticket, but you don't have to show it before you board. Instead, during the ride, a ticket agent might come through the car and demand to see it. If you can't produce it on demand, you become liable for a large fine. So you can evade the fare, but doing so is a high-risk gamble.
The DLR might like to have enough fare inspectors that the gamble would have negative expected payout for the passengers. But at the time I took it, they didn't do so many inspections. The gamble was actually a good one for passengers, if they didn't mind the high risk of a rare large loss in return for small frequent wins. Most people wouldn't accept the risk, so the system worked.
But about fifteen years ago, some guy in East London had an idea. Insurance exists to diffuse risk! You'd pay him a monthly subscription fee, and then you'd ride the DLR that month without buying tickets. If you were caught by the fare inspectors, you'd pay the fine, send him the receipt, and he would reimburse you. You'd win because the insurance premium you paid this guy cost less than what you would have paid for DLR tickets. He'd win because he could set the insurance premiums high enough to cover the relatively few fines he had to pay out.
For a time this went well for everyone except the DLR. Eventually they caught the guy and punished him for conspiring to evade fares or something like that.
Does anyone remember this? Can someone point me to a reference?
[ Addendum 20190914: Leads provided by Florian Ilgenfritz produced a wealth of information about similar schemes. ]
[Other articles in category /misc] permanent link
It has sometimes happened that I couldn't get my git add -p to work. I would carefully
edit a chunk, and then Git would say
Your edited hunk does not apply. Edit again (saying "no" discards!) [y/n]? e
or sometimes also
error: patch fragment without header at line 33: @@ -26,21 +29,20 @@ class Parser():
so I'd do it over, and it still wouldn't work.
Today I learned that at least some of those are because Emacs's
diff-mode has some bug. It's getting the @@ lines wrong. When I
switched to text-mode and composed the @@ line myself, the patch
applied.
[Other articles in category /prog] permanent link
Tue, 27 Aug 2019
Workarounds for semantic problems
At work we have a Git repostory hook (which I wrote) that prevents people from pushing changes to sensitive code without having it reviewed first. But there is an escape hatch for emergencies: if your commit message contains a certain phrase, the hook will allow it anyway. The phrase is:
Craig said I could do this
(Craig is the CTO.)
Recently we did have a semi-emergency situation, and my co-worker Nimrod was delayed because nobody was awake to approve his code. In the discussion after, I mentioned the magic escape phrase. He objected that he could not have used it, because he would have been unwilling to wake up Craig to get the go-ahead. I was briefly puzzled. I hadn't said anything about waking up Craig; all you have to do is put a key phrase in your commit message. Nimrod eventually got me to understand the issue:
Nimrod: what does the phrase Craig said I could do this imply?
I had been thinking of the message as being communicated only to the Git hook. The Git hook thinks you mean only that it should allow the commit into the repo without review, which is true. But Nimrod is concerned about how it will be received by other humans, and to these people he would appear to be telling a lie. Right!
Nimrod had previously suggested a similar feature that involved the magic phrase “I solemnly swear I'm up to no good”.
Me: It seems to me that the only thing lacking from the current feature set is that you want the magic phrase to be
I solemnly swear I'm up to no goodinstead ofCraig said I could do this. Is that correct? It seems to me that alternate universe Nimrod might reasonably object that he may not force a commit unless he can really swear that he is up to no good.So in this case that wouldn't have helped you. Or so I assume.
(I don't know, maybe he really was up to no good? But he did deny it.)
Nimrod: true enough! but it seems less likely to be taken seriously than having to swear that you have Craig's approval…
Me: Perhaps the magic phrase should be
I request that this commit be exempt from review.It would take a very subtle alternate-universe Nimrod to claim that he was too truthful to invoke that magic phrase just because he wanted his commit to be exempt from review.
Nimrod liked that okay, but then I had a better idea:
My suggestion, for the next time this comes up, is that you include the following wording in your commit message:
My mention here of the magic phrase “Craig said I could do this” is not intended to aver that Craig did, in fact, say that I could do this.The Git hook does not understand the use-mention distinction and you can then enable the feature without uttering a falsehood.
Problem solved!
(This reminds me a little bit of those programs that Philippe Bruhat writes that can be interpreted either as Perl or as PostScript, depending on how you understand the quoting and commenting conventions.)
[ Addendum: The actual magic phrase is not “Craig said I could do this”. ]
[ Addendum 20190829: There is a followup article that includes Philippe Bruhat's suggestion. ]
[Other articles in category /tech] permanent link
Wed, 07 Aug 2019
Technical devices for reducing the number of axioms
In a recent article, I wrote:
I guessed it was a mere technical device, similar to the one that we can use to reduce five axioms of group theory to three. …
The fact that you can discard two of the axioms is mildly interesting, but of very little practical value in group theory.
There was a sub-digression, which I removed, about a similar sort of device that does have practical value. Suppose you have a group !!\langle G, \ast \rangle!! with a nonempty subset !!H\subset G!!, and you want to show that !!\langle H, \ast \rangle!! is a subgroup of !!G!!. To do this is it is sufficient to show three things:
- !!H!! is closed under !!\ast!!
- !!G!!'s identity element is in !!H!!
- For each element !!h!! of !!H!!, its inverse !!h^{-1}!! is also in !!H!!
Often, however, it is more convenient to show instead:
For each !!a, b\in H!!, the product !!ab^{-1}!! is also in !!H!!
which takes care of all three at once.
[Other articles in category /math] permanent link
Mon, 05 Aug 2019After decapitating Medusa the Gorgon, Perseus flies home on the winged sandals lent to him by Hermes, But he stops off to do some heroing. Below, he spots the beautiful princess Andromeda, chained to a rock.
Here's the description my kids got from D'Aulaire's Book of Greek Myths:
On the way home, as he flew over the coast of Ethiopia, Perseus saw, far below, a beautiful maiden chained to a rock by the sea. She was so pale that at first he thought she was a marble statue, but then he saw tears trickling from her eyes.
Here's the d’Aulaires’ picture of the pasty-faced princess:

Andromeda has been left there to distract a sea monster, which will devour her instead of ravaging the kingdom. Perseus rescues her, then murders her loser ex-boyfriend, who was conspicuously absent from the rendezvous with the monster. Perseus eventually marries Andromeda and she bears his children.
Very good. Except, one problem here. Andromeda is Princess Royal of Ethiopia, the daughter of King Cepheus and Queen Cassiopeia. She is not pale like a marble statue. She has dark skin.
How dark is not exactly clear. For the Greeks “Aethiopia” was a not entirely specific faraway land. But its name means the land of people with burnt faces, not the land of people who are pale like white marble.
The D'Aulaires are not entirely at fault here. Ovid's Metamorphoses compares her with marble:
As soon as Perseus, great-grandson of Abas, saw her fastened by her arms to the hard rock, he would have thought she was a marble statue, except that a light breeze stirred her hair, and warm tears ran from her eyes.
But he's also quite clear (in Book II) that Ethiopians have dark skin:
It was [during Phaethon episode], so they believe, that the Ethiopians acquired their dark colour, since the blood was drawn to the surface of their bodies.
(Should we assume that Ovid evokes marble for its whiteness? Some marble isn't white. I don't know and I'm not going to check the original Latin today. Or perhaps he only intended to evoke its stillness, for the contrast in the next phrase. Anyway, didn't the Romans paint their marble statuary?)
Andromeda was a popular subject for painting and sculpture over the centuries, since she comes with a a built-in excuse for depicting her naked or at least draped with wet fabric. European artists, predictably, made her white:
 Painting by Gustave
Doré, 1869.
Painting by Gustave
Doré, 1869.
But at least not every time:
[Other articles in category /book/myth] permanent link
Sat, 03 Aug 2019
Git wishlist: aggregate changes across non-contiguous commits
(This is actually an essay on the difference between science and engineering.)
My co-worker Lemuel recently asked if there was a way to see all the
changes to master from the last week that pertained to a certain
ticket. The relevant commit messages all contained the ticket ID, so
he knew which commits he wanted; that part is clear. Suppose Lemuel
wanted to see the changes introduced in commits C, E, and H, but not
those from A, B, D, F, or G.
The closest he could come was git show H E C, which wasn't quite what
he wanted. It describes the complete history of the changes, but what
he wanted is more analogous to a diff. For comparison, imagine a
world in which
git diff A H didn't exist, and you were told to use git show A B C
D E F G H instead. See the problem? What Lemuel wants is more like
diff than like show.
Lemuel's imaginary command would solve another common request: How can
I see all the changes that I have landed on master in a certain
time interval? Or similarly: how can I add up the git diff --stat
line counts for all my commits in a certain interval?
He said:
It just kinda boggles my mind you can't just get a collective diff on command for a given set of commits
I remember that when I was first learning Git, I often felt boggled in this way. Why can't it just…? And there are several sorts of answers, of which one or more might apply in a particular situation:
- It surely could, but nobody has done it yet
- It perhaps could, but nobody is quite sure how
- It maybe could, but what you want is not as clear as you think
- It can't, because that is impossible
- I am not able rightly to apprehend the kind of confusion of ideas that could provoke such a question
Often, engineers will go straight to #5, when actually the answer is in a higher tier. Or they go to #4 without asking if maybe, once the desiderata are clarified a bit, it will move from “impossible” to merely “difficult”. These are bad habits.
I replied to Lemuel's (implicit) question here and tried to make it a mixture of 2 and 3, perhaps with a bit of 4:
Each commit is a snapshot of the state of the repo at a particular instant. A diff shows you the difference between two snapshots. When you do git show commit you're looking at the differences between the snapshot at that commit and at its parent.
Now suppose you have commit A with parent B, and commit C with parent D. I come to you and say I want to see the differences in both A and C at that same time. What would you have it do?
If A and B are on a separate branch and are completely unrelated to C
and D, it is hard to see what to do here. But it's not impossible.
Our hypothetical command could produce the same output as git show A
C. Or it could print an error message Can't display changes from
unrelated commits A, C and die without any more output. Either of
those might be acceptable.
And if A, B, C, D are all related and on the same branch, say with D , then C, then B, then A, the situation is simpler and perhaps we can do better.
If so, very good, because this is probably the most common case by far. Note that Lemuel's request is of this type.
I continued:
Suppose, for example,that C changes some setting from 0 to 1, then B changes it again to be 2, then A changes it a third time, to say 3. What should the diff show?
This is a serious question, not a refutation. Lemuel could quite
reasonably reply by saying that it should show 0 changing to 3, the
intermediate changes being less important. (“If you wanted to see
those, you should have used git show A C.”)
It may be that that wouldn't work well in practice, that you'd find there were common situations where it really didn't tell you what you wanted to know. But that's something we'd have to learn by trying it out.
I was trying really hard to get away from “what you want is stupid” and toward “there are good reasons why this doesn't exist, but perhaps they are surmountable”:
(I'm not trying to start an argument, just to reduce your bogglement by explaining why this may be less well-specified and more complex than you realize.)
I hoped that Lemuel would take up my invitation to continue the discussion and I tried to enocurage him:
I've wanted this too, and I think something like it could work, especially if all the commits are part of the same branch. … Similarly people often want a way to see all the changes made only by a certain person. Your idea would answer that use case also.
Let's consider another example. Suppose some file contains functions X, Y, Z in that order. Commit A removes Y entirely. Commit B adds a new function, YY, between X and Z. Commit C modifies YY to produce YY'. Lemuel asks for the changes introduced by A and C; he is not interested in B. What should happen?
If Y and YY are completely unrelated, and YY just happens to be at the same place in the file, I think we definitely want to show Y being removed by A, and then that C has made a change to an unrelated function. We certainly don't want to show all of YY beind added. But if YY is considered to be a replacement for Y, I'm not as sure. Maybe we can show the same thing? Or maybe we want to pretend that A replaced Y with YY? That seems dicier now than when I first thought about it, so perhaps it's not as big a problem as I thought.
Or maybe it's enough to do the following:
Take all the chunks produced by the diffs in the output of
git show .... In fact we can do better: if A, B, and C are a contiguous sequence, with A the parent of B and B the parent of C, then don't use the chunks fromgit show A B C; usegit diff A C.Sort the chunks by filename.
Merge the chunks that are making changes to the same file:
If two chunks don't overlap at all, there's no issue, just keep them as separate chunks.
If two chunks overlap and don't conflict, merge them into a single chunk
If they overlap and do conflict, just keep them separate but retain the date and commit ID information. (“This change, then this other change.”)
Then output all the chunks in some reasonable order: grouped by file, and if there were unmergeable chunks for the same file, in chronological order.
This is certainly doable.
If there were no conflicts, it would certainly be better than git
show ... would have been. Is it enough better to offset whatever
weirdness might be introduced by the overlap handling? (We're
grouping chunks by filename. What if files are renamed?) We don't
know, and it does not even have an objective answer. We would have to
try it, and then the result might be that some people like it and use
it and other people hate it and refuse to use it. If so, that is a win!
[Other articles in category /prog] permanent link
Tue, 23 Jul 2019
Obtuse axiomatization of category theory
About ten years ago I started an article, addressed to my younger self, reviewing various books in category theory. I doubt I will ever publish this. But it contained a long, plaintive digression about Categories, Allegories by Peter Freyd and Andre Scedrov:
I keep this one around on the shelf just so that I can pick it up ever few months and marvel at its opacity.
It is a superb example of the definition-theorem-remark style of mathematics textbooks. I have heard that this was a style pioneered by a book you are already familiar with, John Kelley's General Topology of 1955. If so, all I can say is, sometimes it works, and sometimes it doesn't. It worked for Kelley in 1955 writing about topology.
Here is an example of what is wrong with this book.
Everyone who knows anything about category theory knows that a category is a sort of abstraction of a domain of mathematical objects, like sets, groups, or topological spaces. A category has a bunch of "objects", which are the sets, the groups, or the topological spaces, and it has a bunch of "morphisms", which are maps between the objects that preserve the objects' special structure, be it algebraic, topological, or whatever. If the objects are sets, the morphisms are simply functions. If the objects are groups, the morphisms are group homomorphisms; if the objects are topological spaces, the morphisms are continuous maps. The basic point of category theory is to study the relationships between these structure-preserving maps, independent of the underlying structure of the objects themselves. We ignore the elements of the sets or groups, and the points in the topological spaces, and instead concentrate on the relationships between whole sets, groups, and spaces, by way of these "morphisms".
Here is the opening section of Categories, Allegories:
1.1 BASIC DEFINITIONS
The theory of CATEGORIES is given by two unary operations and a binary partial operation. In most contexts lower-case variables are used for the 'individuals' which are called morphisms or maps. The values of the operations are denoted and pronounced as:The axioms:
!!□x!! the source of !!x!!, !!x□!! the target of !!x!!, !!xy!! the composition of !!x!! and !!y!!,
!!xy!! is defined iff !!x□ = □y!!, !!(□x)□ = □x!! and !!□(x□) = x□!!, !!(□x)x = x!! and !!x(x□) = x!!, !!□(xy) = □(x(□y))!! and !!(xy)□ = ((x□)y)□!!, !!x(yz) = (xy)z!!.
In light of my capsule summary of category theory, can you figure out what is going on here? Even if you already know what is supposed to be going on you may not be able to make much sense of this. What to make of the axiom that !!□(xy) = □(x(□y))!!, for example?
The explanation is that Freyd has presented a version of category theory in which the objects are missing. Since every object !!X!! in a category is associated with a unique identity morphism !!{\text{id}}_X!! from !!X!! to itself, Freyd has identified each object with its identity morphism. If !!x:C\to D!!, then !!□x!! is !!{\text{id}}_C!! and !!x□!! is !!{\text{id}}_D!!. The axiom !!(□x)□ = □x!! is true because both sides are equal to !!{\text{id}}_C!!.
Still, why phrase it this way? And what about that !!□(x(□y))!! thing? I guessed it was a mere technical device, similar to the one that we can use to reduce five axioms of group theory to three. Normally, one defines a group to have an identity element !!e!! such that !!ex=xe=x!! for all !!x!!, and each element !!x!! has an inverse !!x^{-1}!! such that !!xx^{-1} = x^{-1}x = e!!. But if you are trying to be clever, you can observe that it is sufficient for there to be a left identity and a left inverse:
There must be an identity !!e!! such that !!ex=x!! for all !!x!!, and for each !!x!! there must be an !!x^{-1}!! such that !!x^{-1}x=e!!.
We no longer require !!xe=x!! or !!xx^{-1}=e!!, but it turns out that you can prove these anyway, from what is left. The fact that you can discard two of the axioms is mildly interesting, but of very little practical value in group theory.
I thought that probably the !!□(x(□y))!! thing was some similar bit of “cleverness”, and that perhaps by adopting this one axiom Freyd was able to reduce his list of axioms. For example, from that mysterious fourth axiom !!□(xy) = □(x(□y))!! you can conclude that !!xy!! is defined if and only if !!x(□y)!! is, and therefore, by the first axiom, that !!x□ = □y!! if and only if !!x□ = □(□y)!!, so that !!□y = □(□y)!!. So perhaps the phrasing of the axiom was chosen to allow Freyd to dispense with an additional axiom stating that !!□y = □(□y)!!.
Today I tinkered with it a little bit and decided I think not.
Freyd has:
$$\begin{align} xy \text{ is defined if and only if } x□ & = □y \tag{1} \\ (□x)□ & = □x \tag{2} \\ (□x)x & = x \tag{3} \\ □(xy) & = □(x(□y)) \tag{4} \end{align} $$
and their duals. Also composition is associative, which I will elide.
In place of 4, let's try this much more straightforward axiom:
$$ □(xy) = □x\tag{$4\star$} $$
I can now show that !!1, 2, 3, 4\star!! together imply !!4!!.
First, a lemma: !!□(□x) = □x!!. Axiom !!3!! says !!(□x)x = x!!, so therefore !!□((□x)x) = □x!!. By !!4\star!!, the left-hand side reduces to !!□(□x)!!, and we are done.
Now I want to show !!4!!, that !!□(xy) = □(x(□y))!!. Before I can even discuss the question I first need to show that !!x(□y)!! is defined whenever !!xy!! is; that is, whenever !!x□ = □y!!. But by the lemma, !!□y=□(□y)!!, so !!x□ = □(□y)!!, which is just what we needed.
At this point, !!4\star!! implies !!4!! directly: both sides of !!4!! have the form !!□(xz)!!, and !!4\star!! tells us that both are equal to !!□x!!.
Conversely, !!4!! implies !!4\star!!. So why didn't Freyd use !!4\star!! instead of !!4!!? I emailed him to ask, but he's 83 so I may not get an answer. Also, knowing Freyd, there's a decent chance I won't understand the answer if I do get one.
My plaintive review of this book continued:
Another, briefer complaint about this book: Early on, no later than page 13, Freyd begins to allude to "Lazard sheaves". These are apparently an important example. Freyd does not define or explain what "Lazard sheaves" are. Okay, you are expected to do some background reading, perhaps. Fair enough. But you are doomed, because "Lazard sheaves" is Freyd's own private coinage, and you will not be able to look it up under that name.
Apparently some people like this book. I don't know why, and perhaps I never will.
[Other articles in category /math] permanent link
Thu, 11 Jul 2019
The New York City passport office
Earlier this week I reported on a good visit I had had to the Philadelphia offices of the Social Security Administration.
Philadelphia government offices, in my experience, are generally better than those I have visited elsewhere. I've never been to the New York DMV office (do they even have one?) but the Philadelphia ones are way better than the New Jersey ones I used to use. Instead of standing in line for forty-five minutes, you get a number and sit down until your number is called.
The passport office was the biggest surprise. I first went in to deal with some passport thing shortly after I arrived in Philadelphia, maybe 1990 or so. The office was clean and quiet, the line was short, I got my business done quickly. None of those is the case in the New York passport office.
The New York passport office. Wow. Where to begin? I want to say that it defies description. But, I learned later, it has been described by no less a person than Samuel Beckett:
The abode is a flattened cylinder with rubber walls fifty meters in circumference and eighteen meters high. It is constantly illuminated by a dim, yellow light, and the temperature fluctuates between 5°C to 25°C, sometimes in as small an interval as four seconds. This leads to extremely parched skin, and the bodies brush against each other like dry leaves. Kisses make an "indescribable sound" and the rubber makes the footsteps mostly silent. There are 200 inhabitants, or one per square meter. Some are related to each other. Some are even married to each other, but the conditions make recognition difficult.
Here's a story of the New York passport office told to me by a friend many years ago. He stood in the line for forty-five minutes, and when he reached the window, he handed over his forms. The clerk glared at him for a few seconds, then, without a word, pushed them back.
“Is something wrong?” asked my friend.
There was a long pause. The clerk, too disgusted or enraged to reply immediately, finally said “They're not stapled.”
“Oh,” said my friend. “I see you have a stapler on your desk there.”
“You're supposed to staple them.”
“May I use your stapler?”
“No, your stapler is on the table at the back of the room.”
At this point my friend realized he was dealing with a monster. “Okay, but I can come right back to the window afterward, right?”
“No, you have to wait, like everyone else.”
At that moment my friend felt a tap on his shoulder. A man a few places behind him in line reached into his suit pocket and handed him a stapler. My friend says that as he stapled his papers and turned them in, the look on the clerk's face was of someone whose whole day had just been ruined.
“Thanks so much,” said my friend to Stapler Man. “Why did you happen to have a stapler in your pocket?”
“Oh,” said Stapler Man. “I do a lot of business at the passport office.”
[Other articles in category /misc] permanent link
Sun, 07 Jul 2019[ I wrote this in 2007 and forgot to publish it. Or maybe I was planning to finish it first. But if so I have no idea what I was originally planning to say, so here we are. ]
In computer programs, it's quite common to need a numerical value for π. Often you see something like:
#define PI 3.141592654
This has the drawback of not representing π as exactly as possible. But to do that in C probably requires putting in 16 digits after the decimal point, and most people don't have so much memorized. And anyway, you don't really know at compile time what the floating-point precision will be; some platforms support quad-width floats. So you can do better, maybe, by using the math library to calculate π. And people do:
static double pi = 4*atan2(1,1);
The atan2(y, x) function produces the (almost-)unique value θ from the range !![-\pi, \pi]!! such that a ray from the origin, passing through point (x, y), makes angle θ with the x-axis.
Note that the arguments have y first and x second.
For example, atan2(17, 0) returns !!\frac\pi
2!!, because a line at angle !!\frac\pi 2!! passes through the point
(0, 17). Similarly, atan2(-17, 0) returns -!!\frac\pi 2!!.
You can use atan2 to calculate π, by using
!!4·{\operatorname{atan}}2(1,1)!!, as I mentioned above. Many people
do; Google searching finds hundreds of examples. The manual for the
standard Perl module constant.pm mentions this example.
But this is a bit strange. Why is this so well-known? Why calculate 4*atan2(1,1) when $$\pi = {\operatorname{atan}}2(0,-1)$$ produces the same result and is simpler?
(Obligatory IEEE 754 complaining: atan2 should return an always-unique value from
!!(-\pi, \pi]!!, but I have to say “almost-unique” because as usual IEEE
754 fucks everything up, this time with its stupid distinction between
0 and -0.)
[ Addendum: Leah Neukirchen suggests that the atan2(1,1) is a
translation from earlier systems that provide a single-argument atan
function but no atan2. In those systems, there is no
workable analogue of atan2(0, -1) because the transformation
!!{\operatorname{atan}}2(y, x)\Rightarrow
{\operatorname{atan}}\left(\frac yx\right)!! gives !!{\operatorname{atan}}(0)!!, which doesn't work for this
application as it yields !!0!! instead of the desired !!\pi!!. And
similarly in languages with atan but not atan2 there is no analogue of !!\pi =
2·{\operatorname{atan}}2(1, 0)!!. So the simplest thing you can do is pi = 4 * atan(1),
and after the transformation above one gets !!\pi = 4·{\operatorname{atan}}2(1,1)!!. ]
[Other articles in category /prog] permanent link
Tue, 02 Jul 2019
Philadelphia Slaughterhouse Hotel
More information about the mysterious slaughterhouse hotel has come to light, thanks to Chas. Owens, Pete Krawczyk, and this useful blog post by D.S. Rosenstein.
Most important, the perplexing “hotel” is not intended for humans. “Hotel” is apparently stockyard jargon for a place where livestock are quartered temporarily just prior to slaughter. I am so glad to have this cleared up.
Also, M. Rosenstein has a photograph of the fancy abattoir with the spires:
They don't make industrial buildings like they used to. Check out the ornamental pattern in the bricks on the lower floor and the baluster along the riverside façade.
[ Addendum: Josh Bevan of Hidden City Philadelphia on When Cattle Men Reigned In The West (of Philadelphia). ]
[Other articles in category /history] permanent link
Mon, 01 Jul 2019
Philadelphia Slaughterhouse Hotel
Yesterday on my other blog I posted about the most hilariously mislocated hotel I've ever heard of. It's the hotel that in 1910 was located in the Philadelphia stockyards, just the other side of the railroad tracks from the hog pens, between the slaughter house and the abbatoir:
I thought that would be the end of it, but Chas. Owens did a little digging around and found a picture of the hotel, provided by the Greater Philadelphia GeoHistory Network. It's from R. Hexamer's insurance survey of 1877. At that time, the building was partly a hotel and partly the offices of the Philadelphia Stock Yard Company.
The survey includes a map of the site and a description of the facilities. Here's the detailed plan of the hotel:
The full image is 105 MB:
None of these buildings is still standing. (As I mentioned yesterday, the site is now occupied by the Cira Centre.) But the neighborhood's history as the center of Philadelphia's meatpacking district is not completely lost. According to this marvelous article from Hidden City Philadelphia, in 1906 the D.B. Martin company built a new combination office building and slaughterhouse only two blocks away at 3000 Market Street. Here's my favorite detail from the article:
Five hundred head of cattle at a time would be held on the rooftop cow pens, right above the heads of the company’s executives,
That building still stands, although I believe it's no longer used as a slaughterhouse.
[ Addendum 20190702: The “hotel” is explained: it is a temporary residence for livestock, not for humans. ]
[Other articles in category /history] permanent link
Tue, 25 Jun 2019
Projection morphisms are (not) epic
I don't have a good catalog in my head of basic theorems of category theory. Every time I try to think about category theory, I get stuck on really basic lemmas like “can I assume that a product !!1×A!! is canonically isomorphic to !!A!!?” Or “Suppose !!f:A→B!! is both monic and epic. Must it be an isomorphism?” Then I get sidetracked trying to prove those lemmas, or else I assume they are true, go ahead, and even if I'm right I start to lose my nerve.
So for years I've wanted to make up a book of every possible basic theorem of category theory, in order from utterly simple to most difficult, and then prove every theorem. Then I'd know all the answers, or if I didn't, I could just look in the book. There would be a chapter on products with a long list of plausible-seeming statements:
- If !!P_1!! and !!P_2!! are both products of some !!A!! and !!B!!, then !!P_1\cong P_2!!
- !!A×B \cong B×A!!
- !!(A×B)×C \cong A×(B×C)!!
- !!1×A\cong A!!
- !!0×A\cong 0!!
- !!A×A\cong A!! if and only if !!A!! is initial
- If !!f!! and !!g!! are both monic, then so is !!f×g!!
- If !!f×g!! is monic, so are !!f!! and !!g!!
- (etc…)
and each one would either be annotated, Snopes-style, with “True”, or with a brief description of a counterexample.
On Sunday I thought I'd give it a shot, and I started with:
Suppose !!A×B!! is a product with projection morphism !!π_1:A×B→A!!. Then !!π_1!! is epic.
This seems very plausible, because how could the product possibly work if its left-hand component couldn't contain any possible element of !!A!!?
I struggled with this for rather a long time but I just got more and more stuck. To prove that !!π_1!! is an epimorphism I need to have !!g,h:A→C!! and then show that !!g ∘ π_1 = h ∘ π_1!! only when !!g=h!!. But !!π_1!! being a projection arrow doesn't help with this, because products are all about arrows into !!A!! and !!B!! and here I need to show something about arrows out of !!A!!.
And there's no hope that I could get any leverage by introducing some arrows into !!A!! and !!B!!, because there might not be any arrows into !!B!!. (Other than !!\text{id}_B!!, of course, but then you need an arrow !!B→A!! and that might not exist either.) Or what if I consider how the arrows from !!A×B!! factor through !!C×B!! — ah ah ah, not so fast! !!C×B!! might not exist!
I eventually gave up and looked it up online, and discovered that, in fact, the claim is not true in general. It's not even true in Set. The left projection !!π_1: X×\emptyset → X!! is not epic. (Which answers my rhetorical question above that asks “how could the product possibly work if…”)
So, uh, victory, I guess? I set out to prove something that is false, so failing to produce a proof is the best possible outcome.
And I can make lemonade out of the lemons. I couldn't prove the theorem, and my ideas about why not were basically right. Now I ought to be able to look carefully at what additional tools I might be able to use to make the proof go through anyway, and those then become part of the statement of the theorem, which then would become something like “If all binary products exist in a category with an initial object, then projection morphisms are epic.”
[Other articles in category /math] permanent link
Mon, 24 Jun 2019I just finished Cakes and Ale, by W. Somerset Maugham. I have enjoyed Maugham all my life, and this is considered one of his best books (it was his personal favorite) but I hadn't read it before.
I enjoyed it a lot. It has a story, but at the center instead of a big problem there is a character, Rose Gann. (To other characters she appears to be a big problem, but she sails placidly through the book doing what she wants.) She's really sweet, and I'm glad I had a chance to meet her.
The other side of the book is that it is a very pointed satire of the social-climbing literary circles in which Maugham traveled. Another such satire is his short story The Creative Impulse. That one was exaggerated for comic effect. This one isn't, and because of that it's much more biting. Rose, who is not literary, is contrasted with the literary characters, who are hypocritical, self-serving, manipulative, and pretentious. Rose is none of those things.
The book is quasi-autobiographical, the way Of Human Bondage or the Ashenden stories are. The narrator is named Willie Ashenden and the pattern of his life is the same as Maugham's, growing up in Whitstable with his vicar uncle (in the book it's called “Blackstable”) and then going to medical school in London, etc. Rose Gann was inspired by a woman that Maugham had been in love with. There was a scandal when the book was published; one of the characters was widely understood to be a rather vicious parody of Maugham's literary acquaintance Hugh Walpole. (Maugham denied it, but I've also read that later, when the danger of a libel suit was past, he confessed it was true.)
Parts of Cakes and Ale reminded me strongly of Robertson Davies' The Manticore. In both books, a famous and important man has died and everyone is rushing around to grab a piece of his legacy. In both cases there's also an embarrassing first wife that everyone wants to write out of the story. I imagine Davies had probably read Cakes and Ale and I wondered if he had been thinking of it.
Davies wrote an essay about Maugham, which I suppose I've read, but I don't remember what he said.
[Other articles in category /book] permanent link
Thu, 20 Jun 2019
Sufficiently advanced software
A couple of days ago my sleepy brain mashed up Clarke's Law:
Any sufficiently advanced technology is indistinguishable from magic.
and Hanlon's Razor:
Never attribute to malice what can be explained by stupidity.
to produce these words of wisdom:
Any sufficiently advanced software is indistinguishable from malice.
(Why yes, I had spent the evening dealing with Git. Why do you ask?)
This sounded like something Bryan Horstmann-Allen would have said, so with his permission, I am naming it after him.
BDHA's Law? BDHA's Razor? No!

[Other articles in category /misc] permanent link
Mon, 17 Jun 2019
Don't let the man page write checks that the programmer can't cash
My big work project is called “Greenlight”. It's a Git branch merging
service. After you've pushed a remote branch, say mjd.fix-bugs, you
use a very thin client program to ask the Greenlight server to land your
branch on master and publish it for you:
greenlight submit mjd.fix-bugs
Greenlight analyzes the branch to see if it touches any sensitive code
that requires signoffs. If so it contacts the correct people on
Slack, and asks them to review it. Once they have approved it,
Greenlight rebases the branch onto the current master and pushes the
result back to master. If the push fails, it retries silently.
Throughout, it communicates via Slack what is going on.
 A user, Locksher, complained last week that it didn't do what he had
expected. He had a Git
A user, Locksher, complained last week that it didn't do what he had
expected. He had a Git pre-push hook he had written. Whenever he
ran git push, his pre-push hook would look to see if he was pushing
to master. If so, it would look at the messages of the commits he
was trying to push. If any of them contained WIP or !fixup or !squash,
it would abort the push.
With Greenlight, this check wasn't done, because Locksher never pushed
to master himself. Instead he pushed to some topic branch, and then
asked Greenlight to publish it to master, which it did, including
his WIP commits. Oops!
Locksher asked if it was possible to have Greenlight “respect local
hooks”. Once I understood what he wanted, my first suggestion was
that he wrap the greenlight client in a shell script that did the
check he wanted. My second suggestion, less work for him but also
less immediate, was that the Greenlight client could look in
.git/hooks for a greenlight-pre-submit hook, and run that before
communicating with the server, aborting the request if the hook
failed. I think this would adequately solve the problem, especially
if the calling convention for the new hook was identical to that of
pre-push. Then you would just:
ln -s pre-push .git/hooks/greenlight-pre-submit
and get exactly the desired behavior. I said that if Locksher wanted to implement this, I would include it in the standard client, or alternatively I would open a ticket to implement it myself, eventually.
Locksher suggested instead that the greenlight client configuration
should support this:
[git]
respect-git-hooks = true
I didn't have time then to answer in detail, so I just said:
I consider that very unlikely.
Here's what I said to him once I did have time to answer in detail:
There are currently 23 documented Git hooks, and it's not immediately clear what it would mean to “respect” many of them. I'd have to go over the man page and decide, for each one, what the behavior should be, then possibly implement it, and then document it. Just to pick one example, should Greenlight “respect” your
prepare-commit-messagehook? If so, how?Even for the hooks where the correct behavior seemed clear to me, it might seem clearly something else to someone else. So the feature is severely under-specified and seems likely to cause confusion. I foresee a future of inquiries like “I set
respect-git-hooksbut Greenlight didn't run mypre-auto-gchook.”It is an open-ended promise. The way the option is phrased, it guarantees to “respect” every hook. So it commits me to keep track of what new hooks are introduced in every future version of Git, and to decide what to do about each of them.
Since
greenlightruns on your local machine, the local version of Git may vary. What if the behavior of Git'spre-cake-slicinghook changes between Git 1.24 and Git 1.26? Now Greenlight will have to implement two behaviors, and look at your local Git version to decide what to do.Oh, and 5, it is a YAGNI.
In contrast, the functionality provided by
greenlight-pre-submitis something someone has actually asked for. It is small, sharply bounded in scope and its definition is completely under my control.
 I will elaborate a little on the main items 1–2, that different
people might have different ideas about what it means to “respect” a
local hook. Consider Locksher's specific request, for
I will elaborate a little on the main items 1–2, that different
people might have different ideas about what it means to “respect” a
local hook. Consider Locksher's specific request, for greenlight to
“respect” his pre-push hook. Another user, say Zubi, could object,
quite reasonably, that greenlight submit is not the same as git
push, and that the correct way for it to “respect” her pre-push
hook is to ignore it. “I want my pre-push hook run when I push a
branch,” she might say, “not when I do greenlight submit.” Who
could argue with that? (Other than Locksher, of course.)
So then I would have to add an escape hatch for Zubi, so that everyone who didn't want Locksher's feature would have to affirmatively opt out of it.
Nah.
[Other articles in category /prog] permanent link
Sat, 08 Jun 2019
The inside-outness of category theory
I have pondered category theory periodically for the past 35 years, but not often enough to really stay comfortable with it. Today I was pondering again. I wanted to prove that !!1×A \cong A!! and I was having trouble. I eventually realized my difficulty: my brain had slipped out of category theory mode so that the theorem I was trying to prove did not even make sense.
In most of mathematics, !!1\times A!! would denote some specific entity and we would then show that that entity had a certain property. For example, in set theory we might define !!1\times A!! to be some set, say the set of all Kuratowski pairs !!\langle \varnothing, a\rangle!! where !!a\in A!!:
$$ 1×A =_{\text{def}} \{ z : \exists a\in A : z = \{\{\varnothing\}, \{\varnothing, a\}\} \} $$
and then we would explicitly construct a bijection !!f:A\leftrightarrow 1×A!!:
$$ f(a) = \{\{\varnothing\}, \{\varnothing, a\}\}$$
In category theory, this is not what we do. Everything is less concrete. !!\times!! looks like an operator, one that takes two objects and yields a third. It is not. !!1\times A!! does not denote any particular entity with any particular construction. (Nor does !!1!!, for that matter.) Instead, it denotes an unspecified entity, which happens to have a certain universal property, perhaps just one of many such entities with that property, and there is no canonical representative of the class. It's a mistake to think of it as a single thing, and it's also a mistake to ask the question the way I did ask it. You can't show that !!1×A!! has any specific property, because it's not a specific thing. All you can do is show that anything with the one required universal property must also have the other property. We should rephrase the question like this:
Let !!1×A!! be a product of !!1!! and !!A!!. Then !!1×A\cong A!!.
Maybe a better phrasing is:
Let !!1×A!! be some object that is a product of !!1!! and !!A!!. Then !!1×A\cong A!!.
The notation is still misleading, because it looks like !!1×A!! denotes the result of some operation, and it isn't. We can do a little better:
Let !!B!! be a product of !!1!! and !!A!!. Then !!B\cong A!!.
That it, that's the real theorem. It seems at first to be more difficult — where do we start? But it's actually easier! Because now it's enough to simply prove that !!A!! itself is a product of !!1!! and !!A!!, which is easily done: its projection morphisms are evidently !!! !! and !!{\text{id}}_A!!. And by a previous theorem that all products are isomorphic, any other product, such as !!B!!, must be isomorphic to this one, which is !!A!! itself.
(We can similarly imagine that any theorem that mentions !!1!! is preceded by the phrase “Let !!1!! be some terminal object.”)
[Other articles in category /math] permanent link
Fri, 07 Jun 2019A little while ago I wrote:
I think a disco ball would not be out of place at Versailles.
I just remembered that good mirror technology is perhaps too recent for disco balls to have been at Versailles. Hmmm. Early mirrors were made of polished metal or even stone, clearly unsuitable. Back-silvering of glass wasn't invented until the mid-19th century.
Still, a disco ball is a very forgiving application of mirrors. For a looking-glass you want a large, smooth, flat mirror with no color distortion. For a disco ball you don't need any of those things. Large sheets of flat glass were unavailable before the invention of float glass at the end of the 19th century, but for a disco ball you don't need plate glass, just little shards, leftovers even.
The 17th century could produce mirrors by gluing metal foil to the back of a piece of glass, so I wonder why they didn't. They wouldn't have been able to spotlight it, but they certainly could have hung it under an orbiculum. Was there a technological limitation, or did nobody happen to think of it?
[ Addendum: I think the lack of good spotlighting is the problem here. ]
[ Addendum: Apparently, nobody but me has ever used the word “orbiculum”. I don't know how I started using it, but it seems that the correct word for what I meant is oculus. ]
[Other articles in category /tech] permanent link
Tue, 21 May 2019Say $dt is a Perl DateTime
object.
You are allowed to say
$dt->add( days => 2 )
$dt->subtract( days => 2 )
Today Jeff Boes pointed out that I had written a program that used
$dt->add({ days => 2 })
which as far as I can tell is not documented to work. But it did work. (I wrote it in 2016 and would surely have noticed by now if it hadn't.) Jeff told me he noticed when he copied my code and got a warning. When I tried it, no warning.
It turns out that
$dt->add({ days => 2 })
$dt->subtract({ days => 2 })
both work, except that:
The
subtractcall produces a warning (adddoesn't! and Jeff had changed myaddtosubtract)If you included an
end_of_month => $modeparameter in the arguments tosubtract, it would get lost.
Also, the working-ness of what I wrote is a lucky fluke. It is
undocumented (I think) and works only because of a quirk of the
implementation. ->add passes its arguments to
DateTime::Duration->new, which passes them to
Params::Validate::validate. The latter is documented to accept
either form. But its use by DateTime::Duration is an undocumented
implementation detail.
->subtract works the same way, except that it does a little bit of
preprocessing on the arguments before calling
DateTime::Duration->new. That's where the warning comes from, and
why end_of_month won't work with the hashref form.
(All this is as of version 1.27. The current version is 1.51. Matthew Horsfall points out that 1.51 does not raise a warning, because of a different change to the same interface.)
This computer stuff is amazingly complicated. I don't know how anyone gets anything done.
[Other articles in category /prog/bug] permanent link
Mon, 20 May 2019Alphabetical order in Korean has an interesting twist I haven't seen in any other language.
(Perhaps I should mention up front that Korean does not denote words with individual symbols the way Chinese does. It has a 24-letter alphabet, invented in the 15th century.)
Consider the Korean word “문어”, which means “octopus”. This is made up of five letters ㅁㅜㄴㅇㅓ. The ㅁㅜㄴ are respectively equivalent to English ‘m’, ‘oo‘ (as in ‘moon‘), and ‘n’. The ㅇis silent, just like ‘k’ in “knit”. The ㅓis a vowel we don't have in English, partway between “saw” and “bud”. Confusingly, it is usually rendered in Latin script as ‘eo’. (It is the first vowel in “Seoul”, for example.) So “문어” is transliterated to Latin script as “muneo”, or “munǒ”, and approximately pronounced “moon-aw”.
But as you see, it's not written as “ㅁㅜㄴㅇㅓ” but as “문어”. The letters are grouped into syllables of two or three letters each. (Or, more rarely, four or even five.)
Now consider the word “무해” (“harmless”) This word is made of the four letters ㅁㅜㅎㅐ. The first two, as before, are ‘m’, ‘oo’. The ㅎ is ‘h’ and the ‘ㅐ’ is a vowel that is something like the vowel in “air”, usually rendered in Latin script as ‘ae’. So it is written “muhae” and pronounced something like “moo-heh”.
ㅎis the last letter of the alphabet. Because ㅎfollows ㄴ, you might think that 무해 would follow 문어. But it does not. In Korean, alphabetization is also done at the syllable level. The syllable 무 comes before 문, because it is a proper prefix, so 무해 comes before 문어. If the syllable break in 문어 were different, causing it to be spelled 무너, it would indeed come before 무해. But it isn't, so it doesn't. (“무너” does not seem to be an actual word, but it appears as a consitutent in words like 무너지다 (“collapse”) and 무너뜨리다 (“demolish”) which do come before 무해 in the dictionary.)
As far as I know, there is nothing in Korean analogous to the English alphabet song.
Or to alphabet soup! Koreans love soup! And they love the alphabet, so why no hangeul-tang? There is a hundred dollar bill lying on the sidewalk here, waiting to be picked up.
[ Previously, but just barely related: Medieval Chinese typesetting technique. ]
[Other articles in category /lang] permanent link
Fri, 17 May 2019
What's the difference between 0/0 and 1/0?
Last year a new Math Stack Exchange user asked What's the difference between !!\frac00!! and !!\frac10!!?.
I wrote an answer I thought was pretty good, but the question was downvoted and deleted as “not about mathematics”. This is bullshit, but what can I do?
I can repatriate my answer here, anyway.
This long answer has two parts. The first one is about the arithmetic, and is fairly simple, and is not very different from the other answers here: neither !!\frac10!! nor !!\frac00!! has any clear meaning. But your intuition is a good one: if one looks at the situation more carefully, !!\frac10!! and !!\frac00!! behave rather differently, and there is more to the story than can be understood just from the arithmetic part. The second half of my answer tries to go into these developments.
The notation !!\frac ab!! has a specific meaning:
The number !!x!! for which $$x\cdot b=a.$$
Usually this is simple enough. There is exactly one number !!x!! for which !!x\cdot 7=21!!, namely !!3!!, so !!\frac{21}7=3!!. There is exactly one number !!x!! for which !!x\cdot 4=7!!, namely !!\frac74!!, so !!\frac74\cdot4=7!!.
But when !!b=0!! we can't keep the promise that is implied by the word "the" in "The number !!x!! for which...". Let's see what goes wrong. When !!b=0!! the definition says:
The number !!x!! for which $$x\cdot 0=a.$$
When !!a\ne 0!! this goes severely wrong. The left-hand side is zero and the right-hand size is not, so there is no number !!x!! that satisfies the condition. Suppose !!x!! is the ugliest gorilla on the dairy farm. But the farm has no gorillas, only cows. Any further questions you have about !!x!! are pointless: is !!x!! a male or female gorilla? Is its fur black or dark gray? Does !!x!! prefer bananas or melons? There is no such !!x!!, so the questions are unanswerable.
When !!a!! and !!b!! are both zero, something different goes wrong:
The number !!x!! for which $$x\cdot 0=0.$$
It still doesn't work to speak of "The number !!x!! for which..." because any !!x!! will work. Now it's like saying that !!x!! is ‘the’ cow from the dairy farm, But there are many cows, so questions about !!x!! are still pointless, although in a different way: Does !!x!! have spots? I dunno man, what is !!x!!?
Asking about this !!x!!, as an individual number, never makes sense, for one reason or the other, either because there is no such !!x!! at all (!!\frac a0!! when !!a≠0!!) or because the description is not specific enough to tell you anything (!!\frac 00!!).
If you are trying to understand this as a matter of simple arithmetic, using analogies about putting cookies into boxes, this is the best you can do. That is a blunt instrument, and for a finer understanding you need to use more delicate tools. In some contexts, the two situations (!!\frac00!! and !!\frac10!!) are distinguishable, but you need to be more careful.
Suppose !!f!! and !!g!! are some functions of !!x!!, each with definite values for all numbers !!x!!, and in particular !!g(0) = 0!!. We can consider the quantity $$q(x) = \frac{f(x)}{g(x)}$$ and ask what happens to !!q(x)!! when !!x!! gets very close to !!0!!. The quantity !!q(0)!! itself is undefined, because at !!x=0!! the denominator is !!g(0)=0!!. But we can still ask what happens to !!q!! when !!x!! gets close to zero, but before it gets all the way there. It's possible that as !!x!! gets closer and closer to zero, !!q(x)!! might get closer and closer to some particular number, say !!Q!!; we can ask if there is such a number !!Q!!, and if so what it is.
It turns out we can distinguish quite different situations depending on whether the numerator !!f(0)!! is zero or nonzero. When !!f(0)\ne 0!!, we can state decisively that there is no such !!Q!!. For if there were, it would have to satisfy !!Q\cdot 0=f(0)!! which is impossible; !!Q!! would have to be a gorilla on the dairy farm. There are a number of different ways that !!q(x)!! can behave in such cases, when its denominator approaches zero and its numerator does not, but all of the possible behaviors are bad: !!q(x)!! can increase or decrease without bound as !!x!! gets close to zero; or it can do both depending on whether we approach zero from the left or the right; or it can oscillate more and more wildly, but in no case does it do anything like gently and politely approaching a single number !!Q!!.
But if !!f(0) = 0!!, the answer is more complicated, because !!Q!! (if it exists at all) would only need to satisfy !!Q\cdot 0=0!!, which is easy. So there might actually be a !!Q!! that works; it depends on further details of !!f!! and !!g!!, and sometimes there is and sometimes there isn't. For example, when !!f(x) = x^2+2x!! and !!g(x) = x!! then !!q(x) = \frac{x^2+2x}{x}!!. This is still undefined at !!x=0!! but at any other value of !!x!! it is equal to !!x+2!!, and as !!x!! approaches zero, !!q(x)!! slides smoothly in toward !!2!! along the straight line !!x+2!!. When !!x!! is close to (but not equal to) zero, !!q(x)!! is close to (but not equal to) !!2!!; for example when !!x=0.001!! then !!q(x) = \frac{0.002001}{0.001} = 2.001!!, and as !!x!! gets closer to zero !!q(x)!! gets even closer to !!2!!. So the number !!Q!! we were asking about does exist, and is in fact equal to !!2!!. On the other hand if !!f(x) = x!! and !!g(x) = x^2!! then there is still no such !!Q!!.
The details of how this all works, when there is a !!Q!! and when there isn't, and how to find it, are very interesting, and are the basic idea that underpins all of calculus. The calculus part was invented first, but it bothered everyone because although it seemed to work, it depended on an incoherent idea about how division by zero worked. Trying to frame it as a simple matter of putting cookies into boxes was no longer good enough. Getting it properly straightened out was a long process that took around 150 years, but we did eventually get there and now I think we understand the difference between !!\frac10!! and !!\frac00!! pretty well. But to really understand the difference you probably need to use the calculus approach, which may be more delicate than what you are used to. But if you are interested in this question, and you want the full answer, that is definitely the way to go.
[Other articles in category /math] permanent link
Thu, 02 May 2019A while back I wrote an article about confusing and misleading technical jargon, drawing special attention to botanists’ indefensible misuse of the word “berry” and then to the word “henge”, which archaeologists use to describe a class of Stonehenge-like structures of which Stonehenge itself is not a member.
I included a discussion of mathematical jargon and generally gave it a good grade, saying:
Nobody hearing the term “cobordism” … will think for an instant that they have any idea what it means … they will be perfectly correct.
But conversely:
The non-mathematician's idea of “line”, “ball”, and “cube” is not in any way inconsistent with what the mathematician has in mind …
Today I find myself wondering if I gave mathematics too much credit. Some mathematical jargon is pretty bad. Often brought up as an example are the topological notions of “open” and “closed” sets. It sounds as if they should be exclusive and exhaustive — surely a set that is open is not closed, and vice versa? — but no, there are sets that are neither open nor closed and other sets that are both. Really the problem here is entirely with “open”. The use of “closed” is completely in line with other mathematical uses of “closed” and “closure”. A “closed” object is one that is a fixed point of a closure operator. Topological closure is an example of a closure operator, and topologically closed sets are its fixed points.
(Last month someone asked on Stack Exchange if there was a connection between topological closure and binary operation closure and I was astounded to see a consensus in the comments that there was no relation between them. But given a binary operation !!\oplus!!, we can define an associated closure operator !!\text{cl}_\oplus!! as follows: !!\text{cl}_\oplus(S)!! is the smallest set !!\bar S!! that contains !!S!! and for which !!x,y\in\bar S!! implies !!x\oplus y\in \bar S!!. Then the binary operation !!\oplus!! is said to be “closed on the set !!S!!” precisely if !!S!! is closed with respect to !!\text{cl}_\oplus!!; that is if !!\text{cl}_\oplus(S) = S!!. But I digress.)
Another example of poor nomenclature is “even” and “odd” functions. This is another case where it sounds like the terms ought to form a partition, as they do in the integers, but that is wrong; most functions are neither even nor odd, and there is one function that is both. I think what happened here is that first an “even” polynomial was defined to be a polynomial whose terms all have even exponents (such as !!x^4 - 10x^2 + 1!!) and similarly an “odd” polynomial. This already wasn't great, because most polynomials are neither even nor odd. But it was not too terrible. And at least the meaning is simple and easy to remember. (Also you might like the product of an even and an odd polynomial to be even, as it is for even and odd integers, but it isn't, it's always odd. As far as even-and-oddness is concerned the multiplication of the polynomials is analogous to addition of integers, and to get anything like multiplication you have to compose the polynomials instead.)
And once that step had been taken it was natural to extend the idea from polynomials to functions generally: odd polynomials have the property that !!p(-x) = -p(x)!!, so let's say that an odd function is one with that property. If an odd function is analytic, you can expand it as a Taylor series and the series will have only odd-degree terms even though it isn't a polynomial.
There were two parts to that journey, and each one made some sense by itself, but by the time we got to the end it wasn't so easy to see where we started from. Unfortunate.
I tried a web search for bad mathematics terminology and the top hit was this old blog article by my old friend Walt. (Not you, Walt, another Walt.) Walt suggests that
the worst terminology in all of mathematics may be that of !!G_\delta!! and !!F_\sigma!! sets…
I can certainly get behind that nomination. I have always hated those terms. Not only does it partake of the dubious open-closed terminology I complained of earlier (you'll see why in a moment), but all four letters are abbreviations for words in other languages, and not the same language. A !!G_\delta!! set is one that is a countable intersection of open sets. The !!G!! is short for Gebiet, which is German for an open neighborhood, and the !!\delta!! is for durchschnitt, which is German for set intersection. And on the other side of the Ruhr Valley, an !!F_\sigma!! set, which is a countable union of closed sets, is from French fermé (“closed”) and !!\sigma!! for somme (set union). And the terms themselves are completely opaque if you don't keep track of the ingredients of this unwholesome German-French-Greek stew.
This put me in mind of a similarly obscure pair that I always mix up, the type I and type II errors. One if them is when you fail to ignore something insignificant, and the other is when you fail to notice something significant, but I don't remember which is which and I doubt I ever will.
But the one I was thinking about today that kicked all this off is, I think, worse than any of these. It's really shameful, worthy to rank with cucumbers being berries and with Stonhenge not being a henge.
These are all examples of elliptic curves:
These are not:
That's right, ellipses are not elliptic curves, and elliptic curves are not elliptical. I don't know who was responsible for this idiocy, but if I ever meet them I'm going to kick them in the ass.
[ Addendum 20200510: Several people have earnestly explained to me how this terminological disaster came about. Please be assured that I am well aware of the history here. The situation is similar to the one that gave us “even” and “odd” functions: a long chain of steps each of which made some sense individually, but whose concatenation ended in a completely different place. This MathOverflow post has a good summary. ]
[ Addendum 20200510: Mark Badros has solved the “Type I / II” problem for me. They point out that in the story of the Boy Who Cried Wolf, there are two episodes. In the first episode, the boy and the villagers commit a Type I error by reacting to the presence of a wolf when there is none. In the second episode, they commit a Type II error by failing to react to the actual wolf. Thank you! ]
[Other articles in category /lang] permanent link
Fri, 26 Apr 2019What is the shed in “watershed”? Is it a garden shed? No.
I guessed that it meant a piece of land that sheds water into some stream or river. Wrong!
The Big Dictionary says that this shed is:
The parting made in the hair by combing along the top of the head.
This meaning of “shed” fell out of use after the end of the 17th century.
[Other articles in category /lang/etym] permanent link
This week I learned that there are no fewer than seven fanfics on AO3 that concern the Complaint letter to Ea-Nasir, a 3750-year-old Babylonian cuneiform tablet from an merchant angry at the poor-quality copper ingots he was sold. Truly, we live in an age of marvels.
I've said here before that I don't usually find written material funny, with very rare exceptions. But this story, Pay me Baby, Treat me Right, was a rare exception. I found it completely sidesplitting.
(Caution: sexual content.)
[ Addendum: However, I still demand to know: Where the hell is my Sonar Taxlaw fanfic? Fanfic writers of the world, don't think this gets you off the hook! ]
[ Addendum 20200824: Only 16 months later, there are now eleven works on AO3. ]
[Other articles in category /book] permanent link
This is definitely the worst thing I learned this month. It's way worse than that picture of Elvis meeting Nixon.
Nobel Laureate and noted war criminal Henry Kissinger is also an honorary member of the Harlem Globetrotters.
As Maciej Cegłowski said, “And yet the cruel earth refuses to open and swallow up everyone involved.”
[Other articles in category /misc] permanent link
Thu, 25 Apr 2019
Sometimes it matters how you get there
Katara was given the homework exercise of rationalizing the denominator of $$\frac1{\sqrt2+\sqrt3+\sqrt5}$$ which she found troublesome. You evidently need to start by multiplying the numerator and denominator by !!-\sqrt2 + \sqrt 3 + \sqrt 5!!, obtaining $$ \frac1{(\sqrt2+\sqrt3+\sqrt5)}\cdot \frac{-\sqrt2 + \sqrt 3 + \sqrt 5}{-\sqrt2 + \sqrt 3 + \sqrt 5} = \frac{-\sqrt2 + \sqrt 3 + \sqrt 5}{(-2 +3 + 5 + 2\sqrt{15})} = \frac{-\sqrt2 + \sqrt 3 + \sqrt 5}{6 + 2\sqrt{15}} $$ and then you go from there, multiplying the top and bottom by !!6 - 2\sqrt{15}!!. It is a mess.
But when I did it, it was much quicker. Instead of using !!-\sqrt2 + \sqrt 3 + \sqrt 5!!, I went with !!\sqrt2 + \sqrt 3 - \sqrt 5!!, not for any reason, but just at random. This got me: $$ \frac1{\sqrt2+\sqrt3+\sqrt5}\cdot \frac{\sqrt2 + \sqrt 3 - \sqrt 5}{\sqrt2 + \sqrt 3 - \sqrt 5} = \frac{\sqrt2 + \sqrt 3 - \sqrt 5}{(2 +3 - 5 + 2\sqrt{6})} = \frac{\sqrt2 + \sqrt 3 - \sqrt 5}{2\sqrt{6}} $$
with the !!2+3-5!! vanishing in the denominator. Then the next step is quite easy; just get rid of the !!\sqrt6!!: $$ \frac{\sqrt2 + \sqrt 3 - \sqrt 5}{2\sqrt{6}}\cdot \frac{\sqrt6}{\sqrt6} = \frac{\sqrt{12}+\sqrt{18}-\sqrt{30}}{12} $$
which is correct.
I wish I could take credit for this, but it was pure dumb luck.
[Other articles in category /math] permanent link
Men who are the husbands of someone important
It's often pointed out that women, even famous and accomplished women, are often described in newspaper stories as being someone's wife, but that the reverse rarely occurs. The only really well-known exception I could think of was Pierre Curie, who was a famous, prizewinning scientist (1903 Nobel Laureate, yo), but is often identified as having been the husband of Marie Skłodowska Curie (also 1903 Nobel Laureate).
But last week brought another example to my attention. There ware a great many news articles reporting that Salma Hayek's husband had pledged money to help rebuild Notre Dame cathedral. His name is François-Henri Pinault, and he is a billionaire. And the husband of Salma Hayek.
For example:
Notre Dame fire – Salma Hayek’s French billionaire husband Francois-Henri Pinault pledges £86million
(etc.)
[ Addendum 20190808: Walt Mankowski brings up the excellent example of Sir Max Mallowan, CBE, a famous archaeologist and one of the original excavators of Ur. However, he is better known for having been the husband of Dame Agatha Christie from 1930 until his death in 1976. ]
[ Addendum 20230425: I am proud to announce that I have achieved this distinction! In this article from Slate, I am referred to only as “Lorrie Kim's husband”. ]
[ Addendum 20231215: Antoine Veil is interred in the Panthéon, but only because he was married to Simone Veil ]
[Other articles in category /misc] permanent link
Sun, 31 Mar 2019Yesterday I mentioned the rook:
Wikipedia also tells me that the rook is also named from the sound it makes.
This is the “rook” that is a sort of crow, C. frugilegus. It is not related to the rooks in chess. That word is from Arabic (and earlier, Persian) rukh, which means a chariot. Before the game came to Europe, the rooks were chariots. Europeans didn't use chariots, so when they adopted the game, they changed the chariots to castles. (Similarly the elephants turned into bishops.)
Okay, I've known all this for years, but today I had another thought. Why were there chariots in the Persian form of the game? The Persians didn't use chariots either. Chariots had been obsolete since the end of the Bronze Age, thousands of years, and chess is nothing like that old.
The earliest forerunner of chess was played in India. But I confirmed with Wikipedia that it didn't overlap with chariots:
Chess is believed to have originated in Eastern India, c. 280–550, in the Gupta Empire, where its early form in the 6th century was known as chaturaṅga (Sanskrit: चतुरङ्ग), literally four divisions [of the military] – infantry, cavalry, elephants, and chariotry, represented by the pieces that would evolve into the modern pawn, knight, bishop, and rook, respectively.
Were the Guptas still using chariots in the 6th century? (And if so, why?) I think they weren't, but I'm not sure. Were the chariots intentionally anachronistic, even at the time the game was invented, recalling a time of ancient heroes?
[ Addendum 20200204: Consider the way modern video games, recalling a time of ancient heroes, often involve sword fighting or archery. ]
[ Addendum 20211231: Wikipedia raises the same point: “The first substantial argument that chaturanga is much older than [the 6th century] is the fact that the chariot is the most powerful piece on the board, although chariots appear to have been obsolete in warfare for at least five or six centuries. The counter-argument is that they remained prominent in literature.” ]
[Other articles in category /tech] permanent link
Sat, 30 Mar 2019Katara just read me the story she wrote in Latin, which concerns two men who chase after a corax. “What kind of animal is corax?” I asked.
“It's a raven.”
“Awesome,” I said. “I bet it's onomatopoeic.”
So I looked into it, and yup! It's from Greek κόραξ. Liddell and Scott's Greek-English lexicon says (p. 832):
The Root is to be found in the onomatop. words κράζω, κρώζω, croak, etc.
κράζω (krazo) and κρώζω (krozo) mean “to croak”. “Croak” itself is also onomatopoeic. And it hadn't occurred to me before that English “crow” is also onomatopoeic. Looking into it further, Wikipedia also tells me that the rook is also named from the sound it makes.
(J.R.R. Tolkien was certainly aware of all of this. In The Hobbit has a giant raven named Roäc, the son of Carc.)
Liddell and Scott continues:
The same Root often appears in the sense of curved, cf. κορ-ώνη … Karin cur-vus, etc.
κορώνίς (koronis) means “curved”, and in particular a “corona” or crown. Curvus of course means curved, and is akin to Latin corvus, which again means a crow.
The raven's beak does not look so curved to me, but the Greeks must have found it striking.
[Other articles in category /lang/etym] permanent link
Wed, 02 Jan 2019
More about the happy numeric coincidence
[ Previously ]
Observing three small examples where the digital sum of !!n^k!! was equal to !!n!!, I said:
I supposed that there were few other examples, probably none … Still I hoped there might be one or two…
but in fact there are a great many; for example the digital sum of !!217^{22}!! is !!217!!.
Dave McKee asked what my intuition was. It was something like this. Fix !!n!! and consider the sequence !!n^2, n^3, …!!. The elements become increasingly sparse, and for their digital sum to equal !!n!! requires increasingly improbable coincidences. For example, taking !!n=3!!, we would need to have !!k!! such that $$3^k = 2·10^p + 1.$$ While I can't immediately rule out this possibility, it seems extremely unlikely. This also resembles the Catalan conjecture, which is that the only nontrivial solution of $$ \left\lvert2^i - 3^j\right\rvert = 1$$ is !!i=3, j=2!!. The Catalan conjecture is indeed true, but it was an open problem for 158 years.
[ Addendum 20190205: I have since learned that the Catalan conjecture actually concerns the more general claim about the equation !! \left\lvert a^i - b^j\right\rvert = 1!!. The special case of !!a=2, b=3!! turns out to be elementary. ]
I was quite mistaken, so what went wrong? First, there is one nontrivial solution to the Catalan conjecture, and here we have not one sequence of !!n^k!! but an infinite family, each of which might have an exceptional solution or two. And second, the case of !!n=3!! is atypically bleak. For !!3^k!! to have a digital sum of !!3!! is a tough order because there are very few sequences of digits whose sum is 3. But the number of sequences of !!d!! digits whose sum is !!n!! grows quite rapidly with !!n!!, and for small !!n!! is very misleading.
[Other articles in category /math] permanent link
Tue, 01 Jan 2019A couple of days ago I was pleased to notice the following coincidence:
| !!9^2 = 81!! | and | !!8 + 1 = 9!! |
| !!8^3 = 512!! | and | !!5 + 1 + 2 = 8!! |
| !!7^4 = 2401!! | and | !!2 + 4 + 0 + 1 = 7!! |
I supposed that there were few other examples, probably none, and that at least I could prove that there were only a finite number of examples. My expected proof of this didn't work, but I still supposed that there would be no further examples. Still I hoped there might be one or two, so I set the computer to look for them if there were.
My first run produced:
\begin{array}{rcr} 17^3 &=& 4\;913 \\ 18^3 &=& 5\;832\\ 22^4 &=& 234\;256\\ 25^4 &=& 390\;625\\ 26^3 &=& 17\;576\\ 27^3 &=& 19\;683\\ 28^4 &=& 614\;656\\ 36^4 &=& 1\;679\;616\\ \end{array}
Well, that was a happy surprise.
Wait a minute, though:
\begin{array}{rcr} 18 ^{ 6 } &=& 34\;012\;224 \\ 18 ^{ 7 } &=& 612\;220\;032 \\ 27 ^{ 7 } &=& 10\;460\;353\;203 \\ 28 ^{ 5 } &=& 17\;210\;368 \\ 31 ^{ 7 } &=& 27\;512\;614\;111 \\ 34 ^{ 7 } &=& 52\;523\;350\;144 \\ 35 ^{ 5 } &=& 52\;521\;875 \\ 36 ^{ 5 } &=& 60\;466\;176 \\ 43 ^{ 7 } &=& 271\;818\;611\;107 \\ 45 ^{ 6 } &=& 8\;303\;765\;625 \\ 46 ^{ 5 } &=& 205\;962\;976 \\ 46 ^{ 8 } &=& 20\;047\;612\;231\;936 \\ 53 ^{ 7 } &=& 1\;174\;711\;139\;837 \\ 54 ^{ 6 } &=& 24\;794\;911\;296 \\ 54 ^{ 8 } &=& 72\;301\;961\;339\;136 \\ 54 ^{ 9 } &=& 3\;904\;305\;912\;313\;344 \\ 58 ^{ 7 } &=& 2\;207\;984\;167\;552 \\ 63 ^{ 8 } &=& 248\;155\;780\;267\;521 \\ 64 ^{ 6 } &=& 68\;719\;476\;736 \\ 68 ^{ 7 } &=& 6\;722\;988\;818\;432 \\ 71 ^{ 9 } &=& 45\;848\;500\;718\;449\;031 \\ 81 ^{ 9 } &=& 150\;094\;635\;296\;999\;121 \\ 82 ^{ 10 } &=& 13\;744\;803\;133\;596\;058\;624 \\ 85 ^{ 10 } &=& 19\;687\;440\;434\;072\;265\;625 \\ 94 ^{ 10 } &=& 53\;861\;511\;409\;489\;970\;176 \\ 97 ^{ 10 } &=& 73\;742\;412\;689\;492\;826\;049 \\ 106 ^{ 10 } &=& 179\;084\;769\;654\;285\;362\;176 \\ 117 ^{ 10 } &=& 480\;682\;838\;924\;478\;847\;449 \\ \end{array}
Oh my.
\begin{array}{rcr} 20 ^{ 13 } &=& 81\;920 & · 10^{12} \\ 40 ^{ 13 } &=& 671\;088\;640 & · 10^{12} \\ 80 ^{ 17 } &=& 225\;179\;981\;368\;524\;800 & · 10^{15} \\ \hline 80 ^{ 19 } &=& 1\;441\;151\;880\;758\;558\;720 & · 10^{18} \\ 86 ^{ 13 } &=& 14\;076\;019\;706\;120\;526\;112\;710\;656 \\ 90 ^{ 19 } &=& 13\;508\;517\;176\;729\;920\;890 & · 10^{18} \\ \hline 90 ^{ 20 } &=& 1\;215\;766\;545\;905\;692\;880\;100 & · 10^{18} \\ 90 ^{ 21 } &=& 109\;418\;989\;131\;512\;359\;209 & · 10^{21} \\ 90 ^{ 22 } &=& 9\;847\;709\;021\;836\;112\;328\;810 & · 10^{21} \\ \hline 90 ^{ 28 } &=& 5\;233\;476\;330\;273\;605\;372\;135\;115\;210 & · 10^{27} \\ 91 ^{ 14 } &=& 2\;670\;419\;511\;272\;061\;205\;254\;504\;361 \\ 98 ^{ 11 } &=& 8\;007\;313\;507\;497\;959\;524\;352 \\ \hline 103 ^{ 13 } &=& 146\;853\;371\;345\;156\;431\;381\;127\;623 \\ 104 ^{ 13 } &=& 166\;507\;350\;731\;038\;802\;170\;609\;664 \\ 106 ^{ 13 } &=& 213\;292\;826\;014\;568\;334\;917\;410\;816 \\ \hline 107 ^{ 11 } &=& 21\;048\;519\;522\;998\;348\;950\;643 \\ 107 ^{ 13 } &=& 240\;984\;500\;018\;808\;097\;135\;911\;707 \\ 107 ^{ 15 } & = & 2\;759\;031\;540\;715\;333\;904\;109\;053\;133 & & \\ & & 443 & & \\ \hline 108 ^{ 11 } &=& 23\;316\;389\;970\;546\;096\;340\;992 \\ 108 ^{ 12 } &=& 2\;518\;170\;116\;818\;978\;404\;827\;136 \\ 118 ^{ 14 } &=& 101\;472\;439\;712\;019\;470\;540\;189\;876\;224 \\ \hline 126 ^{ 13 } &=& 2\;017\;516\;459\;574\;609\;153\;391\;845\;376 \\ 127 ^{ 14 } &=& 283\;956\;682\;347\;124\;706\;942\;551\;243\;009 \\ 133 ^{ 16 } & = & 9\;585\;753\;470\;490\;322\;141\;591\;520\;062 & & \\ & & 265\;281 & & \\ \hline 134 ^{ 13 } &=& 4\;491\;199\;828\;872\;408\;503\;792\;328\;704 \\ 134 ^{ 15 } & = & 80\;643\;984\;127\;232\;967\;094\;095\;054\;209 & & \\ & & 024 & & \\ 135 ^{ 13 } &=& 4\;946\;966\;739\;525\;117\;513\;427\;734\;375 \\ \hline 135 ^{ 14 } &=& 667\;840\;509\;835\;890\;864\;312\;744\;140\;625 \\ 136 ^{ 15 } & = & 100\;712\;557\;719\;971\;285\;024\;106\;952\;523 & & \\ & & 776 & & \\ 140 ^{ 25 } &=& 449\;987\;958\;058\;483\;731\;145\;152\;266\;240 & · 10^{24} \\ \hline 142 ^{ 16 } & = & 27\;328\;356\;228\;554\;426\;163\;172\;505\;624 & & \\ & & 313\;856 & & \\ 143 ^{ 17 } & = & 4\;372\;327\;021\;734\;283\;642\;004\;853\;327 & & \\ & & 592\;915\;343 & & \\ 152 ^{ 15 } & = & 534\;138\;422\;146\;939\;893\;094\;821\;310\;496 & & \\ & & 768 & & \\ \hline 154 ^{ 14 } & = & 4\;219\;782\;742\;781\;494\;680\;756\;610\;809 & & \\ & & 856 & & \\ 154 ^{ 15 } & = & 649\;846\;542\;388\;350\;180\;836\;518\;064\;717 & & \\ & & 824 & & \\ 155 ^{ 19 } & = & 413\;335\;079\;574\;020\;313\;162\;122\;296\;733 & & \\ & & 856\;201\;171\;875 & & \\ \hline 157 ^{ 19 } & = & 527\;343\;255\;303\;841\;790\;870\;720\;812\;082 & & \\ & & 050\;804\;460\;293 & & \\ 160 ^{ 28 } & = & 51\;922\;968\;585\;348\;276\;285\;304\;963\;292 & & \\ & & 200\;960 & · 10^{27} & \\ 163 ^{ 16 } & = & 248\;314\;265\;639\;726\;167\;358\;751\;235\;626 & & \\ & & 296\;641 & & \\ \hline 169 ^{ 16 } & = & 442\;779\;263\;776\;840\;698\;304\;313\;192\;148 & & \\ & & 785\;281 & & \\ 169 ^{ 22 } & = & 10\;315\;908\;977\;942\;302\;627\;204\;470\;186 & & \\ & & 314\;316\;211\;062\;255\;002\;161 & & \\ 170 ^{ 31 } & = & 1\;392\;889\;173\;388\;510\;144\;614\;180\;174 & & \\ & & 894\;677\;204\;330 & · 10^{30} & \\ \hline 170 ^{ 33 } & = & 40\;254\;497\;110\;927\;943\;179\;349\;807\;054 & & \\ & & 456\;171\;205\;137 & · 10^{33} & \\ 171 ^{ 17 } & = & 91\;397\;407\;411\;741\;874\;683\;083\;843\;738 & & \\ & & 640\;173\;291 & & \\ 171 ^{ 19 } & = & 2\;672\;551\;590\;126\;744\;157\;608\;054\;674 & & \\ & & 761\;577\;307\;202\;131 & & \\ \hline 172 ^{ 18 } & = & 17\;358\;494\;027\;033\;103\;736\;099\;033\;196 & & \\ & & 316\;709\;617\;664 & & \\ 173 ^{ 19 } & = & 3\;333\;311\;951\;341\;729\;629\;204\;978\;703 & & \\ & & 084\;632\;004\;627\;637 & & \\ 181 ^{ 18 } & = & 43\;472\;473\;122\;830\;653\;562\;489\;222\;659 & & \\ & & 449\;707\;872\;441 & & \\ \hline 181 ^{ 19 } & = & 7\;868\;517\;635\;232\;348\;294\;810\;549\;301 & & \\ & & 360\;397\;124\;911\;821 & & \\ 181 ^{ 20 } & = & 1\;424\;201\;691\;977\;055\;041\;360\;709\;423 & & \\ & & 546\;231\;879\;609\;039\;601 & & \\ 189 ^{ 19 } & = & 17\;896\;754\;443\;176\;031\;520\;198\;514\;559 & & \\ & & 819\;163\;143\;441\;509 & & \\ \hline 193 ^{ 22 } & = & 191\;540\;580\;003\;116\;921\;429\;323\;712\;183 & & \\ & & 642\;218\;614\;831\;262\;597\;249 & & \\ 199 ^{ 21 } & = & 1\;887\;620\;149\;539\;230\;539\;058\;375\;534 & & \\ & & 310\;517\;606\;114\;631\;604\;199 & & \\ 207 ^{ 20 } & = & 20\;864\;448\;472\;975\;628\;947\;226\;005\;981 & & \\ & & 267\;194\;447\;042\;584\;001 & & \\ \hline 211 ^{ 25 } & = & 12\;795\;621\;425\;112\;113\;141\;935\;148\;247 & & \\ & & 655\;082\;376\;252\;275\;523\;500\;373\;035\;251 & & \\ 217 ^{ 22 } & = & 2\;524\;144\;100\;572\;738\;110\;818\;511\;483 & & \\ & & 976\;079\;134\;636\;146\;367\;057\;489 & & \\ 221 ^{ 25 } & = & 40\;719\;913\;064\;560\;249\;818\;128\;041\;081 & & \\ & & 360\;346\;218\;088\;750\;603\;039\;104\;925\;501 & & \\ \hline 225 ^{ 22 } & = & 5\;597\;774\;487\;475\;881\;147\;025\;802\;420 & & \\ & & 102\;991\;163\;730\;621\;337\;890\;625 & & \\ 234 ^{ 23 } & = & 3\;104\;307\;401\;943\;398\;225\;947\;002\;752 & & \\ & & 118\;451\;297\;846\;365\;869\;366\;575\;104 & & \\ 236 ^{ 25 } & = & 210\;281\;019\;656\;164\;214\;863\;109\;519\;134 & & \\ & & 145\;127\;118\;463\;502\;897\;144\;582\;373\;376 & & \\ \hline 250 ^{ 40 } & = & 827\;180\;612\;553\;027\;674\;871\;408\;692\;069 & & \\ & & 962\;853\;565\;812\;110\;900\;878\;906\;250 & · 10^{39} & \\ 265 ^{ 28 } & = & 70\;938\;903\;323\;020\;164\;041\;464\;952\;207 & & \\ & & 191\;804\;150\;246\;813\;586\;391\;508\;579\;254 & & \\ & & 150\;390\;625 & & \\ \end{array}
Holy cow.
I should have been able to foresee some of those, like !!20^{13} = 8192·10^{13}!!, which in hindsight is obvious. But seriously, !!163^{16}!!?
(It rather looks like !!265^{28}!! might be the last one where !!n!! is not a multiple of !!10!!, however. Or maybe that is a misleading artifact of the calculating system I am using? I'm not sure yet.)
Happy new year, all.
[ Addendum 20190102: Several readers have confirmed that there are many examples past !!265^{28}!!. I am probably running into some mismatch between the way the computer represents numbers and the way they actually work. ]
[ Addendum 20190102: Dave McKee asked why I thought there would be few examples. ]
[ Addendum 20220521: I have learned that these numbers are sometimes known as Dudeney numbers after famous puzzlist Henry Dudeney. ]
[Other articles in category /math] permanent link








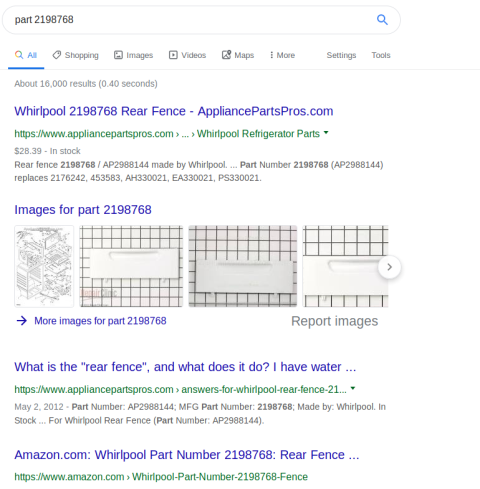







-th.jpg)