Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 08 Sep 2019
The exponential function is a miracle
The Maclaurin series for the exponential function converges for every complex number !!x!!: $$1 - x + \frac{x^2}{2} - \frac{x^3}{6} + \frac{x^4}{24} - \ldots = e^{-x} $$
Say that !!x!! is any reasonably large number, such as 5. Then !!e^{-x}!! is close to zero, But the terms of the series are not close to zero. For !!x=5!! we have: $$ 1 - 5 + 12.5 - 20.83 + 26.04 - 26.04 + 21.7 - 15.5 + 9.69 - 5.38 + \ldots \approx {\Large 0}$$
Somehow all these largish random numbers manage to cancel out almost completely. And the larger we make !!x!!, the more of these largish random numbers there are, the larger they are, and yet the more exactly they cancel out. For even as small an argument as !!x=20!!, the series begins with 52 terms that vary between 1 and forty-three million, and these somehow cancel out almost entirely. The sum of these 52 numbers is !!-0.4!!.
In this graph, the red lines are the various partial sums (!!1-x, 1-x+\frac{x^2}2, !! etc.) and the blue line is the total sum !!e^{-x}!!.
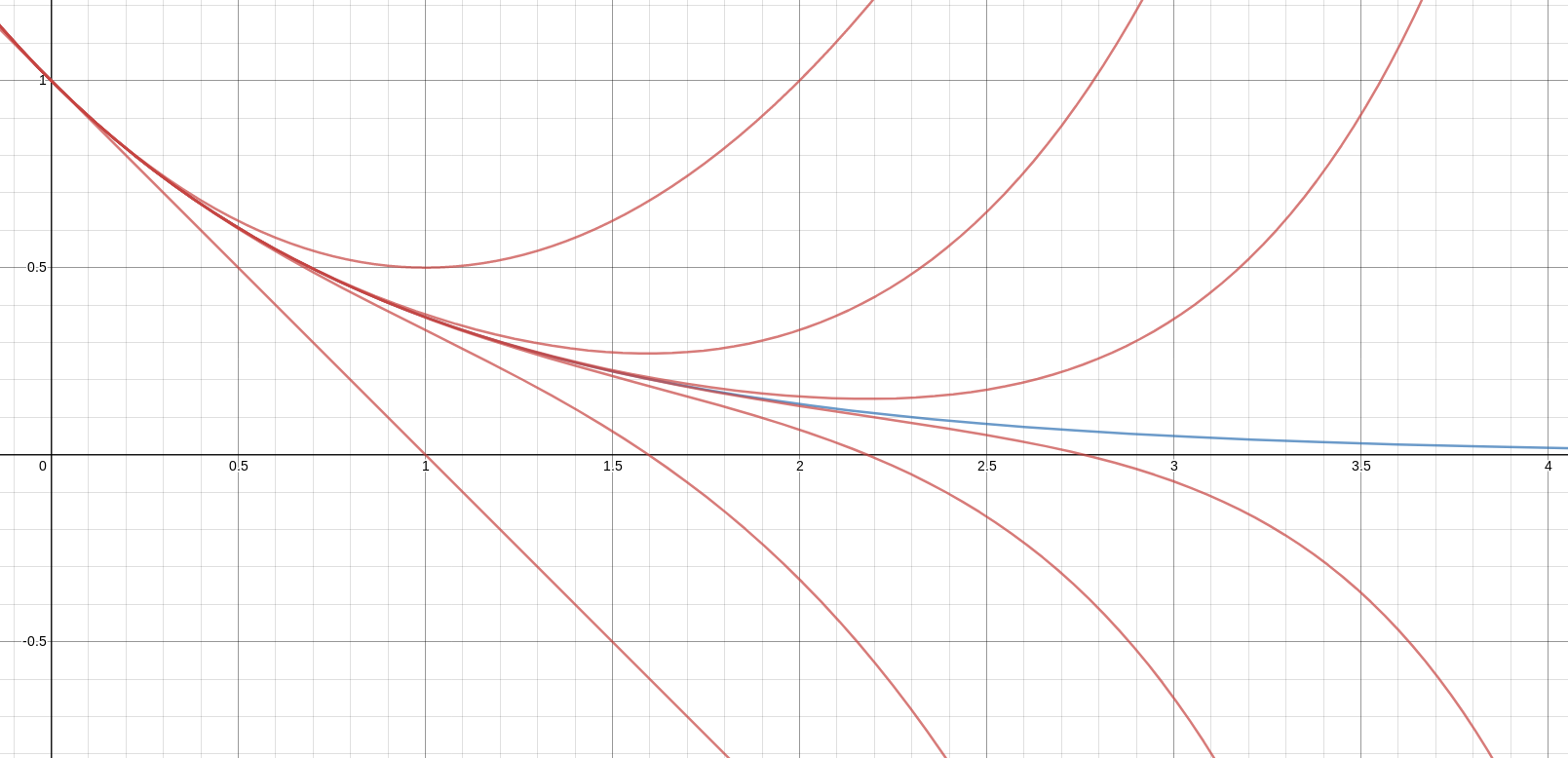
As you can see, each red line is a very bad approximation to the blue one, except within a rather narrow region. And yet somehow, it all works out in the end.
[ (Addendum) ]
[Other articles in category /math] permanent link


