Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Thu, 10 Oct 2019
Incenters of chocolate-iced cakes
A MathOverflow post asks:
Puzzle 1: Grandma made a cake whose base was a square of size 30 by 30 cm and the height was 10 cm. She wanted to divide the cake fairly among her 9 grandchildren. How should she cut the cake?
Okay, this is obvious.
Puzzle 2: Grandma made a cake whose base was a square of size 30 by 30 cm and the height was 10 cm. She put chocolate icing on top of the cake and on the sides, but not on the bottom. She wanted to divide the cake fairly among her 9 grandchildren so that each child would get an equal amount of the cake and the icing. How should she cut the cake?
This one stumped me; the best I could do was to cut the cake into 27 slabs, each !!\frac{10}3×10×10!! cm, and each with between 1 and 5 units of icing. Then we can give three slabs to each grandkid, taking care that each kid's slabs have a total of 7 units of icing. This seems like it might work for an actual cake, but I suspected that it wasn't the solution that was wanted, because the problem seems like a geometry problem and my solution is essentially combinatorial.
Indeed, there is a geometric solution, which is more interesting, and which cuts the cake into only 9 pieces.
I eventually gave up and looked at the answer, which I will discuss below. Sometimes when I give up I feel that if I had had thought a little harder or given up a little later, I would have gotten the answer, but not this time. It depends on an elementary property of squares that I had been completely unaware of.
This is your last chance to avoid spoilers.
The solution given is this: Divide the perimeter of the square cake into 9 equal-length segments, each of length !!\frac{120}{9}!! cm. Some of these will be straight and others may have right angles; it does not matter. Cut from the center of the cake to the endpoints of these segments; the resulting pieces will satisfy the requirements.
“Wat.” I said. “If the perimeter lengths are equal, then the areas are equal? How can that be?”
This is obviously true for two pieces; if you cut the square from the center into two pieces into two parts that divide the perimeter equally, then of course they are the same size and shape. But surely that is not the case for three pieces?
I could not believe it until I got home and drew some pictures on graph paper. Here Grandma has cut her cake into three pieces in the prescribed way:
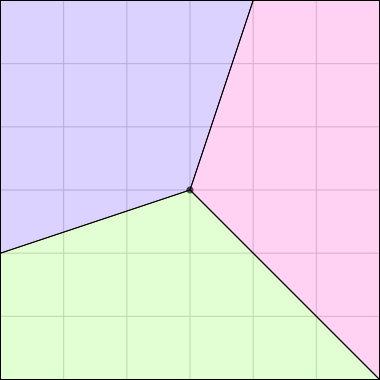
The three pieces are not the same shape! But each one contains one-third of the square's outer perimeter, and each has an area of 12 square units. (Note, by the way, that although the central angles may appear equal, they are not; the blue one is around 126.9° and the pink and green ones are only 116.6°.)
And indeed, any piece cut by Grandma from the center that includes one-third of the square's perimeter will have an area of one-third of the whole square:


The proof that this works is actually quite easy. Consider a triangle !!OAB!! where !!O!! is the center of the square and !!A!! and !!B!! are points on one of the square's edges.
The triangle's area is half its height times its base. The base is of course the length of the segment !!AB!!, and the height is the length of the perpendicular from !!O!! to the edge of the square. So for any such triangle, its area is proportional to the length of !!AB!!.
No two of the five triangles below are congruent, but each has the same base and height, and so each has the same area.
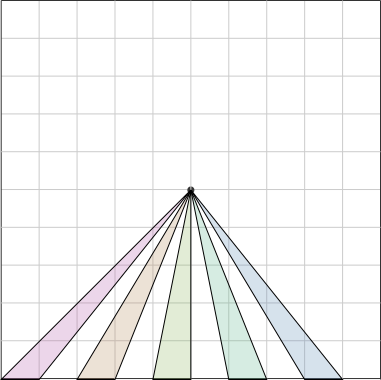
Since the center of the square is the same distance from each of the four edges, the same is true for any two triangles, regardless of which edge they arise from: the area of each triangle is proportional to the length of the square's perimeter at its base. Any piece Grandma cuts in this way, from the center of the cake to the edge, is a disjoint union of triangular pieces of this type, so the total area of any such piece is also proportional to the length of the square's perimeter that it includes.
That's the crucial property of the square that I had not known before: if you make cuts from the center of a square, the area of the piece you get is proportional to the length of the perimeter that it contains. Awesome!
Here Grandma has used the same method to cut a pair of square cakes into ten equal-sized pieces that all the have same amount of icing.
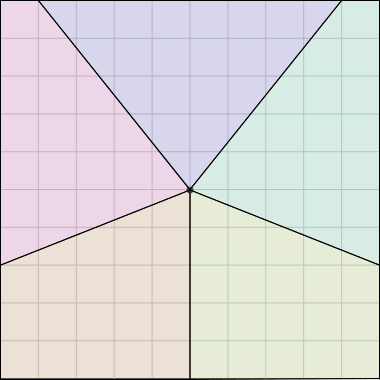
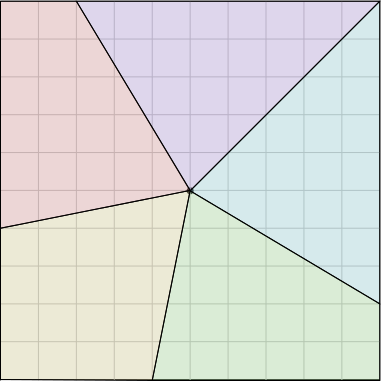
The crucial property here was that the square’s center is the same distance from each of its four edges. This is really obvious, but not every polygon has an analogous point. The center of a regular polygon always has this property, and every triangle has a unique point, called its incenter, which enjoys this property. So Grandma can use the same method to divide a triangular cake into 7 equally-iced equal pieces, if she can find its incenter, or to divide a regular 17-gonal cake into 23 equally-iced equal pieces.
Not every polygon does have an incenter, though. Rhombuses and kites always do, but rectangles do not, except when they are square. If Grandma tries this method with a rectangular sheet cake, someone will get shortchanged. I learned today that polygons that have incenters are known as tangential polygons. They are the only polygons in which can one inscribe a single circle that is tangent to every side of the polygon. This property is easy to detect: these are exactly the polygons in which all the angle bisectors meet at a single point. Grandma should be able to fairly divide the cake and icing for any tangential polygon.
I have probably thought about this before, perhaps in high-school geometry but perhaps not since. Suppose you have two lines, !!m!! and !!n!!, that cross at an acute angle at !!P!!, and you consider the set of points that are equidistant from both !!m!! and !!n!!. Let !!\ell!! be a line through !!P!! which bisects the angle between !!m!! and !!n!!; clearly any point on !!\ell!! will be equidistant from !!m!! and !!n!! by a straightforward argument involving congruent triangles.
Now consider a triangle !!△ABC!!. Let !!P!! be the intersection of the angle bisectors of angles !!∠ A!! and !!∠ B!!.
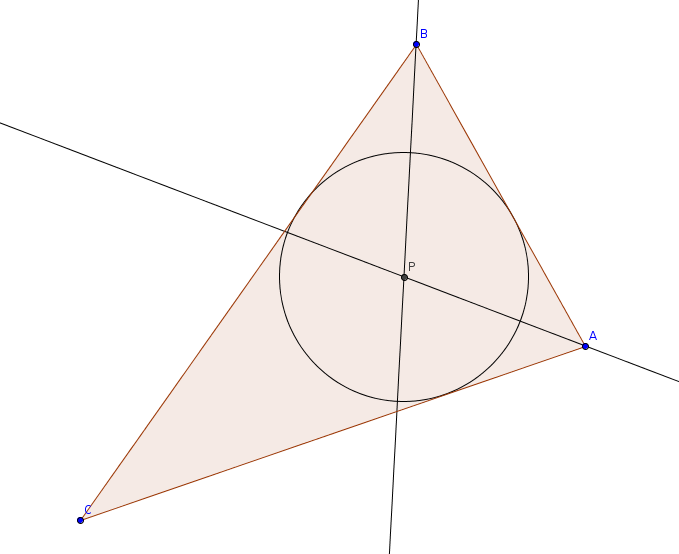
!!P!! is the same distance from both !!AB!! and !!AC!! because it is on the angle bisector of !!∠ A!!, and similarly it is the same distance from both !!AB!! and !!BC!! because it is on the angle bisector of !!∠ B!!.
So therefore !!P!! is the same distance from both !!AC!! and !!BC!! and it must be on the angle bisector of angle !!∠ C!! also. We have just shown that a triangle's three angle bisectors are concurrent! I knew this before, but I don't think I knew a proof.
[ Addendum 20191011: Many illustrated examples. ]
[Other articles in category /math] permanent link


