Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 17 Sep 2019
Suppose you have a bottle that contains !!N!! whole pills. Each day you select a pill at random from the bottle. If it is a whole pill you eat half and put the other half back in the bottle. If it is a half pill, you eat it. How many half-pills can you expect to have in the bottle the day after you break the last whole pill?
Let's write !!H(N)!! for the expected number of half-pills left, if you start with !!N!!. It's easily seen that !!H(N) = 0, 1, \frac32!! for !!N=0,1,2!!, and it's not hard to calculate that !!H(3) = \frac{11}{6}!!.
For larger !!N!! it's easy to use Monte Carlo simulation, and find that !!H(30)!! is almost exactly !!4!!. But it's also easy to use dynamic programming and compute that $$H(30) = \frac{9304682830147}{2329089562800}$$ exactly, which is a bit less than 4, only !!3.994987!!. Similarly, the dynamic programming approach tells us that $$H(100) = \frac{14466636279520351160221518043104131447711}{2788815009188499086581352357412492142272}$$ which is about !!5.187!!.
(I hate the term “dynamic programming”. It sounds so cool, but then you find out that all it means is “I memoized the results in a table”. Ho hum.)
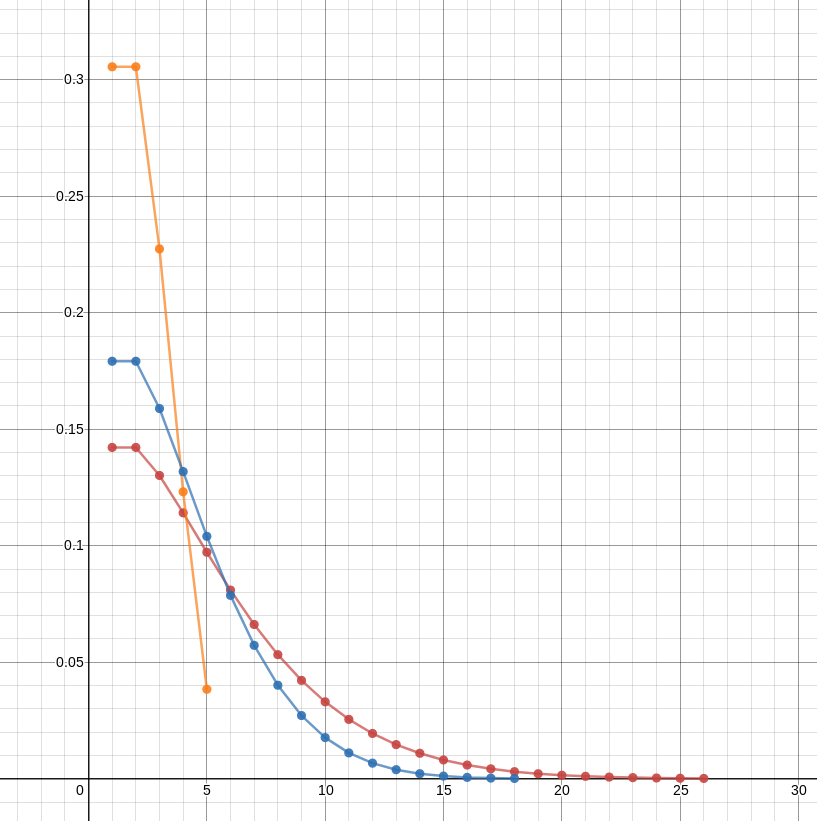
As you'd expect for a distribution with a small mean, you're much more likely to end with a small number of half-pills than a large number. In this graph, the red line shows the probability of ending with various numbers of half-pills for an initial bottle of 100 whole pills; the blue line for an initial bottle of 30 whole pills, and the orange line for an initial bottle of 5 whole pills. The data were generated by this program.
The !!E!! function appears to increase approximately logarithmically. It first exceeds !!2!! at !!N=4!!, !!3!! at !!N=11!!, !!4!! at !!N=31!!, and !!5!! at !!N=83!!. The successive ratios of these !!N!!-values are !!2.75, 2.81,!! and !!2.68!!. So we might guess that !!H(N)!! first exceeds 6 around !!N=228!! or so, and indeed !!H(226) < 6 < H(227)!!. So based on purely empirical considerations, we might guess that $$H(N) \approx \frac{\log{\frac{15}{22}N}}{\log 2.75}.$$
(The !!\frac{15}{22}!! is a fudge factor to get the curves to line up properly.)
I don't have any theoretical justification for this, but I think it might be possible to get a bound.
I don't think modeling this as a Markov process would work well. There are too many states, and it is not ergodic.
[ Addendum 20190919: Ben Handley informs me that !!H(n)!! is simply the harmonic numbers, !!H(n) = \sum_1^n \frac1n!!. I feel a little foolish that I did not notice that the first four terms matched. The appearance of !!H(3)=\frac{11}6!! should have tipped me off. Thank you, M. Handley. ]
[ Addendum 20190920: I was so fried when I wrote this that I also didn't notice that the denominator I guessed, !!2.75!!, is almost exactly !!e!!. (The correct value is !!e!!.) I also suspect that the !!\frac{15}{22}!! is just plain wrong, and ought to be !!e^\gamma!! or something like that, but I need to take a closer look. ]
[ Addendum 20191004: More about this ]
[Other articles in category /math] permanent link


