Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 11 Oct 2019
In a recent article about fair cake division, I said:
Grandma can use the same method … to divide a regular 17-gonal cake into 23 equally-iced equal pieces.
I got to wondering what that would look like, and the answer is, not very interesting. A regular 17-gon is pretty close to a circle, and the 23 pieces, which are quite narrow, look very much like equal wedges of a circle:
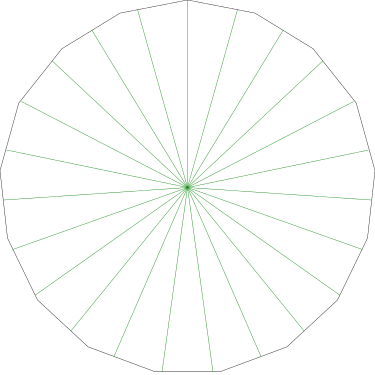
This is generally true, and it becomes more nearly so both as the number of sides of the polygon increases (it becomes more nearly circular) and as the number of pieces increases (the very small amount of perimeter included in each piece is not very different from a short circular arc).
Recall my observation
from last time that even in the nearly extreme case of 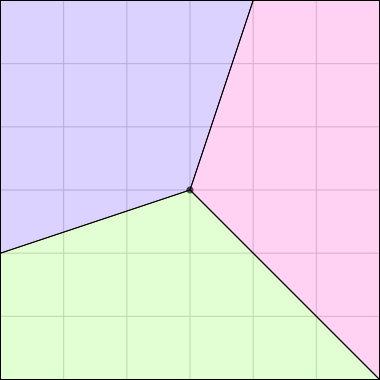 , the central angles deviate from equality by
only a few percent.
, the central angles deviate from equality by
only a few percent.
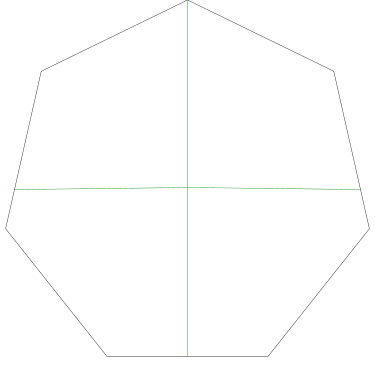
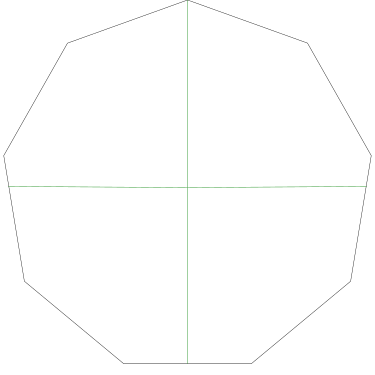
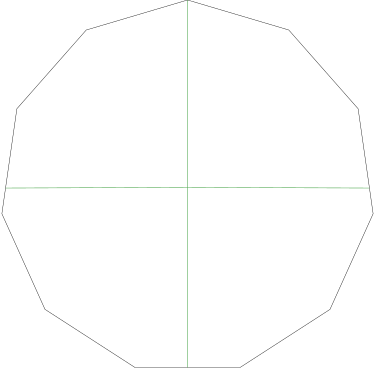
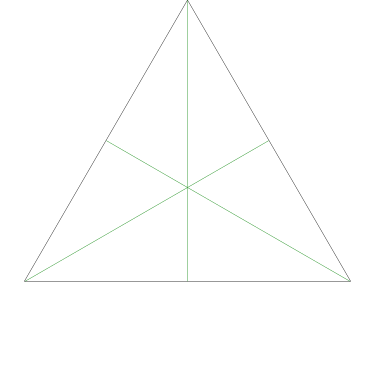
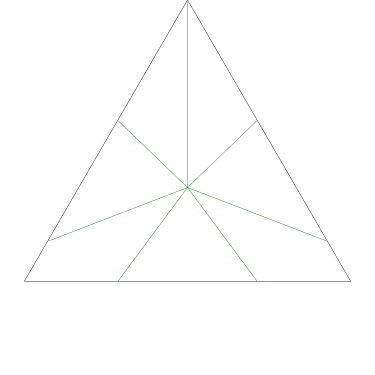
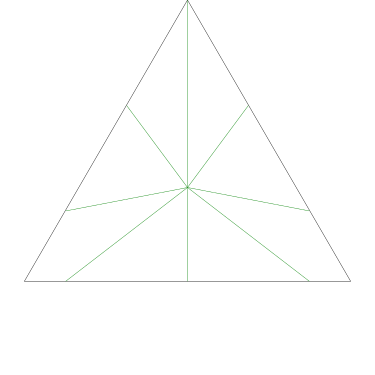
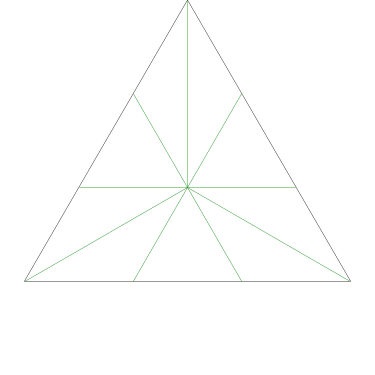
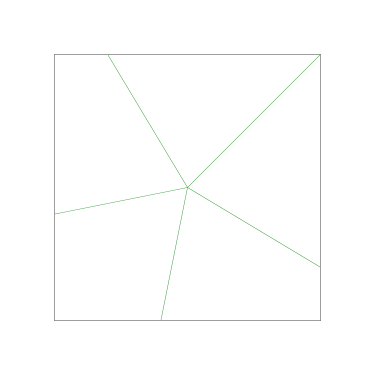
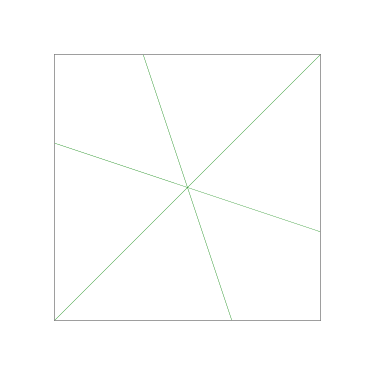
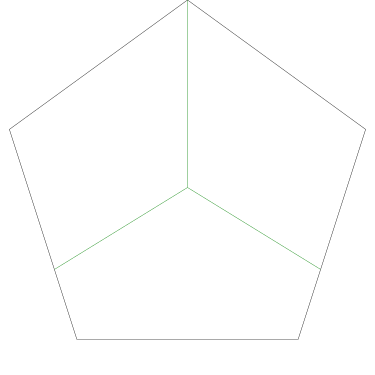
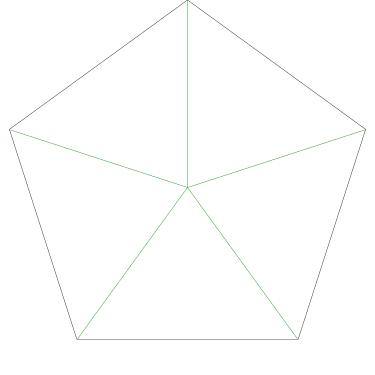
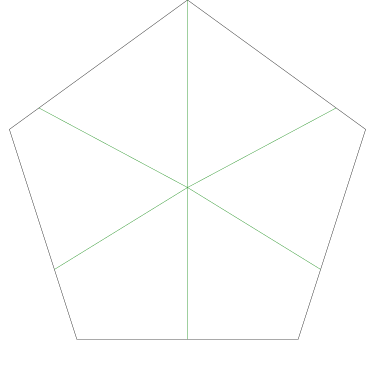
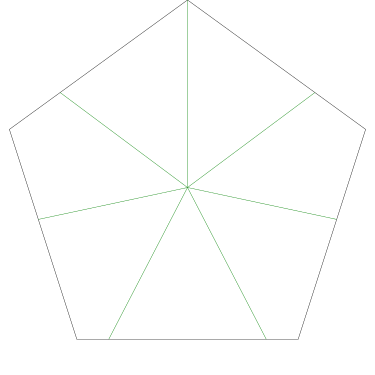
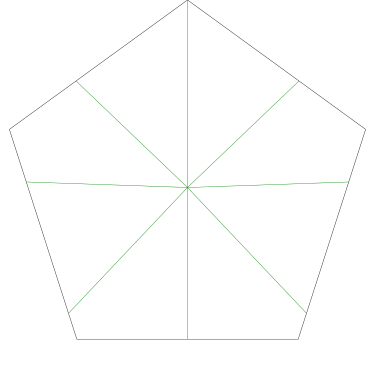
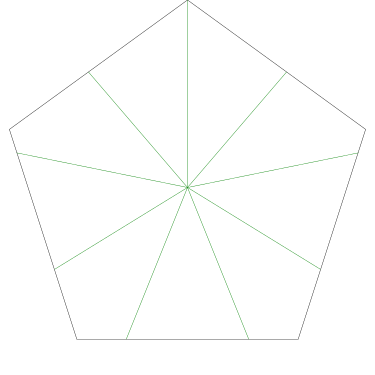
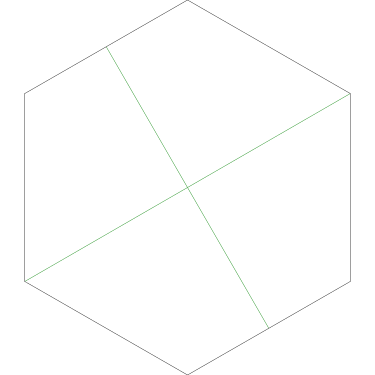
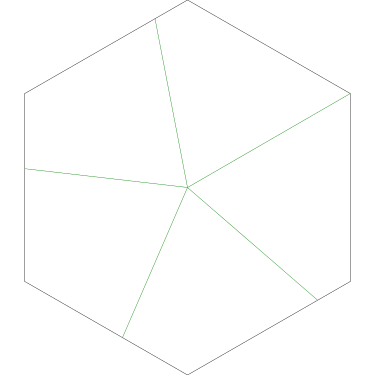
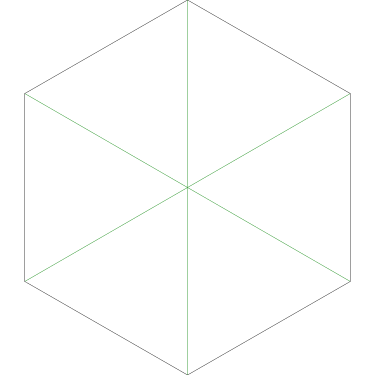
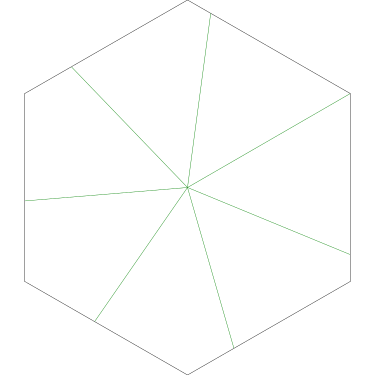
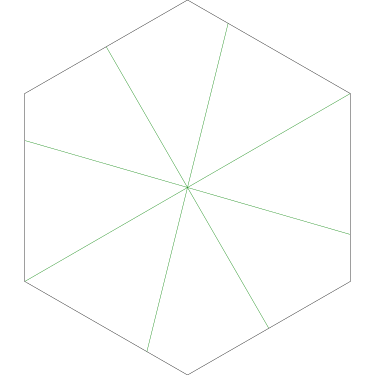
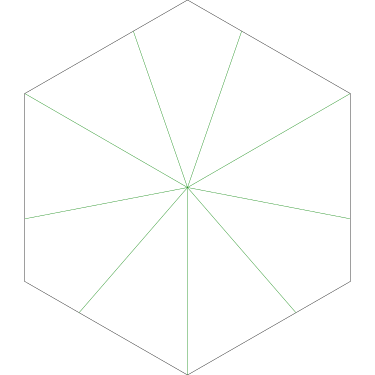
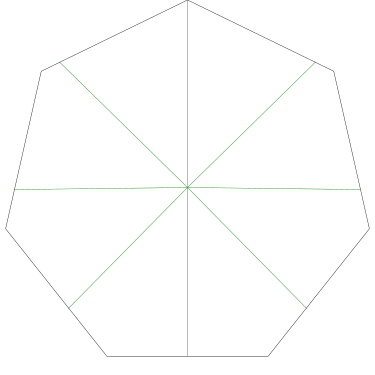
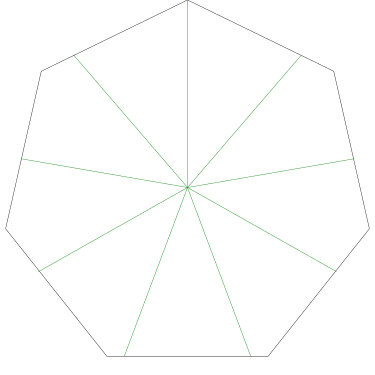
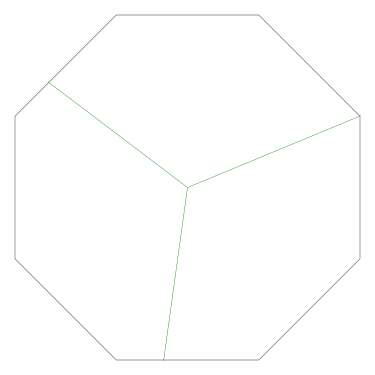
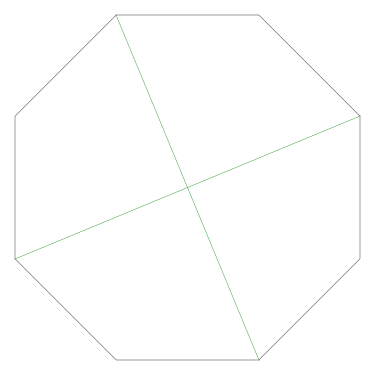
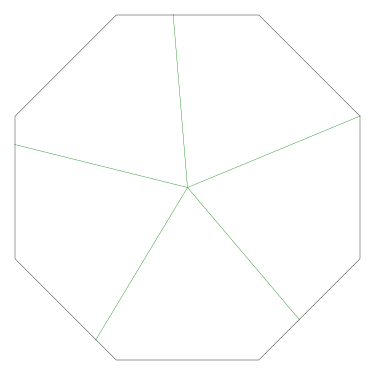
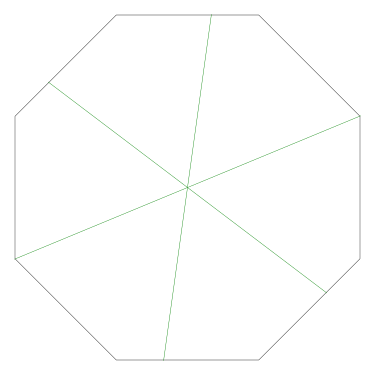
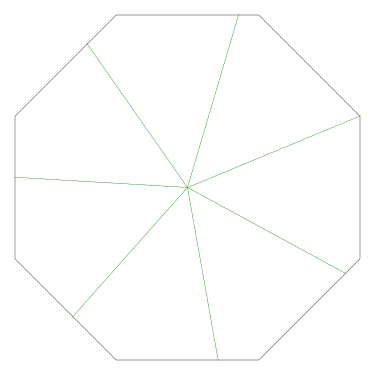
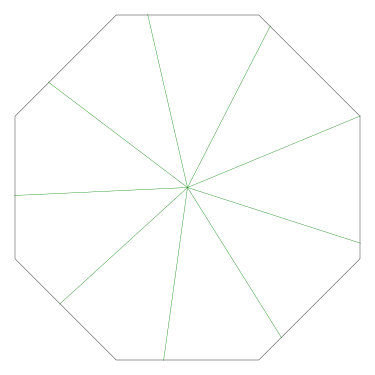
Of particular interest to me is this series of demonstrations of how to cut four pieces from a cake with an odd number of sides:
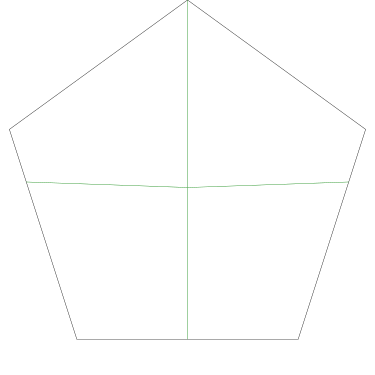
| 
| 
| 
|
I think this shows that the whole question is a little bit silly: if you just cut the cake into equiangular wedges, the resulting slices are very close in volume and in frosting. If the nearly-horizontal cuts in the pentagon above had been perfectly straight and along the !!y!!-axis, they would have intersected the pentagon only 3% of a radius-length lower than they should have.
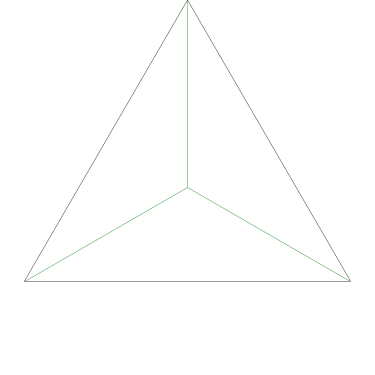
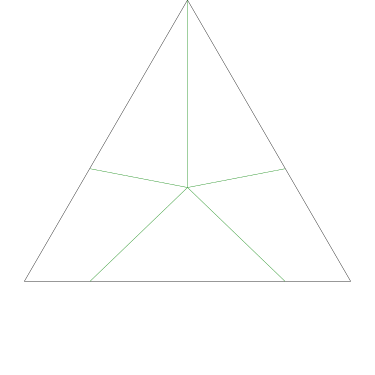
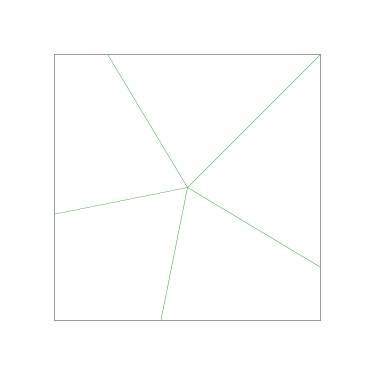
Some of the simpler divisions of simpler cakes are interesting. A solution to the original problem (of dividing a square cake into nine pieces) is highlighted.
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
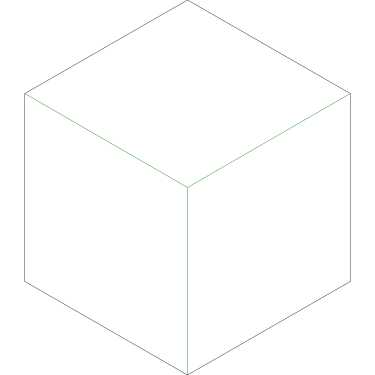
| 
| 
| 
| 
| 
| 
|
| 
| 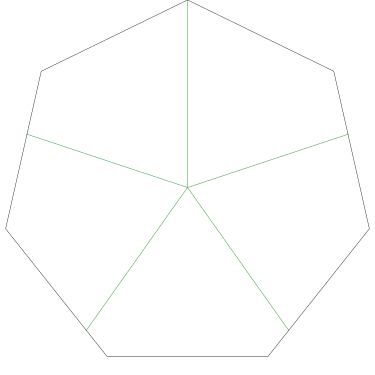
| 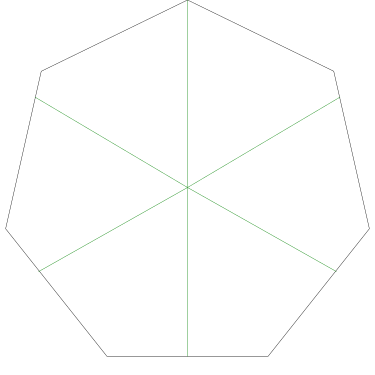
| 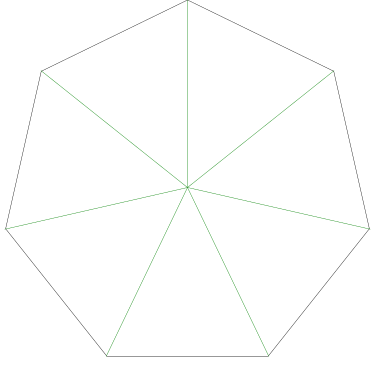
| 
| 
|
| 
| 
| 
| 
| 
| 
|
The method as given works regardless of where you make the first cut. But the results do not look very different in any case:
| 
| 
| 
|
The original SVG files are also available, as is the program that wrote them.
[Other articles in category /math] permanent link


