Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 07 Jul 2019
[ I wrote this in 2007 and forgot to publish it. Or maybe I was planning to finish it first. But if so I have no idea what I was originally planning to say, so here we are. ]
In computer programs, it's quite common to need a numerical value for π. Often you see something like:
#define PI 3.141592654
This has the drawback of not representing π as exactly as possible. But to do that in C probably requires putting in 16 digits after the decimal point, and most people don't have so much memorized. And anyway, you don't really know at compile time what the floating-point precision will be; some platforms support quad-width floats. So you can do better, maybe, by using the math library to calculate π. And people do:
static double pi = 4*atan2(1,1);
The atan2(y, x) function produces the (almost-)unique value θ from the range !![-\pi, \pi]!! such that a ray from the origin, passing through point (x, y), makes angle θ with the x-axis.
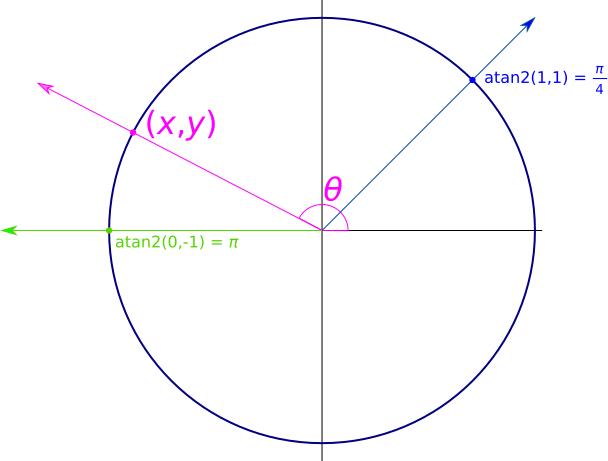
Note that the arguments have y first and x second.
For example, atan2(17, 0) returns !!\frac\pi
2!!, because a line at angle !!\frac\pi 2!! passes through the point
(0, 17). Similarly, atan2(-17, 0) returns -!!\frac\pi 2!!.
You can use atan2 to calculate π, by using
!!4·{\operatorname{atan2}}(1,1)!!, as I mentioned above. Many people
do; Google searching finds hundreds of examples. The manual for the
standard Perl module constant.pm mentions this example.
But this is a bit strange. Why is this so well-known? Why calculate 4*atan2(1,1) when $$\pi = {\operatorname{atan2}}(0,-1)$$ produces the same result and is simpler?
(Obligatory IEEE 754 complaining: atan2 should return an always-unique value from
!!(-\pi, \pi]!!, but I have to say “almost-unique” because as usual IEEE
754 fucks everything up, this time with its stupid distinction between
0 and -0.)
[ Addendum: Leah Neukirchen suggests that the atan2(1,1) is a
translation from earlier systems that provide a single-argument atan
function but no atan2. In those systems, there is no
workable analogue of atan2(0, -1) because the transformation
!!{\operatorname{atan2}}(y, x)\Rightarrow
{\operatorname{atan}}\left(\frac yx\right)!! gives !!{\operatorname{atan}}(0)!!, which doesn't work for this
application as it yields !!0!! instead of the desired !!\pi!!. And
similarly in languages with atan but not atan2 there is no analogue of !!\pi =
2·{\operatorname{atan2}}(1, 0)!!. So the simplest thing you can do is pi = 4 * atan(1),
and after the transformation above one gets !!\pi = 4·{\operatorname{atan2}}(1,1)!!. ]
[Other articles in category /prog] permanent link


