Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 11 Feb 2022
Geometric proof that the mediant lies between its arguments
The mediant of two fractions !!\frac ab!! and !!\frac cd!! is simply !!\frac{a+c}{b+d}!!. It appears often in connection with the theory of continued fractions, and a couple of months ago I put it to use in this post about Newton's method. There the crucial property was that if $$\frac ab < \frac cd$$ then $$\frac ab < \frac{a+c}{b+d} < \frac cd.$$
This can be proved with straightforward algebra:
$$\begin{align} \frac ab & < \frac cd \\ ad & < bc \\ ab + ad & < ab + bc \\ a(b+d) & < (a+c) b \\ \frac ab & < \frac{a+c}{b+d} \end{align}$$
and similarly for the !!\frac cd!! side.
But Reddit user asenseofbeauty recently suggested a lovely visual proof that makes the result intuitively clear:
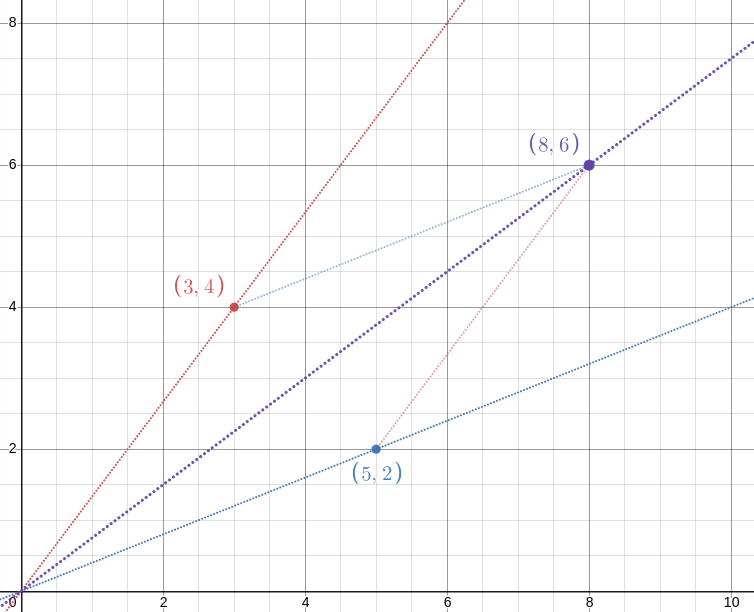
!!\def\pt#1#2{\langle{#1},{#2}\rangle}!! The idea is simply this: !!\frac ab!! is the slope of the line from the origin !!O!! through the point !!P=\pt ba!! (blue) and !!\frac cd!! is the slope of the line through !!Q=\pt dc!! (red). The point !!\pt{b+d}{a+c}!! is the fourth vertex of the parallelogram with vertices at !!O, P, Q!!, and !!\frac{a+c}{b+d}!! is the slope of the parallelogram's diagonal. Since the diagonal lies between the two sides, the slope must also lie in the middle somewhere.
The embedded display above should be interactive. You can drag around the red and blue points and watch the diagonal with slope !!\frac{a+b}{c+d}!! slide around to match.
In case the demo doesn't work, here's a screenshot showing that !!\frac 25 < \frac{2+4}{5+3} < \frac 43!!:
[ Addendum 20220215: The source was this Reddit comment from asenseofbeauty. ]
[Other articles in category /math] permanent link


