Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 23 Jul 2014
When do n and 2n have the same digits?
[This article was published last month on the math.stackexchange blog, which seems to have died young, despite many earnest-sounding promises beforehand from people who claimed they would contribute material. I am repatriating it here.]
A recent question on math.stackexchange asks for the smallest positive integer !!A!! for which the number !!2A!! has the same decimal digits in some other order.
Math geeks may immediately realize that !!142857!! has this property, because it is the first 6 digits of the decimal expansion of !!\frac 17!!, and the cyclic behavior of the decimal expansion of !!\frac n7!! is well-known. But is this the minimal solution? It is not. Brute-force enumeration of the solutions quickly reveals that there are 12 solutions of 6 digits each, all permutations of !!142857!!, and that larger solutions, such as 1025874 and 1257489 seem to follow a similar pattern. What is happening here?
Stuck in Dallas-Fort Worth airport one weekend, I did some work on the problem, and although I wasn't able to solve it completely, I made significant progress. I found a method that allows one to hand-calculate that there is no solution with fewer than six digits, and to enumerate all the solutions with 6 digits, including the minimal one. I found an explanation for the surprising behavior that solutions tend to be permutations of one another. The short form of the explanation is that there are fairly strict conditions on which sets of digits can appear in a solution of the problem. But once the set of digits is chosen, the conditions on that order of the digits in the solution are fairly lax.
So one typically sees, not only in base 10 but in other bases, that the solutions to this problem fall into a few classes that are all permutations of one another; this is exactly what happens in base 10 where all the 6-digit solutions are permutations of !!124578!!. As the number of digits is allowed to increase, the strict first set of conditions relaxes a little, and other digit groups appear as solutions.
Notation
The property of interest, !!P_R(A)!!, is that the numbers !!A!! and !!B=2A!! have exactly the same base-!!R!! digits. We would like to find numbers !!A!! having property !!P_R!! for various !!R!!, and we are most interested in !!R=10!!. Suppose !!A!! is an !!n!!-digit numeral having property !!P_R!!; let the (base-!!R!!) digits of !!A!! be !!a_{n-1}\ldots a_1a_0!! and similarly the digits of !!B = 2A!! are !!b_{n-1}\ldots b_1b_0!!. The reader is encouraged to keep in mind the simple example of !!R=8, n=4, A=\mathtt{1042}, B=\mathtt{2104}!! which we will bring up from time to time.
Since the digits of !!B!! and !!A!! are the same, in a different order, we may say that !!b_i = a_{P(i)}!! for some permutation !!P!!. In general !!P!! might have more than one cycle, but we will suppose that !!P!! is a single cycle. All the following discussion of !!P!! will apply to the individual cycles of !!P!! in the case that !!P!! is a product of two or more cycles. For our example of !!a=\mathtt{1042}, b=\mathtt{2104}!!, we have !!P = (0\,1\,2\,3)!! in cycle notation. We won't need to worry about the details of !!P!!, except to note that !!i, P(i), P(P(i)), \ldots, P^{n-1}(i)!! completely exhaust the indices !!0. \ldots n-1!!, and that !!P^n(i) = i!! because !!P!! is an !!n!!-cycle.
Conditions on the set of digits in a solution
For each !!i!! we have $$a_{P(i)} = b_{i} \equiv 2a_{i} + c_i\pmod R $$ where the ‘carry bit’ !!c_i!! is either 0 or 1 and depends on whether there was a carry when doubling !!a_{i-1}!!. (When !!i=0!! we are in the rightmost position and there is never a carry, so !!c_0= 0!!.) We can then write:
$$\begin{align} a_{P(P(i))} &= 2a_{P(i)} + c_{P(i)} \\ &= 2(2a_{i} + c_i) + c_{P(i)} &&= 4a_i + 2c_i + c_{P(i)}\\ a_{P(P(P(i)))} &= 2(4a_i + 2c_i + c_{P(P(i)})) + c_{P(i)} &&= 8a_i + 4c_i + 2c_{P(i)} + c_{P(P(i))}\\ &&&\vdots\\ a_{P^n(i)} &&&= 2^na_i + v \end{align} $$
all equations taken !!\bmod R!!. But since !!P!! is an !!n!!-cycle, !!P^n(i) = i!!, so we have $$a_i \equiv 2^na_i + v\pmod R$$ or equivalently $$\big(2^n-1\big)a_i + v \equiv 0\pmod R\tag{$\star$}$$ where !!v\in\{0,\ldots 2^n-1\}!! depends only on the values of the carry bits !!c_i!!—the !!c_i!! are precisely the binary digits of !!v!!.
Specifying a particular value of !!a_0!! and !!v!! that satisfy this equation completely determines all the !!a_i!!. For example, !!a_0 = 2, v = \color{darkblue}{0010}_2 = 2!! is a solution when !!R=8, n=4!! because !!\bigl(2^4-1\bigr)\cdot2 + 2\equiv 0\pmod 8!!, and this solution allows us to compute
$$\def\db#1{\color{darkblue}{#1}}\begin{align} a_0&&&=2\\ a_{P(0)} &= 2a_0 &+ \db0 &= 4\\ a_{P^2(0)} &= 2a_{P(0)} &+ \db0 &= 0 \\ a_{P^3(0)} &= 2a_{P^2(0)} &+ \db1 &= 1\\ \hline a_{P^4(0)} &= 2a_{P^3(0)} &+ \db0 &= 2\\ \end{align}$$
where the carry bits !!c_i = \langle 0,0,1,0\rangle!! are visible in the third column, and all the sums are taken !!\pmod 8!!. Note that !!a_{P^n(0)} = a_0!! as promised. This derivation of the entire set of !!a_i!! from a single one plus a choice of !!v!! is crucial, so let's see one more example. Let's consider !!R=10, n=3!!. Then we want to choose !!a_0!! and !!v!! so that !!\left(2^3-1\right)a_0 + v \equiv 0\pmod{10}!! where !!v\in\{0\ldots 7\}!!. One possible solution is !!a_0 = 5, v=\color{darkblue}{101}_2 = 5!!. Then we can derive the other !!a_i!! as follows:
$$\begin{align} a_0&&&=5\\ a_{P(0)} &= 2a_0 &+ \db1 &= 1\\ a_{P^2(0)} &= 2a_{P(0)} &+ \db0 &= 2 \\\hline a_{P^3(0)} &= 2a_{P^2(0)} &+ \db1 &= 5\\ \end{align}$$
And again we have !!a_{P^n(0)}= a_0!! as required.
Since the bits of !!v!! are used cyclically, not every pair of !!\langle a_0, v\rangle!! will yield a different solution. Rotating the bits of !!v!! and pairing them with different choices of !!a_0!! will yield the same cycle of digits starting from a different place. In the first example above, we had !!a_0 = 2, v = 0010_2 = 2!!. If we were to take !!a_0 = 4, v = 0100_2 = 4!! (which also solves !!(\star)!!) we would get the same cycle of values of the !! a\_i !! but starting from !!4!! instead of from !!2!!, and similarly if we take !!a_0=0, v = 1000_2 = 8!! or !!a_0 = 1, v = 0001_2!!. So we can narrow down the solution set of !!(\star)!! by considering only the so-called necklaces of !!v!! rather than all !!2^n!! possible values. Two values of !!v!! are considered equivalent as necklaces if one is a rotation of the other. When a set of !!v!!-values are equivalent as necklaces, we need only consider one of them; the others will give the same cyclic sequence of digits, but starting in a different place. For !!n=4!!, for example, the necklaces are !!0000, 0001, 0011, 0101, 0111, !! and !!1111!!; the sequences !!0110, 1100,!! and !!1001!! being equivalent to !!0011!!, and so on.
Example
Let us take !!R=9, n=3!!, so we want to find 3-digit numerals with property !!P_9!!. According to !!(\star)!! we need !!7a_i + v \equiv 0\pmod{9}!! where !!v\in\{0\ldots 7\}!!. There are 9 possible values for !!a_i!!; for each one there is at most one possible value of !!v!! that makes the sum zero:
$$\begin{array}{rrr} a_i & 7a_i & v \\ \hline 0 & 0 & 0 \\ 1 & 7 & 2 \\ 2 & 14 & 4 \\ 3 & 21 & 6 \\ 4 & 28 & \\ 5 & 35 & 1 \\ 6 & 42 & 3 \\ 7 & 49 & 5 \\ 8 & 56 & 7 \\ \end{array} $$
(For !!a_i=4!! there is no solution.) We may disregard the non-necklace values of !!v!!, as these will give us solutions that are the same as those given by necklace values of !!v!!. The necklaces are:
$$\begin{array}{rl} 000 & 0 \\ 001 & 1 \\ 011 & 3 \\ 111 & 7 \end{array}$$
so we may disregard the solutions exacpt when !!v=0,1,3,7!!. Calculating the digit sequences from these four values of !!v!! and the corresponding !!a_i!! we find:
$$\begin{array}{ccl} a_0 & v & \text{digits} \\ \hline 0 & 0 & 000 \\ 5 & 1 & 512 \\ 6 & 3 & 637 \\ 8 & 7 & 888 \ \end{array} $$
(In the second line, for example, we have !!v=1 = 001_2!!, so !!1 = 2\cdot 5 + 0; 2 = 1\cdot 2 + 0;!! and !!5 = 2\cdot 2 + 1!!.)
Any number !!A!! of three digits, for which !!2A!! contains exactly the same three digits, in base 9, must therefore consist of exactly the digits !!000, 125, 367,!! or !!888!!.
A warning
All the foregoing assumes that the permutation !!P!! is a single cycle. In general, it may not be. Suppose we did an analysis like that above for !!R=10, n=5!! and found that there was no possible digit set, other than the trivial set 00000, that satisfied the governing equation !!(2^5-1)a_0 + v\equiv 0\pmod{10}!!. This would not completely rule out a base-10 solution with 5 digits, because the analysis only rules out a cyclic set of digits. There could still be a solution where !!P!! was a product of a !!2!! and a !!3!!-cycle, or a product of still smaller cycles.
Something like this occurs, for example, in the !!n=4, R=8!! case. Solving the governing equation !!(2^5-1)a_0 + v \equiv 0\pmod 8!! yields only four possible digit cycles, namely !!\{0,1,2,4\}, \{1,3,6,4\}, \{2,5,2,5\}!!, and !!\{3,7,6,5\}!!. But there are several additional solutions: !!2500_8\cdot 2 = 5200_8, 2750_8\cdot 2 = 5720_8, !! and !!2775_8\cdot 2 = 5772_8!!. These correspond to permutations !!P!! with more than one cycle. In the case of !!2750_8!!, for example, !!P!! exchanges the !!5!! and the !!2!!, and leaves the !!0!! and the !!7!! fixed.
For this reason we cannot rule out the possibility of an !!n!!-digit solution without first considering all smaller !!n!!.
The Large Equals Odd rule
When !!R!! is even there is a simple condition we can use to rule out certain sets of digits from being single-cycle solutions. Recall that !!A=a_{n-1}\ldots a_0!! and !!B=b_{n-1}\ldots b_0!!. Let us agree that a digit !!d!! is large if !!d\ge \frac R2!! and small otherwise. That is, !!d!! is large if, upon doubling, it causes a carry into the next column to the left.
Since !!b_i =(2a_i + c_i)\bmod R!!, where the !!c_i!! are carry bits, we see that, except for !!b_0!!, the digit !!b_i!! is odd precisely when there is a carry from the next column to the right, which occurs precisely when !!a_{i-1}!! is large. Thus the number of odd digits among !!b_1,\ldots b_{n-1}!! is equal to the number of large digits among !!a_1,\ldots a_{n-2}!!. This leaves the digits !!b_0!! and !!a_{n-1}!! uncounted. But !!b_0!! is never odd, since there is never a carry in the rightmost position, and !!a_{n-1}!! is always small (since otherwise !!B!! would have !!n+1!! digits, which is not allowed). So the number of large digits in !!A!! is exactly equal to the number of odd digits in !!B!!. And since !!A!! and !!B!! have exactly the same digits, the number of large digits in !!A!! is equal to the number of odd digits in !!A!!. Observe that this is the case for our running example !!1042_8!!: there is one odd digit and one large digit (the 4).
When !!R!! is odd the analogous condition is somewhat more complicated, but since the main case of interest is !!R=10!!, we have the useful rule that:
For !!R!! even, the number of odd digits in any solution !!A!! is equal to the number of large digits in !!A!!.
Conditions on the order of digits in a solution
We have determined, using the above method, that the digits !!\{5,1,2\}!! might form a base-9 numeral with property !!P_9!!. Now we would like to arrange them into a base-9 numeral that actually does have that property. Again let us write !!A = a_2a_1a_0!! and !!B=b_2b_1b_0!!, with !!B=2A!!. Note that if !!a_i = 1!!, then !!b_i = 3!! (if there was a carry from the next column to the right) or !!b_i=2!! (if there was no carry), but since !!b_i\in{5,1,2}!!, we must have !!b_i = 2!! and therefore !!a_{i-1}!! must be small, since there is no carry into position !!i!!. But since !!a_{i-1}!! is also one of !!\{5,1,2\}!!, and it cannot also be !!1!!, it must be !!2!!. This shows that the 1, unless it appears in the rightmost position, must be to the left of the !!2!!; it cannot be to the left of the !!5!!. Similarly, if !!a_i = 2!! then !!b_i = 5!!, because !!4!! is impossible, so the !!2!! must be to the left of a large digit, which must be the !!5!!. Similar reasoning produces no constraint on the position of the !!5!!; it could be to the left of a small digit (in which case it doubles to !!1!!) or a large digit (in which case it doubles to !!2!!). We can summarize these findings as follows:
$$\begin{array}{cl} \text{digit} & \text{to the left of} \\ \hline 1 & 1, 2, \text{end} \\ 2 & 5 \\ 5 & 1,2,5,\text{end} \end{array}$$
Here “end” means that the indicated digit could be the rightmost.
Furthermore, the left digit of !!A!! must be small (or else there would be a carry in the leftmost place and !!2A!! would have 4 digits instead of 3) so it must be either 1 or 2. It is not hard to see from this table that the digits must be in the order !!125!! or !!251!!, and indeed, both of those numbers have the required property: !!125_9\cdot 2 = 251_9!!, and !!251_9\cdot 2 = 512_9!!.
This was a simple example, but in more complicated cases it is helpful to draw the order constraints as a graph. Suppose we draw a graph with one vertex for each digit, and one additional vertex to represent the end of the numeral. The graph has an edge from vertex !!v!! to !!v'!! whenever !!v!! can appear to the left of !!v'!!. Then the graph drawn for the table above looks like this:
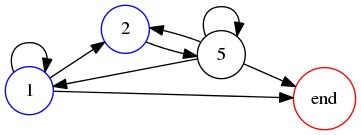
A 3-digit numeral with property !!P_9!! corresponds to a path in this graph that starts at one of the nonzero small digits (marked in blue), ends at the red node marked ‘end’, and visits each node exactly once. Such a path is called hamiltonian. Obviously, self-loops never occur in a hamiltonian path, so we will omit them from future diagrams.
Now we will consider the digit set !!637!!, again base 9. An analysis similar to the foregoing allows us to construct the following graph:
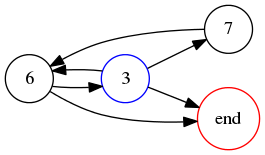
Here it is immediately clear that the only hamiltonian path is !!3-7-6-\text{end}!!, and indeed, !!376_9\cdot 2 = 763_9!!.
In general there might be multiple instances of a digit, and so multiple nodes labeled with that digit. Analysis of the !!0,0,0!! case produces a graph with no legal start nodes and so no solutions, unless leading zeroes are allowed, in which case !!000!! is a perfectly valid solution. Analysis of the !!8,8,8!! case produces a graph with no path to the end node and so no solutions. These two trivial patterns appear for all !!R!! and all !!n!!, and we will ignore them from now on.
Returning to our ongoing example, !!1042!! in base 8, we see that !!1!! and !!2!! must double to !!2!! and !!4!!, so must be to the left of small digits, but !!4!! and !!0!! can double to either !!0!! or !!1!! and so could be to the left of anything. Here the constraints are so lax that the graph doesn't help us narrow them down much:
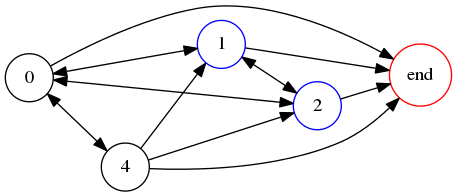
Observing that the only arrow into the 4 is from 0, so that the 4 must follow the 0, and that the entire number must begin with 1 or 2, we can enumerate the solutions:
1042
1204
2041
2104
If leading zeroes are allowed we have also:
0412
0421
All of these are solutions in base 8.
The case of !!R=10!!
Now we turn to our main problem, solutions in base 10.
To find all the solutions of length 6 requires an enumeration of smaller solutions, which, if they existed, might be concatenated into a solution of length 6. This is because our analysis of the digit sets that can appear in a solution assumes that the digits are permuted cyclically; that is, the permutations !!P!! that we considered had only one cycle each.
There are no smaller solutions, but to prove that the length 6 solutions are minimal, we must analyze the cases for smaller !!n!! and rule them out. We now produce a complete analysis of the base 10 case with !!R=10!! and !!n\le 6!!. For !!n=1!! there is only the trivial solution of !!0!!, which we disregard. (The question asked for a positive number anyway.)
!!n=2!!
For !!n=2!!, we want to find solutions of !!3a_i + v \equiv 0\pmod{10}!! where !!v!! is a two-bit necklace number, one of !!00_2, 01_2, !! or !!11_2!!. Tabulating the values of !!a_i!! and !!v\in\{0,1,3\}!! that solve this equation we get:
$$\begin{array}{ccc} v& a_i \\ \hline 0 & 0 \\ 1& 3 \\ 3& 9 \\ \end{array}$$
We can disregard the !!v=0!! and !!v=3!! solutions because the former yields the trivial solution !!00!! and the latter yields the nonsolution !!99!!. So the only possibility we need to investigate further is !!a_i = 3, v = 1!!, which corresponds to the digit sequence !!36!!: Doubling !!3!! gives us !!6!! and doubling !!6!!, plus a carry, gives us !!3!! again.
But when we tabulate of which digits must be left of which informs us that there is no solution with just !!3!! and !!6!!, because the graph we get, once self-loops are eliminated, looks like this:
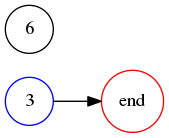
which obviously has no hamiltonian path. Thus there is no solution for !!R=10, n=2!!.
!!n=3!!
For !!n=3!! we need to solve the equation !!7a_i + v \equiv 0\pmod{10}!! where !!v!! is a necklace number in !!\{0,\ldots 7\}!!, specifically one of !!0,1,3,!! or !!7!!. Since !!7!! and !!10!! are relatively prime, for each !!v!! there is a single !!a_i!! that solves the equation. Tabulating the possible values of !!a_i!! as before, and this time omitting rows with no solution, we have:
$$\begin{array}{rrl} v & a_i & \text{digits}\\ \hline 0& 0 & 000\\ 1& 7 & 748 \\ 3& 1 & 125\\ 7&9 & 999\\ \end{array}$$
The digit sequences !!0,0,0!! and !!9,9,9!! yield trivial solutions or nonsolutions as usual, and we will omit them in the future. The other two lines suggest the digit sets !!1,2,5!! and !!4,7,8!!, both of which fail the “odd equals large” rule.
This analysis rules out the possibility of a digit set with !!a_0 \to a_1 \to a_2 \to a_1!!, but it does not completely rule out a 3-digit solution, since one could be obtained by concatenating a one-digit and a two-digit solution, or three one-digit solutions. However, we know by now that no one- or two-digit solutions exist. Therefore there are no 3-digit solutions in base 10.
!!n=4!!
For !!n=4!! the governing equation is !!15a_i + v \equiv 0\pmod{10}!! where !!v!! is a 4-bit necklace number, one of !!\{0,1,3,5,7,15\}!!. This is a little more complicated because !!\gcd(15,10)\ne 1!!. Tabulating the possible digit sets, we get:
$$\begin{array}{crrl} a_i & 15a_i& v & \text{digits}\\ \hline 0 & 0 & 0 & 0000\\ 1 & 5 & 5 & 1250\\ 1 & 5 & 15 & 1375\\ 2 & 0 & 0 & 2486\\ 3 & 5 & 5 & 3749\\ 3 & 5 & 15 & 3751\\ 4 & 0 & 0 & 4862\\ 5 & 5 & 5 & 5012\\ 5 & 5 & 5 & 5137\\ 6 & 0 & 0 & 6248\\ 7 & 5 & 5 & 7493\\ 7 & 5 & 5 & 7513\\ 8 & 0 & 0 & 8624 \\ 9 & 5 & 5 & 9874\\ 9 & 5 & 15 & 9999 \\ \end{array}$$
where the second column has been reduced mod !!10!!. Note that even restricting !!v!! to necklace numbers the table still contains duplicate digit sequences; the 15 entries on the right contain only the six basic sequences !!0000, 0125, 1375, 2486, 3749, 4987!!, and !!9999!!. Of these, only !!0000, 9999,!! and !!3749!! obey the odd equals large criterion, and we will disregard !!0000!! and !!9999!! as usual, leaving only !!3749!!. We construct the corresponding graph for this digit set as follows: !!3!! must double to !!7!!, not !!6!!, so must be left of a large number !!7!! or !!9!!. Similarly !!4!! must be left of !!7!! or !!9!!. !!9!! must also double to !!9!!, so must be left of !!7!!. Finally, !!7!! must double to !!4!!, so must be left of !!3,4!! or the end of the numeral. The corresponding graph is:
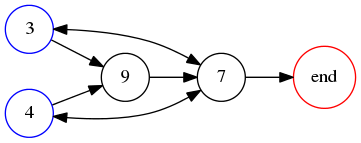
which evidently has no hamiltonian path: whichever of 3 or 4 we start at, we cannot visit the other without passing through 7, and then we cannot reach the end node without passing through 7 a second time. So there is no solution with !!R=10!! and !!n=4!!.
!!n=5!!
We leave this case as an exercise. There are 8 solutions to the governing equation, all of which are ruled out by the odd equals large rule.
!!n=6!!
For !!n=6!! the possible solutions are given by the governing equation !!63a_i + v \equiv 0\pmod{10}!! where !!v!! is a 6-bit necklace number, one of !!\{0,1,3,5,7,9,11,13,15,21,23,27,31,63\}!!. Tabulating the possible digit sets, we get:
$$\begin{array}{crrl} v & a_i & \text{digits}\\ \hline 0 & 0 & 000000\\ 1 & 3 & 362486 \\ 3 & 9 & 986249 \\ 5 & 5 & 500012 \\ 7 & 1 & 124875 \\ 9 & 7 & 748748 \\ 11 & 3 & 362501 \\ 13 & 9 & 986374 \\ 15 & 5 & 500137 \\ 21 & 3 & 363636 \\ 23 & 9 & 989899 \\ 27 & 1 & 125125 \\ 31 & 3 & 363751 \\ 63 & 9 & 999999 \\ \end{array}$$
After ignoring !!000000!! and !!999999!! as usual, the large equals odd rule allows us to ignore all the other sequences except !!124875!! and !!363636!!. The latter fails for the same reason that !!36!! did when !!n=2!!. But !!142857!! , the lone survivor, gives us a complicated derived graph containing many hamiltonian paths, every one of which is a solution to the problem:
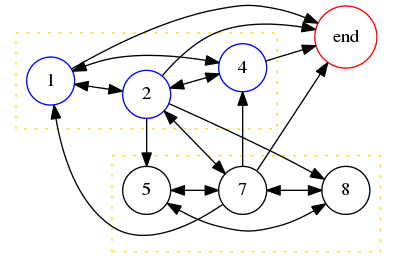
It is not hard to pick out from this graph the minimal solution !!125874!!, for which !!125874\cdot 2 = 251748!!, and also our old friend !!142857!! for which !!142857\cdot 2 = 285714!!.
We see here the reason why all the small numbers with property !!P_{10}!! contain the digits !!124578!!. The constraints on which digits can appear in a solution are quite strict, and rule out all other sequences of six digits and all shorter sequences. But once a set of digits passes these stringent conditions, the constraints on it are much looser, because !!B!! is only required to have the digits of !!A!! in some order, and there are many possible orders, many of which will satisfy the rather loose conditions involving the distribution of the carry bits. This graph is typical: it has a set of small nodes and a set of large nodes, and each node is connected to either all the small nodes or all the large nodes, so that the graph has many edges, and, as in this case, a largish clique of small nodes and a largish clique of large nodes, and as a result many hamiltonian paths.
Onward
This analysis is tedious but is simple enough to perform by hand in under an hour. As !!n!! increases further, enumerating the solutions of the governing equation becomes very time-consuming. I wrote a simple computer program to perform the analysis for given !!R!! and !!n!!, and to emit the possible digit sets that satisfied the large equals odd criterion. I had wondered if every base-10 solution contained equal numbers of the digits !!1,2,4,8,5,!! and !!7!!. This is the case for !!n=7!! (where the only admissible digit set is !!\{1,2,4,5,7,8\}\cup\{9\}!!), for !!n=8!! (where the only admissible sets are !!\{1,2,4,5,7,8\}\cup \{3,6\}!! and !!\{1,2,4,5,7,8\}\cup\{9,9\}!!), and for !!n=9!! (where the only admissible sets are !!\{1,2,4,5,7,8\}\cup\{3,6,9\}!! and !!\{1,2,4,5,7,8\}\cup\{9,9,9\}!!). But when we reach !!n=10!! the increasing number of necklaces has loosened up the requirements a little and there are 5 admissible digit sets. I picked two of the promising-seeming ones and quickly found by hand the solutions !!4225561128!! and !!1577438874!!, both of which wreck any theory that the digits !!1,2,4,5,8,7!! must all appear the same number of times.
Acknowledgments
Thanks to Karl Kronenfeld for corrections and many helpful suggestions.
[Other articles in category /math] permanent link


