Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sat, 22 Apr 2006
Counting squares
Let's take a bunch of squares, and put a big "X" in each one, dividing
each square into four triangular wedges. Then let's take three
colors of ink, say red, blue, and black, and ink in the wedges. How
many different ways are there of inking up the squares?
Well, that's easy. There are four wedges, and each one can be one
of three colors, so the answer is 34 = 81. No, wait,
that's not right, because the two squares below are really the
same:
 |
 |
 |
 |
 |
 |
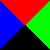
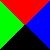 What about turning the squares over? Are the two squares to the right
"the same"?
Let's say that the squares are inked
on only one side, so that those two would not considered the
same, even if we decided to allow squares with green wedges. Later on
we will make the decision the other way and see how things change.
What about turning the squares over? Are the two squares to the right
"the same"?
Let's say that the squares are inked
on only one side, so that those two would not considered the
same, even if we decided to allow squares with green wedges. Later on
we will make the decision the other way and see how things change.


 OK, so let's see. All four wedges might be the same color, and
there are 3 colors, so there are 3 ways to do that, shown at right.
OK, so let's see. All four wedges might be the same color, and
there are 3 colors, so there are 3 ways to do that, shown at right.





 Or there might only be two colors. In
that case, there might be three wedges of one color and one of
another, there are 6 ways to do that, depending on how we pick the
colors; these six are shown at right.
Or there might only be two colors. In
that case, there might be three wedges of one color and one of
another, there are 6 ways to do that, depending on how we pick the
colors; these six are shown at right.
Or it might be two-and-two.
There are three ways to choose the colors (red-blue, red-black, and
blue-black) and two ways to arrange them: same-colored wedges opposite
each other:



or abutting:



so that's another 2·3 = 6 ways.


 If we use all three colors, then two wedges are in one of the colors,
and one wedge in each of the other two colors. The two wedges of the
same color might be adjacent to each other or opposite. In either case, we have three choices for the color of the two wedges that are
the same, after which the colors of the other two wedges are forced.
So that's 3 colorings with two adjacent wedges the same color:
If we use all three colors, then two wedges are in one of the colors,
and one wedge in each of the other two colors. The two wedges of the
same color might be adjacent to each other or opposite. In either case, we have three choices for the color of the two wedges that are
the same, after which the colors of the other two wedges are forced.
So that's 3 colorings with two adjacent wedges the same color:


 And 3 colorings with two opposite wedges the same color:
And 3 colorings with two opposite wedges the same color:
So that's a total of 21. Unless I left some out. Actually I
did leave some
out, just to see if you were paying attention. There are really 24,
not 21. (You
can see the full set, including the three I left out.) What a
pain in the ass. Now let's do the same count for four colors. Whee,
fun!
But there is a better way. It's called the Pólya-Burnside counting lemma. (It's named after George Pólya and William Burnside. The full Pólya counting theorem is more complex and more powerful. The limited version in this article is more often known just as the Burnside lemma. But Burnside doesn't deserve the credit; it was known much earlier to other mathematicians.)
Let's take a slightly simpler example, and count the squares that have two colors, say blue and black only. We can easily pick them out from the list above:
 |
 |
 |
 |
 |
 |
Remember way back at the beginning where we decided that
 and
and
 and
and
 were the same because differences
of a simple rotation didn't count? Well, the first thing you do is
you make a list of all the kinds of motions that "don't
count". In this case, there are four motions:
were the same because differences
of a simple rotation didn't count? Well, the first thing you do is
you make a list of all the kinds of motions that "don't
count". In this case, there are four motions:
- Rotation clockwise by 90°
- Rotation by 180°
- Rotation counterclockwise by 90°
- Rotation by 0°
Now we temporarily forget about the complication that says that some
squares are essentially the same as other squares. All squares are
now different.  and
and  are now different because they are
colored differently. This is a much simpler point of view. There are
clearly 24 such squares, shown below:
are now different because they are
colored differently. This is a much simpler point of view. There are
clearly 24 such squares, shown below:
 |



 |





 |



 |
 |
Which of these 16 squares is left unchanged by motion #3, a counterclockwise quarter-turn? All four wedges would have to be the same color. Of the 16 possible colorings, only the all-black and all-blue ones are left entirely unchanged by motion #3. Motion #1, the clockwise quarter-turn, works the same way; only the 2 solid-colored squares are left unchanged.



 4 colorings are left unchanged by
a 180° rotation. The top wedge and the bottom wedges switch
places, so they must be the same color, and the left and right wedges
change places, so they must be the same color. But the top-and-bottom
wedges need not be the same color as the left-and-right wedges. We
have two independent choices of how to color a square so that it will
remain unchanged by a 180° rotation, and there are 22 =
4 colorings that are left unchanged by a 180° rotation. These are
shown at right.
4 colorings are left unchanged by
a 180° rotation. The top wedge and the bottom wedges switch
places, so they must be the same color, and the left and right wedges
change places, so they must be the same color. But the top-and-bottom
wedges need not be the same color as the left-and-right wedges. We
have two independent choices of how to color a square so that it will
remain unchanged by a 180° rotation, and there are 22 =
4 colorings that are left unchanged by a 180° rotation. These are
shown at right.
So we have counted the number of squares left unchanged by each motion:
| Motion | # squares unchanged |
typical example | |
|---|---|---|---|
| 1 | Clockwise quarter turn | 2 |  |
| 2 | Half turn | 4 |  |
| 3 | Counterclockwise quarter turn | 2 |  |
| 4 | No motion | 16 |  |
Next we take the counts for each motion, add them up, and average them. That's 2 + 4 + 2 + 16 = 24, and divide by 4 motions, the average is 6.
So now what? Oh, now we're done. The average is the answer. 6, remember? There are 6 distinguishable squares. And our peculiar calculation gave us 6. Waaa! Surely that is a coincidence? No, it's not a coincidence; that is why we have the theorem.
Let's try that again with three colors, which gave us so much trouble before. We hope it will say 24. There are now 34 basic squares to consider.
For motions #1 and #3, only completely solid colorings are left unchanged, and there are 3 solid colorings, one in each color. For motion 2, there are 32 colorings that are left unchanged, because we can color the top-and-bottom wedges in any color and then the left-and-right wedges in any color, so that's 3·3 = 9. And of course all 34 colorings are left unchanged by motion #4, because it does nothing.
| Motion | # squares unchanged |
typical example | |
|---|---|---|---|
| 1 | Clockwise quarter turn | 3 |  |
| 2 | Half turn | 9 |  |
| 3 | Counterclockwise quarter turn | 3 |  |
| 4 | No motion | 81 |  |
The average is (3 + 9 + 3 + 81) / 4 = 96 / 4 = 24. Which is right. Hey, how about that?
That was so easy, let's skip doing four colors and jump right to the general case of N colors:
| Motion | # squares unchanged |
typical example | |
|---|---|---|---|
| 1 | Clockwise quarter turn | N |  |
| 2 | Half turn | N2 |  |
| 3 | Counterclockwise quarter turn | N |  |
| 4 | No motion | N4 |  |
Add them up and divide by 4, and you get (N4 + N2 + 2N)/4. So if we allow four colors, we should expect to have 70 different squares. I'm glad we didn't try to count them by hand!
(Digression: Since the number of different colorings must be an integer, this furnishes a proof that N4 + N2 + 2N is always a multiple of 4. It's a pretty heavy proof if it were what we were really after, but as a freebie it's not too bad.)
One important thing to notice is that each motion of the square divides the wedges into groups called orbits, which are groups of wedges that change places only with other wedges in the same orbit. For example, the 180° rotation divided the wedges into two orbits of two wedges each: the top and bottom wedges changed places with each other, so they were in one orbit; the left and right wedges changed places, so they were in another orbit. The "do nothing" motion induces four orbits; each wedge is in its own private orbit. Motions 1 and 3 put all the wedges into a single orbit; there are no smaller private cliques.
For a motion to leave a square unchanged, all the wedges in each orbit must be the same color. For example, the 180° rotation leaves a square unchanged only when the two wedges in the top-bottom orbit are colored the same and the two wedges in the left-right orbit are colored the same. Wedges in different orbits can be different colors, but wedges in the same orbit must be the same color.
Suppose a motion divides the wedges into k orbits. Since there are Nk ways to color the orbits (N colors for each of the k orbits), there are Nk colorings that are left unchanged by the motion.
Let's try a slightly trickier problem. Let's go back to using 3
colors, and see what happens if we are allowed to flip over the
squares, so that
 and
and  are now considered the same.
are now considered the same.
In addition to the four rotary motions we had before, there are now four new kinds of motions that don't count:
| Motion | # squares unchanged |
typical example | |
|---|---|---|---|
| 5 | Northwest-southeast diagonal reflection | 9 |  |
| 6 | Northeast-southwest diagonal reflection | 9 |  |
| 7 | Horizontal reflection | 27 |  |
| 8 | Vertical reflection | 27 |  |
The diagonal reflections each have two orbits, and so leave 9 of the
81 squares unchanged. The horizontal and vertical reflections each
have three orbits, and so leave 27 of the 81 squares unchanged. So
the eight magic numbers are 3, 3, 9, and 81, from before, and now the
numbers for the reflections, 9, 9, 27, and 27. The average of these
eight numbers is 168/8 = 21. This is correct. It's almost the
same as the 24 we got earlier, but instead of allowing both
representatives of each pair like 
 , we allow only one, since they are
now considered "the same". There are three such pairs, so this
reduces our count by exactly 3.
, we allow only one, since they are
now considered "the same". There are three such pairs, so this
reduces our count by exactly 3.
Okay, enough squares. Lets do, um, cubes! How many different ways are there to color the faces of a cube with N colors? Well, this is a pain in the ass even with the Pólya-Burnside lemma, because there are 24 motions of the cube. (48 if you allow reflections, but we won't.) But it's less of a pain in the ass than if one tried to do it by hand.
This is a pain for two reasons. First, you have to figure out what the 24 motions of the cube are. Once you know that, you then have to calculate the number of orbits of each one. If you are a combinatorics expert, you have already solved the first part and committed the solution to memory. The rest of the world might have to track down someone who has already done this—but that is not as hard as it sounds, since here I am, ready to assist.
Fortunately the 24 motions of the cube are not all entirely different from each other. They are of only four or five types:
- Rotations around an axis that goes through one corner to the
opposite corner.
There are 4 such pairs of vertices, and for each pair, you can turn the cube either 120° clockwise or 120° counterclockwise. That makes 8 rotations of this type in total. Each of these motions has 2 orbits. For the example axis above, one orbit contains the top, front, and left faces and the other contains the back, bottom, and right faces. So each of these 8 rotations leaves N2 colorings of the cube unchanged.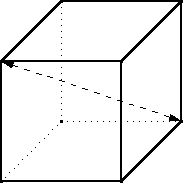
- Rotations by 180° around an axis that goes through the middle
of one edge of the cube and out the middle of the opposite edge.
There are 6 such pairs of edges, so 6 such rotations. Each rotation divides the six faces into three orbits of two faces each. The one above exchanges the front and bottom, top and back, and left and right faces; these three pairs are the three orbits. To be left unchanged by this rotation, the two faces in each orbit must be the same color. So N3 colorings of the cube are left fixed by each of these 6 rotations.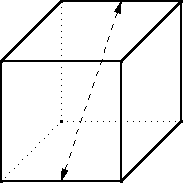
- Rotations around an axis that goes through the center
of a face and comes out the center of the opposite face.
There are three such axes. The rotation can be 90° clockwise, 90 ° counterclockwise, or 180°. The 90° rotations have three orbits. The one shown above puts the top face into an orbit by itself, the bottom face into another orbit, and the four faces around the middle into a third orbit. So six of these nine rotations leave N3 colorings unchanged.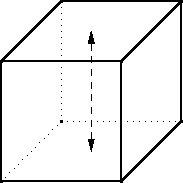
The 180° rotations have four orbits. A 180° rotation around the axis shown above puts the top and bottom faces into private orbits, as the 90° rotation did, but instead of putting the four middle faces into a single orbit, the front and back faces go in one orbit and the left and right into another. Since there are three axes, there are three motions of the cube that each leave N4 colorings unchanged.
- Finally, there's the "motion" that moves nothing. This motion
leaves every face in a separate orbit, and leaves all
N6 colorings unchanged.
- 8N2 from the vertex rotations
- 6N3 from the edge rotations
- 6N3 from the 90° face rotations
- 3N4 from the 180° face rotations
- N6 from the "do nothing" motion
Unfortunately, the Pólya-Burnside technique does not tell you what the ten colorings actually are; for that you have to do some more work. But at least the P-B lemma tells you when you have finished doing the work! If you set about to enumerate ways of painting the faces of the cube, and you end up with 9, you know you must have missed one. And it tells you how much toil to expect if you do try to work out the colorings. 10 is not so many, so let's give it a shot:
- 6 black and 0 white faces: one cube
- 5 black and 1 white face: one cube
- 4 black and 2 white faces: the white faces could be on opposite sides of the cube, or touching at an edge
- 3 black and 3 white faces: the white faces could include a pair of opposite faces and one face in between, or they could be the three faces that surround a single vertex.
- 2 black and 4 white faces: the black faces could be on opposite sides of the cube, or touching at an edge
- 1 black and 5 white faces: one cube
- 0 black and 6 white faces: one cube
Care to try it out? There are 4 ways to color the sides of a triangle with two colors, 10 ways if you use three colors, and N(N+1)(N+2)/6 if you use N colors.
There are 140 different ways to color a the
squares of a 3×3 square array, counting reflections as
different. If reflected colorings are not counted separately, there
are only 102 colorings. (This means that 38 of the colorings have
some reflective symmetry.) If the two colors are considered
interchangeable (so for example  and
and  are considered the same) there are
51 colorings.
are considered the same) there are
51 colorings.
You might think it is obvious that allowing an exchange of the two colors cuts the number of colorings in half from 102 to 51, but it is not so for 2×2 squares. There are 6 ways to color a 2×2 array, whether or not you count reflections as different; if you consider the two colors interchangeable then there are 4 colorings, not 3. Why the difference?
[Other articles in category /math] permanent link


