Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 15 Dec 2023
Recent addenda to articles 202311: Christenings in Tel Aviv
[ Content warning: extremly miscellaneous. ]
Wow, has it really been 7 months since I did one of these? Surprising, then, how few there are. (I omitted the ones that seemed trivial, and the ones that turned into complete articles.)
Back in 2018 I wrote an article that mentioned two alleys in Tel Aviv and quoted an article from Haaretz that said (in part):
A wealthy American businessman … had christened the streets without official permission… .
Every time I go back to read this I am brought up short by the word “christened”, in an article in Haaretz, in connection with the naming of streets in Tel Aviv. A christening is a specifically Christian baptism and naming ceremony. It's right there in the word!
Orwell's essay on Politics and the English Language got into my blood when I was quite young. Orwell's thesis is that language is being warped by the needs of propaganda. The world is full of people who (in one of Orwell's examples) want to slip the phrase “transfer of population” past you before you can realize that what it really means is “millions of peasants are robbed of their farms and sent trudging along the roads with no more than they can carry”. Writers are exposed to so much of this purposefully vague language that they learn to imitate it even when they are not trying to produce propaganda.
I don't mean to say that that's what the Haaretz writer was doing, intentionally or unintentionally. My claim is only that in this one case, because she wasn't thinking carefully about the meanings of the words she chose, she chose a hilariously inept one. Because of an early exposure to Orwell, that kind of mischoice jumps out at me.
This is hardly the most memorable example I have. The prize for that belongs to my mother, who once, when she was angry with me, called me a “selfish bastard”. This didn't have the effect she intended, because I was so distracted by the poor word choice.
Anyway, the Orwell thing is good. Brief and compelling. Full of good style advice. Check it out.
In 2019, I wrote an article about men who are the husbands of someone important and gave as examples the billionaire husband of Salma Hayek and the Nobel prizewinning husband of Marie Curie. I was not expecting that I would join this august club myself! In April, Slate ran an article about my wife in which I am referred to only as “Kim's husband”. (Judy Blume's husband is also mentioned, and having met him, I am proud to be in the same club.)
Also, just today I learned that Antoine Veil is interred in the Panthéon, but only because he was married to Simone Veil.
In an ancient article about G.H. Hardy I paraphrased from memory something Hardy had said about Ramanujan. In latter years Hardy's book become became available on the Internet, so I was able to append the exact quotation.
A few years ago I wrote a long article about eggplants in which I asked:
Wasn't there a classical Latin word for eggplant? If so, what was it? Didn't the Romans eat eggplant? How do you conquer the world without any eggplants?
I looked into this a bit and was amazed to discover that the Romans did not eat eggplant. I can only suppose that it was because they didn't have any, poor benighted savages. No wonder the Eastern Roman Empire lasted three times as long.
[Other articles in category /addenda] permanent link
Thu, 04 May 2023
Recent addenda to articles 202304: Inappropriate baseball team names and anagrams in Russian
In 2006 I wrote an article about sports team names, inspired by the amusing inappropriateness of the Utah Jazz. This month, I added:
I can't believe it took me this long to realize it, but the Los Angeles Lakers is just as strange a mismatch as the Utah Jazz. There are no lakes near Los Angeles. That name itself tells you what happened: the team was originally located in Minneapolis
I missed it when it came out, but in 2017 there was a short article in LanguageHat about my article about finding the best anagram in English. The article doesn't say anything new, but the comments are fun. In particular, January First-of-May presents their favorite Russian anagrams:
- австралопитек (/avstralopitek/, “Australopithecus”)
- ватерполистка (/vaterpolistka/. ”Female water-polo player”)
I will have more to say about this in a couple of days.
Eric Roode pointed out that my animation of cubic Taylor approximations to !!\sin x!! moves like the robot from Lost in Space.
[Other articles in category /addenda] permanent link
Sun, 02 Apr 2023
Recent addenda to articles 202303
I added some notes to the article about mutating consonants in Spanish, about the Spanish word llevar and its connection with Levant, Catalan llevant, the east, the orient, and Latin orior.
I unexpectedly got to use my weird divisibility trick a second time.
John Wiersba informed me that the auction game I described is called “Goofspiel”.
I added a note to my article about spires of the Sagrada Família that mentions that the number twelve (of disciples) symbolizes perfection and is the number of stars in the flag of the European Union.
Lukas Epple wrote to point out that back in 2006 I cited the wrong section for the proof of !!1+1=2!! from the Principia Mathematica. This inspired me to hunt up the actual theorem. My article about this only discussed the precursor theorem ∗54.3. Here's what the !!1+1=2!! proof looks like:

[Other articles in category /addenda] permanent link
Thu, 23 Mar 2023
Addenda to recent articles 202212-202302
I made several additions to articles of the last few months that might be interesting.
I wrote a long article about an unsorted menu in SAP Concur in which I said:
I don't know what Concur's software development and release process is like, but somehow it had a complete top-to-bottom failure of quality control and let this shit out the door.
I would love to know how this happened. I said a while back:
Assume that bad technical decisions are made rationally, for reasons that are not apparent.
I think this might be a useful counterexample.
A reader, who had formerly worked for SAP, provided a speculative explanation which, while it might not be correct, was plausible enough for me to admit that, had I been in the same situation, I might have let the same shit out the door for the same reason. Check it out, it's a great example.
My wife Lorrie suggested that a good emoji to represent Andrew Jackson would be a pigeon. Unfortunately, although there are a dozen different kinds of bird emoji, plus eggs, nests, and including several chickens, there are no pigeons!
My article about the Dutch word kwade was completely broken and will have to be done over again. In December promised an extensive correction “next year”. It is now next year, but I I have not yet written it.
In connection with Rosneft, a discussion of Japanese words for raw petroleum, and whether ナフサ /nafusa/ means that (as Wiktionary claims) or whether it just means ‘naphtha’.
Long ago I observed that in two-person comedy teams, the straight man is usually named before the comedian. I recently realized that Tom and Dick Smothers are a counterexample.
My article about strategies for dealing with assholes on the Internet left out a good one: If you are tempted to end a sentence with something like “you dumbass”, just leave it implicit.
Articles that I started but didn't publish (yet). Based on historical performance, we can expect maybe half of these to see the light of day. My bet would be on numbers 1, 3, and maybe 4 or 5.
How does the assignment of evangelists and apostles to spires on la Sagrada Família work, when (a) the two sets overlap, but only partially, and (b) Judas Iscariot was an apostle? I think I figured this out. (Short answers: (a) Ignore it and (b) Matthias.
[Addendum 20230327: I did this. ]
Something that was supposed to be about the Singularity, but instead turned into a description of my game of playing 21st-century tour guide to Benjamin Franklin.
Why does Unicode recognize five skin-tone modifiers for emoji, when the original document that they reference defined six skin tones? I put in a lot of research effort here and came up with nada.
Notes about the Korean letter ‘ㅓ’ and why it is Romanized as ‘eo’.
An explanation of an interesting sort of mathematical confusion, but I didn't get far enough into the article and now I don't remember what I was planning to say or even what I thought the confusion was.
Also a reader wrote to remind me of my ancient promise to write about why the aliens will play go and not chess, and I sent him paragraphs and paragraphs of stuff about this and related matters like alien card games, but didn't put it into the blog. What is wrong with me?
[Addendum 20230402: I did this. ]
By the way, if anyone happens to know a gender-neutral term for “straight man”, I'm still stumped.
[ Addendum 20230324: Thomas Maccoll suggests “foil”. ]
[Other articles in category /addenda] permanent link
Sun, 04 Dec 2022
Addenda to recent articles 202211
I revised my chart of Haskell's numbers to include a few missing things, uncrossed some of the arrows, and added an explicit public domain notice,
The article contained a typo, a section titled “Shuff that don't work so good”. I decided this was a surprise gift from the Gods of Dada, and left it uncorrected.
My very old article about nonstandard adjectives now points out that the standard term for “nonstandard adjective” is “privative adjective”.
Similar to my suggested emoji for U.S. presidents, a Twitter user suggested emoji for UK prime ministers, some of which I even understand.
I added some discussion of why I did not use a cat emoji for President Garfield. A reader called January First-of-May suggested a tulip for Dutch-American Martin Van Buren, which I gratefully added.
In my article on adaptive group testing, Sam Dorfman and I wondered if there wasn't earlier prior art in the form of coin-weighing puzzles. M. January brought to my attention that none is known! The earliest known coin-weighing puzzles date back only to 1945. See the article for more details.
Some time ago I wrote an article on “What was wrong with SML?”. I said “My sense is that SML is moribund” but added a note back in April when a reader (predictably) wrote in to correct me.
However, evidence in favor of my view appeared last month when the Haskell Weekly News ran their annual survey, which included the question “Which programming languages other than Haskell are you fluent in?”, and SML was not among the possible choices. An oversight, perhaps, but a rather probative one.
I wondered if my earlier article was the only one on the Web to include the phrase “wombat coprolites”. It wasn't.
[Other articles in category /addenda] permanent link
Tue, 08 Nov 2022
Addenda to recent articles 202210
I haven't done one of these in a while. And there have been addenda. I thought hey, what if I ask Git to give me a list of commits from October that contain the word ‘Addendum’. And what do you know, that worked pretty well. So maybe addenda summaries will become a regular thing again, if I don't forget by next month.
Most of the addenda resulted in separate followup articles, which I assume you will already have seen. ([1] [2] [3]) I will not mention this sort of addendum in future summaries.
In my discussion of lazy search in Haskell I had a few versions that used
do-notation in the list monad, but eventually abandoned it n favor of explicitconcatMap. For example:s nodes = nodes ++ (s $ concatMap childrenOf nodes)I went back to see what this would look like with
donotation:s nodes = (nodes ++) . s $ do n <- nodes childrenOf nMeh.
Regarding the origin of the family name ‘Hooker’, I rejected Wiktionary's suggestion that it was an occupational name for a maker of hooks, and speculated that it might be a fisherman. I am still trying to figure this out. I asked about it on English Language Stack Exchange but I have not seen anything really persuasive yet. One of the answers suggests that it is a maker of hooks, spelled hocere in earlier times.
(I had been picturing wrought-iron hooks for hanging things, and wondered why the occupational term for a maker of these wasn't “Smith”. But the hooks are supposedly clothes-fastening hooks, made of bone or some similar finely-workable material. )
The OED has no record of hocere, so I've asked for access to the Dictionary of Old English Corpus of the Bodleian library. This is supposedly available to anyone for noncommercial use, but it has been eight days and they have not yet answered my request.
I will post an update, if I have anything to update.
[Other articles in category /addenda] permanent link
Wed, 08 Jul 2020
Addendum to “Weirdos during the Depression”
[ Previously ]
Ran Prieur had a take on this that I thought was insightful:
I would frame it like this: If you break rules that other people are following, you have to pretend to be unhappy, or they'll get really mad, because they don't want to face the grief that they could have been breaking the rules themselves all this time.
[Other articles in category /addenda] permanent link
Fri, 04 Oct 2019
Addenda to recent articles 201910
Several people have written in with helpful remarks about recent posts:
Regarding online tracking of legislation:
- Ed Davies directed my attention to www.legislation.gov.uk, an official organ of the British government, which says:
The aim is to publish legislation on this site simultaneously, or at least within 24 hours, of its publication in printed form.
M. Davies is impressed. So am I. Here is the European Union (Withdrawal) Act 2018.
Nik Clayton showed me the @unitedstates project, whcih among other things has a program that attempts to parse the United States Code and produce a tree-structured output.
Twitter user
@sunk818pointed out How I changed the law with a GitHub pull request. The title oversells what actually happened: the codified law contained a minor technical error, which could be corrected without requiring any actual legislation. But the takeaway is that the District of Columbia officially publishes its law to a Github repo.
This then led me to Standardizing the World’s Legislative Information — One hackathon at a time on the LII's VOXPOPULII blog.
(Reminder to readers: I do not normally read Twitter, and it is not a reliable way to contact me.)
Regarding the mysteriously wide letter ‘O’ on the Yeadon firehouse. I had I had guessed that it was not in the same family as the others, perhaps because the original one had been damaged. I asked Jonathan Hoefler, a noted font expert; he agreed.
But one reader, Steve Nicholson, pointed out that it is quite common, in Art Deco fonts, for the ‘O’ to be circular even when that makes it much wider than the other letters. He provided ten examples, such as Haute Corniche.
I suggested this to M. Hoefler, but he rejected the theory decisively:
True; it's a Deco mannerism to have 'modulated capitals'… . But this isn't a deco font, or a deco building, and in any case it would have been HIGHLY unlikely for a municipal sign shop to spec something like this for any purpose, let alone a firehouse. It's a wrong sort O, probably installed from the outset.
(The letter spacing suggests that this is the original ‘O’.)
Several people wrote to me about the problem of taking half a pill every day, in which I overlooked that the solution was simply the harmonic numbers.
Robin Houston linked to this YouTube video, “the frog problem”, which has the same solution, and observed that the two problems are isomorphic, proceeding essentially as Jonathan Dushoff does below.
Shreevatsa R. wrote a long blog article detailing their thoughts about the solution. I have not yet read the whole thing carefully but knowing M. Shreevatsa, it is well worth reading. M. Shreevatsa concludes, as I did, that a Markov chain approach is unlikely to be fruitful, but then finds an interesting approach to the problem using probability generating functions, and then another reformulating it as a balls-in-bins problem.
Jonathan Dushoff sent me a very clear and elegant solution and kindly gave me permission to publish it here:
The first key to my solution is the fact that you can add expectations even when variables are not independent.
In this case, that means that each time we break a pill we can calculate the probability that the half pill we produce will "survive" to be counted at the endpoint. That's the same as the expectation of the number of half-pills that pill will contribute to the final total. We can then just add these expectations to get the answer! A little counter-intuitive, but absolutely solid.
The next key is symmetry. If I break a half pill and there are !!j!! whole pills left, the only question for that half pill is the relative order in which I pick those !!j+1!! objects. In particular, any other half pills that exist or might be generated can be ignored for the purpose of this part of the question. By symmetry, any of these !!j+1!! objects is equally likely to be last, so the survival probability is !!\frac1{j+1}!!.
If I start with !!n!! pills and break one, I have !!n-1!! whole pills left, so the probability of that pill surviving is !!\frac1n!!. Going through to the end we get the answer:
$$\frac1n + \frac1{n-1} + \ldots + 1.$$
I have gotten feedback from several people about my Haskell type constructor clutter, which I will write up separately, probably, once I digest it.
Thanks to everyone who wrote in, even people I forgot to mention above, and even to the Twitter person who didn't actually write in.
[Other articles in category /addenda] permanent link
Wed, 02 May 2018
Addenda to recent articles 201804
Andrew Rodland and Adam Vartanian explained ramp metering. Here's M. Rodland's explanation:
ramp metering is the practice of installing signals on freeway onramps that only allow one car every few seconds, so that cars enter the freeway at evenly-spaced intervals instead of in bunches and don't cause as many problems merging.
He added that it was widely used in California. McCain is headquartered in California, and mentions frequently on their web site that their equipment conforms to Caltrans standards.
M. Vartanian and Richard Soderberg also suggested an explanation for why the traffic control system might also control sprinklers and pumps. M. Soderberg says:
DOTs in California and presumably elsewhere often have a need for erosion control on the steep inclines of earth surrounding their highway ramps. So any time you see a 45-degree incline covered in greenery, chances are it has a sprinkler system attached and carefully maintained by the DOT. Those same sprinklers are often within a few feet of the ramp's metering lights…
That makes perfect sense! I had been imagining fire sprinklers, and then I was puzzled: why would you need fire sprinklers at an intersection?
Several readers suggested explanations for why soldier fly larvae are more expensive than pork chops. I rejected several explanations:
Hogs are kept in poor and inhumane conditions (often true, but their accommodations must still be much more expensive than the flies’)
Hog farmers are exempted from paying for the negative externalities of their occupation such as environmental degradation and antibiotic resistance (often true, but the fly farmers cannot be paying that much to offset externalities)
Slaughterhouse waste and rotten fruit are more expensive than the corn and soy on which hogs are fed (I think slaughterhouse waste and waste fruit are available essentially free to anyone who wants to haul them away)
The drying process is difficult and expensive (but the listed price for undried maggots is twice as high)
But I find Marcel Fourné's suggestion much more plausible: the pork price is artificially depressed by enormous government subsidies.
I started looking into the numbers on this, and got completely sidetracked on something only peripherally related:
According to the USDA Census of Agriculture for 2012, in 2012 U.S. farms reported an inventory of 66 million pigs and hogs, and sales of 193 million pigs and hogs. (Table 20, page 22.)
When I first saw this, I thought I must be misunderstanding the numbers. I said to myself:
!!\frac{193}{66}\approx 3!!, so the inventory must be turning over three times a year. But that means that the average hog goes to market when it is four months old. That can't be right.
Of course it isn't right, it isn't even close, it's complete nonsense. I wrote up my mistake but did not publish it, and while I was doing that I forgot to finish working on the subsidy numbers.
James Kushner directed my attention to the MUTCD news feed and in particular this amusing item:
the FHWA issued Official Interpretation 4(09)-64 to clarify that the flash rate for traffic control signals and beacons is a single repetitive flash rate of approximately once per second, and that a combination of faster and slower flash rates that result in 50 to 60 flashes per minute is not compliant…
James writes:
I imagined a beacon that flashed once every ten seconds; after five such iterations, there was one iteration where the beacon would flash fifty times in a second. "But it flashes 55 times every minute, so, you know, it, uh, conforms to the standard..."
But the Official Interpretation also says
You asked whether the FHWA would be willing to consider experimentation with alternative flash rates for warning beacons. Any requests for experimentation would be evaluated on their merits and would be addressed separately from this official ruling.
so there is still hope for James’ scheme.
Two readers suggested musical jokes. Jordan Fultz asks:
Q: How does Lady Gaga like her steak?
A: Raw, raw, raw-raw-raw!(This is Bad Romance)
And betaveros asks:
Q. What kind of overalls does Mario wear?
A. Denim denim denim.(This is the Super Mario Bros. Underworld Theme)
I feel like we might be hitting the bottom of the barrel.
Thanks to all readers who wrote to me, and also to all readers who did not write to me.
[Other articles in category /addenda] permanent link
Sat, 24 Mar 2018
Addenda to recent articles 201803
It's been a while since we had one of these. But gosh, people have sent me quite a lot of really interesting mail lately.
I related my childhood disappointment at the limited number of cool coordinate systems. Norman Yarvin directed me to prolate spheroidal coordinates which are themselves a three-dimensional version of elliptic coordinates which are a system of exactly the sort I escribed in the article, this time parametrized by a family of ellipses and a family of hyperbolas, all of which share the same two foci; this article links in turn to parabolic coordinates in which the two families are curves are up-facing and down-facing parabolas that all share a focus. (Hmm, this seems like a special case of the ellipses, where one focus goes to infinity.)
Walt Mankowski also referred me to the Smith chart, shown at right, which is definitely relevant. It is a sort of nomogram, and parametrizes certain points by their position on circles from two families
$$\begin{align} F_1(c): && (x- c)^2 & + y^2 & =c^2 \\ F_2(c): && x^2 & + (y- c)^2 & =c^2 \\ \end{align} $$
Electrical engineers use this for some sort of electrical engineer calculation. They use the letter !!j!! instead of !!i!! for the imaginary unit because they had already used !!i!! to stand for electrical current, which is totally reasonable because “electrical current” does after all start with the letter !!i!!. (In French! The French word is courant. Now do you understand? Stop asking questions!)
Regarding what part of the body Skaði was looking at when the Norse text says fótr, which is probably something like the foot, Alexander Gurney and Brent Yorgey reminded me that Biblical Hebrew often uses the foot as a euphemism for the genitals. One example that comes immediately to mind is important in the book of Ruth:
And when Boaz had eaten and drunk, and his heart was merry, he went to lie down at the end of the heap of corn: and she came softly, and uncovered his feet, and laid her down. (Ruth 3:7)
M. Gurney suggested Isaiah 6:2. (“Above him were seraphim, each with six wings: With two wings they covered their faces, with two they covered their feet, and with two they were flying.”) I think Ezekiel 16:25 is also of this type.
I mentioned to Brent that I don't think Skaði was looking at the Æsir's genitals, because it wouldn't fit the tone of the story.
Alexander Gurney sent me a lot of other interesting material. I had translated the Old Icelandic hreðjar as “scrotum”, following Zoëga. But M. Gurney pointed out that the modern Icelandic for “radish” is hreðka. Coincidence? Or was hreðjar a euphemism even then? Zoëga doesn't mention it, but he doesn't say what word was used for “radish”, so I don't know.
He also pointed me to Parts of the body in older Germanic and Scandinavian by Torild Washington Arnoldson. As in English, there are many words for the scrotum and testicles; some related to bags, some to balls, etc. Arnoldson does mention hreðjar in the section about words that are bag-derived but doesn't say why. Still if Arnoldson is right it is not about radishes.
I should add that the Skáldskaparmál itself has a section about parts of the body listing suitable words and phrases for use by skálds:
Hönd, fótr.
… Á fæti heitir lær, kné, kálfi, bein, leggr, rist, jarki, il, tá. …
(… The parts of the legs are called thigh, knee, calf, lower leg, upper leg, instep, arch, sole, toe … [ Brodeur ])
I think Brodeur's phrase “of the legs” here is an interpolation. Then he glosses lær as “thigh”, kné as “knee”, kálfi as “calf”, and so on. This passage is what I was thinking of when I said
Many of the words seem to match, which is sometimes helpful but also can be misleading, because many don't.
I could disappear down this rabbit hole for a long time.
Regarding mental estimation of the number of primes less than 1,000, which the Prime Number Theorem says is approximately !!\frac{1000}{\ln 1000}!!, several people pointed out that if I had memorized !!\ln 10\approx 2.3!! then I would have had that there are around !!\frac{1000}{3·2.3}!! primes under 1,000.
Now it happens that I do have memorized !!\ln 10\approx 2.3!! and although I didn't happen come up with it while driving that day, I did come up with it a couple of days later in the parking lot of a Wawa where I stopped to get coffee before my piano lesson. The next step, if you are in a parking lot, is to approximate the division as !!\frac{1000}{6.9} \approx \frac{1000}7 = 142.857\ldots!! (because you have !!\frac17=0.\overline{142857}!! memorized, don't you?) and that gives you an estimate of around 145 primes.
Which, perhaps surprisingly, is worse than what I did the first time around; it is 14% too low instead of 8% too high. (The right answer is 168 and my original estimate was 182.)
The explanation is that for small !!n!!, the approximation !!\pi(N)\sim\frac{N}{\ln N}!! is not actually very good, and I think the interpolation I did, using actual low-value counts, takes better account of the low-value error.
[Other articles in category /addenda] permanent link
Mon, 11 Jul 2016
Addenda to recent articles 201607
Here are some notes on posts from the last couple of months that I couldn't find better places for.
I wrote a long article about tracking down a system bug. At some point I determined that the problem was related to Perl, and asked Frew Schmidt for advice. He wrote up the details of his own investigation, which pick up where mine ended. Check it out. I 100% endorse his lament about
ltrace.There was a Hacker News discussion about that article. One participant asked a very pertinent question:
I read this, but seemed to skip over the part where he explains why this changed suddenly, when the behavior was documented?
What changed to make the perl become capable whereas previously it lacked the low port capability?
So far, we don't know! Frew told me recently that he thinks the
TMPDIR-losing has been going on for months and that whatever precipitated my problem is something else.In my article on the Greek clock, I guessed a method for calculating the (approximate) maximum length of the day from the latitude: $$ A = 360 \text{ min}\cdot(1-\cos L).$$
Sean Santos of UCAR points out that this is inaccurate close to the poles. For places like Philadelphia (40° latitude) it is pretty close, but it fails completely for locations north of the Arctic Circle. M. Santos advises instead:
$$ A = 360 \text{ min}\cdot \frac{2}{\pi}\cdot \sin^{-1}(\tan L\cdot \tan\epsilon)$$
where ε is the axial tilt of the Earth, approximately 23.4°. Observe that when !!L!! is above the Arctic Circle (or below the Antarctic) we have !!\tan L \cdot \tan \epsilon > 1!! (because !!\frac1{\tan x} = \tan(90^\circ - x)!!) so the arcsine is undefined, and we get no answer.
[Other articles in category /addenda] permanent link
Wed, 07 Jan 2009
Addenda to recent articles 200811
- Earlier I discussed an interesting technique for flag variables in
Bourne shell programs. I did a little followup research.
I looked into several books on Unix shell programs, including:
- Linux Shell Scripting with Bash (Burtch)
- Unix Shell Programming 3ed. (Kochan and Wood)
- Mastering UNIX Shell Scripting (Michael)
But two readers sent me puzzled emails, to tell me that they had been using the true/false technique for years are were surprised that I found it surprising. Brooks Moses says that at his company they have a huge build system in Bourne shell, and they are trying to revise the boolean tests to the style I proposed. And Tom Limoncelli reports that code by Bill Cheswick and Hal Burch (Bell Labs guys) often use this technique. Tom speculates that it's common among the old farts from Bell Labs. Also, Adrián Pérez writes that he has known about this for years.
It's tempting to write to Kernighan to ask about it, but so far I have been able to resist.
- My first meta-addendum: In October's
addenda I summarized the results of a paper of Coquand,
Hancock, and Setzer about the inductive strength of various theories.
This summary was utterly wrong. Thanks to Charles Stewart and to
Peter Hancock for correcting me.
The topic was one I had hoped to get into anyway, so I may discuss it at more length later on.
[Other articles in category /addenda] permanent link
Thu, 06 Nov 2008
Addenda to recent articles 200810
- I discussed representing
ordinal numbers in the computer and expressed doubt that the
following representation truly captured the awesome complexity of the
ordinals:
data Nat = Z | S Nat data Ordinal = Zero | Succ Ordinal | Lim (Nat → Ordinal)In particular, I asked "What about Ω, the first uncountable ordinal?" Several readers pointed out that the answer to this is quite obvious: Suppose S is some countable sequence of (countable) ordinals. Then the limit of the sequence is a countable union of countable sets, and so is countable, and so is not Ω. Whoops! At least my intuition was in the right direction.Several people helpfully pointed out that the notion I was looking for here is the "cofinality" of the ordinal, which I had not heard of before. Cofinality is fairly simple. Consider some ordered set S. Say that an element b is an "upper bound" for an element a if a ≤ b. A subset of S is cofinal if it contains an upper bound for every element of S. The cofinality of S is the minimum cardinality of its cofinal subsets, or, what is pretty much the same thing, the minimum order type of its cofinal subsets.
So, for example, the cofinality of ω is ℵ0, or, in the language of order types, ω. But the cofinality of ω + 1 is only 1 (because the subset {ω} is cofinal), as is the cofinality of any successor ordinal. My question, phrased in terms of cofinality, is simply whether any ordinal has uncountable cofinality. As we saw, Ω certainly does.
But some uncountable ordinals have countable cofinality. For example, let ωn be the smallest ordinal with cardinality ℵn for each n. In particular, ω0 = ω, and ω1 = Ω. Then ωω is uncountable, but has cofinality ω, since it contains a countable cofinal subset {ω0, ω1, ω2, ...}. This is the kind of bullshit that set theorists use to occupy their time.
A couple of readers brought up George Boolos, who is disturbed by extremely large sets in something of the same way I am. Robin Houston asked me to consider the ordinal number which is the least fixed point of the ℵ operation, that is, the smallest ordinal number κ such that |κ| = ℵκ. Another way to define this is as the limit of the sequence 0, ℵ0 ℵℵ0, ... . M. Houston describes κ as "large enough to be utterly mind-boggling, but not so huge as to defy comprehension altogether". I agree with the "utterly mind-boggling" part, anyway. And yet it has countable cofinality, as witnessed by the limiting sequence I just gave.
M. Houston says that Boolos uses κ as an example of a set that is so big that he cannot agree that it really exists. Set theory says that it does exist, but somewhere at or before that point, Boolos and set theory part ways. M. Houston says that a relevant essay, "Must we believe in set theory?" appears in Logic, Logic, and Logic. I'll have to check it out.
My own discomfort with uncountable sets is probably less nuanced, and certainly less well thought through. This is why I presented it as a fantasy, rather than as a claim or an argument. Just the sort of thing for a future blog post, although I suspect that I don't have anything to say about it that hasn't been said before, more than once.
Finally, a pseudonymous Reddit user brought up a paper of Coquand, Hancock, and Setzer that discusses just which ordinals are representable by the type defined above. The answer turns out to be all the ordinals less than ωω. But in Martin-Löf's type theory (about which more this month, I hope) you can actually represent up to ε0. The paper is Ordinals in Type Theory and is linked from here.
Thanks to Charles Stewart, Robin Houston, Luke Palmer, Simon Tatham, Tim McKenzie, János Krámar, Vedran Čačić, and Reddit user "apfelmus" for discussing this with me.
[ Meta-addendum 20081130: My summary of Coquand, Hancock, and Setzer's results was utterly wrong. Thanks to Charles Stewart and Peter Hancock (one of the authors) for pointing this out to me. ]
- Regarding homophones of
numeral words, several readers pointed out that in non-rhotic
dialects, "four" already has four homophones, including "faw" and
"faugh". To which I, as a smug rhotician, reply "feh".
One reader wondered what should be done about homophones of "infinity", while another observed that a start has already been made on "googol". These are just the sort of issues my proposed Institute is needed to investigate.
One clever reader pointed out that "half" has the homophone "have". Except that it's not really a homophone. Which is just right!
[Other articles in category /addenda] permanent link
Sun, 01 Jun 2008
Addenda to recent articles 200805
- Regarding the bicameral mind
theory put forth in Julian Jaynes' book The Origin of
Consciousness in the breakdown of the Bicameral Mind, Carl
Witty informs me that the story "Sour Note on Palayata", by James
Schmitz, features a race of bicameral aliens whose mentality is
astonishingly similar to the bicameral mentality postulated by Julian
Jaynes. M. Witty describes it as follows:
The story features a race of humanoid aliens with a "public" and a "private" mind. The "public" mind is fairly stupid, and handles all interactions with the real world; and the "private" mind is intelligent and psychic. The private mind communicates psychically with the private minds of other members of the race, but has only limited influence over the public mind; this influence manifests as visions and messages from God.
This would not be so remarkable, since Jaynes' theories have been widely taken up by some science fiction authors. For example, they appear in Neal Stephenson's novel Snow Crash, and even more prominently in his earlier novel The Big U, so much so that I wondered when reading it how anyone could understand it without having read Jaynes first. But Schmitz's story was published in 1956, twenty years before the publication of The Origin of Consciousness. - Also in connection with Jaynes: I characterized his theory as
"either a work of profound genius, or of profound crackpottery". I
should have mentioned that this
characterization was not lost on Jaynes himself. In his book, he
referred to his own theory as "preposterous".
- Many people wrote in with more commentary about my articles on
artificial Finnish
[1]
[2]:
- I had said that "[The one-letter word 'i'] appears in my sample
in connection with Sukselaisen
I hallitus, whatever that is". Several people
explained that this "I" is actually a Roman numeral 1, denoting the ordinal number
"first", and that Sukselaisen
I hallitus is the first government headed by V. J. Sukselaisen.
I had almost guessed this—I saw "Sukselaisen I" in the source material and guessed that the "I" was an ordinal, and supposed that "Sukselaisen I" was analogous to "Henry VIII" in English. But when my attempts to look up the putative King Sukselaisen I met with failure, and I discovered that "Sukselaisen I" never appeared without the trailing "hallitus", I decided that there must be more going on than I had supposed, as indeed there was. Thanks to everyone who explained this.
- Marko Heiskanen says that the (fictitious) word
yhdysvalmistämistammonit is "almost correct", at least up to the
nonsensical plural component "tammonit". The vowel harmony failure
can be explained away because compound words in Finnish do not respect the
vowel harmony rules anyway.
- Several people objected to my program's generation of the word
"klee": Jussi Heinonen said "Finnish has quite few words that begin with
two consonants", and Jarkko Hietaniemi said "No word-initial "kl":s
possible in native Finnish words". I checked, and my sample Finnish
input contains "klassisesta", which Jarkko explained was a loanword,
I suppose from Russian.
Had I used a larger input sample, oddities like "klassisesta" would have had less influence on the output.
- I acquired my input sample by selecting random articles from
Finnish Wikipedia, but my random sampling was rather unlucky, since it
included articles about Mikhail Baryshnikov (not Finnish), Dmitry Medvevev
(not Finnish), and Los Angeles (also not Finnish). As a result, the
input contained too many strange un-Finnish letters, like B, D, š, and
G, and so therefore did the output. I could have been more careful in
selecting the input data, but I didn't want to take the time.
Medvedev was also the cause of that contentious "klassisesta", since, according to Wikipedia, "Medvedev pitää klassisesta rock-musiikista". The Medvedev presidency is not even a month old and already he has this international incident to answer for. What catastrophes could be in the future?
- Another serious problem with my artificial Finnish is that the
words were too long; several people complained about this, and the
graph below shows the problem fairly clearly:
The x-axis is word length, and the y-axis is frequency, on a logarithmic scale, so that if 1/100 of the words have 17 letters, the graph will include the point (17, -2). The red line, "in.dat", traces the frequencies for my 6 kilobyte input sample, and the blue line, "pseudo.dat", the data for the 1000-character sample I published in the article. ("Ävivät mena osakeyhti...") The green line, "out.dat", is a similar trace for a 6 kb N=3 text I generated later. The long right tail is clearly visible. My sincere apologies to color-blind (and blind) readers.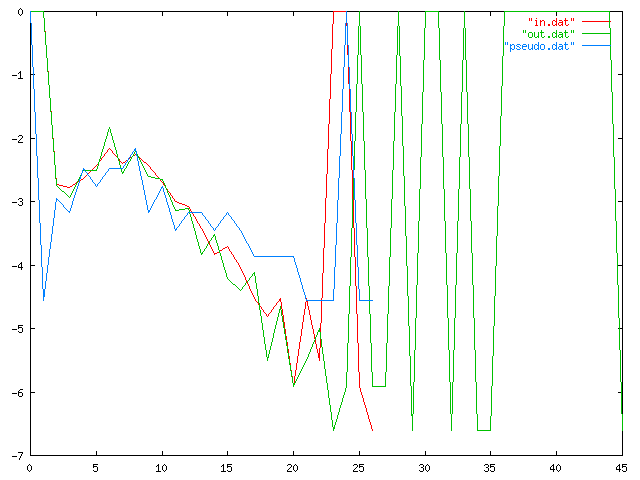
I am not sure exactly what happened here, but I can guess. The Markov process has a limited memory, 3 characters in this case, so in particular is has essentially no idea how long the words are that it is generating. This means that the word lengths that it generates should appear in roughly an exponential distribution, with the probability of a word of length N approximately equal to !!\lambda e^{-\lambda N} !!, where 1/λ is the mean word length.
But there is no particular reason why word lengths in Finnish (or any other language) should be exponentially distributed. Indeed, one would expect that the actual distribution would differ from exponential in several ways. For example, extremely short words are relatively uncommon compared with what the exponential distribution predicts. (In the King James Bible, the most common word length is 3, then 4, with 1 and 8 tied for a distant seventh place.) This will tend to push the mean rightwards, and so it will skew the Markov process' exponential distribution rightwards as well.
I can investigate the degree to which both real text and Markov process output approximate a theoretical exponential distribution, but not today. Perhaps later this month.
My thanks again to the many helpful Finnish speakers who wrote in on these and other matters, including Marko Heiskanen, Shae Erisson, Antti-Juhani Kaijanaho, Ari Loytynoja, Ilmari Vacklin, Jarkko Hietaniemi, Jussi Heinonen, Nuutti-Iivari Meriläinen, and any others I forgot to mention.
- I had said that "[The one-letter word 'i'] appears in my sample
in connection with Sukselaisen
I hallitus, whatever that is". Several people
explained that this "I" is actually a Roman numeral 1, denoting the ordinal number
"first", and that Sukselaisen
I hallitus is the first government headed by V. J. Sukselaisen.
- My explanation of Korean
vowel harmony rules in that article is substantively correct, but
my description of the three vowel groups was badly wrong. I have
apparently forgotten most of the tiny bit I once knew about Middle
Korean. For a correct description, see
the Wikipedia article
or
this
blog post. My thanks to the anonymous author of the blog post for
his correction.
- Regarding the
transitivity of related-by-blood-ness, Toth András told me about a
(true!) story from the life of Hungarian writer Karinthy
Frigyes:
Karinthy Frigyes got married two times, the Spanish flu epidemic took his first wife away. A son of his was born from his first marriage, then his second wife brought a boy from his previous husband, and a common child was born to them. The memory of this the reputed remark: "Aranka, your child and my child beats our child."
(The original Hungarian appears on this page, and the surprisingly intelligible translation was provided by M. Toth and the online translation service at webforditas.hu. Thank you, M. Toth.
- Chung-chieh Shan tells me that the missing
document-viewer feature that I described is available in recent
versions of xdvi. Tanaeem M. Moosa says
that it is also available in Adobe Reader
8.1.2.
[Other articles in category /addenda] permanent link
Fri, 01 Feb 2008
Addenda to recent articles 200801
Here are some notes on posts from the last
month that I couldn't find better places for.
- As a result of my research into the Harriet Tubman mural that was
demolished in 2002, I learned that it had been repainted last year
at 2950 Germantown Avenue.
- A number of readers, including some honest-to-God Italians, wrote
in with explanations of Boccaccio's term
milliantanove, which was variously translated as
"squillions" and "a thousand hundreds".
The "milli-" part suggests a thousand, as I guessed. And "-anta" is the suffix for multiples of ten, found in "quaranta" = "forty", akin to the "-nty" that survives in the word "twenty". And "nove" is "nine".
So if we wanted to essay a literal translation, we might try "thousanty-nine". Cormac Ó Cuilleanáin's choice of "squillions" looks quite apt.
- My article about clubbing
someone to death with a loaded Uzi neglected an essential
technical point. I repeatedly said that
for my $k (keys %h) { if ($k eq $j) { f($h{$k}) } }could be replaced with:
f($h{$j})But this is only true if $j actually appears in %h. An accurate translation is:
f($h{$j}) if exists $h{$j}I was, of course, aware of this. I left out discussion of this because I thought it would obscure my point to put it in, but I was wrong; the opposite was true.
I think my original point stands regardless, and I think that even programmers who are unaware of the existence of exists should feel a sense of unease when presented with (or after having written) the long version of the code.
An example of this error appeared on PerlMonks shortly after I wrote the article.
- Robin Houston provides another example of a
nonstandard adjective in mathematics: a quantum group is not
a group.
We then discussed the use of nonstandard adjectives in biology. I observed that there seemed to be a trend to eliminate them, as with "jellyfish" becoming "jelly" and "starfish" becoming "sea star". He pointed out that botanists use a hyphen to distinguish the standard from the nonstandard: a "white fir" is a fir, but a "Douglas-fir" is not a fir; an "Atlas cedar" is a cedar, but a "western redcedar" is not a cedar.
Several people wrote to discuss the use of "partial" versus "total", particularly when one or the other is implicit. Note that a total order is a special case of a partial order, which is itself a special case of an "order", but this usage is contrary to the way "partial" and "total" are used for functions: just "function" means a total function, not a partial function. And there are clear cases where "partial" is a standard adjective: partial fractions are fractions, partial derivatives are derivatives, and partial differential equations are differential equations.
- Steve Vinoski posted a very interesting solution to my
question about how to set Emacs file modes: he suggested
that I could define a replacement aput function.
- In my utterly useless review of Robert Graves' novel King
Jesus I said "But how many of you have read I,
Claudius and Suetonius? Hands? Anyone? Yeah, I didn't think
so." But then I got email from James Russell, who said he had indeed
read both, and that he knew just what I meant, and, as a
result, was going directly to the library to take out King
Jesus. And he read the article on Planet Haskell. Wow! I am
speechless with delight. Mr. Russell, I love you. From now on,
if anyone asks (as they sometimes do) who my target audience is, I
will say "It is James Russell."
- A number of people wrote in with examples of "theorems" that were
believed proved, and later turned out to be false. I am preparing a
longer article about this for next month. Here are some teasers:
- Cauchy
apparently "proved" that if a sum of continuous functions converges
pointwise, then the sum is also a continuous function, and this error
was widely believed for several years.
- I just learned of a major
screwup by none other than Kurt Gödel concerning the decidability
of a certain class of sentences of first-order arithmetic which went
undetected for thirty years.
- Robert Tarjan proved in the
1970s that the time complexity of a certain algorithm for the
union-find problem was slightly worse than linear. And several people
proved that this could not be improved upon. But Hantao Zhang has a paper
submitted to STOC
2008 which, if it survives peer review, shows that that the
analysis is wrong, and the algorithm is actually O(n).
[ Addendum 20160128: Zhang's claim was mistaken, and he retracted the paper. ]
- Finally, several people, including John Von Neumann, proved that the
axioms of arithmetic are consistent. But it was shown later that no
such proof is possible.
- Cauchy
apparently "proved" that if a sum of continuous functions converges
pointwise, then the sum is also a continuous function, and this error
was widely believed for several years.
- A number of people wrote in with explanations of "more than twenty states"; I
will try to follow up soon.
[Other articles in category /addenda] permanent link
Tue, 02 May 2006
Addenda to recent articles 200604
Here are some notes on posts from the last
month that I couldn't find better places for.
- Stan Yen points out that I missed an important aspect of the
convenience of instant mac & cheese: it has a long shelf life, so
it is possible to keep a couple of boxes on hand for when you want
them, and then when you do want macaroni and cheese you don't have to
go shopping for cheese and pasta. M. Yen has a good point. I
completely overlooked this, because my eating habits are such that I
nearly always have the ingredients for macaroni and cheese on hand.
M. Yen also points out that some of the attraction of Kraft Macaroni and Cheese Dinner is its specific taste and texture. We all have occasional longings for the comfort foods of childhood, and for many people, me included, Kraft dinner is one of these. When you are trying to recreate the memory of a beloved food from years past, the quality of the ingredients is not the issue. I can sympathize with this: I would continue to eat Kraft dinner if it tasted the way I remember it having tasted twenty years ago. I still occasionally buy horrible processed American cheese slices not because it's a good deal, or because I like the cheese, but because I want to put it into grilled cheese sandwiches to eat with Campbell's condensed tomato soup on rainy days.
- Regarding the invention of
the = sign, R. Koch sent me two papers by Florian Cajori, a
famous historian of mathematics. One paper, Note on our sign
of Equality, presented evidence that a certain Pompeo
Bolognetti independently invented the sign, perhaps even before Robert
Recorde did. The = sign appears in some notes that Bolognetti made,
possibly before 1557, when Recorde's book The Whetstone of
Witte was published, and certainly before 1568, when Bolognetti
died. Cajori suggests that Bolognetti used the sign because the dash
----- was being used for both equality and subtraction, so perhaps
Bolognetti chose to double the dash when he used it to denote
equality. Cajori says "We have here the extraordinary spectacle of
the same arbitrary sign having been chosen by independent workers
guided in their selection by different considerations."
The other paper M. Koch sent is Mathematical Signs of Equality, and traces the many many symbols that have been used for equality, and the gradual universal adoption of Recorde's sign. Introduced in England in 1557, the Recorde sign was first widely adopted in England. Cajori: "In the seventeenth century Recorde's ===== gained complete ascendancy in England." But at that time, mathematicians in continental Europe were using a different sign , introduced by René Descartes.
Cajori believes that the universal adoption of Recorde's = sign in
Europe was due to its later use by Leibniz. Much of this material
reappears in Volume I of Cajori's book A History of Mathematical
Notations. Thank you, M. Koch.
, introduced by René Descartes.
Cajori believes that the universal adoption of Recorde's = sign in
Europe was due to its later use by Leibniz. Much of this material
reappears in Volume I of Cajori's book A History of Mathematical
Notations. Thank you, M. Koch.Ian Jones at the University of Warwick has a good summary of Cajori's discussion of this matter.
- Regarding Rayleigh
scattering in the atmosphere, I asserted:
The sun itself looks slightly redder ... this effect is quite pronounced ... when there are particles of soot in the air ... .
Neil Kandalgaonkar wrote to inform me that there is a web page at the site of the National Oceanic and Atmospheric Administration that appears at first to dispute this. I said that I could not believe that the NOAA was actually disputing this. I was in San Diego in October 2003, and when I went outside at lunchtime, the sun was red. At the time, the whole county was on fire, and anyone who wants to persuade me that these two events were entirely unrelated will have an uphill battle.
Fortunately, M. Kandalgaonkar and I determined that the NOAA web page not asserting any such silly thing as that smoke does not make the sun look red. Rather, it is actually asserting that smoke does not contribute to good sunsets. And M. Kandalgaonkar then referred me to an amazing book, M. G. Minnaert's Light and Color in the Outdoors.This book explains every usual and unusual phenomenon of light and color in the outdoors that you have ever observed, and dozens that you may have observed but didn't notice until they were pointed out. (Random example: "This explains why the smoke of a cigar or cigarette is blue when blown immediately into the air, but becomes white if it is been kept in the mouth first. The particles of smoke in the latter case are covered by a coat of water and become much larger.") I may report on this book in more detail in the future. In the meantime, Minnaert says that the redness of the sun when seen through smoke is due primarily to absorption of light, not to Rayleigh scattering:
The absorption of carbon increases rapidly from the red to the violet of the spectrum; this characteristic is exemplified in the blood-red color of the sun when seen through the smoke of a house on fire.
- A couple of people have written to suggest that perhaps the one
science question any high school graduate ought to be able to answer
is "What is the scientific method?" Yes, I quite agree.
Nathan G. Senthil has also pointed out Richard P. Feynman's suggestion on this topic. In one of the first few of his freshman physics lectures, Feynman said that if nearly all scientific knowledge were to be destroyed, and he were able to transmit only one piece of scientific information to future generations, it would be that matter is composed of atoms, because a tremendous amount of knowledge can be inferred from this one fact. So we might turn this around and suggest that every high school graduate should be able to give an account of the atomic theory of matter.
- I said that Pick's theorem
Implies that every lattice polygon has an area that is an integer
multiple of 1/2, "which I would not have thought was obvious." Dan
Schmidt pointed out that it is in fact obvious. As I pointed out in
the Pick's theorem article, every such polygon can be built up from
right triangles whose short sides are vertical
and horizontal; each such triangle is half of a rectangle, and
rectangles have integer areas. Oops.
- Seth David Schoen brought to my attention the fascinating
phenomenon of tetrachromacy. It is believed that some (or all) humans
may have a color sensation apparatus that supports a four-dimensional
color space, rather than the three-dimensional space that it is
believed most humans have.
As is usual with color perception, the complete story is very complicated and not entirely understood. In my brief research, I discovered references to at least three different sorts of tetrachromacy.
- In addition to three types of cone cells, humans also have rod
cells in their retinas. The rod cells have a peak response to photons
of about 500 nm wavelength, which is quite different from the peak
responses of any of the cones. In the figure below, the dotted black
line is the response of the
rods; the colored lines are the responses of the three types of cones.
So it's at least conceivable that the brain could make use of rod cell response to distinguish more colors than would be possible without it. Impediments to this are that rods are poorly represented on the fovea (the central part of the retina where the receptors are densest) and they have a slow response. Also, because of the way the higher neural layers are wired up, rod vision has poorer resolution than cone vision.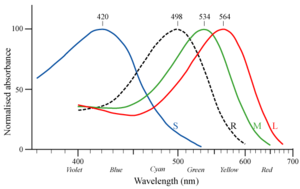
I did not find any scientific papers that discussed rod tetrachromacy, but I didn't look very hard.
- The most common form of color blindness is deuteranomaly,
in which the pigment in the "green" cones is "redder" than it should
be. The result is that the subject has difficulty distinguishing
green and red. (Also common is protanomaly, which is just the
reverse: the "red" pigment is "greener" than it should be, with the
same result. What follows holds for protanomaly as well as
deuteranomaly.)
Genes for the red and green cone pigments are all carried on the X chromosomes, never on the Y chromosomes. Men have only one X chromosome, and so have only one gene each for the red and green pigments. About 6-8% of all men carry an anomalous green pigment gene on their X chromosome instead of a normal one and suffer from deuteranomaly.
Each of these men inherited his X chromosome from his mother, who must also therefore carry the anomalous gene on one of her two X chromosomes. The other X chromosome of such a woman typically carries the normal version of the gene. Since such a woman has genes for both the normal and the "redder" version of the green pigment, she might have both normal and anomalous cone cells. That is, she might have the normal "green" cones and also the "redder" version of the "green" cones. If so, she will have four different kinds of cones with four different color responses: the usual "red", "green" and "blue" cones, and the anomalous "green" cone, which we might call "yellow".
The big paper on this seems to be A study of women heterozygous for colour deficiencies, by G. Jordan and J. D. Mollon, appeared in Vision Research, Volume 33, Issue 11, July 1993, Pages 1495-1508. I haven't finished reading it yet. Here's my summary of the abstract: They took 31 of women who were known to be carriers of the anomalous gene and had them perform color-matching tasks. Over a certain range of wavelengths, a tetrachromat who is trying to mix light of wavelengths a and b to get as close as possible to perceived color c should do it the same way every time, whereas a trichromat would see many different mixtures as equivalent. And Jordan and Mollon did in fact find a person who made the same color match every time.
Another relevant paper with similar content is Richer color experience in observers with multiple photopigment opsin genes, by Kimberly A. Jameson, Susan M. Highnote, and Linda M. Wasserman, appeared in Psychonomic Bulletin & Review 2001, 8 (2), 244-261. Happily, this is available online for free.
My own description is highly condensed. Ryan's Sutherland's article Aliens among us: Preliminary evidence of superhuman tetrachromats is clear and readable, much more so than my explanation above. Please do not be put off by the silly title; it is an excellent article.
- The website Processes in
Biological Vision claims that the human eye normally contains a
color receptor that responds to very short-wavelength violet and even
ultraviolet light, but that previous studies have missed this because
the lens tends to filter out such light and because indoor light
sources tend not to produce it. The site discusses the color
perception of persons who had their lenses removed. I have not yet
evaluated these claims, and the web site has a strong stink of
crackpotism, so beware.
- In addition to three types of cone cells, humans also have rod
cells in their retinas. The rod cells have a peak response to photons
of about 500 nm wavelength, which is quite different from the peak
responses of any of the cones. In the figure below, the dotted black
line is the response of the
rods; the colored lines are the responses of the three types of cones.
- In discussing Hero's
formula, I derived the formula
(2a2b2 + 2a2c2 +
2b2c2 - a4 - b4-
c4)/16 for the square of the area of a triangle with sides of lengths
a, b, and c, and then wondered how to get from
that mess to Hero's formula itself, which is nice and simple:
p(p-a)(p-b)(p-c),
where p is half the perimeter.
François Glineur wrote in to show me how easy it is. First, my earlier calculations had given me the simpler expression 16A2 = 4a2b2 - (a2+b2-c2)2, which, as he says, is unfortunately not symmetric in a, b and c. We know that it must be expressible in a symmetric form somehow, because the triangle's area does not know or care which side we have decided to designate as side a.
But the formula above is a difference of squares, so we can factor it to obtain (2ab + a2 + b2 - c2)(2ab + c2 - a2 - b2), and then simplify the a2 ±2ab + b2 parts to get ((a+b)2 - c2)(c2 - (a-b)2). But now each factor is itself a difference of squares and can be factored, obtaining (a+b+c)(a+b-c)(c+a-b)(c-a+b). From here to Hero's formula is just a little step. As M. Glineur says, there are no lucky guesses or complicated steps needed. Thank you, M. Glineur.
M. Glineur ended his note by saying:
In my opinion, an even "better" proof would not break the symmetry between a, b and c at all, but I don't have convincing one at hand.
Gareth McCaughan wrote to me with just such a proof; I hope to present it sometime in the next few weeks. It is nicely symmetric, and its only defect is that it depends on trigonometry. - Carl Witty pointed out that my equation of the risk of Russian
roulette with the risk of driving an automobile was an
oversimplification. For example, he said, someone playing Russian
roulette, even at extremely favorable odds, appears to be courting
suicide in a way that someone driving a car does not; a person with
strong ethical or religious beliefs against suicide might then reject
Russian roulette even if it is less risky than driving a car. I
hadn't appreciated this before; thank you, M. Witty.
I am reminded of the story of the philosopher Ramon Llull (1235–1315). Llull was beatified, but not canonized, and my recollection was that this was because of the circumstances of his death: he had a habit of going to visit the infidels to preach loudly and insistently about Christianity. Several narrow escapes did not break him of this habit, and he was eventually he was torn apart by an angry mob. Although it wasn't exactly suicide, it wasn't exactly not suicide either, and the Church was too uncomfortable with it to let him be canonized.
Then again, Wikipedia says he died "at home in Palma", so perhaps it's all nonsense.
- Three people have written in to contest my assertion that I did not know
anyone who had used a gas chromatograph. By which I mean that
three people I know have asserted that they have used gas
chromatographs.
It also occurred to me that my cousin Alex Scheeline is a professor of chemistry at UIUC, and my wife's mother's younger brother's daughter's husband's older brother's wife's twin sister is Laurie J. Butler, a professor of physical chemistry at the University of Chicago. Both of these have surely used gas chromatographs, so they bring the total to five.
So it was a pretty dumb thing to say.
- In yesterday's
Google query roundup, I brought up the following search query,
which terminated at my blog:
a collection of 2 billion points is completely enclosed by a circle. does there exist a straight line having exactly 1 billion of these points on each sideThis has the appearance of someone's homework problem that they plugged into Google verbatim. What struck me about it on rereading is that the thing about the circle is a tautology. The rest of the problem does not refer to the circle, and every collection of 2 billion points is completely enclosed by a circle, so the clause about the circle is entirely unnecessary. So what is it doing there?All of my speculations about this are uncharitable (and, of course, speculative), so I will suppress them. I did the query myself, and was not enlightened.
If this query came from a high school student, as I imagine it did, then following question probably has at least as much educational value:
Show that for any collection of 2 billion points, there is a circle that completely encloses them.It seems to me that to answer that question, you must get to the heart of what it means for something to be a mathematical proof. At a higher educational level, this theorem might well be dismissed as "obvious", or passed over momentarily on the way to something more interesting with the phrase "since X is a finite set, it is bounded." But for a high school student, it is worth careful consideration. I worry that the teacher who asked the question does not know that finite sets are bounded. Oops, one of my uncharitable speculations leaked out.
[Other articles in category /addenda] permanent link
Sun, 02 Apr 2006
Addenda to recent articles 200603
Here are some notes on posts from the last
month that I couldn't find better places for.
- In my close attention
to the most embarrassing moments of the Indiana Pacemates, I
completely missed the fact that Pacemate Nikki,
the only one who admitted to farting in public, also reports that she
was born with twelve fingers.
- Regarding the
manufacture of spherical objects, I omitted several kinds of
spherical objects that are not manufactured in any of the ways I
discussed.
 One is the gumball. It's turned out to be surprisingly difficult to
get definitive information about how gumballs are manufactured. My
present understanding is that the gum is first extruded in a sort of
hollow pipe shape, and then clipped off into balls with a pinching
device something like the Civil-War-era bullet mold pictured at right.
The gumballs are then sprayed with a hard, shiny coating, which tends
to even out any irregularities.
One is the gumball. It's turned out to be surprisingly difficult to
get definitive information about how gumballs are manufactured. My
present understanding is that the gum is first extruded in a sort of
hollow pipe shape, and then clipped off into balls with a pinching
device something like the Civil-War-era bullet mold pictured at right.
The gumballs are then sprayed with a hard, shiny coating, which tends
to even out any irregularities.[ Addendum 20070307: the bullet mold at right is probably not used in the way I said. See this addendum for more details. ]
- Glass marbles are made with several processes. One of the most
interesting involves a device invented by Martin Frederick
Christensen. (US Patent #802,495, "Machine For Making Spherical
Bodies Or Balls".) The device has two wheels, each with a deep groove
around the rim. The grooves have a semicircular cross-section. The
wheels rotate in opposite directions on parallel axes, and are aligned
so that the space between the two grooves is exactly circular.
The marble is initially a slug of hot glass cut from the end of a long rod. The slug sits in the two grooves and is rolled into a spherical shape by the rotating wheels. For more details, see the Akron Marbles web site.
Fiberglas is spun from a big vat of melted glass; to promote melting, the glass starts out in the form of marbles. ("Marbles" appears to be the correct jargon term.) I have not been able to find out how they make the marbles to begin with. I found patents for the manufacture of Fiberglas from the marbles, but nothing about how the marbles themselves are made. Presumably they are not made with an apparatus as sophisticated as Christensen's, since it is not important that the marbles be exactly spherical. Wikipedia hints at "rollers".
 The thingies pictured to the right are another kind of
nearly-spherical object I forgot about when I wrote the original
article. They are pellets of taconite ore. Back in the 1950s, the
supply of high-quality iron ore started to run out. Taconite contains
about 30% iron, but the metal is in the form of tiny particles
dispersed throughout very hard inert rock. To extract the iron, you
first crush the taconite to powder, and then magnetically separate the
iron dust from the rock dust.
The thingies pictured to the right are another kind of
nearly-spherical object I forgot about when I wrote the original
article. They are pellets of taconite ore. Back in the 1950s, the
supply of high-quality iron ore started to run out. Taconite contains
about 30% iron, but the metal is in the form of tiny particles
dispersed throughout very hard inert rock. To extract the iron, you
first crush the taconite to powder, and then magnetically separate the
iron dust from the rock dust. But now you have a problem. Iron dust is tremendously inconvenient to handle. The slightest breeze spreads it all over the place. It sticks to things, it blows away. It can't be dumped into the smelting furnace, because it will blow right back out. And iron-refining processes were not equipped for pure iron anyway; they were developed for high-grade ore, which contains about 65% iron.
The solution is to take the iron powder and mix it with some water, then roll it in a drum with wet clay. The iron powder and clay accumulate into pellets about a half-inch in diameter, and the pellets are dried. Pellets are easy to transport and to store. You can dump them into an open rail car, and most of them will still be in the rail car when it arrives at the refinery. (Some of them fall out. If you visit freight rail tracks, you'll find the pellets. I first learned about taconite because I found the pellets on the ground underneath the Conrail freight tracks at 32nd and Chestnut Streets in Philadelphia. Then I wondered for years what they were until one day I happened to run across a picture of them in a book I was reading.)
When the pellets arrive at the smelter, you can dump them in. The pellets have around 65% iron content, which is just what the smelter was designed for.
- Regarding my assertion
that there is no way to include a menu of recent posts in the "head"
part of the Blosxom output, I said:
With stock Blosxom, however, this is impossible. The first problem you encounter is that there is no stories_done callback.
Todd Larason pointed out that this is mistaken, because (as I mentioned in the article) the foot template is called once, just after all the stories are processed, and that is just what I was asking for.My first reaction was "Duh."
My second reaction was to protest that it had never occurred to me to use foot, because that is not what it is for. It is for assembling the footer!
There are two things wrong with this protest. First, it isn't a true statement of history. It never occurred to me to use foot, true, but not for the reason I wanted to claim. The real reason is that I thought of a different solution first, implemented it, and stopped thinking about it. If anything, this is a credit to Blosxom, because it shows that some problems in Blosxom can be solved in multiple ways. This speaks well to the simplicity and openness of Blosxom's architecture.
The other thing wrong with this protest is that it assumes that that is not what foot is for. For all I know, when Blosxom's author was writing Blosxom, he considered adding a stories_done callback, and, after a moment of reflection, concluded that if someone ever wanted that, they could just use foot instead. This would be entirely consistent with the rest of Blosxom's design.
M. Larason also pointed out that even though the head template (where I wanted the menu to go) is filled out and appended to the output before the article titles are gathered, it is not too late to change it. Any plugin can get last licks on the output by modifying the global $blosxom::output variable at the last minute. So (for example) I could have put PUT THE MENU HERE into the head template, and then had my plugin do:
$blosxom::output =~ s/PUT THE MENU HERE/$completed_menu/g;to get the menu into the output, without hacking on the base code.Thank you, M. Larason.
- My article on the 20 most
important tools attracted a lot of attention.
- I briefly considered and rejected the spinning
wheel, on the theory that people have spun plenty of thread with
nothing but their bare fingers and a stick to wind it around.
Brad Murray and I had a long conversation about this, in which he described his experience using and watching others use several kinds of spinning tools, including the spinning wheel, charkha (an Indian spining wheel), drop spindle, and bare fingers, and said "I can't imagine making a whole garment with my output sans tools." It eventually dawned on me that I did not know what a drop spindle was.
A drop spindle is a device for making yarn or thread. The basic process of making yarn or thread is this: you take some kind of natural fiber, such as wool, cotton, or flax fiber, which you have combed out so that the individual fibers are more or less going the same direction. Then you twist some of the fibers into a thread. So you have this big tangled mass of fiber with a twisted thread sticking out of it. You tug on the thread, pulling it out gently, while still twisting, and more fibers start to come away from the mass and get twisted into the thread. You keep tugging and twisting and eventually all the fiber is twisted into a thread. "Spinning" is this tugging-twisting process that turns the mass of combed fibers into yarn.
You can do this entirely by hand, but it's slow. The drop spindle makes it a lot faster. A drop spindle is a stick with a hook stuck into one end and a flywheel (the "whorl") near the other end. You hang the spindle by the hook from the unspun fiber and spin it.
As the spindle revolves, the hook twists the wool into a thread. The spindle is hanging unsupported from the fiber mass, so gravity tends to tug more fibers out of the mass, and you help this along with your fingers. The spindle continues to revolve at a more-or-less constant rate because of the flywheel, producing a thread of more-or-less constant twist. If you feed the growing thread uniformly, you get a thread of uniform thickness.
When you have enough thread (or when the spindle gets too close to the floor) you unhook the thread temporarily, wind the spun thread onto the shaft of the spindle, rehook it, and continue spinning.
A spinning wheel is an elaboration of this basic device. The flywheel is separate from the spindle itself, and drives it via a belt arrangement. (The big wheel you probably picture in your mind when you think of a spinning wheel is the flywheel.) The flywheel keeps the spindle revolving at a uniform rate. The spinning wheel also has a widget to keep the tension constant in the yarn. With the wheel, you can spin a more uniform thread than with a drop spindle and you can spin it faster.
I tried hard to write a coherent explanation of spinning, and although spinning is very simple it's awfully hard to describe for some reason. I read several descriptions on the web that all left me scratching my head; what finally cleared it up for me was the videos of drop spinning at the superb The Joy of Handspinning web site. If my description left you scratching your head, check out the videos; the "spinning" video will make it perfectly clear.
The drop spindle now seems to me like a good contender for one of the twenty most-important tools. My omission of it wasn't an oversight, but just plain old ignorance. I thought that the spinning wheel was an incremental improvement on simpler tools, but I misunderstood what the simpler tools were.
 The charkha, by the way, is an Indian configuration of the spinning
wheel; "charkha" is just Hindi for "wheel". There are several
varieties of the charkha, one of which is the box charkha, a
horizontal spinning wheel in a box. The picture to the right depicts
Gandhi with a box charkha.
The charkha, by the way, is an Indian configuration of the spinning
wheel; "charkha" is just Hindi for "wheel". There are several
varieties of the charkha, one of which is the box charkha, a
horizontal spinning wheel in a box. The picture to the right depicts
Gandhi with a box charkha.
- Doug Orleans asked whether I had considered the key. I hadn't,
but I think it's exempt from consideration for the same kinds of
reasons as those I cited for the remote control: any particular key
serves not a general door-opening function but a specific one. Not
that keys aren't important, but rather, they seem to be outside the
scope of this particular discussion.
- Mike Krell asked why I would list the radio on my third-tier list
and omit the computer. Obviously, the question is not one of
usefulness or of importance, but of whether the "computer" is a "tool"
in the original sense of the list, or whether it is disqualified by
reason of being too general, too abstract, too complex, or something
like that. I made several arguments, most of which I think he
refuted.
My initial answer was that computers are disqualified for the same reason that remote controls are: people do carry calculators, cell phones, personal organizers, handheld GPS devices, and (if they work for FedEx) package tracking gizmos. All of these are tools that incorporate computers, but they don't really seem to be merely different forms of the same thing. Each one is a tool, but "computer" is not, similar to the way that the microscope and the telescope are different tools, and not merely variations of "the lens".
Perhaps so, but then I had a fit of insanity and asserted that people do not walk around toting general-purpose computers in case they happen upon some data that needs processing. M. Krell very gently pointed out that yes, they do exactly that: "I see them every time I fly on an airplane, breaking them out to process some data for work (or play) as soon as the flight attendant says it's OK." Whoops. Quite so.
M. Krell suggested that by restricting the definition of "tool" to devices that perform a single specific function or a few such functions, I have circumscribed the definition of "tool" in an arbitrary way that "does not accurately reflect the realities of our current Information Age". Okay.
- Jon Evans said "Everyone always forgets the hoe." I did indeed
forget the hoe. Not quite a knife, not quite a shovel...
- I briefly considered and rejected the spinning
wheel, on the theory that people have spun plenty of thread with
nothing but their bare fingers and a stick to wind it around.
- Regarding the start of the year prior to 1751, when it
was moved from 25 March to 1 January. You may recall that I had a
series of articles
(1
2
3
4)
in which I was concerned that Benjamin Franklin
might be only 299 years old, not 300, because of confusion about just
what year was meant in discussions of the date "6 January 1706". (The
legal year 1705 ran from 25 March 1705 through 24 March 1706.)
This ambiguity
was confusing at the time as well. It makes little difference to my
life whether Franklin is 300 years old or only 299, but if you were a
person living in 1706, you might like to be sure, when someone said
they would pay you fifty shillings on 6 January 1706, when the payment
would be.
It seems that baroque authors had a convention to disambiguate such dates. Here's a quote from William Derham's 1726 introduction to Robert Hooke's notes on the invention of the barometer:
To this I W.D. shall add another Remark I find in the minutes of the Royal Society, February 20. !!167^8_9!!, viz.…
And similarly, from Richard Waller's summary of The Life of Dr. Robert Hooke:
…they prosecuted their former Inquiries, their first meeting at Arundel house being on the ninth of Jan. !!166^6_7!!.
- * In an
earlier post, I referred to "Ramanujan's approximation to π":
$$ \cfrac{1}{1+ \cfrac{e^{-2\pi}}{1 + \cfrac{e^{-4\pi}}{1 + \cdots}}} = \left( \sqrt{\frac{5+\sqrt5}2} - \frac{\sqrt5-1}2 \right) e^{2\pi/5} $$ But this isn't the formula I was thinking of; I showed the wrong formula! It's obviously not an approximation to π. The approximation formula I was thinking of is no less astonishing:
$${1\over\pi} = {\sqrt8\over9801} \sum_{i=0}^\infty { (4i)! (1103 + 26390i) \over (i!)^4 (396)^{4i} }$$
- Finally, in my article on the
20 most important tools, I said that I didn't think I knew anyone
who had used a gas chromatograph; Geoffrey Young pointed out that he
had used one.
[Other articles in category /addenda] permanent link
Wed, 01 Mar 2006
Addenda to recent articles 200602
Here are some notes on posts from the last month that I couldn't find
better places for.
- Regarding my
bad solution to the problem of preventing multiple simultaneous SMTP
connections from the same place, Chris Siebenmann suggests that a
better strategy is to centralize all SMTP access through a single
server that can manage the connections in any convenient way, without
IPC, and fork child processes to perform the actual SMTP transactions.
I had ended my post with "duh", but this suggestion requires an even
bigger "duh", because I am already running such a server and
modifying it appropriately would have been even easier than the
modification I did make to the SMTP program. Thank you,
M. Siebenmann. Duh!
- Regarding the 3n+1
domain, I should mention first that my use of the word "domain" is
incorrect here. A domain, properly speaking, is required to have both
addition and multiplication; the 3n+1 system supports only
multiplication. Addition doesn't work because (for example) 1+1 is
undefined in this system, 2 having been omitted.
I may discuss this in more detail in a future post.
- Regarding Perl's
accidental s/.../.../ee feature, John Macdonald remarks that
he thinks it was first discovered by Randal Schwartz, not Tom
Christiansen, as I said. M. Macdonald suggests that
M. Schwartz first used it in the form
s/.../.../eieio in a "Just Another Perl Hacker" signature,
and that M. Christiansen then invented the
s/(\$\w+)/$1/ee form as a way to make real use of it.
-
Regarding Robert Hooke's
mismeasurement of the frequency of G above middle C, I referred to
Benjamin Wardhaugh's suggestion that the error was in the length of
the pendulum he used to mention the time. Carl Witty points out that
this is unlikely, for two reasons. First, Hooke would have been quite
familiar with how to make a pendulum of the correct length to time a
one-second interval; indeed, he probably would have had such pendulums
sitting around, ready to be used. And second, the period of a
pendulum is proportional to the square root of its length, so to get
the error of a factor of √2 in the measurement of the frequency
of the brass wire, Hooke's pendulum would have had to be twice
as long as it should have been.
In reply, I suggested several possible causes of error:
- Perhaps the initial wire was not vibrating at precisely 1 Hz.
Synchronization with the 1 Hz pendulum might have been done by eye.
Any error in the original frequency would have been multiplied by 136
in the final result.
- The halving of the wire might not have been exact.
- If the tension in the wire changed during the halving process, the shortened wire would have a frequency different from twice that of the unshortened wire.
- The note produced by the one-foot wire might not have been
exactly G. it could have varied somewhat from true G without being
detected by the musical observers.
- G in 1664 wasn't 384 Hz anyway. In fact, I haven't finished
finding out just what Hooke meant by it, since pitches weren't fully
standardized; I don't know what Hooke intended for the reader to
understand from his assertion that it was 272 Hz. See Wikipedia's
discussion, for example.
- I don't yet know that the second was accurately measured. You
need a pendulum that strokes exactly 86,400 times per day. They would
have had to calibrate it against sandglasses and such things. How
accurate was that calibration?
- Even if the second was accurately measured, was it the same second
that we use today? I'm not sure. I should be able to find this out
by reading Hooke's lectures on gravitation (which I have handy) and
seeing what he gives as the acceleration due to the earth's gravity.
M. Witty also wondered if the fact that apparent error in the measurement was almost exactly √2 was a coincidence. I imagine so, but I could easily be wrong.
- Perhaps the initial wire was not vibrating at precisely 1 Hz.
Synchronization with the 1 Hz pendulum might have been done by eye.
Any error in the original frequency would have been multiplied by 136
in the final result.
-
Regarding non-oral reading,
I said:
Someone once told me that some famous scholar, I think perhaps Thomas Aquinas, was the only one of his contemporaries to read non-orally, that they were astonished at how the information would just fly from the book into his mind without his having to read it.
Ricardo J. B. Signes has confirmed this, except that it wasn't Aquinas. He says that Augustine wrote of Ambrose that "When he read, his eyes travelled over the page and his heart sought the sense, but voice and tongue were silent." Thanks, Ricardo. -
Regarding John Wilkins' artificial
language,
I said:
. . . a certain bishop John Wilkins had invented a language in which the meaning of each word would be immediately apparent from its spelling.
I have now obtained a copy of this book, and it uses "salmon" as an example. Wilkins' word for "salmon" is "zana". The first two letters always identify one of forty primary classifications for things; animal words begin with "z", and fish with "za". Each major group is divided into nine subgroups; the third letter identifies which of the nine subgroups the thing is in, with "n" denoting the ninth. The ninth subgroup of fish are "squamous river fish". Each subgroup is then divided into (usually) nine species, and the fourth letter identifies which of the nine species the thing is in with "a" denoting the second. The "squamous river fish" are divided as follows:(I don't have an example handy, so I will make one up. All words that begin with "p" are animals. Words beginning with "pa" are birds, those with "pe" are fish, and so forth. Words beginning with "pel" are fish with fins and scales. Words for fin-fish that live in rivers and streams all begin with "pela". "pelam" is a salmon.)
Bigger fish Voracious fish With loose scales With one fin, near the tail; wide mouths, and sharp teeth (1) With two fins Common to both fresh and salt water (2) Common to fresh water only Spotted (3) Not spotted More round (4) More broad or compressed (5) With close, compact scales (6) Not voracious Bigger Those that live in standing waters (7) Those that live in running waters Those that are thick and round (8) Those that are broad and deep (9) Lesser (10) Smallest river fish In the lower parts of the water With one fin on the back (11) With two fins and a broad head (12) In the upper parts of the water (13) - Regarding British
assertions that Americans speak of nothing but dollars, John
Bodoni writes in with the following quotation from Ayn Rand's book
Atlas Shrugged:
"If you ask me to name the proudest distinction of Americans, I would choose--because it contains all the others--the fact that they were the people who created the phrase 'to make money.' No other language or nation had ever used these words before; men had always thought of wealth as a static quantity--to be seized, begged, inherited, shared, looted or obtained as a favor. Americans were the first to understand that wealth has to be created."
I looked this up, and I found that it is not true. The OED has citations back to 1472:- 1472 R. CALLE in Paston Lett. (1976) II. 356, I truste be Ester to make of money..at the leeste l marke.
- 1546 O. JOHNSON in H. Ellis Orig. Lett. Eng. Hist. 2nd Ser. II. 175 Besides the monney that I shal make of the said wares.
- 1583 T. STOCKER tr. Tragicall Hist. Ciuile Warres Lowe Countries II. 64 [They] furnished him with all the money they were able to make.
- 1588 R. PARKE tr. J. G. de Mendoza Hist. China 45 Then may the
husband afterwardes sell his wife for a slave, and make money
of her for the dowrie he gaue her.
[Other articles in category /addenda] permanent link



