Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 02 May 2006
Addenda to recent articles 200604
Here are some notes on posts from the last
month that I couldn't find better places for.
- Stan Yen points out that I missed an important aspect of the
convenience of instant mac & cheese: it has a long shelf life, so
it is possible to keep a couple of boxes on hand for when you want
them, and then when you do want macaroni and cheese you don't have to
go shopping for cheese and pasta. M. Yen has a good point. I
completely overlooked this, because my eating habits are such that I
nearly always have the ingredients for macaroni and cheese on hand.
M. Yen also points out that some of the attraction of Kraft Macaroni and Cheese Dinner is its specific taste and texture. We all have occasional longings for the comfort foods of childhood, and for many people, me included, Kraft dinner is one of these. When you are trying to recreate the memory of a beloved food from years past, the quality of the ingredients is not the issue. I can sympathize with this: I would continue to eat Kraft dinner if it tasted the way I remember it having tasted twenty years ago. I still occasionally buy horrible processed American cheese slices not because it's a good deal, or because I like the cheese, but because I want to put it into grilled cheese sandwiches to eat with Campbell's condensed tomato soup on rainy days.
- Regarding the invention of
the = sign, R. Koch sent me two papers by Florian Cajori, a
famous historian of mathematics. One paper, Note on our sign
of Equality, presented evidence that a certain Pompeo
Bolognetti independently invented the sign, perhaps even before Robert
Recorde did. The = sign appears in some notes that Bolognetti made,
possibly before 1557, when Recorde's book The Whetstone of
Witte was published, and certainly before 1568, when Bolognetti
died. Cajori suggests that Bolognetti used the sign because the dash
----- was being used for both equality and subtraction, so perhaps
Bolognetti chose to double the dash when he used it to denote
equality. Cajori says "We have here the extraordinary spectacle of
the same arbitrary sign having been chosen by independent workers
guided in their selection by different considerations."
The other paper M. Koch sent is Mathematical Signs of Equality, and traces the many many symbols that have been used for equality, and the gradual universal adoption of Recorde's sign. Introduced in England in 1557, the Recorde sign was first widely adopted in England. Cajori: "In the seventeenth century Recorde's ===== gained complete ascendancy in England." But at that time, mathematicians in continental Europe were using a different sign , introduced by René Descartes.
Cajori believes that the universal adoption of Recorde's = sign in
Europe was due to its later use by Leibniz. Much of this material
reappears in Volume I of Cajori's book A History of Mathematical
Notations. Thank you, M. Koch.
, introduced by René Descartes.
Cajori believes that the universal adoption of Recorde's = sign in
Europe was due to its later use by Leibniz. Much of this material
reappears in Volume I of Cajori's book A History of Mathematical
Notations. Thank you, M. Koch.Ian Jones at the University of Warwick has a good summary of Cajori's discussion of this matter.
- Regarding Rayleigh
scattering in the atmosphere, I asserted:
The sun itself looks slightly redder ... this effect is quite pronounced ... when there are particles of soot in the air ... .
Neil Kandalgaonkar wrote to inform me that there is a web page at the site of the National Oceanic and Atmospheric Administration that appears at first to dispute this. I said that I could not believe that the NOAA was actually disputing this. I was in San Diego in October 2003, and when I went outside at lunchtime, the sun was red. At the time, the whole county was on fire, and anyone who wants to persuade me that these two events were entirely unrelated will have an uphill battle.
Fortunately, M. Kandalgaonkar and I determined that the NOAA web page not asserting any such silly thing as that smoke does not make the sun look red. Rather, it is actually asserting that smoke does not contribute to good sunsets. And M. Kandalgaonkar then referred me to an amazing book, M. G. Minnaert's Light and Color in the Outdoors.This book explains every usual and unusual phenomenon of light and color in the outdoors that you have ever observed, and dozens that you may have observed but didn't notice until they were pointed out. (Random example: "This explains why the smoke of a cigar or cigarette is blue when blown immediately into the air, but becomes white if it is been kept in the mouth first. The particles of smoke in the latter case are covered by a coat of water and become much larger.") I may report on this book in more detail in the future. In the meantime, Minnaert says that the redness of the sun when seen through smoke is due primarily to absorption of light, not to Rayleigh scattering:
The absorption of carbon increases rapidly from the red to the violet of the spectrum; this characteristic is exemplified in the blood-red color of the sun when seen through the smoke of a house on fire.
- A couple of people have written to suggest that perhaps the one
science question any high school graduate ought to be able to answer
is "What is the scientific method?" Yes, I quite agree.
Nathan G. Senthil has also pointed out Richard P. Feynman's suggestion on this topic. In one of the first few of his freshman physics lectures, Feynman said that if nearly all scientific knowledge were to be destroyed, and he were able to transmit only one piece of scientific information to future generations, it would be that matter is composed of atoms, because a tremendous amount of knowledge can be inferred from this one fact. So we might turn this around and suggest that every high school graduate should be able to give an account of the atomic theory of matter.
- I said that Pick's theorem
Implies that every lattice polygon has an area that is an integer
multiple of 1/2, "which I would not have thought was obvious." Dan
Schmidt pointed out that it is in fact obvious. As I pointed out in
the Pick's theorem article, every such polygon can be built up from
right triangles whose short sides are vertical
and horizontal; each such triangle is half of a rectangle, and
rectangles have integer areas. Oops.
- Seth David Schoen brought to my attention the fascinating
phenomenon of tetrachromacy. It is believed that some (or all) humans
may have a color sensation apparatus that supports a four-dimensional
color space, rather than the three-dimensional space that it is
believed most humans have.
As is usual with color perception, the complete story is very complicated and not entirely understood. In my brief research, I discovered references to at least three different sorts of tetrachromacy.
- In addition to three types of cone cells, humans also have rod
cells in their retinas. The rod cells have a peak response to photons
of about 500 nm wavelength, which is quite different from the peak
responses of any of the cones. In the figure below, the dotted black
line is the response of the
rods; the colored lines are the responses of the three types of cones.
So it's at least conceivable that the brain could make use of rod cell response to distinguish more colors than would be possible without it. Impediments to this are that rods are poorly represented on the fovea (the central part of the retina where the receptors are densest) and they have a slow response. Also, because of the way the higher neural layers are wired up, rod vision has poorer resolution than cone vision.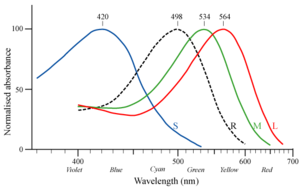
I did not find any scientific papers that discussed rod tetrachromacy, but I didn't look very hard.
- The most common form of color blindness is deuteranomaly,
in which the pigment in the "green" cones is "redder" than it should
be. The result is that the subject has difficulty distinguishing
green and red. (Also common is protanomaly, which is just the
reverse: the "red" pigment is "greener" than it should be, with the
same result. What follows holds for protanomaly as well as
deuteranomaly.)
Genes for the red and green cone pigments are all carried on the X chromosomes, never on the Y chromosomes. Men have only one X chromosome, and so have only one gene each for the red and green pigments. About 6-8% of all men carry an anomalous green pigment gene on their X chromosome instead of a normal one and suffer from deuteranomaly.
Each of these men inherited his X chromosome from his mother, who must also therefore carry the anomalous gene on one of her two X chromosomes. The other X chromosome of such a woman typically carries the normal version of the gene. Since such a woman has genes for both the normal and the "redder" version of the green pigment, she might have both normal and anomalous cone cells. That is, she might have the normal "green" cones and also the "redder" version of the "green" cones. If so, she will have four different kinds of cones with four different color responses: the usual "red", "green" and "blue" cones, and the anomalous "green" cone, which we might call "yellow".
The big paper on this seems to be A study of women heterozygous for colour deficiencies, by G. Jordan and J. D. Mollon, appeared in Vision Research, Volume 33, Issue 11, July 1993, Pages 1495-1508. I haven't finished reading it yet. Here's my summary of the abstract: They took 31 of women who were known to be carriers of the anomalous gene and had them perform color-matching tasks. Over a certain range of wavelengths, a tetrachromat who is trying to mix light of wavelengths a and b to get as close as possible to perceived color c should do it the same way every time, whereas a trichromat would see many different mixtures as equivalent. And Jordan and Mollon did in fact find a person who made the same color match every time.
Another relevant paper with similar content is Richer color experience in observers with multiple photopigment opsin genes, by Kimberly A. Jameson, Susan M. Highnote, and Linda M. Wasserman, appeared in Psychonomic Bulletin & Review 2001, 8 (2), 244-261. Happily, this is available online for free.
My own description is highly condensed. Ryan's Sutherland's article Aliens among us: Preliminary evidence of superhuman tetrachromats is clear and readable, much more so than my explanation above. Please do not be put off by the silly title; it is an excellent article.
- The website Processes in
Biological Vision claims that the human eye normally contains a
color receptor that responds to very short-wavelength violet and even
ultraviolet light, but that previous studies have missed this because
the lens tends to filter out such light and because indoor light
sources tend not to produce it. The site discusses the color
perception of persons who had their lenses removed. I have not yet
evaluated these claims, and the web site has a strong stink of
crackpotism, so beware.
- In addition to three types of cone cells, humans also have rod
cells in their retinas. The rod cells have a peak response to photons
of about 500 nm wavelength, which is quite different from the peak
responses of any of the cones. In the figure below, the dotted black
line is the response of the
rods; the colored lines are the responses of the three types of cones.
- In discussing Hero's
formula, I derived the formula
(2a2b2 + 2a2c2 +
2b2c2 - a4 - b4-
c4)/16 for the square of the area of a triangle with sides of lengths
a, b, and c, and then wondered how to get from
that mess to Hero's formula itself, which is nice and simple:
p(p-a)(p-b)(p-c),
where p is half the perimeter.
François Glineur wrote in to show me how easy it is. First, my earlier calculations had given me the simpler expression 16A2 = 4a2b2 - (a2+b2-c2)2, which, as he says, is unfortunately not symmetric in a, b and c. We know that it must be expressible in a symmetric form somehow, because the triangle's area does not know or care which side we have decided to designate as side a.
But the formula above is a difference of squares, so we can factor it to obtain (2ab + a2 + b2 - c2)(2ab + c2 - a2 - b2), and then simplify the a2 ±2ab + b2 parts to get ((a+b)2 - c2)(c2 - (a-b)2). But now each factor is itself a difference of squares and can be factored, obtaining (a+b+c)(a+b-c)(c+a-b)(c-a+b). From here to Hero's formula is just a little step. As M. Glineur says, there are no lucky guesses or complicated steps needed. Thank you, M. Glineur.
M. Glineur ended his note by saying:
In my opinion, an even "better" proof would not break the symmetry between a, b and c at all, but I don't have convincing one at hand.
Gareth McCaughan wrote to me with just such a proof; I hope to present it sometime in the next few weeks. It is nicely symmetric, and its only defect is that it depends on trigonometry. - Carl Witty pointed out that my equation of the risk of Russian
roulette with the risk of driving an automobile was an
oversimplification. For example, he said, someone playing Russian
roulette, even at extremely favorable odds, appears to be courting
suicide in a way that someone driving a car does not; a person with
strong ethical or religious beliefs against suicide might then reject
Russian roulette even if it is less risky than driving a car. I
hadn't appreciated this before; thank you, M. Witty.
I am reminded of the story of the philosopher Ramon Llull (1235–1315). Llull was beatified, but not canonized, and my recollection was that this was because of the circumstances of his death: he had a habit of going to visit the infidels to preach loudly and insistently about Christianity. Several narrow escapes did not break him of this habit, and he was eventually he was torn apart by an angry mob. Although it wasn't exactly suicide, it wasn't exactly not suicide either, and the Church was too uncomfortable with it to let him be canonized.
Then again, Wikipedia says he died "at home in Palma", so perhaps it's all nonsense.
- Three people have written in to contest my assertion that I did not know
anyone who had used a gas chromatograph. By which I mean that
three people I know have asserted that they have used gas
chromatographs.
It also occurred to me that my cousin Alex Scheeline is a professor of chemistry at UIUC, and my wife's mother's younger brother's daughter's husband's older brother's wife's twin sister is Laurie J. Butler, a professor of physical chemistry at the University of Chicago. Both of these have surely used gas chromatographs, so they bring the total to five.
So it was a pretty dumb thing to say.
- In yesterday's
Google query roundup, I brought up the following search query,
which terminated at my blog:
a collection of 2 billion points is completely enclosed by a circle. does there exist a straight line having exactly 1 billion of these points on each sideThis has the appearance of someone's homework problem that they plugged into Google verbatim. What struck me about it on rereading is that the thing about the circle is a tautology. The rest of the problem does not refer to the circle, and every collection of 2 billion points is completely enclosed by a circle, so the clause about the circle is entirely unnecessary. So what is it doing there?All of my speculations about this are uncharitable (and, of course, speculative), so I will suppress them. I did the query myself, and was not enlightened.
If this query came from a high school student, as I imagine it did, then following question probably has at least as much educational value:
Show that for any collection of 2 billion points, there is a circle that completely encloses them.It seems to me that to answer that question, you must get to the heart of what it means for something to be a mathematical proof. At a higher educational level, this theorem might well be dismissed as "obvious", or passed over momentarily on the way to something more interesting with the phrase "since X is a finite set, it is bounded." But for a high school student, it is worth careful consideration. I worry that the teacher who asked the question does not know that finite sets are bounded. Oops, one of my uncharitable speculations leaked out.
[Other articles in category /addenda] permanent link


