Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 29 Jan 2006
G.H. Hardy on analytic number theory and other matters
| Buy Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work from Bookshop.org (with kickback) (without kickback) |
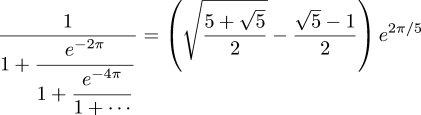
But anyway, the main point of this note is to present the following quotation from Hardy. He is discussing analytic number theory:
The fact remains that hardly any of Ramanujan's work in this field had any permanent value. The analytic theory of numbers is one of those exceptional branches of mathematics in which proof really is everything and nothing short of absolute rigour counts. The achievement of the mathematicians who found the Prime Number Theorem was quite a small thing compared with that of those who found the proof. It is not merely that in this theory (as Littlewood's theorem shows) you can never be quite sure of the facts without the proof, though this is important enough. The whole history of the Prime Number Theorem, and the other big theorems of the subject, shows that you cannot reach any real understanding of the structure and meaning of the theory, or have any sound instincts to guide you in further research, until you have mastered the proofs. It is comparatively easy to make clever guesses; indeed there are theorems like "Goldbach's Theorem", which have never been proved and which any fool could have guessed.(G.H. Hardy, Ramanujan.)
Some notes about this:
- Notice that this implies that in most branches of
mathematics, you can get away with less than absolute rigor. I think
that Hardy is quite correct here. (This is a rather arrogant remark,
since Hardy is much more qualified than I am to be telling you what
counts as worthwhile mathematics and what it is like. But this is my
blog.) In most branches of mathematics, the difficult part is
understanding the objects you are studying. If you understand them
well enough to come up with a plausible conjecture, you are doing
well. And in some mathematical pursuits, the proof may even be
secondary. Consider, for example, linear programming problems. The
point of the theory is to come up with good numerical solutions to the
problems. If you can do that, your understanding of the mathematics
is in some sense unimportant. If you invent a good algorithm that
reliably produces good answers reasonably efficiently, proving that
the algorithm is always efficient is of rather less value. In
fact, there is such an algorithm—the "simplex
algorithm"—and it is known to have exponential time in the worst
case, a fact which is of decidedly limited practical interest.
In analytic number theory, however, two facts weigh in favor of rigor. First, the objects you are studying are the positive integers. You already have as much intuitive understanding of them as you are ever going to have; you are not, through years of study and analysis, going to come to a clearer intuition of the number 3. And second, analytic number theory is much more inward-looking than most mathematics. The applications to the rest of mathematics are somewhat limited, and to the wider world even more limited. So a guessed or conjectured theorem is unlikely to have much value; the value is in understanding the theorem itself, and if you don't have a rigorous proof, you don't really understand the theorem.
Hardy's example of the Goldbach conjecture is a good one. In the 18th Century, Christian Goldbach, who was nobody in particular, conjectured that every even number is the sum of two primes. Nobody doubts that this is true. It's certainly true for all small even numbers, and for large ones, you have lots and lots of primes to choose from. No proof, however, is in view. (The primes are all about multiplication. Proving things about their additive properties is swimming upstream.) And nobody particularly cares whether the conjecture is true or not. So what if every even number is the sum of two primes? But a proof would involve startling mathematics, deep understanding of something not even guessed at now, powerful techniques not currently devised. The proof itself would have value, but the result doesn't.
Fermat's theorem (the one about an + bn = cn) is another example of this type. Not that Fermat was in any sense a fool to have conjectured it. But the result itself is of almost no interest. Again, all the value is in the proof, and the techniques that were required to carry it through.
- The Prime Number Theorem that Hardy mentions is the theorem about
the average density of the prime numbers. The Greeks knew that there
were an infinite number of primes. So the next question to ask is
what fraction of integers are prime. Are the primes sparse, like the
squares? Or are they common, like multiples of 7? The answer turns
out to be somewhere in between.
Of the integers 1–10, four (2, 3, 5, 7) are prime, or 40%. Of the integers 1–100, 25% are prime. Of the integers 1–1000, 16.8% are prime. What's the relationship?
The relationship turns out to be amazing: Of the integers 1–n, about 1/log(n) are prime. Here's a graph: the red line is the fraction of the numbers 1–n that are prime; the green line is 1/log(n):
It's not hard to conjecture this, and I think it's not hard to come up with offhand arguments why it should be so. But, as Hardy says, proving it is another matter, and that's where the real value is, because to prove it requires powerful understanding and sophisticated technique, and the understanding and technique will be applicable to other problems.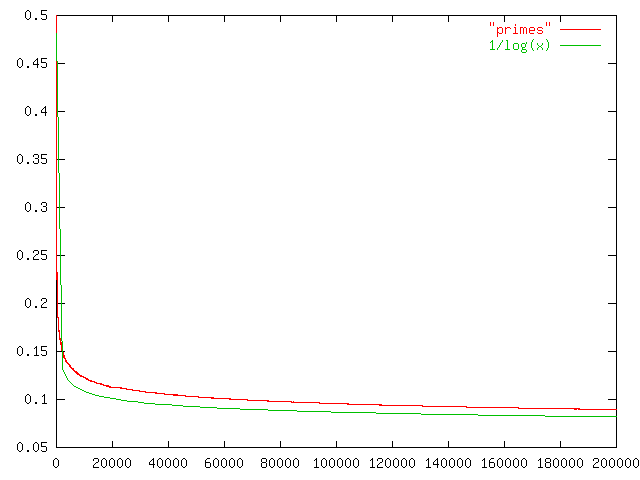
The theorem of Littlewood that Hardy refers to is a related matter.
A man who sets out to justify his existence and his activities has to distinguish two different questions. The first is whether the work which he does is worth doing; and the second is why he does it, whatever its value may be, The first question is often very difficult, and the answer very discouraging, but most people will find the second easy enough even then. Their answers, if they are honest, will usually take one or another of two forms . . . the first . . . is the only answer which we need consider seriously.And that, ultimately, is why I didn't become a mathematician. I don't have the talent for it. I have no doubt that I could have become a quite competent second-rate mathematician, with a secure appointment at some second-rate college, and a series of second-rate published papers. But as I entered my mid-twenties, it became clear that although I wouldn't ever be a first-rate mathematician, I could be a first-rate computer programmer and teacher of computer programming. I don't think the world is any worse off for the lack of my mediocre mathematical contributions. But by teaching I've been able to give entertainment and skill to a lot of people.(1) 'I do what I do because it is the one and only thing I can do at all well. . . . I agree that it might be better to be a poet or a mathematician, but unfortunately I have no talents for such pursuits.'
I am not suggesting that this is a defence which can be made by most people, since most people can do nothing at all well. But it is impregnable when it can be made without absurdity. . . It is a tiny minority who can do anything really well, and the number of men who can do two things well is negligible. If a man has any genuine talent, he should be ready to make almost any sacrifice in order to cultivate it to the full.
When I teach classes, I sometimes come back from the mid-class break and ask if there are any questions about anything at all. Not infrequently, some wag in the audience asks why the sky is blue, or what the meaning of life is. If you're going to do something as risky as asking for unconstrained questions, you need to be ready with answers. When people ask why the sky is blue, I reply "because it reflects the sea." And the first time I got the question about the meaning of life, I was glad that I had thought about this beforehand and so had an answer ready. "Find out what your work is," I said, "and then do it as well as you can." I am sure that this idea owes a lot to Hardy. I wouldn't want to say that's the meaning of life for everyone, but it seems to me to be a good answer, so if you are looking for a meaning of life, you might try that one and see how you like it.
(Incidentally, I'm not sure it makes sense to buy a copy of this book, since it's really just a long essay. My copy, which is the same as the one I've linked above, ekes it out to book length by setting it in a very large font with very large margins, and by prepending a fifty-page(!) introduction by C.P. Snow.)
[ Addendum 20210727: regarding theorems “which have never been proved and which any fool could have guessed” Vladimir Arnol'd once said something similar: “There is a general principle that a stupid man can ask such questions to which one hundred wise men would not be able to answer.” ]
Addendum 20230810
I was quoting from memory above. Hardy's exact words were:[Formulas] (1.10)–(1.12) defeated me completely; I had never seen anything in the least like them before. A single look at them is enough to show that they could only be written down by a mathematician of the highest class. They must be true because, if they were not true, no one would have had the imagination to invent them. Finally… the writer must be completely honest, because great mathematicians are commoner than thieves or humbugs of such incredible skill.This is from page 9 of Ramanujan: Twelve Lectures on Subjects Suggested by his Life and Work, Cambridge University Press, 1940. The two relevant pages may be downloaded here, and the entire book is available in the Internet Archive.
[Other articles in category /math] permanent link


